Introduction

For a long time, a vital subject in fluid dynamics is the problem of steady and unsteady laminar flow over a permeable surface because of its worth from both theoretical and viable point of view and has been studied in detail. It also has abundant applications in engineering and technological processes, such as petroleum industries, groundwater flows, the expulsion of a polymer sheet from a dye, and boundary layer control. The heat transfer mechanisms with non-uniform heat source/sink are an important topic for current researchers due to its comprehensive applications in the fields of physics and engineering. There are various industrial and engineering applications involving non-uniform heat source/sink, for example, nuclear power plants, aircraft, gas turbines, satellites, missiles, polymer industry, biomedicine, and processes concerning high temperature. Mohammadein and El-shear [1] revealed the effect of variable permeability on both free and forced convection. They reported the results of both uniform permeability and variable permeability cases. Later, Seddek and Salma [2] publicized the MHD boundary layer flow attribute of temperature-dependent viscosity and thermal conductivity. Reddy et al. [3] deliberated the numerical analysis for variable viscosity and thermal conductivity across a vertical porous plate. Consequently, several hypothetical and practical features of the flow and heat transfer with regards to power-law fluids have been examined by numerous researchers [4,5,6]. Further, a notable number of various studies has been carried out by innumerable researchers on electromagneto-hydrodynamic viscoelastic fluid [7,8,9].

Problems of the dynamic world led to inquire about analytical and numerical techniques to find out the deserved solutions of highly nonlinear and complex models. Although advancement in programming (like Mathematica, Matlab, Maple, C++, and Java) facilitate to solve such heavy, time-consuming ODEs/PDEs problems, yet it is the focused field for the researcher to erect and scan advance techniques that evaluate results of the nonlinear equations having multiple parameters arising from nature. In literature, the running techniques are the variational iteration method (VIM) [10], homotopy analysis method (HAM) [11], differential transform method (DTM) [12], and finite element method (FEM) [13]. The spectral relaxation method [14] and spectral perturbation method [15] have secured importance these days. Recently, several authors [16,17,18,19,20] have studied different flow parameters considering different fluid flows over different geometries.

There are a couple of reviews in the appurtenant literature concerning the numerical investigation of power-law fluid flow with internal heat generation generated by vertical or di surfaces [21,22,23,24,25,26,27,28]. To the best knowledge of the authors, not many studies have been conducted on the flow of these fluids by considering the impacts of non-uniform heat source/sink, exponential variable viscosity, and thermal conductivity in mathematical model with a Lie group transformation approach. The innovation of this review is the computation of multiple solutions for such kind of physical model for the first time. So, in this article, we simulate free convection flow of over vertical plate.

Influenced by the abovementioned literature, the objective of our study is to explore the effects of internal heat generation on steady, free convective and variable fluid properties past a vertical plate. The effect of exponential variable viscosity and thermal conductivity is also taken into account. The crux of the present study is the discussion of internal heat generation caused by the momentum diffusion. Hence, an effective approach namely Maple symbolic software via dsolve has been adopted for simulations of leading non-linear system. Several plots are assembled to present the effects of involved pertinent parameters on momentum and thermal boundary layers. The equation governs the flow phenomena are solved using Maple symbolic software [29] to execute the computations via dsolve.

Governing equations with a similarity

We consider the flow of an incompressible, viscous fluid with the plane y = 0 considering variable viscosity and thermal conductivity. Figure 1 demonstrates a physical illustration of the flow model past a vertical surface that is designed for the present study. In the flow geometry, the vertical plate is fixed along the x-direction and the fluid is assumed to flow with the plate; the y-axis is taken exactly normal to it. A constant uniform temperature Tw which is greater than T∞ is maintained by the plate. The vertical surface moving continually in the positive x-direction with a velocity u = U∞.with the above assumptions the basic equations for steady flow are the corresponding equations, under the above assumptions, describing the two-dimensional viscous fluid motion, are given by the model of Dinesh et al. [30] leading to

Fig. 1
figure 1

Coordinate system of fluid configuration

Full size image
$$ \frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0 $$
(1)
$$ u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=-\frac{1}{\rho}\frac{\partial }{\partial y}\left(\mu \frac{\partial u}{\partial y}\right) $$
(2)
$$ u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\frac{\partial }{\partial y}\left(\alpha \frac{\partial T}{\partial y}\right)+{q}^{{\prime\prime\prime} } $$
(3)

The boundary conditions of the problem are

$$ {\displaystyle \begin{array}{l}u=0,v=0,T={T}_w={T}_c+C{x}^a,y=0\\ {}u={U}_{\infty },T={T}_{\infty },y\to \infty \end{array}}\Big\} $$
(4)

where q′′′ is the exponential form of internal heat generation which is defined by

$$ q\hbox{'}\hbox{'}\hbox{'}=\frac{U_0\left({T}_w-{T}_c\right)}{2x}{e}^{-\eta } $$

Furthermore, by introducing a dimensional stream function ψ defined into Eqs. (1)–(4), we have

$$ u=\frac{\partial \psi }{\partial y},v=-\frac{\partial \psi }{\partial x},\frac{T-{T}_c}{T_w-{T}_c}=\theta, \mu ={\mu}_0{e}^{-{\beta}_1\theta },\alpha ={\alpha}_0\left(1+{\beta}_2\theta \right) $$

then we have

$$ {\displaystyle \begin{array}{c}\frac{\partial \mu }{\partial \theta }=-{\mu}_0{\beta}_1{e}^{-{\beta}_1\theta },T={T}_c+\left({T}_w-{T}_c\right)\theta ={T}_c+c{x}^a\theta, \\ {}\frac{\partial T}{\partial x}= ca{x}^{a-1}\theta +c{x}^a\frac{\partial \theta }{\partial x},\frac{\partial T}{\partial y}=c{x}^a\frac{\partial \theta }{\partial y},\frac{\partial^2T}{\partial {y}^2}=c{x}^a\frac{\partial^2\theta }{\partial {y}^2}\end{array}} $$

From Eq. (2)

$$ {\displaystyle \begin{array}{c}u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=-\frac{1}{\rho}\frac{\partial \mu }{\partial \theta}\frac{\partial \theta }{\partial y}\frac{\partial u}{\partial y}-\frac{1}{\rho}\mu \frac{\partial^2u}{\partial {y}^2}\\ {}\frac{\partial \psi }{\partial y}\frac{\partial^2\psi }{\partial x\partial y}-\frac{\partial \psi }{\partial x}\frac{\partial^2\psi }{\partial {y}^2}=\frac{1}{\rho }{\mu}_0{\beta}_1{e}^{-{\beta}_1\theta}\frac{\partial \theta }{\partial y}\frac{\partial^2\psi }{\partial {y}^2}-\frac{1}{\rho }{\mu}_0{e}^{-{\beta}_1\theta}\frac{\partial^3\psi }{\partial {y}^3}\end{array}} $$
(5)

From Eq. (3)

$$ {\displaystyle \begin{array}{c}u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\frac{\partial \alpha }{\partial \theta}\frac{\partial \theta }{\partial y}\frac{\partial T}{\partial y}+\alpha \frac{\partial^2T}{\partial {y}^2}+{q}^{{\prime\prime\prime}}\\ {}\frac{\partial \psi }{\partial y}\left( Tw- Tc\right)\frac{\partial \theta }{\partial x}-\frac{\partial \psi }{\partial x}\left( Tw- Tc\right)\frac{\partial \theta }{\partial y}={\alpha}_0{\beta}_2\frac{\partial \theta }{\partial y}\left( Tw- Tc\right)\frac{\partial \theta }{\partial y}+{\alpha}_0\left(1+{\beta}_2\theta \right)\left( Tw- Tc\right)\frac{\partial^2\theta }{\partial {y}^2}+{q}^{{\prime\prime\prime}}\\ {}\frac{\partial \psi }{\partial y}\frac{\partial \theta }{\partial x}-\frac{\partial \psi }{\partial x}\frac{\partial \theta }{\partial y}={\alpha}_0{\beta}_2\frac{\partial \theta }{\partial y}\frac{\partial \theta }{\partial y}+{\alpha}_0\left(1+{\beta}_2\theta \right)\frac{\partial^2\theta }{\partial {y}^2}+{q}^{{\prime\prime\prime}}\end{array}} $$
(6)

The boundary conditions (4) become

$$ {\displaystyle \begin{array}{l}\frac{\partial \psi }{\partial y}=0,\frac{\partial \psi }{\partial x}=0,\theta =1,y=0\\ {}\frac{\partial \psi }{\partial y}\to {U}_{\infty },\theta \to 0,y\to \infty \end{array}}\Big\} $$
(7)

Lie group transformation

The solution of the system of non-similar partial differential Eqs. (5)–(6) subject to the boundary conditions (7) is analytically not possible. Numerical methods are required. However, even with powerful algorithms, the equations remain challenging and expensive also. Therefore, it is necessary to transform these into self-similar ODEs using Lie group transformations (see [31,32,33,34,35]). This effectively reduces the number of independent variables of the governing partial differential equations. Lie algebra is a powerful analytical approach based on continuous symmetry of mathematical structures and objects which has found many uses in modern theoretical physics and applied mathematics. This theory provides a new methodology for analyzing the continuous symmetries of governing equations of many fluid dynamic systems including non-Newtonian transport phenomena. Defining:

$$ \varGamma :{x}^{\ast }=x{e}^{\varepsilon {\alpha}_1},{y}^{\ast }=y{e}^{\varepsilon {\alpha}_2},{\psi}^{\ast }=\psi {e}^{\varepsilon {\alpha}_3},{\theta}^{\ast }=\theta {e}^{\varepsilon {\alpha}_4} $$
(8)

Substituting (8) into (5) and (6), we get

$$ {\displaystyle \begin{array}{l}{e}^{-\varepsilon \left({\alpha}_1+2{\alpha}_2-2{\alpha}_3\right)}\left(\frac{\partial \psi }{\partial y}\frac{\partial^2\psi }{\partial x\partial y}-\frac{\partial \psi }{\partial x}\frac{\partial^2\psi }{\partial {y}^2}\right)=-\frac{1}{\rho }{\mu}_0{\beta}_1{e}^{\beta_1{\alpha}_4\theta }{e}^{-\varepsilon \left(2{\alpha}_2-{\alpha}_3-{\alpha}_4\right)}\frac{\partial \theta }{\partial y}\frac{\partial^2\psi }{\partial {y}^2}\\ {}-\frac{1}{\rho }{\mu}_0{e}^{\beta_1{\alpha}_4\theta }{e}^{-\varepsilon \left(3{\alpha}_2-{\alpha}_3\right)}\frac{\partial^3\psi }{\partial {y}^3}\end{array}} $$
(9)

and

$$ {e}^{-\varepsilon \left({\alpha}_1+{\alpha}_2-{\alpha}_3-{\alpha}_4\right)}\left(\frac{\partial \psi }{\partial y}\frac{\partial \theta }{\partial x}-\frac{\partial \psi }{\partial x}\frac{\partial \theta }{\partial y}\right)+{\alpha}_0{\beta}_2{e}^{-\varepsilon \left(2{\alpha}_2-2{\alpha}_4\right)}{\left(\frac{\partial \theta }{\partial y}\right)}^2+{\alpha}_0\left(1+{\beta}_2{e}^{-\varepsilon {\alpha}_4}\theta \right){e}^{-\varepsilon \left(2{\alpha}_2-{\alpha}_4\right)} $$
(10)

The transformed Eqs. (9) and (10) are invariant under the Lie group of transformation if the following relations among the transform parameters are satisfied.

$$ {\alpha}_1+2{\alpha}_2-2{\alpha}_3=2{\alpha}_1-{\alpha}_3-2{\alpha}_4=3{\alpha}_2-{\alpha}_3-{\alpha}_4 $$
(11)

and

$$ {\alpha}_1+{\alpha}_2-{\alpha}_3-{\alpha}_4=2{\alpha}_2-2{\alpha}_4=2{\alpha}_2 $$
(12)

and the boundary conditions we obtain at y → ∞

$$ {\displaystyle \begin{array}{l}\;\frac{\partial \psi }{\partial y}={U}_{\infty }=>{e}^{\varepsilon \left({\alpha}_2-{\alpha}_3\right)}={U}_{\infty }{e}^0,\\ {}{\alpha}_2-{\alpha}_3=0=>{\alpha}_2={\alpha}_3\end{array}} $$

From (11) and (12)

$$ {\alpha}_4=0,{\alpha}_2={\alpha}_3=\frac{1}{2}{\alpha}_1, $$
(13)

If we insert (13) into the scaling (8), the set of transformations reduces to a one-parameter group of transformations given by

$$ \varGamma :{x}^{\ast }=x{e}^{\varepsilon {\alpha}_1},{y}^{\ast }=y{e}^{\varepsilon \frac{1}{2}{\alpha}_1},{\psi}^{\ast }=\psi {e}^{\varepsilon \frac{1}{2}{\alpha}_1},\kern0.36em {\theta}^{\ast }=\theta $$
(14)

Expanding Eq. (14) by Tailor’s method and the remaining terms up to O (ε2) of the one-parameter group, we further get

$$ {x}^{\ast }-x= x\varepsilon {\alpha}_1+o\left({\varepsilon}^2\right),{y}^{\ast }-y=- y\varepsilon \frac{1}{2}{\alpha}_1+o\left({\varepsilon}^2\right),{\psi}^{\ast }-\psi =\psi \varepsilon \frac{1}{2}{\alpha}_1+o\left({\varepsilon}^2\right),{\theta}^{\ast }-\theta =0 $$
(15)

From Eq. (15), one can easily deduce the set of transformation in the form of the following characteristic equations:

$$ \frac{d x}{x{\alpha}_1}=\frac{d y}{\frac{1}{2}y{\alpha}_1}=\frac{d\psi}{\frac{1}{2}\psi {\alpha}_1}=\frac{d\theta}{0} $$
(16)

Integrating the subsidiary equations (16),

$$ \frac{dx}{x{\alpha}_1}=\frac{dy}{\frac{1}{2}y{\alpha}_1}, $$

we get

$$ \frac{1}{2}\ln x-\ln y=\mathrm{constan}t\;\left(\ln \sqrt{\frac{u_{\infty }}{\nu }}-\ln \eta \right)\left(\mathrm{say}\right) $$

or

$$ \eta =y\sqrt{\frac{u_{\infty }}{\nu x}} $$

From the subsidiary equations

$$ \frac{d x}{x{\alpha}_1}=\frac{d\theta}{0}, $$

we get dθ = 0,that is θ(η)= constant=θ(say).

Also integrating the equation \( \frac{d x}{x{\alpha}_1}=\frac{d\psi}{\frac{1}{2}\psi {\alpha}_1}, \)

we get \( \frac{\psi }{x^{\frac{1}{2}}}= \) constant\( =\sqrt{u_{\infty}\nu }f\left(\eta \right) \)(say),

i.e., \( \psi =\sqrt{u_{\infty}\nu }{x}^{\frac{1}{2}}f\left(\eta \right) \)

or

$$ \psi =\sqrt{u_{\infty}\nu x}f\left(\eta \right) $$

Thus, the new similarity transformations are obtained as follows: \( \eta =y\sqrt{\frac{u_{\infty }}{\nu x}},\psi =\sqrt{u_{\infty}\nu x}f\left(\eta \right),\theta =\theta \left(\eta \right) \)

We introduce the following transformations

$$ \eta =y\sqrt{\frac{U_{\infty }}{\nu x}},\psi =\sqrt{u_{\infty}\nu x}f\left(\eta \right),\mu ={\mu}_0{e}^{-{\beta}_1\theta },\kern0.48em \alpha ={\alpha}_0\left(1+{\beta}_2\theta \right),\theta =\frac{T-{T}_{\infty }}{T_w-{T}_{\infty }} $$
(17)
$$ u=\frac{\partial \psi }{\partial y}={u}_{\infty }f\hbox{'},v=-\frac{\partial \psi }{\partial x}=\frac{1}{2}\sqrt{\frac{u_{\infty}\nu }{x}}\left(\eta f\hbox{'}-f\right) $$

Using the above Eq. (17), the transformed equations yield the following transformed, dimensionless system of ordinary differential equations:

$$ {f}^{{\prime\prime\prime} }+\frac{e^{\beta_1\theta }}{2}f{f}^{{\prime\prime} }-{\beta}_1\;{f}^{{\prime\prime} }{\theta}^{\prime }=0 $$
(18)
$$ \left(1+{\beta}_2\theta \right){\theta}^{{\prime\prime} }+{\beta}_2{\left({\theta}^{\prime}\right)}^2-\frac{1}{2}\Pr \left(2a{f}^{\prime}\theta -f{\theta}^{\prime}\right)+c\Pr {e}^{-\eta }=0 $$
(19)

where Pr = υ/α is the Prandtl number, c = 0 or 1 corresponding to with and without internal heat generation.

The boundary conditions are converted to:

$$ {\displaystyle \begin{array}{l}f=0,{f}^{\prime }=0,\theta =1\;\mathrm{at}\;\eta =0\\ {}{f}^{\prime }=1,\theta =0\kern0.24em \mathrm{as}\;\eta \to \infty \end{array}}\Big\} $$
(20)

Numerical solution

Equations (18) and (19) which are self-similar nonlinear two-point boundary value problem has been solved using Maple via dsolve under boundary conditions (20). This is a very vigorous, legitimate computational algorithm with excellent convergence potentiality. This code has been used by many authors to acquire numerical solutions.

Results and discussion

We solve Eqs. (18) and (19) subject to boundary conditions (20) using the dsolve routine from MAPLE. The numerical solutions are obtained for various values of the parameters such as Prandtl number Pr, viscosity variation parameter β1, thermal diffusivity parameter β2, and temperature exponent parameter a with and without internal heat generation (IGH). We examined our result for positive and negative values of β1 the viscosity of the fluid such as water and lubrication oils for positive values of viscosity while for negative values of β1 the viscosity of the air. From the above discussions, the range of variations of the parameters of the flows β1 and β2 can be taken as follows [36]:

  1. 1)

    For air: −0.7 ≤ β1 ≤ 0, 0 ≤ β2 ≤ 6

  2. 2)

    For water: 0 ≤ β1 ≤ 0.6, 0 ≤ β2 ≤ 0.12

  3. 3)

    For lubricants: 0 ≤ β1 ≤ 3, − 0.1 ≤ β2 ≤ 0

The effects of the physical parameters on the skin friction coefficient and wall temperature gradient for the variable viscosity and thermal conductivity parameter with and without IHG are presented in Table 1. From this table, it is seen that increasing viscosity parameter is to increase the skin friction and rate of heat transfer in both cases (with and without IHG). On the other hand, with increasing thermal conductivity parameter is to increase skin friction and rate of heat transfer for a negative value of viscosity parameter (i.e., gases) but opposite behavior is shown for the positive value of viscosity parameter (i.e., fluid).

Table 1 Skin friction coefficient f '  ' (0), wall temperature gradient for different values β1, and β2 with and without IHG
Full size table

The effect of changes in the viscosity parameter β1 =  − 0.7, − 0.3, 0 and β1 = 0.1, 0.4, 0.6 on velocity and temperature profiles against η with Pr = 1, β2 = 1, a = 1 and without internal heat generation is shown in Figs. 2 and 3. From Fig. 2, it is observed that an increase in the viscosity parameter causes an increase in the velocity profile. Viscosity parameter is inversely proportional to dimensionless viscosity as an exponential form which describes Eq. (17). Therefore, an increase in viscosity parameter results to a decrease in dimensionless viscosity and in turn a decrease in viscous forces which oppose the fluid motion. This translates to inertia forces dominating viscous forces and hence fluid accelerates. It is noticed that the velocity profiles have no significant effect on the presence and absence of internal heat generation. Figure 3 describes the effects of changes in the viscosity parameter β1 on the temperature distribution. An increase in the viscosity parameter β1 causes a decrease in the temperature profile. This is attributed to a decrease in dimensionless viscosity translating into a decrease in viscous forces. These smaller viscous forces result in reduced friction between the fluid and the surface and thus decrease in the dissipation of heat within the boundary layer. Also, internal heat generation induced more flow than that of without internal heat generation for temperature distribution.

Fig. 2
figure 2

Effect of variable viscosity parameter on velocity profile with and without IHG

Full size image
Fig. 3
figure 3

Temperature profiles for the viscosity parameter with and without IHG

Full size image

Figure 4 illustrates the influence of variable thermal conductivity parameter β2 on velocity and temperature profiles. We observed that fluid velocity induces with variable thermal conductivity. We also observed that the fluid temperature enhancement for increasing values of variable thermal conductivity parameter. It is verified that by increasing β2, kinetic energy of fluid particles increases which escalate intensifies in temperature.

Fig. 4
figure 4

Velocity and temperature profiles for the thermal conductivity parameter with and without IHG

Full size image

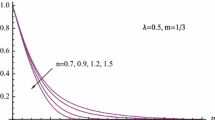
Figure 5 describes the velocity and temperature profile with various values of power exponent parameter a. The value of a = 0 corresponds to uniform surface temperature, whereas a = 0.5 correspond to uniform surface flux and a = 1 correspond to uniform wall temperature. We observed that velocity profile and temperature distribution decreases with increasing values of power exponent parameter a. this effect is more significant for temperature profile than that of the velocity profile. Also, internal heat generation induced more flow than that of without internal heat generation for temperature distribution but there is no significant impact for velocity profile.

Fig. 5
figure 5

Velocity and temperature profiles for the temperature power exponent parameter with and without IHG

Full size image

Figure 6 describes the velocity and temperature profile with various values of Prandtl number with and without internal heat generation. For all the cases, we see that velocity and temperature profiles decrease with the increase in the Prandtl number for all types of heat generation. Physically, when Pr = υ/α increases, α decreases, i.e., thermal diffusivity of fluid decreases. Hence, the heat flow through fluid decreases as Pr increases. Also, internal heat generation induced more flow than that of without internal heat generation, i.e., the mechanical strength in the fluid motion is increased. Note that temperature has a significant impact due to the Prandtl number.

Fig. 6
figure 6

Velocity and temperature profiles for the Prandtl number with and without IHG

Full size image

Conclusion

In this paper, the effect of internal heat generation on free convective power-law variable temperature considering exponential variable viscosity and thermal conductivity past a vertical plate is analyzed. Few of the findings are as follows:

  1. 1)

    Fluid velocity induced with variable viscosity parameter but the fluid temperature reduced for increasing values of viscosity parameter.

  2. 2)

    The effect of variable thermal conductivity parameter is to enhance the temperature in the flow region and is reversed in the case of the wall temperature parameter.

  3. 3)

    The fluid velocity and temperature profiles decrease with the increase in the Prandtl number.

  4. 4)

    The effect of internal heat generation is to induce more flow than that of without internal heat generation for temperature distribution but there is no significant impact for all velocity profiles.