1 Introduction

In the last century, the Korteweg-de Vries (KdV), Boussinesq, Benjamin–Bona–Mahony, Kadomtsev–Petviashvili, Nizhnik–Novikov–Veselov and Kaup-Newell equations are the well-known completely integrable equations that describe the propagation of shallow water [1,2,3,4,5]. A dynamic of shallow water waves in different places like sea beaches are depended by the KdV and Boussinesq equations [6, 7]. Also, the KdV equation has an effect in modeling blood pressure pulses. [8,9,10,11,12]. Besides, Wazwaz [13] presented the nonlinear modified KdV \((3+ 1)\)-dimensional equations and analyze their soliton, kink and periodic solutions. Particularly, Nuruddeen [14] has studied the exact solutions for the following three conformable space-time fractional mKdV equations of \((3+ 1)\)-dimension.

$$\begin{aligned} D^{\gamma }_t u+ 6 D^{\gamma }_{x} u^3+ u^{3\gamma }_{xyz}&= 0,~~0~<\gamma \le ~1, \end{aligned}$$
(1)
$$\begin{aligned} D^{\gamma }_t u+ 6 D^{\gamma }_{y} u^3+ u^{3\gamma }_{xyz}&= 0,~~0~<\gamma \le ~1, \end{aligned}$$
(2)
$$\begin{aligned} D^{\gamma }_t u+ 6 D^{\gamma }_{z} u^3+ u^{3\gamma }_{xyz}&= 0,~~0~<\gamma \le ~1. \end{aligned}$$
(3)

In recently, there are developed miscellaneous mathematical methods to solve nonlinear PDEs or fractional differential equations. Some of these methods are: The ansatz [15, 16], the modified simple equation [17, 18], the extended trial equation [19], the \(\left(\frac{G'}{G}\right)\)-expansion [20, 21], the sine-Gordon expansion [22, 23]. Additionally, some other work like a modified form of Kudryashov and functional variable methods [24,25,26] have been done by several scholars in [27, 28]. In [29,30,31,32,33,34], the auxiliary equation, the extended \(\tanh \)-function, the improved \(\tan \left( \frac{\phi (\eta )}{2}\right) \)-expansion method and the exp function methods have been investigated for difference and fractional order PDEs as well. Especially, the \(exp_{~a}\) function method [35,36,37] and the hyperbolic function method [38,39,40] both have been used to procure the exact solutions of nonlinear partial differential equations.

Among all above approaches, the \(\exp (-\phi (\tau ))\) technique has achieved substantial consideration due to its competency in inaugurating the exact solutions of nonlinear differential equations, see for instance, [41,42,43,44]. In fractional calculus, many definitions of fractional derivatives, Like Hilfer, Riemann–Liouville, Caputo form and so on, have been introduced in the literature but the well known product, quotient and the chain rules were the setbacks of one definition or another [45,46,47,48,49]. Therefore the most fascinating definition of fractional derivative with some of its properties are given in [50].

This paper aims to explore the conformable space-time fractional modified KdV equations of \((3+ 1)\)-dimensional for exact soliton type solutions via the \(\exp (-\phi (\tau ))\) approach using conformable derivative and the traveling wave transformation. The scheme of this paper is as follows: a brief description of the conformable derivative and the \(\exp (-\phi (\tau ))\) expansion approach is given in Sect. 2. Section 3, illustrate how to utilize this approach for producing new solutions with their graphs. The last parts summarized results and discussion of the current study.

2 Conformable fractional derivative approach

We recall the conformable derivative with some of its properties [50].

Definition 1

Suppose \(h:{\mathbb {R}}_{> 0}\rightarrow {\mathbb {R}} \) be a function. Then, for all \(t~>0\),

$$\begin{aligned} D^{\alpha }_t(p(t))=\lim _{\tau \rightarrow 0}\frac{p(t+\tau t^{1-\alpha })-p(t)}{\tau } .\end{aligned}$$

is known as \(\alpha , ~~0 <\alpha \le 1\) order conformable fractional derivative of p. The followings are some useful properties:

\(D^{\alpha }_t (a~p+b~g)=a D^{\alpha }_t(p)+b D^{\alpha }_t (g)\), for all \(a,~ b \in {\mathbb {R}}\)

\( D^{\alpha }_t(p~g)=p~D^{\alpha }_t(g)+g~D^{\alpha }_t(p)\).

Let \(p:{\mathbb {R}}_{> 0}\rightarrow {\mathbb {R}}\) be an \(\alpha \)-differentiable function, g be a differentiable function defined in the range of p.

$$\begin{aligned} D^{\alpha }_t(p\circ g(t))=t^{1-\alpha }~g'(t)~p'(g(t)). \end{aligned}$$

On the top of that, the following rules hold.

\(D^{\alpha }_t(t^{h})=h~t^{h-\alpha }\), for all \(h\in {\mathbb {R}}\)

\(D^{\alpha }_t(\delta )=0\), where \(\delta \) is constant.

\(D^{\alpha }_t(p/g)=\frac{g D^{\alpha }_t(p)-p D^{\alpha }_t(g)}{g^{2}}\).

Conjointly, if p is differentiable, then \(D^{\alpha }_t(p(t))=t^{1-\alpha }\frac{d p(t)}{dt}\).

2.1 Demarcation of the \(\exp (-\phi (\tau ))\) method

The present subsection offers a transitory explanation of \(\exp (-\phi (\tau ))\) expansion approach [42, 44] in fabricating new exact solutions to nonlinear conformable space-time fractional modified KdV equations. Consider the following nonlinear conformable space-time fractional differential equation

$$\begin{aligned} F\left( u, \frac{\partial ^\gamma u}{\partial t^\gamma }, \frac{\partial ^\gamma u}{\partial x^\gamma }, \frac{\partial ^\gamma u}{\partial y^\gamma }, \frac{\partial ^\gamma u}{\partial z^\gamma }, \frac{\partial ^{2\gamma } u}{\partial t^{2\gamma }}, \frac{\partial ^{2\gamma } u}{\partial x^{2\gamma }}, \frac{\partial ^{3\gamma } u}{\partial x^\gamma \partial y^\gamma \partial z^\gamma },... \right) =0. \end{aligned}$$
(4)

With the use of transformation

$$\begin{aligned} u(x, t)=V(\tau ); ~~\tau = q \frac{x^\gamma }{\gamma } +r \frac{y^\gamma }{\gamma } +s \frac{z^\gamma }{\gamma }-l \frac{t^\gamma }{\gamma }. \end{aligned}$$
(5)

Eq. (4) is changed into a nonlinear ODE as

$$\begin{aligned} P(V, V', V'', ..)=0. \end{aligned}$$
(6)

We search a solution for Eq. (6) in the form

$$\begin{aligned} V(\tau )=a_0+a_{1}exp(-\phi (\tau ))+...+a_{N}exp(-N \phi (\tau )), \end{aligned}$$
(7)

where N is calculated using the homogeneous balance principle (HBP) and \(\phi (\tau )\) is a function that satisfies a first-order equation as

$$\begin{aligned} \phi ^{'}(\tau )=exp(-\phi (\tau ))+\mu _{1} exp(\phi (\tau ))+\lambda _1. \end{aligned}$$
(8)

Now, several cases can be taken:

Case 1: If \(\lambda _{1}^{2}-4\mu _{1}>0\) and \(\mu _{1} \ne 0\), then

$$\begin{aligned} \phi _{1}(\tau )=\ln \left( \frac{-\sqrt{\lambda _{1}^{2}-4\mu _{1}}\tanh \left( \frac{\sqrt{\lambda _{1}^{2}-4\mu _{1}}(\tau +\varepsilon )}{2}\right) -\lambda _{1}}{2\mu _{1}}\right) . \end{aligned}$$

Case 2: If \(\lambda _{1}^{2}-4\mu _{1}>0\) , \(\mu _{1}=0\) and \(\lambda _{1} \ne 0\), then

$$\begin{aligned} \phi _{2}(\tau )=-\ln \left( \frac{\lambda _{1}}{\cosh (\lambda _{1}(\tau +\varepsilon ))+\sinh (\lambda _{1}(\tau +\varepsilon ))-1}\right) . \end{aligned}$$

Case 3: If \(\lambda _{1}^{2}-4\mu _{1}<0\) and \(\mu _{1} \ne 0\), then

$$\begin{aligned} \phi _{3}(\tau )=\ln \left( \frac{\sqrt{4\mu _{1}-\lambda _{1}^{2}}\tan \left( \frac{\sqrt{4\mu _{1}-\lambda _{1}^{2}}(\tau +\varepsilon )}{2}\right) -\lambda _{1}}{2\mu _{1}}\right) . \end{aligned}$$

Case 4: If \(\lambda _{1}^{2}-4\mu _{1}=0\) , \(\mu _{1} \ne 0\) and \(\lambda _{1} \ne 0\), then

$$\begin{aligned} \phi _{4}(\tau )=\ln \left( \frac{-2\lambda _{1}(\tau +\varepsilon )+4}{\lambda _{1}^{2}(\tau +\varepsilon )}\right) . \end{aligned}$$

Case 5 If \(\lambda _{1}^{2}-4\mu _{1}=0\) , \(\mu _{1}=0\) and \(\lambda _{1}=0\), then

$$\begin{aligned} \phi _{5}(\tau )=\ln (\tau +\varepsilon ). \end{aligned}$$

Now, by substituting Eq. (7) along with Eq. (8) into left hand side of Eq. (6), a polynomial in \(exp(-\phi (\tau ))\) is acquired. By setting each coefficient of this polynomial to zero, we acquire a nonlinear algebraic system whose solution gives a series of exact solutions for the Eq. (4).

3 Execution of the method

Firstly, we consider the space-time fractional mKdV equation (1).

3.1 Exact solutions of \((3+1)\)-dimensional conformable space-time fractional Eq. (1)

Using the transformation (5), and integrating once w.r.t. \(\tau \) with zero constant of integration, we get

$$\begin{aligned} - l V+ q r s V^{''}+ 6 q V^3=0. \end{aligned}$$
(9)

The balance between \(V^{''}\) and \(V^3\) gives \(N=1\), then the nontrivial solution (7) reduces to:

$$\begin{aligned} V(\tau )=a_1 \exp (-\phi (\tau ))+a_0. \end{aligned}$$
(10)

By inserting the above solution in reduced equation Eq. (9) along with Eq. (8) and equating the coefficients of each \(\exp (-\phi (\tau ))\) to zero, we procure a set of nonlinear algebraic equations

$$\begin{aligned} &a_1 k \lambda _{1} \mu _{1} r s+6 a_0^3 q-a_0 l=0, \\ &a_1 q \lambda _{1} ^2 r s+2 a_1 q \mu _{1} r s+18 a_0^2 a_1 q -a_1 l=0, \\ &3 a_1 q \lambda _{1} r s+18 a_0 a_1^2 q=0,\\ &2 a_1 q r s+6 a_1^3 q=0. \end{aligned}$$

and its solutions

$$\begin{aligned} a_0= & {} \mp \frac{i \lambda _{1} \sqrt{r s}}{2 \sqrt{3}},~a_1=\mp \frac{i \sqrt{r s}}{\sqrt{3}},~q=q, ~r=r, ~s=s,\nonumber \\ l= & {} -\frac{1}{2} q r s \left( \lambda _{1} ^2-4 \mu _{1} \right) , \end{aligned}$$
(11)

yields the following new exact solutions:

If \(\lambda _{1}^{2}-4\mu _{1}>0\) and \(\mu _{1} \ne 0\), then

$$\begin{aligned}V_1(\tau )&=\mp \frac{\iota \lambda _{1} \sqrt{r s}}{2 \sqrt{3}}\nonumber \\&\quad \mp \frac{2 \iota \mu _{1} \sqrt{r s}}{\sqrt{3}\left( -\sqrt{\lambda _{1}^{2}-4\mu _{1}}\tanh \left( \frac{\sqrt{\lambda _{1}^{2}-4\mu _{1}}(q \frac{ x^{\gamma }}{\gamma }+r \frac{ y^{\gamma }}{\gamma }+s \frac{ z^{\gamma }}{\gamma }+\frac{1}{2} q r s \left( \lambda _{1} ^2-4 \mu _{1} \right) \frac{ t^{\gamma }}{\gamma }+\varepsilon )}{2}\right) -\lambda _{1}\right) }; ~~r s > 0. \end{aligned}$$
(12)

If \(\lambda _{1}^{2}-4\mu _{1}>0\), \(\mu _{1}=0\) and \(\lambda _{1} \ne 0\), then

$$\begin{aligned}V_2(\tau )&=\nonumber \\&\quad \mp \frac{\iota \lambda _{1} \sqrt{r s}}{2 \sqrt{3}}\mp \frac{\iota \sqrt{r s}}{\sqrt{3}}\left( \frac{\lambda _{1}}{\cosh (\lambda _{1}(\tau +\varepsilon ))+\sinh (\lambda _{1}(\tau +\varepsilon ))-1}\right) ; ~~r s > 0, \end{aligned}$$
(13)

where \(\tau = q \frac{ x^{\gamma }}{\gamma }+r \frac{ y^{\gamma }}{\gamma }+s \frac{ z^{\gamma }}{\gamma }+\frac{1}{2} \lambda _{1} ^2 q r s \frac{ t^{\gamma }}{\gamma }.\)

If \(\lambda _{1}^{2}-4\mu _{1}<0\) and \(\mu _{1} \ne 0\), then

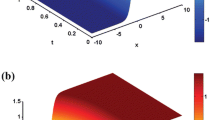
$$\begin{aligned}V_3(x, y, z, t )&=\mp \frac{\iota \lambda _{1} \sqrt{r s}}{2 \sqrt{3}}\nonumber \\&\quad \mp \frac{2 \iota \mu _{1} \sqrt{r s}}{\sqrt{3}\left( \sqrt{4\mu _{1}-\lambda _{1}^{2}}\tan \left( \frac{\sqrt{4\mu _{1}-\lambda _{1}^{2}}(q \frac{ x^{\gamma }}{\gamma }+r \frac{ y^{\gamma }}{\gamma }+s \frac{ z^{\gamma }}{\gamma }+\frac{1}{2} q r s \left( \lambda _{1} ^2-4 \mu _{1} \right) \frac{ t^{\gamma }}{\gamma }+\varepsilon )}{2}\right) -\lambda _{1}\right) }; ~~r s > 0. \end{aligned}$$
(14)

The obtained solutions of Eq. (1) are graphed here for different \(\gamma \)-values corresponding to \(q=\frac{2}{3}\), \(r=1\), \(s=3\) and \(\varepsilon =\frac{1}{2}\).

Fig. 1
figure 1

Solution profile of \(V_1\) appears in Eq. (12) taking \(\mu _{1}=-1\), \(\lambda _{1}=1=z\) and \(y=0\)

Full size image
Fig. 2
figure 2

Solution profile of \(V_2\) appears in Eq. (13) taking \(\mu _{1}=0\), \(\lambda _{1}=1=z\) and \(y=0\)

Full size image
Fig. 3
figure 3

Solution profile of \(V_3\) appears in Eq. (14) taking \(\mu _{1}=1\), \(\lambda _{1}=1=z\) and \(y=0\)

Full size image

3.2 Exact solutions of \((3+1)\)-dimensional conformable space-time fractional Eq. (2)

The Eq. (2) can be transformed into an ordinary differential equation by using the transformation (5), and integrating once w.r.t. \(\tau \), we get

$$\begin{aligned} - l V+ q r s V^{''}+ 6 r V^3=0. \end{aligned}$$
(15)

The balance between \(V^{''}\) and \(V^3\) gives \(N=1\), then the nontrivial solution (7) reduces to:

$$\begin{aligned} V(\tau )=a_1 \exp (-\phi (\tau ))+a_0. \end{aligned}$$
(16)

By inserting the above solution in reduced equation Eq. (15) along with Eq. (8) and equating the coefficients of each \(\exp (-\phi (\tau ))\) to zero, we procure a set of nonlinear algebraic equations

$$\begin{aligned} &-a_0 l+a_1 \lambda _{1} \mu _{1} q r s+6 a_0^3 r=0,\\ &-a_1 l+a_1 \lambda _{1} ^2 q r s+2 a_1 \mu _{1} q r s+18 a_0^2 a_1 r=0,\\ &3 a_1 \lambda _{1} q r s+18 a_0 a_1^2 r=0, \\ &2 a_1 q r s+6 a_1^3 r=0. \end{aligned}$$

and its solutions

$$\begin{aligned} a_0= & {} \mp \frac{i \lambda _{1} \sqrt{q s}}{2 \sqrt{3}}, ~a_1=\mp \frac{i \sqrt{q s}}{\sqrt{3}}, ~q=q, ~r=r, ~s=s\nonumber \\ l= & {} -\frac{1}{2} q r s \left( \lambda _{1} ^2-4 \mu _{1} \right) , \end{aligned}$$
(17)

yields the following new exact solutions:

If \(\lambda _{1}^{2}-4\mu _{1}>0\) and \(\mu _{1} \ne 0\), then

$$\begin{aligned}V_1(\tau )&=\mp \frac{\iota \lambda _{1} \sqrt{q s}}{2 \sqrt{3}}\nonumber \\&\quad \mp \frac{2 \iota \mu _{1} \sqrt{q s}}{\sqrt{3}\left( -\sqrt{\lambda _{1}^{2}-4\mu _{1}}\tanh \left( \frac{\sqrt{\lambda _{1}^{2}-4\mu _{1}}(q \frac{ x^{\gamma }}{\gamma }+r \frac{ y^{\gamma }}{\gamma }+s \frac{ z^{\gamma }}{\gamma }+\frac{1}{2} q r s \left( \lambda _{1} ^2-4 \mu _{1} \right) \frac{ t^{\gamma }}{\gamma }+\varepsilon )}{2}\right) -\lambda _{1}\right) }; ~~q s > 0. \end{aligned}$$
(18)

If \(\lambda _{1}^{2}-4\mu _{1}>0\), \(\mu _{1}=0\) and \(\lambda _{1} \ne 0\), then

$$\begin{aligned}&V_2(\tau )=\mp \frac{\iota \lambda _{1} \sqrt{q s}}{2 \sqrt{3}}\nonumber \\&\quad \mp \frac{\iota \sqrt{q s}}{\sqrt{3}}\left( \frac{\lambda _{1}}{\cosh (\lambda _{1}(\tau +\varepsilon ))+\sinh (\lambda _{1}(\tau +\varepsilon ))-1}\right) ; ~~q s > 0, \end{aligned}$$
(19)

where \(\tau = q \frac{ x^{\gamma }}{\gamma }+r \frac{ y^{\gamma }}{\gamma }+s \frac{ z^{\gamma }}{\gamma }+\frac{1}{2} \lambda _{1} ^2 q r s \frac{ t^{\gamma }}{\gamma }.\)

If \(\lambda _{1}^{2}-4\mu _{1}<0\) and \(\mu _{1} \ne 0\), then

$$\begin{aligned}V_3(\tau )&=\mp \frac{\iota \lambda _{1} \sqrt{q s}}{2 \sqrt{3}}\nonumber \\&\quad \mp \frac{2\iota \mu _{1}\sqrt{q s}}{\sqrt{3}\left( \sqrt{4\mu _{1}-\lambda _{1}^{2}}\tan \left( \frac{\sqrt{4\mu _{1}-\lambda _{1}^{2}}(q \frac{ x^{\gamma }}{\gamma }+r \frac{ y^{\gamma }}{\gamma }+s \frac{ z^{\gamma }}{\gamma }+\frac{1}{2} q r s \left( \lambda _{1} ^2-4 \mu _{1} \right) \frac{ t^{\gamma }}{\gamma }+\varepsilon )}{2}\right) -\lambda _{1}\right) }; ~q s> 0. \end{aligned}$$
(20)

3.3 Exact solutions of \((3+1)\)-dimensional conformable space-time fractional Eq. (3)

The conformable space-time fractional mKdV equation (3), can be reduced into an ordinary differential equation as follows. Using the transformation (5), and integrating once w.r.t. \(\tau \) with zero constant of integration, we get

$$\begin{aligned} - l V + k r s V^{''}+ 6 s V^3=0. \end{aligned}$$
(21)

The balance between \(V^{''}\) and \(V^3\) gives \(N=1\), then the nontrivial solution (7) reduces to:

$$\begin{aligned} V(\tau )=a_1 \exp (-\phi (\tau ))+a_0. \end{aligned}$$
(22)

By inserting the above solution in reduced equation Eq. (21) along with Eq. (8) and equating the coefficients of each \(\exp (-\phi (\tau ))\) to zero, we procure a set of nonlinear algebraic equations

$$\begin{aligned} &-a_0 l+a_1 \lambda _{1} \mu _{1} q r s+6 a_0^3 s=0,\\ &-a_1 l+a_1 \lambda _{1} ^2 q r s+2 a_1 \mu _{1} q r s+18 a_0^2 a_1 s=0,\\ &3 a_1 \lambda _{1} q r s+18 a_0 a_1^2 s=0,\\ &2 a_1 q r s+6 a_1^3 s=0. \end{aligned}$$

and its solution

$$\begin{aligned} a_0= & {} \mp \frac{\iota \lambda _{1} \sqrt{q r}}{2 \sqrt{3}}, ~a_1=\mp \frac{\iota \sqrt{q r}}{\sqrt{3}}, ~q=q, ~r=r, ~s=s, \nonumber \\ l= & {} -\frac{1}{2} q r s \left( \lambda _{1} ^2-4 \mu _{1} \right) , \end{aligned}$$
(23)

yields the following new exact solutions:

If \(\lambda _{1}^{2}-4\mu _{1}>0\) and \(\mu _{1} \ne 0\), then

$$\begin{aligned}V_1(\tau )&=\mp \frac{\iota \lambda _{1} \sqrt{q r}}{2 \sqrt{3}}\nonumber \\&\quad \mp \frac{2 \iota \mu _{1}\sqrt{q r}}{\sqrt{3}\left( -\sqrt{\lambda _{1}^{2}-4\mu _{1}}\tanh \left( \frac{\sqrt{\lambda _{1}^{2}-4\mu _{1}}(q \frac{ x^{\gamma }}{\gamma }+r \frac{ y^{\gamma }}{\gamma }+s \frac{ z^{\gamma }}{\gamma }+\frac{1}{2} q r s \left( \lambda _{1} ^2-4 \mu _{1} \right) \frac{ t^{\gamma }}{\gamma }+\varepsilon )}{2}\right) -\lambda _{1}\right) }; ~~q r > 0. \end{aligned}$$
(24)

If \(\lambda _{1}^{2}-4\mu _{1}>0\), \(\mu _{1}=0\) and \(\lambda _{1} \ne 0\), then

$$\begin{aligned}V_2(\tau )&=\nonumber \\&\quad \mp \frac{\iota \lambda _{1} \sqrt{q r}}{2 \sqrt{3}}\mp \frac{\iota \sqrt{q r}}{\sqrt{3}}\left( \frac{\lambda _{1}}{\cosh (\lambda _{1}(\tau +\varepsilon ))+\sinh (\lambda _{1}(\tau +\varepsilon ))-1}\right) ; ~~q r >0, \end{aligned}$$
(25)

where \(\tau = q \frac{ x^{\gamma }}{\gamma }+r \frac{ y^{\gamma }}{\gamma }+s \frac{ z^{\gamma }}{\gamma }+\frac{1}{2} \lambda _{1} ^2 q r s \frac{ t^{\gamma }}{\gamma }.\)

If \(\lambda _{1}^{2}-4\mu _{1}<0\) and \(\mu _{1} \ne 0\), then

$$\begin{aligned}V_3(\tau )&=\mp \frac{\iota \lambda _{1} \sqrt{q r}}{2 \sqrt{3}}\nonumber \\&\quad \mp \frac{ 2 \iota \mu _{1} \sqrt{q r}}{\sqrt{3}\left( \sqrt{4\mu _{1}-\lambda _{1}^{2}}\tan \left( \frac{\sqrt{4\mu _{1}-\lambda _{1}^{2}}(q \frac{ x^{\gamma }}{\gamma }+r \frac{ y^{\gamma }}{\gamma }+s \frac{ z^{\gamma }}{\gamma }+\frac{1}{2} q r s \left( \lambda _{1} ^2-4 \mu _{1} \right) \frac{ t^{\gamma }}{\gamma }+\varepsilon )}{2}\right) -\lambda _1\right) }; ~~q r> 0. \end{aligned}$$
(26)

The expansion idea given by Eq. (7) was also presented easier in a study on the KPP equation. The general solution to the reduced ordinary differential equations (9), (15) and (21) was also given in [51]. Actually, such travelling solutions should represent sample asymptotic to nonlinear integrable equations [52].

4 Results and discussion

Furthermore, for suitable parametric choices, we plotted three dimensional graphics of some solutions of the fractional mKDV equations for Figs. 1, 2 and 3. The obtained solutions are periodic wave, solitary wave and traveling wave solutions. It is more advantageous than other methods because different, various and more solutions are obtained with our methods. Note that our solutions are new and more extensive than the given ones in [13, 14]. When the parameters are given special values, the optical solitary waves are derived from the travelling waves.

5 Conclusion

In this study, three conformable fractional \((3+1)\)-dimensional mKdV equations have been explored via \(\exp (-\phi (\tau ))\) expansion method. A traveling wave transformation along with conformable derivative has used to transformed the nonlinear fractional differential equation into an ordinary differential equation. We plot some sketches for some of the analytical and exact solutions to express more physical properties of this model. Then, the implementation of \(\exp (-\phi (\tau ))\) expansion method procured a variety of exact solutions of aforementioned fractional mKdV equations. This method and the mathematical tool can be used to derive a localized wave solutions for different nonlinear models in engineering and mathematical physics.