Active scissor-jack for seismic risk mitigation of building structures

Abstract

Active vibration control systems involve sensing and actuation systems to be integrated into a structure. The actuator generates control forces based on sensed external excitation and system response and applies forces directly to the structure in order to reduce its seismic response. One major obstacle with the active vibration control technique is that very large actuator power is often required. This paper studies the effects of positioning an actuator in a scissor-jack configuration within a structural frame. Based on its geometries, the governing equation of motion is derived. A classical optimal control algorithm determines control forces. In a numerical example, a three-level multi-degree of freedom system frame equipped with scissor-jack actuators is compared to an active-tendon system with the same structural characteristics. The results indicate that peak actuator force reduces by 92%. The results indicate that by using the proposed configuration, significant reduction of control forces can be achieved, implying that a much smaller actuator can be used.

1 Introduction

Supplemental energy dissipation systems have recently attracted much attention both in the academia and the construction industry to mitigate seismic hazards in civil structures. In the past three decades, passive, semi-active and active vibration control systems have flourished as many studies have emerged worldwide [1]. In particular, active control systems represent remarkable potentials in suppressing vibration and reduce damages to the structures due to earthquake excitation. Active vibration control systems are smart systems which involve integration of sensing and actuation components acting externally in a structure. The actuators generate control forces based on sensed external excitation and system response and apply forces directly to the structure in order to reduce its seismic response. A comprehensive review including development of control theories, experimental research and practical implementation was carried out by Casciati et al. [2]. The control forces delivered by actuators are determined via control algorithms. Many control algorithms have been developed. Notable algorithms include linear quadratic regulator (LQR) [3], acceleration feedback control [4], H-infinity control [5]. More recent developments include bilinear pole-shifting algorithm [6], fuzzy PID control [7]. Practical implementations of these smart structures in Japan have been summarized [8]. Due to the very large sizes and weights of civil structures, actuators are required to deliver very significant forces. In order to reduce control forces, this paper investigate a method which position the actuator in a scissor-jack configuration. Using the scissor-jack configuration in the vibration reduction in cable systems has been gained the very promising results [9]. This configuration modifies the equation of motion via a coefficient which depends on the geometry of the scissor-jack configuration. The effect of this configuration on the actuator forces will be demonstrated through a numerical example.

2 Active scissor-jack actuator configuration

2.1 Description of system

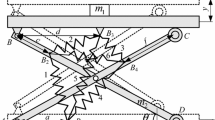
A single degree of freedom system with an Active scissor-jack is presented in Fig. 1. The actuator is pin-connected to four axially rigid members. Due to earthquake excitation, horizontal displacement of floor causes relative displacement between O and O’. To counter the effect of this displacement, the actuator extends or contracts and produces a force via members AO, OC, AO’ and O’C.

Fig. 1

Scissor-jack actuator configuration

2.2 Equation of motion

To establish the equation of motion, Fig. 2 is considered. In this figure u(t) is active actuator force, while T₁, T₂, T₃ and T₄ are axial member forces in brace members.

Fig. 2

Forces in scissor-jack actuator configuration under horizontal excitation

The equilibrium of horizontal and vertical forces in the hinge joints of O and O’ are written as follows, respectively:

$$T_{1} \left( t \right)\cos \theta_{4} - T_{2} \left( t \right)sin\theta_{3} - u\left( t \right)sin\theta_{5} = 0$$

(1)

$$T_{4} \left( t \right)\cos \theta_{1} - T_{3} \left( t \right)sin\theta_{2} - u\left( t \right)sin\theta_{5} = 0$$

(2)

$$T_{1} \left( t \right)sin\theta_{4} - T_{2} \left( t \right)cos\theta_{3} + u\left( t \right)cos\theta_{5} = 0$$

(3)

$$T_{4} \left( t \right)sin\theta_{1} - T_{3} \left( t \right)cos\theta_{2} + u\left( t \right)cos\theta_{5} = 0$$

(4)

Note that θ₅ is the angle that diagonal AC makes with horizon and has been shown in Figs. 1 and 2.

Simultaneously solving Eqs. (1) and (3) as well as Eqs. (2) and (4) gives the following equations:

$$T_{1} \left( t \right) = \alpha_{1} u\left( t \right)$$

(5)

$$T_{3} \left( t \right) = \alpha_{2} u\left( t \right)$$

(6)

where, α₁ and α₂ are as follows:

$$\alpha_{1} = sin(\theta_{5} + \theta_{3} )/cos(\theta_{3} + \theta_{4} )$$

(7)

$$\alpha_{2} = cos(\theta_{5} - \theta_{1} )/cos(\theta_{1} + \theta_{2} )$$

(8)

The equation of motion related to the active control system is derived as follows:

$$m\ddot{x}\left( t \right) + c\dot{x}\left( t \right) + kx\left( t \right) + T_{1} cos\theta_{4} + T_{3} sin\theta_{2} = - m\ddot{x}_{g} \left( t \right)$$

(9)

where m is mass, cis damping coefficient, k is stiffness, u(t) is actuator force in the scissor-jack system and $\ddot{x}_{g} \left( t \right)$ is ground acceleration. Simplifying we have,

$$m\ddot{x}\left( t \right) + c\dot{x}\left( t \right) + kx\left( t \right) = - \alpha_{s} u\left( t \right) - m\ddot{x}_{g} \left( t \right)$$

(10)

where

$$\alpha_{s} = \alpha_{1} cos\theta_{4} + \alpha_{2} sin\theta_{2}$$

(11)

Equation 11 shows that the actuator force u(t) is amplified by the factor α_s. The value of α_s is dependent on geometry of scissor-jack configuration, and it is shown below.

2.3 Scissor-jack coefficient α _s

From Fig. 2 the distance between O’A is L₁, which is the length of the lower brace, and the angle it makes with horizontal is θ₁. For any given building geometries L and h, all other geometric properties, θ₂, θ₃, θ₄ and L₂ in Fig. 2 can be determined as follows:

$$\theta_{2} = 90 - 2\arctan \left( {\frac{h}{L}} \right) + \theta_{4}$$

(12)

$$\theta_{3} = 90 - 2\arctan \left( {\frac{h}{L}} \right) + \theta_{1}$$

(13)

$$\theta_{4} = \arctan \left( {\frac{{\left[ {h - L_{1} cos\left( {\theta_{3} } \right)} \right]}}{{\left[ {L - L_{1} sin\left( {\theta_{3} } \right)} \right]}}} \right)$$

(14)

$$L_{2} = \left[ {L - L_{1} \sin \left( {\theta_{3} } \right)} \right]/cos\left( {\theta_{4} } \right)$$

(15)

To demonstrate the effect of θ₁ and L₁, consider a single storey frame with height h = 3 m and bay width L = 6 m. The resultant α_s is shown in Fig. 3. It is clear that a larger θ₁ and L₁ will result in a larger α_s, which will effectively reduce the required actuator force. There is little effect on α_s until θ₁ becomes larger than 20 degrees, at which α_s sets off rapidly. It should be noted that in practical implementations the physical actuator length would restrict the choice of θ₁ and L₁. Moreover, if the structural designer would like to change the building geometry h and L, their effect on is demonstrated in Fig. 4 and Fig. 5.

Fig. 3

Coefficient α_s as a function of θ₁ and L₁

Fig. 4

Coefficient α_s as a function of θ₁ and L (L₁ = 1.5 m)

Fig. 5

Coefficient α_s as a function of θ₁ and h (L₁ = 1.5 m)

2.4 Formulation of multi-degree of freedom systems

To extend the formulation of active scissor-jack system to a multi-degree of freedom structure, consider a three-level building system shown in Fig. 6. Assuming the geometrical properties of the scissor-jack system is identical on each level, the equation of motion is written in matrix form as follows.

$$\left[ M \right]\ddot{x}\left( t \right) + \left[ C \right]\dot{x}\left( t \right) + \left[ K \right]x\left( t \right) = \left[ {\gamma_{sm} } \right]U\left( t \right) + \left[ \delta \right]\ddot{x}_{g} \left( t \right)$$

(16)

where,

$$\left[ M \right] = \left[ {\begin{array}{*{20}c} {m_{1} } & 0 & 0 \\ 0 & {m_{2} } & 0 \\ 0 & 0 & {m_{3} } \\ \end{array} } \right]$$

(17)

$$\left[ C \right] = \left[ {\begin{array}{*{20}c} {(c_{1} + c_{2} )} & { - c_{2} } & 0 \\ { - c_{2} } & {(c_{2} + c_{3} )} & { - c_{3} } \\ 0 & { - c_{3} } & {c_{3} } \\ \end{array} } \right]$$

(18)

$$\left[ K \right] = \left[ {\begin{array}{*{20}c} {(k_{1} + k_{2} )} & { - k_{2} } & 0 \\ { - k_{2} } & {(k_{2} + k_{3} )} & { - k_{3} } \\ 0 & { - k_{3} } & {k_{3} } \\ \end{array} } \right]$$

(19)

$$\left[ {\gamma_{sm} } \right] = \left[ {\begin{array}{*{20}c} { - \alpha_{sm} } & {\alpha_{sm} } & 0 \\ 0 & { - \alpha_{sm} } & {\alpha_{sm} } \\ 0 & 0 & { - \alpha_{sm} } \\ \end{array} } \right]$$

(20)

$$\left[ {U\left( t \right)} \right] = \left[ {\begin{array}{*{20}c} {u_{1} \left( t \right)} \\ {u_{2} \left( t \right)} \\ {u_{3} \left( t \right)} \\ \end{array} } \right]$$

(21)

$$\left[ \delta \right] = \left[ {\begin{array}{*{20}c} { - m_{1} } \\ { - m_{2} } \\ { - m_{3} } \\ \end{array} } \right]$$

(22)

Fig. 6

MDOF system with active scissor-jack system

In Eq. 16, m₁ to m₃ are masses, c₁ to c₃ are damping coefficients, k₁ to k₃ are stiffness, u₁(t) to u₃(t) are active control forces, $\ddot{x}\left( t \right)$ is the floor acceleration, $\ddot{x}_{g} \left( t \right)$ is the ground acceleration due to earthquakes and $\alpha_{sm}$ is the scissor-jack coefficient. It can be shown that α_sm is a function of geometry of the scissor-jack configuration:

$$\alpha_{sm} = \frac{{sin(\theta_{5} + \theta_{3} )\left( {cos\theta_{4} + sin\theta_{2} } \right)}}{{cos(\theta_{3} + \theta_{4} )}}$$

(23)

2.5 Control strategy

The objective of control strategy is to minimize the displacement x(t) by changing the forces U(t). To facilitate the application of linear optimal control theory, the second-order differential equation in (16) is presented in a first-order state-space form. A 2n-dimensional state vector is declared:

$${\mathbf{Z}}\left( t \right) = \left\{ {\begin{array}{*{20}c} {x\left( t \right)} \\ {\dot{x}\left( t \right)} \\ \end{array} } \right\}$$

(24)

Such that Eq. (16) can be expressed as follows:

$${\dot{\mathbf{Z}}}\left( t \right) = {\mathbf{AZ}}\left( t \right) + {\mathbf{B}}_{{\mathbf{u}}} u\left( t \right)\alpha_{s} + {\mathbf{B}}_{{\mathbf{r}}} \ddot{x}_{g} \left( t \right)$$

(25)

where:

$$\begin{aligned} {\dot{\mathbf{Z}}}\left( t \right) & = \left\{ {\begin{array}{*{20}c} {\dot{x}\left( t \right)} \\ {\ddot{x}\left( t \right)} \\ \end{array} } \right\} \\ {\mathbf{A}} & = \left[ {\begin{array}{*{20}c} 0 & {\mathbf{I}} \\ { - {\mathbf{M}}^{ - 1} {\mathbf{K}}} & { - {\mathbf{M}}^{ - 1} {\mathbf{C}}} \\ \end{array} } \right] \\ {\mathbf{B}}_{{\mathbf{u}}} & = \left[ {\begin{array}{*{20}c} 0 \\ { - {\mathbf{M}}^{ - 1} } \\ \end{array} } \right] \\ {\mathbf{B}}_{{\mathbf{r}}} & = \left[ {\begin{array}{*{20}c} 0 \\ { - 1} \\ \end{array} } \right] \\ \end{aligned}$$

In the above equation, A is system plant matrix, B_u is control location matrix and B_r is earthquake excitation influence matrix. The control force is obtained via a feedback law of a control algorithm:

$$u\left( t \right) = - {\mathbf{GZ}}\left( t \right)$$

(26)

where G is matrix of feedback gain matrix. The determination of the control force can be determined from The Ricatti optimal control algorithm. An optimal solution for state vector Z(t) and control force vector u(t) is calculated based on minimization of a standard performance index J, given by

$$J = \frac{1}{2}\mathop \smallint \limits_{0}^{T} \left( {({\mathbf{Z}}\left( t \right)^{T} {\mathbf{QZ}}\left( t \right) + u\left( t \right)^{T} {\mathbf{R}}u\left( t \right)} \right)dt$$

(27)

where Q and R and weighting matrices for system response and control force. The control gain matrix is determined by

$${\mathbf{G}} = {\mathbf{R}}^{ - 1} {\mathbf{B}}_{{\mathbf{u}}}^{{\mathbf{T}}} {\mathbf{P}}$$

(28)

In which P is the Ricatti matrix obtained from the Ricatti equation.

$${\mathbf{A}}^{{\mathbf{T}}} {\mathbf{P}} + {\mathbf{PA}} - {\mathbf{R}}^{ - 1} {\mathbf{PB}}_{{\mathbf{u}}} {\mathbf{B}}_{{\mathbf{u}}}^{{\mathbf{T}}} {\mathbf{P}} + {\mathbf{Q}} = 0$$

(29)

3 Numerical Study

To demonstrate the effects of scissor-jack configuration, a three-storey MDOF frame is investigated as a numerical study in order to study the performance. Australian sections 200UC59.5 and 250UB37.3 are used for columns and beams, respectively. Lumped masses of 12 tons are assumed for each level. The damping matrix is constructed using Rayleigh proportional damping with 5% damping ratio. Structural properties are listed in Table 1. This structure has natural periods of 0.64 s, 0.23 s and 0.16 s which belongs to modes 1–3, respectively. For comparison, an active tendon system with identical frame structural characteristics is considered. Active tendon systems consist of prestressed tendons located on each floor where active control is delivered by actuators which adjust the level of tension in the tendons. Active tendon systems have been tested in small laboratory scale [10], full scale testing [11], as well as studied numerically [12]. Figure 7a shows the configuration of the 3-storey active scissor-jack system while Fig. 7b shows that of the active-tendon system. All brace members are assumed to be linear elastic and axially rigid. In the active tendon system will have the same equation of motion (Eq. 16) except actuator force is not modified by α_sm. Actuator forces are derived through formulations presented in previous section and results for the both systems are compared.

Table 1 Properties of test structures

Fig. 7

a Scissor-jack system and b active tendon system

The first 20 s of the 1979 Imperial Valley–El Centro M(6.5) and 1994 Northridge M(6.7) is chosen as the input ground excitation. The input acceleration is shown in Fig. 8.

Fig. 8

Ground excitation: a 1979 El Centro earthquake accelerations and b 1994 Northridge earthquake accelerations

Displacements responses of scissor-jack controlled and uncontrolled systems are compared in Fig. 9. It is clear that Active-Scissor Jack system significantly suppress the displacement responses. Using the control algorithm presented in Sect. 3, the control forces u(t) is determined for both active scissor-jack and the active tendon system.

$${\mathbf{U}} = {\mathbf{GZ}}\left( {\mathbf{t}} \right)$$

(30)

Fig. 9

Comparison of displacement response (with and without scissor-jack): imperial Valley–El Centro (left) and Northridge (right)

The control forces are presented in Fig. 10. A 92% reduction of actuator force is resulted. It is clear that the actuator forces from both systems doing the same job, i.e. minimizing the displacements, but actuator in scissor-jack configuration produces smaller control force due to the linear coefficient α_sm.

Fig. 10

Comparison of actuator forces in active scissor-jack and active tendon systems: imperial Valley–El Centro (left) and Northridge (right)

4 Conclusion

In this paper, the effects of the scissor-jack configuration on mitigation of control forces in active control systems have been studied. Equation of motion for a single and multiple degree-of-systems are derived. The equation of motion is linearly influenced by a coefficient, called α_s in this article. Analytical equation of α_s is presented in the paper and its value is determined by geometries of brace members. Using Ricatti optimal control algorithm, a numerical example has demonstrated that the actuator forces in the scissor-jack actuator configuration may reduce the required actuator force by 92%, as compared to that of an active tendon system. The result of this study demonstrates that control forces of an active vibration control system may be reduced via the proposed configuration; consequently increase the feasibility of such system in practice.