Unravelling the scaling characteristics of daily streamflows of Brahmani river basin, India, using arbitrary-order Hilbert spectral and detrended fluctuation analyses

Abstract

This paper presents arbitrary-order Hilbert spectral analysis (AOHSA) and multifractal detrended fluctuation analysis (MF-DFA) approaches to describe the multifractality of daily streamflows from four stations, namely Tilga, Jeraikela, Gomlai and Jenapur of Brahmani river basin in India. In the former method, the spectral slopes of Hilbert spectra for different moment orders depict the multifractality, and in this study, AOHSA method detected the scale invariance between synoptic to intra-seasonal scales (3 days–3 months approximately) in the daily streamflows of all the four stations. The MF-DFA method detected a crossover within 80–110 days (~ 3 months) in the four time series in addition to the crossover at annual scale. The robust estimates of Hurst exponents made by following the adaptive detrending method of pre-processing detrending operation ranged between 0.7 and 0.73 for the four time series which confirmed the universal multifractal properties within Brahmani river basin. The behaviour of spectral slope plot of AOHSA, the characteristics of scaling exponent plot, mass exponent plot and multifractal spectra confirmed that the highest multifractal degree is for the streamflow records of Tilga station which is having the smallest drainage area, and it may be attributed to the faster response of this sub-catchment to local precipitation events. The multifractality of all the four streamflow time series is found to be due to the dominant influence of correlation properties than due to the broadness of probability density function.

1 Introduction

Hydrological system is a complex and dynamical system characterized by non-stationary input (precipitation) and output (runoff/streamflow). Streamflow time series records often possess multiscaling behaviour, and it may display self-similar and exhibit self-affine fractal behaviours over a certain range of timescales. At small scales, turbulence induces stochastic fluctuations, and at larger scales (from days to years) the streamflow fluctuations are the result of complex nonlinear interactions between rainfall processes and global climate system. There exists similarity between large-scale and small-scale streamflow characteristics. The information on long-range correlation in streamflow time series is helpful for its prediction. The procedure of estimation of such long-term correlations was first introduced by Hurst [23], and finding of that research can be considered as the first example referring to the self-affine and fractal behaviour. The science behind the runoff processes in the catchment will be reflected in the time series, and hence the fractal (or multifractal) characterization and scaling analysis can be considered as the fingerprint of the field observations. In the past, researchers have tried different methods to characterize the scaling properties in river flows, which include rescaled range analysis [22, 23], double trace moments [50], Fourier spectral analysis, [44], extended self-similarity principles [6] and wavelet analysis [29]. The hydrological variables possess nonlinear and non-stationary characteristics, and the periodic cycles are inherent in them in most of the cases. Peng et al. [45] proposed an efficient method, namely detrended fluctuation analysis (DFA) to perform the fractal analysis based on a detrending procedure. Kantelhardt et al. [28] proposed the multifractal extension of DFA procedure popularly known as MF-DFA method. Multifractal analysis is an appropriate framework for detecting the scaling fields of time series and eventually it may help for modelling various geophysical processes [44]. For hydrological time series, the multifractal description serves as an efficient nontrivial test bed for the performance of state-of-the-art precipitation–runoff models [30]. These researches provided a broader framework in modelling the rainfall–runoff processes, such as topography and river network, that generate and modify the streamflow processes through the basin [10, 39]. Therefore, the DFA and MF-DFA methods have been applied for a wide range of studies in hydrology.

Kantelhardt et al. [29] applied the MF-DFA procedure to the global river runoff datasets and compared the results with that by wavelet transform modulus maxima (WTMM) method and reported good agreement between the results by the two techniques. They found that the multifractal properties of runoff and precipitation are non-universal and beyond crossover scales to several weeks, there exists noticeable difference in scaling exponents of runoff records in particular. They further reported that for all runoff records, a modified version of the binomial multifractal model fits best, while several precipitation records require different models to describe the processes. Koscielny-Bunde et al. [31] applied DFA, MF-DFA and wavelet analysis to the discharge records from 41 hydrological stations around the globe for investigating their temporal correlations and multifractal properties. The study found that the daily runoff records are long-term correlated with crossover time in the order of weeks, and they are characterized by a correlation function which follow a power law behaviour with exponents varying between 0.1 and 0.9. Kantelhardt et al. [30] studied the multifractal behaviour of 99 long-term daily precipitation records and 42 long-term daily runoff records from different parts of the world. They found that the precipitation records generally show short-term persistence and runoff records show long-term persistence with a mean scaling exponent of ~ 0.73 for runoff records globally. Zhang et al. [51] applied the MF-DFA procedure to analyse the multifractal characteristics of streamflow from four gauging stations of Yangtze river in China. Their study detected the non-stationarity of different time series and analysed the differences in multifractality among the records from stations at upper and lower Yangtze basin. Zhang et al. [52] applied MF-DFA method to study the scaling behaviours of the long daily streamflow series of four hydrological stations in the mainstream of East River in China. The results indicated that streamflow series of the East River basin are characterized by anti-persistence and showed similar scaling behaviour at different shorter timescales. Further, they used the MF-DFA method to investigate the effect of water storage structures on streamflow records, and it was found that the streamflow magnitude is mainly influenced by the precipitation magnitude, while the fluctuations of the streamflow records are affected by the human interventions like construction of control structures. Labat et al. [32] applied DFA to investigate streamflow series of two Karstic watersheds in the southern France, suggesting that the correlation properties exist in small scales and anti-correlated properties exist in large scales. Hirpa et al. [12] analysed and compared the long-range correlations of river flow fluctuations from 14 stations in the Flint River basin in the state of Georgia in the south-eastern USA. Their study investigated the effect of basin area on the multifractal characteristics of streamflow time series at different locations, and it was found that, in general, the higher the basin area, the lower will be the degree of multifractality. Rego et al. [46] applied the MF-DFA to analyse the multifractality of water level records of 12 principal Brazilian rivers, and the results indicated the presence of multifractality and long-range correlations for all the stations after eliminating the climatic periodicity. Li et al. [34] applied the MF-DFA method to the streamflow time series of four stations of Yellow river in China. They detected the crossover point at annual scale in all the time series. After removing the trend by the seasonal trend decomposition, it was found that all decomposed series were characterized by the long-term persistence. Also it was found that the multifractality of streamflow series was due to both correlation properties and the broadness of probability density function of the series. Recently, Tan and Gan [49] used MF-DFA for detecting long-term persistence (LTP) and multifractal behaviour of 100 stations of daily precipitation and 145 stations of streamflow time series of Canada. They reported that all precipitation time series showed LTP at both small and large timescales, while streamflow time series generally showed non-stationary behaviour at small timescales and LTP at large timescales. The multifractal behaviour of Canadian precipitation and streamflow data can be accurately described by the universal multifractal model and with the modified version of multiplicative cascade model. They suggested that the persistence of Canadian streamflow was not only because streamflow is more autocorrelated than precipitation but also due to human interventions such as streamflow regulations.

Since most of the hydrological time series are possessing turbulence at smaller scales and are linked with climatic oscillations at smaller scale, the detection of scaling range using an appropriate technique is of paramount importance in the modelling process. Intermittency and frequency modulations are two dominant properties of turbulent flows, and the influence of flow turbulence is emphasized from high-frequency part (show the intermittence) and low-frequency part (frequency modulations). The time–frequency analysis of such time series based on appropriate multiscale decomposition technique is capable of detecting the intermittency properties and ranges in which scale invariance is present. Hilbert Huang transform (HHT) is one of the popular techniques used for analysing nonlinear and non-stationary time series proposed by Huang et al. [18]. It comprises a data adaptive decomposition method, namely empirical mode decomposition (EMD) as its first phase. The decomposition gives a set of high- and low-frequency oscillatory modes (called intrinsic mode functions or IMFs) and a reminder series (called ‘residue’ which indicates the long-term trend of the dataset) each associated with specific timescales. It is well proven that the different modes obtained by the EMD show filter bank property [8]. Existence of the multiple timescales in the hydrological time series resembles the hierarchy of scales charactering the turbulent flow. Hence, some researchers believe that the hydrological process is an analogy with the stochastic cascade models in a fully developed turbulent flow that generally yield fractals [47]. Hence, one can argue that varying timescales in hydrological time series may display the self-similarity and it is a signature of fractals. As a second phase of HHT, the modes obtained can be subjected to the Hilbert transform (HT) to get the instantaneous frequencies and amplitudes (which form the Hilbert spectrum in time-frequency space). The HHT is hence a useful method for time–frequency characterization of nonlinear and non-stationary time series signals, and the scaling information derived from spectra can be used for a wide range of applications in hydrology like prediction of hydrological variables, teleconnection studies and derivation of intensity–duration–frequency relationships [1, 2, 27]. The integration of Hilbert spectrum in the time domain will help to construct the Hilbert energy spectrum which is often prepared by considering the second-order moment of amplitudes. The energy spectrum is a useful mean to identify the timescale in which the scale invariance is present. As the geophysical time series generally comprises a wide variety of fluctuations, it is logical to assume multifractality of such series. In this circumstance, Huang et al. [19, 17] proposed a modified version of HHT, namely arbitrary-order Hilbert spectral analysis (AOHSA) in which the Hilbert spectra are obtained for specified arbitrary-order moments of amplitudes. This technique was presented as one of the latest additions to the family of techniques to detect multifractality of the time series. In this technique, the multifractal property can be described by evaluating the slope of energy spectrum for different moment orders in the scale-invariant frequency range. The AOHSA method has been applied for assessing the multifractality of passive scalar (temperature) data obtained from a jet experiment [21], wind power fluctuations [3], sunspot time series [53] and financial time series [33]. The method was successfully applied for estimating the multifractality of daily river flow time series Seine River and Wimereux river in France, pertaining to catchments of distinctly different sizes [20]. Also Huang et al. [20] emphasized the comparison of the results of this technique with the more popular methods such as MF-DFA to understand the robustness of the method by applying it for real-field hydrological signals from other part of the world. Motivated from this, the present study (1) applies AOHSA procedure to investigate the multifractality of time series from four hydrological stations Tilga, Jaraikela, Gomlai and Jenapur in Brahmani basin, India; (2) applies MF-DFA procedure for the above set of time series to get useful inferences on multifractality of time series; (3) compares the inferences drawn from the study to comment on the relative merits and demerits of the methods.

Section 2 presents the theoretical description of methodologies used in this study. Section 3 presents the description on datasets used. Section 4 presents the results of multifractal analysis of different time series by both methods supported by relevant discussions. Then, the important observations from the study are concluded.

2 Materials and methods

This section presents the theory of AOHSA method and MF-DFA method along with the respective steps to detect the multifractality of streamflow time series.

2.1 Arbitrary-order Hilbert spectral analysis (AOHSA)

Hilbert Huang transform (HHT) is a recently developed computational paradigm for spectral analysis of nonlinear and non-stationary time series data. The EMD step in HHT is purely a data adaptive process, and hence it decomposes the time series to certain number of oscillatory modes of specific frequency. This method does not involve ‘a priori’ selection of functions, but instead it decomposes the signal into intrinsic oscillation modes derived from the succession of extrema. The original data can be reconstructed by summing each of the modes which are independent of each other. Each IMF must meet the following conditions:

• (a) The number of extreme values in the overall data must match the number of zero crossings or differ by only one

  $$N_{\hbox{max} } + N_{\hbox{min} } = N_{\text{zero}} \pm 1$$

  N_max where N_max = total number of maxima; N_min = total number of minima; and N_zero = total number of zero crossings; and

• (b) At any point of time, the mean value of the envelope of local maxima and envelope of local minima (m(t)) must be zero

  $$m(t) = \frac{{E_{\hbox{max} } (t) + E_{\hbox{min} } (t)}}{2} \approx 0$$

where E_max(t) is the envelope of the local maxima and E_min(t) is the envelope of the local minima, which are often obtained by spline interpolation procedures. The EMD operation primarily involves (1) identification of all extrema (maxima and minima) of the signal X(t), (2) interpolation and construction of upper envelope (E_max(t)) and lower envelope (E_min (t)), (3) computation of the mean of the upper and lower envelope, m(t), (4) finding a difference series by subtraction of mean from the original series, etc. The above process is known as ‘sifting’, and the process is to be repeated iteratively till a zero-mean mode with no riding waves (i.e. there are no negative local maxima and positive local minima) gets evolved. The sifting can be stopped by adopting suitable sifting criteria as proposed by Huang and Wu [17]. Subtraction of a mode from the signal enables us to proceed with the generation of the second mode, and the orthogonality property of modes will enable to proceed with the generation of subsequent modes. The EMD operation will be stopped when the last mode evolved is monotonic or with a single peak. This component is known as residue which represents a low-frequency component representing the long-term trend of the data. More details on EMD operation can be found in Huang et al. [18]. The IMFs of the time series signal X(t) obtained in the first phase (say IMF(t)) are suitable candidates to perform Hilbert transform (HT), to yield instantaneous frequency and amplitudes. Hilbert transform is the convolution of IMF(t) with the function $g(t) = \frac{1}{\pi t}$. Then, an analytic signal (Z(t)) can be represented by combining IMF(t) and Y(t) as follows :

$$Z(t) = {\text{IMF}}(t) + iY(t) = A(t)e^{i\theta (t)}$$

(1)

where Y(t) is the Hilbert transform of the signal; $i = \sqrt { - \,1}$; A(t) is the amplitude, $\theta (t)$ is the phase angle, which are defined as:

$$A(t) = \sqrt {{\text{IMF}}^{2} (t) + Y^{2} (t)}$$

(2)

and

$$\theta (t) = \tan^{ - 1} \left( {\frac{Y(t)}{{{\text{IMF}}(t)}}} \right)$$

(3)

The instantaneous frequency is given by

$$\omega (t) = \frac{1}{2\pi }\left( {\frac{{{\text{d}}\theta (t)}}{{{\text{d}}t}}} \right)$$

(4)

Thus HHT can distribute the amplitudes on the time–frequency plane, and the Hilbert energy spectrum can be defined by considering second-order amplitudes as follows:

$$H(\omega ,t) = A^{2} (\omega ,t).$$

The Hilbert spectrum is representing the energy–time–frequency information at local level, and its integration over the time gives the marginal Hilbert spectrum

$$h(\omega ) = \int\limits_{0}^{\infty } {H(\omega ,t} ){\text{d}}t$$

(5)

An alternative way to define the marginal Hilbert spectrum is to define the joint pdf $p(\omega ,A)$ of instantaneous frequency $\omega$ and amplitude A [19]. Then, the marginal Hilbert spectrum can also be written as the second-order statistical moment

$$h(\omega ) = \int\limits_{0}^{\infty } {p(\omega ,A)A^{2} } {\text{d}}A$$

(6)

The above equation can be expressed as a generalized one by defining arbitrary-order moments, and Huang et al. [19] proposed the arbitrary-order Hilbert spectral analysis

$$L_{q} (\omega ) = \int\limits_{0}^{\infty } {p(\omega ,A)A^{q} } {\text{d}}A\quad {\text{where}}\quad q \ge 0$$

(7)

The AOHSA method can be used to detect the multifractality of the time series. In this process, the Hilbert marginal spectrum is constructed for different q orders. Theoretically, Huang et al. [21] defined the spectrum for q = − 1 onwards, but for stream flow analysis it is recommended to select q in the range 0–5 [18, 44]. The arbitrary-order spectra can be expressed in such a way that it follows scaling law within certain scale range

$$L_{q} (\omega ) = \omega^{ - \,\xi (q)} \quad {\text{where}}\,\xi (q)\,{\text{is}}\,{\text{the}}\,{\text{scaling}}\,{\text{exponent}}\,{\text{in}}\,{\text{the}}\,{\text{Hilbert}}\,{\text{space}}.$$

i.e. the slope of the log–log plot of Hilbert spectra within the chosen scale range corresponding to different q-order moments gives the scaling exponent. If the plot of scaling exponents (corresponding to different q orders) follows a concave shape, it can be concluded that the series is mulifractal in the range chosen. The scaling exponent $\xi (q)$ can be linked to scaling exponent $\zeta (q)$ of structure functions [19] as follows:

$$\xi (q) = \zeta (q) + 1$$

(8)

Further, $\xi (q)$ the scaling exponent can be related to the classical Hurst exponent (H) by the following relation

$$\xi (q) = qH + 1,\quad {\text{where}}\quad H = \xi (1) - 1$$

More mathematical details of the method can be found in Huang et al. [19], and proof for the above relations can be found in Zhou et al. [53].

2.2 Multifractal detrended fluctuation analysis (MF-DFA)

The different steps involved in MF-DFA computational procedure can be described as follows [29, 33, 52].

Consider a streamflow time series X (x₁, x₂, … x_N), N is the length of the time series. The accumulated deviation of the series (known as ‘profile’) is calculated. As $Y(i) = \sum\nolimits_{k = 1}^{i} {\left[ {x_{k} - \bar{x}} \right]}$, where i = 1, 2,…., N, k = 1,2…,N, $\bar{x}$ is the mean of the series x_k

Divide the profile Y(i) into $N_{s} = \text{int} (N/s)$ non-overlapping segments of length, where s is the segment sample size (so-called as scale in MF literature) chosen for the analysis and int(N/s) is the integer part of (N/s). Here, while considering multiple of scales, sometimes a small portion of the time series at the end may remain, as N need not be a multiple of s always. To retain this part of the series, the same procedure is repeated starting from the opposite end, thereby 2N_s segments.

Calculate the local trend for each of the 2N_s segments by a least squares fit of the series as:

$$F^{2} (s,\nu ) = \frac{1}{s}\sum\limits_{i = 1}^{s} {\left\{ {Y[(\nu - 1)s + i] - y_{\nu } (i)} \right\}}^{2} \quad {\text{for}}\;\;\nu = 1,2, \ldots ,N_{s}$$

(9)

and

$$F^{2} (s,\nu ) = \frac{1}{s}\sum\limits_{i = 1}^{s} {\left\{ {Y[N - (\nu - N_{s} )s + i] - y_{\nu } (i)} \right\}}^{2} \quad {\text{for}}\;\;\nu = N_{s} + 1, \ldots ,2N_{s}$$

(10)

Here, $y_{\nu } (i)$ is the fitting polynomial in segment $\nu$. Linear, quadratic, cubic, etc., different types of fitting, can be made, and accordingly DFA procedure is named as DFA1, DFA2,…..DFAm, etc.

Determine the q-order fluctuation function by averaging over all segments

$$F_{q} (s) = \left\{ {\frac{1}{{2N_{s} }}\sum\limits_{\nu = 1}^{{2N_{s} }} {\left[ {F^{2} (s,\,\nu )} \right]^{q/2} } } \right\}^{1/q}$$

(11)

Here, the index variable q can take any real value except zero.

For the zeroth-order, fluctuation function can be computed by following a logarithmic averaging procedure defined as [28]

$$F_{0} (s) = \exp \left\{ {\frac{1}{{4N_{s} }}\sum\limits_{\nu = 1}^{2Ns} {\ln [F^{2} (s,\,\nu )]} } \right\}$$

(12)

Determine the scaling behaviour of the fluctuation functions by analysing the log–log plots of F_q(s) versus s for each values of q. If the time series is long-range power law correlated, F_q(s) increases as F_q(s) ~ s^h(q) and h(q) is the slope of log Fq(s) and log s plot, called as generalized Hurst exponent (GHE).The value of Hurst exponent (H) is reported for h(2) and H is considered as (h(2) − 1)/2, if it is found to be greater than unity.

For an uncorrelated series, the value of Hurst exponent is 0.5. If the Hurst exponent falls between 0.5 and 1, it indicates the long-term persistence (long memory process), and if it falls between 0 and 0.5, it indicates a short-term persistence (short memory process). Long-term persistence implies a positive auto correlation in the time series (i.e. the effect of an observation on future observations remains significant for a long period of time). For example, in an extreme event would have higher probability being followed by another extreme of same character (i.e. a flood followed by another flood). The selection of scale (s), the type of polynomial chosen, etc., are some of the key issues while applying the MF-DFA method. Generally, the minimum scale can be chosen in such way that it is sufficiently larger than the polynomial order chosen to prevent error in computation of local fluctuations and maximum scale can be chosen below 1/2 of the data length. Also the polynomial order can be chosen 1–3 probably sufficient to avoid overfitting problems within small segment sizes [24].

The generalized Hurst exponent (h(q)) is only one of the several types of scaling exponents used to parameterize the multifractal structure of the time series. The q-order mass exponent (τ(q)) and singularity exponent (α) are other useful means for describing the scaling characteristics of time series.

$$\tau (q) = qh(q) - 1$$

(13)

$$\alpha = \frac{{{\text{d}}\tau (q)}}{{{\text{d}}q}}$$

(14)

and $f(\alpha ) = q\alpha - \tau (q)$ where f(α) denotes the dimension of the subset of the series characterized by α. In a multifractal case, different parts of the series are characterized by different values of α, which leads to a spectrum namely singularity spectrum. In short, it is a plot of f(α) versus α. The dependency of h(q) on q infers multifractality of the time series, and the difference in the slopes of the segments before and after (0, τ(0)) in a plot between τ(q) and q will help to comment on the strength of the multifractality. The base width of the spectrum Δα = (α_max− α_min) also reflects the strength of multifractality in the time series.

For each order of q, the scaling behaviour of the fluctuation functions can be determined by the logarithmic plot of Fq(s) versus s. The plot between log Fq(s) and log (s) enable to detect a crossover point which divides the smaller- and larger-scale ranges and useful to detect the dominant cycle in the time series. Also the slope of the segments before and after the crossover point provides useful information on non-stationarity of the series, while the corresponding intercepts provide useful information on the influence of storage structures [52].

3 Study area and datasets

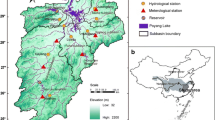
The Brahmani river basin (lies between latitudes 20°30′10″ and 23°36′42″N and longitudes 83°52′55″ and 87°00′38″E) is located in the eastern part of India. The basin is embedded between Mahanadi basin (at the right side) and Baitarani basin (at the left side). It has a total catchment area of ~ 39,315 km², and it comprises the regions from three states in India—Orissa (~ 57% of the basin area), Jharkhand (~ 39% of the basin area) and Chhattisgarh (~ 3.5% of the basin area). The basin is composed of four distinct sub-basins, namely Tilga, Jaraikela, Gomlai and Jenapur, and since the sub-basins are distinctly different in size, more insights into the multifractality can be drawn while comparing the results by a recently developed procedure (AOHSA) and a widely accepted procedure (MF-DFA). Moreover, the lower reaches of this basin near the deltaic area are subject to frequent floods [26]; since Mahanadi, Brahmani and Baitarani are interconnected near their delta, worst flood occurs when there are simultaneous heavy rains in all the three catchments. Breaching of embankments and prolonged submergence are common occurrences during floods. In this context, the information on multifractality may provide valuable inputs to develop robust flood frequency estimation models for the basin. A map showing the location of Brahmani basin and its sub-basin is shown in Fig. 1. The Brahmani river rises near Nagri village in Ranchi district of Jharkhand at an elevation of about 600 m and travels a total length of 799 km before it joins with the Bay of Bengal. The basin has a sub-humid tropical climate with an average annual rainfall of 1305 mm, and southwest monsoon season (June–September/October) is the major contributor of rainfall in the region. Daily streamflow and rainfall data for long periods of four stream gauging stations, namely Tilga, Jaraikela, Gomlai and Jenapur, were collected from Water Resources Information System (WRIS) operated by the Central Water Commission, India (http://www.india-wris.nrsc.gov.in/wris.html). The drainage area corresponding to the four stations along with data span chosen for the study is provided in Table 1.

Fig. 1

Location map of Brahmani basin

Table 1 Datasets used for the study and drainage area of stations

For most of the stations of the database system, the data during an overall span 1970s to 2016 are present with long and short breaks in some of the stations. It is worth mentioning that for Tilga station, data up to 2009 only are available in continuous form and thereafter many breaks are there in the database. Also for the rest of the stations, the data up to 2014 only are available in continuous form, which are chosen for this study. In the time series of Tilga and Jerailkela, both smaller and larger fluctuations are present with many intermittent values (characterized by zero values), while in the data from other stations, the larger magnitude fluctuations are dominant, which indicates that the chances of existence of cycles of a diverse range of frequencies ranging from smaller to larger scales are more in Tilga and Jeraikela stations (Fig. 2).

Fig. 2

Time series plots of daily streamflows of different stations of Brahmani basin. a Tilga; b Jeriakela; c Gomlai; d Jenapur

4 Results and discussion

4.1 Application of AOHSA method for multifractal description

The daily streamflow time series from the four stations are first decomposed adaptively by the EMD method. The decomposition resulted in 21, 19, 20 and 21, respectively, for Tilga, Jeraikela, Gomlai and Jenapur stations. From Table 1, it is noticed that the data length is the highest for Jerailkela station and the least for Tilga station. It is a well-known fact that both the length of the dataset and the complexity of the dataset play a role in deciding the number of modes from the decomposition [8, 17]. For brevity, the modes of decomposition results are not presented here as the multifractality detection is completely based on the final marginal Hilbert spectra estimated by the AOHSA procedure. Now, the modes are subjected to Hilbert transformation and first the Hilbert energy spectrum (for order 2) and Fourier spectrum of different time series is prepared. The spectra of streamflow of different stations are presented in Fig. 3.

Fig. 3

Scaling ranges of daily streamflow series of different stations of Brahmani basin. a Tilga; b Jaraikela; c Gomlai; d Jenapur. The blue line (lower plot) of each panel shows Fourier spectra and red line (upper plot) shows the spectra by HSA method

The visual examination of the spectra clearly shows that both the Fourier and AOHSA methods detect a prominent peak at frequency of (roughly) ~ 0.028 (i.e. a period of ~ 400 days). Thus, it could be ascertained that the annual periodicity is clearly detected by the Fourier and AOHSA methods in the time series from all the stations. It is further noticed that the nature of evolution of both the spectra at inter-annual scales is similar. This suggests the possible link of different climatic oscillations (operating at inter-annual scales) with the streamflow data of the Brahmani river basin. This inference can be logical, as some of the previous studies established the link between Indian monsoon rainfall and large-scale climatic oscillations such as ElNiño Southern Oscillation (ENSO) and Equatorial Indian Ocean Oscillations (EQUINOO) [9]. Moreover, Maity and Nagesh kumar [36] established the linkage of basin scale streamflow with the above large-scale atmospheric circulation patterns at the Mahanadi basin, located adjacent to the study area. Hence, it is logical to ascertain such a linkage of Brahmani river flow with the climatic indices ENSO and EQUINOO which operate at inter-annual scales. The detection of the range of frequency in which the scale invariance holds is the first step in the multifractal detection of streamflow using AOHSA method. The scale invariance is detected for each spectrum, and the vertical bars marked in Fig. 3 indicate the scale invariance range. From the careful perusal of Fig. 3, it is noticed that the scale invariance persists in scale range between 0.4 < ω < 0.01 day⁻¹ approximately (corresponding to a timescale of 2.5–100 days) for different time series. Even though highest frequency is nearly equal (corresponding to 2.5 days), the lowest frequency is varying between 30 days to 100 days (1–3 months) in different stations (frequency values 0.025, 0.035, 0.022, 0.01 for different stations). Hence, it can be concluded that in general the scale invariance is observed between synoptic to intra-seasonal timescales in the Brahmani basin. Further, within the observed scale range, the slope of Hilbert energy spectrum and Fourier spectrum of different time series is computed and marked in the same figure (Fig. 3).

The slopes are also similar for all the time series except that for Jeraikela station. This may be due to inconsistent fluctuations, non-stationarity and high intermittency property of the time series of Jaraikela station. Now, after identifying the scale ranges the plots of the marginal spectra are considered for the moment orders q = 0,1,…,5. The marginal spectra of the time series of four stations for different moment orders are presented in Fig. 4. The large fluctuations of spectral amplitudes for the spectra of higher orders (say q > 3) may introduce error in estimation of scaling exponent, accordingly Lombardo et al. [35] suggested that up to moment order 3 is sufficient to describe the multifractality of hydrological time series. A comparison of different marginal spectra shows that the spectra corresponding to the first three moment orders are stable in all stations. But for the higher-order moments, the spectra show high fluctuation of amplitudes (with lesser fluctuations in Jenapur station) and subsequently this may introduce errors in computation of slope of the spectra for higher-order moments. This also supports the conclusions of Pandey et al. [44] about the consideration of moment orders.

Fig. 4

Marginal spectra of different streamflow time series of different moment orders. a Tilga; b Jaraikela; c Gomlai; d Jenapur

The slopes of the spectra for different moment order q give the scale exponent $\xi (q)$ which enables us to make a plot of $\xi (q)$ versus q. Finally, the slopes of marginal spectra for different moment orders are computed to comment on the multifractality of different time series. The plot between spectral slope and moment order for different stations is presented in Fig. 5.

Fig. 5

Scaling exponents of streamflow time series from Brahmani for different moment orders. Here, $\xi (q)$ is the scaling exponent in Hilbert space. a Tilga; b Jaraikela; c Gomlai; d Jenapur

The spectral slopes for the four series are 1.769 1.886, 1.942 and 1.951, respectively, for the datasets from Tilga, Jeraikela, Gomlai and Jenapur stations. This infers that $\xi (1) - 1$ values are 0.77, 0.87, 0.94 and 0.95 for different stations.

4.2 MF-DFA of daily streamflow

In this section, the results of MF-DF analysis of daily streamflow from Brahmani river basin are discussed. The MF-DFA method is applied to daily streamflow data to evaluate the multifractal properties of the time series: the plots between scale (segment sample size) and fluctuation function for q = 2 (in log scale), the plot between generalized exponent and q order, plot of the mass exponent τ(q) versus q order and the spectral width. The plots between scale and fluctuation function for q = 2 (in log scale) is prepared by considering the maximum scale as half of the data length [11] and presented in Fig. 6.

Fig. 6

Scaling properties of the log–log plots of F_q(s) versus s of daily streamflow of four stations in Brahmani basin. a Tilga; b Jaraikela; c Gomlai; d Jenapur

From Fig. 6, the possibility of multiple crossovers is very much evident in the time series of different time series. Also by AOHSA method, it is found that in addition to annual scales, intra-seasonal cycles play a role in controlling the variability of streamflows of Brahmani basin. In such cases, it is quite difficult to report a unique scaling exponent from the raw data as a signature of multifracatlity; instead, it is quite essential to apply additional pre-processing detrending methods [4, 7, 14, 25]. Many pre-processing methods for denoising are reported in the literature, which include the EMD [18], the Fourier-detrended (Fourier-based filtering) method [5, 40], the singular value decomposition (SVD) method [41, 42] and the adaptive detrending (AD) method [15]. In this paper, we utilize the AD method for the pre-processing detrending operation. A briefing on AD method is provided in “Appendix 1”. After applying the AD method, the dominant trend output data can be subjected to MF-DFA [7]. In this study, a polynomial order of 2 and the number of segmentation 101 are chosen while invoking the AD method, based on past studies [25].

In all the four time series, a crossover point is noticed at between 354 days to 398 days (log10(2.55) to log10(2.65)) which is corresponding to annual scale. In all the cases, the slope of the plot before the annual crossover point is slightly above unity, which indicates the non-staionarity of the series. In all of the series, one crossover point is noticed at intra-seasonal scale ranges. It is noticed that the slope of the two segments before ‘annual’ crossover point is similar and the intra-seasonal scale is least perceptible in the data of Jenapur station. The plots of q-order fluctuation function of different streamflow series are presented in Fig. 7.

Fig. 7

q-Order fluctuation function and corresponding regression computed by MF-DFA. a Tilga; b Jaraikela; c Gomlai; d Jenapur

The plot between h(q) versus q is helpful to assess the multifractality [13]. To represent the scaling exponent, one unit addition is necessary by the relation $\xi (q) = h(q) + 1$, where the behaviour of the plot remains the same. The scaling exponent plot is presented in Fig. 8, which shows the strong nonlinear dependency of $\xi (q)$ on q which suggests that the streamflow time series of all stations possesses multifractality. The strength of multifractality can also be ascertained by GHE plots. Considering the generalized Hurst exponent plot, the difference between GHE for q = − 5 and q = 5 (i.e. h(− 5)–h(5)) gives a value of 4.487, 1.506, 1.547 and 1.339, respectively, for streamflows of Tilga, Jeraikela, Gomali and Jenapur stations. That is, the steeper variation in GHE plots also confirms the highest degree of multifractality of streamflow records of Tilga station.

Fig. 8

The scale exponent plots ($\xi (q)\,\,$ vs q) of daily streamflow data from four stations in Brahmani basin. a Tilga; b Jaraikela; c Gomlai; d Jenapur

The higher the value of total spread of GHE plot (∆h), the greater will be the degree of multifractality. The total spread (∆h), left and right spread (∆h_L and ∆h_R), of the time series of four stations is summarized in Table 2. The Hurst exponent (H) for the q order 2 (i.e. h(2)) for the four time series is found out to be 0.718, 0.703, 0.727 and 0.731, respectively, for Tilga, Jeraikela, Gomlai and Jenapur stations. It is to be recalled that these are the values for generalized Hurst exponent for q = 2 and the values of GHE for q = 1 are equivalent to the classical Hurst exponent (H) by rescaled range analysis [30]. The h(1) values of the four stations are found to be 0.865, 0.854, 0.871, 0.876.

Table 2 Multifractal parameters of daily streamflow series of four stations

Now, the relation between τ(q) and q also is considered to investigate multifractality of different time series. Figure 9 shows that the behaviour is different for q < 0 and q > 0. The slopes of τ(q) and q are also indicated in Fig. 9, which shows that the difference of between the slopes of the two segments is 4.68, 1.605, 1.645 and 1.442, respectively, for streamflows of Tilga, Jeraikela, Gomali and Jenapur stations. The higher slope difference also refers to a higher degree of multifractality; the streamflows of Tilga station show the highest degree, and that of Jenapur display the lowest degree.

Fig. 9

τ(q) versus q curves of daily streamflows of four stations in Brahmani basin. a Tilga; b Jaraikela; c Gomlai; d Jenapur

The multifractal spectra for the streamflow of the four stations are presented in Fig. 10. A wider singularity spectrum indicates a higher degree of multifractality, and a narrow width indicates lesser degree of multifractality. For a multifractal time series, the shape of singularity spectrum will be an inverted parabola whose left- and right-hand wings correspond to positive and negative q. The width of the spectrum f($\alpha )$ reflects the strength of multifractality. The shape and extent of the singularity spectrum f($\alpha )$ curve contain significant information about the distribution characteristics of the examined dataset and describe the singularity content of the time series. The degree of multifractality of a time series is characterized by the difference between the maximum and minimum values of α, $\Delta \alpha = \alpha_{\hbox{max} } - \alpha_{\hbox{min} }$. This parameter is identical to the width of the singularity spectrum $f(\alpha )$ at f = 0. Figure 10 shows that different multifractal spectra exhibit parabolic shape, indicating the multifractal structure of the time series. Spectra of streamflow series show right fluctuation, which indicates that multifractal structure of daily streamflow time series is insensitive to large magnitudes of local fluctuations [24]. The base width of multifractal spectra (α_max− α_min) indicates that the width is largest (4.88) for the spectra of streamflows of Tilga station and minimum for Jenapur station (1.69). This shows that the streamflows of Tilga show the highest degree of multifractality and indicate the faster variation of streamflow to precipitation events in this sub-catchment for which the drainage area is the least (3160 km²). These results support the findings of Hirpa et al. [12] that multifractality degree reduces with an increase in catchment size, and those obtained by AOHSA method, even though it obviously need not be the single factor deciding the degree of multifractality and persistence [48]. The higher multifractal degree of the series indicates more heterogeneity of streamflow records, which is characterized by sudden bursts of high frequency, irregularities or intermittencies. In other words, singularities are highest for the streamflow records of Tilga, in which the changes are more extreme and prediction is more difficult for this station.

Fig. 10

Multifractal spectra of daily streamflow time series of four stations in Brahmani basin. a Tilga; b Jaraikela; c Gomlai; d Jenapur

Asymmetric index (R) is a useful parameter for multifractal analysis [13], which can be derived from the multifractal spectrum. It is obtained by following relation:

$$R = \frac{{\Delta \alpha_{\text{L}} - \Delta \alpha_{\text{R}} }}{{\Delta \alpha_{\text{L}} + \Delta \alpha_{\text{R}} }}$$

(15)

where $\Delta \alpha = \alpha_{\hbox{max} } - \alpha_{\hbox{min} }$; $\Delta \alpha_{\text{L}}$ and $\Delta \alpha_{\text{R}}$ are, respectively, the width of left- and right-hand branches of the multifractal spectrum curve; and their values describe the distribution patterns of high and low fluctuations. The value of R ranges from − 1 to 1. It quantifies the deviations of the multifractal spectrum curve. R > 0 suggests a left-hand deviation of the multifractal spectrum, likely to have resulted from some degree of local high fluctuations; R < 0 suggests a right-hand deviation with local low fluctuations, and R = 0 represents a symmetrical multifractal spectrum. ∆f(α) is the difference between the maximum and minimum values of f(α).The difference ∆f(α) between maximum and minimum values of the singularity provides an estimate of the spread in changes in fractal patterns. Since ∆f(α) denotes the frequency ratio of the largest to the smallest fluctuation, ∆f(α) > 0 means that the largest fluctuations are more frequent than smallest fluctuations, while ∆f(α) < 0 is the reverse. Values of multifractal parameters are presented in Table 2. It is noticed that the R is negative for streamflows of Tilga and Jenapur, while it is positive for that of Jeraikela and Gomali stations. The negative value of R indicates that the spectra are right deviant, i.e. singularity of low streamflow values is larger than high values. Table 2 shows that in the streamflow series of all stations ∆f(α) value is positive, which shows that the largest fluctuations are more frequent than smallest fluctuations in the streamflow series of all stations.

Determination of the cause of multifractality is one of the key steps in multifractal analysis. It is popularly known that the two major causes of multifractality are: (1) due to different long-term temporal correlations for small and large fluctuations and (2) due to the broadness (fatness) of probability density function (PDF), which indicate the variations. In this study, the popular approaches of shuffling and use of surrogate data are adopted to detect the cause of multifractality. The shuffling procedure destroys any temporal correlations in the data, but by retaining the distributions the same. To quantify the influence of the fatness of PDF, the surrogate time series generated from the original can be used. The surrogate series are generated by randomizing their phases in Fourier space so that the surrogate series are Gaussian. If the multifractality is derived from temporal correlations, the generalized Hurst exponent h(q) obtained for shuffled the data is expected to be 0.5. If multifractality is due to broadness of PDF, h(q) obtained for surrogate series will be independent of q [39]. If both long-range correlation and broadness of PDFs are responsible for multifractality, the shuffled and surrogated series will show lower multifractality than the original series. The details of shuffling and the procedure for generating surrogate series through phase randomization can be found elsewhere [13, 37, 38, 43]. The plots of shuffled surrogated and original estimates of generalized Hurst exponent are provided in Fig. 11.

Fig. 11

Generalized Hurst exponent as a function of moment order (q) for original, shuffled and surrogate streamflow time series of four stations in Brahmani basin. a Tilga; b Jaraikela; c Gomlai; d Jenapur

Figure 11 shows that on shuffling the series, the Hurst exponents are practically brought down to 0.5 in all cases, which clearly shows the dominant influence of correlation properties on the multifractality of the series. The changes in Hurst exponents are statistically quantified by reduced Chi-square estimate [39] given by

$$\chi_{r\diamondsuit } 2 = \frac{1}{N}\sum\limits_{i = 1}^{N} {\frac{{[h(q_{i} ) - h_{\diamondsuit } (q_{i} )]^{2} }}{{[\sigma_{o} (q)^{2} + \sigma_{\diamondsuit } (q)^{2} ]}}}$$

(16)

where the symbol $\diamondsuit$ stands for shuffled or surrogate cases and N is the number of degrees of freedom. The values of reduced Chi-square along with the variance of the generalized Hurst exponent estimates of the three cases are provided in Table 3. Also the basic multifractal properties for original, shuffled and surrogate series are provided in Table 4. Results of Table 4 show a significant reduction in these properties for the shuffled series when compared to original and surrogate series. In short, it can be inferred that the multifractality of different series is due to dominant effect of correlation properties, and the effect of broadness of PDF is rather marginal in all the four records.

Table 3 Statistical properties of original, shuffled and surrogate series of streamflow of different stations

Table 4 Multifractal properties of original, shuffled and surrogate series of streamflow of different stations

This study demonstrated an alternate approach for multifractal characterization of daily streamflow, which may eventually help in developing appropriate multifractal models, regional flood frequency analysis and water resources management in different parts of Brahmani basin. AOHSA is applied as an alternative method for explain the science behind the runoff processes of a basin and compared with the popular MF-DFA to examine its competency. However, owing to the infant stage of its theoretical development, more mathematical investigations are to be performed to use it as a tool alternative to MF-DFA for comprehensive multifractal analysis.

5 Conclusions

This paper presents the application of arbitrary-order Hilbert spectral analysis (AOHSA) and MF-DFA methods for describing the scaling characteristics and explaining the scientific reasoning of runoff processes of streamflows of Brahmani basin India. The major conclusions drawn from this study are:

• The daily streamflows of Brahmani basin river basin, India, displayed strong long-term persistence

• AOHSA method clearly detected that the scaling ranges between synoptic to intra-seasonal timescales (3 days–3 months approximately) in the daily streamflow time series of four stations of Brahmani basin

• AOHSA is an efficient alternative to assess the multifractality of daily streamflows which avoid the pre-detrending operation and detect the scaling ranges even under the presence of strong periodic components superposed to scaling regimes which may lead to multiple crossovers in the fluctuation function plots of MF-DFA analysis

• Multiple evaluation properties of the two methods of analysis confirmed that the highest degree of multifractality is for the streamflow of Tilga station, which may be due to the faster response of this sub-catchment to the precipitation events

• The multifractality of all the four streamflow time series is found to be due to the dominant influence of correlation properties than due to the broadness of probability density function.

Appendix 1

1.1 Adaptive detrending (AD) method

A discrete series, X(i) with i = 1,2,….,N, is partitioned with overlapping windows of length (2n + 1). An arbitrary polynomial Y is constructed in each window of length (2n + 1). In order to get a continuous trend function (and to avoid sharp jumps), the following weighted function for the overlapping part of the $\nu$th segment can be used [15]:

$$Y_{\nu }^{\text{overlap}} (j) = \left( {1 - \frac{j - 1}{n}} \right)Y_{\nu } (j + n) + \frac{j - 1}{n}Y_{\nu + 1} (j)$$

J = 1,2,3,…,n + 1, recollecting that there will be (n + 1) overlapping segment for each neighbouring point.

The size of each segment was calculated by $2n + 1 = 2 \times \text{int} \left[ {\frac{N - 1}{{w_{\text{adaptive}} + 1}}} \right] + 1$. It leads to an increase in the value of the adaptive weight $w_{\text{adaptive}}$ and the order of the polynomial. The fluctuations that disappear get suppressed. For the non-overlapping segments, the adaptive detrended data are given by $X_{d} (i) = (X(i) - Y_{\nu } (i))$, while those for overlapping segments are given by $X_{d} (i) = (X(i) - Y_{\nu }^{\text{overlap}} (i))$. The order of the polynomial and the adaptive weight (number of segmentations, $w_{\text{adaptive}}$) are the two control parameters which are to be chosen appropriately during the implementation of AD algorithm.