Introduction

Thanks to the developing technology, working opportunities with nanoscale structures have increased and nanotechnology has started to take an important place today. Rapid developments in nanotechnology and the previously mentioned unique properties of nanoscale structures have enabled these structural elements to be used in the design of micro and nano electro-mechanical systems (MEMS and NEMS) such as atomic force microscopes, switches, sensors. Nanotechnology is a wide field spread across various disciplines such as mechanical engineering, electrical engineering, chemical engineering, applied physics and materials science [1].

The size effect cannot be neglected in the static and dynamic behavior of micro and nanostructures. It is well-known by many researchers that size effects in micro and nanoscale structures can not be explained by classical continuum mechanics. For this reason, non-classical continuum theories depended on size is developed to define the size effect in micro and nanoscale structures by introducing material length scale parameters in the constitutive relations. Because of the various limitations of the classical continuum mechanics, various types of generalized models of continuum mechanics, such as modified couple stress theory [2], gradient theory [3], micropolar theory [4], non-local elasticity theory [5], surface elasticity [6] and micromorphic model [4, 5]. In Romano et al. [7] the authors have introduced the original and important notion of non-redundant strain measures in the micromorphic continuum. For a general presentation of the features of the relaxed micromorphic model in the anisotropic setting, we refer the reader to Barbagallo et al. studies [8]. Recently, various simplified versions of the general micromorphic theory have been developed in [8, 9].

The first studies on vibration were carried out on macro-sized structures. The first study on microstructures was presented on microstructures in linear elasticity properties by Mindlin [10, 11]. Later, Fleck and Hutchinson [12] reformulated the classical stress couple theory used for macro-dimensional structures. Yang et al. [2] developed the modified couple stress and strain gradient theories using the couple stress theory. Park and Gao [13], the researchers who first applied the modified couple stress theory (MCST) to the field of micro technology, is considered a pioneering study in this field. They were first used the MCST in the static deformation analysis of a Euler Bernoulli micro cantilever beam exposed to a point load. They have created a new Euler–Bernoulli beam model using the MCST. This modeling has been the most suitable solution for microstructured beam structures. After this study, many researchers have used the MCST to develop beam models as well as investigate the size-dependent phenomena in microsystems. Linear homogenous Euler–Bernoulli beam model by Kong et al. [14], linear homogenous Timoshenko beam model by Ma et al. [15] and Reddy [16], non-linear homogenous Euler–Bernoulli beam model by Xia et al. [17] and Kahrobaiyan et al. [18], nonlinear homogenous Timoshenko beam model by Asghari et al. [19], a new comprehensive Timoshenko beam element by Kahrobaiyan et al. [20], linear functionally graded Euler–Bernoulli and Timoshenko beam models by Asghari et al. [21, 22] are carried out.

In addition to developing beam models, mechanical behavior of micro and nano systems have also been investigated and analyzed based on the MCST. Postbuckling behavior of Timoshenko and Reddy-Levinson single-walled carbon nanobeams (SWCN)s [23], the buckling analysis of three microbeam models [24], buckling responses of microtubes [25], buckling analysis of axially loaded microscaled beams [26], analytical solution for size dependent response of cantilever microbeams [27] were studied by using MCST.

MCST has been adopted by many researchers to study the vibration of microtubes/beams. For example, Wang [28] developed a new theoretical model for the vibration analysis of fluid conveying microtubes by introducing one internal material length scale parameter based on MCST. Ahangar et al. [29] carried out a study related with the size-dependent vibrational behavior of a microbeam conveying fluid using MCST. Shafiei et al. [30] conducted the transverse vibration of microbeam incorporating rotary effect with Euler Bernoulli tapered beam model based on MCST. The free vibration frequencies of a statically deflected Timoshenko microbeam under uniformly distributed static load was studied based on MCST [31]. Hadian et al. [32] assessed the nonlinear vibration of elastically connected double microbeam system subject to a moving load by applying the non-classical Timoshenko beam and the MCST. Works of Şimşek [33] deal with the study of the nonlinear static and free vibration of a microbeams in presense of three-layered nonlinear elastic foundation modeled with the MCST. Wang et al. [34] focused on nonlinear vibration of a microbeam on the base of MCST. Ghayesh et al. [35] employed the MCST to analyze numerically the nonlinear vibration of microbeam. Kural and Özkaya [36] investigated the transverse vibrations of a microbeam resting on an elastic foundation and conveying fluid with constant velocity using MCST. Utilizing MCST. Hosseini and Bakhshi [37] analytically analyzed the free vibration of nonuniform microbeam in the presence of Poisson’s ratio effects. Şimşek [38] analyzed the forced vibration of an embedded microbeam carrying a moving microparticle on the basis of the MCST within the framework of Euler–Bernoulli beam theory.

MCST is one of the well-known theories used widely by the researchers to analyze the nanotubes/nanobeams vibrations. Zeng et al. [39] performed a study based on MCST to analyze the natural frequency and electromechanical behavior of the flexoelectric cylindrical nanoshell incorporating large deformation. Sourki and Hosseini [40] considered the surface effects on the flexural vibration of a weakened nanobeam based on MCST. Fakhrabadi et al. [41] investigated the nonlinear vibration of carbon nanotubes under step DC voltage for investigating dynamic pull in characteristics and natural frequencies. MCST was used for investigating the vibration and instability of fluid conveying double wall carbon nanotubes [42], the nonlinear vibration and instability of fluid conveying double walled boron nitride nanotubes embedded in viscoelastic medium [43], vibrational behaviors of fluid conveying carbon nanotubes [44] and the vibration and instability of fluid conveying double walled carbon nanotubes [45]. Utilizing MCST, the free vibration behavior of an embedded magneto-elektro-elastic nanoshell subjected to thermo-elektro-magnetic loadings [46] and free vibration of magneto-electro-elastic nanobeams in thermal environment [47] was studied taking into account the size-dependent effect. A detail study on vibration behavior of tensioned nanobeam [48] and also magnetic field effect on nonlocal nanobeam embedded in nonlinear elastic foundation [49] were investigated. Yayli [50] studied torsional vibration of carbon nanotubes with general elastic boundary conditions based on MCST.

More recently the modified couple stress theory has been applied to the study of functionally graded (FG) beams using non-classical Timoshenko beam model for nonlinear free vibration of FG microbeam [51], non-classical Timoshenko beam model for dynamic stability of FG microbeams [52], a third order shear deformation beam theory for static and dynamic analysis of FG microbeams [53], three different beam theories for buckling analysis of a FG microbeam [54], a unified higher order beam theory for buckling of a FG microbeam embedded in elastic Pasternak medium [55], non-classical Euler beam model and non-classical Timoshenko beam model for bending analysis of a FG microbeam [56], Timoshenko beam model for static bending analysis of a FG microbeam [57], various higher order beam theories for static bending and free vibration of functionally graded (FG) microbeams [58], modified Euler–Bernoulli beam model for free vibration of an axially FG tapered cantilever microbeam [59], a third order beam theory for nonlinear analysis of FG beams [60] and Euler–Bernoulli beam theory for free vibration analysis of FG nanobeam incorporating surface effects [61]. In addition to that. MCST has been applied to the study of composite laminated beams using Reddy beam model for the static analysis [62], different beam theories for the vibration analysis [63] and for the bending of a simply supported laminated composite Timoshenko beams subjected to transverse loads [64]. MCST has also been used in a standard experimental method for determining the intrinsic material length scale based on a non-contact laser Doppler vibration measurement system [65]. Nonlocal strain gradient theory is applied to investigate the piezoelectric sandwich nanobeams nonlinear vibration [66]. Nonlocal elasticity theory is applied to analyze the vibration of a rotating FG piezoelectric nanobeam [67]. Togun and Bağdatlı [68] obtained natural frequencies of simply supported Euler-nanobeams resting on elastic foundation based on MCST. Nonlocal elasticity theory was employed in the vibration and stability analysis of a nanobeam conveying fluid was studied [69]. The effect of the axial load on the fundamental vibration frequency was further examined by Wahrhaftig and Brasil [70], who studied a cantilever beam with large initial displacement. Furthermore, analytical and computational methods have been proposed to determine buckling load of slender structures [71,72,73]. Silva et al. [74] presented some research results on the optimization of an impact damper for a structural system excited by a non-ideal power source.

When all of the valuable studies mentioned in the above are examined, it can be seen that analytical techniques dependent on a single mode approximation which is blind to modal interactions are employed. Also, most of these studies has analyzed the free vibrations of the micro and nano systems. The nonlinear transverse vibrations of a tensioned nanobeam under two boundary conditions are studied using modified couple stress theory in [48]. The tensioned effect of nanobeam is examined in [48], where as in the presented study with and without the size effect and Poisson effect is examined. To the best of the authors’ knowledge, there is no paper in the literature that includes nonlinear vibration of a nanobeam based on modified couple stress theory for both with and without the size effect and Poisson effect. Also, the paper is related to applying a model for the four different types of boundary conditions. However, in a study encountered in the literature, only a simply supported beam was considered. The main objective of the current study is to fill this gap. In the present study, the nonlinear free and forced dynamics of a nanoscale beam is investigated numerically based on the modified couple stress theory. Nonlinear equation is obtained considering cubic nonlinearity into the equations included by stretching of the neutral axis. Nonlinear frequency–response curves of the system are constructed for nanobeams with four different boundary conditions named as simply supported. clamped–clamped, clamped-simple and clamped-free nanobeams.

Governing Equation

The Modified Couple Stress Theory

Yang et al. in 2002 [2] initially presented a study related with modified couple stress theory that mentions the strain energy density is a function of not only strain tensor but also curvature tensor. Moreover, it includes two Láme parameters and one length scale parameter. Therefore, the strain energy of a deformed linear isotropic elastic body occupying a volume Ω is given as

$$U = \frac{1}{2}\mathop \int \limits_{{\Omega }} \left( {{\sigma _{ij}}{\varepsilon_{ij}} + {m_{ij}}{\chi_{ij}}} \right)dV\,\, i.j=1.2.3$$
(1)

in this formula. σij, εij, mij and χij are the components of the stress tensor, strain tensor, deviatoric part of the couple stress tensor and the symmetric curvature tensor, respectively. These tensor are defined as follow

$$\sigma_{ij} = \lambda \varepsilon_{kk} \delta_{ij} + 2\mu \varepsilon_{ij}$$
(2)
$$\varepsilon_{ij} = \frac{1}{2}\left( {u_{i,j} + u_{j,i} } \right)$$
(3)
$$m_{ij} = 2\mu l^{2} \chi_{ij}$$
(4)
$$\chi_{ij} = \frac{1}{2}\left( {\theta_{i,j} + \theta_{j,i} } \right)$$
(5)

where ui. δij and l are the displacement vector, the Kronecker delta and the material length scale parameter, respectively. The rotation vector θi is defined as follows

$$\theta_{i} = \frac{1}{2}e_{ijk} u_{k,j}$$
(6)

where eijk is the permutation symbol. λ and μ are the Láme’s constants are expressed as

$$\lambda = \frac{{{\text{E}}\upsilon }}{{\left( {{1} + \upsilon } \right)\left( {1 - 2\upsilon } \right)}}{,}\begin{array}{*{20}c} {} & {\mu = \frac{{\text{E}}}{{2\left( {{1} + \upsilon } \right)}}} \\ \end{array}$$
(7)

where υ is Poisson’s ratio, μ is shear modulus and E is Young’s modulus.

The Governing Equation for Nanobeam

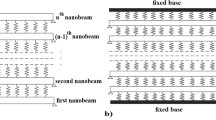
In the present study, nanobeam with four different boundary conditions which are simple-simple, clamped–clamped, clamped- simple and clamped-free cases are considered in Fig. 1. The length of the nanobeam is L and the cross-section dimension is \(b\times h\).

Fig.1
figure 1

Boundary conditions for four different cases

Full size image

The equation of motion of a nanobeam can be formulated by using the Hamilton principle. The potential energy induced by the bending strain energy of the nanobeam due to function of strain and the curvature are given in Eq. (8), respectively. The bending strain energy Um of the nanobeam is written by

$${U}_{m}=-\frac{1}{2}{\int }_{0}^{L}{M}_{x}\frac{{\partial }^{2}w}{\partial {x}^{2}}dx-\frac{1}{2}{\int }_{0}^{L}{Y}_{xy}\frac{{\partial }^{2}w}{\partial {x}^{2}}dx$$
(8)

where the resultant moment \({M}_{x}\) and the couple moment \({Y}_{xy}\) are defined, respectively, by

$${M}_{x}={\int }_{A}{\sigma }_{xx}zdA$$
(9)
$${Y}_{xy}={\int }_{A}{m}_{xy}dA$$
(10)

\({\sigma }_{xx}\) and \({m}_{xy}\) are defined. respectively. by

$${\sigma }_{xx}=-Ez\frac{{\partial }^{2}w}{\partial {x}^{2}}$$
(11)
$${m}_{xy}=-\mu {l}^{2}\frac{{\partial }^{2}w}{\partial {x}^{2}}$$
(12)

using Eqs. (8)-(12), the bending strain energy of the nanobeam based on the modified couple stress theory takes the following form

$${U}_{m}=\frac{1}{2}{\int }_{0}^{L}\left(\frac{E\left(1-\upsilon \right)I}{\left(1+\upsilon \right)\left(1-2\upsilon \right)}+\mu A{l}^{2}\right){\left(\frac{{\partial }^{2}w}{\partial {x}^{2}}\right)}^{2}dx$$
(13)

in which \(\frac{\left(1-\upsilon \right)}{\left(1+\upsilon \right)\left(1-2\upsilon \right)}\) indicates the Poisson effect that included in Equation in order to obtain accurate and reliable results [32]. The potential energy induced by the elastic energy in extension \({U}_{s}\) due to stretching of the neutral axis is written by

$${U}_{s}=\frac{EA}{2L}{\int }_{0}^{L}{\left(\frac{\partial w}{\partial x}\right)}^{2}dx$$
(14)

The kinetic energy of the nanobeam can be expressed as

$$T=\frac{1}{2}{\int }_{0}^{L}\rho A{\left(\frac{\partial w}{\partial t}\right)}^{2}dx$$
(15)

in which \(\rho A\) is the beam mass of per unit length.

The dynamic behavior of a nanobeam and possible boundary conditions can be derived according to the Hamilton’s principle by using the following variational formula;

$$\delta {\int }_{{t}_{1}}^{{t}_{2}}\left[T-{U}_{m}-{U}_{s}-{W}_{ext}\right]dt=0$$
(16)

where \(\delta {W}_{ext}=0;\) inserting Eqs. (13)-(15) into Eq. (16) and integrating by parts, and collecting the coefficients of \(\delta w\), the following equation of motion for the Euler–Bernoulli beam with size dependent considering the modified couple stress theory and including the Poisson effect are obtained

$$\left(\frac{E\left(1-\upsilon \right)I}{\left(1+\upsilon \right)\left(1-2\upsilon \right)}+\mu A{l}^{2}\right)\frac{{\partial }^{4}w}{\partial {x}^{4}}+\rho A\frac{{\partial }^{2}w}{\partial {t}^{2}}=\frac{EA}{2L}{\int }_{0}^{L}\left[{\left(\frac{\partial w}{\partial x}\right)}^{2}dx\right]\frac{{\partial }^{2}w}{\partial {x}^{2}}$$
(17)

Neglecting the Poisson effect in the Eq. 17, the equation of motion of a beam is derived as:

$$\left(EI+\mu A{l}^{2}\right)\frac{{\partial }^{4}w}{\partial {x}^{4}}+\rho A\frac{{\partial }^{2}w}{\partial {t}^{2}}=\frac{EA}{2L}{\int }_{0}^{L}\left[{\left(\frac{\partial w}{\partial x}\right)}^{2}dx\right]\frac{{\partial }^{2}w}{\partial {x}^{2}}$$
(18)

In the classical beam model, beam deflection is associated with material parameters such as ρA, EA and EI. In the beam model where the size effect is included, it is related to \(\mu A{l}^{2}\). In modified couple stress theory, besides the classical beam parameters, additional internal material coefficient parameter (l) comes. This parameter allows us to analyze the size effect.

The boundary conditions at the ends are given in Fig. 1 for each case. Dimensional form of boundary conditions for simply supported (SS), clamped–clamped (CC), clamped- simple (CS) and clamped-free (CF) beams at the both ends (x = 0 and x = L) respectively, can be obtained as.

\(w=0 or \frac{{\partial }^{2}w}{\partial {x}^{2}}=0 at x=0 and x=L\) for SS beam

$$w=0\, or\, \frac{\partial w}{\partial x}=0\, at\, \,x=0\,\, and\, \,x=L\, \,for\, \,CC\, beam$$
(19)

\(w=0 \,or\, \frac{\partial w}{\partial x}=0\, at\, x=0 \,and\, w=0 \,or\, \frac{{\partial }^{2}w}{\partial {x}^{2}}\, at\, x=L\) for CS beam.

\(w=0 \,or \,\frac{\partial w}{\partial x}=0 \,at\, x=0 \,and\, \frac{{\partial }^{2}w}{\partial {x}^{2}} \,\,or \,\,{\left(\mu Al\right)}^{2}\frac{{\partial }^{3}w}{\partial {x}^{3}}-N\frac{\partial w}{\partial x}at\, \,x=L\) for CF beam.

The following dimensionless quantities are expressed because of the independent of geometrical properties and beam material as follows

$$\overline{x} = \frac{x}{L},\begin{array}{*{20}c} {} \\ \end{array} \,\overline{w} = \frac{w}{L},\begin{array}{*{20}c} {} \\ \end{array} \overline{t} = \beta t,\,\begin{array}{*{20}c} {} \\ \end{array} \beta = \frac{t}{{L^{2} }}\sqrt {\frac{EI}{{\rho A}}} ,\,\begin{array}{*{20}c} {} \\ \end{array} \xi = \frac{h}{l},\begin{array}{*{20}c} {} \\ \end{array} \eta = \frac{6(1 - 2\upsilon )}{{\left( {1 - \upsilon } \right)\xi^{2} }},\begin{array}{*{20}c} {} \\ \end{array} \alpha = \frac{(1 - \upsilon )}{{(1 + \upsilon )(1 - 2\upsilon )}},\begin{array}{*{20}c} {} \\ \end{array} \chi = \frac{{EL^{2} }}{{\mu l^{2} }}$$
(20)

Equation (17) may be written in the dimensionless form

$$(1 + \eta ) + \frac{{\partial^{4} \overline{w}}}{{\partial \overline{x}^{4} }} + \frac{1}{\alpha }\frac{{\partial^{2} \overline{w}}}{{\partial \overline{t}^{2} }} = \frac{1}{2\alpha }\left[ {\int\limits_{0}^{1} {\left( {\frac{{\partial \overline{w}}}{{\partial \overline{x}}}} \right)}^{2} \partial \overline{x}} \right]\frac{{\partial^{2} \overline{w}}}{{\partial \overline{x}^{2} }} + \overline{F}{\text{Cos}} \Omega t - 2\overline{\mu }\frac{{\partial \overline{w}}}{{\partial \overline{t}}}$$
(21)

The non-dimensional form of boundary conditions at the beam ends (at x = 0 and x = 1) can be given in Table 1.

Table 1 Non-dimensional boundary conditions of nanobeam at the beam ends
Full size table

Approximate Solutions

In this section, an approximate analytical solution will be acquired with the assist of the multiple scale methods which has a significant perturbation technique. A straight forward asymptotic expansion can be introduced, so there is no quadratic nonlinearity.

$$\overline{w}(x,t\,;\varepsilon ) = \overline{w}_{0} (x,T_{0} ;T_{1} ) + \varepsilon \overline{w}_{1} (x,T_{0} ;T_{1} )$$
(22)

where T0 = t, T1 = εT and ε«1 are the slow time scale, fast time scale and small book-keeping parameter to denote the deflections, respectively [75, 76]. While the fast time scale characterizes the motions of the unperturbed linear system, and the slow time scale characterizes the modulation of the amplitudes and phases due to nonlinearity. \(\overline{\mu } = \varepsilon \mu \,\,\) and \(\overline{F} = \varepsilon \sqrt \varepsilon \,F\,\,\) the transformation is implemented for the forcing and damping terms on the base of the multiple scale method [75, 76]. In order for damping and forcing terms to occur in the same order as the nonlinear terms, damping and forcing terms are ordered.

$$\frac{\partial }{\partial t} = D_{0} + \varepsilon \,D_{1} ,\,\,\,\frac{{\partial^{2} }}{{\partial t^{2} }} = D_{0}^{2} + 2\varepsilon D_{0} D_{1}$$
(23)

where \(D_{n} = {\partial \mathord{\left/ {\vphantom {\partial {\partial T_{n} }}} \right. \kern-0pt} {\partial T_{n} }}\). After making necessarily expansion, the different order of motion equations and boundary conditions are given in the following form:

Order (1):

$$\left( {1 + \eta } \right)\overline{w}_{0}^{iv} + \frac{1}{\alpha }D_{0}^{2} \overline{w}_{0} = 0$$
(24)

Order (ε):

$$\left( {1 + \eta } \right)\overline{w}_{1}^{iv} + \frac{1}{\alpha }D_{0}^{2} \overline{w}_{1} = - \frac{2}{\alpha }D_{0} D_{1} \overline{w}_{0} + \frac{1}{2\alpha }\left[ {\int\limits_{0}^{1} {\overline{w}^{\prime}_{0} \,^{2} dx} } \right]\overline{w}^{\prime\prime}_{0} + F \cos \Omega {\text{t}} - 2\mu D_{0} \overline{w}_{0}$$
(25)

First order expansion gives to linear problem of the system. Also, linear natural frequencies are obtained by solving this equation. But, ε order expansion gives to nonlinear problem of the system.

Linear Problem

The first order equation given in Eq. (24) forms the linear problem. The solution of the problem is written in the complex form as:

$$\overline{w}_{0} \left( {x,T_{0} ,T_{1} } \right) = A\left( {T_{1} } \right)e^{{i\omega {\text{T}}_{0} }} Y\left( x \right) + \overline{A}\left( {T_{1} } \right)e^{{ - i\omega {\text{T}}_{0} }} \overline{Y}\left( x \right)$$
(26)

A is the complex amplitude. Substituting Eq. (26) into Eq. (24). one obtains:

$$\left( {1 + \eta } \right)Y^{iv} (x) - \frac{{\omega^{2} }}{\alpha }Y(x) = 0$$
(27)

Solution of Y(x) will be in the form:

$$Y(x) = c_{1} e^{{i\beta_{1} x}} + c_{2} e^{{i\beta_{2} x}} + c_{3} e^{{i\beta_{3} x}} + c_{4} e^{{i\beta_{4} x}}$$
(28)

Linear natural frequencies are obtained by applying each boundary condition.

Nonlinear Problem

Corrections to the problem can be given by solving the nonlinear Eq. (25). They will have a solution only if a solvability condition is satisfied as explained in reference [75, 76]. The secular and non-secular terms assuming a solution of the form are separated to find the solvability condition

$$\begin{gathered} \hfill \\ w_{1} \left( {x,T_{0} ,T_{1} } \right) = \phi \left( {x,T_{1} } \right)e^{{i\omega {\text{T}}_{0} }} + cc + \,W\left( {x,T_{0} ,T_{1} } \right) \hfill \\ \end{gathered}$$
(29)

and substituting Eq. (29) into Eq. (25), we eliminate the terms producing secularities. Here \(W\left( {x,T_{0} ,T_{1} } \right)\) stands for the solution related with non-secular terms. One obtains

$$\left( {1 + \eta \,} \right)\phi^{{{\text{iv}}}} - \frac{1}{\alpha }\omega^{2} \phi = - \frac{2}{\alpha }i\omega A^{\prime}Y(x) + \frac{3}{{2}}A^{2} \overline{A} \left( {\int\limits_{{0}}^{1} {Y^{{\prime }{2}} } {\text{dx}}} \right)Y^{\prime\prime} + \frac{{1}}{{2}}{\text{Fe}}^{{{\text{i}}\sigma {\text{T}}_{{1}} \, }} - 2i\mu \omega AY(x) + cc + NST$$
(30)

where NST represents the non-secular terms. Excitation frequency is assumed to close to one of the natural frequencies of the system; that is,

$$\Omega = \omega + \varepsilon \sigma$$
(31)

where σ is a detuning parameter of order 1, the solvability condition for Eqs. (30) and (31) are obtained as follows

$$2i\omega \left( {\frac{1}{\alpha }A^{\prime} + \mu A} \right) + \frac{3}{{{2}\alpha }}A^{2} \overline{A} b^{2} - \frac{{1}}{{2}}{\text{e}}^{{{\text{i}}\sigma {\text{T}}_{{1}} \, }} f = 0$$
(32)

where \(\int\limits_{0}^{1} {Y^{2} } dx = 1, \int\limits_{0}^{1} {Y^{{\prime}{2}} } dx = b, \int\limits_{0}^{1} {FY} dx = f\)

Taking into account the real amplitude a and phase θ, the complex amplitude A in Eq. (26) can be written as the following form

$${\text{A}} = \frac{{1}}{{2}}a{\text{(T}}_{{1}} {{)e}}^{{{{i \theta (T}}_{{1}} {)}}}$$
(33)

Then amplitude and phase modulation equations are

$$\frac{\omega }{\alpha }{\text{a}}\psi^{\prime} = \, \frac{\omega }{\alpha }{\text{a}}\sigma - \frac{3}{{{16}}}{\text{a}}^{{3}} b^{2} + \frac{{1}}{{2}}f\cos \psi$$
(34)
$$\frac{\omega }{\alpha }{{a^{\prime}}} + \mu \omega {\text{a}} = \frac{{1}}{{2}}f\sin \psi$$
(35)

where, \(\psi = \sigma \,T_{1} - \theta\) In steady-state case, Eqs. (34) and (35) will be solved in the following section and variation of nonlinear amplitude with forcing will be discussed.

Numerical Results

Numerical solutions belong to each boundary condition are displayed in this part. The linear fundamental frequencies belong to each boundary conditions will be estimated, and then the non-linear frequencies of these boundary conditions for undamped and free vibrations will also be estimated in the case of the μ = f = σ = 0. one obtains.

$${{a^{\prime}}} = {\text{0 and a}} = {\text{a}}_{{0}} \left( {{\text{constant}}} \right)$$
(36)

from Eq. (36). The steady-state real amplitude is represented by \({\text{a}}_{{0}}\). The frequency of non-linear is

$$\begin{gathered} {\upomega }_{{{\text{n1}}}} = {\upomega } + {{\theta^{\prime}}} = {\upomega } + \frac{3}{{{16}}}\frac{{{\text{a}}_{{0}}^{{2}} b^{2} \alpha }}{\omega } \hfill \\ {\upomega }_{{{\text{n1}}}} = {\upomega } + {\text{a}}_{{0}}^{{2}} \lambda \hfill \\ \end{gathered}$$
(37)

where \({\uplambda } = \frac{3}{{{16}}}\frac{{b^{2} \alpha }}{\omega }\) is the nonlinear correction terms.

At the steady state, \({{a^{\prime}}} = 0,\,\,\,\,\,\,\,\psi^{\prime} = 0\) become zero. The detuning parameter of frequency is as follows

$$\sigma = {\text{a}}^{{2}} \lambda \mp \frac{1}{\alpha }\sqrt {\frac{{f^{2} }}{{4\omega^{2} {\text{a}}^{{2}} }} - \mu^{2} }$$
(38)

Simply Supported Nanobeam

The influence of dimensionless material length scale parameter (h/l) on natural frequency is analyzed to take the size-effect due to the couple stress. ξ denotes dimensionless height (i.e., the ratio of beam height to the internal material length scale parameter, h/l). Nanobeam sensitivity is depended on the ξ that informs the nanobeam behavior depended on size. In Table 2, the first three modes are taken into consideration for linear fundamental frequency and nonlinear correction terms. Table 2 lists the dimensionless material length scale parameter ξ and the results for various cases with or without the poisson effect. In that table, dimensionless material length scale parameter can be considered as ξ = 2,4,6,8 and 10, and also Poisson’s ratio as υ = 0, 0.23, 0.38 and 0.45. It is obviously seen in Table 2 that natural frequency of the nanoscale beam is dependent on the ξ value. In non-classical beam theory, when the dimensionless parameter ξ is increased further, it approaches to the natural frequency of the classical beam theory. The natural frequency obtained using MCST is always higher than the frequency of classical beam theory. It is due to the increase in bending rigidity in the non-classical Euler–Bernoulli beam model. It can be concluded that the Poisson's ratio and material length scale parameter have effects to make the beam behave stiffer, and also non-classical beam model obtained by MCST is stiffer than those of classical one. It can be noted that, increasing the ξ value. Poisson’s ratio effect decreases. Taking ξ constant value, the natural frequency at which the Poisson’s ratio is effective is larger than that without the Poisson's ratio effect.

Table 2 Non-dimensional natural frequencies for Case I (simply supported)
Full size table

The characteristic curves of nonlinear vibration frequency versus amplitude of a simply supported nanobeam for cases of including or not including the Poisson effect and under some specific value of the dimensionless material length scale parameter. ξ, are shown in Figs. 2, 3, 4, 5, in which, zero amplitude indicates the natural frequencies given in Table 2. In Figs. 2, 3, 4, 5, the nonlinear frequency versus amplitude curves are drawn for the five different dimensionless parameter (i.e., ξ = 2,4,6,8 and 10) and four different Poisson ratio (i.e., υ = 0.0, 0.23, 0.38 and 0.45) for the first mode, respectively. As it is seen that, for a given value ξ, the nonlinear frequency of nanobeam increases with the increasing in amplitude, and vice versa. It can be inferred that, the vibration of nanobeam was found to have a hardening type behavior at all. Nanobeam with the Poisson effect has the higher nonlinear frequencies than without Poisson effect.

Fig. 2
figure 2

Nonlinear natural frequency versus amplitude change of simply supported nanobeam with different dimensionless length scale parameter, ξ for the first mode and υ = 0.0 a without Poisson effect b with Poisson effect

Full size image
Fig. 3
figure 3

Nonlinear natural frequency versus amplitude change of simply supported nanobeam with different dimensionless length scale parameter, ξ for the first mode and υ = 0.23 a without Poisson effect b with Poisson effect

Full size image
Fig. 4
figure 4

Nonlinear natural frequency versus amplitude change of simply supported nanobeam with different dimensionless length scale parameter, ξ for the first mode and υ = 0.38 a without Poisson effect b with Poisson effect

Full size image
Fig. 5
figure 5

Nonlinear natural requency versus amplitude change of simply supported nanobeam with different dimensionless length scale parameter, ξ for the first mode and υ = 0.45 a without Poisson effect b with Poisson effect

Full size image

The frequency response curves of the nanobeam are constructed in Figs. 6, 7, 8, 9, 10 for examining the effect of each parameter in the equation of motion. In these figures, the detuning parameter σ shows the nearness of the external excitation frequency to the natural frequency of the system. Some figures are plotted using Eq. (38) assuming f = 1 and damping coefficient μ = 0.1. Figures 6, 7, 8, 9 show the frequency response curves of the simply supported nanobeam for the first mode for different values of dimensionless material length scale parameters ξ represented on the curve and for four values of Poisson ratio (i.e., υ = 0.0, 0.23, 0.38 and 0.45), respectively. Moreover, nanobeam with or without the poisson effect are shown in these figures. It is seen that. the dimensionless parameter ξ effect on the frequency response curves for both with or without the Poisson effect. In addition, Figs. 6, 7, 8, 9 show that higher values of ξ. the higher values of steady state amplitude of responses for both including or not including the Poisson effect. In Fig. 10, shows frequency response curves of the first three modes of nanobeam including Poisson effect with υ = 0.38. All the system behavior shown in Figs. 6, 7, 8, 9, 10 are of hardening type. The bending of the frequency response to the right is defined as a hardening nonlinearity and to the left as a softening nonlinearity. More specifically, hardening and softening nonlinearity have two limit point bifurcations. For the first, it jumps from the lower amplitude to the higher one, for the second, the jump phenomenon is the vice-versa.

Fig. 6
figure 6

Frequency–response curves for the first modes of SS nanobeam with υ = 0 a without poisson effect b with poisson effect

Full size image
Fig. 7
figure 7

Frequency–response curves for the first modes of SS nanobeam with υ = 0.23 a without poisson effect b with poisson effect

Full size image
Fig. 8
figure 8

Frequency–response curves for the first modes of SS nanobeam with υ = 0.38 a without poisson effect b with poisson effect

Full size image
Fig. 9
figure 9

Frequency–response curves for the first modes of SS nanobeam with υ = 0.45 a without poisson effect b with poisson effect

Full size image
Fig. 10
figure 10

Frequency–response curves for the SS nanobeam with poisson effect υ = 0.38 a first mode b second mode c third mode

Full size image

Clamped Nanobeam

The linear natural frequencies and the nonlinear correction term obtained for the clamped nanobeam for the first three modes are displayed in Table 3. It is seen in Table 3 that clamped nanobeam linear frequency values are generally close agreement to the simply supported nanobeam. Hovewer, fundamental frequencies and correction term for the clamped nanobeam is higher than the simply supported nanobeam. Because of the reason is that clamped nanobeam type boundary condition rises the nanobeam stiffness.

Table 3 Non-dimensional natural frequencies for Case II (clamped–clamped)
Full size table

Figures 11, 1213, 14 illustrate the nonlinear natural frequency (ωnl) versus amplitude (a) curves of clamped nanobeam considering five distinct dimensionless material length scale parameter values, ξ. This frequency-amplitude graph is a representative properties of nonlinear systems. In linear analysis, the fundamental frequency of any mode is always constant, but in nonlinear analysis, nonlinear frequencies depend on the amplitude. Figures 11–14 demonstrate the effect of Poisson ratio, v, and dimensionless size dependent parameter, ξ, on the first mode of CC nanobeams including or not including the Poisson effect. Examining Figs. 11, 12, 13, 14, it may be inferred that hardening type nonlinearity can be seen at all the graphs.

Fig. 11
figure 11

Nonlinear natural frequency versus amplitude change of CC nanobeam with different dimensionless length scale parameter, ξ for the first mode and υ = 0.0 a without poisson effect b with poisson effect

Full size image
Fig. 12
figure 12

Nonlinear natural frequency versus amplitude change of CC nanobeam with different dimensionless length scale parameter, ξ for the first mode and υ = 0.23 a without poisson effect b with poisson effect

Full size image
Fig. 13
figure 13

Nonlinear natural frequency versus amplitude change of CC nanobeam with different dimensionless length scale parameter, ξ for the first mode and υ = 0.38 a without poisson effect b with poisson effect

Full size image
Fig. 14
figure 14

Nonlinear natural frequency versus amplitude change of CC nanobeam with different dimensionless length scale parameter, ξ for the first mode and υ = 0.45 a without poisson effect b with poisson effect

Full size image

Fig. 15, 16, 17, 18, 19 display the nonlinear frequency response curves in which amplitude, a. versus detuning parameter, σ. Hardening behaviour phenomenon is defined where the maximum amplitudes are obtained, the detuning parameter is higher than zero (σ > 0). In Fig. 15, 16, 17, 18 frequency–response curve is given four different Poisson ratio (υ) which are 0, 0.23, 0.38 and 0.45, respectively. Fig. 15, 16, 17, 18 display that unstable region has a wider area at high dimensionless size dependent parameter (ξ). Furthermore, as the ξ value increases, the steady state amplitude of the first mode of the beam increases. The frequency response curves are generated in Fig. 19 for CC nanobeam with υ = 0.38 at first three modes for different dimensionless size dependent parameter values represented in the figure.

Fig. 15
figure 15

Frequency–response curves for the first modes of CC nanobeam with υ = 0 a without poisson effect b with poisson effect

Full size image
Fig. 16
figure 16

Frequency–response curves for the first modes of CC nanobeam with υ = 0.23 a without poisson effect b with poisson effect

Full size image
Fig. 17
figure 17

Frequency–response curves for the first modes of CC nanobeam with υ = 0.38 a without poisson effect b with poisson effect

Full size image
Fig. 18
figure 18

Frequency–response curves for the first modes of CC nanobeam with υ = 0.45 a without poisson effect b with poisson effect

Full size image
Fig. 19
figure 19

Frequency–response curves for the CC nanobeam with poisson effect υ = 0.38 a first mode b second mode c third mode

Full size image

Clamped- Simple Nanobeam

The next data set in this boundary condition is presented in Table 4. Linear natural frequencies are obtained by using multiple scale method. Examining the data given in Table 4, it is seen that it is similar tendency to the table in other boundary conditions. Linear frequency values incluiding or not incluiding the Poisson effect were calculated for each Poisson ratio. The data given in table shows that the natural frequencies are influenced by the increase of the Poisson ratio υ, as its effect largely in including the Poisson effect. Furthermore, an increase of the dimensionless size dependent parameter ξ, results in an decrease of the natural frequencies.

Table 4 Non-dimensional natural frequencies for Case III (Clamped-simple)
Full size table

Figures 20, 21, 22, 23 is plotted for the typical relationship of the fundamental nonlinear vibration frequency (ωnl) versus amplitude (a) of a nanobeam for different values of dimensionless length scale parameter (ξ). Obviously, the zero value of the amplitude represents the natural linear frequency of the nanobeam listed in Table 4. It is seen that the frequency ωnl is dimensionless size dependent and the nanobeam displays a typical hardening spring behaviour with all boundary conditions mentioned in this study. Also, the nonlinear frequencies obtained by the dimensionless size dependent nanobeam model are higher than those by the classical beam model. In other words, the MCST models the nanobeam stiffer than does the classical beam theory. The effect of the dimensionless length scale parameter of ξ on frequency is noticeable for small values of ξ, but less noticeable or even insignificant for higher ones, fixed all other parameters. Comparing the all of the boundary conditions which are simply supported, clamped and clamped-simple nanobeam, clamped nanobeam frequencies are larger than those of the other boundary conditions. Because clamped type nanobeam is of a higher stiffness than that of the other boundary conditions.

Fig. 20
figure 20

Nonlinear natural frequency versus amplitude change of SC nanobeam with different dimensionless length scale parameter, ξ for the first mode and υ = 0.0 a without poisson effect b with poisson effect

Full size image
Fig. 21
figure 21

Nonlinear natural frequency versus amplitude change of SC nanobeam with different dimensionless length scale parameter, ξ for the first mode and υ = 0.23 a without poisson effect b with poisson effect

Full size image
Fig. 22
figure 22

Nonlinear natural frequency versus amplitude change of SC nanobeam with different dimensionless length scale parameter, ξ for the first mode and υ = 0.38 a without poisson effect b with poisson effect

Full size image
Fig. 23
figure 23

Nonlinear natural frequency versus amplitude change of SC nanobeam with different dimensionless length scale parameter, ξ for the first mode and υ = 0.45 a without poisson effect b with poisson effect

Full size image

Figures 24, 25, 26, 27 represent the frequency response curves for the first mode at different Poisson ratio. It is obviously seen from these figures that frequency response curves for CS nanobeam is generally hardening type behaviour (bend to the right). As shown in Figs. 24, 25, 26, due to increased value of ξ, the steady state amplitude of the nanobeam increase. More specifically, it can be concluded that the MCST predicts the weaker nonlinear behaviour compared to the classical theory. It can also be observed that the nonlinearity of the system increases with increasing ξ. These figures show that there is a noticeable hardening response in the frequency response curve as the dimensionless length scale parameter ξ increases. The studies indicate that this effect is primarily caused by a decrease in the linear frequency. As a result, the nonlinearity of the system increase with increasing ξ (Fig. 28).

Fig. 24
figure 24

Frequency–response curves for the first modes of SC nanobeam with υ = 0.0 a without poisson effect b with poisson effect

Full size image
Fig. 25
figure 25

Frequency–response curves for the first modes of SC nanobeam with υ = 0.23 a without poisson effect b with poisson effect

Full size image
Fig. 26
figure 26

Frequency–response curves for the first modes of SC nanobeam with υ = 0.38 a without poisson effect b with poisson effect

Full size image
Fig. 27
figure 27

Frequency–response curves for the first modes of SC nanobeam with υ = 0.45 a without poisson effect b with poisson effect

Full size image
Fig. 28
figure 28

Frequency–response curves for the SC nanobeam with poisson effect υ = 0.38 a first mode b second mode c third mode

Full size image

Clamped-Free Nanobeam

In the same way, natural frequency for the clamped-free nanobeam is shown in Table 5. The approximate analytical solutions obtained from the multiple scale methods. Linear frequency values incluiding or not incluiding the Poisson effect were calculated for each Poisson ratio. It is observed that constant material length scale parameter leads to considerable errors in the predicted dimensionless frequencies of nanobeams. As the material length scale parameter increases, the predicted frequencies significantly increase and this effect being more remarkable at low values of h/l. Furthermore, for all types of boundary conditions, it is noticeable that natural frequencies are influed by incerase of the Poisson ratio υ, as its effect largely in including the Poisson effect.

The variation of the nonlinear frequency (ωnl) with the amplitude (a) of a nanobeam with and without the Poisson effect for various values of dimensionless length scale parameter (ξ) are shown in Figs. 29, 30, 31, 32 in order to investigate the size-dependent nonlinear vibration. In these figures, in which, amplitudes a = 0 indicates the natural frequencies of the nanobeams, the corresponding values have already been listed in Table 5. It is observed that the nonlinear frequencies increase with a decrease in the ξ value. Furthermore a hardening behavior can be observed in Figs. 29, 30, 31, 32, because the nonlinear frequency increases as the amplitude increases and vice versa. In addition,it is observed that the nonlinear frequencies of the size-dependent beam model are larger than those of the classical beam model, the MCST models the beams stiffer than does the classical beam theory.

Table 5 Non-dimensional natural frequencies for Case IV (Clamped-free)
Full size table
Fig. 29
figure 29

Nonlinear natural frequency versus amplitude change of CF nanobeam with different dimensionless length scale parameter, ξ for the first mode and υ = 0.0 a without poisson effect b with poisson effect

Full size image
Fig. 30
figure 30

Nonlinear natural frequency versus amplitude change of CF nanobeam with different dimensionless length scale parameter, ξ for the first mode and υ = 0.23 a without poisson effect b with poisson effect

Full size image
Fig. 31
figure 31

Nonlinear natural frequency versus amplitude change of CF nanobeam with different dimensionless length scale parameter, ξ for the first mode and υ = 0.38 a without poisson effect b with poisson effect

Full size image
Fig. 32
figure 32

Nonlinear natural frequency versus amplitude change of CF nanobeam with different dimensionless length scale parameter, ξ for the first mode and υ = 0.45 a without poisson effect b with poisson effect

Full size image

Frequency response curves are presented in Figs. 33, 34, 35, 36, 37 for the first mode at different values of the Poisson ratio (υ) which are 0, 0.23, 0.38 and 0.45, respectively. In these figures, nonlinearity is actually observed. The steady-state amplitude of the curve is observed higher for the high size effect in Figs. 33, 34, 35, 36. The hardening behavior and the steady-state amplitude decrease with the small dimensionless size dependent parameter in Figs. 33, 34, 35, 36.

Fig. 33
figure 33

Frequency–response curves for the first modes of CF nanobeam with υ = 0.0, a without poisson effect b with poisson effect

Full size image
Fig. 34
figure 34

Frequency–response curves for the first modes of CF nanobeam with υ = 0.23, a without poisson effect b with poisson effect

Full size image
Fig. 35
figure 35

Frequency–response curves for the first modes of CF nanobeam with υ = 0.38, a without poisson effect b with poisson effect

Full size image
Fig. 36
figure 36

Frequency–response curves for the first modes of CF nanobeam with υ = 0.45, a without poisson effect b with poisson effect

Full size image
Fig. 37
figure 37

Frequency–response curves for the CF nanobeam with poison effect υ = 0.38, a first mode b second mode c third mode

Full size image

Validation Study

In order to verify the proposed solution method, the following linear cases are compared with the studies available in the literature. So, the current method is validated for various of dimensionless length scale parameter in linear natural frequencies with and without the Poisson effect. Numerical results of linear natural frequencies of simply supported nanobeam for various cases of including or not including the Poisson effect are listed in Table 6, and also compared with the numerical results obtained in Refs. [34] and [16]. The present results are in good agreement with the results in the literature.

Table 6 Comparison of the non-dimensional natural frequencies of a beam with υ = 0.38
Full size table

Conclusions

The nonlinear size dependent vibration of the nanobeam with simply supported, clamped supported, clamped simple and clamped free boundary conditions have been investigated numerically. The nanobeam was modelled based on the modified couple stress theory through use of Euler–Bernoulli beam theory. Vibration of nanobeam by considering the effect of the ratio of beam height to the internal material length scale parameter, h/l and with and without the Poisson effect are graphically presented and tabulated. The equation of motion and boundary conditions were derived by means of Hamilton’s principle for the nanobeam. These equations were solved by means of a multiple scale method so as to obtain the natural fundamental frequencies and the nonlinear response of the system. As increasing the dimensionless length scale parameter ξ, linear frequencies decrease. As it increases more, the frequency values get closer to the classical beam value. Moreover, the size effect is significant for small values of ξ. Therefore, considering the size effect is an important parameter in the vibration analysis of nanostructures. Results revealed that increasing the ξ value. Poisson’s ratio effect decreases. Taking ξ constant value, the natural frequency at which the Poisson’s ratio is effective is larger than that without the Poisson's ratio effect. The fundamental frequencies and correction term for the clamped nanobeam is higher than the simply supported, clamped simply and clamped free boundary conditions, respectively. Because of the reason is that, clamped nanobeam type boundary condition rises the nanobeam stiffness due to increase of number of prescribed kinematic boundary condition.