Introduction

Researchers’ interest has recently been drawn to study the problem of a rigid body (RB) in space. The reason is due to the diversity of its engineering, mechanical, and physics applications in daily life. Additionally, a great deal of scientific research has been done to examine the solutions to this problem. This problem demands complicated mathematical techniques because it is controlled by a nonlinear system of DEs besides three first integrals [1, 2]. The key challenge for researchers today is obtaining the full solution to this issue due to the difficulty of obtaining a general added fourth integral. This integral has been achieved for several special cases such as the cases of Euler, Lagrange, Kowalevski, Joukovsky, Volterra, Goryachev–Chaplygin, Kowalevski–Yehia’s case, and others. In these scenarios, both the location of the body's center of mass and the magnitudes of the main moments of inertia are restricted. For more integrable scenarios, check out [2].

Since it is difficult or almost impossible, so far, to obtain the fourth integral in its full generality, attention has been directed toward the approximate solutions to this issue using the perturbation techniques [3,4,5,6] such as the approaches of Krylov–Bogoliubov–Mitropolski, multiple scales (AMS), averaging (AA), APSP, and others. These methods allow many researchers to obtain approximate solutions with great accuracy for the RB motion under the influence of different fields and moments.

The Krylov–Bogoliubov–Mitropolski is utilized in [7,8,9,10] to gain the approximate solutions of the rotatory motion of RB under the impact of a uniform gravitational field [7]. The obtained outcomes were generalized in [8] and [9] when the body is influenced by a GM and a Newtonian field of force, respectively. In [10], the authors constricted the body's motion such that the body’s inertia ellipsoid is close to its inertia rotation. It should be noticed that the established solutions in [7] feature singular points when the body’s frequency has integer data or their inverses, while the corresponding ones in [8,9,10] do not have any singularities. The reason is due to that the authors of [7, 8] used Amer’s frequency which is dependent on the GM.

The AMS is used in a wide range of research related to the planar motion of a RB pendulum, e.g., [11,12,13,14,15] when its suspension is fixed [11], moves in a route of Lissajous curve [12], and moves on an elliptic route [13]. The motion’s regulating systems were obtained using Lagrange’s equations and solved according to the AMS procedure. The gained outcomes are graphed to show how different parameters affect the studied motion. Some of the resonance scenarios are grouped and examined in view of the obtained solvability criteria. The stability and instability criteria of Routh–Hurwitz [14] are used to examine the arisen fixed point. The numerical solutions of a RB pendulum are investigated in [15] near the equilibrium’s location. The motion of a triple RB pendulum with a fixed pivot point was studied in [16, 17] numerically and experimentally. The bifurcation and stability analysis, as well as numerical computing of a dynamical model with limiters rigid motion, are studied in [16]. In [17], it is demonstrated that the numerical and experimental results agree well for the motion of the same model.

The AA has been utilized frequently over the previous four decades to obtain solutions for the spinning motion of a symmetric RB, see [18,19,20,21,22,23]. This motion was investigated when the body is exposed to three different criteria: a uniform field of gravity, a NFF, and the existence of the GM, as studied respectively, in [18,19,20,21], and [22, 23]. The authors have taken into their consideration the impact of the perturbing moments on the body’s motion. The fundamental equation of the body's angular momentum is used to create the guiding equations of motion (EOM), in which a small parameter is inserted according to some applied hypothesis. The proper solutions of the AA systems of the corresponding ones of the EOM are obtained. In [22], it is considered that the inertia’s ellipsoid and rotations of the body are close to each other, in addition to the action of the electromagnetic field (EMF) on the body. The extension of this work is examined in [23], where the EOM are numerically examined by converting them to a system of two second-order DEs. The AA regulating system in [39] is solved numerically when the conditions of Lagrange's gyroscope as well as some initial conditions of the angle of nutation are considered. The attained outcomes in [24] have been generalized in [25] and [26], when the applied perturbing moments slightly change over time and the body is exposed to external forces and moments, respectively. For additional details on how AA might be applied to address the RB's problems, see [27].

The APSP, on the other hand, has been widely used in several studies e.g., [28,29,30,31,32,33,34,35,36,37,38,39,40] to obtain approximate solutions of a RB, whether the movement is considered under the influence of a gravitational field or a NFF, or in the presence of an EMF, or in the existence of the GM, or under the influence of a group of these forces and moments, or even under the influence of all of them. In [28, 29], the RB movement is examined in a field of uniform gravity, while the influence of the NFF on this motion is investigated in [30]. It must be noted that the obtained solutions comprised separate singular points when the system's frequency had integer values or multiple inverses. These singularities have been treated forever in [31] when the motion is impacted only by the third component of the GM in addition to the NFF. In [32] and [33], the conditions of Euler–Poinsot and Kovalevskaya, respectively, were applied to the RB motion taking into account the influence of the entire GM. The achieved solutions are completely free of singularities at all for any value of the system's frequency. Recently, this methodology is applied in [34] to investigate the movement of the RB in accordance with Bobylev–Steklov requirements, in which the body was being affected by the GM, EMF, and NFF. In [35], the authors proposed that the body’s center of mass is somewhat offset from its axis of dynamical symmetry when it is acted by the EMF and the GM. The gained results are considered a generic form of those which were obtained in [36] and [37]. For more information about how the strategy of this approach can be applied to address various SB's problems, see [38] and [39].

The vibrations of the linear time-varying systems using some perturbation techniques have been studied in [40]. Based on analytical approximations of the relevant ordinary linear time-varying DEs, three conventional perturbation methods, namely the AA, harmonic balancing method, and AMS with linear scales have been employed. The accuracy of these techniques has been demonstrated by the study of vibrations with constant and increasing deployment velocities. Also, the dynamic properties of a deployable or retractable damped cantilever beam are examined experimentally and theoretically in [41]. Both the period decrement approach and the enveloped fitting method are used to calculate the time-varying damping as a function of the beam length.

The analytic approximate solutions for the governing equations for a restricted gyrostatic system are presented in [42] and [43] utilizing the large parameter technique. Some applications for the RB motion in a space have been examined in [44] when the body is supposed to be restricted under the influence gravity force, NFF, and GM. The stability is investigated for a free rotation of one-rotor gyrostat with the existence of internal moment in [45]. In an analogy way to Euler's case, the lowest time of reducing rotation for a free dynamically asymmetric RB is examined in [46]. This body is affected by a one component of the GM and a viscous friction torque. The rotational law of optimal control for the sluggish body is defined, and the corresponding time and phase routes are assessed. The generalization of this problem is achieved in [47] when the body is acted by a full GM due to the action of three rotors, a small slowing viscous friction torque, and a minor control torque with close but unequal coefficients. An ideal decelerating law for the body's rotation has been developed to control the body's motion.

In this study, the movement of a RB around a fixed point that is near Lagrange’s gyroscope, under the impact of the NFF and the GM is investigated. The regulating EOM are derived in light of the principal angular momentum equation of the RB motion. This system is reduced via the APSP to one of two acceptable quasi-linear DEs from second order in terms of two variables only, and only one integral. The latter system is solved analytically, and therefore the other variables are achieved. The obtained outcomes are graphed according to various values of the body’s parameters to reveal the impact of these parameters on the motion’s behavior. Angles of Euler are derived to determine the orientation of the body at any instant. Furthermore, the plots of the phase plane are drawn to discuss the dynamical motion's stability. This study's significance stems from its wide-ranging applicability in life as well as in engineering applications where the gyroscopic theory has been used to establish the orientation and maintain the stability of various vehicles such as submarines, spaceships, racing cars, and airplanes.

Problem’s Depiction

This section presents a RB with mass \(M\) rotating in space around a specified fixed point \(O\) in the body, wherein it is regarded as an original of two Cartesian systems. The first one \(O\xi \eta \zeta\) is assumed to be fixed in space while the second frame \(Oxyz\) is fixed in the body’s structure and rotates with it and whose axes are running parallel to the inertia main axes. It should be mentioned that a quick rotation of the body around its \(z\)-axis has been considered to generate an angle \(\theta_{0} \approx {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}\) with \(\zeta\)-axis. The body’s movement is controlled by an NFF that emerges from the center \(O_{1}\) at a significant distance \(R\) from \(O\), in addition to the impact of the GM \(\underline{\ell } \equiv (\ell_{x} ,\;0,\;\ell_{z} )\) about the main inertia’s axes, see Fig. 1.

Fig. 1
figure 1

Displays the problem's dynamic design

Full size image

Let \(I \equiv (A^{0} (1 + \varepsilon \delta_{1} ),\;A^{0} (1 + \varepsilon \delta_{2} ),\;C)\) be the inertia moments tensor, where \(\delta_{j} \,(j = 1,2)\) are dimensionless values of order unity, \(A^{0}\) stands for the unique value of inertia moments, \(C \ne A^{0}\) is the value of the inertia moment about \(z\)-axis, and \(\varepsilon\) is a tiny parameter. Moreover, \(\underline{{r_{G} }} = (x_{0} ,y_{0} ,z_{0} )\) is the coordinates of the body's center of mass, \(\underline{\Lambda } = (\gamma ,\;\gamma^{\prime},\;\gamma^{\prime\prime})\) denotes the cosine directions of the unit vector along \(\zeta\)-axis, \(\underline{\omega } \equiv (p,\;q,r)\) is the RB’s angular velocity along the principal axes \((Ox,Oy,Oz)\), and \(g\) is the gravitational acceleration. Therefore, the regulating system of the EOM can be constructed according to the principal equation of the body’s angular momentum \(\underline{h}_{O}\) and the first time derivative of the unit vector \(\underline{\Lambda }\), as shown below

$$\frac{{d\underline{h}_{O} }}{dt} + \underline{\omega } \wedge (\underline{h}_{O} + \underline{\ell } ) = \underline{G}_{O} ,\,\,\,\,\,\frac{{d\underline{\Lambda } }}{dt} = \underline{\Lambda } \wedge \underline{\omega } .$$
(1)

where \(\underline{G}_{O}\) is an external force given by \(\underline{G}_{O} = Mg(\underline{{r_{G} }} \wedge \underline{\Lambda } ) + N(I\underline{\Lambda } \wedge \underline{\Lambda } )\) and \(N = {{3\lambda } \mathord{\left/ {\vphantom {{3\lambda } {R^{3} }}} \right. \kern-0pt} {R^{3} }},\,\,\lambda\) is the coefficient of the attracting center \(O_{1}\).

The corresponding form to system of Eq. (1) is shown below

$$\begin{gathered} A^{0} (1 + \varepsilon \;\delta_{1} ){\kern 1pt} \,\frac{dp}{{dt}} + [C{\kern 1pt} - A^{0} (1 + \varepsilon \;\delta_{2} )]\,q\,{\kern 1pt} r + q{\kern 1pt} \ell_{z} = Mg(y_{0} {\kern 1pt} \gamma^{\prime\prime} - z_{0} \gamma^{\prime}) + N[C{\kern 1pt} - A^{0} (1 + \varepsilon \;\delta_{2} )]\,\gamma^{\prime}\gamma^{\prime\prime}, \hfill \\ A^{0} (1 + \varepsilon \;\delta_{2} ){\kern 1pt} \,\frac{dq}{{dt}} + [A^{0} (1 + \varepsilon \;\delta_{1} ) - C]\,rp + r\ell_{x} - p\ell_{z} = Mg\,(z_{0} {\kern 1pt} \gamma - x_{0} \gamma^{\prime\prime}) + N[A^{0} (1 + \varepsilon \;\delta_{1} ) - C]\,\gamma \gamma^{\prime\prime}{\kern 1pt} , \hfill \\ C\frac{dr}{{dt}} + A^{0} \varepsilon \;(\delta_{2} - \delta_{1} ){\kern 1pt} {\kern 1pt} p\,q - {\kern 1pt} q{\kern 1pt} \ell_{x} = Mg\,(x_{0} {\kern 1pt} \gamma^{\prime} - y_{0} \gamma ) + NA^{0} \varepsilon \;(\delta_{2} - \delta_{1} )\,\gamma \gamma^{\prime}, \hfill \\ \frac{d\gamma }{{dt}} = {\kern 1pt} r\,\gamma^{\prime} - q{\kern 1pt} {\kern 1pt} \gamma^{\prime\prime},\frac{{d\gamma^{\prime}}}{dt} = p\,\gamma^{\prime\prime} - r\gamma ,\frac{{d\gamma^{\prime\prime}}}{dt} = q\,\gamma - p\gamma^{\prime}, \hfill \\ \end{gathered}$$
(2)

Based on the system of Eq. (2), the available first integrals have the forms

$$\begin{gathered} A^{0} (1 + \varepsilon \;\delta _{1} ) \,p^{2} + A^{0} (1 + \varepsilon \;\delta _{2} ) \,q^{2} + C r^{2} - 2Mg(x_{0} \gamma + y_{0} \gamma^{\prime} + z_{0} \gamma ^{\prime\prime}) \hfill \\ + N[A^{0} (1 + \varepsilon \;\delta _{1} )\,\gamma ^{2} + A^{0} (1 + \varepsilon \;\delta _{2} )\,\gamma ^{{{\prime}2}} + C\gamma ^{{{\prime\prime}2}} ] = A^{0} (1 + \varepsilon \;\delta _{1} ) \,p_{0}^{2} + A^{0} (1 + \varepsilon \;\delta _{2} ) \,q_{0}^{2} \hfill \\ + Cr_{0}^{2} - 2Mg(x_{0} \gamma _{0} + y_{0} \gamma ^{\prime}_{0} + z_{0} \gamma ^{\prime\prime}_{0} ) + N[A^{0} (1 + \varepsilon \;\delta _{1} )\,\gamma _{0}^{2} + A^{0} (1 + \varepsilon \;\delta _{2} )\,\gamma _{0}^{{{\prime}2}} + C\gamma _{0}^{{''2}} ], \hfill \\ [A^{0} (1 + \varepsilon \;\delta _{1} )\,p + \ell _{x} ]\,\gamma + A^{0} (1 + \varepsilon \;\delta _{2} ) \,q\gamma ^{\prime} + (C r + \ell _{z} )\gamma ^{\prime\prime} = [A^{0} (1 + \varepsilon \;\delta _{1} )\,p_{0} + \ell _{x} ]\,\gamma {}_{0} \hfill \\ + A^{0} (1 + \varepsilon \;\delta _{2} ) \,q_{0} \gamma _{0}^{\prime} + (C r_{0} + \ell _{z} )\,\gamma _{0}^{{\prime\prime}} \hfill \\ \gamma ^{2} + \gamma ^{{\prime2}} + \,\gamma ^{{\prime\prime2}} = 1, \hfill \\ \end{gathered}$$
(3)

where \(p_{0} ,q_{0} ,r_{0} ,\gamma_{0} ,\gamma^{\prime}_{0} ,\) and \(\gamma^{\prime\prime}_{0}\) stand, respectively, for \(p,\;q,\;r,\,\gamma ,\;\gamma^{\prime},\) and \(\gamma^{\prime\prime}\) values at initial time.

To proceed with the body’s dynamical motion, the following presumptions are considered

$$\begin{gathered} c\,\sqrt {\gamma^{\prime\prime}_{0} } \,p_{1} = p\,{\kern 1pt} ,c\,\sqrt {\gamma^{\prime\prime}_{0} } \,q_{1} = q,r_{0} \,r_{1} = r,\gamma^{\prime\prime}_{0} \gamma_{1} = \gamma ,\gamma^{\prime\prime}_{0} \gamma^{\prime}_{1} = \gamma^{\prime},\gamma^{\prime\prime}_{0} \,\gamma^{\prime\prime}_{1} = \gamma^{\prime\prime}, \hfill \\ x_{0} = Lx^{\prime}_{0} \,,y_{0} = Ly^{\prime}_{0} \,,z_{0} = Lz^{\prime}_{0} \,,L = \left| {\underline{{r_{G} }} } \right| = \sqrt {x_{0}^{2} + y_{0}^{2} + z_{0}^{2} } \,,\tau = r_{0} \,t, \hfill \\ k = {{N\,\gamma^{\prime\prime}_{0} } \mathord{\left/ {\vphantom {{N\,\gamma^{\prime\prime}_{0} } {c^{2} }}} \right. \kern-0pt} {c^{2} }},c^{2} = MgL/C\,,\varepsilon = {{c\,\sqrt {\gamma^{\prime\prime}_{0} } } \mathord{\left/ {\vphantom {{c\,\sqrt {\gamma^{\prime\prime}_{0} } } {r_{0} ,\,}}} \right. \kern-0pt} {r_{0} ,\,}}A_{1} = \frac{{C - A^{0} (1 + \varepsilon \;\delta_{2} )}}{{A^{0} (1 + \varepsilon \;\delta_{1} )}}, \hfill \\ B_{1} = \frac{{A^{0} (1 + \varepsilon \;\delta_{1} ) - C}}{{A^{0} (1 + \varepsilon \;\delta_{2} )}},C_{1} = \frac{{A^{0} \varepsilon \,(\delta_{2} - \delta_{1} )}}{C},a = \frac{{A^{0} (1 + \varepsilon \;\delta_{1} )}}{C},b = \frac{{A^{0} (1 + \varepsilon \;\delta_{2} )}}{C}, \hfill \\ A_{0} = (A\,r_{0} )^{ - 1} = [A^{0} (1 + \varepsilon \;\delta_{1} )\,r_{0} ]^{ - 1} ,B_{0} = (B\,r_{0} )^{ - 1} = [A^{0} (1 + \varepsilon \;\delta_{2} )\,r_{0} ]^{ - 1} ,C_{0} = (C\,r_{0} )^{ - 1} . \hfill \\ \end{gathered}$$
(4)

where \(r_{0}\) has been assumed to be high and \((x^{\prime}_{0} ,\,y^{\prime}_{0} ,z^{\prime}_{0} )\) are dimensionless values.

The substitution of the presumptions (4) into the EOM (2) and integrals (3) yields

$$\begin{gathered} \dot{p}_{1} + A_{1} q_{1} r_{1} + A_{0} q_{1} \ell_{z} = \varepsilon [a^{ - 1} (y^{\prime}_{0} \gamma^{\prime\prime}_{1} - z^{\prime}_{0} \gamma^{\prime}_{1} ) + kA_{1} \gamma^{\prime}_{1} \gamma^{\prime\prime}_{1} ]{\kern 1pt} , \hfill \\ \dot{q}_{1} + B_{1} r_{1} p_{1} - B_{0} (p_{1} \ell_{z} - \varepsilon^{ - 1} r_{1} \ell_{x} ) = \varepsilon [b^{ - 1} (z^{\prime}_{0} \gamma_{1} - x^{\prime}_{0} \gamma^{\prime\prime}_{1} ) + kB_{1} \gamma_{1} \gamma^{\prime\prime}_{1} ]\,\,, \hfill \\ \dot{r}_{1} + \varepsilon^{2} C_{1} p_{1} {\kern 1pt} q_{1} \, - \varepsilon \,C_{0} q_{1} \ell_{x} = \varepsilon^{2} (x^{\prime}_{0} \gamma^{\prime}_{1} - y^{\prime}_{0} \gamma_{1} + kC_{1} \gamma_{1} \gamma^{\prime}_{1} ), \hfill \\ \dot{\gamma }_{1} = r_{1} \gamma^{\prime}_{1} - \varepsilon \,q_{1} \gamma^{\prime\prime}_{1} ,\quad \,\,\,\,\,\,\,\,\dot{\gamma }^{\prime}_{1} = \varepsilon \,p_{1} \gamma^{\prime\prime}_{1} - r_{1} \gamma_{1} ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dot{\gamma }^{\prime\prime}_{1} = \varepsilon (\,q_{1} \gamma_{1} - p_{1} \gamma^{\prime}_{1} ), \hfill \\ \end{gathered}$$
(5)

and

$$r_{1}^{2} = 1 + {\kern 1pt} \varepsilon^{2} \,S_{1} ,r_{1} \,\gamma_{1}^{^{\prime\prime}} = 1 + \varepsilon \,S_{2} ,\gamma_{1}^{2} + \gamma_{1}^{^{\prime}2} + \,\gamma_{1}^{^{\prime}2} = (\gamma_{0}^{^{\prime\prime}} )^{ - 2} .$$
(6)

Here, the dots denote the differentiation regarding to \(\tau\) and

$$\begin{aligned}{S_1} = a\,(p_{10}^2 - p_1^2) + b(q_{10}^2 - q_1^2) - 2\,\left[ {{{x^{\prime}}_0}({\gamma _{10}} - {\gamma _1}) + {{y^{\prime}}_0}({{\gamma^ {\prime}}_{10}} - {{\gamma ^{\prime}}_1}) + {{z^{\prime}}_0}(1 - {{\gamma^ {\prime\prime}}_1})} \right]\\ + k[a\,(\gamma _{10}^2 - \gamma _1^2) + b(\gamma _{10}^{{\prime}2} - \gamma _1^{{\prime}2}) + (1 - \gamma _1^{{\prime\prime}2})],\\{S_2} = a({p_{10}}{\gamma _{10}} - {p_1}{\gamma _1}) + b({q_{10}}{{\gamma^ {\prime}}_{10}} - {q_1}{{\gamma ^{\prime}}_1}) + {(cC\,\sqrt {{{\gamma^ {\prime\prime}}_0}} )^{ - 1}}[{\ell _x}({\gamma _{10}} - {\gamma _1}) + {\ell _z}(1 - {{\gamma^ {\prime\prime}}_1})],\end{aligned}$$
(7)

One can display \(S_{1}\) and \(S_{2}\) in expressions of power series of \(\varepsilon\) as follows

$$S_{i} = S_{{i{\kern 1pt} 1}} + 2^{2 - i} {\kern 1pt} {\kern 1pt} \varepsilon \,S_{{i{\kern 1pt} 2}} + \cdots ,(\,i = 1,\;2\,).$$
(8)

where

$$\begin{gathered} S_{11} = a\,(p_{20}^{2} - p_{2}^{2} ) + bX^{2} (\dot{p}_{20}^{2} - \dot{p}_{2}^{2} ) - 2\,x^{\prime}_{0} (\gamma_{20} - \gamma_{2} ) - 2\,y^{\prime}_{0} (\dot{\gamma }_{20} - \dot{\gamma }_{2} ) \hfill \\ \quad \quad \quad + k[a(\gamma_{20}^{2} - \gamma_{2}^{2} ) + b(\dot{\gamma }_{20}^{2} - \dot{\gamma }_{2}^{2} )], \hfill \\ S_{12} = a\,[\lambda \,(p_{20} - p_{2} ) + \lambda_{1} (p_{20} \,\gamma_{20} - p_{2} \,\gamma_{2} )\,] - b\,X^{2} \,[a^{ - 1} y^{\prime}_{0} (\dot{p}_{20} - \dot{p}_{2} ) \hfill \\ \quad \;\;\;\; - \lambda_{2} (\dot{p}_{20} \,\dot{\gamma }_{20} - \dot{p}_{2} \,\dot{\gamma }_{2} )] - x^{\prime}_{0} \,\rho_{1} \,(p_{20} - p_{2} ) - y^{\prime}_{0} \,\rho_{2} \,(\dot{p}_{20} - \dot{p}_{2} ) + (z^{\prime}_{0} - k)S_{21} \hfill \\ \quad \quad + k[a\rho_{1} (p_{20} \,\gamma_{20} - p_{2} \,\gamma_{2} ) + b\,\rho_{2} (\dot{p}_{20} \,\dot{\gamma }_{20} - \dot{p}_{2} \,\dot{\gamma }_{2} )\;], \hfill \\ S_{21} = 2\,(\,p_{20} \,\gamma_{20} - p_{2} \,\gamma_{2} \,) - bX\,[\;(\,\dot{p}_{20} \,\dot{\gamma }_{20} - \dot{p}_{2} \,\dot{\gamma }_{2} ) + y_{1} (\gamma_{20} - \gamma_{2} )], \hfill \\ S_{22} = a[\rho_{1} (p_{20}^{2} - p_{2}^{2} ) + \lambda (\gamma_{20} - \gamma_{2} ) + \lambda_{1} (\gamma_{20}^{2} - \gamma_{2}^{2} )] + b\,[\, - X\rho_{2} (\dot{p}_{20}^{2} - \dot{p}_{2}^{2} ) \hfill \\ \quad \quad \quad + Xa^{ - 1} y^{\prime}_{0} \,(\dot{\gamma }_{20} - \dot{\gamma }_{2} ) - X\lambda_{2} (\dot{\gamma }_{20}^{2} - \dot{\gamma }_{2}^{2} ) + y_{1} \rho_{1} \,(p_{20} - p_{2} ) - y_{3} S_{21} ], \hfill \\ \end{gathered}$$
(9)

where

$$\begin{gathered} X = A_{1}^{ - 1} (1 - A^{ - 1} A_{1}^{ - 1} r_{0}^{ - 1} \ell_{z} ),\,\,\,\,\,\,\,\,\,\lambda = \,x^{\prime}_{0} b^{ - 1} \Omega^{ - 2} \,(\,A_{1} \, + A^{ - 1} \,r_{0}^{ - 1} \ell_{z} \,)\,, \hfill \\ \lambda_{1} = (1 - \Omega^{2} )^{ - 1} \,[z^{\prime}_{0} \,(A_{1} b^{ - 1} - a^{ - 1} ) + k(A_{1} - \omega^{2} )\, + (b^{ - 1} z^{\prime}_{0} \, + kB_{1} )A^{ - 1} r_{0}^{ - 1} \ell_{z} ], \hfill \\ \lambda_{2} = \lambda_{1} + a^{ - 1} z^{\prime}_{0} \, - kA_{1} ,\,\,\,\,\,\,\,\,\,\rho_{1} = (1 - \Omega^{2} )^{ - 1} \,(1 + B_{1} - B^{ - 1} r_{0}^{ - 1} \ell_{z} ), \hfill \\ \rho_{2} = \rho_{1} - X,\,\,\,\,\,\,\,\,\,\Omega^{2} = \omega^{2} + (A_{1} B^{ - 1} - A^{ - 1} B_{1} )r_{0}^{ - 1} \ell_{z} ,\,\,\,\,\,\,\,\,\,\omega^{2} = - A_{1} B_{1} , \hfill \\ \,y_{1} = (cC\sqrt {\gamma^{\prime\prime}_{0} } \,)^{ - 1} \ell_{x} ,\,\,\,\,\,\,\,\,\,\,y_{3} = (cC\sqrt {\gamma^{\prime\prime}_{0} } \,)^{ - 1} \ell_{z} \, \hfill \\ \end{gathered}$$
(10)

The \(z\) and \(x\) axes' positive branches have been chosen in a way that prevents them from forming an obtuse angle with the \(\zeta\)-axis direction, i.e.,

$$\gamma_{0} \ge 0\,,0 < \gamma^{\prime\prime}_{0} < 1.$$
(11)

System’s Reduction Processes

The specific objective of this section is to reduce the equations of system (5) and integrals (6) to another suitable quasi-linear system of two second-order DEs and only one integral. To achieve this goal, \(r_{1}\) and \(\gamma^{\prime\prime}_{1}\) must be rewritten in the following way while taking integrals (6) into account

$$\begin{gathered} r_{1} = 1 + \frac{1}{2}\,{\kern 1pt} \varepsilon^{2} \,S_{11} + \cdots ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \hfill \\ \gamma^{\prime\prime}_{1} = 1 + \varepsilon \,S_{21} + \varepsilon^{2} (\,S_{22} - \frac{1}{2}\,{\kern 1pt} S_{11} \,) + \cdots , \hfill \\ \end{gathered}$$
(12)

In this context, we differentiate the first and fourth Equations in (5) and then using (12) to yield

$$\begin{array}{l} {{\ddot p}_1} + {\Omega ^2}{p_1} = {\varepsilon ^{ - 1}}\,({A_1}{B^{ - 1}}r_0^{ - 1}{\ell _x}) + \varepsilon \,\{ - {C^{ - 1}}{A_1}r_0^{ - 1}{\ell _x}q_1^2 + {A_1}{B^{ - 1}}r_0^{ - 1}{\ell _x}{S_1} + {{z{\prime}}_0}({a^{ - 1}} - {A_1}{b^{ - 1}}){\gamma _1}\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + {A_1}{b^{ - 1}}{{x{\prime}}_0} + k({\omega ^2} - {A_1}){\gamma _1} + [{b^{ - 1}}({{x{\prime}}_0} - {{z'}_0}{\gamma _1}) - k{B_1}{\gamma _1}]{A^{ - 1}}r_0^{ - 1}{\ell _z}\} + {\varepsilon ^2}\{ - {\omega ^2}{p_1}{S_1}\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + {A^{ - 1}}{b^{ - 1}}{{x'}_0}{S_2} + {A_1}{C_1}{p_1}q_1^2 - {A_1}{{x{\prime}}_0}{{\gamma {\prime}}_1}{q_1} + {A_1}{{y'}_0}{q_1}{\gamma _1} + {a^{ - 1}}{{y'}_0}{q_1}{\gamma _1} - {a^{ - 1}}{{y{\prime}}_0}{p_1}{{\gamma {\prime}}_1}\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - {a^{ - 1}}{{z{\prime}}_0}{p_1} + {A_1}k[{p_1}(1 - \gamma _1^{'2}) + {q_1}(1 - {C_1}){\gamma _1}{{\gamma '}_1} - {S_2}(1 + {B_1}){\gamma _1}] + \,\frac{1}{2}r_0^{ - 1}{\ell _z}{p_1}({A^{ - 1}}{B_1}\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - {A_1}{B^{ - 1}})[{S_1} + 2{{z'}_0}(1 - {{\gamma ''}_1}) - k(1 - \gamma _1^{{\prime\prime}2})] + {A^{ - 1}}r_0^{ - 1}{\ell _z}({b^{ - 1}}{{x{\prime}}_0} - k{B_1}{\gamma _1}){S_2}\} + \ldots , \end{array}$$
(13)
$$\begin{array}{l} {{\ddot \gamma }_1} + {\gamma _1} = {B_0}{\ell _x} + \varepsilon \,\,[\;{B_0}{\ell _x}{S_2} + {p_1}(1 + {B_1} - {B_0}{\ell _z}) + {C_0}{{\gamma '}_1}{q_1}{\ell _x}] + {\varepsilon ^2}[(1 + {B_1}){p_1}{S_2}\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - {\gamma _1}{S_1} - {B_0}{p_1}{\ell _z}{S_2} + {p_1}{q_1}{{\gamma {\prime}}_1}(1 - {C_1}) + {{x'}_0}\gamma _1^{{\prime}2} - {{y{\prime}}_0}{\gamma _1}{{\gamma {\prime}}_1} - {{z{\prime}}_0}{b^{ - 1}}{\gamma _1} + {b^{ - 1}}{{x{\prime}}_0}\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - q_1^2{\gamma _1} + k({C_1}\gamma _1^{{\prime}2} - {B_1}){\gamma _1}] + ...., \end{array}$$
(14)

We can infer from a close examination of the two equations above that they have frequencies of \(\Omega\) and 1. Amer's frequency [31] is the name given to the frequency \(\Omega\), and it has a real value. The terms \(r_{0}^{ - 2} ,r_{0}^{ - 3} , \ldots\) can be disregarded because it has been assumed that \(r_{0}\) would have a large value. Therefore, using the formulas in (5) and (12), we may rewrite \(q_{1}\) and \(\gamma^{\prime}_{1}\) as follows

$$\begin{gathered} q_{1} = (A_{1}^{ - 1} r_{1}^{ - 1} - A_{1}^{ - 2} A^{ - 1} r_{0}^{ - 1} r_{1}^{ - 2} \ell_{z} + \; \cdots \;)[\varepsilon a^{ - 1} (y^{\prime}_{0} \gamma^{\prime\prime}_{1} - z^{\prime}_{0} \gamma^{\prime}_{1} + kaA_{1} \gamma^{\prime}_{1} \gamma^{\prime\prime}_{1} ) - \dot{p}_{1} ], \hfill \\ \gamma^{\prime}_{1} = r_{1}^{ - 1} (\,\dot{\gamma }_{1} + \varepsilon \,q_{1} \,\gamma^{\prime\prime}_{1} ). \hfill \\ \end{gathered}$$
(15)

Introducing \(p_{2}\) and \(\gamma_{2}\) as two additional variables

$$p_{2} = p_{1} - \varepsilon \,(\,\lambda + \,\lambda_{1} \,\gamma_{2} ),\quad \,\,\,\,\gamma_{2} = \gamma_{1} - \varepsilon \,\rho_{1} \,p_{2} ,$$
(16)

then we can write \(q_{1}\) and \(\gamma^{\prime}_{1}\) in terms of \(p_{2} ,\gamma_{2} ,\dot{p}_{2}\), and \(\dot{\gamma }_{2}\) as follows

$$\begin{gathered} q_{1} = \, - X\dot{p}_{2} + \varepsilon [X(a^{ - 1} y^{\prime}_{0} - \lambda_{2} \dot{\gamma }_{2} )] + \varepsilon^{2} \{ X[(kA_{1} - a^{ - 1} z^{\prime}_{0} )\rho_{1} + S_{11} ]\dot{p}_{2} \hfill \\ - \frac{1}{2}A_{1}^{ - 1} S_{11} \dot{p}_{2} + XS_{21} (kA_{1} \dot{\gamma }_{2} + a^{ - 1} y^{\prime}_{0} )\} + \ldots , \hfill \\ \gamma^{\prime}_{1} = \dot{\gamma }_{2} + \varepsilon \rho_{2} \dot{p}_{2} + \varepsilon^{2} [X(a^{ - 1} y^{\prime}_{0} - \lambda_{2} \dot{\gamma }_{2} - S_{21} \dot{p}_{2} ) - \frac{1}{2}S_{11} \dot{\gamma }_{2} ] + \ldots , \hfill \\ \end{gathered}$$
(17)

The substitution of (8), (9), (12), (16), and (17) into (13) and (14) produces the following quasi-linear autonomous system with two degrees of freedom and just one integral,

$$\begin{gathered} \ddot{p}_{2} + \Omega^{2} p_{2} = CA_{1} B^{ - 1} y_{1} \, + \varepsilon \,F(p_{2} ,\;\dot{p}_{2} ,\;\gamma_{2} ,\;\dot{\gamma }_{2} ,\;\varepsilon ), \hfill \\ \ddot{\gamma }_{2} + \gamma_{2} = B^{ - 1} r_{0}^{ - 1} \ell_{x} + \varepsilon \,\Phi (p_{2} ,\;\dot{p}_{2} ,\;\gamma_{2} ,\;\dot{\gamma }_{2} ,\;\varepsilon ), \hfill \\ \end{gathered}$$
(18)

and

$$\begin{gathered} \gamma_{2}^{2} + \dot{\gamma }_{2}^{2} + 2\,\varepsilon \,(\rho_{1} \gamma_{2} p_{2} + S_{21} ) + \varepsilon^{2} \{ \rho_{1}^{2} p_{2}^{2} + \rho_{2}^{2} \dot{p}_{2}^{2} + 2\dot{\gamma }_{2} [A_{1}^{ - 1} (a^{ - 1} y^{\prime}_{0} - \lambda_{2} \dot{\gamma }_{2} - \dot{p}_{2} S_{21} ) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \frac{1}{2}S_{11} \dot{\gamma }_{2} ] + S_{21}^{2} + 2\,(\,S_{22} - \frac{1}{2}\,{\kern 1pt} S_{11} \,)\;\} = (\gamma^{\prime\prime}_{0} )^{ - 2} - 1\;. \hfill \\ \end{gathered}$$
(19)

Here

$$\begin{array}{l} F = {F_1} + \varepsilon \,{F_2} + {\varepsilon ^2}\,{F_3} + \cdots ,\Phi = {\Phi _1} + \varepsilon \,{\Phi _2} + {\varepsilon ^2}\,{\Phi _3} + \cdots ,\\ {F_1} = - \,\lambda {B^{ - 1}}r_0^{ - 1}{\ell _x} - {C^{ - 1}}r_0^{ - 1}A_1^{ - 1}{\ell _x}\dot p_2^2 + {A_1}{B^{ - 1}}r_0^{ - 1}{\ell _x}{S_{11}} + {{z'}_0}(\,{a^{ - 1}} - {\kern 1pt} {A_1}{b^{ - 1}}){\gamma _2} + {A_1}{b^{ - 1}}{{x'}_0}\\ \,\,\,\,\,\,\,\,\,\,\, + k({\omega ^2} - {A_1}){\gamma _2} + ({b^{ - 1}}{{x'}_0} - {b^{ - 1}}{{z'}_0}{\gamma _2} - k{B_1}{\gamma _2}){A^{ - 1}}r_0^{ - 1}{\ell _z},\\ {F_2} = {f_2} - {\rho _1}{\lambda _1}(1 - {\Omega ^2}){p_2},{F_3} = {f_3} - {\lambda _1}\,{\varphi _2} - {\rho _1}\lambda {\lambda _1}(1 - {\Omega ^2}) - {\rho _1}\lambda _1^2{\gamma _2}(1 - {\Omega ^2}),\\ {\Phi _1} = {B^{ - 1}}\,r_0^{ - 1}{\ell _x}{S_{21}} - {C^{ - 1}}\,r_0^{ - 1}{\ell _x}\,{{\dot \gamma }_2}A_1^{ - 1}{{\dot p}_2},\\ {\Phi _2} = {\rho _1}(1 - {\Omega ^2})(\lambda + {\lambda _1}{\gamma _2}) + {\phi _2},{\Phi _3} = {\phi _3} - {\rho _1}{f_2} - \rho _1^2{\lambda _1}(1 - {\Omega ^2}){p_2},\\ {f_2} = 2{A_1}{B^{ - 1}}r_0^{ - 1}{\ell _x}{S_{12}} + ({A_1}{b^{ - 1}}{{x'}_0}{S_{21}} - {\omega ^2}{S_{11}}{p_2}) + {A_1}{C_1}{p_2}A_1^{ - 2}[\dot p_2^2 - 2{{\dot p}_2}({a^{ - 1}}{{y'}_0} - {\lambda _2}{{\dot \gamma }_2})]\\ \,\,\,\,\,\, + {{x'}_0}{{\dot \gamma }_2}{{\dot p}_2} - {{y'}_0}A_1^{ - 1}({A_1} + {a^{ - 1}}){{\dot p}_2}{\gamma _2} - {a^{ - 1}}{{y'}_0}{p_2}{{\dot \gamma }_2} - {a^{ - 1}}{{z'}_0}{p_2} + {A_1}k{p_2}(1 - \dot \gamma _2^2 - 2{{\dot \gamma }_2}{\rho _1}{{\dot p}_2})\\ \,\,\,\,\,\, + k{\gamma _2}{{\dot \gamma }_2}{{\dot p}_2}({C_1} - 1) - {A_1}k{\gamma _2}{S_{21}}(1 + {B_1}) + \frac{1}{2}r_0^{ - 1}{\ell _z}{p_2}{S_{11}}({A^{ - 1}}{B_1} - {A_1}{B^{ - 1}}) + {\rho _1}{\lambda _1}C{A_1}{B^{ - 1}}{y_1}\\ \,\,\,\,\,\, - {\lambda _1}({B^{ - 1}}r_0^{ - 1}{\ell _x}{S_{21}} - {C^{ - 1}}r_0^{ - 1}{\ell _x}{{\dot \gamma }_2}A_1^{ - 1}{{\dot p}_2}),\\ {\varphi _2} = {B^{ - 1}}r_0^{ - 1}{\ell _x}{S_{22}} - {C^{ - 1}}r_0^{ - 1}{\ell _x}{\rho _2}\dot p_2^2A_1^{ - 1} + {C^{ - 1}}r_0^{ - 1}A_1^{ - 1}{\ell _x}{{\dot \gamma }_2}({a^{ - 1}}{{y'}_0} - {\lambda _2}{{\dot \gamma }_2}) - {\gamma _2}{S_{11}}\\\,\,\,\,\, + (1 + {B_1} - {B^{ - 1}}r_0^{ - 1}{\ell _z}){p_2}{S_{21}} - (1 - {C_1}){p_2}{{\dot \gamma }_2}A_1^{ - 1}{{\dot p}_2} + {{x'}_0}\dot \gamma _2^2 - {{y'}_0}{\gamma _2}{{\dot \gamma }_2} - {{z'}_0}{b^{ - 1}}{\gamma _2}\\\,\,\,\,\, + {{x'}_0}{b^{ - 1}} - {\gamma _2}{X^2}\dot p_2^2 + k{C_1}{\gamma _2}\dot \gamma _2^2 - k{B_1}{\gamma _2},\\{f_3} = {C^{ - 1}}r_0^{ - 1}A_1^{ - 1}{\ell _x}{({a^{ - 1}}{{y'}_0} - {\lambda _2}{{\dot \gamma }_2})^2} - (2{\omega ^2}{p_2}{S_{12}} - {A_1}{b^{ - 1}}{{x'}_0}{S_{22}}) - {\omega ^2}{S_{11}}(\lambda + {\lambda _1}{\gamma _2})\\\,\,\,\,\,\, + A_1^{ - 1}{C_1}(\lambda + {\lambda _1}{\gamma _2})[\dot p_2^2 - 2{{\dot p}_2}({a^{ - 1}}{{y'}_0} - {\lambda _2}{{\dot \gamma }_2})] - {{x'}_0}{{\dot \gamma }_2}({a^{ - 1}}{{y'}_0} - {\lambda _2}{{\dot \gamma }_2}) + {{x'}_0}{\rho _1}\dot p_2^2\\\,\,\,\,\,\, - {\rho _1}{p_2}{{\dot p}_2}{{y'}_0}A_1^{ - 1}({A_1} + {a^{ - 1}}) - {a^{ - 1}}{{y'}_0}{p_2}({\rho _1}{{\dot p}_2} + {q_1}) - {a^{ - 1}}{{y'}_0}{{\dot \gamma }_2}(\lambda + {\lambda _1}{\gamma _2}) - {a^{ - 1}}{{z'}_0}(\lambda \\\,\,\,\,\,\, + {\lambda _1}{\gamma _2}) + {A_1}k(\lambda + {\lambda _1}{\gamma _2})(1 - \dot \gamma _2^2 - 2{{\dot \gamma }_2}{\rho _2}{{\dot p}_2}) + {A_1}k(1 - {C_1})[{\gamma _2}{{\dot \gamma }_2}({A^{ - 1}}{a^{ - 1}}{{y'}_0} - {\lambda _2}{{\dot \gamma }_2})\\\,\,\,\,\, - A_1^{ - 1}{\gamma _2}{\rho _1}\dot p_2^2 - {\rho _1}{p_2}A_1^{ - 1}{{\dot \gamma }_2}{{\dot p}_2}] - {A_1}k{S_{22}}{\gamma _2}(1 + {B_1}) - {A_1}k{S_{11}}{\rho _1}{p_2}(1 + {B_1}) + \frac{1}{2}r_0^{ - 1}{\ell _z}\,\,\\\,\,\,\,\, \times ({A^{ - 1}}{B_1} - {A_1}{B^{ - 1}})\,[{p_2}(2{S_{12}} - 2{{z'}_0}{S_{21}} + 2k{S_{21}}) + (\lambda + {\lambda _1}{\gamma _2}){S_{11}}] + [\frac{1}{2}{{z'}_0}({a^{ - 1}} - {A_1}{b^{ - 1}})\\\,\,\,\, \times {\gamma _2}{S_{11}} + \frac{1}{2}{A^{ - 1}}r_0^{ - 1}{\ell _z}(k{B_1}{\gamma _2} - {b^{ - 1}}{{x'}_0}){S_{11}} + (2k{A_1} - {a^{ - 1}}{{z'}_0}){S_{21}}{p_2}]\, + {A_1}{B^{ - 1}}r_0^{ - 1}{\ell _x}{S_{11}}\\\,\,\, + {\rho _1}{\lambda _1}{{z'}_0}({a^{ - 1}} - {A_1}{b^{ - 1}}){\gamma _2} + {\rho _1}{\lambda _1}{A_1}{b^{ - 1}}{{x'}_0} + k{\rho _1}{\lambda _1}({\omega ^2} - {A_1}){\gamma _2} + {\rho _1}{\lambda _1}({b^{ - 1}}{{x'}_0} - {b^{ - 1}}{{z'}_0}{\gamma _2}\\\,\,\, - k{B_1}{\gamma _2}){A^{ - 1}}r_0^{ - 1}{\ell _z} - {\rho _1}{\lambda _1}{\omega ^2}(\lambda + {\lambda _1}{\gamma _2}),\\{\varphi _3} = - {C^{ - 1}}r_0^{ - 1}A_1^{ - 2}{\ell _x}{{\dot p}_2}({a^{ - 1}}{{y'}_0} - {\lambda _2}{{\dot \gamma }_2} - {{\dot p}_2}{S_{21}} - \frac{1}{2}{S_{11}}{A_1}{{\dot \gamma }_2}) + {C^{ - 1}}r_0^{ - 1}{\ell _x}{{\dot \gamma }_2}\{ [A_1^{ - 1}(k{A_1} - {a^{ - 1}}{{z'}_0}){\rho _1}\\\,\,\,\,\,\,\,\,\, + A_1^{ - 1}{S_{11}}]{{\dot p}_2} - \frac{1}{2}A_1^{ - 1}{S_{11}}{{\dot p}_2} + A_1^{ - 1}(k{A_1}{{\dot \gamma }_2} + {a^{ - 1}}{{y'}_0}){S_{21}}\} + {C^{ - 1}}r_0^{ - 1}A_1^{ - 1}{\ell _x}{\rho _2}{{\dot p}_2}({a^{ - 1}}{{y'}_0} - {\lambda _2}{{\dot \gamma }_2})\,\,\,\,\,\,\,\, - {\rho _1}{p_2}{S_{11}} - 2{\gamma _2}{S_{12}} + (1 + {B_1} + {B^{ - 1}}r_0^{ - 1}{\ell _z})[{p_2}{S_{22}} + (\lambda + {\lambda _1}{\gamma _2}){S_{21}}] + (1 - {C_1}){p_2}A_1^{ - 1}\\\,\,\,\,\,\,\,\, \times ({a^{ - 1}}{{y'}_0} - {\lambda _2}{{\dot \gamma }_2}){{\dot \gamma }_2} - (1 - {C_1}){p_2}A_1^{ - 1}{\rho _2}\dot p_2^2 - (1 - {C_1}){{\dot p}_2}{{\dot \gamma }_2}A_1^{ - 1}(\lambda + {\lambda _1}{\gamma _2}) + 2{{x'}_0}{{\dot \gamma }_2}{\rho _2}{{\dot p}_2}\\ \,\,\,\,\,\,\,\, - {{y'}_0}{\gamma _2}{\rho _1}{{\dot p}_2} - {{y'}_0}{\rho _1}{p_2}{{\dot \gamma }_2} - {{z'}_0}{b^{ - 1}}{\rho _1}{p_2} + 2{\gamma _2}A_1^{ - 2}{{\dot p}_2}({a^{ - 1}}{{y'}_0} - {\lambda _2}{{\dot \gamma }_2}) - {\rho _1}{p_2}A_1^{ - 2}\dot p_2^2 + 2k{C_1}\\\,\,\,\,\,\,\,\, \times {\gamma _2}{{\dot \gamma }_2}{\rho _2}{{\dot p}_2} + k{C_1}{\rho _1}{p_2}\dot \gamma _2^2 - k{B_1}{\rho _1}{p_2}\, + 2{b^{ - 1}}{{x'}_0}{S_{21}} - {b^{ - 1}}{{z'}_0}{\gamma _2}{S_{21}} - 2kB{\gamma _2}{S_{21}} - \frac{1}{2}{B^{ - 1}}r_0^{ - 1}\\\,\,\,\,\,\,\,\, \times \,{\ell _z}{p_2}[{S_{11}} + 2{{z'}_0}(1 - {{\gamma ''}_1}) - k(1 - \gamma _1^{''2})]. \end{array}$$
(20)

Formalization of the Periodic Solution

Determining the periodic solutions of (18) while accounting for the positive sign of \(\Omega^{2}\) is the main objective of this section. According to the autonomously of this system, it is evident that the below requirements have no bearing on the generality of the solutions \(p,q,r,\gamma ,\gamma^{\prime},\) and \(\gamma^{\prime\prime}\).

$$p_{2} (0,0) = CA_{1} B^{ - 1} y_{1} ,\quad \dot{p}_{2} (0,0) = 0,\quad \dot{\gamma }_{2} (0,\varepsilon ) = 0.$$
(21)

The generating form of system (18) has the form

$$\ddot{p}_{2}^{(0)} + \Omega^{2} p_{2}^{(0)} = 0\,,\quad \,\,\,\,\,\,\,\,\,\,\ddot{\gamma }_{2}^{(0)} + \,\gamma_{2}^{(0)} = 0,$$
(22)

which allows solutions with period \(T_{0} = 2\pi \,n\) fill out the form

$$p_{2}^{(0)} = M_{1} \cos \,\Omega \tau + M_{2} \sin \,\Omega \tau ,\quad \,\,\,\,\,\,\,\,\,\,\gamma_{2}^{(0)} = M_{3} \cos \tau ,$$
(23)

where \(M_{j} \;(j = \,1,\;2,\;3\,)\) are determinable constants.

Based on the preceding, the desirable solutions of system (18) can be assumed in the following form with period \(T(\varepsilon ) = T_{0} + \alpha (\varepsilon )\)

$$\begin{gathered} p_{2} (\tau ,\;\varepsilon ) = (M_{1} + \beta_{1} \,)\cos \Omega \tau + (\,M_{2} + \beta_{2} \,)\sin \Omega \,\tau + \sum\limits_{n = 1}^{\infty } {\varepsilon^{n} \,} G_{n} (\tau ), \hfill \\ \gamma_{2} (\tau ,\;\varepsilon ) = (M_{3} + \beta_{3} \,)\cos \tau + \sum\limits_{n = 1}^{\infty } {\varepsilon^{n} \,} H_{n} (\tau ), \hfill \\ \end{gathered}$$
(24)

where \(\beta_{1} ,\Omega \beta_{2} ,\) and \(\beta_{3}\) denote the initial value's deviation of \(p_{2} ,\;\dot{p}_{2} ,\)and \(\gamma_{2}\) for the system (18) from their corresponding values of the system (22). These variations are functions of\(\varepsilon\), in which they are vanishing at \(\varepsilon = 0\). One may establish the required criteria for these solutions (22) at \(t = 0\) by the relations given below

$$\begin{gathered} p_{2} (0,\;\varepsilon ) = M_{1} + \beta_{1} ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\quad \dot{p}_{2} (0,\;\varepsilon ) = \Omega \,(M_{2} + \beta_{2} ),\quad \hfill \\ \gamma_{2} (0,\;\varepsilon ) = M_{3} + \beta_{3} ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\quad \dot{\gamma }_{2} (0,\;\varepsilon ) = 0. \hfill \\ \end{gathered}$$
(25)

Using the next operator, the functions \(G_{n} (\tau )\) and \(H_{n} (\tau ),\;\;(\,n = 1,\;2,\;3,\; \cdots \,)\) can be identified as follows [48]

$$D = d + \frac{{\partial {\kern 1pt} d}}{{\partial M_{1} }}\,\beta_{1} + \frac{{\partial {\kern 1pt} d}}{{\partial M_{2} }}\,\beta_{2} + \frac{{\partial {\kern 1pt} d}}{{\partial M_{3} }}\,\beta_{3} + \frac{1}{2}{\kern 1pt} {\kern 1pt} \frac{{\partial^{2} d}}{{\partial M_{1}^{2} }}\,\beta_{1}^{2} + \cdots ;\quad \left( \begin{gathered} \,D = G_{n} ,\,H_{n} \, \hfill \\ \,d\,\; = g_{n} ,\;h_{n} \; \hfill \\ \end{gathered} \right).$$
(26)

The function \(g_{j} (\tau )\) and \(h_{j} (\tau )\) adopt the following forms.

$$\begin{gathered} g_{n} (\tau ) = \frac{1}{\Omega }\int\limits_{0}^{\tau } {F_{n}^{(0)} (t_{1} )\sin \Omega (\tau - t_{1} )\,d{\kern 1pt} t_{1} } , \hfill \\ h_{n} (\tau ) = \int\limits_{0}^{\tau } {\Phi_{n}^{(0)} (t_{1} )\sin (\tau - t_{1} )\,d{\kern 1pt} t_{1} ,} \quad (n = 1,\;2)\;, \hfill \\ \end{gathered}$$
(27)

where

$$F_{n}^{(0)} (\tau ) = \frac{1}{(n - 1)!}\;(\,\frac{{d^{n - 1} F}}{{d\varepsilon^{n - 1} }}\,)_{{\gamma^{\prime} = \varepsilon = 0}} ,\,\,\,\,\,\,\,\,\,\Phi_{n}^{(0)} (\tau ) = \frac{1}{(n - 1)!}\;(\,\frac{{d^{n - 1} \Phi }}{{d\varepsilon^{n - 1} }}\,)_{{\gamma^{\prime} = \varepsilon = 0}} .$$

It is worthy to mention that system (18), as seen in its right sides, starts with a small parameter of order zero. Consequently, we can determine the functions \(F_{n}^{(0)}\) and \(\Phi_{n}^{(0)}\) as follows

$$F_{n}^{(0)} = F_{n} (\,p_{2}^{(0)} ,\dot{p}_{2}^{(0)} ,\gamma_{2}^{(0)} ,\dot{\gamma }_{2}^{(0)} \,),\,\,\,\,\,\,\,\Phi_{n}^{(0)} = \Phi_{n} (\,p_{2}^{(0)} ,\dot{p}_{2}^{(0)} ,\gamma_{2}^{(0)} ,\dot{\gamma }_{2}^{(0)} \,);\,\,\,\,\,\,\,(\,n = 1,\,2\,).$$

In view of the above, solutions (23) can be rewritten as

$$\begin{gathered} p_{2}^{(0)} = E\cos \,(\Omega \tau - \eta ),\quad \gamma_{2}^{(0)} = M_{3} \cos \tau ;\quad \hfill \\ E = \sqrt {M_{1}^{2} + M_{2}^{2} } ,\quad \mu = \tan^{ - 1} {{M_{2} } \mathord{\left/ {\vphantom {{M_{2} } {M_{1} }}} \right. \kern-0pt} {M_{1} }}. \hfill \\ \end{gathered}$$
(28)

The substitution of (28) into (9) yields

$$\begin{gathered} S_{11}^{(0)} = E^{2} [a(\cos^{2} \eta \, - \frac{1}{2})\; + \,bX^{2} \Omega^{2} (\sin^{2} \eta \, - \frac{1}{2}) + \frac{1}{2}(bX^{2} \Omega^{2} - a)\cos 2(\Omega \tau - \eta )] \hfill \\ \quad \,\,\,\, - 2\,M_{3} [x^{\prime}_{0} (\,1 - \cos \tau \,) + y^{\prime}_{0} \sin \tau ] - \frac{1}{2}kM_{3}^{2} C_{1} (1 - \cos 2\tau ), \hfill \\ S_{21}^{(0)} = M_{3} E\{ a\cos \eta + \frac{1}{2}(bX\Omega - a)\,\cos [(\Omega - 1\,)\tau - \eta ] - \frac{1}{2}(\,b\,X\Omega + a\;) \hfill \\ \,\,\,\,\,\,\,\,\, \times \cos [(\Omega + 1\,)\tau - \eta ]\} + {\kern 1pt} M_{3} y_{1} (1 - \cos \tau ), \hfill \\ S_{12}^{(0)} = aE{\kern 1pt} \{ \lambda [\,\cos \eta - \cos \,{\kern 1pt} (\,\Omega \tau - \eta )\,]{\kern 1pt} + \lambda_{1} M_{3} \cos \eta - \frac{1}{2}\lambda_{1} M_{3} \cos \,{\kern 1pt} [(\Omega + 1)\tau - \eta ] \hfill \\ \,\,\,\,\,\,\,\,\, + \cos \,{\kern 1pt} [(\,\Omega - 1)\tau - \eta \,]\} - bX^{2} E\Omega \{ a^{ - 1} y^{\prime}_{0} [\,\sin \eta + \sin (\Omega \tau - \eta \,)\,]\,\, + \frac{{\lambda^{2} }}{2}M_{3} {\kern 1pt} \hfill \\ \,\,\,\,\,\,\,\,\, \times \,[\cos \,{\kern 1pt} ((\Omega - 1)\tau - \eta )\, - \cos \,{\kern 1pt} ((\,\Omega + 1)\tau - \eta )]\} - \,x^{\prime}_{0} \rho_{1} E[\cos \eta \,\, - \cos \,{\kern 1pt} (\Omega \tau - \eta )] \hfill \\ \,\,\,\,\,\,\,\, - y^{\prime}_{0} \rho_{2} E\Omega [\,\sin \,{\kern 1pt} \eta \,\, + \sin \,{\kern 1pt} (\,\Omega \tau - \eta \,)\,] + (z^{\prime}_{0} - k)S_{21}^{(0)} + ka\rho_{1} EM_{3} \{ \cos \,{\kern 1pt} \eta \, \hfill \\ \,\,\,\,\,\,\, - \frac{1}{2}[\cos \,{\kern 1pt} ((\,\Omega + 1)\tau - \eta \,) + \cos \,{\kern 1pt} ((\,\Omega - 1)\tau - \eta \,)] - \frac{1}{2}kb\rho_{2} EM_{3} \Omega \{ \cos \,{\kern 1pt} [(\,\Omega - 1)\tau - \eta ] \hfill \\ \,\,\,\,\,\,\, - \cos \,[(\Omega + 1)\tau - \eta ]\} , \hfill \\ S_{22}^{(0)} = a\rho_{1} {\kern 1pt} E^{2} \{ \,\cos^{2} \eta - \frac{1}{2}[1 + \cos 2(\,\Omega \tau - \eta \,)]\} + a\lambda M_{3} (\,1 - \cos \tau \;) + \frac{1}{2}\lambda_{1} M_{3}^{2} \hfill \\ \,\,\,\,\,\,\,\,\, \times (1 - \cos \tau )\} - bX\rho_{2} E^{2} \Omega^{2} \{ \sin^{2} \eta - \frac{1}{2}[1 - \cos 2(\Omega \tau - \eta )]\} + bXa^{ - 1} y^{\prime}_{0} M_{3} \sin \tau \hfill \\ \,\,\,\,\,\,\,\, + \frac{1}{2}bX\lambda_{2} M_{3}^{2} (1 - \cos 2\tau ) + y_{1} \rho_{1} E[\cos \eta - \cos (\Omega \tau - \eta \,)] - y_{3} S_{21}^{(0)} . \hfill \\ \end{gathered}$$
(29)

Substituting (28) and (29) into (20), we get

$$\begin{gathered} F_{1}^{(0)} = 0, \hfill \\ \Phi_{1}^{(0)} = - y_{1} r_{0}^{ - 1} B^{ - 1} \ell_{x} M_{3} \cos \tau + \cdots , \hfill \\ F_{2}^{(0)} = L(\Omega )\,(M_{1} \cos \Omega \tau + M_{2} \sin \Omega \tau ) + \cdots , \hfill \\ \Phi_{2}^{(0)} = M_{3} N(\Omega )\cos \tau + \cdots , \hfill \\ \end{gathered}$$
(30)

where

$$\begin{gathered} L(\Omega ) = A_{1} k - [a^{ - 1} z^{\prime}_{0} + \rho_{1} \lambda_{1} (1 - \Omega^{2} )] - 2aA_{1} \lambda r_{0}^{ - 1} B^{ - 1} \ell_{x} + [\frac{1}{2}r_{0}^{ - 1} \ell_{z} (A^{ - 1} B_{1} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\, - A_{1} B^{ - 1} ) - \omega^{2} ][aM_{1}^{2} + bX^{2} \Omega^{2} M_{2}^{2} - \frac{1}{2}(a + bX^{2} \Omega^{2} ) - 2M_{3} x^{\prime}_{0} \hfill \\ \,\,\,\,\,\,\,\,\,\,\, - \frac{1}{2}kM_{3}^{2} C_{1} - \frac{1}{2}(bX^{2} \Omega^{2} - a)(M_{1}^{2} + M_{2}^{2} )] + ..., \hfill \\ N(\Omega ) = - (aM_{1}^{2} + bX^{2} {\kern 1pt} \Omega^{2} M_{2}^{2} ) + (1 + b)(M_{1}^{2} + M_{2}^{2} )X^{2} {\kern 1pt} \Omega^{2} + 2\,x^{\prime}_{0} M_{3} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - [b^{ - 1} z^{\prime}_{0} - \rho_{1} \lambda_{1} (1 - \Omega^{2} )] + k(\frac{1}{2}M_{3}^{2} C_{1} - B_{1} ) - a\lambda r_{0}^{ - 1} B^{ - 1} \ell_{x} + \cdots . \hfill \\ \end{gathered}$$
(31)

The functions \(g_{n} ,\dot{g}_{n} ,h_{n} ,\) and \(\dot{h}_{n} \,\,(n = 1,\,2)\) can be obtained using the expressions (27), (30), and (31) as follows

$$\begin{gathered} g_{1} (T_{0} ) = 0,\,\,\,\,\,\,g_{2} (T_{0} ) = - \,\pi n\,\Omega^{ - 1} M_{2} L(\Omega ),\,\,\,\,\,\,\dot{g}_{1} (T_{0} ) = 0,\,\,\,\,\,\,\dot{g}_{2} (T_{0} ) = \pi nM_{1} L(\Omega \,), \hfill \\ h_{1} (T_{0} ) = 0,\,\,\,\,\,\,h_{2} (T_{0} ) = 0,\,\,\,\,\,\,\dot{h}_{1} (T_{0} ) = 0,\,\,\,\,\,\,\dot{h}_{2} (T_{0} ) = \pi nM_{3} N(\Omega \,). \hfill \\ \end{gathered}$$
(32)

The proposed solutions (24) and their related first derivatives must satisfy the following constraints for periodicity to acquire \(M_{j} ,\beta_{i} ,\) and the correction \(\alpha\) of the period.

$$\begin{gathered} \psi_{1} \,\; = p_{2} (T_{0} + \alpha ,\varepsilon ) - p_{2} (0,\varepsilon ) = 0\;, \hfill \\ \psi_{2} {\kern 1pt} \; = \dot{p}_{2} (T_{0} + \alpha ,\varepsilon ) - \dot{p}_{2} (0,\varepsilon ) = 0\;, \hfill \\ \psi_{3} {\kern 1pt} \; = \gamma_{2} (T_{0} + \alpha ,\varepsilon ) - \gamma_{2} (0,\varepsilon )\;\,\, = 0\;, \hfill \\ \psi_{4} {\kern 1pt} \; = \dot{\gamma }_{2} (T_{0} + \alpha ,\varepsilon ) - \dot{\gamma }_{2} (0,\varepsilon )\;\,\, = 0\;. \hfill \\ \end{gathered}$$
(33)

Notably, the existence of the integral (19) is related to the above mentioned third condition \(\psi_{3} = 0\). Accordingly, one can use the criteria (25) and (33) to get

$$2{\kern 1pt} {\kern 1pt} (\,M_{3} + \beta_{3} \,)\,\psi_{3} + \psi_{3}^{2} + \varepsilon \,h_{1} (\,\psi_{1} ,\psi_{2} ,\psi_{3} ,\psi_{4} ,\varepsilon \,) = 0.$$
(34)

In this case, \(h_{1}\) stands for an entire function where\(h_{1} (0,0,0,\varepsilon ) = 0\). When\(M_{3} \ne 0\), we obtain \(\psi_{3} = k_{1} (\psi_{1} ,\psi_{2} ,\psi_{3} ,\psi_{4} ,\varepsilon ),\) where \(k_{1}\) is a function that fulfills the condition \(k_{1} (0,0,0,\varepsilon ) = 0.\) Then the condition \(\psi_{3} = 0\) in (34) is compatible with the removal of the other conditions, i.e.,

$$\psi_{1} = \psi_{2} = \psi_{4} = 0.$$
(35)

At \(\tau = 0\), the substitution of (25) into (19) yields

$$M_{3}^{2} + 2\,M_{3} {\kern 1pt} \beta_{3} + \beta_{3}^{2} + 2\,\varepsilon \,\rho_{1} \,(\,M_{1} + \beta_{1} \,)(M_{3} + \beta_{3} ) + \cdots = (\,\gamma^{\prime\prime}_{0} )^{ - 2} - 1.$$

If \(\gamma^{\prime\prime}_{0}\) is independent of \(\varepsilon\), then \(M_{3}\) and \(\beta_{3}\) can be produced in the following forms

$${M_3} = {(1 - \gamma _0^{''2})^{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}}{({\kern 1pt} {\gamma ''_0})^{ - 1}},0 < {M_3} < \infty ,{\beta _3} = - \varepsilon {\rho _1}({M_1} + {\beta _1}) + \cdots .$$
(36)

By disregarding terms of order \(\alpha^{2}\) and extending the conditions (33) regarding \(\alpha\) power series, we obtain

$$\begin{gathered} p_{2} (\,T_{0} ,\;\varepsilon \,) + \alpha \,\,\dot{p}_{2} (\,T_{0} ,\;\varepsilon \,) + \cdots - p_{2} (\;0,\;\varepsilon \,) = 0, \hfill \\ \dot{p}_{2} (\,T_{0} ,\;\varepsilon \,) + \alpha \,\,\ddot{p}_{2} (\,T_{0} ,\;\varepsilon \,) + \cdots - \dot{p}_{2} (\,0,\;\varepsilon \,) = 0, \hfill \\ \dot{\gamma }_{2} (\,T_{0} ,\;\varepsilon \,) + \alpha \,\,\ddot{\gamma }_{2} (\,T_{0} ,\;\varepsilon \,) + \cdots - \dot{\gamma }_{2} (\,0,\;\varepsilon \,) = 0. \hfill \\ \end{gathered}$$

Utilizing the criteria (25) into the aforementioned relations, the independent conditions of periodicity (35) can be rewritten as follows

$$\begin{gathered} p_{2} (\,T_{0} ,\;\varepsilon \,) + \alpha \,\Omega {\kern 1pt} {\kern 1pt} (\,M_{2} + \beta_{{{\kern 1pt} 2}} \,) - (\,M_{1} + \beta_{{{\kern 1pt} 1}} \,) = 0, \hfill \\ \dot{p}_{2} (\,T_{0} ,\varepsilon \,) - \Omega {\kern 1pt} {\kern 1pt} {\kern 1pt} (\,M_{2} + \beta_{{{\kern 1pt} 2}} \,) + \alpha \,\Omega {\kern 1pt}^{2} (\,M_{1} + \beta_{{{\kern 1pt} 1}} \,) + \alpha CB^{ - 1} A_{1} y_{1} = 0, \hfill \\ \dot{\gamma }_{2} (\,T_{0} ,\varepsilon \,) - \alpha {\kern 1pt} {\kern 1pt} (\,M_{3} + \beta_{{{\kern 1pt} 3}} \,) + \alpha \,r_{0}^{ - 1} B^{ - 1} \ell_{x} = 0. \hfill \\ \end{gathered}$$
(37)

The correction of period \(\alpha (\varepsilon )\) can be achieved after using (24) and (36) besides the last equation of (37), in the form

$$\alpha (\varepsilon ) = \varepsilon \,(M_{3} + \beta_{{{\kern 1pt} 3}} - r_{0}^{ - 1} B^{ - 1} \ell_{x} )^{ - 1} \,(\,\dot{F}_{1} (T_{0} ) + \varepsilon \,\dot{F}_{2} (T_{0} ) + \varepsilon^{2} \,\dot{F}_{3} (T_{0} ) + \cdots \;).$$
(38)

Utilizing (24), (32), and the first two equations of (37) and (38) to create the below system that determines \(\beta_{{{\kern 1pt} 1}}\) and \(\beta_{{{\kern 1pt} 2}}\)

$$\begin{gathered} - \pi \,n\,\beta_{{{\kern 1pt} 2}} \Omega^{ - 1} \{ L_{1} (\Omega ) - \Omega^{2} {\kern 1pt} N_{1} (\Omega \,)[\,1 + \,(r_{0}^{ - 1} B^{ - 1} \ell_{x} )\,\,(M_{3} + \beta_{{{\kern 1pt} 3}} - r_{0}^{ - 1} B^{ - 1} \ell_{x} )^{ - 1} \,]\} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \varepsilon \,{\kern 1pt} (G_{2} (T_{0} ) + \cdots \,) = 0, \hfill \\ \pi \,n\,\beta_{{{\kern 1pt} 1}} \{ L_{1} (\,\Omega \,) + N_{1} (\,\Omega \,)(CA_{1} B^{ - 1} y_{1} - \Omega \,\beta_{{{\kern 1pt} 1}} )[\,1 + (r_{0}^{ - 1} B^{ - 1} \ell_{x} )\,\,(M_{3} + \beta_{{{\kern 1pt} 3}} - r_{0}^{ - 1} B^{ - 1} \ell_{x} )^{ - 1} \} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \varepsilon \,{\kern 1pt} [\dot{G}_{2} (T_{0} ) + \cdots \,] = 0. \hfill \\ \end{gathered}$$
(39)

Replacing \(M_{1} ,\;M_{2} ,\,M_{3}\) by \(\beta_{{{\kern 1pt} 1}} ,\beta_{{{\kern 1pt} 2}} ,M_{{{\kern 1pt} 3}} + \beta_{{{\kern 1pt} 3}}\), respectively, the functions \(L_{1} (\Omega )\) and \(N_{1} (\Omega )\) can be obtained as follows

$$L_{{{\kern 1pt} 1}} (\Omega ) - \Omega^{2} {\kern 1pt} N_{1} (\Omega ) = (\,\beta_{{{\kern 1pt} 1}}^{2} + \beta_{{{\kern 1pt} 2}}^{2} \,)\,{\kern 1pt} W_{1} (\Omega ) + z^{\prime}_{0} W_{2} (\Omega ) + kW_{3} (\Omega ) + W_{4} (\Omega ),$$
(40)

where

$$\begin{gathered} W_{1} (\Omega ) = \frac{1}{2}\,(b\Omega {\kern 1pt}^{2} X^{2} - a\;)(\Omega^{2} + \frac{1}{2}y) - (1 + b)\Omega {\kern 1pt}^{4} X^{2} , \hfill \\ W_{2} (\Omega ) = b^{ - 1} \Omega {\kern 1pt}^{2} - a^{ - 1} , \hfill \\ W_{3} (\Omega ) = A_{1} + \frac{1}{4}C_{1} y(\,M_{3} + \beta_{3} \,)^{2} + \Omega^{2} \beta_{1} , \hfill \\ W_{4} (\Omega ) = B^{ - 1} r_{0}^{ - 1} a\lambda \ell_{x} (\Omega^{2} - 2A_{1} ) - \rho_{1} \lambda_{1} (1 - \Omega {\kern 1pt}^{4} ) + \frac{1}{2}y[\frac{1}{2}(a + b\Omega {\kern 1pt}^{2} X^{2} ) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\, + 2x^{\prime}_{0} (\,M_{3} + \beta_{3} \,) + (a\beta_{1}^{2} + b\Omega {\kern 1pt}^{2} X^{2} \beta_{2}^{2} )] + \frac{1}{2}\Omega {\kern 1pt}^{2} (a + b\Omega {\kern 1pt}^{2} X^{2} ) \hfill \\ \end{gathered}$$

Based on (39), it is possible to get the formulations for \(\beta_{{{\kern 1pt} n}} \,\,(n = 1,2)\) in terms of \(\varepsilon\) whose first terms begin with \(O(\varepsilon^{3} )\). Consequently, the periodic solutions up to the first approximate order have the following forms

$$\begin{gathered} p_{1} = \varepsilon \{ \Omega^{ - 2} [x^{\prime}_{0} b^{ - 1} (A_{1} + A^{ - 1} r_{0}^{ - 1} \ell_{z} )] + \lambda_{1} M_{3} \cos \tau \} + \cdots , \hfill \\ q_{1} = \varepsilon X(a^{ - 1} y^{\prime}_{0} + \lambda_{2} M_{3} \sin \tau ) + \varepsilon^{2} X(a^{ - 1} y^{\prime}_{0} - kA_{1} M_{3} \sin \tau )[M_{3} y_{1} (\,1 - \cos \tau \,)] + \; \cdots , \hfill \\ r_{1} = 1 + \frac{1}{2}\;\varepsilon^{2} \{ - 2M_{3} [x^{\prime}_{0} \,(\,1 - \cos \tau \,) + y^{\prime}_{0} \sin \tau ] - \frac{1}{2}kM_{3}^{2} C_{1} (\,1 - \cos 2\tau \,)\} + \cdots , \hfill \\ \gamma_{1} = M_{3} \cos \tau + \; \cdots , \hfill \\ \gamma^{\prime}_{1} = - M_{3} \sin \tau + \varepsilon^{2} \,\{ X(a^{ - 1} y^{\prime}_{0} + \lambda_{2} M_{3} \sin \tau ) - \frac{1}{2}M_{3} \sin \tau [2M_{3} [x^{\prime}_{0} (\,1 - \cos \tau \,) + y^{\prime}_{0} \sin \tau ] \hfill \\ \,\,\,\,\, + \frac{1}{2}kM_{3}^{2} C_{1} (\,1 - \cos 2\tau \,)]\} + \; \cdots , \hfill \\ \gamma^{\prime\prime}_{1} = 1 + \varepsilon [M_{3} \,y_{1} \,(\,1 - \cos \tau \,)] + \varepsilon^{2} \{ \;a\lambda M_{3} (\,1 - \cos \tau \,) + \frac{1}{2}M_{3}^{2} (\,1 - \cos 2\tau \,)(a\lambda_{1} + bX\lambda_{2} ) \hfill \\ \,\,\,\,\, + bXa^{ - 1} y^{\prime}_{0} M_{3} \sin \tau - M_{3} y_{1} y_{3} \,(\,1 - \cos \tau \,) + M_{3} [x^{\prime}_{0} \,(\,1 - \cos \tau \,) + y^{\prime}_{0} \sin \tau ] \hfill \\ \,\,\,\,\, + \frac{1}{4}kM_{3}^{2} C_{1} (\,1 - \cos 2\tau \,)\} + \; \cdots , \hfill \\ \alpha (\varepsilon ) = \varepsilon \,\pi \,n\,[\,1 + (M_{3} + \beta_{{{\kern 1pt} 3}} - r_{0}^{ - 1} B^{ - 1} \ell_{x} )^{ - 1} \,(r_{0}^{ - 1} B^{ - 1} \ell_{x} )][2\,x^{\prime}_{0} \,M_{3} - z^{\prime}_{0} b^{ - 1} + \rho_{1} \lambda_{1} (1 - \Omega^{2} ) \hfill \\ \,\,\,\,\,\,\,\,\,\,\, + k(\frac{1}{2}M_{3}^{2} C_{1} - B_{1} ) - r_{0}^{ - 1} B^{ - 1} a\lambda \ell_{x} ] + \; \cdots . \hfill \\ \end{gathered}$$
(41)

A closer examination of the aforementioned solutions revealed that they exhibit periodic behaviors with various values of the gyrostat’s physical parameters. It is emphasized that for any rational value of the frequency \(\Omega\), the gained solutions do not have any singular point. The reason is going back to the use of the frequency of Amer that depends on the third projection of the GM on the \(z\)-axis. As seen from the mathematical forms of these solutions, we expect that the waves of these solutions will behave the forms of periodic waves, due to that these results include trigonometric functions. Moreover, the solutions \(p_{1} ,\,q_{1} ,\) and \(\gamma_{1}^{\prime \prime }\) will be varied with the GM values owing to that these solutions include the components \(\ell_{x}\) and \(\ell_{z}\) of the GM.

Rigid Body Orientations

The goal of the current section is to demonstrate the RB’s orientation at any specific instant in view of the achieved solutions and angles of Euler. Such angles are specified by the angles of nutation, self-rotation, and precession, that are always represented as \(\theta ,\,\,\varphi ,\) and \(\psi\), respectively.

In light of the fact that system (18) is regarded as autonomous (18), the acquired solutions (41) will remain periodic if \(t\) is changed to \((t + t_{0} )\), where \(t_{0}\) denotes any interval. As a result, we may formulate Euler's angles as follows [1]

$$\cos \theta = \gamma^{\prime\prime},\quad \frac{d\psi }{{d{\kern 1pt} t}} = \frac{{p\gamma + q\gamma^{\prime}}}{{1 - \gamma^{{\prime\prime}{2}} }},\quad \tan \varphi_{0} = \frac{{\gamma_{0} }}{{\gamma^{\prime}_{0} }},\quad \frac{d\varphi }{{d{\kern 1pt} t}} = r - \frac{d\psi }{{d{\kern 1pt} t}}\;\cos \theta .$$
(42)

The required Euler's angles for the investigated problem can be obtained by at once substituting (4) and (41) into (42)

$$\begin{gathered} \phi_{0} = (\pi /2) + r_{0} {\kern 1pt} h + \cdots ,\quad \quad \theta_{0} = \tan^{ - 1} M_{3} , \hfill \\ \theta = \theta_{0} - \varepsilon \,\,[\;\theta_{{{\kern 1pt} 1}} (t + h) - \theta_{{{\kern 1pt} 1}} (h)\;] - \varepsilon^{{{\kern 1pt} 2}} \,\,[\;\theta_{{{\kern 1pt} 2}} (t + h) - \theta_{{{\kern 1pt} 2}} (h)\;], \hfill \\ \psi = \psi_{0} + c\,{\kern 1pt} \cos {\text{ec}}{\kern 1pt} {\kern 1pt} \theta_{0} \,\sqrt {\cos \theta_{0} } \;\{ \;[\;\psi_{1} (t + h) - \psi_{1} (h)\;] + \varepsilon \;[\;\psi_{2} (t + h) - \psi_{2} (h)\;] \hfill \\ \;\;\; + \varepsilon^{2} \;[\;\psi_{3} (t + h) - \psi_{3} (h)\;]\;\} , \hfill \\ \phi = \phi_{0} + r_{0} \,t - c\,{\kern 1pt} \cot \theta_{0} \,\sqrt {\cos \theta_{0} } \;\{ [\phi_{1} (t + h) - \phi_{1} (h)] + \varepsilon \;[\phi_{2} (t + h) - \phi_{2} (h)]\} \hfill \\ \quad - \varepsilon^{2} \;\{ \tan \theta_{0} \;[\phi_{3} (t + h) - \phi_{3} (h)] + c\,{\kern 1pt} \cot \theta_{0} \sqrt {\cos \theta_{0} } \;{\kern 1pt} {\kern 1pt} [\phi_{4} (t + h) - \phi_{4} (h)]\} , \hfill \\ \end{gathered}$$
(43)

where

$$\begin{gathered} \theta_{1} (t) = - y_{1} \cos r_{0} {\kern 1pt} t, \hfill \\ \theta_{2} (t) = \,(y_{1} y_{3} - a\lambda - x^{\prime}_{0} \,)\cos r_{0} \,t - (bXa^{ - 1} + 1)y^{\prime}_{0} \sin r_{0} {\kern 1pt} t\, \hfill \\ \,\,\,\,\,\,\,\,\,\,\, - \;\frac{1}{2}\tan \theta_{0} (a\lambda_{1} + bX\lambda_{2} + \frac{1}{2}kC_{1} )\cos 2r_{0} \,t, \hfill \\ \psi_{1} (t) = 0, \hfill \\ \psi_{2} (t) = r_{0}^{ - 1} (\Omega^{ - 2} x^{\prime}_{0} b^{ - 1} A_{1} \sin r_{0} {\kern 1pt} t - A_{1}^{ - 1} a^{ - 1} y^{\prime}_{0} \cos r_{0} t) + \frac{1}{4}\tan \theta_{0} [\lambda_{1} (2t + r_{0}^{ - 1} \,\sin 2r_{0} {\kern 1pt} t) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\, + \lambda_{2} (r_{0}^{ - 1} A_{1}^{ - 1} \sin 2r_{0} t - 2X\,t)], \hfill \\ \psi_{3} (t) = \frac{1}{4}Xy_{1} \tan \theta_{0} \{ a^{ - 1} y^{\prime}_{0} (2\cos r_{0} t - r_{0}^{ - 1} \cos 2r_{0} t) - kA_{1} \tan \theta_{0} [2t \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\, - r_{0}^{ - 1} (\cos 2r_{0} t - 4\sin^{3} r_{0} {\kern 1pt} t)]\} , \hfill \\ \phi_{1} (t) = \psi_{1} (t),\quad \quad \quad \phi_{2} (t) = \psi_{2} (t),\quad \quad \quad \phi_{4} (t) = \psi_{3} (t), \hfill \\ \phi_{3} (t) = x^{\prime}_{0} (r_{0} t - \sin r_{0} t) - y^{\prime}_{0} \cos r_{0} t + \frac{1}{8}kC_{1} \tan \theta_{0} (2r_{0} t - \sin 2r_{0} t). \hfill \\ \end{gathered}$$

By carefully selecting the initial values \(\theta_{0} ,\;\psi_{0} ,\;\phi_{0}\), and \(r_{0}\), we can estimate the orientation of the RB’s motion in view of the previous Eqs. (43) of Euler's angles. According to these equations, we can predict that the behavior of \(\theta\) and \(\varphi\) will be impacted and have periodic forms with the change of the GM, while the behavior of the angle \(\psi\) increases in the opposite direction.

Numerical Simulations

The current section's goal is to analyze the achieved solutions (41) and angles of Euler (43) at various values of the acted parameters on the RB’s motion. Consequently, the following relevant data in Table 1 are used to display the temporary motion and phase plane plots in various graphs.

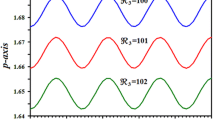
Table 1 Shows the relevant data which are used to display the temporary motion and phase plane plots in various graphs
Full size table

The included curves in potions (a–f) of Figs. 2 and 3 depict the temporal histories of the solutions \(p_{1} ,q_{1} ,r_{1} ,\gamma_{1} ,\gamma^{\prime}_{1} ,\) and \(\gamma^{\prime\prime}_{1}\). These curves are drawn when \(\,\ell_{x} = 30\,{\text{kg}}\,{\text{m}}^{2} \,{\text{s}}^{ - 1} ,\) \(\ell_{z} ( = 30,60,90)\;{\text{kg}}\,{\text{m}}^{2} \,{\text{s}}^{ - 1}\) and \(\,\ell_{z} = 30kg.m^{2} .s^{ - 1} ,\) \(\ell_{x} ( = 30,60,90)\;{\text{kg}}\,{\text{m}}^{2} \,{\text{s}}^{ - 1}\), as presented in Figs. 2 and 3, respectively. It is notable that the represented waves of these solutions have the periodicity forms, as expected before, with the change of the projections of the GM on the main axes of inertia \(\,x\) and \(z\). Moreover, the inspection of the portions of Fig. 2 shows that, the solutions \(q_{1}\) and \(\gamma_{1}^{\prime \prime }\) are influenced with the change of \(\ell_{x}\) values, where the amplitude’s waves increase with the increase of \(\ell_{x}\) values, while the number of oscillations remains stationary. On the other hand, the other solutions are slightly affected to some extent with the variation of \(\ell_{x}\) even though the curves of these solutions are also periodic. Curves of Fig. 3 illustrate that the waves describing the behavior of \(p_{1} ,q_{1} ,\) and \(\gamma_{1}^{\prime \prime }\) have been impacted with the various values of \(\ell_{z}\), in which the waves’ amplitudes increase with the increase of \(\ell_{z}\), as displayed in portions (a) and (b) of Fig. 3, while the amplitudes of the waves illustrating the solution \(\gamma_{1}^{\prime \prime }\) decrease with the increase of \(\ell_{z}\), as drawn in Fig. 3f. The reminder waves of the solutions \(p_{1} ,q_{1} ,\) and \(\gamma_{1}^{\prime }\) have no variation with the same values of \(\ell_{z}\). These remarks agree with the obtained solutions (41). The phase plane plots of the explored curves in Figs. 2 and 3 are graphed in the corresponding potions of these figures with portions of Figs. 4 and 5. The latter Figs. 4 and 5 included closed curves which assert that the behaviors of the plotted solutions are stable and free of chaos. Based on the variation of the solutions with the values of \(\ell_{x}\) and \(\ell_{z}\), we find that there is a corresponding change in plotted closed curves in Figs. 4 and 5.

Fig. 2
figure 2

The time history of the obtained approximate solutions \(p_{1} ,q_{1} ,r_{1} ,\gamma_{1} ,\gamma^{\prime}_{1} ,\) and \(\gamma^{\prime\prime}_{1}\) over time \(t\) when \(\,\ell_{z} = 30\,{\text{kg}}\,{\text{m}}^{2} \,{\text{s}}^{ - 1}\) with different values of \(\ell_{x} ( = 30,60,90)\;{\text{kg}}\,{\text{m}}^{2} \,{\text{s}}^{ - 1}\)

Full size image
Fig. 3
figure 3

The fluctuation of \(p_{1} ,q_{1} ,r_{1} ,\gamma_{1} ,\gamma^{\prime}_{1} ,\) and \(\gamma^{\prime\prime}_{1}\) versus \(t\) when \(\ell_{x} = 30\,{\text{kg}}\,{\text{m}}^{2} \,{\text{s}}^{ - 1}\) with the increase of \(\ell_{z} ( = 30,60,90)\,{\text{kg}}\,{\text{m}}^{2} \,{\text{s}}^{ - 1}\) values

Full size image
Fig. 4
figure 4

The phase plane diagrams of the solutions \(p_{1} ,q_{1} ,r_{1} ,\gamma_{1} ,\gamma^{\prime}_{1} ,\) and \(\gamma^{\prime\prime}_{1}\) at \(\,\ell_{z} = 30\;{\text{kg}}\,{\text{m}}^{2} \,{\text{s}}^{ - 1}\) with distinct values of \(\ell_{x} ( = 30,\;60,90)\;{\text{kg}}\,{\text{m}}^{2} \,{\text{s}}^{ - 1}\)

Full size image
Fig. 5
figure 5

The graphs of the solutions’ phase plane when \(\ell_{x} = 30\,{\text{kg}}\,{\text{m}}^{2} \,{\text{s}}^{ - 1}\) according to the various values of \(\ell_{z} ( = 30,60,90)\,{\text{kg}}\,{\text{m}}^{2} \,{\text{s}}^{ - 1}\)

Full size image

The curves shown in portions of Figs. 6 and 7 are meant to demonstrate the temporal evolution of the angles \(\theta ,\psi ,\) and \(\phi\) under distinct values for \(\ell_{x}\) and \(\ell_{z}\). The represented curves in portions (a–c) of Figs. 6 and 7 have been impacted with the change of the GM values. It is obvious that the waves of the angles \(\theta\) and \(\varphi\) oscillate periodically, as seen in potions (a) and (b) of these figures, respectively. As contrasted to this, the behavior of the angle \(\psi\) has a negative direction when time goes on, as drawn in part (c) of the same figures. These curves are in full agreement with Eqs. (43).

Fig. 6
figure 6

Reveals the variation of \(\theta (t),\phi (t),\) and \(\psi (t)\) at \(\,\ell_{z} = 30\,{\text{kg}}\,{\text{m}}^{2} \,{\text{s}}^{ - 1}\) for various values of \(\ell_{x} ( = 30,60,90)\,{\text{kg}}\,{\text{m}}^{2} \,{\text{s}}^{ - 1}\)

Full size image
Fig. 7
figure 7

Shows the waves of \(\theta (t),\varphi (t),\) and \(\psi (t)\) at \(\,\ell_{x} = 30\;{\text{kg}}\,{\text{m}}^{2} \,{\text{s}}^{ - 1}\) for various values of \(\ell_{z} ( = 30,60,90)\,{\text{kg}}\,{\text{m}}^{2} \,{\text{s}}^{ - 1}\)

Full size image

Conclusion

The positive impact of the NFF and the GM on the rotatory motion of a RB, about one of its fixed points has been examined for an analogs case of Lagrange's gyroscope. The governing system of motion that consists of six nonlinear DEs of first order has been derived using the principal equation of the angular momentum for the body’s motion. The three first integrals of this system related to energy, area, and geometric integral have been obtained. This system is reduced, using the APSP, to an appropriate one of two quasi-linear DEs of second order and one integral in terms of just two variables. It has been found that the obtained approximate solutions are valid for any value of the RB’s frequency and do not have any singularities at all. The body’s geometric interpretations have been estimated at any given time using Euler’s angles. The achieved results have been drawn according to the values of the impacted parameters to show the behavior of the body’s motion. Additionally, the stability of the dynamical motion is discussed using phase plane plots. These results are regarded as a generalization of those that were obtained in [7, 28, 30] for the absence of all applied forces and moments except NFF, and in [31] at (\(\ell_{x} = 0,\;A \ne B\)). This study presents an important contribution in a variety of critical domains, including the industrial uses of spacecraft, aircraft, and submarines.