Introduction

The problem of the free rotatory movement of a gyrostat is considered to be one of the significant problems in the field of mechanics. The relevance of the topic of the present paper is due to the use of various gyroscopic devices in technology like gyroscopic platforms’ stabilization, controlling and stabilization of artificial Earth satellites’ motion, and also in the calculation and design of various gyroscopic instruments. The gyrostat’s motion in the simple notification (free rotation of gyrostat) and in more complicated expression (heavy gyrostat's movement in a Newtonian field) was examined in the various works as [1,2,3,4,5,6,7,8]. Despite this, it is implausible to claim that even the gyrostat’s fundamental case-free rotation has been thoroughly examined. In [1], the author illustrated and collected the familiar rotatory motions of a rigid body (motion about a fixed point and without a fixed point, in fluids, under the action of potential forces in uniform and Newtonian fields). The problem of free rotation of a body carrying a smoothly rotating one was investigated in [2] while in [3], the stabilization of gyroscopic platforms is studied. In [4], the author investigated a gyrostat’s rotation with an absence of 2nd component of a gyrostatic moment when the body is considered to be subjected to external forces. In [5,6,7], both the theoretical foundations of rigid bodies and various practical applications, including gyroscopic effects in rotors, are considered in detail. In the work [8], matrix tools are used to represent vectors and tensors for the rigid body’s motion.

The study of the solid mass problem and the different gyroscopic movements have been drawn the attention of many researchers over the years, e.g., [9,10,11,12,13,14]. The book [9] offers an analytical solution for the free gyrostatic problem, in which some basic motions of the rigid body are investigated. The solutions for the motion of a charged gyrostat under the influence of various applied forces and moments are obtained analytically in [10]. The authors presented various applications on the averaging system of the corresponding controlling one. It is crucial to note that the achieved outcomes generalize that were obtained in [11] for the motion of uncharged gyrostat.

Perturbation methods [12, 13] played an important role to obtain the required solutions of the gyrostatic motion analogous to Lagrange’s gyroscope. In [14], the authors used Poincaré method of the tiny parameter to obtain the approximate solutions for the gyrostatic movements when the body’s center of mass is slightly displaced. The motion is restricted to the action of the Newtonian field and the gyrostatic moment. The periodic motions for the scenario of irrational frequencies are obtained. The examination of this problem is studied in [15] when the effectiveness of an electromagnetic field is taken into account. The same procedure of perturbation is tested in [16] for the rigid body’s motion similar to Bobylev-Steklov case. Other methods were used in several works to gain the desired approximate solutions of various gyrostatic models e.g., [17,18,19,20].

In [21,22,23,24] some dynamical vibrating models are studied using Li–He’s modified homotopy perturbation method and the enhanced homotopy perturbation method.

In the absence of engine torque, the classical problem of a heavy rigid body motion that has a fixed point was examined in several works e.g., [25,26,27,28,29]. In [25], the equilibria, asymptotic stability conditions, and bifurcations of equilibria for a gyrostatic satellite in a perfectly circular orbit are explored. It is assumed that the gyrostatic moment has a tangent direction of the orbital plane, and it has a collinear relationship with the orbital velocity. The dynamical behavior of a moving ball inside a fixed cavity is investigated analytically in [26], in which the authors have used a dependent approach on the governing Lagrangian system. At the point where the ball touches the cavity, rolling of the ball is thought to be slipping-free and dampen-free. In [27], the rotational motion of a heavy gyrostat subjected to external forces and moments is examined. The periodic solutions of the controlling system of motion are obtained using a perturbation approach. The stability of the gyrostatic behavior is examined and analyzed. The stationary permanent rotational motion is studied in [28]. Perturbed motions of a rigid body under the action of restoring torques are investigated in [29,30,31].

In our work, the turn tensor calculations have been used and the application of the tensor of rotation in the dynamics of a rigid body is described as in [32]. The problem of rigid mass without rotors is investigated to describe rotations and turns of solid bodies, the turn tensor is considered one of the best tools. As a result, the method of constructing the solution to the problem is mainly determined based on the use of the rotation tensor below.

The present work aims to derive the EOM of the free rotation of a single rotor and construct a desired analytical solution. Moreover, studying both the merits of the gained solution and the asymptotic properties of the gyrostatic motion for a rotation rotor case through a motor of limited power. The derivation of differential EOM is carried out based on the fundamental laws of mechanics using the tool of direct tensor calculus. The asymptotic method [33] for constructing the approximate solutions is used. In more general situations, which are typical in some sense, numerical methods are used. Besides, computer methods of symbolic calculations are widely used in the work. The results of this article may be used in gyroscopic platforms’ stabilization, controlling, and stabilization of artificial Earth satellites.

Dynamical Modeling’s Description

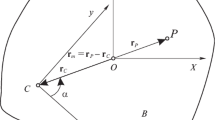
The objective of this section is to get the system of equations that governs the gyrostat’s motion. For this purpose, let's consider the motion of a single rotor gyrostat without any acting external forces and moments, in which there are no friction forces between the rotor and the carrier, see Fig. 1. We suggest that the moment \(\underline{M}\) which is acting on the rotor has the form

$$\underline{M} = - S\left( {\dot{\beta } - \omega_{ * } } \right)\underline{\underline{P}} \cdot \underline{e} \,,$$
(1)

where

Fig. 1
figure 1

One rotor gyrostat with an internal moment

Full size image

\(S\) an arbitrary positive constant,

\(\beta\) the rotation’s angle of the rotor relative to the carrier body (CB),

\(\omega_{ * }\) an arbitrary constant,

\(\underline{e}\) a unit vector directed along the rotor’s axis in the initial placement,

\(\underline{\underline{P}}\) turn tensor (rotation’s tensor) of the CB, the engine torque in Eq. (1) is an internal moment with respect to the gyrostat.

At the starting position, the inertia’s tensor of the CB is denoted by \(\underline{\underline{\Theta }}_{1}\), while in the actual position it is pointed by \(\underline{\underline{\Theta }}_{1}^{\left( t \right)}\).

The relationship between \(\underline{\underline{\Theta }}_{1}^{\left( t \right)}\) and \(\underline{\underline{\Theta }}_{1}\) is given by the formula:

$$\underline{\underline{\Theta }}_{1}^{\left( t \right)} = \underline{\underline{P}} (t) \cdot \underline{\underline{\Theta }}_{1} \cdot \underline{\underline{P}}^{T} (t),$$
(2)

It must be noted that the rotor is inserted into the hollow cavity, in which its inertia’s tensor \(\underline{\underline{\Theta }}_{2}\) is calculated relative to the centroid of rotor. In order for the rotor’s rotation remains the mass distribution without change in the gyrostat, it must be transversely isotropic, i.e., \(\underline{\underline{\Theta }}_{2}\) must have:

$$\underline{\underline{\Theta }}_{2} = \lambda \underline{e} \otimes \underline{e} + \mu \left( {\underline{\underline{E}} - \underline{e} \otimes \underline{e} } \right)\,,$$
(3)

where

\(\lambda\) the moment of inertia along the axis of rotation of the rotor,

\(\mu\) the inertia’s equatorial moment of the rotor,

\(\underline{\underline{E}}\) the unity tensor.

In the actual position, the inertia’s tensor of the rotor has a form similar to the expression (2):

$$\underline{\underline{\Theta }}_{2}^{\left( t \right)} = \underline{\underline{P}}_{ * } (t) \cdot \underline{\underline{\Theta }}_{2} \cdot \underline{\underline{P}}_{ * }^{T} (t),$$
(4)

where

\(\underline{\underline{P}}_{ * } (t)\) turn tensor of rotor; \(\underline{\underline{P}}_{ * } (t) = \underline{\underline{P}} \cdot \underline{\underline{Q}} \left( {\beta \underline{e} } \right)\); \(\underline{\underline{Q}} \left( {\beta \underline{e} } \right)\) is the relative turn tensor of the rotor with respect to the CB.

According to the formula for adding angular velocities [32].

$$\underline{\omega }_{ * } = \underline{\omega } + \dot{\beta }\underline{\underline{P}} \cdot \underline{e} \,,$$
(5)

where

\(\underline{\omega }\) the angular velocity (AV) vector of the CB,

\(\underline{\omega }_{ * }\) the AV vector of the rotor.

System’s Equations of Motion

It must remember that we considered the free motion of the gyrostat. Therefore, the first law of Euler’s dynamics [34] has the form

$$\underline{{\dot{K}}}_{1} = 0\,,$$
(6)

where \(\underline{K}_{1}\) is the momentum of the system.

The formulation of Euler’s second law of dynamics for a system of bodies

$$\underline{{\dot{K}}}_{2} = \underline{M}_{ext} \,,$$
(7)

where \(\underline{K}_{2}\) is the kinetic moment (KM) of the gyrostat relative to its center of mass \(C\), and \(\underline{M}_{ext}\) is the external moment that acting on the gyrostat. In this problem, Euler's second law of dynamics has the form

$$\underline{{\dot{K}}}_{2} = 0\,,$$
(8)

Because the external moment is zero. For the rotor, Euler’s second law of dynamics written relative to its centroid and has the form

$$\underline{{\dot{K}}}_{2}^{{\left( {B_{{c_{2} }} } \right)}} = \underline{M}^{ * } ,\,\,\,$$
(9)

where \(\underline{K}_{2}^{{\left( {B_{{c_{2} }} } \right)}}\) is the KM of the rotor relative to its centroid \(c_{2}\), and.

\(\underline{M}^{ * }\) is the moment acting on the rotor.

Then the vector \(\underline{M}^{ * }\) has the following form

$$\underline{M}^{ * } = \underline{M}^{ * }_{ext} + \underline{M} ,\,\,\,$$
(10)

where \(\underline{M}^{ * }_{ext}\) is the acted moment on this rotor due to the bearing body. The substitution of Eq. (10) into Eq. (9), yields

$$\underline{{\dot{K}}}_{2}^{{\left( {B_{{c_{2} }} } \right)}} = \underline{M}^{ * }_{ext} + \underline{M} .\,\,\,$$
(11)

Let’s substitute Eq. (1) into Eq. (11) and then multiply both sides of the resulted equation by the vector \(\underline{\underline{P}} \cdot \underline{e}\) to get

$$\left( {\underline{\underline{P}} \cdot \underline{e} } \right).\,\underline{{\dot{K}}}_{2}^{{\left( {B_{{c_{2} }} } \right)}} = \left( {\underline{\underline{P}} \cdot \underline{e} } \right).\underline{M}^{ * }_{ext} - S\left( {\dot{\beta } - \omega_{ * } } \right).\,\,\,$$
(12)

Since the friction forces between the rotor and the carrier are neglected. Therefore, the vector \(\underline{M}^{ * }_{ext}\) must be perpendicular to the rotor’s axis and consequently Eq. (12) has the form

$$\left( {\underline{\underline{P}} \cdot \underline{e} } \right).\,\underline{{\dot{K}}}_{2}^{{\left( {B_{{c_{2} }} } \right)}} = - S\left( {\dot{\beta } - \omega_{ * } } \right).\,\,\,$$
(13)

Considering that \(m\) is the gyrostat’s mass, \(m_{1}\) is the mass of the CB, and \(m_{2}\) is the rotor’s mass. Then the gyrostat’s momentum has the form

$$\underline{K}_{1} = m_{1} \,\underline{v}_{{c_{1} }} + m_{2} \,\underline{v}_{{c_{2} }} = m\,\underline{v}_{c} ,$$
(14)

where \(\underline{v}_{{c_{1} }} ,\underline{v}_{{c_{2} }} ,\) and \(\underline{v}_{c}\) are the velocities of the points \(c_{1} ,c_{2} ,\) and \(c\), respectively.

Substituting expression (14) into Eq. (6) we get

$$\,\underline{v}_{c} = const$$
(15)

Since the KM of the gyrostat is the sum of the KMs of the CB and the rotor, then we can write

$$\underline{K}_{2} = \underline{K}_{2}^{\left( A \right)} + \underline{K}_{2}^{\left( B \right)} ,$$
(16)

where \(\underline{K}_{2}^{\left( A \right)}\) is the angular momentum of the CB relative to gyrostat's centroid, and \(\underline{K}_{2}^{\left( B \right)}\) is the angular momentum of the rotor relative to the center of the gyrostat’s mass.

$$\left\{ \begin{gathered} \underline{K}_{2}^{\left( A \right)} = \underline{K}_{2}^{{\left( {A_{{c_{1} }} } \right)}} + \left( {\underline{\tau }_{1} \times m_{1} \,\underline{v}_{{c_{1} }} } \right), \hfill \\ \underline{K}_{2}^{{\left( {A_{{c_{1} }} } \right)}} = \underline{\underline{\Theta }}_{1}^{\left( t \right)} \cdot \,\underline{\omega } \,, \hfill \\ \underline{K}_{2}^{\left( B \right)} = \underline{K}_{2}^{{\left( {B_{{c_{2} }} } \right)}} + \left( {\underline{\tau }_{2} \times m_{2} \,\underline{v}_{{c_{2} }} } \right), \hfill \\ \underline{K}_{2}^{{\left( {B_{{c_{2} }} } \right)}} = \underline{\underline{\Theta }}_{2}^{\left( t \right)} \cdot \,\underline{\omega }_{ * } \,, \hfill \\ \underline{v}_{{c_{1} }} = \underline{v}_{c} + \,\underline{\omega } \times \underline{\tau }_{1} \hfill \\ \underline{v}_{{c_{2} }} = \underline{v}_{c} + \,\underline{\omega } \times \underline{\tau }_{2} \,, \hfill \\ \end{gathered} \right.\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$
(17)

where

\(\underline{\tau }_{1}\) the vector \(\underline{cc}_{1}\),

\(\underline{\tau }_{2}\) the vector \(\underline{cc}_{2}\),

\(\underline{K}_{2}^{{\left( {A_{{c_{1} }} } \right)}}\) the KM of the CB relative to its centroid \(c_{1}\).

Substituting the system of equalities (17) into Eq. (16) to get

$$\underline{K}_{2} = \underline{\underline{\Theta }}_{1}^{\left( t \right)} \cdot \,\underline{\omega } \, + \underline{\tau }_{1} \times m_{1} \left( {\underline{v}_{c} + \,\underline{\omega } \, \times \,\,\underline{\tau }_{1} \,} \right) + \underline{\underline{\Theta }}_{2}^{\left( t \right)} \cdot \,\underline{\omega }_{ * } \, + \underline{\tau }_{2} \times m_{2} \left( {\underline{v}_{c} + \,\underline{\omega } \, \times \,\,\underline{\tau }_{2} \,} \right).$$
(18)

Inserting Eqs. (2), (3), (4), (5), and (15) into Eq. (18), to obtain

$$\begin{gathered} \underline{K}_{2} = \underline{\underline{P}} \cdot \underline{\underline{\Theta }}_{1} \cdot \underline{\underline{P}}^{T} \cdot \,\underline{\omega } \, + m_{1} \underline{\tau }_{1} \times \left( {\underline{v}_{c} + \,\underline{\omega } \, \times \,\,\underline{\tau }_{1} \,} \right) + \underline{\underline{P}} \cdot \underline{\underline{Q}} \left( {\beta \underline{e} } \right) \cdot \underline{\underline{\Theta }}_{2} \cdot \underline{\underline{Q}}^{T} \left( {\beta \underline{e} } \right) \cdot \underline{\underline{P}}^{T} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\, \cdot \,\left( {\underline{\omega } + \dot{\beta }\underline{\underline{P}} \cdot \underline{e} } \right)\, + m_{2} \underline{\tau }_{2} \times \left( {\underline{v}_{c} + \,\underline{\omega } \, \times \,\,\underline{\tau }_{2} \,} \right)\,\,\,\,\,\,\,\,\,\,\,\, \Rightarrow \hfill \\ \end{gathered}$$
$$\begin{gathered} \underline{K}_{2} = \underline{\underline{P}} \cdot \left( {\underline{\underline{\Theta }}_{1} + \underline{\underline{\Theta }}_{2} } \right) \cdot \underline{\underline{P}}^{T} \cdot \,\underline{\omega } \, + \left( {m_{1} \underline{\tau }_{1} + m_{2} \underline{\tau }_{2} } \right) \times \underline{v}_{c} + m_{1} \underline{\tau }_{1} \times \left( {\,\underline{\omega } \, \times \,\,\underline{\tau }_{1} \,} \right) \hfill \\ + m_{2} \underline{\tau }_{2} \times \left( {\,\underline{\omega } \, \times \,\,\underline{\tau }_{2} \,} \right) + \underline{\underline{P}} \cdot \underline{\underline{\Theta }}_{2} \cdot \underline{\underline{P}}^{T} \cdot \dot{\beta }\underline{\underline{P}} \cdot \underline{e} \,\,\,\,\,\,\,\,\,\,\,\,\,\, \Rightarrow \hfill \\ \end{gathered}$$
$$\underline{K}_{2} = \underline{\underline{P}} \cdot \left\{ {\underline{\underline{\Theta }} + \left( {m_{1} \tau_{1}^{2} + m_{2} \tau_{2}^{2} } \right)\underline{\underline{E}} - \left( {m_{1} \underline{{\tilde{\tau }}}_{1} \otimes \underline{{\tilde{\tau }}}_{1} + m_{2} \underline{{\tilde{\tau }}}_{2} \otimes \underline{{\tilde{\tau }}}_{2} } \right)} \right\} \cdot \underline{\Omega } + \lambda \dot{\beta }\underline{\underline{P}} \cdot \underline{e} \Rightarrow$$
$$\underline{K}_{2} = \underline{\underline{P}} \cdot \left\{ {\left[ {\underline{\underline{\Theta }} + \left( {m_{1} \tau_{1}^{2} + m_{2} \tau_{2}^{2} } \right)\underline{\underline{E}} - \left( {m_{1} \underline{{\tilde{\tau }}}_{1} \otimes \underline{{\tilde{\tau }}}_{1} + m_{2} \underline{{\tilde{\tau }}}_{2} \otimes \underline{{\tilde{\tau }}}_{2} } \right)} \right] \cdot \underline{\Omega } + \lambda \dot{\beta }\underline{e} } \right\},$$
(19)

where

$$\begin{gathered} \underline{\underline{\Theta }} = \underline{\underline{\Theta }}_{1} + \underline{\underline{\Theta }}_{2} ,\underline{\Omega } = \underline{\underline{P}}^{T} \cdot \underline{\omega } ,\underline{\tau }_{1} (t) = \underline{\underline{P}} \left( t \right) \cdot \underline{{\tilde{\tau }}}_{1} \hfill \\ \,\,\,\,\,\,\,\,,\underline{{\tilde{\tau }}}_{1} = \underline{\tau }_{1} (0),\underline{\tau }_{2} (t) = \underline{\underline{P}} \left( t \right) \cdot \underline{{\tilde{\tau }}}_{2} ,\underline{{\tilde{\tau }}}_{2} = \underline{\tau }_{2} (0). \hfill \\ \end{gathered}$$

Integrating Eq. (8) to obtain

$$\underline{K}_{2} = \underline{L} \,,$$
(20)

where \(\underline{L}\) is a constant vector that can be determined using the initial conditions.

Making use of Eqs. (19) and (20) to get

$$\underline{K}_{2} = \underline{\underline{P}} \cdot \left\{ {\left[ {\underline{\underline{\Theta }} + \left( {m_{1} \tau_{1}^{2} + m_{2} \tau_{2}^{2} } \right)\underline{\underline{E}} - \left( {m_{1} \underline{{\tilde{\tau }}}_{1} \otimes \underline{{\tilde{\tau }}}_{1} + m_{2} \underline{{\tilde{\tau }}}_{2} \otimes \underline{{\tilde{\tau }}}_{2} } \right)} \right] \cdot \underline{\Omega } + \lambda \dot{\beta }\underline{e} } \right\} = \underline{L} .$$
(21)

Let’s denote \(\underline{\underline{\theta }}_{ * }\) the tensor of inertia of gyrostat

$$\underline{\underline{\theta }}_{ * } = \underline{\underline{\Theta }} + \left( {m_{1} \tau_{1}^{2} + m_{2} \tau_{2}^{2} } \right)\underline{\underline{E}} - \left( {m_{1} \underline{{\tilde{\tau }}}_{1} \otimes \underline{{\tilde{\tau }}}_{1} + m_{2} \underline{{\tilde{\tau }}}_{2} \otimes \underline{{\tilde{\tau }}}_{2} } \right).$$

Therefore, Eq. (21) can be rewritten as follows

$$\underline{\underline{P}} \cdot \left\{ {\underline{\underline{\theta }}_{ * } \cdot \underline{\Omega } + \lambda \dot{\beta }\underline{e} } \right\} = \underline{L} .$$
(22)

Let us consider the notations \(l = \left| {\underline{L} } \right|\), and \(\underline{m} = \underline{\underline{P}}^{T} \cdot \underline{{\hat{L}}} \,;\,\,\,\,\underline{{\hat{L}}} = \frac{{\underline{L} }}{{\left| {\underline{L} } \right|}}\), then we can write the previous Eq. (22) in the form

$$\underline{\Omega } = \underline{\underline{\theta }}_{ * }^{ - 1} \cdot \left\{ {l\underline{m} - \lambda \dot{\beta }\underline{e} } \right\}.$$
(23)

Substituting Eqs. (5), (17) into Eq. (13). It is easy to write:

$$\left( {\frac{d}{dt}\left\{ {\underline{\underline{P}} \cdot \underline{\underline{\Theta }}_{2} \cdot \underline{\underline{P}}^{T} \cdot \,\underline{\omega } + \lambda \dot{\beta }\underline{\underline{P}} \cdot \underline{e} } \right\}} \right) \cdot \underline{\underline{P}} \cdot \underline{e} = - S\left( {\dot{\beta } - \omega_{ * } } \right)$$
(24)

After some simple reductions, the previous equation takes the form

$$\frac{d}{dt}\left\{ {\dot{\beta } + \underline{e} \cdot \underline{\Omega } } \right\} = - S\left( {\dot{\beta } - \omega_{ * } } \right).$$
(25)

Hence, the EOM of system have the form

$$\left\{ \begin{gathered} \underline{\Omega } = \underline{\underline{\theta }}_{ * }^{ - 1} \cdot \left\{ {l\underline{m} - \lambda \dot{\beta }\underline{e} } \right\}, \hfill \\ \frac{d}{dt}\left\{ {\dot{\beta } + \underline{e} \cdot \underline{\Omega } } \right\} = - S\left( {\dot{\beta } - \omega_{ * } } \right). \hfill \\ \end{gathered} \right.$$
(26)

For this system to be closed, it must be supplemented the following kinematical relation:

$$\underline{{\dot{m}}} = - \underline{\Omega } \times \underline{m} \,,$$
(27)

which can be proved as follows:

$$\begin{gathered} \,\,\,\,\,\,\,\,\underline{\underline{P}} \cdot \underline{m} = \underline{{\hat{L}}} \hfill \\ \Rightarrow \,\,\underline{\underline{{\dot{P}}}} \cdot \underline{m} = - \underline{\underline{P}} \cdot \underline{{\dot{m}}} \hfill \\ \Rightarrow \underline{\underline{P}} \cdot \left( {\underline{\Omega } \times \underline{m} + \underline{{\dot{m}}} } \right) = \underline{0} \hfill \\ \Rightarrow \underline{{\dot{m}}} + \underline{\Omega } \times \underline{m} = 0. \hfill \\ \end{gathered}$$

Making use of (27) and (26), we can obtain directly

$$\left\{ \begin{gathered} \underline{{\dot{m}}} = - \left\{ {\underline{\underline{\theta }}_{ * }^{ - 1} \cdot \left( {l\underline{m} - \lambda \omega \underline{e} } \right)} \right\} \times \underline{m} \,, \hfill \\ \dot{\omega } + \underline{e} \cdot \underline{\underline{\theta }}_{ * }^{ - 1} \cdot \left\{ {l\underline{{\dot{m}}} - \lambda \dot{\omega }\underline{e} } \right\} = - S\left( {\omega - \omega_{ * } } \right), \hfill \\ \end{gathered} \right.$$
(28)

where \(\omega = \dot{\beta }.\) Thus, the problem now is transformed to the integration of system (28).

Asymptotic Properties Solutions for Large Time

Let’s prove that \(\omega\) is a bounded function. To accomplish this aim, one can write Eq. (28) as follows

$$\frac{d}{dt}\left( {\omega - \omega_{ * } } \right) + \tilde{S}\left( {\omega - \omega_{ * } } \right) = \underline{e}^{ * } \cdot \underline{{\dot{m}}} \,\,,$$
(29)

where

$$\tilde{S} = \frac{S}{{1 - \lambda \underline{e} \cdot \underline{\underline{\theta }}_{ * }^{ - 1} \cdot \underline{e} }}\,\,,\,\,\,\,\,\underline{e}^{ * } = \frac{{l\underline{e} \cdot \underline{\underline{\theta }}_{ * }^{ - 1} }}{{1 - \lambda \underline{e} \cdot \underline{\underline{\theta }}_{ * }^{ - 1} \cdot \underline{e} }}\,\,.$$

Based on the computer algebra system with helping Mathematica program, we can prove that the expression \(\left( {1 - \lambda \underline{e} \cdot \underline{\underline{\theta }}_{ * }^{ - 1} \cdot \underline{e} } \right)\) has the form

$$1 - \lambda \underline{e} \cdot \underline{\underline{\theta }}_{ * }^{ - 1} \cdot \underline{e} = \frac{Q}{R}\,\,,$$

where \(Q = P_{0} + \sum\limits_{i = 1}^{12} {P_{i} } Q_{i} \,,\,\,\,\,\,R = R_{0} + \sum\limits_{i = 1}^{12} {P_{i} } Q_{i} \,,\,\,\,\,\,P_{0} ,\,R_{0} \,,\,P_{i}\) represent themselves sums of positive values,

$$\begin{gathered} Q_{1} = e_{3}^{2} ,\,\,\,\,\,\,Q_{2} = 1 - e_{2}^{2} ,\,\,\,\,\,\,\,Q_{3} = 1 - e_{1}^{2} ,\,\,\,\,\,\,\,Q_{4} = 1 - e_{2}^{2} - e_{3}^{2} , \hfill \\ Q_{5} = e_{1}^{2} - e_{3}^{2} ,\,\,\,\,\,\,\,Q_{6} = 1 - e_{1}^{2} - e_{2}^{2} ,\,\,\,\,\,\,\,Q_{7} = 1 - e_{1}^{2} - e_{2}^{2} - e_{3}^{2} , \hfill \\ \end{gathered}$$
$$\begin{aligned} Q_{8} & = t_{1}^{2} - e_{1}^{2} t_{1}^{2} - 2e_{1} e_{2} t_{1} t_{2} + t_{2}^{2} - e_{2}^{2} t_{2}^{2} + 2t_{3}^{2} - e_{1}^{2} t_{3}^{2} - e_{2}^{2} t_{3}^{2} \\ & = \left( {e_{2}^{2} + e_{3}^{2} } \right)t_{1}^{2} + \left( {e_{1}^{2} + e_{3}^{2} } \right)t_{2}^{2} - 2e_{1} e_{2} t_{1} t_{2} + \left( {2 - e_{1}^{2} - e_{2}^{2} } \right)t_{3}^{2} \\ & = \left( {e_{2} t_{1} - e_{1} t_{2} } \right)^{2} + e_{3}^{2} t_{1}^{2} + e_{3}^{2} t_{2}^{2} + \left( {2 - e_{1}^{2} - e_{2}^{2} } \right)t_{3}^{2} \ge 0, \\ \end{aligned}$$
$$\begin{aligned} Q_{9} & = 2t_{1}^{2} - e_{2}^{2} t_{1}^{2} - e_{3}^{2} t_{1}^{2} + t_{2}^{2} - e_{2}^{2} t_{2}^{2} - 2e_{2} e_{3} t_{2} t_{3} + t_{3}^{2} - e_{3}^{2} t_{3}^{2} \\ & = \left( {e_{2}^{2} + e_{1}^{2} } \right)t_{3}^{2} + \left( {e_{1}^{2} + e_{3}^{2} } \right)t_{2}^{2} - 2e_{2} e_{3} t_{2} t_{3} + \left( {2 - e_{3}^{2} - e_{2}^{2} } \right)t_{1}^{2} \\ & = \left( {e_{2} t_{3} - e_{3} t_{2} } \right)^{2} + e_{1}^{2} t_{3}^{2} + e_{1}^{2} t_{2}^{2} + \left( {2 - e_{3}^{2} - e_{2}^{2} } \right)t_{1}^{2} \ge 0, \\ \end{aligned}$$
$$\begin{aligned} Q_{10} & = t_{1}^{2} - e_{1}^{2} t_{1}^{2} + 2t_{2}^{2} - e_{1}^{2} t_{2}^{2} - e_{3}^{2} t_{2}^{2} - 2e_{1} e_{3} t_{1} t_{3} + t_{3}^{2} - e_{3}^{2} t_{3}^{2} \\ & = \left( {e_{2}^{2} + e_{1}^{2} } \right)t_{3}^{2} + \left( {e_{2}^{2} + e_{3}^{2} } \right)t_{1}^{2} - 2e_{1} e_{3} t_{1} t_{3} + \left( {2 - e_{3}^{2} - e_{1}^{2} } \right)t_{2}^{2} \\ & = \left( {e_{1} t_{3} - e_{3} t_{1} } \right)^{2} + e_{2}^{2} t_{3}^{2} + e_{2}^{2} t_{1}^{2} + \left( {2 - e_{3}^{2} - e_{1}^{2} } \right)t_{2}^{2} \ge 0, \\ \end{aligned}$$
$$\begin{aligned} Q_{11} & = 2t_{1}^{2} - 2e_{1}^{2} t_{1}^{2} - e_{2}^{2} t_{1}^{2} - e_{3}^{2} t_{1}^{2} - 2e_{1} e_{2} t_{1} t_{2} + 2t_{2}^{2} - e_{1}^{2} t_{2}^{2} - 2e_{2}^{2} t_{2}^{2} - e_{3}^{2} t_{2}^{2} \\ & \, - 2e_{1} e_{3} t_{1} t_{3} - 2e_{2} e_{3} t_{2} t_{3} + 2t_{3}^{2} - e_{1}^{2} t_{3}^{2} - e_{2}^{2} t_{3}^{2} - 2e_{3}^{2} t_{3}^{2} = \left( {e_{2}^{2} + e_{3}^{2} } \right)t_{1}^{2} \\ & \, + \left( {e_{1}^{2} + e_{3}^{2} } \right)t_{2}^{2} + \left( {e_{1}^{2} + e_{2}^{2} } \right)t_{3}^{2} - 2e_{1} e_{2} t_{1} t_{2} - 2e_{1} e_{3} t_{1} t_{3} - 2e_{2} e_{3} t_{2} t_{3} \\ \, & = \left( {e_{2} t_{1} - e_{1} t_{2} } \right)^{2} + \left( {e_{1} t_{3} - e_{3} t_{1} } \right)^{2} + \left( {e_{3} t_{2} - e_{2} t_{3} } \right)^{2} \ge 0, \\ \end{aligned}$$
$$\begin{aligned} Q_{12} & = t_{1}^{4} - e_{1}^{2} t_{1}^{4} - 2e_{1} e_{2} t_{1}^{3} t_{2} + 2t_{1}^{2} t_{2}^{2} - e_{1}^{2} t_{1}^{2} t_{2}^{2} - e_{2}^{2} t_{1}^{2} t_{2}^{2} - 2e_{1} e_{2} t_{1} t_{2}^{3} + t_{2}^{4} - e_{2}^{2} t_{2}^{4} - 2e_{1} e_{3} t_{1}^{3} t_{3} \\ & \, - 2e_{2} e_{3} t_{1}^{2} t_{2} t_{3} - 2e_{1} e_{3} t_{1} t_{2}^{2} t_{3} - 2e_{2} e_{3} t_{2}^{3} t_{3} + 2t_{1}^{2} t_{3}^{2} - e_{1}^{2} t_{1}^{2} t_{3}^{2} - e_{3}^{2} t_{1}^{2} t_{3}^{2} - 2e_{1} e_{2} t_{1} t_{2} t_{3}^{2} + 2t_{2}^{2} t_{3}^{2} \\ & \, - e_{2}^{2} t_{2}^{2} t_{3}^{2} - e_{3}^{2} t_{2}^{2} t_{3}^{2} - 2e_{1} e_{3} t_{1} t_{3}^{3} - 2e_{2} e_{3} t_{2} t_{3}^{3} + t_{3}^{4} - e_{3}^{2} t_{3}^{4} \\ \end{aligned}$$
$$\begin{gathered} = t_{1}^{2} \left\{ {t_{1}^{2} \left( {e_{2}^{2} + e_{3}^{2} } \right) - 2e_{1} e_{2} t_{1} t_{2} - 2e_{1} e_{3} t_{1} t_{3} - 2e_{2} e_{3} t_{2} t_{3} } \right\} + t_{2}^{2} \left\{ {t_{2}^{2} \left( {e_{1}^{2} + e_{3}^{2} } \right) - 2e_{1} e_{2} t_{1} t_{2} } \right. \hfill \\ \left. { - 2e_{1} e_{3} t_{1} t_{3} - 2e_{2} e_{3} t_{2} t_{3} } \right\} + t_{3}^{2} \left\{ {t_{3}^{2} \left( {e_{1}^{2} + e_{2}^{2} } \right) - 2e_{1} e_{2} t_{1} t_{2} - 2e_{1} e_{3} t_{1} t_{3} - 2e_{2} e_{3} t_{2} t_{3} } \right\} \hfill \\ + t_{1}^{2} t_{2}^{2} \left( {e_{1}^{2} + e_{2}^{2} + 2e_{3}^{2} } \right) + t_{1}^{2} t_{3}^{2} \left( {e_{1}^{2} + e_{3}^{2} + 2e_{2}^{2} } \right) + t_{2}^{2} t_{3}^{2} \left( {e_{2}^{2} + e_{3}^{2} + 2e_{1}^{2} } \right) \hfill \\ \end{gathered}$$
$$\,\,\,\,\, = \left\{ {t_{1}^{2} + t_{2}^{2} + t_{3}^{2} } \right\}\left\{ {\left( {e_{2} t_{1} - e_{1} t_{2} } \right)^{2} + \left( {e_{3} t_{1} - e_{1} t_{3} } \right)^{2} + \left( {e_{2} t_{3} - e_{3} t_{2} } \right)^{2} } \right\} + 2\left( {t_{1}^{2} t_{2}^{2} e_{3}^{2} + t_{1}^{2} t_{3}^{2} e_{2}^{2} + t_{2}^{2} t_{3}^{2} e_{1}^{2} } \right) \ge 0,$$

where \((t_{1} ,t_{2} ,t_{3} )\) and \((e_{1} ,e_{2} ,e_{3} )\) are the components of the vector \(\underline{\tau }_{1}\) and the unit vector \(\underline{e}\), respectively.

Therefore, \(Q_{i} \ge 0\,\,\,\left( {i = 1,2,...,12} \right).\) Thus, \(\left( {1 - \lambda \underline{e} \cdot \underline{\underline{\theta }}_{ * }^{ - 1} \cdot \underline{e} } \right)\) > 0 is proved.

Integrating Eq. (29) to get

$$\omega - \omega_{ * } = e^{{ - \tilde{S}\,t}} \left\{ {c + \int {(\underline{e}^{ * } \cdot \underline{{\dot{m}}} )e^{{\tilde{S}\,t}} dt} } \right\};\,\,\,\,\,c = const,$$
(30)

In the previous equation, the integral may be expanded by parts to have the following form

$$\omega - \omega_{ * } = c\,e^{{ - \tilde{S}\,t}} + \underline{e}^{ * } \cdot \underline{m} - \tilde{S}\,e^{{ - \tilde{S}\,t}} \int {(\underline{e}^{ * } \cdot \underline{m} )e^{{\tilde{S}\,t}} dt} .$$

The function \((\underline{e}^{ * } \cdot \underline{m} )\) is limited, since \(\left| {\underline{e}^{ * } } \right| = const,\,\left| {\underline{m} } \right| = 1.\) Therefore, \(\left| {\,\underline{e}^{ * } \cdot \underline{m} } \right| \le \left| {\underline{e}^{ * } } \right|\). Then

$$\left| {\omega - \omega_{ * } } \right| \le \left| c \right|\,e^{{ - \tilde{S}\,t}} + \left| {\underline{e}^{ * } } \right| + \tilde{S}\,e^{{ - \tilde{S}\,t}} \int {\left| {\underline{e}^{ * } } \right|e^{{\tilde{S}\,t}} dt} = \left| c \right|\,e^{{ - \tilde{S}\,t}} + 2\left| {\underline{e}^{ * } } \right|.$$

Then the value \(\omega - \omega_{ * }\) is bounded. Since \(\omega_{ * } = const.,\) \(\omega\) is bounded.

Now, we are going to prove that \(\omega\) tends to \(\omega_{ * }\) at \(t\) tends to infinity. To gain this purpose multiplying the first equation of the system (28) by \(\left( {\underline{\underline{\theta }}_{ * }^{ - 1} \cdot \left( {l\underline{m} - \lambda \,\omega \,\underline{e} } \right)} \right)\) to get

$$\underline{{\dot{m}}} .\,\underline{\underline{\theta }}_{ * }^{ - 1} \cdot \left( {l\underline{m} - \lambda \,\omega \,\underline{e} } \right) = 0.$$
(31)

This equation can be converted to the form

$$\frac{{l^{2} }}{2}\left( {\underline{m} .\,\underline{\underline{\theta }}_{ * }^{ - 1} \cdot \underline{m} } \right)^{ \cdot } + \lambda \,\omega \left( {1 - \lambda \underline{e} \cdot \underline{\underline{\theta }}_{ * }^{ - 1} \cdot \underline{e} } \right)\underline{e}^{ * } \cdot \underline{{\dot{m}}} = 0,$$
(32)

where

$$\underline{e}^{ * } = \frac{{l\,\underline{e} \cdot \underline{\underline{\theta }}_{ * }^{ - 1} }}{{1 - \lambda \underline{e} \cdot \underline{\underline{\theta }}_{ * }^{ - 1} \cdot \underline{e} }}\,\,$$

Substituting Eq. (29) into Eq. (32), we have

$$\omega \left( {\omega - \omega_{ * } } \right) = - \frac{1}{{2\lambda \,\tilde{S}}}\left\{ {\frac{{l^{2} \,\underline{m} \cdot \underline{\underline{\theta }}_{ * }^{ - 1} \cdot \underline{m} }}{{1 - \lambda \underline{e} \cdot \underline{\underline{\theta }}_{ * }^{ - 1} \cdot \underline{e} }} + \lambda \,\omega^{2} } \right\}^{ \cdot } ,$$
(33)

Integrating Eq. (33) to get

$$\int {\omega \left( {\omega - \omega_{ * } } \right)} \,dt = - \frac{1}{{2\lambda \,\tilde{S}}}\left\{ {\frac{{l^{2} \,\underline{m} \cdot \underline{\underline{\theta }}_{ * }^{ - 1} \cdot \underline{m} }}{{1 - \lambda \underline{e} \cdot \underline{\underline{\theta }}_{ * }^{ - 1} \cdot \underline{e} }} + \lambda \,\omega^{2} } \right\}.$$
(34)

Integrating Eq. (29), it follows

$$\int {\omega_{ * } \left( {\omega - \omega_{ * } } \right)} \,dt = \frac{{\omega_{ * } }}{{\tilde{S}}}\left\{ {\underline{e}^{ * } \cdot \underline{m} - \left( {\omega - \omega_{ * } } \right)} \right\}.$$
(35)

Subtracting Eq. (35) from Eq. (34), to yield

$$\int {\left( {\omega - \omega_{ * } } \right)^{2} } \,dt = - \frac{1}{{\,\tilde{M}}}\left\{ {\frac{{l^{2} \,\underline{m} \cdot \underline{\underline{\theta }}_{ * }^{ - 1} \cdot \underline{m} }}{{2\lambda \left( {1 - \lambda \underline{e} \cdot \underline{\underline{\theta }}_{ * }^{ - 1} \cdot \underline{e} } \right)}} + \frac{{\omega^{2} }}{2} + \omega_{ * } \left( {\underline{e}^{ * } \cdot \underline{m} } \right) - \omega + \omega_{ * } } \right\}.$$

Since \(\left| {\underline{m} } \right| = 1,\,\,\omega\)—bonded value, the right side of the last equation is also bounded.

Therefore, \(\int {\left( {\omega - \omega_{ * } } \right)^{2} } \,dt \le D;\,\,D - {\text{bounded}}\,{\text{value}}.\,\) Then, \(\omega\) tends to \(\omega_{ * }\) at \(t\) tends to infinity, i.e., \(\omega \mathop{\longrightarrow}\limits^{t \to \infty }\omega_{ * } .\)

Let's prove that:

$$\begin{gathered} \,\,\underline{m} \mathop{\longrightarrow}\limits^{t \to \infty }const, \hfill \\ \,\underline{\underline{P}} \mathop{\longrightarrow}\limits^{t \to \infty }\underline{\underline{P}} (\psi (t)\underline{{\hat{L}}} ) \cdot \underline{\underline{P}}_{0} ,\, \hfill \\ \end{gathered}$$

where \(\psi (t)\) the rotation angle about the vector \(\underline{{\hat{L}}}\) and \(\,\underline{\underline{P}}_{0} = const.\)

Since \(\omega \mathop{\longrightarrow}\limits^{t \to \infty }\omega_{ * } ,\) then from Eq. (33), it is easy to write

$$\mathop {\lim }\limits_{t \to \infty } \left\{ {\,\underline{m} \cdot \underline{\underline{\theta }}_{ * }^{ - 1} \cdot \underline{m} + \frac{{\lambda \,\omega^{2} }}{{l^{2} }}\left( {1 - \lambda \underline{e} \cdot \underline{\underline{\theta }}_{ * }^{ - 1} \cdot \underline{e} } \right)} \right\}^{ \cdot } = 0,$$
(36)

and then, we can obtain

$$\mathop {\lim }\limits_{t \to \infty } \,\,\,\underline{m} \cdot \underline{\underline{\theta }}_{ * }^{ - 1} \cdot \underline{m} = const$$
(37)

Consequently, using (26), we can write

$$\mathop {\lim }\limits_{t \to \infty } \,\,\,\underline{e} \cdot \underline{\Omega } = const$$
(38)

Multiplying both sides of the first Eq. (26) scalar by \(\underline{e}\), it easy to have:

$$\,\,\underline{e}_{ * } \cdot \underline{m} = \frac{{\underline{e} \cdot \underline{\Omega } }}{{l\left| {\underline{e} \cdot \underline{\underline{\theta }}_{ * }^{ - 1} } \right|}} + \frac{\lambda \,\omega }{l}\underline{e}_{ * } \cdot \underline{e} \,\,,$$
(39)

where \(\underline{e}_{ * } = \frac{{\,\underline{e} \cdot \underline{\underline{\theta }}_{ * }^{ - 1} }}{{\left| {\underline{e} \cdot \underline{\underline{\theta }}_{ * }^{ - 1} } \right|}}\,.\)

Therefore,

$$\mathop {\lim }\limits_{t \to \infty } \,\,\,\underline{e}_{ * } \cdot \underline{m} = const$$
(40)

Now, we have three scalar Eqs. (37), (40), and \(\left| {\underline{m} } \right| = 1\) that containing the components of the vector \(\underline{m}\). The right-hand side of each equation equals constant for the large values of time t. Therefore, we get

$$\mathop {\lim }\limits_{t \to \infty } \,\,\underline{m} = const$$
(41)

The turn tensor of CB is \(\underline{\underline{P}}\). It takes the form:

$$\underline{\underline{P}} = \underline{\underline{P}} (\psi (t)\underline{{\hat{L}}} ) \cdot \underline{\underline{P}}_{0} \,.$$

Since \(\underline{m} = \underline{\underline{P}}^{T} \cdot \underline{{\hat{L}}} = \underline{\underline{P}}_{0}^{T} \cdot \underline{{\hat{L}}} \,,\,\,\mathop {\lim }\limits_{t \to \infty } \,\underline{m} = const,\,{\text{then }}\underline{\underline{P}}_{0} { = }const \,\).

Left and right AV of the CB have the form:

$$\underline{\omega } = \dot{\psi }\underline{{\hat{L}}} + P(\psi \underline{{\hat{L}}} ) \cdot \underline{\omega }_{0} ,\,\,\underline{\Omega } = \dot{\psi }\underline{m} + \underline{\Omega }_{0}$$

Thus, from the first Eq. (26) follows:

$$\mathop {\lim }\limits_{t \to \infty } \,\,\underline{\Omega } = \mathop {\lim }\limits_{t \to \infty } \,\dot{\psi }\,\underline{m} = const$$
(42)

Then

$$\mathop {\lim }\limits_{t \to \infty } \,\dot{\psi }\, = const$$

Asymptotic Solutions of the Problem for Large Time

To transform the EOM of the system (26) to another appropriate one at a large time, let us introduce the notations:

$$\begin{gathered} \underline{\underline{P}}_{\infty } = \mathop {\lim }\limits_{t \to \infty } \,\underline{\underline{P}} (t), \hfill \\ \underline{m}_{\infty } \, = \mathop {\lim }\limits_{t \to \infty } \,\underline{m} (t),\, \hfill \\ \,\underline{\Omega }_{\infty } \, = \mathop {\lim }\limits_{t \to \infty } \,\underline{\Omega } (t),\,\, \hfill \\ \dot{\psi }_{\infty } \, = \mathop {\lim }\limits_{t \to \infty } \,\dot{\psi }(t)\,. \hfill \\ \end{gathered}$$

Then at large time \(t\), we will look for a solution in the form

$$\left\{ \begin{gathered} \dot{\beta }(t) = \omega_{ * } + \dot{\beta }_{ * } (t), \hfill \\ \dot{\psi }(t) = \dot{\psi }_{\infty } + \dot{\psi }_{ * } (t), \hfill \\ \underline{m} (t) = \underline{m}_{\infty } + \underline{m}_{ * } (t), \hfill \\ \underline{\Omega } (t) = \underline{\Omega }_{\infty } + \underline{\Omega }_{ * } (t), \hfill \\ \end{gathered} \right.\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$
(43)

where \(\dot{\beta }_{ * } \,,\dot{\psi }_{ * } ,\,\left| {\underline{m}_{ * } } \right|,\) and \(\left| {\underline{\Omega }_{ * } } \right|\) are much less than \(\omega_{ * } \,,\dot{\psi }_{\infty } ,\,\left| {\underline{m}_{\infty } } \right|,\) and \(\left| {\underline{\Omega }_{\infty } } \right|\), respectively.

Inserting the expressions (43) into (26) to obtain the following system which determines the values \(\dot{\beta }_{ * } \,,\dot{\psi }_{ * } ,\,\underline{m}_{ * } ,\) and \(\underline{\Omega }_{ * }\)

$$\left\{ \begin{gathered} \underline{\Omega }_{ * } = \underline{\underline{\theta }}_{ * }^{ - 1} \cdot \left\{ {l\underline{m}_{ * } - \lambda \dot{\beta }_{ * } \underline{e} } \right\} \hfill \\ \frac{d}{dt}\left\{ {\dot{\beta }_{ * } + \underline{e} \cdot \underline{\Omega }_{ * } } \right\} = - S\dot{\beta }_{ * } \,\,. \hfill \\ \end{gathered} \right.$$
(44)

At large \(t\), it may be represented \(\underline{\underline{P}}\) in the form

$$\underline{\underline{P}} = \underline{\underline{P}}_{\infty } \cdot \underline{\underline{P}} (\underline{\gamma } ),$$

where \(\left| {\underline{\gamma } } \right|\)—small value.

So that

$$\underline{\underline{P}} (\underline{\gamma } ) = \underline{\underline{E}} + \underline{\gamma } \times \underline{\underline{E}} .$$
(45)

The left AV vector of the CB has the form

$$\underline{\omega } = \underline{\omega }_{\infty } + \underline{\underline{P}}_{\infty } \cdot \underline{{\dot{\gamma }}} \,\,\,.$$
(46)

The right AV vector of the CB can be written as

$$\underline{\Omega } = \underline{\underline{P}}^{T} \cdot \underline{\omega } = \underline{\Omega }_{\infty } + \underline{\Omega }_{\infty } \times \underline{\gamma } + \underline{{\dot{\gamma }}} \,\,\,.$$
(47)

Substituting the last equation of the system (43) into Eq. (47) to obtain

$$\underline{\Omega }_{ * } = \underline{\Omega }_{\infty } \times \underline{\gamma } + \underline{{\dot{\gamma }}} \,\,\,,$$
(48)

where the vector \(\underline{m}\) can be calculated as follows

$$\underline{m} = \underline{\underline{P}}^{T} \cdot \,\underline{{\hat{L}}} = \left( {\underline{\underline{P}}_{\infty } \cdot \underline{\underline{P}} \left( {\underline{\gamma } } \right)} \right)^{T} \cdot \,\underline{{\hat{L}}} = \underline{\underline{P}}^{T} \left( {\underline{\gamma } } \right) \cdot \underline{\underline{P}}_{\infty }^{T} \cdot \,\underline{{\hat{L}}} = \left( {\underline{\underline{E}} - \underline{\gamma } \times \underline{\underline{E}} } \right) \cdot \underline{m}_{\infty } \,\,.$$

Thus

$$\underline{m} = \underline{m}_{\infty } + \underline{m}_{\infty } \times \underline{\gamma } \cdot \,$$
(49)

Substituting expressions (43) into Eq. (49), to have

$$\underline{m}_{ * } = \underline{m}_{\infty } \times \underline{\gamma } \cdot \,$$
(50)

Equation (42) can be rewritten as follows

$$\underline{\Omega }_{\infty } = \dot{\psi }_{\infty } \underline{m}_{\infty } \,$$
(51)

Using (48) and (50) in system (44) to get

$$\left\{ \begin{gathered} \underline{\Omega }_{\infty } \times \underline{\gamma } + \underline{{\dot{\gamma }}} = \underline{\underline{\theta }}_{ * }^{ - 1} \cdot \left\{ {l\underline{m}_{\infty } \times \underline{\gamma } - \lambda \dot{\beta }_{ * } \underline{e} } \right\} \hfill \\ \frac{d}{dt}\left\{ {\dot{\beta }_{ * } + \underline{e} \cdot \underline{\underline{\theta }}_{ * }^{ - 1} \cdot \left( {l\underline{m}_{\infty } \times \underline{\gamma } - \lambda \dot{\beta }_{ * } \underline{e} } \right)} \right\} = - S\dot{\beta }_{ * } \,\,. \hfill \\ \end{gathered} \right.$$
(52)

The previous system of Eqs. (52) represents a system of four scalar linear differential equations of first order, which can be abbreviated to a system of three scalar differential equations of the same order in addition to one independent equation. Therefore, let us introduce the following notation

$$\underline{\gamma } = \gamma_{3} \underline{m}_{\infty } + \underline{{\tilde{\gamma }}} \,\,\,;\,\,\,\underline{{\tilde{\gamma }}} \, \cdot \underline{m}_{\infty } = 0.\,$$
(53)

Inserting (51) and (53) into the system (52) to get

$$\left\{ \begin{gathered} \dot{\psi }_{\infty } \underline{m}_{\infty } \times \underline{{\tilde{\gamma }}} + \underline{{\dot{\tilde{\gamma }}}} = \left( {\underline{\underline{E}} - \underline{m}_{\infty } \otimes \underline{m}_{\infty } } \right) \cdot \underline{\underline{\theta }}_{ * }^{ - 1} \cdot \left\{ {l\underline{m}_{\infty } \times \underline{\gamma } - \lambda \dot{\beta }_{ * } \underline{e} } \right\} \hfill \\ \frac{d}{dt}\left\{ {\dot{\beta }_{ * } + \underline{e} \cdot \underline{\underline{\theta }}_{ * }^{ - 1} \cdot \left( {l\underline{m}_{\infty } \times \underline{\gamma } - \lambda \dot{\beta }_{ * } \underline{e} } \right)} \right\} = - S\dot{\beta }_{ * } \,\,, \hfill \\ \end{gathered} \right.$$
(54)

and

$$\dot{\gamma }_{3} = \underline{m}_{\infty } \cdot \underline{\underline{\theta }}_{ * }^{ - 1} \cdot \left( {l\underline{m}_{\infty } \times \underline{{\tilde{\gamma }}} - \lambda \dot{\beta }_{ * } \underline{e} } \right)\,\,.\,$$
(55)

Using \(\dot{\beta }_{ * } = B\,e^{\delta t}\) and \(\underline{{\tilde{\gamma }}} = \underline{\Gamma } e^{\delta t}\) in (54), we get an equation of third degree in terms of \(\delta\) that depends on all parameters of the problem. The numerical analysis of the obtained outcomes can be described: for any parameters \(\left( {Re\,\delta < 0\,} \right).\). Figures 2, 3 show the two projections of the vector \(\underline{{\tilde{\gamma }}}\) and the plots of the functions \(\dot{\beta }_{ * }\) and \(\gamma_{3} .\)

Fig. 2
figure 2

Projections of \(\underline{{\widetilde{\gamma }}}\)

Full size image
Fig. 3
figure 3

\(\mathop \beta \limits^{ \cdot }_{ * } ,\gamma_{3}\)

Full size image

For more description, the previous Eqs. (54) and (55) can be rewritten in scalar forms according to selected parameters in addition to the given initial conditions. Then, let us consider the following chosen values of these parameters

$$\begin{gathered} \underline{e} = \left( {0.5,0.5,\frac{1}{\sqrt 2 }} \right),\dot{\psi }_{\infty } = 1{\text{rad}}/\sec ,l = 1, \hfill \\ \lambda = 2{\text{kg}}{\text{.m}}^{{2}} ,S = 4{\text{kg}}.{\text{m}}^{{2}} {\text{/sec}},\underline{m}_{\infty } = (0,0,1), \hfill \\ \theta_{1} = 3{\text{kg}}{\text{.m}}^{{2}} ,\theta_{2} = 5{\text{kg}}{\text{.m}}^{{2}} ,\theta_{3} = 7{\text{kg}}{\text{.m}}^{{2}} ,\underline{{\tilde{\gamma }}} = \left( {\tilde{\gamma }_{1} ,\tilde{\gamma }_{1} ,0} \right), \hfill \\ \tilde{\gamma }_{1} \left( 0 \right) = 10,\tilde{\gamma }_{2} \left( 0 \right) = 11,\beta_{*} \left( 0 \right) = 2,\dot{\beta }_{*} \left( 0 \right) = 0.01,\gamma_{3} \left( 0 \right) = 5. \hfill \\ \end{gathered}$$

Then the Eqs. (54) and (55) may be reduced to the following four differential equations

$$- \dot{\tilde{\gamma }}_{1} - \frac{{2\tilde{\gamma }_{2} }}{3}\, + \,\frac{{\dot{\beta }_{*} }}{3}\, = \,0$$
$$\dot{\tilde{\gamma }}_{2} + \frac{{4\tilde{\gamma }_{1} }}{5} + \frac{{\dot{\beta }_{*} }}{5} = 0$$
$$- 0.1\dot{\tilde{\gamma }}_{1} + 0.167\dot{\tilde{\gamma }}_{2} + 4\,\dot{\beta }_{*} + 1.41\ddot{\beta }_{*} = 0$$
$$\dot{\gamma }_{3} + \frac{\sqrt 2 }{7}\dot{\beta }_{*} = 0$$

Based on these equations, one can observe that the first three ones depend on the same three independent variables. They constitute a system of linear differential equations of the third order, while the last equation is given in terms of the fourth variable. Curves of Fig. 2 show that the time behaviors of the functions \(\tilde{\gamma }_{1}\) and \(\tilde{\gamma }_{2}\) have decay manner as time go on till the end of time interval. Moreover, the temporal histories of the functions \(\dot{\beta }_{*}\) and \(\gamma_{3}\) approach to constant values, as plotted in Fig. 3. Therefore, we can conclude that the behaviors of the interpretation functions of the gyrostat have stable manners.

Conclusion

Using the asymptotic technique, the analytical solution, for large time, of the problem of a one-rotor gyrostat moving freely under the action of a motor with restricted power has been investigated. The kinematic EOM have been derived using the mechanics’ basic laws and according to the procedure of the direct tensor calculus tools. The asymptotic characteristics of large-time solutions have been examined. It has been proved that the motion of the CB tends to rotate around a fixed axis and the direction of which depends on all parameters of the problem besides the initial conditions. A set of linear differential equations that approximates the motion of a gyrostat over a large time has been derived. It has been demonstrated that, the parameters and initial conditions of the problem affect the motion of the carrier body that is near to the rotation around a fixed axis. Numerical analysis was used to support the stability of motion.