1 Introduction

With the development of technologies such as propulsion systems and sensors, the intelligent game between exoatmospheric vehicles has become a worthwhile research topic. Due to the extremely high speeds and the lack of aerodynamic forces, maneuverability for these vehicles is limited by their finite energy, making exoatmospheric pursuit-evasion game a challenging problem.

Many researchers have studied pursuit-evasion problems using geometry analysis method, optimal control, and differential game methods. Extensive research has been conducted on the interception problem for pursuers, focusing on aspects such as convergence of line-of-sight angle, time constraints, terminal angle constraints, and energy consumption. The Apollonius circle geometry analysis method is perhaps the most classic research approach in this field. However, this method significantly simplifies problems by assuming a constant velocity and neglecting realistic complex dynamics. In recent years, some researchers have explored Apollonius circles geometric analysis method to address pursuit-evasion problems with multiple participants [1]. However, the problem is still modeled as a simplified two-dimensional scene. Liu et al. [2] addressed the problem of a low-speed missile intercepting a hypersonic vehicle in the longitudinal plane. The guidance system is established by defining the LOS angular rate as the state variable. He et al. [3] and Reisner et al. [4] studied exoatmospheric the interception problem based on optimal control theory, taking into account finite time and interception angle constraints. Liang et al. [5, 6] investigated the guidance problem for interceptors against spacecraft with active defense, considering fuel cost, control saturation, chattering phenomenon and parameters selection. Wang et al. [7] proposed a cooperative augmented proportional guidance for proximity to uncooperative space targets.

For the evader, the primary objective is to avoid entering the pursuer’s kill radius. However, the evader also has an ultimate goal of striking a specific target or flying to a particular area. Evading the pursuer becomes a necessary condition for accomplishing the final goal. Therefore, the evader often needs to compromise between the evasion task and the ultimate objective. Consequently, it becomes difficult for the evader to choose a suitable evasion strategy. Therefore, several literatures have investigated scenarios in which the evader carries a defender for active defense [8,9,10]. With assistance, the evasion task for the evader becomes significantly simpler. However, only a few studies have focused on investigating a single evader’s strategies. Shaferman et al. [11] proposed a Near-optimal evasion strategies for an evader, exploiting the inherent time delay associated with the pursuer’s estimate of the evader’s acceleration to maximize the miss distance. Carr Ryan et al. [12] investigates]d a scenario where proportional navigation is nearly optimal for the pursuer and solves the differential game solution for the evader in this scenario. Fonod Robert et al. [13] proposed a multiple model adaptive evasion strategies and analyzed several specific limiting cases in which the attacking missile uses proportional navigation, augmented proportional navigation, or an optimal guidance law.

The references mentioned above mostly employ optimal control or differential game approaches which had two shortcomings. Firstly, simplifying the problem to two dimensions and linearize complex dynamic equations [14] due to the difficulty of solving nonlinear models. However, exoatmospheric missile engagements are characterized by high speeds, short durations, and small kill radii. Achieving high simulation accuracy is crucial, and any model simplification may result in significant errors in terminal miss distance. Secondly, previous research had focused on minimizing energy consumption as one of the evader's goals, but no literature considered the total energy limit as a constraint for the evader. The two approaches are different. The former aims to minimize energy consumption while ensuring a successful evasion, whereas the latter tries to find the optimal evasion strategy within the energy constraints. In exoatmospheric environment, only direct force can be utilized as there is no aerodynamic force. Consequently, the evader must consider the constraint of energy consumption. Therefore, it is necessary to develop a real-time decision-making method that can directly solve the evasion guidance law with nonlinear dynamic equations and strict energy constraint.

Reinforcement learning (RL) is an iterative decision-making method that allows an agent to interact with its environment in real-time, which can solve the two problems above effectively. The decision-making entity, referred to as an agent, observes the current state of the environment and makes decisions based on these observations. The agent then evaluates and enhances its strategy by receiving feedback in the form of reward values from the environment. However, applying reinforcement learning methods to address the problem studied in this paper encounters two significant challenges: firstly, how to effectively handle constraints, and secondly, how to achieve precise control. Traditional reinforcement learning methods typically optimize an agent’s strategy through a reward function. However, when energy consumption is incorporated into the reward function, ensuring compliance with total energy constraints that the agent must satisfy becomes challenging. In certain related research, some researchers refer to the constraints an agent must satisfy as cost. Subsequently, the agent’s objective becomes twofold: to maximize the expected reward value while accumulating sufficient cost to meet the constraint. This approach is known as constrained reinforcement learning (CRL) [15,16,17]. On one hand, the evader’s acceleration command was defined as cost. The accumulated cost of a trajectory must satisfy the total energy constraints. On the other hand, reinforcement learning is commonly employed with stochastic policies to enhance the exploration capability of an agent. However, in missile guidance problems, excessive randomness can result in unnecessary energy consumption. Therefore, a maximum-minimum entropy learning method is proposed to reduce the randomness of acceleration commands without compromising the exploration capability of the agent. In this game, evader’s maneuvering capability is less than that of the pursuer. Simulation results have shown that constrained reinforcement learning can effectively address such constrained decision-making problems. The evader agent is capable of completing the evasion task while satisfying the energy consumption constraint.

The main contributions of this paper are as follows:

  1. 1.

    Constrained reinforcement learning method was proposed to solve the problem of exoatmospheric evasion guidance with total energy constraints.

  2. 2.

    To minimize the randomness of acceleration commands while preserving the agent's exploration capability, we introduce the Maximum-Minimum Entropy Learning method, which is integrated into the agent's learning objective as a constraint term.

  3. 3.

    The effectiveness and robustness of the proposed method have been validated on a randomly generated dataset.

2 Related Work

In recent years, the remarkable advancements of RL in various domains have prompted researchers to explore its application in computational missile guidance. The researchers first demonstrated that reinforcement learning guidance laws have certain advantages compared to proportional navigation methods. He et al. [18] and Hong Daseon et al. [19] studied the comparison between the reinforcement learning guidance law and the traditional proportional guidance law, and the experiment verified that the guidance law based on reinforcement learning can be applied to the missile guidance law. Gaudet et al. [20] showed that the guidance law of reinforcement learning performs better than the proportional guidance method and the enhanced proportional guidance method when considering the noise and time delay of the sensors and actuators.

Reinforcement learning method is also capable of addressing constraint problems in missile guidance, like interception angle constraints. Gong et al. [21] presented an all-aspect attack guidance law for agile missiles based on deep reinforcement learning (DRL), which can effectively cope with the aerodynamic uncertainty and strong nonlinearity in the high angle-of-attack flight phase. Li et al. [22] proposed an assisted deep reinforcement learning (ARL) algorithm to optimize the neural network-based missile guidance controller for head-on interception. Based on the relative velocity, distance, and angle, ARL can control the missile to intercept the maneuvering target and achieve large terminal intercept angle.

Subsequently, reinforcement learning has been further applied to missile active defense [23, 24], spacecraft pursuit-evasion games [25,26,27,28], as well as exoatmospheric missile guidance [29,30,31]. Shalumov et al. [24] tried to find an optimal launch time of the defender and an optimal target guidance law before and after launch using DRL. A policy suggesting at each decision time the bang-bang target maneuver and whether or not to launch the defender was obtained and analyzed via simulations. Simulations showed the ability of the reinforcement learning based method to obtain a close to optimal level of performance in terms of the suggested cost function. Yang et al. [25] proposed a closed-loop pursuit approach using reinforcement learning algorithms to solve and update the pursuit trajectory for the incomplete-information impulsive pursuit-evasion missions. Brandonsio et al. [26] focused towards enhanced autonomy on-board spacecrafts for on-orbit servicing activities using deep reinforcement learning method. Zhao et al. [27] investigated the problem of impulsive orbital pursuit-evasion games using Multi-Agent Deep Deterministic Policy Gradient approach. A closed-loop pursuit approach using reinforcement learning algorithms was proposed to solve and update the pursuit trajectory for the incomplete-information impulsive pursuit-evasion missions. Zhang et al. [28] studied an one-to-one orbital pursuit-evasion problem. A near-optimal guidance law using deep learning is proposed to intercept the evader inside the capture zone. For the games that start outside the barrier, a learning algorithm for the capture zone embedding strategy is presented based on deep reinforcement learning to help the game state cross the barrier surfaces. In [30], reinforcement learning algorithm was applied to the mid-course penetration of extra-atmospheric ballistic missiles. In [31], reinforcement learning combined with meta-learning is applied to the guidance law of extra-atmospheric interceptor. The reinforcement learning algorithm outputs four propulsion instructions for steering thrusters. The results show that reinforcement learning guidance law is superior to the traditional ZEM guidance law in interception rate and energy consumption.

3 Problem Formulation

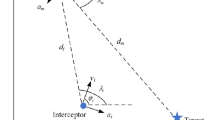
This paper aims to analyze the terminal guidance phase of a 3D exoatmospheric pursuit-evasion problem. The 3D relative kinematics relationship is shown in Fig. 1. The centroid of the evader is represented by the red dot, while the centroid of the pursuer is represented by the blue dot. The inertial coordinate system is denoted as XYZ, while the virtual inertial coordinate system, obtained by shifting the inertial coordinate system to the centroid of the evader, is denoted as X'Y'Z'. The missile body coordinate system is denoted as XmYmZm, where the Xm axis aligns with the missile axis, the Ym axis is perpendicular to the missile in an upward direction, and the Zm axis follows the right-hand rule. The line-of-sight (LOS) coordinate system is denoted as XlYlZl, with the Xl axis coinciding with the line of sight, the Yl axis pointing upward in the vertical plane of the Xl axis, and the Zl axis following the right-hand rule. θ and φ represent the pitch angle and yaw angle, respectively, of the moving coordinate system in relation to the inertial system.

Fig. 1
figure 1

3D relative kinematics relationship

Full size image

3.1 Kinematic and Dynamic Formulas in the Inertial Coordinate System

The kinematic formulas for the evader and pursuer in the inertial frame are:

$$ \left\{ \begin{gathered} {\dot{\mathbf{r}}}_{e} = {\mathbf{v}}_{e} \hfill \\ {\dot{\mathbf{v}}}_{e} = {\mathbf{a}}_{e} \hfill \\ \end{gathered} \right., $$
(1)
$$ \left\{ \begin{gathered} {\dot{\mathbf{r}}}_{p} = {\mathbf{v}}_{p} \hfill \\ {\dot{\mathbf{v}}}_{p} = {\mathbf{a}}_{p} \hfill \\ \end{gathered} \right., $$
(2)

where \({\mathbf{r}} = \left[ {x,y,z} \right]\), \({\mathbf{v}} = \left[ {v_{x} ,v_{y} ,v_{z} } \right]\), \({\mathbf{a}} = \left[ {a_{x} ,a_{y} ,a_{z} } \right]\). The subscripts e and p represent the evader and pursuer, respectively.

Exoatmospheric hypersonic vehicles usually rely on the divert control system located on the side of the vehicle body and near the center of gravity to provide direct forces during the orbit flight phase [32]. As depicted in Fig. 1, the evader’s thrust accelerations are applied along the Ym and Zm axes, and the thrust acceleration of the evader in the missile coordinate system can be expressed as \({\mathbf{a}}_{t}^{m} = \left[ {0,a_{ty} ,a_{tz} } \right]^{m}\). Suppose there is a maximum limit on the thrust acceleration of the evader, denoted as at_max, that is \(\left| {{\mathbf{a}}_{ty} } \right| \le a_{t\_\max }\) and \(\left| {{\mathbf{a}}_{tz} } \right| \le a_{t\_\max }\). The thrust acceleration of the evader in the inertial frame is denoted as \({\mathbf{a}}_{t}^{i} = {\mathbf{C}}_{mi} {\mathbf{a}}_{t}^{m}\), where Cmi is the transformation matrix from the missile body coordinate system to the inertial coordinate system.

The exoatmospheric dynamics equation of the evader is:

$$ {\mathbf{a}}_{e}^{i} = {\mathbf{a}}_{g}^{i} + {\mathbf{a}}_{t}^{i} , $$
(3)

where ag represents the gravitational acceleration of the Earth in the inertial frame, and its expression is:

$$ {\mathbf{a}}_{g} = \left[ \begin{gathered} \frac{GM \cdot x}{{\sqrt {\left( {x^{2} + y^{2} + z^{2} } \right)^{3} } }} \hfill \\ \frac{GM \cdot y}{{\sqrt {\left( {x^{2} + y^{2} + z^{2} } \right)^{3} } }} \hfill \\ \frac{GM \cdot z}{{\sqrt {\left( {x^{2} + y^{2} + z^{2} } \right)^{3} } }} \hfill \\ \end{gathered} \right], $$
(4)

where GM is the gravitational constant, with a value of 3.9753×1014.

Assuming that the pursuer uses proportional guidance, the formula is [33]:

$$ {\mathbf{a}}_{c}^{i} = N\frac{zem}{{t_{{{\text{go}}}}^{{2}} }}, $$
(5)

where N is a guidance gain, zem is the Zero Effort Miss (ZEM) [33] that is perpendicular to the LOS and tgo represents the remaining flight time, which is approximated as:

$$ t_{{{\text{go}}}} = - \frac{R}{{\dot{R}}}. $$
(6)

The exoatmospheric dynamics equation of the pursuer is:

$$ {\mathbf{a}}_{p}^{i} = {\mathbf{a}}_{g}^{i} + {\mathbf{a}}_{c}^{i} . $$
(7)

In this paper, it is assumed that the pursuer's initial ZEM is 0 [34], and the initial velocity vector of the pursuer is determined by solving the two-body Lambert equation.

3.2 Kinematic Formulas in the LOS Coordinate System

Denote the rotation matrices that transform the ECI coordinate system to the LOS coordinate system around the Z, Y, and X axes as CZ, CY, and CX, respectively. The matrix representing the angular velocities of rotation is denoted as \(\Omega^{i}\), which can be expressed as:

$$ {{\varvec{\Omega}}}^{i} = {\mathbf{C}}_{X} {\mathbf{C}}_{Y} {\mathbf{C}}_{Z} \left[ \begin{gathered} 0 \hfill \\ 0 \hfill \\ \dot{\varphi }_{l} \hfill \\ \end{gathered} \right] + {\mathbf{C}}_{X} {\mathbf{C}}_{Y} \left[ \begin{gathered} 0 \hfill \\ \dot{\theta }_{l} \hfill \\ 0 \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} - \dot{\varphi }_{l} \sin \theta_{l} \hfill \\ \, \dot{\varphi }_{l} \cos \theta_{l} \hfill \\ \, - \dot{\theta }_{l} \hfill \\ \end{gathered} \right]. $$
(8)

The kinematic formula in the LOS coordinate system is:

$$ {\mathbf{V}}_{r} = \left[ {\frac{{\delta {\mathbf{R}}}}{\delta t}} \right]^{l} + \left[ {{{\varvec{\Omega}}}^{i} } \right]^{l} \times {\mathbf{R}}. $$
(9)

Substituting Eq. 8 into Eq. 9 yields:

$$ {\mathbf{V}}_{r} = \left[ {\begin{array}{*{20}c} {\dot{R}} \\ { - R\dot{\theta }_{l} } \\ { - R\dot{\varphi }_{l} \cos \theta_{l} } \\ \end{array} } \right]. $$
(10)

Assuming the pursuer utilizes a direct collision interception method with a kill radius of 0.5 m, successful interception by the pursuer is defined when \(R \le 0.5\). Conversely, successful evasion by the evader is defined when \(\dot{R} \ge 0\).

The decision time interval and simulation interval is crucial for the convergence of the algorithm and the accuracy of simulation. Considering the algorithm search space and practical engineering conditions, we set the decision time interval to 0.1 s, which means that an acceleration command is output every 0.1 s. For ballistic simulation, a smaller simulation interval can improve simulation accuracy, but it also increases the training time cost. To accelerate the training process, we set the initial simulation step size to be the same as the decision step size, which is 0.1 s. Meanwhile, to accurately calculate the miss distance at the end, the simulation interval is adjusted to 0.0001 s when the relative distance is less than 2000 m, as depicted in Fig. 2. If the simulation interval is directly set to 0.0001 s, the training time cost will increase by more than 40 times, which would be unacceptable. Additionally, the motion differential equation is updated using the 4th order Runge–Kutta method.

Fig. 2
figure 2

Diagram illustrating simulation accuracy

Full size image

4 Method

To solve the constrained evasion problem in RL framework, we firstly build a Constrained Markov Decision Process (CMDP) and then present the Constrained Proximal Policy Optimization (CPPO) based evasion guidance law.

4.1 CMDP

CMDP differs from the classical MDP by incorporating cost as feedback during the decision-making process. A CMDP can be represented by \(\left( {{\mathbf{S}},{\mathbf{A}},{\mathbf{P}},{\mathbf{R}},{\mathbf{C}}} \right)\), where S is the state space, A is the action space, R denote the reward function and C denote the cost function, respectively, and P is the transition probability function with \(p\left( {{\mathbf{s}}^{\prime } |{\mathbf{s}},{\mathbf{a}}} \right)\) denoting the transition probability from state s to state s′ given action a. A stochastic policy \(\pi :S \to A\) is a mapping from states to probabilities of selecting each possible action. The goal is to find the optimal policy \(\pi^{*}\) that provides the highest expected sum of rewards:

$$ \pi^{ * } = \arg \max E_{\pi } \left\{ {\sum\limits_{t}^{T} {\gamma^{t} r_{t + 1} \left| {s_{0} = s} \right.} } \right\}, $$
(11)

where \(\gamma \in [0,1][0,1]\) is the discount factor. The CMDP problem can be generalized into:

$$ \begin{gathered} \mathop {\max }\limits_{\pi } {\text{ E}}_{\pi } \left\{ {\sum\limits_{t}^{T} {\gamma^{t} r_{t + 1} \left| {s_{0} = s} \right.,a_{0} = a} } \right\} \hfill \\ {\text{ s}}{\text{.t}}{. }\sum\limits_{t}^{T} {c_{t + 1} } \le C, \end{gathered} $$
(12)

where C is the cost limit, and the \(\sum\nolimits_{t}^{T} {c_{t + 1} }\) is the total cost during a trajectory.

This paper assumes that the evasion agent can only observe partial information about the engagement state. Therefore, in the subsequent description, the state s is replaced by the observed variable o. The observation space, action space, cost function, and reward function of CMDP are set as follows.

4.1.1 Environment States and Agent Observations

The environment states can be described in both the inertial coordinate system and the LOS coordinate system. In the inertial coordinate system, the environmental state includes the positional coordinates, velocity vectors, and acceleration vectors of both the pursuer and the evader. In the LOS coordinate system, the environmental state can be described by relative distance and its rate, line-of-sight angles and its rate, as well as elevation angle and its rate.

In this paper, the environment information is only partially observable for the evader. Assuming that the evader is equipped with an infrared sensor, it can directly measure the line-of-sight angles in the missile body coordinate system, as depicted in Fig. 3. Although these two angles can be transformed into the inertial coordinate system or the LOS coordinate system, we choose to directly use these two angles as observations of the agent to minimize errors. However, the information provided by these two angles is insufficient. Therefore, it is assumed that the agent can estimate the relative distance to the pursuer using a filtering algorithm, resulting in a total of three observations, denoted as \(\left[ {\varphi_{m} ,\theta_{m} ,R} \right]\). Furthermore, the evader does not require knowledge of the rate of line-of-sight angle and the rate of relative distance.

Fig. 3
figure 3

Diagram of observations for the evader

Full size image

4.1.2 Action Space

The action output of the actor network is the thrust acceleration in the y-axis and z-axis directions defined in the missile body coordinate system. Specifically, it can be represented as \({\mathbf{a}} = \left[ {a_{y} ,a_{z} } \right]^{m}\), where the superscript m denotes the missile body coordinate system.

4.1.3 Cost Function

The role of the cost function is to calculate the cumulative constraints. For each interaction during training, the single-step constraint is determined by summing the absolute values of the current thrust acceleration, which can be represented as \(c = \tau \left( {\left| {a_{v} } \right| + \left| {a_{z} } \right|} \right)\), where τ is a hyperparameter and is set to 0.1 in this paper.

4.1.4 Reward Function

The reward function plays a crucial role in the reinforcement learning environment as it guides the agent's learning process. Reward functions can be categorized into shaping rewards and end rewards. Shaping rewards are used to guide the agent's exploration during training, while end rewards indicate whether the task has been successfully accomplished or not. In our case, since the acceleration constraint is already accounted for by the cost function, we only employ a sparse reward approach, specifically using an end reward function. If the evader is hit, the task fails and a penalty is given; if the evader successfully avoids being hit, the task succeeds, and a positive reward is given. The expression is as follows:

$$ \left\{ \begin{gathered} r = - \left( {1 - \frac{\left| R \right|}{{R_{kill} }}} \right)\quad {\text{ if }}R \le R_{kill} \hfill \\ r = 0.2\log \left( {2R} \right)\quad \quad {\text{ if }}R > R_{kill} {\text{ and }}\dot{R} \ge {0} \hfill \\ \end{gathered} \right. . $$
(13)

The reward function curve is shown in Fig. 4. The relationship between terminal miss distance and reward is a continuous curve, and the range of reward values is approximately from -1 to 1. When the miss distance is equal to the kill radius, the reward is 0. If the miss distance is smaller than the kill radius, a penalty value is assigned, and the magnitude of the penalty increases as the miss distance decreases. As the miss distance approaches 100 m, the reward value gradually increases, but the rate of change becomes smaller, which informs the agent that the current miss distance is sufficiently large.

Fig. 4
figure 4

Reward function curve

Full size image

4.2 Traditional PPO Algorithms

The PPO [35] algorithm, which is a state-of-art reinforcement learning algorithm, is used as the basic algorithm in this paper. PPO is an on-policy algorithm that operates within the Actor-Critic (AC) framework. The traditional framework of continuous PPO algorithm has two main components: the actor network and the critic network. The actor network is responsible for outputting the distribution of actions, while the critic network evaluates the state value function.

The PPO algorithm utilizes importance sampling method to calculate the ratio of the old policy to the new policy to measure the quality of the new policy, which as shown in formula (14),

$$ p_{n} (\theta ) = \frac{{\pi_{\theta } ({\mathbf{a}}_{n} \left| {{\mathbf{o}}_{n} } \right.)}}{{\pi_{\theta old} ({\mathbf{a}}_{n} \left| {{\mathbf{o}}_{n} } \right.)}}. $$
(14)

The samples obtained through importance sampling can be reused multiple times, and the number of sample usages, denoted as nreuse in this paper, is a crucial hyperparameter in the PPO algorithm. Following the proposal of the PPO algorithm, several versions have been developed, with the clip version being the most commonly used. The clip function is responsible for controlling the gap between the old policy and the new policy. The objective of the PPO algorithm is to maximize the expected value of the advantage function through importance sampling. The objective function is shown in formula (15).

$$\begin{aligned} & J(\theta ) \hfill \\ & = {\text{E}}_{p(\tau )} \left[ {\min \left[ {p_{n} (\theta ),{\text{clip}}(p_{n} (\theta ),1 - \varepsilon ,1 + \varepsilon )} \right]A_{{\mathbf{w}}}^{\pi } ({\mathbf{o}}_{n} ,{\mathbf{a}}_{n} )} \right].\end{aligned} $$
(15)

The advantage function is defined as the difference between the state-action value function and the state value function, and it encourages actions with values greater than the average value. There are various forms to express the advantage function, and the Generalized Advantage Estimation (GAE) is an effective method that provides a good balance between estimation bias and variance. Its expression is given by formula (16).

$$ \begin{aligned}& A_{{\mathbf{w}}}^{\pi } ({\mathbf{o}}_{t} ,{\mathbf{a}}_{t} )_{GAE} \hfill \\ & \quad = \sum\limits_{t = 0}^{T - n - 1} {\left( {\gamma \lambda } \right)^{n} \left[ {r_{t + n} + \gamma V\left( {{\mathbf{o}}_{t + n + 1} } \right) - V\left( {{\mathbf{o}}_{t + n} } \right)} \right]} . \end{aligned}$$
(16)

The objective of the critic network is to predict the value of a given state. The loss function of the critic network is shown in formula (17).

$$ L({\mathbf{w}}) = \sum\limits_{i = 1}^{M} {\left( {V_{{\mathbf{w}}}^{\pi } ({\mathbf{o}}_{n}^{i} ) - \left[ {\sum\limits_{t = n}^{T} {\gamma^{t - n} r({\mathbf{o}}_{t}^{i} ,{\mathbf{a}}_{t}^{i} )} } \right]} \right)^{2} } . $$
(17)

4.3 Maximum-Minimum Entropy Learning method

The formulas (15) to (17) represent the traditional PPO algorithm, where the policy is typically described using a Gaussian distribution. The acceleration command is generated by sampling from the policy distribution, resulting in a certain level of randomness. In general application scenarios like competitive games, random policies are favored because they enhance exploration capabilities, reduce the likelihood of getting stuck in local optima, and exhibit better robustness. For instance, the authors of the Soft Actor-Critic (SAC)[36] algorithm propose incorporating the maximization of entropy learning into the objective of the agent. However, in missile guidance problems, where there are strict limitations on the sum of acceleration commands, excessive randomness can lead to energy waste and hinder the learning of the optimal policy under total energy constraints. Therefore, this paper introduces the maximum-minimum entropy learning method to address this issue. The idea is to encourage exploration during the early stages of training and gradually reduce the randomness of the policy in later stages, thus reducing the randomness of acceleration commands without compromising the exploration capability of the agent.

The classic definition of entropy is \(- \sum {p\left( x \right)\log p\left( x \right)}\), and Ref. [36] defined the entropy as \({\text{E}}_{{{\mathbf{a}}_{n} \sim \pi }} \left[ { - \log \left( {\pi \left( {{\mathbf{a}}_{n} \left| {{\mathbf{s}}_{n} } \right.} \right)} \right)} \right]\). However, the former has excessively large gradients in the direction of entropy reduction, while the latter has excessively small gradients in the direction of entropy reduction. Therefore, this paper constructs a logistic entropy function as shown in formula (18).

$$ H\left( {p\left( {{\mathbf{a}}_{n} \left| {{\mathbf{o}}_{n} } \right.} \right)} \right) = {\text{E}}_{{{\mathbf{a}}_{n} \sim \pi }} \left[ { - \frac{{k_{n} e^{{ - \eta p\left( {{\mathbf{a}}_{n} \left| {{\mathbf{o}}_{n} } \right.} \right)}} }}{{\left( {1 + \left( {{{k_{n} } \mathord{\left/ {\vphantom {{k_{n} } {k_{0} }}} \right. \kern-0pt} {k_{0} }} - 1} \right)} \right)}}} \right], $$
(18)

where kn = 100, k0 = 2, ƞ = 0.2, and \(p\left( {{\mathbf{a}}_{n} \left| {{\mathbf{o}}_{n} } \right.} \right)\) is the value of probability density. The images of the three entropy functions are shown in Fig. 5. It can be observed that neither \(p\left( x \right)\log p\left( x \right)\) nor \(\log \left( {p\left( x \right)} \right)\) is suitable when the learning objective is entropy reduction. \(p\left( x \right)\log p\left( x \right)\) has a derivative that is too large in the entropy reduction direction, while \(\log \left( {p\left( x \right)} \right)\) has a derivative that is too small. Function \(p\left( x \right)\log p\left( x \right)\) exhibits an excessive derivative in the direction of entropy reduction, whereas derivative of \(\log \left( {p\left( x \right)} \right)\) is insufficient. In contrast, the logistic entropy function exhibits a derivative in the direction of entropy reduction that initially progresses slowly but gradually accelerates, eventually converging. This is in line with the requirements of the training objective.

Fig. 5
figure 5

Comparison of three entropy functions

Full size image

The logistic entropy function is incorporated as a constraint term in the objective function of the policy network, as shown in formula (19).

$$\begin{aligned} J(\theta ) &= - {\text{E}}_{p(\tau )} \Bigg[ \min \left[ {p_{n} (\theta ),{\text{clip}}(p_{n} (\theta ),1 - \varepsilon ,1 + \varepsilon )} \right] \\ & \quad \quad \quad A_{{\mathbf{w}}}^{\pi } ({\mathbf{o}}_{n} ,{\mathbf{a}}_{n} ) \Bigg] - \alpha H\left( {p\left( {{\mathbf{a}}_{n} \left| {{\mathbf{o}}_{n} } \right.} \right)} \right), \end{aligned}$$
(19)

where α is an adaptive parameter, and its value affects whether the policy distribution increases or decreases in entropy. The objective function of α is given by formula (20).

$$ J(\alpha ) = \left\{ \begin{gathered} \mathop {\text{E}}\limits_{{\left( {{\mathbf{o}}_{t} ,{\mathbf{a}}_{t} } \right)\sim \rho_{z} }} \left[ {\alpha \sum\limits_{t} {\gamma^{t} r\left( {{\mathbf{o}}_{t} ,{\mathbf{a}}_{t} } \right)} } \right],{\text{ if E}}\left( {\gamma^{t} r\left( {{\mathbf{o}}_{t} ,{\mathbf{a}}_{t} } \right)} \right) \le {0 } \hfill \\ \mathop {\text{E}}\limits_{{\left( {{\mathbf{o}}_{t} ,{\mathbf{a}}_{t} } \right)\sim \rho_{z} }} \left[ {\alpha \left( {H_{0} - \log \left( {p\left( {{\mathbf{a}}_{n} \left| {{\mathbf{o}}_{n} } \right.} \right)} \right)} \right)} \right],{\text{ otherwise}} \hfill \\ \end{gathered} \right., $$
(20)

where H0 is an objective entropy, and its value is set to 3 in this paper. The explanation of the influence of exploration randomness and H0 value can be found in Appendix.

4.4 CPPO Evasion Guidance Law

After controlling the randomness of the policy, we can proceed to solve the constrained optimization problem described in formular (12). The challenge lies in incorporating the cost and cost limit within the reinforcement learning algorithm framework. In the CMDP problem, it is crucial to calculate the cumulative cost following a specific state. Therefore, we propose an Actor-Critic-Cost (AC2) structure by incorporating a cost network into the traditional AC framework to predict the cumulative cost value. The AC2 framework is illustrated in Fig. 6.

Fig. 6
figure 6

CPPO algorithm framework

Full size image

In general, a constrained optimization problem can be solved by the Lagrange Multiplier method. By introducing the Lagrange Multiplier β, formula (12) becomes an unconstrained optimization problem:

$$ \begin{gathered} \max_{\pi } { \mathcal{L}}(\pi ,\beta ) \doteq f(\pi ) - \beta g(\pi ) \hfill \\ \, f(\pi ) = \mathop {\text{E}}\limits_{{\left( {{\mathbf{o}}_{t} ,{\mathbf{a}}_{t} } \right)\sim \rho_{z} }} \left[ {\sum\limits_{t} {\gamma^{t} } r\left( {{\mathbf{o}}_{t} ,{\mathbf{a}}_{t} } \right)} \right] \hfill \\ \, \quad \, g(\pi ) = \mathop {\text{E}}\limits_{{\left( {{\mathbf{o}}_{t} ,{\mathbf{a}}_{t} } \right)\sim \rho_{\pi } }} \left[ {\sum {c\left( {{\mathbf{o}}_{t} ,{\mathbf{a}}_{t} } \right)} } \right] - C. \end{gathered} $$
(21)

As a result, the complete objective function of the actor network in this paper can be described by formula (22).

$$\begin{aligned} J(\theta ) &= {\text{E}}_{p(\tau )} \Bigg[ \min \left[ {p_{k} (\theta ),{\text{clip}}(p_{k} (\theta ),1 - \varepsilon ,1 + \varepsilon )} \right]\\ & \qquad \times\left( {A_{{\mathbf{w}}}^{\pi } ({\mathbf{o}}_{k} ,{\mathbf{a}}_{k} ) + \beta Q^{c} \left( {{\mathbf{o}}_{k} ,{\mathbf{a}}_{k} } \right)} \right) \Bigg] - \alpha H\left( {p\left( {{\mathbf{a}}_{n} \left| {{\mathbf{o}}_{n} } \right.} \right)} \right),\end{aligned} $$
(22)

where \(Q^{c} \left( {{\mathbf{o}}_{k} ,{\mathbf{u}}_{k} } \right)\) is obtained from the cost critic network. Similar to the critic network, the loss function of the cost critic network is described by formula (23).

$$ L^{c} ({\mathbf{w}}) = \sum\limits_{i = 1}^{M} {\left( {C_{{\mathbf{w}}}^{\pi } ({\mathbf{o}}_{k}^{i} ) - \left[ {\sum\limits_{t = k}^{T} {\gamma^{t - k} c({\mathbf{o}}_{t}^{i} ,{\mathbf{a}}_{t}^{i} )} } \right]} \right)^{2} } . $$
(23)

It is worth noting that the β in formula (21) is continuously updated based on the relationship between the cost limit and the average cumulative cost of the current episode. The objective function of β is shown in formula (24).

$$ J(\beta ) = \beta \left( {C - \max \left( {\sum {c\left( {{\mathbf{o}}_{t} ,{\mathbf{a}}_{t} } \right)} } \right)} \right)j, $$
(24)

where j is an adaptive parameter that adjusts the update speed of β under different conditions. The updating process of β is outlined in Algorithm 1.

Algorithm 1
figure a

Adaptive update algorithm for β

Full size image

In Algorithm 1, the values of j1, j2, j3 and j4 need to be tuned, which are set to 1, − 0.1,  – 1 and 5 in this paper. The updates of parameters α and β are not synchronized with the updates of network parameters. Network parameters are updated multiple times within each episode based on the value of parameter nreuse, while parameters α and β are updated at a slower frequency, only once at each episode. The complete process of the proposed CPPO algorithm is shown in Algorithm 2.

Algorithm 2
figure b

CPPO algorithm

Full size image

The complete flowchart of the proposed method is shown in Fig. 7. The left side of the flowchart represents the interaction phase, while the right side represents the training phase. The final output is the well-trained actor network parameters, which represent the mapping relationship between observations and actions. These parameters can be used for testing and application purposes.

Fig. 7
figure 7

Research methodology flowchart

Full size image

5 Experiment and Results

5.1 Training Results and Parameter Sensitivity Experiments

In this section of the experiment, we compared the classical PPO algorithm with the CPPO algorithm proposed in this paper. The parameter settings and environment setup for the PPO algorithm are consistent with CPPO. The difference between them is that CPPO describes energy cost using a cost function, while PPO describes energy cost using a reward function, as shown in formula (25).

$$ r = - k\left( {e^{{\left( {{\raise0.7ex\hbox{${a_{y} }$} \!\mathord{\left/ {\vphantom {{a_{y} } {a_{\max } }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${a_{\max } }$}}} \right)^{2} }} + e^{{\left( {{\raise0.7ex\hbox{${a_{z} }$} \!\mathord{\left/ {\vphantom {{a_{z} } {a_{\max } }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${a_{\max } }$}}} \right)^{2} }} } \right), $$
(25)

where k is a parameter that needs to be tuned, and its value will affect the weight of energy cost in the learning objective of the PPO agent.

Before each training episode, the situation needs to be initialized. With the evader as the center, the position vectors [θ, φ, R] of the pursuer are randomly initialized in the visual coordinate system. Assuming that the maximum thrust acceleration of the pursuer is greater than that of the evader, and both sides have a decision frequency of 10 Hz. The initial values of the situation parameters are shown in Table 1.

Table 1 Initial values of the situation parameters
Full size table

The hyperparameters of the CPPO algorithm have been fine-tuned, and their corresponding values are presented in Table 2.

Table 2 Hyperparameters of the CPPO algorithm
Full size table

To demonstrate the superiority of the proposed CPPO algorithm in this paper, we conducted a comparison between multiple groups of PPO and CPPO algorithms with different energy consumption constraints. In the CPPO algorithm, we set total energy constraints C = 5, 10, and 15, respectively. As for the PPO algorithm, we set k = 0.00025, 0.0005, and 0.001, respectively. The training results are shown in Fig. 8. Figure 8a–d illustrate the reward curve, maximum energy consumption curve, policy distribution standard deviation curve, and penalty parameter β curve, respectively. In Fig. 8a, both the CPPO and PPO algorithms exhibit robust convergence. The reward curve of PPO appears relatively stable, whereas the CPPO reward curve shows some fluctuations. This can be attributed to the fact that the primary learning objective of the PPO agent is to maximize the reward function, whereas CPPO may encounter a reduction in rewards due to the influence of constraints throughout the training process. The characteristics of the CPPO algorithm are demonstrated in Fig. 8b. The energy consumption of the CPPO agent can converge with high accuracy to the specified constraint C (often slightly below the C value). In contrast, it is difficult for the PPO algorithm to precisely control the energy consumption of the agent through the parameter k. For instance, when k = 0.0005 and 0.001, despite doubling the parameter values, there is no significant difference in the energy consumption between them. Figure 8 (c) illustrates the effect of the Maximum-Minimum Entropy Learning method. The method enables the standard deviation of the policy distribution to converge to 0.01, which aligns with the target value set in formula (20). However, when α is set to 0, indicating the absence of the Maximum-Minimum Entropy Learning method, the agent’s policy distribution will always maintain a certain level of randomness. Figure 8d illustrates the trend of the penalty parameter β in the CPPO algorithm. When β shows an increasing trend, it indicates that the agent has not yet satisfied the energy consumption constraint, requiring a further increase in the weight of the cost loss compared to the policy loss. Conversely, when the agent meets the energy consumption constraint, the value of β starts to slowly decrease. Therefore, β is a crucial parameter in the CPPO algorithm.

Fig. 8
figure 8

Training results

Full size image

5.2 Effectiveness Experiment

In this section, we introduced the classic step maneuver as a comparative method and defined two sets of different maneuver parameters. The expressions for two maneuvers are given by formulas (26) and (27) respectively. They are referred to as “step maneuver 1” and “step maneuver 2” in the subsequent text.

$$ a_{y} = a_{z} = \left\{ \begin{gathered} 0, \, t \le 20{\text{s}} \hfill \\ a_{\max } , \, t{\text{ > 20s}} \hfill \\ \end{gathered} \right., $$
(26)
$$ a_{y} = a_{z} = \left\{ \begin{gathered} 0, \, t \le 15{\text{s}} \hfill \\ 0.7a_{\max } , \, t{\text{ > 15s}} \hfill \\ \end{gathered} \right.. $$
(27)

5.2.1 Experiment in Typical Situations

In this section of the experiment, we compare the performance of CPPO, PPO, and two types of step maneuvering in specific situations, analyzing the trajectories, acceleration commands and LOS angle rates. The situational parameters of this scene are φm = 0.873, θm = − 0.261 and R=220,000. Figure 9 displays the trajectories of evaders and pursuers using different methods. In this particular scenario, the two step maneuver methods are intercepted, while RL methods successfully evade by performing slight maneuvers.

Fig. 9
figure 9

Trajectories of evader and pursuer

Full size image

Figure 10 illustrates the acceleration and LOS angular rate curves of the evader in this scenario. Figure 10a and b shows the accelerations in the y-axis and z-axis directions of the missile body coordinate system, respectively. It is apparent that the results acquired through RL learning also demonstrate an approximation of step maneuvering. In the initial stage of the game, no maneuvering is performed, and at a specific time in the final stage, the maneuvering starts and gradually increases until reaching maximum acceleration. The distinction among RL methods with different parameters lies in the timing of maneuver initiation and the rate of acceleration variation. Figure 10c and d depicts the LOS angular rate curves. Due to the assumption that the ZEM for pursuers is 0 at the beginning of the game, the LOS angular rate remains constant at 0 until the evader initiates maneuvering. In this state, the pursuer can successfully intercept the evader without any maneuvers. The main difference between RL methods and traditional methods lies in the rate of change of the yaw angle. In RL methods, there is a noticeable variation in the yaw angular rate at the end stage of game, whereas the yaw angular velocity remains almost constant at 0 in traditional maneuvering methods.

Fig. 10
figure 10

Acceleration and LOS angle curve

Full size image

The energy consumption and miss distance of various methods are shown in Table 3, indicating a clear advantage of RL methods over traditional maneuvering methods. RL methods achieve a larger miss distance with lower energy consumption. RL methods with larger constraint parameter values have higher energy consumption but also result in safer miss distances. In particular, the CPPO (C = 5) method achieves successful evasion with only 441.41 units of energy consumption. On the contrary, step maneuvers 1 and 2 have energy consumptions of 2000 and 2800, respectively, but are eventually intercepted by the pursuer.

Table 3 Results on the typical scenario
Full size table

5.2.2 Experiment on Test Dataset

To comprehensively evaluate the agent’s performance, we generated a test dataset of 100 scenarios randomly, as shown in Fig. 11.

Fig. 11
figure 11

Test dataset

Full size image

The trained agent and the traditional step maneuvering method were subjected to 100 experiments on the test dataset, and the results are shown in Table 4. According to Table 4, both CPPO and PPO algorithms have a success rate of 100%, while traditional maneuvering methods, despite consuming a large amount of energy, cannot achieve successful escape in all situations. For instance, CPPO (C = 15) and step maneuver 2 have similar energy consumption. However, the former demonstrates approximately twice the success rate of escape and terminal miss distance compared to the latter. This indicates that intelligent methods can significantly enhance maneuvering efficiency compared to traditional approaches. Both PPO and CPPO are capable of effective maneuvering, and higher energy consumption often leads to a larger terminal miss distance.

Table 4 Results on test dataset
Full size table

Figure 12 shows the scatters of energy consumption and terminal miss distance for CPPO agent and PPO agent on the test dataset, clearly demonstrating the advantages and characteristics of the CPPO algorithm. Figure 12a and c depict scatters of the energy consumption for CPPO and PPO, respectively. It can be observed that the energy constraint parameter C has a significant influence on the agent in the CPPO algorithm. The agent is able to control its energy consumption below the corresponding constraint value in all situations, while obtaining the maximum terminal miss distance. Conversely, accurately controlling the agent's energy consumption is challenging for the PPO algorithm. The difference in miss distance scatters between CPPO and PPO is more evident. Figure 12b demonstrates that CPPO has a more uniform distribution of miss distance, exhibiting noticeable distinctions among CPPO agents with different constraint values.

Fig. 12
figure 12

Test dataset

Full size image

5.3 Robustness Experiments Under Information Error Conditions

The experiments above were conducted under perfect information conditions, where the observations of the agent were completely accurate. However, in real-life scenarios, the observations of the agent are often inaccurate due to the environmental noise, and filtering algorithm performance. Therefore, the robustness of RL algorithms in information error conditions is also an important evaluation metric.

In the aforementioned assumptions, the LOS angles are directly measured by the evader through an infrared sensor, while the relative distance information is obtained through a data fusion and filtering algorithm. Therefore, we assume that the angle measurements have only minor random errors that follow a normal distribution. As for the relative distance, we assume that errors consist of two components: random errors that follow a normal distribution and systematic errors that follow a uniform distribution. The error representations of the observations are given by formulas (28) and (29).

$$ Err_{{\varphi_{m} }} , \, Err_{{\theta_{m} }} \sim N\left( {0, \, \sigma_{a}^{2} } \right) ,$$
(28)
$$ Err_{R} \sim N\left( {0, \, \sigma_{b}^{2} } \right) + U\left( {e_{1} , \, e_{2} } \right) \times \frac{{R_{err} }}{{R_{\max } }} ,$$
(29)

where \(\sigma_{a} = 5 \times 10^{ - 4}\), \(\sigma_{b} = 5 \times 10^{ - 2}\), \(R_{err} = 10^{4} {\text{m}}\). We have established 6 levels of error based on different values of e1 and e2, as shown in Table 5.

Table 5 Error level
Full size table

The comparison between the error values and the accurate values for a specific simulation are illustrated in Fig. 13.

Fig. 13
figure 13

Observation with error

Full size image

The performance of CPPO agents under different error levels is shown in Table 6.

Table 6 Results on test dataset with information error
Full size table

According to Table 6, the CPPO (C = 5) agent is highly affected by information errors. Under error level 0, the task success rate decreases to 81%. The performance of CPPO (C = 5) under the 4th error level and above is almost unacceptable. On the other hand, the CPPO (C = 10) and CPPO (C = 15) agents demonstrate remarkable robustness, maintaining a 100% task success rate under all error levels. However, both the maximum energy consumption and terminal miss distance are significantly impacted, as depicted in Fig. 14.

Fig. 14
figure 14

Agent performance under information error conditions

Full size image

From Fig. 14, it is evident that both energy consumption and miss distance show considerable fluctuations under error conditions. The energy consumption of all three CPPO algorithms slightly surpasses the constraints at error levels 2 and 3. In general, larger constraint values lead to safer strategies for the agents, which in turn enhance their robustness.

Based on the above analysis, it seems that C = 10 is a highly balanced choice. By relying on reasonable energy consumption, it not only ensures a sufficient safety margin for the miss distance but also possesses the capability to counteract noise environments. Therefore, C = 10 can be considered as the preferred option in the absence of strict energy constraints. However, in practical scenarios, energy reserves may not be sufficient, implying that energy constitutes a strict constraint. In this context, we can only determine the corresponding C value based on the total amount of available energy at the time. This necessitates training multiple agents under different C values (e.g., C = 5, 6, 7, …, 10) during the offline training phase so that we can flexibly invoke different agents based on varying circumstances during the online application phase.

6 Conclusions

  1. (1)

    Constrained reinforcement learning is capable of addressing decision-making problems under constraints. Unlike traditional reinforcement learning algorithms, constrained reinforcement learning decouples the constraints from the decision objectives. The intelligent agent trained with constrained reinforcement learning knows how to find optimal policies while satisfying the constraints. The learned policies can even reflect the relationship between the constraints and decision objectives. In this paper, the agent trained with the CPPO algorithm has learned the correlation between energy consumption and deviation, while the PPO algorithm does not produce such an effect.

  2. (2)

    The constrained reinforcement learning method introduced in this paper is characterized as a soft constraint approach. Consequently, when under certain constraint conditions, the agent will initially prioritize the reward function and may bypass the constraints. Nevertheless, it will gradually converge to the constraints.

  3. (3)

    The constraint value is correlated with the level of risk-taking by the intelligent agent. Agents with larger constraint values tend to adopt safer strategies, while agents with smaller constraint values are inclined towards more adventurous strategies. Therefore, the robustness of an agent is also influenced by the magnitude of the constraint value. To obtain a more robust intelligent agent, it is necessary to provide the agent with looser constraints (such as enough resources or a broader decision space), enabling the agent to make safer decisions without resorting to risky choices.

  4. (4)

    Observation noise is an important factor that affects the performance of agents, especially when the available energy is not sufficient (e.g., C = 5), the performance of agents under observation noise may become unacceptable. Therefore, the development of robust reinforcement learning guidance laws under observation noise is a promising research direction for the future.