Missile guidance with assisted deep reinforcement learning for head-on interception of maneuvering target

Abstract

In missile guidance, pursuit performance is seriously degraded due to the uncertainty and randomness in target maneuverability, detection delay, and environmental noise. In many methods, accurately estimating the acceleration of the target or the time-to-go is needed to intercept the maneuvering target, which is hard in an environment with uncertainty. In this paper, we propose an assisted deep reinforcement learning (ARL) algorithm to optimize the neural network-based missile guidance controller for head-on interception. Based on the relative velocity, distance, and angle, ARL can control the missile to intercept the maneuvering target and achieve large terminal intercept angle. To reduce the influence of environmental uncertainty, ARL predicts the target’s acceleration as an auxiliary supervised task. The supervised learning task improves the ability of the agent to extract information from observations. To exploit the agent’s good trajectories, ARL presents the Gaussian self-imitation learning to make the mean of action distribution approach the agent’s good actions. Compared with vanilla self-imitation learning, Gaussian self-imitation learning improves the exploration in continuous control. Simulation results validate that ARL outperforms traditional methods and proximal policy optimization algorithm with higher hit rate and larger terminal intercept angle in the simulation environment with noise, delay, and maneuverable target.

Introduction

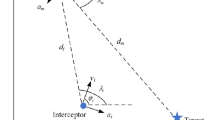
The modern missile is expected to cause the maximum damage to the target under complicated conditions such as target maneuver, measurement noise, and detection delay. As shown in Fig. 1, to increase the damage to the target, the missile should hit the front of the target, which means the terminal intercept angle and terminal missile velocity should be as large as possible. These requirements make the missile guidance task a hard problem.

The problem of designing missile controller can be solved by many traditional guidance methods, such as sliding mode tracking control [12], optimal guidance law [19], finite-time guidance law [28], and Lyapunov-based guidance law [22]. With the support of radar and other active sensors, the relative information of the target can be measured, which greatly improves the controller performance [3, 33]. However, it is still difficult to design a missile guidance law that is capable of adapting complex environmental conditions [2, 4]. On one hand, due to the limitations of radar technology, the precise information required by the algorithm is difficult to obtain, such as the acceleration of the target [8]. On the other hand, the target can escape out of the range of the guidance method, which causes the guidance method to be invalid.

In recent years, deep reinforcement learning (DRL) provides a simple way to design the missile guidance controller [7]. In DRL, the neural network-based agent chooses an action according to its policy and gathers data from the environment [24, 30]. According to the collected trajectories, the agent adjusts its policy to maximize the sum of future rewards. In DRL, conditions and objectives of the task are naturally set in the environment and reward function. By interacting with the environment, the algorithm can optimize the policy to achieve the objective without additional human knowledge [27]. DRL algorithms can be divided into model-based and model-free methods. The former ones use a model that predicts the future states and rewards to derive optimal actions [25], while the latter ones optimize policy by collected trajectories from interacting with the environment. Some model-based DRL methods [7, 17, 29, 35] consider tracking maneuverable targets in a noiseless environment. If there exists a mismatch modeling error between the model and the simulator, the learned policy may be a suboptimal solution and lack robustness. To enhance the robustness, some methods introduce the model-free DRL to design controller [8]. When there is uncertainty in the observation, due to the low efficiency of model-free DRL, it needs more data to optimize its strategy [1]. Auxiliary tasks are a way to improve the efficiency of reinforcement learning. Auxiliary tasks can take many forms, including supervised learning [10, 31] and unsupervised learning [13]. By designing auxiliary learning tasks, the agent can reduce noise interference and extract information more efficiently.

Fig. 1

Example of missile guidance engagement geometry. When the missile intercepts the target, the intercept angle $\varphi$ should be as large as possible

In this work, the objective of the agent is to achieve the largest intercept angle when intercepting the target. The observation of the agent will have different sizes of the Gaussian white noise and steps of observation delay. During the interception, the target will try to escape the interception of the missile in a random direction. The terminal intercept angle will be considered as the evaluation of the performance. The maneuverability of the missile is limited, and the speed of the missile decreases according to aerodynamics. There are two difficulties in training a DRL controller. The first is the large-scale observation space with noise, which increases the difficulty in extracting information. The second is the long simulation step, which increases the difficulty of exploration and makes a large variance on the value of the state.

To solve the problem, we propose ARL to learn a missile guidance controller. The main contribution of ARL is that we introduce assisted learning including auxiliary learning and Gaussian self-imitation learning to improve training missile guidance controller for better performance. Auxiliary learning (AL) requires the agent to predict the acceleration based on noisy observation. The key idea of AL is to use the acceleration of the target as a clean label to train the agent to model the target. Gaussian self-imitation learning (GSIL) makes the agent imitate its sampled action if the return of the state is better than the value of the current policy. The key idea of GSIL is to imitate the good action and encourage the exploration in good trajectories. Simulation results show that ARL achieves better performance than proximal policy optimization (PPO) and traditional methods in both the hit rate and intercept angle in intercepting 9$g$-maneuverability target.

This paper is organized as follows. The next section reviews the related work mentioned in this paper, including auxiliary learning, self-imitation learning, and guidance laws with neural network. The third section describes the interception scenario, including dynamics, maneuverability, and noise. The fourth section describes the proposed DRL algorithm with auxiliary supervised learning and self-imitation learning. The fifth section shows the simulation and results in different scenarios. Finally, the last section gives the conclusion.

Related work

Auxiliary learning

Noisy observation will significantly reduce training efficiency because the difficulty of extracting information increases. Research has shown that even for low-dimensional problems, the efficiency of training agents can be improved through auxiliary learning [16, 18, 34]. Auxiliary learning considers multiple related sub-tasks or objectives simultaneously. Pablo et al. [10] proposed two architectures to make the agent learn other agent’s policies as auxiliary tasks. Their experiments showed that the auxiliary tasks stabilized learning and outperformed baselines. Laskin et al. [15] proposed contrastive unsupervised representations for reinforcement learning, which greatly improved the efficiency of training.

Self-imitation learning

The performance of DRL suffered from the inefficiency of exploration [6]. Self-imitation learning is a simple way that makes the policy learn to reproduce the past collected trajectories with high returns. Junhyuk et al. [20] introduced the self-imitation learning in advantage actor-critic and proximal policy optimization to improve the performance of the algorithm in hard exploration environments. Ecoffet et al. [5] showed the self-imitation learning can significantly improve the performance of the agent in sparse reward environments such as Montezuma’s Revenge and Pitfall.

Guidance law with neural network

There are lots of elegant methods that have been proposed in guidance laws, including sliding mode control [9], dynamics surface control [11], and other traditional control methods. Gaudet et al. [7] introduced reinforcement learning in two-dimensional homing-phase guidance law design. DRL based missile controller shows more flexibility and efficiency than traditional methods. Recently, Gaudet [8] introduced meta-learning and reinforcement learning to solve the angle-only intercept guidance of maneuvering targets. The algorithm achieved remarkable robustness in intercepting exo-atmospheric targets. Liang et al. [17] proposed guidance law based on meta-learning and model predictive path integral control. The algorithm built an environmental model based on meta-learning and searched trajectories through Monte Carlo trees. By introducing stochastic optimal control and neural networks, the performance of model predictive control methods can satisfy complex environmental conditions. It should be noted that the above methods mainly focused on miss distance and line-of-sight angle. They paid less attention to the target posture and neglected the effect of environmental noise.

Problem formulation

The three-dimensional missile–target model can be described by a six-degree-of-freedom system. Considering aircraft as a particle, changes in roll angle can be ignored to simplify the model. The geometry of the guidance system is shown in Fig. 1, where missile and target share the uniform coordinate system $O_{XYZ}$. Both the missile and target kinematic models are represented as follows:

$$\begin{aligned}&a^{i}_t=[N_{y}^{i},N_{z}^{i}] \end{aligned}$$

(1)

$$\begin{aligned}&{{\dot{\theta }}^{i}} =g\frac{N_{y}^{i}}{{v}^{i}}\end{aligned}$$

(2)

$$\begin{aligned}&{{\dot{\psi }}^{i}} =-g\frac{N_{z}^{i}}{{v}^{i}\cos \theta ^{i}}\end{aligned}$$

(3)

$$\begin{aligned}&{{\dot{x}}^{i}}={v}^{i}\cos (\theta ^{i})\cos (\psi ^{i})\end{aligned}$$

(4)

$$\begin{aligned}&{{\dot{y}}^{i}}={v}^{i}\sin (\theta ^{i})\end{aligned}$$

(5)

$$\begin{aligned}&{{\dot{z}}^{i}}={v}^{i}\cos (\theta ^{i})\sin (\psi ^{i})\end{aligned}$$

(6)

$$\begin{aligned}&[{\theta }^{i},{\psi }^{i},x^{i},y^{i},z^{i}]_{t+1}=[{\theta }^{i},{\psi }^{i},x^{i},y^{i},z^{i}]_{t}+\varDelta t[{\dot{\theta }}^{i},\nonumber \\&{\dot{\psi }}^{i},{\dot{x}}^{i}, {\dot{x}}^{i}, {\dot{x}}^{i}]_{t}, \end{aligned}$$

(7)

where the superscript $i$ indicates that the variable is about the missile (M) or the target (TG), $x^{i}, y^{i}, z^{i}$ are the coordinate of the missile or target, $a_t^{i}$ is the acceleration, ${v}^{i}$ is the velocity, with direction being defined by $\theta ^{i}$ and $\psi ^{i}$, the projection of acceleration command at pitch and yaw angles as $N_{y}^{i},N_{z}^{i}$, the projection of the acceleration on pitch $\theta ^{i}$ and yaw $\psi ^{i}$ as ${\dot{\theta }}^{i}, {\dot{\psi }}^{i}$ respectively, the universal gravitational constant as $g$, $D$ is the distance, $\varphi$ is the intercept angle, and $t$ is the step. The three-dimensional relative coordinates between the missile and the target can be expressed as follows:

$$\begin{aligned} \overrightarrow{d^{r}}=[\overrightarrow{x^{r}},\overrightarrow{y^{r}},\overrightarrow{z^{r}}]&=[x^{\text {TG}},y^{\text {TG}},z^{\text {TG}}]-[x^{\text {M}},y^{\text {M}},z^{\text {M}}]\end{aligned}$$

(8)

$$\begin{aligned} \overrightarrow{v^{r}}=[\dot{\overrightarrow{x^{r}}},\dot{\overrightarrow{y^{r}}},\dot{\overrightarrow{z^{r}}}]&=[{\dot{x}}^{\text {TG}},{\dot{y}}^{\text {TG}},{\dot{z}}^{\text {TG}}]-[{\dot{x}}^{\text {M}},{\dot{y}}^{\text {M}},{\dot{z}}^{\text {M}}], \end{aligned}$$

(9)

where $\overrightarrow{x^{r}},\overrightarrow{y^{r}},\overrightarrow{z^{r}}$ are the projection of relative position $\overrightarrow{d^{r}}$ on the coordinate axis and $\dot{\overrightarrow{x^{r}}},\dot{\overrightarrow{y^{r}}},\dot{\overrightarrow{z^{r}}}$ are the projection of relative velocity $\overrightarrow{v^{r}}$ on the coordinate axis.

Fig. 2

Three stages in the missile–target problem. a The beginning phase and its constraints in yoz plane. b All three phases in zox plane

There are three stages in this missile–target problem, including the beginning phase, maneuvering phase, and terminal phase. The beginning phase and its constraints are shown in Fig. 2a. The missile is launched to capture the target when the relative distance is smaller than $D_b$. The initial coordinates and velocity direction of the target satisfy that the intercept angle is greater than the threshold of angle $\varphi _{b}$ if the target maintains the velocity direction. At each step $t$ in the episode, the distance between missile and target is $D_t$ and the interception angle is $\varphi _t$.

In our scenario, the velocity of the target is constant at ${v}^{\text {TG}}$, and the initial angle of velocity is $\theta ^{\text {TG}}_{0}$. The velocity of the missile is set at ${v}^{\text {M}}_{0}$ and decreased by the aerodynamic coefficient $C_{a}$ shown in Appendix Table 8. The speed decay of missile can be calculated as follows:

$$\begin{aligned}&H_{dk}= y^{\text {M}} + \frac{{x^{\text {M}}}^{2}+{y^{\text {M}}}^{2}+{z^{\text {M}}}^{2}}{12756490} \end{aligned}$$

(10)

$$\begin{aligned}&H_{q}=\left\{ \begin{array}{ll} {0.06e^{\lambda _{h1} \cdot H_{dk}}{v^{\text {M}}}^{2}} &{} {H_{dk} \le 1.1 \times 10^{4}} \\ {0.01e^{\lambda _{h2} \cdot (H_{dk}-1.1 \times 10^{4})}{v^{\text {M}}}^{2}} &{} {H_{dk} > 1.1 \times 10^{4}}\\ \end{array} \right. \end{aligned}$$

(11)

$$\begin{aligned}&{v}^{\text {M}} = v^{\text {M}} + {\varDelta }t g\left( -\frac{C_{a}H_{q}S_{a}}{600}-sin(\psi ^{\text {M}})\right) , \end{aligned}$$

(12)

where $H_{dk}$ is the altitude of the missile in the geometry coordinate system, $H_{q}$ is the dynamic pressure, $S_{a}=0.1$ is the effective area, the coefficient $\lambda _{h1}$ is set to $-1.15 \times 10^{-4}$, and the coefficient $\lambda _{h2}$ is set to $-1.62\times 10^{-4}$. The speed of the missile is required to be higher than $500\, {\text {m/s}}$ , otherwise, the episode is considered a failure.

When the missile enters the detection range $D_{m}$ of the target, the target begins the maneuvering phase as shown in Fig. 2b. The target chooses a random direction and escapes at a fixed acceleration. When $D_t$ is smaller than distance threshold $D_c$, the interception is considered a hit and the episode ends. If the terminal intercept angle $\varphi _{T}$ is greater than angle threshold $\varphi _{c}$ at the terminal step $T$, the interception is considered a true hit. After the episode ends, the terminal reward of the agent is settled according to the miss distance and intercept angle. However, the terminal reward is sparse, which causes a high variance in value estimation. To stabilize the learning process, we add the immediate reward to reshape the reward function at each step. There are two components in immediate reward, including distance reward and angle reward. The distance reward is calculated by $D_{t}-D_{t+1}$ and the angle reward is defined as $-\cos (\varphi _t)$. The whole reward function can be described as follows:

$$\begin{aligned} r_{t}&=w_{0}(D_{t}-D_{t+1}) - \cos (\varphi _t)\end{aligned}$$

(13)

$$\begin{aligned} r_{T}&=\left\{ \begin{array}{ll} (-\cos (\varphi _T)+1)\times {10}, &{} {\text { if } D_T \le D_{c}} \\ {0,} &{} {\text { if } D_T > D_{c}} \end{array}\right. , \end{aligned}$$

(14)

where $w_0$ is the weight of the distance reward. The immediate reward guides the behavior of the agent to hit the target and get the terminal reward. The objective of the DRL based guidance law is to maximize the cumulative reward $\sum _{t=0}^{T}{\gamma }^{t}r_t$.

With the relative coordinates, the observation of the missile $o^{\text {M}}$ can be described as follows:

$$\begin{aligned} D&={\sqrt{{({\overrightarrow{x^{r}})}^{2}+{(\overrightarrow{y^{r}})}^{2}+{(\overrightarrow{z^{r}})}^{2}}}}\end{aligned}$$

(15)

$$\begin{aligned} {\dot{D}}&=\frac{\overrightarrow{x^{r}}\dot{\overrightarrow{x^{r}}}+\overrightarrow{y^{r}}\dot{\overrightarrow{y^{r}}}+\overrightarrow{z^{r}}\dot{\overrightarrow{z^{r}}}}{D}\end{aligned}$$

(16)

$$\begin{aligned} q_{e}&=\arctan \frac{\overrightarrow{y^{r}}}{\sqrt{{(\overrightarrow{x^{r}})}^{2}+{(\overrightarrow{z^{r}})}^{2}}}\end{aligned}$$

(17)

$$\begin{aligned} q_{b}&=\arctan \frac{\overrightarrow{y^{r}}}{\overrightarrow{x^{r}}}\end{aligned}$$

(18)

$$\begin{aligned} {\dot{q}}_{e}&={({(\overrightarrow{x^{r}})}^{2}+{(\overrightarrow{z^{r}})}^{2})\dot{\overrightarrow{y^{r}}}}-\frac{\overrightarrow{y^{r}}(x^{r}\dot{\overrightarrow{x^{r}}})}{\sqrt{{(\overrightarrow{x^{r}})}^{2}+{(\overrightarrow{z^{r}})}^{2}}}\end{aligned}$$

(19)

$$\begin{aligned} {\dot{q}}_{b}&=\frac{\overrightarrow{z^{r}}\dot{\overrightarrow{x^{r}}}+x^{r}\dot{\overrightarrow{z^{r}}}}{{(\overrightarrow{x^{r}})}^{2}+{(\overrightarrow{z^{r}})}^{2}}\end{aligned}$$

(20)

$$\begin{aligned} s^{\text {M}}&=[D,{\dot{D}},q_{e},q_{b},{\dot{q}}_{e},{\dot{q}}_{b}]\end{aligned}$$

(21)

$$\begin{aligned} o^{\text {M}}&=Z(s^{\text {M}}), \end{aligned}$$

(22)

where $q_{e}$ is the pitch angle of the line of sight, $q_{b}$ is the yaw angle of the line of sight, ${\dot{q}}_{e}$ is the rate of pitch angle, ${\dot{q}}_{b}$ is the rate of yaw angle, and $Z$ represents the process of adding noise and delay to the observation.

In this paper, we consider the influence of Gaussian random noise on the observation. In most studies, these noises are considered white Gaussian distribution with zero means [26]. The noise we introduce includes a Gaussian noise with a variance correlated with distance and a Gaussian noise that is independent of distance.

Methods

State representation

Among the observation list, the value span of distance information $D$ is quite large and easy to cause catastrophic forgetting [14]. For example, it is difficult to adjust the weight of the neural network for the distance input because the value of the relative distance spans from 10 to 10,000. Therefore, we clip and normalize $D$ to $[0,5000]/5000$ and ${\dot{D}}$ to $[0,1000]/1000$.

To further enhance the robustness of the algorithm, we design a binary mask $C_m$ to randomly choose elements from observation in one episode:

$$\begin{aligned} c&=C_m\cdot {o^{\text {M}}}. \end{aligned}$$

(23)

The observation is covered by $C_m$ to simulate the different combinations of sensors. Different combinations of observations prevent agent from relying on a certain sensor. The observation $o_t$ has ten dimensions, and can be described as

$$\begin{aligned} o_t=[c_t,c_{t-2}]. \end{aligned}$$

(24)

We take two consecutive observations with one-step skipping as the controller input to overcome the uncertainty and target maneuvering. The reason for not using adjacent observations is that the correlation of the observations is very serious, which makes the algorithm difficult to converge during the training process.

Reinforcement learning

An interception problem can be described as a Partially Observable Markov Decision Process (POMDP) with a 7-tuple $\langle S,A,R,O,T,Z,\gamma \rangle$, where $S$ is the state space, $A$ is the space of available actions, $R:S \times A \rightarrow {\mathbb {R}}$ is the reward function, $O$ is the set of observations, $Z$ is the set of conditional observation probabilities, $T:S\times A\times S \rightarrow [0,1]$ is a transition function, $T(s,a,{s}{'})$ is the probability of ending in state $s{'}$ given that action $a$ is taken in state $s$, $r(s,a)$ is the expected payoff for taking action $a \in A$ in state $s \in S$, and $\gamma \in [0,1)$ is the discount factor. The policy $\pi$ of the agent with parameters $\theta$ specifics an action $a_t\sim \pi _{\theta }(o_t)$ for any observation $o_t=Z(s_t)$, $o_t \in O$ at step $t$. The objective of the agent is to learn an optimal policy $\pi ^{*}$ to maximize the expected cumulative discounted rewards $G(o_t, a_t)=\sum _{k=t}^{T} \gamma ^{k-t} r_k(o_k, a_k)$, which is the total discounted cumulative of rewards from step $t$. The policy optimization directly optimizes the policy $\pi _{\theta }$ by gradient ascent on the performance objective $J(\theta , o_t)={\mathbb {E}}_{a_t\sim \pi _{\theta }}G(o_t, a_t)$. Usually, policy optimization uses value function $V^{\pi _{\theta }}(o_t)={\mathbb {E}}_{a\sim \pi _{\theta }}[r(s,a)+\gamma V^{\pi _{\theta }}(o_{t+1})]$ to provide the estimated advantage values $A^{\pi _{\theta }}(o,a)=G^{\pi _{\theta }}(o,a)-V^{\pi _{\theta }}(o)$. The weights $\theta$ of the agent are updated following the gradient $\nabla _{\theta }J(\theta )={\mathbb {E}}_{a\sim \pi _{\theta }}[\nabla _{\theta }{\log }\pi _{\theta }(o,a)A^{\pi _{\theta }}(o,a)]$.

The proposed ARL algorithm is based on the actor-critic framework. Table 1 and Fig. 3 show the architecture of ARL networks. The policy network, prediction network, and the value function network share the same first and second hidden layers. The hidden layer is defined by a fully connected (FC) neural network, and uses the rectified linear unit (ReLU) activation function for the network nonlinearity. The policy network outputs the mean $m$ and the variance $\sigma$ of the Gaussian distribution for agent action. We use the tangent activation function for the mean value and exponential activation function for the variance. The action is sampled from the outputs of the distribution. The action $a$ of the agent is limited to $[-1,1]$ and scaled according to the actual maneuverability of the missile. The value is calculated by a fully connected neural network.

Fig. 3

The learning framework of ARL, including neural network architecture of the agent, reinforcement learning, auxiliary learning, and self-imitation learning

Table 1 ARL neural network architecture

To avoid the gradient explosion, we use the huberloss instead of mean square error:

$$\begin{aligned} {\text {huberloss}}(a,b)=\left\{ \begin{array}{ll} \frac{1}{2}{(a-b)^2} &{} {\text { if } |a-b| \le 1} \\ {|a-b|-\frac{1}{2}} &{} {\text { otherwise}}.\\ \end{array} \right. \end{aligned}$$

(25)

We deploy PPO-clip [23] to train our agent. The critic is updated to estimate the value $V(o_t)$ of the observation $o_t$. The loss of critic is given by

$$\begin{aligned}&{\mathcal {L}}_{\text {critic}}(o_t)={\text {huberloss}}\Bigg ({\mathbb {E}}_{a\sim \pi _{\theta }}\sum ^{T}_{k=t} \gamma ^{k-t}r(o_k,a_k),V(o_{t})\Bigg ).\nonumber \\ \end{aligned}$$

(26)

The reinforcement loss of the actor is given by

$$\begin{aligned}&{\mathcal {L}}_{\text {ppo-clip}}(o_t,a_t,\pi _{\text {old}},\pi _{\theta }) \nonumber \\&\quad =\min \Bigg [\frac{\pi _{\theta }(a_t|o_t)}{\pi _{\text {old}}(a_t|o_t)}A^{\pi _{\text {old}}}(o_t,a_t),\nonumber \\&\quad {\text {clip}}\left( \frac{\pi _{\theta }(a_t|o_t)}{\pi _{\text {old}}(a_t|o_t)},1-\epsilon ,1+\epsilon \right) A^{\pi _{\text {old}}}(o_t,a_t)\Bigg ], \end{aligned}$$

(27)

where $\pi _{\text {old}}$ is the policy of collecting trajectories, and $\epsilon$ is clip hyperparameter which limits the updated policy to go far away from the old policy. To encourage exploration, PPO introduces entropy regularization. The policy is trained to maximize a trade-off between future reward and entropy. Appropriate entropy loss can enhance the exploration ability of the agent. The loss of the entropy is given by

$$\begin{aligned} {\mathcal {L}}_{\text {ent}}(o_t)=\ln (\sigma _t\sqrt{2\pi e}), \end{aligned}$$

(28)

where $\sigma _t$ is the Gaussian variance output of the agent according to the observation $o_t$, and $e$ is the Euler’s numbers. The PPO loss is given by ${\mathcal {L}}_{\text {ppo-clip}} + w_1{\mathcal {L}}_{\text {ent}}$, where $w_1$ is the weight of the entropy.

Auxiliary supervised learning

The noise in measurements significantly reduces the efficiency of reinforcement learning because the agent needs more training steps to extract the relationship between observations and actions. To improve the efficiency of extracting information, we consider labeled data to construct a supervised learning task to assist the agent to extract information. Directly predicting the coordinates and state of the target is a high-dimensional task, which is too complicated for the agent. Since the target’s acceleration is strongly related to the transition of the state, we choose to predict the target’s acceleration as an auxiliary supervised task. The acceleration of the target and missile can be estimated based on the changes of observations. Based on the relative position changes of observations on the trajectory, the relative acceleration relationship between the missile and target can be estimated. At the same time, because AL and RL share the same network layer, AL has the ability to infer the acceleration of the input based on the shared layer. During the training phase, the state and acceleration of the target can be obtained from environment. We record the target acceleration at each step to establish the dataset of AL training. The agent predicts the acceleration of the target according to the input observation $o_t$. The error loss between the prediction and the acceleration of the target can be defined for the AL during the training phase, and the corresponding network parameters can be trained using the gradient backpropagation. In practice, only the action is needed, and prediction is no longer needed. The loss ${\mathcal {L}}_{\text {AL}}$ is computed from ${\text {huberloss}}$ for every step

$$\begin{aligned} {\mathcal {L}}_{\text {AL}}({\hat{u}}^{\text {TG}}_{t},{a}^{\text {TG}}_{t})={\text {huberloss}}({\hat{u}}^{\text {TG}}_{t},{a}^{\text {TG}}_{t}), \end{aligned}$$

(29)

where ${\hat{u}}^{\text {TG}}_{t}$ is the predicted value and ${a}^{\text {TG}}_{t}$ is the acceleration command of the target at step $t$. The auxiliary learning guides the agent to extract information from the observation, which enhances the robustness of the agent.

Fig. 4

The example of measurement and true value during one episode

Fig. 5

Comparison results of training in the scenario, including ARL (blue line), PPO+GSIL (gray line), PPO+AL (red line), PPO (green line), PPO+SIL (yellow line), PNG (purple line) and IGL (teal line). Each experiment was repeated three times with three different random seeds. The line represents the statistical mean, and the shaded represents the statistical variance

Gaussian self-imitation learning

Although we add dense rewards related to the intercept angle, the objective of intercept angle is still hard to be achieved. The main reason is that when we train the agent, multiple constraints and targets may conflict with distance minimization. For example, in the head-pursuit process, the dense interception angle reward is the opposite of the distance reward. Therefore, we need to use self-imitation learning (SIL) [20] to assist the agent to reproduce trajectories that reach the final goal. An action whose advantage value is greater than zero will be considered as a demonstration of the good action. The vanilla SIL can be described as follows:

$$\begin{aligned}&{\mathcal {L}}_{\text {SIL}}({m_t},a_{t},o_t)\nonumber \\&=-{\max (G(o_t, a_{t})-V(o_t),0)}\log {\pi }_{\theta }(a|s) \nonumber \\&\frac{\partial L_{\text {SIL}}}{\partial m_t}=\frac{1}{{\sigma _t}^2}(a_t-m_t)\varDelta _{+}\nonumber \\&\frac{\partial L_{\text {SIL}}}{\partial \sigma _t}=(\frac{1}{{\sigma _t}}-\frac{(m_t-a_t)^2}{{\sigma _t}^3})\varDelta _{+}, \end{aligned}$$

(30)

where $\varDelta _{+}={\max (G(o_t, a_{t})-V(o_t),0)}$. ${\partial L_{\text {SIL}}}/{\partial \sigma _t}$ is nonnegative when the sampled $a_t$ is in the range of $\sigma _t$. Therefore, $\sigma _t$ will be decreased when minimizing $L_{\text {SIL}}$, which is harmful to exploration. We hope that SIL will not affect the exploration, so $\sigma _t$ is expected to be unchanged by SIL. Therefore, we treat $\sigma _t$ as a constant and integrate ${\partial L_{\text {SIL}}}/{\partial m_t}$ over ${m_t}$ to get a loss form $(a_t-m_t)^2\varDelta _{+}$. The type of our Self-imitation learning is called Gaussian self-imitation learning (GSIL) to distinguish with vanilla SIL. To prevent gradient exploration, we replace mean square error with ${\text {huberloss}}$:

$$\begin{aligned}&{\mathcal {L}}_{\text {GSIL}}({m_t},a_{t},o_t)\nonumber \\&\quad ={\max (G(o_t, a_{t})-V(o_t),0)}{\text {huberloss}}({m_t},a_{t}), \end{aligned}$$

(31)

where $o_t$ is the observation in the sampled trajectories, $a_{t}$ is the action in the sampled trajectories, and $m_t$ is the mean of the Gaussian distribution.

The whole policy loss is given by

$$\begin{aligned} {\mathcal {L}}_{{{\text {policy}}}} = - {\mathcal {L}}_{{{\text {ppo - clip}}}} - w_{1} {\mathcal {L}}_{{{\text {ent}}}} + w_{2} {\mathcal {L}}_{{{\text {AL}}}} + w_{3} {\mathcal {L}}_{{{\text {GSIL}}}} , \end{aligned}$$

(32)

where $w_2$ is the weight of the auxiliary tasks, and $w_3$ is the weight of the GSIL. The procedure of the algorithm is shown in Algorithm 1.

Simulation and results

In this section, we describe the simulation scenarios and training results. In the following experiments, we choose proportional navigation guidance (PNG) law [21] and impact angle constraint method [32] as our benchmark. We discuss the contribution of various parts of ARL, including AL and GSIL, and show the robustness of ARL in different measurement noise and delays.

Proportional navigation guidance law

Proportional navigation guidance law dictates that the missile velocity vector should rotate at a rate proportional to the rotation rate of the line of sight, and in the same direction:

$$\begin{aligned}&[N_y,N_z]=N|\overrightarrow{v^r}|\frac{{v}^M}{|{v}^M|}\times \overrightarrow{\varOmega }\end{aligned}$$

(33)

$$\begin{aligned}&\overrightarrow{\varOmega }=\frac{\overrightarrow{d^r}\times \overrightarrow{v^r}}{\overrightarrow{d^r}\overrightarrow{d^r}}, \end{aligned}$$

(34)

where $N$ is optimally set to 3 for proportional navigation guidance law after manual tuning and testing. We use PNG to represent this guidance method. Without considering the intercept angle and velocity, PNG can be applied in many situations.

Guidance law for impact angle constraints

The guidance law for impact angle constraints [32] generated the acceleration command that could meet the intercept angle and position constraints according to the accurate relative position and velocity between the missile and target, which can be described as follows:

$$\begin{aligned}&[N_y,N_z]=-4{\dot{\theta }}_{\text {LOS}} - 2\frac{\theta _{\text {LOS}}+\theta _{f}}{t_{\text {go}}}\end{aligned}$$

(35)

$$\begin{aligned}&{\dot{\theta }}_{\text {LOS}}=\frac{{v^r}\sin {(\theta _{\text {LOS}}-\theta )}}{D}\end{aligned}$$

(36)

$$\begin{aligned}&t_{\text {go}}=\frac{\overrightarrow{d^r}}{v_c}\end{aligned}$$

(37)

$$\begin{aligned}&v_c =\frac{\overrightarrow{d^r}\cdot \overrightarrow{v^r}}{||\overrightarrow{d^r}||}, \end{aligned}$$

(38)

where $\theta _{f}$ is the desired impact angle, and $\theta$ is the velocity angle of the missile. We use IGL to represent this guidance method.

Simulation scenarios

Table 2 summarizes the Gaussian noise standard deviation in the scenario. Correlation variance is consistent with the percentage of measurements. Independent variance is not related to measurement. Figure 4 shows the measurement error during the episode.

Fig. 6

The prediction error of target acceleration. The ordinate is a logarithmic scale. The gray line is the prediction error of the ARL when the weight of the auxiliary loss is set to 0. The blue line is the prediction error of the ARL. With auxiliary learning, ARL can predict the acceleration of the target, which improves the performance of the algorithm

Table 2 Typical measurements’ noise standard deviations

Fig. 7

Sampled simulation trajectories generated by IGL and ARL

Parameters for scenarios are shown in Table 3. The ${\text {unif}}(a,b)$ means the value sampled from uniform distribution between $a$ and $b$. The guidance integration step size is 10$\,{\text {ms}}$. The missile maneuverability is set to $40g$. The measurement includes the noise described in Table 2. The response delay is set to 10 steps and the maneuverability of the target is set to $9g$. Any singular value caused by noise will be set to 0. To maintain head-on acute angle interception, we require that the range of the boundary of the interception angle should be less than 90. If the terminal intercept angle $\theta _{3}>135$ and $d_{3}<5m$, the hit is considered as a true hit.

Table 3 Parameters for experimental and learning scenarios

Fig. 8

The lines represent the acceleration generated by the agent in the process of intercepting the target. Each sampled result is marked with a different color for distinction. The specific colors only represent different rounds

Simulation results: ablation study

Figure 5 shows the training results in the scenario, including hit rate, true hit rate. Figure 5a shows the hit rate during the training process and Fig. 5b shows the results of the true hit rate. Due to the interference of noise and delay, the improvement of PPO is very slow at the beginning of training. Both AL and SIL can improve training efficiency of PPO. The red line shows that under the assistance of AL, the agent improves information extraction ability and stabilizes the training process. AL improves the extracting ability and SIL improves the learning efficiency. However, the performance of SIL is very poor because the gradient on the variance of the Gaussian distribution limits the exploration of the agent. GSIL avoids the exploration problems by changing the loss function. The gray curve indicates that GSIL improves the performance of the agent in the whole process of training. By combining the advantages of GSIL and AL, ARL obtains more stable and higher performance and achieves 99% hit rate after 2500 steps. Compared with IGL and PNG, ARL also has significant advantages. PNG does not consider delay, noise and intercept angle. Therefore, although PNG has a high hit rate, its true hit rate is relatively low. IGL can satisfy the objective of intercept angle. But IGL cannot distinguish between head-on interception and head-pursuit interception. When the maneuvering of the target causes the problems to change from head-on interception to head-pursuit interception, IGL may fail. The average true hit rate of ARL reaches 17.5%, which is much better than the IGL and PNG.

Figure 6 shows the results of prediction error. The gray line shows the prediction error when the ARL does not minimize the auxiliary loss. The blue line shows the prediction error of ARL. The error of blue line indicates that the ARL can predict the acceleration of the target. The prediction training can be divided into several stages according to the number of iterations. At the early iterations, the agent policy is randomly initialized around 0 and is not good enough to guide the missile within the target range. The target maneuverability is rarely triggered and the target acceleration of collected data remains mostly zero. With large training batch size, the prediction error of samples with large error are diluted. After about 100 iterations, because the policy improves, the number of samples with maneuvering targets increases, so the error increases in the middle of the training. Around 400 iterations, the agent explores more new trajectories to achieve higher interception angle, so the prediction error increases again. After that, as the auxiliary training continues, the prediction error drops again. The results illustrate the ability of the agent to extract information is improved by AL, which naturally improves the performance of the algorithm.

To illustrate the obtained policy, we evaluate ARL and IGL in scenarios with maneuverability target, noise, randomly maneuver directions, and delay. The target’s position is initialized to $[x,y,z]=[4500,2500,4500]$, and it flies at the same altitude toward the origin direction. Figure 7a shows the 100 interception trajectories generated by IGL. The results show that the IGL method fails in many interception directions. On the one hand, IGL does not consider the limitation of the velocity, so some flight is terminated early. On the other hand, if the target escapes from head-on to head-pursuit, IGL will be invalid. Figure 7b shows the 100 interception trajectories generated by ARL. When the required angle could not be obtained, ARL does not follow the optimal trajectory to intercept the target but chooses to hit directly.

In engineering, we hope that the acceleration curve will be smooth to reduce sudden acceleration and deceleration. To illustrate the effect of the observation mask, we compare the acceleration of the agent with and without the observation mask. The acceleration of the agent is shown in Fig. 8. Figure 8a shows that with the observation mask, the agent will use the available information as much as possible to get a more robust strategy. When the agent can access the relative distance, the agent can reduce the miss distance by a large acceleration at a close relative distance. However, if there is no distance information, the agent cannot distinguish the relative distance, and naturally it cannot choose a large acceleration at a close relative distance. Without distance information, the agent has to minimize the miss distance at each step, which means the agent needs to maintain correct acceleration. Since the observation changes continuously, the reasonable output acceleration should also change smoothly. Therefore, the agent chooses gradually accelerating instead of abruptly accelerating to intercept the target. Figure 8b shows that with more information, the agent will exploit more acceleration ability to intercept the target. This sudden acceleration is impractical in engineering.

Performance evaluation on delay and maneuverability

Table 4 Comparison of hit rate in different maneuverability of the target

Table 5 Comparison of true hit rate in different maneuverability of the target

Table 6 Comparison of hit rate in different measurement delay

Table 7 Comparison of true hit rate in different measurement delay

Tables 4 and 5 show the hit rate and true hit rate of intercepting different maneuverability targets in the scenario with ten steps delay and noise. We compare the learning algorithm and optimal control methods, including PPO, PNG, and IGL. PNG method only considers the miss distance, so its hit rate

is very high but the true hit rate is very low. On the contrary, IGL has a high true hit rate when the maneuverability of the target is small. As the maneuverability of the target increases, the target can shift from head-on interception to head-pursuit interception faster. The head-pursuit interception is out of the domain of IGL method, so the method fails in intercepting the target.

Tables 6 and 7 show details about the test results of the methods under different delays in the scenarios with $9g$-maneuverability targets, 5% correlation variance noise, and independent noise. The results show that although the maneuvering method of the target is simple, the performance of the traditional approach is not ideal under noise interference. Compared with the PNG and IGL, ARL shows robust to the scenarios with different delays. The IGL algorithm using $t_{\text {go}}$ is more time-sensitive, and high latency will cause the algorithm to completely fail. It is concluded from the results that the proposed method is well adapted to noisy and delayed scenarios.

Conclusion

This paper focuses on designing guidance law based on DRL in the noisy and delayed environment to intercept the maneuvering target. We propose ARL with additional methods to improve the performance of PPO, including auxiliary learning and self-imitation learning. Auxiliary learning provides accurate auxiliary supervised gradients. Self-imitation learning reproduces the good experience without limiting its exploration. ARL can achieve 99.6% in intercepting the maneuvering target, which is better than PNG method. At the same time, ARL can intercept targets up to 17.5% within the intercept angle requirement, which is over twice than that of the guidance method considering angle constraints. We discuss the contribution of each part of ARL and analyze the training result in detail. Empirical simulations show that when intercepting different maneuvering targets in noisy-delayed environments, ARL can obtain a larger terminal intercept angle than PPO, PNG, and IGL.

Appendix

See Table 8.

Table 8 Aerodynamic coefficient $C_{a}$