Abstract
In this paper, we report on an enhanced hydrogen permeation effect along grain boundaries in tungsten. Sputtered nanocolumnar tungsten layers (column lateral dimensions 100–150 nm and layer thickness 2 μm) were analysed by hydrogen permeation measurements in the temperature range 520–705 K. The experiments constitute a direct observation of this effect, previously postulated by means of a combination of indirect experiments and simulations and considered controversial due to the lack of direct measurements. DFT results support this observation since (i) the hydrogen binding energy to the grain boundary is 1.05 eV and (ii) the migration energies along the grain boundary and along the bulk are 0.12 eV and 0.20 eV, respectively. OKMC simulations, parametrized by DFT data, were used as a supporting tool to attain a better understanding of the involved phenomena. The OKMC results are also compatible with the observations. Indeed, they show that the fraction of hydrogen flux along grain boundaries in the steady-state permeation regime increases when decreasing the ratio of lateral dimensions to length of the nanocolumns, rapidly approaching unity when this ratio is < 2. Therefore, grain boundaries act as preferential migration pathways for H atoms at the studied temperature range in the studied samples. This behaviour has interesting implications to reduce the retention of hydrogen in several applications, in particular, fusion materials exposed to plasma discharges.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
One of the main challenges that must be overcome in order to attain energy production by means of nuclear fusion reactions is the development of materials, by any fabrication method able to provide functional solutions (e.g., protective coatings) with superior properties to withstand realistic power plant conditions [1,2,3,4,5,6,7,8]. Tungsten (W) is nowadays considered the most reliable material to fulfil this role due to its outstanding properties, such as high melting point (Tmelt = 3695 K) and high thermal conductivity (160 W m−1 K−1) [1]. However, it also presents certain drawbacks, particularly regarding the retention of light species, mainly hydrogen and helium [9, 10]. This leads to a series of detrimental effects such as surface blistering, exfoliation and cracking [5, 11]. In order to avoid or at least to minimise these effects, one of the proposed strategies consists in scaling down the grain size from micrometre dimensions to tens to hundreds of nanometres (nanostructuration), as it has been reported that nanostructured materials present a higher resistance against radiation than their coarse-grained counterparts [12,13,14,15,16]. The superior resistance is attributed to the high density of grain boundaries (GBs), which enables a self-healing behaviour based on the annihilation of point defects (such as vacancies and interstitial atoms) under certain conditions [12,13,14,15,16]. However, in the specific case of nanostructured tungsten, there are still some discrepancies regarding the effect of the GBs in the transport of hydrogen: some publications report an enhanced hydrogen transport through GBs [17, 18], whereas, other authors attribute a strong trapping behaviour to the GBs [19, 20]. These discrepancies have been ascribed to different factors, like the nature and structure of the GB [21, 22], as well as the different temperature range of the performed analysis (as thermal-activated mechanisms can play additional roles in defect transport), not only in tungsten, but also in other metals [23,24,25,26]. We should emphasise that the information regarding the influence of GBs in hydrogen transport has been obtained through indirect observation, not only in our previous reports but in all the literature mentioned above.
This work intends to shed some light regarding the role of GBs in hydrogen transport in tungsten by direct observation of hydrogen permeation in nanostructured tungsten samples in the temperature range from 520 to 705 K grown by DC magnetron sputtering. In addition, object kinetic Monte-Carlo (OKMC) simulations, parametrized by means of density functional theory (DFT) data, have been extensively used to analyse the experimental data and attain a better understanding about the underlying phenomena. The combination of experiments and simulations provide a clear evidence of an efficient H trapping at the GBs and an enhanced 2D diffusion along them. Thus, the GBs act as efficient H migration pathways in our samples and therefore, contribute to a significant H permeation flux enhancement along nanostructured W in the temperature range of this study.
2 Materials and methods
2.1 Sample preparation
Pure α-phase, nanostructured W (NW) coatings preferentially oriented along the α-(1 1 0) direction were deposited by DC magnetron sputtering from a pure (99.95%) W commercial target at normal incidence angle on nickel substrates for mechanical support during the permeation experiments. The coatings have a thickness of approximately 2 μm as determined from cross-sectional scanning electron microscopy (SEM) images. The deposition setup consists of a high vacuum chamber with a base pressure in the range of 10−6 Pa, equipped with a 5-cm diameter magnetron designed and manufactured by Nano4Energy SL (www.nano4energy.es). The coatings consist of columns that grow perpendicular to the substrate, presenting an inverted pyramidal shape (compatible with zone T in Thornton’s morphology diagram [27]). The diameter of the columns at the coating surface is around 150 nm (Fig. 1). A more detailed description of the deposition method and the morphological and microstructural properties of the coatings can be found elsewhere [28]. The Ni substrate (99.95% pure Ni foil, with a thickness of 100 μm) was provided by Goodfellow. The effect of the coating on the hydrogen transport was studied by means of permeation experiments on an uncoated Ni substrate.
Top view and cross-sectional (detail) scanning electron microscopy images of pure α-phase nanostructured W coatings deposited by sputtering following the procedure described in [28]. The coating is made of columns with an average diameter of ∼100 nm, which grow perpendicular to the substrate
2.2 Permeation measurements
The permeation measurements rely on the determination of the hydrogen flux along a sample that acts as a membrane separating the high-pressure side from the vacuum side where detectors to determine the flux are located. This process consists of several steps that involve the adsorption and dissociation of the hydrogen molecule at the sample surface, diffusion of the hydrogen atoms through the sample and, finally, the recombination of the hydrogen atoms and desorption of the hydrogen molecule on the other side of the sample. The steady-state permeation flux along a single material membrane in this case can be written as follows:
where J represents the permeation rate, C0 the surface region concentration, S and D are the solubility and the diffusivity, respectively, φ represents the permeability of the material, P is the hydrogen pressure in the high-pressure side, and d the thickness of the sample. It is important to note that the value of the inlet pressure exponent, n, varies depending on the limiting step of the whole process: for purely diffusion-limited permeation, the exponent takes a value n = 1/2, whereas for purely surface-limited permeation, n = 1 [29,30,31]. The permeability is represented by φ = SD and, in most cases, it follows an Arrhenius law over a broad range of temperatures, as the solubility and the diffusivity do.
where φ0 is the permeability preexponential factor, Ea the activation energy, k the Boltzmann’s constant, and T, the temperature. In the case of coated, multi-layered samples, hydrogen must permeate through the whole system, and therefore a reduction of the permeation flux with respect to that along an uncoated substrate is expected. In this situation, an experimental proof of the coating efficiency is the reduction of the steady-state hydrogen permeation flux at identical conditions for coated and uncoated substrates. Thus, we can define a permeation reduction factor (PRF) [32], which can be written as:
where Juncoated refers to the steady state flux along the substrate and Jcoated to the stead-state flux along the whole-coated sample. In the diffusion-limited permeation scenario, the PRF of a bilayer sample is related to the permeability (φ) and thickness (d) of each layer (i) through the following expression [32]:
where the subscript f corresponds to the coating film and the subscript s, to the substrate. Thus, we can obtain the permeability of the film provided we know the thickness of the layers, the permeability of the uncoated substrate (Ni in our case) and the PRF (i.e., the Jcoated and Juncoated).
Permeation measurements were performed in a home-built all-metal permeation cell, which operates with a base pressure of 10−6 Pa. It is divided in three different modules, schematically shown in the inset of Figure 2. Module 1 is the gas supply, module 2 contains two sample holders with the heating elements and module 3 is the detection chamber with the necessary instrumentation. Module 1 consists of stainless steel tubes connected to the gas supply, a membrane pump and a pressure gauge to control the pressure. The sample is mounted in one of the stainless steel flanges (module 2), in such a way that the sample acts as a membrane separating the high-pressure side (module 1) from the high vacuum side (module 3). The sample can be exposed to pressures of up to 106 Pa. The temperature is controlled with a thermocouple attached to the flange that holds the sample. Finally, module 3 is made of stainless steel and contains a vacuum gauge and a quadrupole mass spectrometer (QMS). Thus, we can estimate the hydrogen permeation rate with both instruments. The measurements were performed following the dynamic method, i.e., exposing the heated sample to a constant pressure and determining the permeation flux on the other side of the sample.
Hydrogen permeation flux obtained at 520 K for a sample composed of a Ni substrate coated with a nanostructured W layer. The flux was stabilised for several days at the maximum pressure. Then, the pressure was successively dropped to the indicated pressures and the permeation fluxes were recorded. The inset shows schematically the experimental arrangement
In this paper, the permeation experiments were performed at different temperatures, ranging from 520 to 705 K, in order to determine the permeability of the material according to Equation (2). At least five measurements were carried out at every single temperature at different inlet hydrogen pressures from 106 down to 105 Pa to verify the rate limiting mechanism of the permeation process through the value of the pressure exponent, n, in Equation (1). Between two consecutive experiments, the sample and neighbouring tubes were heated for several hours above the maximum analysis temperature value, in order to minimise the influence of hydrogen desorption contributions. An example of the hydrogen permeation flux obtained at 520 K is shown in Figure 2. During these experiments, the sample was heated to the target temperature in vacuum (aprox. 10−6 Pa) and kept at that temperature for several hours to reduce the background signal. Then, the highest hydrogen pressure (777.6 kPa) was set. At this relatively low temperature, long times are required to stabilise the permeation flux, in the example, more than 2 days. Once stable, the inlet pressure was decreased to the indicated values and the permeation flux was recorded in every case.
2.3 DFT simulations
DFT simulations were performed by means of the VASP package [33,34,35]. In all these calculations, we have used the approximation developed by Perdew, Burke and Ernzerhof (PBE) [36] for the exchange and correlation functional and the Projector Augmented Wave [37] pseudo-potentials provided by the code. A cutoff energy of 400 eV was fixed for the plane waves and the structures were relaxed until the energy difference was less than 10−4 eV and the forces were lower than 0.025 eV/Å. We have modelled the W atoms using six valence electrons (4 4d and 2 5s) and a single electron in the 1s orbital for H. Following these conditions, the lattice parameter obtained for the bulk (bcc) structure was 3.172 Å, in agreement with the experimental room temperature value 3.165 Å [38]. The 1×1×1 cubic unit cell was repeated 5 times along the three Cartesian directions, thereby forming a 5×5×5 supercell (250 atoms), where we have created all the defects included in the parametrization. The first Brillouin zone was sampled with a 2×2×2 k-mesh following the Monkhorst–Pack methodology [39]. We presented and successfully used all these values in a previously published work [10].
On the other hand, the GB was modelled with a slab formed by 6 layers of a W <110> surface adjoined to 6 additional layers of a W <112> surface (for a total of 288+168=456 atoms). This particular choice of surfaces has been suggested by experimental data (XRD). The interface was formed after the alignment of the (−111) directions of both surfaces (see Fig. 1 in Ref. [40]). We repeated the unit cell four times along this direction and defined the full unit cell when a mismatch between the surfaces of less than 1% was found in the perpendicular direction. Due to the difference in the length of the lattice vectors, the k-space was sampled asymmetrically by means of a 2×4 k-mesh. The last atomic layers of each surface were fixed, in order to mimic bulk behaviour, while the remaining ones were allowed to move during relaxation. A vacuum of 12 Å was included in the calculation to avoid spurious interactions between surface images. A more exhaustive description of the interface construction process can be found in [40].
2.4 OKMC simulations
OKMC simulations were performed with the open source code MMonCa [9, 10, 41]. The parametrization used in this work is identical to the one recently employed in [9], except for some modifications introduced to consider hydrogen incorporation to GBs and hydrogen migration along GBs, based on the results of the DFT calculations. Figure 3 depicts the simplified schematic energy diagram used for the simulations. We obtained a smaller value for the migration energy along GBs than that in the bulk (0.12 eV and 0.20 eV, respectively) [10], which implies an enhanced mobility for H atoms along the GBs. We take into account the 2D migration mechanism along the GBs and the 3D migration mechanism in the interior of the grains. In addition, our DFT simulations leads to a binding energy of a hydrogen atom to an empty GB is 1.05 eV. Hence, hydrogen atoms are efficiently trapped at the GB at low occupation levels and at the experimental temperatures. In our simplified scheme, we used this value instead of a binding energy dependant on the GB occupation density. However, we considered the hydrogen occupation by varying the allowed maximum occupation density from 0.25 to 6.25 H/nm2. Thus, the GBs are not considered perfect sinks for H, on the contrary, hydrogen incorporation to the GB is only possible through empty sites. In this way, the effect of GB occupation is considered in a simple model that provides information about the relationship between occupation density and effective permeability.
In order to analyse the influence of the GB density on the permeation behaviour, several simulation boxes were used with different sample dimensions, i.e., different length (d) and grain size (lateral dimensions, L×L). The box length was d = 50, 100 and 200 nm and the lateral dimensions L2 = 50×50, 100×100 and 150×150 nm2. The four lateral surfaces of the boxes were defined as GB in terms of energies and migration mechanisms.
We carried out the permeation simulations by means of two different methods. The first one consists in keeping a constant concentration at the box surface, while the second one relies on keeping a constant flux along the simulation box. The first method is more intuitive because it is similar to the experiments performed in diffusion-limited materials such as tungsten. However, it requires to count the number of atoms in the surface region every certain number of steps and replace the lost ones. There are some issues that arise from this method, namely, the definition of the surface region is not trivial, and the small dimensions of the simulation boxes lead to statistical errors in counting and replacing atoms. Regarding the second method, we added a fixed number of atoms every certain number of simulation steps. In this way, we properly reproduce the steady-state permeation once it is reached (which is actually the final goal of the simulations) without the statistical fluctuations produced by the random movement of atoms in and out the surface region. For this reason, most results shown in this paper were obtained with this method. Certainly, with this method, we cannot describe the concentration build-up prior to the steady-state regime. However, this is not the main point of interest, which would actually require, for a proper description, a more sophisticated model including molecule adsorption from the gas phase and dissociation at surface cracking centres. Without such a detailed surface model, we need to rely on published values of solubility to estimate the external pressure in equilibrium for a certain surface concentration (steady state in diffusion-limited permeation).
3 Results and discussion
3.1 Permeation measurements
As described in the previous Section, Figure 2 shows an example of hydrogen permeation experiments at 520 K across a NW sample on a Ni substrate. We carried out the same experiments at different temperatures and inlet pressures, as mentioned above, in order to study the steady-state permeation flux dependence on these variables. The steady-states fluxes (Jcoated) are summarised as a function of the square root of the inlet pressure for five experiments performed at different temperatures in Figure 4. The linear trend followed by the experimental points can be fitted with the least square method, showing a high goodness of the fits (R2 > 0.999 in all the cases). This indicates that the steady-state permeation flux follows Equation (1) with an exponent n = 1/2, which, as discussed in the previous Section, is an evidence of a diffusion-limited permeation process. Thus, the atomic hydrogen concentration at the sample surface region is in equilibrium with the external gas pressure.
In order to determine the PRF, we need to know the permeability value of the uncoated Ni substrates. Instead of using values reported in literature, we carried out similar experiments to those shown in Figure 4 on our uncoated substrates (not shown). We confirmed a diffusion-limited permeation behaviour (n = 1/2) and obtained Ni permeability values with the following Arrhenius temperature dependence in the studied temperature range:
which is in good agreement with the literature [42, 43]. With this expression and Equation (1), we obtain Juncoated for all the temperature and inlet pressure values of the experiments represented in Fig. 4. By using Equation (3), with Jcoated values represented in Fig. 4 and its corresponding Juncoated value, we obtain the PRF, which is ~4 for all temperatures and inlet pressure values. Then, and taking into account that the substrate (df) and the coating depth (ds) are 100 μm and 2 μm, respectively, Equation (4) provides the permeability of the NW coatings at every temperature. The permeability values are plotted in Figure 5. Assuming an Arrhenius behaviour, we get the following expression for the permeability of the NW layers (fitting line in the figure):
Permeability of H in tungsten obtained by means of the experiments reported in this paper and compared to experiments by Frauenfelder [44], Zakharov [45], Esteban et al. [46], Zhao et al. [47], Liang et al. [48], and Liu et al. [49, 50]. The continuous lines are fits to the experimental data obtained from samples with different microstructure. In the case of Esteban et al. the continuous line corresponds to the permeability of bulk tungsten as estimated from their results when considering the effect of traps
For comparison purposes, along with our results, Figure 5 contains permeability results obtained by Frauenfelder [44, 45], Zakharov [45], Esteban et al. [46], Zhao et al. [47], Liang et al.[48], and Liu et al.[49, 50]. The results shown in the figure were obtained for samples with different microstructure and defect level; thus, the values shown in the figure are effective permeabilities affected by the details of the samples under study, their microstructure and their defect level. The estimation of the permeability value of a non-ideal sample is not straightforward, in particular at low temperatures, due to the myriad of effects that can occur in a real sample containing point defects, dislocations and grain boundaries [51]. However, it is very remarkable that the permeability of our nanostructured layers is considerably higher than the permeability reported in every one of the other experiments carried out on samples with much larger grain size. Only at very elevated temperatures, an extrapolation of our results seems to point to the experimental results of Frauenfelder [44, 45]. This observation agrees with the fact that, at elevated temperatures, H emission from the GBs is possible, which suppresses the preferential migration pathway of H along the GBs. On the other hand, at low temperatures, H cannot escape from the GB region due to its binding energy (1.05 eV, according to our DFT results). Therefore, at low temperatures, GBs play an important role in H transport and permeation. Based on DFT calculations and indirect observations on hydrogen transport in NW, we proposed that the presence of GBs perpendicular to the sample surface significantly enhances the H migration to the surface [9, 10], from where H can escape in molecular form upon recombination. The direct observation of hydrogen transport through the permeation experiments shown in this paper strongly supports our suggestion. The recent permeation results obtained by Zhao et al. [47] (green line in Figure 5) on microstructured tungsten samples with elongated grains perpendicular to the surface also support our proposal of an enhanced permeation favoured by the GBs. In addition, the results shown by Liang et al. (grey line) and Liu et al. (various green lines and pink line) do correspond with the projection of the results attained by Frauenfelder and Zakharov, respectively for samples with grain sizes of several hundreds of nanometres, even few micrometres [48,49,50], where the effect of the GBs is negligible.
3.2 DFT simulations
DFT calculations allowed us to determine the binding energy of the most stable site for a single H atom in an empty (100)/(112) interface, obtaining a value of 1.05 eV, in agreement with the result found by several authors [52,53,54,55,56,57]. Its migration energy along the (−111) direction was also estimated, and the barrier found was 0.12 eV, clearly below the migration energy through bulk W (0.20 eV). Additionally, in an attempt to achieve a better understanding of the GB occupation process, we have tried to fill completely the interface with H atoms, as it is shown in Figure 6. It was possible to insert a maximum of 39 H/nm2 in the designed interface.
Representation of the results attained during the filling process of the (100)/(112) interface (W atoms as grey spheres) with H atoms (white spheres). A maximum H density of 39 H/nm2 was achieved at 0 K. The inclusion of additional H atoms provokes a decrease in the binding energy and the migration of several H atoms to first and second neighbour sites
This process leads to an important modification of the energy diagram and the migration of a significant number of H atoms to first and second nearest neighbour sites. This means, effectively, a reduction in the binding energy of H to the GB. These calculations have been performed following a standard DFT methodology, thus all processes take place at 0 K. Reaching this huge H occupation at the GB is not expected at higher temperatures, as the binding energy of H decreases when the amount of H atoms that access to the GB increases, to a point that the reemission mechanism dominates over the incorporation to the GB.
These values confirm, firstly, the ability of GBs to act as efficient traps for H atoms at he analysed temperatures, avoiding the return of these atoms back to the grain and forcing them to migrate along the GBs, where the migration energy barrier to overcome is smaller than inside the grain. It is important to note that the value found for the binding energy (1.05 eV) corresponds to a hydrogen-empty GB, and therefore might change depending on the amount of H already present at this GB. However, considering the model proposed in previous sections and further developed in the following one, the proposed value is high enough to assume that GBs behave as traps for H, impeding their reemission back to the interior of the grain. If the accumulation of hydrogen at the grain boundaries is too high, hydrogen atoms will pile up; however, since this situation is far from our experimental situation, we have not considered it in detail.
3.3 OKMC simulations
We carried out OKMC simulations to understand the effect of the GBs on the hydrogen transport along our NW samples. Rather than a quantitative fit to the experimental data, we pursued a semi-quantitative explanation of the transport processes. As discussed in Section ‘Materials and methods’, the simplified GB model we used does not consider a variable hydrogen-binding energy to the GB as a function of the GB occupation. On the other hand, we set the maximum occupation number to study its influence. We did not consider surface effects, on the contrary, we introduced hydrogen in the surface region by two methods, either keeping the concentration constant or the flux constant. It was not possible to carry out simulations with boxes of the experimental dimensions (2 μm thick) because the simulation times for such boxes are excessively long. However, we show next that this is not a major drawback. In fact, in order to provide a comparison with the experiments for validation purposes, we show in Figure 7 the permeability values obtained from our experiments (previous discussion) and permeability values obtained by means of the OKMC simulations, calculated with Equation (1), provided we can connect the concentration in the surface region (from the simulations) and the external equilibrium pressure. For that purpose, we need the hydrogen solubility in tungsten, which is actually a non-well established value, especially at low temperatures, at which different traps do play an important role [51]. In our case, we used the solubility obtained by Esteban et al. [46] considering traps at temperatures similar to those of our experiments. Thus, to provide an example with the values employed, with Esteban’s solubility, the equilibrium pressure to keep a fixed concentration of 5.6 H/nm3 varies from 0.1 to 1 GPa depending on the temperature. These inlet pressures are considerably higher than the experimental ones, which is appropriate to avoid the statistical fluctuations related to the low concentrations reached in our simulations even when carrying out the simulation in constant flux mode (Section ‘Materials and methods’). Certainly, at these high pressures, one would expect additional effects, such as the appearance of strain/stress fields in the material and a hydrogen behaviour far from ideal gas conditions, which affect physical parameters such as solubility and permeability. However, since these effects are not considered in our model, the results obtained at high pressures can be extrapolated to low pressures with the mentioned advantage of reducing the statistical fluctuations. Indeed, the good agreement between the experiments and the simulations in the whole temperature range of the experiments for boxes with lateral dimensions similar to those of the experimental samples (L2 = 150×150 nm2) and a sufficiently large thickness (d = 100–200 nm) in simulations with a maximum GB occupation density of 6.25 H/nm2 is remarkable. According to the figure, the permeability curve significantly changes when d varies from 50 to 100 nm. However, the variation is small when d varies from 100 to 200 nm. Further increase in the box thickness will likely lead to similar results, making possible to extract useful conclusions with boxes smaller than those of the experiments. Thus, despite the simplified model, the permeability values obtained by OKMC simulations reproduce fairly well the experimental values, making us confident about the explanation on hydrogen transport given in the following.
Comparison of permeability values obtained in our experiments and by means of OKMC simulations using boxes of the indicated dimensions (in nm3, the first number refers to the box length, d) and a maximum GB occupation of 6.25 H/nm2. For the simulations, the concentration was kept constant (5.6 H/nm3) in the near surface region (0.4 nm). The continuous line is the fit to the experimental values given in Eq. (6). The dashed line was obtained by OKMC simulations of a GB-free (monocrystalline) tungsten sample
For comparison, similar simulations for a GB-free (monocrystalline) sample are included in Figure 7 (dashed line). The obtained permeability is much lower than the one found for the NW cases. Once again, the enhancement due to the high GB density is very evident. The permeabilities shown in Figure 7 for NW samples are effective permeabilities, i.e., a fraction of the hydrogen flux diffuses along the grain boundaries through a 2D diffusion process and the rest along the grain, following the normal 3D diffusion along monocrystalline W.
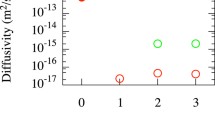
The OKMC simulations provide the fraction of hydrogen flux along the GB (JGB/J) once the steady state is reached. Figure 8 contains this fraction at 705 K as a function of the ratio of lateral size to depth (L/d) for different box dimensions and for the indicated maximum GB occupation densities. The role of the maximum occupation densities is clearly visible; if the number of accessible sites for H atoms is limited, the flux along the GB is reduced with respect to the same case with a larger number of accessible sites. It is interesting to realise that, in a first approach, the ratio L/d determines the value of JGB/J, even when using boxes of different dimensions, as for L/d = 0.5 and L/d = 1.0 (note the overlapping symbols in the figure). The flux fraction along the GB increases with decreasing L/d. For L/d ≤ 1.5, JGB/J tends to saturate to values close to 1. This explains why in Figure 7, the permeability curves do not vary significantly when increasing d beyond 100 nm since the major contribution to the total permeability is the one of the GBs in these scenarios. In addition to the JGB/J dependency on L/d, the lateral area (GB area) plays a role. In other words, if the box length is greater than the box side, hydrogen will easily reach the GB, get trapped and diffuse along it. Therefore, the flux fraction along the GB approaches unity. On the other hand, if the box side is greater than the box length, hydrogen will diffuse a long way along the grain before getting trapped at the GB. However, the probability of hydrogen trapping at the GB followed by 2D diffusion along it is not negligible at all. For example, for the box with dimensions 50×150×150 nm3 (L/d = 3.0), the flux fraction along the GB is JGB/J = 0.6 − 0.7, which indicates, that H can effectively reach the GB and leave the sample from it even for cases with high L/d ratios. If we observe the cases for boxes with dimensions L2 = 150×150 nm2, the flux along the GB appears higher than the one for the L/d ratios 0.75 and 1.5. Thus, as expected, we can state that the larger the GB, the higher the JGB/J fraction that can be reached, due to the additional available H sites at the GB.
Fraction of hydrogen flux along the GB in steady-state conditions as a function of the ratio of lateral box size to box depth. The results were obtained by means of OKMC simulations with the indicated boxes at 705 K keeping a constant flux of 1023 H2 m-2 s−1. The maximum GB occupation density varied from 0.25 to 4 H/nm2 (legend)
By means of the OKMC simulations we can obtain the hydrogen concentration profiles in any simulated box and distinguish where H is located, i.e., at the GB or in the interior of the grains. Figure 9 contains the H atoms concentration profiles for a number of illustrative cases to understand the effect of the GBs on the hydrogen transport. Columns A to C display the concentration profile of thin columnar grains (L2 = 50×50 nm2). The constant parameter is the hydrogen flux; therefore, the steady state is reached with different surface concentrations. In these columns, it is easy to observe that the total concentration gradient is less pronounced for increasing box length. From Equation (1), we can deduce that the permeability increases for increasing depth, similar to the observations in Figure 7. The explanation to this effect is related to the GBs: in all cases, the H fraction trapped at the GBs increases with increasing box length. Due to the fact that according to our DFT results, the migration energy along the GB (0.12 eV) is lower than along the grain (0.20 eV), the increase of H concentration at GBs leads to the experimentally observed effective permeation enhancement. It is interesting to note that the surface concentration basically increases by trapping and accumulating more H atoms at the GB (red curves).
Atomic hydrogen concentration profiles (in the interior of the grain, in the grain boundary and total) in steady state as obtained by means of OKMC simulations. The inlet hydrogen flux was kept constant at a value of 1023 H2 m-2 s−1. Box dimensions, temperatures, and maximum occupation densities (in H/nm2) are indicated
If we compare columns A and B, we can observe the effect of varying the maximum GB occupation density from 1 to 4 H/nm2. In all cases, but especially relevant for the boxes with a length of 200 nm, the concentration profiles rises for increasing maximum occupation densities. Note that the surface GB concentrations in these cases are far from the maximum values (0.08 H/nm3 and 0.32 H/nm3, respectively for maximum occupations of 1 and 4 H/nm2). Anyhow, it is obvious that increasing the availability of sites to accommodate H at the GB significantly contributes to increase the surface concentration.
The effect of the temperature can be understood by comparison of columns B and C. According to Equation (1), reducing the temperature from 705 (column B) to 615 K (column C), results in a decrease in the permeability and, therefore, a higher external pressure is needed to maintain the hydrogen flux constant. This fact leads to an increase in the concentration profiles of H in the sample, which is easily seen when comparing these columns, e.g., the maximum H concentration in the 200-nm-thick sample rises from a value of approximately 0.03 H/nm3 at 705 K to a value of almost 0.04 H/nm3 at 615 K.
The previous cases obtained with thin boxes (L2 = 50×50 nm2) and side to length ratios L/d ≤ 1.0 are examples of GB-dominated permeation (JGB/J~1). Column D shows the effect of using broader columnar grains L2 = 100×100 nm2 and L2 = 150×150 nm2. As the lateral dimensions increase (L/d ratios increase), the probability of reaching the GBs decreases, thus the H fraction trapped at the GB decreases to the extent that in the panel D3 the H diffusion along the box mainly occurs through 3D diffusion along the grain.
It is important to note that the flux fraction (JGB/J) along the GB shown in Figure 8 was estimated by means of the flux that escapes from the GB (JGB) at the end of the simulation box but this fraction does not consider how the hydrogen transport took place along the box. Therefore, the values obtained in this way may lead to misguiding interpretations if not considered carefully. For instance, we showed that for the box with dimensions 50×150×150 nm3 (L/d = 3.0) in Figure 8, the flux fraction along the GB is JGB/J = 0.6 − 0.7, thus, one may misinterpret that H transport mainly occurs along the GB. However, we have just discussed invoking panel D3 in Figure 9 that the transport in this case is dominated by 3D diffusion along the grain, despite the probability for H trapping at the GB is high, it mainly occurs near the exit surface of the sample, once the migration has taken place mainly along the grain. The fact that for the 50×150×150 nm3 box (as an example of a high L/d ratio sample), the permeation process mainly occurs along the grain explains why, in Figure 7, the permeability approaches the grain-free permeability (dashed line): the small thickness of this sample favours the diffusion along the grain until the exit surface, and only a small amount of the H atoms (the ones closest to the lateral surfaces) will access the GB and diffuse along it. In samples with a high L/d ratio such as the one considered, H atoms tend to diffuse along the grain before reaching the GB (as the thickness of the simulation box is shorter than the existing distance between its lateral surfaces), although the atoms that eventually reach the GB will therefore be trapped, and will contribute to the fraction of the H flux that permeates through GB instead of along the grain.
4 Conclusions
We performed hydrogen permeation experiments in nanostructured tungsten samples in the temperature range of 520 to 705 K and for inlet pressures ranging from 105 to 106 Pa in order to determine by direct observation analysis the influence of GBs on the hydrogen transport in tungsten. The experimental results were compared with the information provided by several OKMC simulations, parametrized by means of DFT simulations, which provided a better understanding of the phenomena involved.
The permeability values obtained from our experiments were consistently higher than the ones found in literature. We ascribed this effect to the presence of GBs with a perpendicular orientation regarding the sample surface, which act as preferential migration paths (as we postulated earlier) for H atoms at relatively low temperatures, such as the ones employed here. However, at higher temperatures, the extrapolation of the obtained data suggests the suppression of these preferential paths as H emission from GBs becomes possible, leading to permeability values similar to the ones found in literature.
We performed several OKMC simulations, parametrized by DFT values, employing a simplified GB model. Different box sizes were designed to improve the interpretation of the experimental results, confirming the assumption of an enhanced H permeation along GBs, particularly at low temperatures. It is important to note that the flux fraction along GBs follows the ratio of lateral dimensions to box length (L/d) even for simulation boxes of different sizes. In addition, different GB occupation densities were studied, and we found that increasing the availability of sites for H atoms in the GBs leads to an increase of the permeation flux along the GB, as well as an obvious increase of the H concentration in the GB, especially in the longest simulation boxes.
These results, attained by a combination of experimental and computational simulations, indicate that the GBs play an essential role in H transport in tungsten, especially at low temperatures, acting as preferential migration paths (Em, GB = 0.12 eV vs. Em, grain = 0.20 eV) as well as traps for H atoms, although parameters such as the nature of the sample, the size of the grain, the arrangement of the GBs and the tortuosity of the GB network might play an important role on the transport process. This has interesting implications to reduce the retention of hydrogen in several applications, in particular, fusion materials exposed to plasma discharges.
Further work should consider the most common types of grain boundaries properly characterised with experiments, such as, electron backscatter diffraction studies. Additional permeation experiments along with DFT calculations (as in this paper) for well characterised grain boundary types will help understand the hydrogen behaviour on the most common types of grain boundaries and will provide a unified understanding on the hydrogen transport mechanisms in tungsten samples fabricated and processed by means of different methods.
Data availability
The data that support the findings of this study are available from the corresponding author, Pablo Díaz-Rodríguez, upon reasonable request.
Code availability
The code employed that support the findings of this study is available from the corresponding author, Pablo Díaz-Rodríguez, upon reasonable request.
References
J. Linke, J. Du, T. Loewenhoff, G. Pintsuk, B. Spilker, I. Steudel, M. Wirtz, Challenges for plasma-facing components in nuclear fusion. Matter Radiat. Extrem. 4, 056201 (2019)
A.J.H. Donné, The European roadmap towards fusion electricity. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 377, 20170432 (2019)
I.T. Chapman, A.W. Morris, UKAEA capabilities to address the challenges on the path to delivering fusion power. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 377, 20170436 (2019)
N. Castin, A. Bakaev, G. Bonny, A.E. Sand, L. Malerba, D. Terentyev, On the onset of void swelling in pure tungsten under neutron irradiation: An object kinetic Monte Carlo approach. J. Nucl. Mater. 493, 280–293 (2017)
K.D. Hammond, Helium, hydrogen, and fuzz in plasma-facing materials. Mater Res. Express 4, 104002 (2017)
R. Gonzalez-Arrabal, A. Rivera, J.M. Perlado, Limitations for tungsten as plasma facing material in the diverse scenarios of the European inertial confinement fusion facility HiPER: Current status and new approaches. Matter Radiat Extrem. 5, 055201 (2020)
Viswanathan, V., Kumar, N., Goel, G., Matthews, A. and Goel, S. (2021). Role of Thermal Spray in Combating Climate Change. Emergent Materials. https://doi.org/10.1007/s42247-021-00307-1
Katiyar, N.K., Goel, G. & Goel, S. Emergence of machine learning in the development of high entropy alloy and their prospects in advanced engineering applications. emergent mater. (2021). https://doi.org/10.1007/s42247-021-00249-8
M. Panizo-Laiz, P. Díaz-Rodríguez, A. Rivera, G. Valles, I. Martín-Bragado, J.M. Perlado, F. Munnik, R. González-Arrabal, Experimental and computational studies of the influence of grain boundaries and temperature on the radiation-induced damage and hydrogen behavior in tungsten. Nucl Fusion 59, 086055 (2019)
G. Valles, M. Panizo-Laiz, C. González, I. Martin-Bragado, R. González-Arrabal, N. Gordillo, R. Iglesias, C.L. Guerrero, J.M. Perlado, A. Rivera, Influence of grain boundaries on the radiation-induced defects and hydrogen in nanostructured and coarse-grained tungsten. Acta Mater. 122, 277–286 (2017)
E. Gao, N.M. Ghoniem, A coupled rate theory-Monte Carlo model of helium bubble evolution in plasma-facing micro-engineered tungsten. J. Nucl. Mater. 509, 577–590 (2018)
E. Aradi, J. Lewis-Fell, R.W. Harrison, G. Greaves, A.H. Mir, S.E. Donnelly, J.A. Hinks, Enhanced radiation tolerance of tungsten nanoparticles to He Ion irradiation. Nanomaterials 8, 1052 (2018)
E.M. Bringa, J.D. Monk, A. Caro, A. Misra, L. Zepeda-Ruiz, M. Duchaineau, F. Abraham, M. Nastasi, S.T. Picraux, Y.Q. Wang, D. Farkas, Are Nanoporous materials radiation resistant? Nano Lett. 12, 3351–3355 (2012)
R.A. Andrievski, Behavior of radiation defects in nanomaterials. Rev. Adv. Mater. Sci. 29, 54–67 (2011)
R.A. Andrievskii, Radiation stability of nanomaterials. Nanotechnologies Russ. 6, 357–369 (2011)
G. Ackland, Controlling radiation damage. Science 327, 1587–1588 (2010)
U. von Toussaint, T. Schwarz-Selinger, K. Schmid, First-passage kinetic Monte Carlo on lattices: Hydrogen transport in lattices with traps. J. Nucl. Mater. 463, 1075–1079 (2015)
H.-B. Zhou, Y.-L. Liu, S. Jin, Y. Zhang, G.-N. Luo, G.-H. Lu, Investigating behaviours of hydrogen in a tungsten grain boundary by first principles: from dissolution and diffusion to a trapping mechanism. Nucl Fusion 50, 025016 (2010)
T. Oda, D. Zhu, Y. Watanabe, Kinetic Monte Carlo simulation on influence of vacancy on hydrogen diffusivity in tungsten. J. Nucl. Mater. 467, 439–447 (2015)
Y. Yu, X. Shu, Y.-N. Liu, G.-H. Lu, Molecular dynamics simulation of hydrogen dissolution and diffusion in a tungsten grain boundary. J. Nucl. Mater. 455, 91–95 (2014)
J. Chai, Y.-H. Li, L.-L. Niu, S.-Y. Qin, H.-B. Zhou, S. Jin, Y. Zhang, G.-H. Lu, First-principles investigation of the energetics of point defects at a grain boundary in tungsten. Nucl. Instrum. Methods Phys Res. Sect. B Beam Interact. Mater. At. 393, 144–149 (2017)
W.Z. Han, M.J. Demkowicz, E.G. Fu, Y.Q. Wang, A. Misra, Effect of grain boundary character on sink efficiency. Acta Mater. 60, 6341–6351 (2012)
A. Oudriss, J. Creus, J. Bouhattate, E. Conforto, C. Berziou, C. Savall, X. Feaugas, Grain size and grain-boundary effects on diffusion and trapping of hydrogen in pure nickel. Acta Mater. 60, 6814–6828 (2012)
P.A. Thorsen, J.B. Bilde-Sørensen, B.N. Singh, Influence of grain boundary structure on bubble formation behaviour in helium implanted copper. Mater. Sci. Forum 207–209, 445–448 (1996)
C.M. Barr, O. El-Atwani, D. Kaoumi, K. Hattar, Interplay between grain boundaries and radiation Damage. JOM 71, 1233–1244 (2019)
P. Mao, J. Cui, Y. Chen, J. Qiu, Q. Jin, J. Qiao, Y. Zhao, K. Cui, N. Gao, K. Tai, Quantitative investigation on sink strength of nano-grain boundary for irradiation resistance. J. Nucl. Mater. 526, 151741 (2019)
J.A. Thornton, Influence of substrate temperature and deposition rate on structure of thick sputtered Cu coatings. J. Vac. Sci. Technol. 12, 830–835 (1975)
N. Gordillo, M. Panizo-Laiz, E. Tejado, I. Fernandez-Martinez, A. Rivera, J.Y. Pastor, C.G.d. Castro, J. del Rio, J.M. Perlado, R. Gonzalez-Arrabal, Morphological and microstructural characterization of nanostructured pure α-phase W coatings on a wide thickness range. Appl. Surf. Sci. 316, 1–8 (2014)
A. Pisarev, A. Bacherov, Hydrogen gas driven permeation through asymmetric membranes in diffusion limited and surface limited regimes: Interplay between analytical and numerical calculations. Phys. Scr. 2004, 124 (2004)
P.M. Richards, Surface-limited hydrogen release and uptake in metals. J. Nucl. Mater. 152, 246–258 (1988)
B. Zajec, V. Nemanič, Determination of parameters in surface limited hydrogen permeation through metal membrane. J. Membr. Sci. 280, 335–342 (2006)
V. Nemanič, B. Zajec, D. Dellasega, M. Passoni, Hydrogen permeation through disordered nanostructured tungsten films. J. Nucl. Mater. 429, 92–98 (2012)
G. Kresse, J. Hafner, Abinitio molecular-dynamics for liquid-metals. Phys. Rev. B 47, 558–561 (1993)
G. Kresse, J. Furthmuller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996)
G. Kresse, D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999)
J.P. Perdew, K. Burke, M. Ernzerhof, Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996)
P.E. Blöchl, Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994)
A.M.L.M.P. James, Macmillan’s chemical and physical data (Basingstoke: Macmillan). Biochem. Educ. 21, 109–110 (1993)
H.J. Monkhorst, J.D. Pack, Special points for Brillouin-zone integrations. Phys. Rev. B 13, 5188–5192 (1976)
C. González, M. Panizo-Laiz, N. Gordillo, C.L. Guerrero, E. Tejado, F. Munnik, P. Piaggi, E. Bringa, R. Iglesias, J.M. Perlado, R. González-Arrabal, H trapping and mobility in nanostructured tungsten grain boundaries: a combined experimental and theoretical approach. Nucl Fusion 55, 113009 (2015)
I. Martin-Bragado, A. Rivera, G. Valles, J.L. Gomez-Selles, M.J. Caturla, MMonCa: an object kinetic Monte Carlo simulator for damage irradiation evolution and defect diffusion. Comput. Phys. Commun. 184, 2703–2710 (2013)
S.K. Lee, Y.G. Ohn, S.J. Noh, Measurement of hydrogen permeation through nickel in the elevated temperature range of 450 – 850 °C. J. Korean Phys. Soc. 63, 1955–1961 (2013)
S.J. Noh, S.K. Lee, H.S. Kim, S.-H. Yun, H.G. Joo, Deuterium permeation and isotope effects in nickel in an elevated temperature range of 450–850 °C. Int. J. Hydrog. Energy 39, 12789–12794 (2014)
R. Frauenfelder, Permeation of hydrogen through tungsten and molybdenum. J. Chem. Phys. 48, 3966 (1968);https://doi.org/10.1063/1.1669721
A.P. Zakharov, V.M. Sharapov, É.I. Evko, Hydrogen permeability of polycrystalline and monocrystalline molybdenum and tun gsten. Sov. Mater. Sci. 9, 149–153 (1975)
G.A. Esteban, A. Perujo, L.A. Sedano, K. Douglas, Hydrogen isotope diffusive transport parameters in pure polycrystalline tungsten. J Nucl Mater. 295(1), 49–56 (2001), ISSN 0022-3115, https://doi.org/10.1016/S0022-3115(01)00486-X
M. Zhao, M. Nakata, F. Sun, Y. Hatano, Y. Someya, K. Tobita, Y. Oya, Deuterium permeation behavior in Fe ion damaged tungsten studied by gas-driven permeation method. Fusion Sci Technol. 76, 246–251 (2020)
C. Liang, D. Wang, W. Jin, Y. Lou, W. Wang, X. Ye, C. Chen, K. Liu, H. Xu, X. Wang, A.W. Kleyn, Deuterium permeation behaviors in tungsten implanted with nitrogen. J. Nucl. Mater. 505, 174–182 (2018)
F. Liu, H. Zhou, X.-C. Li, Y. Xu, Z. An, H. Mao, W. Xing, Q. Hou, G.-N. Luo, Deuterium gas-driven permeation and subsequent retention in rolled tungsten foils. J. Nucl. Mater. 455, 248–252 (2014)
F. Liu, H. Zhou, Y. Xu, X.-C. Li, M. Zhao, T. Zhang, Z. Xie, Q.-Z. Yan, X. Zhang, F. Ding, S. Liu, G.-N. Luo, Gas-driven permeation of deuterium through tungsten with different microstructures. Fusion Eng Des. 113, 216–220 (2016)
T. Tanabe, Review of hydrogen retention in tungsten. Phys. Scr. 2014, 014044 (2014)
C. Guerrero, C. González, R. Iglesias, J.M. Perlado, R. González-Arrabal, First principles study of the behavior of hydrogen atoms in a W monovacancy. J Mater Sci 51, 1445–1455 (2016)
N. Fernandez, Y. Ferro, D. Kato, Hydrogen diffusion and vacancies formation in tungsten: Density functional theory calculations and statistical models. Acta Mater. 94, 307–318 (2015)
K. Heinola, T. Ahlgren, Diffusion of hydrogen in bcc tungsten studied with first principle calculations. J. Appl. Phys. 107, 113531 (2010)
D.F. Johnson, E.A. Carter, Hydrogen in tungsten: Absorption, diffusion, vacancy trapping, and decohesion. J. Mater. Res. 25, 315–327 (2010)
K. Heinola, T. Ahlgren, K. Nordlund, J. Keinonen, Hydrogen interaction with point defects in tungsten. Phys. Rev. B 82, 094102 (2010)
K. Ohsawa, J. Goto, M. Yamakami, M. Yamaguchi, M. Yagi, Trapping of multiple hydrogen atoms in a tungsten monovacancy from first principles. Phys. Rev. B 82, 184117 (2010)
Funding
The research leading to these results has received funding from Spanish MICINN Project PID2019-105325RB-C32 and TechnoFusion Project (P2018/EMT-4437) of the CAM (Comunidad Autónoma Madrid), EUROfusion Consortium project AWP15-ENR-01/CEA-02 and Madrid Region project (II)-CM (S2018/EMT-4437). The authors acknowledge the computer resources and technical assistance provided by CESVIMA (UPM) and the computer resources provided by the Spanish Supercomputing Network (RES) (projects QCM-2017-2-0012 and QCM-2017-3-0009 from the resource Calendula based at the FCSCL, Leon, Spain; and projects QCM-2019-1-0002 and QS-2019-2-0002 from the resource Caesaragusta based at the BIFI, Zaragoza, Spain. The author also acknowledges the Convenio Plurianual with Universidad Politécnica de Madrid regarding the Programa de Excelencia para el Profesorado Universitario of the CAM for the financial support.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Díaz-Rodríguez, P., Panizo-Laiz, M., González, C. et al. Direct observation of hydrogen permeation through grain boundaries in tungsten. emergent mater. 5, 1075–1087 (2022). https://doi.org/10.1007/s42247-021-00344-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s42247-021-00344-w