1 Introduction

Fusion reactors can provide a safe, clean power supply using readily available raw materials. However, developing materials that are able to withstand the extreme conditions is key to making fusion viable. The International Thermonuclear Experimental Reactor (ITER) will be a tokamak reactor, which confines the plasma within a torus, as shown in Fig. 1 [1].

Fig. 1
figure 1

Reproduced with permission from Ref. [1]. Copyright 2013. ITER.org

ITER scale model. Arrows indicate the tungsten divertor at the base of the torus.

Full size image

The divertor is at the torus base, where waste material exits. It must protect surrounding components from extreme heat, impinging ions, and neutrons [2]. In ITER, the divertor will be made of tungsten, selected for its high melting point, high thermal conductivity, and low sputter yields (the number of tungsten ions ejected from the material per incident ion) [3].

Both hydrogen and helium ions impinge upon the divertor, but this review focusses only on the microstructural change named fuzz, caused by helium ions (He+). Fuzz is a porous layer that forms on top of the tungsten bulk, shown in Fig. 2 [4]. The layer can grow beyond several micrometres thick and consists of individual tendrils with diameters of 10–50 nm [5].

Fig. 2
figure 2

Reproduced with permission from Ref. [4]. Copyright 2009. International Atomic Energy Agency

SEM image showing initial fuzz formation on tungsten bulk.

Full size image

The conditions for fuzz formation, which is expected during ITER operation [6], are discussed in Sect. 2.3. The fuzz layer could reduce the divertor’s thermal conductivity [7] and contaminate the plasma [8]. Understanding the fuzz formation mechanism will be key to preventing these problems, and could allow fuzz to be used for beneficial purposes, such as catalysing water splitting [9] or organic compound breakdown [10].

Due to the extreme conditions of fuzz formation, mechanisms are commonly investigated by simulation studies. The available experimental data can then be used to validate predictions from these studies. Simulations are effective at modelling the first stages of fuzz formation, where helium ions impact on perfect tungsten bulk material, and the subsequent motion of helium within the bulk. This has led to a good understanding of the bubble growth and rupture mechanism [11], discussed in Sect. 2.2. However, it has not been possible for simulations to reproduce a complete fuzz structure [8] and outstanding questions remain.

The current consensus on fuzz formation conditions and mechanism is presented in Sect. 2. Sections 3 and 4 discuss mechanisms proposed to explain tungsten and helium migration, respectively. Section 5 examines which of these is rate-limiting. Section 6 presents the conclusions and identifies areas for further study.

For clarity, in this review, the overall microstructure change is described as fuzz, which consists of individual tendrils.

2 Current consensus

This section introduces the accepted mechanism of bubble growth and rupture, and the outstanding questions of fuzz formation. The conditions, and the variation of growth with these conditions, are also presented. The different theories presented in Sects. 3 and 4 can then be evaluated on how well they explain the experimental evidence.

2.1 Bubble growth and rupture

It is accepted that He ions implant into the W surface, leading to the nucleation of He bubbles underneath the surface. These bubbles then grow and rupture; subsequently fuzz forms. Continued bubble rupture leads to extremely high-specific surface areas [12, 13], highlighting the potential of W fuzz-based catalysts. Different mechanisms have been proposed to explain how this bubble growth leads to fuzz formation. The mechanism of bubble growth and rupture is summarised below and in Fig. 3 [14].

  1. 1.

    A He ion implants within the W bulk, where there is low He solubility. This leaves a He atom that diffuses until it desorbs from the surface [15] or encounters another He atom, forming a mobile cluster of He atoms. These clusters can grow by absorbing other clusters or lone He atoms [11].

  2. 2.

    Once large enough, these clusters can eject a W atom into an interstitial site, leaving the He cluster bound to the lattice vacancy, a Frenkel pair. The cluster could also combine with a vacancy already present in the lattice instead [16]. Immobile clusters bound to vacancies are called bubbles [11].

  3. 3.

    These bubbles absorb more He and grow by trap mutation. This is where a VHen bubble (consisting of one vacancy, V) grows to V2Hen and produces another interstitial W atom, which remains bound to the bubble surface.

  4. 4.

    Once the number of interstitials is high enough, they form a dislocation loop (the loop surrounds a disc of W interstitials forming an extra plane of atoms in the lattice) [11]. The loop is no longer bound to the bubble, and is free to travel to the surface and annihilate. This is loop punching, which causes the surface to grow outwards [16]; the disc of interstitials is now a group of adatoms—atoms on the W surface.

  5. 5.

    As loop punching continues, the distance from the bubble to the initial surface decreases, causing the bubble to rupture. This leaves protrusions and pits which form the basis of the fuzz tendrils [14], illustrated in Fig. 3. Simulations can reproduce this, showing that protrusions are caused by bubble bursting [17,18,19]. Transmission electron microscopy (TEM) images have shown that in addition to the large bubbles that rupture, there are many small bubbles within the bulk and the individual tendrils [14]. The stresses within the large bubbles, and from the surrounding smaller bubbles, likely drive bubble rupture [20].

Fig. 3
figure 3

Reproduced with permission from Ref. [14]. Copyright 2011. Elsevier

Schematics of initial fuzz growth from TEM images, with labelled fluences. The red dotted line marks the initial surface. a shows the initial formation of many small bubbles. b and c illustrate the growth of large bubbles, causing outward surface growth. d shows the sharp protrusions formed by bubble rupture.

Full size image

2.2 Conditions

Table 1 shows the conditions for fuzz formation. The observed incubation fluence (the minimum fluence before fuzz growth) is required for bubbles to form [21] which are required for fuzz growth [22].

Table 1 Observed conditions of fuzz formation. Data from Ref. [6]
Full size table

At high temperatures, due to the low thermal conductivity of the fuzz [7, 23], tendrils heat up and reintegrate back into the bulk. Irradiation by impurities or high-energy He ions (> 120 eV) can lead to sputtering, the emission of W atoms from the sample, which erodes surface features [24]. This erosion competes with fuzz growth and the fuzz reaches a steady-state thickness, where these effects balance [25]. Increasing ion energies reduce this thickness significantly. At even higher ion energies (> 10 keV), larger fuzz-like structures form again [11]. However, the ITER divertor will be subject to energies in the range 0–100 eV, which we focus upon.

The minimum energy occurs because ions below ~ 20 eV are more likely to be reflected by the surface [11] so cannot easily form bubbles. For example, 12 eV ions only formed fuzz at extremely high fluences (> 1027 m−2) [26], due to the high reflectance. Thus, 20 eV is taken as a practical minimum energy.

It has been observed that the growth rate decreases over time, and is proportional to the square root of the exposure time. It was therefore concluded that diffusion through the fuzz is rate-limiting [27]. Thicker fuzz leads to greater diffusion distances, slowing the growth rate. Since this conclusion, growth has been analysed using the one-dimensional diffusion length (from Fick’s laws) [28]:

$$x= \sqrt{2Dt,}$$
(1)

where \(x\) is fuzz thickness and \(D\) is an effective diffusion coefficient. Since He flux,\(\Gamma\), is typically constant, fluence, \(\Phi = \Gamma t\). There is a square-root dependence on fluence too, as fluence is proportional to time. Substituting for \(t\) and including the incubation fluence, \({\Phi }_{0}\), gives the relationship between fuzz thickness and He fluence:

$$x= \sqrt{\frac{2D}{\Gamma }\left(\Phi - {\Phi }_{0}\right).}$$
(2)

The incubation time is related by \({\Phi }_{0}= \Gamma {t}_{0}\).

However, which species is responsible for diffusion was not clear. A logarithmic model has also been proposed to explain the decreasing growth rate, based on the penetration of He ions. These areas of debate are discussed in Sect. 5. Until then, we compare mechanisms to the currently accepted \(\sqrt{t}\) dependence.

This leaves interesting questions for the proposed mechanisms to answer:

  • Is W migration, He migration, or both responsible for fuzz formation?

  • If a He supply is required, how does He move through the thickening fuzz layer?

  • Is W or He migration rate-limiting?

3 Tungsten migration

This section explores the proposed mechanisms for W migration during late-stage fuzz formation. The theory, evidence supporting it, and evidence against it is examined in turn for each model.

3.1 Electrostatic growth

This theory proposes that fuzz could be formed from metal whiskers growing on the W surface. Protrusions would induce large electric fields, favouring whisker growth [29]. The interaction with the electric field from the plasma present could accelerate this.

However, two studies have shown that electric field variation has no effect on fuzz growth [30, 31], so this mechanism has been rejected.

3.2 Viscoelastic flow

This was proposed by Krasheninnikov [32], suggesting that bubbles within the growing tendrils exert stresses which cause plastic deformation—creep—where W flows up tendrils causing growth, shown in Fig. 4. The bubbles in tendrils experience a drift force attracting them to free surfaces, which causes them to push upwards to the top of the tendrils [11].

Fig. 4
figure 4

Reproduced with permission from Ref. [32]. Copyright 2011. IOP Publishing

Side-on tendril views explaining the viscoelastic mechanism. a illustrates the initial tendril, b and c show the viscous flow of W to the tip due to the bubble pressure.

Full size image

Krasheninnikov et al. [32] concluded that whichever of the He or W supply was slower would lead to the \(\sqrt{t}\) dependence. At a constant He flux, the growth rate decreases over time [33] (as thickness is proportional to \(\sqrt{t}\)); this was interpreted as evidence that W supply was limiting. This model was also able to reproduce the \(\sqrt{t}\) dependence. Subsequent molecular dynamics (MD) calculations have shown that large amounts of He reduce the yield strength of W [34], supporting the proposal of plastic deformation.

However, there is opposing evidence. It has been found that He concentrations do not reach the necessary level to cause W yield [35]. Also, a recent experiment using 3He and 4He isotopes [36] found that bubbles continually rupture during growth. Only 4He was released for the final part of plasma exposure and only 4He was found in the bulk or fuzz. Thus, all 3He was released, by bubble rupture, and 4He was able to move through the fuzz layer. This theory does not consider the continual rupture of bubbles. In addition, the assumption that W supply is limiting is premature. Even at constant flux of He ions, the transport of He through the fuzz layer to the bulk could be rate-limiting, as considered later.

3.3 Adatom diffusion

In this theory, He+ ion bombardment leads to the formation of adatoms, i.e. atoms on the W surface. These diffuse along the sides of tendrils, to the tips. Whilst this appears unphysical, explanations for this phenomenon are given in the next paragraph. This mechanism is diffusive, thus explaining the \(\sqrt{t}\) dependence of growth. An MD study [37] calculated the effective adatom diffusion coefficients, which were similar to those obtained experimentally [27].

It has been proposed that adatoms diffuse to tendril tips due to stresses from He bubbles, which lower the chemical potential in the high-curvature tip regions [38]. This is supported by recent work finding that stresses from He bubbles can drive W adatom diffusion [12]. Additionally, an experimental study [22] found that fuzz formed when a sample was irradiated with He+, then held above 1273 K without any further irradiation. Thus, if He bubbles pre-exist, no more He is needed to form fuzz initially. Fuzz even formed on very thin regions of this sample without any He bubbles present. This was attributed to W adatoms diffusing driven by surface tension. Under further He irradiation, bubbles formed in the thin regions, increasing the growth rate. The rate increase provides evidence that bubbles enhance surface diffusion of adatoms. In a thick sample (relevant to fusion reactors), He bubbles are required for fuzz initiation; this could be to drive adatom diffusion. Finally, annealing fuzz [23] leads to He release and subsequent destruction of the fuzz nanostructure; without the stresses from He bubbles, the metastable fuzz disappears when heated.

Fiflis et al. [30] replaced He+ ions with Ne+ which did not lead to fuzz. Both should produce adatoms by bombardment, so both should form fuzz. The authors concluded that adatoms were not responsible for fuzz growth. However, the different penetrations of He+ and Ne+ mean the Ne+ will not lead to bubble formation [39] which we have seen is necessary for adatom diffusion. Thus, their conclusion was premature.

Recent studies [40,41,42] have deposited W atoms on the sides of growing tendrils, like those in Fig. 3d. They found that this increases the growth rate significantly, such that there is no longer a \(\sqrt{t}\) dependence. This is evidence that adatom diffusion is responsible for growth. However, this does not establish whether adatom migration or adatom generation is limiting during normal growth because both processes are enhanced by deposition. Adatom migration is increased as adatoms deposited on the sides of tendrils have a shorter distance to the tip than those generated at the base. It was also observed that the tendril widths remain constant even with extra W deposition on the sides, further supporting adatom diffusion along tendril surfaces to the tip.

Hammond [11] argues that adatoms alone cannot account for fuzz growth. Their migration is too slow, and there is little uphill diffusion, where an adatom diffuses to an island of many adatoms. This means the island cannot grow to form the initial protrusions. However, adatoms do not need to be responsible for this; bubble rupture can form protrusions, as seen in Fig. 3, and adatoms can then diffuse to the protrusion tips [43].

The original theory suggested adatoms would form on the side of tendrils due to He bombardment. However, experimental studies with W isotope films [36] on W, thin Mo films on W (Mo forms similar fuzz) [30, 44, 45], and thin W films on Mo [45] have found that the surface and bulk materials mix in fuzz formation. Thus, bubble growth, rupture and loop punching (discussed in Sect. 2.2) are responsible for forming adatoms [46], bringing material up from the bulk. If adatoms formed immediately due to He bombardment, mixing would not occur as only surface material would form adatoms. Instead, He bubbles are responsible for adatom formation, which can diffuse over the surface with a net upward flux to the tip, as detailed above. The continual bubble rupture, evidence for which is discussed in Sect. 2.2, is responsible for generating adatoms throughout the process.

This explains why the supply of new material is from the bulk. It was also observed that there is greater concentration of bulk material at the edge of tendrils [36, 44]. This supports adatom migration over viscoelastic flow. If flow occurred within the tendrils, shown in Fig. 4, a large concentration of atoms from the bulk would not be seen at the edges of tendrils. During late-stage growth, bubbles within the fuzz could also lead to adatom formation on the side of tendrils by the same mechanism [8].

To summarise:

  • Unlike the original theory suggested, adatoms are not formed directly due to He bombardment.

  • Adatoms are created on the W surface by bubble growth and loop punching.

  • Bubble rupture then forms a crater with protrusions.

  • Adatoms diffuse to the tips of these protrusions (the precursors to tendrils) along the surfaces causing growth.

  • Adatoms continue to be generated by loop punching of He bubbles during late-stage growth.

This means a continuous supply of He through the fuzz layer to the W bulk is necessary for bubbles to continue to produce adatoms. The rate-limiting process is either adatom migration (diffusion along tendril surfaces) or generation. If generation is rate-limiting, this must depend on the rate of He migration through the fuzz.

4 He migration

We now consider how He continues to reach the W bulk through the fuzz layer (as isotopic studies showed [36], see Sect. 3.2). Two proposals are explored: diffusion of He down the tendrils, and direct penetration of He through the fuzz.

4.1 Diffusion

Fiflis et al. [30] proposed that growth continued by He bubbles in the bulk loop punching to the surface. He is implanted at the top of the fuzz layer and diffuses down tendrils to the bulk to form bubbles, potentially aided by compressive stress fields of bubbles. Whilst the diffusion of He in bulk W is much faster than the diffusion coefficients observed, it was proposed that diffusion through the porous fuzz layer would be slower [27].

Klaver et al. [47] listed a series of objections. First, He will diffuse horizontally to tendril edges (~ 30 nm diameter) and desorb well before it manages to diffuse several micrometres vertically to the tendril base. Second, He would become trapped by other interstitial He atoms, bubbles or defects before it reached the bulk. Finally, this diffusion should allow heat conduction, yet fuzz has an extremely low thermal conductivity [7], even when accounting for its high porosity.

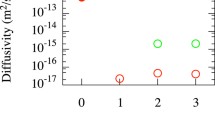
A recent MD study [48] placed He atoms in model tendrils, with and without He bubbles present, to model diffusion. They found that bubbles exerted stresses, driving diffusion as Fiflis et al. [30] proposed. Diffusion coefficients were calculated; these decreased over time as more He clusters form, interacting with the diffusing He. Accounting for desorption at the surface, it was concluded that He could feasibly diffuse to the base of 1 and 10 μm tendrils during formation times. However, this assumed a constant diffusion coefficient for simplicity, despite the findings that coefficients decrease with time. In addition, the possibility of the diffusing He atoms being absorbed by bubbles was not accounted for.

It appears possible for diffusion to contribute to He migration; however, further simulations are needed to clarify this. The MD simulations [48] only ran for 20 ns due to the high computational cost, so coarser methods are needed to extrapolate the findings to longer distances and times. Simulations that could account for He absorption by existing bubbles would also help to identify if diffusion is valid.

4.2 Ballistic penetration

Since fuzz layers have been found to have around 90% porosity, Klaver et al. [47, 49] proposed that He+ ions may be able to penetrate much further than the several nanometres expected. They observed that tendrils favour growing perpendicular to the W surface, leading to open channels that He could scatter down. MD studies showed that He is able to bounce off fuzz tendrils before implanting, allowing penetrations of the order of micrometres in the most porous fuzz.

Their studies showed an exponential decay in flux with distance into fuzz. This led to the proposal of thickness having logarithmic dependence on fluence or time (fluence = flux \(\times\) time) instead of the diffusional square-root dependence seen in Sect. 1:

$$x={x}_{0} \mathrm{ln}\left(\frac{A}{{x}_{0}}\left(\Phi - {\Phi }_{0}\right)+1\right).$$
(3)

\(x\): fuzz thickness; \(\Phi\): fluence; \({\Phi }_{0}\): incubation fluence; \(A\), \({x}_{0}\): constants.

The MD calculations were repeated with the computationally simpler binary collision approximation (BCA) approach [49], where ion movement is treated as a sequence of collisions. BCA produced similar results for all but the lowest ion energies, where the approximation is inaccurate. BCA systematically underestimates penetration; however, this can be accounted for, allowing BCA to be used instead of MD calculations taking months. This is significant because a recent BCA study [50] accounted for electronic stopping power (inelastic collisions between ions and bound electrons), which was not included in the original model. The new study reported decreased penetration, but still of several hundred nanometres, indicating penetration remains a viable mechanism when electronic stopping is included.

It should be noted that these simulations must approximate the three-dimensional (3D) structure of fuzz, which has still not been fully determined [50]. TEM observation [51] has shown that tendrils favour growing upwards from the surface; however, they are still interconnected by branches in a complex manner. Figure 5 shows the cylinders used in Ref. [50] to build the structure, whilst [47, 49] used ellipsoids instead. Determination of the complete structure would allow much more accurate modelling to be done, so long as the representations of the structure can be constructed in a way that do not increase computing times.

Fig. 5
figure 5

Reproduced with permission from Ref. [50]. Copyright 2019. Elsevier

Fuzz structure used to model He ballistic penetration. a shows the full fuzz structure, with dimensions labelled in nanometres. b is an enlarged view illustrating the cylinders used to build the fuzz.

Full size image

Further support for ballistic penetration comes from studies using isotopic He [36]; the ratio of 3He in the sample bulk is similar to the ratio of 3He fluences, which is expected from a direct penetration mechanism. Instead, diffusive He transport would cause a square-root ratio.

The evidence suggests that ballistic penetration is the primary mechanism for He migration through the fuzz, although it could be aided by diffusion once implanted. We now examine whether penetration is rate-limiting.

5 Rate-limiting process

We have established that W migration is likely due to adatom diffusion, and He migration due to ballistic penetration. If adatom diffusion is rate-limiting, the diffusive (square-root) model should be a good fit to thickness-fluence data. If He penetration (needed to generate adatoms) is limiting, the logarithmic model should apply. Now, we apply these models to experimental data.

5.1 Flux dependence

Rewriting the ballistic relationship in terms of flux gives,

$$x={x}_{0} \mathrm{ln}\left(\frac{A}{{x}_{0}}\left( \Gamma t- {\Phi }_{0}\right)+1\right),$$
(4)

so that for constant time, \(t\), fuzz thickness, \(x\), will increase if there is greater flux, \(\Gamma\), allowing more He to reach the fuzz base. The constants and incubation fluence, \({\Phi }_{0}\), are unaffected.

Instead the diffusional relationship,

$$x= \sqrt{\frac{2D}{\Gamma }(\Phi - {\Phi }_{0})}= \sqrt{2D\left(t-{t}_{0}\right),}$$
(5)

is independent of flux (using \(\Phi = \Gamma t\)), as adatom diffusion distances only depend upon time. However, there is expected to be a flux threshold below which adatom generation becomes rate-limiting.

Figure 6 shows the variation of thickness with flux. Previously it was concluded that thickness was independent of flux above ~ 1022 m−2·s−1, as expected for a diffusional mechanism. Here, the ballistic model has been fitted, assuming He migration is limiting across the entire flux range. Due to the large uncertainties in the fluxes, it is difficult to accept or reject the logarithmic fit of all the data.

Fig. 6
figure 6

Variation of fuzz thickness with He flux after 3600 s. The logarithmic dependence proposed by the ballistic penetration model was fitted and shown in red. Data from Ref. [33]

Full size image

It is also possible that the ballistic penetration is only limiting below a threshold flux, which will depend on the irradiation conditions. Thus, the logarithmic fit may only apply to data below this threshold. Above this, adatom diffusion becomes limiting and thickness is independent of flux.

5.2 Fluence dependence

The two models will be used to see if there is a different relationship between thickness and fluence at different fluxes. It should be noted that adatom diffusion is independent of the amount of He supplied; however, there is a square-root dependence on fluence simply because fluence is proportional to time.

The data in Fig. 7 were recorded at a flux of ~ 1.7 \(\times\) 1022 m−2·s−1, close to the proposed threshold above which growth is independent of flux. The diffusional model is clearly a worse fit, and predicts a higher incubation fluence (x-intercept) of 6 \(\times\) 1024 m−2, which is much greater than observed values [21]. At this lower flux, the ballistic model is a much better fit.

Fig. 7
figure 7

Fuzz thickness as a function of He fluence. The sample was irradiated with a constant flux of ~ 1.7 × 1022 m2 s−1 of 50 eV He+ ions at 1400 K. Data from Ref. [14]

Full size image

The data in Fig. 8 were recorded at a higher flux ~ 5 \(\times\) 1022 m−2·s−1. The ballistic model predicts an unphysical and negative incubation fluence, which also occurred applying the model to similar data [47]. However, applying the ballistic model with \({\Phi }_{0}=0\) can produce a good fit to the data. The diffusional fit is better than either ballistic fit and has a lower \({\chi }^{2}\) value (the reduced \({\chi }^{2}\) is slightly less than 1 but is likely due to an underestimation of errors rather than overfitting). The quantity \({\chi }^{2}\) is used to evaluate ‘goodness of fit’ for different models by comparing the residuals to the standard deviation of the original data; a small \({\chi }^{2}\) implies the model fits the data well. The reduced \({\chi }^{2}\) accounts for the number of free parameters in a model; ideally this would be close to 1 [52].

Fig. 8
figure 8

Fuzz thickness as a function of He fluence. The sample was irradiated with a constant flux of ~ 5 × 1022 m2 s−1 of 60 eV He+ ions at 1120 K. Data from Ref. [33]

Full size image

Although the ballistic fit at the higher flux cannot be rejected, there is further evidence that diffusion is rate-limiting at higher fluxes. Experiments with identical flux and energy conditions have found that growth rate increases with temperature [27] which is explained by diffusion. Instead, there is no clear reason why the growth rate would increase if ballistic penetration were limiting.

This could imply a flux threshold above which the rate-limiting process switches from He ballistic penetration to W adatom diffusion, with the fluence dependence switching from logarithmic to square-root. This would depend upon irradiation conditions, as diffusion will be faster at higher temperatures. Further experiments needed to confirm this are proposed in Sect. 6.

Simulations [16] revealed that the random nature of the loop punching and bubble rupture process, which generates adatoms, could also lead to a \(\sqrt{t}\) dependence. However, this also fails to explain the temperature dependence of growth rate.

6 Conclusion

Experiments and simulations to clarify the mechanism of late-stage tungsten fuzz growth have been reviewed, looking at helium and tungsten migration in turn. In Sect. 2.3 three questions were presented:

  • Is tungsten migration, helium migration, or both responsible for fuzz formation?

  • If a helium supply is required, how does it move through the thickening fuzz layer?

  • Is tungsten or helium migration rate-limiting?

The answers are summarised below, with areas of debate and further work identified.

Firstly, tungsten adatom migration is likely responsible for growth, shown by the growth rate increase when extra tungsten adatoms are deposited on tendrils [40,41,42]. However, bubble growth and rupture are needed to form initial protrusions. Adatoms are generated by loop punching as bubbles grow, and can diffuse to protrusion tips to form tendrils. Bubble growth and rupture continue during late-stage growth, and adatoms continue to be generated at the tendril bases.

Second, a constant helium supply to the bottom of the fuzz layer is required for the continued bubble growth and rupture [36]. Ballistic penetration of helium through the porous fuzz layer can explain this, even when electronic stopping is accounted for [50]. However, it appears diffusion could still play a part; for example, diffusion may occur after ballistic penetration. Simulations over longer periods that can account for helium absorption by bubbles during diffusion will help to resolve this.

It would useful to simulate implantation and diffusion together, or to model diffusion starting from the much greater helium implantation distances predicted by ballistic penetration. This requires a better understanding of the fuzz structure, as modelling diffusion through the cylinder structure in Fig. 5 will not be accurate. TEM images of fuzz exist, but Klaver et al. [47] suggest filling the open space with a setting fluid or deposited atoms. This would allow removal of the intact fuzz layer from which TEM topography could identify the complete structure. Using a complete structure determined this way could improve the accuracy of many simulations, not only those related to helium migration but tungsten migration too.

Finally, it is difficult to determine whether helium ballistic penetration or tungsten adatom diffusion is rate-limiting. There is evidence for a flux threshold above which the rate-limiting process switches from helium penetration (logarithmic thickness–fluence relationship) to adatom diffusion (square-root relationship).

High fluence experiments are needed to differentiate accurately between the two models. Repeats at identical temperature and ion energy could investigate if there is a different thickness–fluence relationship at high and low flux. Additional measurements at low helium fluences to determine the incubation fluence could also differentiate between the two models, as the curves fitted in Figs. 7 and 8 have different incubation fluence parameters.

It would also be useful to see if there is a different thickness–fluence relationship at very high fuzz thicknesses if the mechanism changes. Meyer [8] speculates whether adatoms would be generated midway upon tendril sides instead of at the base. To avoid the long times needed for this, tungsten deposition (see Sect. 3.3) could be used to grow a thick fuzz layer, which is then irradiated under normal conditions.

For a phenomenon first observed in 2006 [26], great progress has been made in identifying the mechanism of tungsten fuzz formation. As nuclear fusion enters the DEMOnstration Power Station (DEMO) phase, it will be interesting to see whether fuzz prevents the use of all-tungsten divertors. Understanding the mechanism helps design suppression and removal techniques for reactors, as well as aiding in the production of porous catalysts with high-specific surface areas.