Renal Pathology Images Segmentation Based on Improved Cuckoo Search with Diffusion Mechanism and Adaptive Beta-Hill Climbing

Abstract

Lupus Nephritis (LN) is a significant risk factor for morbidity and mortality in systemic lupus erythematosus, and nephropathology is still the gold standard for diagnosing LN. To assist pathologists in evaluating histopathological images of LN, a 2D Rényi entropy multi-threshold image segmentation method is proposed in this research to apply to LN images. This method is based on an improved Cuckoo Search (CS) algorithm that introduces a Diffusion Mechanism (DM) and an Adaptive β-Hill Climbing (AβHC) strategy called the DMCS algorithm. The DMCS algorithm is tested on 30 benchmark functions of the IEEE CEC2017 dataset. In addition, the DMCS-based multi-threshold image segmentation method is also used to segment renal pathological images. Experimental results show that adding these two strategies improves the DMCS algorithm's ability to find the optimal solution. According to the three image quality evaluation metrics: PSNR, FSIM, and SSIM, the proposed image segmentation method performs well in image segmentation experiments. Our research shows that the DMCS algorithm is a helpful image segmentation method for renal pathological images.

1 Introduction

Renal pathology is a subspecialty of general pathology based on the diagnostic evaluation of light microscopy, immunofluorescence microscopy, and electron microscopy for medical and transplant kidney disease characteristics. Renal pathologists examine renal biopsies to provide a definitive clinicopathologic diagnosis, working closely with nephrologists, which is particularly significant for Lupus Nephritis (LN) [1]. LN is a significant cause of morbidity and mortality in systemic lupus erythematosus and has a broad histopathological spectrum [2, 3]. Renal biopsy is not necessary to confirm the diagnosis of LN but is essential to define the quality and severity of the renal injury and is a guide for treatment [4]. However, histopathological changes of LN are complex, varied, and sometimes unstructured; it needs expertise and effort to assess the biopsies. Nowadays, large amounts of digital image data from renal biopsies are being generated. Accordingly, there is a strong demand for developing computer-based image analysis systems for nephropathology, especially for the challenging images of LN.

Aiming development of intelligent medical systems [5], researchers apply more image processing techniques [6, 7]. The segmentation of kidney structure is an early step in computer-assisted nephropathological image analysis systems. In the early days, renal biopsies were manually visualized and interpreted by renal pathologists, but due to the need to reduce the consumption of time and resources and the support of science and technology, researchers began to seek ways to automate the process [8]. Albayrak et al. [9] proposed a two-stage image segmentation to obtain cellular structures in high-dimensional renal cell carcinoma histopathological images. In this method, a simple linear iterative clustering means is utilized to segment the image into superpixels, and then the superpixels are clustered by the latest segmentation method based on clustering. Experimental results show that a super-pixel segmentation algorithm can be used as a pre-segmentation method to improve the performance of cell segmentation.

Yoruk et al. [10] introduced a fully automated kidney segmentation technology for evaluating Glomerular Filtration Rate (GFR) in children, which improves iterative graph cut-based image segmentation methods by training a random forest classifier to segment kidney tissue into cortical, medullary and collecting systems. According to GFR, this automatic segmentation method has similar segmentation results to manual segmentation results to manual segmentation methods and saves much time, even reducing segmentation time from several hours to 45 s. Gadermayr et al. [11] proposed and studied a two-order pipeline consisting of weak supervision-based patch detection and accurate segmentation for glomerular segmentation. This pipeline does not require any previously acquired training data, thus reducing manual effort and manual annotation costs. Li et al. [12] put forward a novel graphic construction scheme that uses the optimal surface search method to solve, construct differences, and model the relationship between surfaces in the graph. The innovation of this graphic construction scheme is that it can simultaneously segment the outer and inner surface of the kidney, which solves the problem of renal cortex segmentation, which is rarely studied. Yang et al. [13] proposed a kidney partitioning method that achieves robust segmentation accuracy for dynamic contrast-enhanced MRI with little manual manipulation and parameter settings. The segmentation results match well with the manually generated results, which is superior to the segmentation results of existing technical methods.

The work mentioned above mainly draws on machine learning and deep learning methods to achieve image segmentation; however, such methods have disadvantages, such as a long training cycle, large time and resource consumption, large data demand, and the inability of the trained model to be universal. The other image segmentation method, i.e., multi-threshold image segmentation technology, which is the most basic image segmentation technique, obtains appropriate thresholds by combining with swarm intelligence algorithms, which can solve the problems of large computation, long computation time, and low segmentation accuracy of traditional multi-threshold image segmentation methods [14]. In the last few years, this method has been recognized by many scholars and put into research due to its remarkable effect. Nguyen et al. [15] proposed a novel method for improving Moth Flame Optimization (MFO) [16] by mixing lévy flight and flame update formulations of logarithmic functions and proved that it has an excellent performance in the field of multi-threshold image segmentation. Zhou et al. [17] put forward a multi-threshold image segmentation technology based on the Moth Swarm Algorithm (MSA) and used Kapur's entropy method to optimize the threshold of the test image, and experiments verified the robustness and availability of the technique.

Zhao et al. [18] intensely studied the introduction of Horizontal Cross-Search (HCS) and Vertical Cross-Search (VCS) into a variant of Ant Colony Optimization (ACOR), improved the original ACOR mechanism, formed an improved algorithm called CCACO, and achieved a higher level of powerful results in image segmentation. Sharma et al. [19] proposed a new hybrid Butterfly Optimization Algorithm (BOA) called MPBOA by combining the BOA with the symbiotic and parasitic stages of the Symbiosis Organisms Search (SOS) algorithm. This method obtains the optimal threshold in the multi-threshold problem of single image segmentation, and the overall performance in search behavior and the convergence time is satisfactory. To increase the diversity of Whale Optimization Algorithm (WOA) solutions and avoid falling into local optimum, Chakraborty et al. [20] changed the random solution selection process in the search prey phase. They integrated the cooperative hunting strategy of whales into the exploitation phase of the algorithm. An Improved WOA (ImWOA) algorithm was proposed. The authors used the ImWOA method to effectively solve the multi-threshold image segmentation problem. Chakraborty et al. [21] also used the improved WOA algorithm to enhance the diagnostic efficiency of a computational tool that can quickly use COVID-19 chest X-ray photos to determine the severity of the disease. The improved WOA algorithm, called mWOAPR, integrates the random initialization population in the global search phase. The COVID-19 chest X-ray images are segmented using the multi-threshold method and the Kapur's entropy fitness function calculated from the two-dimensional histogram of the gray image.

Bio-inspired computing is roughly defined as using computers to model the underlying mechanisms of biological phenomena and to study the use of computing from the perspective of intelligent populations [22]. Swarm intelligence-based computing is an essential branch of biological computing. To solve various problems, many computing algorithms based on swarm intelligence to simulate natural swarm models have been invented [23, 24]. The more well-known and standard swarm intelligence optimization algorithms involve Particle Swarm Optimization(PSO) [25], Differential Evolution(DE) [26], Gray Wolf Optimization(GWO) [27], Ant Colony Optimization(ACO) [28], Harris Hawks Optimization(HHO) [29], Whale Optimization Algorithm(WOA) [30], Genetic Algorithm(GA) [31], Cuckoo Search Algorithm(CS) [32] and Sine and Cosine Algorithm(SCA) [33] and so on. In addition, the swarm intelligence algorithm and its improved version have been effectively applied and developed in many aspects of life and production. Gharehchopogh et al. [34] introduced the lévy mutation operator, Cauchy mutation operator, and Gaussian mutation operator to improve the performance of the Tunicate Swarm Algorithm (TSA) to evaluate six large-scale engineering problems, named QLGCTSA algorithm. Tree Seed Algorithm (TSA) has been developed in hybridization, improvement, mutation, and optimization with its ability and advantages since it was proposed in 2015 [35, 36]. The Sparrow Search Algorithm (SSA) [37] is robust. Nowadays, its application in the structural improvement of artificial neural networks and the optimization of hyperparameter parameters of deep learning has also been recognized by scholars [38]. Since its introduction in 2014, the Symbiotic Organisms Search (SOS) has had improved versions, multi-objective versions, and hybrid discrete types, which are very effective in solving complex and NP-hard problems [39, 40]. WOA is a very popular optimization algorithm, and its improved versions are even more numerous. They play an important role in engineering, clustering, classification, robot path, image processing, network, task scheduling and other engineering applications [41]. The Moth Flame Optimization (MFO) algorithm is also a widely used optimization algorithm, and the butterfly optimization algorithm is a relatively new algorithm. Sahoo et al. combined the two and proposed a novel hybrid algorithm h-MFOBOA, which solves the two practical problems of optimal gas production capacity and three-bar truss design [42]. In besides, swarm intelligence algorithms have been applied to solve many other problems [21, 43,44,45,46,47].

Among the numerous swarm intelligence algorithms, the CS algorithm has only two control parameters, so it does not need to readjust every new problem. The algorithm is simpler and more general, has good scenarios in many fields, such as optimization and computational intelligence [48,49,50,51,52], and has excellent application scenarios. This paper uses the CS algorithm based on the original multi-threshold image segmentation technology to be improved. Following the no-free lunch theorem [53], no learning algorithm can consistently produce the most accurate learner in any field. Talking about which algorithm is better is meaningless when divorced from the actual situation. When dealing with optimization and multi-threshold image segmentation problems, the CS algorithm also has problems such as falling into local optimum and slowing convergence speed. Therefore, this paper introduces the Diffusion Mechanism (DM) and the Adaptive β-Hill Climbing (AβHC) mechanisms into the algorithm. DM strategy can generate more solutions by dispersing the population, increasing the cuckoo population diversity, and avoiding the algorithm from stagnation and local optimum. AβHC strategy makes the algorithm continuously explore more appropriately, contributing to the search for better solutions in the algorithm exploitation stage. In this article, the CS algorithm is chosen to be studied, and multi-threshold image segmentation experiments test the performance of the improved version. To verify the performance of the above strategies in the CS algorithm, the IEEE CEC2017 [54] dataset test experiment and renal pathology image segmentation experiment were carried out. The experimental results demonstrate that the proposed algorithm has improved its optimization ability to find the optimal solution for CEC2017 functions. The image segmentation effect is better according to the image quality evaluation metrics.

To summarize, the contributions of this article are as follows:

• (1) An improved CS algorithm, DMCS, is proposed based on the DM and AβHC strategies.

• (2) Combining the multi-threshold medical image segmentation method of renal pathology image with DMCS results in more accurate and higher-quality image segmentation results.

• (3) Different image quality metrics are employed to assess the experimental results of image segmentation. The evaluation results show that the DMCS algorithm significantly improves its convergence and segmentation ability.

The rest of this paper is arranged as follows. Section 2 presents the proposed DMCS. Section 3 gives the experiment results and discussions on the CEC2017 dataset, and Sect. 4 offers the renal pathology image segmentation experiment. Finally, Sect. 5 summarizes the conclusions and future works.

2 Proposed DMCS

This part introduces the original CS algorithm and the proposed DMCS algorithm. Firstly, the rules and processes of the original CS algorithm are introduced. On this basis, the principles and mathematical formulas of the two mechanisms used in the DMCS algorithm and how to combine them with the original CS algorithm are introduced.

2.1 The Cuckoo Search (CS)

The CS algorithm is based on the parasitic brood behavior of cuckoo [32]. Furthermore, it is enhanced by Lévy flight instead of a simple random walk. Some experiments have proved that the CS algorithm, such as PSO, may be more efficient than others. Besides, the CS algorithm has been applied to many optimizations and computational intelligence fields, such as engineering design applications, data fusion, wireless sensor networks, thermodynamic calculation, image segmentation, etc. The CS algorithm summarizes the cuckoo's parasitic brood behavior into three rules [55]:

• Each cuckoo will lay an egg at a time in a randomly placed nest.

• The best nest with a good egg will be passed on to the next generation.

• The number of host nests used is fixed, and the probability of a host finding the cuckoo egg is $0\le {P}_{\alpha }\le 1$. If the host finds out that the egg in the nest is not its own, it can kill it or erect a new nest.

The search methods of the CS algorithm can be divided into two types: local search and global search. The switching parameter ${P}_{\alpha }$ controls the balance between the two search methods. Furthermore, local search is described by Eq. (1).

$$x_{i}^{t + 1} = x_{i}^{t} + \alpha s \otimes H\left( {P_{\alpha } - \varepsilon } \right) \otimes \left( {x_{j}^{t} - x_{k}^{t} } \right),$$

(1)

where $x_{i}^{t}$ denotes the location of the $i$-th nest in the generation $t$, $\alpha > 0$ denotes the scaling factor of step size. s is the step size. $H\left( x \right)$ is the Heaviside function. $x_{j}^{t}$ and $x_{k}^{t}$ are two different solutions randomly selected in the $t$ generation, $\varepsilon$ is extracted from the uniform distribution, which is a random number. $\otimes$ means the dot product between two vectors.

The global search is performed by Lévy flight with Eq. (2).

$$x_{i}^{t + 1} = x_{i}^{t} + \alpha L\left( {s,\lambda } \right),$$

(2)

where usually $\alpha = {\rm O}\left( \frac{L}{10} \right)$, $L$ is the feature scale of the problem in question; the value of $\alpha$ in Eqs. (1) and (2) may be different. To simplify the calculation, the value of $\alpha$ in two formulas is set to be the same. $L\left( {s,\lambda } \right)$ is a Lévy flight, which can be described by Eq. (3).

$$L\left( {s,\lambda } \right) = \frac{{\lambda {\Gamma }\left( \lambda \right){\text{sin}}\left( {\frac{\pi \lambda }{2}} \right)}}{\pi } \frac{1}{{s^{1 + \lambda } }},\left( {s \ge s_{0} > 0} \right),$$

(3)

where $\Gamma \left( \lambda \right) = \mathop \int \limits_{0}^{\infty } t^{z - 1} e^{ - t} {\text{d}}t$, and $0 \le \lambda \le 2$.

Given $r \in \left[ {0,1} \right]$, let $r$ be compared with the switching probability $P_{\alpha }$ to get the global branch with Eq. (4).

$$x_{i}^{{\left( {t + 1} \right)}} = \left\{ {\begin{array}{*{20}c} {x_{i}^{\left( t \right)} {\text{ if}}\ r < P_{\alpha } } \\ {x_{i}^{\left( t \right)} + \alpha \otimes L\left( {s,\lambda } \right) {\text{ if}}\ r > P_{\alpha } } \\ \end{array} } \right..$$

(4)

Figure 1 illustrates the flowchart of the CS algorithm.

Fig. 1

The CS algorithm flowchart

2.2 The Proposed DMCS

The original CS algorithm uses Lévy flight to update its agents' position. Although this strategy does an excellent job of searching global optima and jumping out from local optima, it still has some search space it cannot reach. Thus, some more suitable solutions may be missed. Here, the diffusion mechanism is used to address this shortcoming.

The exploration ability of the algorithm is enhanced by introducing the DM strategy into the CS algorithm. To further improve the algorithm exploitation capability, AβHC is introduced. AβHC is a simple and greedy local search algorithm. Although AβHC is not an intelligent optimization algorithm, it is a typical improvement strategy for other intelligent optimization algorithms. AβHC works after cuckoos seek new nests, using AβHC to find solutions with higher fitness values and thus develop better solutions.

2.2.1 The Diffusion Mechanism (DM)

The diffusion mechanism is the process by which the original particle randomly generates new particles around it using established strategies. The mathematical model of DM can be described by Eq. (5).

$$x_{i} = {\text{Gaussian}} \, \left( {{\text{Bestposition}},\varepsilon ,m} \right) + \sigma \times \left( {{\text{Bestposition}} - x_{i} } \right),$$

(5)

where $x_{i}$ represents the position of a new particle generated by the diffusion strategy, and ${\text{Gaussian}}\left( {{\text{Bestposition}},\varepsilon ,m} \right)$ denotes the generation of a random matrix obeying Gaussian distribution.${ }Bestposition$ is the position of global optima, and $\sigma$ is a random number obeying normal distribution, which is between 0 and 1. The $m$ vector is a determinant of the form of the matrix generated.

2.2.2 Adaptive β-Hill Climbing (AβHC)

The adaptive β-hill-climbing algorithm [56] is an improved version of the β-hill-climbing algorithm [57], published in 2019 by Al-Betar et al. A detailed definition of this algorithm is presented below. Supposed that the mathematical description of the optimization problem is like this:

$$\min \left\{ {g\left( s \right){|}s \in S} \right\},$$

(6)

where $s = \left\{ {s_{1} ,s_{2} , \ldots ,s_{N} } \right\}$ denote a series of feasible solutions in the range of $S$. $S_{i} \in \left[ {LB_{i} ,UB_{i} } \right]$, $LB_{i}$ and $UB_{i}$ represent the lower and upper limits of the solutions severally. $g\left( s \right)$ is the objective function. $N$ represents the population size.

Define the starting provisional solution to $s_{i}$. The solutions generated in each iteration are improved using the $\eta - {\text{operator}}$ and $\beta - {\text{operator}}$. $\eta - {\text{operator}}$ mainly play a role in the exploitation phase, using random walks for neighborhood search, and $\beta - {\text{operator}}$ is similar to uniform mutation operator and mainly play a role in the exploration phase.

$\eta - {\text{operator}}$ employs a concept called "random walk". The mathematical description using the $\eta - {\text{operator}}$ can be described by Eq. (7):

$$s_{i}^{^{\prime}} = s_{i} \pm U\left( {0,1} \right) \times \eta ,$$

(7)

where the current solution $s_{i}$ can produce a new solution $s_{i}^{^{\prime}}$ nearby by Eq. (7). $U\left( {0,1} \right)$ denotes a random number with a normal distribution ranging from 0 to 1, and the distance between $s_{i}$ and $s_{i}^{^{\prime}}$ is determined by $\eta$. In the $A\beta HC$, $\eta$ is an adaptive coefficient. The larger the value of $\eta$, the wider the search scope. Thus, to balance the exploitation and exploration phases, η needs a larger value to keep the algorithm searching more place in the early iterations and needs a small value to help the algorithm converge near the optimum. So it is reduced in each iteration from 1 to 0 according to Eq. (8):

$$\eta_{t} = 1 - \frac{{t^{\frac{1}{p}} }}{{T^{\frac{1}{p}} }},$$

(8)

where $t$ and $T$ are the number of current iterations and the maximum number of iterations, respectively. $p$ is a constant that brings the value of $\eta$ closer to 0 as the number of iterations increases. This work set the value of $p$ to 2.$s^{\prime}$, which is obtained by using $\eta - {\text{operator}}$ to update the position, is used as the current solution, and the new position $s^{\prime\prime}$ gets further updated based on the current solution $s^{\prime}$ by using $\beta - {\text{operator}}$, as follows:

$$ s_{i}^{{^{\prime\prime}}} = \left\{ {\begin{array}{*{20}c} {s_{k} , r \le \beta } \\ {s_{i}^{^{\prime}} , \, {\text{otherwise}}} \\ \end{array} } \right., $$

(9)

where $r$ is a random number between 0 and 1, $k$ is a random number selected from the range of $i$. Equation (9) states that if $r$ is not bigger than $\beta$, then an individual from the current population will be randomly selected to replace the individual. Otherwise, it will remain unchanged. $\beta$ is computed by a linearly increasing formula and depends on the $\beta_{\max }$ and $\beta_{\min }$. In the original paper, the author set $\beta_{\min }$ to 0.01 and $\beta_{\max }$ to 0.1. The formula is as follows:

$$\beta_{t} = \beta_{\min } + \frac{t}{T} \times \left[ {\beta_{\max } - \beta_{\min } } \right].$$

(10)

2.2.3 DMCS’s Overall Framework

The proposed algorithm DMCS is dedicated to improving convergence speed and accuracy, and Algorithm 1 is the pseudo-code of DMCS. The DM mechanism is deployed innovatively to improve the algorithm convergence speed in the early iteration, while AβHC plays a role in improving the convergence accuracy of the algorithm in a later iteration. In addition, the flowchart of the DMCS is illustrated in Fig. 2.

Fig. 2

Flowchart of the DMCS algorithm

The computational complexity of the DMCS algorithm is determined by the maximum generations $MaxFEs$, the number of individuals in the population $N$, and the dimensionality of individual $dim$. Thus, the computational complexity is $O\left( {MaxFEs \times N \times {\text{dim}}} \right)$.

3 Experiments for Benchmark Functions Performance Testing

In this section, many experiments are done to assess the performance of the DMCS. To verify the effect of DM and AβHC on DMCS, the single strategy, and the combined strategy are tested on 30 benchmark functions from CEC 2017, respectively. Furthermore, to demonstrate that the DMCS algorithm has the ability of fast convergence, high convergence accuracy, and jumping out of local optimum, this paper compares DMCS with seven conventional algorithms on 30 benchmark functions of CEC 2017 to nine other advanced algorithms.

3.1 Experiment Setup

This subsection shows three experimental results on CEC 2017: the comparison experiments with the mechanisms, the traditional algorithm, and the advanced DMCS algorithm. These composition functions of the CEC 2017 are the combination of multiple shifted, rotation, and based multimodal functions. Therefore, they can broadly challenge the ability of the DMCS algorithm to solve real-world and complex optimization problems. We respected the universal rules of fair evaluations for all methods in this study [58,59,60,61]. These universal rules help researchers to ensure computing conditions are not biased, or some techniques do not perform superior only because of better conditions of tests [62, 63]. To compare the experimental results more clearly, the results were treated with the Wilcoxon signed-rank test and the Freidman test [64]. The Friedman test is a nonparametric test of manifold judgment that can be utilized to evaluate the performance of different algorithms. Also, the lowest ordering is among the best-performing algorithms.

The population size is set as 30, and 30 independent runs are performed to test the algorithm's stability. Each test was carried out under the same conditions. The maximum function evaluation $MaxFEs$ is set at 30,000 for the mechanism comparison experiment and 300,000 for other experiments. All experiments were performed on the desk computer with Windows 10, Intel Core i5, 2.90 GHz, 8 GB RAM, and MATLAB R2021b.

3.2 Mechanism Comparison Experiment

To study the impact of the two mechanisms on the global optimization performance improvement of DMCS, the three improvement schemes combining the two mechanisms with CS were experimentally studied on the 30 benchmark test functions of CEC 2017 to find the best improvement scheme for CS. These three improved CS are denoted as MCS, DCS, and DMCS, respectively, as shown in Table 1. In the table, DM and AβHC represent the Diffusion Mechanism and the Adaptive β-hill-Climbing, respectively. "1" indicates that the algorithm uses this mechanism, and "0" indicates that it does not. For example, DCS uses the DM rather than the AβHC mechanism to improve.

Table 1 The combinatorial variants of CS

Table 2 displays the Average (Avg), and Standard deviation (Std) of all algorithms generated by the experiments, where the best results are emboldened. The smaller the Avg, the better solution the algorithm finds on the benchmark functions. The smaller the Std, the more stable the algorithm is. Therefore, after adding the mechanism, the CS algorithm obtains better solutions and higher stability on more than 80% of the functions. Table 3 shows the results of the Wilcoxon signed-rank test analysis of the data in Table 2, where the best results are emboldened. The "mean" represents the average ranking results of each algorithm on all benchmark functions, and "rank" is the final ranking according to the "mean". Otherwise, " + /-  / = " represents the number of corresponding performances of DMCS and other comparison algorithms on benchmark functions, where " + " denotes that DMCS performs better than the competitor, "-" denotes that DMCS performs worse than the competitor, " = " means that DMCS is similar to the competitor.

Table 2 The results achieved by combinatorial variants

Table 3 The results of Avg and Std analysis of the mechanism comparison experiment

From Table 3, we can see that DMCS ranks first with an average value of 1.5, and DCS, and MCS rank second and third with average values of 1.9 and 2.43, respectively. DMCS, DCS, and MCS all rank ahead of CS; it can be seen that both strategies have a specific improvement on CS, and DM strategy plays a significant role. Figure 3 clearly shows the four algorithms' convergence speed and convergence accuracy. DM strategy makes a significant difference in accelerating the convergence speed of the DMCS algorithm. That is because DM can further strengthen the exploitation capability of the CS algorithm. Taking advantage of the characteristics of the diffusion process so that each cuckoo individual can spread around the current location to enhance the exploitation ability of the algorithm increases the chance of the algorithm finding the global optimum while also avoiding being trapped in the local optimum. The DM is used regularly during the function optimization process, enabling individuals in the algorithm to explore the search space more efficiently. Therefore, introducing the DM into the optimization algorithm can enhance the exploitation ability of CS and improve the algorithm's convergence rate and accuracy. AβHC strategy can improve the accuracy in the late stage.

Fig. 3

The convergence curves of DMCS, MCS, DCS

3.3 Comparison with Conventional Algorithms

In this subsection, the proposed DMCS compared with seven conventional algorithms, namely Differential Evolution (DE) [26], Gray Wolf Optimizer (GWO) [27], Harris Hawks Optimization (HHO) [29], Slime Mould Algorithm (SMA) [65], Cuckoo Search (CS) algorithm [32], Multi-Verse Optimizer (MVO) [66] and Farmland Fertility Algorithm (FFA) [67].

Table 4 displays the Avg, and Std of all algorithms, where the best results are emboldened. DMCS obtained the smallest Avg and Std on F1, F2, F4, F12, F18, and F19, the smallest Std on F10 and F21, and tied with HHO for the best results on F23-F30. These indicate that DMCS has a significant advantage in both optimization ability and stability compared with the conventional algorithms in the experiment. Table 5 displays the results that analyze the data in Table 4 through the Wilcoxon signed-rank test, where the best results are emboldened. As shown in Table 5, DMCS gets the first in the "rank", in which DMCS ranks first in sixteen and second in five functions. It is clear that DMCS ranks best on more than 60% of the benchmark functions and significantly outperforms the competitors on at most 28 and at least 13 functions.

Table 4 The results achieved by DMCS against the seven conventional algorithms

Table 5 The results of Avg and Std analysis of conventional algorithms comparison experiment

Moreover, Fig. 4 shows the Freidman test result of DMCS and its competitors. This figure shows that DMCS ranks NO.1 with a Freidman test value of 2.852, a clear advantage over the SMA, which ranks second with a mean value of 3.701, and even far below the other competitors. Figure 5 plots and shows the convergence curves of the methods for some functions when solving the benchmark functions of IEEE CEC 2017. It can also be seen that DMCS has higher convergence accuracy and faster convergence on most benchmark functions, which also shows that DMCS is easier to jump out of local optimization solutions and obtain a higher-quality global optimization solution.

Fig. 4

The Freidman test result of DMCS and other conventional algorithms

Fig. 5

The convergence curves of DMCS and the other seven conventional algorithms

3.4 Comparison with Advanced Algorithms

In this subsection, the performance of DMCS was further verified by comparing it with nine advanced algorithms on 30 benchmark functions from CEC 2017. They are Boosted Grey Wolf Optimizers (OBLGWO) [68], Modified Sine Cosine Algorithm (MSCA) [69], Hybridizing Gray Wolf Optimization with Differential Evolution (HGWO) [70], Orthogonal Learning-driven Multi-swarm Sine Cosine Algorithm (OMGSCA) [71], Comprehensive Learning Particle Swarm Optimizer (CLPSO) [72], Particle Swarm Optimization with an Aging Leader and Challengers (ALCPSO) [25], Lévy flight trajectory-based Whale Optimization Algorithm (LWOA) [73], Double Adaptive Random Spare Reinforced Whale Optimization Algorithm (RDWOA) [74], Gaussian Barebone Harris Hawks Optimizer (GBHHO) [75].

Table 6 displays the Avg and Std of all algorithms, where the best results are emboldened. The DMCS achieved the smallest Avg or Std on F1–F4, F13–F15, F18, F19, F21, and F23–F30, which indicates that DMCS is still intensely competitive with advanced algorithms. Table 7 displays the results that further analyze the data in Table 6 through the Wilcoxon signed-rank test. Analyzing the Avg and Std obtained in the experiment, it can be concluded that the quality of the optimal solution obtained by the DMCS algorithm is of better quality and more stable for most functions. DMCS generally ranks first with an average of 2.7 in Table 7, first in 17 functions, and second in two cases, significantly better than the competition for at least 14 functions and significantly better than the LWOA algorithm for all 30 functions. Especially for several multimodal functions from F23 to F30, DMCS has breakneck convergence speed and high solution accuracy. Besides, Fig. 6 shows the bar graphs of the Friedman test result of DMCS and other competitors. From the graph of the result of the Friedman ranking, one conclusion can be drawn: the DMCS algorithm is different from the other nine comparison algorithms and significantly outperforms the other comparison algorithms. The DMCS algorithm is ranked first in the Friedman test with a value of 3.161, slightly smaller than the CLPSO algorithm with a value of 3.462. Figure 7 plots and shows the convergence curves of the methods while solving the benchmark functions from CEC 2017. The curve corresponding to the DMCS algorithm decreases quickly and is close to the optimal value in the early stage. The optimal can search for solutions with higher accuracy, which indicates that the DMCS algorithm increases the population diversity, prevents the algorithm from falling into local optima, and improves the convergence efficiency.

Table 6 The results achieved by DMCS against the nine advanced algorithms

Table 7 The results of Avg and Std analysis of advanced algorithms comparison experiment

Fig. 6

The Friedman test result of DMCS and other advanced algorithms

Fig. 7

The convergence curves of DMCS and other nine advanced algorithms

4 Experiment for Renal Pathology Image Segmentation

To test the effectiveness of the DMCS algorithm for maximum entropy multi-threshold image segmentation, this subsection used the DMCS algorithm and six other algorithms, which are CS [32], WOA [30], Bat Algorithm (BA) [76], PSO [25], Salp Swarm Algorithm (SSA) [77], MVO [66], Biogeography-based Learning Particle Swarm Optimization (BLPSO) [78] and an Improved WOA (IWOA) [79], to conduct multi-threshold image segmentation comparison experiments on eight renal pathology images of LN. In any image processing task [80,81,82,83], the utilized metric should be chosen so carefully. Hence, we used three indicators of Peak Signal to Noise Ratio (PSNR) [84], Feature Similarity Index (FSIM) [85] and Structural Similarity Index (SSIM) [86] to access the effect of the experiment. For further analysis, the experiment results are subjected to the Friedman test. The eight renal pathology images were obtained from electronic medical records of LN patients in the first affiliated hospital of Wenzhou medical university, China. This study was approved by the Medical Ethics Committee of the hospital and following the Declaration of Helsinki.

4.1 Experiment Setup

In this experiment, the population size of the swarm intelligence algorithm is set to 20 and runs independently 20 times, with each iteration running 100 times. The algorithm's fitness function is 2D Rényi entropy, and the image size was set to 512 $\times$ 512. The thresholds of image segmentation were taken as 4, 5, and 6 for three independent experiments. All experiments were carried out on a desk computer with Windows 10, Intel Core i5, 2.90 GHz, 8 GB of RAM, and MATLAB R2021b.

4.2 Multi-threshold Image Segmentation

Image segmentation is an essential technique in image processing that determines the quality of object detection, recognition, and tracking. The choice of image segmentation method directly influences the performance of an image analysis system. Thresholding has become a fundamental technique for image segmentation because of its stable performance and simplicity. The threshold segmentation method can be classified into two categories: single-threshold segmentation and multi-threshold segmentation. Multi-thresholds are used to set the multi-threshold to the image's grayscale, then compare each pixel's grayscale with the threshold, and then classify it, which is a pattern recognition classification process [87, 88]. The traditional method has high computational intensity and inaccurate results [89]. The current swarm intelligence algorithm searches for the best threshold for simple calculation. This work uses the DMCS algorithm to search for the optimal threshold and compare it with six other swarm intelligence algorithms.

4.2.1 Non-Local Means (NLM) for 2D Histogram

French scholars Buades et al. [90] proposed an image denoising algorithm, the Non-Local Means (NLM) denoising algorithm, in 2005. Although image denoising and image segmentation method are two independent stages, the quality of image denoising can significantly impact image segmentation. The original threshold segmentation method uses a 1D grayscale histogram to select the threshold, but it cannot segment the image containing noise. A 2D histogram-based multi-threshold image segmentation combining local pixel grayscale averages and original grayscale histograms proposed by Abutaleb et al. [91] solves this problem. However, using a 2D histogram to find the optimal threshold has high computational complexity, and the traditional 2D histogram cannot make the best of the edge and noise information of the image, resulting in inaccurate image segmentation [92, 93]. Hence, in this paper, the NLM image and grayscale image are used to generate a 2D histogram and then combined with the proposed DMCS algorithm to find the optimal threshold for medical image segmentation purposes while reducing the to reduce the computational complexity.

NLM denoising algorithm calculates the weighted sum of the pixel values of all pixels in the rectangular window, and the weights obey the Gaussian distribution. It uses the similarity between the neighborhood block of the current filter point and the neighborhood blocks of other points in the rectangular window to calculate the weight. The greater the similarity, the greater the weight. A simple formula for NLM will be given below:

$$NL\left[ v \right]\left( i \right) = \mathop \sum \limits_{j \in I} w\left( {i,j} \right)v\left( j \right),$$

(11)

$$w\left( {i,j} \right) = \frac{1}{Z\left( i \right)}e^{{\frac{{ -\| v\left( {N_{i} } \right) - v\left( {N_{j} } \right)\|_{2,a}^{2} }}{{h^{2} }}}} ,$$

(12)

$$Z\left( i \right) = \mathop \sum \limits_{j} e^{{\frac{{ -\| v\left( {N_{i} } \right) - v\left( {N_{j} } \right)\|_{2,a}^{2} }}{{h^{2} }}}} .$$

(13)

The formulas will be explained below in conjunction with Fig. 8. In the figure, the window with a black border is the search window centered on the target pixel $i$. The small red and blue windows are the domain windows centered on pixels $i$ and $j$ severally. $v = \left\{ {v\left( i \right){|}i \in I} \right\}$ denotes a discrete noisy image. $NL\left[ v \right]\left( i \right)$ is the filter value of point $v\left( i \right)$, it is obtained from the weighted average of the pixel values of all points in the search window. $w\left( {i,j} \right)$ denotes the Gaussian weight between $v\left( i \right)$ and any point $v\left( j \right)$ in the search window, calculated from the mean-squared error $v\left( {N_{i} } \right) - v\left( {N_{j} } \right)_{2,a}^{2}$ of the respective domain block of the two points, and $w\left( {i,j} \right)$ lies between 0 and 1, and $\sum\nolimits_{j} {w\left( {i,j} \right) = 1}$. $v\left( {N_{i} } \right)$ and $v\left( {N_{j} } \right)$ are the intensity gray level vectors, where $N_{k}$ denotes a square window centered at pixel $k$. The more similar $v\left( {N_{i} } \right)$ and $v\left( {N_{j} } \right)$ are, the larger $w\left( {i,j} \right)$ is. The similarity between pixel $i$ and pixel j is determined by the similarity of $w\left( {i,j} \right)$. $a$ > 0 is the standard deviation of the Gaussian kernel. $Z\left( i \right)$ is a normalizing factor. $h$ is a coefficient to control the decay of the exponential function. The size of the $h$-value is proportional to the denoising effect and inversely proportional to the degree of image distortion. In other words, the larger the $h$, the better the denoising effect, but the more blurred the image will be. The smaller the $h$, the worse the denoising effect, but the smaller the denoising distortion.

Fig. 8

The schematic diagram of NLM

Suppose an image $I$ with a total number of $m*n$ pixels is divided into $L$ gray levels, then the gray value range of pixels in the original image $I$ is from $0$ to $L - 1$, and the gray value range of pixels in the NLM image is from $0$ to $L - 1$, too. The grayscale probability density of pixels in the NLM for 2D histogram generated by combining the grayscale image and the NLM image is calculated by Eq. (14) [94].

$$p\left( {i,j} \right) = \frac{{f\left( {i,j} \right)}}{m \times n},$$

(14)

where the frequency of occurrence of the binary group $\left( {i,j} \right)$ is denoted by $f\left( {i,j} \right)$. $i$ denotes the pixel gray level of the original image $I$, $j$ denotes the pixel gray level of the NLM image, and Fig. 9 shows the NLM 2D histogram, where the pixel values of the original grayscale image $I$ are represented by the horizontal axis and the NLM image are represented by the vertical axis, with the axis intervals determined by the corresponding threshold levels of the image.

Fig. 9

NLM 2D histogram

4.2.2 2D Rényi Entropy Mode

2D Rényi entropy is a generalization of Shannon entropy, which differs from Shannon entropy in those variable parameters $\alpha$ are introduced into it. Then in 2008, Leila et al. defined the conditional 2D Rényi entropy and showed that the so-called chain rule holds for 2D Rényi entropy [95,96,97]. In this paper, the coefficient of $\alpha$ is 0.5. Here, we introduce the 2D Rényi entropy method of multi-threshold.

Given an image $I$ divided into $L$ gray levels, the distribution probability of each gray level is $\left\{p\left(1\right),p\left(2\right),\dots ,p\left(i\right),\dots ,p(L)\right\}$. Assuming that there are $N$ thresholds $\left\{{t}_{1},{t}_{2},\dots ,{t}_{N}\right\}$, the histogram is divided into $N+1$ regions, and the grayscale probability of the first threshold $t$ can be described as Eq. (15):

$$w_{j} \left( t \right) = \left\{ {\begin{array}{*{20}c} {\mathop \sum \limits_{i = 1}^{{t_{1} }} p\left( i \right),j = 1} \\ {\mathop \sum \limits_{{i = t_{n - 1} + 1}}^{{t_{n} }} p\left( i \right),1 < j < N} \\ {\mathop \sum \limits_{{i = t_{N - 1} + 1}}^{L - 1} p\left( i \right),{\text{otherelse}}} \\ \end{array} } \right..$$

(15)

The 2D Rényi entropy of each region $Rt_{\alpha }^{n}$ can be calculated by Eq. (16):

$$Rt_{\alpha }^{n} = \frac{1}{1 - \alpha }ln\mathop \sum \limits_{{i = t_{n - 1} + 1}}^{{t_{n} }} \left( {\frac{p\left( i \right)}{{w_{n} \left( t \right)}}} \right)^{\alpha } ,{ }n = 1 \ldots N.$$

(16)

The selected optimal threshold by the algorithm should meet Eq. (17):

$$\left[ {t_{1} ,t_{2} , \ldots ,t_{N} } \right] = arg{ }\max \left( {\mathop \sum \limits_{n = 1}^{N} Rt_{\alpha }^{n} \left( {t_{n} } \right)} \right).$$

(17)

4.3 Evaluation Metrics for Image Segmentation

This subsection details three commonly used image quality evaluation metrics: FSIM, PSNR, and SSIM. They evaluate the image feature similarity, image distortion degree, and image structural integrity.

(1) FSIM is an image quality metric based on a low-level feature, which uses both Phase Congruency (PC) and the Gradient Magnitude (GM) [85] features. PC and GM indicate complementary aspects of the visual quality of an image. Below we will explain Eqs. (18)–(21).

${PC}_{1}$ and ${PC}_{2}$ represent the PC map extracted from images ${f}_{1}$ and ${f}_{2}$, respectively, and ${G}_{1}$ and ${G}_{2}$ represent the GM maps extracted from them. The similarity measure ${S}_{PC}(x)$ for ${PC}_{1}(x)$ and ${PC}_{2}(x)$ is calculated by Eq. (18), and the similarity measure $S_{G} \left( x \right)$ is defined as Eq. (19):

$$S_{PC} \left( x \right) = \frac{{2PC_{1} \left( x \right) \cdot PC_{2} \left( x \right) + T_{1} }}{{PC_{1}^{2} \left( x \right) + PC_{2}^{2} \left( x \right) + T_{1} }},$$

(18)

$$S_{G} \left( x \right) = \frac{{2G_{1} \left( x \right) \cdot G_{2} \left( x \right) + T_{2} }}{{G_{1}^{2} \left( x \right) + G_{2}^{2} \left( x \right) + T_{2} }},$$

(19)

where $T_{1}$, $T_{2}$ both are positive constants, and $T_{1}$ plays a role in enhancing the stability of $S_{PC}$. The dynamic range of GM values determines the value of $T_{2}$. Define $S_{L}$ as the similarity between $f_{1}$ and $f_{2}$, which is calculated by combining $S_{PC}$ and $S_{G}$, and the calculation method is shown in Eq. (20):

$$S_{L} \left( x \right) = \left[ {S_{PC} \left( x \right)} \right]^{\alpha } \cdot \left[ {S_{G} \left( x \right)} \right]^{\beta } ,$$

(20)

where $\alpha$ and $\beta$ are relative importance parameters that can be used to adjust the PC and GM values. From the above description. The FSIM index between $f_{1}$ and $f_{2}$ can be defined as Eq. (21).

$${\text{FSIM}} = \frac{{\mathop \sum \nolimits_{x \in \Omega } S_{L} \left( x \right) \cdot PC_{m} \left( x \right)}}{{\mathop \sum \nolimits_{x \in \Omega } PC_{m} \left( x \right)}}{ ,}$$

(21)

where $\Omega$ denotes the whole image space domain, and $PC_{m}$ is obtained through equation ${\text{max}}\left( {PC_{1} \left( x \right),PC_{2} \left( x \right)} \right)$.

(2) PSNR is a simple and commonly used fidelity measurement method and has traditionally been used in analog systems as a consistent quality metric. Due to its mathematical convenience and simplicity, it is an attractive measure of image quality (loss) [84, 98].

The mathematical formula for PSNR is as follows:

$${\text{PSNR}}\left( {x,y} \right) = 10\log_{10} \frac{{255^{2} }}{{{\text{MSE}}\left( {x,y} \right)}},$$

(22)

$${\text{MES}}\left( {x,y} \right) = \frac{1}{N}\mathop \sum \limits_{I = 1}^{N} \left( {x_{i} - y_{i} } \right)^{2} ,$$

(23)

where $x$ and $y$ denote the vector of reference and test image signals, respectively. ${\text{MES}}\left( {x,y} \right)$ means the mean-squared error between $x$ and $y$. $N$ denotes the total number of pixels in the image [99].

(3) SSIM is a metric to measure the quality by the similarity of the captured images. The SSIM index is obtained by three aspects of similarity: luminance, contrast, and structure. Defined $x$ and $y$ are two images, the luminance comparison function $l\left( {x,y} \right)$ is defined as Eq. (24):

$$l\left( {x,y} \right) = \frac{{2\mu_{x} \mu_{y} + C_{1} }}{{\mu_{x}^{2} + \mu_{y}^{2} + C_{1} }},$$

(24)

where $\mu$ means the mean value of the image, and $C_{1}$ is a constant to avoid instability when $\mu_{x}^{2} + \mu_{y}^{2}$ is very close to zero. Similarity, the contrast comparison function $c\left( {x,y} \right)$ can be defined as Eq. (25):

$$c\left( {x,y} \right) = \frac{{2\sigma_{x} \sigma_{y} + C_{2} }}{{\sigma_{x}^{2} + \sigma_{y}^{2} + C_{2} }},$$

(25)

where $\sigma$ is the standard deviation of two contrasting images, and $C_{{2{ }}}$ is a constant. The structure comparison function $s\left( {x,y} \right)$ is calculated by Eq. (26):

$$s\left( {x,y} \right) = \frac{{\sigma_{xy} + C_{3} }}{{\sigma_{x} \sigma_{y} + C_{3} }}.$$

(26)

The mathematical formula for SSIM is as follows:

$${\text{SSIM}}\left( {x,y} \right) = l\left( {x,y} \right) \cdot c\left( {x,y} \right) \cdot s\left( {x,y} \right) = \frac{{\left( {2\mu_{x} \mu_{y} + C_{1} } \right)\left( {2\sigma_{xy} + C_{2} } \right)}}{{\left( {\mu_{x}^{2} + \mu_{y}^{2} + C_{1} } \right)\left( {\sigma_{x}^{2} + \sigma_{y}^{2} + C_{2} } \right)}}{ ,}$$

(27)

where set $C_{3} = \frac{1}{2}C_{2}$ according to [86].

4.4 Experimental Result Analyses

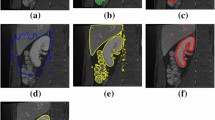
The original color images and 2D histograms of the eight images used in the experiments are shown in Fig. 10. Column A in Fig. 10 is the color image of the original images, and column B represents the 2D histogram generated by combining the NLM graph and grayscale image. Tables 8, 9 and 10 show the results of the analysis of the experimental results using the image quality evaluation metrics, where "K" is the threshold value, "Avg" denotes the average, and "Std" means the standard deviation. According to the results of FSIM, the DMCS algorithm achieves the best results on all eight images at a threshold of 4; at thresholds of 5 and 6, it fails to achieve the optimal Avg or Std only on images 2, 4 and 4, 5. This indicates that most of the images segmented using the DMCS algorithm are closer to the test images than the competitors. According to the results of PSNR, the DMCS algorithm performs well on all eight images at thresholds 4, and 5, and achieves the maximum Avg and the minimum Std on images except images 3 and 4 at threshold 6. This indicates that most of the images segmented using the DMCS algorithm have less distortion than the competitors. According to the results of SSIM, the DMCS algorithm achieves the best results on all eight images at a threshold of 4. At a threshold of 5 and 6, it fails to achieve the optimal Std only on images 4 and 3. This indicates that most of the images segmented using the DMCS algorithm are more structurally complete than the competitors. Therefore, DMCS can effectively avoid stagnation of the algorithm and is more stable. In addition, the accuracy of image segmentation improves as the threshold increases. The Wilcoxon signed-rank test was performed on the results of Tables 8, 9 and 10 to obtain Tables 11 , 12 and 13, and the best results are bolded. Based on the results of " + / - / = ", it can be found that DMCS significantly outperforms the comparison algorithm on 8 images. Therefore, DMCS ranks first overall and has the best performance. Tables 14, 15 and 16 show the results of further analysis with the Friedman test, where the DMCS algorithm gets the largest average and the first ranking with a large advantage on all thresholds. In addition, Fig. 11 shows the convergence curves of the DMCS algorithm and the contrast algorithm for the two-dimensional Rényi entropy for a threshold of 4 in 8 images; the larger the value of the curve convergence, the more information it contains about the image. The figure shows that the DMCS algorithm has the fastest convergence speed and accuracy. Figure 12 offers the best thresholds of the DMCS algorithm and its contrast algorithm for a threshold of 5 on image 1. The best thresholds have been marked in red font on the image, and the comparison reveals that the DMCS algorithm can over-obtain reasonable thresholds. Figure 13 visualizes the images after the segmentation of image 4 at a threshold of 6 for each algorithm in the experiment, the first image in each group is the segmented grayscale image, and the second is the colormap map. It can be seen from the segmented grayscale images that the DMCS algorithm has more transparent and more complete details in the segmented images compared with the CS algorithm, and the results are not inferior compared with other comparison algorithms.

Fig. 10

Original images and corresponding 2D histograms of the eight images used in the experiment

Table 8 The FSIM of each algorithm

Table 9 The PSNR of each algorithm

Table 10 The SSIM of each algorithm

Table 11 Wilcoxon signed-rank test result for each algorithm on FSIM

Table 12 Wilcoxon signed-rank test result for each algorithm on PSNR

Table 13 Wilcoxon signed-rank test result for each algorithm on SSIM

Table 14 Friedman test result for each algorithm on FSIM

Table 15 Friedman test result for each algorithm on PSNR

Table 16 Friedman test result for each algorithm on SSIM

Fig. 11

2D Rényi entropy convergence curves for eight images at the threshold of 4

Fig. 12

Thresholds for image 1 obtained by each algorithm at level 5

Fig. 13

Segmentation results for each method at threshold level 6 of image 4

5 Conclusions and Future Works

This paper proposes a multi-threshold image segmentation model combining NLM 2D histogram and an improved CS algorithm to segment LN images. To improve the defects of the original CS algorithm and increase the efficiency of image segmentation, an enhanced algorithm named DMCS is proposed by introducing the DM and AβHC strategies in the CS algorithm. Introducing the DM and AβHC strategies increases the cuckoo population diversity and helps search for better solutions. DMCS is tested on the CEC 2017 dataset. Among the mechanism comparison, experimental results prove that the DM strategy can accelerate the algorithm's convergence. In contrast, the AβHC strategy is beneficial to improve the quality and accuracy of the solution, and the experimental results with the traditional and advanced algorithms also show that the proposed improved algorithm performs better function optimization. Finally, the ability of DMCS to solve practical problems is verified on real LN image segmentation. However, the proposed method has some limitations. Adding the mechanisms inevitably increases the algorithm's time complexity, which can be improved by parallel computing and high-performance computing techniques in the future. In addition, for other optimization problems, such as feature selection and energy parameter optimization with different search space characteristics and objectives, the optimization effect of the DMCS algorithm will be affected. The DMCS algorithm can continue to be improved in the next step to be applied to more cases, such as optimizing machine learning models.