Abstract
Despite advances in techniques for exploring reciprocity in brain-behavior relations, few studies focus on building neurocognitive models that describe both human EEG and behavioral modalities at the single-trial level. Here, we introduce a new integrative joint modeling framework for the simultaneous description of single-trial EEG measures and cognitive modeling parameters of decision-making. As specific examples, we formalized how single-trial N200 latencies and centro-parietal positivities (CPPs) are predicted by changing single-trial parameters of various drift-diffusion models (DDMs). We trained deep neural networks to learn Bayesian posterior distributions of unobserved neurocognitive parameters based on model simulations. These models do not have closed-form likelihoods and are not easy to fit using Markov chain Monte Carlo (MCMC) methods because nuisance parameters on single trials are shared in both behavior and neural activity. We then used parameter recovery assessment and model misspecification to ascertain how robustly the models’ parameters can be estimated. Moreover, we fit the models to three different real datasets to test their applicability. Finally, we provide some evidence that single-trial integrative joint models are superior to traditional integrative models. The current single-trial paradigm and the simulation-based (likelihood-free) approach for parameter recovery can inspire scientists and modelers to conveniently develop new neurocognitive models for other neural measures and to evaluate them appropriately.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Recent decades have seen a remarkable growth in the development of both the fields of mathematical psychology and cognitive neuroscience to interpret and predict cognition from behavioral and brain data (Usher & McClelland, 2001; Brown & Heathcote, 2008; Ditterich, 2006; Gold & Shadlen, 2007; Drugowitsch et al., 2012; Turner et al., 2013; Ratcliff et al., 2016). In particular, neurocognitive theories of perceptual decision-making have been proposed to explain how evoked electroencephalography (EEG) measures and behavioral data from experiments result from the specific time course of visual encoding, evidence accumulation, and motor preparation (O’Connell et al., 2012a; van Ravenzwaaij et al., 2017; Nunez et al., 2019; Lui et al., 2021). Models derived from these theories can then be fit to data and predict and explain both evoked EEG and behavioral data. These neurocognitive models utilize trial- or individual-level signatures of EEG or magnetoencephalography (MEG) signals to assess, constrain, replace, or add cognitive parameters in models (Nunez et al., 2017; 2022). Moreover, Turner et al. have proposed many approaches for directly or indirectly relating neural data to a cognitive model; for instance, the field of model-based cognitive neuroscience has used BOLD responses and EEG waveforms simultaneously and separately to predict and constrain cognitive parameters and behavioral data (Turner et al., 2013, 2016, 2019; Bahg et al., 2020; Kang et al., 2021). Also, Nunez et al. have introduced some neurocognitive models to study the effect of selective attention, the role of visual encoding time (VET), and the relationship of readiness potentials (RPs) in motor cortical areas to evidence accumulation during perceptual decision-making tasks (Nunez et al., 2017, 2019; Lui et al., 2021). Furthermore, Ravenzwaaij et al. have suggested an explicit and confirmatory model that reveals that the drift rate parameter can describe simultaneously the behavioral data and the neural activation in a mental rotation task (van Ravenzwaaij et al., 2017).
Motivation
Are EEG measures able to track parameters of sequential sampling models? Sequential sampling models (SSMs), especially drift-diffusion models (DDMs), assume that human and animal decision-making are based on the integration of evidence over time which reaches a specific threshold. The accumulation and non-accumulation parameters for a decision are usually measured by the firing rate of neurons and ERP signatures (O’Connell et al., 2018). Even though some joint models incorporate neural dynamics in classical DDMs, only some models have been developed that consider EEG signatures as a participant response similar to reaction time (RT) and accuracy (van Ravenzwaaij et al., 2017). There are however many studies linking event-related potential (ERP) components and behavioral performance (O’Connell et al., 2012a; Gluth et al., 2013; Philiastides et al., 2014; Loughnane et al., 2016), as well as using EEG to constrain models’ parameters at the level of the experimental trial (Frank, 2015; Nunez et al., 2017; Ghaderi-Kangavari et al., 2022). Models should be further developed that explain ERP data at the trial level with generative models similar to response times (RTs) and accuracy. Therefore, there is an impetus to build a few of these models, develop associated model fitting procedures, and then assess the idealized models to test how robustly their parameters can be estimated. In this paper, we introduce some practical models and model fitting procedures which will help researchers in the field of cognitive neuroscience to make better inferences about individual differences and trial-to-trial changes in neurocognitive underpinnings during perceptual decision-making tasks. These new neurocognitive models are advantageous compared to the traditional models. The benefits of these models and model-fitting procedures are listed in two categories.
First, we used model-fitting procedures that estimate posterior distributions through invertible neural networks (INNs). In particular, we used a new method named BayesFlow https://github.com/stefanradev93/BayesFlow; (Radev et al., 2020a). This allowed us to flexibly test complex models of joint data without solving for closed-form likelihoods, as well as test models that have no closed-form likelihood. Specifically, we used BayesFlow to apply amortized deep learning to build networks that quickly estimate posterior distributions of complicated and likelihood-free models rather than applying case-based inference. Note here that the training of neural networks did depend on particular types of prior distributions, similar to other Bayesian workflows, and we felt that uniform distributions can be a good option for generating sample parameters. After training, these posterior approximators can be widely shared and applied because they require less knowledge of computational and model fitting procedures rather than Markov chain Monte Carlo (MCMC) methods, non-amortized simulation-based methods, and other amortized Bayesian inference methods (Turner & Sederberg, 2012; Gelman et al., 2014; Lueckmann et al., 2019; Hermans et al., 2020; Turner & Van Zandt, 2012; Fengler et al., 2021). These posterior approximators still allow the estimation of full posterior distributions instead of summary statistics of the posterior (e.g., posterior mean or mode). The BayesFlow method has been recently modified to distinguish correct posterior distributions from posterior errors when there are some deviations between the assumed (simulated) model and the true model that generated the observed data, a situation known as model misspecification (Schmitt et al., 2021). This advantage is mostly due to the use of the summary network, which usually obtains the most important information and helps to detect the presence of unexpectedly contaminated data or misspecified simulators (i.e., simulation gaps). We endeavored to manage contaminated behavioral and neurological data by building some neurocognitive models which contain explicit mixtures of contaminants. For instance, the mixture model of a DDM model and a lapse process (uniform distribution) can be a good option to handle contaminated behavioral data (Ratcliff & Tuerlinckx, 2002; Nunez et al., 2019).
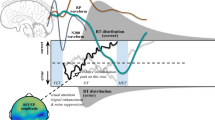
The second category of benefit is that these models explain EEG as single-trial-dependent variables. For example, specific models can generate event-related potential (ERP) latencies or ERP waveform shapes (ERPs explained below) in addition to RT and accuracy data from latent cognitive parameters. Some of these models separate visual encoding times (VETs) from other non-decision times (see Fig. 1), while some of these models also predict contaminants (e.g., “lapse” trials) in EEG measures and behavioral performance. Other models constrain evidence accumulation rate (i.e., drift-rate) parameters to make better parameter estimates (see Fig, 1). With these models, we can test research questions about correlates of behavioral performance and neural data (e.g., O’Connell et al., 2012a, Nunez et al., 2019, 2022), new research questions (such as about spatial attention, see Ghaderi-Kangavari et al., 2022), and explain and predict ERP measures jointly with behavioral measures. Another benefit is that these models are measurement models in that the estimated parameters reflect interpretations of cognitive processes. Finally, these models are easily extendable, such as similar models with linear and non-linear collapsing boundaries (Evans et al., 2020b; Voss et al., 2019).
A theoretical presentation of novel neurocognitive models for the study of human cognition that explain single-trial neural activities and behavioral data simultaneously. Three types of decision boundaries (static, linear collapsing, and Weibull collapsing) have been used to design neurocognitive models. Single-trial EEG, such as single-trial event-related potentials (ERPs) from the occipito-parietal area, can be explained by these joint models; for example, N200 latencies (blue line) and centro-parietal positivities (CPP) (green line). These data constrain and predict latent parameters. Distributions of behavioral performance such as RT and choice for correct and error are displayed on both sides of the two choice boundaries. Latent parameters of the DDM are also displayed, which reflect N200 latencies and CPP slopes. Prior evidence has found that N200 waveforms track visual encoding time (VET) and the onset of evidence accumulation (Loughnane et al., 2016; Nunez et al., 2019). Moreover, P300 or CPP slope are assumed to account for the accumulation time rather than non-decision time and possibly reflect the mean of drift rate (O’Connell et al., 2012a). The minimum N200 waveform has initiated the onset of the evidence accumulation as well as the P300/CPP slope is similar to the mean slope of the evidence accumulation
Single-Trial ERP Analysis
EEG activity time-locked to particular events in an experimental task and averaged-across trials, i.e., event-related potentials (ERPs), have been frequently utilized as a powerful method in the past century to study both clinical and research applications such as the information processing in the brain, biomarkers for a variety of disorders, neural mechanisms involving cognitive processes, highlighting differences in brain activity, prediction of future cognitive functioning, identifying cognitive dysfunction, individual differences, etc. (Philiastides et al., 2006; Cavanagh et al., 2011; Luck, 2014; Zwart et al., 2018; Manning et al., 2022). Some advantages of using ERPs over other EEG measures include as follows: enhancing signal-to-noise ratios, less variance across conditional manipulations, and decreased type II errors (Luck, 2014; Luck et al., 2000). However, some disadvantages of trial-averaged ERPs are that: a large number of participants are needed to achieve robust inferences, there is a loss of abundant information contained in EEG across trials, and it is difficult to use ERPs to constraint cognitive models to estimate parameters within-trials. Nevertheless, correlation and multiple linear regression methods on the individual level have been crucial parts of analysis for researchers who assessed statistical relationships between models’ parameters, ERPs components, and behavioral performance (Nunez et al., 2015; Schubert et al., 2019; Clayson et al., 2019; Manning et al., 2022). In fact, the two-stage inference is a statistically attenuated approach because parameters are estimated, and then their summary measures are put into a regression model, resulting in missing information.
Improving upon the aforementioned disadvantages of trial-averaged ERPs, ERPs can also be measured on single trials under certain conditions (Nunez et al., 2017; Bridwell et al., 2018). Single-trial ERPs can help the neurocognitive models estimate and restrict cognitive parameters simultaneously because of fluctuations in cognition across experimental trials (Nunez et al., 2017). However, one of the main difficulties in using single-trial ERPs is the amount of noisy information due to artifacts (electromyographic—EMG—signals, electrical noise, and other unrelated brain activity). Therefore, modern techniques are required to discard irrelevant information and amplify relevant cognitive activity. In general, there are two approaches to extracting single-trial ERPs: manual and automatic. Using the manual method, researchers might spatially average single-trial EEG waveforms across electrodes in occipital, occipito-parietal, motor regions, etc. However, using an automatic method, researchers can apply machine learning approaches to identify linear spatial weightings to generate a single waveform, such that this single waveform contributes to the activity of many electrodes. One example is to find single-trial ERPs using a weighted map resulting from singular value decomposition (SVD) of the traditional trial-averaged ERPs at every electrode. This procedure has been successful in our previous work (Nunez et al., 2019; Ghaderi-Kangavari et al., 2022). In other work, a single-trial multivariate linear discriminant analysis (LDA) has been used to determine linear spatial weightings of the EEG electrodes for maximal discrimination of target (faces) and non-target (cars) trials during a simple categorization task (Philiastides et al., 2006; Diaz et al., 2017).
N200 Latencies Can Reflect Visual Encoding Time
Estimating the time of visual encoding for perceptual decision-making is challenging because it depends on distinct variables, for instance: uncertainty of stimuli, target selection, and figure-ground segregation (Lamme et al., 2002; Loughnane et al., 2016). Consequently, researchers have reported on the verity of time to encode visual stimulus, and this research has converged on a specific window of latency. We first review the previous literature on visual processing and then the specific literature related to decision-making.
Note that encoding for some emotional and threatening stimuli project to the amygdala nuclei, and thus visual encoding of these stimuli are expected to take a little time to make innate and unconscious reaction (Tamietto & De Gelder, 2010; Baars & Gage, 2013). In this work, we are concerned with stimuli where the mechanism of visual encoding is the transmission of information through the LGN of the thalamus to the primary visual cortex, and involves a different network to further process visual information (Baars & Gage, 2013; Hall & Hall, 2020). The visual path has a long way to go, and it takes a little longer than the auditory pathway. The C1 (60–80 ms), P100 (around 100 ms, also known as the P1), and N200 (120–180 ms, also known as the N1) are exogenous ERP waves over the visual cortex that are thought to reflect sensory stages of processing visual stimuli; such that the C1 wave is not manipulated by attention, and both P100 and N200 peaks were manipulated by attention and visual perceptual learning (Cobb & Dawson, 1960; Clark et al., 1994; Luck et al., 2000; Ahmadi et al., 2018). The N200 latency component between sessions correlates negatively with behavioral improvement in a texture discrimination task (Ahmadi et al., 2018). Di Russo et al. showed by studying ERPs and the combination of structural and functional magnetic resonance imaging (fMRI) that the spatio-temporal patterns of the calcarine sulcus, primary visual cortex, extrastriate and occipito-parietal activities were in the latency range of 80–225 ms in response to flash stimuli (Di Russo et al., 2003).
We define visual encoding time (VET) as the time between the onset of stimuli and the relative starting of the evidence accumulation process (Nunez et al., 2019). VET is thought to take place sequentially before, not in parallel to, the accumulation process (Weindel, 2021). This is not necessarily true for all cognitive components in decision-making; for instance, there is evidence to suggest that motor planning evolves concurrently with the evidence accumulation process (Dmochowski & Norcia, 2015; Servant et al., 2015, 2016; Verdonck et al., 2021). Researchers proposed that the process of VET can be completed from 150 ms to 225 after the appearance of stimulus (Thorpe et al., 1996; VanRullen & Thorpe, 2001; Nunez et al., 2019). Shadlen et al. demonstrate that the evidence accumulation from the lateral intraparietal area (LIP) begins at around 200 ms after the onset of random dot motion with difference phase coherence (Roitman & Shadlen, 2002; Kiani & Shadlen, 2009; Shadlen & Kiani, 2013). In addition, Thorpe et al. revealed that the visual processing demanded a go/no-go categorization task can be reached around 150 ms after the onset of stimulus (Thorpe et al., 1996). Furthermore, Nunez et al. found evidence that the latency of the negative N200 between 150 and 275 after stimulus onset in the occipito-parietal electrodes reflects the VET needed for figure-ground segregation before the accumulation of evidence (Nunez et al., 2019). Finally, Ghaderi-Kangavari et al. used hierarchical Bayesian models that included single-trial N200 latencies to identify the effects of spatial attention on perceptual decision-making and found evidence that perceptual decision-making manipulates both VET before evidence accumulation and other non-decision time process after or during evidence accumulation (Ghaderi-Kangavari et al., 2022).
Centro-parietal Positivities Can Reflect Evidence Accumulation
Analogous to well-known findings of invasive single cell recordings that identified markers of how animals accumulate information to make perceptual decisions (Shadlen & Newsome, 2001; Roitman & Shadlen, 2002; Gold & Shadlen, 2007; Shadlen & Kiani, 2013; Kiani & Shadlen, 2009; Jun et al., 2021), some researchers have shown that non-invasive EEG recordings can also describe how humans accumulate information towards a specific bound to make a decision (Kelly & O’Connell, 2013; O’Connell et al., 2012a, 2018). O’Connell et al. discovered an ERP signiture called the centro-parietal positivity (CPP) identifying a build-to-threshold decision variable (O’Connell et al., 2012a). They also clarify that the CPP evoked by gradual decreases in the contrast of stimuli is highly correlated to the classic P300 peak elicited by invariant contrast of targets. In addition, the P300/CPP dynamic taken from three electrodes centered on CPz, the standard site for the P300, can predict both timing and accuracy of perceptual decision-making in humans (O’Connell et al., 2012a; Kelly & O’Connell, 2013; McGovern et al., 2018). On the other hand, Loughnane et al. showed that a pair of early negative deflections at lateral occipito-temporal sites around 200 ms after stimulus appearance can influence the onset of the centro-parietal positivity (CPP) during a random dot motion task (Loughnane et al., 2016). In summary, researchers have shown that the CPP steadily increases at a certain rate and is assumed to reflect the integration of evidence to reach a particular peak at the time of response execution (O’Connell et al., 2012a; Kelly & O’Connell, 2013). It should be noted that the drift rate in drift-diffusion models (DDMs) is the mean rate of evidence accumulation. Therefore, the slope of the CPP can be assumed to be related to the drift rate (Nunez et al., 2022), which is line with previous findings (Ratcliff et al., 2009; Philiastides et al., 2014; van Ravenzwaaij et al., 2017).
Simulation-Based Approaches
Neuro-cognitive models that describe both brain and behavior could have complicated non-linear relationships between parameters. In order to obtain estimates (or full posterior distributions p(Θ|X)) of parameters of neurocognitive models, component likelihood functionsL(Θ|X) (or the probability density of the data given the parameters p(X|Θ)) can be derived to fit models using maximum likelihood estimation (MLE) or MCMC methods. However, in this paper, we will present plausible single-trial integrative joint models for which the component closed-form likelihoods are complicated, necessitating clever mathematical derivations to derive component likelihoods, if they are even tractable, i.e., possible to derive analytically.
Rejection-based approximate Bayesian computation (ABC) is an alternative to the calculation of likelihood functions with models only based on simulation (Csilléry et al., 2010; Turner & Van Zandt, 2012; Sunnåker et al., 2013). Rejection-based ABC algorithms estimate posterior distributions by taking proposal samples from a prior distribution \(\theta _{i} \sim p(\theta )\) and then generating an artificial dataset from the estimator model called the forward model \(x_{i} \sim p(x | \theta _{i})\) for xi = 1,…,N. If the artificial dataset is close enough to the observed dataset by a tolerance (𝜖), the sample (𝜃i) is chosen as a sample of the posterior (Csilléry et al., 2010; Klinger et al., 2018). One can use a sufficient statistic S(.) to summarize both artificial and observed data before comparing them (Palestro et al., 2018b). However, sufficient statistics are hard to obtain for complex models with intractable likelihoods, and using insufficient statistics may incur significant approximation error.
The pass/fail rule of rejection-based ABC is simple to implement but does not optimally use all simulated data, therefore kernel-based ABC algorithms can be an effective alternative (Turner & Sederberg, 2012). Moreover, synthetic likelihood methods and probability density approximations have been used as likelihood-free algorithms to fit mechanistic models to observed data (Wood, 2010; Turner & Sederberg, 2014; Palestro et al., 2018b). Both rejection-based methods need to include predetermined tolerance thresholds and the distributions of sufficient summary statistics, while synthetic likelihood methods and probability density approximation are computationally costly. Furthermore, these kinds of approaches have been identified as performing case-based inference which has a few drawbacks, such as expensive computations, inability to generate effective samples from posterior distributions, only approximating posteriors for specific data, and sensitivity to tolerance values.
Amortized Bayesian approaches are alternative methods to approximate joint posterior distributions, which can be applied quickly to new data. These methods also use simulated data for training. However, this training step is not necessary for each new dataset. For instance, some researchers have used masked autoregressive flows (Papamakarios et al., 2019) and probabilistic neural emulator networks (Lueckmann et al., 2019) to learn approximate likelihoods L(Θ|X) rather than instantaneous posterior distributions p(Θ|X). Moreover, Hermans et al. (2020) introduced a likelihood-to-evidence ratio estimator to compute an approximation of acceptance ratios in MCMC in order to draw posterior samples rather than evaluating the likelihood directly. Fengler et al. (2021) focused on two classes of architectures, multilayered perceptrons (MLPs), and convolutional neural networks (CNNs), to approximate likelihoods as well as estimate cognitive models with varying trial numbers. In this workflow by Fengler et al. (2021), two different posterior sampling methods, MCMC and importance sampling, are used for taking samples from posterior in each iteration. Estimating summary measures of the posteriors by constructing new artificial architectures for Bayesian inference can be useful for many research topics. These methods include as follows: fully convolutional neural networks as end-to-end architecture (Radev et al., 2020b), deep neural networks (Jiang et al., 2017), autoencoders (Albert et al., 2022), ABC random forests (Raynal et al., 2019), and different approaches to approximate likelihood and posteriors (Cranmer et al., 2020).
Radev et al. (2020a) have proposed a novel pathway to find posterior distributions using neural networks for globally amortized Bayesian inference. They proposed a fitting procedure with two neural networks: a summary network and an invertible neural network (INN). INNs are neural network architectures in which the mapping from input to output can be efficiently reversed (Ardizzone et al., 2018), while permutation-invariant summary networks are responsible for summarizing the independent and identically distributed (i.i.d.) observation datasets with a fixed-size vector automatically. The summarized data and the true posteriors are then transformed directly through an INN in the training phase into a simple latent space (e.g., Gaussian). This network is trained to learn simulated parameters, and then in the inference phase can then be inverted to estimate the joint (and marginal) posteriors. These networks are used to estimate posteriors in two main phases: a relatively expensive training phase and a very cheap inference phase (Radev et al., 2020a). Many of the models we propose in this paper fit with the procedure by (Radev et al., 2020a), although the models could also conceivably fit with other methods, such as that proposed by (Fengler et al., 2021) in the future.
Types of Joint Models
There are several strategies to link brain-behavior relationships in modeling (Turner et al., 2017; Palestro et al., 2018a). However, only two general strategies are relevant to our work. Directed and integrative models have been investigated to relate both unobserved parameters of behavior and the brain, and these models could either be employed for each participant or each experimental trial (see Fig. 2 to visualize modeling strategies relevant to our work).
Graphical models of a directed joint models, b a common integrative joint model, and c the single-trial integrative joint model. These graphical models represent approaches for linking EEG and behavioral data. These figures follow standard graphical model notation (Lee, 2014; Palestro et al., 2018b) with one new notation addition for c. Observed data are represented by shaded nodes, where node Z is the EEG data and node X is the behavioral data. Unobserved variables are represented by unshaded nodes. Nodes Λ are vectors of parameters that represent cognitive variables that describe both EEG and behavioral data. Nodes Ψ are vectors of computational parameters that only describe EEG data. Nodes Θ are vectors of cognitive parameters that only describe behavioral data. The double-bordered node in the directed model (a) refers to parameters that are not estimated and deterministic, such that their posterior distributions can be derived directly from posterior distributions of other parameters. The shaded double-bordered node in the single-trial integrative model (c) refers to parameters that are not necessarily estimable and are stochastic in simulation. It means that the posterior of the mentioned node must be estimated if we use closed-form likelihood approaches, but there is no need to estimate if we use a simulation-based approach. The plates that border the nodes represent replication over each trial i. Note that there are two differences between a and c: the changing direction of the arrow between Z and Λ, and the nature of the Λ node
In directed joint modeling, one assumes connections directly between EEG measures, denoted ϕ, and cognitive parameters, denoted 𝜃, that explain behavioral data (Turner et al., 2019). This connection is usually applied via a linking function. For instance, the linking function could be an embedded regression model. Note that a regression model the linking function allows EEG measures to be on any non-standardized scale for mapping from ϕ to 𝜃 (e.g., in the original scale of milliseconds for N200 latencies or micro-volts μV per second for CPP latencies). Directed neurocognitive models have been successfully used for studying the effect of visual attention, noise suppression, and spatial attention in perceptual decision-making tasks (Nunez et al., 2017, 2019; Ghaderi-Kangavari et al., 2022) as well as deployed to answer any other questions in related to the cognitive control of single-trial EEG in decision-making (Wiecki et al., 2013; Frank, 2015; Yau et al., 2021). Note that directed joint models can often produce better estimate parameter relationships between EEG measures and cognitive parameters than other methods because these models fit in a single step, as opposed to methods that fit cognitive models and linear regression sequentially (Ghaderi-Kangavari et al., 2021). However, while directed models are extremely useful for discovering the relationship between EEG data and cognition in exploratory research (Nunez et al., 2022), directed models can neither easily explain nor predict EEG data.
Integrative joint models describe, predict, and constrain both behavioral and EEG data simultaneously (Palestro et al., 2018a; Nunez et al., 2022). These models also allow us to fit models closer to the theoretical process models suspected to underlie both data types, as well as include computational parameters of EEG measures that are sometimes not necessarily tied to cognition. In this investigation, we focus on parameter recovery and robustness of novel integrative neurocognitive models to predict data on individual experimental trials. As a result, the models make both EEG measures (N200 and CPP) and behavioral data (RT and accuracy) explainable and predictable at the single-trial level.
Integrative model specification and formalization can explicitly reflect our understanding of cognition. So, different mathematical models can represent different theories of cognitive processes. Thus, another reason to model neurocognitive theory is to help understand the possible relationships between the brain, cognition, and behavior that can then be compared to data and tested in experimentation (Guest and Martin, 2021; Nunez et al., 2022). Therefore, the models presented here can help researchers who want to understand human cognition using EEG signals and behavioral data. Specifically, researchers can consider these models in terms of underlying neurocognitive theory, find parameter estimates of these models and compare them across experimental conditions and participants, and also compare models to find evidence for the most reasonable theory. We also believe the current approaches will be highly beneficial when applied to animal studies and when extended to other electrophysiology (e.g., single-unit and LFP data). Extensions of these models and simulation-based model fitting procedures can be easily applied in the future.
Mathematical Models for Neurocognitive Theory
We propose several neurocognitive models that reflect certain hypotheses and can be used to analyze data and answer research questions. These types of models can be considered integrative approaches to joint modeling (Turner et al., 2019). Specifically, they provide an architecture to apply behavioral and neural responses simultaneously at the single-trial level. These models also serve as examples and modeling architecture for psychological, cognitive, and neuroscience researchers who plan to construct explicit statistical models to connect data with theory.
From a methodological point of view, after formalization of these models, we implement them as simulation for a range of realistic parameter values (draws from prior distributions), and then submit these simulations through the BayesFlow Python pipeline to train INNs that yield samples from the parameter’s posterior distributions given any observed data set. We then test the robustness of the model fitting. We also provide saved fitted models, e.g., checkpoints in BayesFlow, of each trained model to be applied in a fast and single step on new data.
A General Framework for Integrative Joint Models
As mentioned before, in the following we propose a few models particular to the study of decision-making using single-trial EEG, response times, and choice data. However, our proposed models in this paper could be considered a part of a general framework to describe and predict single-trial EEG/behavior relationships. These models can be considered true integrative models as previously discussed. An important point to note here is that while known joint likelihood functions and approximations exist for choice-RTs (Tuerlinckx, 2004; Wagenmakers et al., 2007; Navarro & Fuss, 2009), and common likelihood functions exist that can be applied to single-trial EEG data (such as the Normal distribution), known joint likelihoods that describe all three data types on single trials do not exist. In such cases, joint likelihoods are likely necessary to estimate the parameters of these models using MCMC algorithms. However, the primary model-fitting technique we used for this work, BayesFlow, depends only upon being able to simulate the model. We can therefore express each model as a series of prior distributions and simulation equations from conditional probability distributions.
The general form to describe (joint) behavioral data X and neural data Z with shared latent single-trial cognitive parameters Λ is the following, with i being the index for one experimental trial, prior indicating a prior distribution, and sim indicating a simulation block:
where \(\mathcal {K}\) is the joint prior probability density over all non-single trial parameters, \({\mathscr{H}}\) is the marginal probability density function describing latent single-trial cognitive parameters, \(\mathcal {F}\) is the probability density function of behavior conditional on latent single-trial parameters, and \(\mathcal {G}\) is the probability density function of EEG conditional on latent single-trial parameters. Note that the three simulation blocks could be considered as simulations from one joint likelihood \((\mathbf {X}_{i},\mathbf {Z}_{i}) \sim \mathcal {J}(\mathbf {\Gamma },\mathbf {\Theta }, \mathbf {\Psi })\). However, it is often useful to think about three simulation blocks that share parameters instead, for example, to connect non-joint models developed in mathematical psychology and cognitive neuroscience. Here it is worth considering that behavioral parameters Θ, EEG measurement parameters Ψ, and shared cognitive parameters Γ can be estimated by BayesFlow under certain conditions for identified models, as we show later in this paper. Meanwhile, the issue to be highlighted here is that single-trial cognitive parameters Λi often cannot be estimated. However, using BayesFlow, estimation of Λi is not necessary because we can simulate Λi using the Γ parameters without needing to directly estimate Λi nor treating Λi as observed data.
These models can be fit to data using MCMC algorithms under certain conditions. The true joint likelihood of (Xi,Zi) must either be solved analytically by integrating out the so-called nuisance parameters Λ or approximated via estimation algorithms (Fengler et al., 2021) before sampling. Note however that sampling statements similar to the equations above written in programs such as JAGS (Plummer, 2003) and Stan (Carpenter et al., 2017), programs that fit MCMC models from a language of distributional sampling statements, will attempt to find posterior distributions for the nuisance parameters Λi for every trial i. For instance, a similar model with like lihoods, priors, and hyper priors is fundamentally different in that the density \({\mathscr{H}}\) is no longer assumed as part of the assumed model and instead reflects a prior belief about each single-trial parameter:
These similar models with priors for every trial do not easily converge to solutions due to a large number of parameters compared to data observations. Note also that the prior shape for single-trial parameters Λi in these models are influenced both by the functional form of \({\mathscr{H}}\) as well as the uncertainty of the hyperparameters Γ, while the models above have only an assumed probability density function \({\mathscr{H}}\) as part of the assumed joint density. Therefore, these are similar, but different, models (Gelman et al., 2014; Merkle et al., 2019).
As a consequence, a fixed probability distribution \({\mathscr{H}}\) must often be assumed that cannot result in a new hierarchical posterior distribution for the nuisance parameters Λi on every trial. This could be considered analogous to certain problems in decision-making models of behavior. For instance, a normal distribution for trial level drift rates δi is often assumed in DDMs (Ratcliff et al., 2016). Single-trial drift rates δi as nuisance parameters in this example are analogous to the single-trial Λi nuisance parameters in our framework. In order to estimate across-trial drift-rate variability parameters η with MCMC (and many other parameter estimation techniques), the trial-specific drift-rate parameter δi must be integrated out of the likelihood function, instead of estimating posterior distributions for each trial’s drift rate (Tuerlinckx, 2004; Ratcliff et al., 2016; Shinn et al., 2020). In these appropriate MCMC procedures and BayesFlow, single-trial drift rates are not estimated for every trial. However, integrating out this parameter is not necessary with BayesFlow because the entire model is instantiated in simulation.
Another similar model framework would be one in which there is no nuisance parameter Λi that varies over single trials, but that both EEG and behavioral model likelihoods (\(\mathcal {F}\) and \(\mathcal {G}\)) share some common parameters Γ and both predict single trial data. These are models that can be fit in using MCMC procedures, and similar joint models of EEG and behavioral data have been proposed (Nunez et al., 2022):
However, the key difference between this model framework and our proposed model framework is that the single-trial data is completely independent. That is, the same parameter estimates will result from a random permutation of the single-trial index i for EEG data Z if the single-trial index of behavioral data X remains the same. This essentially implies that the EEG data and behavioral data in these traditional integrative models are not assumed to be related on single-trials. This is not true of our proposed models which share a joint (estimated) likelihood on the single-trial level. A random permutation of EEG data will result in different parameter estimates in our framework. We will show later that these parameter estimates are intuitive in our specific models, and that the true relationship between behavioral data X and EEG data Z can also be assessed with our modeling framework.
Assuming Two Sources of Variance in Single-Trial EEG
In directed models, it is intrinsically assumed that the independent variable, the EEG measure Z, is a perfect descriptor of the true neural signal (see Fig. 2). However, for most electrophysiology and brain imaging, a perfect measure of the brain is unrealistic. This is especially true for EEG where derived measures of EEG are expected to be influenced by muscle and electrical artifacts, even when the measure of EEG is somewhat robust to artifact (Nunez et al., 2016). While other forms of integrated neurocognitive models could be beneficial for studying human cognition (see Appendix), the key benefit of our frameworks is that these models contain at least one source of measurement noise for the EEG measures, σ2, as well as variance in the underlying cognition that can change across trials s2. By measurement noise, we mean the combination of electrical noise, artifacts due to EMG, and unrelated cognitive processes embedded in all measures of EEG (Whitham et al., 2007; Nunez et al., 2016). Measurement noise is especially relevant for EEG on single trials (Bridwell et al., 2018) because we are often not using measures that are robust to EEG artifacts, like trial-averaged ERPs (although even trial-averaged ERPs are not completely robust to artifact either) (Nunez et al., 2016). Note also that preprocessing steps for EEG measures often have many degrees of freedom (Clayson et al., 2021), and therefore models should provide some quantification of the amount of relevant cognition described by single-trial EEG measures compared to the amount of extraneous information.
One would expect that both sources of variance, measurement noise and variance related to cognition, could contribute to the single-trial EEG. In our models, we operationalize the sum of these two sources of variance (e.g., (γ2s2 + σ2) in model 2) to describe the variance in the observed EEG measure for every trial i. However, only the variance in the underlying cognition (e.g., s2 in model 2) also describes the behavioral data. Therefore, an important property of these models is that they can assess the amount of variance in single-trial EEG related to cognition, given by the fraction of variance r. As a specific example, in model 2 (discussed below), the fraction of variance in EEG related to cognition is r = (γ2s2/(γ2s2 + σ2)). We will discuss further assessment of these models below. Note that the exact equation for the fraction of variance varies across models (e.g. r = (s2/(s2 + σ2)) in model 1 and r = (γ2η2/(γ2η2 + σ2)) in model 8.
The Base Evidence Accumulation Process of All New Models
The base processes that describe a portion of behavior and EEG data in our models are drift-diffusion models (DDMs) (Ratcliff, 1978; Ratcliff & Rouder, 1998; Ratcliff & McKoon, 2008). However, this framework can easily be extended with various other decision models (e.g., Usher & McClelland, 2004, Brown & Heathcote, 2008, Hawkins et al., 2015, Voss et al., 2019, van Ravenzwaaij et al., 2020, Hawkins & Heathcote, 2021), especially when using BayesFlow, because the base DDM can be replaced with any decision-making process that can be simulated. DDMs presume that participants integrate continuous information during choice tasks via a Wiener process (i.e., Brownian motion), typically for one choice over another or a correct over incorrect response. Once enough evidence is acquired, by passing one of two boundaries, a decision is made. This is one of many classes of ‘first pass time distributions’ that share the same boundary crossing properties, such as linear ballistic accumulators (LBAs) (Brown & Heathcote, 2008). Mathematically, this flowing evidence accumulation is assumed to be a diffusion process which can be represented as:
and a form of discrete approximation as a random walk process with a small size time scale for use in simulation in digital computers is as follows:
where \({\Delta } t \rightarrow 0\) is a very small time scale (5 ms or 1 ms in our simulations) that approximates an infinitesimal time step, Xt is the diffusion state, dWt represents the independent increment of the Wiener process, e is noise generated from the standard normal distribution \(\mathcal {N}(0,1)\), the δ parameter is drift rate, and the ς parameter is instantaneous variance (scaling parameter). Note that in simulation-based model fitting, we use 5 ms to approximate the very small time scale Δt. We experimented with using 1 ms to see if this affected model fitting performance, but it did not.
Standard DDMs have four major parameters. The first parameter is the amount of evidence required to make a decision, which is denoted by α. Psychologically, when this parameter is changed, it can index a speed-accuracy trade-off (Ratcliff & McKoon, 2008; Hanks et al., 2014). The second parameter is the drift rate of the diffusion process. It is the mean rate of evidence accumulation within a trial which is denoted by δ, and psychologically, it is determined by the quality of the stimulus. The third parameter β is the start point of the evidence accumulation path within a trial, shown to empirically reflect bias in a decision (Voss et al., 2004; Bowen et al., 2016). The fourth parameter is the non-decision time. It is often assumed to be only the summation of encoding and execution time (Ratcliff, 1978; Voss et al., 2015), although this assumption has rarely been tested (Ghaderi-Kangavari et al., 2022). Total non-decision time is denoted by τ. One additional parameter is sometimes estimated (Nunez et al., 2015, 2017), the instantaneous variance within a trial, “diffusion coefficient” ς. However, we fixed ς = 1 for all parameter recoveries.
Some integral formations have been derived to capture intrinsic trial-to-trial variability of the cognitive parameters in DDMs. However, only certain model likelihoods have known integral solutions. For instance, there is a an exact solution to estimate the four main variables (δ, α, β, τ), in addition to the trial-to-trial variance in the drift rate η. This is achieved by assuming a normal distribution of the nuisance parameter and integrating out the nuisance parameter (see Tuerlinckx 2004; Voss et al., 2015, for more information). Note however that in the simulation approach to fitting models using BayesFlow, it is acutely convenient to add across-trial variability parameters.
The General Structure of All New Single-Trial Integrative Models
Figure 3 provides a graphical description of the overview of the example neurocognitive models, including the relationship and difference between them, in the paper. Schematically, we use only the simulation statements to describe the models. However, each model is defined by both priors (listed below) and implicit likelihoods derived from the simulation statements. A common sampling statement is given by \(r_{i}, x_{i} \sim DDM(\lambda _{i}, \mathbf {\Theta } )\) which refers to a drift-diffusion model with single-trial nuisance parameter λi (either single-trial non-decision times τ(e)i or single-trial drift rates δi) and additional parameters Θ. The specific parameters will be defined in each sampling statement. Here, ri is the response time and xi is accuracy, coded with 1 for correct response and − 1 for incorrect response. Also, zi denotes the EEG measure in each model. Note that x, r, and z change on each trial i and for each participant.
Our methods here could be considered extensions of models by Ratcliff and others (Ratcliff et al., 2016) that allow trial-to-trial variability in the cognitive model parameters. These models are also similar to previously published directed models in which the single-trial EEG data describes trial-to-trial variability in the model parameters through embedded linear linking functions to cognitive parameters (Frank, 2015; Nunez et al., 2017; Ghaderi-Kangavari et al., 2022). However, the models proposed here allow some of the noise in the EEG to be described by measurement noise unrelated to behavior, thus improving the ultimate reflection of the true process and improving the estimation of single-trial behavior and EEG. Note that estimating the trial-to-trial variability parameters of DDMs is difficult with MCMC methods (Boehm et al., 2018). Using the current neurocognitive models and deep learning approximations of posteriors, parameters encoding across-trial variability of non-decision time and drift rate can be recovered well and conveniently.
We present specific models to represent specific hypotheses in the neurocognitive decision-making literature. However, many of our models could also be considered extensions of simple linear regressions on single-trial nuisance parameters. For instance, if we consider λi to be a specific nuisance cognitive parameter of a DDM that changes on each trial i that describes both choices xi and response times ri, then we can assume that the EEG measures zi come from linear regression with the nuisance parameter as the predictor variable. That is \(z_{i} \stackrel {\text {\textit {sim}}}{\sim } \mathcal {N}(\gamma \cdot \lambda _{i} + \rho , \sigma ^{2})\), where γ is the effect of the single-trial cognitive parameter on EEG, ρ is the residual mean cognitive variable unexplained by EEG, and σ2 is the measurement noise in EEG unexplained by this cognitive variable. Note that in some models we have performed parameter transformations and reordering of variables to reflect hypotheses in the neurocognitive literature. Also note that in some models γ = 1, such as in the class of model 1 which assumes single-trial N200 latencies are described by an additive component of non-decision times. While in some models ρ = 0, such as in model 8 which describes single-trial CPP slopes as scaled descriptors of drift rates. Unless otherwise specified as fixed, all parameters on the right side of distributional statements are free model parameters to be estimated.
Basic Single-Trial Integrative Models That Describe N200 Latencies
One idea, which has been used in our recent work (Nunez et al., 2019; Ghaderi-Kangavari et al., 2022), is that N200 peak-latencies can separate measures of visual encoding time (VET), τe from other non-accumulation times during decision making, e.g., motor encoding time (MET), τm. The following models were designed to test and use this idea with N200 latencies as the EEG data, although the models could also be used with other EEG data types. We will consider the separation of VET and MET in the first set of new models, such that they do not depend upon the assumption that single-trial N200s exactly reflect the onset of VET but are instead driven by VET with measurement noise.
The first, most simple, integrative joint model, model 1a, adds two sources of variance: measurement noise of EEG measures σ2 and variance related to non-decision time on single trials \(s_{(\tau )}^{2}\) to a DDM framework. This model assumes that one source of across-trial variance in non-decision time is contained in an EEG measure and that this source of variance in non-decision time is additive to fixed non-decision time across trials. For instance, we could use this model if we presume that the sources of non-decision time variance arise from the variance of visual encoding time, which is also reflected in N200 latencies, and not other sources of variance. However, note that this model is more general than this specific case:
Note that we assume normal distributions for both the EEG generation from single-trial cognitive variables as well as the generation of across-trial variance in non-decision time itself. We use normal distributions to be most flexible for various EEG inputs, and not because we think the normal distribution is the true data generation process of N200 latencies. We test these assumptions in simulation and with real data, see “Robustness to Model Misspecification and Fitting the Proposed Single-Trial Neurocognitive Models on Experimental Data.” It is important to observe that the mean non-decision time across-trials is τ = μ(e) + τ(m), where μ(e) reflects the mean EEG measure and τ(m) reflects the residual non-decision time after subtracting the mean EEG measure across trials. The key point here is that the posteriors of parameters reflecting cognitive-variability across trials \(s_{(\tau )}^{2}\) and measurement noise across trials σ2, and the percentage variance resulting from a transformation of these measures, are more informative about the true relationship between EEG and behavior than the mean parameters (see discussion below). In this particular additive model of non-decision time, the mean parameter μ(e) reflects the mean EEG measure and the residual parameter is just the mean non-decision time minus the mean EEG measure: τ(m) = τ − μ(e).
A specific example is the case of the N200 latencies reflecting visual encoding time (VET) (Nunez et al., 2019). In this case, we might expect μ(e) to reflect the mean visual encoding time (and N200 latencies) across trials, while the residual non-decision time τ(m) would reflect the motor execution time (MET). Thus, τ(e)i would reflect the fact that visual encoding time depends on both trials and individual levels. The residual non-decision time τ(m) would reflect MET that does not change trial-to-trial.
It should be noted that the above formulas can be transformed by instead parameterizing the models with a single-trial non-decision time τi = τ(e)i + τ(m). This model, labeled model 1b has the following form:
As it turns out, model 1b is just a more specific case of the embedded linear regressions framework presented in “The General Structure of All New Single-Trial Integrative Models,” where γ = 1. Note we do not consider model 1b to be truly different from model 1a. However, we tested whether parameter recovery would be different between the two parameterizations.
Because of the positive quantity of N200 latencies, we should confine them to a specific time window, for instance, a window from 50 to 500 ms. Therefore, we also constructed a neurocognitive model based on model 1b to evaluate whether using a truncated normal distribution \(\mathcal {T}\mathcal {N}(.)\) lies within the interval (a,b), as well as a uniform distribution \(\mathcal {U}\)(.) for non-decision time variability, can be identifiable well. The following equations reflect model 1c:
where the mean and variance of the uniform distribution in Eq. (8c) are the same as the mean and variance in Eq. (7c) in model 1b.
An obvious extension to model 1a is one in which the component of non-decision time that changes trial-to-trial τ(e)i describes a portion of the EEG variance up to a certain scalar value γ, called an “effect” parameter. We therefore propose model 2 which changes only the second equation from equation set Eq. (6a) to \(z_{i} \stackrel {\text {\textit {sim}}}{\sim } \mathcal {N}(\gamma \cdot \tau _{(e)i}, \sigma ^{2})\). In previous work, Nunez et al. (Nunez et al., 2019) discovered some evidence of a 1 to 1 ms (albeit noisy) relationship between non-decision time and N200 latencies. This evidence was, in part, shown using Savage-Dickey density ratios (Wagenmakers et al., 2010) to estimate Bayes Factors (van Ravenzwaaij & Etz, 2021) that compare the hypothesis of a slope of 1 in the linear link function of a directed neurocognitive model. In this new model, we also use the Savage-Dickey density ratio to test the relationship between N200 latencies and non-decision time by again testing whether γ = 1.
Extensions of Models That Describe N200 Latencies
Researchers often use cut-off values to truncate behavioral data in order to remove so-called contaminant data. For instance, for decision-making, these include slow outlier response times (RTs) and fast-guess responses (Vandekerckhove & Tuerlinckx, 2007; Ratcliff & Kang, 2021). Removing RTs outside a window from around 150 to 3000 ms has been frequently deployed, as well as using an exponentially weighted moving average to find an optimal lower cutoff (Vandekerckhove & Tuerlinckx, 2007). Ratcliff and Tuerlinckx proposed a mixture distribution model between standard DDM and a contaminant lapse process described by a uniform distribution to estimate a certain proportion of contaminant data (Ratcliff & Tuerlinckx, 2002). Recently, to describe response times due to fast guesses, Ratcliff and Kang have proposed a mixture of DDM and a normal distribution that describe some properties of observed choice-RT data that could not be easily described by DDMs alone (Rafiei & Rahnev, 2021; Ratcliff & Kang, 2021). Therefore, in neurocognitive models, we may would like to estimate automatically the amount of contaminated data, including very fast responses (e.g., due to lack of attention), very slow responses (e.g., due to mind wandering), and some other possible contaminant data that arises from the research environment. As an example, we propose a mixture model of the neurocognitive model and uniform distribution (\(\mathcal {U}\)), labeled model 3, with a new certain parameter 𝜃(l) describing the probability of a lapse process, and the resulting eight cognitive/computational parameters:
where max(r) is the maximum observed response time over a vector of response times r. Note that we have encoded both a Bernoulli(0.5) choice (with the mathematical convenience of encoding each choice x with a − 1 and 1 and then multiplying by the response time) as well as a uniform \(\mathcal {U}\) response time from 0 ms to max(r). The 𝜃 parameter represents the probability of a lapse response and exists only in the [0,1] interval.
Trial-averaged ERPs are somewhat robust to contaminants since averaging can increase signal proportions and decrease noise. However, single-trial EEG analysis often relies on the development of specific signal processing techniques (e.g., independent component analysis) (Shlens, 2014). Thus, single-trial EEG data could be contaminated with external noise (equipment and environmental sources) and internal noise (head motion, eye blinking, etc.). To handle possible contaminated data in EEG measures, that is not due to simple measurement noise as encoded by σ parameters in previous models, we may wish to find the percentage of data that is described by a relationship to EEG. Thus, to manage different sources of variance in single-trial N200 latencies, the following neurocognitive model, labeled Model 4a, is proposed which has seven free parameters:
where τ is non-decision time parameter (visual encoding time and motor execution time), \(\sigma ^{2}_{(e)}\) is the measurement noise in z (N200 latencies) when observed values arise from the neurocognitive model, \(s^{2}_{(\tau )}\) is across-trial variance in non-decision time when observed values arise from the neurocognitive model, and v and \(\sigma ^{2}_{(v)}\) parameters are the mean and variance of z (N200 latencies) when observed values are not derived from the neurocognitive model.
As it turns out, the 𝜃 parameter can detect the existence of the relationship between the brain and behavior, measuring the proportion of experimental trials that come from the neurocognitive model and what proportion that cannot be examined by the neurocognitive model. In fact, model 4a represents a new approach for comparing two competing models across experimental trials. In this case, a neurocognitive model versus two simple models: a DDM that describes the behavioral data ri,xi and normal distribution of EEG measures zi. That is, the first mixture is model 1a as a neurocognitive model and another mixture is the following model as a cognitive model:
We used model 4a as the joint mixture model to see the amount of actual relationship between neural data and behavior across trials, as discussed below. This model has eleven parameters, but for better recovery, we reduced the number of parameters to nine parameters. In model 1a, the variance of the EEG measures zi in the first mixture is \(s^{2}_{(m)} + \sigma ^{2}_{(e)}\) while the variance of the EEG measures in the second mixture is an independent parameter, \(\sigma ^{2}_{(v)}\). Therefore, we removed a free parameter by forcing the variance of the second mixture to be the same as the first. We similarly forced the non-decision times and mean of EEG measures to be the same in both mixture distributions. The equations of the reduced model 4b are as follows:
Models with Collapsing Boundaries
Drift-diffusion models with collapsing boundaries encode participant behavior such that participants require less and less amount of evidence to trigger a decision as time passes (Drugowitsch et al., 2012; Hawkins et al., 2015; Forstmann et al., 2016; Ratcliff et al., 2016). Mathematical models with collapsing boundaries have gained remarkable attention in some experimental and theoretical accounts. Such models outperform the fixed boundary DDM in certain circumstances and implement optimal decision-making (Ratcliff et al., 2016; Drugowitsch et al., 2012; Evans et al., 2020a). Other evidence for the accuracy of these models has been mixed in the literature. Hawkins et al. (Hawkins et al., 2015) consider both types of models for humans and nonhuman primates over three different paradigms and then by applying using model-selection methods showed that fixed boundary models are generally better than collapsing boundaries, although there is occasional evidence for a collapsing-bound DDM. These authors also concluded that models with collapsing boundaries are not a descriptive model for the majority of human participants, while they can be useful for interpreting the underlying components of non-human cognition. Moreover, Voskuilen et al. (Voskuilen et al., 2016) found that the fixed boundary model was superior to the collapsing boundary model for all data obtained from numerosity discrimination experiments and motion discrimination experiments in human subjects. Voss et al. (Voss et al., 2019) compared six distinct types of accumulator models based on Wiener diffusion, Cauchy-flight, and Lévy-flight models in four number-letter classification tasks to examine if decision bounds can be dynamic over times. They found some evidence in favor of collapsing boundary rather than a fixed boundary. Also, Evans et al. (Evans et al., 2020b) evaluated five different collapsing boundary models based on DDM, linear ballistic accumulator model (LBA), and urgency gating model and then found out the linear collapsing boundary for DDM can fit better in caution/urgency modulation as well as an urgency-gating model with a leakage process. It has also been shown that the drift-diffusion model with a time-variant boundary can well explain both behavioral and neural electrophysiological data in non-human primates (Roitman & Shadlen, 2002; Ditterich, 2006). Smith et al. (Smith & Ratcliff, 2022) showed that the standard DDM was the best model for conditions with constant stimulus and time-variant boundary models were similar to the standard DDM on changing-stimulus conditions.
Most of the findings support the idea that models with collapsing boundaries are optimal for animal’s cognition, in accordance with the idea that adept animals, which are trained on fixed juice feedback, adjust their behavior with urgency (Smith & Ratcliff, 2022). As a result, regardless of whether collapsing boundaries are optimal for humans and some paradigms or not, we deploy the use of collapsing boundaries and analyze their parameter recoveries as a generalization of our neurocognitive models.
We expand the previous neurocognitive models to include collapsing boundary models that allow for decreasing evidence used to make a decision over time. These models are the same as model 1a with collapsing instead of static boundaries. Specifically, we implemented two types of collapsing boundary models: linear and Weibull functions (Voss et al., 2019; Evans et al., 2020b). These are labeled model 5, with seven free parameters, and model 6, also with seven free parameters, respectively (Evans et al., 2020b; Voss et al., 2019).
The linear collapsing boundary is instantiated as follows:
where aslope is the slope of the linear collapsing boundary, α is the initial boundary value before any time elapses, u(t) is the upper threshold, and l(t) is the lower threshold.
A scaled Weibull cumulative distribution function describes the collapsing boundaries in model 6:
where u(t) is the upper threshold and l(t) is the lower threshold. The parameter k indicates the shape of collapse (early vs. late). Also, ω is the scale parameter and shows the onset at which the collapse begins, d encodes the amount of collapse, and finally α again represents the initial boundary before any time elapses. We fixed parameters of k = 3 and d = − 1.
Single-Trial Integrative Models That Describe CPP Slopes
In this section, we propose an integrative neurocognitive model that predicts CPP slope is related to the rate of accumulation evidence variable on single trials. The following model 7 assumed that trial-to-trial variability of drift rate parameters at the model level comes from CPP variance at ERPs signals as well as there is source noise of CPP slope which is denoted by the parameter c as follows:
In one final model, we impose a γ = 1 effect of CPP slope, changing the second equation of Eq. (17a). This results in \(c_{i} \sim \mathcal {N}(\gamma \cdot \delta _{i}, \sigma ^{2})\), i.e., model 8. Note that both models are specific forms of linear regressions presented in “The General Structure of All New Single-Trial Integrative Models,” with trial-to-trial drift rate δi as the nuisance variable λi. In the models of the previous sections, the nuisance parameter was trial-to-trial non-decision time τi or an additive non-decision time component τ(e)i for the same fit.
Traditional Integrative Models That Describe N200 Latencies
As a comparison to our models built in our new single-trial integrative framework, we also fit some similar traditional integrative models using BayesFlow. The models in this section predict single-trial behavior and EEG data but are not described by (estimated) joint likelihoods. Therefore, a random permutation of one of the data types will result in the same model fit. This type of model is shown in Fig. 2b. In these models, we replace the \(\stackrel {\text {\textit {sim}}}{\sim }\) notation with the \(\sim \) notation because these models can all be fit using MCMC algorithms and do not need to be directly simulated for model inference. Thus, they can be directly written in languages such as Stan for specific MCMC algorithms. However, we used BayesFlow for fitting the traditional integrative models in order to directly compare to previously described single-trial integrative models that were fit using BayesFlow.
The first model is analogous to model 1a. This non-single-trial integrative neurocognitive model has six parameters, labeled model 9. This model assumes that both behavioral and brain data are independent at the level of single trials, but it assumes that a non-decision time component τ(e) (for instance VET) describes EEG on single trials. Mathematically, the model equations are as follows:
As already pointed out, integrative neurocognitive models can be divided into two groups based on how two neural and behavior modalities constrain each other (see Fig. 2): first, those models that have shared parameters on a group level but predict independent behavior and neural data on the single-trial level, and second, those models that produce dependent data on the single-trial level. For instance, model 9 has two independent relations which constrain the non-decision parameter. It means that both sets of random variables of Xi = {ri,xi} and Zi = {zi} are independent on single trials. Therefore, by permutation of zi across trials, the same posteriors will be estimated for all parameters.
Meanwhile, there is another issue that should be highlighted here. Actually, another problem with model 9 is that it cannot provide any inference about the relationship between EEG measures and behavior. This is because τ(e) provides an estimate of the mean EEG measure that is not constrained at all by the non-decision time τ = τ(e) + τ(m), because the estimate of τ(m) will just be the estimate of non-decision time τ from behavior while τ(m) = τ − τ(e). Note that in the class of model 1, we can judge the relationship of EEG to behavior by exploring the posterior distributions of \(s_{\tau }^{2} / (s_{\tau }^{2} + \sigma ^{2})\), which does not exist in model 9.
Now, consider the following model, labeled model 10, with an additional parameter γ, ostensibly to solve the aforementioned problem:
When proposing a new neurocognitive model, it is important to note that the model’s parameters must be constrained by data in order to draw inference about the parameters. In the above model, it is obvious that this model is not a single-trial model; thus, the random variables ri,xi and the random variable zi are independent statistically. From the neural data zi, we can estimate both the mean (μ) and the variance (σ2 ) of the normal distribution, and on the other hand, by the random variables ri,xi, we can estimate non-decision time from DDM, which is the sum of τ(e) and τ(m). Thereby, the following two relations are introduced:
It should be noted that there are three variables and two equations which make it impossible for each parameter to be recovered perfectly. Figure 24 is the result of the parameter recovery of model 10. As we expected, the latent parameters can not be recovered and so this model cannot inform us at all about cognition nor the brain-behavior relationship.
Traditional Integrative Models That Describe CPP Latencies
To build a traditional neurocognitive model with CPP slope, we used the following model, model 11, to constrain the drift rate by CPP slope for each participant. In fact, CPP is denoted by parameter ci as follows:
We also tested the following neurocognitive model that predicts CPP slopes on single trials are described by both the mean drift rate and trial-to-trial variance in drift rate. Therefore, we use the following model, model 12:
The above model assumes that single-trial CPPs are explained by both the mean and variability of the drift rate, but single-trial CPPs and choice-RTs are still independent. Remember that both model 11 and model 12 are traditional integrative models in that they predict the same parameters for a random permutation of either the choice-RT pair (ri,xi) or CPP slopes ci with respect to the other data.
Directed Joint Models That Incorporate N200 Latencies
Directed joint models are another approach to constrain both behavioral data at the single-trial level. Recently, a new linear formation of τi = τ(e)i + τ(m) = λ ⋅ zi + τ(m) has been proposed to describe behavioral data directly by both cognitive parameters and neural data (Nunez et al., 2019; Ghaderi-Kangavari et al., 2022). Although note that these models do not describe neural data. More precisely, these approaches are able to make predictions of behavioral data with only neural activity, but cannot easily predict neural data from behavioral data. Parameter τ(m) is residual of the linear formation, assumed to represent MET (Nunez et al., 2019; Ghaderi-Kangavari et al., 2022), λ is the effect of N200 latencies on single-trial non-decision times and the zi parameter represents the N200 negative peak latencies for each trial, such that λ ⋅ zi is assumed to represent VET. This model has seven (non-nuisance) parameters, labeled model 13:
where μ(z) is the mean of N200 latencies.
In the above neurocognitive model, the single-trial non-decision time variability is related to the N200 latencies single-trial variability. This means that the source of the non-decision time variability is assumed to come only from variability in a noiseless neural measure. Therefore, this model is only more appropriate than model 2 if we expect the EEG measure z to reflect the true cognitive process without noise. To calculate the variability of τ, consider the following equations:
Therefore, in this model, the trial-to-trial variability of non-decision time is given by s(τ) = λ2 ⋅ σ2, which is also true of model 2 above.
Priors
We assume “weakly informative” prior distributions for all models (Gelman et al., 2014). For model 1a, model 1b, and model 1c, we assume uniform distributions as the following the prior distributions:
It is important to note here that the parameters shared by the models presented here had the same prior distributions. For instance, model 2 has an additional parameter γ with prior distribution \(\gamma \sim \mathcal {U} (0,3)\). Other parameters, which are similar to parameters in the class of model 1, have the same prior distributions. For the sake of brevity, for the following models, we do not mention prior distributions that were previously mentioned in a previous models. Model 3 contains a prior distribution of the lapse parameter as \(\theta _{(l)} \sim \mathcal {U} (0,0.3)\). Other parameters, which are similar to parameters in the class of model 1, have the same prior distributions. Model 4a has additional prior distributions \(\tau \sim \mathcal {U} (0.1,1)\), \(\sigma _{(v)} \sim \mathcal {U} (0,0.3)\), \(\sigma _{(e)} \sim \mathcal {U} (0,0.3)\), \(v \sim \mathcal {U} (0.04,0.4)\), and \(\theta _{(m)} \sim \mathcal {U} (0,1)\). Also, model 4b has additional a prior distribution \(\theta _{(m)} \sim \mathcal {U} (0,1)\). On the other hand, model 5 contains a prior distribution of \(a_{\text {slope}} \sim \mathcal {U} (0.01,0.9)\). For model 6, it contains a prior distribution of \(\omega \sim \mathcal {U} (0.5,4)\). For model 7, we assume uniform distributions as the following the prior distributions:
Model 8 has an additional prior of \(\gamma \sim \mathcal {U}(-3, 3)\). Also, for this model has the parameter β = .5. Other parameters, which are similar to parameters in model 7, have the same prior distributions. Note that we used a wider prior for the parameter γ in model 8 compared to the range of γ in model 2. This is because negative CPP slopes are reported in the literature (e.g., see van Vugt et al., 2019) and thus negative γ estimates were assumed to be possible.
For model 9, we also assume uniform distributions as the following the prior distributions:
Model 10 has an additional prior of \(\gamma \sim \mathcal {U}(.1, 4)\). Finally, by viewing Figs. 25, 26, and 27 in the Appendix, the range of parameters will be clear.
Recovering Parameters from Simulated Models
Results of parameter recovery reveal whether the proposed models reliably recover true parameters. We first tested whether our model fitting procedure can extract reliable parameter estimates for the data given that the data is generated from the same model. Then we tested whether the some models are robust to slight model misspecification, another important test of models and model fitting procedures before being applied to real experimental data. These procedures indicate whether the estimation method and the neurocognitive assumptions can successfully apply to real data.
We used point parameter recovery to assess how well the posterior mean of a proposed neurocognitive model resembles data-generating parameters. In Bayesian statistics, parameter recovery is conceptually beyond point recovery, so we also report the uncertainty of parameter approximations parameters as well as coverage percentages of free posterior.
Training the Model Fitting Procedure
We train neural networks in BayesFlow via experience-replay learning. Experience-replay learning has had success recently within the deep learning community and is a type of reinforcement optimization which uses a replay memory technique to store trajectories of experiences (Sutton & Barto, 2018). This technique will keep an experience replay buffer from past simulations for taking samples randomly for each iteration, so the networks will likely use some simulations multiple times. This training can efficiently simulate data on-the-fly for fast generation and is optimal in comparison to pure online training (Radev et al., 2020a). By increasing the number of epochs and iterations of deep learning, the parameters gradually become more convergent. In the training phase, we used 500 epochs, 1000 iterations per epoch, a batch size of 32, and a buffer size of 100 for the hyperparameter of memory for training weights of the deep learning structure. Also, we simulate a variable number of trials from 60 to 300 trials from a uniform distribution during the training phase. Note that we purposefully use a small number of trials in order to explore parameter recovery of realistic observation counts in real data. More precisely, we train these neural networks only in one training period with the same prior distributions, and then we generate posterior distributions from the trained neural networks in each subsequent analysis (including fitting real data in the next section).
Models Recover Simulated Parameters Accurately
Here, we generate figures of true parameters plotted against parameter posterior estimates and credible intervals. These parameter recovery figures are generated using 100 simulated datasets with 300 simulated trials each. It should be noted that we obtain 2000 samples from posteriors in the inference phase. Figure 4 as well as Figs. 13 and 14 in the Appendix show parameter recovery of the seven parameters from model 1a, model 1b, and model 1c, respectively, with the x-axis as true parameters and the y-axis as posterior distributions. Each figure includes the mean, median, 95%, and 99% credible intervals related to each data point of parameters. Also, Figs. 15, 16, and 17 in the Appendix represent the result of parameter recovery for model 2, model 3, and model 4a, respectively. Another parameter recovery figure can be seen in the Appendix is Fig. 18, which corresponds to model 4b with 100 datasets and 1000 trials for each. Looking further into the Appendix, it is clear that this parameter recovery approach is clearly confirmed for other proposed models in the same procedure. For instance, we observe that Figs. 19 and 20 show the results of parameter recovery of model 5 and model 6, respectively. In addition, for models including CPP slope results, Figs. 21 and 22 in the Appendix are related to model 7 and model 8, respectively. We used the fixed parameter β = .5 from model 8 to provide the accuracy-based model fitting of data in “2.” Furthermore, Figs. 23, 24, 25, and 26 in the Appendix represent the parameter recovery of traditional integrative joint modeling related to models 9, 10, 11, and 12. Finally, Fig. 27 presents the parameter recovery of the directed joint modeling of model 13.
The plot of true parameters versus posteriors of estimated parameters for model 1a. The x-axis of each graph are simulated parameters and the y-axis represents posterior distributions. The mean of the posteriors is shown by teal star symbols and the median of the posterior of parameters is shown by black circles. Also, uncertainty of parameters is indicated by 95% credible intervals (dark blue lines) and 99% credible intervals (green lines). Note that the orange line is the function of y = x, where we expected recovered posterior distributions to be centered. The estimated parameters follow the orange line, corresponding to the true recovery of these parameters
We also assess the performance of the current models in parameter recovery by calculating R2, the normalized root mean square error (NRMSE) statistic, and the coverage percentages of 95% and 99% credible intervals derived from the posterior distributions of each parameter. In fact, we use the estimated posterior means and the ground-truth parameter values to calculate both R2 and NRMSE measures. Note that using only the posterior mean is not mandatory and the full joint posterior should be used for model-based predictions. The R2 measure, also known as the coefficient of determination, evaluates how well the model explains the variability of the grand-truth parameters, while the NRMSE measure represents the standardized prediction errors, which facilitates the comparison between models of different scales. Mathematically, NRSME and R2 formula are defined as:
where \(\hat {y}_{i}\) are the posterior means, yi are the ground-truth parameters, and \(\max \limits (\mathbf {y})\) and \(\min \limits (\mathbf {y})\) are the maximum and minimum of the ground-truth parameters, respectively.
In Table 1, these statistics to assess the performance of each neurocognitive model in recovering true parameters are reported. Note that both R2 and NRMSE statistics are calculated using the mean posteriors of parameters and true parameters. The coverage percentage of a specific parameter represents the number of datasets whose parameter’s credible interval contains the true parameter. The coverage percentages for 95% and 99% credible intervals are calculated in Table 1. We expect that 95% and 99% of simulated datasets have true parameters which are located inside 95% and 99% of the credible interval respectively. Furthermore, we developed simple metrics to express the uncertainty of estimated parameters by calculating the (1) mean of the variances of the estimated posterior distributions as well as (2) the variance of the variances of the estimated posterior distributions. Table 8 in the Appendix contains these values.
Looking more closely at Table 1, it can be seen that the majority of the current models’ parameters are exceptionally well recovered, although a number of parameters have challenges in recovery. If there are few trials with no single-trial relationship, the recovery of cognitive parameters in model 4a will be inaccurate. However, by decreasing the number of parameters in model 4a to model 4b, the uncertainty of estimated cognitive parameters was shortened (see Figs. 17 and 18). However, overall, the results show that many of the parameters of the proposed models can be recovered with real data to obtain information about the neurocognitive process.
The Proportion of Cognitive Variance in Permuted and Non-permuted EEG Measures
We probe how associations of single-trial choice-RTs and EEG measures affected posterior distributions when fitting the neurocognitive models to simulated data. The current single-trial integrative paradigm has two different sources of variance that explain variance in EEG measures: cognitive variability s2 (or γ2s2 in model 2) and EEG measurement noise (or noise not associated with cognition) σ2. We found that the posterior ratio r = s2/(s2 + σ2) of these parameters provides some information about the degree to which single-trial EEG measures explain cognition.
To do so, we simulate model 1a but then randomly permute the index of the EEG measures across trials compared to the index of choice-RT. Thus, the EEG and behavioral data are no longer paired per trial (see Fig. 5). We then fit the permuted data using our model fits above. We generate 100 datasets with 500 simulated trials for each dataset and then take 5000 samples from the posteriors in the inference phase. Figure 6 shows the percentage of EEG measures explaining cognition related to both real and permuted EEG measures. The model fit of the permuted data provides larger estimates of EEG measurement noise (σ) and smaller estimates of cognitive non-decision time variability (\( s_{(\tau )}^{2}\)) than the model fit of the original data. Thus, the model fit of the permuted data results in smaller estimates of the proportion of cognitive variance r than in the non-permuted data.
Regressions of EEG measures versus response times simulated from model 1a when we permute EEG measures compared to response times as well as the original simulation data. We picked five datasets drawn at random from five parameter sets. Each dataset was simulated with a different parameter set from model 1a resulting in 1000 trials for each dataset
The proportion of EEG variance explaining cognition of model 1a. Left: Posterior distributions of r = s2/(s2 + σ2) when we fit the model to the original simulated data. Right: Posterior distributions of r when we permuted EEG measures before fitting model 1a to the original behavioral and permuted EEG data. See the caption of Fig. 4 for additional details of these plots
These results imply that the fitted model not only describes latent cognitive variables under the assumption of the model given the data but can also be used to discover the relationship of EEG to behavior. Thus, in model 1a fits of experimental data, posterior means of r ≈ .27 (95% credible interval of mean posteriors across 1000 simulations) and below could be considered evidence that EEG and behavior data are not related on the single-trial level (see Fig. 6). Note however that EEG and behavior data may or may not be related to the participant or condition level if r < .27. Note also that the observed empirical cutoff is not r = 0, likely because there is true trial-to-trial variability in non-decision time that described behavior better than fixed non-decision time. Figure 5 illustrates the comparison of simulated and permuted EEG across trials compared to simulated (non-permuted) RT for five random datasets with different parameter sets. As a comparison, Fig. 28 in the Appendix demonstrates the regression between simulated (no-permuted) EEG measures and response times collapsed across 100 datasets and 1000 trials from each dataset collapsed across datasets, simulated from model 1a. However, note that a more extensive discussion on model comparison can be found in the section below.
Figure 29 in the Appendix displays parameter recovery in the model when EEG measures are permuted for many different parameter sets in one figure. It should be noted that we use 100 datasets and 500 trials for each dataset to estimate posteriors of parameters (with 1000 posterior samples each).
Robustness to Model Misspecification
The proposed neurocognitive models, like any cognitive model, have specific assumptions. However, we expect some of those assumptions could be robust to various model misspecifications. Therefore, for a subset of models, we keep the original assumptions when fitting data (and thus the original trained neural networks) using slight differences in the simulated data. The robustness tests fell into two categories: robustness to normal distributional assumptions and robustness to contaminant processes.
In the first set of robustness tests, we test the robustness to normal distributional assumptions. In one misspecification, we fit model 1a to sets of simulated data where various Gamma distributions, \(\mathcal {G(\alpha , \beta )}\), with shape parameter \(\alpha = \mu _{(e)}^{2} / s^{2}_{(\tau )}\) and an inverse scale parameter \(\beta = \mu _{(e)} / s^{2}_{(\tau )}\) which are used to simulate the single-trial non-decision times τ(e)i. Note that we calculate the non-decision time variability \(s^{2}_{(\tau )}\) and the mean directly from the simulated Gamma distribution parameters. The deviation of the Gamma distribution from normality can be summarized in part by the kurtosis, such that normal distributions always have a kurtosis of 3. The mean and standard deviation values of the kurtosis of the Gamma distributions were approximately 10.30 and 16.05 across simulations. Figure 7 shows the parameter recovery when Gamma distributions were used to simulate data. By looking at this figure, it can be seen that all parameters are recovered well besides some misestimation of non-decision time variability \(s^{2}_{(\tau )}\) for a few datasets, with the model estimating somewhat lower variability than what was actually simulated.
Parameter recovery when fitting model 1a to a simulation of a similar model with trial-to-trial non-decision time being simulated by a Gamma distribution, \(\tau _{(e)i} \sim Gamma\), instead of a normal distribution as assumed by the model-fitting procedure. See the caption of Fig. 4 for additional details of these plots
We also conduct a robustness test to the normal distribution assumption of N200 latencies zi. Indeed, we apply a Gamma distribution instead of a normal distribution for simulating zi. To do so, we fit model 1a to sets of simulated data where various Gamma distributions with shape parameter \(\alpha = \tau _{(e)i}^{2} / \sigma ^{2}\) and an inverse scale parameter β = τ(e)i/σ2 are used to simulate the N200 latencies zi. The mean and standard deviation values of the kurtosis statistics of the Gamma distributions were approximately 10.40 and 20.84 across simulations. The results are reported in Fig. 32 in the Appendix. Apparently, the parameters are well recovered besides a slight misestimation of mean EEG and the non-decision time variability.
We also investigate the robustness of model model 1a to contaminant processes. In the first such robustness test of model 1a, we simulate a contaminant process where 5% of choice-response times are generated by uniform distribution between 0 and 2 s, while all other parameters are simulated following model 1a (Ratcliff & Tuerlinckx, 2002). Figure 30 in the Appendix reveals that parameters of model 1 with 5% lapse distribution are recovered well with a slight underestimation of extreme drift rates and larger boundaries. The second contaminant process we simulate is one in which of uniform noise within the N200 latencies, with a 5% probability of trial coming from a uniform distribution between 0 and 300 ms instead of the cognitive generation process. Figure 31 in the Appendix shows parameter recovery of this situation. This model recovers parameters incredibly well besides an occasional misestimation of larger boundaries.
Posterior Predictive Checks
One of the main purposes of presenting and assessing different models is to select the most appropriate model for neurocognitive phenomena. The first step would be to conduct a model comparison based on simulated and observed data. Winning models can then be tested in further confirmatory work and tests of selective influence (Heathcote et al., 2015; Lee et al., 2019).
Due to the lack of likelihoods for the models (estimated with the deep learning approach), we cannot report model selection criteria such as Bayesian information criterion (BIC), Akaike information criterion (AIC), Deviance Information Criteria (DIC), Watanabe-Akaike information criterion (WAIC), the effective number of parameters (PWAIC), and log pointwise predictive density (LPPD). Instead, we use data generation to compare models by posterior prediction checks. However, some deep learning approaches estimate the likelihoods of models and therefore could be used for calculating models selection criteria, e.g., (Fengler et al., 2021). Anyway, we think that this is beyond the scope of this work and can be pursued in future work.
To evaluate models without known likelihoods, we focus on posterior predictive checks to choose which model fits well for particular data. The posterior predictive is the distribution over new data (unobserved data) given observed data. Thus, the posterior predictive check predicts new data. Its formula is calculated for replications ypred and the observed data y by integrating out the parameters 𝜃 as follows:
To sample from the above distribution, we first use the BayesFlow deep learning architecture to estimate posteriors of model parameters and then simulate new data under the fitted model.
Moreover, we use a cross-validation paradigm to evaluate a model in which the original dataset is divided into two datasets: training data (in-sample data) and test data (out-of-sample data). In this analysis, we randomly assigned 80% of the trials as in-sample data and 20% of the trials as out-of-sample data. The in-sample prediction is used as an indicator to show the performance of a model because it shows how likely the data used to fit a model is anticipated by the model itself (Blohm et al., 2019; Nunez et al., 2022). On the other hand, out-of-sample prediction can represent the generality of a model, which is one of the main goals of cognitive scientists who intend to introduce a model (Busemeyer & Wang, 2000; Wagenmakers et al., 2006; Nunez et al., 2017; Lee et al., 2019). Actually, out-of-sample predictions are thought to better reflect how much a model can anticipate data that has not been seen before, or how much a model can anticipate similar behavioral performance and neural activity in other experiments.
To do so, we simulate data from the current models with certain parameters, and then split the data with 80% labeled “in-sample” and 20% labeled “out-of-sample.” For example, in model 1a, we consider a certain set of parameters {δ = 1,α = 1.5,β = .6,τ(e) = 0.180,τ(m) = 0.2,σ = 0.05} to generate data from 1000 trials. We next take 2000 samples from posterior distributions of parameters and then use all these samples to generate posterior predictive distributions. The results of model 1a are shown in Fig. 8. In this figure, you can discern how well both in-sample and out-of-sample data matches the posterior predictive distribution, which was estimated only by in-sample data.
Fitting the Proposed Single-Trial Neurocognitive Models on Experimental Data
We used three existing datasets to test the applicability of our new proposed modeling framework. Different analysis methods had been used on all three datasets previously. The first public data set arises from a car-face perceptual decision task by Georgie et al. (2018), which we previously analyzed to see how spatial prioritization can affect latent cognitive parameters. We found evidence with this data that both visual encoding time and other non-decision times can be manipulated by spatial cueing in decision-making (Ghaderi-Kangavari et al., 2022). The second dataset is related to a perceptual decision-making task with some embedded visual signal-to-noise manipulations (Nunez et al., 2019). Nunez et al. (2019) found evidence that N200 latencies were linearly related to non-decision times, with a slope of 1, in different visual signal-to-noise conditions. The third dataset contains CPP slopes estimated on single trials in memory and perceptual decision-making tasks (van Vugt et al., 2019). The goal of this data collection was to test whether CPP slopes are a general EEG signature to track evidence accumulation in multiple task domains (van Vugt et al., 2019).
Face-Car Perceptual Decision-making Task
In this section, we evaluate neurocognitive models related to N200 latencies for some participants who completed a face-car perceptual decision-making task. This data is publicly available (Georgie et al., 2018), and we have previously analyzed this data for another specific purpose (Ghaderi-Kangavari et al., 2022). In this analysis, we estimate the participants’ parameters for models 1–6. We also compare observed data with predicted data by the models to see if the results are reasonable.
In terms of extracting EEG signals to fit the models, we applied some preprocessing steps including down-sampling the raw data, a Butterworth IIR band-pass filter of 1-10 Hz, re-referencing to the average reference, epoching the EEG data into − 100- to 400-ms time segments that are time-locked to the face/car onset, baseline correction, and eliminating irrelevant and noisy components by independent component analysis (ICA). Then, to capture single-trial N200 latencies, we use singular-value decomposition (SVD) for calculating the weighted map on the window from 125 to 225 ms. We then multiply the first or second component of its right singular matrix to the preprocessed EEG in the time window from 100 to 250 ms after stimulus for all 64 electrodes. This results in a single N200 waveform with less noise related to each trial. These steps match our previous work (see Ghaderi-Kangavari et al., 2022, for more details).
Figure 9 shows the single trial N200 histogram, waveform, and a weighted map indicating the positive activation on occipito-parietal electrodes during the single-trial N200s peaks for three example participants (sub-001, sub-003, and sub-006). Also, Table 2 reports the mean and standard deviation (STD) of each parameter related to nine models which capture N200 latencies for a specific participant (sub-003). It is important to note that the values of the parameters across the models are relatively stable. In addition, the proportion of cognitive variance is estimated around r = 0.44 across participants by model 1a. Furthermore, it is important to observe that the result γ ≈ 1 from model 2 in Table 2 seems to support previous results by Nunez et al. (2019), who found initial evidence that N200 latencies track non-decision times with a 1-to-1-ms correspondence.
Weighted maps, waveforms, and distributions of N200 latencies for three participants from the dataset by Georgie et al. (2018). These figures are derived from the first SVD component. The weighted maps in the first column indicate the positive activation of occipito-parietal electrodes during the single-trial negative N200s peaks between 100 and 250 ms after stimulus appearance. In the middle column, shading bands around the bold line is the standard error across trials. Also, the last column shows the distribution of single-trial N200 waveforms. Note that the single-trial estimates (in red) which are boundary effects are not used in the model fitting, see our previous work for more details (Ghaderi-Kangavari et al., 2022)
To clarify even more, Fig. 10 shows posterior prediction distributions of response times and N200 latencies for each model for participant sub-003, in which 5000 samples from posterior parameters and 5000 trials for each sample are used. Figure 33 in the Appendix displays the posterior predictive distributions of response times and N200 latencies for participants sub-001 and sub-006, respectively.
Re-analysis of (Nunez et al., 2019) Data
To further show the reliability and feasibility of the current models, we use all data from (Nunez et al., 2019) in which 14 participants were recruited to perform two different perceptual decision-making tasks. Data from experiment 1 included EEG and behavioral performance with 12 participants, and data from experiment 2 included EEG and behavioral performance with 4 participants. Two participants were common in both experiments resulting in 14 unique participants for both experiments. In order to estimate the N200 waveforms, five steps have been implemented consecutively, applying bandpass forward-backward Butterworth IIR filter over raw EEG data from 1 to 10 Hz, basedline correction using − 100 ms of the stimulus appearance, calculating traditional trial-averaged ERP at 128 electrodes for each participant, applying a singular value decomposition (SVD) over the ERPs for each condition and EEG session, and extracting the first SVD component as a spatial filtering or weighted-map to estimate the N200 waveforms see the paper by Nunez et al. for more details (Nunez et al., 2019).
We fit model 2 to all participants from two experiments to estimate the posterior of its parameters. Table 3 reports the mean and standard deviation (STD) of the parameters’ posteriors. Note that the STD of estimated parameters is reasonably small, and mean parameters are also feasible. We calculate the ratio of the fraction of two sources of variance called r(σ,s(τ),γ) to show the proportion of cognitive variance to EEG variance. As previously mentioned in more detail, this ratio shows the amount of variance of cognition explained by EEG measures. Here, the mean posterior ratio of explained variance is about r = 0.45 across all participants in the two experiments. Interestingly, we expected γ ≈ 1 for most participants due to the findings of the original analysis of this data by Nunez et al. (2019), but the results of the model fits in Table 3 clearly show positive γ below 1.
Experiment 2 consists of three conditions to manipulate visual noise contrast at high, medium, and low levels. Figure 11 shows the posterior predictive distribution of RT and N200 latencies for two participants across SRN conditions of experiment 2. The results show that model 1a can describe observed RT and N200 latencies simultaneously, even in the presence of censored EEG data that were removed outside a pre-determined range (see Nunez et al., 2019, for more details). Table 4 in the Appendix shows the mean and STD of posterior of participants from experiment 2 across the signal-to-noise ratio (SRN) conditions for model 1a.
Comparing observed response times and N200 latencies of two specific participants (1 and 14) of experiment 2 from (Nunez et al., 2019) with posterior predictive distributions from fitted values of model 1a
Re-analysis of (van Vugt et al., 2019) Data
In this section, we assess models 7 and 8 that describe CPP slopes and behavior in real data. We first repeat the some of the data extraction methods from the paper by van Vugt et al. (2019) for clarity.
The data contained 23 participants with an age range of 17 to 36 (average 23.9) in which 11 participants were female (van Vugt et al., 2019). Participants were recruited to perform two different tasks with alternating blocks. In the perceptual decision-making task, participants were presented two images of human faces on either side of the screen and then asked to determine whether the two faces on the screen belonged the same person. In recognition memory task, participants had to memorize two faces and after a variable delay in the range of several seconds, they answered whether a probe face matched one of the two memorized faces or not. To obtain the appropriate number of trials for each task, participants did 12 four-minute blocks in a quadruple cycle, in which there were two blocks of the memory task followed by one block of the perceptual decision task. During the process of performing tasks, EEG activity was recorded from participants using 30 scalp electrodes electrodes based on the 10/20 system. For preprocessing of behavioral data, trials with response time outside of 3 standard deviations from the mean were excluded from further analyses. For EEG preprocessing, neuronal data were re-referenced to the average mastoids and a bandstop filter at 50 Hz was applied to remove power line noise. Also, approximately 5.4% of channels and 8.0% of trials were excluded across all participants using three different criteria (see the paper by van Vugt et al. (2019) for more details). Finally, CPP was identified at three electrodes CPz, CP1, and CP2 in accordance with O’Connell et al. (2012b).
At first, we fit model 7 and model 8 to all participants from two tasks to estimate the posterior of their parameters. The results show that model 7 model cannot provide a suitable account of the observed data for both experiments but model 8 can because of existence of γ parameter. Figure 12 shows the posterior predictive distributions over the observed data for some participants in each task.
Comparing observed response times and CPP slope of three specific participants from (van Vugt et al., 2019) with posterior predictive distributions from fitted values of model 7 and model 8
Table 5 in the Appendix shows the posterior probability of the γ parameter from model 8 where the distribution is above 0 for each task. We also reported Table 6 containing the mean and standard deviation (STD) of the parameters’ posteriors of model 8 for some participants from two experiments. The mean posterior ratio of explained variance of perceptual decision-making is about r = 0.06 and recognition memory tasks is r = 0.07 across all participants.
These results suggest that little variance of the single-trial CPP is explained by cognition. It may be that trial-averages in this data are necessary to find better cognitive representations. It also is possible that other single-trial EEG estimation techniques should be used for this data, such as using the Mexican hat function used by Jin et al. (2019). We could even compare single-trial estimation techniques to see which techniques yield the largest posterior ratios r across multiple model fits with different single-trial CPP estimations as data input (with appropriate out-of-sample posterior predictive comparisons). However, we felt this study was outside the scope of the current work.
How to Apply the Proposed Single-Trial Neurocognitive Models to New Data
The results of these three datasets show that the proposed single-trial framework and example neurocognitive models can be conveniently used to estimate latent processes underlying perceptual decision-making. Like other model fitting procedures, a researcher can compare related models in order to answer research questions related to experimental hypotheses. The models can then be compared using posterior predictive distributions to decide on the best interpretation of the data.
Future researchers may would like to extract the single-trial N200 latencies and CPP slope with methods to increase signal-to-noise on single trials. We recommend researchers use SVD or other decomposition methods to extract single-trial N200 latencies, single-trial CPP estimates, and other EEG measures. In this way, the main component can be selected which describes the high variance of the original signal. For more information about how to apply SVD in ERP data, you can see the references of (Nunez et al., 2017, 2019; Ghaderi-Kangavari et al., 2022).
All pre-trained neural networks that we fit in this paper are provided as checkpoints to be implemented in BayesFlow on https://github.com/AGhaderi/NDDM. These checkpoints allow future researchers to fit selected models to new data quickly in order to quickly obtain posterior distributions of the example models in this paper. If a researcher wishes to test different single-trial neurocognitive models which do not incorporate perceptual decision-making nor N200 latencies or CPPs in EEG, it is completely feasible to build new models based on the current paradigm and then evaluate them using posterior predictive distributions.
Discussion
The neurocognitive models assume latent parameters of the brain and cognition simultaneously to better predict unobserved data and discover underlying mechanisms of cognition. Our investigation aimed to introduce a framework for integrative models to consolidate neural activity and behavioral data at the single-trial level. The current models contained nuisance parameters shared with both brain measures and behavioral data at the single-trial level. These models are difficult to fit, with at least some of them being intractable in that they do not have closed-form likelihoods.
In some example models, we proposed that single-trial non-decision times in drift-diffusion models reflected particular ERP components from EEG, N200 latencies, on each trial. In other models, we proposed that single-trial drift rates reflected another particular ERP component, CPP measures, in every single trial. To fit these models, we used a deep learning approach to learn the feed-forward model in a training phase. To assess the reliability of estimated latent parameter values of interests, we then recovered parameters in a single step during the inference phase. The results show that many of the proposed models recovered parameters reasonably well. Also, investigation of model misspecification showed that the single-trial integrative models are robust to contaminant data and some assumption violations. We also used three real experimental datasets to test the reliability of the models. In general, the results of using real data show that our models have a high degree of flexibility and practicability. Therefore, even when the models’ assumptions are violated and misspecified in real data, their parameters can be informative for measuring the neurocognitive process.
Moreover, by evaluating the ratios of noise parameters, evaluating parameters in fits of mixture models (model 4), and performing the model comparison, it can be discovered whether the extracted neural activity is helpful to constrain cognitive latent parameters. Specific parameters are also able to provide some information about the relation between EEG measures and behavior. For example, we can examine if the effect parameters (e.g., γ in model 2) are close to zero to identify the existence of a relationship between cognitive parameters and EEG measurements, e.g., by calculating Bayes factors (van Ravenzwaaij and Etz, 2021).
Limitations to Our Framework and Models
The main limitations of our approach stem from the fact that the joint likelihood of paired single-trial EEG and behavioral data is not solved, and likely cannot be solved for most models. Therefore, approximate Bayesian computation (ABC) should be used (Palestro et al., 2018b). We choose to use BayesFlow in this paper (Radev et al., 2020a); however, other algorithms and programs could be used in the future to fit these same models or new models in our framework (Palestro et al., 2018b; Klinger et al., 2018; Fengler et al., 2021).
Another limitation is that fitting hierarchical models that use our proposed models or modeling framework as a base is somewhat difficult. There are often scientific questions that are best asked by creating a model in which multiple participants’ data are fit. Participants are expected to differ in their parameters sets but also expected to share some overall effect across two experimental conditions. To the best of our knowledge, it is not currently known how to fit these models using BayesFlow that properly accounts for participant differences with both priors and hyperpriors. However, we believe that recent techniques (Fengler et al., 2021) and future techniques are solving this problem.
Fitting the same neurocognitive models with fixed parameters requires the neural networks as approximators to be retrained. This is especially relevant when comparing nested models. This type of design for model comparison typically has a number of fixed and free parameters within models.
Many of the joint models proposed here assume intrinsic relationships between the EEG and behavioral data. Posterior distributions of variance parameters can indicate the reliability of this assumed relationship, and model comparison can be performed to test assumed relationships. However, fitting models in this framework should be used in conjunction with fitting directed models when discovering new EEG + behavioral relationships.
The proposed framework assumed normal distributions for both describing EEG measures with measurement noise as well as the connections between EEG measures and cognitive parameters. Such assumptions may be somewhat controversial for real data, though we showed the robustness of the present models to model misspecifications. It is likely that noise measurement of EEG is not normal since lots of embedded physical and environment noise exists in the real EEG signal. Theoretical development is necessary to test models with different distributions. We felt assuming normal distributions was a good first step, despite obvious censored and skewed real EEG data.
The source of the less precise recovery of the linear collapsing parameter in model 5 may be due to a failure of our particular model estimation procedure, instead of the model specifications. Previous findings have shown that the mean of slope parameter is recovered relatively well (Evans et al., 2020b; Fengler et al., 2021). On the other hand, the poor recovery of the Weibull collapsing parameter in model 6 may be due to an unavoidable intrinsic unidentifiability of the model (Evans et al., 2020b; Fengler et al., 2021).
Considerations About Parameter Estimation Methods
Although it is not generally required to use simulation to estimate posteriors of parameters, we have used it because the closed-form likelihood of the current models is unknown and common software such as Stan and JAGS can not easily estimate parameters’ posterior when the models contain nuisance parameters. Also, the INNs are based on standard neural networks (not Bayesian neural networks) which are able to directly take samples of the posterior portions of the parameters (Adler et al., 2019; Radev et al., 2020a). Summary neural networks help likelihood-free inference by concentrating training only on valuable information in the data. As a result, the fusion of a summary and INNs have been constructed to estimate the parameters of each model.
All neurocognitive models were run on PC with a CPU: Intel(R) Xeon(R) Gold 6226R CPU @ 2.90GHz 32 Core X64, RAM: 64 GB = 2 × 32 GB, Model: SK Hynix 2x 32GB DDR4-2933 RDIMM and Operating System: Debian 4.19.181-1 (2021-03-19) x86_64 GNU/Linux. We suspect that using a graphics processing unit (GPU) for training weights of deep learning would lead to faster processing times. Programming languages for deep learning (e.g., Keras and TensorFlow) with GPUs are great for highly parallel processing.
Recommended Steps in Introducing New Models in This Framework
These three concepts are important to test new neurocognitive models in our proposed framework: simulation, parameter recovery, and model comparison. In this paper, we elucidated our new single-trial modeling framework, and in “Mathematical Models for Neurocognitive Theory,” we sought to illuminate the theory and specification of the framework. We used a deep learning implementation, BayesFlow, and simulation in Python to fit and test the current models. “Recovering Parameters from Simulated Models” showed the results of parameter recovery related to each single-trial integrative model and then “Posterior Predictive Checks” and “Fitting the Proposed Single-Trial Neurocognitive Models on Experimental Data” evaluated the models by simulated and real data respectively. Note that each type of distinct joint modeling approach contains specific assumptions about the relation between the brain and behavior. It is worthwhile to simulate these different approaches with a plausible range of parameters’ values in order to learn about the model and assess parameter recovery.
There are some investigations into the meta-scientific process on how to build robust models to address hypothetical questions (Lee et al., 2019; Blohm et al., 2019; Guest & Martin, 2021). Confirmatory models could be determined in preregistration before data collection and should anticipate the pattern of data that we want to collect. However, the aim of the present research is to develop an overall framework as well as example explanatory models that make some explicit assumptions about data generation and cognitive processes. These models could ultimately inspire future confirmatory approaches.
Inspiring New Research Questions
Neurocognitive models can identify underlying latent processes. Latent parameters are the power of neurocognitive models, which can show individual- and group-level differences in experimental data. Our proposed models are based on specific theories and concepts. They not only have the characteristics of descriptive models that identify individual differences in task performance but also describe compactly the underlying psychological parameters related to neural activity. Thus, these neurocognitive models could be considered measurement models if they pass future tests of selective influence in experimental work. That is, changes in the neurocognitive processes as induced by experimental conditions should be reflected in the corresponding parameters in the models.
Our example models are intended to propose some intuitive research questions in order to answer questions about neurocognitive processes. Indeed, the models intrinsically provide some criteria and inspirations for designing new experiments. In particular, models 1a, 1b, and 1c can answer some questions about visual encoding time (VET) and motor execution time (MET) in perceptual decision making tasks. Which one of VET and MET can be changed significantly by specific experimental manipulation, for instance by a visual attention manipulation? Which of VET and MET is typically longer than the other across individuals? Under noninvasive brain stimulation, e.g., transcranial alternating current stimulation (tACS) and transcranial magnetic stimulation (TMS), how are motor execution and visual encoding disturbed? Or does the trial-to-trial variability of drift rate come from the CPP variability? These are just some of the example questions that could be answered with our models. We expect many research questions can be answered with our proposed single-trial integrative framework.
The Future of Neurocognitive Modeling
Our framework can easily be extended to different data types (e.g., single-trial fMRI data) and multiple data types (e.g., single-trial fMRI, EEG, and behavioral data). Also, a benefit of these models is that they are easily extended to multiple EEG variables. For instance, one could extend the class of model 1 so that the non-decision time variable influences both the visual sensory system and motor performance, by explaining both single-trial N200 latencies and readiness potentials (Lui et al., 2021; Nunez et al., 2022). This model would be achieved with an additional equation that describes the second peak in the RP potential from a second trial-to-trial nuisance parameter.
Recent models have proposed the use of accumulation processes to describe on- versus off-task behavior, as well as keeping track of the time to response (Hawkins et al., 2019; Hawkins & Heathcote, 2021). We did not implement such models, but these models could conceivably be implemented for joint models using our integrative single-trial framework.
Neuro-cognitive extensions of these models within our framework could be improvements upon our proposed models, specifically our mixture models: model 3 and model 4. In the future, using a similar method to model 4, researchers can easily compare two or more models to draw an inference about whether a specific neural measure can constrain and predict cognitive processes effectively.
The single-trial integrative models impose dependency between neural and behavioral data at the single-trial level. As a result, the authors of this article envisage that the single-trial approach will be very worthwhile and practical in interpreting cognitive processes in the future, and researchers will endeavor to further develop it.
Conclusions
There is now rich literature on the relationships between EEG measures, behavioral data, and latent cognitive parameters. However, few studies focus on building models for the combination of EEG data and behavioral data at the trial level simultaneously. Here, we introduced a novel integrative framework to connect both brain and behavior modalities in single trials. We then approximated posteriors of parameters in example models directly via a deep learning approach named BayesFlow. We also showed the robustness of the models to model misspecification. The results of using the current models for fitting three real data show that they can be applicably and easily used by researchers. Future researchers can introduce new single-trial integrative joint models via the current paradigm to set their explicit assumptions. Although we focused on EEG measures to build some relevant models, the present ideas can be also feasible for other data, including magnetoencephalography (MEG) data, fMRI, and invasive single-cell recordings in animal studies.
Code Availability
Implementations for simulating, parameter recovery, and model comparison in the context of DDM and EEG signals are accessible in https://github.com/AGhaderi/NDDM. Checkpoints for fitting our example models using BayesFlow are also available in this repository.
References
Adler, T.J., Ardizzone, L., Vemuri, A., Ayala, L., Gröhl, J., Kirchner, T., Wirkert, S., Kruse, J., Rother, C., Köthe, U., & et al. (2019). Uncertainty-aware performance assessment of optical imaging modalities with invertible neural networks. International Journal of Computer Assisted Radiology and Surgery, 14, 997–1007.
Ahmadi, M., McDevitt, E.A., Silver, M.A., & Mednick, S.C. (2018). Perceptual learning induces changes in early and late visual evoked potentials. Vision Research, 152, 101–109.
Albert, C., Ulzega, S., Ozdemir, F., Perez-Cruz, F., & Mira, A. (2022). Learning summary statistics for Bayesian inference with autoencoders. arXiv:2201.12059.
Ardizzone, L., Kruse, J., Wirkert, S., Rahner, D., Pellegrini, E.W., Klessen, R.S., Maier-Hein, L., Rother, C., & Köthe, U. (2018). Analyzing inverse problems with invertible neural networks. arXiv:1808.04730.
Baars, B., & Gage, N.M. (2013). Fundamentals of cognitive neuroscience: A beginner’s guide. Academic Press.
Bahg, G., Evans, D.G., Galdo, M., & Turner, B.M. (2020). Gaussian process linking functions for mind, brain, and behavior. Proceedings of the National Academy of Sciences, 117, 29398–29406.
Blohm, G., Kording, K.P., & Schrater, P.R. (2019). A how-to-model guide for neuroscience. eNeuro, 7, 1–12.
Boehm, U., Annis, J., Frank, M.J., Hawkins, G.E., Heathcote, A., Kellen, D., Krypotos, A.M., Lerche, V., Logan, G.D., Palmeri, T.J., & et al. (2018). Estimating across-trial variability parameters of the diffusion decision model: Expert advice and recommendations. Journal of Mathematical Psychology, 87, 46–75.
Bowen, H.J., Spaniol, J., Patel, R., & Voss, A. (2016). A diffusion model analysis of decision biases affecting delayed recognition of emotional stimuli. PloS One, 11, e0146769.
Bridwell, D.A., Cavanagh, J.F., Collins, A.G., Nunez, M.D., Srinivasan, R., Stober, S., & Calhoun, V.D. (2018). Moving beyond ERP components: A selective review of approaches to integrate EEG and behavior. Frontiers in Human Neuroscience, 12, 106.
Brown, S.D., & Heathcote, A. (2008). The simplest complete model of choice response time: Linear ballistic accumulation. Cognitive Psychology, 57, 153–178.
Busemeyer, J.R., & Wang, Y.M. (2000). Model comparisons and model selections based on generalization criterion methodology. Journal of Mathematical Psychology, 44, 171–189.
Carpenter, B., Gelman, A., Hoffman, M.D., Lee, D., Goodrich, B., Betancourt, M., Brubaker, M., Guo, J., Li, P., & Riddell, A. (2017). Stan: A probabilistic programming language. Journal of Statistical Software, 76, 1–32.
Cavanagh, J.F., Bismark, A., Frank, M.J., & Allen, J.J. (2011). Larger error signals in major depression are associated with better avoidance learning. Frontiers in Psychology, 2, 331.
Clark, V.P., Fan, S., & Hillyard, S.A. (1994). Identification of early visual evoked potential generators by retinotopic and topographic analyses. Human Brain Mapping, 2, 170–187.
Clayson, P.E., Baldwin, S.A., Rocha, H.A., & Larson, M.J. (2021). The data-processing multiverse of event-related potentials (ERPs): A roadmap for the optimization and standardization of ERP processing and reduction pipelines. NeuroImage, 245, 118712.
Clayson, P.E., Carbine, K.A., Baldwin, S.A., & Larson, M.J. (2019). Methodological reporting behavior, sample sizes, and statistical power in studies of event-related potentials: Barriers to reproducibility and replicability. Psychophysiology, 56, e13437.
Cobb, W.A., & Dawson, G. (1960). The latency and form in man of the occipital potentials evoked by bright flashes. The Journal of Physiology, 152, 108.
Cranmer, K., Brehmer, J., & Louppe, G. (2020). The frontier of simulation-based inference. Proceedings of the National Academy of Sciences, 117, 30055–30062.
Csilléry, K., Blum, M.G., Gaggiotti, O.E., & François, O. (2010). Approximate Bayesian computation (ABC) in practice. Trends in Ecology & Evolution, 25, 410–418.
Di Russo, F., Martínez, A., & Hillyard, S.A. (2003). Source analysis of event-related cortical activity during visuo-spatial attention. Cerebral Cortex, 13, 486–499.
Diaz, J.A., Queirazza, F., & Philiastides, M.G. (2017). Perceptual learning alters post-sensory processing in human decision-making. Nature Human Behaviour, 1, 1–9.
Ditterich, J. (2006). Stochastic models of decisions about motion direction: Behavior and physiology. Neural Networks, 19, 981–1012.
Dmochowski, J.P., & Norcia, A.M. (2015). Cortical components of reaction-time during perceptual decisions in humans. PloS one, 10, e0143339.
Drugowitsch, J., Moreno-Bote, R., Churchland, A.K., Shadlen, M.N., & Pouget, A. (2012). The cost of accumulating evidence in perceptual decision making. The Journal of Neuroscience, 32, 3612–3628.
Evans, N.J., Hawkins, G.E., & Brown, S.D. (2020a). The role of passing time in decision-making. Journal of Experimental Psychology: Learning, Memory, and Cognition, 46, 316.
Evans, N.J., Trueblood, J.S., & Holmes, W.R. (2020b). A parameter recovery assessment of time-variant models of decision-making. Behavior research methods, 52, 193–206.
Fengler, A., Govindarajan, L.N., Chen, T., & Frank, M.J. (2021). Likelihood approximation networks (LANs) for fast inference of simulation models in cognitive neuroscience. Elife, 10, e65074.
Forstmann, B.U., Ratcliff, R., & Wagenmakers, E.J. (2016). Sequential sampling models in cognitive neuroscience: Advantages, applications, and extensions. Annual Review of Psychology, 67, 641–666.
Frank, M.J. (2015). Linking across levels of computation in model-based cognitive neuroscience. In B.U. Forstmann E.J. Wagenmakers (Eds.) An introduction to model-based cognitive neuroscience. Springer, New York, pp. 159–177.
Gelman, A., Carlin, J.B., Stern, H.S., Dunson, D.B., Vehtari, A., & Rubin, D.B. (2014). Bayesian data analysis. 3rd edn., Taylor & Francis Group, LLC, Boca Raton, FL.
Georgie, Y.K., Porcaro, C., Mayhew, S.D., Bagshaw, A.P., & Ostwald, D. (2018). A perceptual decision making EEG/fMRI data set. bioRxiv, vol. 253047.
Ghaderi-Kangavari, A., Rad, J.A., Parand, K., & Ebrahimpour, R. (2021). How spatial attention affects the decision process: Looking through the lens of bayesian hierarchical diffusion model & EEG analysis. bioRxiv.
Ghaderi-Kangavari, A., Rad, J.A., Parand, K., & Nunez, M.D. (2022). Neuro-cognitive models of single-trial EEG measures describe latent effects of spatial attention during perceptual decision making. Journal of Mathematical Psychology, 111, 102725.
Gluth, S., Rieskamp, J., & Büchel, C. (2013). Classic EEG motor potentials track the emergence of value-based decisions. NeuroImage, 79, 394–403.
Gold, J.I., & Shadlen, M.N. (2007). The neural basis of decision making. Annual Review of Neuroscience, 30, 535–574.
Guest, O., & Martin, A.E. (2021). How computational modeling can force theory building in psychological science. Perspectives on Psychological Science, 16, 789–802.
Hall, J.E., & Hall, M.E. (2020). Guyton and hall textbook of medical physiology e-Book. Elsevier Health Sciences.
Hanks, T., Kiani, R., & Shadlen, M.N. (2014). A neural mechanism of speed-accuracy tradeoff in macaque area LIP. Elife, 3, e02260.
Hawkins, G.E., Forstmann, B.U., Wagenmakers, E.J., Ratcliff, R., & Brown, S.D. (2015). Revisiting the evidence for collapsing boundaries and urgency signals in perceptual decision-making. Journal of Neuroscience, 35, 2476–2484.
Hawkins, G.E., & Heathcote, A. (2021). Racing against the clock: Evidence-based versus time-based decisions. Psychological Review, 128, 222.
Hawkins, G.E., Mittner, M., Forstmann, B.U., & Heathcote, A. (2019). Modeling distracted performance. Cognitive Psychology, 112, 48–80.
Heathcote, A., Brown, S.D., & Wagenmakers, E.J. (2015). Springer an introduction to good practices in cognitive modeling. In B.U. Forstmann E.J Wagenmakers (Eds.) An, introduction to model-based cognitive neuroscience. New York, pp. 25–48.
Hermans, J., Begy, V., & Louppe, G. (2020). Likelihood-free mcmc with amortized approximate ratio estimators. In International conference on machine learning, organizationPMLR, pp. 4239–4248.
Jiang, B., Wu, T. y., Zheng, C., & Wong, W.H. (2017). Learning summary statistic for approximate Bayesian computation via deep neural network. Statistica Sinica, pp. 1595–1618.
Jin, C.Y., Borst, J.P., & Van Vugt, M.K. (2019). Predicting task-general mind-wandering with EEG. Cognitive, Affective, & Behavioral Neuroscience, 19, 1059–1073.
Jun, E.J., Bautista, A.R., Nunez, M.D., Allen, D.C., Tak, J.H., Alvarez, E., & Basso, M.A. (2021). Causal role for the primate superior colliculus in the computation of evidence for perceptual decisions. Nature Neuroscience, 24, 1121–1131.
Kang, I., Yi, W., & Turner, B.M. (2021). A regularization method for linking brain and behavior. Psychological Methods.
Kelly, S.P., & O’Connell, R.G. (2013). Internal and external influences on the rate of sensory evidence accumulation in the human brain. Journal of Neuroscience, 33, 19434– 19441.
Kiani, R., & Shadlen, M.N. (2009). Representation of confidence associated with a decision by neurons in the parietal cortex. Science, 324, 759–764.
Klinger, E., Rickert, D., & Hasenauer, J. (2018). pyABC: Distributed, likelihood-free inference. Bioinformatics, 34, 3591–3593.
Lamme, V.A., Zipser, K., & Spekreijse, H. (2002). Masking interrupts figure-ground signals in V1. Journal of Cognitive Neuroscience, 14, 1044–1053.
Lee, M.D., Criss, A.H., Devezer, B., Donkin, C., Etz, A., Leite, F.P., Matzke, D., Rouder, J.N., Trueblood, J.S., White, C.N., & et al. (2019). Robust modeling in cognitive science. Computational Brain & Behavior, 2, 141–153.
Lee, M.D. (2014). Bayesian cognitive modeling: A practical course. Cambridge University Press.
Loughnane, G.M., Newman, D.P., Bellgrove, M.A., Lalor, E.C., Kelly, S.P., & O’Connell, R.G. (2016). Target selection signals influence perceptual decisions by modulating the onset and rate of evidence accumulation. Current Biology, 26, 496– 502.
Luck, S.J. (2014). An introduction to the event-related potential technique. MIT press.
Luck, S.J., Woodman, G.F., & Vogel, E.K. (2000). Event-related potential studies of attention. Trends in Cognitive Sciences, 4, 432–440.
Lueckmann, J.M., Bassetto, G., Karaletsos, T., & Macke, J.H. (2019). Likelihood-free inference with emulator networks. In Symposium on advances in approximate Bayesian inference, organizationPMLR, pp. 32–53.
Lui, K.K., Nunez, M.D., Cassidy, J.M., Vandekerckhove, J., Cramer, S.C., & Srinivasan, R. (2021). Timing of readiness potentials reflect a decision-making process in the human brain. Computational Brain & Behavior, 4, 264–283.
Manning, C., Hassall, C.D., Hunt, L.T., Norcia, A.M., Wagenmakers, E.J., Snowling, M.J., Scerif, G., & Evans, N.J. (2022). Visual motion and decision-making in dyslexia: Reduced accumulation of sensory evidence and related neural dynamics. Journal of Neuroscience, 42, 121–134.
McGovern, D.P., Hayes, A., Kelly, S.P., & O’Connell, R.G. (2018). Reconciling age-related changes in behavioural and neural indices of human perceptual decision-making. Nature Human behaviour, 2, 955–966.
Merkle, E.C., Furr, D., & Rabe-Hesketh, S. (2019). Bayesian comparison of latent variable models: Conditional versus marginal likelihoods. Psychometrika, 84, 802–829.
Navarro, D.J., & Fuss, I.G. (2009). Fast and accurate calculations for first-passage times in wiener diffusion models. Journal of Mathematical Psychology, 53, 222–230.
Nunez, M.D., Gosai, A., Vandekerckhove, J., & Srinivasan, R. (2019). The latency of a visual evoked potential tracks the onset of decision making. Neuroimage, 197, 93–108.
Nunez, M.D., Nunez, P.L., & Srinivasan, R. (2016). Electroencephalography (EEG): Neurophysics, experimental methods, and signal processing. In H. Ombao, M. Lindquist, W. Thompson, & J Aston (Eds.) Handbook of Neuroimaging data analysis. Chapman & Hall/CRC, pp. 175-197.
Nunez, M.D., Srinivasan, R., & Vandekerckhove, J. (2015). Individual differences in attention influence perceptual decision making. Frontiers in Psychology, 6, 18.
Nunez, M.D., Vandekerckhove, J., & Srinivasan, R. (2017). How attention influences perceptual decision making: Single-trial EEG correlates of drift-diffusion model parameters. Journal of Mathematical Psychology, 76, 117–130.
Nunez, M.D., Vandekerckhove, J., & Srinivasan, R. (2022). A tutorial on fitting joint models of M/EEG and behavior to understand cognition. PsyArXiv.
O’Connell, R.G., Dockree, P.M., & Kelly, S.P. (2012a). A supramodal accumulation-to-bound signal that determines perceptual decisions in humans. Nature Neuroscience, 15, 1729–1735.
O’Connell, R.G., Dockree, P.M., & Kelly, S.P. (2012b). A supramodal accumulation-to-bound signal that determines perceptual decisions in humans. Nature Neuroscience, 15, 1729–1735.
O’Connell, R.G., Shadlen, M.N., Wong-Lin, K., & Kelly, S.P. (2018). Bridging neural and computational viewpoints on perceptual decision-making. Trends in Neurosciences, 41, 838–852.
Palestro, J.J., Bahg, G., Sederberg, P.B., Lu, Z.L., Steyvers, M., & Turner, B.M. (2018a). A tutorial on joint models of neural and behavioral measures of cognition. Journal of Mathematical Psychology, 84, 20–48.
Palestro, J.J., Sederberg, P.B., Osth, A.F., Van Zandt, T., & Turner, B.M. (2018b). Likelihood-free methods for cognitive science. Springer.
Papamakarios, G., Sterratt, D., & Murray, I. (2019). Sequential neural likelihood: Fast likelihood-free inference with autoregressive flows. In The 22nd international conference on artificial intelligence and statistics, PMLR, pp. 837–848.
Philiastides, M.G., Heekeren, H.R., & Sajda, P. (2014). Human scalp potentials reflect a mixture of decision-related signals during perceptual choices. Journal of Neuroscience, 34, 16877– 16889.
Philiastides, M.G., Ratcliff, R., & Sajda, P. (2006). Neural representation of task difficulty and decision making during perceptual categorization: A timing diagram. Journal of Neuroscience, 26, 8965–8975.
Plummer, M. (2003). JAGS: a program for analysis of Bayesian graphical models using Gibbs sampling. In Proceedings of the 3rd international workshop on distributed statistical computing (DSC 2003), Vienna, Austria.
Radev, S.T., Mertens, U.K., Voss, A., Ardizzone, L., & Köthe, U. (2020a). BayesFlow: Learning complex stochastic models with invertible neural networks. IEEE Transactions on Neural Networks and Learning Systems, 33, 1452–1466.
Radev, S.T., Mertens, U.K., Voss, A., & Köthe, U. (2020b). Towards end-to-end likelihood-free inference with convolutional neural networks. British Journal of Mathematical and Statistical Psychology, 73, 23–43.
Rafiei, F., & Rahnev, D. (2021). Qualitative speed-accuracy tradeoff effects that cannot be explained by the diffusion model under the selective influence assumption. Scientific Reports, 11, 1–19.
Ratcliff, R. (1978). A theory of memory retrieval. Psychological Review, 85, 59.
Ratcliff, R., & Kang, I. (2021). Qualitative speed-accuracy tradeoff effects can be explained by a diffusion/fast-guess mixture model. Scientific Reports, 11, 1–9.
Ratcliff, R., & McKoon, G. (2008). The diffusion decision model: Theory and data for two-choice decision tasks. Neural Computation, 20, 873–922.
Ratcliff, R., Philiastides, M.G., & Sajda, P. (2009). Quality of evidence for perceptual decision making is indexed by trial-to-trial variability of the EEG. Proceedings of the National Academy of Sciences, 106, 6539–6544.
Ratcliff, R., & Rouder, J.N. (1998). Modeling response times for two-choice decisions. Psychological Science, 9, 347–356.
Ratcliff, R., Smith, P.L., Brown, S.D., & McKoon, G. (2016). Diffusion decision model: Current issues and history. Trends in Cognitive Sciences, 20, 260–281.
Ratcliff, R., & Tuerlinckx, F. (2002). Estimating parameters of the diffusion model: Approaches to dealing with contaminant reaction times and parameter variability. Psychonomic Bulletin & Review, 9, 438–481.
van Ravenzwaaij, D., Brown, S.D., Marley, A., & Heathcote, A. (2020). Accumulating advantages: A new conceptualization of rapid multiple choice. Psychological Review, 127, 186.
van Ravenzwaaij, D., & Etz, A. (2021). Simulation studies as a tool to understand Bayes factors. Advances in Methods and Practices in Psychological Science, 4, 2515245920972624. Publisher: SAGE Publications Inc.
van Ravenzwaaij, D., Provost, A., & Brown, S.D. (2017). A confirmatory approach for integrating neural and behavioral data into a single model. Journal of Mathematical Psychology, 76, 131–141.
Raynal, L., Marin, J.M., Pudlo, P., Ribatet, M., Robert, C.P., & Estoup, A. (2019). ABC random forests for Bayesian parameter inference. Bioinformatics, 35, 1720–1728.
Roitman, J.D., & Shadlen, M.N. (2002). Response of neurons in the lateral intraparietal area during a combined visual discrimination reaction time task. Journal of Neuroscience, 22, 9475– 9489.
Schmitt, M., Bürkner, P.C., Köthe, U., & Radev, S.T. (2021). Detecting model misspecification in amortized Bayesian inference with neural networks. arXiv:2112.08866.
Schubert, A.L., Nunez, M.D., Hagemann, D., & Vandekerckhove, J. (2019). Individual differences in cortical processing speed predict cognitive abilities: A model-based cognitive neuroscience account. Computational Brain & Behavior, 2, 64–84.
Servant, M., White, C., Montagnini, A., & Burle, B. (2015). Using covert response activation to test latent assumptions of formal decision-making models in humans. Journal of Neuroscience, 35, 10371–10385.
Servant, M., White, C., Montagnini, A., & Burle, B. (2016). Linking theoretical decision-making mechanisms in the Simon task with electrophysiological data: A model-based neuroscience study in humans. Journal of Cognitive Neuroscience, 28, 1501–1521.
Shadlen, M.N., & Kiani, R. (2013). Decision making as a window on cognition. Neuron, 80, 791–806.
Shadlen, M.N., & Newsome, W.T. (2001). Neural basis of a perceptual decision in the parietal cortex (area LIP) of the rhesus monkey. Journal of Neurophysiology, 86, 1916–1936.
Shinn, M., Lam, N.H., & Murray, J.D. (2020). A flexible framework for simulating and fitting generalized drift-diffusion models. ELife, 9, e56938.
Shlens, J. (2014).
Smith, P.L., & Ratcliff, R. (2022). Modeling evidence accumulation decision processes using integral equations: Urgency-gating and collapsing boundaries. Psychological Review, 129, 235– 267.
Sunnåker, M., Busetto, A.G., Numminen, E., Corander, J., Foll, M., & Dessimoz, C. (2013). Approximate Bayesian computation. PLoS Computational Biology, 9, e1002803.
Sutton, R.S., & Barto, A.G. (2018). Reinforcement learning: An introduction. MIT press.
Tamietto, M., & De Gelder, B. (2010). Neural bases of the non-conscious perception of emotional signals. Nature Reviews Neuroscience, 11, 697–709.
Thorpe, S., Fize, D., & Marlot, C. (1996). Speed of processing in the human visual system. Nature, 381, 520–522.
Tuerlinckx, F. (2004). The efficient computation of the cumulative distribution and probability density functions in the diffusion model. Behavior Research Methods Instruments & Computers, 36, 702–716.
Turner, B.M., Forstmann, B.U., Love, B.C., Palmeri, T.J., & Van Maanen, L. (2017). Approaches to analysis in model-based cognitive neuroscience. Journal of Mathematical Psychology, 76, 65–79.
Turner, B.M., Forstmann, B.U., Steyvers, M., & et al. (2019). Joint models of neural and behavioral data. Springer.
Turner, B.M., Forstmann, B.U., Wagenmakers, E.J., Brown, S.D., Sederberg, P.B., & Steyvers, M. (2013). A Bayesian framework for simultaneously modeling neural and behavioral data. NeuroImage, 72, 193–206.
Turner, B.M., Rodriguez, C.A., Norcia, T.M., McClure, S.M., & Steyvers, M. (2016). Why more is better: Simultaneous modeling of EEG, fMRI, and behavioral data. NeuroImage, 128, 96– 115.
Turner, B.M., & Sederberg, P.B. (2012). Approximate bayesian computation with differential evolution. Journal of Mathematical Psychology, 56, 375–385.
Turner, B.M., & Sederberg, P.B. (2014). A generalized, likelihood-free method for posterior estimation. Psychonomic Bulletin & Review, 21, 227–250.
Turner, B.M., & Van Zandt, T. (2012). A tutorial on approximate Bayesian computation. Journal of Mathematical Psychology, 56, 69–85.
Usher, M., & McClelland, J.L. (2001). The time course of perceptual choice: The leaky, competing accumulator model. Psychological Review, 108, 550.
Usher, M., & McClelland, J.L. (2004). Loss aversion and inhibition in dynamical models of multialternative choice. Psychological Review, 111, 757–769.
Vandekerckhove, J., & Tuerlinckx, F. (2007). Fitting the ratcliff diffusion model to experimental data. Psychonomic Bulletin & Review, 14, 1011–1026.
VanRullen, R., & Thorpe, S.J. (2001). The time course of visual processing: From early perception to decision-making. Journal of Cognitive Neuroscience, 13, 454–461.
Verdonck, S., Loossens, T., & Philiastides, M.G. (2021). The leaky integrating threshold and its impact on evidence accumulation models of choice response time (rt). Psychological Review, 128, 203.
Voskuilen, C., Ratcliff, R., & Smith, P.L. (2016). Comparing fixed and collapsing boundary versions of the diffusion model. Journal of Mathematical Psychology, 73, 59–79.
Voss, A., Lerche, V., Mertens, U., & Voss, J. (2019). Sequential sampling models with variable boundaries and non-normal noise: A comparison of six models. Psychonomic Bulletin & Review, 26, 813–832.
Voss, A., Rothermund, K., & Voss, J. (2004). Interpreting the parameters of the diffusion model: An empirical validation. Memory & Cognition, 32, 1206–1220.
Voss, A., Voss, J., & Lerche, V. (2015). Assessing cognitive processes with diffusion model analyses: A tutorial based on fast-dm-30. Frontiers in Psychology, 6, 336.
van Vugt, M.K., Beulen, M.A., & Taatgen, N.A. (2019). Relation between centro-parietal positivity and diffusion model parameters in both perceptual and memory-based decision making. Brain research, 1715, 1–12.
Wagenmakers, E.J., Grünwald, P., & Steyvers, M. (2006). Accumulative prediction error and the selection of time series models. Journal of Mathematical Psychology, 50, 149–166.
Wagenmakers, E.J., Lodewyckx, T., Kuriyal, H., & Grasman, R. (2010). Bayesian hypothesis testing for psychologists: A tutorial on the savage–dickey method. Cognitive psychology, 60, 158–189.
Wagenmakers, E.J., Van Der Maas, H.L., & Grasman, R.P. (2007). An EZ-diffusion model for response time and accuracy. Psychonomic Bulletin & Review, 14, 3–22.
Weindel, G. (2021). On the measurement and estimation of cognitive processes with electrophysiological recordings and reaction time modeling.
Whitham, E.M., Pope, K.J., Fitzgibbon, S.P., Lewis, T., Clark, C.R., Loveless, S., Broberg, M., Wallace, A., DeLosAngeles, D., Lillie, P., Hardy, A., Fronsko, R., Pulbrook, A., & Willoughby, J.O. (2007). Scalp electrical recording during paralysis: Quantitative evidence that EEG frequencies above 20Hz are contaminated by EMG. Clinical Neurophysiology, 118, 1877– 1888.
Wiecki, T.V., Sofer, I., & Frank, M.J. (2013). HDDM: Hierarchical Bayesian estimation of the drift-diffusion model in Python. Frontiers in neuroinformatics, 7, 14.
Wood, S.N. (2010). Statistical inference for noisy nonlinear ecological dynamic systems. Nature, 466, 1102–1104.
Yau, Y., Hinault, T., Taylor, M., Cisek, P., Fellows, L.K., & Dagher, A. (2021). Evidence and urgency related EEG signals during dynamic decision-making in humans. Journal of Neuroscience, 41, 5711–5722.
Zwart, F.S., Vissers, C.T.W., Kessels, R.P., & Maes, J.H. (2018). Implicit learning seems to come naturally for children with autism, but not for children with specific language impairment: Evidence from behavioral and ERP data. Autism Research, 11, 1050–1061.
Acknowledgements
Marieke van Vugt is kindly thanked for sharing data with the authors. Konrad Mikalauskas is thanked for his related work on models of inhibition. We would also like to thank Stefan Radev for engaging the authors in a discussion on the future of BayesFlow. The anonymous reviewers are thanked for their helpful suggestions and comments.
Funding
JAR was supported in part by IRAN Cognitive Sciences & Technologies Council (Grant No. 9311), and Iran National Science Foundation, INSF (Grant No. 99010447 and 4003215).
Author information
Authors and Affiliations
Contributions
MDN developed the study concept. All authors contributed to the study design. AGK implemented and conducted the simulation experiments. All the authors contributed to analyzing and interpreting the results. AGK drafted the manuscript. MDN and JAR provided critical revisions. All the authors approved the final version of the manuscript for submission.
Corresponding author
Ethics declarations
Ethics Approval
Not applicable.
Consent to Participate
Not applicable.
Consent for Publication
Not applicable.
Conflict of Interest
The authors declare no competing interests.
Open Practices Statement
Checkpoints for fitting our example models using BayesFlow are available in https://github.com/AGhaderi/NDDM. The three datasets used in this publication are all available. The data from Georgie et al. (2018) are available at https://osf.io/jg9u3 upon request. Pre-calculated EEG measures and behavioral data from Nunez et al. (2019) are available at https://osf.io/jg9u3/ and https://github.com/mdnunez/encodingN200. EEG data and behavioral data from van Vugt et al. (2019) are available at https://unishare.nl/index.php/s/CNNUyD3r16ZC5hy.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix:
Appendix:
Simulation
We used the following code to simulate model 3 in Python. For other models, little changes in code are required.

Figures Associated with Parameter Recovery Results
The plot of true parameters versus posteriors of estimated parameters for model 1b. See the caption of Fig. 4 for additional details of these plots
The plot of true parameters versus posteriors of estimated parameters for model 1c. See the caption of Fig. 4 for additional details of these plots
The plot of true parameters versus posteriors of estimated parameters for model 2. See the caption of Fig. 4 for more details
The plot of true parameters versus posteriors of estimated parameters for model 3. See the caption of Fig. 4 for more details
True parameters versus posteriors of estimated parameters for model 4a. See the caption of Fig. 4 for more details
True parameters versus posteriors of estimated parameters for model 4b. See the caption of Fig. 4 for more details
True parameters versus posteriors of estimated parameters for model 5. See the caption of Fig. 4 for more details
True parameters versus posteriors of estimated parameters for model 6. See the caption of Fig. 4 for more details
The plot of true parameters versus posteriors of estimated parameters for model 7. See the caption of Fig. 4 for more details
True parameters versus posteriors of estimated parameters for model 8. See the caption of Fig. 4 for more details
True parameters versus posteriors of estimated parameters for model 9. See the caption of Fig. 4 for more details
True parameters versus posteriors of estimated parameters for model 10. We demonstrated that the model cannot recover the related parameters when we are going to add a γ effect parameter to the model in an irrational and non-technical way. Therefore, we are very uncertain about the parameters. Although this model is convergent, we did not actually add any information to the model with brain data compared to when we only had behavioral data
True parameters versus posteriors of estimated parameters for model 11. See the caption of Fig. 4 for more details
True parameters versus posteriors of estimated parameters for model 12. See the caption of Fig. 4 for more details
True parameters versus posteriors of estimated parameters for model 13. See the caption of Fig. 4 for more details
Parameter recovery when fitting model 1a to a simulation of a similar model with a contaminant process of choice-response times. On 5% of trials, choice-response times are simulated by a uniform distribution, \(r_{i}, x_{i} \sim Uniform(0, 2)\) seconds, instead of a drift-diffusion model distribution. See the caption of Fig. 4 for additional details of these plots
Parameter recovery when fitting model 1a to a simulation of a similar model with a contaminant process of N200 latencies. On 5% of trials, N200 latencies are simulated by a uniform distribution, \(z_{i} \sim Uniform(0, 0.3)\) seconds, instead of the original generation process that was influenced by trial-to-trial variability in non-decision time. See the caption of Fig. 4 for additional details of these plots
Assessing Model Fits Experimental Data
Parameter recovery when fitting model 1a to a simulation of a similar model with the single-trial N200 latencies zi instead being simulated by a Gamma distribution, \(z_{i} \sim Gamma\), instead of a normal distribution as assumed by the model-fitting procedure. See the caption of Fig. 4 for additional details of these plots
Comparing observed response times and N200 latencies of two specific participants (sub-001 and sub-006) with predicted values by six of the current neurocognitive models. Left side: The comparison of observed and predicted response times. Right side: The comparison of observed and predicted N200 latencies
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ghaderi-Kangavari, A., Rad, J.A. & Nunez, M.D. A General Integrative Neurocognitive Modeling Framework to Jointly Describe EEG and Decision-making on Single Trials. Comput Brain Behav 6, 317–376 (2023). https://doi.org/10.1007/s42113-023-00167-4
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s42113-023-00167-4