Bayesian Comparison of Latent Variable Models: Conditional Versus Marginal Likelihoods

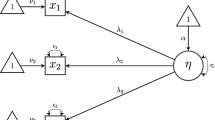
Abstract

Typical Bayesian methods for models with latent variables (or random effects) involve directly sampling the latent variables along with the model parameters. In high-level software code for model definitions (using, e.g., BUGS, JAGS, Stan), the likelihood is therefore specified as conditional on the latent variables. This can lead researchers to perform model comparisons via conditional likelihoods, where the latent variables are considered model parameters. In other settings, however, typical model comparisons involve marginal likelihoods where the latent variables are integrated out. This distinction is often overlooked despite the fact that it can have a large impact on the comparisons of interest. In this paper, we clarify and illustrate these issues, focusing on the comparison of conditional and marginal Deviance Information Criteria (DICs) and Watanabe–Akaike Information Criteria (WAICs) in psychometric modeling. The conditional/marginal distinction corresponds to whether the model should be predictive for the clusters that are in the data or for new clusters (where “clusters” typically correspond to higher-level units like people or schools). Correspondingly, we show that marginal WAIC corresponds to leave-one-cluster out cross-validation, whereas conditional WAIC corresponds to leave-one-unit out. These results lead to recommendations on the general application of the criteria to models with latent variables.

Appendices

A. Posterior Expectations of Marginal and Conditional Likelihoods

Following Trevisani and Gelfand (2003), who studied DIC in the context of linear mixed models, we can use Jensen’s inequality to show that the posterior expected value of the marginal log-likelihood is less than the posterior expected value of the conditional log-likelihood.

First, consider the function $h(x) = x\log (x)$. It is convex, so Jensen’s inequality states that

$$\begin{aligned} h(\mathrm {E}(x)) \le \mathrm {E}(h(x)). \end{aligned}$$

(13)

Setting $x = f_{\text {c}}(\varvec{y} | \varvec{\omega }, \varvec{\zeta })$ and taking expected values with respect to $\varvec{\zeta }$, we have that

$$\begin{aligned} h(\mathrm {E}(x))&= \displaystyle \log \left[ \displaystyle \int f_{\text {c}}(\varvec{y} | \varvec{\omega }, \varvec{\zeta }) g(\varvec{\zeta } | \varvec{\psi }) \text {d}\varvec{\zeta } \right] \int f_{\text {c}}(\varvec{y} | \varvec{\omega }, \varvec{\zeta }) g(\varvec{\zeta } | \varvec{\psi }) \text {d}\varvec{\zeta } \end{aligned}$$

(14)

$$\begin{aligned} \mathrm {E}(h(x))&= \displaystyle \int \log (f_{\text {c}}(\varvec{y} | \varvec{\omega }, \varvec{\zeta })) f_{\text {c}}(\varvec{y} | \varvec{\omega }, \varvec{\zeta }) g(\varvec{\zeta } | \varvec{\psi }) \text {d}\varvec{\zeta }, \end{aligned}$$

(15)

so that

$$\begin{aligned}&\displaystyle \log \left[ \displaystyle \int f_{\text {c}}(\varvec{y} | \varvec{\omega }, \varvec{\zeta }) g(\varvec{\zeta } | \varvec{\psi }) \text {d}\varvec{\zeta } \right] \int f_{\text {c}}(\varvec{y} | \varvec{\omega }, \varvec{\zeta }) g(\varvec{\zeta } | \varvec{\psi }) \text {d}\varvec{\zeta }\nonumber \\&\le \displaystyle \int \log (f_{\text {c}}(\varvec{y} | \varvec{\omega }, \varvec{\zeta })) f_{\text {c}}(\varvec{y} | \varvec{\omega }, \varvec{\zeta }) g(\varvec{\zeta } | \varvec{\psi }) \text {d}\varvec{\zeta }. \end{aligned}$$

(16)

We now multiply both sides of this inequality by $p(\varvec{\omega }, \varvec{\psi })/c$, where $p(\varvec{\omega }, \varvec{\psi })$ is a prior distribution and

$$\begin{aligned} c = \displaystyle \int _{\varvec{\psi }} \displaystyle \int _{\varvec{\omega }} \displaystyle \int _{\varvec{\zeta }} f_{\text {c}}(\varvec{y} | \varvec{\omega }, \varvec{\zeta }) g(\varvec{\zeta } | \varvec{\psi }) \text {d}\varvec{\zeta } \cdot p(\varvec{\omega }, \varvec{\psi }) \text {d}\varvec{\omega } \text {d}\varvec{\psi } \end{aligned}$$

(17)

is the posterior normalizing constant. Finally, we integrate both sides with respect to $\varvec{\omega }$ and $\varvec{\psi }$ to obtain

$$\begin{aligned}&\displaystyle \int _{\varvec{\psi }} \displaystyle \int _{\varvec{\omega }} \log \left( \displaystyle \int _{\varvec{\zeta }} f_{\text {c}}(\varvec{y} | \varvec{\omega }, \varvec{\zeta }) g(\varvec{\zeta } | \varvec{\psi }) \text {d}\varvec{\zeta } \right) \displaystyle \int _{\varvec{\zeta }} f_{\text {c}}(\varvec{y} | \varvec{\omega }, \varvec{\zeta }) g(\varvec{\zeta } | \varvec{\psi }) \text {d}\varvec{\zeta } \cdot \left[ p(\varvec{\omega }, \varvec{\psi })/c \right] \text {d}\varvec{\omega } \text {d}\varvec{\psi } \le \nonumber \\&\quad \displaystyle \int _{\varvec{\psi }} \displaystyle \int _{\varvec{\omega }} \displaystyle \int _{\varvec{\zeta }} \log \left( f_{\text {c}}(\varvec{y} | \varvec{\omega }, \varvec{\zeta }) \right) f_{\text {c}}(\varvec{y} | \varvec{\omega }, \varvec{\zeta }) g(\varvec{\zeta } | \varvec{\psi }) \text {d}\varvec{\zeta } \cdot \left[ p(\varvec{\omega }, \varvec{\psi })/c \right] \text {d}\varvec{\omega } \text {d}\varvec{\psi }. \end{aligned}$$

(18)

We can now recognize both sides of (18) as expected values of log-likelihoods with respect to the model’s posterior distribution, leading to

$$\begin{aligned} \mathrm {E}_{\varvec{\omega }, \varvec{\psi } | \varvec{y}} \left[ \log f_\text {m}(\varvec{y} |\varvec{\omega }, \varvec{\psi } ) \right] \le \mathrm {E}_{\varvec{\omega }, \varvec{\zeta } | \varvec{y}} \left[ \log f_\text {c}(\varvec{y}|\varvec{\omega }, \varvec{\zeta }) \right] . \end{aligned}$$

(19)

Note that the above results do not rely on normality, so they also apply to, e.g., the two-parameter logistic model estimated via marginal likelihood.

B. Effective Number of Parameters for Marginal and Conditional DIC

To consider the effective number of parameters for normal likelihoods, we rely on results from Spiegelhalter et al. (2002). They showed that the effective number of parameters $p_D$ can be viewed as the fraction of information about model parameters in the likelihood, relative to the total information contained in both the likelihood and prior. Under this view, a specific model parameter gets a value of “1” if all of its information is contained in the likelihood, and it gets a value below “1” if some information is contained in the prior. We sum these values across all parameters to obtain $p_D$.

Spiegelhalter et al. (2002) relatedly showed that, for normal likelihoods, $p_D$ can be approximated by

$$\begin{aligned} p_D \approx \text {tr}(\varvec{I}(\hat{\varvec{\theta }}) \varvec{V}), \end{aligned}$$

(20)

where $\varvec{\theta }$ includes all model parameters (including $\varvec{\zeta }$ in the conditional model), $\varvec{I}(\hat{\varvec{\theta }})$ is the observed Fisher information matrix, and $\varvec{V}$ is the posterior covariance matrix of $\varvec{\theta }$. When the prior distribution of $\varvec{\theta }$ is non-informative, then $\varvec{I}(\hat{\varvec{\theta }}) \approx \varvec{V}^{-1}$. Consequently, matching the discussion in the previous paragraph, the effective number of parameters under non-informative priors will approximate the total number of model parameters.

This result implies that the conditional $p_D$ will tend to be much larger than the marginal $p_D$. In particular, in the conditional case, each individual has a unique $\varvec{\zeta }_j$ vector that is included as part of the total parameter count. The resulting $p_D$ will not necessarily be close to the total parameter count because the “prior distribution” of $\varvec{\zeta }_j$ is a hyperdistribution, whereby individuals’ $\varvec{\zeta }_j$ estimates are shrunk toward the mean. Thus, for these parameters, the “prior” is informative. However, even when the fraction of information in the likelihood is low for these parameters, the fact that we are summing over hundreds or thousands of $\varvec{\zeta }_j$ vectors implies that the conditional $p_D$ will be larger than the marginal $p_D$.

C. Adaptive Gaussian Quadrature for Marginal Likelihoods

We modify the adaptive quadrature method proposed by Rabe-Hesketh et al. (2005) for generalized linear mixed models to a form designed to exploit MCMC draws from the joint posterior of all latent variables and model parameters. Here, we describe one-dimensional integration, but the method is straightforward to generalize to multidimensional integration as in Rabe-Hesketh et al. (2005) . We assume that $\zeta _j$ represents a disturbance with zero mean and variance $\tau ^2$ so that there is only one hyperparameter $\psi =\tau$.

In a non-Bayesian setting, standard (non-adaptive) Gauss–Hermite quadrature can be viewed as approximating the conditional prior density $g(\zeta _j|\tau )$ by a discrete distribution with masses $w_m$, $m=1,\ldots , M$ at locations $a_m\tau$ so that the integrals in (2) are approximated by sums of M terms, where M is the number of quadrature points,

$$\begin{aligned} f_\text {m}(\varvec{y}| \varvec{\omega }, {\tau })\ \approx \ \prod _{j=1}^J \sum _{m=1}^M w_m f_\text {c}(\varvec{y}_{j} | \varvec{\omega }, \zeta _j=a_m\tau ) . \end{aligned}$$

(21)

To obtain information criteria, this method can easily be applied to the conditional likelihood function for each draw $\varvec{\omega }^s$ and $\tau ^s$ ($s=1,\ldots ,S$) of the model parameters from MCMC output. This approximation can be thought of as a deterministic version of Monte Carlo integration. Adaptive quadrature is then a deterministic version of Monte Carlo integration via importance sampling.

If applied to each MCMC draw $\varvec{\omega }^s$ and $\tau ^s$, the importance density is a normal approximation to the conditional posterior density of $\zeta _j$, given the current draws of the model parameters. Rabe-Hesketh et al. (2005) used a normal density with mean and variance equal to the mean $\text {E}(\zeta _j|\varvec{y}_j, \varvec{\omega }^s, \tau ^s)$ and variance $\mathrm {var}(\zeta _j|\varvec{y}_j, \varvec{\omega }^s, \tau ^s)$ of the conditional posterior density of $\zeta _j$, whereas Pinheiro and Bates (1995) and some software use a normal density with mean equal to the mode of the conditional posterior and variance equal to minus the reciprocal of the second derivative of the conditional log posterior. Here, we modify the method by Rabe-Hesketh et al. (2005) for the Bayesian setting by using a normal approximation to the unconditional posterior density of $\zeta _j$ as importance density. Specifically, we use a normal density with mean

$$\begin{aligned} {\tilde{\mu }}_j = \widetilde{E}(\zeta _j | \varvec{y}) = \frac{1}{S} \sum _{s=1}^S \zeta _j^s , \end{aligned}$$

(22)

and standard deviation

$$\begin{aligned} {\tilde{\phi }}_j = \sqrt{{\widetilde{\mathrm {var}}}(\zeta _j | \varvec{y}) } = \sqrt{\frac{1}{S-1} \sum _{s=1}^S (\zeta _j^s- {\tilde{\mu }}_j)^2}, \end{aligned}$$

(23)

where $\zeta _j^s$ is the draw of $\zeta _j$ from its unconditional posterior in the sth MCMC iteration. The tildes indicate that these quantities are subject to Monte Carlo error.

Note that this version of adaptive quadrature is computationally more efficient than the one based on the mean and standard deviation of the conditional posterior distributions because the latter would have to be evaluated for each MCMC draw and would require numerical integration, necessitating a procedure that iterates between updating the quadrature locations and weights and updating the conditional posterior means and standard deviations. A disadvantage of our approach is that the quadrature locations and weights (and hence importance density) are not as targeted, but the computational efficiency gained also makes it more feasible to increase M.

The adaptive quadrature approximation to the marginal likelihood for cluster j at posterior draw s becomes

$$\begin{aligned} f_\text {m}(\varvec{y}| \varvec{\omega }, {\tau })\ \approx \ \prod _{j=1}^J \sum _{m=1}^M w_{jm}^s f_\text {c}(\varvec{y}_{j} | \varvec{\omega }, \zeta _j=a_{jm}) , \end{aligned}$$

(24)

where the adapted locations are

$$\begin{aligned} a_{jm} = {\tilde{\mu }}_j + {\tilde{\phi }}_j \times a_m, \end{aligned}$$

(25)

and the corresponding weights or masses are

$$\begin{aligned} w_{jm}^s = \sqrt{2\pi } \times {\tilde{\phi }}_j \times \exp \left( \frac{a_{m}^2}{2} \right) \times g \left( a_{jm}; 0, \tau ^{2,s} \right) \times w_m, \end{aligned}$$

(26)

where $g \left( a_{jm}; 0, \tau ^{2,s} \right)$ is the normal density function with mean zero and variance $\tau ^{2,s}$, evaluated at $a_{jm}$.

The number of integration points M required to obtain a sufficiently accurate approximation is determined by evaluating the approximation of the target quantity (DIC, WAIC) with increasing values of M (7, 11, 17, etc.) and choosing the value of M for which the target quantity changes by less than 0.01 from the previous value. Here, the candidate values for M are chosen to increase approximately by 50% while remaining odd so that one of the quadrature locations is at the posterior mean. Furr (2017) finds this approach to be accurate in simulations for linear mixed models where the adaptive quadrature approximation can be compared with the closed-form integrals.

D. Monte Carlo Error for the DIC and WAIC Effective Number of Parameters

For the DIC effective number of parameters, $p_\text {D}$, we can make use of the well-known method for estimating the Monte Carlo error for the mean of a quantity across MCMC iterations. Let a quantity computed in MCMC iteration s ($s=1,\ldots ,S$) be denoted $\gamma _s$, so the point estimate of the expectation of $\gamma$ is

$$\begin{aligned} \overline{\gamma } \ = \ \frac{1}{S}\sum _{s=1}^S \gamma _s. \end{aligned}$$

Then the squared Monte Carlo error (or Monte Carlo error variance) is estimated as

$$\begin{aligned} \mathrm{MCerr}^2(\overline{\gamma })\ =\ \frac{1}{S_\mathrm{{}eff}}\left[ \frac{1}{S-1} \sum _{s=1}^S (\gamma _s-\overline{\gamma })^2\right] , \end{aligned}$$

(27)

where $S_\mathrm{{}eff}$ is the effective sample size.

For the effective number of parameter approximation in (6) proposed by Plummer (2008), we can obtain the Monte Carlo error variance by substituting

$$\begin{aligned} \gamma _s\ =\ \frac{1}{2} \log \left\{ \frac{f(\varvec{y}_s^{\text {r}1} | \varvec{\theta }_s^1)}{f(\varvec{y}_s^{\text {r}1} | \varvec{\theta }_s^2)} \right\} + \frac{1}{2} \log \left\{ \frac{f(\varvec{y}_s^{\text {r}2} | \varvec{\theta }_s^2)}{f(\varvec{y}_s^{\text {r}2} | \varvec{\theta }_s^1)} \right\} \end{aligned}$$

in (27).

For the effective number of parameter approximation in (4) proposed by Spiegelhalter et al. (2002), we assume that the variation due to $\text {E}_{\varvec{\theta }|\varvec{y}}[-2\log f(\varvec{y}|{\varvec{\theta }})]$ dominates and use

$$\begin{aligned} \gamma _s = -2\log f(\varvec{y}|{\varvec{\theta }_s}). \end{aligned}$$

For the WAIC effective number of parameters, $p_\text {W}$, we use expressions for the Monte Carlo error of sample variances (see, e.g., White, 2010). Let the variance of $\gamma _s$ over MCMC iterations be denoted $v(\gamma )$,

$$\begin{aligned} v(\gamma )\ = \ \frac{1}{S-1} \sum _{s=1}^S (\gamma _s-\overline{\gamma })^2 = \frac{1}{S} \sum _{s=1}^S T_s,\quad \quad T_s = \frac{S}{S-1}(\gamma _s-\overline{\gamma })^2. \end{aligned}$$

Then the Monte Carlo error variance is estimated as

$$\begin{aligned} \mathrm{MCerr}^2(v(\gamma ))\ =\ \frac{1}{S_\mathrm{{}eff}\times S} \sum _{s=1}^S (T_s-v(\gamma ))^2, \end{aligned}$$

(28)

The conditional version of the effective number of parameters is given by the sum over all units of the posterior variances of the pointwise log posterior densities,

$$\begin{aligned} p_{\text {W}\text {c}} \ = \ \sum _{j=1}^J\sum _{i=1}^{n_j} \text {Var}_{\varvec{\omega },\varvec{\zeta }|\varvec{y}} \left[ \log f_\text {c}({y}_{ij}|\varvec{\omega },\varvec{\zeta }_j)\right] . \end{aligned}$$

The posterior variance $\text {Var}_{\varvec{\omega },\varvec{\zeta }|\varvec{y}} \left[ \log f_\text {c}({y}_{ij}|\varvec{\omega },\varvec{\zeta }_j)\right]$ for a given unit is estimated by $v(\gamma _{ij})$ with

$$\begin{aligned} \gamma _{ijs}\ =\ \log f_\text {c}({y}_{ij}|\varvec{\omega }_s,\varvec{\zeta }_{js}), \end{aligned}$$

where we have added subscripts ij to identify the unit, and has Monte Carlo error variance $\mathrm{MCerr}^2(v(\gamma _{ij}))$ given in (28). The variance of the sum of the independent contributions $v(\gamma _{ij})$ to $\hat{p}_{\text {W}\text {c}}$ is the sum of the variances of these contributions,

$$\begin{aligned} \mathrm{MCerr}^2(\hat{p}_{\text {W}\text {c}})\ = \ \sum _{j=1}^J\sum _{i=1}^{n_j} \mathrm{MCerr}^2(v(\gamma _{ij})). \end{aligned}$$

For the marginal version of the effective number of parameters, $p_{\text {W}\text {m}}$, we define

$$\begin{aligned} \gamma _{js}\ =\ \log f_\text {m}(\varvec{y}_{j}|\varvec{\omega }_s,\varvec{\psi }_s) \end{aligned}$$

and

$$\begin{aligned} \mathrm{MCerr}^2(\hat{p}_{\text {W}\text {m}})\ = \ \sum _{j=1}^J\mathrm{MCerr}^2(v(\gamma _{j})). \end{aligned}$$

E. Additional Results

This section contains additional results from the CFA example that were not included in the main text.

Figure 7 shows Spiegelhalter DIC values for models that use the uninformative priors described in the “Prior sensitivity” subsection. Of note here is that Models 2 and 2a sometimes failed to converge, resulting in fewer than ten points in the graphs. Because we used the automatic convergence procedure described in the main text, “failure to converge” here means that the chains did not achieve Gelman–Rubin statistics below 1.05 in the five minutes allotted. When we removed the 5-minute maximum time to convergence, we encountered situations where chains ran for days without converging. In our experience, these convergence issues are often observed for CFA models in JAGS with flat priors. Chains sometimes get stuck in extreme values of the parameter space and cannot recover.

Fig. 7

Marginal and conditional DICs (Spiegelhalter et al. definitions) under uninformative prior distributions for nine models from Wicherts et al.

Figure 8 shows Plummer DIC values for models that use the informative priors described in the “Prior sensitivity” subsection. The figure also contains error bars ($\pm 2$ SDs) from a single replication, similarly to Figure 3 in the main text. These error bars appear to continue to track Monte Carlo error in DIC. Comparing Figure 8 to Figure 4, we observe a different pattern in the conditional DICs across the Plummer and Spiegelhalter definitions. The Spiegelhalter conditional DICs (Figure 4) consistently prefer Model 2a, whereas the Plummer conditional DICs (Figure 8) generally decrease across models and become lowest for the final models, labeled 5b and 6 (though Models 4 and 5a are also similar). On the other hand, the marginal DICs are similar across the Spiegelhalter and Plummer definitions.

Fig. 8

Marginal and conditional DICs (Plummer definitions) under informative prior distributions for nine models from Wicherts et al.