Benefits of Bayesian Model Averaging for Mixed-Effects Modeling

Abstract

Bayes factors allow researchers to test the effects of experimental manipulations in within-subjects designs using mixed-effects models. van Doorn et al. (2021) showed that such hypothesis tests can be performed by comparing different pairs of models which vary in the specification of the fixed- and random-effect structure for the within-subjects factor. To discuss the question of which model comparison is most appropriate, van Doorn et al. compared three corresponding Bayes factors using a case study. We argue that researchers should not only focus on pairwise comparisons of two nested models but rather use Bayesian model selection for the direct comparison of a larger set of mixed models reflecting different auxiliary assumptions regarding the heterogeneity of effect sizes across individuals. In a standard one-factorial, repeated measures design, the comparison should include four mixed-effects models: fixed-effects H₀, fixed-effects H₁, random-effects H₀, and random-effects H₁. Thereby, one can test both the average effect of condition and the heterogeneity of effect sizes across individuals. Bayesian model averaging provides an inclusion Bayes factor which quantifies the evidence for or against the presence of an average effect of condition while taking model selection uncertainty about the heterogeneity of individual effects into account. We present a simulation study showing that model averaging among a larger set of mixed models performs well in recovering the true, data-generating model.

Linear mixed-effects modeling has become a popular approach for analyzing within-subjects designs (Pinheiro & Bates, 2000; Singmann & Kellen, 2019). Besides many other advantages, mixed models offer researchers a lot of flexibility in modeling experimental data. When testing hypotheses via Bayes factors, the large number of possible model specifications leads to the question of how to define a suitable pair of (nested or non-nested) mixed-effects models for comparison. van Doorn et al. (2021) (vDAHSW) presented three pairwise model comparisons for testing within-subjects factors in repeated measures designs. These comparisons differ in the specification of the random-effects structure, especially for the mixed-effects model under the null hypothesis.

Here, we argue that there is no general answer to the question of which pairwise model comparison is the most appropriate one. Instead of using the Bayes factor as a tool for comparing only two specific, nested models, Bayesian model averaging allows researchers to compare a larger set of theoretically interesting models at once. Moreover, the inclusion Bayes factor provides a means for quantifying the amount of evidence for or against the average effect of condition in a repeated measures design while accounting for the uncertainty in model specification (Gronau et al., 2021; Hinne et al., 2020).

Mixed Models for Repeated Measures Designs

We follow vDAHSW in using a simple lexical decision task as a running example. In such a task, N participants have to decide as quickly and accurately as possible whether a letter string is a word or a non-word. Each participant runs through two conditions j = 1, 2. For half of the M presented letter strings, participants have to respond by using their index fingers to press the buttons, whereas they have to use their thumbs in the remaining trials. The experiment thus uses a one-factorial, within-subjects design with two conditions and response time as the dependent variable. The aim is to test whether the two conditions differ with respect to the mean response time.

Specification of Mixed-Effects Models

When using mixed models, it is necessary to choose an appropriate specification of the fixed- and random-effects structure (Pinheiro & Bates, 2000). What renders the situation difficult is that there is not a unique, “correct” way of specifying mixed-effects models (Barr et al., 2013; Bates et al., 2018). From a theoretical perspective, researchers have to commit to a range of specific auxiliary assumptions regarding the specification of a model in order to test the core theoretical question (Kellen, 2019; Suppes, 1966).

In a one-factorial repeated measures design, the fixed-effects parameter ν is defined as half the difference between the means of the two conditions using sum-to-zero coding (cf. vDAHSW). Regarding the random effects, it is uncontroversial that random intercepts α_i are required to model differences in the absolute level of mean response times between individuals. However, it is less clear whether it is necessary to specify random slopes θ_i, that is, individual differences in the effect of the within-subjects factor. Whether the effect is assumed to vary across individuals is not only a theoretical question (Davis-Stober & Regenwetter, 2019; Heck, in press; Rouder & Haaf, in press), but also a methodological one as statistical inference can be biased if the additional variance induced by random slopes is not accounted for by a mixed-effects model.

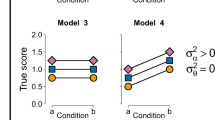
These considerations lead to six possible model specifications which differ with respect to the included fixed and random effects. The corresponding model equations for the i^th individual, in the j^th condition, and for the m^th trial are:

M1 : yijm =μ			+ϵim	(Intercept-only model)
M2 : yijm =μ	+	νxj	+ϵim	(Fixed effect of condition)
M3 : yijm =μ	+αi		+ϵim	(Random intercept)
M4 : yijm =μ	+αi +	νxj	+ϵim	(Random intercept and fixed effect)
M5 : yijm =μ	+αi +	θixj	+ϵim	(Random intercept and random slope)
M6 : yijm =μ	+αi +	(ν + θi)xj	+ϵim	(Full model)

These six models already represent a subset of all 2³ = 8 possible models which are obtained by including or excluding the fixed effect ν, the random intercept α_i, and the random slope θ_i. This selection of models is justified because each model version corresponds to a specific theoretical position (see vDAHSW, for a discussion). The list does not include mixed-effects models that can possibly be defined but are deemed to be highly implausible a priori. For instance, we do not define a model with random slopes but without random intercepts as this would require that variation in individual effects perfectly cancels out across conditions (Rouder, Engelhardt, et al., 2016).

When considering which of the six models actually provide a plausible account of the data-generating mechanism, the first two models M₁ and M₂ can also be criticized. Both of these models assume a complete absence of random intercepts and random slopes and, therefore, of any individual differences. As this is clearly problematic, we follow vDAHSW in discarding the first two models from further discussion. The remaining (reduced) model space contains only the four models M₃ to M₆.

Hypothesis Testing via Pairwise Model Comparisons

In a repeated measures design, hypothesis testing focuses on the question whether the within-subjects factor has an effect on the dependent variable. Hence, the test-relevant parameter of interest is the fixed effect of condition (ν). This leads to the two substantive hypotheses H₀ : ν = 0 (i.e., the means in the two conditions are identical) versus H₁ : ν ≠ 0 (i.e., the means in the two conditions differ). The evidence for the null versus the alternative hypothesis is quantified by the Bayes factor BF₀₁ (Kass & Raftery, 1995), with BF₀₁≈1 indicating that the data are not informative for discriminating between the two models. The Bayes factor provides an ideal method for selecting between two competing models as it achieves an optimal trade-off between model fit and complexity (Myung & Pitt, 1997; Rouder et al., 2012). Before computing a Bayes factor, however, it is necessary to translate the null and the alternative hypotheses into specific mixed-effect models which assume ν = 0 and ν ≠ 0, respectively.

Considering the (reduced) model space, the alternative hypothesis H₁ can be represented either by model M₄ or M₆. Model M₄ makes the auxiliary assumption that by-subject random slopes are irrelevant from a theoretical point of view (i.e., θ_i = 0), which means that all individuals show exactly the same effect across experimental conditions. In contrast, model M₆ assumes the maximal random-effects structure, meaning that the effect of condition is allowed to vary across individuals (i.e., θ_i ≠ 0).

Statistically, model M₄ offers the benefit of being more parsimonious, thus leading to less overfitting, which is especially relevant if there are only few responses in each condition. However, model M₆ is often recommended as a baseline model for (frequentist) tests of within-subject factors due to ensuring more robust results (Barr et al., 2013).

To represent the null hypothesis H₀, we can again select between two candidate models from the (reduced) model space. Model M₃ only includes the by-subject random intercept, whereas model M₅ additionally includes random slopes. The latter model has been criticized as being implausible because it assumes that the variability in individual effects perfectly cancels out on average (i.e., ν = 0; Rouder, Engelhardt, et al., 2016).

To investigate the consequences of the flexibility in model specification, vDAHSW compared three pairwise Bayes factors that have been proposed in the literature for quantifying the evidence for the null versus the alternative hypothesis:

$$\mathrm{RM}\ \mathrm{ANOVA}\ \mathrm{comparison}:{\mathrm{BF}}_{01}^{M_3-{M}_4}\Longleftrightarrow \frac{H_0:v=0\ \mathrm{with}\ {\theta}_i=0}{H_1:v\ne 0\ \mathrm{with}\ {\theta}_i=0}$$

(1)

$$\mathrm{Strict \ null \ comparison}:{\mathrm{BF}}_{01}^{M_3-{M}_6}\Longleftrightarrow \frac{H_0:v=0\ \mathrm{with}\ {\theta}_i=0}{H_1:v\ne 0\ \mathrm{with}\ {\theta}_i\ne 0}$$

(2)

$$\mathrm{Balanced \ null \ comparison}:{\mathrm{BF}}_{01}^{M_5-{M}_6}\Longleftrightarrow \frac{H_0:v=0\ \mathrm{with}\ {\theta}_i \ne 0}{H_1:v\ne 0\ \mathrm{with}\ {\theta}_i\ne 0}$$

(3)

The superscript in ${\mathrm{BF}}_{01}^{M_{3}-M_{4}}$ denotes that the Bayes factor is computed as the ratio of marginal likelihoods of the models M₃ versus M₄.

It is an open question which of the three pairwise comparisons should be preferred as each is based on different auxiliary assumptions and involves different drawbacks and advantages. For example, the comparison M₃ vs. M₄ ignores by-subject random slopes, in turn leading to inflated Bayes factors in favor of H₁, or similarly, to increased Type-I error rates (Barr et al., 2013). The comparison M₃ vs. M₆ suffers from low diagnosticity as the alternative and the null hypothesis differ with respect to the presence of two parameters simultaneously (i.e., the fixed effect ν and the by-subject random slope θ_i). Hence, any evidence in favor of the alternative hypothesis might be due to the fixed effect of condition, the by-subject random slope, or both. While the comparison M₅ vs. M₆ does not suffer from this low diagnosticity, the theoretical underpinning of the null model might be questionable (Rouder, Engelhardt, et al., 2016). Moreover, as both models M₅ and M₆ only differ with respect to the mean ν of the distribution of random slopes (i.e., the average effect of condition either equals zero or differs from zero), a large sample size is required to discriminate between these two statistically complex models empirically (see simulation below).

Model Selection Among Larger Sets of Mixed Models

To account for the uncertainty of which of the three pairwise model comparisons should be preferred, we propose a simple solution. Bayesian model selection via Bayes factors does not only allow researchers to compare two nested models in a pairwise fashion, but also enables the comparison of a larger set of models. By comparing multiple models simultaneously, researchers can express uncertainty with respect to the auxiliary assumptions about the fixed- and random-effects structure (Kellen, 2019). The question of which comparison is most suitable can thus be answered empirically based on the data.

The possibility to compare multiple models does not release the researcher from the challenge to specify a set of candidate models. On the one hand, it may be preferable to limit the potential model space by including only theoretically relevant model versions (Rouder, Engelhardt, et al., 2016). This strategy increases the chances of finding substantial evidence for one of the models and may facilitate the substantive interpretation of the results. On the other hand, including a larger number of candidate models increases the chances that one of the models provides a satisfactory approximation of the data-generating process (Aho et al., 2014). Statistical model selection can be misleading if the set of models is too small because the results are conditional on the specific set of candidate models. It follows that limiting model selection to the comparison of only two model versions comes with the risk of overlooking that both models actually perform poorly. From this perspective, including a larger set of models in the comparison can be beneficial in order to prevent misspecification.

For the present scenario of a one-factorial repeated measures design, the comparison should include the maximal mixed-effects model M₆ as a “catch-all” alternative. The inclusion of this model allows researchers to test whether more simple, constrained models actually provide a satisfactory fit to the data (Barr et al., 2013; Hilbig & Moshagen, 2014). If this is not the case, the more complex, full model will be automatically preferred, thereby reducing the chances of selecting an overly simple, misspecified model. Moreover, models M₃ and M₅ should be included as alternative specifications for the null hypothesis ν = 0 which differ merely with respect to the random slope specification. Note that model selection among these three models provides a direct comparison of all models that occur in the two pairwise comparisons that either use the balanced or the strict null model. Finally, model M₄ should also be included because it is often of interest to test whether the effect of condition varies across individuals or not (Davis-Stober & Regenwetter, 2019; Heck, in press).

An important requirement for performing model selection among a larger set of models is that each model is fitted to exactly the same data set. This implies that it is not possible to compare models fitted to the raw data at the trial level against models fitted to aggregated data at the participant level. Extending the set of candidate models thus allows us to combine the balanced and strict null comparisons within a single analysis, but we cannot make a direct comparison to the RM-ANOVA analysis by vDAHSW based on aggregated data.¹ In selecting among the four candidate models, the two models without random slopes (i.e., M₃ and M₄) are thus fitted at the trial level. We can then compare these models to those with random slopes (i.e., M₅ and M₆) to test whether there is any evidence for the presence of individual differences in the effect of condition. Including all four mixed-effects models M₃ to M₆ shown in Fig. 1 renders the model selection problem diagnostic with respect to both the overall effect of condition and the heterogeneity of individual effects.

Fig. 1

Nested mixed-effects models included in Bayesian model averaging for a repeated measures design with one within-subjects factor

Bayesian Model Averaging

There are practical issues of model selection when using a larger set of models. When comparing M models, one obtains M(M − 1)/2 pairwise Bayes factors. The number of Bayes factors thus rapidly increases as more models are being assessed, which can be a hurdle for interpreting and communicating results. Moreover, when selecting only a single model that is preferred by the Bayes factor, posterior uncertainty on how much evidence the data provide for a specific model is ignored (Hinne et al., 2020; Hoeting et al., 1999). For instance, it may be the case that all four models M₃ to M₆ are supported to a similar degree, in which case researchers should not be very confident in selecting one of the models at all. This gives rise to the question of how to account for model selection uncertainty in drawing substantive conclusions.

As a remedy, we propose to focus on posterior model probabilities which allow researchers to communicate results more concisely and intuitively. Instead of reporting M(M − 1)/2 pairwise Bayes factors, it is sufficient to report M posterior model probabilities. For instance, the results of a repeated measures analysis may show that the two models representing the alternative hypothesis are only slightly more supported, P(M₄| y) = .12 and P(M₆| y) = .35, compared to the two models representing the null hypothesis, P(M₃| y) = .07 and P(M₅| y) = .46. Furthermore, presenting the model selection results by four posterior probabilities shows that the two models assuming random slopes for the effect of condition (M₅ and M₆) have slightly larger posterior probabilities than those without random slopes (M₃ and M₄). However, the computation of posterior model probabilities requires researchers to make assumptions about prior model probabilities which is not the case when focusing on Bayes factors only.

As a default, one may assume uniform prior model probabilities (e.g., P(M_i) = 1/4). In repeated measures designs involving multiple experimental factors, more advanced strategies might be applied to assign prior weights to all combinations of including or excluding specific model terms (e.g., fixed- and random-effects for the main effects and interactions, Scott & Berger, 2010, see Discussion).

Once posterior model probabilities have been computed, we are still faced with the issue of how to answer the core question of whether there is an effect of condition. Bayesian model averaging can be used to contrast one subset of (null) models against the remaining set of (alternative) models. Figure 1 shows that the alternative hypothesis H₁ is represented by the models M₄ and M₆ as both models include the fixed-effects parameter ν. Similarly, the null hypothesis H₀ is represented by the two models not including this parameter (i.e., M₃ and M₅). These two subsets of models can be compared by computing the sum of the corresponding posterior model probabilities. For instance, we can simply add up the posterior model probabilities for the two models corresponding to the null hypothesis, P(M₃| y) + P(M₅| y). By considering the posterior probabilities of all four models, we fully take “into account model uncertainty with respect to choosing a fixed-effect or random-effects model” (Gronau et al., 2021, p. 13). This is in contrast to the common approach of merely selecting one of the competing models.

To answer the core hypothesis whether there is an effect of condition, we can compute the inclusion Bayes factor which compares all mixed-effects models representing H₀: ν = 0 against all models representing H₁: ν ≠ 0. First, it is necessary to sum the prior and posterior model probabilities for the two model sets as discussed above. Second, the inclusion Bayes factor is obtained by dividing the posterior inclusion odds by the prior inclusion odds (Gronau et al., 2021):

$$\mathrm{BF}^\mathrm{inclusion}_{01}=\frac{P(\mathcal{M}_3\mid y)+P(\mathcal{M}_5\mid y)}{\underbrace{P(\mathcal{M}_4\mid y)+P(\mathcal{M}_6\mid y)}_{\mathrm{posterior~inclusion~odds}}} {\bigg /} \frac{P(\mathcal{M}_3)+P(\mathcal{M}_5)}{\underbrace{P(\mathcal{M}_4)+P(\mathcal{M}_6)}_{\mathrm{prior~inclusion~odds}}}.$$

(4)

The inclusion Bayes factor can be interpreted as the factor by which the prior plausibility for the absence of an effect is updated in light of new data, while considering uncertainty whether random slopes should be included in the mixed-effects models representing H₀ and H₁. Equation (4) shows that, in contrast to Bayes factors for pairs of models, the inclusion Bayes factor depends on the prior model probabilities of all four models. When assuming uniform prior model probabilities, the prior inclusion odds in (4) will be one, meaning that the inclusion Bayes factor is thus identical to the ratio of the summed posterior model probabilities of the two subsets of models representing the null and the alternative hypothesis.

The simple definition of the inclusion Bayes factor in (4) allows us to draw direct conclusions about the mechanism of how evidence in the data informs the test of the null versus the alternative hypothesis. If Bayesian model selection clearly indicates that random slopes are necessary to account for the data (i.e., the posterior probabilities of M₃ and M₄ are very small), the inclusion Bayes factor will be very similar to that of the balanced null comparison of model M₅ versus M₆. Similarly, if the results indicate that random slopes are not necessary to account for the data (i.e., the posterior probabilities of M₅ and M₆ are very small), the inclusion Bayes factor will be very similar to that of the RM-ANOVA comparison of model M₃ versus M₄. This means that the inclusion Bayes factor can utilize benefits of both types of model comparisons depending on the evidence in the data regarding the presence of random slopes.

Monte Carlo Simulation

vDAHSW used a single, simulated data set to highlight qualitative differences in the results when using different models for comparison. We think that this approach is beneficial for the purpose of illustration, but it is not sufficient for drawing strong conclusions about the general behavior of the Bayes factor for the selection of mixed-effects models. For instance, results may depend on the specifics of the parameters and the random noise used to generate a simulated data set. Moreover, relying on a single case study can be especially critical for the Bayes factor as it can show a large variability across different data sets even if these were simulated using the same data-generating process (Tendeiro & Kiers, 2019).

As a remedy, we relied on a Monte Carlo simulation to obtain more informative and robust patterns of results (see Linde & van Ravenzwaaij, 2021 for a similar approach). The simulation illustrates the behavior of the Bayes factor when including the four mixed-effects models in Fig. 1 in the comparison while varying the size of the fixed effect and the variance of the random effects. The R scripts of the simulation are available at the Open Science Framework (https://osf.io/tavnf) and may also be useful for sample size planning and design optimization (e.g., Heck & Erdfelder, 2019).

Methods

We used the R scripts provided by vDAHSW to simulate data from a mixed-effect model for a one-factorial within-subjects design with two conditions. Bayes factors were computed using the BayesFactor package (Morey & Rouder, 2015) using default JZS priors with scale parameters r_fixed = 0.5 and r_random = 1. In the Appendix, we provide further simulation results for other prior scale settings. However, varying the prior scales does not change the conclusions substantially.

We chose true, data-generating parameters similar to vDAHSW and simulated 200 data sets within each cell of the factorial design. We varied the fixed effect of condition by generating raw differences of the two means of 2 · ν = 0, 0.2, 0.5, and 0.8. Furthermore, we varied the variance of the random slopes of condition on four levels, Var(θ_i) = 0, 0.25, 1, and 4. The variance of the random intercepts was fixed to 0.5 while assuming independence of random intercepts and random slopes. Concerning the number of observations, we varied the number of items between 1, 5, 10, 15, 20, and 25. Note, however, that the random slopes model with only one observation per condition is not identified (see vDAHSW). We also varied the number of individuals between 10, 20, 30, and 40 but only report the results for N = 20 individuals since the results were qualitatively similar for the other cases.²

Results: Posterior Model Probabilities

Instead of focusing on pairwise Bayes factors, we summarize the results of the simulation by focusing on the posterior probabilities of the four candidate models when assuming equal prior model probabilities. Figure 2 shows the average posterior probability across 200 replications for N = 20 individuals with varying strengths of the fixed effect (column panels) and varying variances of the random slope (row panels).

Fig. 2

Average posterior model probabilities for 200 simulated data sets of N = 20 individuals. The data-generating model is highlighted by a bold line. The label “Random Slope” refers to the variance of the random slopes θ_i. The random intercept is included in all models and fixed to 0.5 in the data simulation

Across all panels, when there is only one item per condition, the average posterior model probabilities are often close to the prior probabilities P(M_i) = .25 meaning that the data do not provide much evidence for distinguishing between the four models. Partly, this reflects the fact that the data are informative only for the overall effect of condition ν ≠ 0 (which determines only the sum of the posterior probabilities of M₄ and M₆), but not for detecting the presence of random slopes because the corresponding models M₅ and M₆ are not identified.

Despite having only a single observation, however, the sum of the posterior probabilities of M₄ and M₆ is not equal to .50 because the Bayes factor takes the complexity of the four models into account while also considering the expected magnitude of the random effects as specified by the prior distributions. Note that the non-informativeness of the model comparison for a single item leads to a “hump” in the pattern of posterior model probabilities in some of the panels in Fig. 2 (e.g., those in the second row).

In the first row of Fig. 2, it is assumed that the variance of random slopes is zero, meaning that the effect of condition is constant for all individuals. Reflecting the data-generating mechanism, the two models assuming random slopes (M₅ and M₆) have a very small posterior probability with as few as five items. If the null hypothesis holds (ν = 0), evidence for the corresponding model M₃ increases for larger numbers of items. If the alternative hypothesis holds and the effect size is medium to large (2 · ν = 0.5 and 2 · ν = 0.8),³ evidence for model M₄ increases with the number of items. Moreover, evidence in favor of the correct model M₄ shows a faster convergence compared to the convergence in favor of model M₃ if the null hypothesis holds (see panel 4 vs. panel 1, respectively, in the first row of Fig. 2). In the former case, the posterior probability also reaches a larger value almost equal to one compared to the latter case. These differences in the rates of accumulating evidence reflect a general behavior of the Bayes factor when testing a point null against an alternative hypothesis (Tendeiro & Kiers, 2019). Moreover, if the alternative hypothesis holds and the effect size is small (2 · ν = 0.2), the Bayes factor indicates a slight preference for the more parsimonious model M₃ with few items, but indicates evidence for the true, data-generating model M₄ as the number of items increases.

Next, we consider the remaining rows of Fig. 2 across which the variance of the random slopes increases. Given a rather small variance of Var(θ_i) = 0.25 (second row), posterior model probabilities favor the random-effects models M₅ and M₆ only when there are 15 or more items per condition. Given less items, the Bayes factor prefers the fixed-effects models M₃ and M₄ as these are more parsimonious while still providing a satisfactory fit to the data. For larger random-effect variances of Var(θ_i) = 1 and 4 (third and fourth row), the Bayes factor reliably detects that individual effects vary across individuals even with only five items per condition. If the random slope variance is large (forth row), the posterior model probabilities of the two random slope models M₅ and M₆ are similar or differ only by a rather small amount. In such cases, it is more difficult to provide evidence for the null versus the alternative hypothesis since the variability of the individual effects has to be considered. This resembles the well-known finding that, in frequentist analyses, including random slopes in mixed-effects models reduce statistical power (Barr et al., 2013). Whereas the amount of evidence for the two models is generally limited, the results show that M₅ is preferred if the null hypothesis is true, whereas M₆ is preferred if there is a medium to large effect size of the fixed effect (2 · ν = 0.5 and 2 · ν = 0.8). However, if the effect size is only small (2 · ν = 0.2), Bayesian model selection provides evidence for the model M₅ even though M₆ was the data-generating model (e.g., second panel in the last row). Overall, the results show that substantial evidence for an average effect of condition can only be obtained if the fixed effect is relatively large compared to the random slope variance (i.e., when the signal-to-noise ratio is high).

Results: Inclusion Bayes Factor

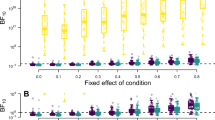
To assess the performance of Bayesian model averaging, Fig. 3 compares the average Bayes factor based on the strict null comparison, the balanced null comparison, and the inclusion Bayes factor for N = 20 individuals. To facilitate the comparison for the varying scales of the Bayes factor on the y-axis across rows, Bayes factors of BF₀₁ = 10 and BF₀₁ = 1/10 are highlighted by dashed horizontal lines.

Fig. 3

Average Bayes factors for 200 simulated data sets of N = 20 individuals. The limits of the y-axis differ for the first row. The solid horizontal line indicates absence of evidence (i.e., BF₀₁ = 1), whereas the two dashed horizontal lines refer to evidence for and against the null hypothesis (i.e., BF₀₁ = 10 and BF₀₁ = 1/10, respectively)

The panels in the first row of Fig. 3 highlight a particular feature of the strict null comparison (cf. case study by vDAHSW). In the presence of random slopes and for at least 10 items, the Bayes factor indicates overwhelming evidence for the alternative model M₆ relative to the null model M₃ irrespective of whether the null hypothesis is actually true or not (i.e., for all values of the fixed effect on the x-axis). This is due to the limited diagnosticity of this model comparison because model M₆ includes both the fixed effect ν and the random slope θ_i, whereas M₃ includes neither of these terms. In this specific setting, the presence of the random effect outweighs the absence of a fixed effect. If the random slope variance is zero, the Bayes factor provides substantial evidence for the null hypothesis if it is true (i.e., if the fixed effect is zero) but also if the fixed effect is small (i.e., 2 · ν = 0.2).

The panels in the second row of Fig. 3 show that the balanced null comparison provides a better discrimination between the null and the alternative hypothesis. Across all numbers of items, the Bayes factor indicates stronger evidence for the alternative hypothesis H₁ as the size of the fixed effect of condition (x-axis) increases. This behavior is expected and desirable: the larger the effect of condition, the easier it will be to find evidence for the presence of the effect. If there is no effect of condition (i.e., ν = 0), the Bayes factor indicates evidence for the null model M₅. Moreover, the more items are included in the repeated measures design, the better the Bayes factor of the balanced null comparison discriminates between the two hypotheses. This can be concluded by the observation that the slope of the lines increases as the number of items across the column panels increases.

Figure 3 shows that the random slope variance has a pronounced effect on the size of the Bayes factor of the balanced null comparison. Discrimination between the null and the alternative hypothesis is highest when the random slope variance is zero, as indicated by the steep slope of the green line (marked with circles): If there is no effect of condition (ν = 0), the Bayes factor favors M₅, the null hypothesis; if there is a large effect of condition (2 · ν = 0.8), the Bayes factor favors M₆, the alternative hypothesis. As the random slope variance increases, it becomes more difficult to discriminate between both models. Often, the average value of the Bayes factor is within the interval of 1/10 to 10, thus indicating that it is difficult to draw strong conclusions based on the balanced null comparison. Whereas this can be interpreted as robust and conservative behavior of the Bayes factor, it also has the drawback that the balanced null comparison has a low sensitivity of detecting the presence of a fixed effect of condition in the absence of random slopes. In this case, the Bayes factor provides only weak evidence for the null hypothesis if it is true, and it provides evidence for the alternative hypothesis only if the fixed effect of condition is sufficiently large (i.e., 2 · ν = 0.5) but not if the effect is small (i.e., 2 · ν = 0.2). This is due to the fact that both models M₅ and M₆ assume random slopes which are not required to fit the data but still render model selection less efficient due to the increased statistical complexity of the models.

The inclusion Bayes factor provides a solution to the low sensitivity of the balanced null comparison while maintaining its robustness. If random slopes are not required to account for the data, the inclusion Bayes factor assigns a smaller weight to the two random slope models M₅ and M₆. In turn, the inclusion Bayes factor will have a higher sensitivity with respect to the presence of the fixed effect of condition as the comparison now mainly relies on the posterior probabilities of M₃ and M₄ (i.e., the RM-ANOVA comparison). Figure 3 highlights a beneficial consequence of this mechanism. If the random slope variance is zero, the inclusion Bayes factor better discriminates between the null and the alternative hypothesis compared to the balanced null comparison. This means that the inclusion Bayes factor indicates stronger evidence for H₀ and for H₁ depending on which model is true, and it indicates at least weak evidence for H₁ even if the fixed effect is small (2·ν = 0.2, panels 3 and 4 in the third row of Fig. 3). If the random slope variance is larger than zero, the inclusion Bayes factor provides almost identical results as the balanced null comparison because the posterior probabilities of the fixed-effects models M₃ and M₄ rapidly drop towards zero (cf. Fig. 2). Overall, the results highlight a major benefit of model averaging: Depending on the information in the data, those mixed-effects models with the highest posterior probability inform the test of the null versus the alternative hypothesis. Thereby, we gain the robustness of the balanced null comparison if random slopes are required but retain the higher sensitivity of the RM-ANOVA comparison otherwise.

Across all panels, the results also show that the Bayes factor does in general provide stronger evidence for the alternative than for the null hypothesis irrespective of which type of model comparison is used. This is due to the well-known fact that, when testing a point null hypothesis, the Bayes factor has a faster rate of convergence towards H₁ if an effect is present than towards H₀ if there is no effect (van Ravenzwaaij & Wagenmakers, in press). This asymmetry in the rate of evidence accumulation is desirable and in line with common sense. In terms of plausible reasoning (Jaynes, 2003), the claim that something is absent is more difficult to support than the claim that something is present, at least when one is uncertain about the effect size of the assumed phenomenon. The asymmetry of the amount of evidence in favor of H₁ and H₀ in Fig. 3 can thus be attributed to a general feature of the Bayes factor and not to a specific shortcoming of the (inclusion) Bayes factor for mixed-effect modeling.

Discussion

vDAHSW raised the question of which pairwise test of mixed-effects models is most appropriate. Here, we highlighted the benefits of directly comparing a larger set of models against each other. For a repeated measures design with one within-subjects factor, the comparison of the four model versions M₃ to M₆ in Fig. 1 allows researchers to draw conclusions about both the average effect of condition and the presence of individual differences concerning this effect. Both of these aspects can be addressed within a single analysis by focusing on the posterior model probabilities.

Bayesian model averaging provides an ideal solution for testing specific substantive hypotheses while taking uncertainty about the auxiliary assumptions into account. Given a possibly large model space, Bayesian model averaging proceeds by bundling models into two non-overlapping subsets. Thereby, multiple mixed-effects models can be used to represent the null and the alternative hypotheses which are of substantive interest. In a simple repeated measures design, we can test for the presence (models M₄ and M₆) or absence (models M₃ and M₅) of an effect of condition while considering the remaining uncertainty about individual differences (Gronau et al., 2021; Hinne et al., 2020). The inclusion of multiple candidate models in the analysis increases transparency regarding the auxiliary assumptions about the fixed- and random-effects structure (Rouder, Morey, & Wagenmakers, 2016). Based on the sum of the corresponding posterior model probabilities, one obtains the inclusion Bayes factor in favor of one subset of models against another subset.

Model Averaging for More Complex Factorial Designs

For more complex experimental designs, the model space grows exponentially with the number of predictor terms. For example, in a 2 × 2 within-subjects design, a model may include the two main effects A and B and the interaction A × B. Accordingly, there are 2³ combinations of fixed effects and 2³ combinations of random effects, leading to model space of 2³ × 2³ = 64 model versions in total. Besides the fact that working with such a large model space is computationally expensive, the plausibility and usefulness of particular model versions can be called into question. To illustrate this, consider a model without any fixed effects but with random slopes for the interaction A × B. Such a model would require that the individual interaction effects do not only cancel out with respect to A, B, and A × B on average, but also with respect to the random slopes for factors A and B within each individual. Often, these assumptions may neither be plausible nor represent any meaningful theoretical position (Rouder, Engelhardt, et al., 2016).

In higher factorial designs, there are two general approaches for dealing with the issue of selecting a set of appropriate mixed-effects models. One can either use the full model space irrespective of the plausibility of specific model versions or specify a reduced model space by selecting a subset of models a priori. The first approach emphasizes the core idea of Bayesian model averaging by considering the full uncertainty with respect to the auxiliary assumptions about model specification. However, when the model space consists of models that are implausible or difficult to interpret, it is not clear what can be learned if these models are supported by the data.

The second approach already rules out some models a priori, in which case it is important to select models according to a certain rationale. One possibility for reducing the model space is to adopt the principle of marginality which states that higher-order interactions should only be included in a model if the corresponding main effects are also included (Rouder, Engelhardt, et al., 2016). This principle also underlies the strict null comparison since random slopes can be interpreted as an interaction of the within-subjects factor with individuals (cf. vDAHSW). Table 1 shows the 14 possible model versions which are obtained by applying the principle of marginality to a 2 × 2 within-subjects design. Essentially, random slopes are only added to a model if it also contains (1) the corresponding fixed effects and (2) the lower-order random slopes. For instance, a model with varying interaction effects across individuals (i.e., with the term A × B × id) must include (1) the three fixed effects A, B, and A × B as well as (2) the random slopes A × id and B × id. Hence, this results in the maximal model which includes all terms.

Table 1 Reduced model space when applying the principle of marginality to a 2 × 2 within-subjects design

As discussed by vDAHSW, excluding some models a priori lead to a lack of diagnosticity since it is not possible to discriminate between the presence of an average effect at the group level and individual heterogeneity of the effect. The simulation results in Fig. 2 also show that models with random slopes but without the corresponding fixed effect (i.e., model M₅ in the one-factorial example) may often obtain a substantial posterior probability. Excluding such models a priori may thus lead to overconfidence with respect to testing the null versus the alternative hypothesis.

As an alternative strategy for selecting a subset of mixed-effects models, one may apply the principle of marginality separately for fixed effects and random slopes. The first five rows in Table 1 show all possible combinations of fixed-effects terms for a 2 × 2 design. When crossed with all five combinations of adding random slopes, this results in 5 × 5 = 25 mixed-effects models. This alternative strategy thus provides a compromise between considering the complete model space (64 models) and applying the principle of marginality to fixed effects and random slopes jointly (14 models). However, it also comes with a lack of interpretability regarding some model versions (e.g., A + B × id). In sum, it remains a challenging question which models to include in the comparison for more complex experimental designs.

Prior Model Probabilities

Irrespective of which models are included in the comparison a priori, model averaging and the inclusion Bayes factor depend on the choice of the prior model probabilities (see Eq. (4)). As the set of models increases, specifying a prior also becomes more complex. At first glance, the reliance on a uniform prior, as introduced above for the one-factorial, within-subjects design, seems to be a straightforward and innocuous solution. However, this choice can be problematic when the number of predictor terms increases as in complex factorial designs (Clyde, 2003; Montgomery & Nyhan, 2010; Zeugner et al., 2015). When assuming a uniform prior for all possible models, most of the prior mass will be on the relatively large subset of models that include an average number of terms (e.g., in a 2 × 2 design, 20 out of 64 models include three of six possible terms). In comparison, the prior probability for the null and the maximal model will be relatively small (i.e., 1/64) which may result in a bias against these models. Moreover, a uniform prior implicitly assumes that the inclusion or exclusion of different terms is independent. However, this assumption is violated when adding interaction effects in a factorial ANOVA. When applying the principle of marginality to exclude particular model versions a priori, the probability of including an interaction depends on the presence of the corresponding main effects which should be expressed in the prior belief of the respective models (Chipman et al., 2001).

Steel (2020) provides an overview about the ongoing debate regarding the specification of prior model probabilities. In principle, either prior choice is acceptable as long as it reflects the prior assumptions of the researcher regarding the plausibility of the different models. A prominent prior choice is the beta-binomial prior which accounts for all combinations of including or excluding specific parts of a model (Scott & Berger, 2010). This prior provides a correction for multiplicity by being less informative with respect to model size (i.e., the number of included terms). Alternatively, one may account for the dependence among predictor terms by using a heredity prior (Chipman et al., 1997). Strong heredity requires that a model with an interaction also includes both main effects (thus resembling the principle of marginality), whereas weak heredity only requires that at least one of the main effects is included. Instead of excluding certain models a priori, Chipman et al. (1997) also proposed relaxed weak heredity priors which leave a small probability (e.g., .01) for implausible models to be included in the comparison. However, future research is required to adopt beta-binomial and heredity priors for mixed-effects models with complex random-effects structures.

Conclusion

The paper by vDAHSW addresses many important issues regarding the use of Bayes factors for mixed-effects modeling in factorial designs. Most importantly, the paper shows that researchers should be aware that auxiliary assumptions are required for translating substantive hypotheses to specific statistical models (Kellen, 2019; Suppes, 1966). While Bayesian model selection is ideally suited for testing substantive theories in psychology (Heck et al., 2021), Bayes factors for mixed models necessarily depend on details of the model specification such as the inclusion of fixed and random effects and the prior distributions. Bayesian model averaging allows researchers to make such researchers degrees of freedom transparent by considering multiple model versions at once, thereby accounting for the inherent uncertainty about auxiliary assumptions in mixed-effects modeling.

Appendix. Different prior settings

Figure 4 and Fig. 5 show the simulation results for varying prior settings based on 200 simulated data sets for N = 20 individuals. The parameters r_fixed and r_random refer to the prior scales for the fixed effect and the random slope, respectively.

Fig. 4

Average posterior model probabilities for varying prior settings. The label “Random Slope” refers to the variance of the random slopes θ_i. The random intercept is included in all models and fixed to 0.5 in the data simulation

Fig. 5

Average Bayes factor for varying prior settings. The limits of the y-axis differ for the first row. The solid horizontal line indicates absence of evidence (i.e., BF₀₁ = 1), whereas the two dashed horizontal lines refer to evidence for and against the null hypothesis (i.e., BF₀₁ = 10 and BF₀₁ = 1/10, respectively)