Bayes Factor Model Comparisons Across Parameter Values for Mixed Models

Abstract

Nested data structures, in which conditions include multiple trials and are fully crossed with participants, are often analyzed using repeated-measures analysis of variance or mixed-effects models. Typically, researchers are interested in determining whether there is an effect of the experimental manipulation. These kinds of analyses have different appropriate specifications for the null and alternative models, and a discussion on which is to be preferred and when is sorely lacking. van Doorn et al. (2021) performed three types of Bayes factor model comparisons on a simulated data set in order to examine which model comparison is most suitable for quantifying evidence for or against the presence of an effect of the experimental manipulation. Here, we extend their results by simulating multiple data sets for various scenarios and by using different prior specifications. We demonstrate how three different Bayes factor model comparison types behave under changes in different parameters, and we make concrete recommendations on which model comparison is most appropriate for different scenarios.

Introduction

The presence of nested or hierarchical data structures is common in various fields of science. van Doorn et al. (2021, henceforth vDAHSW) describe a typical example of a response time experiment where multiple trials are nested within conditions, and conditions are fully crossed with participants (i.e., condition is a within-subjects variable). In such experiments, researchers are typically interested in the effect of the experimental manipulation (i.e., the condition) on the dependent variable (i.e., some measure of the response time). Critically, there are multiple statistical approaches towards that end and, as alluded to by vDAHSW, the choice among them depends on many factors.

Traditionally, the observations in all trials of each participant within each condition are aggregated by calculating the mean, leaving one value of the dependent variable per participant and condition. Subsequently, a repeated-measures analysis of variance (RM-ANOVA) is conducted on this aggregated data set and information on the effect of the experimental manipulation can be extracted. Such an effect is typically labeled a fixed effect and it represents a shift in the population mean between conditions (see, e.g., the top-row panels of Fig. 1 in vDAHSW).

Fig. 1

Bayes factors for RM-ANOVA (purple) on the aggregated data, Balanced null (green) on the full data, and Strict null (yellow) on the full data as a function of the fixed effect of the independent variable “condition.” Panel B displays a zoomed-in version of panel A. The empty dots show the Bayes factors for 50 repetitions with the same parameter values

Alternatively, mixed-effects models (also called multilevel, hierarchical, varying-effects, or random-effects models; cf. McElreath, 2020) have gained popularity and are considered to be one of the most important developments in the statistical sciences in recent years (Gelman and Vehtari, 2021). These models are able to capitalize on the full unaggregated data structure, providing information on potential baseline differences between participants (random intercepts; see, e.g., the middle-row panels of Fig. 1 in vDAHSW) and the potential differential impact of the experimental manipulation on participants (random slopes; see, e.g., the bottom-row panels of Fig. 1 in vDAHSW) in addition to information on the effect of the experimental manipulation (fixed effect; see, e.g., the top-row panels of Fig. 1 in vDAHSW). Random intercepts and random slopes vary at the participant level (i.e., one of each per participant) and can characterize differences in effects on the level of condition, but also on the level of individual trials. For the remainder of this paper, random intercepts and slopes strictly refer to individual effects on the level of condition. We refer the reader to, for instance, Baayen et al. (2008), Gelman and Hill (2006), Kruschke (2015), Snijders and Bosker (2011), McElreath (2020), and Singmann and Kellen (2019) for general introductions to mixed-effects models.

Independent of whether RM-ANOVA or mixed-effects models are used, testing for the presence or absence of an effect of the experimental manipulation requires the specification of a null model ${\mathscr{M}}_{0}$ that does not contain the effect of interest and an alternative model ${\mathscr{M}}_{1}$ that does contain the effect of interest. In the Bayesian inference framework, a Bayes factor can be calculated that quantifies the likelihood of the data y under ${\mathscr{M}}_{1}$ relative to the likelihood of y under ${\mathscr{M}}_{0}$ (or vice versa):

$$ \text{BF}_{10}=\frac{P\left( y\left|\mathcal{M}_{1}\right.\right)}{P\left( y\left|\mathcal{M}_{0}\right.\right)}\text{.} $$

(1)

Bayes factors can range from 0 to $\infty$, where BF₁₀ > 1 indicates evidence in favor of ${\mathscr{M}}_{1}$ and BF₁₀ < 1 evidence in favor of ${\mathscr{M}}_{0}$ (see, e.g., Jeffreys, 1961; Kass & Raftery, 1995; van Ravenzwaaij & Etz, 2021; Etz & Vandekerckhove, 2018; Heck et al., 2020).

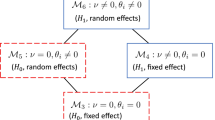
As emphasized by vDAHSW, there is no consensus yet on which models should be used as ${\mathscr{M}}_{0}$ and ${\mathscr{M}}_{1}$ for the Bayes factor model comparison regarding the effect of the experimental manipulation. vDAHSW list two possibilities for selecting ${\mathscr{M}}_{0}$, two possibilities for selecting ${\mathscr{M}}_{1}$, and three comparisons between those: RM-ANOVA, comparing ${\mathscr{M}}_{0-RM}$ to ${\mathscr{M}}_{1-RM}$, Balanced null, comparing ${\mathscr{M}}_{0-BN}$ to ${\mathscr{M}}_{1-BN}$, and Fixed null, comparing ${\mathscr{M}}_{0-RM}$ to ${\mathscr{M}}_{1-BN}$ (see vDAHSW for more details). The two versions of ${\mathscr{M}}_{0}$ under consideration are:

• ${\mathscr{M}}_{0-RM}$, containing random intercepts for participants α_i but no random slopes for participants 𝜃_i and no fixed effect of condition ν:

  $$ \begin{aligned} Y_{ijm}&\sim\text{N}\left( \alpha_{i}, \sigma^{2}_{\epsilon}\right)\\ \alpha_{i}&\sim\text{N}\left( \mu, \sigma^{2}_{\alpha}\right) \end{aligned} $$

  (2)

• ${\mathscr{M}}_{0-BN}$, containing random intercepts for participants α_i and random slopes for participants 𝜃_i but no fixed effect of condition ν:

  $$ \begin{aligned} Y_{ijm}&\sim\text{N}\left( \alpha_{i}+x_{j}\theta_{i}, \sigma^{2}_{\epsilon}\right)\\ \alpha_{i}&\sim\text{N}\left( \mu, \sigma^{2}_{\alpha}\right)\\ \theta_{i}&\sim\text{N}\left( 0, \sigma^{2}_{\theta}\right) \end{aligned} $$

  (3)

Thus, the difference between ${\mathscr{M}}_{0-RM}$ and ${\mathscr{M}}_{0-BN}$ lies in the inclusion of random slopes for participants. The two versions of ${\mathscr{M}}_{1}$ under consideration are:

• ${\mathscr{M}}_{1-RM}$, containing the fixed effect of condition ν and random intercepts for participants α_i but no random slopes for participants 𝜃_i:

  $$ \begin{aligned} Y_{ijm}&\sim\text{N}\left( \alpha_{i}+x_{j}\nu, \sigma^{2}_{\epsilon}\right)\\ \alpha_{i}&\sim\text{N}\left( \mu, \sigma^{2}_{\alpha}\right) \end{aligned} $$

  (4)

• ${\mathscr{M}}_{1-BN}$, containing the fixed effect of condition ν, random intercepts for participants α_i, and random slopes for participants 𝜃_i:

  $$ \begin{aligned} Y_{ijm}&\sim\text{N}\left( \alpha_{i}+x_{j}\theta_{i}, \sigma^{2}_{\epsilon}\right)\\ \alpha_{i}&\sim\text{N}\left( \mu, \sigma^{2}_{\alpha}\right)\\ \theta_{i}&\sim\text{N}\left( \nu, \sigma^{2}_{\theta}\right) \end{aligned} $$

  (5)

Again, the difference between ${\mathscr{M}}_{1-RM}$ and ${\mathscr{M}}_{1-BN}$ lies in the inclusion of random slopes for participants. The three comparisons between these, as described in vDAHSW, are:

• RM-ANOVA: ${\mathscr{M}}_{0-RM}$ versus ${\mathscr{M}}_{1-RM}$ using the aggregated data. Both models allow for different intercepts between participants ($\sigma ^{2}_{\alpha }\neq 0$): The only difference between the two models being compared is that in ${\mathscr{M}}_{0-RM}$ the fixed effect of condition is ν = 0, whereas in ${\mathscr{M}}_{1-RM}$ the fixed effect of condition is ν≠ 0.

• Balanced null: ${\mathscr{M}}_{0-BN}$ versus ${\mathscr{M}}_{1-BN}$ using the full data. Both models allow for different intercepts and slopes between participants ($\sigma ^{2}_{\alpha }\neq 0$ and $\sigma ^{2}_{\theta }\neq 0$): The only difference between the two models being compared is that in ${\mathscr{M}}_{0-BN}$ the fixed effect of condition is ν = 0, whereas in ${\mathscr{M}}_{1-BN}$ the fixed effect of condition is ν≠ 0.

• Strict null: ${\mathscr{M}}_{0-RM}$ versus ${\mathscr{M}}_{1-BN}$ using the full data. Both models allow for different intercepts between participants ($\sigma ^{2}_{\alpha }\neq 0$): The difference between the two models being compared is that in ${\mathscr{M}}_{0-RM}$ the fixed effect of condition is ν = 0 and the variance of random slopes for participants is $\sigma ^{2}_{\theta }=0$, whereas in ${\mathscr{M}}_{1-BN}$ the fixed effect of condition is ν≠ 0 and the variance of random slopes for participants is $\sigma ^{2}_{\theta }\neq 0$.

Therefore, these three Bayes factor model comparison methods ask different questions. The essence of the RM-ANOVA and the Balanced null methods is to examine whether there is an average effect of the experimental manipulation across participants. In contrast, the Strict null method examines whether there is an average effect of the experimental manipulation across participants or whether there is variation of the effect of the experimental manipulation for individual participants.

vDAHSW give examples in which the RM-ANOVA, Balanced null, and Strict null model comparison methods give very different results depending on whether or not the data are aggregated.

The Current Study

The results of Example 1 in vDAHSW offer important insights on the usability of the different Bayes factor model comparison methods for nested data. However, the Bayes factors obtained by vDAHSW only apply to a single simulated data set and a unique prior specification. Since the data simulation entails sampling variability, it is worthwhile to examine the robustness of the Bayes factors applied to multiple simulated data sets with the same parameter values. Moreover, although the choice of parameter values for the data simulation of vDAHSW is plausible, it is unclear whether the behavior of the three Bayes factor model comparison methods is similar for data sets that were generated using different parameter values. Lastly, vDAHSW used one specific setting for the priors. It is possible that different settings for the priors affect the three types of Bayes factor comparisons differently. In the current study, we explore the scenario of Example 1 by vDAHSW more thoroughly in order to assess the robustness of the Bayes factor comparison results for data generated using different parameter values and for different choices of priors.

Methods

We calculated Bayes factors corresponding to the RM-ANOVA, the Balanced null, and the Strict null model comparison types for various scenarios of data sets and prior specifications. As a reference point, we print here the parameter values vDAHSW used in their Example 1:

• M = 15 trials,

• I = 20 participants,

• J = 2 conditions,

• ν = 0.5, the fixed effect of condition,

• $\sigma ^{2}_{\alpha }=0.5$, the variance of the random intercepts for participants,

• $\sigma ^{2}_{\theta }=1$, the variance of the random slopes for participants,

• ρ_α𝜃 = 0, the correlation between random intercepts and random slopes for participants.

In both the original simulation and our simulations, trials, participants, and conditions are fully crossed. The authors used multivariate Cauchy priors with scales of r_fixed = 0.5 and r_random = 1 for fixed and random effects, respectively.

We simulated data sets using the parameter values of vDAHSW, while varying one parameter at a time. Doing this allowed us to inspect the effect of variations in each of the parameters individually on the results reported by vDAHSW (see the Appendix for two-way interactions between parameters and the Supplementary Material, available at https://osf.io/gz57a/, for higher-way interactions). The parameter values we used are (parameter values shown in bold font correspond to the default values employed by vDAHSW):

• $\nu =\left \{0, 0.1, \dots , \textbf {0.5}, \dots , 0.8\right \}$,

• $\sigma ^{2}_{\alpha }=\left \{0, 0.25, \textbf {0.5}, \dots , 2\right \}$,

• $\sigma ^{2}_{\theta }=\left \{0, 0.25, \dots , \textbf {1}, \dots , 2\right \}$,

• $\rho _{\alpha \theta }=\left \{-0.8, -0.6, \dots , \textbf {0}, \dots , 0.8\right \}$,

• $I=\left \{5, 10, \dots , \textbf {20}, \dots , 50\right \}$,

• $M=\left \{5, 10, \textbf {15}, \dots , 50\right \}$,

• $r_{fixed}=\left \{0.2, 0.3, \dots , \textbf {0.5}, \dots , 0.8\right \}$,

• $r_{random}=\left \{0.4, 0.6, \dots , \textbf {1}, \dots , 1.6\right \}$,

yielding 70 different combinations of parameter values.

The ranges of parameter values were chosen in a way such that they entail a broad spectrum of values that we consider to be realistic. For instance, the values for ν are oriented at rules of thumb for effect sizes by Cohen (1988), where ν = 0.2, ν = 0.5, and ν = 0.8 are considered small, medium, and large effects, respectively; ν = 0 was included to be able to compare Bayes factor model comparison methods when no effect of the experimental manipulation is present and the Bayes factors should thus indicate pro ${\mathscr{M}}_{0}$ evidence. As another example, the range of mathematically possible correlations is $\left [-1, ~ 1\right ]$, which gave us a natural restriction for ρ_α𝜃; since we deemed correlations of − 1 or 1 highly unlikely, we limited the range for ρ_α𝜃 to be $\left [-0.8, ~ 0.8\right ]$.

Note that in our simulations, we limited the number of conditions to J = 2. Presently, the data generation function provided by vDAHSW (available at https://osf.io/tjgc8/) only works for J = 2 conditions (personal communication with vDAHSW). Moreover, equivalent to the methods of vDAHSW, we keep the fixed effect of trial, the variance of random intercepts of trial, the variance of random slopes of trial, and the correlation of random intercepts and random slopes of trial constant at 0. Because of sampling variability, we created 50 data sets for each of the 70 possible parameter value combinations, which allowed us to assess the robustness of the resulting Bayes factors to sampling fluctuations.

Of all 3500 full unaggregated data sets, we calculated an additional aggregated data set by taking the mean of the scores on the dependent variable of the trials for each participant and each condition, yielding 3500 full data sets and 3500 corresponding aggregated data sets. Analogous to the procedure followed by vDAHSW, we calculated the RM-ANOVA, the Balanced null, and the Strict null Bayes factors with the BayesFactor package (Morey and Rouder, 2018) written in R (R Core Team, 2021). The relevant files can be accessed at https://osf.io/gz57a/, which strongly rely on the files from vDAHSW (accessible at https://osf.io/p74wk/).

Results

The results of the comparisons between the RM-ANOVA, the Balanced null, and the Strict null Bayes factor model comparisons for (1) the fixed effect of condition ν; (2) the variance of random intercepts for participants $\sigma ^{2}_{\alpha }$; (3) the variance of random slopes for participants $\sigma ^{2}_{\theta }$; (4) the correlation of random intercepts and random slopes for participants ρ_α𝜃; (5) the number of subjects I; (6) the number of trials M; (7) the scale of the multivariate Cauchy prior for fixed effects r_fixed; and (8) the scale of the multivariate Cauchy prior for random effects r_random are shown in Figs. 1, 2, 3, 4, 5, 6, 7, and 8, respectively. Importantly, in each figure, only the parameter shown on the x-axis is varied; all other parameters are kept constant at the values used in vDAHSW. Panel A of each figure shows the obtained Bayes factors; Bayes factors higher than the highest 75% quantile (i.e., the upper edge of the highest boxplot) are not shown. In order to enhance the visibility of the differences in the Bayes factors for the RM-ANOVA and Balanced null comparisons, panel B of each figure displays a zoomed-in version of panel A. Moreover, results for the RM-ANOVA Bayes factors were obtained on the aggregated data and results for the Balanced null and Strict null Bayes factors on the full data. In the Appendix and Supplementary Material, we present simulations that vary multiple parameters at once. The Appendix shows potential two-way interactions between parameters. Higher-way interactions can be inspected in the Supplementary Material, available at https://osf.io/gz57a/.

Figure 1 shows that for the full data sets the Strict null method always provides overwhelming evidence in favor of ${\mathscr{M}}_{1}$, even when the fixed effect of condition is ν = 0. This strongly suggests that the Strict null Bayes factor is largely driven by the presence of random slopes for participants, which are part of ${\mathscr{M}}_{1}$ but not ${\mathscr{M}}_{0}$ (see also vDAHSW). This behavior is likely to be undesirable in most practical applications: when the fixed effect of condition is of interest, pro ${\mathscr{M}}_{0}$ evidence should be obtained when the true fixed effect of condition is (close to) ν = 0. In contrast, the Balanced null method produces Bayes factors that vary meaningfully with the fixed effect of condition; that is, the higher the fixed effect of condition, the higher the Bayes factors. Nevertheless, the Balanced null Bayes factors are conservative, only providing weak evidence towards ${\mathscr{M}}_{1}$ even for large fixed effects of condition (i.e., ν > 0.5). For the aggregated data, the RM-ANOVA method varies meaningfully with the fixed effect of condition. When ν = 0 evidence in favor of ${\mathscr{M}}_{0}$ is usually obtained. For moderate and large fixed effects of condition (i.e., ν > 0.5), the evidence is relatively weak but still quite clearly points towards ${\mathscr{M}}_{1}$.

Figure 2 indicates that for the full data sets the Bayes factors for the Balanced null and Strict null methods are unaffected by the variance of random intercepts for participants. For all variances of random intercepts for participants, the Strict null method provides overwhelming evidence for ${\mathscr{M}}_{1}$, whereas the Balanced null method displays ambiguous evidence. Similarly, for the aggregated data sets, the RM-ANOVA method also produces Bayes factors that do not depend on the variance of random intercepts for participants (at least, not strongly). Generally, the RM-ANOVA method provides relatively weak evidence in favor of ${\mathscr{M}}_{1}$. The invariance of all three types of Bayes factor model comparison methods to the variance of random intercepts for participants is as it should be because this term is included in all null models and alternative models used in the corresponding comparisons.

Fig. 2

Bayes factors for RM-ANOVA (purple) on the aggregated data, Balanced null (green) on the full data, and Strict null (yellow) on the full data as a function of the variance of the random intercepts for participants. Panel B displays a zoomed-in version of Panel A. The empty dots show the Bayes factors for 50 repetitions with the same parameter values

As shown in Fig. 3, for the full data sets, the Strict null method still provides extreme evidence in favor of ${\mathscr{M}}_{1}$ for all variances of random slopes for participants. It is further visible that the Bayes factors obtained with the Strict null method sharply increase as the variance of random slopes for participants increases. In contrast, the Balanced null method yields Bayes factors providing ambiguous evidence for relatively high variances of random slopes for participants (i.e., $\sigma ^{2}_{\theta }>0.5$). As the variance of random slopes for participants decreases, the Balanced null Bayes factors indicate clear evidence towards ${\mathscr{M}}_{1}$. When the aggregated data are used, the RM-ANOVA method also yields Bayes factors providing ambiguous evidence for high variances of random slopes for participants (i.e., $\sigma ^{2}_{\theta }>0.5$) and clear pro ${\mathscr{M}}_{1}$ evidence for lower variances of random slopes for participants. We believe that the Balanced null and RM-ANOVA Bayes factors are higher for low variances of the random slopes for participants due to the posterior being more narrow. The reason for this is that the fixed effect of condition can be estimated more precisely in the absence of noise (i.e., variance of random slopes for participants). This effect should be even more pronounced for RM-ANOVA, as the models no longer have to compensate for the existence of variance of random slopes for participants which is not present in the model specification.

Fig. 3

Bayes factors for RM-ANOVA (purple) on the aggregated data, Balanced null (green) on the full data, and Strict null (yellow) on the full data as a function of the variance of the random slopes for participants. Panel B displays a zoomed-in version of panel A. The empty dots show the Bayes factors for 50 repetitions with the same parameter values

The Balanced null and Strict null Bayes factors on the full data sets as well as the RM-ANOVA Bayes factors on the aggregated data sets are largely unaffected by the correlation of the random intercepts and random slopes for participants (see Fig. 4). While the Strict null Bayes factors provide overwhelming evidence in favor of ${\mathscr{M}}_{1}$, the Balanced null and RM-ANOVA Bayes factors indicate ambiguous evidence.

Fig. 4

Bayes factors for RM-ANOVA (purple) on the aggregated data, Balanced null (green) on the full data, and Strict null (yellow) on the full data as a function of the correlation between the random intercepts and random slopes for participants. Panel B displays a zoomed-in version of panel A. The empty dots show the Bayes factors for 50 repetitions with the same parameter values

The results displayed in Fig. 5 suggest that the evidence towards ${\mathscr{M}}_{1}$ for the Balanced null, Strict null, and RM-ANOVA model comparisons is bolstered by an increasing number of participants. This is as it should be, because having more participants reduces the uncertainty around the estimate of the fixed effect of condition ν. In contrast, Fig. 6 shows that an increasing number of trials leads to stronger evidence for ${\mathscr{M}}_{1}$ in case of the Strict null Bayes factors on the full data sets but not in case of the Balanced null Bayes factors on the full data sets and the RM-ANOVA Bayes factors on the aggregated data sets. Related to the conclusions of vDAHSW, we suspect that the Strict null Bayes factors increase in magnitude with an increasing number of trials because more trials ensure a reduced uncertainty around the estimate of the variance of the random slopes for participants, demonstrating more clearly that $\sigma ^{2}_{\theta }\neq 0$.

Fig. 5

Bayes factors for RM-ANOVA (purple) on the aggregated data, Balanced null (green) on the full data, and Strict null (yellow) on the full data as a function of the number of subjects. Panel B displays a zoomed-in version of panel A. The empty dots show the Bayes factors for 50 repetitions with the same parameter values

Fig. 6

Bayes factors for RM-ANOVA (purple) on the aggregated data, Balanced null (green) on the full data, and Strict null (yellow) on the full data as a function of the number of trials. Panel B displays a zoomed-in version of panel A. The empty dots show the Bayes factors for 50 repetitions with the same parameter values

Figures 7 and 8 demonstrate that the Bayes factors resulting from the RM-ANOVA, Balanced null, and Strict null model comparisons are quite robust against variations of the multivariate Cauchy priors for fixed and random effects, respectively. That is, none of the three Bayes factor model comparison types changes substantially as a function of the multivariate Cauchy prior scales.

Fig. 7

Bayes factors for RM-ANOVA (purple) on the aggregated data, Balanced null (green) on the full data, and Strict null (yellow) on the full data as a function of the scale of the multivariate Cauchy prior for fixed effects. Panel B displays a zoomed-in version of panel A. The empty dots show the Bayes factors for 50 repetitions with the same parameter values

Fig. 8

Bayes factors for RM-ANOVA (purple) on the aggregated data, Balanced null (green) on the full data, and Strict null (yellow) on the full data as a function of the scale of the multivariate Cauchy prior for random effects. Panel B displays a zoomed-in version of panel A. The empty dots show the Bayes factors for 50 repetitions with the same parameter values

In terms of two-way interactions, we found effects for some of the dyads of fixed effect, variance of slopes for participants, variance of intercepts for participants, and number of participants, depending on the specific Bayes factor model comparison. More details can be found in the Appendix.

Discussion

In Example 1 of vDAHSW, the RM-ANOVA, Balanced null, and Strict null Bayes factor model comparison types were compared on a nested data set, where multiple trials were nested within conditions, and conditions and participants were fully crossed. The authors concluded that the RM-ANOVA and Strict null Bayes factors were unreasonably large for a modest effect of condition of ν = 0.5 and only I = 20 participants due to the presence of variance of random slopes for participants. Only the Balanced null Bayes factor was appropriately conservative, due to the fact that the variance of random slopes for participants is present in both the null and alternative models being compared.

We extended their findings by comparing the three Bayes factor types for various scenarios. We found that the RM-ANOVA Bayes factor on aggregated data sets and the Balanced null Bayes factor on full data sets varied meaningfully with changes in the fixed effect of condition ν, showing pro ${\mathscr{M}}_{0}$ evidence when appropriate. The Strict null Bayes factor on the full data sets is largely driven by the presence of variance of random slopes for participants $\sigma ^{2}_{\theta }$. A larger sample size benefits all three Bayes factors, whereas a larger number of trials increases the Strict null Bayes factor, but not the Balanced null and RM-ANOVA Bayes factors. The variance of random intercepts for participants, the correlation between random intercepts and slopes for participants, and the settings of the priors had no qualitative effect on the results of vDAHSW. We also observed considerable variation of the Bayes factors for all three Bayes factor model comparison methods for multiple data sets that were sampled with identical population parameters, which in some cases led to qualitatively different conclusions. This variability mainly stems from sampling fluctuations. Clearly then, any single Bayes factor resulting from a single data set should be judged with caution (as is the case for all measures that are data-dependent and thus subject to sampling variability, e.g., p-values, confidence intervals).

In general, we agree with the conclusions of vDAHSW. More specifically, with the settings we used in our simulations, the Strict null Bayes factor always provides overwhelming evidence in favor of ${\mathscr{M}}_{1}$, even when the fixed effect of condition is around ν = 0. In contrast, the Balanced null Bayes factor varies meaningfully with the fixed effect of condition, providing evidence towards ${\mathscr{M}}_{0}$ when the fixed effect of condition is around ν = 0 and at least weak evidence towards ${\mathscr{M}}_{1}$ when the fixed effect of condition is approximately ν > 0.5. The flipside is that the Balanced null Bayes factor appears to be quite conservative, habitually producing Bayes factors of a magnitude of about 10 even when the fixed effect of condition is ν = 0.5. We should keep in mind though, that these results are for the scenario when the sample size is I = 20. Arguably it should be difficult to obtain decisive evidence for such a small sample size in case of all but the most extravagant effect sizes.

The Strict null Bayes factor clearly asks a different question from the Balanced null Bayes factor. Where the latter asks “Is there a mean effect of condition?” the former asks “Is there any effect of condition?” Traditionally, the focus of testing and quantifying effects has been on the mean, so in that sense the Balanced null comparison is more in line with tradition, but it is certainly conceivable that the variance of random slopes for participants is the focal interest of the researcher. In that case, we recommend a more gradual comparison of models, comparing ${\mathscr{M}}_{0-RM}$ to ${\mathscr{M}}_{0-BN}$ (i.e., the models that differ only in their inclusion of variance of random slopes for participants), so that there is no conflation of effects in the Bayes factor.

Another approach is to calculate an inclusion Bayes factor. Inclusion Bayes factors allow one to compare all models that include a predictor (e.g., fixed effect of condition or variance of random slopes for participants) with all those that do not, to determine the relative strength of evidence for each factor on the dependent variable based on the data (van den Bergh et al., 2020). For instance, the inclusion Bayes factor for the fixed effect of condition for the four previously discussed models would be:

$$ \text{BF}_{\nu\neq0, \nu=0} = \frac{\left( \frac{P\left( \mathcal{M}_{1-RM}| y\right)+P\left( \mathcal{M}_{1-BN}| y\right)}{P\left( \mathcal{M}_{0-RM}| y\right)+P\left( \mathcal{M}_{0-BN}| y\right)}\right)}{\left( \frac{P\left( \mathcal{M}_{1-RM}\right)+P\left( \mathcal{M}_{1-BN}\right)}{P\left( \mathcal{M}_{0-RM}\right)+P\left( \mathcal{M}_{0-BN}\right)}\right)}\text{;} $$

(6)

and the inclusion Bayes factor for the variance of the random slopes for participants for the four previously discussed models would be:

$$ \text{BF}_{\sigma^{2}_{\theta}\neq0, \sigma^{2}_{\theta}=0} = \frac{\left( \frac{P\left( \mathcal{M}_{0-BN}| y\right)+P\left( \mathcal{M}_{1-BN}| y\right)}{P\left( \mathcal{M}_{0-RM}| y\right)+P\left( \mathcal{M}_{1-RM}| y\right)}\right)}{\left( \frac{P\left( \mathcal{M}_{0-BN}\right)+P\left( \mathcal{M}_{1-BN}\right)}{P\left( \mathcal{M}_{0-RM}\right)+P\left( \mathcal{M}_{1-RM}\right)}\right)}\text{.} $$

(7)

For a more extensive discussion on inclusion Bayes factors, see Heck and Bockting (2021).

Conclusion

Bayes factors are not magic. They can answer the question researchers ask. In that sense, none of the three comparisons is strictly superior to any other. In practice, our intuition is that researchers are most often interested in testing for the presence of a fixed effect of condition. In such a case, the Balanced null comparison using full unaggregated data or possibly the RM-ANOVA comparison using aggregated data are to be preferred. If the focus is on the variance of random slopes for participants alone, we believe an entirely different model comparison is in order. Regardless, we echo the sentiment by vDAHSW that “a discussion on best practices in Bayes factor model comparison in mixed models” is in order and we hope that our simulation results contribute to this discussion.

Appendix A: Two-way Interactions Between Parameters

Here, we present results from our extended parameter simulation in terms of pairs of parameters. This should allow for a qualitative inspection of the presence of two-way interactions for each of the three Bayes factor model comparisons. Figure 9 presents the results for RM-ANOVA Bayes factors, Fig. 10 presents the results for Balanced null Bayes factors, and Fig. 11 presents the results for Strict null Bayes factors.

Fig. 9

Median RM-ANOVA Bayes factors on aggregated data for all combinations of values of two respective parameters. The median is calculated for the Bayes factors over all values of the six remaining parameters. Note that the y-axes in the panels display different ranges of Bayes factors

Fig. 10

Median Balanced null Bayes factors on aggregated data for all combinations of values of two respective parameters. The median is calculated for the Bayes factors over all values of the six remaining parameters. Note that the y-axes in the panels display different ranges of Bayes factors

Fig. 11

Median Strict null Bayes factors on aggregated data for all combinations of values of two respective parameters. The median is calculated for the Bayes factors over all values of the six remaining parameters. Note that the y-axes in the panels display different ranges of Bayes factors

Turning first to the results of the RM-ANOVA Bayes factors (Fig. 9), we see interactions for (1) fixed effect of condition versus variance of random intercepts for participants (highest for high fixed effect of condition and zero variance of random intercepts for participants), (2) fixed effect of condition versus variance of random slopes for participants (highest for high fixed effect of condition and zero variance of random slopes for participants), (3) fixed effect of condition versus number of participants (highest for high fixed effect of condition and high number of participants), and (4) variance of random slopes for participants and number of participants (highest for high number of participants and zero variance of random slopes for participants). Generally, these results make sense: since the relevant comparison of RM-ANOVA focuses on the fixed effect of condition, any reduction in variance of nuisance parameters will bolster the Bayes factor. Its susceptibility to zero variance of random intercepts for participants mirrors the change that can be observed for RM-ANOVA specifically for the main effects (see leftmost result in Fig. 2).

For the Balanced null Bayes factors (Fig. 10), we see interactions for (1) fixed effect of condition versus variance of random slopes for participants (highest for high fixed effect of condition and zero variance of random slopes for participants), (2) fixed effect of condition versus number of participants (highest for high fixed effect of condition and high number of participants), and (3) variance of random slopes for participants and number of participants (highest for high number of participants and zero variance of random slopes for participants). These results mirror the results for RM-ANOVA, except that there are no interactions involving the variance of random intercepts for participants.

For the Strict null Bayes factors (Fig. 11), we see interactions for (1) fixed effect of condition versus number of participants (highest for high fixed effect of condition and high number of participants), (2) number of participants versus variance of random slopes for participants (highest for high number of participants and high variance of random slopes for participants), (3) fixed effect of condition versus number of trials (highest for high fixed effect of condition and high number of trials), (4) number of trials versus variance of random slopes for participants (highest for high number of participants and high variance of random slopes for participants), and (5) number of trials versus number of participants (highest for high number of participants and high number of trials). Interestingly, two-way interactions for the Strict null Bayes factor always feature the number of participants or trials. The pattern is always the same: high values for both parameters lead to the largest Bayes factor. As for the previous two model comparisons, generally two-way interactions were observed for parameters that also showed main effects (see Figs. 5 and 6). As a result, we caution against over-interpreting these two-way interactions.