Analysis of Dirichlet–Robin Iterations for Solving the Cauchy Problem for Elliptic Equations

Abstract

The Cauchy problem for general elliptic equations of second order is considered. In a previous paper (Berntsson et al. in Inverse Probl Sci Eng 26(7):1062–1078, 2018), it was suggested that the alternating iterative algorithm suggested by Kozlov and Maz’ya can be convergent, even for large wavenumbers $k^2$, in the Helmholtz equation, if the Neumann boundary conditions are replaced by Robin conditions. In this paper, we provide a proof that shows that the Dirichlet–Robin alternating algorithm is indeed convergent for general elliptic operators provided that the parameters in the Robin conditions are chosen appropriately. We also give numerical experiments intended to investigate the precise behaviour of the algorithm for different values of $k^2$ in the Helmholtz equation. In particular, we show how the speed of the convergence depends on the choice of Robin parameters.

1 Introduction

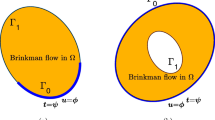
Let $\Omega$ be a bounded domain in ${{\mathbb {R}}}^d$ with a Lipschitz boundary $\Gamma$ divided into two disjoint parts $\Gamma _0$ and $\Gamma _1$ such that they have a common Lipschitz boundary in $\Gamma$ and ${\overline{\Gamma }}_0\cup {\overline{\Gamma }}_1=\Gamma$, see Fig. 1.

The Cauchy problem for an elliptic equation is given as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} {{\mathcal {L}}}u=D_ja^{ji}(x)D_i u + a(x) u = 0 &{} \quad \text{ in } \quad \Omega ,\\ u = f &{} \quad \text{ on } \quad \Gamma _0,\\ N u = g &{} \quad \text{ on } \quad \Gamma _0, \end{array}\right. } \end{aligned}$$

(1.1)

where $\nu =(\nu _1,\ldots ,\nu _d)$ is the outward unit normal to the boundary $\Gamma$, $D_j=\partial /\partial _{x_j}$, $a^{ji}$ and a are measurable real-valued functions such that a is bounded, $a^{ij} = a^{ji}$ and

$$\begin{aligned} \lambda |\xi |^2 \le a^{ij}\xi _i\xi _j \le \lambda ^{-1}|\xi |^2,\;\;\xi \in {\mathbb {R}}^d,\;\;\lambda =\mathrm{const}>0. \end{aligned}$$

The conormal operator N is defined as usual

$$\begin{aligned} Nu=\nu _ja^{ji}D_iu \end{aligned}$$

and the functions f and g are specified Cauchy data on $\Gamma _0$, with a certain noise level. We are seeking real-valued solutions to problem (1.1). We will always assume that there is only trivial solution to ${{\mathcal {L}}}u=0$ in $H^1(\Omega )$ if $u=0$, $Nu=0$ on $\Gamma _0$ or $u=0$, $Nu=0$ on $\Gamma _1$. This is certainly true for the Helmholtz equation.

This Cauchy problem (1.1), which includes the Helmholtz equation [1, 12, 17, 21], arises in many areas of science and engineering related to electromagnetic or acoustic waves. For example, in underwater acoustics [8], in medical applications [22], etc. The problem is ill-posed in the sense of Hadamard [9].

The alternating iterative algorithm was first introduced by V.A Kozlov and V. Maz’ya in [13] for solving Cauchy problems for elliptic equations. For the Laplace equation, a Dirichlet–Neumann alternating algorithm for solving the Cauchy problem was suggested in [14], see also [10, 11].

It has been noted that the Dirichlet–Neumann algorithm does not always work even if ${{\mathcal {L}}}$ is the Helmholtz operator $\Delta +k^2$. Thus, several variants of the alternating iterative algorithm have been proposed, see, for instance, [2, 7, 18, 19], and also [3, 4] where an artificial interior boundary was introduced in such a way that convergence was restored. Also, it has been suggested that replacing the Neumann conditions by Robin conditions can improve the convergence [6].

The alternating iterative algorithm has several advantages compared to other methods. Most importantly, it is easy to implement as it only requires solving a sequence of well-posed mixed boundary value problems. In contrast most direct methods, e.g. [16, 23] or [12], are based on an analytic solution being available and are thus more difficult to apply for general geometries or in the case of variable coefficients. On the other hand, the alternating iterative algorithm, in its basic form, suffers from slow convergence, see [4], and in the presence of noise additional regularization techniques have to be implemented, see, e.g. [5]. Thus, a practically useful form of the alternating algorithm tends to be more complicated than the variant analyzed in this paper.

In this work, we formulate the Cauchy problem for general elliptic operator of second order and consider the Dirichlet–Robin alternating iterative algorithm. Under the assumption that the elliptic operator with the Dirichlet boundary condition is positive we show that the Dirichlet–Robin algorithm is convergent, provided that parameters in the Robin conditions are chosen appropriately. The proof follows basically the same lines as that in [13] but with certain changes due to more general class of operators and the Robin boundary condition. We also make numerical experiments to investigate more precisely how the choice of the Robin parameters influences the convergence of the iterations.

Fig. 1

Description of the domain considered in this paper with a boundary $\Gamma$ divided into two parts $\Gamma _0$ and $\Gamma _1$

2 The Alternating Iterative Procedure

In this section, we describe the Dirichlet–Robin algorithm and introduce the necessary assumption.

The main our assumption is the following:

$$\begin{aligned} \int _\Omega (a^{ji}D_iuD_ju+au^2) \,\mathrm{d}x >0\;\;\hbox { for all}\ u\in H^1(\Omega ,\Gamma )\backslash \big \{0\big \}, \end{aligned}$$

(2.1)

where $H^1(\Omega ,\Gamma )$ consists of functions $u\in H^1(\Omega )$ vanishing on $\Gamma$. It is shown below in Sect. 3.2 that condition (2.1) is equivalent to existence of two real-valued measurable bounded functions $\mu _0$ and $\mu _1$ defined on $\Gamma _0$ and $\Gamma _1$, respectively, such that

$$\begin{aligned} \int _\Omega (a^{ji}D_iuD_ju+au^2) \,\mathrm{d}x + \int _{\Gamma _0 }\mu _0u^2 \,\mathrm{d}S+ \int _{\Gamma _1 }\mu _1u^2 \,\mathrm{d}S>0, \end{aligned}$$

(2.2)

for all $u\in H^1(\Omega )\backslash \big \{0\big \}$. Actually, we prove that for $\mu _0=\mu _1$ to be a sufficiently large positive constant, but we think that it can be useful to have here two functions (as we will see in numerical examples the convergence of the Dirichlet–Robin algorithm weakens when $\mu _0$ and $\mu _1$ become large).

With these two bounded real-valued measurable functions $\mu _0$ and $\mu _1$ in place, we consider the two auxiliary boundary value problems

$$\begin{aligned} {\left\{ \begin{array}{ll} {{\mathcal {L}}}u = 0 &{}\quad \text{ in }\quad \Omega , \\ u = f_{0} &{} \quad \text{ on }\quad \Gamma _0, \\ Nu+ \mu _1 u =\eta &{}\quad \text{ on }\quad \Gamma _1,\\ \end{array}\right. } \end{aligned}$$

(2.3)

and

$$\begin{aligned} {\left\{ \begin{array}{ll} {{\mathcal {L}}}u = 0 &{}\quad \text{ in }\quad \Omega ,\\ N u+ \mu _0 u= g_{0} &{}\quad \text{ on }\quad \Gamma _0, \\ u = \phi &{}\quad \text{ in }\quad \Gamma _1.\\ \end{array}\right. } \end{aligned}$$

(2.4)

Here, $f_{0}\in H^{1/2}(\Gamma _0)$, $g_{0}\in H^{-1/2}(\Gamma _0)$, $\eta \in H^{-1/2}(\Gamma _1)$ and $\phi \in H^{1/2}(\Gamma _1)$. These problems are uniquely solvable in $H^{1}(\Omega )$ according to [20].

The algorithm for solving (1.1) is described as follows: take $f_{0}=f$ and $g_{0}=g+\mu _0 f$, where f and g are the Cauchy data given in (1.1). Then

• (1) The first approximation $u_{0}$ is obtained by solving (2.3) where $\eta$ is an arbitrary initial guess for the Robin condition on $\Gamma _1$.

• (2) Having constructed $u_{2n}$, we find $u_{2n+1}$ by solving (2.4) with $\phi =u_{2n}$ on $\Gamma _1$.

• (3) We then obtain $u_{2n+2}$ by solving (2.3) with $\eta =N u_{2n+1}+ \mu _1 u_{2n+1}$ on $\Gamma _1$.

3 Function Spaces, Weak Solutions and Well-Posedness

In this section, we define the weak solutions to the problems (2.3) and (2.4). We also describe the function spaces involved and show that the problems solved at each iteration step are well-posed.

3.1 Function Spaces

As usual, the Sobolev space $H^1(\Omega )$ consists of all functions in $L^2(\Omega )$ whose first-order weak derivatives belong to $L^2(\Omega )$. The inner product is given by

$$\begin{aligned} (u,v)_{H^1(\Omega )}=(u,v)_{L^2(\Omega )}+\sum _{j=1}^d(\partial _{j}u,\partial _{j}v)_{L^2(\Omega )},\quad u,v\in H^1(\Omega ) \end{aligned}$$

(3.1)

and the corresponding norm is denoted by $\Vert u \Vert _{H^1(\Omega )}$.

Further, by $H^{1/2 }(\Gamma )$, we mean the space of traces of functions in $H^{1 }(\Omega )$ on $\Gamma$. Also, $H^{1/2 }(\Gamma _0)$ is the space of restrictions of functions belonging to $H^{1/2 }(\Gamma )$ to $\Gamma _0$, and $H^{1/2 }_{0}(\Gamma _0)$ is the space of functions from $H^{1/2 }(\Gamma )$ that vanish on $\Gamma _1$. The dual spaces of $H^{1/2 }(\Gamma _0)$ and $H^{1/2 }_{0}(\Gamma _0)$ are denoted by $(H^{1/2 }(\Gamma _0))^*$ and $H^{-1/2 }(\Gamma _0)$, respectively.

Similarly, we can define the spaces $H^{1/2 }(\Gamma _1)$, $H^{1/2 }_{0}(\Gamma _1)$, $(H^{1/2 }(\Gamma _1))^*$ and $H^{-1/2 }(\Gamma _1)$, see [20].

3.2 The Bilinear Form $a_\mu$

Lemma 3.1

The assumption (2.1) is equivalent to the existence of a positive constant $\mu$ such that

$$\begin{aligned} \int _{\Omega }(a^{ji}D_iuD_ju-a(x)u^2) \,\mathrm{d}x + \mu \int _{\Gamma } u^2 \,\mathrm{d}S >0 \end{aligned}$$

(3.2)

for all $u\in H^1(\Omega )\backslash \big \{0\big \}$.

Proof

Clearly the requirement (3.2) implies (2.1). Now assume that (2.1) holds and let us prove (3.2). Let

$$\begin{aligned} \lambda _0=\inf _{\begin{array}{c} u\in H^1(\Omega ,\Gamma )\\ {\Vert u \Vert _{L_2(\Omega )}=1} \end{array}} \int _\Omega (a^{ji}D_iuD_ju-au^2) \,\mathrm{d}x. \end{aligned}$$

By (3.1) $\lambda _{0}>0$. Let also

$$\begin{aligned} \lambda (\mu )=\inf _{\begin{array}{c} u\in H^1(\Omega )\\ {\Vert u \Vert _{L_2(\Omega )}=1} \end{array}} \int _{\Omega } (a^{ji}D_iuD_ju-au^2) \,\mathrm{d}x + \mu \int _{\Gamma } u^2 \,\mathrm{d}S. \end{aligned}$$

The function $\lambda (\mu )$ is monotone and increasing with respect to $\mu$ and $\lambda (\mu )\le \lambda _{0}$ for all $\mu$. Therefore, there is a limit $\lambda _*:=\lim _{\mu \rightarrow \infty }\lambda (\mu )$ which does not exceed $\lambda _0$. Furthermore, $\lambda _0$ is the first eigenvalue of the operator $-{{\mathcal {L}}}$ with the Dirichlet boundary condition and $\lambda (\mu )$ is the first eigenvalue of $-{{\mathcal {L}}}$ with the Robin boundary condition $Nu+ \mu u =0$ on $\Gamma$.

Our goal is to show that $\lambda (\mu )\rightarrow \lambda _0$ as $\mu \rightarrow \infty$ or equivalently $\lambda _*=\lambda _0$. We denote by $u_{\mu }$ an eigenfunction corresponding to the eigenvalue $\lambda (\mu )$ normalised by $\Vert u_{\mu } \Vert _{L_2(\Omega )}=1$. Then

$$\begin{aligned} \lambda _{0}\ge \lambda (\mu )= \int _{\Omega }(a^{ji}D_iu_{\mu }D_ju_{\mu }-au_{\mu }^2) \,\mathrm{d}x + \mu \int _{\Gamma } u_{\mu }^2 \,\mathrm{d}S. \end{aligned}$$

Therefore,

$$\begin{aligned} \Vert u_{\mu } \Vert _{H^{1}(\Omega )}^2+ \mu \int _{\Gamma } u_{\mu }^2 \,\mathrm{d}S\le C, \end{aligned}$$

where C does not depend on $\mu$. This implies that we can choose a sequence $\mu _j$, $1\le j<\infty$, $\mu _{j}\rightarrow \infty$ as $j\rightarrow \infty$ such that $u_{\mu _{j}}$ is weakly convergent in $H^{1}(\Omega )$, $u_{\mu _{j}}$ is convergent in $L_2(\Omega )$ and $\mu _j u_{\mu _j}$ is bounded. We denote the limit by $u\in H^1(\Omega )$. Clearly, $\Vert u \Vert _{L_2(\Omega )}=1$ and, therefore, $u\ne 0$. Moreover, $u\in H^{1}(\Omega ,\Gamma )$ since $\int _{\Gamma } u_{\mu }^2 \,\mathrm{d}S\le \frac{C}{\mu }$. We note also that $\lim _{j \rightarrow \infty }\lambda (\mu _{j})=\lambda _{*}$. Since

$$\begin{aligned} \int _\Omega (a^{ji}D_iu_{\mu }D_jv-au_{\mu }v) \,\mathrm{d}x = \lambda (\mu )\int _{\Omega } u_{\mu }v\,\mathrm{d}x, \end{aligned}$$

for all $v\in H^1(\Omega ,\Gamma )$ we have that

$$\begin{aligned} \int _\Omega (a^{ji}D_iuD_jv-auv) \,\mathrm{d}x = \lambda _{*}\int _{\Omega } uv\,\mathrm{d}x. \end{aligned}$$

Therefore, $\lambda _{*}$ is the eigenvalue of the Dirichlet–Laplacian and u is the eigenfunction corresponding to $\lambda _{*}$. Using that $\lambda _*\le \lambda _0$ and that $\lambda _0$ is the first eigenvalue of $-{{\mathcal {L}}}$ with the Dirichlet boundary condition we get $\lambda _{*}=\lambda _{0}$. This argument proves that $\lambda (\mu )\rightarrow \lambda _{0}$ as $\mu \rightarrow \infty$. $\square$

According to Lemma 3.1, we can choose two functions $\mu _0$ and $\mu _1$ such that (2.2) holds. Let us introduce the bilinear form on $H^1(\Omega )$

$$\begin{aligned} a_\mu (u,v) = \int _\Omega (a^{ji}D_iuD_jv+auv) \,\mathrm{d}x + \int _{\Gamma _0 }\mu _0uv \,\mathrm{d}S+ \int _{\Gamma _1 }\mu _1uv \,\mathrm{d}S. \end{aligned}$$

According to our assumption (2.2), $a_\mu (u,u)>0$, for $u\in H^1(\Omega )\backslash \big \{0\big \}$. The corresponding norm will be denoted by $\Vert u \Vert _{\mu }=a_\mu (u,u)^{1/2}$.

Let us show that the norm $\Vert \cdot \Vert _{\mu }$ is equivalent to the standard norm on $H^1(\Omega )$.

Lemma 3.2

There exist positive constants $C_{1}$ and $C_{2}$ such that

$$\begin{aligned} C_{1}\Vert u \Vert _{H^{1}(\Omega )}\le \Vert u \Vert _{\mu } \le C_{2}\Vert u \Vert _{H^{1}(\Omega )}, \quad \text { for all }u\in H^1(\Omega ). \end{aligned}$$

(3.3)

Proof

Suppose that $u \in H^1(\Omega )$. Then

$$\begin{aligned} a_\mu (u,u)\le & {} C\left( \Vert u \Vert _{H^{1}(\Omega )}^2 + \Vert u \Vert _{L_2(\Gamma _0)}^2 + \Vert u \Vert _{L_2(\Gamma _1)}^2\right) \\\le & {} C \Vert u \Vert _{H^{1}(\Omega )}^2. \end{aligned}$$

This proves the second inequality of (3.3).

To prove the first inequality, we argue by contradiction and, assume that the inequality does not hold. This means that we can find a sequence $\{v_{k}\}^{\infty }_{k=1}$ of non-zero functions in $H^1(\Omega )$ such that

$$\begin{aligned} \Vert v_{k}\Vert ^{2}_{H^{1}(\Omega )}\ge k a_{\mu }(v_{k},v_{k}). \end{aligned}$$

Let $u_{k}=\Vert v_{k} \Vert _{H^{1}(\Omega )}^{-1} v_{k}$ and note that the sequence of functions $(u_{k})^{\infty }_{k=0}$ in $H^1(\Omega )$ satisfies

$$\begin{aligned} \Vert u_{k} \Vert ^{2}_{H^{1}(\Omega )}=1. \end{aligned}$$

(3.4)

Therefore,

$$\begin{aligned} a_{\mu }(u_{k},u_{k})< \frac{1}{k}. \end{aligned}$$

(3.5)

Since the sequence $\{u_{k}\}^{\infty }_{k=0}$ is bounded in $H^1(\Omega )$, there exists a subsequence, denoted by $\{u_{k_{n}}\}^{\infty }_{n=0}$, of $\{u_{k}\}$, and a function u in $H^1(\Omega )$ such that $u_{k_{n}}$ converges weakly to u in $H^1(\Omega )$. Since $H^1(\Omega )$ is compactly embedded in $L^2(\Omega )$, the subsequence $\{u_{k_{n}}\}^{\infty }_{n=0}$ converges strongly in $L^2(\Omega )$. Moreover, the trace operator from $H^1(\Omega )$ to $L^2(\Gamma )$ is compact; hence, the restrictions of $u_{k_{n}}$ to $\Gamma _0$ and $\Gamma _1$ converge strongly to the corresponding restrictions of u in the $L^2$-norm. Finally, $\nabla u_{k_{n}}$ converges weakly to $\nabla u$ in $L^2(\Omega )$ and

$$\begin{aligned} \Vert \nabla u\Vert _{L^2(\Omega )}\le \liminf _{n \rightarrow \infty }\Vert \nabla u_{k_{n}}\Vert _{L^2(\Omega )}. \end{aligned}$$

Thus, we get that

$$\begin{aligned} a_{\mu }(u,u)\le \liminf _{n \rightarrow \infty }a_{\mu }(u_{k_n},u_{k_n}). \end{aligned}$$

By (3.5), this tends to zero as $n\rightarrow \infty$ and hence $\Vert u \Vert ^{2}_{\mu }=0$, which implies $u=0$. Therefore, $u_{k_{n}}\rightarrow 0$ in $L^2(\Omega )$, $u_{k_{n}}|_{\Gamma _0}\rightarrow 0$ in $L^2(\Gamma _0)$ and $u_{k_{n}}|_{\Gamma _1}\rightarrow 0$ in $L^2(\Gamma _1)$. Using these facts and (3.5), we find that

$$\begin{aligned} \limsup _{n\rightarrow \infty }\int _{\Omega } |\nabla u_{k_{n}}|^2 \,\mathrm{d}x = 0, \end{aligned}$$

which contradicts (3.4). This proves the first inequality in (3.3). $\square$

We define the following subspaces of $H^1(\Omega )$. First, $H^1(\Omega ,\Gamma )$ is the space of functions from $H^1(\Omega )$ vanishing on $\Gamma$. Second, $H^1(\Omega ,\Gamma _0)$ and $H^1(\Omega ,\Gamma _1)$ are the spaces of functions from $H^1(\Omega )$ vanishing on $\Gamma _0$ and $\Gamma _1$ respectively. The bilinear form defined on $H^1(\Omega ,\Gamma _0)$ will be denoted by $a_1(u, v)$ and the bilinear form $a_\mu$ defined on $H^1(\Omega ,\Gamma _1)$ is denoted by $a_0(u, v)$. They are defined by the expressions

$$\begin{aligned} a_0(u,v) = \int _\Omega (a^{ji}D_iuD_jv+auv) \,\mathrm{d}x + \int _{\Gamma _0 }\mu _0uv \,\mathrm{d}S \end{aligned}$$

and

$$\begin{aligned} a_1(u,v) = \int _\Omega (a^{ji}D_iuD_jv+auv) \,\mathrm{d}x + \int _{\Gamma _1 }\mu _1uv \,\mathrm{d}S. \end{aligned}$$

3.3 Preliminaries

Let $u\in H^2(\Omega )$ satisfy the elliptic equation,

$$\begin{aligned} {{\mathcal {L}}}u = 0 \quad \text{ in }\quad \Omega . \end{aligned}$$

(3.6)

By Green’s first identity, we obtain

$$\begin{aligned} \int _\Omega (a^{ji}D_iuD_jv+auv) \,\mathrm{d}x = \int _{\Gamma } (N u)v \, \mathrm{d}S. \end{aligned}$$

(3.7)

We add $\int _{\Gamma _0 }\mu _0uv\,\mathrm{d}S$ and $\int _{\Gamma _1 }\mu _1uv\,\mathrm{d}S$ to both sides and obtain

$$\begin{aligned} a_\mu (u,v)= \int _{\Gamma _0 }(N u+\mu _0u)v\,\mathrm{d}S+\int _{\Gamma _1 }(N u+\mu _1u)v \,\mathrm{d}S. \end{aligned}$$

Definition 3.3

A function $u\in H^1(\Omega )$ is a weak solution to equation (3.6) if

$$\begin{aligned} \int _\Omega (a^{ji}D_iuD_jv+auv) \,\mathrm{d}x=0 \end{aligned}$$

for every function $v\in H^1(\Omega ,\Gamma )$.

Let H denote the space of the weak solutions to (3.6). Clearly it is a closed subspace of $H^1(\Omega )$. Let us define the conormal derivative of functions from H. We use identity (3.7) to define the conormal derivative Nu on $\Gamma$. By the extension theorem [15], for any function $\psi \in H^{1/2 }(\Gamma )$, there exists a function $v\in H^1(\Omega )$, such that $v=\psi$ on $\Gamma$ and

$$\begin{aligned} \Vert v \Vert _{H^{1}(\Omega )}\le C\Vert \psi \Vert _{H^{1/2 }(\Gamma )}, \end{aligned}$$

(3.8)

where the constant C is independent of $\psi$. Moreover, this mapping $\psi \rightarrow v$ can be chosen to be linear.

Lemma 3.4

Let $u\in H$. Then there exists a bounded linear operator

$$\begin{aligned} F:H \rightarrow H^{-1/2 }(\Gamma ), \end{aligned}$$

such that

$$\begin{aligned} \left\langle F(u), \psi \right\rangle =\int _\Omega (a^{ji}D_iuD_jv+auv) \,\mathrm{d}x, \end{aligned}$$

where $\psi \in H^{1/2 }(\Gamma )$, $v\in H^1(\Omega )$ and $v|_{\Gamma }=\psi$. Moreover,

$$\begin{aligned} F(u)=N u \;\;\text{ if } u\in C^2(\Omega ) \text{ and } \text{ the } \text{ coefficients } a^{ij} \text{ are } \text{ smooth }. \end{aligned}$$

Proof

Consider the functional

$$\begin{aligned} {{\mathcal {F}}}(\psi )=\int _\Omega (a^{ji}D_iuD_jv+auv) \,\mathrm{d}x. \end{aligned}$$

(3.9)

Let us show that the right-hand side of (3.9) is independent of the choice of v. If $v_{1},v_{2}\in H^1(\Omega )$ and $v_{1}|_{\Gamma }=v_{2}|_{\Gamma }=\psi$, then the difference $v=v_{1}-v_{2}$ belongs to $H^1(\Omega ,\Gamma )$ and, since $u\in H$, we have

$$\begin{aligned} \int _\Omega (a^{ji}D_iuD_jv+auv) \,\mathrm{d}x =0, \end{aligned}$$

and, therefore,

$$\begin{aligned} \int _\Omega (a^{ji}D_iuD_jv_1+auv_1) \,\mathrm{d}x =\int _\Omega (a^{ji}D_iuD_jv_2+auv_2) \,\mathrm{d}x. \end{aligned}$$

Hence, the definition of ${{\mathcal {F}}}(\psi )$ does not depend on v. Next by the Cauchy–Schwartz inequality, and (3.8), we obtain

$$\begin{aligned} | {{\mathcal {F}}}(\psi )|\le C \Vert u\Vert _{H^{1}(\Omega )}\Vert \psi \Vert _{H^{1/2 }(\Gamma )}. \end{aligned}$$

Thus, ${{\mathcal {F}}}$ is a bounded operator in $H^{1/2 }(\Gamma )$. Therefore,

$$\begin{aligned} {{\mathcal {F}}}(\psi )=\langle F(u),\psi \rangle ,\;\;F(u)\in H^{-1/2}(\Gamma ) \end{aligned}$$

and

$$\begin{aligned} ||F(u)||_{H^{-1/2}(\Gamma )}\le C\Vert u\Vert _{H^{1}(\Omega )}. \end{aligned}$$

$\square$

Remark 3.5

We will use the notation Nu for the extension of the conormal derivative of functions from H. For the distribution $Nu\in H^{-1/2}(\Gamma )$, the restrictions $Nu|_{\Gamma _0}$ and $Nu|_{\Gamma _1}$ are well defined and

$$\begin{aligned} ||Nu\Big |_{\Gamma _0}||_{H^{-1/2}(\Gamma _0)}+||Nu\Big |_{\Gamma _1}||_{H^{-1/2}(\Gamma _1)}\le C||Nu||_{H^{-1/2}(\Gamma )}. \end{aligned}$$

3.4 Weak Solutions and Well-Posedness

In this section, we define weak solution to the two well-posed boundary value problems (2.3) and (2.4) and we show that the problems are well posed.

Definition 3.6

Let $f_{0}\in H^{1/2 }(\Gamma _0)$ and $\eta \in H^{-1/2 }(\Gamma _1)$. A function $u\in H^{1}(\Omega )$ is called a weak solution to (2.3) if

$$\begin{aligned} a_1(u,v)=\int _{\Gamma _1} \eta v\,\mathrm{d}S, \end{aligned}$$

for every function $v\in H^{1}(\Omega ,\Gamma _0)$ and $u=f_0$ on $\Gamma _0$.

We now show that problem (2.3) is well-posed.

Proposition 3.7

Let $f_{0}\in H^{1/2 }(\Gamma _0)$ and $\eta \in H^{-1/2 }(\Gamma _1)$. Then there exists a unique weak solution $u \in H^1(\Omega )$ to problem (2.3) such that

$$\begin{aligned} \Vert u \Vert _{H^{1}(\Omega )}\le C\left( \Vert f_{0}\Vert _{H^{1/2 }(\Gamma _o)}+\Vert \eta \Vert _{H^{-1/2 }(\Gamma _1)}\right) , \end{aligned}$$

(3.10)

where the constant C is independent of $f_0$ and $\eta$.

Proof

The proof presented here is quite standard. Let $w\in H^{1}(\Omega )$ satisfy $w|_{\Gamma _0}=f_{0}$ and

$$\begin{aligned} \Vert w \Vert _{H^{1}(\Omega )} \le C\Vert f_{0}\Vert _{H^{1/2 }(\Gamma _0)}. \end{aligned}$$

(3.11)

Again let $u=w+h$, where $h\in H^{1}(\Omega ,\Gamma _0)$, then

$$\begin{aligned} a_{1}(h, v)= \int _{\Gamma _1} \eta v \,\mathrm{d}s -a_{1}(w, v), \end{aligned}$$

(3.12)

for all $v\in H^{1}(\Omega ,\Gamma _0)$. The right-hand side of (3.12) is a continuous linear functional. Thus, we can write

$$\begin{aligned} a_{1}(h, v) = G(v):=\int _{\Gamma _1} \eta v \,\mathrm{d}s -a_{1}(w, v). \end{aligned}$$

(3.13)

By applying the trace theorem, the Cauchy–Schwartz inequality, and (3.11), we obtain

$$\begin{aligned} |G(v)|\le C (\Vert \eta \Vert _{H^{1/2 }(\Gamma _1)^*}+\Vert f_{0}\Vert _{H^{1/2 }(\Gamma _0)} )\Vert v\Vert _{H^{1}(\Omega )}. \end{aligned}$$

According to Riesz’ representation theorem, there exists a unique solution $h\in H^{1}(\Omega ,\Gamma _0)$ of (3.13) such that

$$\begin{aligned} \Vert \ h\Vert _{H^{1 }(\Omega )}\le C (\Vert \eta \Vert _{H^{-1/2 }(\Gamma _1)}+\Vert f_{0}\Vert _{H^{1/2 }(\Gamma _0)} ). \end{aligned}$$

One can verify that $u=w+h$ by triangular inequality and (3.11) satisfies (3.10). $\square$

Definition 3.8

Let $g_{0}\in H^{-1/2 }(\Gamma _0)$ and $\phi \in H^{1/2 }(\Gamma _1)$. A function $u\in H^{1}(\Omega )$ is called a weak solution to (2.4) if

$$\begin{aligned} a_0(u,v) =\int _{\Gamma _0} g_{0}v\,\mathrm{d}S, \end{aligned}$$

for every function $v\in H^{1}(\Omega ,\Gamma _1)$ and $u=\phi$ on $\Gamma _1$.

In the same manner, one can show that problem (2.4) is well posed. We will state the last result without a proof.

Proposition 3.9

Let $g_{0}\in H^{-1/2 }(\Gamma _0)$ and $\phi \in H^{1/2 }(\Gamma _1)$. Then there exists a unique weak solution $u \in H^1(\Omega )$ to problem (2.4) such that

$$\begin{aligned} \Vert u \Vert _{H^{1}(\Omega )}\le C\Big (\Vert \phi \Vert _{H^{1/2 }(\Gamma _1)}+\Vert g_{0}\Vert _{H^{-1/2 }(\Gamma _1)}\Big ), \end{aligned}$$

where C is independent of $g_{0}$ and $\phi$.

4 Convergence of the Algorithm

We now prove the convergence of the Robin–Dirichlet algorithm. We denote the sequence of solutions of (1.1) obtained from the alternating algorithm described in Sect. 2 by $(u_n(f_0,g_0,\eta ))_{n=0}^\infty$. The iterations linearly depend on $f_0$, $g_0$ and $\eta$.

Theorem 4.1

Let $f_0\in H^{1/2}(\Gamma _0)$ and $g_0\in H^{-1/2 }(\Gamma _0)$, and let $u\in H^{1}(\Omega )$ be the solution to problem (1.1). Then for $\eta \in H^{-1/2}(\Gamma _1)$, the sequence $(u_n)_{n=0}^\infty$, obtained using the algorithm described in Sect. 2, converges to u in $H^{1}(\Omega )$.

Proof

Lemma 3.4 together with Remark 3.5 shows that $N u+\mu _1 u_{\vert _{\Gamma _1}} \in H^{-1/2}(\Gamma _1)$. Since

$$\begin{aligned} u = u_n(f_0,g_0,(N+\mu _1)u\big |_{\Gamma _1} ) \end{aligned}$$

for all n, we have

$$\begin{aligned} u_n(f_0,g_0,\eta )-u =u_n(0,0,\eta -(N+\mu _1) u_{\vert _{\Gamma _1}} ). \end{aligned}$$

Therefore, it is sufficient to show that the sequence converges in the case when $f_0=0$, $g_0=0$ and $\eta$ is an arbitrary element from $H^{-1/2}(\Gamma _1)$. To simplify the notation, we will denote the elements of this sequences by $u_n=u_n(\eta )$ instead of $u_n(0,0,\eta )$.

Then $u_0$ solves (2.3) with $f_0=0$, $u_{2n}$ is a solution to (2.3) with $f_0= 0$ and $\eta = N u_{2n-1}+\mu _1 u_{2n-1}$, and $u_{2n+1}$ satisfies (2.4) with $g_0=0$ and $\phi =u_{2n}$. From the weak formulation of (2.3) , we have that

$$\begin{aligned} a_\mu (u_{2n-1},u_{2n})= & {} \int _{\Gamma _1} (N u_{2n-1}+\mu _1 u_{2n-1})u_{2n} \,\mathrm{d}S \\= & {} \int _{\Gamma _1} (N u_{2n}+\mu _1 u_{2n})u_{2n} \,\mathrm{d}S=a_\mu (u_{2n},u_{2n}). \end{aligned}$$

Similarly $u_{2n+1}$ solves problem (2.4) with $N u_{2n+1}+\mu _0 u_{2n+1} = 0$ on $\Gamma _0$, $u_{2n+1} =u_{2n}$ on $\Gamma _1$. Again, it follows from the weak formulation of (2.4) that

$$\begin{aligned} a_\mu (u_{2n+1},u_{2n})= & {} \int _{\Gamma _1} (N u_{2n+1}+\mu _1 u_{2n+1})u_{2n} \,\mathrm{d}S\\= & {} \int _{\Gamma _1} (N u_{2n+1}+\mu u_{2n+1})u_{2n+1} \,\mathrm{d}S\\= & {} a_\mu (u_{2n+1},u_{2n+1}). \end{aligned}$$

From these relations, we obtain

$$\begin{aligned} a_\mu (u_{2n+1}-u_{2n},u_{2n+1}-u_{2n})= a_\mu (u_{2n},u_{2n})-a_\mu (u_{2n+1},u_{2n+1}) \end{aligned}$$

and

$$\begin{aligned} a_\mu (u_{2n}-u_{2n-1},u_{2n}-u_{2n-1})= a_\mu (u_{2n-1},u_{2n-1})-a_\mu (u_{2n},u_{2n}), \end{aligned}$$

which implies

$$\begin{aligned} a_\mu (u_{2n-1},u_{2n-1}) \ge a_\mu (u_{2n},u_{2n}) \ge a_\mu (u_{2n+1},u_{2n+1}). \end{aligned}$$

(4.1)

We introduce the linear set R consisting of functions $\eta \in H^{-1/2}(\Gamma _{1})$ such that $u_n(\eta )\rightarrow 0$ in $H^{1}(\Omega )$ as $n\rightarrow \infty$. Our goal is to prove that $R=H^{-1/2}(\Gamma _{1})$. Let us show first that R is closed in $H^{-1/2}(\Gamma _{1})$. Suppose that $\eta _{j} \in R$ and $\eta _{j} \rightarrow \eta \in H^{-1/2}(\Gamma _1)$. Since $a_\mu ^{1/2}$ is a norm and $u_n(\eta )$ is a linear function of $\eta$, we have

$$\begin{aligned} a_\mu (u_{n}(\eta ),u_{n}(\eta ))^{1/2} \le a_\mu (u_{n}(\eta -\eta _{j} ),u_{n}(\eta -\eta _{j} ))^{1/2} + a_\mu (u_{n}(\eta _{j} ),u_{n}(\eta _{j} ))^{1/2}. \end{aligned}$$

By squaring both sides, we have

$$\begin{aligned} a_\mu (u_{n}(\eta ),u_{n}(\eta )) \le 2a_\mu (u_{n}(\eta -\eta _{j} ),u_{n}(\eta -\eta _{j} ))+ 2a_\mu (u_{n}(\eta _{j} ),u_{n}(\eta _{j} )). \end{aligned}$$

(4.2)

Since $a_\mu (u_n, u_n,)_{n=0}^\infty$ is a decreasing sequence, we obtain that

$$\begin{aligned} a_\mu (u_{n}(\eta -\eta _{j} ),u_{n}(\eta -\eta _{j} )) \le a_\mu (u_{0}(\eta -\eta _{j} ),u_{0}(\eta -\eta _{j} )). \end{aligned}$$

Since $u_{0}$ is a solution to problem (2.3), we obtain that

$$\begin{aligned} a_\mu (u_{n}(\eta -\eta _{j} ),u_{n}(\eta -\eta _{j} ))\le C \Vert \eta -\eta _{j} \Vert _{H^{-1/2 }(\Gamma _1)}. \end{aligned}$$

Therefore, the first term in the right- hand of (4.2) is small for all n if j is sufficiently large and the second term in (4.2) can be made small by choosing sufficiently large n. Therefore, the sequence $(u_n(\eta ))_{n=0}^\infty$ converges to zero in $H^{1}(\Omega )$ and thus $\eta \in H^{-1/2 }(\Gamma _1)$.

To show that $R =H^{-1/2}(\Gamma _{1})$, it suffices to prove that R is dense in $H^{-1/2}(\Gamma _{1})$. First, we note that the functions $(N+\mu _1)u_1(\eta )-\eta$ belong to R for any $\eta \in H^{-1/2}(\Gamma _{1})$. Indeed, $u_k((N+\mu _1)u_1(\eta )-\eta )=u_{k+2}(\eta )-u_k(\eta )$ and

$$\begin{aligned} a_\mu (u_{k+2}(\eta )-u_k(\eta ),u_{k+2}(\eta )-u_k(\eta ))\le 2(a(u_{k+2}(\eta ),u_{k+2}(\eta ))-a(u_{k}(\eta ),u_{k}(\eta ))). \end{aligned}$$

Due to (4.1), the right-hand side tends to zero as $k\rightarrow \infty$,which proves $(N+\mu _1)u_1(\eta )-\eta \in R$.

Assume that $\varphi \in H_0^{1/2}(\Gamma _{1})$ satisfies

$$\begin{aligned} \int _{\Gamma _1}\Big ( (N u_{1}(\eta )+\mu _{1} u_{1}(\eta ))-\eta \Big )\varphi \,\mathrm{d}S=0, \end{aligned}$$

(4.3)

for every $\eta \in H^{-1/2}(\Gamma _{1})$. We need to prove that $\varphi =0$. Consider a function $v\in H^{1}(\Omega )$ that satisfies (2.4) with $g_0=0$ and $\phi =\varphi$. From Green’s formula

$$\begin{aligned} \int _{\Gamma _1} (N u_{1}(\eta )+\mu _{1} u_{1}(\eta ))v \,\mathrm{d}S=a_\mu (u_1,v)=\int _{\Gamma _1} (N v+\mu _{1}v)u_{1}(\eta )\,\mathrm{d}S. \end{aligned}$$

Therefore, (4.3) is equivalent to

$$\begin{aligned} \int _{\Gamma _1} (N v+\mu _1 v)u_1\,\mathrm{d}S-\int _{\Gamma _1}\eta \varphi \,\mathrm{d}S=0. \end{aligned}$$

Since $u_0=u_1$ on $\Gamma _{1}$, we have

$$\begin{aligned} \int _{\Gamma _1} (N v+\mu _{1} v)u_0\,\mathrm{d}S-\int _{\Gamma _1}\eta \varphi \,\mathrm{d}S=0. \end{aligned}$$

(4.4)

Now let $w\in H^{1}(\Omega )$ be a solution of (2.3) with $f_0=0$ and $\eta =N v+\mu _{1} v$. Using again Green’s formula, we get

$$\begin{aligned} \int _{\Gamma _1} (N w+\mu _{1} w)u_0 \,\mathrm{d}S=a_\mu (w,u_0)=\int _{\Gamma _1} (N u_0+\mu _{1}u_0)w\,\mathrm{d}S, \end{aligned}$$

which together with (4.4) and $N w+\mu _{1} w=N v+\mu _{1} v$ on $\Gamma _1$ gives

$$\begin{aligned} \int _{\Gamma _1} (Nu_0+\mu u_0)w\,\mathrm{d}S-\int _{\Gamma _1}\eta \varphi \,\mathrm{d}S=0. \end{aligned}$$

Since $Nu_0+\mu u_0=0$ on $\Gamma _1$, we obtain

$$\begin{aligned} \int _{\Gamma _1} \eta (w-\varphi ) \,\mathrm{d}S=0\quad \text{ for } \text{ all } \eta \in H^{-1/2}(\Gamma _1). \end{aligned}$$

This implies $w=\varphi$ on $\Gamma _1$. On the other hand, $Nw+\mu _{1} w=N v+\mu _{1} v$ on $\Gamma _{1}$ and by uniqueness of the Cauchy problem we get $w=v$ on $\Omega$. But from the fact that $w=0$ on $\Gamma _{0}$, it follows that $w=v=0$ on $\Gamma _0$. Thus, $\varphi =0$. This shows that R is dense in $H^{-1/2}(\Gamma _{1})$ and, therefore, $R=H^{-1/2}(\Gamma _{1})$. This means that for any $\eta \in H^{-1/2}(\Gamma _{1})$, the sequence $(u_n(\eta ))_{n=0}^\infty$ converges to zero in $H^{1}(\Omega )$. $\square$

5 Numerical Results

In this section, we present some numerical experiments. To conduct our tests we need to specify a geometry $\Omega$ and implement a finite difference method for solving the two well-posed problems that appear during the iterative process. For our tests, we chose a relatively simple geometry. Let L be a positive number and consider the domain

$$\begin{aligned} \Omega =(0,1)\times (0,L),\quad \text {with}\quad \Gamma _0=(0,1)\times \{0\}\quad \text {and}\quad \Gamma _{1}= (0,1) \times \{L\}. \end{aligned}$$

For our tests, we consider the Cauchy problem for the Helmholtz equation in $\Omega$, i.e.

$$\begin{aligned} {\left\{ \begin{array}{ll} \Delta u(x,y) + k^2 u(x,y) = 0,&{}\quad \quad 0< x< 1,0< y <L,\\ u_{y}(x,0) = g(x),&{} \quad \quad 0\le x \le 1,\\ u(x,0) = f(x),&{} \quad \quad 0\le x \le 1,\\ u(0,y) = u(1,y)=0&{} \quad \quad 0\le y \le L. \end{array}\right. } \end{aligned}$$

(5.1)

Due to zero Dirichlet boundary condition on a part of the boundary, where $x=0$ or $x=1$ we keep them to be zero on each iteration. Therefore, our theoretical result gives convergence of the Dirichlet–Robin iterations for

$$\begin{aligned} k^2<\pi ^2+\frac{\pi ^2}{L^2} \end{aligned}$$

and for the Dirichlet–Neumann iterations for $k^2<\pi ^2$.

In our finite difference implementation, we introduce a uniform grid on the domain $\Omega$ of size $N\times M$, such that the step size is $h=N^{-1}$, and thus $M=\text {round}(Lh^{-1})$, and use a standard ${\mathcal {O}}(h^2)$ accurate finite difference scheme. In the case of Robin conditions, on $\Gamma _0$ or $\Gamma _1$, we use one sided difference approximations. See [4] for further details. For all the experiments presented in this section, a grid of size $N=401$ and $M=201$ was used.

To test the convergence of the algorithm, we use an analytical solution. More specifically, we use

$$\begin{aligned} u(x,y)=\sin \pi x\left( \cosh \sqrt{\pi ^2-k^2} y+\sinh \sqrt{\pi ^2-k^2} y\right) , \end{aligned}$$

which satisfies both the Helmholtz equation in $\Omega$ and also the conditions $u(0,y)=u(1,y)=0$. The corresponding Cauchy data, for the problem (5.1), are

$$\begin{aligned} f(x):=u(x,0)=\sin \pi x, \quad \text {and}\quad g(x)=u_{y}(x,0)=\sqrt{\pi ^2-k^2} \sin \pi x. \end{aligned}$$

We also find that the unknown data, at $y=L$, is

$$\begin{aligned} u(x,L)=\sin \pi x\left( \cosh \sqrt{\pi ^2-k^2} L+\sinh \sqrt{\pi ^2-k^2} L\right) \end{aligned}$$

and

$$\begin{aligned} u_{y}(x,L) = \sqrt{\pi ^2-k^2} \sin \pi x\left( \sinh \sqrt{\pi ^2-k^2} L+ \cosh \sqrt{\pi ^2-k^2} L\right) . \end{aligned}$$

The analytical solution is illustrated in Fig. 2. Note that the solution depends on both L and $k^2$.

Fig. 2

$k^2=20.5$ and $L=0.5$, is shown (left, graph). Also the Dirichlet data $f(x)=u(x,L)$ (right, solid) and $g(x)=u(x,0)$ (right, dashed)

Example 5.1

In an initial test, we use Cauchy data f(x) and g(x) obtained by sampling the analytical solution, with $k^2=20.5$ and $L=0.5$, on the grid. Previously it has been shown that the Dirichlet–Neumann algorithm, e.g. the case $\mu _0=\mu _1=0$, is divergent [4] for this set of parameters. To illustrate the properties of the Dirichlet–Robin algorithm, we pick the initial guess $\phi ^{(0)}(x)=\eta ^{(0)}=0$ and compute a sequence of approximations $\phi ^{(k)}(x)$ of the exact data f(x), as illustrated in Fig. 2.

For this test, we used the same value for the Robin parameters, i.e. $\mu :=\mu _0=\mu _1$. The results show that for small values of $\mu$, the Dirichlet–Robin algorithm is divergent but for sufficiently large values of $\mu$, we obtain convergence. The results are displayed in Fig. 3. To see the convergence speed, we display the number of iterations needed for the initial error $\Vert \phi ^{(0)}-f\Vert _2$ to be reduced, or increased, by a factor $10^{3}$. We see that for small values of $\mu$, we have divergence and the speed of the divergence becomes slower as $\mu$ is increased. At $\mu \approx 2.6$, we instead obtain a slow convergence. As $\mu$ is increased further, the rate of convergence is improved up to a point. For very large values of $\mu$, we have slower convergence. It is interesting to note that the transition from divergence to convergence is rather sharp. The optimal choice for $\mu$ is just above the minimum required to achieve convergence.

Fig. 3

We illustrate the error during the iterations for the case $\mu =2.5$ (right, red curve) and for $\mu =2.7$ (right, blue curve). We see that the rate of convergence is clearly linear. We also show the specific dependence on the parameter $\mu$ in the Robin conditions (left graph). Here we show the number of iterations needed for the magnitude of the error to change by a factor $10^3$

Example 5.2

For our second test we use the same analytical solution, with $\lambda =20.5$ and $L=0.5$. We test the convergence of the Dirichlet–Robin algorithm for a range of values $0\le \mu _0,\mu _1\le 15$. As previously, we find the number of iterations needed for the magnitude of the error to change by a factor $10^3$. In Fig. 4 we display the results. We see that both $\mu _0$ and $\mu _1$ need to be positive for the iteration to be convergent. We also see that the effect of $\mu _0$ and $\mu _1$ is slightly different.

Fig. 4

We illustrate the convergence speed for different values of $\mu _0$ and $\mu _1$ (left graph). The graphs represents level curves for the number of iterations needed to change the error by a factor $10^3$. The cases where the iteration diverges are illustrated by negative numbers (blue curves) and the cases where the iteration is convergent correspond to positive values (black curves). We also show the convergence speed as a function of the Robin parameter where either $\mu _0$ or $\mu _1$ is fixed. The case when $\mu _0=5$ is displayed (right,black curve) and the case when $\mu _1=5$ (right,blue curve). Here we see that the curves are similar in shape but not identical

Example 5.3

In the third test, we keep $L=0.5$ but vary $\lambda$ in the range $12.5<\lambda <45$. Recall that $k^2\approx 12.5$ is where the Dirichlet–Neumann algorithm stops working [4]. For this experiment, we use the same value for the parameters $\mu :=\mu _0=\mu _1$ in the Robin conditions. We are interested in finding the smallest value for $\mu$ needed to obtain convergence as a function of $\lambda$. The results are shown in Fig. 5. We see that a larger value for $k^2$ also means a larger value for $\mu$ is needed to obtain convergence. We also fix $k^2=35$ and display the number of iterations needed for the initial error $\Vert \phi ^{(0)}-f\Vert _2$ to be reduced, or increased, by a factor $10^{3}$. This illustrates the convergence speed of the iterations. In this case, $\mu \approx 12.7$ is needed for convergence. A comparison with the results of Example 5.1 shows that the shape of the graph is similar in both cases. We have very slow convergence, or divergence, only in a small region near $\mu \approx 12.7$.

Fig. 5

We display the minimum Robin-parameter $\mu$ required for convergence as a function of $k^2$, for the case $L=0.5$, and $\mu =\mu _0=\mu _1$ (left graph). We also show the number of iterations needed to change the initial error by a factor of $10^3$ for the case $k^2=35$ (right graph). Here negative numbers mean divergence and positive numbers correspond to convergent cases

6 Conclusion

In this paper, we investigate the convergence of a Dirichlet–Robin alternating iterative algorithm for solving the Cauchy problem for general elliptic equations of second order. In the Dirichlet–Robin algorithm, two functions $\mu _0$ and $\mu _1$ are chosen to guarantee the positivity of a certain bilinear form associated with the two well-posed boundary value problems, (2.3) and (2.4), that are solved during the iterations.

For the Helmholtz equation, we have shown that if we set $\mu =\mu _0=\mu _1$ is a positive constant then for small values of $\mu$, the Dirichlet–Robin algorithm is divergent but for sufficiently large values of $\mu$, we obtain convergence. However, for very large values of $\mu$, the convergence is very slow. We also investigated how $\mu _0$ and $\mu _1$ influences the convergence of the algorithm in detail. The results show that both $\mu _0$ and $\mu _1$ need to be positive for the iteration to be convergent. Finally, we investigated the dependence of $\mu$ on $k^2$ for convergence of the algorithm, i.e the smallest value of $\mu$ needed to obtain convergence as a function of $k^2$. The results show that a larger value for $k^2$ also means a larger value for $\mu$ is needed to obtain convergence.

For future work, we will investigate how to improve the rate of convergence for very large values of $\mu _0$ and $\mu _1$ using methods such as the conjugate gradient method or the generalized minimal residual method. We will also investigate implementing Tikhonov regularization based on the Dirichlet–Robin alternating procedure, see [5]. Also a stopping rule for inexact data will be developed. It will also be interesting to study the convergence of the algorithm in the case of unbounded domains.