Mono- and Multi-Representational Learning of the Covariational Aspect of Functional Thinking

Abstract

Using multiple external representations is advocated for learning in STEM education. This learning approach assumes that multiple external representations promote richer mental representations and a deeper understanding of the concept. In mathematics, the concept of function is a prototypical content area in which multiple representations are used. However, there are hardly any experimental studies investigating the effect of learning functional thinking with multiple representations compared to learning with only one form of representation. Therefore, this article reports on a quasi-experimental intervention study with students from Grade 7, using three measurement time points. The study compared the multi-representational learning of functional thinking with both tables and graphs with mono-representational learning with either tables or graphs. The results show that multi-representational learning led to advantages in learning qualitative functional thinking. However, in quantitative functional thinking, learning with both graphs and tables did not result in higher learning gains than learning exclusively with graphs. Furthermore, students were better able to transfer their knowledge from graphs to tables than vice versa. The results also indicate that multi-representational learning requires more time than mono-representational learning but can lead to higher learning gains. In sum, the results show that the effect of learning with representations is a complex interaction process between learning content and the forms of representation.

Introduction

Mathematics and science classes often deal with concepts (e.g., function, energy, atom) that are not directly accessible through the senses. Therefore, STEM learners are often provided with oral or written information about the concepts in question. The learning process consists of performing tasks that prompt the processing of the information given. The information is frequently provided in written form and combines different forms of external representation (e.g., texts, pictures, charts, graphs, tables, formulas). The learner’s goal in working with these external representations is to process them in their mind and generate adequate internal mental representations of the concept to be learned.

Consequently, over the last decades, the interplay between external and internal representations while learning has been an essential topic of educational psychology (e.g., Mayer, 2014; van Meter et al., 2020) as well as chemistry education (Gilbert & Treagust, 2009), physics education (Treagust et al., 2017), biology education (Treagust & Tsui, 2013), and mathematics education (e.g., Duval, 2006, 2017; Heinze et al., 2009). In this research, there is a consensus that learners should have rich mental representations that allow them to solve problems related to the concept flexibly.

However, the question of how external representations in learning foster or hinder the generation of elaborate and flexible mental representations is still open. It is often assumed that to develop rich mental representations, learning with multiple external representations is helpful. To justify this assumption, it is stressed that each form of representation highlights only certain aspects of a concept; therefore, multiple representations complement each other, and learning with multiple representations thus confers advantages (Cuoco, 2001; Gagatsis & Shiakalli, 2004; Kaput, 1992; Lesh et al., 1987). It is also argued that representations differ in terms of the information they contain or the actions that they support (e.g., Ainsworth, 1999). Thus, learners can gain from the complementarity of the benefits derived from different forms of representation in multi-representational learning environments. As a result, students are not limited to the strengths and weaknesses of one particular form of representation (Ainsworth et al., 2002).

However, results from empirical research challenge the simple principle that two representations are better than one. Multiple representations can confuse the learner and can result in higher cognitive demand that hinders learning (e.g., Sweller et al., 1998). For example, the split-attention effect (see Schroeder & Cenkci, 2018) shows that the combination of different external representations (e.g., text and picture) is not always conducive to the learning process. It may even be that some representations are better suited to learning a particular concept than others (Cobb et al., 1992). Furthermore, it has become increasingly apparent that complex interactions occur between external representations and the mental representations constructed by learners (Schnotz, 2014). The potential effectiveness of multi-representational learning materials is likely to be influenced by how the learning environment accommodates these complex interactions. Therefore, it is necessary to better understand the requirements for processing different forms of representation.

Theoretical background

In mathematics, learning with multiple representations plays an essential role when learning the concept of function. As an abstract mathematical concept, it is only accessible through external representations (Duval, 2006). Representing a function through an equation, a graph, a table, a verbal description, or a real-world situation are five common methods (Moschkovich et al., 1993). Because of the importance of the function concept for mathematics and its permeation of everyday life, one goal of mathematics education is the development of functional thinking in both primary education (Blanton & Kaput, 2011) and secondary education (Doorman et al., 2012; Günster & Weigand, 2020; Lichti & Roth, 2018). Functional thinking can be defined as “a way of thinking that is typical for dealing with functions” (Vollrath, 1989, p. 6, translated by the authors). A common approach that is used to further elaborate on functional thinking is to highlight three aspects of the function concept: correspondence, covariation, and mathematical object (e.g., Doorman et al., 2012; Günster & Weigand, 2020; Lichti & Roth, 2018; Vollrath, 1989). The aspect of covariation or covariational reasoning has received increasing attention in mathematics education research in recent years (e.g., Johnson, 2012, 2015; Thompson & Carlson, 2017; Wilkie, 2020). Although there are slightly different perspectives on covariation (see Thompson & Carlson, 2017), a common perspective on covariational reasoning for functions with one single variable is the investigation of the following question: What effect does varying the value of one variable (e.g., x-value) have on the value of the other variable (e.g., the y-value)?

One situational context proposed to foster functional thinking with a particular focus on covariation is the bottle problem (Carlson, 1998; Johnson et al., 2017; Swan, 1985; Thompson & Carlson, 2017). In this problem context, bottles (or other vessels that can contain water, such as vases) of different shapes are imagined, and water is poured in at a constant rate. The students then have to investigate the functional relationship between time and the bottle’s water level in various ways.

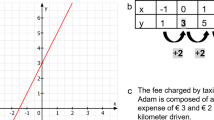
Figure 1 shows an exemplary task of a bottle problem in which the information about the filling process is given as a graph. Sometimes, a graph is considered to be especially suitable for developing functional thinking because it offers a view of the function as a whole (Vollrath, 1989) and it has the advantages of an iconic representation (Vogel, 2006). The task in Fig. 1 illustrates that functional thinking’s covariational aspect can be further divided into quantitative functional thinking and qualitative functional thinking (Rolfes et al., 2018). In subtask (a), the students have to determine the rate of change, which is an elementary concept of the covariational aspect (see Carlson et al., 2002). In this subtask, students could determine the rate of change by drawing a slope triangle and calculating rise over run (e.g., 3 cm/3 s = 1 cm/s). Calculating the rate of change requires quantitative functional thinking because the solution is based on precise function values that have to be inferred from the graph, that is, it deals with functional thinking in a quantitative way. To solve subtasks (b) and (c), on the contrary, is possible without inferring particular function values from the graph. For these tasks, it is sufficient to investigate the shape of the graph qualitatively. The steeper the graph, the higher the function values’ change (in this case: the water level’s height). Moreover, if the water level rises faster, the bottle has to become narrower. Therefore, subtasks (b) and (c) require qualitative functional thinking. As a previous empirical study with function tasks showed (Rolfes, 2018), the ability in quantitative functional thinking and the ability in qualitative functional thinking are connected but different abilities because a two-dimensional model that assumed different psychometric dimensions for these two abilities fitted substantially better than a one-dimensional model. The discriminatory validity of the two-dimensional model was satisfactory, with a latent correlation between the two dimensions quantitative and qualitative functional thinking of 0.79.

Fig. 1

Exemplary task concerning the bottle problem, supplemented by possible notes from students (in blue)

In Fig. 1, the tasks are based on a graph. However, it would also be possible to present the task and its relevant information with a table (see Fig. 2). In this form of representation, students could analyze the aspect of covariation by calculating the difference values of the x-values and the y-values, as illustrated in Fig. 2. In almost the same way as in a graph with a slope triangle, the rate of change can be calculated in a table by calculating the difference quotient (e.g., 3 cm/3 s = 1 cm/s). Students can solve subtask (b) by realizing that the difference in the y-values is higher between 6 and 12 s than between 0 and 6 s.

Fig. 2

Exemplary task with a table as form of representation, supplemented by possible notes from students (in blue)

The possibility of conveying information in different forms of representation raises the question of how external representations can be compared. According to Larkin and Simon (1987), two representations are computationally equivalent if the relevant information can be obtained from both representations just as quickly and easily. Thus, a representation A is computationally more efficient than a representation B if representation A makes it possible to solve the task more easily and faster than representation B. Therefore, the representation with the highest computational efficiency is the most advantageous representation for a task (Larkin & Simon, 1987). In the tradition of cognitive psychology, computational efficiency describes the interaction between the form of representation and the task regarding the human mind in general.

The computational efficiency of forms of representation depends on which type of functional thinking has to be performed (Rolfes et al., 2018). For example, for quantitative functional thinking (e.g., numerically calculating a rate of change), previous research has shown that a table had greater computational efficiency than a graph (Rolfes et al., 2018). However, for qualitative functional thinking (e.g., evaluating in which part of a piecewise linear function the increase is the fastest), a graph turned out to be more computationally efficient than a table because one could visually solve the task by assessing the slope of the graph (Rolfes et al., 2018). However, computational efficiency primarily refers to the performance on a task: Which form of representation is best for using students’ existing cognitive structures? Up until now, no statement has been made in previous research about the advantages of forms of representation in learning. Learning involves the experiential and relatively permanent modification of the cognitive structure (Anderson, 1995). Studies examining performance dependent on different forms of representation do not measure a change in cognitive structures. Hence, such studies provide only limited information about the effect of different forms of representation on learning procedures and concepts.

Therefore, the question about which influence the forms of representation have on learning functional thinking remains open. In addition to the term computational efficiency (Larkin & Simon, 1987), we refer to the effect of representational forms on the learning process as learning efficiency: A representation A is more learning efficient than a representation B if learning with representation A more efficiently modifies or extends cognitive structures for a particular requirement than learning with representation B does. That is, when learning within a certain amount of time with a representation A has a higher effect on learning a specific content than when learning with a representation B in the same amount of time, representation A has more learning efficiency than representation B.

Present study

Tables and graphs are two forms of representation very commonly used for teaching the concept of function. Therefore, this empirical study aimed to compare tables’ and graphs’ learning efficiency for learning functional thinking. Additionally, we examined the efficiency of multi-representational learning (i.e., learning with both tables and graphs) compared with mono-representational learning (i.e., learning with either tables or graphs).

Research question: When learning functional thinking, does the learning efficiency differ depending on whether students learn with tables only, with graphs only, or with both tables and graphs?

There were three different, in part competing, hypotheses to our research question:

• Hypothesis 1 (Multiple representation hypothesis): Functional thinking can be learned more efficiently in a multi-representational than in a mono-representational manner. That is, it is more learning-efficient to learn with both graphs and tables than to learn only with graphs or only with tables.

  Justification: It is often assumed from a theoretical perspective that learning with multiple representations brings advantages. This is based on the assumption that using multiple representations broadens the spectrum of cognitive possibilities and therefore enhances the learning outcome.

• Hypothesis 2 (Representational congruence hypothesis): Functional thinking should be learned with the same representation that the students later use for solving problems that require functional thinking. That is, graphs are the most efficient representation for learning graph-based functional thinking; tables are the most efficient representation for learning table-based functional thinking.

  Justification: Every representation requires different cognitive schemata. Therefore, students need to learn how to deal with each representation separately. For example, if a person wants to work out the piecewise linear function’s section with the highest rate of change (see Figs. 1 and 2), the procedures will differ between graphs and tables. When using a graph, the slopes of the lines can be compared visually. When using a table, a visual strategy is not possible and, therefore, changes must be numerically examined by, for example, calculating difference values.

• Hypothesis 3 (Master representation hypothesis): Functional thinking can be learned more efficiently with graphs than with tables.

  Justification: The representation that better supports the development of suitable cognitive schemata for functional thinking is more efficient for learning. Applying this argument to graphs and tables, it can be assumed that when learning with graphs, more diverse and flexible cognitive schemata can be developed than when learning with tables. Graphs contain many global features (e. g., general shape, intervals of increase or decrease) that can be interpreted (Leinhardt et al., 1990). For example, it is possible to analyze change behavior with a graph numerically (e.g., by calculating the rate of change) and qualitatively using the graph’s visual properties (e.g., from the graph’s slope). However, when using tables, the change behavior can only be analyzed numerically by calculating difference values or difference quotients. Therefore, the graph can be considered to be a superior form of representation to a table.

Method

Participants

The study included N = 331 students from 13 Grade 7 classes from five academic-track coeducational secondary schools (Gymnasium) in the German federal state of Rhineland-Palatinate. The study took place in proximate learning in the first quarter of the school year. The participating students were recruited by the teachers who were willing to participate with their classes in the study. The students’ parents or legal guardians gave their informed consent for the students to participate in the research study. The teachers provided the information that the students had not yet been formally introduced to the concept of function (scheduled, according to the curriculum, to happen in Grades 7 or 8).

Design and materials

Design

The study consisted of three experimental groups and one control group (see Fig. 3). One experimental group learned exclusively with tables, another learned exclusively with graphs, and the third learned with both tables and graphs. The control group received instruction on a topic other than the concept of function (e.g., geometry). The study was quasi-experimental in that the nine classes willing to participate in the intervention were randomly assigned to an experimental group. The three experimental groups completed a pretest, a short intermediate test in the middle of the intervention, and a post-test at the end of the intervention. Four classes were willing to act as the control group, which only completed the pre- and post-test to estimate the pretest’s testing effect.

Fig. 3

Quasi-experimental design of the study (EG experimental group, CG control group)

Learning environment

During the intervention, the students in the experimental groups received instruction on essential covariational aspects of functional thinking. For this purpose, a lesson sequence (the complete learning environment is presented in Online Supplement 1) was administered according to direct instructions (see Hattie, 2009), which means the explicit teaching of content followed by an exercise phase. Direct instruction has been shown to be highly effective in empirical studies (Hattie, 2009). This teaching method was chosen in our study mainly because it made it possible to administer a highly standardized lesson sequence in each participating class. New content was typically developed in an introductory phase and then consolidated and deepened by individual exercises or exercises solved with a classmate. Throughout the lesson sequence, flower vases served as the context because bottle-filling problems have been proven fruitful for teaching functional thinking (see Introduction). Lessons in all three experimental groups followed a strictly parallel structure and were carried out in all classes by the first author of this article. The class’s regular mathematics teacher was present only as an observer during the lessons and was not involved in the intervention. The process of filling vases with water at a constant rate was demonstrated with four differently shaped vases at the beginning of the learning sequence in the whole learning group. In the three experimental groups, the learning materials for the lessons differed only in the form of representation used (see Fig. 4): the table-only group used tables exclusively; the graph-only group used graphs exclusively; and in the table-graph group, tables and graphs were used alternately for the introductory examples and tasks. The students in the table-graph group had to work with both tables and graphs because the relevant information for an exercise was given either in one particular table or in one particular graph (see Online Supplement 1). Aside from the variation of the forms of representation, the teaching materials used were identical because the functional context, tasks, and layout were the same in all three experimental groups.

Fig. 4

Example task of the intervention (translated into English)

In the first half of the intervention, functional thinking was learned mainly through piecewise linear functions. For this purpose, according to the given functional relationship in the tables or graphs, change behavior was quantitatively analyzed either by determining rates of change or by extrapolation. To determine rates of change using the tables, the students were instructed to note the difference values beside the table (see Fig. 2).

Next, change behavior was qualitatively analyzed by producing qualitative descriptions (“uniformly increasing”), qualitatively comparing the change behavior (“water level increases quicker in the first section than in the second”) or inferring possible vase shapes from the rise in water level. At the end of the first half of the intervention, an intermediate test was performed containing questions on piecewise linear functions.

In the second half of the intervention, functional thinking was extended to nonlinear relationships, for example, by discussing the processes of filling spherical vases. For these nonlinear functions, similar tasks to those in the first half of the intervention were used (e.g., determining average rates of change, inferring possible vase forms, and qualitatively describing change behavior)..

Strictly speaking, the term mono-representational learning does not accurately characterize the experimental groups that learned solely with graphs or solely with tables. This is because, in addition to the tables or graphs, the students also had to deal with verbal descriptions (e.g., “the water level increases faster”) and images (e.g., a cross-sectional drawing of a vase). The learning environment’s central learning goal was even to translate between tables or graphs and verbal descriptions or images. However, because tables and graphs constituted the factorial variation of the quasi-experiment and the fundamental difference of the intervention, the learning process of the two groups that did not learn with both tables and graphs was nevertheless called mono-representational learning.

Pre-, intermediate, and post-test

Eighty-two items were developed to evaluate the learning effect of the intervention (typical test items are provided in Online Supplement 2). To calculate the ability on a common scale, a linked multimatrix design test (Frey et al., 2009) was administered (see Table 1). Six different booklets were developed from the item clusters for the pre-, intermediate, and post-test. The item clusters were distributed to the pre-, intermediate, and post-test booklets so that each student of the experimental groups received all 82 items, albeit at different time points. The pre- and post-test each consisted of 36 items, in which piecewise linear and non-linear functions were included. The intermediate test consisted of 10 items from the item clusters A, B, and C, which contained piecewise linear functions because only this function type had been addressed in the intervention up to this point. To adequately take account of differences between booklets, the item cluster L_V was used in all booklets of the pretest and thereby formed a link (Frey et al., 2009) to the pretest. Similarly, the item cluster L_N was included in all booklet variants of the post-test and served as a link to the posttest.

Table 1 Booklets

The items’ psychometric fit was evaluated by scaling the data with a two-dimensional Rasch model (quantitative vs. qualitative functional thinking). Three items showed values for the INFIT greater than 1.2 and were therefore excluded from the following analyses. All remaining 79 items met the defined quality criteria (INFIT ≤ 1.20, item-total correlation ≥ 0.20).

Data analysis

Learning effect analysis

The item response theory (IRT) in the form of a linear logistic test model (LLTM) was used to measure the learning effect (see Fischer, 1995). In a Rasch model, the basic model of the IRT, a specific item difficulty is estimated for every item. As a Rasch model’s extension, an LLTM decomposes item difficulties into components. Where an LLTM is used to measure change, the difficulty parameter of an item at the second time point is estimated as the sum of the item’s difficulty parameter at the first time point and one or more group-specific or global change parameters (Fischer, 1995). The basic idea is that, with no loss of generality, any change in a person’s ability can be regarded as a change in the item parameters (Mair & Hatzinger, 2007). A group contrast can be included to allow item difficulty to vary between groups (Mair & Hatzinger, 2007). For example, if ${\sigma }_{T}$ denotes the item difficulty of an item administered in the table-only group in the post-test, the item difficulty of the same item administered in the graph-only group in the post-test can be formulated as σ_G = σ_T – δ. The parameter δ estimates the difficulty difference parameter between the two experimental groups and indicates the ability difference between the graph-only and the table-only groups (see Fig. 5). When the graph-only group learned more than the table-only group, an item was easier for the graph-only group than for the table-only group, resulting in a positive difficulty difference parameter δ. Whether a difficulty difference parameter δ differed significantly from zero was tested by conducting a Gaussian Z-test because the parameters δ are asymptotically normally distributed.

Fig. 5

Illustration of the linear logistic test model (LLTM). The difficulty difference parameter indicates the difference in posttest achievement between the table-only group and the graph-only group

In the IRT framework, persons’ abilities and item difficulties are estimated in logits. Figure 6 shows the relationship between the ability on the logit scale and the probability of solving a task with medium item difficulty. As can be seen there, a change of δ = 0.5 logits approximately corresponds to an increase in the solution probability P of 10 percentage points (∆P). Because values on the logit scale are independent of the population, they can be interpreted as effect measures. The δ-values can be roughly interpreted similar to values of Cohen’s d, for which a value of 0.2 can be considered a small effect, a value of 0.5 represents a medium effect, and values of 0.8 and above are large effects.

Fig. 6

Relationship between the logit scale and the solution probability. An increase of 0.5 logits approximately indicates an increase in the solution rate of 10 percentage points

Two-dimensional LLTM

First, a two-dimensional LLTM was calculated (LLTM-2D). With this model, the learning efficiency of the different experimental groups on quantitative and qualitative functional thinking was evaluated. The first 79 parameters σ₁ to σ₇₉ of the LLTM-2D calculated the item difficulties in the table-only group in the pretest as the baseline item difficulties. The other 20 parameters δ₁ to δ₂₀ estimated the group differences in the two dimensions at the various time points. Of these group difference parameters, the first six basic parameters (δ₁ to δ₆) each estimated the ability difference between the four groups in the pretest. Six further parameters (δ₇ to δ₁₂) estimated the learning gain from pretest to intermediate test, taking into account the ability difference of the groups in the pretest. Hence, it should be pointed out that it was not analyzed whether the ability level differed in the intermediate test, but whether the learning gain differed. The parameters δ₁₃ to δ₂₀ estimated the learning gain from pre- to post-test while partitioning out the ability differences in the pretest.

Four-dimensional LLTM

Additionally, a four-dimensional model that took the form of representation (table or graph) into account was estimated (LLTM-4D). This four-dimensional model (Dimension 1: quantitative table items; Dimension 2: qualitative table items; Dimension 3: quantitative graph items; and Dimension 4: qualitative graph items) enabled us to analyze students’ ability to transfer their knowledge from graphs to tables and vice versa. Overall, the four-dimensional model showed a satisfactory model fit and satisfactory EAP/PV reliabilities (Dimension 1: .786; Dimension 2: .724; Dimension 3: .807; Dimension 4: .648).

Assessment of model fit

The LLTM-2D and the LLTM-4D models assumed a particular two-dimensional or, respectively, four-dimensional structure of the construct functional thinking. Therefore, confirmatory factor analyses were conducted with the pretest data to assess whether these modeling approaches were psychometrically reasonable. Because all items were dichotomously scored, a full-information item factor analysis (Bock et al., 1988) was performed.

As a baseline model, we estimated the one-dimensional model 1D, in which all items loaded on one factor. This baseline model was compared with three different multidimensional models. In the model 2D–Quan × Qual, functional reasoning was divided into the two factors quantitative functional thinking (factor Quan) and qualitative functional thinking (factor Qual). The model 2D–T × G assumed the two latent dimensions table-based functional thinking (factor T) and graph-based functional thinking (factor G). Furthermore, the model 4D–QuanT × QualT × QuanG × QualG split quantitative and qualitative functional thinking according to whether the tasks had to be solved with tables or graphs.

To assess which of these models fitted best, model comparisons were performed using the Akaike information criterion (AIC, Akaike, 1974) and the Bayesian information criterion (BIC, Schwarz, 1978). Furthermore, the latent correlations of the dimensions were estimated. Finally, the EAP-PV reliability of the models was calculated.

Assessment of multilevel effect

The quasi-experiment had a design-related multilevel structure (Goldstein, 1987), with students (Level 1 units) nested in classes (Level 2 units). One problematic effect of a multilevel structure can be that measurements violate the assumption of independence because measurements within a class might be more homogeneous than those between different classes. However, hierarchical linear models should only be applied with a high number of Level 2 units (i.e., school classes) (see Maas & Hox, 2005). Nevertheless, to investigate the possible influence of the multilevel structure on the results, the extent of nonindependence can be estimated using the intraclass correlation (Gelman & Hill, 2006). The higher the intraclass correlation, the higher the dependence within classes and the higher the multilevel effect. Therefore, for the quasi-experiment, intraclass correlations for the pretest results were calculated for each model and each dimension with 10 plausible values (Adams et al., 2007). If the intraclass correlation does not deviate significantly from zero, there is no evidence that the multilevel structure affects the results.

Software

The calculations were made using the software package R (R Core Team, 2020). Dimension analyses were performed using the package Mirt (Chalmers, 2012), and the IRT scaling and calculation of the LLTMs were performed using the package TAM (Robitzsch et al., 2020).

Results

Assessment of model fit

The data analyses were based on the models LLTM-2D and LLTM-4D. The LLTM-2D was based on a two-dimensional model, 2D–Quan × Qual, which assumed the two dimensions of quantitative and qualitative functional thinking. The LLTM-4D additionally separated quantitative and qualitative functional thinking, depending on whether it was performed with tables or graphs. To assess the appropriateness of these modeling approaches, model comparisons were performed.

The model comparison with the information criteria AIC and BIC showed that the model 2D–Quan × Qual and the model 4D–QuanT × QualT × QuanG × QualG fitted best (see Table 2). The one-dimensional model had substantially higher values for AIC and BIC and, therefore, fitted substantially worse. The two-dimensional model, 2D–T × G, which separated table-based and graph-based functional thinking, fitted even worse than the one-dimensional model.

Table 2 Model comparisons

The analyses of the latent correlations (see Table 3) confirmed the results of the model comparisons. The models 2D–Quan × Qual and 4D–QuanT × QualT × QuanG × QualG showed the highest discriminatory validity. In contrast, the dimensions table-based and graph-based functional thinking in the model 2D–T × G were highly correlated.

Table 3 Latent correlations of the models

Overall, the models 2D–Quan × Qual and 4D–QuanT × QualT × QuanG × QualG showed a similar model fit. Furthermore, the EAP/PV reliabilities of the models were satisfactory (2D–Quan × Qual: .809 and .772, 4D–QuanT × QualT × QuanG × QualG: .786, .724, .807, and .648).

Assessment of multilevel effect

This study was a quasi-experiment because the random assignment to experimental conditions occurred on the level of the learning groups. Therefore, it is possible that a multilevel effect distorted the results. To evaluate the extent of this multilevel effect, intraclass correlations were calculated.

In the two-dimensional model, 2D–Quan × Qual, the mean intraclass correlation in the first dimension was .015 with a mean 95% confidence interval [–.012, .099], and in the second dimension .014 with a mean 95% confidence interval [–.012, .098]. This means that in both dimensions, the intraclass correlation did not differ significantly from zero because zero was always included in the mean confidence interval. In the four-dimensional model, 4D–QuanT × QualT × QuanG × QualG, the mean intraclass correlations also did not differ significantly from zero in any of the dimensions: Dimension 1: 95% CI [–.021, .062]; Dimension 2: 95% CI [–.007, .120]; Dimension 3: 95% CI [–.013, .094]; and Dimension 4: 95% CI [–.011, .105].

These results show that a significant multilevel effect was not detected, either in the two-dimensional model, 2D–Quan × Qual, or in the four-dimensional model, 4D–QuanT × QualT × QuanG × QualG. Hence, it was reasonable to neglect the effect of the multilevel structure of the data in the analyses.

Learning effect analysis

Overall, the experimental groups showed a substantial increase in performance. The average p value of the experimental groups concerning the items administered in the pretest was .34. This average p value rose in the post-test to .64. That is, on average, across all experimental groups and dimensions, there was an increase of 30 percentage points.

To provide a more detailed insight into the learning effects, the results of the data analyses using the two models LLTM-2D (based on the two-dimensional model 2D–Quan × Qual) and LLTM-4D (based on the four-dimensional model 4D–QuanT × QualT × QuanG × QualG) are presented below. Supplementary tables with the parameter values of both LLTMs are available in Online Supplement 3.

LLTM-2D: quantitative versus qualitative functional thinking

The LLTM-2D estimated gain scores (in logits) for the two constructs, quantitative functional thinking and qualitative functional thinking.

Quantitative functional thinking

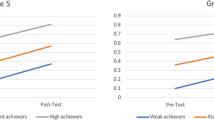
From pretest to intermediate test (see Fig. 7, left-hand side), the table-only group showed a significant learning gain (δ₇ = 1.93, z = 25.7, p < .001) in quantitative functional thinking. However, the graph-only group demonstrated an even (significantly) higher learning gain (δ₉ = 0.55, z = 6.05, p < .001) than the table-only group. Up to the intermediate test, the table-graph group showed a significantly lower learning gain than the graph-only group (by δ₁₁ =  − 0.54, z =  − 4.37, p < .001), but almost as much learning gain as the table-only group.

Fig. 7

Average scores of experimental groups and control group in terms of quantitative and qualitative functional thinking based on the results of the LLTM-2D (G graph-only group, TG table-graph group, T table-only group, C control group)

From pre- to post-test, the learning gain in quantitative functional thinking in the control group (i.e., the testing effect) was significant, δ₁₃ = 0.74, z = 21.07, p < .001. The table-only group displayed a significantly higher learning gain than the control group, δ₁₅ = 1.19, z = 27.9, p < .001. At the intermediate test stage, the learning gain in the graph-only group was significantly higher than the learning gain in the table-only group, with a difference in learning gain of δ₁₇ = 0.59, z = 11.3, p < .001, even though the magnitude of the intermediate test result was almost identical. However, there was no significant difference (δ₁₉ =  − 0.10, z =  − 1.4, p = .15) in the learning gain from pre- to post-test between the table-graph group and the graph-only group.

Qualitative functional thinking

Overall, learning gains in qualitative functional thinking were lower than in quantitative functional thinking (see Fig. 7, right-hand side). From pretest to intermediate test, the ability level in the table-only group increased significantly by δ₈ = 0.99, z = 11.6, p < .001. The graph-only group showed a significantly higher learning gain than the table-only group, δ₁₀ = 0.31, z = 3.0, p = .003. However, there was no significant difference between the table-graph group and the graph-only group in qualitative functional thinking up to the intermediate test (δ₁₂ = 0.16, z = 1.1, p = .27).

From pre- to posttest, ability in qualitative functional thinking in the control group increased significantly, by δ₁₄ = 0.23, z = 6.9, p < .001. The table-only group showed a significantly higher learning gain than that of the control group, δ₁₆ = 0.90, z = 21.7, p < .001, while the graph-only group had a significantly higher increase in ability than the table-only group, δ₁₈ = 0.15, z = 2.9, p = .004. However, the highest learning gain was recorded for the table-graph group, δ₂₀ = 0.42, z = 5.7, p < .001, again significantly higher than that of the graph-only group.

LLTM-4D: quantitative and qualitative functional thinking with graphs and tables

To evaluate whether the students were able to transfer their acquired knowledge in functional thinking from graphs to tables and vice versa, a four-dimensional model was estimated. However, the four dimensions could not be measured reliably in the intermediate test because it consisted of only 10 items; therefore, in the LLTM-4D, unlike the LLTM-2D, only learning gains from pre- to posttest were calculated.

Quantitative functional thinking with tables and graphs

In quantitative functional thinking with tables (see Fig. 8, left-hand side), the control group had significantly higher ability values in the posttest than in the pretest, δ₁ = 0.82, z = 16.2, p < .001, while the table-only group showed a significantly higher learning gain than the control group, δ₅ = 1.50, z = 24.0, p < .001. Moreover, the learning gain of the graph-only group did not differ significantly from that of the table-only group, δ₉ = 0.09, z = 1.1, p = .25; likewise, there was no significant difference between the learning gain of the table-graph group and that of the graph-only group, δ₁₃ = 0.03, z = 0.2, p = .81. The finding that the three experimental groups’ learning gains were approximately equal is strikingly illustrated in Fig. 8 (on the left-hand side) by the fact that the lines are nearly parallel.

Fig. 8

Average scores of experimental groups and control group in terms of quantitative functional thinking with tables and graphs based on the results of the LLTM-4D (G graph-only group, TG table-graph group, T table-only group, C control group)

Turning to quantitative functional thinking with graphs (see Fig. 8, right-hand side), the control group showed a significant learning gain from pre- to post-test, by δ₃ = 0.64, z = 13.0, p < .001. The table-only group showed a significantly higher learning gain than the control group, δ₇ = 0.66, z = 11.1, p < .001, while the graph-only group demonstrated a significantly higher learning gain than the table-only group, δ₁₁ = 1.24, z = 17.0, p < .001. There was no significant difference in learning gain between the graph-only group and the table-graph group, δ₁₅ =  − 0.08, z =  − 0.8, p = .43. Visually, Fig. 8 (on the right-hand side) shows that the lines for the table-graph group and the graph-only group are nearly parallel, whereas the table-only group’s line is obviously less steep, indicating a lower learning gain.

Qualitative functional thinking with tables and graphs

In qualitative functional thinking with tables (see Fig. 9, left-hand side), the control group showed a significant increase from pre- to post-test by δ₂ = 0.19, z = 4.2, p < .001. The learning gain of the table-only group was significantly higher than that of the control group, δ₆ = 0.96, z = 17.4, p < .001. The graph-only group had a significantly lower gain than the table-only group, δ₁₀ =  − 0.26, z =  − 3.9, p < .001. In turn, the table-graph group showed a significantly higher learning gain than the graph-only group, δ₁₄ = 0.24, z = 2.5, p = .01.

Fig. 9

Average scores of experimental groups and control group in terms of qualitative functional thinking with tables and graphs based on the results of the LLTM-4D (G graph-only group, TG table-graph group, T table-only group, C control group)

In qualitative functional thinking with graphs (see Fig. 7, right-hand side), the control group’s ability increased significantly from pre- to posttest, δ₄ = 0.20, z = 4.8, p <.001. The learning gain in the table-only group was significantly higher than in the control group, δ₈ = 0.28, z = 5.3, p < .001, while the graph-only group showed a significantly higher learning gain than the table-only group, δ₁₂ = 0.54, z = 8.2, p < .001. Again, the table-graph group recorded the highest learning gain. Its learning gain was significantly higher than that of the graph-only group, δ₁₆ = 0.31, z = 3.4, p < .001.

Discussion

In the following, we discuss the results of our study. In the first section, the results on learning functional thinking with representations are summarized and evaluated with regard to the three hypotheses. We then infer what practical implications for learning functional reasoning could follow from the results. Finally, the limitations of the study are presented, and future research desiderata are formulated.

Learning functional thinking

Multiple representation hypothesis

In the multiple representation hypothesis (Hypothesis 1), we assumed that multi-representational learning would be more efficient than mono-representational learning. We found some support for this hypothesis in the finding that the table-graph group had the significantly highest learning gain from pre- to posttest in qualitative functional thinking. However, in quantitative functional thinking, there was no significant difference between mono-representational learning using graphs exclusively and multi-representational learning using both tables and graphs. In the four-dimensional model, multi-representational learning with tables and graphs had the significantly highest learning gain for qualitative functional thinking. In contrast, the two dimensions of quantitative functional thinking with tables and graphs showed no significant difference between the mono-representational experimental group that learned with graphs only and the multi-representational experimental group that learned with both tables and graphs.

What is striking about the results is that the table-graph group showed an apparent increase from intermediate to posttest, whereas the mono-representational learning groups showed little change from intermediate to post-test. For example, up until the intermediate test, multi-representational learning with tables and graphs was no more efficient than mono-representational learning using graphs exclusively for either quantitative or qualitative functional thinking. Up until the intermediate test, the multi-representational group even showed a lower learning gain in quantitative functional thinking than the group that learned with graphs only. In contrast, the increase in qualitative functional thinking between these two experimental groups did not differ significantly. Overall, the results indicate that multi-representational learning might require more time than mono-representational learning. The reason for this result could be that working with multiple representations requires initially higher cognitive demands since more information has to be processed simultaneously and held in working memory. Conversely, however, multi-representational learning presents an opportunity to achieve higher learning gains than are possible with mono-representational learning alone. The present study also shows that the added value of multi-representational learning depends on both the learning object and the learning time. The generality of the assumption that multi-representational learning always leads to higher learning gains was not confirmed in our study.

Representational congruence hypothesis

The representational congruence hypothesis (Hypothesis 2) assumed that it is best to learn with the form of representation that is used later in the assessment. Essentially, this hypothesis suggests that tables are best for learning table-based functional thinking, whereas graphs are most effective for learning graph-based functional thinking. The empirical data from the quasi-experiment provides some evidence for this hypothesis, albeit with some limitations. The graph did prove more efficient than the table for learning graph-based quantitative and qualitative functional thinking. In the same manner, the table proved more efficient than the graph for table-based qualitative functional thinking. However, concerning table-based quantitative functional thinking, learning with tables was not more efficient than learning with graphs. Instead, table-based quantitative functional thinking was learned with graphs as efficiently as it was with tables. In other words, the cognitive schemata constructed by learning quantitative functional thinking with a graph appear to be relatively easily applicable to a table.

Master representation hypothesis

In the master representation hypothesis (Hypothesis 3), we assumed that graphs are a superior form of representation and are more efficient than tables for functional thinking. Support for this hypothesis was found in the results for both the two-dimensional and the four-dimensional models. Thus, with the two-dimensional model, a graph was found to be more efficient than a table for learning quantitative functional thinking. Likewise, in the four-dimensional model, graphs were more efficient than tables for learning both table-based and graph-based quantitative functional thinking. In graph-based quantitative functional thinking, the difference in learning between the table-only group and the graph-only group was relatively high (1.24 logits). This finding supports the thesis that transferring procedures learned with a table to a graph poses considerable difficulty. Applying quantitative functional thinking to a table, on the other hand, can be learned with graphs as well as with tables. The transfer of graph-based schemata to a table in quantitative functional thinking seems to pose relatively little difficulty. Therefore, a graph seems to be a more suitable form of representation for learning quantitative functional thinking than a table.

For qualitative functional thinking, however, the graph was not always more learning-efficient than the table. In the four-dimensional model, a table was more learning-efficient than a graph for table-based qualitative functional thinking, whereas, for graph-based qualitative functional thinking, a graph was more learning-efficient. This result is also plausible from a subject-matter perspective. Qualitative functional thinking, for example, includes the ability to assess in which section the increase is highest in a piecewise linear function. When using a graph, this problem can be solved by comparing the slope of the line. The same problem can be solved numerically with a table only by calculating the difference between the x- and y-values in each section and comparing the differences’ size. Thus, using a table requires different procedures than those required when using a graph.

Computational efficiency versus learning efficiency

Overall, one can surmise from the results that the transfer’s success depends on the underlying cognitive processes. If the necessary cognitive processes are very similar, a transfer from one representation to another is relatively easy. However, if the cognitive processes differ substantially between representations, a transfer is relatively difficult. The results also show a difference between the computational efficiency of a form of representation and its learning efficiency. Students learn quantitative functional thinking better with a graph than with a table, as this study shows. That is, a graph promotes the construction of mental representations for quantitative functional thinking better than a table does, and a graph is better suited to learn, for example, the concept of the rate of change than a table. However, if students have understood the concept of the rate of change, previous research showed (Rolfes et al., 2018) that a table is better suited than a graph for actually calculating the rate of change.

Practical implications

The present study’s findings appear to justify the dominance of graphs over tables in learning the concept of function. A graph is a richer representation than a table because, besides the numeric data, it provides a visual impression that a table lacks. Therefore, it is reasonable to assume that a graph offers more learning opportunities than a table. Accordingly, a graph is more efficient than a table for learning many facets of functional thinking. Only in table-based qualitative functional thinking was a table more beneficial than a graph in the current study. Therefore, when planning lessons, teachers should reflect as much as possible on the benefit of a particular form of representation concerning the learning process. The selection of the form of representation during the learning process should be determined not only by the question of which particular form of representation provides the most straightforward way to solving the given problem; sometimes, a more cumbersome approach with another form of representation might provide more learning opportunities and might be more rewarding for the learning process.

Being able to connect different representations of functions is in itself already an important learning goal of mathematics education. Besides this rationale for using multiple representations, the present study identified further benefits. Multi-representational learning can lead to higher learning gains than those achieved through mono-representational learning. Put simply, one can learn more with multiple forms of representation. This result provides empirical evidence that adopting an approach that uses multiple representations is beneficial for learning functional thinking. For example, this study showed that it is better to learn qualitative functional thinking using a graph and a table rather than only a graph. This leads to the initially counterintuitive conclusion that teaching qualitative functional thinking should not exclusively use graphs. Instead, the way in which qualitative problems (e.g., “In which time period do the function values change the quickest?”) might be solved with tables should also be considered. In general, these results show that computational efficiency and learning efficiency do not always correspond. Therefore, students should also be taught with representations that are computationally less efficient for the task to be learned; that is, quantitative functional thinking should also be taught with graphs, and qualitative functional thinking should also be taught with tables.

However, the benefits of multi-representational learning have limits. In general, multi-representational learning takes more time than mono-representational learning because students first have to learn how to deal with the different representations. This fact presents a representation dilemma (Rau, 2017) that not only the content but also the representation itself must be learned. Furthermore, multi-representational learning was not superior to mono-representational learning for all learning content. For quantitative functional thinking, for example, the effect of learning with both tables and graphs was lower than learning with graphs alone from the pretest to the intermediary test. However, the effect from pre- to post-test was comparable for both groups. Therefore, it seems appropriate to initially begin the learning process with a representation that is particularly suitable for the particular content being learned. When the learning content has been mastered to a satisfactory degree with this “first” representation, a second and possibly third representation can be added. This approach can potentially maximize the learning success, as conferred by our results. However, further representations only provide additional value if they require a different approach to the learning content than that of the first representation. If a transfer of what has been learned with the first form of representation to other forms is relatively easy, the addition of further representations might not add any further value.

Thus, the simple action motto “The more, the better!” is only partially supported by the present study’s results. Working with additional representations requires additional learning time; therefore, whether an additional form of representation justifies the additional time required must be weighed up. In classroom practice, it is not always easy to determine whether another form of representation truly adds value to the learning process. Here, the insight and experience of the teacher are required to make the right decision. Hence, further empirical research on learning with representations would be desirable to support teachers with this difficult decision.

Limitations

In the study’s learning environment, the connection between tables and graphs was not explicitly highlighted in the multi-representational learning group. Instead, the students had to implicitly link the two forms of representation by solving similar problems using a table and a graph. Kaput (1989), for example, highlights the importance of connecting the forms of representation while teaching and learning. Hence, learning multi-representationally with tables and graphs in the current study may have resulted in even higher learning benefits had the connection between tables and graphs been explicitly discussed. Future experiments should investigate this possibility further.

Some of our results are limited for methodological reasons. The problem of our multilevel structure (students nested in classes) has already been pointed out, although the insignificant intraclass correlations suggest that the multilevel effect did not lead to a severe distortion of the results. Furthermore, the intermediate test did not have the same reliability as the pre- and posttest because the intermediate test consisted of only 10 items on linear functional relationships. In contrast, the pre- and posttest each consisted of 36 items on both piecewise linear and nonlinear functional relationships.

Finally, the learning environment and the test items focused on the bottle problem. Although this situational context is often recommended for fostering functional thinking, the empirical question of how representative the bottle problem is for measuring functional thinking remains open.

Research desiderata

The present study considered learning efficiency as a characteristic of a form of representation with regard to the human mind in general. However, interindividual differential effects of the efficiency of mono- or multi-representational learning are possible and should be investigated further in detail. For example, against the backdrop of the cognitive load theory (Sweller et al., 2011), a plausible assumption is that learning with multiple representations creates a higher cognitive burden than mono-representational learning. Therefore, it could be hypothesized that students with considerable cognitive capacity (e.g., high working-memory capacity, high intelligence) in particular would benefit from multi-representational learning because they can handle the higher cognitive load. Students with somewhat low cognitive capacity, on the other hand, could be overwhelmed by multiple representations in the learning process. On that basis, it would be worthwhile to empirically investigate the interaction between cognitive capacity and learning gains in multi-representational learning.

Furthermore, our study focused on the quantitative measurement of the effects of learning with different forms of representations. Based on our hypotheses, which were derived from theoretical considerations and empirical evidence from previous studies, we were able to gain valuable insights into learning with representations. However, a follow-up study could explore the findings via qualitative research. Such a study could provide more information on students’ thinking and how students specifically deal with external representations such as tables and graphs in the learning process.

Finally, tables and graphs are only two of several forms of representation of functional relationships. In addition, the learning environment and the test items on the bottle problem focused on one particular context. Therefore, studies on the efficiency of learning with other forms of representation (e.g., symbolic algebra, verbal descriptions, real-life situations) and in other situational contexts should be conducted. For example, the symbolic-algebraic representation of functional relationships forms a central subject in mathematics education at the secondary school level. Although studies exist on the translation between, for example, a graph and a symbolic-algebraic form of representation, future studies should investigate which particular aspects of functional thinking can be learned using the symbolic-algebraic form of representation.