1 Introduction

Functional thinking has been extensively studied over the last 20 years by mathematics educators, policymakers, and researchers. They argue that functional thinking contributes towards understanding important mathematical ideas as a unifying principle across the K-12 mathematics curriculum and as being a major gateway to algebraic thinking (Blanton et al., 2015b; National Council of Teachers of Mathematics, 2000; Pittalis et al., 2020). Research findings have shown that functional thinking can be nurtured among primary school students under appropriate conditions (Blanton et al., 2015a). For example, students can generalize and represent functional relationships (Stephens et al., 2017) and manipulate different representations of functions (Rolfes et al., 2022). Findings showing that functional thinking can be developed are drawn from early-algebra intervention programs that are founded upon hypothesized learning progressions and include patterning problems in real-life contexts that require exploring functional relationships, constructing input–output function tables, identifying recursive patterns and covariational relationships, making far-transfer predictions for values according to a functional relationship, and representing an identified correspondence rule in words or symbols (Pang & Sunwoo, 2022). There is also evidence that learning environments utilizing computer-based simulations, real materials, or multiple external representations (e.g., graphs, tables, equations) facilitate the development of functional thinking (Lichti & Roth, 2018; Rolfes et al., 2022).

However, primary school curricula worldwide offer limited support for students' functional thinking and many questions about how exactly to nurture functional thinking with primary school students remain unanswered (Carraher & Schliemann, 2018; Kieran, 2022). Considering that digital approaches have shown to be fruitful for fostering functional thinking (e.g., Lichti & Roth, 2018), further research in this field should focus on such digital settings to enhance functional thinking. As new digital technology tools continue to evolve, it remains essential to provide both theoretical and empirical justifications for how such tools could support functional thinking development (Günster & Weigand, 2020). Researchers recommend investigating embodied approaches using digital technology (Wei et al., 2023), as digital learning environments can support learning by linking embodied experiences with mathematical discourse (Duijzer et al., 2017; Shvarts & van Helden, 2023; Skulmowski & Rey, 2018). For example, portable and handheld digital technologies offer opportunities for enacting embodied learning through hand-held dragging of objects on screen (Abrahamson & Bakker, 2016; Duijzer, et al., 2017; Xie et al., 2018).

In this sense, our study aims to empirically investigate the effects of an intervention program for upper primary school students. The program is designed to foster functional thinking by utilizing the affordances of digital learning environments and by developing different aspects of functions. The purpose of this study was twofold: (a) to examine whether fifth and sixth grade students’ participation in a dynamic mathematics functional thinking intervention program leads to significant effects on their functional thinking development and corresponding strategy usage and (b) to explore whether these effects vary based on students' grade, gender, prior functional thinking performance, mathematics- and functions-related self-concept, and interest.

2 Theoretical framework

In the following, we present the theoretical framework, which encompasses the aspects of function, students’ modes of functional thinking and research findings related to corresponding intervention programs.

2.1 Aspects of functions

Beyond formally defining function in mathematics education, this concept is associated with various aspects of functions, including input–output relationships, dynamic process of covariation, the correspondence relation, and the nature of functions as mathematical objects (Dubinsky & Harel, 1992; Pittalis et al., 2020; Thompson & Carlson, 2017). The input–output aspect entails the computations given by a rule and does not necessitate an awareness of the causal relationship between input and output. Students perceive functions as a request for calculation, where one variable (the input) is entered, and the resulting variable represents the output (Doorman et al., 2013). The covariational aspect entails the analysis, manipulation, and comprehension of the relationships between at least two quantities that change simultaneously. It focuses on the conceptualization of the simultaneous variation of two or more quantities, with the aim of coordinating the values of these two variables as they change (Confrey & Smith, 1995; Thompson & Carlson, 2017). The correspondence aspect is often used to formally introduce functions at school (Vinner & Dreyfus, 1989) and underscores the comprehension of the structural conceptualization of functions by perceiving the relation between the independent and dependent variables. The fourth aspect entails considering a function as a mathematical object that can be represented in different ways, such as arrow chains, tables, graphs, formulas, and verbal descriptions, each providing a different view on the same object (Doorman et al., 2013). Based on Sfard (1991), we observe a gradual transition from a process-oriented perspective (input–output aspect) to a more structural viewpoint (object aspect). That said, it's essential to recognize that these different aspects are often intertwined, making it challenging for teaching and learning.

During primary and lower secondary grades, students are primarily expected to engage with functions through the input–output, covariation, and correspondence approaches (Eisenberg, 1992). Hence, we adopt the stance that functional thinking among primary school students focuses on the invariant relation between two varying quantities/variables. This understanding leads from specific relationships to the generalization across different instances, emphasizing that each value of one quantity/variable determines a value of the other (Pittalis et al., 2020). In this context, functional thinking involves (a) recognizing, generalizing, and abstracting relations between covarying quantities/variables; (b) expressing these relations using verbal language, symbols, and appropriate representations; and (c) employing these generalized representations to solve problems (Blanton et al., 2015a; Cañadas et al., 2016; Warren & Cooper, 2005). To do so, students use different strategies that are related to the conceptions of functions described above.

2.2 Modes of functional thinking

Research on students' strategies to explore functional relationships in various scenarios has shown three modes of functional thinking (Confrey & Smith, 1995). The first mode is a recursive strategy, which encompasses identifying variations within a single sequence of values, describing the rule between successive terms, and using a rule to predict data without taking a second variable into account. The second mode is a covariational strategy and involves articulating the rule that governs the covariation of two quantities, aiming to coordinate the underlying rate of change. The third mode refers to correspondence and focuses on recognizing the relationship between the involved variables and utilizing the function rule to predict distant-function values or to determine the value of one variable based on the value of the other. For example, to determine the 20th term of the pattern 5, 8, 11, …. an individual employing a recursive strategy would extend the pattern (by repeatedly adding 3) until reaching the 20th term. A covariational strategy involves conceptualizing that 3 is added for every additional term; hence 17 times 3 should be added to the third term (11) to find the 20th term. Finally, a correspondence strategy requires recognizing that the nth term is calculated by the linear relationship \(3(n-1)+5\).

The mode of correspondence can be characterized more detailed through two sub-modes of functional thinking: correspondence-particular, which involves the ability to identify the correspondence relation using specific values, and correspondence-general, which reflects students' capacity to recognize and articulate the general relation between the involved variables (Pang & Sunwoo, 2022; Pittalis et al., 2020). Research has indicated a potential developmental progression from recursive to covariational and (particular and general) correspondence strategies (Cooper & Warren, 2011).

2.3 Functional thinking intervention programs

Developing functional thinking is not easy – neither for students, nor for their teachers. Difficulties arise for instance from the abstract nature of functions, which are only accessible through specific representations such as graphs, equations, tables, and verbal descriptions (Sproesser et al., 2022), and from the need to change between mathematics and real-world contexts in the processes of vertical and horizontal mathematization (Michelsen, 2006). Effective interventions recognize the developmental progression of functional thinking modes and provide students with opportunities to engage with functions in meaningful and relevant ways.

Several intervention studies targeted students in the lower primary grades (Blanton et al., 2015a). A common aspect of these studies was the use of typical patterning tasks through problem scenarios that serve as a bridge to functional relationships. Students are asked to generate a set of covarying data based on the given scenario, organize the data in a table, explore relationships in the data, find the covariation rule, predict near, and far function values, and generalize the relationship between the two quantities using verbal or variable notation. An intervention study with first graders included scenarios with relations of the form \(y=m\bullet x\), \(y=x+b\), and \(y=m\bullet x+b\) (Blanton et al., 2015a). For example, students engaged with the relationship between the number of cuts of a straight piece of string and the number of pieces of string made \((y=x+1)\) (Blanton et al., 2015a, p. 520). The program of this study included 16 lessons in an 8-week session and followed a design research approach. Findings of the project, based on student interviews, showed that first graders can learn to think in quite sophisticated and generalized ways about functional relationships. Another intervention study from Blanton, Stephens and colleagues (2015b) examined the impact of a comprehensive early algebra intervention in third grade and showed a statistically significant effect on the ability of students to identify and represent generalizations about covarying quantities. The study also revealed a change in students’ strategy usage, as they utilized function rules to extend patterns or to find far function values.

A longitudinal experimental study examined students’ development in dealing with various types of functional relationships from Grade 3 to 5. In Grade 3, students examined linear relationships, in Grade 4, they moved to quadratic relationships of the form \(y={x}^{2}\) (using a growing geometric pattern) and \(y={x}^{2}+b\), and, finally, in Grade 5, students moved to exponential relationships (e.g., for each succeeding good-work day, the reward doubles) (Blanton et al., 2019; Stephens et al., 2017). During and after the intervention, students from the experimental group were significantly better able than those from the control group to generalize a functional relationship verbally or using variable notation at each time-point from Grade 3 to 5. Findings showed that Grade 5 students faced more difficulties in symbolically representing functional relationships compared to symbolically representing an arithmetic property or a varying quantity. This difficulty seemed to be attributed to the task’s complexity (quadratic and exponential) and its divergence from the regular curriculum (Blanton et al., 2019). This finding raises questions regarding the type of functional relationships that are appropriate for each grade in primary school. Further, the study showed that students’ responses progressed from a recursive to a correspondence mode, noticing a main path from a recursive strategy to considering both variables in a general way (e.g., “times 2”) before expressing a correspondence rule in variables and words (Stephens et al., 2017). A retention study showed that the experimental students retained a significant advantage over their control peers one year after completing the intervention. Nonetheless, the experimental students experienced a significant decline in all functional thinking tasks, giving support to the argument that a functional approach to algebra must be treated as a continuous K-12 curriculum strand (Stephens et al., 2021).

So far, various research studies provide empirical evidence supporting the effectiveness of four key instructional elements for nurturing functional thinking: using a variety of patterning tasks, learning about correspondence relationships in real-life contexts, giving opportunities of exploring correspondence relationships and using symbol variables to represent these relationships in a variety of situations (e.g. Warren et al., 2006; Wilkie, 2022). For example, a study conducted by Pang and Sunwoo (2022) aimed to enhance students’ functional thinking with a particular focus on correspondence relations, patterning tasks, and the use of symbolic variables to represent relationships. Further, a study from Wilkie (2022) showed that figural pattern generalization can be enhanced by teaching strategies that encourage students to verbally describe the features of a pattern, using hands-on material to explore the structure of figures, and engaging in activities that discourage recursive strategies (Küchemann, 2010). Beyond the use of patterning tasks in generalizing and representing, Warren et al. (2006) explored the use of function tables by focusing on the relationships between input and output numbers in a teaching experiment with Grade 4 students.

A study conducted by Rolfes et al. (2022) in Grade 6 focused on the aspect of covariation by examining the impact of using mono- and multi-representational learning environments on the development of the covariational aspect of functional thinking. The findings indicate that multi-representational learning offers advantages in acquiring qualitative functional thinking. Qualitative functional thinking included the ability to interpret the covariation of the measures involved based on the shape of graphs, all without relying on quantitative data. In terms, of quantitative functional thinking, the study showed that learning with both graphs and tables did not lead to higher learning gains than learning exclusively with graphs. It also provided evidence for the superiority of graphs over tables, as graphs offer a richer representation by combining numeric data and a visual impression of the examined relationship. The early use of graphs facilitates the development of a covariation perspective by visually depicting how the involved quantities vary simultaneously (Carlson et al., 2002).

A growing number of studies focus on the ways digital tools could foster students’ functional thinking and how the effect of such approaches is compared to more traditional teaching methods. For example, Lichti and Roth (2018) compared sixth-grade students’ functional thinking in a learning environment using hands-on material or computer-based simulations. The results of the study showed that functional thinking could be better fostered by using simulations than by hands-on material. Another study with Grade 6 students examined the effect of an online game on solving problems with covarying quantities (Kolovou et al., 2013). The study demonstrated a significant positive effect of the intervention on the post-test, in understanding how two quantities covary, even after controlling for pretest performance, mathematical ability, and gender.

2.4 Purpose of this study and research questions

The purpose of this study is to develop, implement and evaluate an intervention program aimed at nurturing functional thinking in upper primary school students. The development of the program lies on research findings indicating that students can engage with functional thinking from an early age and can also improve it over time through an adequate intervention. Most of the studies described above appear to focus on specific aspects of functions, such as input–output, e.g., related to function tables (e.g., Francisco & Hähkiöniemi, 2012; Warren et al., 2006), or covariation and correspondence, e.g., through pattern tasks (e.g., Blanton et al., 2019; Pang & Sunwoo, 2022; Rolfes et al., 2022; Stephens et al., 2017). Contrarily, the present study contributes to the field by addressing various aspects of functions simultaneously.

In response to the research objective of considering students' affective characteristics in such programs (as suggested, e.g., by Kolovou et al., 2013), we are investigating how the intervention works for students with varying levels of self-concept and interest in mathematics. Consistent with numerous studies, including those of PISA and TIMSS, which have documented significant correlations between motivational variables and mathematics achievement (e.g., Abín et al., 2020), we believe it is essential to empirically assess the impact of students' mathematics interest and self-concept on their functional thinking improvement. With respect to the empirical finding that affective measures are more closely connected when they are as domain-specific as possible (Hansford & Hattie, 1982), we examine not only the influence of students' overall mathematics-related interest and self-concept but also their interest and self-concept specifically related to functions. Further, we investigate possible gender differences in the benefits of the intervention, as gender effects are well documented in the literature (e.g., Kaiser & Steisel, 2000). For example, Sproesser et al., (2022) found that girls and boys showed different strength and weaknesses when dealing with functions.

Based on the presented theoretical considerations, our research questions are the following: (a) Does the participation in a functional thinking intervention program improve fifth and sixth graders performance in situations involving functions as an input–output, dynamic covariation, and correspondence relation? (b) Do students of different initial functional thinking performance level profit in the same manner from the intervention? (c) Does students’ gender, mathematics- and functions-related interest and self-concept relate to their gain score magnitude? (d) Does the participation in the intervention program impact on students’ strategies in dealing with functional thinking situations by shifting from variational to covariational and correspondence strategies?

3 Framework for the development of the intervention

Beyond the four aspects of functions that provide a framework for designing tasks and analyzing student work in the field of functional thinking, in the present study, we embrace promising didactical approaches to functional thinking education. These approaches include connecting mathematical concepts with familiar real-world situations and utilizing figural pattern generalization (Pang & Sunwoo, 2022), and early graphing of functions (Wilkie, 2020). To do so, students engage in activities that integrate embodiment, dynamic mathematics learning environments and adopt an inquiry-based approach (Ramírez et al., 2022; Rolfes et al., 2022). In the following section, we present these didactical approaches – the so-called design principles of this study.

3.1 Design principles

Drawing on the fundamental principles of inquiry-based approaches (Artigue & Blomhøj, 2013), the design of the program asserts that teachers encourage students to observe and investigate the relationships between quantities, experiment by manipulating functions, make conjectures regarding the functional rules, generalize, model, and shift their focus towards the properties of functions. Further, understanding the various aspects of functions necessitates students’ engagement in an inquiry-based approach that facilitates (inter)acting with functions and their properties (or any preliminary understanding of functions that students may possess).

The second design principle is rooted in the theory of embodied cognition, which suggests that cognition is positively influenced by bodily activities (Barsalou, 2010; Dackermann et al., 2017). Research has demonstrated that various aspects of mathematical understanding exhibit embodiment, underscoring the importance of engaging students in perceptual-motor experiences (Flood et al., 2020; Radford, 2009). These experiences involve a broad spectrum of bodily activities, spanning from observing and affecting other human movements to performing movements oneself (Duijzer et al., 2019). These various methods of directly and indirectly engaging the body within learning processes can be considered as "embodied" (Pouw et al., 2014). Drawing from the embodied action-based design genre (Abrahamson, 2014), our approach involved activities where students are actively engaged in physical actions that support their learning goals. These activities incorporated continuous feedback on students' movements, thereby facilitating specific perception and action. For instance, we implemented activities like "walking a graph" (Duijzer et al., 2019), designed to enhance graphical comprehension and to promote understanding of functional relationships, such as those between distance and time. In this activity, students walked in front of a motion sensor and observed the resulting graph displayed on a screen. In classroom discussions, students endeavoured to interpret the graphical depiction of their own movement, leading to perceptual, perceptual-motor, and imaginative experiences, as indicated by the students' verbal articulation of their thoughts (ibid).

To foster the development of functional thinking in students, we leveraged dynamic mathematics environments with selected perceptual-motor activities. We refer to learning environments that utilize portable and handheld digital technologies that offer opportunities for enacting learning through hand-held dragging of objects on screen (Duijzer et al., 2017; Xie et al., 2018). The touch interface brings sensorimotor interaction back into mathematics learning activities and allows a more natural interaction with better flow and control of the interaction compared to textbooks and oral instruction (Abrahamson & Sánchez-García, 2016; Yeung, & Ng, 2023). It provides a kinaesthetic orientation of learning, while multiple senses were incorporated and offered opportunities to do justice to the embodied character of mathematical cognition (Abrahamson & Bakker, 2016). These learning environments offered the opportunity to actively merge action-perception experiences with mathematical discourse through the interplay between touchscreen actions and mathematical concepts in touchscreen-based applications (Duijzer et al., 2017; Shvarts & van Helden, 2023). We employed a dynamic mathematical learning environment that provided the capability to construct the graph of a motion scenario by observing another person or object in motion, and to view an animation of the situation displayed in a graph. Students were prompted to anticipate the impact of a described motion on the graph and engage in reasoning about the interrelated quantities and graph properties. This approach offers several benefits. First, it fosters a sense of ownership over the animated object's motion, a sense of agency (akin to manipulating a part of one's own body for motor tasks), and a sense of self-location within the space (Duijzer et al., 2017). Second, the evolving mathematical discourse could contribute to the development of conceptual understanding regarding functional relationships (Lichti & Roth, 2018). This experience established connections between real-world situations, verbal descriptions, and graphical representations, and could even be complemented, for example, by the animated video.

Finally, a crucial design principle of this study was situatedness, which pertains to the need for organizing or mathematizing meaningful situations (Gravemeijer & Terwel, 2000). The inclusion of "meaningful" in the description indicates that situatedness depends on what the learner perceives as meaningful. For advanced mathematics learners, a formula or abstract functional relationship can be inherently meaningful. For primary school students, we employed real-world situations that hold significance for students, helping them to identify a functional relationship that corresponded to the given situation.

3.2 Intervention program and learning objectives

The intervention program comprised of four progressive modules, each of which focused on the different aspects of functions to varying degree. The four modules are presented in Table 1 with the corresponding learning objectives.

Table 1 Modules of the program
Full size table

The overarching goal of Module 1 was to facilitate students’ transit from understanding variation in one quantity to recognizing, manipulating, and describing the covariation of two quantities. To achieve this, it primarily emphasized the aspect of a function as an input–output process and to a lesser extent, the aspects of a function as covariation and correspondence. Students were expected to implicitly grasp arithmetic operations as functions through activities involving function machines. Students should be able to identify, generalize, and express the functional relationship between input and output values generated by the function machines. Students provided rules for function machines to model given tables and real-life scenarios. For example, students provided the rule for a digital function machine that offers output values for inserted values based on given rules (see Table 1). Within this context, students experimented with machines that exhibit additive, multiplicative, or linear structures. There were tasks asking to find input values for given output values, to determine output values for large input values, and to predict output values when symbols are entered into the machine. Targeted questions prompted students to calculate the differences between output values for consecutive input values and discuss the relationship between the covariation rule of the machine and the functional relationship between the input and output values. This approach integrated multiple aspects of functions within a single activity. As students progressed, they gained experience in combining function machines with different rules to create linear ones.

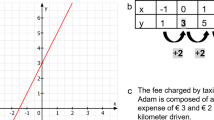
Module 2 aimed to support the development of students' understanding of functions by interpreting and manipulating various representations, including double number lines and graphs. In this module, students were expected to conceptualize functions as correspondence between two sets of values on a double number-line diagram. They experimented how the covariational rule of a function influences the mapping of values between the two lines. Additionally, students connected double number-line mappings with graphs on a coordinate system and discussed how the function rule determines the graph's shape, after expressing the rule based on the double number lines. Students engaged with a digital app presenting three double number lines with different functional rules. They interacted by moving a point on the left line and observing the mapping between points on the two lines (left and right). They compared how the line connecting the mapped values on each double number line moves vertically, depending on the covariation rule of each one. For instance, they noticed that the connecting line on the double number line with an additive rule (\(y=x+2\)) moved up and down in a parallel manner, while in the case of the double number line with a multiplicative rule (\(y=2\bullet x\)), it moved more steeply for larger values. Subsequently, students utilized a digital app that generates a graph's trace for each double number line, as they moved the point along the left axis of the double number line. Students were encouraged to analyze the shape of the constructed graph based on the functional rule of the double number line. They also suggested real-life scenarios that can be modeled using various types of functional relationships and explained how the structure of each scenario differs in relation to each functional rule.

In Module 3, students engaged in activities that involved identifying, coordinating, and representing covarying quantities. The expected learning outcomes included intuitively grasping the formal definition of a function within the context of distance-time scenarios (walking graph environment and constructing graphs with the “Turtle walking” app); in the context of such distance-time scenarios, students were asked to interpret the corresponding graphical representations, to compare distance-time graphs and to conceptualize the rate of change in terms of distance-time. Students connected experiences in both physical and digital environments and constructed their own graphs. Our focus centered on enhancing students' understanding of graphing motion. For example, students were tasked with constructing a graph in a digital app that models a given distance-time scenario (whether verbal or demonstrated by the teacher). Subsequently, they validated their construction by comparing it to the feedback provided by the app in the form of an animated video.

Module 4 built upon previous studies focused on developing functional thinking in the context of growing figural patterns (e.g., Wilkie, 2020, 2022). Students engaged in identifying, describing, generalizing, and representing growing patterns. They used recursive, covariational, and correspondence strategies, aiming to understand the underlying structure. Then, students were expected to express generalized relations verbally and symbolically and make predictions. For instance, students worked on a digital app that presented a growing figural pattern governed by a covariational rule of + 2. This app allowed students to adjust the first term of the pattern using a slider, creating patterns with the same underlying structure but varying initial values. Through this exploration, students developed hypotheses about the pattern's rule and responded to questions that approach the pattern from multiple perspectives.

4 Methodology

To address the research questions, the intervention program described above was implemented and evaluated. The following sections present the participants, the procedure, the data collection instrument, and the methods for analyzing the data.

4.1 Participants, setting and procedure

The study involved students in Grades 5 and 6 (see Table 2), with an average age of 11.1 years, all of whom attended a single public school in Nicosia (the age range for students in Grades 5 to 6 is typically 10.5 to 12.5 years old). This school had three 5th-grade classes and three 6th-grade classes, resulting in a total of 104 participants, comprising 50 students in Grade 5 and 54 students in Grade 6. Among the participants, there were 49 girls and 55 boys and, all ethical guidelines were meticulously followed. Informed consent was obtained from the parents, and privacy and confidentiality were strictly maintained to protect the children's personal information.

Table 2 Demographics of the participants
Full size table

According to the corresponding curricula and teachers, students had limited prior experience with functional relationships before participating in this study. Students were informed the program’s rationale and the type of intended activities. Emphasis was placed on explaining how digital tools would be utilized, with the main goal being to actively engage students into interactive, embodied activities. We highlighted that students could freely pose questions during the program and that testing would not be used to formative evaluation purposes, but solely for assessing the program’s effectiveness.

In the context of the Cyprus mathematics curriculum and textbooks, Grade 4 students are expected to investigate repeated and growing number and figural patterns. By Grade 5, students begin to explore functional relationships through activities involving function machines. They also learn to express the n-th term of the machine in symbolic form, typically dealing with simple functional rules, either additive or multiplicative.

Each intervention module consisted of three 40-min lessons. These modules underwent testing in a pilot study conducted during the previous year, which included 120 Grade 5 and 6 students. In the pilot study, a design research approach was used for each lesson. Initially, it was introduced in one class, and based on feedback (with all lessons being recorded on video), revisions were made before implementing it in a different class. This evaluation and refinement process followed a two-cycle procedure, with each lesson being tested in both a Grade 5 and a Grade 6 class. Revisions included strengthening the interactivity of the digital activities and adding reflections regarding the structure of the identified functional relationships.

All lessons were taught by the same teacher (first author) and were implemented during student’s regular mathematics classes in the school’s computer lab. There was one tablet for each student and an accompanying paper-and-pencil worksheet. Students worked on their own or discussed in pairs. The teacher and a teacher assistant (fourth author) moved from pair to pair, listened to their dialogues and asked further questions to trigger students’ reflection on their work. After two or three activities, the teacher called students to present their work to the whole class and discussed their findings. Lessons were spread over a three-month period, from March to May 2023. During this period, students received no related additional training outside of the intervention program.

4.2 Test instrument—scoring

Students completed a pre-test and post-test before and after the implementation of the intervention program in paper-and-pencil format (see Table 3). The test was a familiar setting for the students as a paper-and-pencil worksheet was accompanying students’ work during the lessons. The available time for completing each test was 30 min. Pre- and post-tests consisted of three items that measured functional thinking in input–output, covariation, and correspondence situations. The internal consistency of the test measured by Cronbach’s alpha was satisfactory for both the pre- and post-test (a = 0.81 and a = 0.83 correspondingly), based on the total number of sub-items. Additionally, 18 items to measure functions-related interest and self-concept were used in the post-test.

All items respectively scales are presented in more detail in the following.

Table 3 Test items
Full size table

4.3 Input–output aspect

Item 1 was developed for the purpose of this study, based on ideas suggested by Ng (2018). It measured students’ ability to find the input or output value of a function machine by identifying the numerical relation between two sets of values. Students were required to show their calculations, provide the output value for two given input values and the input value for two given output values. Students received a score of either correct or incorrect for each value. These tasks assessed students' performance in correspondence-particular situations (see Pittalis et al., 2020). Students were also asked to express the rule of the machine using symbols, which measured their performance in a correspondence-general situation (see Table 3). The item was scored as correct if the answer contained the correct linear structure with appropriate symbols (or explained the structure of the relation using natural language, making it clear that this relation is valid for any natural number), and half a score was given if the answer included the correct linear structure but had incorrect manipulation of symbols (i.e., ** + 3 instead of 2* + 3). Students also received a full score if they provided the rule using verbal explanations (i.e., multiplying the given number by 2 and then adding 3).

4.4 Covariation aspect

The covariation item (Item 2 in Table 3) was based on prior work by Duijzer and colleagues (2020) and measured graph interpretation and construction. Students were given a graph with data about a remote car (distance-time). The first two questions required mainly a global interpretation of the graph, as students had to identify which parts of the graph represented the car moving away from or towards a person, based on the direction of the graph. The question about moving away was scored as correct if the answer contained both correct time intervals and half a score if the answer included only one of these time intervals. Students received a score of either correct or incorrect for finding the time interval during which the car moved towards a person, as the answer included only one interval. The third question asked students to identify when the car moved the fastest. An answer that contained both correct time intervals was scored as correct, while providing only one time interval was considered as half score, regardless of the provided explanation. The third question required students to extend the graph for the following four seconds based on a given description. The provided description involved two actions: first, it moved away from the person for one second, and then it moved towards the person. Students received half a point for accurately representing each of these actions.

4.5 Correspondence aspect

Item 3 (see Table 3) was an adaptation of the Birthday Party task used by Blanton, Stephens et al. (2015b). The first question required finding the 8th term of the pattern. Students could answer this using different strategies (see corresponding part of the Theoretical Background). The second question required calculating a far-transfer term and necessitated either a correspondence-particular or a covariation mode of functional thinking. Students received a score of either correct or incorrect for each term of the pattern. The third question asked for the general rule of the pattern. An answer that contained an explicit description of the rule in verbal or symbolic form was scored as correct, while providing only the covariation rule (i.e., adding two persons for every additional table) was considered a half score.

4.6 Scales for self-concept and interest

Further, students completed a test measuring their interest and self-concept towards mathematics and functions after the completion of the program. This test comprised four 5-point Likert scales. The first scale included three items that assessed students’ interest toward mathematics, such as “Doing mathematics is one of my favorite activities.” (Pekrun et al., 2007). The second scale contained three items about students’ interest toward functions (Sproesser et al., 2019). For example, students expressed their agreement with the statement, “I like to deal with functions the most”. The third scale pertained with six items to students’ self-concept regarding mathematics. We used statements of the form, “Concerning mathematics, I am a talented student.” (Pekrun et al., 2007). The fourth scale concentrated on students’ self-concept concerning functions with six items, using statements like, “I can solve most tasks related to functions correctly.” (Sproesser et al., 2019). The internal consistency was satisfactory for students’ mathematics- and functions-related interest (α = 0.84 and α = 0.87, respectively) and self-concept (α = 0.83 and α = 0.89, respectively).

4.7 Data analysis

To analyze the data from both the pre- and post-test, we employed the SPSS 29 statistical package. Initially, we conducted paired t-tests to determine if there was a significant change in students' functional thinking performance between the two measuring times, separately for each grade (addressing Research Question 1). To achieve this, we normalized the total score for each item to 1, and the resulting mean value of the three items served as the dependent variable in our analysis. Furthermore, we categorized students from each grade into three groups based on their pre-test performance. The first group comprised students with initial performance ranking below the 33rd percentile (the ‘weak-achievers group’). The second group, referred to as the ‘standard-achievers group,' included students with initial performance ranking between the 33rd and 67th percentiles. Finally, the ‘high-achievers group' consisted of students whose performance exceeded the 67th percentile.

To address the second research question, we examined whether the categorization of students based on their gain score magnitude was independent of their initial functional thinking performance. To do this, we classified students into three groups based on their gain score (the difference between pre- and post-tests) ranking and conducted a Chi-Square test of independence, considering both the initial performance ranking group and gain score ranking group. Next, we conducted a regression analysis to examine whether students’ gender, mathematics- and functions-related interest and self-concept influenced their gain score (Research Question 3).

Finally, to address Research Question 4, we analyzed students’ strategies and explanations in each item and then conducted a Chi-Square test of independence to examine whether students’ adoption of strategies was independent of time (pre- or post-test). In Item 1, to identify students’ strategies, we analyzed students’ calculations to find the requested input and output values and their response to show what the output of the machine is when a symbol is entered. First, we used a theory-driven approach to identify emerging strategies. That is, we began with a predefined theoretical framework based on previous studies describing modes of functional thinking and students’ conceptualization of structure in functional thinking situations (Pittalis, 2023; Pittalis et al., 2020). We included codes that refer to correspondence particular, correspondence general and covariational strategies. We categorized students’ responses and explanations using the a-priori framework described in the theoretical framework (modes of functional thinking). However, these initial categorizations needed adjustment based on students’ work. We further developed and refined the a-priori framework to incorporate the observed data, considering also unsuccessful strategies such as identifying additive rules in specific instances (as discussed in Venkat et al., 2019) or identifying and repeating additive rules. We used the same method for the other two items. In Item 2, we analyzed students’ explanations concerning the time periods when the car moved the fastest. To accomplish this, we employed the framework proposed by Duijzer et al. (2020). Responses were classified as either single-variable reasoning, which considered a single variable (distance or time), or multiple-variable reasoning, which took into account multiple variables such as distance and time or speed. For Item 3, we utilized the framework introduced by Blanton, Stephens et al. (2015b), which distinguished between recursive, covariational, and correspondence strategies. A recursive strategy in Item 3 involved determining the number of people for 8 tables based on the number of people for 2 tables. This method entails adding two for each subsequent term until the eighth one is reached. A covariational strategy relied on coordinating the variation in the number of tables with the variation in the number of people. For instance, to calculate the number of people for 20 tables, the number of tables changes from 2 tables to 20, so the number of people should increase by 36 (2 people for each of the added 18 tables). Finally, a correspondence approach involved finding the general term of the pattern and then applying the formula for the requested values.

To establish interrater reliability of the data analysis, a second researcher coded 50% of the data after establishing the final coding framework. Agreement among coders reached 80%. Any discrepancies were discussed until full agreement was reached.

5 Results

The results of the study are presented in relation to the corresponding four research questions. Hence, we start with the results related to the first research question focusing on the change in students’ performance from pre- to post-test.

5.1 Difference in students’ performance between pre- and post-tests

A paired samples t-test was conducted to assess whether there was a difference in students’ functional thinking performance between the pre-test and post-test. The results indicated that students’ performance in the post-test (Grade 5: \(M = 0.58\), \(SD = 0.28\); Grade 6: \(M = 0.60\), \(SD = 0.28\)) was significantly higher than in the pre-test for both grades (Grade 5: \(M = 0.29\), \(SD = 0.22\), \(t(47) = 8.91\), \(p < 0.001\), \({Cohen}^{\prime}s d = 1.30\); Grade 6: \(M = 0.37\), \(SD = 0.24\), \(t(48) = 6.38\), \(p < 0.001\), \({Cohen}^{\prime}s d = 0.92\)). The effect size of the intervention for both grades was large.

To examine the progression of students with different initial levels of functional thinking performance, we calculated the mean performance of the three achievement groups in the pre-test and post-test for both grades. In Grade 5, the weak-achievers group’s mean performance progressed from 0.06 to 0.36 (see Table 4). The standard-achievers group’s performance increased from 0.26 to 0.57, while the high-achievers group improved from 0.54 to 0.81. In respect to gain scores (difference between post- and pre-test scores), the mean gain score of the three groups were quite similar. The standard-achievers group (Mgain = 0.31, SDgain = 0.21) and the weak-achievers group (Mgain = 0.30, SDgain = 0.25) exhibited the largest gain score, followed by the high-achievers group (Mgain = 0.27, SDgain = 0.22), which had the smallest progression (see Fig. 1). In Grade 6, the weak-achievers' mean increased from 0.10 to 0.37, the standard-achievers group from 0.36 to 0.58, and the high-achievers group from 0.63 to 0.80, respectively. The mean gain score for the weak-achievers group was 0.27 (SDgain = 0.29). The corresponding score for the standard-achievers group was 0.22 (SDgain = 0.21), followed by the high-achievers group that had the smallest gain score (Mgain = 0.17, SDgain = 0.18).

Table 4 Mean Values and standard deviation in the pre- and post-tests
Full size table
Fig. 1
figure 1

Progression of students

Full size image

5.2 Initial functional thinking performance group and gain score

To examine whether students’ gain scores were affected by their initial functional thinking score (operationalized by the classification into the group of weak-, standard- and high-achievers), we divided students in each grade into three groups based on the magnitude of their gain scores. To accomplish this, we used percentiles, with the low gain score group representing the bottom third, the medium gain score group representing the middle third, and the high gain score group representing the upper third. Table 5 presents the distribution of students of each initial functional thinking group (weak, standard, high) to the three gain score groups for both grades. A Chi-square test of independence revealed that there was no significant association between a student’s initial functional thinking group and the gain score due to the intervention in both grades (Grade 5: χ2(4) = 0.35, p = 0.98, Grade 6: χ2(4) = 5.09, p = 0.28). For instance, in Grade 5, the fifteen students that had the highest gain score were equally distributed in the weak-, standard- and high-achievers groups. In Grade 6, 6 out of the 17 students that had the highest gain belonged to the weak-achievers group, 7 to the standard-achievers group and 4 to the high-achievers group, respectively.

Table 5 Distribution of students with low, medium and high gain score across the three initial functional thinking (F.T.) Groups
Full size table

5.3 Covariates affecting the gain score

To investigate research question 3, we conducted a multiple regression analysis to examine the relationship between students’ gender, mathematics- and functions-related self-concept and interest with their gain score magnitude (see Table 6). The mean interest for mathematics was 3.46 out of 5 (SD = 1.19) and 3.31 for functions (SD = 1.05). The mean value for mathematics-related self-concept was 3.82 (SD = 0.78) and 3.48 for functions-related self-concept (SD = 0.89). The regression model displayed in Table 6 yielded an R-square of 0.05 (F(5, 85) = 0.90, p = 0.49), indicating that the model cannot significantly explain the variance in students’ gain score. Furthermore, none of the other predictor variables reached statistical significance (all p > 0.05). Analysis showed that there were no multicollinearity restrictions (Tolerance values > 0.2 and VIF < 5). While none of the predictor variables was statistically significant, it is worth noting that students’ mathematics interest had the highest beta value compared to the others with a marginally significant p-value of p = 0.07. In conclusion, our regression analysis did not identify any statistically significant predictors of gain score magnitude.

Table 6 Regression analysis
Full size table

5.4 Students’ strategies in handling functional thinking tasks

In the following, we present the results related to research question 4, that addressed students’ strategies when solving the three items. In Item 1 (Function as input–output perspective), we identified three set of categories according to the degree of correctness (see Table 7).

Table 7 Students’ strategies in item 1
Full size table

First, fully correct strategies that effectively conveyed the general rule of the function machine through symbols or verbal explanations. For example, a correspondence general strategy, such as expressing in words that the rule of the function machine is “multiply the input value by two and then add three to get the output value” or representing the output value when the symbol ‘*’ is entered in the machine as ‘2* + 3’.

Second, partially correct strategies are primarily focused on discerning the function rule within specific instances. For instance, a correspondence particular strategy referred to the case that a student showed that the output value for the requested values is calculated by multiplying by two and then adding three, without showing that this rule stands also for the general case that an arbitrary symbol enters the machine.

Finally, incorrect strategies, such as identifying additive rules within particular examples or employing random calculations. These incorrect strategies indicated a lack of recognition that a function rule applies universally to all paired values extracted from the machine. For example, a student showed that when 5 enters the machine you add 8 to get 13 and when 7 enters the machine you add 10 to get 17. Then, he applied the first rule to find the output value when 12 enters the machine and the second rule for the output value of 15. A Chi-square test for the independency of time and the categories of strategies unveiled a noteworthy shift regarding the three categories of strategies employed by students between the pre-test and post-test for both grades (Grade 5: Χ2(70) = 99.66, p = 0.01; Grade 6: Χ2(49) = 67.53, p = 0.04).

In Grade 5, during the pre-test, 17% of the students employed a correspondence general strategy, 8.5% utilized a partially correct strategy, while 38.3% identified additive rules in local examples, and 12.8% relied on random calculations. In the post-test, 60% of the students applied a correspondence general strategy, with the percentage of students focusing on additive rules or employing random calculations dropping to 22%. During the pre-test, 25.5% of the students did not complete this task, whereas in the post-test, only 12% did not respond to it. In Grade 6, the percentage of students utilizing a correspondence general strategy increased from 40.4% in the pre-test to 76% in the post-test, while the percentage of those relying on additive rules and random calculations slightly decreased from 17.3% in the pre-test to 16%. It is worth noting that 25% of students did not complete this task during the pre-test, but in the post-test, this percentage dropped to 4%.

In Item 2 (Function as covariation), we examined students’ explanations for the time intervals during which the car moved the fastest. This question provided evidence of their reasoning in terms of adopting a variational or covariational approach. We classified students’ strategies into three categories, namely no answer, variational and covariational answers (see Tables 8 and 9). To examine whether students’ strategies preference was independent of time, we conducted a Chi-square test. The analysis revealed a significant change in students’ strategies between the pre-test and post-test for both grades (Grade 5: Χ2(4) = 15.25, p < 0.001; Grade 6: Χ2(4) = 30.43, p < 0.001). In Grade 5, 51% of the students in the pre-test were unable to provide an explanation. Among those who did, 42.6% relied on a single-variable explanation, specifically that the car covered the longest distance, while 6.4% explained their answer from a covariation perspective, by considering the relationship between distance and time. Typical examples of covariational explanations were “the car moved the fastest during the first two seconds because it covered 8 m in two seconds and in the fourth second because it covered 4 m in one second” and “the first two seconds covered 4 m per second, while in the last two seconds it covered half a meter per second”. In the post-test, the percentage of students who did not provide an explanation decreased from 51% to 14.9%. Of the remaining students, 55.3% provided a single-variable explanation, while 29.8% provided an explanation based on the relationship distance/time. It should be noted that among the students that did not provide an explanation in the pre-test, 13 out of the 24 managed to give an explanation in the post-test by focusing solely on time, and 4 of them provided a comprehensive covariation explanation. Seven out of the 10 students that provided a single-variable explanation in the pre-test explained their answer in the post-test by adopting a covariational perspective.

Table 8 Grade 5 Students’ strategies in item 2
Full size table
Table 9 Grade 6 Students’ strategies in item 2
Full size table

In Grade 6, 51% of the students did not provide an explanation in the pre-test, 34.7% used a single-variable explanation, and only 14.3% exhibited a covariational perspective in their reasoning (see Table 9). In the post-test, the percentage of students who justified their answers using a covariation approach increased to 32.7%, while 36.7% used a single-variable explanation. Only 30.6% of the students did not provide an explanation. This change was attributed to the fact that 7 out of the 25 students who did not provide an explanation in the pre-test managed to provide in the post-test a single-variable explanation, and 4 of them offered a covariation-based response. Further, 6 out of the 17 who provided a single-variable explanation in the pre-test moved to a covariation-based approach in the post-test.

In Item 3 (Birthday Party), we analyzed students' strategies for finding the 8th and 20th terms of the pattern. We identified three types of strategies (in addition, we coded if no answer was given). The first, a recursive approach, involved extending the + 2 rule from the given terms. The second, the covariational approach, relied on recognizing that for each additional table, the number of people increased by 2. Therefore, for the 8th term, students added 12 more people (6 × 2) to the 2nd term. Students who applied the third, the correspondence approach, identified the pattern's rule as multiplying the term number by two and then adding 2. They applied this rule to determine the two requested terms. A Chi-square test showed a significant change in the types of strategies used between the pre-test and post-test for both grades (Grade 5: Χ2(9) = 27.7, p < 0.001; Grade 6: Χ2(9) = 17.53, p = 0.04).

Table 10 presents the frequency of the strategies used by Grade 5 students in Item 3. In the pre-test, 68.1% of Grade 5 students used a recursive strategy, while only 17% of the students employed a correspondence strategy. In the post-test, 44.7% adopted a recursive strategy, 36.2% preferred a correspondence one, 12.8% applied a covariational one, and 6.4% did not complete this task. Eleven out of the 32 students that used a recursive strategy in the pre-test switched to a covariational (3 out of 32) or a correspondence strategy (8 out of 32) in the post-test. Further, five out of the six students that did not complete the task in the pre-test, used a recursive, covariational or correspondence strategy in the post-test.

Table 10 Grade 5 students’ strategies in item 3
Full size table

In the pre-test in Grade 6, 58.3% of the students used a recursive strategy, 10.4% applied a covariational approach, 22.9% utilized a correspondence strategy, and the remaining 8.3% did not complete the task (see Table 11). In the post-test, the dominant strategy was the correspondence one (50%), followed by the recursive approach (25%), and the covariational one (16.7%). Once again, 8.3% of the students did not complete the task. Out of the 28 students who used a recursive approach in the pre-test, 17 preferred a covariational approach (7 out of 28) or a correspondence approach (10 out of 28) in the post-test. Four out of the five students who applied a covariational approach in the pre-test switched to a correspondence approach, which was more efficient and suitable for explaining the general pattern rule.

Table 11 Grade 6 Students’ strategies in item 3
Full size table

6 Discussion

The present study responded to the research call for describing explicitly the nature of instructional interventions that are found to be pivotal to developing functional thinking as a core facet of students’ early algebraic thinking (Kieran, 2022). We described and presented the results of the implementation of an intervention program designed to enhance functional thinking among upper primary school students. The innovative aspect of the developed program lies in the fact that it aimed to develop simultaneously different aspects of function and adopt promising design principles based on previous research (Blanton et al., 2015a, 2015b; Pang & Sunwoo, 2022; Warren et al., 2006; Wilkie, 2022). The results of the intervention are discussed in terms of the observed outcomes in respect to students’ performance and strategy usage, implications for educational practice, limitations, and directions for future research.

Considering our first research question, the results of the study revealed a significant improvement in Grade 5 and 6 students’ performance in functional thinking between the pre- and post-tests, with a large effect size observed in both grades. The effect size found in this study is larger than typical effect size of instructional improvement programs in algebra education (Rakes et al., 2010). The average gain score exhibited a similar pattern in both grades across weak-, standard-, and high-achievers. In particular, we found that students improved in their ability to notice, manipulate, and symbolize linear relationships in input–output functional thinking situations, grasp varying quantities, interpret graphs that represent covarying quantities in a qualitative and quantitative way and generalize and symbolically represent functional relationships in correspondence situations. We reaffirmed previous research findings suggesting that functional thinking can be nurtured in primary school under appropriate teaching conditions (Blanton et al., 2015a, 2015b; Pang & Sunwoo, 2022; Warren et al., 2006; Wilkie, 2022).

Regarding our second research question, the analysis indicated that the gain score magnitude was independent of students’ initial functional thinking achieving group. Being part of the low, medium, or high gain score group did not depend on whether a student was classified as a weak, standard, or high achiever. The finding that even weak-achievers exhibited the largest gain score compared to their peers highlights a particularly compelling aspect of our results: engaging students, irrespective of their initial functional thinking performance, can successfully develop critical components of functional thinking that are foundational for later years. We interpret these findings as a strong indicator that students with varying performance potential in developing functional thinking are likely to be significantly affected by an intervention program in understanding functional thinking in primary school.

Further, in respect to the third research question, analysis showed that students’ gender, mathematics- and functions-related self-concept and interest did not serve as predictive factors of students’ gain score magnitude. Hence, the program works for students with different abilities and affective profiles, subsequently, the extent to which each student benefited from the program was not related to the examined factors, such as gender, initial functional thinking performance, mathematics- and functions-related self-concept and interest.

Moreover, our findings did not provide supporting evidence to previous studies reporting significant correlations between motivational factors and mathematics achievement (Abín et al., 2020), as students’ gain score magnitude was independent of the examined affective measures. We interpret this as an indication that the intervention provided an authentic mathematical challenge to all participants and may be particularly effective in engaging students with low self-concept and interest in mathematics. This is a promising finding that could indicate the potential of meticulously designed teaching overcoming barriers such as the aforementioned affective factors.

Regarding our fourth research question, an analysis of the shifts in strategies used from pre- to post-test showed that students increasingly engaged in functional thinking. For example, in the input–output situation in the pre-test, most of the students could not identify a functional relationship between the input and output values, or they focused only on recursive rules, or noticed a relation that characterized only particular instances. In the post test, 60% of Grade 5 and 76% of Grade 6 students identified and expressed the general relation between the involved variables. Students’ engagement in functional thinking was also evident in the covariational situation. In the pre-test, a small percentage of students in both grades exhibited a covariation reasoning, while in the post-test, about one third of the students provided covariational explanations, by coordinating the variation of the involved quantities. Furthermore, in the correspondence situation, the percentage of students applying a correspondence strategy doubled from the pre-test to the post-test for both grades. Our findings are in line with previous studies that explained students’ progression in functional thinking intervention studies due to students’ shifts in strategies used (Blanton et al., 2015b). The study provided evidence that appropriate learning conditions can facilitate students’ shifting away from recursive thinking to functional thinking what is considered a challenging task (Cooper & Warren, 2011).

Based on our theoretical background, we could argue that the following characteristics of the intervention program contributed to students’ functional thinking development: (a) addressing different aspects of function simultaneously facilitates the development of multiple understandings and ways of exploring functional relationships; (b) digital learning environments using inquiry-based approach that prompt the manifestation of physical movements provide entry-points for students of different performance level by investigating multiple representations of functions, grasping function as covariation by experimenting with the effect of specific actions on the involved covarying measures; (c) manipulating functional relationships in situated contexts makes it possible to experience the abstract aspects of functions within concrete scenarios; (d) activities that integrate bodily movements with graphical representations, leveraging the sensory aspects of the motion experience, facilitated the initial conceptualization of how changes in one quantity influence the concurrent changes in another quantity, and the abstraction of covariational functional relationships by constructing graphs that simulate real-life motion scenarios.

The above research findings should be interpreted in light of three limitations. First, we caution that our findings are not intended to be generalized across all populations of students and we can only make claims for the students participating in the study. Second, this study did not include a control group as all fifths and sixth graders of the involved school participated in the intervention. We acknowledge the need to more precisely define the conditions under which an intervention program takes place to strengthen the argument that student’s progression is due to the intervention itself. Finally, we did not measure student’s general arithmetic skills, which would allow classifying students as weak-, standard- and high-achievers based on general mathematics and arithmetic abilities. Future studies that include random assignment of groups to instructional conditions and measurement of cognitive measures would allow further clarification of the effect of the intervention program. For instance, a future large-scale study could include three groups: one that attends a dynamic mathematics functional thinking program, a second group that fosters functional thinking without using digital tools, and a control group that follows the official school curriculum. Such a study could include measures of a variety of abilities and self-related factors, such as rational number sense, reasoning abilities, and computer anxiety. More analysis is needed, however, to understand the impact of student’s engagement in dynamic mathematics learning environments on their understanding of functional relationships from an embodied-instrumental approach (Pittalis & Drijvers, 2023), as the intervention program engaged students in selected perceptual-motor activities that seem to have triggered students’ embodied actions. Therefore, a future study could include a variety of embodied activities and focus on analysing the intertwining of the body with the affordances of the digital tools and mathematical concepts.

7 Conclusion

The overarching results of the study indicate that upper primary school students can engage with rather abstract aspects of functions that are traditionally introduced in middle school or later. This achievement is possible with appropriate teaching interventions, given that traditional curricula may not adequately prepare students to engage with functional relationships in a variety of situations. Therefore, these results hold significance for researchers, teachers, curriculum developers, and policy makers to consider.

The findings highlight the feasibility of a comprehensive approach to functional thinking. An exclusive focus on patterns in primary school as a route to functional thinking as commonly seen in mathematics curricula might be a narrow interpretation of functional thinking development. Engaging students with the different aspects of function seems a critical aspect of progressing towards the correspondence and covariational modes of thinking. Different sense-making contexts as well as dynamic connections between various representations of functions using digital tools and perceptual-motor activities exposes students into a rich and comprehensive understanding of function. Teachers should avoid traditional teaching approaches and instead design and implement activities that engage students in a variety of perceptual-motor activities. These activities should help students concretize abstract mathematical ideas through exploration. For instance, using embodied distance-time activities to model dynamic functional situation could facilitate connections between real-life scenarios and graphical representations, thereby enhancing students’ understanding of the covariational perspective of function (Pittalis, et al., 2024).

Moreover, students’ engagement with functional thinking in primary school at the level described here, could support students in developing a nuanced understanding of the abstract concept of function at secondary school. It should also be noted that participating in such a program is beneficial for all students, irrespectively of their academic performance. This type of dynamic learning mathematic environment appears to have the potential to challenge all students by providing multiple authentic experiences that engage them in functional thinking situations.

Interventions, similar to the one presented in this paper, call to rethink the approach to functional thinking traditionally adopted in curricula. In line with Pang and Sunwoo (2022), we assert that there is no need to wait for curriculum changes to enhance primary school students’ functional thinking; immediate actions are necessary. This study offers specific suggestions for designing contemporary functional thinking intervention programs that leverage digital tool affordances and align with promising didactical principles, such as inquiry-based learning with selected perceptual-motor activities and situated contexts. The evidence presented herein paves the way for further explorations in the field and the development of innovative, effective instructional designs in functional thinking.