FormalPara Key Points for Decision Makers

High structural uncertainty existed in extrapolation models when simulating the long-term economic evaluation results of cancer immunotherapies, especially when dealing with immature data.

Flexible techniques show better performances when standard parametric models are not flexible enough to capture the complexity of survival hazards from cancer immunotherapy. Model validity will be reinforced if external evidence exists.

Identifying and reporting the structural uncertainty caused by extrapolation model selection in an economic evaluation is recommended as researchers lack evidence to identify the ‘right’ model among several models in most cases.

1 Introduction

Decision making for anti-cancer drugs usually requires a lifetime projection including survival benefit and cost when mature data are quite often unobtainable [1]. Especially with the emergence of immune checkpoint inhibitors (ICIs), time-to-event data with long-enough follow-up that could fully capture the complex survival hazards is rarely available. To be specific, median overall survival (OS) data reported in these clinical trials are not necessarily reached. Meanwhile, individual patient data (IPD) is usually unavailable for peer replication. This results in high uncertainties when conducting an economic evaluation under these conditions. Modeling techniques are therefore used both to capture the key features of survival functions (model fitness) and to simulate the survival data to a longer term (extrapolation performance).

The most widely used parametric models in economic evaluation are standard parametric models [2], including exponential, Weibull, Gompertz, lognormal, and log-logistic [3]. A study by Djalalov et al. (2019) introduced a method to fit parametric survival distributions and provided a systemic approach to estimating transition probabilities from survival data using parametric distributions [3]. However, survival curves for ICIs tend to be more complex and variable in shape, with declining survival after the initial phase followed by plateaus [4]. Note that standard parametric models are limited in the types of hazard functions they can reproduce, which means that they may not be flexible enough to model survival curves during all phases where there are multiple changes in the slope of the hazard function [4, 5].

In comparison, flexible parametric models including fractional polynomials (FP), restricted cubic splines (RCS), Royston–Parmar (RP) models, and generalized additive models (GAM) can capture the inflection points of survival curves [6,7,8]. Other models including landmark models, parametric mixture models (PMM), and mixture cure models (MCM) can also model complex hazard shapes. A rich literature has demonstrated the improved fit performance of these flexible models [4, 6, 8,9,10,11,12,13,14,15]. It can be concluded that flexible models performed better in fitting and extrapolating survival outcomes than standard parametric models. However, selecting survival models based only on goodness-of-fit (GOF) statistics is unsuitable since good within-sample fit does not guarantee good extrapolation performance. The National Institute for Health and Care Excellence (NICE) has already published some guidelines regarding the process of fit and extrapolation [16, 17]. Some current studies have also discussed different flexible modeling techniques in extrapolating survival outcomes regarding immunotherapies [7, 18,19,20,21,22]. Through these studies, we can conclude that methods that provide more degrees of freedom may accurately represent survival for anti-cancer drugs, particularly if data are more mature or external data are available to inform the long-term extrapolations.

Despite rich literature focused on survival extrapolation, few studies evaluated the impacts of model selection on economic evaluations for cancer immunotherapy. Several items including the immature survival data and the long-term extrapolation which may lead to high uncertainty in economic evaluations of cancer immunotherapy still need to be examined when using flexible models [19]. In this work, we aimed to evaluate the GOF and extrapolation performance of different modeling technologies through a case study of Checkmate 067. We present the results of the model differences in extrapolated survival outcomes, and the resulting structural uncertainties in economic evaluation. Further recommendations on how to deal with immature data and model selection through this case study are also provided.

2 Methods

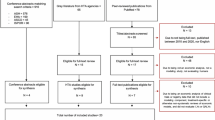
The study process for this article is shown in Fig. 1. All algorithms for fit, extrapolation, and economic evaluation in this study were implemented in R (version 4.0.2, https://www.r-project.org/). R Codes for reproducing this study can be found on GitHub (https://github.com/TaihangShao/uncertainty-of-CEA-flexible-extrapolation-techniques).

Fig. 1
figure 1

Flow chart of study process. AIC Akaike information criterion, ICER incremental cost-effectiveness ratio, IPD individual patient data, MSE mean squared errors

Full size image

2.1 Clinical Data Sources

The clinic trial selected for this research was Checkmate 067 (a phase III, randomized, double-blind study of nivolumab monotherapy or nivolumab plus ipilimumab versus ipilimumab monotherapy in subjects with previously untreated unresectable or metastatic melanoma) because it has the longest survival data so far for cancer immunotherapy [23, 24]. We extracted both progression-free (PFS) and OS data of nivolumab plus ipilimumab (NI) and ipilimumab (I) from this study. IPD was obtained through reconstruction. Results published in 2017 with 3 years of data (with a minimum follow-up of 36 months) [24] and 2021 with 6.5 years (minimum follow-up of 77 months) [23] were all included to test model performance with data maturity. The 3-year data were used for fit and extrapolation (considered immature in this study) [24], while the 6.5-year data were used for fit and validation (considered mature in this study) [23]. The hypothesis here is that the data was immature when the median OS was not reached, and vice versa.

2.2 Model Fit, Extrapolation, and Validation

We used GetData Graph Digitizer (version 2.26) to extract survival plots from PFS and OS curves. Guyot’s method, as NICE recommended, was used to reconstruct individual patient data through the SurvHE package in R [25,26,27].

In this study, 3-year and 6.5-year survival data were both used to test the model GOF (as compared with the original KM data). We further extrapolated 3-year survival data to 6.5 years to compare the GOF with the original 6.5-year KM data, for the purpose of testing the model impact when only immature data is available.

The models used for fit and extrapolation in our study included standard parametric models (exponential, Weibull, Gompertz, lognormal, log-logistic, gamma, and generalized gamma distributions) and six flexible models (FP, RCS, RP, GAM, PMM, and MCM) [1]. Note that generalized gamma has three parameters that can assume a variety of hazard shapes (e.g., unimodal, monotonically increasing or decreasing, or bathtub) [19]. Landmark models that require patients’ response status for choosing a landmark time point were not included in this study since we only had summary data instead of detailed IPD information [17, 18]. For FP models, the best models for both first-order and second-order were included. For RP models, the best models for all three scales (‘odds’, ‘normal’, and ‘hazard’) were considered. For RCS, GAM, PMM, and MCM models, we only considered the models with the best performance. Therefore, we included a total of 16 models in the comparisons. Methodologies and details of implementing these modeling techniques are provided in Supplementary file 3 (see electronic supplementary material [ESM]).

GOF for specific types of models was checked by Akaike’s information criterion (AIC) and visual inspection. AIC is described by the following formula [28]:

$$ AIC = - 2\log L + 2k $$

L refers to the likelihood of the model and k refers to the number of parameters.

GOF between models was checked by two indicators. The primary measure was mean squared errors (MSE), and the secondary measure was bias [8, 15]. MSE could penalize positive and negative deviations from the estimand of mean equally. Besides, MSE could be interpreted as penalizing both for bias (how close are the model estimates to the truth) and variance (how much do estimates vary across cycles). How the bias and variance contributed to the MSE could be provided by the measure of bias.

MSE and bias are described by the following formula:

$$ {\text{MSE}} = \frac{1}{n}\sum\limits_{{i = 1}}^{n} {(Y_{i} - \hat{Y}_{i} )^{2} } $$
$$ {\text{bias}} = \frac{1}{n}\sum\limits_{{i = 1}}^{n} {(Y_{i} - \hat{Y}_{i} )} $$

n refers to the number of samples, Yi refers to the real value, and \(\hat{Y}_{i}\) refers to the predicted value.

Extrapolation performance was also evaluated by MSE and bias. That is, we checked the MSE/bias of model-estimated survival data and observed survival data at each time point from 3 years [3, 6, 29]. The check of extrapolation performance was also supplemented with visual inspection. For AIC and MSE, smaller values indicated better model performance; for bias, performance was examined by how close values are to zero.

To improve the accuracy of extrapolating survival outcomes [17, 18], we conducted the external validation. However, due to lack of data, the only external data found was from I-OS (overall survival data of ipilimumab), for which the longest follow-up time of 10 years has been reached. Therefore, we only conducted the external validation for 3-year data of I-OS. The choice of external data was made following a recently published guideline [19]. Other external data were obtained from a pooled analysis of long-term survival data from 12 studies of ipilimumab in unresectable or advanced melanoma [30]. A KM curve was reconstructed. The MSE/bias of model-estimated survival data and external data at each time point between 3 years and 10 years was checked.

2.3 Economic Evaluation

For economic evaluation, we considered three groups of models, including models with best fit of 3-year data, models with the best extrapolation performance after the third year, and models with the best fit of 6.5-year data. Four survival outcomes were needed for each cost-effectiveness analysis, including both PFS and OS for the treatment and comparator. For every outcome, we sought the best model with the lowest MSE. Therefore, a total of 34 combinations were considered for a specific group of models. Model combinations were excluded only when they were not clinically realistic (PFS higher than OS at specific time points).

There already existed a rich literature that studied the cost effectiveness of nivolumab plus ipilimumab versus ipilimumab monotherapy in subjects with previously untreated unresectable or metastatic melanoma according to a current systematic review [31]. Therefore, we chose to reproduce and simplify high-quality research instead of building a new model. Kohn et al. evaluated the cost effectiveness of five first-line immunotherapies for advanced melanoma with a Markov model [32]. This research considered both nivolumab plus ipilimumab and ipilimumab monotherapy as their first-line therapies. The parameters reported in this study were comprehensive and had authoritative sources. Medication, dosage, and subsequent treatment were also close to the original Checkmate 067 (first-line NI + I followed by second-line carboplatin and paclitaxel; first-line I followed by second-line NI). Thus, based on Kohn’s study, we constructed a simplified partitioned survival model since some parts of the original model were not needed in our study. A summary of Kohn’s study is reported in Supplementary file 4 (see ESM). Parameters including costs, utilities, and incidence of adverse events were obtained from the original study. End-of-life cost was not reported by Kohn et al., and we obtained it from a similar study [33]. The detailed parameter inputs are shown in Table 1, Supplementary file 1 (see ESM). Simulation times were set at 6.5 years and 20 years. Outcomes included incremental costs, incremental quality-adjusted life-years (QALYs), and incremental cost-effectiveness ratio (ICER).

The impacts of model choices were reflected on the structural uncertainties of economic evaluation. We used the variability of the modeled ICERs to measure this structural uncertainty. Tornado diagrams were drawn to show the variability. However, to quantify and visualize this structural uncertainty, we used the distances of modeled ICER plots to the referencing ICER to indicate the model variability. We first defined the referencing ICER as the one with the smallest distance among all modeled ones, and then decided the variability by calculating the distance between each observed ICER and the reference dot. For distance calculation, we did it in two steps: first to standardize all modeled outcomes (cohort point estimates of incremental QALYs and incremental costs for each PFS and OS using selected model), and second to calculate the discrete degree of modeled ICER estimate to the referencing one. The standardization process was conducted as follows:

$$ Z = \frac{X - \mu }{\sigma } $$

Z refers to the standardized data, X refers to the original data, μ refers to the mean, σ refers to the standard deviation. Therefore, new outcome points (x = standardized incremental costs, y = standardized incremental QALYs) were obtained after the standardization.

To measure the discrete degree between the ICER points and the reference point, the Euclidean Distance was used (see following formula).

$$ dist = \sqrt {(x_{2} - x_{1} )^{2} + (y_{2} - y_{1} )^{2} } $$

dist refers to the Euclidean Distance between two points, x and y refer to the coordinate of points. The mean and standard deviation of these calculated distances were then determined. The larger mean and the wider standard deviation indicated a more discrete degree of the results. Note that this study did not evaluate parameter uncertainty because we only focused on the uncertainty caused by the choice of extrapolation models.

3 Results

3.1 Assessment of Fit and Extrapolation Performance Among Different Models

Figure 2 shows the visualized results of fit and extrapolation performance among different models. Detailed results are shown in Supplementary file 1 Tables 2–4 (including MSE, estimated log-likelihood, AIC, and coefficients) (see ESM).

Fig. 2
figure 2

Visualized results of fit and extrapolation performance among different models. ‘3-year data fit’ means that this MSE is calculated by fitted 3-year data and original 3-year data; ‘3-year data extrapolate’ means that this MSE is calculated by extrapolated 6.5-year data and original 6.5-year data; ‘6.5-year data fit’ means that this MSE is calculated by fitted 6.5-year data and original 6.5-year data. Current MSE value = original MSE value * 10,000. The lower the point is located, the lower the MSE value it presents, meaning the model had better performance. Exp exponential, FP fractional polynomial, GAM generalized additive models, gengamma generalized gamma, IPI ipilimumab, lnorm lognormal, llogis log-logistic, mix-cure mixture cure model, MSE mean squared errors, NIV nivolumab plus ipilimumab, OS overall survival, param-mix parameter mixture model, PFS progression-free survival, RCS restricted cubic spline models, RP Royston-Parmar models

Full size image

3.1.1 Goodness-of-Fit (GOF)

Smoothed hazard plots and survival plots based on observed and modeled data are shown as S1 Figs. 1–2 and 5–6 (see ESM). Visually, almost all the models provided a good fit of the observed hazard data for both 3-year and 6.5-year OS data (S1 Figs. 2 and 6, see ESM), although there were differences in the extent to which local fluctuations were captured (S1 Figs. 1 and 5, see ESM). However, most models failed to capture the steep descents in the early stages of PFS. They either underestimated or overestimated the survival rate, which was particularly obvious in I-PFS (progression-free survival data of ipilimumab) (S1 Figs. 2 and 6, see ESM).

3.1.2 GOF Under Flexible Techniques and Data Maturity

According to Fig. 2, the average MSE of flexible modeling techniques was less than that of standard parametric models, which indicated that flexible modeling techniques had better GOF. The bias of 6.5-year modeled data with standard parametric models was greater than that of 3-year modeled data. However, it was the opposite in the flexible techniques. For specific models, RP models performed well when fitting the data (MSE always ranked top 3). To compare between model groups, the 6.5-year data fit group had a smaller MSE than the 3-year data fit group. This indicated that GOF could be improved by modeling with longer follow-up data.

3.1.3 Goodness of Extrapolation

More variation could be seen in the extrapolated parts of the survival curves (S1 Fig. 3, see ESM). It was found that more flexible techniques outperformed standard parametric models on average. Gompertz and FP models performed well for extrapolation. Interestingly, it could be observed in Fig. 2 (all models included) that the top-ranked models in the 3-year data extrapolate group were different from those in the 3-year data fit group. This indicated that models with best fit are not always the ones with best extrapolation performance. Notably, according to Fig. 2 (top five models included), although we provided the models that rank top for each comparison, several models had similar MSE results and the statistical difference among them could not be assessed.

3.2 External Validation

Details of external validation are shown in Supplementary file 2 (see ESM). MSE results of different models are shown in S2 Table 1 and survival plots are shown in S2 Fig. 2. By comparing the modeled I-OS data with 10-year external data, we found that RCS and GAM, which performed well in extrapolating the 3-year data for longer horizons, also showed a better performance when validated by the external data. This indicated that RCS and GAM might provide a good long-term extrapolation performance. However, second-order FP, which showed the best performance in extrapolating 3-year data to 6.5 years, had a poor performance in external validation due to over-fit. In addition, it was hard to tell which model performed better without external data since the GOF statistics were close (MSE of six models had a difference within 1).

3.3 Economic Evaluation Results

The process of economic evaluation is given in Supplement 4 (see ESM). For a total of 81 potential modeled curves, 45 were included with 3-year fitted data combined with a 20-year extrapolated data, and 54 models were included with extrapolated data from the beginning. Table 1 shows the summary results of the impacts of model selection on economic evaluation. According to Table 1, it was obvious that the estimated ICER varied by the simulation time and model selection. However, it was hard to evaluate the association between them. The 3-year data fit group had the largest summed mean of distances away from reference ICERs regardless of simulation time, while the 6.5-year data fit group had the smallest. The 3-year data extrapolate group performed almost the same as the 3-year data fit group when the simulation time was set to 6.5 years. However, with a 20-year horizon, the 3-year data extrapolate group performed better than the 3-year data fit group. However, no significant statistical difference could be observed among the three groups.

Table 1 Summary results of the impacts of model selection on economic evaluation
Full size table

Tornado diagrams are provided in Supplementary file 4, Figs. 1–6 (see ESM). Based on S4 Figs. 1–6, we found that the model choice for a specific survival curve might lead to significant changes in estimated ICER (e.g., selecting the RP-hazard model in I-OS always brought huge fluctuations in estimations). Standardized ICERs for three groups with different study horizons are shown in Fig. 3. According to Fig. 3, more discrete results could be observed when simulation time progressed. The 3-year data fit group appeared more scattered than the other two groups regardless of the simulation time, and the 3-year data extrapolate group appeared less scattered than the 6.5-year data fit group. A possible reason was that many groups of models were excluded from the 3-year data extrapolate group.

Fig. 3
figure 3

Standardized economic evaluation result points for three groups of models under different simulation times. Red points refer to the reference points. Reference points were selected as the point with the closest distance to all the other points. Result points were standardized from incremental costs and incremental QALYs calculated in the economic evaluations. Black dashed lines represent the line y = 0. 3-year data was considered immature. 6.5-year data was considered mature. The three groups of models refer to (1) models with best fit of 3-year data, (2) models with best extrapolation performance of 3-year data, and (3) models with best fit of 6.5-year data. ICER incremental cost-effectiveness ratio, QALYs quality-adjusted life-years

Full size image

4 Discussion

In this study, we explored the effect of modeling technique selection on fitting and extrapolation of survival curves through a case study of cancer immunotherapy. A simplified partitioned survival model was constructed to evaluate the impacts of model selection on the structural uncertainties in economic evaluation, including the variability of estimated ICER and the discrete degree of ICER.

Model selection could influence the prediction of survival outcomes, leading to the uncertainty of economic evaluation. Based on our results targeted on 3-year data, we found that models selected only based on GOF statistics did not show a superior MSE when validated by the 6.5-year original data, and the economic evaluation showed that the results from choosing models through GOF were more discrete than choosing models through goodness of extrapolation. This showed that selecting survival models based only on GOF statistics was unsuitable and might lead to biased cost-effectiveness results. An alternative approach was to search for external evidence [17, 26]. In our case study, models with good extrapolation performance could be identified through external validation. In addition, over-fitted models could also be identified. A recently published guide has pointed out the potential available sources of external evidence (e.g. long-term survival data of the same products used in the same indication or more mature data from the same products but used in a later line of treatment for the same disease) [19]. However, despite several available approaches [26, 34, 35], a standard approach to using external evidence still needs future studies. A necessary point that should be highlighted is that although researchers could identify the best model through statistical indicators, there still existed uncertainty in estimated ICER under different model choices and study horizons. All these results should be reported in an economic evaluation of cancer immunotherapy to show the structural uncertainty [19] (e.g., tornado diagrams).

Data maturity could also influence the survival outcomes and economic outcomes. Our findings showed that the estimated ICERs calculated from immature data appeared more discrete than those from mature data. This indicated that different model selections based on immature data brought more uncertainty. Unfortunately, a high proportion of current cost-effectiveness analyses for cancer immunotherapy were conducted based on immature data. Although using flexible techniques can be helpful in reducing the uncertainty of capturing complex survival hazards, few studies take a full model choice into consideration. A recent systematic review of French health technology assessment (HTA) reports indicated that only one study applied a flexible technique among 11 assessed targeted cancer immunotherapies [36]. Although using external evidence could be helpful when dealing with immature data [17, 19], results generated from the immature data should be carefully considered for decision making because of unaddressed uncertainties.

Our study validated several peer studies and guidelines [4, 6,7,8,9,10,11,12,13,14,15, 18]. Firstly, models with the best GOF might not necessarily provide improved extrapolation performance. Secondly, extrapolation uncertainty would be raised with prolonged model horizon. Thirdly, external evidence can be helpful to validate the model choice, especially when dealing with immature data. Among previous studies, two have already compared the different extrapolation models through the case study of Checkmate 067 [4, 18]. Gibson et al. compared RCS with standard parametric models and found that RCS performed better in modeling PFS [4]. Federico et al. included six survival models to fit the OS from different data cuts [18]. They both found that survival models explicitly incorporating survival heterogeneity showed greater accuracy for earlier data cuts than standard parametric models. However, the two studies only focused on either PFS or OS outcomes. Our study further explored the impacts of model selection on economic evaluation. Our study further proved that estimated ICERs could show great variability with model choices and horizons. We also present this kind of structural uncertainty in a visualized and quantitative way to make it easier to understand. Finally, we suggest that sometimes researchers might lack evidence to select the ‘best’ model, so reporting the uncertainty is recommended.

However, this study is not without limitations. First, the lack of IPD data and reconstructed IPD might lead to some biases, although one study showed that using reconstructed IPD had little influence on economic evaluation results [3]. Second, we considered the effects of different models and simulation time in our economic evaluation; however, we ignored the impact of sample size and the parameters. In other words, the sample size and the parameters were controlled constant in our analysis. Third, the economic model we used was simplified based on published studies. The original model was Markov [32], and we used a partitioned survival model. Deficiencies in model structures and model assumptions might bias the cost-effectiveness results. Thus, we only focused on the uncertainty of the results instead of the practical significance. Finally, using a single case study might also be viewed as a limitation. Further studies that include more cancer immunotherapies and more cancer types could help to test the generalizability of our findings.

5 Conclusions

Flexible techniques present better performance in the case of Checkmate 067 regardless of data maturity. Model selections matter to ICERs of cancer immunotherapy, especially when dealing with immature survival data. Finally, under usual cases when researchers lack evidence to identify the ‘right’ model, a recommended approach is to identify and report these structural uncertainties even when external data could help to exclude some of the models considered.