1 Introduction

Dusty plasmas are ubiquitous in astrophysical environments, they are relevant in the industrial context of plasma etching or thin film deposition and they are of high interest for the fundamental understanding of strongly-coupled many-body systems. Dusty plasmas are multi-species systems consisting of electrons, ions, neutrals and massive (dust) particles, often in the nanometer to micrometer size range. The dust particles in the plasma environment acquire a usually negative net charge from the collection of plasma electrons and ions. In laboratory dusty discharges, a \(10~\upmu \)m particle carries charges of the order of \(Z_\mathrm {d}=10^4\) elementary charges (Piel 2010; Bellan 2004; Melzer 2019). Then, the electrostatic interaction energies among the dust particles exceed their thermal energy leading to strongly coupled systems and even ordered dust arrangements (Ikezi 1986; Chu 1994; Thomas et al. 1994; Melzer et al. 1994). In astrophysical environments, also other charging mechanisms such as secondary electron emission or photo-electron emission can become dominant (Goertz 1989). In industrial discharges for plasma etching or thin film deposition reactive gases are employed that often tend to polymerize and to form nanometric dust particles (Bouchoule 1999; Hollenstein 2000; Boufendi and Bouchoule 2002; Boufendi et al. 2011; Kortshagen 2016).

In all these situations, the charged dust particles provide, in addition to the electrons and ions, another plasma constituent that potentially reacts to the presence of magnetic fields. In many natural dusty plasmas magnetic fields are present and play an essential role (Verheest 2000; Shukla and Mamun 2002). Also, over the past years, strong magnets have been installed in various laboratories to study magnetic field effects in laboratory dusty plasmas (Schwabe et al. 2011; Carstensen et al. 2012; Tadsen et al. 2014; Thomas et al. 2015; Bates et al. 2016; Dzlieva et al. 2018; Melzer et al. 2019; Choudhary et al. 2020). As a consequence, the interest in the physical behavior of magnetized dusty plasmas has grown dramatically, recently.

The charge-to-mass ratio of the plasma charge carriers governs the sensitivity to the presence of a magnetic field: Electrons become magnetized at the lowest magnetic fields of the order of a few milliteslas. Ion magnetization requires a much higher field strength of typically more than 100 mT. Despite their high charge the dust particles have a very low charge-to-mass ratio meaning that very high magnetic field strengths (certainly above 1 T) are expected to be required to magnetize the dust (Thomas et al. 2012; Kählert et al. 2018).

On the other side, this low charge-to-mass ratio of the dust in laboratory discharges results in slow time-scales and enables us to study the dust dynamics with high-resolution video diagnostics. Also the involved spatial scales are ideally suited to study dust systems on the individual particle level. Moreover, the dust dynamics usually is only weakly damped. All this allows to study the dust dynamics on the kinetic level of individual particles. Now, clearly, the goal is to reveal the dynamics of a magnetized dust ensemble.

The reaction of a dusty plasma to magnetic fields can be quite complex: there are indirect effects where the magnetization of the plasma electrons and, subsequently at increased fields, ions lead to modified electron and ion transport processes in the plasma. These consequently alter the plasma conditions to which the dust particles then react. Also, the magnetization of the plasma electrons (and ions) leads to altered charging currents to the dust particles influencing the dust charging processes. Moreover, the plasma-mediated forces on the dust are changed by the magnetic field and the particle-particle interaction might be influenced, e.g. by changed screening properties. In addition, the propagation of dust waves might be altered by changed electron and ion dynamics. Ultimately, the goal is to identify unique signs for a magnetized dust component, such as a dust gyro motion or wave types such as the electrostatic dust-cyclotron wave. So far, however, a magnetization of the dust component has not been clearly demonstrated in experiments, yet.

This review aims at illustrating the physical properties of dusty plasmas at (strong) magnetic fields. From the wealth of material we will focus on phenomena where laboratory findings are available. We will also mainly discuss only situations where strong magnetic fields prevail, i.e., where the electrons are magnetized and the ions can be considered, at least, as partially magnetized. On the one hand, we will look into situations where the dust responds to changes in the plasma environment due to magnetized electrons and ions. On the other hand, we will more specifically address the charging and the wake field structure of the dust under magnetic fields. Finally, we will also study wave propagation of the dust component with magnetic fields. All these topics are looked upon from an experimentalist’s perspective.

2 Fundamental parameters of magnetized dusty plasmas

In the presence of a magnetic field \(\mathbf {B}\) the charged plasma constituents (electrons, ions and dust particles) are subject to the magnetic Lorentz force \(\mathbf {F}_{L\alpha }=Z_{\alpha }e\, \mathbf {v}_{\alpha } \times \mathbf {B}\) where \(Z_{\alpha }\) is the charge number and \(\mathbf {v}_{\alpha }\) is the velocity of species \(\alpha =\mathrm {e,i,d}\) (for electrons, ions and dust). Further, e denotes the elementary charge.

Then, the equation of motion of a charged particle under magnetic field influence can be written as

$$\begin{aligned} m_{\alpha }\dot{\mathbf {v}}_{\alpha } = Z_{\alpha }e\, {\mathbf {v}}_{\alpha } \times \mathbf {B} + \mathbf {F}_{p\alpha } \quad , \end{aligned}$$
(1)

where \(m_{\alpha }\) is the particle mass and \(\mathbf {F}_{p,\alpha }\) are the other (plasma) forces acting on the species \(\alpha \). In case of a dust particle these forces are, among others, the electric field force, the ion drag, thermophoresis, gravity or the neutral gas drag (Nitter 1996; Fortov et al. 2005; Piel 2010; Shukla and Mamun 2002; Melzer 2019).

In the absence of the plasma forces the charges perform a gyro motion around the magnetic field lines with the cyclotron frequency

$$\begin{aligned} \omega _{c\alpha } = \frac{Z_{\alpha } e B}{m_{\alpha }} \end{aligned}$$
(2)

at a gyro- (or Larmor) radius

$$\begin{aligned} r_{L\alpha } = \frac{m_{\alpha } v_{\alpha \perp }}{Z_{\alpha } e B} \end{aligned}$$
(3)

with \(v_{\alpha \perp }\) being the magnitude of the velocity of species \(\alpha \) perpendicular to the magnetic field \(\mathbf {B}\), and \(B=|\mathbf {B}|\).

The relevance of the Lorentz force on the particle dynamics can be classified by different parameters. The Hall parameter

$$\begin{aligned} h_{\alpha } = \frac{\omega _{c\alpha }}{\nu _{\alpha n}} \end{aligned}$$
(4)

compares the cyclotron frequency of species \(\alpha \) with its collision frequency \(\nu _{\alpha n}\). Here, we take specifically the collision frequency of species \(\alpha \) with neutrals since this usually is the dominant collision mechanism. When \(h_{\alpha }>1\) the particle \(\alpha \) performs (on average) a full gyro-orbit before experiencing a collision. Hence, then magnetic field effects can be considered to be significant (Piel 2010).

A second parameter, the magnetization \(M_{\alpha }\) compares the cyclotron frequency with the electrostatic plasma frequency

$$\begin{aligned} \omega _{p\alpha } = \sqrt{\frac{Z_\alpha ^2 e^2 n_\alpha }{\epsilon _0 m_\alpha }} \quad . \end{aligned}$$
(5)

Here, \(n_{\alpha }\) is the density of species \(\alpha \) and \(\epsilon _0\) is the electric field constant. The magnetization then is defined as

$$\begin{aligned} M_{\alpha } = \frac{\omega _{c\alpha }}{\omega _{p\alpha }}= \sqrt{\epsilon _0}\frac{B}{\sqrt{m_\alpha n_\alpha }} \end{aligned}$$
(6)

and is seen to be independent of \(Z_\alpha \). For \(M_{\alpha }>1\) the magnetic field induced dynamics exceeds the electrostatic dynamics (Kählert et al. 2018; Feng et al. 2019. Hence, this parameter is suitable for the description and classification of collective modes.

From these parameters it is clear that the light electrons already will become magnetized with magnetic fields B as low as a few milliteslas under the typical conditions of plasma discharges. For the heavier ions to be magnetized usually much higher magnetic fields of the order of 100 mT and more are required. For the heavy dust particles even larger fields are required. To enter regimes where magnetic field effects become visible for the dust, i.e. where \(h_\mathrm {d}>1\) and/or \(M_\mathrm {d}>1\), one needs to increase the magnetic field and/or the charge-to-mass ratio of the dust. Since in the basic orbital-motion-limit (OML) model the charge scales proportional to the the particle radius a (\(Z_\mathrm {d}\sim a\)) (Whipple et al. 1985 and the dust mass naturally scales with \(a^3\), one needs, in essence, to maximize the parameter B/a at a low gas pressure to reduce the dust neutral friction \(\nu _\mathrm {dn}\) (Thomas et al. 2012. For example, for a particle of about \(1~\mu \)m diameter at a gas pressure of only 0.1 Pa a very high magnetic field of about 3 T is required to achieve \(h_\mathrm {d}\ge 1\). To arrive at \(M_\mathrm {d} \ge 1\) even smaller particles or larger fields are needed. At these field strengths the electrons and ions are already magnetized indicating that magnetized dust is inevitably connected to magnetized electrons and ions.

Due to the formal equivalence of the magnetic Lorentz force \(\mathbf {F}_\mathrm {Ld}=Z_\mathrm {d} e\, \mathbf {v}_\mathrm {d} \times \mathbf {B}\) and the Coriolis force \(\mathbf {F}_\mathrm {Cd}=2 m_\mathrm {d} \mathbf {v}_\mathrm {d} \times \omega _{rot}\) a rotating dust ensemble (with the angular rotation frequency \(\omega _{rot}\)) behaves as if magnetized (Kählert et al. 2018, 2012; Bonitz et al. 2013; Hartmann et al. 2013. Even small rotation frequencies \( \omega _{rot}\) would correspond to extremely high pseudo-magnetic fields \(B_\mathrm {p}=2m_\mathrm {d}/(Z_\mathrm {d} e) \omega _{rot}\) (where actually the small charge-to-mass ratio of the dust is advantageous). This allows to observe “magnetic field” effects from rotations of the dust ensemble mimicking \(h_\mathrm {d},M_\mathrm {d} \gg 1\). In an experiment (Kählert et al. 2012), using a rotating dust cluster, its normal mode frequencies scale with rotation frequency as would be expected for the huge pseudo-magnetic fields \(B_\mathrm {p}\). In extended systems (Hartmann et al. 2013) the longitudinal and transverse modes in a rotating dust layer are determined and found to behave equivalently to magnetoplasmons. However, while the dust behaves as if magnetized, this pseudo-magnetization leaves the electrons and ions unmagnetized (\(h_\mathrm {e,i},M_\mathrm {e,i} \approx 0\)). Hence, a rotating dust system is different from a “real” magnetized dusty plasma since this is, as just discussed, inherently associated with magnetized electrons and ions.

3 Dust reaction to magnetized plasmas

Here, we like to summarize effects and phenomena observed in experiments on dusty plasmas under strong magnetic fields. Here, a survey of selected, available experimental findings will be addressed, see also (Block and Melzer 2019).

We start with a description of the response of the dust particles to the changed plasma conditions when electrons and ions become magnetized. The influence on the charging properties of the dust and the wave propagation will be discussed in the following Sections.

Laboratory experiments on dusty plasmas are usually performed in low-pressure gas discharges where a plasma is ignited by applying a DC or radio-frequency (RF) voltage between two electrodes. While the behavior of magnetically confined plasmas, e.g. in fusion devices, are well established and widely studied, see e.g. Ref. Stacey (2012), the influence of magnetic fields on low-pressure gas discharges that are bounded by walls and electrodes is much less investigated. Over the past few years DC and RF discharges have been installed into the bore of strong magnets (Schwabe et al. 2011; Carstensen et al. 2012; Tadsen et al. 2014; Thomas et al. 2015; Bates et al. 2016; Dzlieva et al. 2018; Melzer et al. 2019; Choudhary et al. 2020) and their behavior has been studied. The various reactions of the dust in such discharges under magnetic fields are compiled below. In all these experiments, generally, the electrons are magnetized (with \(h_\mathrm {e}\gg 1\) and \(M_\mathrm {e}\gg 1\)) and the Hall parameter of the ions usually is of the order of unity, \(h_\mathrm {i}\approx 1\), but \(M_\mathrm {i} < 1\). The dust, however, remains unmagnetized with \(h_\mathrm {d}, M_\mathrm {d} \ll 1\).

Fig. 1
figure 1

a Side view of filaments in an argon plasma at B = 0.75 T. Filaments aligned with the vertically oriented magnetic field are seen throughout the plasma volume. b Filaments coexisting with dust particles trapped in the mapped grid structures at B = 2 T. The dust particles follow the square pattern of the grid electrode. From Thomas et al. (2019). Copyright IOP Publishing. Reproduced with permission. All rights reserved

Full size image

3.1 Filamentation

One of the main observations is that under strong magnetic fields the gas discharges (with and without dust) undergo an instability where a filamentation of the plasma occurs, see e.g. (Schwabe et al. 2011; Thomas et al. 2016; Menati et al. 2020; Thomas et al. 2019; Jung et al. 2018; Jaiswal et al. 2020 and Fig. 1a). These filaments are regions of elevated light emission and thus presumably elevated plasma density and they are extended along the magnetic field lines, but quite localized perpendicular to the field. The filamentation transition occurs in different types of gases and seem to favor low gas pressures. The filaments influence the dust motion in that micron-sized dust particles seem to encircle the filaments (Schwabe et al. 2011). In contrast, filamentation seems to be suppressed in dense dust clouds (Tadsen et al. 2014). Recent experiments in argon discharges (Menati et al. 2020) identified filamentary columns as well as circular or spiral-like structures. Accompanying plasma simulations (without dust) using a fluid model for the electrons and ions show that filamentary structures are indeed regions of higher (electron) density that emerge from an initial density perturbation. The simulations also show, in line with the experiments, that the filaments are reduced with increasing neutral gas pressure. While the electrons are fully magnetized at strong fields, the ions still retain some limited diffusion across the magnetic field lines which gives rise to non-ambipolar diffusion (Menati et al. 2019, 2020). The cross-field scale lengths associated with these filaments seem to be connected to the collisional mean free path of the ions, their gyro-radius and the Debye length.

3.2 Imposed structures

Apart from filamentation, inhomogeneities of the boundaries (electrodes and walls) can be mapped onto the plasma due to the directionality induced by the magnetic field. For instance, a grid structure of the electrode is inscribed into the plasma and, in turn, modifies the trapping condition for the dust component. In a series of experiments (Thomase et al. 2015; Thomas et al. 2019; Hall et al. 2018; Hall and Thomas 2020), a grid and a “waffle”-like structure with holes and conducting elements at a larger length scale have been used as an electrode in the discharge. It is then demonstrated that the dust cloud follows the pattern imposed by these structured electrodes. In detail, the plasma is mainly restricted to the “holes” in the electrode structure where the plasma forms a potential structure in which the dust particles become trapped, see Fig. 1b). This also correlates with the plasma glow observations and hints at the role of the filaments (Hall and Thomas 2020).

3.3 Rotation

Further, it is observed that, even at relatively low magnetic fields (where still \(h_\mathrm {i}< 1\)), ensembles of trapped dust particles rotate as a whole around the magnetic field axis, see e.g. (Nunomura et al. 1997; Konopka et al. 2000; Sato et al. 2001; Cheung et al. 2003; Carstensen et al. 2009; Dzlieva et al. 2006, 2018; Karasev et al. 2006, 2019). The rotation direction usually is in the \(\mathbf {E}_\mathrm {r} \times \mathbf {B}\) direction where \(\mathbf {E}_\mathrm {r}\) is the (horizontal, radial, perpendicular) electric field that confines the dust particles transverse to the magnetic field. The typical rotation frequency \(\omega _{rot}\) is of the order of 0.1–1 s\(^{-1}\). Such a behavior has been observed for dusty plasmas in DC and RF discharges. In anodic plasmas with horizontally oriented fields rotating dust tori have been produced and studied (Reichstein et al. 2012; Pilch et al. 2008; Wilms et al. 2015; Piel and Wilms 2016; Piel 2018).

The origin of the rotation often lies in the motion of the ions. The ions are subject to the \(\mathbf {E}_\mathrm {r} \times \mathbf {B}\) drift and thus rotate around the discharge axis. The rotary ion motion is then eventually transferred to the dust via the ion drag force. In experiments at very low gas pressure (Nunomura et al. 1997) this direct interaction of the ions with the dust via the ion drag force is found to yield rotation speeds that are compatible with the observed speeds. However, for typical plasma experiments with gas pressures around a few Pascal, due to neutral gas friction, this direct ion drag mechanism provides too low rotation speeds as compared to experiments (Carstensen et al. 2009). There, one finds a quantitative agreement between observed and calculated speeds when assuming that the rotating ion species first excites a rotation of the entire neutral gas background via ion-neutral collisions. Then, the rotating neutral gas (together with the ions) drives the dust particle rotation by the neutral gas drag. Neutral gas motion has been demonstrated to play an important role in the rotation of dust clusters in a magnetic field (Carstensen et al. 2009).

In another experiment, an ordered 2D dust cloud was found to rotate as a rigid body at low magnetic fields. At higher fields with magnetic fields of the order of 1 T (\(h_\mathrm {i}\approx 1\)) the shear in the rotation speed of inner and outer parts of the dust cloud eventually disrupts the ordered dust arrangement (Jaiswal et al. 2017). Similarly, in DC discharges at strong magnetic fields of up to 1 T a notable variation of the rotation speed with magnetic field strength was observed as well as redistributions of the dust particle density within the dust clouds (Dzlieva et al. 2018; Pavlov et al. 2020). Using inhomogeneous magnetic fields of the order of 0.1 T the dust particles are found to rotate in opposite direction in different parts of the dust cloud leading to a dust shear flow (Saitou 2016).

3.4 Forces

In low-pressure discharges a sheath is formed in front of the electrodes and the ions usually perform a streaming motion through the sheath due to the sheath electric field \(\mathbf {E}_\mathrm {z}\). The ion motion in this direction remains unaffected when a magnetic field along the sheath electric field is applied. The dust particles, in turn, are usually trapped in the sheath electric field by the upward electric field force and the downward action of gravity. Under such conditions, it was measured that the horizontal confining electric field is steepened by the presence of the magnetic field and that also the charge on the particles exhibits a horizontal gradient. These gradients then drive a vortex motion of the dust cloud (Choudhary et al. 2020). The influence of a magnetic field on the plasma sheath and the resulting forces on dust particles have been studied using dust particles as probes indicating that the sheath structure is modified by the magnetic field and, as a consequence, also the forces on the dust (Dropmann et al. 2015). Another experiment (Puttscher et al. 2017) has shown that laser illumination of the particles under strong magnetic field can lead to self-excited particle oscillations. This might be due to an interplay of the laser drive and a position-dependent dust charge in the sheath leading to delayed charging (Nunomura et al. 1999; Ivlev et al. 2000; Puttscher et al. 2017).

When however the magnetic field is aligned horizontally, perpendicular to the sheath electric field \(\mathbf {E}_\mathrm {z}\), a complex reaction of the dust particles is observed. This is on the one hand due to the \(\mathbf {E}_\mathrm {z} \times \mathbf {B}\) drifts of the electrons that sets up a horizontal ambipolar electric field (Maemura et al. 1998; Pandey et al. 2011). This ambipolar field then gives rise to horizontal electric field forces as well as ion and neutral drag forces that influence the dust motion in a quite intricate way. Nevertheless, the calculated forces are found to be in good agreement with the observed behavior of the dust particles (Puttscher and Melzer 2014; Melzer and Puttscher 2017).

Also the ion drag force (Barnes et al. 1991; Khrapak et al. 2002; Hutchinson 2006; Hutchinson and Patacchini 2007) that describes the interaction of streaming ions with the charged dust becomes influenced by the magnetic field. From recent simulations and accompanying calculations it is found that the gyro motion of magnetized ions results in a reduced momentum transfer from the ions to the dust. Hence, the ion drag force becomes more and more suppressed by the actions of a magnetic field (James and Coppins 2020). However, this effect seems to become important only when the ion gyro radius is of the order of the particle radius (for a 10 micron dust particle this requires a magnetic field of about 10 T).

3.5 Nanodusty clouds in magnetic fields

One possible way to enter the regime of magnetized dusty plasmas is to reduce the particle size, see Sect. 2. Hence, dust clouds with nanometric dust particles under strong fields are of special interest. As a drawback, however, individual particles and their trajectories will no longer be observable. Nevertheless, experiments (Tadsen et al. 2014, 2018) have been performed where dust particles have been grown in argon-acetylene plasmas without magnetic field to a desired particle size of about \(a=150\) nm. The cloud of these nanometric particles then fills almost the entire plasma volume. By subsequently applying a magnetic field of up to 500 mT it was observed that the dust cloud changes its shape. It becomes more confined into the space right between the electrodes and also the dust density distribution within the cloud changes. It has been argued that this is, on the one hand, due to changes of the plasma properties and, on the other hand, due to rotation of the entire dust cloud induced by the Hall component of the ion drag (Tadsen et al. 2014, 2018), see above.

4 Dust charge and wake field

In this chapter we like to review experiments to measure the dust charge under increased magnetic fields together with accompanying simulations and calculations. Associated with the dust charge is the formation of the wake field downstream of the dust particle by streaming ions. Since the dynamics of electrons and ions are strongly influenced by the magnetic field an influence on the charging of the dust particles and the wake field might be expected.

4.1 Dust charge

Dedicated experiments on the measurement of dust charges under strong magnetic fields are rare. One of the earliest experiments exploits a vertically aligned pair of particles trapped in the sheath of an RF discharge in a magnetic field of up to 2.5 T. From a refined version (Carstensen et al. 2011, 2012) of the resonance method (Melzer et al. 1994; Trottenberg et al. 1995; Tomme et al. 2000; Samarian and James 2001; Basner et al. 2009; Carstensen et al. 2012) measured the oscillation frequencies of each of the two particles as well as their interaction strength. From that they concluded that the dust charge essentially stays constant with increased magnetic field, but that the non-reciprocal interaction among the two particles is reduced (see below).

Here, we will review another experiment (Melzer et al. 2019) where finite clusters of micron-sized dust particles are trapped in the sheath of an RF discharge under an axial magnetic field of up to nearly 6 T, see Fig. 2a, b). At the highest field strengths, both the electrons and ions are magnetized, but the dust itself still remains unmagnetized (\(h_\mathrm {d}\ll 1\), \(M_\mathrm {d}\ll 1\)).

Fig. 2
figure 2

Scheme of the experimental setup. a Overview of superconducting magnet and discharge chamber. b Details of the chamber and observation and illumination geometry for the cluster experiment. The inset shows, as an example, a snap shot of a dust cluster with 34 particles. c Setup for the wave investigations with cuvette. A snap shot of the recorded dust-density wave in the cloud of the 3.55 micron particles is also shown. The dashed rectangle indicates the region over which the image intensity is averaged horizontally. This region has a width of 80 pixels (1.4 mm)

Full size image

In this experiment, micrometer-sized particles form a two-dimensional cluster (Schweigert and Peeters 1995; Juan et al. 1998; Klindworth et al. 2000; Melzer 2003; Cheung et al. 2005). Their motion has been measured at a frame rate of 200 frames per second (fps) for magnetic field strengths between 0 and 5.8 T. For each magnetic field setting the dust particle motion has been recorded in sequences of 5 s duration (corresponding to 1000 frames), see Fig. 3. The particles mainly exhibit only thermal Brownian motion around their equilibrium positions. Only at the highest field strengths, Fig. 3d, e, one sees a slight rotation of the dust ensemble, as discussed in the previous section.

Now, first, the temporally resolved positions \(\mathbf {r}_i(t)\) and corresponding velocities \(\mathbf {v}_i(t)\) of all particles i have been extracted from the video sequences (Crocker and Grier 1996; Melzer et al. 2016; Melzer 2019). The Brownian cluster dynamics is then decomposed into its 2N Eigen mode spectrum which is sensitive to the interaction between the dust particles (Schweigert and Peeters 1995; Nelissen et al. 2006; Melzer 2003). Assuming a shielded Coulomb (Debye–Hückel or Yukawa) interaction between the particles and a harmonic confining potential (of frequency \(\omega _0\)) the total energy of the cluster can be written as

$$\begin{aligned} E=\frac{1}{2}m_\mathrm {d}\omega _0^2\sum \limits _{i=1}^N {r}_i^2 + \frac{Z_\mathrm {d}^2e^2}{4\pi \epsilon _0}\sum \limits _{i>j}\frac{1}{r_{ij}}e^{-r_{ij}/\lambda _\mathrm {s}} \quad . \end{aligned}$$
(7)

Here, \(r_{i}\) is the distance of particle i from the trap center, \(r_{ij}\) is the distance between particles i and j and \(\lambda _\mathrm {s}\) is the screening length. The Eigen modes are determined as the Eigen values (describing the oscillation frequency of the particular mode) and Eigen vectors (describing its oscillation pattern) of the dynamical matrix \(A_{ij} = \partial ^2 E/(\partial r_i^{\{1,2\}}\partial r_j^{\{1,2\}})\) with \(r_i^{\{1,2\}}\) being the x or y component of \(r_i\). The measured particle velocities \(\mathbf {v}_i(t)\) are then projected onto each of the the Eigen modes and the corresponding oscillation frequencies are extracted. These mode frequencies finally yield the dust charge \(Z_\mathrm {d}\) for an assumed screening length \(\lambda _\mathrm {s}\), see Melzer (2003); Melzer et al. (2019) for details. In Fig. 4, \(\lambda _\mathrm {s} = 580~\upmu \)m has been used which is well in the range of screening lengths found in (unmagnetized) dusty plasmas (Homann et al. 1997; Nunomura et al. 2002; Konopka et al. 2000). With interparticle distances of the order of \(500~\upmu \)m this corresponds to moderate screening effects.

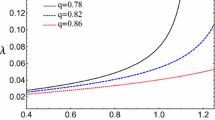
Now, for each magnetic field value, the Eigen mode spectrum is derived from the measured particle dynamics and, in turn from that, the corresponding dust charge \(Z_\mathrm {d}\). Figure 4 shows the so retrieved dust charges as a function of the magnetic field over the entire range of up to 5.8 T. It is seen that the dust charge is around \(Z_\mathrm {d}\approx 11\,000\) elementary charges and does not vary very much with magnetic field strength: only a minor variation of the charge of about 10 % with magnetic field is seen (Melzer et al. 2019). There might be a little variation of the dust charge in correlation with the magnetization parameters (as indicated in Fig. 4), but this needs further clarification.

Fig. 3
figure 3

Trajectories of the dust clusters at various field strengths over a time span of about 5 seconds

Full size image

On the one hand, the fact that the dust charge varies so little with magnetic field might not necessarily be expected since the electron and ion dynamics change a lot with magnetic field and some models also suggest a strong variation of the dust charge with magnetic field strength (Tsytovich et al. 2003; Kalita et al. 2015). However, recent collisionless PIC (particle-in-cell) simulations (Lange 2016) have shown that the electron and ion charging currents are influenced by the magnetic field, but in a similar manner, so that the dust floating potential (and thus dust charge) is not strongly affected by the presence of a magnetic field. Only when the ion gyro radius becomes smaller than the dust radius the particle potential becomes decisively more negative (again: for a 10 micron dust particle this requires a magnetic field of about 10 T). This finding of nearly constant dust charges also holds for streaming ions (Simons and Coppins 2020). In other simulations of particles in a collisionless plasma with flowing ions under strong magnetic fields a slightly larger variation of dust charge with magnetic field of the order of 25 % was found (Darian et al. 2019). However, in MD (molecular dynamics) simulations under realistic experimental conditions including ion-neutral collisions where the particles are trapped in the sheath of a plasma discharge the dust charge is found to decrease by only about 5 % when the magnetic field is varied from 0 to 10 T (Piel et al. 2018, 2018).

In contrast to the above measurements that yielded almost constant charges, in a different experiment a decisive change of the dust charge with magnetic field was observed. There, submicron particles have been dropped through the plasma. Under the action of gravity and a sideways oriented magnetic field the charged dust experiences a \(\mathbf {g} \times \mathbf {B}\) force with a drift velocity \(\mathbf {v}_\mathrm {d}=m_\mathrm {d}/(Z_\mathrm {d}e) \mathbf {g} \times \mathbf {B}/B^2\). From the deflection of the falling particles due to this force the charge then has been measured. It was found that the dust charge considerably drops by about a factor of 5 when the magnetic field ranges from 0.5 to 2.2 T (Lynch 2017). However, in this study, the absolute values of the dust charges were much less than expected from OML charging.

4.2 Wake fields

Closely connected to the dust charge is the formation of a wake field structure downstream of the dust along the ion streaming motion (Vladimirov and Nambu 1995; Nambu et al. 1995; Schweigert and Obrekht 1995; Melzer et al. 1996; Takahashi et al. 1998; Hebner et al. 2003; Samarian et al. 2005; Zhdanov et al. 2009; Couëdel et al. 2011, 2010; Liu et al. 2010; Kroll et al. 2010; Hutchinson 2011, 2012; Ludwig et al. 2012; Röcker et al. 2012; Qiao et al. 2013). Ions that stream past a dust particle in the plasma sheath are scattered into a region downstream of the dust particle due to the ions’ electrostatic interaction with the dust. There the deflected ions form a region of positive space charge. This positive space charge in the wake of the dust, also called “ion focus” (Schweigert et al. 1996; Melzer et al. 1996), gives rise to non-reciprocal attractions and instabilities on lower-layer particles in a dusty plasma (Schweigert et al. 1996, 1999; Ivlev et al. 2015). At strong magnetic fields the ions are bound to the field lines and they perform a gyro motion. Hence, the scattering dynamics of the streaming ions in the field of the dust particle is quite different from the no-field situation and one can expect changes to the ion focus structure and strength.

Fig. 4
figure 4

Charge number retrieved from the normal mode as a function of magnetic field strength. Here a screening length of \(\lambda _\mathrm {s} = 580~\upmu \)m has been assumed. Also, the magnetic field strengths are indicated where the hall parameter and the magnetization of electrons and ions reach unity. See also (Melzer et al. 2019)

Full size image

In a wave picture, the dust excites waves at various frequencies in the streaming ion component that superimpose to form a wake potential structure downstream of the dust (Vladimirov and Nambu 1995; Nambu et al. 1995). In linear response theory calculations the plasma potential \(\phi (\mathbf {r})\) around a dust particle can be written as

$$\begin{aligned} \varPhi (\mathbf {r})=\int \frac{Z_\mathrm {d}e}{8\pi ^2\epsilon _0 q^2}\frac{\exp (i\mathbf {q}\cdot \mathbf {r})}{\epsilon (\mathbf {q},\omega -q_\mathrm {z} u_\mathrm {i})}d\mathbf {q} , \end{aligned}$$
(8)

where \(\omega \) is the wave frequency at the wavenumber \(q=|\mathbf {q}|\) and \(\epsilon (\mathbf {q},\omega )\) is the appropriate dispersion function. The dispersion function is to be evaluated at the Doppler-shifted wave frequency of the ions \(\omega -q_\mathrm {z} u_\mathrm {i}\) with \(u_\mathrm {i}\) being their streaming velocity (along \(\mathbf {B}\)) and \(q_\mathrm {z}\) being the component of the wavevector in streaming direction.

In analytical calculations for the case of no magnetic field, assuming a Boltzmann electron component and a Doppler-shifted fluid ion component, the dust is found to excite ion-acoustic waves, i.e. longitudinal acoustic-like oscillations of the ions and electrons, in the streaming ion component that generate an oscillating wake potential downstream of the dust (Vladimirov and Nambu 1995; Nambu et al. 1995). Downstream, close to the dust, a region of positive, attractive potential forms. With magnetic fields, the dispersion function is modified to include electrostatic ion cyclotron waves or dust-lower-hybrid waves. These are two types of longitudinal oscillations of the ions (and electrons) in a magnetized plasma that propagate nearly perpendicular to the magnetic field; they differ in the allowed range of angles. This modified dispersion function leads to a different wake field structure. There, analytical calculations show that the amplitude of the wake field (i.e. the strength of the positive space charge) is reduced with increasing magnetic field strength (Nambu et al. 2001; Salimullah et al. 2003, 2004; Shukla 1999). This is further confirmed by numerical linear response theory calculations (Joost et al. 2015) that employ kinetic dispersion functions \(\epsilon (\mathbf {q},\omega )\), similar to those used in Sect. 5.1. Thereby, the response of the streaming plasma to a dust particle can been described including collisional effects, wave-ion and wave-electron interactions as well as sub- and supersonic ion flows in addition to the magnetic field. It is seen that, in supersonic ion flows, the magnetic field compresses the wake field structure towards the symmetry axis and at the highest fields (around \(M_\mathrm {i}> 5\)) the wake field vanishes.

PIC simulations (Miloch et al. 2017; Darian et al. 2019) as well as MD simulations (Piel et al. 2018) have confirmed that, in collisionless plasmas up to field strengths of the order of 1 T, the ion focus becomes somewhat weaker with magnetic field. Also the maximum of the positive space charge moves closer to the dust particle. This means that the effect of this ion focus/wake field attraction reduces with magnetic field strength. With even larger magnetic fields, a region of reduced ion density (an “ion shadow”) appears downstream of the dust particle. This is since the magnetized ions adhere to the magnetic field lines and cannot be effectively scattered into the region downstream of the dust. As a consequence, for lower magnetic fields, the non-reciprocal attraction remains present, but for higher field strengths this turns into a repulsive force (Piel et al. 2018).

When ion-neutral collisions are taken into account, a similar behavior is observed: the transition from an attractive to a repulsive ion focus still occurs, but at decisively larger fields of about 10 T (Piel et al. 2018). From Fig. 5 it is seen that with increasing magnetic field, the ion focus (i.e. region of highest ion density) shifts upward to the particle. Along with that the density maximum is substantially reduced. This means that the positive space charge becomes weaker until it gradually disappears at the higher field strengths. Finally, at the highest field strength of 10 T the ion shadow region with a reduced ion density is fully developed.

Fig. 5
figure 5

Ion density distribution (in units of the electron Debye length cubed) for different magnetic field strengths: a \(B=0\), b \(B=2\) T, c \(B=4\) T, d \(B=10\) T. Dotted lines indicate negative plasma potentials, sold lines positive potentials. Reprinted from (Piel et al. 2018), with the permission of AIP Publishing

Full size image

There are only a few experiments on the wake field interaction of microparticles in a dusty plasma (Carstensen et al. 2012; Jung et al. 2018). In these experiments, using a system of two vertically aligned particles, the mutual interaction due to the wake field is probed by analyzing the vertical resonances of the particle pair. These experiments indeed indicate that the wake field strength reduces with increasing magnetic field strength, but a transition to repulsive forces has not been observed, yet.

5 Waves in magnetized dusty plasmas

In this section we will focus on the propagation of dust waves in a magnetized dusty plasma. Without field, strong wave activities of the dust component (so called dust-acoustic or dust density waves) are observed in a vast variety of situations. These waves are easily identified from (typically quite violent) spatio-temporal modulations of the dust density. At strong magnetic fields, a new wave mode arises when the dust becomes magnetized. This wave mode then can serve as an indicator for the dust species being magnetized.

5.1 Wave dispersion in magnetized dusty plasmas

Dust-acoustic waves have been introduced as an analog to ion-acoustic waves into the field of dusty plasmas in its early years by Rao et al. (1990). Similar to ion-acoustic waves, in dust-acoustic waves the dust particles perform longitudinal oscillations where the dust provides the inertia and the electrons and ions provide the shielding (Piel 2011). Almost always these waves are destabilized in a dusty plasma environment by the streaming ions. The ions are the energy source for the motion of the dust particles against the friction with the neutral gas background. Since this ion destabilization modifies the dispersion behavior of the wave it has been argued that this driven wave is better termed dust density wave (Piel 2011).

Such dust-density waves (DDWs) without magnetic field have been analytically predicted and discussed by various authors, e.g., in Refs. Rao et al. (1990); Rosenberg (1996); D’Angelo and Merlino (1996); Kaw and Sen (1998). Experimentally, they have been observed in a variety of systems, for example, just to name a few, in anodic plasmas (Barkan et al. 1995; Thompson et al. 1997; Prabhakara and Tanna 1996; Williams and Thomas 2008), in DC discharges (Molotkov et al. 1999; Ratynskaia et al. 2004; Dietz et al. 2018; Liu et al. 2018) or in the bulk and the sheath of RF discharges (Piel et al. 2008; Flanagan and Goree 2010; Menzel et al. 2010; Chang and Teng 2012), see e.g. Ref. Merlino (2014) for an overview.

The dispersion relation \(\omega (q)\) of these driven dust-density waves (without magnetic field) as derived from fluid equations can be written as (Merlino 2014; Khrapak et al. 2003; Ratynskaia et al. 2004; Thomas 2010; Tadsen et al. 2015; Melzer 2019)

$$\begin{aligned} \varepsilon (\omega ,q) = 1 + \sum \limits _\alpha \chi _\alpha = 0 \end{aligned}$$
(9)

with the susceptibilities of the different species

$$\begin{aligned} \chi _\mathrm {e}= & {} \frac{1}{q^2\lambda _\mathrm {D,e}^2}\nonumber \\ \chi _\mathrm {i}= & {} \frac{\omega _\mathrm {pi}^2}{q^2v_\mathrm {th,i}^2 - \varOmega _\mathrm {i}(\varOmega _\mathrm {i} + \mathrm {i}\nu _\mathrm {in})}\nonumber \\ \chi _\mathrm {d}= & {} \frac{\omega _\mathrm {pd}^2}{q^2v_\mathrm {th,d}^2 - \omega (\omega +\mathrm {i}\nu _\mathrm {dn})}. \end{aligned}$$
(10)

Here, \(\varOmega _\mathrm {i} = \omega - q u_\mathrm {i}\) is the Doppler-shifted wave frequency that the drifting ions “see”. Further, \(\lambda _\mathrm {De}\) is the electron Debye length and \(v_\mathrm {th,\alpha }\) is the corresponding thermal velocity of species \(\alpha \) = (e, i, d) for electrons, ions and dust.

For the electron susceptibility \(\chi _\mathrm {e}\) the low-frequency dust-wave dynamics is neglected. The ion susceptibility \(\chi _\mathrm {i}\) includes the ion drift motion as well as ion-neutral collisions by the ion-neutral collision frequency \(\nu _\mathrm {in}\). Finally, for the dust the effects of a finite temperature and the friction with the neutral gas with the collision frequency \(\nu _\mathrm {dn}\) (Epstein 1924) are included.

With magnetic field, the electron, ion and dust susceptibilities under an arbitrary angle \(\vartheta \) between wave propagation and magnetic field have been given in a fluid picture, e.g. by (D’Angelo 1998). They can be written as Tadsen et al. (2018)

$$\begin{aligned} \chi _\alpha = \frac{\omega _\mathrm {p\alpha }^2 \varOmega _\mathrm {1c\alpha }^2}{q^2v_\mathrm {th,\alpha }^2\varOmega _\mathrm {1c\alpha }^2 - \varOmega _\mathrm {1\alpha }\varOmega _\mathrm {2\alpha }\varOmega _\mathrm {2c\alpha }^2}\quad . \end{aligned}$$
(11)

There, the following abbreviations have been used

$$\begin{aligned} \varOmega _\mathrm {1\alpha }= & {} \omega -\mathbf {q} \cdot \mathbf {u}_{\alpha }\\ \varOmega _\mathrm {2\alpha }= & {} \omega -\mathbf {q} \cdot \mathbf {u}_{\alpha }+\mathrm {i}\nu _\mathrm {\alpha n}\\ \varOmega _\mathrm {1c\alpha }^2= & {} \varOmega _\mathrm {2\alpha }^2-\omega _\mathrm {c\alpha }^2\cos ^2\vartheta \\ \varOmega _\mathrm {2c\alpha }^2= & {} \varOmega _\mathrm {2\alpha }^2-\omega _\mathrm {c\alpha }^2 \end{aligned}$$

with the streaming velocity \(\mathbf {u}_{\alpha }\) of species \(\alpha \). For \(\vartheta = 0\) or without magnetic field this dispersion relation reduces to the field-free case of Eq. (10). Hence, interestingly, for a magnetized dusty plasma the same dispersion relation (10) as for the unmagnetized case holds for a wave propagation along magnetic field direction, see e.g. Refs. (Bharuthram and Pather 1996; Salimullah and Salahuddin 1998; Tadsen et al. 2015).

A kinetic dispersion relation for a magnetized dusty plasma is obtained when the (Maxwellian) velocity distributions for the different species are taken into account (Shukla 1999; Shukla and Rahman 1998; Rosenberg 2010). Hence, this requires warm dust where the dust thermal velocity is of the order of the wave speed. Following (Rosenberg 2010), the susceptibilities for the kinetic dispersion relation can then be written as

$$\begin{aligned}&\chi _\alpha = \frac{1}{q^2\lambda _{D\alpha ^2}}\left[ 1+\frac{\varOmega _\mathrm {2\alpha }}{\sqrt{2}q_z v_\mathrm {th,\alpha }}\mathrm {e}^{-b_\alpha }\sum \limits _{m=-\infty }^{\infty } I_m(b_\alpha )Z(\zeta _\alpha )\right] \times \nonumber \\&\quad \times \left[ 1+\frac{\mathrm {i}\nu _{\alpha n}}{\sqrt{2}q_z v_\mathrm {th,\alpha }}\mathrm {e}^{-b_\alpha }\sum \limits _{m=-\infty }^{\infty } I_m(b_\alpha )Z(\zeta _\alpha )\right] ^{-1} \end{aligned}$$
(12)

with

$$\begin{aligned} \zeta _\alpha =\frac{\varOmega _\mathrm {2\alpha }-m\omega _{\mathrm {c\alpha }}}{\sqrt{2}q_z v_\mathrm {th,\alpha }}. \end{aligned}$$

Further, \(q_\perp , q_z\) are the wave numbers perpendicular and parallel to \(\mathbf {B}\), \(I_m\) is the modified Bessel function of order m and Z is the plasma dispersion function. The parameter \(b_\alpha = q_\perp ^2 v_\mathrm {th,\alpha }^2/\omega _{\mathrm {c}\alpha }^2\) is the (square of the) perpendicular wave number normalized by the respective Larmor radius of species \(\alpha \). For the strongly magnetized electrons and ions only the \(m=0\) contribution needs to be considered. This considerably simplifies the expressions for electrons and ions, see (Rosenberg 2010; Shukla 1999; Shukla and Rahman 1998).

5.2 The electrostatic dust cyclotron wave

From the analysis of the dispersion relation, another fundamental dust wave mode exists, the electrostatic dust cyclotron (EDC) wave (D’Angelo 1990; Shukla and Rahman 1998; D’Angelo 1998; Rosenberg and Chow 1999; Shukla 1999; Rosenberg 2010). This wave mode is an analog to the electrostatic ion cyclotron wave. The EDC wave frequency is near the dust cyclotron frequency \(\omega _\mathrm {cd}\), hence, at very low frequencies. The EDC propagates nearly perpendicular to the magnetic field, but has a small component of the wave vector along the magnetic field and can thus be destabilized by ion streaming along \(\mathbf {B}\).

The observation and identification of a EDC wave would clearly indicate the magnetization of the dust component. From theoretical considerations (D’Angelo 1998; Rosenberg 2010), it can be expected that the EDC wave can be excited at lower ion drift velocities compared to the excitation of DDWs. Hence, given a magnetized dust component, the excitation of EDC could be realized without masking it by the presence of a DDW.

For a numerical example, we adopt the values for case II of Ref. Rosenberg (2010) where dust particles of radius \(a=100\) nm with a charge of \(Z_\mathrm {d}=350\) are trapped in a nitrogen plasma with \(T_\mathrm {e} = 2\) eV and \(T_\mathrm {i} = 0.1\) eV. The dust density is \(n_\mathrm {d} = 2\times 10^9\) m\(^{-3}\), the ion density \(n_\mathrm {i} = 2.5\times 10^{12}\) m\(^{-3}\). The drift velocity of the electrons is considered as \(u_\mathrm {e} = v_\mathrm {th,e}/8\). The magnetic field strength is taken as \(B= 4\) T. These are parameters that might be achievable in experiments and that result in a magnetized dust component. The dust cyclotron frequency under these conditions is \(\omega _\mathrm {cd} = 45\) s\(^{-1}\).

We have solved the dispersion relation \(\omega (q)=\omega _\mathrm {R}(q) + \mathrm {i}\omega _\mathrm {I}(q)\) of the EDC according to Eq. (12) and have retrieved the real and imaginary part of the EDC wave frequency \(\omega \). From that, the most unstable wave number \(q_\mathrm {I}\) is identified where \(\omega _\mathrm {I}\) takes its maximum. Then, the wave frequency \(\omega _\mathrm {R}(q_\mathrm {I})\) of that corresponding wave vector is determined. This has been done for all angles \(\vartheta \) between wave propagation direction \(\mathbf {q}\) and magnetic field \(\mathbf {B}\).

Fig. 6
figure 6

a Most unstable wave number (left) and corresponding wave frequency (right) for the EDC wave and the DDW. The EDC wave is obtained for ion drifts of \(u_\mathrm {i} = v_\mathrm {th,i}\) whereas the DDW is found for larger drift velocities \(u_\mathrm {i} = 1.5 v_\mathrm {th,i}\). Here, the magnetic field and the ion drift are pointing downwards. See text for details. b Example dispersion relation for the EDC under an angle of \(\vartheta = 85^\circ \). c Example dispersion relation for the DDW under an angle of \(\vartheta = 10^\circ \). For both dispersions, the most unstable wave number \(q_\mathrm {I}\) is marked together with the resulting wave frequency \(\omega _\mathrm {R}(q_\mathrm {I})\)

Full size image

The results are shown in Fig. 6. On the left half the most unstable wave number \(q_\mathrm {I}(\vartheta )\) is shown, in the right half the corresponding wave frequency \(\omega _\mathrm {R}(q_\mathrm {I}(\vartheta ))\). The EDC wave becomes destabilized already at an ion drift velocity of \(u_\mathrm {i} = v_\mathrm {th,i}\). It can be seen that EDC wave propagation is observed for angles in the range \(77.8^\circ<\vartheta <87.4^\circ \). The wave frequency is around \(\omega \approx 50\) s\(^{-1}\), slightly larger than \(\omega _\mathrm {cd}\), as expected. The most unstable wave number is around \(q_\mathrm {I}\approx 60\) m\(^{-1}\) corresponding to a wavelength of the order of 10 cm. This wavelength is decisively larger than for a typical DDW. The observation and support of an EDC wave thus requires a relatively large dust cloud.

In contrast, the DDW is destabilized under these conditions only when the ion drift velocity is increased to \(u_\mathrm {i} = 1.5 v_\mathrm {th,i}\). The DDW is found at all angles, the wave frequency is of the order of \(\omega \approx 130\) s\(^{-1}\), the most unstable wave number is near \(q_\mathrm {i}\approx 180\) m\(^{-1}\) (wavelength approximately 3 cm). At the largest angles an influence of the EDC component is observable from the increase in wave velocity (and a slight reduction of the wave number).

Although these calculations are done with hypothetical parameters they indicate under which conditions a magnetized dusty plasma can be realized and identified from the presence of an EDC wave: one needs to use small dust particles at high magnetic fields, as already discussed above. The dust cloud needs to be large to support at least a few wavelengths of the EDC. An advantage is that EDC waves can be excited at lower ion drifts than the DDW and the wave propagation is preferably nearly perpendicular to the magnetic field \(\mathbf {B}\).

5.3 Dust density waves in experiments at strong magnetic fields

In situations without magnetic field, dust density waves have been exploited as a diagnostic tool for dusty plasmas with nanometer or micrometer dust particles as well as dust under weightlessness conditions (Tadsen et al. 2015, 2018; Flanagan and Goree 2010; Williams 2014; Menzel et al. 2010; Yaroshenko et al. 2019). It is now intriguing too see how the dust density waves are affected in a dusty plasma under (strong) magnetic fields.

Tadsen et al. (2018) have studied dust density waves in dusty plasmas with nanometric dust. There dust particles have been grown in an argon-acetylene plasma to sizes of about 150 nm. A magnetic field of up to 100 mT has been applied and the immanent dust density waves have been analyzed to retrieve a (spatially resolved) wave frequency and wavenumber. The authors have proposed a method (Tadsen et al. 2015, 2018) to retrieve plasma parameters from the comparison of the measured wave frequencies and wave numbers (\(f_\mathrm {m}, q_\mathrm {m}\)) with the dispersion relation. The dispersion of the dust density waves, Eq. (10), yields the real and imaginary part of the wave frequency \(\omega _\mathrm {R}(q) + \mathrm {i} \omega _\mathrm {I}(q)\). Then, the authors seek, by variation of the plasma and dust parameters, the solution of the model dispersion, Eq. (10), that reproduces the observed wave frequency \(2\pi f_\mathrm {m}=\omega _\mathrm {R}(q_\mathrm {m})\) where the observed wavenumber \(q_\mathrm {m}\) matches the point of maximum wave growth rate, i.e. where \(\omega _\mathrm {I}(q_\mathrm {m})\) is maximum. From that, they were able to deduce the spatial distribution of ion densities and velocities that in turn are used to derive the dust charge. In their dense cloud they found evidence for strong charge depletion (Tadsen et al. 2015, 2018; Havnes et al. 1987). Under the conditions of their experiment, the dispersion relation of the dust density wave in presence of magnetized electrons (and possibly) ions, still coincides with the dispersion relation (10) for unmagnetized species. This is due to the relatively small ion cyclotron frequency in comparison to \(\mathbf {q}\cdot \mathbf {u}_\mathrm {i}\) and \(\nu _\mathrm {in}\) as well as the small dust cyclotron frequency (Tadsen et al. 2018).

Thomas et al. (2016) have observed self-excited dust-density waves at different magnetic field strengths of up to 1 T. They have measured wave frequency and wavenumber, \(f_\mathrm {m}\) and \(q_\mathrm {m}\), in their dust clouds of micron-sized dust particles trapped in the sheath of an RF discharge. They found, quite independent of magnetic field strength, an acoustic dispersion \(f_\mathrm {m} = C_\mathrm {DDW} q_\mathrm {m}\) with a dust density wave speed of about \(C_\mathrm {DDW} = 38\) mm/s.

Similarly, Choudhary et al. (2020 have studied dust-density waves of micron-sized particles in the discharge sheath under varying magnetic field strength of up to 0.1 T. They measured wave frequencies of the order of \(f_\mathrm {m} \approx 8\) Hz and wave speeds of about \(C_\mathrm {DDW} = 13\) mm/s under their conditions. Moreover, they found that the wave activity became overdamped at magnetic fields above 0.1 T.

In the case of the experiments of Thomas et al. (2016) and Choudhary et al. (2020) also the dispersion relation (10) for unmagnetized species is valid since the wave propagation is along the magnetic field (Bharuthram and Pather 1996; Salimullah and Salahuddin 1998; Tadsen et al. 2015).

In our experiments, that are reviewed here, we have trapped dust clouds of \(1.04~\mu \)m and \(3.55~\mu \)m diameter particles inside a cuvette placed on the lower electrode of an RF discharge at a gas pressure of 7–9 Pa, see Fig. 2c. In this cuvette a dust cloud forms and the ions excite dust density waves that propagate along the magnetic field. The dust density waves then have been recorded for magnetic field strengths of up to 2 T.

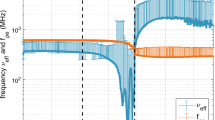
The spatio-temporal evolution of the dust-density waves is obtained by averaging the image intensity along the horizontal image coordinate x (dashed rectangle in Fig. 2c) yielding I(z, t) for each frame (temporal instant t), see also (Schwabe et al. 2007; Flanagan and Goree 2010). The wave frequency \(f_\mathrm {m}\) is measured from the Fourier transform of I(z, t). Then the instantaneous phases have been calculated from the wave intensity I(z, t) by a Hilbert transform, see e.g. Refs. (Menzel et al. 2010, 2011; Williams 2014, 2014; Tadsen et al. 2015). There, I(z, t) is transformed into its analytical signal \(A(z,t)=I(z,t)+\mathrm {i}{\hat{I}}(z,t)\) where \({\hat{I}}(z,t)\) is the Hilbert transform of I(z, t). From that, the instantaneous phase is derived as \(\phi (z,t)=\mathrm {atan2}({\hat{I}}(z,t)/I(z,t))\). The resulting instantaneous phase \(\phi (z,t)\) is shown in Fig. 7a for the dust cloud of \(3.55~\mu \)m dust at different magnetic field strengths. The phase speed \(c_\mathrm {DDW}\) then is obtained from the slope of areas of constant phase \(\phi \) and subsequently the wave number is retrieved from \(q_\mathrm {m} = 2\pi f_\mathrm {m}/ c_\mathrm {DDW}\).

Fig. 7
figure 7

a Maps of the instantaneous phase \(\phi (z,t)\) of the dust-density waves under a magnetic field strength of a 8 mT, b 113 mT, and c 690 mT. d Frequency, wave number and phase speed retrieved from the wave field as a function of magnetic field strength. For presentation purposes the case of no magnetic field (0 mT) is arbitrarily set to \(5\times 10^{-3}\) T on the horizontal axis

Full size image

For the case of \(3.55~\mu \)m particles it is found that the wave frequency slightly drops from about 24 to 19 Hz with increasing magnetic field strength. The phase speed of the waves is around 55 to 60 mm/s with somewhat higher values at intermediate field strengths (0.02–0.3 T). This results in slightly dropping wave numbers from about 2800 m\(^{-1}\) to about 2200 m\(^{-1}\) with somewhat smaller values (1900 m\(^{-1}\)) at those intermediate field strengths. The stronger variation of the wave properties is due to the fact that at field strengths above about 20 mT the dust density waves are not as coherent as at low field strengths, but rather show competing wave modes which makes it difficult to assign a unique wave speed and corresponding wave number (Melzer et al. 2020).

For the smaller dust particles of \(1.04~\mu \)m diameter a similar behavior is observed. There the wave speed is quite constant with \(c_\mathrm {DDW}\approx 40\) mm/s. The wave number decreases with magnetic field from about 8000 m\(^{-1}\) to about 4000 m\(^{-1}\) and the wave frequency decreases correspondingly from about 40 Hz to 20 Hz. Here, we also find competing wave modes at intermediate field strengths, however, in this case it is quite difficult to assign a unique wave frequency (Melzer et al. 2020). In both cases, at the highest magnetic fields, the dust density waves become overdamped, a wave propagation cannot be observed any more (Melzer et al. 2020). A damping of the waves has also been observed by Choudhary et al. (Choudhary et al. 2020), however at much lower magnetic field strengths of about 100 mT. This is probably due to the fact that their experiments have been run under decisively higher pressure, around 25 Pa, compared to 7 Pa in our experiment.

From the comparison of the measured wave frequencies and wave numbers \(f_\mathrm {m}\) and \(q_\mathrm {m}\) with the model dispersion relation (10) we can extract parameters of the dust-plasma system. As for the experiments (Thomas et al. 2016; Choudhary et al. 2020), for our system the unmagnetized dispersion is valid due to the wave propagation along the magnetic field. By variation of the ion density \(n_\mathrm {i}\) and the dust charge \(Z_\mathrm {d}\) the model dispersion is matched to the measured wave properties (Tadsen et al. 2015, 2018), so that the real part of the model dispersion matches the measured wave frequency \(\omega _\mathrm {R}(q_\mathrm {m})=2\pi f_\mathrm {m}\) at the most unstable wavenumber, i.e. \(\omega _\mathrm {I}(q_\mathrm {m})\) is maximum. Figure 8a shows an example of a matched dispersion relation for the case at \(B=113\) mT shown in Fig. 7b. Here, \(f_\mathrm {m}=21\) Hz and \(q_\mathrm {m}=2025\) m\(^{-1}\), yielding \(n_\mathrm {i}=2.6\times 10^{14}\) m\(^{-3}\) and \(Z_\mathrm {d}=1710\). The other parameters were: dust density \(n_\mathrm {d} = 1\times 10^{11}\) m\(^{-3}\), electron density \(n_\mathrm {e} = 0.5 \times n_\mathrm {i}\), electron temperature \(T_\mathrm {e} = 3\) eV, ion temperature \(T_\mathrm {i} = 0.03\) eV, and Epstein drag coefficient (Epstein 1924) \(\nu _\mathrm {dn} = 24\) s\(^{-1}\), see Melzer et al. (2020) for details. The ion-neutral collision frequency results in \(\nu _\mathrm {in} = 2.4\times 10^6\) s\(^{-1}\) and the ion drift velocity in \(u_\mathrm {i} = 1300\) m/s from the electric field necessary to trap the dust (Frost 1957).

Fig. 8
figure 8

a Real and imaginary part of the model dispersion relation fitting the observations: at the measured wavenumber \(q_\mathrm {m}\) the imaginary part has its maximum while the real part coincides with the measured value \(2\pi f_\mathrm {m}\). b Ion density and dust charge number extracted from the dispersion relation for the dust cloud of \(3.55~\mu \)m particles. Again, the data point for B = 0 mT has been arbitrarily set to \(5\times 10^{-3}\) T

Full size image

As already found from the charge analysis using the normal mode, the dust charge extracted from the DDW in Fig. 8b shows only little variation with magnetic field for the \(3.55~\mu \)m particles. The dust charge slightly drops from \(Z_{\mathrm{d}} \approx 2000\) at no field to \(Z_{\mathrm{d}} \approx 1500\) at the highest field. The ion density is found to vary even less and values around \(3\times 10^{14}\) m\(^{-3}\) are found (there is a slightly larger scatter at intermediate field strength due to the uncertainties in the wavenumber). For the smaller particles of \(1.04~\mu \)m the dust charge is also quite constant with values just below \(Z_{\mathrm{d}} \approx 500\) (Melzer et al. 2020). The relative charge ratio between the smaller and larger particles nicely coincides with the dust size ratio, as one would expect from simple OML charging models. Also the absolute values of the dust charge are nicely compatible with other experiments (Khrapak et al. 2003; Schwabe et al. 2007; Flanagan and Goree 2010).

Summarizing, dust density wave propagation at (relatively) strong fields has already been studied in some experiments. However, in none of these cases the EDC wave propagation could have been tested since either the magnetic field was too low, e.g. in Ref. (Tadsen et al. 2018), or the wave propagation was in the direction of the magnetic field, e.g. in (Thomas et al. 2016; Choudhary et al. 2020; Melzer et al. 2020). Also, due to their relatively large wavelength, the EDC wave requires large dust clouds. This requirement of a large magnetized dust volume is a challenging task.

6 Summary and open issues

We have compiled experimental observations in dusty plasmas under strong magnetic fields. Such experiments have been performed with magnetic fields of up to some teslas. Nevertheless, in the experiments available so far, with these high fields only magnetization of the electrons and ions has been achieved, the dust component remained unmagnetized. A magnetization of the dust component requires the use of quite small dust particles at very large fields. Nevertheless, magnetized dust should be achievable in future experiments.

The magnetization of the plasma electrons and ions lead to modified plasma dynamics that in turn influence the dust behavior. Examples include, among others, imposed ordered structures, dust cloud rotation and modified forces on the dust.

The dust charge on micrometer-sized dust particles generally is found to be only weakly influenced by a magnetic field which is in agreement with recent numerical simulations. The attractive ion focus downstream of a dust particle is expected to be weakened under magnetic fields, eventually turning it into a repulsive ion shadow. While the weakening of the ion focus is confirmed by experiments, the formation of an ion shadow remains to be shown.

Dust density waves have been studied in plasmas at strong fields. The wave dynamics also is only weakly modified by the presence of a magnetic field. At intermediate field strengths a competition between different wave modes is observed, before at very high fields the wave motion eventually is damped. So far, only the dust density wave mode has been observed either due to a too low magnetic field or due to wave propagation along the magnetic field. The electrostatic dust cyclotron wave with a propagation nearly perpendicular to the field would indicate a magnetized dust component, however, it also requires large dust clouds.

Not been addressed in this review are dust particles in fusion devices or magnetized dust in astrophysical situations.

In fusion devices dust particles are formed by the interaction of the plasma with the plasma facing components, e.g. by brittle destruction of carbon layers, by melting of surfaces or by desintegration of surface layers, see e.g. (Winter and Gebauer 1999; Sharpe et al. 2002; Krasheninnikov et al. 2010). Dust particles can then cover optics and diagnostics. More important, material from the wall entering the core plasma can lead to strong radiation losses, and in a real deuterium-tritium fusion plasma, the radioactive tritium can be chemically bound to carbonaceous dust particles. Therefore, an understanding of the dust behavior in fusion devices that also operate at high magnetic field strengths is of vital importance. For an overview of dust-related issues in fusion plasmas the reader is referred to recent overviews (Krasheninnikov et al. 2011; Krasheninnikov and Kukushkin 2020).

Dusty plasmas are ubiquitous in astrophysical situations, such as solar and planetary nebulae or molecular clouds and often magnetic fields are involved (Goertz 1989; Crutcher 2012; Reissl et al. 2020; Li 2021). For instance, the cores of molecular cloud cores, which are birth places for protostars and protoplanetary disks, are considered strongly magnetized (Apai and Lauretta 2014; Wardle 2007). While the magnetic field strength can be derived from measurements of the Faraday rotation and the Zeeman effect, the orientation of the magnetic field is obtained, e.g. from the polarization of starlight in extinction by non-spherical dust grains aligned in the magnetic field.

Laboratory studies of magnetized dusty plasmas will help in understanding the physical properties of magnetized dusty plasmas also in for fusion devices and in astrophysical systems.