Stable volumes for persistent homology

Abstract

This paper proposes a stable volume and a stable volume variant, referred to as a stable sub-volume, for more reliable data analysis using persistent homology. In prior research, an optimal cycle and similar ideas have been proposed to identify the homological structure corresponding to each birth-death pair in a persistence diagram. While this is helpful for data analysis using persistent homology, the results are sensitive to noise. The sensitivity affects the reliability and interpretability of the analysis. In this paper, stable volumes and stable sub-volumes are proposed to solve this problem. For a special case, we prove that a stable volume is the robust part of an optimal volume against noise. We implemented stable volumes and sub-volumes on HomCloud, a data analysis software package based on persistent homology, and show examples of stable volumes and sub-volumes.

1 Introduction

Topological data analysis (TDA) (Edelsbrunner and Harer 2010; Carlsson 2009) is a data analysis method utilizing the mathematical concept of topology. In recent years, persistent homology (PH) (Edelsbrunner et al. 2002; Zomorodian and Carlsson 2005) has become one of the most important tools of TDA. PH is mathematically formalized by using homology on a filtration. We can characterize the geometric information by encoding the information regarding the scale of the data on the filtration. PH has developed rapidly over the most recent decade and has been applied in a variety of areas, including natural image analysis (Carlsson et al. 2008), biology (Chan et al. 2013), geology (Suzuki et al. 2021), and materials science (Hiraoka et al. 2016; Saadatfar et al. 2017; Onodera et al. 2019; Hirata et al. 2020).

PH information can be described by a persistence diagram (PD) or a persistence barcode.¹ A PD is a scatter plot on the XY plane, where each point (called a birth-death pair) on the plot corresponds to a homological structure in the input data.

1.1 Persistent homology and volume-optimal cycles

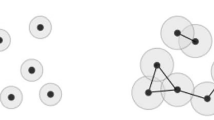
Figure 1 can be used to intuitively explain how a PD is determined from data. The input data in the example constitute a pointcloud with five points, as shown in Fig. 1a. Let a be the length of the edges of the regular triangle and the square. Since the five points themselves do not carry any interesting topological information, we construct a topological structure by putting circles with values of radii r as indicated in Fig. 1b–e.

Fig. 1

How to compute a PD for 5 points a Input pointcloud b Pointcloud and circles with radii $r < a/2$. c $r = a/2$, d $r = a / \sqrt{3}$, e $r = a / \sqrt{2}$, f PD

We now face the problem of how to determine the proper size of the circles. If the circles are too small, as in Fig. 1b, the topology is simply equivalent to the five points. On the other hand, if the circles are too large, as in Fig. 1e, the shape becomes acyclic, which makes it impossible to uncover any interesting topological information. PH solves this problem by considering the appearance and disappearance of homology generators associated with radii changes; that is, PH considers the increasing sequence from Fig. 1b–e.

In the Fig. 1 example, two holes (homology generators in the 1st homology) appear at Fig. 1c, one of which disappears at d. The other hole disappears at Fig. 1e. The pair of radii of the appearance and disappearance of each homology generator is called a birth-death pair, and the multiset of all birth-death pairs is called a persistence diagram. In this example, the PD for the 1st homology is $\{(a/2, a/\sqrt{3}), (a/2, a/\sqrt{2})\}$. The PD is visualized by a scatter plot or a 2D histogram (Fig. 1f). The two pairs correspond to a regular triangle and a square. We can extract the geometric information of the pointcloud in Fig. 1a using the PD.

It is beneficial in data analysis using PH to detect the original homological structures corresponding to each birth-death pair. This is sometimes called “inverse analysis on PH”. Some applications of PH (Hiraoka et al. 2016; Hirata et al. 2020) already use inverse analysis on PH. However, detection is not an easy task, as the representative cycle corresponding to a homology generator is not unique.

To solve this problem, various methods involving the solution of an optimization problem in homology algebra have been proposed (Chen and Freedman 2011; Escolar and Hiraoka 2016; Dey et al. 2019; Erickson and Whittlesey 2005; Dey et al. 2011; Obayashi 2018; Tahbaz-Salehi and Jadbabaie 2008; Schweinhart 2015) in various settings. For PH, optimal cycles (Escolar and Hiraoka 2016), persistence trees (Schweinhart 2015), volume-optimal cycles (Obayashi 2018), and persistent 1-cycles (Dey et al. 2019), have been proposed. The “tightest” or “minimal” cycle is considered the best to interpret, and solving the optimization problem in homology algebra produces the tightest cycle. Persistence cycles (Iuricich 2022) is also proposed for a similar purpose using discrete Morse theory.

1.2 Problems of homology optimization

The existing methods have problems with noise. The example in Fig. 1 can be used to demonstrate these problems. The pointcloud in Fig. 1 has two minimal building blocks, a triangle and a square, and two birth-death pairs correspond to these shapes. However, the optimization technique sometimes fails to find these minimal building blocks when a small noise is added. Figure 2a shows the pointcloud in Fig. 1a when a small noise is added. This figure also shows circles, and, as can be seen, a pentagon appears before either a triangle or a square appears. By applying the homology optimization technique to the data in Fig. 2a, we produce a triangle and a pentagon, as shown in Fig. 2b. On the other hand, consider the pointcloud in Fig. 2c. The pointcloud here is also very close to that in Fig. 1a; however, while a square appears first, the homology optimization technique gives a square and a triangle, as shown in Fig. 2d.

Fig. 2

Two types of optimization results

The example demonstrates the following problems: (1) A small noise can change the result, and (2) The optimization technique sometimes fails to give minimal building blocks of the data. The first problem is related to the reliability of the analysis; the second problem is related to the interpretability of the result.

This means that the stability theorem does not hold for the solutions of the homology optimization problems. Previous studies (Cohen-Steiner et al. 2007; Chazal et al. 2009; Bauer and Lesnick 2014; Lesnick 2015) have proved the stability theorem for PDs. The literature indicates that a PD is continuously changed by a small noise in the input data if we consider reasonable metrics. The stability of other PH outputs has also been studied in the context of machine learning and PH (Bubenik 2015; Kusano et al. 2018; Adams et al. 2017) or pointcloud summary method (Kurlin 2015; Smith and Kurlin 2021). Although these types of stability play an important role in the study of PH, such a stability theorem does not hold for optimized results.

These problems are practically significant, especially when we analyze crystalline structures using PH. We can demonstrate the problems using the synthetic crystalline data in Fig. 3. Here, the pointcloud consists of 27 points, arranged in a $3~\times ~3~\times ~3$ cubical lattice. The distance between two vertices on the cube is 1. A small noise is added to the pointcloud. Figure 3a shows the 1st PD of the pointcloud. As can be seen here, some birth-death pairs are concentrated around $(1/4, 1/\sqrt{2}) \approx (0.5, 0.7)$. These pairs correspond to 1x1 squares in the lattice. By applying volume-optimal cycles (Obayashi 2018), we found some loops corresponding to the pairs in Fig. 3b and c. Some of the cycles shown in Fig. 3b are squares, as expected; however, others in Fig. 3c are larger structures resembling chairs. These larger structures were detected with the same mechanism in Fig. 2.

Fig. 3

Optimal volumes for $3~\times ~3~\times ~3$ cubical lattice. a 1st PD, b Optimal volumes of two pairs, c Optimal volumes of other two pairs

The purpose of this paper is to present a new method to solve these problems. That is, we propose a method to find minimal building blocks that is robust to noise.

1.3 Statistical approach in previous research

Bendich et al. (2020) proposed a statistical approach for the problem, which can be outlined as follows:

• 1. Computing a PD from the input data and choosing a birth-death pair to analyze

• 2. Adding a small noise to the input data, computing a PD, and applying inverse analysis

• 3. Repeating 2. multiple times

• 4. Computing an average of the results of the inverse analysis

By applying this method to the birth-death pair $(1/2, 1/\sqrt{2})$ in Fig. 1, we produce the result shown in Fig. 4. The result indicates that the four points on the square are robust to noise and that the leftmost point is less robust. This result is consistent with the fact that the pair $(1/2, 1/\sqrt{2})$ corresponds to a square.

Fig. 4

Schematic result of applying the statistical approach to the birth-death pair $(1/2, 1/\sqrt{2})$

The stability of the method in a probabilistic sense was also proved in the paper. Notably, the method provides a more reliable inverse analysis. The idea is quite clever, simple, and easy to implement. However, the method has a high computation cost since it requires the user to compute PDs and optimal cycles a large number of times. In the paper, the authors repeat the computation of the generators 1,000 or 10,000 times. We suspect that fewer repetitions may be sufficient, but ten or a hundred trials will be necessary. Multiple trials and errors are typically needed to tune the noise bandwidth in order to apply the method, and thus the cost is not ignorable.

1.4 Reconstructed shortest cycles in Ripserer.jl

The “reconstructed shortest cycles” functionality of Ripserer.jl² by Čufar (2020) gives another solution of the problem. The functionality reconstructs the tightest 1-cycle using the shortest path algorithm and the representative of persistent cohomology. The functionality accepts a noise bandwidth parameter and computes a tighter loop.³

The advantage of reconstructed shortest cycles is their efficiency. Since it uses the shortest path algorithm, the computational complexity is small. However, reconstructed shortest cycles can be applied only to 1st PH since it uses the shortest path algorithm. Another disadvantage is the lack of mathematical justification for the functionality. Now⁴ the functionality is declared as experimental⁵ and gives no mathematical documentation. We explain the algorithm in Appendix A.

1.5 Results

In this paper, we propose stable volumes and a variant of stable volumes, called stable sub-volumes. The proposed method is based on the volume-optimal cycles and optimal volumes (Obayashi 2018). Stable volumes produce minimal building blocks with a lower computation cost than the statistical approach. The following list shows the outline of the results:

• A stable volume for the $(n-1)$th PH embedded in ${\mathbb {R}}^n$ is defined in a similar way to an optimal volume using persistence trees (Definition 3)

• We prove that the stable volume is considered to be the “robust part” against noise (Theorem 3.1)

• The stable volume is reformalized using an optimization problem on homology algebra (Definition 6, Theorem 4.1)

• A stable volume without dimension conditions is also defined using the optimization problem (Sect. 4.2)

• A stable sub-volume is also defined in a similar way (Definition 7)

As the stable volume method has already been implemented in HomCloud (Obayashi et al. 2021),⁶ stable volumes can now be used to analyze the data.

We can demonstrate stable volumes by using the same input data as in Fig. 3. Figure 5 shows the optimal volumes (Fig. 5a) and stable volumes (Fig. 5b) of the same two birth-death pairs. The birth-death pairs correspond to 1x1 squares in the lattice points, but Fig. 5a shows larger loops than expected. In contrast, Fig. 5b shows the expected 1x1 squares. The author confirmed that all stable volumes are 1x1 squares. This example suggests that stable volumes give better results and help promote a better intuitive understanding of PDs.

Fig. 5

Optimal and stable volumes computed for $3~\times ~3~\times ~3$ cubical lattice. a Optimal volumes of two pairs (the same as Fig. 3c), b Stable volumes of the same two pairs

1.6 Organization of the paper

The remainder of the paper is organized as follows: Sect. 2 introduces the concept of PH, optimal volumes, and volume-optimal cycles. Section 3 defines stable volumes for the $(n-1)$th PH embedded in ${\mathbb {R}}^n$. In this section, we also discuss the limitation of stable volumes. Section 4 shows an alternative formalization of stable volumes using mathematical optimization. Section 4.1 provides a proof that the two formalizations are consistent for the $(n-1)$th PH when the simplicial complex is embedded in ${\mathbb {R}}^n$. Section 4.2 extends the formalization to other cases, and Sect. 4.3 defines a stable sub-volume, which is another variant of stable volume. Section 5 discusses the software implementation of stable volumes. Section 6 gives examples using synthetic and real data. This section also provides a comparison with previous methods, the statistical approach, and the reconstructed shortest cycles. Section 7 discusses the way in which the noise bandwidth parameter can be tuned. Section 8 compares stable volumes and sub-volumes. Section 9 summarizes the paper and offers concluding remarks. In this section, we also discuss the differences between the proposed method and the methods of previous works.

2 Persistent homology, optimal volumes, and volume-optimal cycles

In this section, we introduce the mathematical concepts of PH, PDs, optimal volumes, and volume-optimal cycles, which provide the foundation for our discussion.

2.1 Persistent homology

PH is defined on a filtration of topological spaces. Let X be a finite simplicial complex and

$$\begin{aligned} {\mathbb {X}}: \emptyset = X_0 \subsetneq X_1 \subsetneq \cdots \subsetneq X_N = X \end{aligned}$$

(1)

be a filtration of subcomplexes of X. The kth persistent homology $H_k({\mathbb {X}}; \Bbbk )$ with a coefficient field $\Bbbk$ is defined as

$$\begin{aligned} H_k({\mathbb {X}}; \Bbbk ): H_k(X_0; \Bbbk ) \rightarrow H_k(X_1; \Bbbk ) \rightarrow \cdots \rightarrow H_k(X_N; \Bbbk ), \end{aligned}$$

(2)

where $H_k(X_i; \Bbbk )$ is the kth homology $\Bbbk$-vector space of $X_i$ and $\rightarrow$ is the linear map induced by the inclusion maps. We define the direct sum of the sequences of linear maps to describe the fundamental theorem of PH.

Definition 1

For sequences of linear maps with the same length $N+1$, $\{{\mathbb {V}}_m\}_{m=1}^L = \{V_{m,0} \xrightarrow {f_{m,1}} \cdots \xrightarrow {f_{m,N}} V_{m,N}\}_{m=1}^L$, the direct sum of these sequences $\bigoplus _{m=1}^L {\mathbb {V}}_i = V_0 \xrightarrow {f_1} \cdots \xrightarrow {f_{N}} V_N$ is defined as follows:

$$\begin{aligned} V_i = \bigoplus _{m=1}^L V_{m,i} \ (i=0,\ldots ,N), \ \ f_i = \bigoplus _{m=1}^L f_{m,i} \ (i=1,\ldots ,N). \end{aligned}$$

The fundamental theorem of PH is as follows.

Theorem A

There exists a unique decomposition of $H_k({\mathbb {X}}; \Bbbk )$,

$$\begin{aligned} H_k({\mathbb {X}}; \Bbbk ) \simeq \bigoplus _{m=1}^L I(b_m, d_m), \end{aligned}$$

(3)

where $0< b_m < d_m \le \infty$, $\Bbbk \rightarrow \Bbbk$ is an identity map, $0 \rightarrow \Bbbk , \Bbbk \rightarrow 0$ are zero maps, and I(b, d) are as shown below:

$$\begin{aligned} I(b, d) =&0 \rightarrow \cdots \rightarrow 0 \rightarrow \overbrace{\Bbbk }^{b\text {th}} \rightarrow \cdots \rightarrow \overbrace{\Bbbk }^{(d-1)\text {th}} \rightarrow \overbrace{0}^{d\text {th}} \rightarrow \cdots \rightarrow 0, \ \ \text { if } d_m \not = \infty , \end{aligned}$$

(4)

$$\begin{aligned} I(b, d) =&0 \rightarrow \cdots \rightarrow 0 \rightarrow \overbrace{\Bbbk }^{b\text {th}} \rightarrow \cdots \rightarrow \Bbbk , \ \ \text { if } d_m = \infty . \end{aligned}$$

(5)

On an intuitive level, the map $0 \rightarrow \Bbbk$ indicates the appearance of a homology generator, $\Bbbk \rightarrow \Bbbk$ indicates the persistence of the generator, and $\Bbbk \rightarrow 0$ indicates the disappearance of the generator.

We note that we should use a field as a coefficient ring of the homology module since the theorem holds only when $\Bbbk$ is a field.

2.2 Order with level

We earlier introduced the idea of a level function. We now introduce the concept of total order consistent with the level function. The total order is used to rigorously describe the algorithms; the level function is needed to rigorously describe the noise. Simplices with the same level often appear in an alpha filtration or a Vietoris-Rips filtration; thus, the concept of the total order is required to deal with such filtrations. The pair consisting of the total order and the level function is called an order with level.

Let $\prec$ be a total order on the set of all simplices of X. We assume that

$$\begin{aligned} \sigma \subsetneq \sigma ' \text { implies } \sigma \prec \sigma '. \end{aligned}$$

(6)

We can number all simplices in X by this ordering as follows:

$$\begin{aligned} \sigma _1 \prec \sigma _2 \prec \cdots \prec \sigma _N. \end{aligned}$$

(7)

From the condition (6), $X_i = \{\sigma _1, \ldots , \sigma _i\}$ is always a subcomplex of X and

$$\begin{aligned} \emptyset = X_0 \subsetneq X_1 \subsetneq \cdots \subsetneq X_N = X \end{aligned}$$

(8)

is a filtration of simplicial complexes. In this filtration, the number of simplices is increased one by one, which simplifies the mathematical description.

To include additional information in the filtration, we consider an order with level.

Definition 2

A pair $r = ({\hat{r}}, \preceq _r)$ of a real-valued map on X and a total order on X satisfying the following conditions is called an order with level.

• 1. $\sigma \preceq _r \sigma '$ implies ${\hat{r}}(\sigma ) \le {\hat{r}}(\sigma ')$

• 2. The order $\preceq _r$ satisfies (6)

From the total order $\preceq _r$, a filtration ${\mathbb {X}}_r$ is defined by (7) and (8). Theorem A gives the unique decomposition $H_k({\mathbb {X}}_r; \Bbbk ) \simeq \bigoplus _{m=1}^L I(b_m, d_m)$. For each $(b_m, d_m)$, the simplex $\sigma _{b_m}$ is called a birth simplex, $\sigma _{d_m}$ is called a death simplex, and the pair $(\sigma _{b_m}, \sigma _{d_m})$ is called a birth-death simplices pair. When $d_m = \infty$, we write the pair as $(\sigma _{b_m}, \star )$ using the special symbol $\star$. $D_k({\mathbb {X}}_r)$ denotes the set of all birth-death simplices pairs. Moreover, ${\hat{r}}(\sigma _{b_m})$ is called a birth time, ${\hat{r}}(\sigma _{d_m})$ is called a death time, and the pair of the birth time and death time, $({\hat{r}}(\sigma _{b_m}), {\hat{r}}(\sigma _{d_m}))$, is called a birth-death pair. When $\sigma _{d_m} = \star$, ${\hat{r}}(\star )$ is defined as $+\infty$. The multiset of birth-death pairs is called a persistence diagram:

$$\begin{aligned} \{({\hat{r}}(\sigma _{b_m}), {\hat{r}}(\sigma _{d_m})) \mid m=1,\ldots ,L; {\hat{r}}(\sigma _{b_m}) \not = {\hat{r}}(\sigma _{d_m})\}. \end{aligned}$$

(9)

We write the persistence diagram as $\textrm{PD}_k(X, r)$.

2.3 Optimal volumes

Optimal volume is proposed by Obayashi (2018) as a way to extract homological structures corresponding to a birth-death pair. For an order with levels $r = ({\hat{r}}, \preceq _r)$ and a birth-death simplices pair $(\tau _0, \omega _0) \in D_k({\mathbb {X}}_r)$ with $\omega _0 \not = \star$, the optimal volume for the pair is formalized as the solution to the following minimization problem:

$$\begin{aligned} \begin{aligned}&\text {minimize } \Vert z\Vert _0, \text { subject to } \\ z&= \omega _0 + \sum _{\omega \in {\mathcal {F}}_{k+1}} \alpha _\omega \omega \in C_{k+1}(X; \Bbbk ), \\ \tau ^*(\partial z)&= 0 \text { for every } \tau \in {\mathcal {F}}_k, \\ \tau _0^*(\partial z)&\not = 0, \end{aligned} \end{aligned}$$

(10)

where $C_{k+1}(X; \Bbbk )$ is a chain complex whose coefficient field is $\Bbbk$, ${\mathcal {F}}_k = \{ \sigma \in X^{(k)} \mid \tau _0 \prec _r \sigma \prec _r \omega _0\}$, $\tau ^*$ is an element of the dual basis of cochain complex $C^k(X; \Bbbk )$, and $\Vert z\Vert _0 = \{ \omega \mid \alpha _\omega \not = 0 \}$ is the $\ell ^0$ norm of z. For solution z, $\partial z$ is called a volume-optimal cycle.

Obayashi (2018) shows the following theorem, which indicates that the volume-optimal cycle is suitable for representing a birth-death pair.

Theorem B

Let $(\tau _0, \omega _0) \in D_k({\mathbb {X}}_r)$ be a birth-death simplices pair and z an optimal volume of that pair. Then the following relations hold:

$$\begin{aligned} \partial z&\not \in Z_k(\{\sigma \in X \mid \sigma \prec _r \tau _0\}), \end{aligned}$$

(11)

$$\begin{aligned} \partial z&\in Z_k(\{\sigma \in X \mid \sigma \preceq _r \tau _0\}), \end{aligned}$$

(12)

$$\begin{aligned} \partial z&\not \in B_k(\{\sigma \in X \mid \sigma \prec _r \sigma _0\}), \end{aligned}$$

(13)

$$\begin{aligned} \partial z&\in B_k(\{\sigma \in X \mid \sigma \preceq _r \sigma _0\}), \end{aligned}$$

(14)

where $Z_k(\cdot )$ represents the cycles and $B_k(\cdot )$ represents the boundaries.

2.4 Optimal volumes for the $(n-1)$th PH and persistence trees

In this section, we consider a triangulation of a convex set in ${\mathbb {R}}^n$ and its $(n-1)$th PH with $n \ge 2$. More precisely, we assume the following:

Condition 1

A simplicial complex X in ${\mathbb {R}}^n$ satisfies two conditions.

• Any k-simplex ($k < n$) is a face of an n-simplex

• $|X|:= \bigcup _{\sigma \in X}\sigma$ is contractible

Any alpha filtration for a pointcloud with more than $(n+1)$ points in general position (Edelsbrunner and Mücke 1994) satisfies the above conditions.

Delfinado and Edelsbrunner (1995) presented an efficient algorithm to compute the second Betti number of a simplicial complex on the 3-sphere or ${\mathbb {R}}^3$ using a dual graph and union-find algorithm (Section 19, Cormen et al (2022)).

Schweinhart (2015) pointed out that the $(n-1)$th PH was isomorphic to the 0th persistent cohomology of the dual filtration by Alexander duality. Zeroth cohomology is deeply related to the connected components in the dual filtration. This gives rise to another formalization of $(n-1)$th PH. The algorithm is the PH version of Delfinado and Edelsbrunner (1995)’s algorithm. Obayashi (2018) generalizes the idea to optimal volumes.

We now examine an order with levels r on X. Consider the filtration ${\mathbb {X}}_r$ in (7) and (8) given by $\preceq _r$. For simplicity, we will use ${\mathbb {Z}}_2$ as the coefficient field. Then the following theorems hold (Schweinhart 2015; Obayashi 2018).

Theorem C

For any birth-death pair in $\textrm{PD}_{n-1}(X, r)$, the death time is not infinity. Therefore we can always define the optimal volume of the pair. Moreover, the optimal volume is uniquely determined.

Theorem D

If z and $z'$ are the optimal volumes for two different birth-death pairs, one of the following holds:

• $z \cap z' = \emptyset$

• $z \subsetneq z'$

• $z \supsetneq z'$

Note that we can naturally regard any $z = \sum _{\omega \in X^{(n)}} k_{\omega } \sigma \in C_{n}(X)$ as a subset of n-simplices of X, $\{\omega \in X^{(n)} \mid k_{\omega } \not = 0\}$, since we use ${\mathbb {Z}}_2$ as the homology coefficient field.

From Theorem D, we know that $D_{n-1}({\mathbb {X}}_r)$ can be regarded as a forest (i.e., the union of distinct trees) by the inclusion relation. Schweinhart (2015) calls the forest persistence trees. Moreover, we can compute the persistence trees by the merge-tree algorithm (Algorithm 1).

To describe the algorithm, consider the one-point compactification space ${\mathbb {R}}^n \cup \{\infty \} \simeq S^n$. The following facts from Condition 1 are well known.

• $X \cup \{\omega _\infty \}$ is a cell decomposition of ${\mathbb {R}}^n \cup \{\infty \}$, where $\omega _\infty = ({\mathbb {R}}^n \cup \{\infty \}) \backslash |X|$

• For any $\tau \in X^{(n-1)}$, the proper cofaces⁷ of $\tau$ are just two n-cells in $X \cup \{\omega _\infty \}$

We can extend the order with levels r onto $X \cup \{\omega _\infty \}$ by regarding $\omega _\infty$ as the maximum element and ${\hat{r}}(\omega _\infty ) = +\infty$. To describe the algorithm, we consider a directed graph $\bar{G}$ whose nodes are n-cells in $X \cup \{\omega _{\infty }\}$. An edge has extra data in $X^{(n-1)}$, and we can write the edge from $\omega$ to $\omega '$ with extra data $\tau$ as $(\omega \xrightarrow {\tau } \omega ')$. The directed graph $\bar{G}$ is increasingly updated in Algorithm 1.

Since the graph is always a forest throughout the algorithm (Obayashi 2018), we can find a root of a tree that contains an n-cell $\omega$ in the graph $\bar{G}$ by recursively following the edges from $\omega$. We call this procedure ( $\omega , \bar{G}$).

The following theorem gives the interpretation of the result of the algorithm as persistence information.

Theorem E

Let $\bar{G}_*$ be the result of Algorithm 1. That is, $\bar{G}_*$ is the final graph of $\bar{G}$. Then the following holds:

• 1. $\bar{G}_*$ is a tree whose root is $\omega _\infty$

• 2. $D_{n-1}({\mathbb {X}}_r) = \{(\tau , \omega ) \mid (\omega \xrightarrow {\tau } *) \text { is an edge of } \bar{G}_*\}$. Here $*$ means another vertex

• 3. If there is an edge $\omega ' \xrightarrow {\tau } \omega$ is in $\bar{G}_*$, we have $\omega ' \prec _r \omega$

• 4. The optimal volume for $(\tau , \omega ) \in D_{n-1}({\mathbb {X}}_r)$ is $\textrm{dec}(\omega , \bar{G}_*)$, where $\textrm{dec}(\omega , \bar{G}_*)$ the set of all descendant nodes of $\omega$ in $\bar{G}_*$ including $\omega$ itself

• 5. $\bar{G}_*$ gives the persistence trees. That is, $(\tau , \omega )$ is the parent of $(\tau ', \omega ')$ in the persistence trees if and only if there are edges $\omega ' \xrightarrow {\tau '} \omega$

We can prove the above theorems using Alexander duality. Appendix A in (Obayashi 2017)⁸ provides a detailed discussion.

We also remark that the merge-tree algorithm is remarkably accelerated by adding a shortcut path to the root in a similar way as in the union-find algorithm.

3 Stable volumes for the (n-1)th PH

We can now describe stable volume for $(n-1)$th PH using persistence trees under Condition 1. The parameter $\epsilon$ in the following definition is called a bandwidth parameter.

Definition 3

Let X be a simplicial complex and r an order with levels on X, and ${\mathbb {X}}_r$ be the filtration of X given by (7) and (8). Let $\bar{G}_*$ be the persistence trees of the filtration ${\mathbb {X}}_r$. For $(\tau _0, \omega _0) \in D_{n-1}({\mathbb {X}}_r)$ and a positive number $\epsilon$, the stable volume of the birth-death simplices pair with a noise bandwidth parameter $\epsilon$, $\textrm{SV}_\epsilon (r, \tau _0, \omega _0)$, is defined as follows:

$$\begin{aligned} \textrm{SV}_\epsilon (r, \tau _0, \omega _0) = \{\omega _0\} \cup \left( \bigcup _{\omega \in C_\epsilon (\tau _0, \omega _0)} \textrm{dec}(\omega , \bar{G}_*) \right) , \end{aligned}$$

(15)

where $C_\epsilon (\tau _0, \omega _0)$ is given as

$$\begin{aligned} C_\epsilon (\tau _0, \omega _0)&= \{ \omega \in X^{(n)} \mid \omega \xrightarrow {\tau } \omega _0,\text { and } {\hat{r}}(\tau ) \ge {\hat{r}}(\tau _0) + \epsilon \}. \end{aligned}$$

(16)

We can compute $\textrm{SV}_\epsilon (r, \tau _0, \omega _0)$ by traversing persistence trees as shown in Algorithm 2.

We specify the following $(r, \omega _0)$-order condition in order to describe the main theorem.

Definition 4

Let r and q be two orders with levels on a simplicial complex X and $\omega _0$ be an n-simplex. Then q satisfies an $(r, \omega _0)$-order condition if $\sigma \prec _{r} \omega _0$ implies $\sigma \prec _q \omega _0$ for all $\sigma \in X$.

We also define the symbol $\tau _{q, \omega _0}$. For an order with levels q and an n-simplex $\omega _0$, $\tau _{q, \omega _0}$ is the birth simplex paired with $\omega _0$ in $D_{n-1}({\mathbb {X}}_q)$. That is, $(\tau _{q, \omega _0}, \omega _0) \in D_{n-1}({\mathbb {X}}_q)$.

The following theorem is the first main theorem of the paper. It states that the stable volume is an invariant part of optimal volumes in the presence of small noise.

Theorem 3.1

$$\begin{aligned} \textrm{SV}_{\epsilon }(r, \tau _0, \omega _0) = \bigcap _{q \in {\mathcal {R}}_\epsilon } \textrm{OV}(q, \omega _0), \end{aligned}$$

(17)

where

$$\begin{aligned} \begin{aligned} {\mathcal {R}}_\epsilon = \{&q = ({\hat{q}}, \preceq _{q}): \text { an order with levels } \mid \\&\Vert {\hat{q}} - {\hat{r}}\Vert _{\infty } < \epsilon / 2 \text { and } q \text { satisfies }(r, \omega _0)\text {-order condition} \}, \end{aligned} \end{aligned}$$

(18)

and

$$\begin{aligned} \begin{aligned} \textrm{OV}(q, \omega _0)&= \text {the optimal volume of } (\tau _{q, \omega _0}, \omega _0) \in D_{n-1}({\mathbb {X}}_q). \end{aligned} \end{aligned}$$

(19)

The theorem treats two different filtrations, ${\mathbb {X}}_r$ and ${\mathbb {X}}_q$, on the same simplicial complex X. It should be noted that the reader needs to treat these filtrations carefully.

The following two claims immediately imply Theorem 3.1 and are discussed in the next three subsections.

Claim 1

For any $q \in {\mathcal {R}}_\epsilon$, the following relation holds:

$$\begin{aligned} \textrm{SV}_\epsilon (r, \tau _0, \omega _0) \subseteq \textrm{OV}(q, \omega _0). \end{aligned}$$

(20)

Claim 2

For any $\tilde{\omega } \not \in \textrm{SV}_\epsilon (r, \tau _0, \omega _0)$, there is an order with levels $q \in {\mathcal {R}}_\epsilon$ satisfying $\tilde{\omega } \not \in \textrm{OV}(q, \omega _0)$.

3.1 Dual graph and its subgraphs

To show Theorem 3.1, we introduce a dual graph of X and its subgraphs.

Definition 5

$V_X$ and $E_X$ are defined as follows:

$$\begin{aligned} \begin{aligned} V_X&= X^{(n)} \cup \{\omega _\infty \}, \\ E_X&= X^{(n-1)}. \end{aligned} \end{aligned}$$

(21)

$G_X = V_X \cup E_X$ is an undirected graph when the two endpoints of $\tau \in E_X$ are defined as the two cofaces of $\tau$.

We call the graph $G_X$ the dual graph of X. We define the subgraphs of $G_X$, $G_X(\succeq _{r} \sigma )$ and $G_X({\hat{r}} \ge s)$, as

$$\begin{aligned} \begin{aligned} G_X(\succeq _{r} \sigma )&= V_X(\succeq _{r} \sigma ) \cup E_X(\succeq _{r} \sigma ), \\ V_X(\succeq _{r} \sigma )&= \{\omega \in V_X \mid \omega \succeq _r \sigma \},\\ E_X(\succeq _{r} \sigma )&= \{ \tau \in E_X \mid \tau \succeq _r \sigma \}, \\ G_X({\hat{r}} \ge s)&= V_X({\hat{r}} \ge s) \cup E_X({\hat{r}} \ge s), \\ V_X({\hat{r}} \ge s)&= \{\omega \in V_X \mid {\hat{r}}(\omega ) \ge s \}, \\ E_X({\hat{r}} \ge s)&= \{ \tau \in E_X \mid {\hat{r}}(\tau ) \ge s \}, \end{aligned} \end{aligned}$$

(22)

where $\sigma$ is a simplex in X and s is a real number. The condition (6) ensures that $G_X(\succeq _{r} \sigma )$ and $G_X({\hat{r}} \ge s)$ are subgraphs of $G_X$. We also define $G_X(\succ _{r} \sigma )$ by replacing $\succeq _r$ with $\succ _r$.

We introduce the notation $\bar{G}_\sigma$ as $\bar{G}$ in Algorithm 1 when the inside of the (LOOP) is finished at $\sigma$. The following facts are essential for the proof of Theorem 3.1. The facts are shown as Fact 17 and Fact 18 in (Obayashi 2017).

Fact 1

The topological connectivity of vertices in $\bar{G}_\sigma$ is the same as $G_X(\succeq _{r} \sigma )$. That is, $\omega _1, \ldots , \omega _k \in V_X(\succeq _{r} \sigma )$ are all vertices of a connected component in $G_X(\succeq _{r} \sigma )$ if and only if there is a tree in $\bar{G}_\sigma$ whose vertices are $\omega _1, \ldots , \omega _k$.

Fact 2

For each tree in $\bar{G}_\sigma$, the root of the tree is the $(\preceq _r)$-maximum vertex in the tree.

The next lemma describes the role of the birth and death simplices. $K(G, \omega )$ denotes the connected component of a graph G which contains a vertex $\omega$. $K_{\textrm{V}}(G, \omega )$ and $K_{\textrm{E}}(G, \omega )$ denote all the vertices and all the edges of $K(G, \omega )$.

Lemma 3.2

Let $(\tau _0, \omega _0) \in D_{n-1}({\mathbb {X}}_r)$. Then $\omega _0$ is the $(\preceq _r)$-maximum n-simplex in $K(G_X(\succ _{r} \tau _0), \omega _0)$ and the optimal volume of $(\tau _0, \omega _0)$ is $K(G_X(\succ _{r} \tau _0), \omega _0)$. Furthermore, there exists $\omega _1 \in V_X$ satisfying the following conditions:

• $\omega _0 \xrightarrow {\tau _0} \omega _1$ in $\bar{G}_*$

• $\omega _1 \succ _r \omega _0$

• $K(G_X(\succeq _{r} \tau _0), \omega _0) = K(G_X(\succ _{r} \tau _0), \omega _0) \cup K(G_X(\succ _{r} \tau _0), \omega _1) \cup \{\tau _0\}$. That is, $\tau _0$ is the edge between $K(G_X(\succ _{r} \tau _0), \omega _0)$ and $K(G_X(\succ _{r} \tau _0), \omega _1)$

We can easily prove the lemma by considering Algorithm 1 and Facts 1 and 2.

3.2 Proof of Claim 1

The following equality holds from the definition of stable volume (15), Theorem E, Facts 1 and 2, and Lemma 3.2.

$$\begin{aligned} \textrm{SV}_\epsilon (r, \tau _0, \omega _0) = K_{\textrm{V}}(G_X({\hat{r}} \ge {\hat{r}}(\tau _0) + \epsilon ), \omega _0). \end{aligned}$$

(23)

The following equality also holds from Lemma 3.2.

$$\begin{aligned} \textrm{OV}(q, \omega _0) = K_{\textrm{V}}(G_X(\succ _{q} \tau _{q,\omega _0}), \omega _0). \end{aligned}$$

(24)

Therefore, we can show the following relationship to prove Claim 1.

$$\begin{aligned} K_{\textrm{V}}(G_X({\hat{r}} \ge {\hat{r}}(\tau _0) + \epsilon ), \omega _0) \subseteq K_{\textrm{V}}(G_X(\succ _{q} \tau _{q,\omega _0}), \omega _0). \end{aligned}$$

(25)

The following lemma is essential to prove Claim 1.

Lemma 3.3

Let $(\tau _0, \omega _0) \in D_{n-1}({\mathbb {X}}_r)$ be a birth-death simplices pair and $q \in {\mathcal {R}}_\epsilon$. Then the following inequality holds:

$$\begin{aligned} {\hat{q}}(\tau _{q, \omega _0}) - \epsilon / 2 < {\hat{r}}(\tau _0). \end{aligned}$$

(26)

Proof

We assume that ${\hat{q}}(\tau _{q, \omega _0}) - \epsilon / 2 \ge {\hat{r}}(\tau _0)$ and will show a contradiction. Since $\Vert {\hat{q}} - {\hat{r}}\Vert _{\infty } < \epsilon / 2$, for any $\sigma \in G_X$ with $\tau _{q, \omega _0} \preceq _q \sigma$, we have

$$\begin{aligned} {\hat{r}}(\tau _0) \le {\hat{q}}(\tau _{q, \omega _0}) - \epsilon / 2 \le {\hat{q}}(\sigma ) - \epsilon /2 < ({\hat{r}}(\sigma ) + \epsilon /2) - \epsilon /2 = {\hat{r}}(\sigma ). \end{aligned}$$

(27)

From the definition of order with levels, the inequality immediately implies $\tau _0 \prec _r \sigma$ and $G_X(\succeq _{q} \tau _{q, \omega _0})$ is a subgraph of $G_X(\succ _{r} \tau _0)$.

Since $(\tau _{q, \omega _0}, \omega _0) \in D_{n-1}({\mathbb {X}}_q)$, Lemma 3.2 gives $\omega _1 \in V_X$ satisfying

$$\begin{aligned} \omega _1&\succ _q \omega _0, \end{aligned}$$

(28)

$$\begin{aligned} K(G_X(\succeq _{q} \tau _{q, \omega _0}), \omega _0)&= K(G_X(\succ _{q} \tau _{q, \omega _0}), \omega _0) \cup K(G_X(\succ _{q} \tau _{q, \omega _0}), \omega _1) \cup \{\tau _{q, \omega _0}\}. \end{aligned}$$

(29)

(28) leads to $\omega _1 \succ _r \omega _0$ from the $(r, \omega _0)$-order condition. At the same time, (29) leads to $\omega _1 \in K(G_X(\succ _{r} \tau _0), \omega _0)$ since $G_X(\succeq _{q} \tau _{q, \omega _0})$ is a subgraph of $G_X(\succ _{r} \tau _0)$. These facts lead to a contradiction since $\omega _0$ is the $(\preceq _r)$-maximum vertex in $K(G_X(\succ _{r} \tau _0), \omega _0)$, but $K(G_X(\succ _{r} \tau _0), \omega _0)$ contains $\omega _1$ and $\omega _1 \succ _r \omega _0$. $\square$

Using Lemma 3.3, we prove that $G_X({\hat{r}} \ge {\hat{r}}(\tau _0) + \epsilon )$ is a subgraph of $G_X(\succ _{q} \tau _{q, \omega _0})$ to show (25). For any $\sigma \in G_X({\hat{r}} \ge {\hat{r}}(\tau _0) + \epsilon )$, we have

$$\begin{aligned} {\hat{q}}(\sigma )> {\hat{r}}(\sigma ) - \epsilon / 2 \ge ({\hat{r}}(\tau _0) + \epsilon ) - \epsilon / 2 = {\hat{r}}(\tau _0) + \epsilon /2 > {\hat{q}}(\tau _{q, \omega _0}), \end{aligned}$$

(30)

and hence $\sigma \succ _q \tau _{q, \omega _0}$. This means that $G_X({\hat{r}} \ge {\hat{r}}(\tau _0) + \epsilon )$ is a subgraph of $G_X(\succ _{q} \tau _{q, \omega _0})$.

3.3 Proof of Claim 2

If $\tilde{\omega } \not \in OV(r, \omega _0)$, the conclusion of Claim 2 is trivial. Therefore, we assume $\tilde{\omega } \in OV(r, \omega _0)$.

Since

$$\begin{aligned} \tilde{\omega }&\in \textrm{OV}(r, \omega _0) = K_{\textrm{V}}(G_X(\succ _{r} \tau _0), \omega _0), \\ \tilde{\omega }&\not \in \textrm{SV}_\epsilon (r, \tau _0, \omega _0) = K_{\textrm{V}}(G_X({\hat{r}} \ge {\hat{r}}(\tau _0) + \epsilon ), \omega _0), \end{aligned}$$

and $G_X({\hat{r}} > {\hat{r}}(\tau _0) + \epsilon )$ is a subgraph of $G_X(\succ _{r} \tau )$, there is $\tilde{\tau } \in E_X$ satisfying the following conditions:

$$\begin{aligned} \begin{aligned} \tau _0&\prec _r \tilde{\tau }, \\ {\hat{r}}(\tau _0)&\le {\hat{r}}(\tilde{\tau }) < {\hat{r}}(\tau _0) + \epsilon , \\ \tilde{\omega }&\not \in K_{\textrm{V}}(G_X(\succ _{r} \tilde{\tau }), \omega _0), \\ \tilde{\omega }&\in K_{\textrm{V}}(G_X(\succeq _{r} \tilde{\tau }), \omega _0). \end{aligned} \end{aligned}$$

(31)

Let $\epsilon _* = {\hat{r}}(\tilde{\tau }) - {\hat{r}}(\tau _0)$ and $\eta = (\epsilon _* + \epsilon ) /4$. From (31), we have

$$\begin{aligned} \begin{aligned} \epsilon /2&> \eta > \epsilon _* / 2 \ge 0. \end{aligned} \end{aligned}$$

(32)

Lemma 3.2 gives $\omega _1 \in V_X$ satisfying

$$\begin{aligned} \omega _1&\succ _r \omega _0, \text { and } \end{aligned}$$

(33)

$$\begin{aligned} K(G_X(\succeq _{r} \tau ), \omega _0)&= K(G_X(\succ _{r} \tau _0), \omega _0) \cup K(G_X(\succ _{r} \tau _0), \omega _1) \cup \{\tau _0\}. \end{aligned}$$

(34)

Let $\omega _e$ be the endpoint of $\tau _0$ contained in $K(G_X(\succ _{r} \tau _0), \omega _0)$. A path from $\omega _0$ to $\omega _e$ exists in $K(G_X(\succ _{r} \tau _0), \omega _0)$. We consider the following two cases regarding the path.

• Case 1 There is a path P from $\omega _0$ to $\omega _e$ in $G_X(\succ _{r} \tau _0)$ without passing through $K(G_X(\succ _{r} \tilde{\tau }), \tilde{\omega })$.

• Case 2 Any path $\omega _0$ to $\omega _e$ in $K(G_X(\succ _{r} \tau _0)$ passes through $K(G_X(\succ _{r} \tilde{\tau }), \tilde{\omega })$.

We will divide the proof into the above two cases.

3.3.1 Case 1

Fig. 6 shows the relationship between connected components and the path P in Case 1. We can construct an order with levels q satisfying $\tilde{\omega } \not \in K_{\textrm{V}}(G_X(\succ _{q} \tau _{q, \omega _0}), \omega _0)$ based on this relationship.

Fig. 6

The relationship between connected components and path P in Case 1. Circles represent vertices, rectangles by dotted lines represent connected components, solid lines represent edges between connected components, and dashed curves represent paths

Using $\eta$, we define a function ${\hat{q}}$ on X as follows:

$$\begin{aligned} {\hat{q}}(\sigma ) = \left\{ \begin{array}{ll} {\hat{r}}(\sigma ) + \eta &{} \text {if } \sigma \in X^{(n)}, \\ {\hat{r}}(\sigma ) + \eta &{} \text {if } \sigma \in Q_{\textrm{E}}, \\ {\hat{r}}(\sigma ) - \eta &{} \text {if } \sigma \in X^{(n-1)} \backslash Q_{\textrm{E}}, \\ {\hat{r}}(\sigma ) - \eta &{} \text {if } \sigma \in X^{(0)} \cup \cdots \cup X^{(n-2)}, \end{array} \right. \end{aligned}$$

(35)

where $Q = P \cup \{\tau _0\} \cup K(G_X(\succ _{r} \tau ), \omega _1)$, and $Q_{\textrm{E}}$ is the set of all edges in Q. We can easily show that ${\hat{q}}$ is a level function from the fact that ${\hat{r}}$ is a level function. We define the order on $X \cup \{\omega _\infty \}$, $\preceq _q$, as follows:

$$\begin{aligned} \begin{aligned}&\sigma \prec _q \sigma ' \text { if and only if} \\&{\hat{q}}(\sigma ) < {\hat{q}}(\sigma '), \text { or }\\&{\hat{q}}(\sigma ) = {\hat{q}}(\sigma ') \text { and } \sigma \subsetneq \sigma ', \text { or } \\&{\hat{q}}(\sigma ) = {\hat{q}}(\sigma ') \text { and } \sigma \cap \sigma ' = \emptyset \text { and } \sigma \prec _r \sigma '. \end{aligned} \end{aligned}$$

(36)

This is a kind of lexicographic order by the total preorder $(\sigma , \sigma ') \mapsto {\hat{q}}(\sigma ) \le {\hat{q}}(\sigma ')$, the partial order $\subseteq$, and the total order $\preceq _r$. Therefore $\preceq _q$ is a total order.

The following two facts are easily shown.

Fact 3

$q = (\preceq _q, {\hat{q}})$ is an order with levels.

Fact 4

The order $\preceq _q$ coincides with $\preceq _r$ on $V_X$. The same is true on $Q_{\textrm{E}}$ or $X^{(n-1)} \backslash Q_{\textrm{E}}$.

We also show the following fact.

Fact 5

$q \in {\mathcal {R}}_\epsilon$.

Proof

From the definition, we have $\Vert {\hat{q}} - {\hat{r}}\Vert \le \eta < \epsilon / 2$. To show the $(r, \omega _0)$-order condition, we assume $\sigma \prec _r \omega _0$ and show $\sigma \prec _r \omega _0$. From the assumption, we have ${\hat{r}}(\sigma ) \le {\hat{r}}(\omega _0)$. Since $\omega _0$ is n-simplex, ${\hat{q}}(\omega _0) = {\hat{r}}(\omega _0) + \eta$, and so ${\hat{q}}(\omega _0) \ge {\hat{q}}(\sigma )$. Therefore, we consider the following cases:

• 1. ${\hat{q}}(\omega _0) > {\hat{q}}(\sigma )$. In this case, we can see $\omega _0 \succ _q \sigma$ from the definition of order with levels.

• 2. ${\hat{q}}(\omega _0) = {\hat{q}}(\sigma )$ and $\omega _0 \supsetneq \sigma$. In this case, we have $\omega _0 \succ _q \sigma$ from the definition of $\preceq _q$.

• 3. ${\hat{q}}(\omega _0) = {\hat{q}}(\sigma )$ and $\omega _0 \subsetneq \sigma$. In this case, the condition $\omega _0 \subsetneq \sigma$ leads to a contradiction since $\prec _r$ satisfies (6) but $\sigma \prec _r \omega _0$.

• 4. ${\hat{q}}(\omega _0) = {\hat{q}}(\sigma )$ and $\omega _0 \cap \sigma = \emptyset$. In this case, we have $\omega _0 \succ _q \sigma$ from the assumption of $\sigma \prec _r \omega _0$.

In all cases except 3, we have $\sigma \prec _r \omega _0$. $\square$

The following fact comes from Fact 4.

Fact 6

$\tau _0$ is the $(\preceq _q)$-minimum element in Q.

The above fact leads to the following.

Fact 7

Q is a subgraph of $K(G_X(\succeq _{q} \tau _0), \omega _0)$.

We also prove the following fact about $K(G_X(\succ _{q} \tau _0), \omega _0)$ and $K(G_X(\succ _{q} \tau _0), \omega _1)$.

Fact 8

$K(G_X(\succ _{q} \tau _0), \omega _0)$ and $K(G_X(\succ _{q} \tau _0), \omega _1)$ are different connected components in $G_X(\succ _{q} \tau _0)$.

Proof

We assume that $K(G_X(\succ _{q} \tau _0), \omega _0) = K(G_X(\succ _{q} \tau _0), \omega _1)$ and this will lead to a contradiction. From the assumption, there is a path $Q'$ from $\omega _0$ to $\omega _1$ in $G_X(\succ _{q} \tau _0)$. Any edge $\tau$ on $Q'$ satisfies $\tau \succ _q \tau _0$ and so ${\hat{q}}(\tau ) \ge {\hat{q}}(\tau _0)$. Therefore, since $|{\hat{r}}(\tau ) - {\hat{q}}(\tau )| \le \eta$ and ${\hat{q}}(\tau _0) = {\hat{r}}(\tau _0) + \eta$, the inequality ${\hat{r}}(\tau ) \ge {\hat{r}}(\tau _0)$ holds for any $\tau \in Q_{\textrm{E}}'$, where $Q_{\textrm{E}}'$ is the set of all edges on $Q'$.

We conclude that $\tau \succ _r \tau _0$ for any $\tau \in Q_{\textrm{E}}'$ from (36), $\tau \succ _q \tau _0$, and ${\hat{r}}(\tau ) \ge {\hat{r}}(\tau _0)$. This means that $Q'$ is a subgraph of $G_X(\succ _{r} \tau _0)$. However, this contradicts the fact that $\omega _0$ and $\omega _1$ are contained in different connected components of $G_X(\succ _{r} \tau _0)$. $\square$

From Facts 4, 7, and 8, and (33), we have the following fact.

Fact 9

$\tau _{q,\omega _0} = \tau _0$.

Next, we examine $\tilde{\tau }$.

Fact 10

$\tau _0 \succ _q \tilde{\tau }$.

Proof

Since $\tau _0 \in Q_{\textrm{E}}$ and $\tilde{\tau } \not \in Q_{\textrm{E}}$, we have

$$\begin{aligned} {\hat{q}}(\tau _0) - {\hat{q}}(\tilde{\tau })&= ({\hat{r}}(\tau _0) + \eta ) - ({\hat{r}}(\tilde{\tau }) - \eta ) \\&= {\hat{r}}(\tau _0) - {\hat{r}}(\tilde{\tau }) - 2\eta \\&= \epsilon _* - 2\eta > 0. \end{aligned}$$

The inequality leads to $\tau _0 \succ _q \tilde{\tau }$ since q is an order with levels. $\square$

We can prove the following fact in a similar way to Fact 8.

Fact 11

$\tilde{\omega } \not \in K(G_X(\succ _{q} \tilde{\tau }), \omega _0)$.

From Facts 9, 10, and 11, the following fact is easily established.

Fact 12

$\tilde{\omega } \not \in K(G_X(\succ _{q} \tau _{q, \omega _0}), \omega _0)$.

Finally, since $\textrm{OV}(q, \omega _0) = K_{\textrm{V}}(G_X(\succ _{q} \tau _{q, \omega _0}), \omega _0)$, we conclude that $\tilde{\omega } \not \in \textrm{OV}(q, \omega _0)$.

3.3.2 Case 2

In Case 2, there is a path T from $K(G_X(\succ _{r} \tilde{\tau }), \tilde{\omega })$ to $\omega _e$ without passing through $K(G_X(\succ _{r} \tilde{\tau }), \omega _0)$. Figure 7 shows the relationship between connected components and paths between the components in this case.

Fig. 7

The relationship between connected components and path T in Case 2. Circles represent vertices, rectangles by dotted lines represent connected components, solid lines represent edges between connected components, and dashed curves represent paths

We now define a function ${\hat{s}}$ on X as follows:

$$\begin{aligned} {\hat{s}}(\sigma ) = \left\{ \begin{array}{ll} {\hat{r}}(\sigma ) + \eta &{} \text {if } \sigma \in X^{(n)}, \\ {\hat{r}}(\sigma ) + \eta &{} \text {if } \sigma \in S_{\textrm{E}}, \\ {\hat{r}}(\sigma ) - \eta &{} \text {if } \sigma \in X^{(n-1)} \backslash S_{\textrm{E}}, \\ {\hat{r}}(\sigma ) - \eta &{} \text {if } \sigma \in X^{(0)} \cup \cdots \cup X^{(n-2)}, \end{array} \right. \end{aligned}$$

(37)

where $S = K(G_X(\succ _{r} \tilde{\tau }), \tilde{\omega }) \cup T \cup \{\tau _0\} \cup K(G_X(\succ _{r} \tau _0), \omega _1)$ and $S_{\textrm{E}}$ is the set of all edges of S.

We also define the total order on X, $\preceq _s$, as follows:

$$\begin{aligned} \begin{aligned}&\sigma \prec _s \sigma ' \text { if and only if} \\&{\hat{s}}(\sigma ) < {\hat{s}}(\sigma '), \text { or }\\&{\hat{s}}(\sigma ) = {\hat{s}}(\sigma ') \text { and } \sigma \subsetneq \sigma ', \text { or } \\&{\hat{s}}(\sigma ) = {\hat{s}}(\sigma ') \text { and } \sigma \cap \sigma ' = \emptyset \text { and } \sigma \prec _r \sigma '. \end{aligned} \end{aligned}$$

(38)

We can prove the following fact in a similar way to Facts 3 and 5.

Fact 13

$s = (\preceq _s, {\hat{s}})$ is an order with levels on X, and $s \in {\mathcal {R}}_\epsilon$.

The following fact arises directly from the definition of ${\hat{s}}$ and $\preceq _s$.

Fact 14

The order $\preceq _s$ coincides with $\preceq _r$ on $V_X$. The same is true on $Q_{\textrm{E}}$ or $X^{(n-1)} \backslash Q_{\textrm{E}}$.

The following fact can be shown in a similar way to Facts 6 and 7.

Fact 15

S is a subgraph of $K(G_X(\succeq _{s} \tau _0), \tilde{\omega })$.

We can show the following fact in the same way as Fact 10. From the following fact, we have $K(G_X(\succeq _{s} \tau _0), \tilde{\omega }) \subseteq K(G_X(\succ _{s} \tilde{\tau }), \tilde{\omega })$.

Fact 16

$\tau _0 \succ _s \tilde{\tau }$.

We can prove the following in a similar way to Facts 8 and 9 using Facts 14, 15, and 16.

Fact 17

$K(G_X(\succ _{s} \tilde{\tau }), \tilde{\omega })$ and $K(G_X(\succ _{s} \tilde{\tau }), \omega _0)$ are different connected components in $G_X(\succ _{s} \tilde{\tau })$ and $\tilde{\tau }$ connects the two connected components. Therefore, $\tau _{s, \omega _0} = \tilde{\tau }$.

From the above facts, we have the following.

Fact 18

$\tilde{\omega } \not \in K(G_X(\succ _{s} \tau _{s, \omega _0}), \omega _0)$.

Finally, since $\textrm{OV}(q, \omega _0) = K_{\textrm{V}}(G_X(\succ _{q} \tau _{q, \omega _0}), \omega _0)$, we conclude that $\tilde{\omega } \not \in \textrm{OV}(q, \omega _0)$.

3.4 Limitation of stable volumes

In this subsection, we discuss some of the limitations of stable volumes.

The first relates to the $(r, \omega _0)$-order condition. Theorem 3.1 requires the $(r, \omega _0)$-order condition; however, this condition seems somewhat curious. To clarify, we offer a brief discussion of the role of the condition.

First, we examine what happens when orders with levels q and r satisfy $\Vert {\hat{q}} - {\hat{r}}\Vert \le \epsilon /2$ but not the $(r, \omega _0)$-order condition. Figure 8 shows an example. In this example, we assume the following conditions:

$$\begin{aligned} Y&= Y_0 \cup \{ \tau _1, \tau _2, \omega _1, \omega _2 \} \text { is a simplicial complex}, \end{aligned}$$

(39)

$$\begin{aligned} {\hat{r}}(\sigma )&\approx {\hat{q}}(\sigma ) \text { for any } \sigma \in Y, \end{aligned}$$

(40)

$$\begin{aligned} {\hat{r}}(\omega _1)&\approx {\hat{r}}(\omega _2), {\hat{q}}(\omega _1) \approx {\hat{q}}(\omega _2), \end{aligned}$$

(41)

$$\begin{aligned} {\hat{r}}(\sigma )&< {\hat{r}}(\tau _1) \text { for any } \sigma \in Y_0, \end{aligned}$$

(42)

$$\begin{aligned} {\hat{q}}(\sigma )&< {\hat{q}}(\tau _1) \text { for any } \sigma \in Y_0, \end{aligned}$$

(43)

$$\begin{aligned} {\hat{r}}(\tau _1)&< {\hat{r}}(\tau _2)< {\hat{r}}(\omega _1) < {\hat{r}}(\omega _2) \text { for any } \sigma \in Y_0, \end{aligned}$$

(44)

$$\begin{aligned} {\hat{q}}(\tau _1)&< {\hat{q}}(\tau _2)< {\hat{q}}(\omega _2) < {\hat{q}}(\omega _1) \text { for any } \sigma \in Y_0 . \end{aligned}$$

(45)

Fig. 8

Two filtrations on the same simplicial complex

Here, we have

$$\begin{aligned} ({\hat{r}}(\tau _1), {\hat{r}}(\omega _2)), ({\hat{r}}(\tau _2), {\hat{r}}(\omega _1))&\in \textrm{PD}_1(X, r), \\ ({\hat{q}}(\tau _1), {\hat{q}}(\omega _1)), ({\hat{q}}(\tau _2), {\hat{q}}(\omega _2))&\in \textrm{PD}_1(X, q), \\ ({\hat{r}}(\tau _1), {\hat{r}}(\omega _2))&\approx ({\hat{q}}(\tau _1), {\hat{q}}(\omega _1)), \\ ({\hat{r}}(\tau _2), {\hat{r}}(\omega _1))&\approx ({\hat{q}}(\tau _2), {\hat{q}}(\omega _2)). \end{aligned}$$

The optimal volumes are

$$\begin{aligned} \{\omega _1, \omega _2 \}&= \textrm{OV}({\hat{r}}, {\hat{r}}(\tau _1), {\hat{r}}(\omega _2)) = \textrm{OV}({\hat{q}}, {\hat{q}}(\tau _1), {\hat{q}}(\omega _1)), \end{aligned}$$

(46)

$$\begin{aligned} \{\omega _1 \}&= \textrm{OV}({\hat{r}}, {\hat{r}}(\tau _2), {\hat{r}}(\omega _1)), \end{aligned}$$

(47)

$$\begin{aligned} \{\omega _2 \}&= \textrm{OV}({\hat{q}}, {\hat{q}}(\tau _2), {\hat{q}}(\omega _2)). \end{aligned}$$

(48)

Therefore, $({\hat{r}}(\tau _2), {\hat{r}}(\omega _1)) \approx ({\hat{q}}(\tau _2), {\hat{q}}(\omega _2))$; however, $\textrm{OV}({\hat{r}}, {\hat{r}}(\tau _2), {\hat{r}}(\omega _1))$ does not intersect with $\textrm{OV}({\hat{q}}, {\hat{q}}(\tau _2), {\hat{q}}(\omega _2))$. Thus, the example shows that $\textrm{OV}({\hat{r}}, {\hat{r}}(\tau _2), {\hat{r}}(\omega _1))$ does not have a robust part to small noise if we do not assume the $(r, \omega _0)$-order condition.

In contrast, (46) indicates that $\textrm{OV}({\hat{r}}, {\hat{r}}(\tau _1), {\hat{r}}(\omega _2))$ has a stable part even if we do not assume the $(r, \omega _0)$-order condition. We expect that if an optimal volume is large in some sense, then the optimal volume has a stable part even if the $(r, \omega _0)$-order condition is not satisfied. Mathematically clarifying what is meant by “large in some sense” is a subject for future research.

Next, we focus on the construction of simplicial filtrations. An alpha shape (Edelsbrunner and Mücke 1994) is often used to construct a filtration from a pointcloud. Alpha complexes have some good properties. If a pointcloud is in ${\mathbb {R}}^d$ and satisfies the general position condition, then the alpha shape is embedded in ${\mathbb {R}}^d$. An alpha shape has the same information as the union-balls model. More precisely, an alpha shape is homotopy equivalent to the union of balls. However, the alpha shape may vary discontinuously with noise. Theorem 3.1 assumes that the simplicial complex X does not change with noise; however, the assumption does not hold if the noise is large. On the other hand, if the noise is small, the assumption holds and the theorem works perfectly. In Sect. 6, we show that a large noise bandwidth parameter gives unexpected results. Therefore, it is reasonable to assume that the noise is small; however, care should be taken.

4 Another formalization of a stable volume as the solution to an optimization problem

The formalization of stable volumes is based on persistence trees. Importantly, however, persistence trees are available only for the $(n-1)$th persistence homology, and we cannot apply the concept directly to another degree. Another version of a stable volume can be defined as the solution to an optimization problem.

Definition 6

Let r be an order with levels and $(\tau _0, \omega _0) \in D_k({\mathbb {X}}_r)$. $\tilde{\textrm{SV}}_\epsilon (r, \tau _0, \omega _0)$ is defined by the solution to the following minimization problem.

$$\begin{aligned} \text {minimize }&\Vert z\Vert _0, \text { subject to } \nonumber \\ z&= \omega _0 + \sum _{\omega \in {\mathcal {F}}_{\epsilon , k+1} } \alpha _\omega \omega \in C_{k+1}(X; \Bbbk ), \end{aligned}$$

(49)

$$\begin{aligned} \tau ^*(\partial z)&= 0 \text { for any } \tau \in {\mathcal {F}}_{\epsilon , k}, \end{aligned}$$

(50)

where $\Bbbk$ is the coefficient field and ${\mathcal {F}}_{\epsilon , k} = \{\sigma \in X^{(k)} \mid {\hat{r}}(\tau _0) + \epsilon \le {\hat{r}}(\sigma ) \text { and } \sigma \prec _r \omega _0 \}$.

4.1 Another formalization of a stable volume: a special case

For $(n-1)$th PH, we will prove the following second main theorem, which guarantees the validity of the definition.

Theorem 4.1

If X satisfies Condition 1, $\Bbbk ={\mathbb {Z}}/2{\mathbb {Z}}$, and $(\tau _0, \omega _0) \in D_{n-1}({\mathbb {X}}_r)$, $\tilde{\textrm{SV}}_\epsilon (r, \tau _0, \omega _0)$ coincides with $\textrm{SV}_\epsilon (r, \tau _0, \omega _0)$ for $k=n-1$.

Recall the remark associated with Theorem D that $\tilde{\textrm{SV}}_\epsilon (r, \tau _0, \omega _0)$ can be regarded as a subset of $X^{(n)}$.

For $z = \omega _0 + \sum _{\omega \in {\mathcal {F}}_{\epsilon ,n}} \alpha _\omega \omega \in C_n(X; {\mathbb {Z}}/2{\mathbb {Z}})$, we define $V_z$ and $E_z$ as follows.

$$\begin{aligned} \begin{aligned} V_z&= \{ \omega \in {\mathcal {F}}_{\epsilon , n} \mid \alpha _\omega = 1\} \cup \{\omega _0\}, \\ E_z&= \{ \tau \in {\mathcal {F}}_{\epsilon , n-1} \mid \exists \omega \in V_z\ \tau ^* (\partial \omega ) = 1\}. \end{aligned} \end{aligned}$$

(51)

To prove the theorem, we show the following lemma.

Lemma 4.2

If z satisfies (49) and (50), $G_z:= V_z \cup E_z$ is a subgraph of $G_X$ and $G_z$ is a disjoint union of some connected components of $G_X({\hat{r}} \ge {\hat{r}}(\tau _0) + \epsilon )$.

We now assume that z satisfies (49) and (50). To show the above lemma, we show the following three facts, Fact 19, 20, and 21.

Fact 19

For any $\tau \in E_z$, $\tau$ is not a face of $\omega _\infty$.

Proof

Assume $\tau$ is a face of $\omega _\infty$. Then there is a unique n-simplex $\omega _1 \in X^{(n)}$ which is the coface of $\tau$. From the definition of $E_z$ and $\omega _\infty \not \in V_z$, $V_z$ should contain $\omega _1$. However,

$$\begin{aligned} \tau ^*(\partial z) = \tau ^*(\partial (\sum _{\omega \in V_z} \omega )) = \sum _{\omega \in V_z} \tau ^*(\partial \omega ) = \tau ^*(\partial \omega _1) = 1 \not = 0, \end{aligned}$$

(52)

which contradicts (50). $\square$

The following fact guarantees that $G_z$ is a subgraph of $G_X$.

Fact 20

For any $\tau \in E_z$, both cofaces of $\tau$, $\omega _1$ and $\omega _2$, are contained in $V_z$.

Proof

From the definition $E_z$, $V_z$ contains either $\omega _1$ or $\omega _2$ and one of the following holds: $\alpha _{\omega _1}= 1$ or $\alpha _{\omega _1} = 1$. From the condition (50),

$$\begin{aligned} \tau ^*(\partial z) = \sum _{\omega \in {\mathcal {F}}_{\epsilon , n}} \alpha _\omega \tau ^*(\partial ( \omega )) = \alpha _{\omega _1} + \alpha _{\omega _2} = 0. \end{aligned}$$

(53)

Therefore, $\alpha _{\omega _1} = \alpha _{\omega _2} = 1$, which means that both $\omega _1$ and $\omega _2$ are contained in $V_z$. $\square$

Fact 21

For $\omega _1 \in V_X$, $A_{\omega _1}$ denotes the set of all $(n-1)$-dimensional faces of $\omega _1$. If $\omega _1 \in V_z$, then the following holds:

$$\begin{aligned} A_{\omega _1} \cap E_X({\hat{r}} \ge {\hat{r}}(\tau _0) + \epsilon ) = A_{\omega _1} \cap E_z. \end{aligned}$$

(54)

Proof

Since $E_z \subseteq {\mathcal {F}}_{\epsilon , n-1} \subseteq E_X({\hat{r}} \ge {\hat{r}}(\tau _0) + \epsilon )$, $A_{\omega _1} \cap E_X({\hat{r}} \ge {\hat{r}}(\tau _0) + \epsilon ) \supseteq A_{\omega _1} \cap E_z$ is trivial. Therefore, we assume $\tau \in A_{\omega _1} \cap E_X({\hat{r}} \ge {\hat{r}}(\tau _0) + \epsilon )$ and will show $\tau \in A_{\omega _1} \cap E_z$. Since $\tau \prec _r \omega _1$ and $\omega _1 \in V_z \subset {\mathcal {F}}_{\epsilon , n} \cup \{\omega _0\}$, we have $\tau \prec _r \omega _0$. Therefore, $\tau \in {\mathcal {F}}_{\epsilon , n-1}$ since $\tau \in E_X({\hat{r}} \ge {\hat{r}}(\tau _0) + \epsilon )$. We also have $\tau ^*(\partial \omega _1) = 1$ because $\tau \in A_{\omega _1}$ and we conclude $\tau \in E_z$. $\square$

By repeatedly using Fact 21, we can see that any path in $G_X({\hat{r}} \ge {\hat{r}}(\tau _0) + \epsilon )$ starting from $\omega _1 \in V_z$ is also a path in $G_z$. This means that $G_z$ is a disjoint union of some connected components of $G_X({\hat{r}} \ge {\hat{r}}(\tau _0) + \epsilon )$, and Lemma 4.2 is shown.

Lemma 4.3

$z_1 = \sum _{\omega \in K_{\textrm{V}}(G_X({\hat{r}} \ge {\hat{r}}(\tau _0) + \epsilon ), \omega _0) } \omega$ satisfies (49) and (50).

Proof

First, we show (49). The condition (49) is equivalent to the following inclusion relationship:

$$\begin{aligned} K_{\textrm{V}}(G_X({\hat{r}} \ge {\hat{r}}(\tau _0) + \epsilon ), \omega _0) \subset {\mathcal {F}}_{\epsilon , n} \cup \{\omega _0\}. \end{aligned}$$

(55)

Since $G_X({\hat{r}} \ge {\hat{r}}(\tau _0) + \epsilon )$ is a subgraph of $G_X(\succ _{r} \tau _0)$ and $\omega _0$ is $(\succeq _r)$-maximum element in $K(G_X(\succ _{r} \tau _0), \omega _0)$, $\omega \preceq _r \omega _0$ holds for any $\omega \in K_{\textrm{V}}(G_X({\hat{r}} \ge {\hat{r}}(\tau _0) + \epsilon ), \omega _0)$. This equates to (55).

Next we show (50). We can show the following relationship in a similar way to (55).

$$\begin{aligned} K_E(G_X({\hat{r}} \ge {\hat{r}}(\tau _0) + \epsilon ), \omega _0) \subseteq {\mathcal {F}}_{\epsilon , n-1}. \end{aligned}$$

(56)

Let $\tau$ be an element of ${\mathcal {F}}_{\epsilon , n-1}$. We consider the following two cases to show $\tau ^*(\partial z) = 0$.

• 1. $\tau \in K_E(G_X({\hat{r}} \ge {\hat{r}}(\tau _0) + \epsilon ), \omega _0)$. In this case, $K_E(G_X({\hat{r}} \ge {\hat{r}}(\tau _0) + \epsilon ), \omega _0)$ contains both cofaces $\omega _1, \omega _2$ of $\tau$, and

  $$\begin{aligned} \tau ^*(\partial z_1) = \tau ^*(\partial \omega _1) + \tau ^*(\partial \omega _2) = 1 + 1 = 0. \end{aligned}$$

  (57)

• 2. $\tau \in {\mathcal {F}}_{\epsilon , n-1} \backslash K_E(G_X({\hat{r}} \ge {\hat{r}}(\tau _0) + \epsilon ), \omega _0)$. In this case, $K_E(G_X({\hat{r}} \ge {\hat{r}}(\tau _0) + \epsilon ), \omega _0)$ does not contain both cofaces of $\tau$, and $\tau ^*(\partial z_1) = 0$.

In both cases, we have $\tau ^*(\partial z_1) = 0$. $\square$

From Lemma 4.2 and Lemma 4.3, we can show that $z_1$ in Lemma 4.3 is the solution to the optimization problem in Definition 6. This means that $K_{\textrm{V}}(G_X({\hat{r}} \ge {\hat{r}}(\tau _0) + \epsilon ), \omega _0) = \tilde{\textrm{SV}}_{\epsilon }({\hat{r}}, \tau _0, \omega _0)$. From (23), this set is equal to $\textrm{SV}(r, \tau _0, \omega _0)$, which completes the proof of the theorem.

4.2 Another formalization of a stable volume: general case

We can apply Definition 6 to cases other than $k=n-1$. In such cases, we also call the solutions of the optimization problems the stable volumes. In such cases, Theorem 4.1 does not hold in general, and it is difficult to mathematically ensure the good property shown in Theorem 3.1. Empirically, however, the stable volumes often work well. (We examine the property using computer experiments in Sect. 6.)

The reason for this is likely that an optimal volume is often included in a lower-dimensional structure (a submanifold or a lower-dimensional simplicial complex) and the solution of the stable volume is also included in the structure.

4.3 Stable sub-volume

In the previous subsection, we expressed our belief that a lower-dimensional structure may make the stable volume work well. We can develop a variant of stable volume using this idea. If we find such a lower-dimensional structure, we can consider the stable volume constrained on the structure. An optimal volume is one possible lower-dimensional structure. We define a stable sub-volume as follows.

Definition 7

Let r be an order with levels and $(\tau _0, \omega _0) \in D_k({\mathbb {X}}_r)$. The stable sub-volume of $(\tau _0, \omega _0)$ is defined by the solution to the following minimization problem:

$$\begin{aligned} \text {minimize }&\Vert z\Vert _0, \text { subject to } \nonumber \\ z&= \omega _0 + \sum _{\omega \in {\mathcal {F}}_{\epsilon , k+1} \cap \textrm{OV}(r, \tau _0, \omega _0)} \alpha _\omega \omega \in C_{k+1}(X; \Bbbk ), \end{aligned}$$

(58)

$$\begin{aligned} \tau ^*(\partial z)&= 0 \text { for any } \tau \in {\mathcal {F}}_{\epsilon , k}, \end{aligned}$$

(59)

where $\Bbbk$ is the coefficient field and ${\mathcal {F}}_{\epsilon , k} = \{\sigma \in X^{(k)} \mid {\hat{r}}(\tau _0) + \epsilon \le {\hat{r}}(\sigma ) \text { and } \sigma \prec _r \omega _0 \}$.

For stable sub-volumes, the parameter $\epsilon$ is also called a noise bandwidth parameter.

The following proposition holds for the $(n-1)$th PH in ${\mathbb {R}}^n$ since the stable volume is a subset of an optimal volume.

Proposition 4.4

Let X be a simplicial complex embedded in ${\mathbb {R}}^n$ satisfying Condition 1. Let r be an order with levels. For $(\tau _0, \omega _0) \in D_{n-1}({\mathbb {X}}_r)$ and $\epsilon > 0$, the stable volume of $(\tau _0, \omega _0)$ with bandwidth parameter $\epsilon$ coincides with the stable sub-volume of $(\tau _0, \omega _0)$ with bandwidth parameter $\epsilon$.

The advantages and disadvantages of a stable sub-volume will be discussed in Sect. 8.

5 Implementation

In this section, we discuss how to produce a stable volume using a computer.

While we can directly implement stable volumes by persistence trees (Definition 3) using the persistence trees constructed by Algorithm 1, implementing stable volumes as an optimization problem is more difficult. As discussed in (Chen and Freedman 2011; Dey et al. 2019), these kinds of optimization problems are NP-hard in general, which makes them difficult to solve on a computer. To resolve this problem, we can apply the following approximation techniques (Tahbaz-Salehi and Jadbabaie 2008; Escolar and Hiraoka 2016; Obayashi 2018):

• Use ${\mathbb {R}}$ as a coefficient field instead of ${\mathbb {Z}}/2{\mathbb {Z}}$

• Change $\ell ^0$ norm to $\ell ^1$ norm

The second technique is often used in sparse modeling. Following the above approximations, the optimization problem can be formulated as a linear programming problem.

We need to translate the problem into an acceptable form for a linear programming solver. That is, we need to specify the variables, the objective function (the function to be minimized), and the constraints in the following form:

• The objective function should be $(\text{ a } \text{ linear } \text{ combination } \text{ of } \text{ variables}) + (\text{ constant})$

• Each constraint should be $(\text{ a } \text{ linear } \text{ combination } \text{ of } \text{ variables}) + (\text{ constant})\ \text {OP}\ (\text{ another } \text{ constant})$, where $\text {OP}$ is any of the relational operators $=, \ge , \le$

Algorithm 3 shows the algorithm of a stable volume. We can also compute a stable sub-volume using the same algorithm expect that ${\mathcal {F}}_{\epsilon , k+1}$ is replaced by ${\mathcal {F}}_{\epsilon , k+1} \cap \textrm{OV}(r, \tau _0, \omega _0)$. It should be noted that ${\mathbb {R}}$ is used as the coefficient field and that we need to consider the sign of $c_{\omega , \tau }$.

Section 4.2 in (Obayashi 2018) introduced the idea of accelerating the computation of optimal volume using locality. The same idea is applicable to stable volumes.

HomCloud already implements Algorithm 2 and Algorithm 3, and was used for the examples in Sect. 6.

6 Examples

In this section, we give examples of stable volumes and stable sub-volumes. Alpha filtration (Edelsbrunner and Mücke 1994) is used to compute the PDs.

6.1 2D lattice with random defects

Figure 9 shows an example of stable volume. Here, we consider 2D lattice points with defects (Fig. 9a). We prepared 30x30 lattice points in a 2D space. The distance between the two closest vertices is 1. The configuration of the points is perturbed from the complete lattice using random noises sampled from a uniform distribution on $(-0.1, 0.1)^2$, and some points are removed randomly with a probability of 0.5 except for the outermost points.

Fig. 9

An optimal volume and a stable volume for a 2D lattice with defects. a The input pointcloud, b 1st PD, c The optimal volumes of (0.705, 2.091), d The stable volume of the same birth-death pair, e Bandwidth parameter versus the size of stable volume

Figure 9b shows the 1st PD of the points, and Fig. 9c shows the optimal volume of (0.705, 2.091). Figure 9d shows the stable volume of the same birth-death pair with bandwidth parameter $\epsilon = 0.12$. The optimal volume in Fig. 9d seems to surround the holes in the pointcloud more naturally than is the case in Fig. 9c.

We also examined the effect of changing the bandwidth parameter, computing stable volumes for bandwidth parameter $\epsilon = 0.0, 0.01, 0.02, \ldots , 0.40$. Figure 9e shows the graph of the bandwidth parameter versus the size of the stable volumes. The size was measured as the number of simplices in the stable volume.

From the optimal volume ($\epsilon = 0$), the size of the stable volume rapidly decreases. A wide plateau appears at $\epsilon = 0.04$ and is completely flat from $\epsilon = 0.06$ to $\epsilon = 0.27$, meaning that the stable volume is stable to changes in bandwidth parameter over the range [0.06, 0.27]. This suggests that $\epsilon$ should be somewhere within this range. It should be noted that the scale of this range coincides with the scale of the noise. This is consistent with the fact that the bandwidth parameter indicates the strength of the virtual noise.

6.2 Comparison with previous studies

We apply the statistical approach by Bendich et al. (2020) and reconstructed shortest cycles by Ripserer.jl using the same data as in Fig. 9 to compare with our method. The two methods are applied to the same birth-death pair as in the example of Sect. 6.1.

Fig. 10

Result of the statistical approach. Upper two figures: Noise source is the uniform distribution on $[-0.03, 0.03]^2$. Lower two figures: Noise source is the uniform distribution on $[-0.06, 0.06]^2$. The left two figures: The points with frequencies > 70% are marked. The right two figures: The points with frequencies > 90% are marked

Figure 10 shows the results of the statistical approach. The distribution of the noise is the uniform distribution on $[-0.03,0.03]^2$ (left) and $[-0.06,0.06]^2$ (right). In the computation, the optimal volumes are computed 100 times. We put large black dots in the figure to indicate points whose frequencies are more than 70% or 90%. The result is consistent with Fig 9 and has richer information. However, the result looks more difficult to interpret than Fig 9.

Fig. 11

Result of reconstructed shortest cycles. Left: The noise bandwidth parameter is 0.1. Right: The noise bandwidth parameter is 0.3

Figure 11 shows the reconstructed shortest cycles with two noise bandwidth parameters, 0.1 (left) and 0.3 (right). As shown in the figure, the result for 0.3 is consistent with other results, but the result for 0.1 is not consistent. This means that the shortest loop criterion sometimes gives a result inconsistent with the structure of persistent homology. Figure 12 shows the reason for the phenomenon using schematic pictures. The 1st PD for the pointcloud Fig. 12a has two prominent birth-death pairs corresponding to $\ell _1$ and $\ell _2$ in Fig. 12b, but the shortest loop criterion finds the loop $\ell _3$ instead of $\ell _2$ since $\ell _2$ and $\ell _3$ share the two cross-marked points and $\ell _3$ is shorter than $\ell _2$.

Fig. 12

Schematic pictures to explain why the shortest loop criterion sometimes gives a result inconsistent with the structure of persistent homology

In this comparison, we also remark that the meaning of noise bandwidth parameters used in those three methods is different. Therefore a direct comparison of the results with the same parameter is meaningless. We should focus on the changes in the results to the change of noise bandwidth parameters.

6.3 Atomic configuration of amorphous silica

The proposed approach was applied to more realistic data. In this case, we used the atomic configuration of amorphous silica. The data are from ISAACS (Rouxa and Petkova 2010), generated by Reverse Monte Carlo simulations guided by synchrotron X-ray radiation data. The data are available at http://isaacs.sourceforge.net/ex.html.

The PDs were computed from the atomic configuration. Two types of atoms, silicons and oxygens, were mixed in a 1:2 ratio in the data. The atomic type was ignored in this example, and only the positions of the atoms were used. Figure 13 shows the 1st PD.

Fig. 13

1st PD for amorphous silica

The PD has birth-death pairs on the vertical line with $(\text {birth time}) \approx 0.7$. The birth-death pairs on the vertical line correspond to rings formed by the chemical bonds between oxygen and silicon. Oxygen and silicon atoms appear alternatively on these rings. Previous studies (Hiraoka et al. 2016; Onodera et al. 2019) have found that the existence of the vertical line on a PD implies network structures.

Fig. 14

a Optimal volume and stable volume of (0.677, 5.007). The orange ring is the boundary of the optimal volume; the green ring is the boundary of the stable volume. The red and blue points are oxygen atoms and silicon atoms, respectively. b The plot of the bandwidth parameter $\epsilon$ versus the size of stable volumes and stable sub-volumes

Figure 14a shows the boundary of the optimal volume (orange) and the boundary of the stable volume (green) with $\epsilon = 0.2$ of (0.677, 5.007). The red and blue points are oxygen atoms and silicon atoms, respectively. In this case, the stable volume and stable sub-volume are identical. The optimal volume is a large twisted ring, while the stable volume is a simpler ring. Figure 14b shows the $\epsilon$ versus volume plot. The plot indicates that the size of the stable volume quickly decreases from $\epsilon =0$ to $\epsilon =0.1$, meaning that the optimal volume is sensitive to noise. Therefore, we can consider that the stable volume is the essential part of the birth-death pair.

It should be noted that the stable volume with $\epsilon \in [1.1, 1.6]$ on the second plateau is not a reasonable representation of the birth-death pair since only oxygen atoms exist on the boundary of the volume. The large $\epsilon$ causes the removal of the information of the silicon atoms.

Figure 15a shows the optimal volume (orange) of (0.669, 5.053) and the stable volume (green) of the same pair with $\epsilon =0.2$. In this case, the optimal volume and the stable sub-volume are identical. However, the stable volume and sub-volume are not identical since the stable volume is not included in the optimal volume. Figure 15b shows the plot of $\epsilon$ against the volume.

Fig. 15

a Optimal volume and stable volume of (0.669, 5.053). The orange ring is the boundary of the optimal volume; the green ring is the boundary of the stable volume. The red and blue points are oxygen atoms and silicon atoms, respectively. b Plot of the bandwidth parameter $\epsilon$ versus the size of the stable volumes and stable sub-volumes. c Schematic of the optimal volume and the stable volume. The orange area is the optimal volume, the dark orange ring is its boundary, and the green ring is the boundary of the stable volume

In Fig. 15a, the stable volume is tighter than the stable sub-volume. Figure 15c shows the schematic of the optimal volume and the stable volume. The stable volume and sub-volume are different since path Z in the figure is not included in the optimal volume. In our opinion, the stable volume appears superior since it surrounds the tunnel in the pointcloud more tightly. However, we do not have a theoretical guarantee. In general, the stable volume is tighter than the stable sub-volume since the optimization for a stable volume is more aggressive than that for a stable sub-volume.

7 Tuning of noise bandwidth parameter

In applying stable volumes, properly tuning the noise bandwidth parameter $\epsilon$ is essential. The examples shown in the previous section suggest two possible approaches to such tuning:

• The scale of $\epsilon$ should be the same scale as the noise of the data

• A value on the plateau shown in the plot of $\epsilon$ against volume size (Sect. 6.1) should be used

In applying the first approach, we can use the domain knowledge about the data to tune the parameter. Here, the scale of the system noise gives an estimate of the parameter. For example, the scale of thermal fluctuation can be used as the parameter if the data consist of the atomic configuration, and thermal fluctuation is the dominant noise.

To apply the second approach, we need to plot the figure. As noted in Sect. 6.3, when there are multiple plateaus, we need additional criteria to determine which is better.

If we use stable volumes by persistence trees, such a plot is easy to produce. From Definition 3, the size of a stable volume is computable as follows:

$$\begin{aligned} 1 + \sum _{\omega \in C_\epsilon (\tau _0, \omega _0)} (\text {size of }\textrm{dec}(\omega , V, E)). \end{aligned}$$

(60)

We can compute the size of $\textrm{dec}(\omega , V, E)$ by counting all the descendant elements of $\omega$. It is also easy to judge whether $\omega \in C_\epsilon (\tau _0, \omega _0)$ by comparing ${\hat{r}}(\tau _0)$ and ${\hat{r}}(\tau )$ in (16). HomCloud already has this functionality.

When we cannot use stable volumes by persistence trees and we want to plot $\epsilon$ against volume size, a stable sub-volume is more useful than a stable volume.

8 Comparison between stable volumes and stable sub-volumes

The question of whether stable volumes or stable sub-volumes are better requires further discussion. The differences between stable volumes and stable sub-volumes can be described as follows:

• If we want to compute stable volumes or stable sub-volumes using multiple bandwidth parameters, the computation cost of stable sub-volumes is smaller than that of stable volumes. Thus, stable sub-volumes are desirable for constructing $\epsilon$ versus volume plots.

• If the size of the optimal volume is large, a stable volume often gives a more aggressive and likely better result than a stable sub-volume. In other words, a stable sub-volume gives a more conservative result than a stable volume.

The first listed characteristic shows the advantage of using a stable sub-volume, while the second characteristic implies that the choice between stable volumes and stable sub-volumes depends on the problem.

In the author’s opinion, stable sub-volumes are easy to handle in general. However, users should compare both options and make a decision as to which is better for their data.

9 Concluding remarks

We have proposed the concept of stable volumes and stable sub-volumes as a means for identifying good geometric realization of homology generators that, unlike many of the methods proposed in prior research, is robust to noise. The idea of stable volumes and stable sub-volumes is based on optimal volumes by Obayashi (2018).

The statistical approach taken by Bendich et al. (2020) offers another solution to our problem. However, one advantage of stable volumes and stable sub-volumes is that they do not require a large number of repeated computations. Moreover, stable volumes and sub-volumes are easier to visualize than the output of the statistical approach since they give a deterministic rather than a probabilistic description. On the other hand, the advantage of the statistical approach is its flexibility. For 1st PH, we can only apply the statistical approach when we want to minimize the length of a loop rather than minimize the volume. The statistical approach is also applicable to the spatial distribution of points. Another advantage of the statistical approach is that it gives richer probabilistic information than stable volumes and sub-volumes.

Reconstruct shortest cycles in Ripserer.jl by Čufar (2020) offers the other solution. The approach uses the representative of persistent cohomology and the shortest path algorithm. Our proposed method has two advantages over reconstructed shortest cycles. The first is its mathematical background. We prove Theorem 3.1 to show the good property of stable volumes and stable sub-volumes. Reconstruct shortest cycles do not have such mathematical justification. The second is the difference in the scope of the application. Stable volumes and sub-volumes can apply to the PH of any degree; however, reconstructed shortest cycles are only applicable to 1st PH. On the other hand, the advantage of reconstructed shortest cycles is computation efficiency. The algorithm of reconstructed shortest cycles uses the shortest path algorithm and is faster than stable volumes and sub-volumes in general.

Although we used the number of simplices as the volume size in this paper, it is possible to use the real volume by changing the objective function from $\sum _{\omega \in {\mathcal {F}}_{\epsilon , k+1}} |\bar{\alpha }_\omega |$ to $\sum _{\omega \in {\mathcal {F}}_{\epsilon , k+1}} \textrm{vol}(\omega ) |\bar{\alpha }_\omega |$, where $\textrm{vol}(\omega )$ is the volume of the simplex $\omega$. This idea may improve the result.

In this paper, we presented algorithms only for the filtration of a simplicial complex; however, the concept can be easily applied to other filtrations, such as cubical and cell filtrations. The proposed algorithms should be helpful in the study of two-dimensional, three-dimensional, or higher-dimensional digital images.

Some problems raised in Sect. 3.4 are still unresolved. A more reliable mathematical justification for stable volumes other than $(n-1)$th PH is also an open problem. These problems show the limitation of our research and are worth addressing in future research for the further development of homology optimization.

Appendix A: Reconstructed shortest cycles in Ripserer.jl

We illustrate the mechanism of reconstructed shortest cycles in Ripserer.jl using an example.

Figure 16 shows the example filtration, and we consider ${\mathbb {Z}}/2{\mathbb {Z}}$-persistent homology. In this filtration, a homology generator appearing at $X_2$ disappears at $X_7$. That is, (2, 7) is a birth-death pair in the 1st PD. The representative cycle corresponding to the pair is $\sum _{\sigma \in X_2^{(1)}} \sigma$. This representative cycle is the loop appearing at $X_2$.

Now we consider persistent cohomology. The diagram defined by persistent cohomology is identical to the diagram by persistent homology since we use a field as a coefficient, but the representative cocycle is, of course, different. The representative cocycle corresponding to (2, 7) is $\sigma _1^* + \sigma _2^* + \sigma _3^*$.

From the observation of the example, we find that the representative cocycle is the “cut” of the loop. This means that any representative cycle corresponding to the birth-death pair disappears if we remove all 1-simplices in the representative cocycle from the 1-skeleton of $X_7$ as shown in Fig. 17a.

Using this fact, we can compute representative cycles using the shortest path algorithm. Let C be $\{\sigma _1, \sigma _2, \sigma _3\}$, the set of all 1-simplices in the representative cocycle. Now $X_2^{(1)}$ is divided into two parts, one is $X_2^{(1)} \backslash C$ and another is $X_2^{(1)} \cap C = \{\sigma _1\}$. Then we compute the shortest path in $X_4^{(1)} \backslash C$ whose two endpoints are the endpoints of $\sigma _1$. The result is shown in Fig. 17b.

We can extend the idea to compute tighter cycles. We can similarly divide $X_4^{(1)}$ into $X_4^{(1)} \backslash C$ and $X_4 ^{(1)} \cap C = \{\sigma _1, \sigma _2\}$. For each $\sigma \in X_4^{(1)} \cap C$, we compute the shortest path in $X_4^{(1)} \backslash C$ whose two endpoints are the endpoints of $\sigma$. The results are (b) and (c) in Fig. 17, and we choose (c) as the shortest loop in these loops. Using $X_5$ instead of $X_4$, we compute an even tighter loop (d). This is the mechanism of the reconstructed shortest cycles.

Fig. 16

Example filtration for reconstructed shortest cycles

Fig. 17

a Representative cocycle, b Reconstructed shortest cycle for $X_2$ c for $X_4$ d for $X_5$

The algorithm is summarized as follows.

• 1. The 1st PD, $\textrm{PD}_1({\mathbb {X}})$ for a filtration ${\mathbb {X}}: X_1 \subset \cdots \subset X_N$, is computed using persistent cohomology. The representative cocycles are also computed

• 2. We choose a birth-death pair (b, d), and take the corresponding representative cocycle $\sum _{\sigma \in C} \sigma ^*$

• 3. We also choose k between b and d

• 4. For each $\sigma \in X_k^{(1)} \cap C$, we compute the shortest path in $X_k^{(1)} \backslash C$, $P(\sigma )$, whose two endpoints are the endpoints of $\sigma$

• 5. We search the shortest one from $\{P(\sigma )\}_{\sigma \in C}$

The mathematical justification of the algorithm is not yet given, but empirically it works. A deeper analysis of the algorithm is beyond the scope of this paper.