Abstract
Neutron star mergers are the canonical multimessenger events: they have been observed through photons for half a century, gravitational waves since 2017, and are likely to be sources of neutrinos and cosmic rays. Studies of these events enable unique insights into astrophysics, particles in the ultrarelativistic regime, the heavy element enrichment history through cosmic time, cosmology, dense matter, and fundamental physics. Uncovering this science requires vast observational resources, unparalleled coordination, and advancements in theory and simulation, which are constrained by our current understanding of nuclear, atomic, and astroparticle physics. This review begins with a summary of our current knowledge of these events, the expected observational signatures, and estimated detection rates for the next decade. I then present the key observations necessary to advance our understanding of these sources, followed by the broad science this enables. I close with a discussion on the necessary future capabilities to fully utilize these enigmatic sources to understand our universe.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Two Neutron Stars (NSs) from the galaxy NGC 4993 merged, emitting two messengers that traveled together from the age of dinosaurs through the age of civilization. As the messengers neared Sirius the Fermi Space Telescope was launched; after they passed Alpha Centauri the Advanced Gravitational wave (GW) interferometers were turned on for the first time. On August 17th, 2017 the messengers arrived at Earth (Abbott et al. 2017b): the GWs observed as GW170817 (Abbott et al. 2017c) by the Advanced Laser Interferometer Gravitational-Wave Observatory (LIGO; Aasi et al. 2015) and Advanced Virgo (Acernese et al. 2015) and the gamma rays as GRB 170817A (Goldstein et al. 2017b; Savchenko et al. 2017) by Fermi (Meegan et al. 2009) and INTEGRAL (von Kienlin et al. 2003). This joint detection resulted in the greatest follow-up observation campaign in the history of transient astrophysics (Abbott et al. 2017d), which resulted in six independent detections of AT2017gfo (Coulter et al. 2017; Valenti et al. 2017; Tanvir et al. 2017; Lipunov et al. 2017; Soares-Santos et al. 2017; Arcavi et al. 2017), the theoretically predicted radioactively-powered kilonova, whose precise location enabled the identification of “off-axis” afterglow emission (Troja et al. 2017b; Margutti et al. 2017; Haggard et al. 2017) that has been detected until more than two years later.
These discoveries culminated in a suite of papers published only two months after the first detection, with contributions from thousands of astronomers and astrophysicists, ushering in the new era of GW multimessenger astrophysics. For decades, the scientific promise of these sources has been known, and the first event certainly met expectations with, on average, more than three papers written per day over the first two years.
There have been only three convincing multimessenger detections of individual astrophysical sources: neutrinos and photons from the core-collapse supernova SN 1987A (Hirata et al. 1987), gravitational waves and photons from a binary neutron star merger (this event; Abbott et al. 2017d), and likely neutrinos and photons from a flaring blazar (Aartsen et al. 2018). The modern era of time domain, multimessenger astrophysics will hopefully result in multiple detections of multiple source classes with multiple messengers. Binary Neutron Star (BNS) and Neutron Star–Black Hole (NSBH) mergers, collectively referred to here as NS mergers, will be important astrophysical multimessenger sources for the foreseeable future.
Several papers and reviews on the astrophysics of NS mergers have been written, both before and after GW170817. Several papers have been written on science beyond astrophysics enabled by observations of these events. When available, we reference manuscripts that contain more detailed discussions. This review collates and advances this information into a coherent summary, to ensure the information carried by messengers from NS mergers, already long into their journey to Earth, will be captured and utilized to understand our Universe. Our view of these mergers will depend on the ground- and space-based assets available to observe them and our strategies and scientific gains are placed in the context of our current outlook on these future capabilities.
In Sect. 2 we give a broad overview of our current understanding of NS mergers and how we observe them. This section contains rough detection rate predictions through the next decade. In Sect. 3 we discuss the astrophysical inferences on NS mergers that are important for several additional scientific studies and those that are not otherwise discussed. The later science sections are separated into the broad topics: Short gamma-ray bursts and ultrarelativistic jets (Sect. 4), Kilonovae and the origin of heavy elements (Sect. 5), Standard sirens and cosmology (Sect. 6), Dense matter (Sect. 7), and Fundamental physics (Sect. 8). The individual science sections are, as much as possible, self-contained. Based on the science sections, Sect. 9 makes recommendations for future capabilities. This discusses both current and funded missions, and identifies where gaps may occur.
Given the broad scope of this paper, particular attention is given to avoid or carefully define field-specific terminology and to use language that should prevent confusion for readers of various backgrounds. We use the astrophysical definition of “gamma-rays”, referring to all photons with energies \(\gtrsim 100\,\text{keV}\). We will directly state when we are discussing gamma-rays that originate from nuclear processes. We assume, unless otherwise stated, that our general understanding of science is correct, e.g., that BNS mergers and (some) NSBH mergers are the progenitors of most Short Gamma-Ray Bursts (SGRBs) and all kilonovae, or that the relative propagation of gravity and light is zero. We assume a standard \(\varLambda \)CDM cosmology, with \({H}_0=67.4\,\text{km}\,/\text{s}\,/\text{Mpc}\) and \(\varOmega _m=0.315\), from Planck Collaboration (2020). Canonical NSs are those with masses of \(1.4\,M_{\odot }\); canonical Black Holes (BHs) refer to those with masses of \(10\,M_{\odot }\). All rates are reported for a calendar year and refer to the prediction of the true rate (i.e. they do not account for Poisson variation). Variables and constants have their usual definition, e.g., c is the speed of light, G the gravitational constant, M represents masses, etc. Subscript \(\odot \) denote solar units. When referring to stars in a binary, both massive and compact, the heavier star is always referred to as the primary and is denoted by a subscript 1 and the lighter star is referred to as the secondary with a subscript 2, to match convention. Heavy elements here refers to those beyond-iron.
2 Neutron star mergers
NSs are the densest matter in the Universe, with BHs the only known denser object. Binary star systems emit GWs causing them to slowly inspiral as they lose energy. Tightly bound BNS and NSBH systems can lose energy fast enough to merge within the age of the Universe. The merging of the two objects can significantly disrupt the NS, releasing large amounts of matter and energy that can power the observed Electromagnetic (EM) and predicted neutrino signatures.
In Sect. 2.1 we provide a succinct overview of our current understanding of how these systems form, their behavior shortly before, during, and after merger, and potential longer-term signatures. We discuss the intrinsic event rates in Sect. 2.2, followed by subsections on the canonical signals, their individual detection rates, and what we learn from these observations. Interspersed are subsections on the necessary steps for combining information: Sect. 2.5 details the conditions required for robust statistical association, Sect. 2.6 joint detection rates for independent detections, and Sect. 2.7 methods for follow-up searches. Section 2.10 briefly discusses additional signatures that are expected and prospects of detection. We summarize our predicted future detection rates in Sect. 2.11.
2.1 Overview
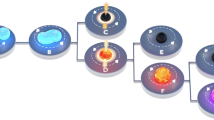
Information on NS mergers can be gleaned from observations of these systems from eons before coalescence to long after merger. This section contains an overview of the lives of these systems; each subsection discusses a stage of their evolution and contains references for further detail. For an in-depth review of the expected EM signatures from NS mergers see the opening figure of Fernández and Metzger (2016), which we borrow as Fig. 1. We do not here give an overview on the history of our understanding of these events as we are unlikely to exceed existing literature; for a brief general history we refer the reader to the introduction of Abbott et al. (2017d).
An overview of the expected GW and EM signatures from minutes before until years after merger, as discussed in Sects. 2.1.2, 2.1.3, 2.1.4 and 2.1.5. The bottom represents what occurs as a function of time with the corresponding observational signature on top. Image reproduced with permission from Fernández and Metzger (2016), copyright by Annual Reviews
2.1.1 System formation
The formation and evolution of stellar systems is a broad topic in astrophysics. We are focused on the science enabled with NS mergers. The events of interest are then BNS and NSBH systems that will form and merge within the age of the Universe. For relevant reviews see Sadowski et al. (2008) and Faber and Rasio (2012). Before discussing how such systems can form, we show the time until merger as a function of orbital separation radius R for two compact objects inspiraling only through GW emission, which is
individual masses \(M_1\) and \(M_2\), and mass ratio \(q=M_2/M_1\). This equation, and others in this section, assume quasi-circular orbits as compact object systems circularize quickly compared to their total inspiral time (Faber and Rasio 2012).
A star with mass between \(\sim 8\) and \(50\,M_{\odot} \) will end as a Core-Collapse Supernova explosion (CCSNe). Stars on the lower end of this mass range will result in a NS and those on the high end will result in a BH (see da Silva Schneider et al. 2020, and references therein for details). Such heavy stars become supergiants near the end of their lives with sizes \(R \gtrsim 30\,R_{\odot }\). When two of these stars form already bound together, as a field binary, they can result in compact object binaries once both have undergone supernova. For canonical BNS systems with initial separations larger than the size of the progenitor supergiant the GW-only inspiral time will be a thousand times the age of the Universe.
For canonical BNS systems to merge within one current age of the Universe, inspiraling only through GW radiation, they must have initial separation of \(\lesssim 5\,R_{\odot} \). This requires a common envelope stage, where either the two massive stars are not distinct or the primary forms a compact object before being enveloped by the secondary during its supergiant phase. This greatly accelerates the inspiral and results in tighter initial separation of the two compact objects.
If the primary compact object is a NS the second is most often also a NS. This likely forms a BNS system, but could form a NSBH system if the primary accretes sufficient mass to collapse into a BH during the common envelope phase. If the primary collapses directly to a BH the system becomes an NSBHFootnote 1 if the secondary is light enough to form a NS, otherwise it is a Binary Black Hole (BBH) system.
The prior discussion focused on what is thought to be the standard formation channel for BNS and NSBH systems whose mergers we can observe. It is also believed that a smaller number of systems can be formed dynamically, where two compact objects form separately but become gravitationally bound when they travel close enough to each other. NSs and BHs in globular clusters will tend to gravitate towards the center due to dynamical friction, leading to both a higher likelihood of dynamical capture and an accelerated inspiral aided by three-body interactions with other objects. This could contribute \(\sim \) 10% of merger events (e.g., Belczynski et al. 2002). There may be rare head-on collisions that would behave quite differently. These are beyond the scope of this paper, but investigations of their relative importance can be studied from the information relevant for Sect. 3.5.
2.1.2 Inspiral
After the BNS or NSBH system is formed, the two compact objects will lose energy to GWs, causing the two compact objects to inspiral towards one another. Long before merger this emission is weak and the orbital evolution is slow. Close to merger time the energy released greatly increases and the orbital evolution accelerates. We discuss these two cases and how we can best observe them separately.
Observations of the inspiral long before merger are best performed using EM observations of galactic BNS systems. An overview of the known galactic BNS systems and their observed parameters is available in Tauris et al. (2017). These BNS systems have inspiral times from \(\sim \) 85 Myr to greater than a Hubble time. There is no known galactic NSBH system.
The discovery of the Hulse-Taylor binary system (Hulse and Taylor 1975) enabled precise measures of the orbital decay of a compact binary system for the first time. Years of careful observation enabled a determination of the properties of the stars and the first proof of GW radiation (Taylor and Weisberg 1982).
These systems spend only a tiny fraction of their lives in the late inspiral phase, which is roughly hours to minutes before merger. We are unlikely to observe a NS system at this phase within the Milky Way, and are thus left to detecting extragalactic events. BNS and NSBH systems beyond the local group will likely be undetectable in photons during the early inspiral stage. Within the last \(\sim \) 100 s before merger it is possible that precursor EM emission could be detectable for some nearby events. The strongest observational evidence is the claim of precursor activity preceding the main episode of prompt SGRB emission (Troja et al. 2010); however, this question remains unsettled. There are theoretical models that predict precursor emission in gamma-rays, X-rays, and radio, with typical luminosities \(\sim 10^{42}\) to \(10^{47}\,\text{erg/s}\). These are discussed in Sects. 2.10 and 4.7.
GW observations of stellar mass compact object inspirals provide a new method to study these systems at this stage. Because of their extremely dense nature, compact binary inspirals are among the strongest sources of GWs. As they approach merger time, where the orbital radius is similar to the size of the NSs themselves, the luminosity of this signal increases and the emitted GW frequency enters the band of the ground-based interferometers. Shortly thereafter the objects enter the merger stage.
2.1.3 Merger
The loss of energy to GW radiation shrinks the orbital separation, increases the orbital frequency (with \(f_{\mathrm{GW}}=2f_{\mathrm{orb}}\) as the dominant GW emission is quadrupolar) and strengthens the GW emission. This frequency evolution results in well-known Compact Binary Coalescence (CBC) chirp signal. The peak GW luminosity approaches \(10^{56}\,\text{erg/s}\) around merger time (e.g., Abbott et al. 2019b; Zappa et al. 2018). In the surrounding \(\sim \) seconds the NS can be so disrupted that it releases matter which can power ultrarelativistic polar jets (Sect. 2.1.4) and mildly relativistic quasi-isotropic outflows (Sect. 2.1.5) that produce the known EM and likely neutrino counterparts.
There are several potential contributions to the matter freed from the NS. We follow the discussions from Margalit and Metzger (2019), Kawaguchi et al. (2020), Metzger (2020). Dynamical ejecta is released within milliseconds of the merger. The deformation of the NS late in the inspiral and efficient angular momentum transport from the remnant can release matter through tidal tails that can become spiral arms, which eject matter predominantly in the equatorial region. Shock-heating occurs at the interface of two NSs, squeezing out matter through quasi-radial oscillations at the interface region, which can dominate the polar region due to the lower densities in this region and solid angle spin effects.
Additional matter is ejected starting after the dynamical timescale and continuing for up to \(\sim \) 10 s after merger and is referred to as post-merger or wind ejecta. Disk winds can occur due to several physical processes. Magnetic fields can drive fast outflows with much of the ejection occurring within the first \(\sim \) 1 s (Siegel and Metzger 2017; Fernández et al. 2018). Longer term ejection after \(\sim \) 1 s can occur when viscous heating and nuclear combination dominate over neutrino cooling (Metzger et al. 2008a, 2009). There can also be significant contributions from a remnant NS which can power neutrino winds, magnetically driven outflows, and even strip material from the surface of the remnant itself (e.g., Dessart et al. 2008; Fernández and Metzger 2016).
The unbound material, or ejecta, is characterized by total mass, average velocity, and electron fraction \(Y_e \equiv n_p/(n_n +n_p)\) where \(n_n\) and \(n_p\) are the number densities for neutrons and protons, respectively. More detailed treatments consider additional behavior, such as the spatial and density distributions. Winds from the central engine can alter these properties, broadening the spatial distributions, accelerating and heating the outflows, providing additional matter, and altering the electron fraction through neutrino irradiation via the charged-current interactions
Given the much larger initial fraction of neutrons to protons, these interactions will drive \(Y_e\) to higher values until equilibrium is achieved. The origin of these thermal neutrinos are from the accretion disk or, when one is present, created in pair interactions near the surface of the remnant NS
We expect enormous variation between NS mergers. BNS and NSBH mergers should be quite different. Each of these can be further divided into sub-classes, which are discussed in detail below. Within these sub-classes we expect additional variety depending on the intrinsic parameters of the system.
NSBH mergers can be split into two classes. The delineation depends on whether \(r_{\mathrm{tidal}}\), the orbital separation at which the NS disrupts, is less than or greater than \(r_{\mathrm{ISCO}}\), the Innermost Stable Circular Orbit (ISCO) of the BH (Foucart 2012; Foucart et al. 2018). For a non-spinning BH \(r_{\mathrm{ISCO}}=6GM/c^2\). The spin of the BH alters this distance, approaching \(r_{\mathrm{ISCO}}=9GM/c^2\) for maximal retrograde spin and approaching the event horizon for maximal prograde spin. The NS disruption occurs when tidal acceleration due to the inspiral exceeds the self-gravity of the NS, and depends on the properties of the NS, including the NS Equation of State (EOS) (Sect. 7.2). Disruption is favored for low mass BHs, for BHs with high prograde spin, and for large NSs. When no disruption occurs we refer to these as Heavy NSBH mergers; when disruption does occur we refer to them as Light NSBH mergers as they have lower mass and should produce bright EM radiation.
-
Heavy NSBH Mergers
Heavy NSBH mergers swallow the NS whole. They will produce significant GW emission during inspiral and coalescence, with BH ringdown frequencies up to \(\sim \) 1–2 kHz (Pannarale et al. 2015). Note the frequencies discussed here are the expected maximum values in a given NS merger type, not the ISCO frequencies. This is likely to be the only observable signal for these events.
-
Light NSBH Mergers
NSBH mergers with tidal disruption can release a sizable fraction of the total NS before it enters the BH. The GW emission from these events is, in general, weaker than the heavy NSBH cases due to the lower mass. They will tend to reach higher frequencies, \(\sim \) 3–4 kHz (Pannarale et al. 2015), owing to the generally smaller BH size.
Light NSBH mergers are more exciting for traditional (that is, EM) and neutrino astronomers. Disruption of the NS releases ejecta in the equatorial plane due to tidal effects. This dynamical ejecta moves outward at \(\sim \) 0.2–0.3c, roughly corresponding to the orbital velocity at \(r_{\mathrm{tidal}}\), and is incredibly neutron-rich with \(Y_e \lesssim 0.1\) (Kiuchi et al. 2015; Foucart et al. 2014). The bound material stretches around the BH into an accretion disk with a total mass up to \(\sim 0.1\,M_{\odot} \). The disk is initially maintained as neutrino cooling dominates other effects, with peak luminosities approaching \(\sim 10^{53}\,\text{erg/s}\) (e.g., Just et al. 2016). The main disk ejection phase can release tens of percent of the total disk mass at \(\sim 0.1c\); while this material initially also has \(Y_e \lesssim 0.1\), neutrino irradiation can significantly raise the electron fraction of polar ejecta due to geometric exposure effects to the disk torus and lower densities in this region (e.g., Fernández et al. 2018).
The structure of NSs is determined by the counterbalance of the combination of degeneracy pressure and nuclear forces against gravity. NSs have a maximum mass, beyond which they will collapse to a BH; however, when there are additional mechanisms supporting the star against gravitational collapse this mass threshold can be temporarily altered. The heaviest NSs that do not immediately collapse to a BH are supported against collapse by internal differential rotation, and are referred to as HyperMassive Neutron Stars (HMNSs; Baumgarte et al. 1999). Slightly lighter NSs can be supported against collapse by uniform rotation, referred to as Supramassive Neutron Stars (SMNSs). NSs that do not require additional support mechanisms are referred to as Stable NSs.
BNS mergers can be broadly split into four possible outcomes. Cases with the heaviest progenitor NSs are expected to promptly collapse to a BH in \(\lesssim 10\,\text{ms}\). Slightly lighter progenitors should result in a short-lived HMNS remnant with typical lifetimes of \(\lesssim 1\,\text{s}\) due to efficient energy losses to internal torques (Shibata and Taniguchi 2006; Sekiguchi et al. 2011). At lower masses the remnant object can survive as a SMNS with inefficient energy losses through magnetic dipole and quadrupolar GW radiation. Shortly after merger the (meta)stable NS is expected to have strong magnetic fields, which results in lifetimes as short as hundreds or thousands of seconds (Ravi and Lasky 2014). Finally, it may be possible for two low-mass progenitor NSs to combine into a Stable NS. We separate the following paragraphs to discuss our current understanding of these events from the most to least massive cases. Here the Stable NS and SMNS cases are combined as their lifetimes greatly exceed the merger and ejecta timescales, making these events very similar at this stage.
-
Prompt Collapse
With sufficiently heavy NSs the system will collapse to a BH within milliseconds. These will be the loudest BNS mergers during inspiral due to their higher masses. In this case the GW frequencies reach \(\sim \) 6–7 kHz (e.g., Shibata and Taniguchi 2006; Clark et al. 2014), the highest achieved for any NS mergers. The inspiral is followed by BH ringdown, which has much weaker GW emission.
Near merger, angular momentum transport stretches the NSs, forming tidal tails in the equatorial plane. Equal-mass binaries have been show to release dynamical ejecta with a low electron fraction \(Y_e \lesssim 0.1\) with mass \(10^{-4}\)–\(10^{-3}\,M_{\odot} \) and outwards velocity \(\sim 0.3c\) (Hotokezaka et al. 2013; Just et al. 2015). Asymmetric mass ratios have been shown to achieve \(5\times 10^-3\,M_{\odot} \) (Kiuchi et al. 2019). This is far lower total ejecta than the Light NSBH merger case as NSs are larger than similar mass BHs. The other main dynamical ejecta mechanism in BNS mergers is negligible for this case as it is immediately swallowed by BH formation.
The tidal tails stretch until they form an accretion disk which can range from \(10^{-4}-10^{-2}\,M_{\odot} \), depending on the NS EOS (e.g., Shibata and Taniguchi 2006; Hotokezaka et al. 2013; Just et al. 2015; Ruiz and Shapiro 2017). Magnetically-driven outflows and thermally-driven winds can both release up to 20% of the disk mass.
-
Hypermassive Neutron Star Remnant
BNS mergers that result in HMNS remnants will have similar inspirals as the prompt collapse case, though a bit quieter. During the HMNS phase the internal differential rotation releases GWs about as loud as the peak emission at coalescence, which occurs at \(\sim \) 2–4 kHz (Zhuge et al. 1994; Shibata and Uryū 2000; Hotokezaka et al. 2013; Maione et al. 2017). When the HMNS collapses there is BH ringdown emission.
The tidal ejecta for these mergers (Hotokezaka et al. 2013; Bauswein et al. 2013b) behave differently than the previously discussed cases. For disks around a BH the material accretes in the equatorial region. For a NS remnant the presence of a hard surface causes the in-falling matter to envelope the surface, resulting in additional material in the polar regions (Metzger and Fernández 2014). The unbound tidal ejecta for BNS mergers with a HMNS remnant will expand outwards at \(\sim 0.15{-}0.25c\). These are also the heaviest mergers that will have significant dynamical ejecta from the shock interface between the two NSs; this ejecta will dominate in the polar regions due to solid angle effects and the lower densities in this region. If the HMNS lives for \(\gtrsim \)50 ms the neutrino luminosity can strip \(\sim 10^{-3}\,M_{\odot} \) of material from the surface of the remnant itself (Dessart et al. 2008; Fernández and Metzger 2016).
During these ejection processes the HMNS has formed and is of sufficient temperature (few MeV) to produce significant amounts of \(e^+e^-\) pairs at its surface. The total MeV neutrino emission can be \(10^{53}\,\text{erg/s}\) with contributions from both the disk and the temporary NS (e.g., Sekiguchi et al. 2011). The tidal tail ejecta is sufficiently massive, dense, and distant that its electron fraction is largely unchanged (\(Y_e \approx 0.1{-}0.2\)). However, the polar material is closer, has lower densities, and a greater geometric exposure to the disk allowing the combined neutrino irradiation to significantly alter the electron fraction of the dynamical material in this region (\(Y_e \approx 0.3{-}0.4\); Wanajo et al. 2014).
Given the larger amount of disruption and the lower overall velocity of the disrupted material, HMNS remnants have larger disk masses than the prompt collapse case. The HMNS collapses in under a second during the disk wind phase. So long as the HMNS lives, the neutrino luminosities will cause an increase in the amount of ejected material and monotonically increase the electron fraction. From Metzger and Fernández (2014), the amount of disk wind ejecta can exceed the dynamical ejecta; if the HMNS lives for 100 (300) ms the effects of the HMNS can eject up to \(\sim \) 10% (\(\sim \) 30%) of the total disk mass into the equatorial region and \(\sim \) 5% (\(\sim \) 10%) into the polar region. For disk wind ejecta the equatorial material will be distributed between \(Y_e \approx 0.1{-}0.5\) and the polar material will be \(Y_e \gtrsim 0.3\), and move outwards at up to \(\sim 0.1c\).
The combination of the dynamical and post-merger ejecta and their alteration due to the HMNS surface and winds summarizes into a reasonably simple picture. The dynamical ejecta leaves first being lanthanide-rich in the equatorial region and relatively lanthanide-free in the polar region, with a roughly comparable contribution from each component. Behind this is the ejecta from the disk winds which follows a similar spatial distribution of lanthanide-fraction. This combines to the representative Fig. 7 of Metzger (2020) and our similar representation in Fig. 9.
-
Stable and Supramassive Neutron Star Remnants
SMNS remnants survive for (e.g., Ravi and Lasky 2014) longer than the ejection phase, meaning they are quite similar to Stable NS remnants during merger and ejection. The GW emission is similar to the HMNS case; the emission is slightly weaker during inspiral, they transition to significant GW release to internal differential rotation, but would be followed by secular GW radiation (e.g., Foucart et al. 2016) at twice their rotational frequencies for some time. The longevity of this last phase of GW emission is not well constrained, but when the SMNS collapses there will be weak BH ringdown emission. The neutrino flux is similar to the HMNS case, but would be significantly greater total irradiation as the cooling time for the full NS is longer than the lifetime of HMNSs.
The initial ejecta is similar to the HMNS case, but the longer life of the NS provides additional ejecta and wind to the system. This results in greater total ejecta material moving at somewhat larger velocities and the polar dynamical and disk wind ejecta achieving electron fractions approaching the equilibrium value (e.g., Sekiguchi et al. 2011).
The neutrino heating likely causes ejection of the majority of the total disk mass (Metzger and Fernández 2014). These systems can potentially approach an ejection up to \(0.1\,M_{\odot} \) (e.g., Coughlin et al. 2018; Margalit and Metzger 2019), with the disk wind ejecta dominating over dynamical ejecta, though large uncertainty remains. Stripping of material from the NS surface due to the neutrino-driven wind from the hot NS remnant can be more important here than in the HMNS case (e.g., Dessart et al. 2008).
Lastly, the spin-down energy from these remnants should provide massive continued energy injection into the system. This is reviewed in detail in Metzger (2020).
Our understanding of what occurs during BNS and NSBH mergers comes from detailed simulations accounting for several incredibly complicated, coupled, non-linear effects. Despite the lengthy description in the preceding paragraphs, we have omitted several in-depth investigations into the effects of varying individual parameters, such as eccentricity, mass ratio, total mass, spins, the NS EOS, etc. The outcome of these variations is not immediately obvious. For a thorough review of these effects we refer to Fernández and Metzger (2016) and Metzger (2020). The large uncertainty range in the previously described parameters includes both the intrinsic effects of variation of these parameters and differences in the simulations, which vary their approximations.
However, some general effects are robust. For NSBH mergers there is larger mass ejection for lower mass BHs with higher values of spin. For BNS mergers there is a positive correlation for the total ejecta mass and electron fraction with the lifetime of the NS. Combining information from population synthesis models, numerical modeling, and the current constraints on the maximum mass of a NS we generally expect to eventually observe all of these cases. The exception might be a BNS merger with a Stable NS, which may or may not be possible, depending on if the lightest NSs are less than half the maximum NS mass (Sect. 7.1).
2.1.4 Jets
The disrupted but still bound material accretes onto the remnant object. In at least some cases, this produces a highly collimated, ultrarelativistic jet that results in a SGRB, as confirmed with GW170817 and GRB 170817A. As much of this process is still poorly understood we here pull the phenomenological arguments from Fernández and Metzger (2016).
These jets have enormous kinetic energies and produce some of the most luminous EM events in existence, with each approaching \(10^{50}\,\text{erg}\) (Fong et al. 2015). These are powered by the accretion disks (Oechslin and Janka 2006), with \(10^{-4}\)–\(0.3\,M_{\odot} \) available according to simulations (the range includes extreme conditions but neglects heavy NSBH mergers with no released matter). The pure conversion of a typical value of \(0.1\,M_{\odot} \) into energy gives \(0.1\,M_{\odot} c^2 \approx 10^{53}\,\text{erg}\), which is sufficient to power a SGRB with reasonable overall efficiencies.
How this energy reservoir is converted into the jet is somewhat unsettled (Sect. 4.3). However, it is agreed that an enormous amount of energy, predominantly from the accreting matter, is deposited in the relatively empty polar regions near the surface of the compact object, which launches an ultrarelativistic fireball away from the central engine. This outflow is collimated into a jet by the material encroaching on the polar region, e.g., the thick accretion disk (or torus) and by the magnetic fields emanating from the system. The emission from the collimated ultrarelativistic jet is only detectable for observers within the jet opening angle, \(\theta _j\), due to Doppler beaming limiting the visibility region to \(1/\varGamma \), where \(\varGamma \) is the bulk Lorentz factor with typical value \(\sim 100\). The statements here are detailed and referenced in Sect. 4.
If there is significant baryonic matter in this region it is expected to sap the available energy and prevent jet launch (Sect. 4.2). If a jet launches and there is ejecta above the launch site in the polar region the jet must propagate through to successfully break-out; otherwise it could, in principle, be choked. The collimation and the jet interaction with polar material imparts structure onto the jet itself (Sect. 4.4).
For jets that successfully break-out they move outwards at nearly c. At \(\sim 10^{12}\)–\(10^{13}\,\text{cm}\) the jet reaches the photospheric radius where light can escape for the first time (Beloborodov and Mészáros 2017). At around the same distance the jet may release the prompt SGRB emission due to the occurrence of internal shocks (though there are alternative models with much higher distances, see Sect. 4.6). The emission is characterized by a total duration of \(\sim 0.01{-}5\,\text{s}\) predominantly in the \(\sim 10\,\text{keV}\) to \(\sim 10\,\text{MeV}\), with peak isotropic luminosities \(\sim 10^{51}\,\text{erg}\,/\text{s}\) (e.g., von Kienlin et al. 2020; Abbott et al. 2017b).
After the prompt SGRB, the ultrarelativistic jet continues to speed away from the central engine, with a total kinetic energy \(\sim 10^{50}\,\text{erg}\), and interacts with the surrounding circumburst material with typical densities \(\sim 10^{-4}\)–\(0.1\,\text{cm}^{-3}\) (Fong et al. 2015). As the jet interacts its bulk Lorentz factor slows, the observable angle grows, and it emits synchrotron radiation across nearly the entire EM spectrum, which has been detected from radio to GeV energies (e.g., Ackermann et al. 2010; Fong et al. 2015). This emission is referred to as Gamma-ray burst (GRB) afterglow.
In Sect. 4.7 we discuss other high energy signatures potentially related to the ultrarelativistic jet. For now it is sufficient to note that observations strongly suggest late-time energy injection into the system from the central engine, which likely has implications for other observable signatures.
2.1.5 Quasi-isotropic outflows
The unbound matter from the system evolves far differently than the bound material that powers the ultrarelativistic jet. This ejecta is neutron-rich, contains roughly \(\sim 10^{-3}\)–\(10^{-1}\,M_{\odot} \), and moves outward at a \(\sim 0.1{-}0.3 c\). The rest of this section borrows heavily from Metzger and Fernández (2014), Metzger et al. (2014), Fernández and Metzger (2016), Tanaka (2016) and Metzger (2020). The merger process significantly raises the temperature of the NS(s). As the ejecta expands and releases energy as thermal neutrinos it rapidly cools, entering relatively slow homologous expansion in only \(\sim 10\)–\(100\,\text{ms}\).
At \(\lesssim 10^{10}\,/\text{K}\) free nuclei combine into \(\alpha \) particles. At \(\lesssim 5 \times 10^{9}\,/\text{K}\) the \(\alpha \)-process forms seed nuclei with \(A \sim 90{-}120\) and \(Z \sim 35\) (Woosley and Hoffman 1992). The neutron-to-seed ratio results in rapid neutron captures at rates exceeding the \(\beta \) decay of the seeds, rapidly synthesizing the heaviest elements. This is the so-called r-process, responsible for half the heavy elements (here meaning beyond iron) in the universe. This continues until the nuclei reach \(A \gtrsim 250\) where fission splits the atoms in two, which are subsequently pushed to higher atomic mass in a process referred to as fission recycling. This generically returns peaks near the closed shell numbers \(A = 82, 130, 196\), observed in the solar system elemental abundances. A few seconds have passed.
The heavy nuclei are undergoing heavy radioactive decay, producing copious amounts of neutrinos (\(\sim 0.1{-}10\,\text{MeV}\)), nuclear gamma-rays (dozens of keV to a few MeV), and elements that approach the line of stability over time (e.g., Hotokezaka et al. 2016b). At early times the overwhelming majority of released energy escapes as neutrinos because the ejecta material is dense and opaque for photons (see Fig. 4, discussion, and references in Metzger 2020). In base kilonova models, the earliest photons that can escape are the nuclear gamma-rays, beginning on the order of a few hours. Neutrinos escape with \(\sim \) 30–40% of the energy; gamma-rays carry 20–50% of the total energy. This significantly lowers the remaining energy in the system before it reaches peak luminosity (e.g., Barnes et al. 2016; Hotokezaka et al. 2016b).
The main frequency range of interested for EM observations of kilonova is Ultraviolet, Optical, and Infrared (UVOIR). The opacity in this energy range is driven by atomic transitions of bound electrons to another bound energy state. The open f shell for lanthanides (\(Z = 58-72\)) have angular momentum quantum number of \(l=3\), with the number of valence electron states \(g=2(2l+1)=14\), where n electrons can be setup in \(C = g!/n!(g-n)!\) possible configurations, with bound-bound transitions scaling as \(C^2\), resulting in millions of transition lines in the UVOIR range. As the ejecta is expanding with a significant velocity gradient (e.g., Bauswein et al. 2013b) all of these lines are Doppler broadened. This blankets the entire range, preventing this light from escaping at early times.
As time continues the ejecta loses energy to neutrinos and gamma-rays, cools as it expands, the radioactive heating rate slows, and it transitions to lower densities until eventually the UVOIR photons can escape, resulting in a quasi-thermal transient known as a kilonova. The energy deposition rate of most forms of radioactivity of interest here decay as a power law with index \(-1.1\) to \(-1.4\) (see][and references therein]metzger2020kilonovae. In the hours to days post-merger this maintains high temperatures in the ejecta, with values \(\sim 10^4{-}10^3\,/\text{K}\). Ejecta with relatively high initial electron fraction \(Y_e \gtrsim 0.3\) will produce mostly lanthanide-free material which will result in a blue kilonova with peak luminosity on the \(\sim \) 1 day timescale (e.g., Metzger et al. 2010). Ejecta with low electron fraction \(Y_e \lesssim 0.3\) will produce lanthanide-rich material (and potentially actinides) that will produce a red kilonova with a peak luminosity timescale of \(\sim \) 1 week (e.g., Barnes and Kasen 2013).
The prior paragraphs in this section discuss the base-kilonova model, but there may be significant additional signals or alteration of these observables from the quasi-isotropic outflows. These include the radioactive decay of neutrons that are not captured into nuclei, the effects of jet interactions on the previously ejected polar material, and late-time energy injection from the central engine. These are summarized in Sect. 3.4, which references detailed works covering each.
2.1.6 Aftermath
After the energy ejection ends and the kilonova cools and fades, the quasi-isotropic ejecta will continue moving outwards. Over the next few months and years the event will transition to the nebular phase. Once it reaches the deceleration radius, where it has swept up a comparable amount of mass from the surrounding environment, the ejecta will transition to a Sedov–Taylor blast wave that releases synchrotron radiation in the radio bands (Nakar and Piran 2011; Piran et al. 2013; Hotokezaka and Piran 2015), analogously described as a kilonova afterglow.
Over decades, centuries, and millennia it forms a Kilonova remnant (KNR). These are bound by a shock wave at the interaction of the merger ejecta and surrounding material, providing a transition edge. They may be similar to supernova remnants but have lower total kinetic energies and will tend to occur in regions with lower surrounding material (due to occurring outside of their host galaxies). Even long after merger they will be radioactive, with emission dominated by isotopes with half-lives of similar order to the age of the remnant (Wu et al. 2019; Korobkin et al. 2020). Longer still, the kinetic energy will eventually be used up and the shock-front will dissipate. Ejecta that is bound to the host galaxy will eventually return and become part of the diffuse galactic material where long-term mixing distributes the heaviest elements throughout the galaxy (Wu et al. 2019). Some will eventually join new planets and stars, and a bit may eventually be dug out of the ground by advanced life. Heavy elements unbound from the host galaxy will be lonely for a reasonable part of eternity.
2.2 Intrinsic event rates
The rates of compact object mergers is of interest to several fields. The true value sets how quickly we can achieve specific scientific outcomes, and will determine the necessary devotion of observational resources and prioritization on telescopes with shared time. Estimates have arisen through several means with predicted rates spanning several orders of magnitude. The most direct measurement comes from GW observations, calculated from a detection number in a known spacetime volume. These are the basis for our assumed rates, and the large existing uncertainty should rapidly shrink in the next few years. The local volumetric rates assumed in this paper are explained below and summarized in Table 1.
The latest reported local volumetric rate measurements from LIGO/Virgo come from the discovery paper in GW190425, the second GW-detected BNS merger (Abbott et al. 2020a). The full 90% range reported for BNS mergers is 250–2810 \(\text{Gpc}^{-3}\,\text{yr}^{-1}\). This value is the union of two measurements, one considering a uniform mass prior between 1 and \(2\,M_{\odot} \) for each NS in a BNS merger and the second adding the sum of the rates of events like GW170817 to those like GW190425. The median value is approximately \(1000\,\text{Gpc}^{-3}\,\text{yr}^{-1}\). Following the initial release of this paper, which occurred before the publication on GW190425, and to enable for ease of scaling as these reported rates are updated, we chose to use the BNS local volumetric rate of \(R=1000_{-800}^{+2000}\) (200–3000) \(\text{Gpc}^{-3}\,\text{yr}^{-1}\).
The rates of NSBH mergers are known with less precision. Abbott et al. (2019b) bound the local upper limit of NSBH mergers as a function of BH mass. Since we do not know the distribution of BH mass in NSBH merger systems we take the least constraining value of \(<610\,\text{Gpc}^{-3}\,\text{yr}^{-1}\), which is for \(M_{\mathrm{BH}}=5\,M_{\odot} \). The lower and mid-range value come from the merger rates expectations paper prior to the initialization of Advanced LIGO (Abadie et al. 2010), where the high rate is similar to the constraints reported above.
The LIGO Scientific Collaboration and Virgo Collaboration (LVC) has also reported the discovery of a CBC with a high mass ratio, GW190814 (Abbott et al. 2020c). Owing to the strength of the signal and the large mass asymmetry this allowed for a precise determination of the individual masses, with the secondary being between 2.50 and \(2.67\,M_{\odot} \). This is potentially the first NSBH merger identified, but is more likely to be a BBH merger. We do not inform our NSBH rates with this event. We may expect a directly measured value once a GW-detected event is unambiguously classified as an NSBH merger.
For comparison, we report the inferred volumetric local BBH merger rates with a mass function that is self-consistent with the observed BBH mergers from O1 and O2 (Abbott et al. 2019a). This gives a range of 24.4–111.7 \(\text{Gpc}^{-3}\,\text{yr}^{-1}\) with a central value of 54.4 \(\text{Gpc}^{-3}\,\text{yr}^{-1}\). This has a factor of four uncertainty. This range is far narrower due to the larger number of detected BBH system. As the number of detected NS mergers increases the precision of the local rates measure will similarly improve.
The rates of NS mergers vary through cosmic time. Under the standard formation channel, it should track the stellar formation rate modulo their inspiral times. The peak rate of SGRBs occurred at a redshift of \(\sim 0.5{-}0.8\) (e.g., Berger et al. 2013) before declining to the current rate. This is a useful proxy to estimate the largest average inspiral range due to the Malmquist bias in detecting SGRBs. The furthest known SGRBs occurred at a redshift of \(>2\) and few are expected beyond a redshift of \(\sim \) 5. We do not explicitly account for intrinsic source evolution for our detection rates in this manuscript. The rates of NS mergers do not evolve significantly over the distances we can detect these events through GWs, neutrinos, or as kilonovae for at least a decade. Source evolution does matter for SGRB observations, both prompt and afterglow, but our rates for those events are determined from empirical observations and thus source evolution is accounted for intrinsically.
We lastly close with the rates of rare events that may provide unique understanding of these mergers. Particularly nearby events will be able to be characterized to vastly greater detail; as such, we report the nearest event we may expect on fiducial timescales. Assuming the usual number density of Milky Way (MW)-like galaxies of \(\sim 0.01\,\text{Mpc}^{-3}\) (e.g., Hotokezaka et al. 2018), we show the rates per Milky Way-like galaxy per million years, and how many millennia we may expect between events in the Milky Way itself.
From Table 1 we can draw a few immediate conclusions. BNS mergers are locally more common than BBH mergers and likely more common than NSBH mergers. We may expect a BNS merger to occur within \(\sim \) 30 Mpc about once a decade. Events within \(\sim \) 20 Mpc are rare, occurring about as often as an average human lifetime. We should expect a BNS merger in the Milky Way about every 10 millennia.
Strongly lensed events are prize astrophysical occurrences. They provide both complementary and unique tests in cosmology (Refsdal 1964; Linder 2011; Blandford and Narayan 1992) and fundamental physics (Biesiada and Piórkowska 2009; Collett and Bacon 2017; Minazzoli 2019), and unique studies of transient events (e.g., Goobar et al. 2017; Perna and Keeton 2009). The detection and successful identification of a strongly lensed NS merger would be momentous, which is discussed in more detail in Sect. 6.2 and a few subsections of Sect. 8. The intrinsic rates of strongly lensed NS mergers are likely to be low but likely non-zero (e.g., Biesiada et al. 2014, after accounting for new rates estimates). These rates could be increased in the future by targeted known strongly lensed systems (see Collett 2015, for these prospects), analogous to the current galaxy targeting approach EM follow-up to GW-detected NS mergers.
2.3 Gravitational waves
GWs are detected by measuring their effect on spacetime itself as the strain \(h = \varDelta L/L\) where \(\varDelta L\) is the fractional change of length L (Abbott et al. 2009). At the reasonably nearby distance of \(\sim \) 100 Mpc (Sect. 2.2) the strain at Earth for a canonical BNS merger is \(\sim 10^{-21}\). Detection then requires the most sensitive ruler ever built. Weak GWs can be described by the ordinary plane wave solution. In General Relativity (GR) GWs have only two independent polarization modes (Will 2014). They can be distinguished by a \(\pi /4\) rotation in the plane perpendicular to the direction of motion, which, by convention, are referred to as the plus and cross polarization modes. The strain h from these modes are \(h_+\) and \(h_{\times} \), respectively.
Following Schutz (2011), the antenna response function can be written in terms of the two GR polarization modes as
where \(\theta \) and \(\phi \) are spherical coordinates relative to detector normal, and \(\psi \) the polarization angle for the merger relative to this same coordinate system. \(F_+\) and \(F_{\times} \) are the interferometer response to the two polarization modes
The antenna power pattern, which the Signal-to-Noise Ratio (SNR) is proportional to, is
GW emission is omnidirectional but not isotropic. For CBCs we can define the radiated power as a function of inclination angle \(\iota \), which goes from 0 to 180 because orientation matters for GW observations (as opposed to the 0 to 90 convention used for most EM observations). This relation can be represented as as \(F_{\mathrm{rad}}\), referred to as the binary radiation pattern, and is defined as
It is equivalent to the \(\phi \)-average of the interferometer antenna pattern. It is strongest along the total angular momentum axis (\(\iota = 0, 180\)) and weakest in the orbital plane (\(\iota = 90\)).
The sensitivity of individual ground-based interferometers is usually quoted in terms of detection distances for canonical BNS mergers (e.g., Abbott et al. 2018a). The detection horizon is the maximum detection distance, which occurs for face-on events (\(\iota \approx \)0 or 180, where the rotation axis is oriented towards Earth) that are directly overhead (or under). Converting the total sensitive volume to a spherical equivalent gives a radius referred to as the detection range, which is the usual figure of merit for (single) ground-based interferometer sensitivity. The horizon is 2.26 times the range (e.g., Abadie et al. 2012b).
NS mergers are identified in GW strain data through CBC searches, where CBC refers to BNS, NSBH, and BBH mergers for ground-based interferometers, which are found by looking for signals that match waveforms from a template bank of GW inspirals (e.g., Usman et al. 2016; Messick et al. 2017). Because the signals of interest are so weak and background noise is significant, a GW detection generally requires two or more interferometers to jointly trigger on an event. The interferometers are separated by thousands of kilometers, which results in generally uncorrelated background, giving a massive increase in search sensitivity. Signal significance has historically been quantified through the use of a False Alarm Rate (FAR), measuring how often an event with a given value of the ranking statistic occurs in background (e.g., Abbott et al. 2016a, b, 2017c). Recently, the development of \(P_{\mathrm{astro}}\), the probability that an event is astrophysical in origin, has provided additional information, conveying the chance a given event has an astrophysical origin based on an assumed volumetric event rate against the rate of detector noise in that region of parameter space. This is a more powerful method that should result in increased detection rates, but its effect on detection rates has not been quantified.
Interferometers directly measure amplitude, which falls as 1/d (e.g., Aasi et al. 2015), rather than the typical \(1/d^2\) for most astrophysical instruments. That is, an increase in sensitivity gives a cubic increase in detection rates, rather than the typical 3/2. For signal-dominated events this corresponds to a cubic increase in detection rates.
Through kilometer-scale modified Michelson interferometers the direct detection of GWs has recently been achieved (Abbott et al. 2016b). We first discuss the US-based observatories. The current design sensitivity of the Advanced LIGO interferometers is expected to achieve a BNS range of 175 Mpc (Barsotti et al. 2018) by \(\sim \) 2020.Footnote 2 The NSF has funded the Advanced LIGO+ upgrade which has a target BNS range of 330 Mpc (Zucker et al. 2016).
Beyond A+, there are proposed concepts. The LIGO Voyager upgrade would push the existing interferometers close to their theoretical maximum sensitivity, and we use a representative BNS range of 1 Gpc (McClelland et al. 2014). Lastly, third generation interferometers (e.g., Abbott et al. 2017a; Punturo et al. 2010) will detect these events throughout the universe. Converting from values in Reitze et al. (2019), the early stage Cosmic Explorer (\(\sim \) 2035) would have a BNS range of \(\sim \) 12 Gpc and the late-stage version (\(\sim \) 2045) \(\sim \) 60 Gpc. We take \(\sim \) 10 Gpc as a representative value.
The LIGO interferometers are only part of the ground-based GW detection network. The active GW detectors are the two Advanced LIGO interferometers and the Advanced Virgo (Acernese et al. 2015) interferometer. LIGO and Virgo work together as the LVC. They are to be joined by the Kamioka Gravitational Wave Detector (KAGRA) interferometer (Aso et al. 2013) in late 2019 and eventually by LIGO-India which would enter at the A+ version (Iyer et al. 2011). These interferometer sites are generally referred to by letters, H for LIGO-Hanford, L for LIGO-Livingston, V for Virgo, K for KAGRA, and I for LIGO-India. A summary of the currently expected ground-based GW network sensitivity and planned observing runs through \(\sim \) 2026 is shown in Fig. 2. The plan updates will be available online.Footnote 3
In Table 2 we report reasonable and conservative detection rates for NS mergers for the four representative sensitivities. Our base estimate accounts for only two, coaligned interferometers, equivalent to the HL configuration for at least the next decade. This enables easy calculation of a particularly conservative estimate. We also provide a broader network estimate as a function of time based on the network figures of merit in Schutz (2011, which are not directly comparable given the differing interferometer sensitivities) and simulations in Abbott et al. (2016c). All estimates assume individual interferometer livetime fractions of 70%, corresponding to 50% livetime for the HL(-like) configuration(s).
The Advanced and A+ rates are calculated with the intrinsic rates from Table 2 and their sensitivity volume. Source evolution at these distances are unimportant and neglected. The NSBH rates assume they are detected \(\sim \) 2 times further, corresponding to a reasonably light BH (giving conservative estimates) which should produce EM emission. The Voyager and Gen 3 rates assumes no source evolution, which is a conservative estimate. The Gen 3 rates further only consider events within a redshift of 0.5, providing a very conservative limit. These ranges are 90% confidence, giving lower limits at 95% confidence.
Beyond just detecting them, characterization of NS mergers is an additional priority for design requirements. The high end frequency is set by the wish to directly observe the merger events themselves. From Sect. 2.1.3 the highest expected maximum frequency is for the BNS prompt collapse case reaching \(\sim \) 6–7 kHz. Sufficiently capturing this range should also enable sensitive searches for NS modes above the primary frequency in the BNS (meta)stable remnant cases (see Ackley et al. 2020, and references therein).
Pushing to lower frequencies has a number of benefits, such as providing vastly improved parameter estimation precision due to a far greater SNR for a given event. A canonical BNS (NSBH) merger emitting GWs at 0.1 Hz will merge in about a decade (a year) (e.g., Graham et al. 2017). For NS mergers that will merge within an instrument lifetime this provides a reasonable lower frequency goal. This range is also ideal for the best-case GW localizations, as we will show. Thus, absent funding or technical considerations, the best range to study these events is \(\sim 0.1\) to \(\sim \) 10 kHz. The rough frequency range for the four ground-based GW interferometer sensitivity examples is given in Table 2. For the next decade we are largely limited to the \(\sim \) 10–1000 Hz regime. Achieving higher frequencies may be possible, but pushing lower than 5 Hz on the ground is nearly impossible.
Generic GW observations of CBCs measure more than a dozen parameters. The extrinsic system parameters include the location (\(\theta \), \(\phi \), and the luminosity distance \(d_L\)), inclination (\(\iota \)), polarization angle (\(\psi \)), eccentricity (e), coalescence phase (\(\phi _0\)), and merger time \(t_{\mathrm{GW}}\). The intrinsic parameters include the mass and spin components of each pre-merger object (\(m_1\), \(m_2\); \(\overrightarrow{S}_1\), \(\overrightarrow{S_2}\)). Most of these parameters have strong correlations (often referred to as degeneracies). One example is the amplitude dependence on both \(\iota \) and \(d_L\), contributing to greater uncertainty on both measures (Schutz 2002). For NS mergers matter effects accelerate the late inspiral which can be captured into the tidal deformability parameter (\(\varLambda \)).
Eccentricity is generally expected to be zero for these systems, as circularization happens on a shorter interval than the expected inspiral time to merger (Peters and Mathews 1963; Faber and Rasio 2012). The polarization can be constrained for events detected by interferometers that are not coaligned, based on the SNRs and antenna response as a function of position. These detections will tend to have more precisely measured inclinations, as the parameters are correlated. The merger time and coalescence phase are precisely measured for NS mergers given the long inspirals (e.g., Abbott et al. 2017b). Tidal deformability is determined by the (non-)detection of accelerated inspirals due to matter effects, and for NSBH mergers, by determining the frequency at which tidal disruption occurs, which tends to happen at high frequencies where we currently have insufficient sensitivity.
The remaining GW-determined parameters are mass and spin. The masses are determined from the chirp mass
where \(M_1\) and \(M_2\) are the masses of the primary and secondary, and the mass ratio \(q = M_2/M_1\) which is by definition \(q \le 1\). For NS mergers the chirp mass measurement is extremely precise as the GW observation covers thousands of cycles, giving a great measure on the frequency evolution of the inspiral. The mass ratio effect on the inspiral is perfectly correlated to first order with one of the spin parameters, requiring high SNR near merger to be well constrained. q will be poorly constrained for BNS mergers so long as the merger occurs out of band of the GW interferometers (Abbott et al. 2019b), except for particularly loud events. The spin components are usually written in terms of dimensionless spin \({\chi } \equiv c \mathbf{S}/(GM^2)\).
A unique aspect of GW observations is knowledge of the distance to the source. Both the strain amplitude h and \(\dot{f}_{\mathrm{GW}}\) depend on the \(\mathcal{M}_c\), defined in Eq. 8, enabling a determination of the luminosity distance to the source (Schutz 1986, 2002). For ground-based interferometers typical distance uncertainty is tens of percent (e.g., Chen et al. 2017), with improved uncertainty for higher SNR events. Given the distance-inclination correlation, the constraint can be improved when external inclination information is provided (e.g., Guidorzi et al. 2017).
The earliest detectable signal for NS mergers are GWs. As such, they play an important role in both the detection and characterization of these events, but also in providing localization information for searches with other instruments. Current ground-based GW interferometers can measure BNS merger times to sub-ms accuracy. As they are separated by thousands of kilometers and GWs travel at the speed of light (Abbott et al. 2017b) we can combine pairs of detections into narrow timing annuli on the sky. The narrowness is determined by \(\delta t/d_I\) where \(d_I\) is the distance between contributing instruments. The precise timing for BNS mergers (\(\lesssim \)ms) enables narrow annuli, despite the (comparatively) short baselines between interferometers.
For two interferometer detections the typical 90% confidence region is a few hundred square degrees, with large variation in each case (e.g., Singer et al. 2014). Three interferometer detections decrease to a median of few 10s of square degrees. Additional interferometers improve this accuracy (e.g., Abbott et al. 2018a). Table 3 shows the absolute and cumulative livetimes for a number of active interferometers from a network of a given size. Extreme loud single interferometer events can be reported without independent confirmation; in this case the localization will match the antenna pattern of that interferometer, giving a 90% confidence region of order half the sky. When one interferometer is significantly more sensitive than another the joint detection rate will decrease and two interferometer localizations will be the antenna pattern of the more sensitive instrument, slightly modified by the other, with 90% confidence region covering several thousand square degrees, as shown by GW190425 (LVC 2019).
Because inspirals can be detected before merger, GW detections can be reported before merger, i.e. act as early warning systems. Knowing the event time in advance can be beneficial for several reasons, such as pointing wide-field telescopes, switching observational modes, increasing temporal resolution, etc, but perhaps the greatest potential outcome would be the pointing of EM telescopes to observe the source at merger time, which would uncover vastly greater understanding of these sources. The localizations available before merger using the method discussed above will give typical accuracies about a thousand square degrees a minute before merger (e.g., Cannon et al. 2012) because the timing uncertainty is not precise until just before merger. Loud events could have improved, but still poor, localizations.
There are additional mechanisms for constraining source position from GW observations, relying on the motion of the interferometer. Ground-based interferometers are bound to the surface of Earth and their antenna patterns sweep over the sky as Earth rotates through the day. For signals that are \(\sim \) hours long this change causes time-dependent exposure that depends primarily on the source position, refining the location. For the recent listed frequency range of Cosmic Explorer, the U.S. third generation proposal, it will achieve 5 Hz on the low end (Reitze et al. 2019), which would begin to observe BNS mergers about an hour before merger. Therefore, even with third generation interferometers we will not be able to rely on additional localization methods and will likely be limited to accuracies of order \(\sim \) 100 square degrees a minute before merger. For comparison, 30 s is among the current fastest repoint times (from reception of alert to observation) currently available in time domain astronomy.
Space-based interferometers will localize primarily through measuring Doppler shifts as their orbit moves towards/away the source (e.g., Cutler 1998). The longer integration time can give higher SNR, providing more precisely determined distances. This is the dominant localization method for the funded satellite constellation mission Laser Interferometer Space Antenna (LISA), which would have an Earth-like orbit around the Sun and would cover the \(\sim \) mHz frequency range. LISA may detect BNS and NSBH systems, but they would be long before merger.
There are proposed mid-range interferometers, referring to instruments that cover frequencies between LISA and the ground-based network, (e.g., Dimopoulos et al. 2008; Kawamura et al. 2011; Canuel et al. 2018; Mueller et al. 2019; Kuns et al. 2020). Such devices would measure BNS systems years before merger and are likely the only way to achieve good pre-merger localizations. The details vary, but even conservative instruments/predictions give sub-degree accuracy for at least a few systems per year. These would enable broadband EM observations of NS mergers during coalescence through the first few hours. There is no funded mission in this range, precluding launch within a decade, but we discuss them as they would enable unique science with NS mergers inaccessible through other means.
2.4 Prompt gamma-ray bursts
The easiest method to detect NS mergers is through their prompt SGRB emission. The GRB monitors have detected more than a thousand SGRBs, which is (currently) three orders of magnitude more than GW detections of NS mergers, two more than claimed kilonovae, and one more than SGRBs afterglow. These events emit primarily in the \(\sim 10\,\text{keV}\)–10 MeV energy range, which is only observable from space. There are two classes of GRBs, short and long, separated in the prompt phase by a duration threshold. These classes have different origins, as proven by follow-up observations. Long Gamma-Ray Bursts (LGRBs) origin from a specific type of core-collapse supernova; SGRBs originate from BNS mergers and likely NSBH mergers. Short and long colloquially refer to these separate classes, despite the fact that the duration distributions overlap.
The most prolific active detector of SGRBs is the Fermi Gamma-ray Burst Monitor (GBM) (Meegan et al. 2009) which identifies more SGRBs than all other active missions combined. It is this instrument we will use to baseline our rates. GBM consists of two types of scintillators to cover \(\sim 10\,\text{keV}\)–10 MeV. The duration threshold where events are equally likely to belong to the short or long distributions for Fermi GBM is 5 s (Bhat et al. 2016). From the combined fit to the short and long log-normal distributions, the weight of each distribution is 20% and 80%, respectively. This gives a Fermi GBM SGRB detection rate of 48 SGRBs/yr. The low-energy detectors are oriented to observe different portions of the sky and, to first order, have a cosine response from detector normal. Localization is done by deconvolving the observed counts in each detector with the response of the instrument as a function of energy and constraining the sky region where the event is consistent with a point source origin. The median GBM SGRB localization, including systematic error, has a 90% containment region of \(\sim 500\,\text{deg}^2\). The typical localization accuracy is a few hundred square degrees, comparable to the two-interferometer GW localizations, but are quasi-circular blobs rather than narrow arcs.
The Swift Burst Alert Telescope (BAT) consists of an array of gamma-ray scintillators below a partial coding mask, which imparts shadows in a unique pattern (Barthelmy et al. 2005). This detector setup trades effective area for localization accuracy, detecting \(\sim \) 8–9 SGRBs/yr with localizations to 3’ accuracy (e.g., Lien et al. 2016). Swift has two narrow-field telescopes, the X-ray telescope (XRT) and Ultraviolet/Optical Telescope (UVOT), which are repointed to the BAT localizations for bursts within their field of regard. The XRT recovery fraction of BAT SGRBs is 75%, and is 85% of those it observes promptly. This enables localization accuracy to a few arcseconds. This is sufficient for follow-up with nearly any telescope, and was the prime mission for Swift. The BAT is sensitive over 15–150 keV, preventing it from performing broadband spectral studies of SGRBs.
There are two other instrument types that can promptly detect SGRBs. The Large Area Telescope (LAT) is the primary instrument on-board the Fermi satellite and is a pair-conversion telescope that observe from \(\sim \) 100 MeV–100 GeV (Atwood et al. 2009). It detects about \(\sim \) 2 SGRBs/yr, though some of these are afterglow-only detections (Ajello et al. 2019). Compton telescopes are phenomenal SGRB detectors that detect photons within the \(\sim \) 100 keV–10 MeV energy range, with great sensitivity, wide fields of view, and localization accuracy of order a degree. They can provide a large sample of SGRBs with localizations sufficient for follow-up with wide-field instruments.
Beyond autonomous localizations by individual satellites, the Interplanetary Network (IPN) pioneered using the finite speed of light to constrain events with timing annuli on the sky (see Hurley et al. 2011, and references therein). GRB temporal evolution is fit by empirical functions and their intrinsic variability is limited to \(\gtrsim \)50 ms. That is, to achieve annuli similarly narrow to the GW network localizations we require baselines longer than can be achieved in Low Earth Orbit (LEO). By placing gamma-ray detectors on spacecraft bound for other planets the baseline increases by orders of magnitude, enabling very bright events to be localized to arcminute accuracy. The limitation of the IPN is the high data downlink latency, generally too long for the purposes of following SGRB afterglow and early kilonova observations. The other issue is the lack of gamma-ray detectors on recent planetary spacecraft, threatening an end to massive baselines for the IPN.
The KONUS-Wind instrument has broadband energy coverage comparable to GBM, no autonomous localization capability, but sits at the Sun \(L_1\) point (Aptekar et al. 1995). The INTErnational Gamma-Ray Astrophysics Laboratory (INTEGRAL) SPectrometer onboard INTEGRAL—Anti-Coincidence Shield (SPI-ACS) is an anticoincidence shield sensitive to \(\gtrsim 100\,\text{keV}\) with no energy or spatial information, but has a highly elliptical orbit that brings it up to half a light second from Earth (von Kienlin et al. 2003). With the LEO GRB monitors they form the backbone of the modern IPN, with sufficient distances from Earth and detection rates to regularly constrain the localizations of GRBs to sub-degree accuracy.
Once a burst is identified it is characterized by its temporal and spectral properties. The GRB time is often set to the trigger time, though this definition varies for a given instrument. The on-set time of GRB emission can be refined when necessary by fitting a field-specific pulse function and defining the start time as when some amount of the peak height (e.g., 5% of the maximum) is achieved. The duration of a burst is determined through the \(T_{90}\) measure, the time from when 5–95% of the total fluence is observed, which gives a first assignment as short or long. Out of this analysis comes an estimate of the peak photon and energy flux, and total energy fluence for the event. Spectral analysis of GRBs is performed with the forward-folding technique, where an empirical functional form is convolved with the detector responses and compared with the data. The usual forms are a basic power law, a smoothly broken power law, or a power law with an exponential cutoff. These functions are not selected with any theoretical motivation. Spectral analysis is often done in a time-integrated manner, which averages out the spectral evolution of the event. Generally a power law fit indicates a burst that is too weak to constrain spectral curvature. When this curvature is constrained it is parameterized as \(E_{\mathrm{peak}}\), where most of the power is radiated.
When the distance to the source is known (Sect. 3.5) the observed flux and fluence can be converted into the isotropic-equivalent energetics, \(L_{\mathrm{iso}}\) and \(E_{\mathrm{iso}}\) for the peak luminosity and total energy released, respectively. These are calculated by assuming the observed brightness is constant over a spherical shell with radius \(D_L\) to the source, and are reported in the bolometric range 1 keV–10 MeV, after accounting for cosmological redshift through the k-correction factor (Bloom et al. 2001). These values can be refined to jet-corrected energetics if the half-jet opening angle is determined through observations of the afterglow (Fong et al. 2015).
These are the basic parameters in wide use within the field. There are additional analyses that can be done that are quite useful. Examples include fitting multiple spectral functions simultaneously has provided evidence for additional components (e.g., Guiriec et al. 2011; Tak et al. 2019) and a potential spectro-temporal signature indicative of nearby BNS mergers (Burns et al. 2018).
The SGRB rate as a function of sensitivity. Orange is the histogram of observed 64 ms peak flux in the 50–300 keV energy range for GBM SGRBs over an 11-year period. The 64 ms duration is chosen to encompass most SGRBs (e.g., the majority of bursts are longer than this timescale) and 50–300 keV is the dominant triggering range for GBM. The grey line is the cumulative logN-logP yearly detection rate. GBM has an average exposure of \(\sim \) 60% (conservatively ignoring sky regions GBM observes with poor sensitivity), which is scaled to give the all-sky detection rate of SGRBs above GBM’s on-board trigger sensitivity in black. We fit a power-law to this curve for events above \(7\,\text{ph/s/cm}^2\) as this should be a reasonably complete sample. The fit has an index of \(-1.3\)
Lastly, we discuss how the detection rate of SGRBs varies with sensitivity, as shown in Fig. 3. The result is an estimation of the all-sky SGRB rate above the on-board trigger threshold for GBM of \(\sim \) 80/yr and an extrapolation to higher sensitivity by a logN-logP power-law with an index of \(-1.3\), varying by \(\sim \) 0.1 depending on where the fit threshold is applied. That is, instruments with 2 (10) times GBM sensitivity corresponding to a detection rate multiplier of 2.5 (20). Given sensitivity scales as the square root of effective area, to maximize detection rates with a fixed amount of scintillators one should prioritize all-sky coverage over depth in a given direction, though depth is preferred for characterization of individual events.
The SGRB detection rates discussed in the previous paragraph were for on-board triggers, which are basic to ensure sample purity, minimize the use of limited bandwidth, and due to the limitations of flight computers. The initial data downlinked after a trigger is limited. Most GRB monitors also provide continuous data which is generally binned with somewhat coarse temporal or energy resolution, owing to bandwidth considerations. Fermi GBM is able to downlink continuous Time-Tagged Event (TTE) data, which enables deep searches for additional SGRBs. There is a blind untargeted search for SGRB candidates that reports the results publicly with a few hours delay, limited by the data downlink latency.Footnote 4 The targeted search of GBM data (Blackburn et al. 2015; Goldstein et al. 2016; Kocevski et al. 2018) is the most sensitive SGRB search ever developed. Based on the maximal detection distance for GRB 170817A with the targeted search against the detection limit of the on-board trigger (Goldstein et al. 2017a), the inefficiencies of the on-board trigger due to non-uniform sky coverage, and the logN-logP relation, the GBM targeted search should be capable of recovering a few times as many SGRBs as the on-board trigger, or a few per week.
2.5 Statistical association and joint searches
Multimessenger science is incredible. It requires detections in multiple messengers and the robust statistical association of those signals. This is often neglected or totally ignored. As such, we focus on this problem before proceeding to other detections of NS mergers. Much work has been done in this endeavor during the past several years, with varied focus and applicability. For example, Ashton et al. (2018) developed a general Bayesian framework to associate signals based on commonly measured parameters. For our purposes it is sufficient to use a representative frequentist method using the three dominant parameters that provide association significance: temporal and spatial information, and the rarity of the event itself.
We first discuss time. The rate of GW-detected NS mergers will remain at less than one per day for the better part of a decade. The rate of NS mergers detected as SGRBs will remain similarly rare. The time offset of these two events is expected to be only seconds long. For example, the chance coincidence of a GBM triggered SGRB occurring within a few seconds of a GW detection of a NS merger is \(\sim \text{few}\times 10^{-6}\). Then, with the inclusion of spatial information, even with the independent localizations spanning hundreds of square degrees, the association easily surpasses \(5\sigma \) (see Abbott et al. 2017b; discussions in Ashton et al. 2018). A pure sample is readily maintained even for large numbers.
Spatial information can be even more powerful. For much of observational astronomy localization alone is sufficient to associate multiwavelength signals because the uncertainty on the localization from radio to X-ray can be a trillionth of the sky, which enables easy association of steady sources. These are so precise that association significance is generally not calculated. We use the nominal Swift operations as our example here. Swift has a GRB rate (both long and short) of \(\sim \) 100/year which are localized to 3’ accuracy with the BAT. Swift autonomously repoints to the majority of these events within about a minute. Fading X-ray signals above the limit of the ROSAT All-Sky Survey (Voges et al. 2000) within the BAT localization are effectively always the GW afterglow.
Among the hidden issues exposed by GW170817 is the association of kilonovae signals to a GW event. For GW170817 the last non-detection with sufficient limits was the DLT40 observation 21 days before merger time (Yang et al. 2017). With our median BNS merger rate and the \(380\,\text{Mpc}^3\) volume from the final GW constraint (Abbott et al. 2017c), \(P_{\mathrm{chance}} \approx (380\,\text{Mpc}^3) \times (1000\,\text{Gpc}^{-3}\text{yr}^{-1}) \times 21 \text{days} \approx 10^{-5}\), which is a reasonably robust association.
To examine a worse-case scenario we can imagine a similar EM detection in the follow-up of GW190425 which has a distance estimate of \(156 \pm 41\,\text{Mpc}\) and a 90% confidence region covering \(7461\,\text{deg}^2\) (LVC 2017d). Then, \(P_{\mathrm{chance}} \approx 0.5\), a rather questionable association. As the GW interferometers improve their reach, events will tend to have similar fractional uncertainty on their distance determination which corresponds to a far larger total localization volumes. Take a middle example with a typical localization region of \(500\,\text{deg}^2\), distance \(200 \pm 50\,\text{Mpc}\), and a last (constraining) non-detection a week before, then \(P_{\mathrm{chance}} \approx 1\%\). So, even if we know the event is a kilonova, we may not be able to robustly associate it. This effect is even more important when relatively pure samples are strongly preferred (e.g., standard siren cosmology). This issue can either be solved by increasing the spatial association significance (either through better GW or GRB localizations) or the temporal association significance. The latter can be accomplished in two ways. More recent non-detections help, but may require sensitivity to \(\sim \) 23–24 Mag (Cowperthwaite and Berger 2015). Alternatively, one can determine the start time to \(\sim \) 1 day accuracy either by directly constraining the rise or through inferring the age of the kilonova for well-sampled events.
Joint searches for NS mergers can be more powerful than individual searches by elevating the significance of a true signal and repressing background. Most work in joint searches for NS mergers has focused on GW-GRB searches. Owing to the rarity of GRBs and the \(\sim \) seconds intrinsic time offset, current joint searches can improve the GW detection distance by 20–25% (Williamson et al. 2014), which is a corresponding search volume increase of nearly double.Footnote 5 Further, for at least the next few years we will have a significant amount of time where only a single GW interferometer is active (Table 3, Fig. 2). SGRBs are so rare that association with a single interferometer trigger could confirm the event. This improves the effective livetime of the GW network for GW-GRB searches.
In addition to increasing the number of multimessenger detections of NS mergers, joint GW-GRB searches also provide improved localization constraints by combining the two independent, morphologically different localizations. We demonstrate with GW170817. The first localization reported by the LVC was the GBM localization (LVC 2017a). This was because Virgo data was not immediately available, a massive glitch occurred contemporaneously in LIGO-Livingston (LVC 2017c), and the GBM localization is more constraining than the single interferometer antenna pattern from LIGO-Hanford. The first GW network localization (HLV) was reported 5 hours after event time, with a 90% containment region covering \(31\,\text{deg}^2\) (LVC 2017b). If we take the HL localization region and combine it with the independent GBM localization, the 90% confidence region covers \(60\,\text{deg}^2\). These combined localizations also improve the estimate of the distance to the host galaxy. This information was available much earlier than the Virgo information, but was not reported publicly.
Even with the poor localization accuracy of Fermi GBM, the different morphologies of the typical GBM and GW confidence regions enable greatly improved joint localizations. GBM will tend to reduce the 90% confidence regions for single interferometer events by \(\sim \) 90%, for double interferometer localizations by \(\sim \) 80%, but will tend to not improve localizations from three or more interferometers (Burns 2017). Should a joint GW-GRB detection occur with Swift, the BAT (or XRT) localization would be sufficient for immediate follow-up. IPN localizations will be between the two, but with much longer reporting latency (hours-days instead of a minute).
The other promising joint search is GW-neutrino or neutrino-GRB searches, for cases where the neutrino emission is nearly immediate (e.g., Van Elewyck et al. 2009), though the prospects for neutrino detections of NS mergers are pessimistic or uncertain. Some work has been done on prospects for elevating sub-threshold GW detections through association with a kilonova or afterglow. Lynch et al. (2018) find that to double the number of true GW events the FAR threshold would increase by five orders of magnitude. They advocate for LVC reporting thresholds to be determined by \(P_{\mathrm{astro}}\), which we support. However, weak events have to overcome the likelihood that the GW event is not real for confirmation (Ashton et al. 2018). For example, the LVC initial classification for S190718y is 98% terrestrial (noise) and 2% BNS (LVC 2017e), lowering the claim of a joint detection by more than an order of magnitude. With the prior established difficulty in associating kilonova to GW detections, it seems performing follow-up searches of sub-threshold GW signals is not a good use of observational resources. Then, for joint searches, the most promising prospect is the identification of a kilonova or afterglow by an optical (or other) survey in its normal operating mode which is then associated to a GW or SGRB trigger. Such joint searches should be developed and automated.
Because of the importance of this section we summarize the results:
-
Robust associations are necessary to enable multimessenger astronomy, and are not possible for all events.
-
Spatial constraints from the discovery instruments are critical for robust statistical association.
-
Temporal constraints for follow-up instruments are critical for robust statistical association. This can either be through a constraint on rise-time or previous non-detection from wide-field surveys.
-
Follow-up observations of sub-threshold GW signals is ill-advised, but automatically associating signals found in independent surveys should be done.
The observed inclination angle distributions for NS mergers detected through GWs and prompt SGRB observations. The GW solution comes from Schutz (2011) and the SGRB from slight modification (to handle solid angle) from observational results in Fong et al. (2015). We use the astrophysical convention of \(0 \le \iota \le 90\), ignoring handedness relative to Earth. Against the rather naive assumption of a solid-angle distribution, roughly 1 in 8 GW-detected NS mergers that produce jets will have those jets oriented towards Earth
2.6 Joint GW-GRB detection rates
Prior to GW170817 it was considered somewhat unlikely, though possible, for a joint GW-GRB detection to occur with the Advanced network of interferometers. This belief was continued due to several misconceptions or misunderstandings. We briefly describe these and their resolution:
-
Inclination Biases SGRBs have an observed half-jet opening angle distribution of \(16^\circ \pm 10^\circ \) (Fong et al. 2015), which does not include GRB 170817A. Then, from solid angle effects only a few percent of successful SGRB jets will be oriented towards Earth. Therefore, the assumption was that only a few percent of GW-detected NS mergers would have an associated SGRB (or less, if not all NS mergers produce successful jets).
The emission of GWs is omnidirectional but not isotropic. It is strongest when the system is face on. Convolving this with solid angle gives an observed inclination angle probability distribution for GW-detected NS mergers of
$$\begin{aligned} \rho _{\mathrm{GW-detected}}(\iota ) = 0.002656\Big (1+6\cos ^2(\iota )+\cos ^4(\iota )\Big )^{3/2}\sin (\iota ) \end{aligned}$$(9)Schutz (2011). Note that we have altered the distribution to be in terms of degrees (not radians) and removed directionality from \(\iota \) (GW measures of inclination go from 0 to 180 but EM studies of NS mergers generally only go to 90).
The effect of this is shown in Fig. 4. The GW distribution comes from Eq. (9). The SGRBs distribution is a Gaussian convolved with solid angle that roughly recreates the observed distribution compiled in Fong et al. (2015), accounting for the intrinsic vs observed differences. The outcome is that roughly 1 in 8 GW-detected NS mergers that produce SGRBs will have Earth within the jet angle.
-
The Minimum Luminosity of SGRBs Shifting a typical cosmological SGRB with \(L_{\mathrm{iso}} \approx 10^{52}\,\text{erg/s}\) within the GW detection volume would have an observed flux \(\sim 10^4\) times the typical value. Such a burst has not been observed in half a century of observations.
The implicit assumption is that SGRBs have a minimum luminosity, which was widely assumed (see e.g., Wanderman and Piran 2015, references therein, and references to). The was an implicit assumption that SGRBs arise from top-hat jets, where the jet has uniform properties within its cone, which largely explained observations until GRB 170817A. Structured jets, where there is variation within the jet cone, have now been considered (see Sect. 4.4). For these models the intrinsic luminosity function of SGRBs refers to the peak luminosity of the jet, generally corresponding to the face-on value. Then, for the same jet, the isotropic-equivalent luminosity as viewed from Earth depends on the inclination angle. Prior to GRB 170817A, there were papers that avoided this implicit assumption, such as Ghirlanda et al. (2016) who predicted joint detect rates without requiring an imposed minimum luminosity.
Evans et al. (2015) was the first paper to consider that we may not identify nearby SGRBs based on flux measurements if they are “systematically less luminous than those detected to date”. Burns et al. (2016) investigated the observed brightness of SGRBs as a function of redshift and found no relation, empirically showing that we likely had not observed the bottom of the luminosity function, and suggested that subluminous SGRBs exist. From the knowledge gained from GRB 170817A these subluminous bursts would arise from nearby off-axis events.
-
The limited GW Detection Distance and the Redshift Distribution of SGRBs There were no known SGRBs within the Advanced interferometer design BNS range of 200 Mpc. Neglecting the full GW network fails to account for the true spacetime volume observed, as shown in Fig. 7. Joint GW-GRB detections will have a restricted inclination angle, giving a sky-averaged GW-GRB BNS range 1.5 times greater than the GW-only range. Further, with joint searches we can increase the detection distance by \(\sim \) 25% (Sect. 2.5).
The GW-GRB detection distances and the observed redshift distribution of SGRBs are shown in Fig. 5 with relevant information in Fig. 7. This suggests a few percent of SGRBs are within the joint detection horizon, corresponding to a few events per year with current sensitivities.
Prior observations of NS mergers. The grey shaded region is the cumulative redshift distribution observed for SGRBs, bounded by the pessimistic and optimistic samples from Abbott et al. (2017b). Blue squares and triangles are the claimed kilonova and cases with constraining upper limits. The top axis marks the approximate KN170817 magnitude as a function of distance, based on an assumed 17.5 Mag (within half a Mag of most bands Villar et al. 2017) and neglecting redshift effects. Overlaid are the joint GW-GRB detection horizons
Combining this information together, Burns (2017), published before GW170817, stated that we should expect joint detections with the Advanced network at design sensitivity, and potentially before. With GW170817 and GRB 170817A we confirmed that nearby bursts exist, that subluminous SGRBs exist, and that joint detections should be expected with existing instruments. As a result, in predicting future joint detection rates we use the same underlying principles.
Another issue, that remains unsolved and is not considered in the prior paragraph, is the fraction of observed SGRBs from NSBH mergers. NSBH mergers are heavier and can be detected in GWs roughly an order of magnitude greater volume (for those expected to produce SGRBs). That is, even a low fraction of detected SGRBs originating from NSBH mergers would result in a sizable fraction of GW-GRB detections from NSBH mergers (as compared to joint detections from BNS mergers). The fractional contribution from each progenitor can then significantly alter the expected joint rates.
However, this requires a very important caveat. Since GW170817, several papers have been published that estimate future joint detection rates with the intrinsic BNS merger rate, a half-jet opening angle (typically \(\sim 16^\circ \) from Fong et al. 2015), that all BNS mergers produce SGRBs, and a 100% recovery efficiency for the EM instrument. This last assumption is fundamentally flawed. As a sanity check, applying this calculation to GBM vastly overestimates the expected joint detection rate by a factor of several. It is necessary to account for the low recovery fraction of weak SGRBs due to detection distances like GRB 170817A.
For the joint rates estimates we use existing literature to determine a reasonable range of the fraction of SGRBs that will be detected by NS mergers, which has the benefit of avoiding the uncertainty on the fraction of NS mergers that produce SGRBs. These rates consider the detections of off-axis events, being built on literature that considers this either explicitly or implicitly. To start, we assume only a two-interferometer network with a 50% network livetime (70% each) and that all SGRBs originate from BNS mergers. For the Advanced network at design sensitivity we assume that 0.8–4.5% of SGRBs are detected in GWs. This is consistent with limits on the fraction of nearby SGRBs from comparing their localizations against galaxy catalogs (Mandhai et al. 2018) and on the inverse fraction of GWs detections with associated SGRB detections (Song et al. 2019; Beniamini et al. 2019). These values come from the methods described in Abbott et al. (2017b, 2019f), as well as the simulations from Howell et al. (2019) and Mogushi et al. (2019). For the A+ network we take 2–10%, based on a \(\sim \) 2.5\(\times \) scaling relative to the Advanced network from Howell et al. (2019). For Voyager we assume 10–20% as a representative recovery fraction based on the observed SGRB redshift distribution (Fig. 5). The Gen 3 interferometers have a joint BNS range beyond the furthest SGRB ever detected; therefore, we assume they recover all events when the network is live.
To calculate an absolute base rate we scale these fractions by the rate of GBM on-board triggers. We note that this is a particularly conservative estimate. It ignores single interferometer GW triggers that are confirmed by an associated SGRB trigger (\(\sim \) 80% increase for a two interferometer network), the effects of adding interferometers to the network (\(\sim \) 2–3\(\times \) for a five interferometer network, with slightly asymmetric sensitives, due to higher network livetime and more uniform coverage), the increase in recovered SGRBs (a factor of a few, see Sect. 2.4), and the contributions from the rest of the active GRBs monitors (\(\sim \) 30–40% more than the GBM on-board trigger rate). These effects are not fully independent (e.g., a five interferometer network will have negligible single interferometer livetime). As a conservative estimate of the effects of these additional detections we provide the final column in Table 4, which doubles the rate of GBM+HL triggers. For Advanced LIGO at design sensitivity we should expect a few joint detections per year. With A+ this should happen several times per year.
We also provide an estimate for Swift-BAT+HL joint detection rates by scaling the GBM+HL values. This is reasonable because they have similar detection thresholds. However, this is a lower limit. By reordering the observation list to bias the BAT Field of View (FoV) to overlap with the LIGO sensitivity maximum the joint detection rates can be increased by several tens of percent. Scaling to instruments with different sensitivities requires accounting for the bias of brighter events being more likely to occur in the nearby universe.
2.7 Follow-up searches
As of the time of this writing, no NS merger has ever been discovered without a prompt SGRB or GW detection. This is not particularly surprising. Using optical as an example, only a few LGRB afterglows have been detected without an associated prompt trigger. Detections of SGRBs are rarer than LGRBs and have systematically fainter afterglows. Similarly, there are thousands of known supernova identified through optical surveys but they are orders of magnitude brighter and more common than kilonovae.
As such, the dominant mode for finding SGRB afterglows, kilonovae, and the other expected EM transients from NS mergers will be through follow-up observations of prompt SGRB and GW triggers. This is true at least until the era of Large Synoptic Survey Telescope (LSST). These follow-up observations can be performed in a few different ways. The most common method is through follow-up of Swift-BAT SGRBs with afterglow detections approximately every other month (generally detected by XRT).
As previously discussed, GW detections of NS mergers provide localizations of tens to hundreds, and sometimes thousands, of square degrees. They also provide an estimate of the distance to the event, with typical uncertainty of tens of percent. These 3D localizations are distributed as HEALPix maps (Gorski et al. 2005) through Gamma-ray Coordinates Network (GCN), with the distance reported as a function of position (Singer and Price 2016). These localization regions are massive, and difficult to follow-up with the vast majority of telescopes. However, for the initial GW era detections will tend to be in the nearby universe (\(\lesssim 200\,\text{Mpc}\)), where galaxy catalogs are reasonably complete. That is, narrow-field telescopes can prioritize the position of known galaxies within the GW-identified search volume, a technique referred to as galaxy targeting (e.g., Kanner et al. 2012; Gehrels et al. 2016).
The other solution to this problem is to build sensitive telescopes with a large FOV. When a localization is reported these facilities tile the large error region and rapidly cover the observable containment region to a depth sufficient for a reasonable recovery fraction. This technique can also apply to GRB localizations. Such optical facilities identify enormous numbers of transients that have to be down-selected to a small subset of events of interest. A great demonstration of this technique is the Zwicky Transient Facility (ZTF) follow-up of GW190425, covering \(\sim \) 10% of the sky on successive nights, in two bands, identifying more than 300,000 candidate transients, and quickly down-selecting to 15 events of interest (Coughlin et al. 2019a).
In estimating follow-up detection rates we should not expect to recover those events that occur near the Sun. The space-based observing constraint is within \(\sim 45^\circ \) of the Sun for many narrow-field space-based telescopes (e.g., Swift, Hubble, Chandra). The ground-based limitation is generally a few hours of RA from the Sun, for a comparable exclusion zone size. An exception to this is for events detectable long enough for the Sun to move across the sky, requiring \(\sim \) months of detectability. We neglect this here, only considering events identified in the first \(\sim \) week. Either case rules out about 15% of the sky. We may also not be able to recover SGRB afterglow and kilonovae if they occur within about \(5^\circ \) of the galactic plane because of extinction and the insane rate of transients at lower energies. Therefore, follow-up observations could be capable of recovering up to 80% of GW or GRB triggers.
We briefly remark on the possibility of separating afterglow and kilonova observations. SGRB afterglow can be bright and dominate kilonova emission, or faint and undetectable below a given kilonova. From observations it appears afterglow will dominate in \(\sim \) 25% of cases (Gompertz et al. 2018). When they are of comparable strength, or the observations sufficient, the different spectral signatures and their temporal evolution of these events should enable disentanglement. Further, afterglow will tend to fade away long before the dominant emission of red kilonova.
2.8 Gamma-ray burst afterglows
Swift identified the first SGRB afterglow and has provided a sampleFootnote 6 of about 100. These detections and broadband EM observations from radio to GeV have shown afterglow is well described by synchrotron radiation. This radiation spans the EM spectrum and is described as power laws with three breaks: the self-absorption break \(\nu _a\), the minimum Lorentz factor break \(\nu _m\), and the synchrotron cooling break \(\nu _c\) (Sari et al. 1998).
As summarized in Berger (2014), broadband observations and closure relations enable determination of these break energies and their temporal evolution allow determination of several parameters. This includes the kinetic energy of the blastwave \(E_k\), the half-jet opening angle \(\theta _j\) (historically calculated assuming a top-hat jet), the density in the circumburst region n (on \(\sim \) parsec scales), the power law index of the electron distribution in the jet, and a few microphysical parameters. In response to GRB 170817A excluding the base top-hat jet models, closure relations for structured jet models have been derived (Ryan et al. 2020). Afterglow detection also enables arcsecond localizations and thus distance determination (see Sect. 3.5), which allows for the calculation of \(E_{\mathrm{iso}}\) and \(L_{\mathrm{iso}}\) of the prompt emission, and the half-jet opening angle allows for the jet-corrected values of these parameters and \(E_k\).
The rates of SGRB afterglow detections is well understood for Swift bursts. With the rate of SGRB detections by BAT and the fraction detected in XRT, there are \(\sim \) 6–7 X-ray detections of SGRBs/yr. The XRT sample of GRB afterglows is shown in Fig. 6. The recovery fraction at other wavelengths is poor. The summary in Fong et al. (2015) covers observations of 103 SGRBs; X-rays have a 74% recovery fraction, optical and Near infrared (NIR) 34% and radio 7%. Note that these pessimistic recovery fractions are for narrow-field telescopes, which are effectively always more sensitive than wide-field telescopes covering the same energy range.
The Swift XRT afterglow sample. LGRBs are orange and SGRB in red, showing they are systematically dimmer by \(\sim \) 1–2 orders of magnitudes. XRT has an 85% recovery fraction for SGRBs it observes in the first 100 s. The black markers are the nearest SGRBs with known redshift. The upper limits (triangles) are for GRBs 170817A and 150101B. The lines are for GRBs 061201, 080905A, and 100628A. Like the prompt SGRB emission, they are not brighter at Earth than the full sample
The temporal decay of afterglow is steeper than the sensitivity gain most telescopes get for longer observation times. The faster an observation begins after event time the higher a likelihood of recovery, which was the main technical driver for Swift. Alternatively, vastly more sensitive telescopes can be pointed at later times and still recover these signals, such as Chandra detections days later.
Beyond the typical cosmological SGRB afterglows, off-axis afterglows were thought to be promising EM counterparts to GW detections. From Metzger and Berger (2012), and references therein, when top-hat jets interact with the surrounding material they slow and broaden. Over long enough timescales this emission can become observable to wider angles than the prompt SGRB emission, but can still be bright enough to be detected from nearby events. GW170817 and GRB 170817A proved that afterglow can be detected significantly off-axis, but it also showed that off-axis afterglows may not be promising EM counterparts unless the precise source localization is known through other means (i.e. identification of the kilonova). Fermi-GBM, an all-sky monitor that is secondary on its own spacecraft, could detect GRB 170817A nearly as far as the narrow-field X-ray Great Observatory Chandra. Indeed without the kilonova determination of the source position the afterglow for GRB 170817A event would not have been identified.
For the previously discussed reasons, searches for blind discovery of SGRB afterglow using current wide-field monitors are unlikely to be successful. This is unlikely to change at least until LSST operation. The most likely follow-up technique to succeed is then the galaxy targeting technique, as it enables follow-up with more sensitive telescopes; however, this is limited to well-localized and nearby events. The instrument most likely to identify a SGRB afterglow following a GW detection is the Swift-XRT, as it is the only fast response X-ray instrument.
Estimating the number of SGRB afterglow detections following NS mergers is difficult because we do not understand their structure and therefore their brightness distribution. We will lose some events due to Sun constraints, transient contamination Milky Way, or relative sensitivity issues, which we estimate as \(\sim \) 25% based on the Swift XRT recovery fraction of BAT bursts. However, we may also recover some events undetectable by GBM due to Earth occultation or livetime considerations. These two effects are likely of similar order. Therefore, we roughly estimate the rates by assuming they have similar recovery fractions as the prompt GBM on-board triggers.
2.9 Kilonovae
The first widely discussed claim of a kilonova detection came from follow-up observations of the Swift SGRB 130603B (Tanvir et al. 2013). There are a handful of other claims of kilonova signals in follow-up of Swift GRBs, (e.g., Perley et al. 2009; Yang et al. 2015; Jin et al. 2016). Inferred color and luminosity distributions for the claimed events are summarized in Gompertz et al. (2018) and Ascenzi et al. (2019). However, the only well studied kilonova is KN170817. This event likely had a HMNS remnant (see Sect. 3.2), suggesting the brightness was near the middle of the possibilities (with SMNS and Stable NS being brighter and prompt collapse fainter). However, the early emission was on the bright end of expectations and the exact reason remains a matter of debate (see discussions and references in Arcavi 2018, Metzger et al. 2018, but see Kawaguchi et al. 2020).
If we assume that this unexpected bright behavior is due to our lack of understanding of these sources, rather than being a rare occurrence, we can use it as a representative kilonova, which we do in this paper. Villar et al. (2017) compiled a large sample of the UVOIR observations of KN170817. At the distance of \(\sim \) 40 Mpc the Ultraviolet (UV) emission peaked at \(\sim \) 19th Mag (thought it may have peaked before the first observations), blue bands at \(\sim \) 18th Mag, with red and infrared approaching almost \(\sim \) 17th Mag. With a limiting Mag of \(\sim \) 26, within the reach of existing sensitive telescopes, around 30–40% of Swift SGRBs occur close enough for a KN170817-like event to be detected and studied. The majority of Swift SGRBs do not have follow-up at these sensitivities. This is in part because the primary goal of Swift follow-up was afterglow studies, and SGRB afterglow usually fade before the on-set of kilonova emission. With the devotion of sufficient observational resources \(\sim \) 1–2 kilonova per year can be identified by following up Swift SGRBs, though we note that many of the nearby bursts have claims of kilonova or interesting upper limits as shown in Fig. 5.
KN170817 was independently identified in the follow-up of GW170817 through both the wide-field tiling and galaxy targeting techniques (e.g., Coulter et al. 2017; Soares-Santos et al. 2017; Valenti et al. 2017; Arcavi et al. 2017; Tanvir et al. 2017; Lipunov et al. 2017). Both methods will continue to be useful for future events, with the best technique depending on a given event. For events that are nearby (where galaxy catalogs are relatively complete) and reasonably well-localized galaxy targeting will be quite beneficial, with methods that account for galaxy incompleteness being particularly powerful (Evans et al. 2016). For events that are nearby and poorly localized (e.g., several hundreds of square degrees or more), or events that are further away, the wide-field tiling technique will be dominant, provided the telescopes are sufficiently sensitive. There is no active wide-field UV monitor. The band with the current best wide-field telescopes for identifying kilonova are in optical, where instruments like ZTF (Bellm 2014) can tile a large fraction of the sky to \(\sim \) 21st–22nd Mag in one or two filters in a single night, as demonstrated by the (current) worse-case event (Coughlin et al. 2019a). However, even these depths may be insufficient to recover the majority of kilonova following GW detections (Sagués Carracedo et al. 2020).
Reliably predicting the detection rates of kilonova in follow-up of GW-detected NS mergers may be a fools errand. The values depend on the volumetric rate of NS mergers (each with more than an order of magnitude uncertainty), predictions on the sensitivity of the GW network years in advance (that is an attempt to predict how some of the most sensitive machines ever built will change), the color and luminosity distribution of kilonova themselves (and how the intrinsic system parameters affect this, with only a single well-studied event to base our knowledge on), and would have to account for dozens of follow-up instruments scattered over the surface of Earth and teams with different observational strategies.
Here we bound the rate. To calculate the number of kilonova detected through follow-up of GW detected BNS mergers we start with the rate of such events within 200 Mpc. This is estimated using KN170817 as a baseline, with observations achieving a sensitivity of \(\sim \) 21st Mag, we can recover KN170817 out to the Advanced design range of LIGO and Virgo. At 22nd Mag this reaches to \(\sim \) 250 Mpc. This is roughly the sensitivity of ZTF (depending on the observation time) which has a \(47\,\text{deg}^2\) FOV, covers the g, r, and i filters (effectively, green, red, and infrared), and observes the northern sky. For our estimate of kilonova detection rates we assume that we can achieve ZTF-like depths in the majority of optical filters over the observable night sky, which is a reasonable assumption given active and potential upcoming comparable facilities (e.g., Diehl et al. 2012; Bloemen et al. 2015).
We do not attempt to estimate the gain from wide-field telescope sensitivity (e.g., LSST) as the rate of optical transients becomes too great for this simple method to be accurate. Galaxy-targeting campaigns or smaller field of view telescopes that are more sensitive (e.g., DECam) generally require 3 or more interferometer localizations to succeed. This will not be common for events beyond 200 Mpc in the Advanced era, but will be in the A+ era where our provided numbers are conservative. This is shown in Fig. 7.
The first estimation is the GW-recovery fraction of these events, which is shown in Fig. 7. We multiply the GW detection efficiency with differential volume to determine the distance distribution for GW-detected NS mergers. From this, we can also calculate the recovery fraction of a network for BNS mergers within 200 Mpc, roughly corresponding to the discovery distance for kilonova until LSST. This value is calculated by taking the time a network will spend with specific detector combinations and multiplying by the recovery fraction of the second-best live interferometer. We assume 70% livetime for each individual interferometer and treat Virgo and KAGRA as roughly equivalent (taking the higher recovery fraction). For the Advanced era this suggests the network will recover \(\sim \) 30% of BNS mergers within 200 Mpc and about 75% in the A+ HLVKI era. These assumptions neglect the fact that most detectors are not copointed, but this is somewhat counteracted by the additional sensitivity of three and four detector livetimes.
The GW detection efficiency and distance distributions for GW-detected NS mergers by he Advanced and A+ networks. These are constructed with the projection parameter from Finn and Chernoff (1993), as used in the literature (e.g., Howell et al. 2019), and the tables from (Dominik et al. 2015). The left panels are for the Advanced interferometer era and the right for the A+ era. The top panels shows the GW detection efficiency for canonical BNS mergers as a function of distance. The middle and lower panels scale this by the differential volume to show the cumulative and differential distance distributions for GW-detected NS mergers. The assumed distances for the different interferometers are the median value for the interferometers (Advanced: LIGO-175 Mpc, Virgo-105 Mpc, KAGRA-77.5 Mpc; A+: LIGO-330 Mpc, Virgo-205 Mpc, KAGRA-130 Mpc) from Abbott et al. (2018a)
Multiplying this fraction by the 5% and 95% bounds on the local volumetric rate of BNS mergers gives the expected rates as a function of distance. To estimate the rate of kilonova detections following GW detections of BNS mergers we account for the 20% loss of events that occur close to the Sun or in the galactic plane, where follow-up observations are either impossible or likely to be too contaminated to reliably identify as discussed in Sect. 2.7. We calculate reasonable values for pessimistic and optimistic scenarios, as well as a mid-range estimate. For the representative estimate we assume 70% will be like AT2017gfo or brighter (the remaining 30% being assumed to be prompt collapse and too faint to detect), and for the high-end estimate we assume 100% (assuming prompt collapse events are rare). These values come from Margalit and Metzger (2019), which is conservative compared to predicted remnant object fractions from other estimates Lü et al. (e.g., 2015).
For the low-end estimate we remove the assumption of kilonova brightness being predominantly determined by the progenitor, e.g., due to properties of the merger or inclination effects, which also removes the assumed mass distributions for BNS mergers. Gompertz et al. (2018) investigate kilonova brightness based on SGRBs follow-up. They find that three kilonova candidates would be brighter than KN170817 and that four events have non-detections with upper limits sufficient to rule out a KN170817-like event. We here assume 25% of kilonova would be as bright as KN170817, corresponding to 2 of the 3 candidates being real detections. We caution that this may still prove to be optimistic.
These calculations give a representative estimate of 5.6 GW-kilonova detections per year with the Advanced network, with pessimistic and optimistic scenarios estimating between 0.4 and 24 per year. For the Advanced network this is 14/yr in the representative case, and between 1.0 and 60/yr in the other scenarios. For Voyager and Gen 3 we adopt a lower limit of detections of at least once a month, corresponding to the recovery of BNS mergers (assuming the 95% intrinsic lower limit) within 300 Mpc (with the previously mentioned losses). Should wide-field telescopes sufficiently advance in sensitivity, or should LSST prioritize the follow-up of GW detected NS mergers, this rate could greatly increase. The rate of kilonova detected following-up NSBH mergers is likely to be low in comparison, due to the generally greater distances and emission peaking in infrared (where wide-field telescopes are much less sensitive), though the intrinsic rates are broadly unknown.
These estimates neglect inclination effects on recovery fraction. As KN170817 was thought to be oriented for maximal brightness this may suggest the rates are somewhat optimistic. However, this is counteracted by the observed inclination distribution GW-detected NS mergers. This is discussed in Sects. 2.6 and 2.11.
Earlier detections are necessary for characterization of the kilonova and for robust statistical association to the GW (or GRB signal). The earliest light expected from these events is in UV. The only active mission that does UV discovery searches is Swift, which relies on the galaxy targeted technique. Otherwise, observations in b and g filters within about a day (for blue kilonova), and r and i filters on timescales of a week (for red kilonova) are likely the discovery bands (Cowperthwaite and Berger 2015). However, separation of kilonovae from other optical transients must rely on color information, and we likely need detection in multiple bands for discovery. Once the source position is known, either through identification of afterglow or kilonova, broadband study of the kilonova begins. Telescopes covering these wavelengths are abundant, which can make use of both follow-up techniques; however, NIR wide-field telescopes are significantly less sensitive than optical ones.
UVOIR observations from the earliest detection until they fade from detectability (in each wavelength) enable us to infer properties of the ejected material. The ejecta mass, velocity, and opacity (or lanthanide fraction, depending on the formulation) can be determined from the broadband evolution of the quasi-thermal signature. This relies on an underlying assumed kilonova model. This is discussed in detail in Sect. 5.
2.10 Other signatures
GW inspirals, prompt SGRBs, afterglow, and kilonova are the primary signals for detecting and characterizing these events. This section briefly summarizes several other possible signals expected on observational or theoretical grounds. Detecting any of these signatures would provide incredible insight into the physics of NS mergers. The discussion here is limited to observational requirements with a base scientific motivation, with more detailed discussion in later sections.
2.10.1 MeV neutrinos
As discussed, BNS mergers can have neutrino luminosities a few times greater than CCSNe. The Supernova Early Warning System (SNEWS) was developed to cross-correlate short-duration signal excesses from multiple \(\sim \) MeV neutrino telescopes to identify and localize nearby CCSNe and alert the astronomical community before the first light (from shock break-out) is detectable (Antonioli et al. 2004). It should also work for NS mergers, where the very short intrinsic time offset from a GW trigger can enable sensitive joint searches.
To discuss potential detection rates we focus on Hyper-Kamiokande, which is a 0.5 Megaton detector under construction in Japan (Abe et al. 2018). It follows the Nobel Prize winning detectors Kamiokande and Super-Kamiokande, will increase our neutrino detection rate of CCSNe by an order of magnitude, and provides a potential path forward from the Standard Model. Unfortunately, it will probably not inform our understanding of NS mergers as they can only be detected to \(\sim \) 15 Mpc. The closest BNS merger every century should be roughly \(13_{-4}^{+9}\,\text{Mpc}\), suggesting during a decade run of Hyper-Kamiokande there is a \(\lesssim \)10% chance of detecting a BNS merger.
2.10.2 Other observed non-thermal signatures
Observations of SGRBs have uncovered several additional non-thermal signatures. These signatures provide unique insight into these events, the possibilities and implications of which are discussed in Sect. 4.7. The main peak in prompt emission is sometimes observed with preceding emission referred to as precursor activity and sometimes with extended emission that can last up to \(\sim \) 100 s. These are reliably identified with the prompt GRB monitors. Gamma-ray precursors may require pre-trigger data with high temporal resolution (if the trigger is due to the main emission), and are generally expected to be softer, requiring energy coverage near \(\sim \) 10–100 keV. There may also be precursor emission at other energies. Clear identification of extended emission requires well-behaved backgrounds after trigger and generally emits at \(\lesssim \)100 keV.
SGRB afterglow emission has large variation in addition to the base temporal decay. The Swift-XRT sample of SGRB afterglows with X-ray flares and plateau activity in excess of the base temporal decay. These appear to be signatures of late-time energy injection into the jet. They require prompt X-ray observations, generally concluding within 10,000 s of trigger time.
2.10.3 High-energy neutrinos
We may also expect high-energy (\(\sim \) TeV-EeV) neutrino emission from NS mergers. The most sensitive instrument at these energies is the gigaton-class IceCube detector. The prompt and extended emission of SGRBs and the extra components seen in some SGRB afterglow may produce significant amounts of neutrinos (e.g., Kimura et al. 2017, and references therein). These signals are favorable for joint detections given the short time offset and rough localization capability of IceCube. Extended emission appears to be the most favorable signature, but only occurs for a fraction of NS mergers. In light of the neutrino search around GW170817 (Albert et al. 2017) approaching interesting limits and the relatively new consideration of the SGRB jet interaction with polar kilonova ejecta, new theoretical studies have been performed that suggest we may be able to detect SGRBs in high energy neutrinos (Kimura et al. 2018). This generally requires a GW-GRB event within \(\sim \) 50 Mpc and occurring in the northern hemisphere, where IceCube is far more sensitive. Such an event occurs about once per decade.
Murase et al. (2009) opened the possibility of observing \(\sim \) EeV neutrinos over days to weeks after merger from proton acceleration by a new, long-lived NS remnant with a high magnetic field, referred to as a magnetar. Fang and Metzger (2017) applied this to BNS mergers and their model was tested in Albert et al. (2017), which suggests we are 2 orders of magnitude away from interesting limits. This high energy neutrino signature is unrelated to the prescence of a jet. The understanding gained through the multimessenger observations of GW170817 have led to reevaluation of potential coincident detections (e.g., Kimura et al. 2017) and additional mechanisms for high energy neutrino production, such as choked jet scenarios (e.g., Kimura et al. 2018). Precise predictions of detection rates are difficult, but are generally expected to be rare.
2.10.4 Very-high energy electromagnetic detections
Gamma-rays refers to about half of the electromagnetic spectrum. The primary energy range of SGRBs (\(\sim \) keV–MeV energies) are soft gamma-rays. The mid-energy range is covered by the Fermi-LAT. In its first decade of observation is has detected 186 GRBs, 155 of which are with its normal data (\(\gtrsim \)100 MeV). The seed information for LAT GRB searches is usually GBM triggers, with about 30% of GBM detections observed within the nominal LAT FOV, giving a LAT recovery efficiency of \(\sim \) 25%. Of that 25%, 30% (2%) is seen above 5 GeV (50 GeV) (Ajello et al. 2019). Notably, of those with measured redshift 80% (12%) have source-frame photons above 5 GeV (100 GeV). These detections appear to be a mixture of prompt and afterglow emission, which can occur during the prompt phase even for SGRBs.
Beyond the reach of Fermi are Very High Energy (VHE) gamma-rays, roughly defined as \(\gtrsim 100\,\text{GeV}\), that are observed by ground-based facilities utilizing Cherenkov radiation. Detections at these energies are expected observationally from extrapolation of the LAT power-law measurements and theoretically, e.g., from synchrotron self-Compton afterglow emission. There are two classes of VHE telescopes. Water Cherenkov telescopes like High-Altitude Water Cherenkov Array (HAWC Wood 2016) which observe a large fraction of the sky instantaneously (day or night). Imaging Atmospheric Cherenkov Telescopes (IACTs) are pointed observations, though by most definitions they are wide-field telescopes (\(\sim \text{few deg}^2\) FOV) that are far more sensitive but can only observe at night.
The first report of a VHE detection of a GRB occurred earlier this year, with the Major Atmospheric Gamma Imaging Cherenkov Telescopes (MAGIC) detection of LGRB 190114C (Mirzoyan et al. 2019). The LAT observations of this burst are impressive, but within the observed distribution. This suggests that the MAGIC observation resulted in detection because it was the first early VHE observation of a very bright afterglow. It is sufficiently bright that it could have been detected by HAWC in the sensitive region of its FOV. There are also two reports from H.E.S.S. of VHE detection of afterglow from the LGRBs 180720B and 190829A (Velasco 2019; de Naurois 2019). This suggests a detection rate of a few LGRBs per decade with existing telescopes, which is consistent with extrapolation from the LAT rates.
To estimate the detection rate of SGRBs with VHE telescopes we can scale the rate by the fraction of SGRBs to the total GRBs rate. The LGRB-to-SGRB ratio for GBM is 4:1. The same ratio for the LAT is 10:1. This is not surprising as a large portion of the LAT detections are from only afterglow emission (which is fainter for SGRBs). Then, an optimistic VHE detection rate of NS mergers with existing instrumentation is \(\sim \) 1/decade. The planned Cherenkov Telescope Array (CTA) is an IACT that is roughly an order of magnitude more sensitive than its predecessors. Then, we may expect a VHE detection of a SGRB every few years. However, we emphasize this is a very rough estimate.
2.10.5 Neutron precursors to kilonova and additional energy injection
Among the surprises of KN170817 that remains unsolved is the origin of the early bright UV/blue emission. This topic is discussed in Sect. 3.4. The possibilities range from the decay of free neutrons, shock-heated contributions from jet interactions with polar ejecta, additional heating supplied through a temporary magnetar, etc. In all cases these require observations in UV and blue optical wavelengths as early as \(\sim \) 1–2 hours after merger.
2.10.6 Late-time radio emission
The quasi-isotropic ejecta will emit late-time radio emission as it interacts with the circumburst material (Nakar and Piran 2011). Their estimate of the detectability distances for a representative set of sensitive radio telescope reaches a few hundred Mpc. This signal should therefore be detectable, but we note the assumed densities are higher than most of the observed distribution following SGRBs (Fong et al. 2015). We emphasize that this cannot be the only counterpart to a GW detection for it to be reliably associated, given the massive delay time preventing robust association.
2.10.7 Gamma-ray detections of prompt kilonova and kilonova remnants
Kilonova are nuclear powered transients. Our observational understanding of the properties of the ejecta material comes from indirect, model-dependent inferences. We could directly measure the nuclear yield by detecting the nuclear gamma-rays that emit from \(\sim \) tens of keV to a few MeV with a flat spectrum across this range due to Doppler broadening of many lines (Hotokezaka et al. 2016b; Korobkin et al. 2020). No existing telescope can detect this emission unless the event occurs within the local group. The current design of the most sensitive proposed instruments (e.g., McEnery et al. 2019) could detect these signals up to \(\sim \) 15 Mpc, comparable to the prospects for MeV neutrino detections of these events.
However, another option has recently been identified. Based on fiducial BNS merger rates and kilonova ejecta properties both Korobkin et al. (2020) and Wu et al. (2019) discuss the possibility of identifying KNRs in the Milky Way. They make different assumptions but come to the same conclusion that detecting kilonova remnants in the galaxy may be within reach with next-generation nuclear astrophysics missions. The use of these observations is discussed in Sect. 5.2.
Wu et al. (2019) also consider potential diffuse emission from ancient NS mergers that have fully diffused with the Milky Way. The spatial distribution would likely differ from usual galactic distributions given the natal kicks to these systems, but detection prospects are hopeless for decades.
2.11 Detections summary
Given the breadth of this total section we provide a short summary tying the observations together. NS mergers may produce observable signatures in all astrophysical messengers across wide ranges in energy and time, as shown in Fig. 8. In Tables 5 and 6 we summarize the rates results of this full section. See the text for a full understanding of the assumptions underlying each number.
The observing timescales when detectable emission is known or expected from NS mergers. Because of our greater history (and therefore understanding) of EM observations, we divide this messenger into bands. Intervals where signals were detected for GW170817 are outlined with black boxes. The full color regions are for times with known observations of other SGRBs. The shaded regions cover times where we expect to detect signals in the future
We provide a short summary here for convenience. We assume a base intrinsic BNS merger rate, neglecting any contribution from NSBH mergers. This is used to calculate the GW detections where each network assumes only two co-aligned interferometers (corresponding to the two US-based LIGO interferometers for the next several years). Advanced refers to the current design sensitivity, A+ is the funded upgrade, with Voyager and Gen 3 referring to the proposed future interferometers.
The prompt SGRB and SGRB afterglow rates are based on empirical observations. The joint rates assume a fixed fractional recovery of SGRBs by GW interferometers of a given sensitivity. The Swift BAT joint detection rate comes from scaling the Fermi-GBM values by their relative SGRBs rates. Note that the GW and GW-GRB rates for GBM and BAT are for two interferometer GW networks and are therefore a lower bound. See Sect. 2.6 for a broader explanation.
The kilonova rates are very broad bounds, which account for a more complete GW network than the GW or GRB rates shown in this table. The low end is bound by a base recovery fraction of the low end of the GW detection rates and on the high end by assuming recovery of the majority of intrinsic event rates within a fixed distance. The detections of kilonova following SGRBs assume KN170817-like events and the fraction of SGRBs with measured redshift from following within the maximum detection distance for an assumed sensitivity.
In broad strokes, all the canonical signals from NS mergers are brighter when observed from a polar position than an equatorial one. In Sect. 2.6 we discuss the effects of inclination bias on joint GW-GRB detection rates, where SGRBs are only visible when Earth is within the jet and GWs are stronger along the total angular momentum axis. Observed kilonova brightness also depends on the inclination angle (e.g., Kasen et al. 2017). If polar ejecta is faster moving than the equatorial ejecta then its brightness is fairly constant regardless of the observer angle. If it is slower then its emission is obscured when viewed from an equatorial region (e.g., Kawaguchi et al. 2020). Equatorial ejecta is brighter when viewed on-axis due to viewing a larger cross section. These conclusions hold for most putative signatures as well (e.g., MeV neutrinos from a thick disk). Overall this may be viewed as a beneficial selection effect for multimessenger astronomy and will result in a larger sample of particularly well characterized events, but will induce biases that must be handled carefully for some science (e.g., standard siren cosmology).
3 Astrophysical inferences
From the observable parameters for individual events, we may make a number of additional inferences and draw new information from combined information. Section 3.1 discusses the observations that allow identification of NS mergers and classification into BNS and NSBH mergers; and Sect. 3.2 discusses how to determine the immediate remnant object formed in BNS mergers. The potential contribution to the origin of the observed time delay between the GW and GRB emission is discussed in Sect. 3.3. The origin of the early bright UV/blue emission in KN170817, and potential contributions to future events, is discussed in Sect. 3.4. Lastly, how to determine where these events occur, both in spatial position and redshift, and the inferences this information allows with respect to formation channels, stellar formation and evolution, and redshift determination for individual events is discussed in Sect. 3.5.
3.1 Progenitor classification and the existence of neutron star–black hole systems
There is no known NSBH system. These systems are thought to be formed through the same field binary formation channel as BNS systems (which we know exist), where instead the primary remnant is either born a BH or becomes one through accretion during the common envelope phase. Determining the astrophysical rates and intrinsic properties of these systems has important implications for the science that can be done with NSBH mergers.
As discussed in Sect. 2.1.3 some NSBH mergers are not expected to have EM signals. Based on current population synthesis models for intrinsic system parameters, the inferred BH spins from LIGO/Virgo observations, and our understanding of which systems will release NS material to power the EM transients it seems likely that EM-dark NSBH mergers exist and that EM-bright mergers could exist (e.g., Foucart 2020). Once we have observed them, they provide a separate handle on stellar evolution (Sect. 3.5), may enable a precise determination of NS radius in a NS merger (Sect. 7.1.4), and may allow for some more stringent measures of fundamental physics (e.g., speed of gravity) with a given network sensitivity (Sect. 8). As they can be detected through GWs to greater distances and are phenomenologically different, they would require different EM capabilities to understand.
Classifying events as BNS or NSBH mergers is critical to ensure pure samples and understanding how these events differ. GW detections of CBC provide information on the progenitor masses. Events with the primary constrained to be under the maximum mass of a NS can be assumed to be BNS systems. Events with the secondary constrained to be over this value can be classified as BBH mergers. This value is currently not known (see Sect. 7.2) but is almost certainly between 2 and 3\(M_{\odot} \). Systems with one mass below this value and one above can be classified as NSBH mergers.
These classifications assume that there are no exotic stars in this mass range and that there is a clear separation between NS and BH masses. For low-mass systems we will tend to precisely measure the chirp mass but poorly measure the mass ratio (unless the event is particularly nearby/loud), so we may expect a significant fraction of events to have inferred individual mass posteriors that cross this boundary. This mass range is particularly difficult to precisely constrain for most events as was shown in Littenberg et al. (2015) who investigate the possibility of probing the existence of the first mass gap of compact objects, i.e. the lack of known NS or BH between \(\sim \) 2 and \(\sim \) 5 \(M_{\odot} \). Assuming this gap exists would make GW classification easier, but this is a strong assumption to make.
Further, the first GW detections of NS mergers require a higher standard of proof for strong classification claims. GW observations can conclusively distinguish between progenitors by finding or ruling out matter effects on the inspiral, characterized by the tidal deformability parameter \(\varLambda \). Constraining this value to be non-zero would exclude a BBH merger and classify the event as a NS merger. Determining between BNS and NSBH merger would then rely on the mass constraints of the primary.
The difficulty of GW measurement of tidal deformability with the current high-frequency sensitivity is demonstrated with GW170817 as despite being one of the loudest events detected thus far and utilizing the precise position from the kilonova detection the final LVC results cannot rule out a BBH merger origin from GW observations alone (Abbott et al. 2020b). In fact, the LVC discovery paper for GW170817 comments that the GW observations alone do not classify the event as a BNS merger, relying on the information provided by the EM counterparts and to make the firm claim (Abbott et al. 2017c), which additionally relied upon the assumption that BHs do not exist in this mass range (Hinderer et al. 2019; Coughlin and Dietrich 2019). For NSBH mergers the inspiral can be dominated by the heavier BH and appear similar to a BBH merger (e.g., Foucart 2020). GW-only classification of these events will not be unambiguous for a large fraction of these events until they achieve sensitivity at higher frequencies.
In the O3 observing run LIGO and Virgo reported the GW trigger GW190814 (Abbott et al. 2020c) which demonstrates many of these difficulties. The precisely determined secondary mass requires the object to be either the heaviest known NS or the lightest known BH, but it cannot be assigned to either class as the boundary between the two is unknown. The precise secondary mass measurement was enabled by a large mass asymmetry and the loud signal, but no evidence for matter effects was observed.
MeV neutrino observations provide another potential direct determinant of the presence of a NS, or even determination of a BNS progenitor if it observes the (meta-)stable NS remnant, but these detections will be very rare for at least a decade (Sect. 2.10).
Given these difficulties, multimessenger detections provide a solution. If there is an associated SGRB we can immediately infer the presence of at least one NS. If the inferred BH mass is sufficiently heavy then the GW-GRB observations can classify the event as a NSBH merger. Otherwise, they can only conclusively state the system is not a BBH merger. This information may be useful in real-time to prioritize follow-up observations once we are in an era where GW-detections of NS mergers are a regular occurrence. There have been searches for quasi-periodic oscillations in prompt SGRB emission (Dichiara et al. 2013), which may occur in NSBH mergers if the spin-axis of the BH was misaligned with the orbital angular momentum axis (Stone et al. 2013). However, it is unknown if the accretion disk will align with the BH equator and precession of the jet may or may not occur (Liska et al. 2017, 2019) in NSBH mergers.
Kilonova observations will provide the strongest indirect evidence for system classification. The predictions for the inferred ejecta mass, average velocity, and electron fraction differs for NSBH mergers and BNS mergers. Delineation between the progenitors and remnants will have to rely on combinations of ejecta mass, velocities, kilonova color, and multimessenger determination of inclination (Barbieri et al. 2019, 2020). A self-consistent picture with GW-determined masses SGRB and kilonova observations will strengthen such claims.
3.2 The immediate remnant object in binary neutron star mergers
In NSBH mergers the remnant object will always be a BH because one already exists. In BNS mergers we have the previously discussed (Sect. 2.1.3) four cases: Stable NS, SMNS, HMNS, and prompt collapse to a BH. Determining what mergers produce which immediate remnant objects is key to understanding NS mergers themselves and informs on the NS EOS studies, our understanding of the central engines of ultrarelativistic jets, the heavy element yield distribution, and biases in standard siren cosmology. Figure 9 summarizes the expected differences, collating information from several sections (2.1.2, 2.1.3, 2.1.4, 2.1.5) and is relied upon throughout the paper. While the text and figure represent generally robust expectations and are based on the current understanding of these cases, these will invariably be updated as future multimessenger detections occur and simulations improve. Some current limitations are discussed in Sect. 5.
The key expected signatures for the different classes of NS mergers. Left to right corresponds to increasing mass: BNS mergers classed into a Stable NS, SMNS, HMNS, or prompt collapse scenarios, then EM-bright NSBH mergers and lastly EM-dark NSBH mergers. The differing prompt SGRB and kilonovae signatures are shown for each scenario, providing a potential method to distinguish them. Dashed lines indicate the assignment of this signature to a specific scenario is not yet certain, or that the signature is theoretically expected but not yet confirmed observationally. The geometric representations are approximate and intended only as guidelines
Directly classifying remnants can likely only be done with GW or neutrino signals. With neutrino observations we could infer a NS remnant because the \(\sim \) MeV neutrino flux would be in excess of that from the accretion disk. EeV neutrinos should be emitted at late times around long-lived magnetars. Neutrino detections are unlikely to occur with upcoming neutrino telescopes.
The GW merger frequency and strain evolution could reliably differentiate between most of the four cases. For prompt collapse we expect BH ringdown at \(\sim \) 6–7 kHz and an immediate drop in amplitude. For (meta)stable NS remnants the merger would occur at \(\sim \) 2–4 kHz and significant GW emission would remain after merger. In the HMNS case this emission would cutoff in \(\lesssim \)1 s as the object collapsed to a BH. For the Stable NS and SMNS case the amplitude of the GW emission would decrease as the remnant transitioned to the isotropic rotation phase where secular GWs may be released at twice the rotation frequency, which will slowly decrease with time. Distinguishing between Stable NS and SMNS classes with GW observations is unlikely.
With the planned high frequency sensitivity for the Advanced interferometers it may be possible to detect GW emission from a HMNS remnant at 10–25 Mpc, where 25 Mpc is of order a once a decade event (Clark et al. 2014). A direct GW determination requires improved GW sensitivity up to at least \(\sim \) 4 kHz. The A+ upgrade (and similar upgrades) are currently not aiming to be sensitive beyond \(\sim \) 1 kHz. Therefore, we are unlikely to have direct determination of the immediate remnant object within a decade. Then indirect determination using EM observations is the only viable option. Fortunately, there are expectations for significant EM signal variation between remnant classes, guided by theory and simulation.
Below we summarize how the kilonova, SGRBs, and other EM signatures are expected to vary depending on the immediate merger remnant. Because these rely on model-dependent predictions on the behavior of matter in extreme regimes and the scientific results we wish to claim have incredibly important implications, we require a self-consistent understanding to emerge from these distinct predictions and the GW determined masses.
Kilonovae will be the most common EM counterpart, and they should vary significantly between remnant classes. The understanding of the expected differences has come about over the past decade of improvements in simulation and theoretical understanding. The subject was broached with regards to disk winds in Metzger and Fernández (2014), refined for general ejecta type in Metzger (2020), and well described in Margalit and Metzger (2019) and Kawaguchi et al. (2020). We summarize those arguments here and plot representative early spectra to show how this can be done. We emphasize that these are representative cases and variation on observed emission within a specific remnant class is expected to be significant depending on orientation effects, the mass, mass ratio, spins, etc.
However, the underlying differences are robust. In general, the longer the remnant NS lives the more total ejecta will be unbound and it will be systematically bluer. Given enough time, the tidal tails become spiral arms that collide with the dominant NS mass and are released. In the HMNS case ejection at the shock-interface terminates during collapse, but it can continue in the lower-mass cases. The disk-wind ejecta increases with lifetime as a higher fraction of its total mass is unbound. The massive neutrino luminosities alter the electron fraction for much of this ejecta. These are all generic outcomes.
Second, it also will help resolve the origin of the early UV emission. The origin of the early bright UV/blue emission in KN170817 is generally debated. As discussed in detail in Sect. 3.4 the resolution to this question should not affect the relative differences between the cases discussed above, as the UV brightness expected for different models generally scales with NS remnant lifetime. One potential exception is if magnetars cannot power SGRBs, meaning we would only expect jet interactions in the HMNS case.
Representative early spectra for the Stable NS and SMNS, HMNS, and prompt collapse cases for events at 100 Mpc. We here assume KN170817 originated from a HMNS remnant and represent this case with the finely tuned model from Kasen et al. (2017). The spectra for the prompt collapse and Stable NS/SMNS cases are generated using the toy kilonova model described in Metzger (2020), using the code to generate the lightcurves in Villar et al. (2017), and were generated by P. Cowperthwaite (private communication). The Stable NS/SMNS case was generated assuming ejecta mass with the properties \(M_{ej}^\mathrm{Blue} = 0.1\,M_{\odot} \), \(v_{ej}^\mathrm{Blue} = 0.3c\), \(\kappa ^\mathrm{Blue}=0.1\,\mathrm{cm}^{2}/\mathrm{g}\) and \(M_{ej}^\mathrm{Red} = 0.005\,M_{\odot} \), \(v_{ej}^\mathrm{Red} = 0.25c\), \(\kappa ^\mathrm{Red}=10\,\mathrm{cm}^{2}/\mathrm{g}\). The prompt collapse case has \(M_{ej}^\mathrm{Red} = 0.005\,M_{\odot} \), \(v_{ej}^\mathrm{Red} = 0.25c\), \(\kappa ^\mathrm{Red}=10\,\mathrm{cm}^{2}/\mathrm{g}\), which neglects a potential subdominant blue component
Kawaguchi et al. (2020) focus on timescales between about a day and a week post-merger and conclude that the peak timescale and luminosity of the infrared emission may enable delineation between the remnant classes. In Fig. 10 we show early spectra for the different cases using representative parameters from Sect. 2.1.3. The early UV/blue emission should very easily distinguish prompt collapse from other scenarios for any observation in the first day or so. The fast evolution of the peak in the HMNS case can be distinguished from the Stable NS/SMNS case, as the latter should brighten over time. This method is advantageous as the initial classification can be done relatively soon after merger, allowing for follow-up prioritization and more precise inferences based on the more complete dataset.
SGRB observations will provide complementary information on the remnant object, and may provide a key signature to discern between a fully Stable NS and a SMNS remnant. It is debated if magnetars can power SGRBs (discussed in Sect. 4.2).
If magnetars cannot power ultrarelativistic outflows, we would only ever observe SGRB emission from mergers that undergo prompt collapse or have a HMNS, where in the latter case the jet will not launch until the NS has collapsed. Stated another way, there should never be a SGRB observed in a SMNS or Stable NS remnant case. We would also observe the non-thermal plateau emission in the HMNS and prompt collapse cases, which would require work to identify its origin.
If magnetars can power ultrarelativistic jets then SGRB observations still provide distinguishing characteristics. The non-thermal signatures of extended emission following the prompt peak and X-ray plateaus in the afterglow suggest late-time energy injection into the jet and led to the development of magnetar central engine theory (this is discussed in Sect. 4.7). Then, we should expect to detect these signatures only in the Stable NS and SMNS remnant cases, and will not observe them in the HMNS or prompt collapse cases. A sharp drop in X-ray flux at the end of the plateau is thought to occur when the NS collapses, providing an observational signature between a Stable NS and SMNS remnant. The X-ray plateaus have been modeled by late-time fallback accretion, but we should be able to distinguish this from a magnetar central engine (see discussions and references in Sect. 4.7).
The time delay from GW to GRB emission is another key piece of distinguishing information, which may provide another way to disentangle what occurs in these sources. From Zhang (2019), the time delay could be up to \(\sim \) 10 s in cases with a magnetar central engine. This is roughly the timescale for the hot NS to cool enough to stop driving baryons from the surface, enabling a clean enough environment for the jet to launch. In other cases the time delay should not exceed a few seconds.
In additional to the potential plateau signature, there are other methods of distinguishing between the Stable NS and SMNS cases. Long-lived remnants will result in a significantly brightened kilonova signature, which could distinguish the cases as Stable NS remnants will be even brighter than SMNS remnants (e.g., Yu et al. 2013; Metzger and Piro 2014; Metzger et al. 2018). There may be an increase in the radio emission from the quasi-isotropic outflow interactions with the circumburst material \(\sim \) years after merger (Metzger and Piro 2014; Fong et al. 2016). There may be differences in the \(\sim \) EeV neutrino emission weeks after merger (e.g., Gao et al. 2013; Murase et al. 2018).
To summarize, with current planned instruments a direct determination of the remnant object for all but the most fortuitous mergers is unlikely for a decade. Until then, we can rely on broadband EM observations to characterize these events. Should a self-consistent picture emerge between the observed kilonova, GRBs, and other signature behavior with the inferred masses from GW observations then we can reliably infer the remnant object outcome indirectly. As much of the science from NS mergers relies on remnant object classification and it likely has significant effects on the observed signatures, determination of the merger remnant for a sample of events is a key goal of observations of NS mergers.
3.3 The time delay from merger to prompt gamma-ray burst emission
The total observed time offset for two astrophysical messengers is
with \(\varDelta t_{\mathrm{intrinsic}}\) the intrinsic time delay which is affected by cosmological time dilation \((1+z)\) and \(\varDelta t_{\mathrm{propagation}}\) the induced arrival delays caused during propagation of the messengers from source to observation. Much of the science in this paper relies on \(\varDelta t_{\mathrm{GRB-GW}}\), the observed time offset from the coalescence time as measured by GW measurements and the on-set of the prompt gamma-ray emission. Separating the individual contributions to this term could enable us to determine or better constrain the lifetimes of HMNSs, the speed of gravity, and the emission mechanism of SGRBs, to name a few.
We will show that possible propagation effects for GW to SGRB reduce to violations of fundamental physics. So far these all appear to be zero, which simplifies separation of the total individual terms. Should the propagation term be non-zero we can separate them from intrinsic delays as the cosmological redshift effects on the latter should be negligible for the foreseeable future. Alternatively, if they are hard to disentangle we may require future GW interferometers to detect NS mergers to distances where the redshift will become the dominant term. However, the relevant fundamental physics currently seems rather well supported. We discuss the intrinsic and propagation delay for GW to SGRB emission separately. We discuss the individual terms to show how we can distinguish the relative contributions of each term, or separately constrain their maximal effects.
For BNS mergers we can write (assuming the standard GRB BH central engine, relativistic jet, internal shock scenario):
\(\varDelta t_{\mathrm{collapse}}\) is the time from coalescence to the formation of the BH; \(\varDelta t_{\mathrm{collapse}}\approx 0\) if the event undergoes prompt collapse, else \(\varDelta t_{\mathrm{collapse}} \lesssim 1\,\text{s}\) in the HMNS case. \(\varDelta t_\mathrm{formation}\) is the time until jet formation once the BH has formed, which is expected to be \(\lesssim \)1 s (limited by the cooling time in the neutrino powered jet scenario and the accretion timescale in the magnetically powered case; see Sect. 4.3). If there is previously ejected material in the polar region then the newly formed jet must breakout, where \(\varDelta t_\mathrm{breakout} \approx 1\,\text{s}\) following known closure relations (from Nakar et al. 2012 as applied to SGRBs in Abbott et al. 2017b). Lastly, the jet must propagate outwards until the prompt SGRB emission. The various SGRB emission mechanisms (Sect. 4.6) usually require at least a few minutes of propagation, but with typical bulk Lorentz factors of \(\varGamma \approx 100\) the jet effectively matches the speed of the GWs and the observed time delay is short (generally of order the duration of the burst).
Equation 11 can be modified for different NS merger cases. Another formulation more useful for GRB-specific studies is described in Zhang (2019); we do not use this here for clarity with our immediate remnant object discussion. If magnetars can power SGRBs then \(\varDelta t_{\mathrm{collapse}}\) should be removed from the discussion. In cases with little polar ejecta (prompt collapse BNS and NSBH) \(\varDelta t_\mathrm{breakout}\) is negligible. These differences should enable us to disentangle the relative importance of these individual terms. For example, NSBH mergers have \(\varDelta t_{\mathrm{collapse}} = \varDelta t_\mathrm{breakout} = 0\). Should we observe a particularly short SGRB then \(\varDelta t_{\varGamma }\) is small and \(\varDelta t_{\mathrm{intrinsic}} = \varDelta t_\mathrm{formation}\).
One can write a very general equation to capture the total possible propagation effects:
where each term captures induced relative delay during propagation by different effects: \(\varDelta t_{\varDelta v}\) represents different intrinsic velocities, \(\varDelta t_\mathrm{LIV}\) Lorentz Invariance Violation (LIV), \(\varDelta t_\mathrm{WEP}\) relative Shapiro delay, \(\varDelta t_\mathrm{massive}\) capturing velocities of massive particles with a given energy according to Special Relativity (SR), \(\varDelta t_\mathrm{dispersion}\) for dispersion, \(\varDelta t_\mathrm{deflection}\) the delay induced for magnetic deflection of charged particles, and \(\varDelta t_\mathrm{other}\) represents other effects or the unknown. Note that some of these terms are subsets of the other; they are separated in this manner for pedagogical purposes, but see Sect. 8 for a full explanation.
For GWs and SGRBs we can neglect several of these terms. That is, \(\varDelta t_\mathrm{deflection}=0\) because (inter)galactic plasma and magnetic fields do not affect \(\sim \) MeV gamma-rays nor GWs. The gamma-rays have \(\varDelta t_\mathrm{dispersion}=0\), but the GWs may not. We assume \(\varDelta t_\mathrm{other}=0\) for simplicity. This then leaves
These terms correspond to specific violations of fundamental physics. \(\varDelta t_{\varDelta v}\) is the induced propagation delay for \(v_{\mathrm{GW}} \ne c\). \(\varDelta t_\mathrm{LIV}\) is for different LIV by gravity and light; \(\varDelta t_\mathrm{WEP}\) is the same except for the Weak Equivalence Principle (WEP). \(\varDelta t_\mathrm{massive}\) is the delay induced for a graviton with non-zero mass; and \(\varDelta t_\mathrm{dispersion}\) capturing other potential forms of GW dispersion. Each of these terms and the scientific importance of determining them is discussed in subsections in Sect. 8.
By convention, limits on individual fundamental physics terms are set by assuming the other contributions are 0. Should any of these terms be non-zero a sample of events will be required to determine relative contributions, which is possible because the separate possible propagation terms are most strongly dependent on different parameters.
The precision of the tests of fundamental physics (Sect. 8) that rely on the GW-GRB time offset is determined by how accurately we can model the intrinsic time offset for the event of interest, the redshift, and the observed time offset. We can remove the cosmological time dilation of \(\varDelta t_{\mathrm{intrinsic}}\) if we know z, or calculate z from a known distance and an assumed cosmology. Redshift is likely negligible during the Advanced interferometer era. For the A+ era it may begin to be important, and could become the dominant effect for third generation interferometers.
The observed time delay from GW170817 to GRB 170817A. The top panel is the 50–300 keV lightcurve from Fermi GBM and the bottom is a time-frequency map from combining the LIGO observations. Figure is from NASA Goddard which is modified from Fig. 2 in Abbott et al. (2017b)
The total intrinsic time delay is expected to be a few seconds (e.g., Zhang 2019), and potentially up to 10 s in extreme scenarios. Separately constraining the different contributions to the intrinsic time delay unveils great insight into these events (e.g., Li et al. 2016; Abbott et al. 2017b; Zhang 2019). The more precisely we can determine the intrinsic time delay the greater our constraints on fundamental physics. Before GW170817 the LVC prior on this time offset was \([0, +4]\,\text{s}\) with a 1 second addition on either side for safety (e.g., to account for light travel time from distance spacecraft or differing GRB triggering methodologies; see Abbott et al. 2017b and references therein). The time offset from GW170817 to GRB 170817A fell right in the middle of this range, as shown in Fig. 11.
When this redshift is accounted for, and allowing for two-sided constraints, we write \(\varDelta t_\mathrm{intrinsic,z}^{\pm } = \varDelta t_{\mathrm{intrinsic}}^{\pm }(1+z)\). Throughout this paper we assume \(\delta t_{\mathrm{intrinsic,z}} = 2\) s for individual events, giving 1 s uncertainty for two-sided constraints. This is only twice the precision of the prior set by the LVC based only on theory prior to GW170817 (Abbott et al. 2017g). This assumption also makes the results easily scalable, should this precision be unachievable for some events, given each side of a two-sided constraint are set to 1 s precision. This assumption is used in Sect. 8.
3.4 The origin of early ultraviolet emission
The observations of KN170817 were broadly consistent with a two-component kilonova: bright blue emission that peaks on the order of a day which fades to redder emission that peaks on the order of a week before fading out of detectability. It was brighter and bluer than expected, including a somewhat surprising UV detection half a day post-merger (Evans et al. 2017). The origin of this emission is debated. Metzger et al. (2018) and Arcavi (2018) discuss most of the theoretical explanations that have been invoked, their successes and limitations, and how future early UV/blue observations can resolve this question. We summarize the options below but refer to these papers for more detail.
The most basic explanation is a kilonova origin for the emission (Villar et al. 2017). This is potentially feasible but has some difficulties, which led to the discussion of other models (e.g., Metzger et al. 2018; Arcavi 2018). Before proceeding we point out a peculiar outcome of these theoretical models: in all cases we may expect the brightest early UV/blue emission to occur for BNS mergers with Stable NS, SMNS, and HMNS cases (in expected brightness listed in decreasing order) with little to no early bright UV/blue emission from prompt collapse or NSBH mergers. This may complicate delineation between these models, but has the benefit that the phenomenological description on indirectly differentiating between BNS merger remnants (Sect. 3.2) is unaffected by the true origin of the early bright UV/blue emission in KN170817.
Jet-interaction effects were invoked by a few teams (e.g., Evans et al. 2017; Kasliwal et al. 2017). In these models the jet is launched after material already exists in the polar region. This can release a portion of very high velocity radioactive ejecta which allows the light to escape much earlier and can provide an additional source of energy through shock-heating. If magnetars can power SGRBs (Sect. 4.2) then we expect jet interaction effects in the Stable NS, SMNS, and HMNS cases with the amount of polar material related to the lifetime of the NS. If magnetars cannot power ultrarelativistic outflows then we only expect jet interactions in the HMNS case. The BNS prompt collapse and NSBH mergers should not have significant material in the polar regions at jet-launch time and should thus have much dimmer blue emission compared to the other cases. However, this model struggles to reproduce the observations of KN170817 as it would require jet kinetic energies beyond anything previously seen (Metzger et al. 2018) but may impart observable signatures in future events.
Metzger et al. (2018) argue the emission can be explained by a neutrino-heated, magnetically accelerated wind from a short-lived magnetar, resulting in mildly-relativistic outflows. Again brightness scales with remnant NS lifetime. Observing a more traditional SGRB or directly inferring relativistic motion through radio interferometry observations or detection of high energy photons can clearly distinguish between these possibilities.
Lastly, free neutrons decay as \(n^0 \rightarrow p^+ + w^- \rightarrow p^+ + e^- + \bar{\nu }_e\) with a half-life of \(\sim \) 10 min. If the fastest moving initial neutrons escape capture they lead the ejecta material, allowing the majority of their decay energy to escape while the photospheric temperatures are still high. This can provide a very blue signature that peaks on the timescale of \(\sim \) hours, before kilonova emission, with a comparable peak luminosity (Metzger et al. 2014). This model is applied to KN170817 in Metzger et al. (2018).
Both Arcavi (2018) and Metzger et al. (2018) point out that early UV and optical observations should be able to distinguish between these potential contributions as their temporal and spectral evolution differ. GRB observations will provide additional information on distinguishing jet interaction effects from the other models. Early UV emission may arise from combinations of these potential contributions.
3.5 Host galaxy, redshift, and where neutron star mergers occur
Understanding where these events occur determines their source evolution and thus the (volumetric and detection) rates of these events through cosmic time, inform on their formation channels, and provide information on stellar evolution through constraints on rare evolutionary pathways. The best current observational evidence to answer these questions come from observations of SGRB afterglows, which provided the strongest evidence tying these events to NS mergers prior to GRB 170817A; for an overview see Fong et al. (2015). For a study on how GRB 170817A compares to these observed distributions see Fong et al. (2017). For reviews on the formation channels of BNS systems see Lorimer (2008), for reviews on compact object binaries see Kalogera et al. (2007), Postnov and Yungelson (2014). The standard formation channel for NS mergers is described in Sect. 2.1.1. See Belczynski et al. (2002) for a discussion on other possible formation channels.
There are two methods to determine the redshift of GRBs. The first is from direct measurement of redshift from the afterglow itself. This is common for LGRBs but has only occurred twice for SGRBs, due to the lower overall brightness. The second method is through statistical association to a host galaxy, and then determining the redshift of that galaxy (e.g., Fong et al. 2015, and references therein).
The natal kicks during supernova explosion send a large fraction of NS mergers outside of their host galaxies. More SGRBs are observed outside of the half-light radius of the inferred host galaxy than within, with typical physical offset \(\sim \) 10 kpc and the largest inferred of 75 kpc (see Fong and Berger 2013, and references therein). The assignment of a host galaxy is relatively robust when it is within the half-light radius, and becomes more difficult as the offset increases. The assignment is probabilistic, counting the likelihood of a chance alignment of the source with likely host galaxies. Note that we observe the 2D projection of the 3D offset, e.g., for an event 10 kpc from the host galaxy we can observe it anywhere from 10 kpc offset to directly aligned, depending on our viewing geometry. There is no way to directly separate this effect.
The assignment of a SGRB (or kilonova) to a host galaxy requires localizations with \(\sim \) arcsecond accuracy to be robust. Swift XRT localizations are not sufficient, as the chance alignment of galaxies within typical error regions is non-negligible. There are some SGRBs where no robust host galaxy assignment can be done as there are no potential hosts very nearby in 2D angular offset (\(\lesssim 1'\)), despite deep observational searches. These hostless SGRBs have bright galaxies somewhat nearby in 2D offset (\(\sim \) few arcminutes) in excess of random chance, suggesting at least some belong to these galaxies (Tunnicliffe et al. 2013). This creates an observational bias against associating some particularly nearby SGRBs with their true host galaxy, which is shown in Fig. 12. That is, for a fixed intrinsic offset the maximum observed 2D offset (the vector from host to source being perpendicular to that of host to Earth) can vary by more than an order of magnitude over the observed distance range for SGRBs. This directly corresponds to the host association probability. There is also the obvious bias of more difficult host galaxy detection for distant events.
Both arcseconds per kpc and kpc per arcsecond as a function of redshift. This figure shows how we require arcsecond precision for distant events to distinguish host from source, and we may fail to associate nearby events as the probability of this depends on the observed 2D offset for a fixed distance. The black dashed line is the distance to NGC 4993, the grey line is the distance to the furthest claimed redshift for a SGRBs
The figure also demonstrates that the largest inferred intrinsic offset of 75 kpc at the distance of GW170817 would have a 6’ offset from the host galaxy. With EM-only observations we could not associate the source to host in this circumstance. Distance determination through GW observations will alleviate these issues and will resolve some systematic problems with redshift determination of SGRBs (and NS mergers) These observations require sensitive spectrometers, such as the X-shooter instrument on the VLT.
The cosmic rate evolution of NS mergers is not well known. The peak cosmic star formation rate occurred at a redshift of \(\sim \) 1.5–3.0 (e.g., Hopkins and Beacom 2006, or Madau and Dickinson 2014a for a review). We expect the peak rate of NS mergers to track the peak star formation rate modulo the average inspiral time (the lifetimes of massive stars that result in Compact Objects (COs) are negligible). SGRBs will provide the only constraints on the source evolution of NS mergers for at least the next decade. The observed median redshift for SGRBs is inferred to be \(\langle z \rangle_{\rm SGRB} \approx 0.5-0.8\) (Berger 2014), which corresponds to an average inspiral time of \(\lesssim \)5 Gyr; this is a lower limit on the average redshift due to the Malmquist bias and the detection threshold of BAT.
Population synthesis studies are being provided with much improved data from EM observations to test data against (e.g., Brown et al. 2018; Bellm 2014; Ivezić et al. 2019). This will be commensurate with GW observations from LIGO/Virgo and in the future by additional ground-based interferometers and LISA. GW and EM detections of BNS and NSBH mergers will provide some unique information (e.g., Belczynski et al. 2008) to the overall understanding of how stars form and evolve (e.g., Abbott et al. 2017f). The formation channels can be tested from these studies and by greater understanding of the source evolution of these events. However, results on the inspiral time distribution may require \(\sim \) 100 nearby events (Safarzadeh et al. 2019). A detailed description of the input physics and how they are constrained with GW observations of BNS, NSBH, and NSBH mergers is given in Kruckow et al. (2018).
One example is the primary mass gap, i.e., the idea that there is a gap between the heaviest NSs and the lightest BHs (Belczynski et al. 2012). This is borne from the lack of observed compact objects between 2 and \(5\,M_{\odot}\). With the NS merger determination of the maximum mass of a NS (Sect. 7.1.1) we can set a strict boundary threshold. Then, if the mass gap does not exist we would expect to eventually detect a loud CBC merger with a BH posterior contained within the putative mass gap. If it does exist then this would never occur. This would have a number of important implications from the CCSNe mechanism (Belczynski et al. 2012), that implication on stellar evolution, and potentially robust CBC classification from GW-only observations.
This understanding has implications for future detection rates of these events. The SGRBs detection rate is empirically determined and unaffected, but the GW detection rates for Voyager or third generation ground-based interferometers are altered significantly by the evolution of the rates of these events. Further, this has implications for other outstanding questions. Perhaps the best example is the origin of heavy elements, which depends on the source evolution as the modern abundances are determined by the time-integrated history of their creation rate (Sect. 5).
4 Short gamma-ray bursts and ultrarelativistic jets
During the cold war the Vela satellites were launched to monitor Earth for gamma-ray signatures of nuclear detonations in the atmosphere to enforce the Partial Test Ban treaty between the United States and the Soviet Union. The detection of GRBs in 1967 were initially slightly concerning, before timing annuli placed their origin as outside the solar system, enabling their declassification (Klebesadel et al. 1973). This was the beginning of the study of GRBs, and therefore the beginnings of our observational study of NS mergers.
The first three decades of GRB study were limited to observations of the prompt phase. The high peak energies, and short duration tended to suggest very energetic phenomena as their source (e.g., Strong et al. 1974; Mazets et al. 1981). A cosmological origin for these events would require energetics well beyond anything previously known which strongly suggested a galactic origin. In Euclidean space the observed flux distribution from sources with a homogeneous distribution is \(P^{-3/2}\). Deviation from this power law would require a source distribution where space is non-Euclidean, i.e., to cosmological distances (Meegan et al. 1992; Mao and Paczynski 1992). Sources with a galactic origin have an anisotropic source distribution concentrated in the galactic plane. Data favored an isotropic, inhomogeneous distribution requiring a cosmological origin, with the Burst and Transient Source Experiment (BATSE) on-board Compton Gamma-Ray Observatory (CGRO) the first to hit discovery significance (Briggs et al. 1996).
Another key result from this era was the discovery of two classes, short and long, separated by their prompt duration and spectral hardness (Dezalay et al. 1991; Kouveliotou et al. 1993). This separate has been confirmed by broadband afterglow studies. LGRBs arise from host galaxies, and regions within those hosts, with high rates of star formation (e.g., Fruchter et al. 1999; Le Floc’h et al. 2003; Christensen et al. 2004; Fruchter et al. 2006). Nearby LGRBs usually are followed by a CCSNe (Galama et al. 1998; Cano et al. 2017), giving direct evidence that these events are powered by a subset of CCSNe referred to as collapsars (Woosley and Bloom 2006). SGRBs track older host environments (e.g., Leibler and Berger 2010; Fong et al. 2013), occur outside of their host galaxies (e.g., Church et al. 2011; Fong and Berger 2013), and varied properties of those hosts (e.g., Gehrels et al. 2005; Fong et al. 2013) all matched expectations from NS mergers (e.g., Belczynski et al. 2006). As previously mentioned, the association of GW170817 and GRB 170817A directly confirmed that at least some SGRBs arise from BNS mergers. For a review on these properties see Berger (2014). For a summary of the multiwavelength studies from the first decade of the Swift mission, which largely confirmed these predictions, see Fong et al. (2015).
The measured isotropic-equivalent energetics for GBM GRBs with measured redshift. \(L_{\mathrm{iso}}\) is the peak 64 ms luminosity; \(E_{\mathrm{iso}}\) is the total energetics measured over the burst duration. GRB 170817A is both the closest and the faintest by large margins. This figured is modified from Fig. 4 in Abbott et al. (2017b)
With base values the observed fluence of GRBs at Earth from cosmologically distant GRBs would require intrinsic isotropic-equivalent energetics of \(\gtrsim 10^{50}\,\text{erg}\). The prompt emission of GRBs have small intrinsic variability timescales, with the most extreme values being sub-millisecond (e.g., Bhat et al. 1992). Structure at this timescale constrains the size of the central engine, in the non-relativistic case, to \(R \approx c\delta t \lesssim 300\,\text{km}\), requiring a compact central engine. This amount of energy being emitted from such a small volume would result in an enormous opacity for \(\gtrsim \)MeV photons due to pair creation, i.e., \(\gamma + \gamma \rightarrow e^+ + e^-\). The resulting spectrum then must be thermal, incompatible with observations. Paczynski (1986), Goodman (1986) stepped through these issues and determined that GRBs from cosmological distances require bulk relativistic motion. As calculated through various means, typical values of the bulk Lorentz factor \(\varGamma \) are \(\sim \) 100 (e.g., Fenimore et al. 1993; Baring and Harding 1997; Lithwick and Sari 2001; Hascoët et al. 2012).
It was hypothesized that the fast outflows from GRBs would interact with the surrounding matter, emitting synchrotron radiation at lower energies (Paczynski and Rhoads 1993). The first detections of GRB afterglow by BeppoSAX confirmed the cosmological origin by localizing events to distant host galaxies (e.g., Van Paradijs et al. 1997; Reichart 1998). Tying specific bursts to specific distances enables a direct determination of the intrinsic isotropic energetics with some approaching a few times \(10^{54}\,\text{erg}\)s (Fig. 13), which is an energy equivalent to the total mass of the Sun after all of the relevant efficiency factors have been accounted for. This strongly suggested that the emission was not isotropic.
It is now known that the bulk relativistic outflow from GRBs is not isotropic, but is collimated into jets. The isotropic-equivalent energetics are corrected by the factor \(1-\cos (\theta _j)\) where \(\theta _j\) is the half-jet opening angle. With a representative values of \(\theta _j=1-10\,\text{deg}\) this reduces the required energetics by \(\sim 10^2\)–\(10^4\) (e.g., Sari et al. 1999; Frail et al. 2001; Panaitescu and Kumar 2001; Racusin et al. 2009; Cenko et al. 2010). Observational evidence in favor of relativistic jets as the origin of GRBs includes constraints on the angular size from the detection of radio scintillation (Goodman 1997; Frail et al. 1997) and direct measurement of superluminal motion of compact emitting regions in both long and short SGRBs (Taylor et al. 2004; Mooley et al. 2018).
We can determine the collimation angle by measuring the jet-break with afterglow studies (Rhoads 1997). The afterglow undergoes early temporal decay that is somewhat counteracted by the increase in the observable region due to the change in Doppler beaming, \(1/\varGamma \), as \(\varGamma \) slows due to jet interaction with the circumburst material. Once the beaming angle encompasses the entire jet the temporal decay steepens to the intrinsic value. This signature was first observed in LGRBs in the late 1990s (Kulkarni et al. 1999; Fruchter et al. 1999; Harrison et al. 1999) while jet-break measurements for SGRBs required the Swift era, where a sample now suggests a typical half-jet opening angle for SGRBs of \(\sim 16\pm 10\,\deg \) ( Fong et al. 2015, and references therein). These jet-break measurements relied on a top-hat model, which is consistent with observations for these GRBs.
The preceding paragraphs discuss the understanding of GRBs that is generally agreed upon. However, there are many important questions related to GRBs that remain unresolved. For a thorough and quantitative discussion on GRBs in general see Kumar and Zhang (2015) for a review article and Zhang (2018) for a book. These publications discuss a number of key outstanding questions relevant to understand GRBs. Multimessenger studies of NS mergers, especially those with detected SGRBs emission in the prompt or afterglow phase, may provide new pieces of information to answer these questions. Section 4.1 focuses how GW-GRB studies can probe the types and relative contributions of progenitors of GRBs. Section 4.2 discusses the possibility of magnetar central engines for ultrarelativistic jets. Determining the possible formation mechanisms for these jets is discussed in Sect. 4.3. The propagation and structure is explored in Sect. 4.4. Their role in the production of other high energy particles is discussed in Sect. 4.5. How GW observations may help us understand the prompt emission mechanism is provided in Sect. 4.6. Lastly, Sect. 4.7 discusses the other non-thermal signatures seen in GRBs and how we can uncover their origin.
4.1 The progenitors of gamma-gay bursts
As discussed, the circumstantial but convincing evidence enabled by the Swift mission tied most SGRBs to a NS merger origin. There are two key questions where GW observations and multimessenger studies may improve this question. The first is the direct knowledge of the progenitor system for events detected both in in GWs and as GRBs, as demonstrated by the association of GW170817 to GRB 170817A and the classification as a BNS merger (Abbott et al. 2017b, c). With a larger population of confidently classified events we can constrain the fraction of SGRBs that arise from BNS mergers and those from NSBH mergers, providing a method to determine if their GRBs properties differ.
Second, future GRBs that are determined via EM observations to originate within the BNS merger sensitive volume for the GW network can be conclusively classified as arising from other sources. There are some events that have some properties of the short class and some of the long class, such as GRB 060614 (e.g., Zhang et al. 2007), where a sufficiently sensitive GW network will confirm or reject a merger origin, providing some insight into these ambiguous events.
Further, some fraction of SGRBs may arise from a different origin. Magnetars are NSs with magnetic fields of order \(\sim 10^{15}\,\text{G}\). Some of them produce soft gamma-ray repeater flares, which are \(\sim 10\,\text{ms}\) long and generally softer than SGRBs (e.g., Lazzati et al. 2005). These magnetars sometimes produce a magnetar giant flare, with three having been observed in the Milky Way and its satellite galaxies (e.g., Mazets et al. 1979; Hurley et al. 1999; Palmer et al. 2005). As noted in Hurley et al. (2005), observing such flares that originate in other galaxies, out to a few tens of Mpc, would result in temporal and spectral properties largely consistent with cosmological GRBs. From basic rates estimates it follows that a small fraction of SGRBs, between \(\sim \) 1 and 10%, are from extragalactic giant flares (Ofek 2007; Svinkin et al. 2015).
There are two previously published SGRBs that are strongly suggested to be extragalactic magnetar giant flares (e.g., Frederiks et al. 2007; Mazets et al. 2008) and an initial report of a third case (LVC 2020). Non-detections by the LVC constrain a NS merger origin for the first two to be beyond the likely nearby host galaxy, reducing the options to a giant flare from that galaxy, a SGRBs from that galaxy with an unknown origin, or chance alignment of a cosmologically distant SGRBs (Abadie et al. 2012a; Abbott et al. 2008). These measurements were interesting with the previous generation of LIGO. As joint observations proceed in the coming years with far more sensitive GW interferometers we can more clearly separate SGRBs arising from different progenitors.
4.2 The central engines of short gamma-ray bursts
As summarized in Kumar and Zhang (2015), viable central engines of GRBs must be able to launch a jet with enormous luminosities, the jet must be relatively clean of baryons to enable ultrarelativistic speeds, and it likely needs to be intermittent to recreate the observed variability timescales and likely able to reactivate to power the later X-ray flares. Based on these criteria, a hyper-accreting stellar-mass BH is generally accepted as a viable option (e.g., Woosley 1993; Popham et al. 1999; Lee et al. 2000; Lei et al. 2017). Magnetar central engines have also been invoked (Usov 1992; Thompson 1994; Zhang and Mészáros 2001) and appear to easily explain observational signatures observed in tens of percent of SGRBs that require late-time energy injection into the system (Sect. 4.7).
So far, simulations suggest this cannot happen as they may fail to meet the second criterion: if the (meta)stable NS remnant lives for \(\gtrsim 50\,\text{ms}\) the neutrino luminosity strips \(\sim 10^{-3}\,M_{\odot} \) of material from the surface of the remnant itself (Dessart et al. 2008; Fernández and Metzger 2016). Even with \(10^{52}\,\text{ergs}\) (\(\approx 0.1\,M_{\odot} c^2\), the rough total mass of the accretion disk) to power the jet, this small amount of baryonic material could only be accelerated to \(\varGamma \approx 10\), an order of magnitude below the typical values expected for SGRBs (e.g., Lee and Ramirez-Ruiz 2007; Murguia-Berthier et al. 2014). However, we note the observational signatures requiring ultrarelativistic outflows for SGRBs is more sparse than in LGRBs, as demonstrated by Ghirlanda et al. (2018) providing a measurement for 1 SGRBs compared to 67 LGRBs. While this baryon loading has not been resolved theoretically, there are potential paths forward (see e.g., discussions in Metzger 2020).
If magnetars can power ultrarelativistic jets then SGRBs may be generated in the low-mass BNS merger cases so long as the remnant object forms a magnetar (Giacomazzo and Perna 2013; Giacomazzo et al. 2015), could alter the kilonova signatures in the Stable NS and SMNS cases due to jet interactions with the polar material and enormous energy deposition into the system during spin-down (e.g., Yu et al. 2013; Metzger and Piro 2014; Metzger 2020). Magnetar central engines have also been studied for a subset of LGRBs (e.g., Bucciantini et al. 2008; Ioka et al. 2016); however, the baryon content issues for collapsars is different than for mergers, and it is possible that magnetars may only be viable central engines in the latter case.
If these magnetars cannot power ultrarelativistic jets, then only higher-mass BNS mergers produce SGRBs, we would only expect potential jet interactions in the HMNS case and it may suggest magnetars cannot power LGRBs. Resolving this question is related to confirming the origin of the additional non-thermal emission (Sect. 4.7) as originating from magnetar spin-down energy or fall-back accretion, would alter EM signatures of the remnant object (Sect. 3.2), and has implications on the inferred properties of the ejecta from kilonova observations and therefore their production of the heavy elements (Sect. 5).
Either way we can use this information to classify BNS remnant cases, but in different ways (Sect. 3.2). Observing a SGRB, with the non-thermal plateau emission, from a BNS merger confidently classified as a Stable NS or SMNS merger is suggestive of a magnetar central engine. Given the various possible explanations for the plateau emission we will require several detections with confident classification to prove magnetars can power ultrarelativistic jets (Sect. 3.2).
Otherwise, we will never observe SGRBs for these events. Approximately 5% of GW-detected NS mergers in the Advanced era will have jets oriented towards Earth with SGRB emission detectable with current (or funded) missions (Song et al. 2019). With the unknown fraction of mergers that result in long-lived magnetars, and the unknown viable viewing angles for the plateau emission, we likely require several tens of GW detections of NS mergers to confidently rule out this possibility. This will likely be resolved in the A+ era.
4.3 Ultrarelativistic jet formation
A related question to the central engines of SGRBs is how the jet itself is launched. With the required bulk Lorentz factors and total energetics seen in GRBs, the jet formation condition requires an enormous energy deposition into environments nearly devoid of baryonic matter, as previously discussed. From Sects. 2.1.3 and 3.2, some NS mergers have relatively empty polar regions (referenced to the total angular momentum axis) providing a natural jet launching site. The viable jet-launch mechanisms depend on the central engine, intimately tying this question to the previous section. As summarized in Kumar and Zhang (2015), there are three mechanisms thought to be viable for BH central engines. We will describe the two most widely discussed options. We refer the reader to that review for more details on all three cases.
One mechanism is through neutrino-antineutrino annihilation (Ruffert and Janka 1998), whereby enormous neutrino luminosities interact as \(\nu + \bar{\nu } \rightarrow e^+ + e^-\) occurs with moderate efficiency and drives a relativistically expanding fireball away from the central engine (e.g., Katz and Canel 1996). The origin of these neutrinos would generally be the thermal emission from the disk which are geometrically exposed to both polar regions. In cases with, providing
with \(\dot{E}\) the annihilation power, M the BH mass, and \(\dot{M}\) the accretion rate (Zalamea and Beloborodov 2011; Lei et al. 2013).
The other commonly discussed option is the Blandford–Znajek mechanism which can extract the rotational power of the BH from the magnetic field of the disk (Blandford and Znajek 1977). These Poynting flux jets appear capable of recreating GRBs observations with representative power
with \(a_{\star} \) the spin parameter \(Jc/GMc^2\) where J is the angular momentum of the BH and \(F(a_{\star} )\) is the spin-dependent function that is often approximated (Blandford and Znajek 1977; Mészáros and Rees 1997; Lee et al. 2000; Lei et al. 2013). Note that in this case the neutrino-antineutrino annihilation energy can still be provided to the jet.
Lei et al. (2013) investigate the capability of these two jet-launch mechanisms to reproduce the bulk Lorentz factor and observed intrinsic energetics seen in GRBs by considering the effects of baryon loading. They find that both mechanisms can produce highly energetic bursts with values spanning order of magnitudes, but that the neutrino-antineutrino case generally results in bulk Lorentz factors lower than has been observed. The high magnetic fields required for the Blandford–Znajek case acts as a barrier preventing protons from entering the jet (Li 2000) resulting in a jet with lower numbers of baryons. Given the much larger mass of baryons, compared with electrons, the higher the baryon content the lower the total velocity of the jet (for a given amount of energy).
If magnetars are to be GRB central engines then the jet launch mechanism is related to the enormous large-scale magnetic field (e.g., Usov 1992; Metzger et al. 2008b). From Metzger et al. (2011), Kumar and Zhang (2015), the initially hot magnetar drives baryons from the surface, preventing the launch of an ultrarelativistic jet. Once it cools and the baryonic wind stops, the rapid spindown generates magnetic energy via a dynamo mechanism, launching the ultrarelativistic outflow. The total available energy for this case is related to the spin energy of the magnetar, \(\sim 2\times 10^{52}\,\text{erg}\), which does not appear violated in the GRBs with plateau emission suggestive of a magnetar origin (Lü and Zhang 2014).
Multimessenger observations of GWs and SGRBs provide new information to investigate the viable jet launching mechanisms. In the magnetar case you would expect a longer time delay from the GW-inferred merger time to the on-set of GRBs emission (Zhang 2019). Remnant classification (Sect. 3.2) may provide conclusive evidence proving the viability of the magnetar mechanism. Delineating between the leading mechanisms to power a GRB with a BH will benefit from (future) direct GW measures on the final BH mass and inferred spin, allowing the input of measured instead of assumed values in the above equations. Considering additional information from kilonova and afterglow observations may enable tighter constraints on other parameters, which in the future may favor one method over the other for individual bursts (e.g., Salafia and Giacomazzo 2020).
4.4 Propagation and structure
Forming a jet also requires some method of collimation. In SGRBs this can be done by matter surrounding the launch site originating from the expansion of the equatorial ejecta or the dynamical ejecta already in the polar regions (e.g., Mochkovitch et al. 1993; Aloy et al. 2005; Nagakura et al. 2014). The observed half-jet opening angle is \(\sim 16^\circ \pm 10^\circ \) (Fong et al. 2015), with a range of observed values from \(\sim 3^\circ \) to \(\gtrsim 25^\circ \). Given solid angle effects the median observed value is wider than the true value.
The top-hat jet model refers to a conical emitting regions with uniform parameters as a function of angle (Rhoads 1997). They have historically been used to model GRBs because they involve (comparatively) simple math and were capable of reproducing (most) observations. However, structured jets of various forms where the properties vary within the jet opening angle have been considered (Mészáros et al. 1998; Rossi et al. 2002; Zhang and Mészáros 2002; Granot and Kumar 2003; Kumar and Granot 2003; Perna et al. 2003; Panaitescu 2005a) and have been applied to some particularly well observed bursts (e.g., Berger et al. 2003; Starling et al. 2005; Racusin et al. 2008).
GRB 170817A had a few unusual properties. Its isotropic-equivalent energetics were several orders of magnitude less energetic than the known sample (see Fig. 13), there was no detection of the X-ray afterglow from the earliest observation at \(\sim \) 0.5 days post-merger (Evans et al. 2017), and was first detected in X-rays nine days later by Chandra (Troja et al. 2017b). Some key observations since this time are discussed below. Several models were invoked to explain these characteristics, which can be classified into three options:
-
A Top-hat Jet GW170817 was so close that we were able to use radio interferometry observations to prove superluminal motion of the main emitting region, confirming compact bulk relativistic motion, proving a successful jet (e.g., Mooley et al. 2018; Ghirlanda et al. 2019). However, in top-hat jets the afterglow fades in time as a power-law, so the lack of detection in X-rays at first observation rules out a top-hat jet origin (e.g., Troja et al. 2017b; Margutti et al. 2017; Fong et al. 2019).
-
A Structured Jets A structured jet origin is the leading explanation remaining for GRB 170817A (e.g., Margutti et al. 2018; Alexander et al. 2018; Hajela et al. 2019b; Nynka et al. 2018; Lazzati et al. 2018; Fong et al. 2019; Troja et al. 2019). In this scenario GRB 170817A is usually referred to as off-axis, implying the most luminous section of the GRB was oriented away from Earth. The long term monitoring of GRB 170817A has allowed for broadband characterization of the temporal evolution from X-ray to radio over years timescales. This has shown a slow temporal rise to a smooth peak followed by the usually decay rate seen from on-axis jets, as expected once the full jet has slowed enough to be fully visible (see Hajela et al. 2019a, and references therein).
-
Cocoon emission refers to the hot envelope that develops around a jet propagating through dense media (Nakar et al. 2012). Some groups invoked a fully choked jet resulting in cocoon (and shock breakout) emission to simultaneously explain the low luminosity of GRB 170817A, the early afterglow behavior, and the early UV emission of the kilonova (e.g., Kasliwal et al. 2017; Gottlieb et al. 2018). Successfully choking a jet generally requires large amounts of material in the path of the jet (i.e., the polar region) in absorb the large kinetic energies and prevent successful propagation of the jet. As such, choked jets in SGRBs was not widely considered before GRB 170817A given the generally low expected densities in that region, as discussed in Sect. 2.1.3. This has been confirmed by simulations performed after GRB 170817A of jet dynamics in NS mergers (Duffell et al. 2018). While the prompt emission of GRB 170817A is consistent with cocoon closure relations, it would require chance coincidence for this event to occur at the correct distance to produce a burst within all of the normal gamma-ray parameters as measured at Earth (Goldstein et al. 2017a; Abbott et al. 2017b). Such emission is expected to produce spectra with peak energies much below those seen in time-resolved analysis of this burst (Lazzati et al. 2017; Veres et al. 2018). The late-time afterglow emission favors a structured jet origin and disfavor a cocoon origin, as discussed and referenced in the previous bullet. The radio observations of the bulk relativistic motion of the compact emitting region also favors a structured jet (Ghirlanda et al. 2019). Further, powering the early UV emission would require a jet with kinetic energies beyond the previously known sample (Metzger et al. 2018). Together these results strongly suggest that a fully choked jet is incompatible with the broadband observations of GRB 170817A.
A major result of GRB 170817A is the exclusion of the top-hat jet model for this burst. While the choked jet cocoon origin for GRB 170817A now appears unlikely, it may be viable for future events (Gottlieb et al. 2018) and in cases with prompt detection can be tested by the cocoon closure relations in Nakar et al. (2012) to check for consistency (e.g., Abbott et al. 2017b; Burns et al. 2018). This test can be performed within hours of the merger time, allowing for informed follow-up observations. These studies can confirm the viability of GRBs originating from a shock breakout origin or exclude this option shortly after event time and may be particularly interesting when tied to investigations of the merger remnant given the different expectations for material in the polar region (Sect. 3.2).
Jets can be collimated by a density gradient in the polar region, preventing particles from expanding too far from the polar region (e.g., Mochkovitch et al. 1993; Aloy et al. 2005; Nagakura et al. 2014). Magnetic fields can accelerate charged particles in a preferential direction, where ordered poloidal fields can also contribute to jet collimation (e.g., Rezzolla et al. 2011). These interactions impart structure onto the jet where dependencies on the amount and distribution of polar material and the jet launch time are important (e.g., Xie et al. 2018; Geng et al. 2019; Kathirgamaraju et al. 2019; Gill et al. 2019). GW observations provide new information to investigate this question and additional constraints to be met with future models and simulation. The first is a measure of inclination, \(\iota \), where variations in the jet should alter the observed prompt GRBs properties, such as the observed energetics, and combined study may elucidate their structure or, at least, constrain the properties of assumed functional forms (e.g., Mogushi et al. 2019; Williams et al. 2018; Song et al. 2019; Beniamini et al. 2019; Biscoveanu et al. 2020). These studies require detections with non-aligned GW interferometers and sensitive sky coverage in gamma-rays, as stringent non-detections are also informative. Combining this information with the jet-opening angle determined from afterglow observations will be particularly powerful.
The second benefit of GW detections for these purposes is immediate identification of particularly nearby SGRBs; GRB 170817A is so close that it has been observed \(\sim \) 100 times longer than prior SGRB afterglows. Among the key parameters to study GRB structure is the late-time temporal decay of the afterglow, which can distinguish between jetted and quasi-spherical outflows (e.g., Fong et al. 2019). Top-hat jets are predicted to have achromatic jet breaks, but chromatic jet breaks, which are often observed, may allow for inferences on the structure of these outflows (e.g., Panaitescu 2005b), though this explanation is not unique (e.g., Fox et al. 2003; Curran et al. 2007).
GW detections also constrain the jet launch time from studies of the GW-GRB time delay (e.g., Xie et al. 2018; Gottlieb et al. 2018; Geng et al. 2019). Jets that are launched earlier will experience less polar material, potentially providing less collimation and would be more likely to breakout. Jets that launch later may be more collimated, given thick disk expansion or additional dynamical polar ejecta. If they launch too late they could potentially be choked and fail. Studies seeking to understand the delay time are strongly tied to understanding the remnant object in the case of a BNS merger because of the expected variations in the amount ejecta, the distribution of that ejecta, and the expected time to launch the jet (Sect. 3.2).
So far studies of the structure of GRB 170817A and SGRBs in general have focused on either the prompt or afterglow emission separately. This is for the perfectly understandable reason that it is difficult to address the two together, but a successful, general structured jet model will have to simultaneously explain all observables, including historic constraints. For example, it would need to be capable of recreating the inferred \(\varGamma \gtrsim 1000\) observed for GRB 090510 based on Fermi LAT observations of this event (Ackermann et al. 2010), will also have to reasonably reproduce the observed SGRB redshift distribution, reproduce GRB 170817A, and the observed intrinsic energetics distribution (Beniamini and Nakar 2018).
4.5 Gamma-ray burst jet composition and ultra high energy cosmic rays
Cosmic rays were first identified more than a century ago, through Victor Hess’s high altitude balloon flight (Hess 1912). This was before the formulation of GR or the postulated existence of the neutrino. These particles carried new information from the Universe to Earth and led to the creation of a new field of study. One of the greatest outstanding questions in astrophysics is the origin of Ultra-High Energy Cosmic Rays (UHECRs), i.e., cosmic rays with energies in excess of 1 EeV. For reviews see Nagano and Watson (2000) or Sokolsky (2018)
When protons are accelerated to high energies in dense environments they generically undergo photohadronic processes, e.g., \(p + \gamma \rightarrow \varDelta ^+ \rightarrow n + \pi ^+\) (e.g., Rachen and Mészáros 1998). These can be followed by leptonic decays \(\pi ^+ \rightarrow \mu ^+ + \nu _\mu \) and \(\mu ^+ \rightarrow e^+ + \nu _e + \bar{\nu }_\mu \), which tie the predicted energies of gamma-rays, neutrinos, and cosmic rays produced in the same interactions; the total observed flux of these messengers are relatively equal, which is suggestive of a common origin (see e.g., Halzen and Hooper 2002, and references therein). Among the problems in determining the origin of UHECRs is the deflection of charged particles by the (inter)galactic magnetic fields and large gyro radii, causing both a propagation delay and altering the arrival direction. In principle we can reconstruct the source direction for a particle with known properties (e.g., mass, energy), but this relies on our imperfect understanding of the (inter)galactic magnetic fields, obscuring the origin even in the best case. It is for this reason that the quest to detect gamma-rays and neutrinos from a common source, with appropriate relative energies, have been used to search for the origin of UHECRs.
Given the ultrarelativistic nature of GRBs and the enormous energetics involved, it is natural to assume they will accelerate some amount of protons to high energies, with simulations showing some level of baryon loading even in the Poynting flux case (e.g., Lei et al. 2013). This led to the suggestion that they may be responsible for UHECRs (Vietri 1995; Waxman 1995) and the idea that a large scale neutrino detector could be used to investigate their potential common origin (Waxman and Bahcall 1997). The short intrinsic timescales and external trigger information would make association (after detection) relatively easy.
While IceCube has indeed found an astrophysical flux of high energy neutrinos (Aartsen et al. 2014), deep searches have never robustly associated these signals with GRBs (Abbasi et al. 2011; Aartsen et al. 2015). This is somewhat of a puzzling finding, as it suggests a very low baryon loading in GRBs jets, despite the general expectation that the baryons are present above the jet-launching site and should be accelerated. It could be that these protons are accelerated to high velocities, but the prompt emission radius is significantly larger than the internal shock scenario, where the photohadronic interactions become less likely due to the lower densities and neutrino production is suppressed (Zhang and Kumar 2013). These non-detections led to suggestions that choked LGRBs, where the jet fails to breakout through the massive star, may be significant sources of neutrinos (e.g., Mészáros and Waxman 2001; Senno et al. 2016).
LGRBs are generally more favorable for these studies than SGRBs, as their higher total energetics should produce a higher neutrino flux and their greater total matter above the jet launch site should result in a higher proportion of choked jets. However, the detection of GW170817 and GRB 170817A resulted in renewed interest in SGRBs as neutrino sources. First, among the issues of choked LGRBs is that they are EM-dark (or at least, extremely fainter than successful jets). If there are NS mergers with choked jets we can identify nearby events through GW detections, which will provide a time and location for joint sub-threshold searches (Kimura et al. 2018) as well as inform on the expected EM counterparts and their behavior. Second, the inferred structure of SGRB jets suggests a higher likelihood of neutrino detection for nearby events identified by GW detections (e.g., Ahlers and Halser 2019).
It is not known for certain what GRBs observations are the most likely to produce detectable neutrinos; however, because neutrino telescopes are all-sky monitors we will have observations of nearly all events. Ideally future studies will be able to detect neutrinos from these events and allow us to study baryon presence in the jet. Alternatively more stringent limits may show that the launch of a relativistic outflow in the presence of baryons is not a sufficient condition for the production of UHECRs or that UHECR production may not require significant neutrino production if the emission radius is large enough (Zhang and Kumar 2013), which may have implications for multimessenger searches for the origin of UHECRs from other sources.
A simplified picture of the emission from GRBs. Thermal emission is possible once the jet has passed the photospheric radius. Internal dissipation of the jet releases the prompt GRBs signal, shown here with the internal shocks model. Then, the on-set of afterglow emission occurs when the external shock develops as the jet interacts with the surrounding media. This figure is courtesy of Dan Kocevski (private communication)
4.6 The prompt emission mechanism(s) of gamma-ray bursts
GRB jets are often discussed as an ultrarelativistically expanding fireball (e.g., Piran 1999; Yost et al. 2003; Willingale et al. 2007). A basic representation of the emission stages is shown in Fig. 14. The energy density is truly enormous preventing gamma-rays from escaping until the jet reaches the photospheric radius, where opacity becomes low enough to allow light to escape from within the jet for the first time, at \(\sim 10^{11}\)–\(10^{12}\,\text{cm}\) (Beloborodov 2010; Kumar and Zhang 2015). Inhomogeneities from the central engine result in shells that propagate outwards with differing bulk Lorentz factors. Fast-moving shells catch slow-moving shells that were emitted at earlier times at \(\sim 10^{12}\)–\(10^{13}\,\text{cm}\), releasing the main prompt GRB emission through internal shocks (Rees and Meszaros 1994). Lastly, the jet propagates outwards until the interaction with the local environment creates the afterglow emission via synchrotron radiation (Kobayashi and Zhang 2007).
Except, maybe not. There are those that argue the dominant emission of GRBs originates from a photospheric origin (reviewed in Beloborodov and Mészáros 2017). Or that a Poynting flux jet can release the prompt signal once turbulence and magnetic reconnection hit a critical point, at a distance \(\sim 10^{16}\,\text{cm}\) from the central engine (Zhang and Yan 2010), which has implications for GRBs as the origin of UHECR (Sect. 4.5).
Observations have provided insight, but no full resolution. The broader energy coverage of Fermi has enabled the study of more complex spectral models. For example, Guiriec et al. (2010) fit the prompt emission of three bright SGRB with multiple components, including a thermal component, the main non-thermal component, and an extra power law, which has been seen in additional bursts (e.g., Tak et al. 2019). These components could originate from the three stages (photospheric, internal dissipation, external shock) which can have temporally overlapping signals given the enormous bulk Lorentz factors involved. Alternatively, some explain similar features through synchrotron radiation (e.g., Ravasio et al. 2018). The detector response of gamma-ray scintillators is non-linear, requiring a forward-folding spectral analysis method that still (usually) relies on empirical functions rather than theoretically motivated ones, which significantly complicates these studies.
There are two capabilities that are providing new insight into the prompt GRB emission mechanism. Polarization probes the existence of large-scale magnetic fields, where significant detection of high polarization implies Poynting flux jets (Toma et al. 2009). Population analyses have only recently become available, as these require Compton telescope observations of particularly bright bursts, given the probabilistic scattering angle. Results are not yet conclusive, given the varied results (e.g., Lyutikov et al. 2003; Yonetoku et al. 2012; Chattopadhyay et al. 2019; Zhang et al. 2019; Burgess et al. 2019). Continued advancement in these studies is a promising method to understand the prompt emission mechanism of GRBs. We note that the lower fluence of SGRBs implies their polarization will be measured an order of magnitude less often than LGRBs, but, under the general assumption that GRBs have the same emission mechanism(s), results from LGRBs are likely to be informative.
The other new parameter is the time offset from the GW to GRB emission. These were explored for GW170817 and GRB 170817A in Abbott et al. (2017b) and followed by several wonderful analyses (e.g., Granot et al. 2017; Shoemaker and Murase 2018; Zhang et al. 2018a), as well as those that sought to test or distinguish between leading models (e.g., Meng et al. 2018) or alternative scenarios (e.g., Kasliwal et al. 2017). The separate intrinsic time delay parameters each provide unique information on these events (Zhang et al. 2019). With a large enough sample we can independently constrain the separate parameters, providing tighter constraints, e.g., on the jet launch time and the size of the emitting region at emission time. Tying specific bursts to a known central engine type (Sect. 4.2) or potentially constrained to a dominant jet formation mechanism (Sect. 4.3) will provide additional insights into the viable models.
These studies then require polarization measurements of GRBs, which will be difficult given there is no active Compton telescope. We also need broadband characterization of the prompt SGRB emission in joint GW-GRB detections. Currently, only KONUS-Wind and Fermi-GBM cover the necessary range (\(\sim \) 10 KeV–10 MeV). Several proposed SmallSats cover only a restricted energy range (\(\sim \) 50 keV–2 MeV), largely due to mass limitations (e.g., Racusin et al. 2017; Grove et al. 2019). To constrain the time-resolved \(E_{peak}\) in a majority of SGRBs we require sensitivity to several MeV.
There have been a few detections of the prompt phase of GRBs by telescopes at lower energies, (e.g., Guiriec et al. 2016; Troja et al. 2017a). Broadband characterization, beyond the energy range of the GRB monitors, of the prompt emission would be phenomenally informative for prompt emission mechanisms (see discussion in Kumar and Zhang 2015), so long as their contribution can be separated from a external shock component. This would require either telescopes with massive fields of view, or sufficient early warning from GW detectors.
4.7 The origin of other non-thermal signatures
Discussed below are observed or predicted signatures that are likely to be tied to the central engine activity. These includes flares and plateaus in the prompt and early afterglow emission, which are separate from the dominant components. Determining if these events exist and their origin can enable greater understanding of NS mergers, as discussed below.
4.7.1 Short gamma-ray burst precursors
Precursors generally refer to short emission episodes that occur 100 s or less before the main GRB episode. Troja et al. (2010) analyzed Swift data to identify precursor signals, claimed confirmation of these pulses in other instruments, and argue \(\sim \) 10% of SGRBs have precursor activity. Other analyses suggest a lower fraction of potential SGRB precursors in other instruments (e.g., Zhu 2015; Burns 2017; Minaev and Pozanenko 2017; Li et al. 2018). A similar fraction of SGRBs have secondary pulses that succeed the main pulse. There is no analysis showing SGRBs precursors are spectrally distinct from the main emission. As discussed below, the majority of SGRBs occur at distances beyond where we would theoretically expect to detect precursors. Therefore, it appears feasible that previously observed precursors are just lower-flux SGRB pulses. None were observed before GRB 170817A to constraining limits (Abbott et al. 2017b; Li et al. 2018).
There are theoretical models (mentioned below) that predict precursor emission in gamma-rays, X-rays, and radio, with typical luminosities (\(\sim 10^{42}-10^{47}\,\text{erg s}^{-1}\)) and potentially UHECR production. Signals at these luminosities would only be detectable by all-sky monitors if the events are particularly nearby, precluding these models as the origin of some claimed precursors (e.g., the precursor for GRB 090510, which occurred at a redshift of 0.9; Ackermann et al. 2010). Isotropic precursor emission may be expected in these wavelengths from magnetospheric interactions (Hansen and Lyutikov 2001; Metzger and Zivancev 2016; Wang et al. 2018), disruption of the NS crust could produce a short gamma-ray flash (Tsang et al. 2012), or emission from the crust can power an EM chirp (Schnittman et al. 2018). These could give unique constraints on the magnetic fields of the progenitors or on the NS EOS (Sect. 7.2). While these signatures would be emitted before merger time, radio precursors may arrive at Earth after merger being delayed by dispersion.
GW observations will enable a resolution to this question. First, they select nearby events where the expected precursor brightness from theory may be detectable by existing or future GRB instruments. In some models the precursor emission is more isotropic than the jet, and do not necessarily require an associated prompt SGRB. Second, they provide the merger time. This will unambiguously determine if the observed SGRB precursors (relative to the main EM peak) occur before or after the GW merger time, more directly tying precursors to the theoretically-motivated regime or classifying them as prompt SGRBs pulses.
4.7.2 Extended emission and X-ray plateaus
Extended emission describes an observed behavior of longer, lower flux tails following the main peak of some SGRBs. While the main peak of SGRBs is \(\lesssim 5\,\text{s}\), the extended emission can persist for up to \(\sim \) 100 s with the two components having comparable total fluence. This signature was first identified in BATSE data (Lazzati et al. 2001; Connaughton 2002) and has been found in BAT data (Norris and Bonnell 2006). BAT allows for the exclusion of extended emission down to stringent flux limits, and suggests it occurs in \(\gtrsim \)15% of SGRBs, but is not ubiquitous (Lien et al. 2016). Extended emission has rapid variability, tying it to late-time energy injection from the central engine. It could be powered by the spin-down energy of a fast-rotating magnetar which can naturally explain the relatively flat emission over the times of interest, corresponding to the Stable NS or SMNS remnant cases (e.g., Dai and Lu 1998; Gao and Fan 2006; Metzger et al. 2008b; Bucciantini et al. 2011; Fan et al. 2013; Lü et al. 2015). Matching observations may require significant energy losses to GW emission, which would be beneficial for future direct GW detections of long-lived remnants.
A somewhat similar plateau signature has been observed on top of the temporal decay of the X-ray afterglow in some SGRBs (e.g., Rowlinson et al. 2010) and in LGRBs. Evidence for which may exist in up to half of SGRBs afterglows (Rowlinson et al. 2013). These signatures can also be reasonably explained by a magnetar central engine (e.g., Gompertz et al. 2013). It may be possible to detect similar signatures from proto-magnetar winds outside of the observable prompt GRB line of sight (Sun et al. 2017). There are potentially two such detections already (Xue et al. 2019; Sun et al. 2019).
However, there are other models that can result in plateau emission. In the fall-back accretion scenario material is launched with some velocity away from the remnant, but remains gravitationally bound (Rosswog 2007; Kisaka and Ioka 2015). The variability seen can then arise from interactions of this material during fallback (e.g., Coughlin et al. 2020). Other models have been considered, such as a two-component jet model (e.g., Barkov and Pozanenko 2011; Matsumoto et al. 2020). Another explanation that arose with the increased consideration of structured jets following GRB 170817A is high latitude emission creating the observed plateaus (Oganesyan et al. 2020; Ascenzi et al. 2020). For each of these models there are additional predictions that will allow for exclusion in some cases, pending sufficient broadband follow-up detections.
Multimessenger observations could provide an unambiguous resolution to the origin of these non-thermal signatures. If magnetars are the origin then we should only expect these signatures following Stable NS and SMNS cases, corresponding to low-mass GW inspirals and bright blue kilonovae (Sect. 3.2). If they are observed in other cases, and incompatible with a late-time fall-back origin, then we must search for a different origin. It is also possible that there could be multiple causes for the observed plateau emission, which would require a larger number of multimessenger observations to fully understand.
4.7.3 X-ray flares in the afterglow
X-ray flares above the afterglow have also been observed, which differ from plateaus by having a distinct rise and fall (Burrows et al. 2007). Long-lived remnants with high magnetic fields could potentially explain this emission as well (e.g., Dai et al. 2006; Gao and Fan 2006); however, these signatures are more often explained via late-time fall-back accretion (e.g., Fan et al. 2005; Rosswog 2007; Kocevski et al. 2007). Time-resolved multiwavelength observations should be able to distinguish between these models (e.g., Lamb et al. 2019).
There are predicted differences between the progenitor systems, with NSBH mergers having up to an order of magnitude more fall-back material than in BNS mergers (Rosswog 2007). There should also be differences based on the properties of these systems, likely corresponding to the amount of tidal ejecta and being related to the mass ratio of the system. GW measurement of these intrinsic parameters and the multimessenger classification of progenitor system and BNS remnant type should confirm if observations follow expectations and determine if the X-ray flares are indeed caused by late-time fallback accretion.
4.7.4 Synchrotron self Compton
It is generally agreed that the radio to gamma-ray afterglow emission is synchrotron radiation from the external shock (Sari et al. 1998). From the conditions in GRB jets we generically expect Synchrotron Self Compton (SSC) emission. The first public claim of VHE detection of a GRB was for GRB 190114C (Mirzoyan et al. 2019), which has been modeled with a SSC origin (e.g., Fraija et al. 2019; Derishev and Piran 2019; Wang et al. 2019). However, no analysis published so far has performed robust multi-instrument spectral analysis showing a statistical preference for a SSC origin against a base synchrotron explanation, which may also fit the data. Regardless of this specific burst, the detection of SSC emission in GRBs would give phenomenal constraints on several microphysical parameters which would inform a wide range of GRB studies. These would require sensitive VHE observations as close to the on-set of prompt emission time as possible. These constraints will likely be most sensitive for LGRB observations, but the GW identification of nearby SGRBs and the upcoming CTA provide a promising combination to seek SSC emission from a NS merger. The ideal scenario would be distributed CTA coverage of the highest probability region from a GW early warning localization.
5 Kilonovae and the origin of heavy elements
The origin of the elements is among the most basic questions in existence. As discussed in Sect. 6, Hydrogen, Helium, and Lithium were produced at recombination. Despite 13.8 Gyr of the production of all other elements, these are still the most common by an overwhelming margin. Some of these atoms coalesced into the first stars. Stellar fusion combine the light elements into heavier elements through well understood nuclear reactions. In massive stars these reactions progress to heavier elements until iron, beyond which fusion becomes endothermic. Eventually the star will explode and release copious amounts of elements from carbon through the \(\sim \) fifth row of the periodic table. Boron, Beryllium, and nearby elements are created mostly from cosmic ray spallation.
The heavy elements, those beyond iron, are created by slow and rapid neutron capture processes. The s-process (s for slow) occurs mostly in asymptotic giant branch stars where, over thousands of years, neutrons can be captured into iron seeds from prior supernovae and create heavier elements (Johnson 2019). Here beta-decay is more rapid than the neutron capture. The reverse is true in the r-process (r for rapid), responsible for the heaviest elements including most of the lanthanides and all of the actinides (Burbidge et al. 1957; Cameron 1957), which generally requires material with particularly high neutron density and a low electron fraction. The heaviest (stable) elements must have more neutrons than protons to overcome the massive Coulomb repulsion or else they will radioactively decay to lighter elements. For a recent review on the origin of the heaviest elements see Cowan et al. (2019).
In all the universe, the highest neutron density occurs in NSs. It seems reasonable to investigate the violent births and deaths of NSs as potential r-process generation sites. For a long time the leading candidate for r-process element production were CCSNe (e.g., Meyer et al. 1992; Woosley et al. 1994). However, as simulations improved they showed the large neutrino irradiation of the material shifting the electron fraction to higher values, preventing the formation of significant amounts of lanthanides and actinides (e.g., Martínez-Pinedo et al. 2012; Roberts et al. 2012; Wanajo 2013). There are more complicated scenarios that could potentially resolve these issues. For a very nice summary of the current understanding of r-process sites, particularly with respect to common and rare CCSNe, we refer to the Supplementary Methods in Siegel et al. (2019).
The necessary enrichment rate to reproduce the amount of heavy elements (\(A > 140\)) in the Milky Way, as inferred from the solar system abundances, is \(\sim 2 \times 10^{-7}\,M_{\odot} /\text{yr}\) (Qian 2000). With a fiducial rate of CCSNe per Milky Way-like galaxy of 2.84 per century (Li et al. 2011), or 0.0283/yr, if CCSNe do produce r-process elements the lanthanide yield of individual events must be low, giving an effective constant enrichment of the heavy elements. There are observational evidence that tend to argue against such a scenario as the dominant r-process site. The first comes from observations of \({}^{244}\)Pu in the ocean floor at two orders of magnitude below the expected value from constant r-process enrichment, favoring a rare process (Wallner et al. 2015). Such a measurement relies on using the radionuclide as a natural clock. A second key piece of evidence was the detection of heavy neutron-capture elements in several stars in the dwarf spheroidal galaxy Reticulum II with abundances two orders of magnitude higher than in other such galaxies, again arguing against (relatively) common low-yield events (Ji et al. 2016), with inferred total production capable of reproducing the total r-process production of the Milky Way, suggesting a common origin (Beniamini et al. 2016). The actinide abundances in the early solar system also favor a rare origin (Côté et al. 2019; Bartos and Marka 2019).
Ripping apart NSs promises a neutron-dense, low electron fraction environment. Lattimer and Schramm (1974) were the first to suggest NSBH mergers as r-process sites, followed by Symbalisty and Schramm (1982) suggesting BNS mergers. Freiburghaus et al. (1999) demonstrated the first simulations showing NS mergers could roughly reproduce the observed relative elemental abundances, a result which has been confirmed as simulations have improved. With the apparent r-process production problems in CCSNe and observations favoring rare, high-yield sites, NS mergers became prime candidates for the dominant r-process sites owing to their much lower rate (\(\sim \) 1 per 10,000 years) in the Milky Way. For a review with a historical discussion on the r-process origin and the role of NS mergers see Metzger (2020).
The identification of KN170817 following GW170817 with the broadly expected behavior for a kilonova was the first firm detection of r-process nucleosynthesis. With the inferred ejecta mass from KN170817 and the GW-determined local NS merger rate it appears that NS mergers can be the dominant r-process sites, though large uncertainties remain (Côté et al. 2018). It appeared then, that we had a reasonably consistent understanding of the origin of heavy elements from theory, simulation, and observation.
Then, Siegel et al. (2019) decided to complicate things, by using knowledge gained from KN170817 to re-energize an old suggestion (e.g., Pruet et al. 2004). We briefly summarize their arguments. The observed properties of KN170817 suggest the dominant ejection method came from accretion disk outflows, from a total disk mass \(\sim 0.1\,M_{\odot} \). LGRBs originate from collapsars, which are fast-rotating massive stars that undergo core-collapse, and are powered by accretion disks with characteristic mass \(\sim 3\,M_{\odot} \). In short, the thick disk can maintain an electron fraction (in cases with a BH central engine) sufficiently low to produce actinides. Despite CCSNe being rarer than NS mergers (by a factor of a few, based on the inferred LGRB and SGRB rates) the higher yields (more than an order of magnitude more) of CCSNe suggest they have been the dominant r-process production sites over the life-age of the Universe. The viability of this explanation based on current observational evidence is the subject of on-going work (e.g., Macias and Ramirez-Ruiz 2019; van de Voort et al. 2020).
As noted in Siegel et al. (2019), collapsars would be consistent with the observational evidence that support rare, high yield production sites. They predict an infrared signature somewhat similar in evolution to a red kilonova (though from a much larger ejecta mass) that would follow LGRBs and could be detectable by sufficiently sensitive infrared telescopes such as James Webb Space Telescope (JWST). Should this signature be observationally identified then delineating between the relative importance of collapsars and NS mergers will require a more precise yield measurement for each class, their distributions, as well as their relative rates through cosmic time. More generally, there are other suggested rare types of supernova that would produce high yields of the heavy elements, also discussed in Siegel et al. (2019). We use collapsars as the representative case but note most tests of the two options apply to the larger case of rare supernova.
In Sect. 5.1 we discuss the nucleosynthetic yield of NS mergers, both relative and absolute abundances, and prospects for improving our understanding through simulation and observation of kilonova. Section 5.2 discusses prospects for determining the current lanthanide and actinide enrichment of our own galaxy. Section 5.3 ties these observations to the source evolution of the potential r-process sites and determination of the dominate sites as a function of time through cosmic history.
5.1 Heavy element production in candidate r-process sites
There are at least three important observational constraints that r-process sites must explain: they must be able to reproduce the relative and absolute heavy element abundances, and they need to be able to explain the varied r-process enrichment in stars. This latter constraint was relied upon to narrow the candidate sites to NS mergers and rare types of supernova. The relative values can be inferred from the observed solar system abundances, predicated on the assumption that we do not live in an unusual place. Lower electron fractions may not reproduce the low-mass heavy elements (e.g., iron to lanthanides), and higher electron fractions \(Y_e \gtrsim 0.3\) cannot reproduce lanthanides and actinides. Wanajo et al. (2014) first demonstrated with high fidelity simulations that NS merger ejecta composed of varying electron fraction successfully reproduce the full range of r-process elements. However, despite the optimal dataset of KN170817 there were suggestions, but no unambiguous observational proof of production of the heaviest elements (corresponding to the third r-process abundance peak) and an answer may require capabilities that do not yet exist (Kasliwal et al. 2019).
From the arguments suggesting collapsars as potential r-process sites and as checked with initial simulation, collapsars show similar capability to reproduce the observed abundances (Siegel et al. 2019). As stated, most simulations of standard CCSNe scenarios appear unable to reproduce the observed relative abundance pattern. It is a reasonable assumption that the dominant r-process production sites should produce these elements with the relative abundances that are observed in the solar system. We assume this is true in ensemble (e.g., the average production from these events, but not necessarily every individual event) when discussing absolute production.
A great deal of simulation work has been performed to tie the observed UVOIR behavior to the ejecta properties (e.g., Barnes and Kasen 2013; Barnes et al. 2016; Tanaka 2016; Metzger 2020, and references therein). With prior kilonova candidates (e.g., Perley et al. 2009; Tanvir et al. 2013; Berger et al. 2013; Gompertz et al. 2018; Ascenzi et al. 2019) the data was insufficient to reliably constrain elemental production of individual NS mergers (with some published claimed kilonova signatures relying on a single single data point), especially after accounting for the Malmquist bias towards detecting brighter events (and thus inferring higher average yield per event than the true value).
In the first detection of a kilonova following a GW detection the observers hit the limit of precision of existing models. Villar et al. (2017) collated the UVOIR data reported by various groups for KN170817; the results are shown in Fig. 15. Like most authors they identify a red and a blue component, but they favor the addition of a third component with opacity in between the other two.Footnote 7
We list some of the complications with inferring ejecta properties from the current kilonova models and methods to improve these uncertainties. This is not a criticism of these works. They combined several complicated processes into software frameworks that run sets of efficient simulations to predict the signatures of kilonovae before one was ever observed and studied in detail, sometimes hitting the limits of human knowledge itself. The discussion here to show where progress will have to be made in the next few years to determine the true nuclear production in these events.
In order for kilonova models to be easily utilized to infer ejecta properties from observations they need to provide a range of considered parameter values for comparison. We discuss only two examples out of several options. The kilonova models used in Villar et al. (2017) are constructed from the toy model presented in Metzger (2020), allowing for a broad range of considered ejecta parameters. Kasen et al. (2017) generated a set of models covering a reasonable parameter space using full radiative transport, reproducing KN170817 with a specially tailored model, presenting a range of specific models that data can be compared to. They are broadly similar in behavior, but some important differences remain, e.g., the predicted early UV flux. Coughlin et al. (2018) generated an effective method to interpolate between the available grid models from Kasen et al. (2017), providing an important step towards tying observations to simulations.
Laboratory astrophysics is critical. Early work on tying ejecta parameters to lightcurves that predicted a bright blue kilonova with a peak timescale of about a day by assuming iron-like opacities (Metzger et al. 2010). Using more realistic opacities for ejecta with lanthanides and actinides results in values orders of magnitude higher, which prevents the quasithermal emission from escaping for longer times, resulting in a redder kilonova with lower peak emission on the timescale of a week (Kasen et al. 2013; Barnes and Kasen 2013; Tanaka and Hotokezaka 2013). The dominate contribution to the UVOIR opacities are the bound-bound transitions of the lanthanides and actinides. As discussed in Sect. 2.1.5, the opacities in these papers are calculated from reasonable approximations because we lack the atomic orbital information for these heavy elements which determine the bound-bound transitions. Over the past few years we have improved laboratory and computational determination of these values, work which is critical to improving our estimates of ejecta properties in kilonovae. However, we still do not have key information on individual atoms and much uncertainty remains on how to calculate the ensemble opacities (see discussions in Metzger 2020, and references therein).
Similarly, our current understanding of nuclear physics with regards to the heaviest elements, particularly those far from the region of stability, also limits the accuracy of kilonova lightcurve models. For example, Barnes et al. (2016) investigate a few nuclear mass models to check abundance yields which produce variations in the relative elemental abundances, particularly in the actinides, as well as the fraction of total radioactive energy combined in different decay species as a function of time. The relative \(\alpha \), \(\beta \), and fission decay differences between nuclear models determines the amount of energy deposited into these products, including neutrinos which can escape very quickly, and gamma-rays which can escape before the peak luminosity time. This alters the thermalization efficiency, i.e. how much energy is converted into heat rather than lost, of the radioactivity as a function of time, which effects the lightcurves and thus our inferences of the total ejecta mass (Hotokezaka et al. 2016b; Barnes et al. 2016). Fortunately, upcoming atom smashers, particularly the Facility for Rare Isotope Beams (Balantekin et al. 2014), which has astrophysics as a core science goal, will help improve our understanding of the heaviest elements over the next several years.
The simulations themselves make different assumptions and contain different approximations. They vary the assumed velocity gradients of the ejecta, neutron capture fraction, neutrino treatments, radiative transport schemes, nuclear model, opacities, thermalization efficiencies, magnetic fields, entropies, grid formulations and resolution, NS EOS, etc (e.g., Tanaka 2016; Wollaeger et al. 2018; Kawaguchi et al. 2020; Metzger 2020, and references therein). Over the years papers have been published to resolve the importance of these different assumptions which has led to significant improvements in the accuracy of the models and, in general, trends within models based on different input parameters. As examples, that longer-lasting remnants in BNS mergers result in more and bluer ejecta, that increasing lanthanide and actinide fraction results in redder kilonova, and that the same kilonova can appear with different color based on the inclination angle. However, uncertainty remains with respect to absolute behavior.
As a particular example we consider the magnetically-driven disk winds. Siegel and Metzger (2017) investigated these outflows using 3D GRMHD simulations with approximate neutrino transport, running for \(\sim \) 0.4 s. Extrapolating beyond the end time they conclude that these outflows could ejecta similar amounts of matter as the viscously driven outflows. Fernández et al. (2018) ran simulations for several seconds, providing direct evidence for those conclusions and additional suggest this ejecta could produce a kilonova precursor signal. Miller et al. (2019a) consider full 3D GRMHD simulations with full neutrino transport which significantly altered the electron fraction of the ejected material, suggesting these outflows could power a blue kilonova.
With each increase in fidelity the conclusions were strengthened or even altered, and this may be expected to continue for some time. As an important example, each still assume idealized initial conditions of the magnetic field. MHD instabilities can significantly amplify magnetic fields (e.g., Balbus and Hawley 1991) and their topology is not necessarily simple. Kiuchi et al. (2014) and Kiuchi et al. (2015) study the magnetic fields that develop in BNS and NSBH mergers respectively, showing strong and complicated fields in both cases, but with different topology. Using the information from careful merger simulations as initial conditions for studies focusing on post-merger effects, as in Nouri et al. (2018), may provide more accurate results. These currently limit our ability to infer ejecta parameters from kilonova lightcurves.
Most kilonova models have assumed spherical symmetry for simplicity, but accounting for more realistic spatial distribution results in inclination effects on the observed lightcurves for the same event (e.g., Kasen et al. 2017; Wollaeger et al. 2018). In measuring the ejecta properties of the components in KN170817 nearly every group assumed spherical symmetry for each contributing ejecta region, which is not necessarily a good assumption (e.g., Metzger 2020, ). If a red kilonova emitting region is between a blue kilonova emitting region and the observer the blue emission will be blocked by the bound-bound opacity of the intervening material (Kasen et al. 2017). Even if the view is unobstructed the spatial distribution can alter the inferred ejecta properties. Indeed, accounting for the expected equatorial distribution for the lanthanide-rich material and the polar distribution for the lanthanide-free material for KN170817 suggests a lower overall yield, removing some of the tension with kilonova simulations (Kawaguchi et al. 2020). This is also considered in Bulla (2019) with the additional consideration of the polarization which may provide key additional information.
These are further complicated by the intrinsic variations in mergers themselves. The progenitor system and different immediate remnant cases have vastly different ejecta morphology, velocity, opacity, neutrino irradiation, etc. Within each case the mass ratios, spins, and other intrinsic parameters also cause variation in the observational signature. These are further complicated by potential additional sources of energy and heat into the kilonova, like late-time fallback accretion onto the remnant object (see Sect. 4.7). Astrophysical observations of a large population of varied NS mergers will be particularly helpful in understanding these effects.
Assuming our general understanding is correct, NSBH mergers could release no matter or up to \(0.1\,M_{\odot} \) of lanthanide and actinide-rich ejecta. BNS mergers that undergo prompt collapse will produce similar elements, but in lower abundances. Though, these cases could produce the lighter elements if fast magnetically-driven disk outflows occur. HMNS could release the full range of beyond-iron elements with higher mass elements from the tidal and disk wind and lower mass elements in the polar ejecta, perhaps up to \(\sim 0.05\,M_{\odot} \) based on KN170817. Stable NS and SMNS remnants can release \(0.1\,M_{\odot} \) of the lower mass beyond-iron elements, but only a smaller portion of lanthanides and actinides. To understand the enrichment of heavy elements from NS mergers we will likely need to determine the distribution of yield for these different cases, as well as how often these cases occur.
The periodic table showing the heavy elements produced in NS mergers. The color shading is a simplified representation of the wavelengths that probe production of that element, with violet representing UV and near-UV, light blue representing optical and some NIR, and red showing NIR and IR. Figure from Judy Racusin (private communication)
In order to both precisely test existing models and to accurately infer the ejecta properties for a given event, UVOIR observations of GW-detected NS mergers are absolutely critical. Figure 16 shows a basic representation of the elemental yield probed by the different wavelengths. UV observations will help understand the unusual excess seen in KN170817 (Sect. 3.4) which will separate out the contributions of radioactive heating from other potential sources and enable more accurate inferred mass yields. The discovery of the arcsecond position of EM counterparts will almost certainly be dominated by optical observations. Infrared uniquely probe the contributions of lanthanide and actinide-rich ejecta, and provide the latest observations of these events. A full understanding of these sources requires the broadband observations from early to late times, noting that limited band observations can be consistent with multiple parameter combinations. GW detections provide information on the intrinsic parameters which, with the multimessenger determination of the merger remnant (Sect. 3.2), will enable a broad understanding of these sources. The inclination information will be particularly helpful in understanding inclination effects.
Given the complicated nature of these events and our models to understand them, direct determination of nucleosynthetic yield would be helpful. Nuclear gamma-rays can escape beginning a few hours after merger and can carry tens of percent of the total energy of the system (e.g., Hotokezaka et al. 2016b). The emission would be concentrated from a few dozen KeV to a few MeV, bright for a few days, and be a relatively flat spectrum due to Doppler broadening. Such a detection would provide another handle on the ejecta properties that is not dependent on a number of assumptions that the UVOIR determination is. However, this is beyond the capability of existing instruments, and likely beyond the capability of proposed instruments unless we are lucky (Timmes et al. 2019).
Alternatively, one could potentially measure yields of individual elements. This can be direct spectroscopic measurements of individual absorption lines with sensitive IR telescopes weeks after merger when the ejecta has sufficiently slowed to minimize Doppler broadening. Late-time temporal decay in the infrared may be dominated by the decay of individual (or a few) isotopes. These prospects are reviewed in Metzger (2020), who suggest the approaches are promising, though some uncertainty remains.
Observationally measuring or constraining the lanthanide production in collapsars appears phenomenologically similar to that of NS mergers. Siegel et al. (2019) argue a late-time infrared signature following LGRBs detections would arise if they are significant r-process sites. Then, similar modeling to tie the observed light curves to the ejecta properties are required. This may be the only observable signature as the Milky Way is generally too metal-rich for collapsars to occur, preventing study of nearby LGRB remnants.
5.2 On-going heavy element nucleosynthesis in the Milky Way
Combining yields from individual events with the GW-determined volumetric NS merger rate measures the local heavy element production from these events. This rate currently has an order of magnitude uncertainty in the 90% range, which should rapidly shrink over the next few years. With the inferred ejecta for KN170817 and the merger rates in the Milky Way from Table 1, BNS mergers alone can robustly create the r-process elements in the Milky Way at the rate required to be the dominant site of r-process.
However, as we begin to constrain the yield distribution of BNS mergers, better constrain the local rate of NS mergers, and determine the relative contribution of NSBH mergers, we will have to consider additional effects. From Tunnicliffe et al. (2013) about 30% of SGRBs are hostless, implying no nearby potential galaxy to deep observational limits. From Fong et al. (2015) some of the SGRBs with reliable hosts also appear to be significantly outside of the galaxy itself. This implies that a few tens of percent of NS mergers are nearly or totally unbound from their host galaxy. Then, the nucleosynthetic yield of these mergers will not contribute to the observed abundances in their galaxies, and we should expect a similar effect for BNS and NSBH systems born in the Milky Way. This consideration does not apply to either CCSNe or collapsars which should track the stellar mass within the galaxy.
The use of radionuclides can uncover recent nucleosynthesis in our own galaxy. That is, explosive nucleosynthesis results in radioactive isotopes. With nuclear reaction networks we can calculate the expected isotopic ratios of some key elements as a function of time for various initial relative abundances. These natural clocks allow constraints on past explosions in the Milky Way. These studies usually rely on recent Supernova explosion (SNe), supernova remnants, or observations of diffuse radioactive emission. Wu et al. (2019) consider diffuse emission from NS mergers suggesting they are well beyond the capability even of any proposed telescope.
Searches for KNR in the galaxy have been proposed (Wu et al. 2019; Korobkin et al. 2020), suggesting detections are possible with proposed \(\sim \) MeV gamma-ray telescopes. The detection of \(^{126}\)Sn lines would identify a past r-process production site, likely limited to events occurring in the last \(\sim \) Myr. Detection of additional lines would enable constraints on the age of the remnant and the relative production of actinides.
Distinguishing between the potential r-process sites could be done through spatial information and yield determination. If the events occur outside of the galactic plane it will favor a BNS/NSBH merger origin; otherwise a rare CCSNe origin. Events with low initial yields will favor basic CCSNe. Events with incredible yields (\(\sim 1\,M_{\odot} \)) would favor a collapsar origin but we do not expect to identify these in the Milky Way. Events with yields \(\sim 10^{-2}\)–\(0.1\,M_{\odot} \) would favor a NS merger origin. Delineating between BNS and NSBH merger remnants may be difficult unless multiple lines are detected. In general, the inferred actinide fraction will be informative, with NSBH mergers generally requiring a high value. Most BNS cases do not. The exception is the prompt collapse scenario which may be difficult to distinguish from an NSBH merger with low (\(\sim 0.01\,M_{\odot} \)) initial ejection. Being able to reliably determine what the origin of the r-process site is would require a MeV telescope with line sensitives a factor of a few better than the current advanced proposals.
The other method of direct isotopic determination is through careful cosmic ray studies. Binns et al. (2019) argue that uncovering the relative isotopic abundances of the actinides and comparison of their ratios would constrain the rarity of the currently dominant r-process sites, similar to the constraints of observing \(^{244}\)Pu on the sea floor. They discuss this specifically delineating between base CCSNe and BNS mergers.
5.3 The heavy element enrichment history of the Universe
The prior subsection discusses how to resolve the dominant r-process site in the current time. This answer may differ from the site that has produced most of the lanthanides and actinides that now exist. That is, current elemental abundances in the solar system are the cumulative effect of all prior r-process events in the Milky Way. We know that the rates of BNS mergers were higher in the past than they are today (e.g., Berger 2014). The peak rates for CCSNe occur earlier, and the rates of collapsars earlier still. Then, the relative contributions of each potential source varies through the history of the Universe.
The best understood source evolution of these potential sites is CCSNe. Stars that undergo core collapse are massive and have short lifetimes, measured in tens of millions of years, or less than 0.1% the age of the universe. Their creation should largely track the cosmic star formation history which peaked at roughly \(z \approx 1.9\) when the universe was \(\sim \) 3.5 Gyr old (see e.g., Madau and Dickinson 2014b; Hopkins and Beacom 2006). The e-folding scale is \(\sim \) 3.9 Gyr, suggesting half the stellar mass was created before \(z \approx 1.3\). These are effectively the source evolution of CCSNe, with the normalization determined by the current local rate.
In the early universe the source evolution of collapsars should track that of CCSNe (and thus the stellar formation evolution). However, overall, collapsars do not track the environments of CCSNe (Fruchter et al. 2006). It is empirical fact that collapsars strongly prefer low metallicity environments. Given the increase in average metallicity as the universe ages due to elemental enrichment from supernovae (and other processes), then the peak collapsar rate should occur earlier than the peak Star Formation Rate (SFR). This has been confirmed observationally, suggesting a peak rate before \(z \approx 2{-}3\) (e.g., Langer and Norman 2006; Wanderman and Piran 2010).
As previously discussed the formation of BNS and NSBH mergers likely follows the SFR evolution, as they are thought to originate in field binaries of stars that undergo CCSNe, but they have long inspirals that delay the merger times. The observed peak rate is around (or greater than) \(z \approx 0.5{-}0.8\) (e.g., Berger 2014), or when the universe was about half its current age.
Then, we can discuss the relative importance of these sites through cosmic time. If collapsars are important r-process producers they are almost certainly the dominant sites for the first several billion years of the Universe. Heavy elements before a redshift of \(\sim \) 3 are likely attributable to these sources. If CCSNe are r-process sites then they are likely most important around the times of peak SFR, potentially still being sub-dominant during that time. NS mergers of either type are likely to be important in the latest half of the universe and currently the dominant sites, with BNS and NSBH mergers having different yields per event and likely different source evolution.
These studies will have to be done in concert with studies of ancient elemental enrichment (e.g., Macias and Ramirez-Ruiz 2019; Johnson et al. 2019), and as we improve our determination of the SFR. These are key questions in astrophysics and we can rely on continued investment in these areas. We should seek to determine the SGRB source evolution through follow-up observations of prompt signals detected by more sensitive telescopes as a proxy for NS merger source evolution. Identical instruments can provide the same for LGRBs as a proxy for collapsar evolution. We support the use of JWST to seek the infrared lanthanide signature in follow-up of LGRBs.
6 Standard sirens and cosmology
Cosmology is the study of the Universe on the grandest scales, using observations of the past to understand how it began, how it evolved to its present state, and how it will end. For much of recorded history humanity largely believed in a Geocentric Universe. Copernicus moved us to Heliocentrism through mathematical description. This world view stood until the onset of observational cosmology, little more than a century ago.
Standard candles are EM sources with known intrinsic luminosities, which enable us to determine their distance from the observed brightness and known \(1/d^{2}\) behavior. Cepheid variables were the first known standard candles with luminosities described by the Leavitt Law (Leavitt 1908; Leavitt and Pickering 1912). Harlow Shapley switched us to Galactocentrism when he used Cepheids to infer the distance to the galactic center (Shapley 1918). Soon after, Edwin Hubble used Cepheids to identify other galaxies in the local group as island universes (of Kant’s imagination) distinct from the Milky Way (Hubble 1925, 1929b), moving us to Acentrism, and then used them to prove the Universe was expanding in 1929 (Hubble 1929a). George Lemaître found evidence and provided a theoretical explanation for Hubble’s results in 1927 (Lemaître 1927) and used them to envision the Big Bang (Lemaître 1931). In twenty years the first known standard candle took us from an eternal, static Universe with the solar system at the center to an evolving Universe with a beginning and our galaxy as one of many. As a bit of a cosmic joke, in Hubble’s expanding Universe (with a finite propagation speed) we are the center of our observable Universe.
Lemaître argued that time reversal of an expanding Universe naturally rewound to a single point. Such a Universe would explode outwards, beginning as a super-heated place that cooled as it expanded. Once it was sufficiently cool to allow electrons to bind to nuclei the first atoms were formed, referred to as recombination for historical reasons, which occurred only 380,000 years from the beginning. Careful study of this Big Bang Nucleosynthesis (BBN) predicts the relative abundances of the light elements (H, He, Li; Alpher et al. 1948; Burles et al. 1999), which reliably match current measured values (see e.g., Planck Collaboration 2020), providing additional support for the theory.
At recombination the Universe became transparent, allowing photons to travel freely for the first time, decoupling radiation and matter. As the Universe expanded these photons were cosmologically redshifted to lower energies until the present time when these photons are microwaves. The prediction of the Cosmic Microwave Background (CMB; Alpher and Herman 1948) and its accidental discovery (Penzias and Wilson 1965) was the third key piece of evidence in favor of the Big Bang. The detection of its blackbody spectrum as the most perfect ever observed added further confirmation (Mather et al. 1994).
In the 1980s, the idea of inflation (which does not have an agreed upon physical explanation) was developed (e.g., Starobinskiǐ 1979; Guth 1981; Linde 1982), which resolved a number of outstanding issues such as the lack of magnetic monopoles, the homogeneity and isotropy of the local Universe, and the observed flatness of the Universe. Separately, the inferred baryon matter density in the early Universe is a factor of several below the inferred (total) matter density. This provides strong evidence for the existence of dark matter (Zwicky 1933, 1937; though there are discussions of the idea back to Lord Kelvin) with similar relative abundances inferred from galaxy rotation curves (Rubin et al. 1978, 1980) and other methods. Altogether, the small anisotropies in the CMB (Smoot et al. 1992) requires inflation (for overall smoothness) and cold dark matter (for some clumping), which made “Cold Dark Matter” the standard cosmological model at the time.
The most famous standard candle in astrophysics are type Ia supernovae due to their high intrinsic luminosities and rates enabling distance-redshift studies deep into the Universe (and because explosions are cool). Observations of them gave us the last great surprise in 1998: the expansion rate of the Universe is accelerating (Riess et al. 1998; Perlmutter et al. 1999). The currently unknown origin of this acceleration is referred to as dark energy.
Of the four known fundamental forces, gravity dominates on cosmological scales. Our modern theory of gravity, GR, allows for a cosmological constant. A positive cosmological constant (a positive energy density in the vacuum of spacetime) will tend to counteract the pull of gravity. Einstein had originally used it to maintain a static Universe, the need for which was discarded with Hubble’s discovery of the expansion of the Universe. Currently, our observations of dark energy are consistent with a positive cosmological constant, \(\varLambda \), with sufficient magnitude to accelerate universal expansion. That is, despite the great observational surprise of dark energy, GR is still valid on cosmological scales. Adding this to the prior CDM cosmological model gives us \(\varLambda \)CDM, which has a cosmological constant dark energy, dark matter, and a Big Bang with inflation. For a full understanding of the Standard Model of Cosmology we suggest the reader find a good modern cosmology textbook.
This section is presented with a brief historical overview to make a key point: since the beginning of observational cosmology our understanding of the Universe undergoes a revolution about once a generation as observations achieve the necessary precision to show old models as incomplete. Following this pattern, there are some unsolved issues with \(\varLambda \)CDM. Quantum Field Theory (QFT) expects a zero-point energy of spacetime with a value one hundred orders of magnitude larger than the observed value; the so-called “vacuum catastrophe” (also known as the worst prediction in physics) (Adler et al. 1995). The relative amounts of light isotopes in the early Universe formed by BBN are in general agreement except for the abundance of Lithium-7 which is significantly rarer than expected (see Fields et al. 2014, for a review). \(\varLambda \)CDM has remarkable success at predicting the large scale structure of the Universe, but simulations currently have less success on smaller scales; the so-called “small scale crisis” (see Bullock and Boylan-Kolchin 2017, for a review). The total amount of baryons in the local Universe is predicted to be much higher from both BBN (Fields et al. 2014) or CMB observations (Planck Collaboration 2020) than is actually observed (Shull et al. 2012); the “Missing Baryon Problem”. The names show that cosmologists have a flare for the dramatic, but the identified problems suggest considering that \(\varLambda \)CDM is incomplete.
6.1 The Hubble Constant
Perhaps the greatest current issue with \(\varLambda \)CDM is related to the value of the local expansion rate of the Universe, \(H_0\), first measured by Hubble generations ago. \(H_0\) sets the scale of the Universe, both its age and size, and is one of the fundamental cosmological parameters. In the local Universe one can directly measure \(H_0\) through a distance-redshift relation.
In cosmology it is convenient to define the dimensionless scale factor a, using the Friedmann equations (Friedmann 1922), which grows through time representing the expansion of the Universe with a unity value in the current age. The Hubble Constant is now known to be the local value of the Hubble Parameter which evolves with time and is \(H(z) \equiv \dot{a}/a\). Cosmological distance measures are determined by integrating the inverse of this value, e.g., the luminosity distance is
where the evolution of H(z) is determined by an assumed cosmological model. With a FLRW metric, \(a = 1/(1+z)\). Thus, we can calculate \(H_0\) by setting the scale of the Hubble Parameter in the distant Universe and evolved to the present value (the Hubble Constant) by assuming a cosmological model.
Measuring the value from observations of opposite ends of the Universe provides a stringent test of any cosmology. The most precise value of \(H_0\) as measured in the nearby (late) Universe is \(H_0 = 74.03 \pm 1.42\) (Riess et al. 2019) and the most precise value of \(H_0\) from the distance (early) Universe is \(H_0 = 67.66 \pm 0.42\) (Planck Collaboration 2020), which currently disagree at more than 4 \(\sigma \) (Riess et al. 2019).
In the local Universe (\(z \ll 1\)), \(d=cz/H_0\), where d is the distance (we here neglect peculiar velocities as they are not important to our general conclusions). Therefore, we can use the distance inferred from observations of type Ia supernovae and their associated redshift to measure \(H_0\). Redshift is fairly easy to measure (and at cosmological distances the redshift due to the local motion of the galaxies is negligible).
The cosmological distance ladder is the method used to determine distances to cosmological objects. For an overview of the cosmological ladder and using it to measure \(H_0\), see Freedman and Madore (2010). Standard candles have known relations, but their zero points (their true intrinsic luminosities) must be properly calibrated for their distance measures to be correct. Galaxies with large numbers of Cepheid variables can have distances determined through the average inferred distance from each variable. The calibration of Cepheid variables can be set through several means, but all require some independent distance measure for the first ladder rung. To move to the distant Universe, a key data set are galaxies where we have observed a type Ia supernova and several Cepheid variables, which enable a calibration of the type Ia distance through comparison. If the zero point is set incorrectly in any of these steps, then a systematic error will be induced in the inferred distance.
The exact construction of a cosmological ladder can now rely on several different rungs. Regardless of this choice, similar results arise for several other calibration methods. As it is unlikely that all of these calibration methods would be systematically incorrect in the same direction and magnitude, an incorrect distance ladder calibration seems somewhat unlikely to be the origin of the disagreement. For a broad discussion on suggested systematic errors and an investigation into their possible contribution, see Riess et al. (2016).
The recent value of \(H_0\) from the distant Universe come from studies of the CMB with the full data set from the Planck mission (Planck Collaboration 2020) which is connected to the nearby Universe by assuming \(\varLambda \)CDM. There are several correlations between parameters inferred from CMB data. Density fluctuations at recombination (observed through the CMB) result in anisotropies in the large-scale structure of the Universe referred to as Baryon acoustic oscillations (BAOs). BAOs are standard rulers, and combining CMB+BAO observations can break geometric correlations from CMB data alone. The most precise value of \(H_0\) from Planck Collaboration (2020) come from CMB+BAO data, with the BAO measures taken from the latest BOSS results (Alam et al. 2017). The predecessor to Planck was WMAP, and WMAP+BAO measures give a value of \(H_0\) that disagrees with Riess et al. (2019) at more than 3\(\sigma \) significance. Planck Collaboration (2020) give a thorough discussion of systematics within Planck data, resolve some issues between WMAP and Planck, and conclude that any simple modification to the CMB+BAO (with \(\varLambda \)CDM) value of \(H_0\) to match the value from Riess et al. (2018) is disfavored through comparison with other cosmological observations.
A clever approach to determine the value of \(H_0\) sets the calibration of type Ia supernovae from the distant Universe using BAOs, a so-called “inverted distance ladder” (see e.g., Heavens et al. 2014). This is also done assuming \(\varLambda \)CDM, which results in a value of \(H_0\) consistent with the CMB+BAO value (Planck Collaboration 2020). While the precision of the type Ia and CMB+BAO values of \(H_0\) has improved over the past few years, the central value from each method remains largely unchanged. Therefore, it is worth considering that this is evidence against \(\varLambda \)CDM being the correct cosmological model, which would not be surprising given the historic pace of such advancements.
The most boring outcome is the \(H_0\) disagreement is entirely due to statistical chance, but this appears to be unlikely given the disagreement arises through several measures, has persisted for several years, and has become more significant as each measure became more precise. If there is a systematic error in our study of type Ia supernovae or in the calibration of the cosmological ladder, which would not be entirely surprising since we do not understand the explosion mechanism nor the progenitor(s), then it would have implications beyond just the value of \(H_0\). Similarly, if there is a systematic error in our study of the CMB then our inferred values for several correlated parameters would be wrong, and the ramifications would be far reaching. If the inferred disagreement is not statistical, and there is no (dominant) systematic error in these studies, then it provides strong evidence that \(\varLambda \)CDM must be extended.
A quirk of GR is that both GW amplitude and \(\dot{f}_{GW}\) depend on the chirp mass, which enables a determination of the luminosity distance from GW observations of chirping binaries (Schutz 1986), which led to their designation as standard sirens. Their importance for cosmology has long been known (see e.g., Schutz 2002, for a review). With the first GW detection of a NS merger as GW170817, the associated redshift enabled the first demonstration of this technique (Abbott et al. 2017h). NS mergers will provide a resolution to the disagreement on the value of \(H_0\) in the next few to several years (strictly speaking, there is a possibility that standard sirens give a third value inconsistent with the other two). This requires a precision comparable to that of type Ia supernovae, or about 2%.
Several people have calculated the number of joint events necessary to hit some level of precision (Dalal et al. 2006; Nissanke et al. 2013; Chen et al. 2018; Feeney et al. 2019; Hotokezaka et al. 2019; Vitale and Chen 2018; Kyutoku and Seto 2017). There exists a luminosity distance-inclination correlation that limits the precision of the distance estimate. The different results from these papers arise from the different assumptions on how well inclination can be constrained, from the number of active GW interferometers (with more giving increased determination of inclination/distance), from the different source classes (with NSBH potentially more useful per event than BNS), and from using EM information to constrain inclination (which is generally done with information from the SGRB jet).
There are also methods that attempt to infer \(H_0\) from CBCs without associated redshifts (e.g., Messenger and Read 2012; Taylor and Gair 2012), but these are inherently model dependent. While they should be useful for constraining parameters in a given cosmology, it would be difficult to falsify a standard cosmology with such a measurement. For comparison, some of the scientists that showed CDM was incomplete (Riess et al. 1998) are now using the same sources to suggest \(\varLambda \)CDM may also be incomplete and have been moving towards discovery significance (e.g., Riess et al. 2019), but significant works into alternative explanations such as observational biases, source evolution, and underestimates of errors as sources of the disagreement continue (see discussions in Riess et al. 2016; Planck Collaboration 2020). We here make generic arguments on prospects for \(H_0\) precision with NS mergers and, separately, for those with associated GRBs. We discuss the latter here for organizational purposes, but it is more relevant in the next section.
As the number of NS mergers with GW measured distances and associated redshift increases, the precision of the \(H_0\) measure from standard sirens should scale as \(1/\sqrt{N}\). This is only valid outside low-number statistics as the uncertainty on the luminosity distance can vary greatly for individual events (due to SNR, orientation, number of contributing interferometers, etc). The scaling from Chen et al. (2018) for the HLV network is \(15/\sqrt{N}\), which we adopt here. To achieve the necessary 2% precision to prefer either the type Ia or CMB+BAO \(H_0\) value, this would require \(\sim \) 50 NS mergers with associated redshift.
Early discussions of using NS mergers as standard sirens focused on SGRBs as the EM counterpart to enable redshift determination (e.g., Dalal et al. 2006; Nissanke et al. 2013). GW-GRB detections are advantageous as they can be easily detected deeper into the Universe and the collimation and relativistic beaming of the associated SGRB enable inclination constraints that can reduce the distance uncertainty by a factor of a few. If we conservatively say this improvement is a factor of \(\sim \) 2–3 (which is reasonable given uncertainties on the half-jet opening angle distribution and effects of jet structure), then a 2% determination of \(H_0\) could be done with about a dozen events. The GW+kilonova approach will likely resolve the \(H_0\) tension before the GW+GRB approach, but the GW+GRB approach will become more important as the GW interferometers search deep into the Universe. In practice, combining the two will provide the best measurement. If our representative estimates are accurate this would be resolved in the A+ era.
Other studies of the distance-redshift relation are all inherently limited by systematic errors, in part because they have achieved sensitivity beyond the statistical uncertainty. These include instrumental calibration uncertainty and zero-point luminosity uncertainties that calibrate the steps of the cosmological ladder. For standard sirens the instrinsic luminosity is determined by well-understood differential geometry, so long as GR correctly predicts the inspiral of CBCs. This leaves the absolute amplitude calibration of the observing intereferometers. The best calibration in a final report of the O2 observing run from Advanced LIGO/Virgo is 2.6% for LIGO-Hanford (Abbott et al. 2019b). Should the calibration uncertainty affect the precision of future standard siren studies there is no obvious technological limitation to achieving sub-percent precision (Karki et al. 2016; Estevez et al. 2018). Therefore, we do not expect classical systematics to prevent resolution of the \(H_0\) controversy with standard sirens. Implicit in this discussion is that standard sirens will also provide a fully independent calibration of the cosmological ladder.
However, there is a different potential systematic that has not been discussed in the case of GW+kilonova studies. Determination of redshift for NS mergers is done by achieving a precise localization with EM observations, identifying the host galaxy (Sect. 3.5), and measuring the redshift to that host galaxy. The first step requires identification of an EM counterpart with follow-up telescopes; if there is an inclination-dependence on the observed EM brightness then GW-detected mergers with associated redshift will have an inclination bias relative to the total sample of GW-detected mergers. This would bias a determination of \(H_0\) due to the correlation of distance and inclination on GW amplitude. This has been considered in the cases of GW-GRBs because it is an obvious effect. As discussed in Sect. 2.11, we expect significant inclination effects on EM brightness for the majority of counterparts. We support investigations into the level of systematic error this effect can produce.
6.2 Beyond \(\varLambda \)CDM
Base-\(\varLambda \)CDM is the standard model of cosmology as it reliably describes our observations of the Universe with only six parameters. As discussed, one of these is the Hubble constant. The expansion rate of the Universe through cosmic time is determined by opposing effects: the pull of gravity opposed by dark energy. These effects are conveniently described through the cosmological density parameters. The density parameter is defined as \(\varOmega \equiv \rho /\rho _c\) where \(\rho _c = 3H^2/8\pi G\) is the critical density necessary for a flat Universe.
The density of matter is \(\varOmega _M = \varOmega _c + \varOmega _b + \varOmega _\nu \) with the densities of cold dark matter as \(\varOmega _c\), baryonic matter \(\varOmega _b\), and neutrinos \(\varOmega _\nu \). Returning to the use of the dimensionless scale parameter a, \(\varOmega _M\) evolves as \(a^{-3}\) as the total amount of matter is largely constant, so the density scales as the inverse volume. The density of radiation, \(\varOmega _R\), scales as \(a^{-4}\) for the same reason with the addition of cosmological redshift (lowering the energy of each photon). The density of dark energy is captured as \(\varOmega _{DE}\), which is represented as \(\varOmega _\varLambda \) when it is specifically referring to a cosmological constant. In a flat Universe \(\varOmega \equiv 1 = \varOmega _M+\varOmega _{DE}\) (when neglecting terms that are small in the late Universe).
Several extensions to the base \(\varLambda \)CDM are generally considered. We list a few here and describe the implications of these extensions.
-
What is the Shape of the Universe?
Observations of the observable Universe may provide insights into the topology of the Universe as a whole. For ease of use, we can capture curvature as an effective density \(\varOmega _k = 1-\varOmega \) which will scale as \(a^{-2}\). If the Universe is flat then \(\varOmega _k = 0\) and the Universe is infinite (assuming it is simply connected). If the Universe is curved, this is not necessarily true. If \(\varOmega _k\) is negative then the Universe has positive curvature and is hyperbolic. If \(\varOmega _k\) is positive then there is negative curvature and we live in a finite, spherical Universe. Allowing this parameter as the only extension to base-\(\varLambda \)CDM, joint CMB+BAO observation from Planck and Boss data constrain \(\varOmega _k = 0.0007 \pm 0.0037\) at 95% confidence (Planck Collaboration 2020).
-
Is Dark Energy a Cosmological Constant?
We represent dark energy as a cosmological constant because it reliably matches observations, was a simple extension to CDM, and is still consistent with GR. However, it may be that dark energy evolves with time (or, equivalently, a). If true, this would prove \(\varLambda \)CDM incomplete or invalidate GR on cosmological scales, either of which would be a monumental discovery. There are alternative theoretical models to explain dark energy as arising from a dynamic effect, such as Quintessence (Ratra and Peebles 1988; Caldwell et al. 1998).
The EOS of dark energy is defined with the dimensionless parameter \(w=p/\rho \), the ratio of the pressure to the energy density of a perfect fluid. In \(\varLambda \)CDM these values are equal and opposite, i.e., \(w=-1\). To investigate if dark energy is not a cosmological constant, the dark energy EOS is often parameterized as \(w = w_0 +w_a (1-a) = w_0 + w_a z/(1+z)\) (Chevallier and Polarski 2001; Linder 2003; Planck Collaboration 2020).
For \(\varLambda \)CDM \(w_0=-1\) and \(w_a=0\). If \(w_0 \ne -1\), the dark energy density is not constant as the Universe expands, and \(w_a\) not being equal to 0 would imply a time-varying EOS. Fixing \(w_a=0\), Planck Collaboration (2020) combine CMB measures with BAO measurements from BOSS to limit \(w_0 = -1.04 \pm 0.10\) at 95% confidence. Including SNe information allows for constraints on \(w_0\) and \(w_a\) together, with \(w_0 = -0.961 \pm 0.077\) and \(w_a = -0.28^{+0.31}_{-0.27}\), both at 68% confidence, and they are anticorrelated.
-
The Mass of Neutrinos
This is discussed in Sect. 8.1.
These extensions modify the equations for the cosmological observables in the nearby Universe. Allowing for \(\varOmega _k\) and \(w_0\) to separately deviate from their base values (but not \(w_a\) for simplicity), the Hubble Parameter is modified into:
We here introduce the comoving distance:
Which enables us to write the luminosity distance:
Here the dark energy density is \(\varOmega _{DE}\) since it may not be a cosmological constant. In the case that \(\varOmega _k = 0\) and \(w_0=-1\) these reduce to the previous equations.
Answering these questions could change our fundamental understanding of the Universe. The early Universe was radiation dominated. Because of cosmological redshift of photons, it quickly transitioned from radiation dominated to a matter-dominated Universe, referred to as the deceleration era as the pull of gravity slowed the expansion rate of the Universe. Over billions of years \(\varOmega _M\) was diluted until the effects of dark energy became dominant, bringing us to the dark energy-dominated Universe, also referred to as the acceleration phase. When this transition occurred, and the shape of the transition, is sensitive to the EOS of dark energy and the shape of the Universe.
The effect on the Hubble Parameter and luminosity distance from allowing \(\varOmega _k\) and \(w_0\) to individually vary, with values taken from Table 7. We show the base \(\varLambda \)CDM values from Planck Collaboration (2020) and the range of the allowed parameter space for a non-flat Universe and non-constant dark energy. The top is for the Hubble parameter, scaled by \((1+z)\), the middle is the fractional deviation of this value, and the bottom the fractional deviation of the luminosity distance, with the latter two corresponding to the necessary measurement precision for informative results on these cases
To demonstrate how changes in these additional parameter models affect observables we match the approach often used for future cosmology experiments (e.g., Weinberg et al. 2013; Gehrels et al. 2015). We vary the cosmological parameters in a way that the effect on the CMB power spectra should be minimized. Specifically, with the convention of \(h = H_0/(100 \text{ km s}^{-1} \text{Mpc}^{-1})\), we maintain the distance to the last scattering surface and we fix both \(\varOmega _M h^2\) and \(\varOmega _b h^2\). These values for the various cases considered here are given in Table 7. The effect of these modifications on the observables is given in Fig. 17. We would like to emphasize that what is shown is two separate 1-parameter extensions to the base \(\varLambda \)CDM. Considering additional options, such as jointly varying \(\varOmega _k\) and \(w_0\) or allowing \(w_a\) to vary as well, opens up a vastly larger range of still-acceptable parameter space with correlated variables. Understanding these effects in the middle-age of the Universe is a prime goal of upcoming cosmology experiments like WFIRST, LSST, and EUCLID.
It is evident from the figure that constraining \(H_0\) is a particularly powerful method to constrain beyond-\(\varLambda \)CDM models. The precision from Riess et al. (2019) is sufficient to provide useful degeneracy breaking information (e.g., as discussed in Sect. 8.1, its inclusion could resolve the neutrino mass hierarchy, due to their anticorrelation), but this is not done because the value is inconsistent with the CMB+BAO measures and the reason why is not known. Enter NS mergers. With current GW interferometers we can study the luminosity distance-redshift relation in the nearby Universe. A 1% measure of \(H_0\) in the local Universe corresponds to a \(\sim \) 7% measure of the EOS of dark energy when combined with Planck data, and a \(\sim \) 3% measure with future CMB experiments (Riess et al. 2016). If standard siren studies show that other nearby measures of \(H_0\) are flawed, then combining CMB+BAO and standard siren information would be useful for exploring multi-parameter extensions to \(\varLambda \)CDM (e.g., Di Valentino et al. 2018). Otherwise, the combined nearby measurement of \(H_0\) can be used to study beyond-\(\varLambda \)CDM models or to further investigate potential issues with the early universe measures.
Further, this also shows why we require a resolution of the \(H_0\) tension using standard sirens even with upcoming cosmological experiments: in order to jointly constrain \(\varOmega _k\) and both \(w_0\) and \(w_a\) for the time-varying dark energy EOS, as well as other additional parameters, we need precise measures of these observables throughout the Universe (Linder 2005; Knox 2006; Dalal et al. 2006; Bernstein 2006). Within the decade, the combination of CMB observations with information from LSST, EUCLID, and WFIRST as well as standard siren and other local measures of \(H_0\) will provide the greatest test of any proposed cosmological model.
As GW detectors peer deeper into the Universe, they will enable the most precise Hubble diagram, with a redshift range rivaling or exceeding even type Ia supernovae. These tests are key goals for third generation ground-based interferometers (e.g., Sathyaprakash et al. 2010, 2012), LISA (e.g., Tamanini et al. 2016), and mid-range space-based interferometers (Cutler and Holz 2009). LISA is expected to detect CBCs to greater redshifts than the other options, but prospects for the EM emission is more uncertain. Third generation ground-based interferometers will tend to have poorer distance uncertainty on an event by event basis, than would a mid-range interferometer. We note the beneficial property for these studies that the peak SGRB merger rate (a proxy for NS mergers) is around the transition era (Berger 2014).
Traditional cosmology experiments being constructed to answer these questions seek several methods with orthogonal systematics to maximize precision. This is discussed in every document justifying these experiments, for good reasons. We refer to Weinberg et al. (2013) for an in-depth discussion of these methods. They mention the promising prospects for standard sirens but do not consider them in detail because at the time their rates and our capability to detect EM counterparts was not known. It is for this reason that, despite these future interferometers coming online in an era where we already expect precision cosmology in the Universe, we still consider this a strong science driver for NS mergers. They provide an entirely independent method of distance determination and will become key sources in cosmology.
In the current era we require the capability to detect kilonovae and measure redshift in the local Universe. As we transition to future GW interferometers we will require the capability for localizations sufficient for follow-up searches to identify the GRB afterglow (as kilonovae will be too faint at these distances). This can be done with a large-scale gamma-ray mission to jointly detect the associated GRB, with the added benefit of restricting the inclination angle in the analysis. With mid-range interferometers the localizations should be sufficient in their own right. In all cases, we require the capability to measure the redshift for host galaxies to a reasonable fraction of the GW horizon.
Lastly, we briefly comment on the possibility of using lensed NS mergers to measure \(H_0\). For lensed standard candles we can directly measures \(H_0\) (Refsdal 1964; Blandford and Narayan 1986), and potentially additional cosmological parameters (Linder 2011). A lensed type Ia has been found (Goobar et al. 2017), but cosmological information is still unavailable due to the correlation with the properties of the lensing system. With a GW-GRB event or mid-range interferometers we could robustly associated multiple detections of the same event (noting that in the GW-GRB case the jets are sufficiently small that we would not fall out of the jet in most path cases Perna and Keeton 2009), which would have a precisely (\(\sim \) ms) measured event time. This would be several orders of magnitude more precise than, e.g., a type Ia supernova. However, this analysis is incredibly difficult and at the time these detections occur they will likely be more important as independent confirmation rather than discovery cases, and we consider them a nice free bonus rather than a driving capability.
7 Dense matter
Quantum Chromodynamics (QCD) is the QFT description of the strong force. It describes the interactions between its force boson known as gluons and the elementary particles named quarks, which come in six flavors and three colors (the origin of the chromo- prefix). Gluons bind quarks into hadrons, which are classified as mesons composed of a (valence) quark antiquark pair or baryons composed of three (valence) quarks. Protons and neutrons are baryons that are the composite particles that constitute atomic nuclei, referred to together as nucleons. For a review focused on the nuclear physics description we refer to Baym et al. (2018). For a review focused on the astrophysical determination of the NS EOS we refer to Özel and Freire (2016).
QCD is a reliably well tested theory and a foundational aspect of the Standard Model; however, it is incredibly complicated. Constructing large-scale predictions of QCD relies on approximate methods. The nuclear saturation density is where baryons begin to overlap, and occurs at \(\rho _0 \approx 2.7 \times 10^{14}\,\text{g cm}^{-3}\) (e.g., Baym et al. 2018). Up to about \(2\rho _0\) nucleon interactions dominate with some additional exchanges. In this regime QCD lattice methods provide sufficient description to enable tests of QCD. At incredibly high densities, \(\rho \gtrsim 10-100\rho _0\), the color confinement of quarks to mesons and baryons breaks down. The resulting quark-gluon plasma is well-described by perturbative QCD, which have resulted in the most precise tests of QCD to date (e.g., Altarelli 1989; Gyulassy and McLerran 2005).
We know less about the behavior of matter in the range \(2\rho _0 \lesssim \rho \lesssim 10\rho _0\). It is not known how matter at these densities behaves, i.e. if there is a firm or smooth phase transition between baryon-dominated and quark-dominated interactions. For example, do baryons begin sharing quarks or does color confinement breakdown quickly at some specific density. Constructing predictions at these densities from QCD may not be able to directly rely on the previously discussed methods to sufficient accuracy and cannot be built from first principles as this is beyond any existing computational power, and will continue to be for the foreseeable future. Therefore, we rely on varying approximations, often attempting to adapt the approaches viable at either the lower density or higher density end. A description of these methods is beyond the scope of this work and reviewed in Baym et al. (2018).
These extreme densities are unobtainable in terrestrial laboratories. NSs are natural experiments. The collapsing core of massive stars converts electrons and protons into the neutrons, resulting in the densest known matter and the only known cold supranuclear matter in the universe, where cold means temperatures \(\lesssim \)1 MeV. NSs can be hot supranuclear matter for comparatively short times when they are born as CCSNe or during merger and coalescence in NS mergers. In the former case several layers of a large star are between object and observer, a region that is significantly cleaner in the case of NS mergers. Their crusts, while incredibly dense by any reasonable measure, have low enough densities that lattice methods may be applicable. Between the crust and the center the densities fall in the 2–10\(\rho _0\) range. Therefore, understanding the intrinsic nature of these enigmatic objects allows for unique constraints on the behavior of supranuclear matter, which nicely complement current and upcoming ground-based facilities like the Facility for Rare Isotope Beams (Balantekin et al. 2014).
The key to tying astrophysics to nuclear physics is the NS EOS, which prescribes the assumed pressure-density relationship. Such a relation can be constructed from the approximate methods described above. From this, one can make testable predictions. Like any star, the structure of NSs is described from the balance of gravitational forces against internal processes. Oppenheimer and Volkoff (1939) and Tolman (1939) derived the equations to calculate NS structure and their mass-radius relation from an assumed EOS, which are now referred to as the Tolman–Oppenheimer–Volkoff (TOV) equations.
Soft EOS are those with lower pressure for a given mass density, which tend to have lower maximal masses. Stiff EOS have higher pressures for a given mass density, and tend to have higher maximal masses. Above \(\sim 1.5\,M_{\odot} \) NSs have a peculiar property: heavier masses correspond to smaller radii, with as asymptotic behavior towards \(M_\mathrm{TOV}\), which is the maximum mass of a stable, non-rotating NS. Models exist for more exotic dense stars. We do not discuss these models in detail here, but note that constraints on the parameters relevant for the NS EOS will constrain viable exotic stars. For example, other stars can have significantly increased mass beyond the range typically considered for NSs (e.g., the three curves that reach the upper right of Fig. 18).
The mass-radius relations for several representative EOSs are shown as lines. Constraints are shown in red and green; the viable models must fall into the green regions and must avoid the red regions. The lower band of constraints is set by the mass-radius constraints from multimessenger studies of GW170817. The upper red constraint corresponds to upper limits on \(M_\mathrm{TOV}\) (also referred to in this paper as \(M_\mathrm{Stable}^\mathrm{Max}\)). These values come from the results in Coughlin et al. (2019b). The lower limit of the upper green constraint is from the lower limit of \(M_\mathrm{TOV}\) (Antoniadis et al. 2013). Nonviable NS EOS, according to Coughlin et al. (2019b), are shown in grey; viable models have thicker, colored lines and the names are labeled at the top. Image reproduced with permission from Coughlin et al. (2019b), copyright by the authors
Astrophysical constraints on NS EOS, prior to GW170817, were set by careful temporal or spectral observations of galactic NSs, as reviewed in Özel and Freire (2016). A variety of techniques are used, with varying levels of precision. The mass-radius relationship is the most well known prediction that astrophysical observations seek to constrain; examples from a representative set of NS EOS are shown in Fig. 18. Determination of the NS EOS is important enough to warrant a space-based mission dedicated to this goal. NICER seeks to measure the mass-radius relation of three NSs through observations of their X-ray emission to 5–10% precision (Gendreau et al. 2012). Current results from NICER begin to approach the 10% limit in both mass and radius (Miller et al. 2019b; Riley et al. 2019).
To be clear, constraining the NS EOS will not provide a new understanding of the fundamentals of QCD itself. This is why this section is distinct from Sect. 8.Footnote 8 Determining the NS EOS will inform on reliable methods to construct large-scale predictions from QCD in an otherwise inaccessible regime, which can be informative for other purposes.
For example, it is related to the thickness of the neutron skin of heavy nuclei, which are 18 orders of magnitude smaller in size (e.g., Horowitz and Piekarewicz 2001). Neutron skin thickness is probed with terrestrial laboratories (e.g., Horowitz et al. 2014), providing comparable precision. Constraining these distinct but related properties over such a massive size range gives a particularly stringent test of our understanding of the large-scale behavior of QCD in this density regime. The next generation ground-based experiments will provide early results in the mid-2020s.
A full understanding of such densities requires the intersection of nuclear physics and astrophysics. Following discussions in Zhang et al. (2018b), we can approximate the energy per nucleon \(E(\rho , \delta ) \approx E_0(\rho ) + E_\mathrm{sym}(\rho )\delta ^2\), with the isospin asymmetry \(\delta = (\rho _n-\rho _p)/\rho \) and \(E_0(\rho )\) the energy in symmetric matter. \(E_\mathrm{sym}\) captures the effects of the neutron-richness of the system. Determining the nuclear symmetry energy density dependence is a key goal for nuclear astrophysics (Aprahamian et al. 2015; Bracco 2017). \(E_0\) and \(E_\mathrm{sym}\) near the saturation density can be described with characteristic parameters of the EOS. Some of these parameters are reasonably well determined from terrestrial experiments and can be used to inform astrophysical inferences, e.g., excluding a Stable NS remnant for GW170817 (Zhang et al. 2018b). Otherwise, improved measurements on the properties of NSs and understanding of the NS EOS can provide new understanding on the nuclear symmetry energy at supranuclear densities (Li et al. 2019).
GW detections of NS mergers provide new ways to constrain the NS EOS. A review of inferences from the observations of GW170817 is available in Raithel (2019). We discuss these here, as well as future prospects. The parameters of interest and how observations of NS mergers constrain them are discussed in Sect. 7.1. Using these measurements together to constrain the NS EOS is discussed in Sect. 7.2. We close with a brief discussion on a potential unique QCD measurement from GW observations of BNS mergers in Sect. 7.3.
7.1 Observables from neutron star mergers
The unique constraints on the NS EOS utilizing NS mergers generally rely on the GW measurements. We briefly discuss some the relevant limitations of these measurements here.
Precise knowledge of the NS masses is critical. As previously stated, the GW measurement of the chirp mass in NS mergers is precise, but the measurement of the mass ratio is usually not. From observations of galactic BNS systems the individual masses cluster around \(1.33 \pm 0.09\) (Tauris et al. 2017; Abbott et al. 2019b). This also implies that \(q \approx 1\) for BNS systems, a result generally confirmed by population synthesis models, which would allow for a precise value of the total mass of the system for these events, and much stronger constraints in the masses of the individual progenitors.
The detection of GW190425 has shown that GW-detected merger events do not closely follow the galactic mass distribution, but it is still consistent with \(q\approx 1\) (Abbott et al. 2020a). However, new measurements suggest between 2 and 30% of the total population of BNS mergers will be asymmetric based on the identification of an asymmetric binary in the Milky Way (Ferdman et al. 2020). In what follows we generally assume that the majority of BNS mergers will be reasonably symmetric, but this absolutely needs to be verified from observations of loud events. Should asymmetric cases be non-negligible all of the following science results will still be possible, but some will require a significantly larger number of events. We note that the low mass of BNS systems allows for a reasonable determination of the total mass even if the mass ratio is not precisely known, e.g., for a fixed chirp mass varying q from 0.7 to 1 alters \(M_t\) by only 10%. This may bias measurements if BNS mergers do not have \(q\approx 1\) as expected, but is reasonably accurate for current measurements.
The reason the mass ratio can not be measured for most of these events is its perfect correlation, at leading order, with one of the spin parameters. The highest observed dimensionless spin for NSs in galactic BNS systems are \({\chi } \approx 0.05\). The GW parameter estimation can be run assuming this as the maximum allowed spin value for the individual NSs, referred to as the low-spin prior (e.g., Abbott et al. 2019c). This assumption allows for tighter constraints on the mass ratio, and therefore tighter constraints on the individual masses and total mass of the system. Again, this assumption is informed from prior EM observation, appears to be reasonably valid, but should be tested with particularly loud events. This is demonstrated with GW190814 which has the most precisely measured secondary mass to date as it is both asymmetric and loud (Abbott et al. 2020c).
When discussing BNS mergers there are two masses of interest: \(M_b\) is the baryonic mass and \(M_g\) the gravitational mass, which is \(M_b\) minus the binding energy. Conservation of mass applies to \(M_b\), but \(M_g\) is the GW observable. To determine the total mass of the remnant object in BNS systems one must convert \(M_{g,t}\) (with subscript denoting total, as before) into \(M_{b,t}\), use mass conservation for \(M_{b,\mathrm remnant} = M_{b,t} - M_{ej}\), then convert back to \(M_{g,\text{remnant}}\). Below we refer to \(M_{g, \mathrm remnant}\) as \(M_\mathrm{remnant}\). An in-depth discussion of this is presented in Gao et al. (2020), who provide EOS-insensitive relations to convert between these two.
Quasi-universal relations refer to properties or relations that appear preserved over a wide range of (still viable) NS EOS. In fact, there are some that exist without an intuitive reason as to why (e.g., Yagi and Yunes 2013). There are also parametrized forms for NS EOS (see e.g., Abbott et al. 2018b, and references therein) that are used as phenomenological tools to allow for application of observational constraints to a wide range of EOS and are powerful methods to advance our understanding in this complicated, interdisciplinary field of study. However, we note that there are known errors associated with these approaches. Any final assessment on the viability of a NS EOS may require the direct test of that EOS if the measurement is near the level of the quantified errors.
7.1.1 The maximum mass of neutron stars
For the purposes of this subsection we refer to \(M_\mathrm{TOV}\) as \(M_\mathrm{Stable}^\mathrm{Max}\) for reasons that will be immediately obvious. We label the maximum mass of a NS undergoing only isotropic rotation as \(M_\mathrm{SMNS}^\mathrm{Max}\) and the maximum mass of a differentially rotating NS as \(M_\mathrm{HMNS}^\mathrm{Max}\). Note that \(M_\mathrm{Stable}^\mathrm{Max} \le M_\mathrm{SMNS}^\mathrm{Max} \le M_\mathrm{HMNS}^\mathrm{Max}\). NS EOS-insensitive scalings relate these values (e.g., Cook et al. 1994; Gao et al. 2020; Köppel et al. 2019).
The determination of the immediate remnant object for BNS mergers (Sect. 3.2) relates to these quantities. If \(M_\mathrm{HMNS}^\mathrm{Max} < M_\mathrm{remnant}\) the system will undergo prompt collapse; if \(M_\mathrm{SMNS}^\mathrm{Max}< M_\mathrm{remnant} < M_\mathrm{HMNS}^\mathrm{Max}\) the remnant will undergo a HMNS stage before collapsing to a BH; if \(M_\mathrm{Stable}^\mathrm{Max}< M_\mathrm{remnant} < M_\mathrm{SMNS}^\mathrm{Max}\) the remnant undergoes a phase of internal differential rotation before transitioning to a long-lived SMNS stage; otherwise \(M_\mathrm{remnant} < M_\mathrm{Stable}^\mathrm{Max}\) and the remnant object is a permanently stable NS.
Then, we can use the multimessenger determination of the BNS remnant classification to determine \(M_\mathrm{TOV}\). This has been a promising prospect for science with NS mergers for some time (e.g., Bauswein et al. 2013a; Rezzolla et al. 2018). The broad approach discussed here was described in Margalit and Metzger (2019), who argue the detection of \(\sim \) 10 BNS mergers in GWs with confident remnant classification would constrain \(M_\mathrm{TOV}\) to the level of a few percent, under the assumption that \(q\approx 1\). This value is largely determined by the pressure at the core of the NS.
The current constraints are \(1.97\,M_{\odot} \le M_\mathrm{TOV}\) and \(M_\mathrm{TOV} \lesssim 2.3\,M_{\odot} \). The lower limit comes from observations of a galactic NS with mass \(2.01 \pm 0.04\,M_{\odot} \) from Antoniadis et al. (2013), which ruled out a significant fraction of soft EOS that were otherwise viable (e.g., Lattimer 2012). The maximum value is set by considering several published results (e.g., Lü et al. 2015; Shibata et al. 2019). We note that more stringent upper limits have been published (e.g., Margalit and Metzger 2019), but these results are somewhat in tension. Future observations will resolve this question.
Constraints may improve here with the discovery/characterization of galactic NSs, especially if they identify NSs with \(M>2.0\,M_{\odot} \) (with small uncertainties). They will certainly improve with additional GW detections of BNS mergers (with sufficient EM characterization). These multimessenger studies have the advantage that the number of known events will grow rapidly and that we can separately constrain the maximum mass of SMNS and HMNS with a large enough sample, which can provide additional information to constrain the EOS. As shown in Fig. 18 these limits are powerful constraints on viable EOS as they inform on an asymptotic limit (note the maximum \(M_\mathrm{TOV}\) in that figure slightly differs from discussions here). Future constraints at the percent level will provide an incredible constraint on viable NS EOS.
7.1.2 The lifetimes of metastable neutron stars
There is another key parameter that can constrain the NS EOS that relies on the determination of the merger remnant, that may be unique to multimessenger studies of BNS mergers: the lifetimes of HMNSs or SMNSs. From simulations, the lifetime of HMNSs is \(\lesssim 1\,\text{s}\) (e.g., Sekiguchi et al. 2011) and the lifetime of SMNSs with massive magnetic fields and potential energy losses to GWs (as may be expected during these mergers) is \(\sim 10{-}10^5\,\text{s}\) (e.g., Ravi and Lasky 2014). Though much uncertainty remains (e.g., Baiotti and Rezzolla 2017).
The lifetimes of these metastable NSs depends on the NS EOS (though not exclusively, e.g., the mass ratio). There have been studies on the effects of remnant lifetime on observable parameters, especially in the case of neutrino irradiation altering the colors of kilonovae (e.g., Metzger and Fernández 2014; Lippuner et al. 2017). The lifetimes may be directly measured by GW or neutrino observations, though this will not occur for a decade. We here propose a method to determine the lifetimes of either HMNSs or SMNSs (but not both).
If only BHs are central engines of SGRBs (Sect. 4.2) then in the HMNS case the jet cannot launch until the collapse of the NS. Interesting constraints on this lifetime likely require \(\sim 1\,\text{s}\) accuracy. Advancements in understanding the relative contributions of these terms and fortunate events (Sect. 3.3) will allow an interesting measure. The most interesting scientific question related to this measure (Sect. 7.3) requires precision that is likely impossible without direct measures.
Alternatively, if magnetars can power SGRBs, then we can directly determine the lifetime of a SMNS from the non-thermal observations. This could either be the duration of the extended emission in gamma-rays following the prompt emission or the duration of the X-ray plateaus in the afterglow (Sect. 4.7). That is, the sharp drop in flux is expected to correspond to the collapse time of the SMNS. Indeed such interpretations have already been applied to a small number of GRBs (e.g., Zhang and Mészáros 2001; Troja et al. 2007). Multimessenger studies confirming these interpretation will enable they use to study the NS EOS.
Either option will provide insight on the internal dynamics of the NSs. The application of these measurements to a broad range of EOS is not straightforward. Should an observational measure occur we would expect the necessary simulations to be performed.
7.1.3 Tidal deformability
The GW determination of the tidal deformabilityFootnote 9\(\varLambda \) of a NS is another parameter that can constrain the EOS that is uniquely constrained from observations of NS mergers, in this case with high-frequency GW observations. The inspiral of NS mergers are effectively identical to BBH mergers with similar intrinsic parameters until very near merger, when the effects of matter and the larger size of NSs begin to be important.
NSs undergo tidal deformation in an EOS-dependent manner, which results in an acceleration of the inspiral, generally at \(\gtrsim 500\,\text{Hz}\). This tidal deformability is often parametrized as
where \(k_2\) is the quadrupole love number (Read et al. 2013). Note that some formulations utilize a parameter that scales as \(R^6\) (e.g., De et al. 2018). Detection of non-zero \(\varLambda \) is how GW observations alone can infer the presence of a NS. Detection of \(\varLambda \) is likelier to be measured for BNS mergers as these inspirals are slower and the larger mass of the BH can dominate the inspiral of NSBH mergers, hiding the matter effects signature. In either case, a NS with a larger radius will be more strongly deformed.
This parameter was constrained for GW170817. Several analyses provided upper limits on tidal deformability and some also claim lower limits (e.g., Abbott et al. 2018b; Most et al. 2018; Raithel et al. 2018; Coughlin et al. 2019b), providing somewhat varied results. However, it shows the capability of GW measurements of this parameter, suggesting the Advanced network can (or already has) constrain this parameter. Providing significantly more accurate constraints likely requires both improved GW models that account for matter effects and improved high-frequency response beyond the current funded upgrades.
7.1.4 The mass-radius relation
We have already discussed how to infer the masses of the progenitor and remnant object. Then, measurement of the radius, largely determined by the pressure at \(\rho \approx 2.5\rho _0\) (Lattimer and Prakash 2000), enables constraints in the mass-radius plane. There are a few ways to do this with observations of NS mergers.
The definition of the tidal deformability being proportional to a high power of the radius relates the parameters, and enables constraints on the NS radius from GW observations (e.g., Abbott et al. 2018b; Hotokezaka et al. 2016a). These measurement are of order 10% accuracy, approaching the precision goal of new EM NS EOS instruments and analyses.
The determination of the merger remnant and the total mass of the remnant enables a constraint on the radius (Bauswein et al. 2017). This relies on the NS-insensitive relation between \(M_\mathrm{HMNS}^\mathrm{Max}\) and \(M_\mathrm{Stable}^\mathrm{Max}\) (labeled differently between these papers), which depends on \(R_{1.6}\), the radius of a \(1.6\text{M}_{\odot} \) NS for a given EOS. Assuming GW170817 did not undergo prompt collapse they limit \(R_{1.6} > 10.68_{-0.04}^{+0.15}\,\text{km}\) and demonstrate the identification of a BNS merger that undergoes prompt collapse would provide complementary upper bounds. Köppel et al. (2019) expanded this relation to the non-linear regime, giving a tighter constraint.
NSBH mergers may also provide a similarly precise determination of the NS radius (Foucart 2012). With a reasonable sample of events, or fortunate single events, we can determine the conditions for tidal disruption of the NS and the release of the EM counterparts. As discussed in Sect. 2.1.3, this condition is \(r_{\mathrm{tidal}} > r_{\mathrm{ISCO}}\). The latter is easily calculated if we can determine \(\chi _\mathrm{eff}\) of the BH. \(r_{\mathrm{tidal}}\) depends strongly on the NS radius.
Therefore, BNS and NSBH mergers provide unique methods to constrain the allowable mass-radius relation of NSs. With GW170817 the GW-only observations achieved precision of 10–20% on these parameters (Abbott et al. 2018b). As the Advanced network approaches design sensitivity this precision will improve.
Beyond even multimessenger studies within astrophysics, interdisciplinary studies in physics can also provide better constraints using astrophysical observations of these events. Capano et al. (2020) combine the astrophysical observations of GW170817 with detailed NS EOS from nuclear theory, which are more advanced than generally considered. They claim a NS radius measurement of \(11_{-0.6}^{+0.9}\,\text{km}\), or \(\sim \) 7% precision. This suggest future observations of nearby BNS mergers will surpass the 5% precision goal of other methods.
7.1.5 Ejecta properties
As described in detail in Sect. 2.1.3, the properties of the ejecta that power the kilonova emission are tied to the NS EOS. This implies that observations of the kilonova ejecta can be tied back to the NS EOS and provide interesting constraints.
For example, Radice et al. (2018) use the observed properties of KN170817 to set a lower limit on \(\varLambda \), necessary to reproduce the total ejecta mass observed. With the upper limit on \(\varLambda \) from the GW observations they conclude that we prefer Goldilocks EOS, that is, not too soft and not too stiff.
Similar inferences show the promise of multimessenger astronomy, and have been applied by a few groups (e.g., Coughlin et al. 2019b). We note that these constraints rely on simulations that reliably predicted the broad behavior of KN170817 before any kilonova had been well-observed and this is evidence supporting their claims. However, we caution against strong inferences based on the current implementations. The existing uncertainty in kilonova modeling (see Sect. 5) is not negligible. These methods will prove valuable when modeling has sufficiently advanced (e.g., more realistic initial conditions) and when they have been shown to reliably reproduce a sample of observed events.
7.1.6 Post-merger gravitational waves
The NS EOS should also have an observable imprint on the post-merger GWs, providing and independent GW measure from the pre-merger signal. The most important frequency range is between \(\sim \) 1 and 4 kHz where the spectral behavior can be complex. For an overview on our understanding of these signals and prospects for their detection see Clark et al. (2016).
The primary frequency depends predominantly on the total mass and the NS EOS (Oechslin and Janka 2007). Detections of post-merger GWs from NS mergers will be limited to particularly nearby events, where we may be able to reliable detector higher order modes in the inspiral and precisely measure the mass ratio. Otherwise we can infer the total mass from the chirp mass, so long as \(q\approx 1\) is valid. Thus, we can directly tie the primary frequency to tests of the NS EOS. There are secondary peaks whose prescence or absence will inform on the dynamics of the merger itself (Bauswein and Stergioulas 2015).
These tests rely on quasi-universal relations that have been confirmed for several NS EOS over a wide range of parameter space (e.g., Rezzolla and Takami 2016). These tie the maximum GW post-merger frequency to the tidal deformability and thus the radius of the NS (Bose et al. 2018). These measurements provide additional constraints on parameters also measured through other means, with independent systematics, and in a much higher range of NS mass. Therefore, we very strongly encourage an emphasis on high-frequency sensitivity for future GW interferometers.
7.2 Supranuclear matter and the equation of state of neutron stars
Determining the NS EOS will be greatly aided by the general assumption that all NSs are governed by the same EOS. This requires that any viable NS EOS has to be consistent with all observed properties of all observed NSs. It must simultaneously fall into the acceptable range in the mass-radius plane, be capable of producing (stable, non-rotating) NSs up to \(M_\mathrm{TOV}\), have tidal deformability in the constrained range, live the proper amount of time when metastable, and release approximately the correct amount of ejecta and it must do so for every observed NS merger. It must also reasonably match the emitted GW frequencies during merger for the different BNS merger remnant cases, once it is measured. It must do all of this while also satisfying the NS EOS constraints from other observations, such as the new and upcoming results from NICER (Riley et al. 2019; Miller et al. 2019b).
We can further apply a few more requirements, as summarized in Abbott et al. (2018b). The first is causality, limiting the sound speed at the highest pressure region for a \(M_\mathrm{TOV}\) star to be less than the speed of light. Second, each EOS must be self-consistent, e.g., it must be able to create the remnant object with the correct class for the total mass of the system while also be capable of sustaining the inferred properties of the progenitor NSs. Last, the NS must be thermodynamically stable.
Folding all of these methods into a coherent set of constraints greatly reduces the range of viable NS EOS. We look forward to the future constraints that the coming years of multimessenger astronomy will provide. As a closing remark on this science, we cite Coughlin et al. (2019b) which creates a multimessenger Bayesian framework to constrain the observed properties of the system based on GW, kilonova, and GRB constraints. While the results are model-dependent and make a number of assumptions, they provide the first demonstration of a technique that will likely prove invaluable for future studies of NS mergers. Additionally, Capano et al. (2020) demonstrate the promise of interdisciplinary work with non-astrophysicists.
7.3 The phase transitions of quantum chromodynamics
We briefly discuss a prospect that has recently been identified as a potential science goal with NS mergers. QCD has phase transitions, analogous to the phase transitions of water. That is, regions of parameter space where the behavior of matter changes significantly, such as transition to a quark-gluon plasma at particularly high densities or pressure.
GW observations of NS mergers may be able to constrain or measure a phase transition in QCD by direct determination of the lifetimes of HMNSs and the peak GW frequencies obtained during merger (Most et al. 2019; Bauswein et al. 2019). Both require GW sensitivity at several kHz. The precision required on the merger lifetime likely necessitates direct determination through GW (or neutrino) observations, as it is beyond the capability of what we can infer through indirect EM methods. As this is potentially the only way to measure QCD phase transitions we consider this a critical technical driver for future GW interferometer development.
8 Fundamental physics
Since 1900, our understanding of the Universe has fundamentally changed. Space and time were thought to be absolute until Einstein showed us space and time were relative and manifestations of spacetime (Einstein 1905). SR has now been woven throughout modern physics. Newtonian gravity had stood since the Age of Exploration until it was supplanted by GR (Einstein 1916), which has withstood a century of observational and experimental inquiries. We went from no inkling of quantum mechanics to the Standard Model of Particle Physics that brings quantum field theories for three fundamental forces into a single framework. Between them, these theories encompass all known fundamental forces of nature; they have been exquisitely tested, and, so far, observational evidence suggests they are largely correct, though incomplete. As it stands, the two theories are fundamentally incompatible. In a beautiful universe all forces could be described together, which, if possible, is generally thought to require a QFT of gravity. However, gravity could be truly distinct, and a not a force in the particle physics definition (i.e., not governed by a gauge boson). For now, true unification eludes us. Observers should strive for ever more stringent tests of these theories until they breakdown and illuminate the path forward.
NS mergers have important discovery space, providing insight into the behavior of neutrinos and GWs according to expectations from the Standard Model and GR. The non-zero mass of neutrinos is the clearest evidence for the incompleteness of the Standard Model. The use of NS mergers as standard sirens to break geometric correlations from observations of the CMB help determine the absolute neutrino mass eigenstates (Sect. 8.1). Small timescales against cosmological baselines enable unmatched timescale ratio tests of fundamental physics. The short intrinsic timescales between messengers for GW-GRB detections enable for the most precise determination of the speed of gravity relative to the speed of light (Sect. 8.2). The GR-calculated frequency evolution of GWs, and the time of flight difference for GW-GRBs, allow for precise determinations of dispersion within GWs (Sect. 8.3) which also constrains the mass of the graviton (should it exist). A network of several GW interferometers allows for searches of beyond-GR GW polarization modes (Sect. 8.4). The comparison of GW determined distance and EM determined distance allow for searches of large extra dimensions (Sect. 8.5) and, with an associated GRB, for searches of gravitational parity violation through enhancement/suppression of the two GR polarization modes (Sect. 8.6). The short intrinsic timescale for prompt GRB emission over several decades of energy in EM radiation allow for the best constraints on EM dispersion (Sect. 8.7).
Noting several of the other subsections are versions of LIV, we discuss general LIV in Sect. 8.8. Lastly, we discuss multimessenger tests of the WEP in Sect. 8.9. We also note these last two are two-thirds of the Einstein Equivalence Principle that underlie all metric theories of gravity (Will 2014). Because more stringent tests will be performed through other means, we do not consider GW dispersion as a science driver for NS mergers, but discuss it here to show the unique time of flight tests these sources enable will be less constraining than other measures.
For general overviews on the known and expected behavior of particles we refer to the Particle Data Group reviews, Tanabashi et al. (2018). For a discussion on testing GR in general we refer to Will (2014). For discussions on the tests of GR with ground-based interferometers or Pulsar Timing Arrayss (PTAs) we refer to Yunes and Siemens (2013) and to Gair et al. (2013) for LISA.
8.1 The nature of neutrinos
Neutrinos are bizarre particles. They interact only with the weak nuclear force and gravity, are the lightest (known) particles by a factor of a million, and as a result only rarely interact. Their non-zero mass requires new physics beyond the Standard Model, their role in the primordial plasma have left an imprint in the Universe, and they are important carriers of astrophysical information. Studies of these particles have already resulted in four Nobel Prizes. Below we briefly summarize the evolution of our understanding of these particles and how observations of NS mergers complement terrestrial experiments to further elucidate their nature. For a comprehensive overview of our current understanding and expected future results we refer the reader to the Particle Data Group reviews “Neutrino Masses, Mixing, and Oscillations” and “Neutrinos in Cosmology” (Tanabashi et al. 2018). See Bilenky et al. (2003) for a review of measuring absolute neutrino masses, Qian and Vogel (2015) for a review on the neutrino mass hierarchy, and Drewes (2013) for a review of right-handed neutrinos and their implications. The Hyper-Kamiokande design report contains a very nice overview for the state of existing, and prospects for upcoming, terrestrial neutrino experiments (Abe et al. 2018).
Neutrinos were first proposed by Pauli (1930) to maintain energy and momentum conservation during beta decay.Footnote 10 A few years later Majorana published his relativistic wave equation valid for neutral fermions which are their own antiparticles (Majorana 1937). So-called “Majorana particles” can generate mass in a unique way and the original publication suggested the then-theoretical neutrino as a possible case. Within a few decades the neutrino was observed for the first time (Reines and Cowan 1953; Cowan et al. 1956).
Particles with left-handed chirality have spin opposite to their direction of motion. For massive particles, helicity (effective chirality) differs for frames of reference moving faster or slower than the particle of interest, as the observed direction of motion inverts while the spin direction does not. Pontecorvo investigated the implications if neutrinos had non-zero masses and left-handed neutrinos oscillate into left-handed antineutrinos (and right-handed antineutrinos into right-handed neutrinos), analogous to neutral kaon oscillations (Pontecorvo 1957, 1958). These would be two Majorana particles. Only left-handed neutrinos (right-handed antineutrinos) enter the weak interaction Lagrangian, i.e., they only interact with gravity. Therefore, right-handed neutrinos (left-handed antineutrinos) are referred to as “sterile” neutrinos.
In 1962, two important developments regarding neutrinos occurred. The muon neutrino was directly detected for the first time, confirming a second neutrino type (Danby et al. 1962). Neutrino flavors are named to match the charged lepton involved in their usual interactions (e.g., the electron neutrino \(\nu _e\) involves interactions with electrons). That same year, Maki, Nakagawa, and Sakata developed the two-neutrino mixing matrix relating neutrino flavor to mass eigenstates (Maki et al. 1962). We here describe the modern version of this matrix following Abe et al. (2018). Formally, if we have neutrino flavors \(\nu _{\alpha} \) which are superpositions of the neutrino mass eigenstates \(\nu _i\) we have
\(U_{\alpha i}\) is the unitary Pontecorvo–Maki–Nakagawa–Sakata matrix (PMNS matrix; also known as the MNS matrix, lepton mixing matrix, or neutrino mixing matrix; Maki et al. 1962; Pontecorvo 1968). For a modern description of the general matrix see Tanabashi et al. (2018). Here we discuss the case of three neutrino flavors (electron, muon, tau; \(\alpha = e, \mu , \tau \)) with three mass eigenstates (i = 1, 2, 3)
with \(c_{ij} = \cos (\theta _{ij})\) and \(s_{ij} = \sin (\theta _{ij})\). The matrix is characterized by three mixing angles \(\theta _{ij}\) and three CP phase terms. The “Dirac” CP phase term is \(\delta \); the Majorana CP phase terms \(\alpha _{21}\) and \(\alpha _{31}\) only matter if neutrinos are Majorana particles. These phase terms are still unmeasured.
Neutrinos from weak interactions are generated as definite flavors, but, from a basic wave equation, their mass eigenstates propagate at different velocities. As a result, propagating neutrinos are a superposition of flavors and can be detected as a different flavor than their origination. This is referred to as neutrino oscillation and its observation requires non-zero neutrino mass.
The dominant fusion reactions in the Sun produce vast amounts of electron neutrinos. In 1967 Pontecorvo argued that neutrino oscillations would cause a deficit of solar electron neutrinos at Earth, relative to theoretical flux predictions (Pontecorvo 1967). Also in 1967, the Higgs mechanism (Higgs 1964; Englert and Brout 1964; Guralnik et al. 1964) was incorporated into the electroweak interaction (Weinberg 1967; Salam 1968). The Higgs field gives rise to the mass of the Higgs boson itself. The Higgs mechanism explains the origin of the W and Z boson masses. Fermions (leptons and quarks) gain mass through Yukawa-type couplings between left-handed fermions, the Higgs field, and their right-handed counterparts (reviewed in Tanabashi et al. 2018).
The treatment of neutrinos in the Standard Model was constructed in a way that it matched existing observational data. It was thought that individual lepton numbers were conserved within a given flavor (e.g., electrons with electron neutrinos, etc). We have only observed left-handed neutrinos (right-handed antineutrinos). Under the assumption that right-handed neutrinos do not exist, neutrinos cannot gain mass through couplings with the Higgs field, requiring them to be massless in the Standard Model. The suggestion that particles other than gauge bosons could be massless is, in principle, fine, because masses are not predictions of the Standard Model.
So when the first results from the Homestake experiment in the 1970s suggested a deficit of Solar (electron) neutrinos people wanted to believe that either the experiment (Davis et al. 1968) or the theory (Bahcall 1964) was wrong. Three decades later the Sudbury Neutrino Oscillation (SNO) experiment, built to detect all three neutrino flavors, directly confirmed the observed deficit arose from neutrino oscillation (Ahmad et al. 2002). A few years earlier Super-Kamiokande observations of muon neutrinos produced in atmospheric interactions had already proven neutrino oscillations due to matter interaction effects ( Fukuda et al. 1998). The incompleteness of the Standard Model has now been known for more than two decades. Modern studies of neutrinos observe oscillations from Solar and atmospheric neutrinos, as well as those produced in accelerators or reactors, in order to measure the values of the mixing angles (\(\theta _{ij}\)) and the squared differences of the neutrino mass eigenstates (\(\varDelta m_{ij}^2 \equiv m_i^2 - m_j^2\); Tanabashi et al. 2018).
We provide a historical overview as ideas about neutrinos that predate the formulation of the Standard Model may provide a path beyond it. There are several outstanding questions that experimental observations hope to answer (e.g., Tanabashi et al. 2018):
-
What is the neutrino mass ordering?
-
What gives rise to mass in neutrinos? Are they Dirac or Majorana fermions?
-
What is the value of the CP phase(s)?
-
Is there a theory of flavor that encompasses both quarks and leptons?
-
Why are neutrino masses so much smaller than other particles?
Depending on the answers to these questions, studies of neutrinos could uncover solutions to foundational problems. Neutrino parity violation could explain leptogenesis and baryogenesis in the early Universe (Fukugita and Yanagida 1986; Kuzmin et al. 1985), explaining why the universe is filled with matter and not antimatter. They may prove Majorana particles exist and require a second method for mass generation. If right-handed “sterile” neutrinos exist (Drewes 2013) they should be dark matter constituents. As one example of answering several questions at once, the Type I seesaw mechanism assumes that right-handed neutrinos exist and have Majorana mass terms (see Tanabashi et al. 2018, for a more detailed explanation), which could explain the small neutrino mass arising from the difference between the electroweak symmetry breaking scale and the unification scale of the electroweak and strong interactions, baryogenesis, and (at least some) dark matter.
Understanding these particles requires all available information, and answering any one question can resolve or inform future work to answer the others. Ground based experiments have led much of our understanding of these particles and will continue to do so; however, astrophysical observations provide some unique information. The (effective) number of active neutrino species (\(N_\mathrm{eff}\)) and the sum of the neutrino mass eigenstates (\(m_\nu = \sum _i \nu _i\)) can be measured from observations of the CMB (e.g., Planck Collaboration 2020). The latter is particularly important as the combination of the cosmological measurements of \(m_\nu \) and of oscillation experiment measurements of \(\varDelta m_{ij}^2\) provides a method to determine the absolute values of the neutrino mass eigenstates.
If the values of the neutrino mass eigenstates are larger than the differences between them, then we have the “quasi-degenerate case” of \(m_1 \approx m_2 \approx m_3\). Otherwise the ordering is hierarchical in nature, with either the “normal hierarchy” (\(m_1< m_2 < m_3\)) or the “inverted hierarchy” (\(m_3< m_1 < m_2\)). The resolution to this question will inform on theory (e.g., Mohapatra and Smirnov 2006) and expected results from future experiments (e.g., the search for the 0\(\nu \beta \beta \) decay signature of Majorana particles is easier for the inverted case).
From combining Planck measurements, with degeneracy-breaking information and assuming base \(\varLambda \)CDM, \(m_\nu < 0.12\) eV (Planck Collaboration 2020), which rules out the quasi-degenerate mass ordering. For the squared differences of the mass eigenstates, the current measured values are \(\varDelta m_{21} \approx 7.5 \times 10^{-5}\,\text{eV}\) and \(\left| \varDelta m_{32}\right| \approx 2.5 \times 10^{-3}\,\text{eV}\) (Tanabashi et al. 2018). Therefore, the lowest that \(m_\nu \) can be in the inverted hierarchy case is \(\sim \) 0.1 eV and in the normal hierarchy case \(\sim \) 0.06 eV (see Fig. 19).
The sum of the neutrino mass eigenstates as a function of the lightest eigenstate. The values are shown for both the Normal and Inverted Hierarchy ordering, with the current Planck 2018 results (Planck Collaboration 2020), which excludes the quasi-degenerate case. Standard siren cosmology will tighten these constraints
As the scale of the Hubble parameter and \(m_\nu \) and anticorrelated, the inclusion of the Riess et al. (2019) data may exclude the inverted hierarchy case but this is not done because of the disagreement in the value of \(H_0\) (Planck Collaboration 2020). If the disagreement originates with a systematic error in the measure of \(H_0\) from type Ia supernovae then information added by upcoming cosmological experiments will enable \(m_\nu \) detection at \(>3\sigma \) significance (e.g., Carbone et al. 2011; Audren et al. 2013; Cuesta et al. 2016). If the disagreement originates because the base 6-parameter \(\varLambda \)CDM is incomplete, then standard siren measurements become crucial as they improve \(m_\nu \) measurements by \(\sim \) 30%, even with multi-parameter extensions (Di Valentino et al. 2018). The timescales for using standard siren cosmology to study neutrino mass are well-suited to complement upcoming direct neutrino mass experiments (Mertens 2016).
We consider this a science driver for NS mergers. As the required observation is the standard siren Hubble diagram, the required observations are the same as discussed in Sect. 6. Time of flight tests to directly measure the neutrino mass are briefly discussed in Sect. 8.8, but the use of NS mergers is generally uninteresting as CCSNe observed by the same detectors are likely to be more stringent, but still less constraining than the cosmological determination.
8.2 The speed of gravity
The speed of gravity is infinite in Newtonian gravity. In the 1800s, attempts were made to include finite propagation speed into theories of gravity. In 1905, SR showed that space and time are manifestations of spacetime, and defined c as the conversion factor between the two, where massless particles do not experience time and travel through space at speed c. In GR GWs travel at c but there are some alternative theories of gravity where this may not be true. For example, some explained our evidence for the existence of dark energy as arising from \(v_{\mathrm{GW}} \ne v_\mathrm{EM}\), where \(v_\mathrm{EM}\) in a vacuum is c (e.g., De Felice and Tsujikawa 2012; Bellini and Sawicki 2014; Gleyzes et al. 2015). Therefore, observational determination of the speed of gravity is critical. In this section we report constraints on \(\delta _{\mathrm{GW}} \equiv (v_{\mathrm{GW}}-v_\mathrm{EM})/v_\mathrm{EM}\), the fractional deviation of the speed of gravity to the speed of light. Past, present, and expected future limits on this parameter are given in Table 8.
Measuring the speed of gravity has proven difficult. The detection of high energy Cosmic Rays (CRs) at Earth constrains a subluminal graviton, as it would cause energy loss to gravi-Cherenkov radiation (Caves 1980; Moore and Nelson 2001); however, we do not include this in Table 8 because it presupposes the existence of the graviton and is only valid for very high energy GWs. Observations of binary pulsars set two-sided limits of \(\delta _{\mathrm{GW}} \lesssim 10^{-2}\) (Jiménez et al. 2016). The first direct measure came from comparing the signal arrival times between the LIGO interferometers from the merging of two black holes (Blas et al. 2016). These are currently not particularly constraining (\(\delta _{\mathrm{GW}} \lesssim 0.5\)) but could improve to the \(\sim \) 1% level within a few years with several BBH merger detections by a multiple interferometer network (Cornish et al. 2017).
It was recognized that the multimessenger detection of a cosmological event in GWs and EM radiation, where the two messengers are emitted close in time, would provide an extremely constraining measure of the speed of gravity relative to the speed of light (Will 1998). For NS mergers we have the coalescence measured by GWs followed within seconds by a SGRB in \(\sim \) keV–MeV gamma-rays. All other proposed GW-EM transients either have timescales that are orders of magnitudes larger or are galactic in origin (meaning orders of magnitude smaller baselines); therefore, GW-GRB observations of NS mergers are the ideal multimessenger transient for this test. This method of constraining the speed of gravity was laid out in Will (1998) for nearby events. It was first (correctly) extended to cosmological distances in Jacob and Piran (2008). Nishizawa and Nakamura (2014) directly applied this equation to GW-GRB studies. We summarize, modify, and develop arguments from those authors here, with the inclusion of new observational information.
We are here concerned with the \(\varDelta t_{v_{\mathrm{GW}}}\) term from Eq. (13), assuming all other propagation terms are 0. We can write \(\delta _{\mathrm{GW}} \approx v_\mathrm{EM} \varDelta t_\mathrm{propagation}/d_c\) when \(\varDelta t_{propagation} \ll d_c/v_\mathrm{EM}\). The distance can be determined from the GW measure of \(d_L\) or an EM determination of redshift and converted to \(d_c\) with an assumed cosmological model. For two-sided constraints on the intrinsic time offset we can set sub- and superluminal constraints as
where \(\varDelta t_\mathrm{intrinsic,z}^{\pm }\) is described in Sect. 3.3. We could alternatively replace \(1/d_c\) with \((1+z)/d_L\), depending on the specific observables or assumptions used for a given event.
Indeed, the current best constraints are from the joint detection of GW170817 and GRB 170817A (Abbott et al. 2017b). With a conservative assumed distance, \(\varDelta t_\mathrm{intrinsic,z}^{\pm } = [0, 10]\) s, and neglecting redshift effects, we improved the measure by ten orders of magnitude. This single constraint has ruled out large classes of alternative theories of gravity (Creminelli and Vernizzi 2017; Baker et al. 2017; Ezquiaga and Zumalacárregui 2017; Sakstein and Jain 2017). There are additional theories that expect deviations at \(\delta _{\mathrm{GW}} \sim 10^{-40}\), though no yet-imagined test could approach this limit. However, constraining the speed of gravity is intrinsically important as it is a fundamental parameter of the universe. Either we will measure \(\delta _{\mathrm{GW}} = 0\) ever more precisely and further constrain where deviations from our understanding of fundamental physics occur, or we find one of those deviations. In Fig. 20 we show the expected sensitivities of the GW-GRB time of flight approach as the GW detection distance for BNS mergers improves, showing both the naive intrinsic time offsets used for GW170817 and GRB 170817A, and the informed \(\varDelta t_\mathrm{intrinsic,z}^{\pm }\) method.
Future \(\delta _{\mathrm{GW}}\) constraints with individual joint GW-GRB measurements. The sensitivity for a detection at a given distance corresponds to where that redshift interacts with the Naive or Informed limits. The naive (tan) limits are from assuming the conservative intrinsic time offset of [0, 10] s from Abbott et al. (2017b). The constraints weaken at high redshift due to cosmological time dilation of the intrinsic time offset. The informed (orange) limits assume 1 s time offset uncertainty on either side and removes the cosmological time dilation of the intrinsic emission offset. The GW170817 and GRB 170817A distance is shown with the purple vertical line; the grey line shows the maximum claimed redshift for a SGRB. The joint BNS detection horizons for the assumed GW network are taken from Sect. 2.3. Note that canonical NSBH mergers could be detected to greater distances, corresponding to more stringent limits, within a given network sensitivity
We consider determination of the speed of gravity to be a science driver for NS mergers, as it is fundamental in the universe and best done with these sources. The most important observational capability is increasing the maximum detection distance of ground-based GW interferometers, through increasing their low-frequency sensitivity. Beyond the uncertainty on the intrinsic time delay, the dominant source of error is the uncertainty on the luminosity distance, which could be removed with a measured redshift and assumed cosmology, and the on-set of gamma-ray emission which can be tens of ms. The best measurement of the latter will come from prompt GRB detectors sensitive to the tens of keV energy range, as these energies tend to precede the harder EM emission.
Nishizawa and Nakamura (2014) also raised the prospect of using a population of GW-GRB detections to jointly determine the intrinsic time offset and further constrain the speed of gravity. In short, the intrinsic time delay will have an additional redshift term, allowing for joint constraints once GW interferometers detect events to distances where cosmological redshift is no longer negligible. We add our support to investigations determining how precise these measures can be, but do not perform them here as such work could only improve these limits with the same observational requirements as individual detections. The most precise tests will be enabled through greater understanding of the intrinsic time delay.
8.3 Gravitational dispersion and the mass of the graviton
In GR GWs experience no dispersion. But like any aspect of GR, there are alternative theories of gravity that expect the opposite. This section is included in the paper because NS mergers provide a unique way to search for GW dispersion, but as we will show, other investigations into GW dispersion will prove superior to what is possible with NS mergers. As such, this section contains fewer details.
We can observationally search for dispersion by modifying the standard energy relation from SR to \(E^2 = p^2c^2 + A_{\alpha} p^\alpha c^\alpha \) with E, p, and c, their usual meaning and \(A_{\alpha} \) and \(\alpha \) parameters capturing the scale and type of dispersion (Mirshekari et al. 2012). This is the phenomenological form that the LVC have used in tests of GW170817 and the BBHs from GWTC-1 (Abbott et al. 2019d, e). They consider values of \(\alpha \) from 0 to 4 in steps of 0.5, excluding \(\alpha =2\) where the effect is an achromatic alteration of the speed of GWs (see Sect. 8.2). \(\alpha =2.5,3,4\) correspond to specific beyond-GR models (Mirshekari et al. 2012). For \(A_0>0\) this test corresponds to a massive graviton, i.e., \(E^2 = p^2c^2+m^2c^4\) from \(m_g = A_0^{1/2}/c^2\). This case is useful for pedagogical purposes and projected sensitivities have been reported for several future instruments. We focus on this case, but note our conclusions apply generally (except where stated otherwise). More general formulations of these tests are available in Tso et al. (2017) and Mewes (2019) and further discussed in Sect. 8.8.
Because of GR, the speed of GWs being the speed of light, and the effects of gravity being felt on galactic scales it is generally expected that the graviton, if it exists, must be a massless spin-2 gauge boson.Footnote 11 However, there are alternative theories of gravity where the graviton is massive (for a review see de Rham 2014), though some difficulties have yet to be worked out. Since we are unlikely to be able to directly detect gravitons in the next few years, limits on the mass of the graviton presuppose its existence and come from observations of natural extraterrestrial laboratories.
There are observable effects of a massive graviton. Several of the tests directly limit the Compton wavelength of the graviton, \(\lambda _g = h/(m_g c)\), rather than \(m_g\) itself. We list prior measurements and predicted future constraints in Table 9. We do not discuss details here (which are available in the relevant citations).
There are two tests for GW dispersion that are of interest for NS mergers. Time of flight tests can constrain the mass of a particle through measurement of its arrival time offset from a massless particle (or one with known mass and energy). Taking the energy of a massive particle in the usual form from SR, with the definition of group velocity \(v \equiv \partial p /\partial E \approx c(1-(mc^2)^2/2E^2)\) for light particles, a massive particle experiences a propagation delay of \(\varDelta t_{\mathrm{massive}} = (d_c/c) (mc^2)^2/2E^2\) compared to a massless particle. This allows for mass constraints of
Using Eq. 24 and the time offset and distance values for GW170817 and GRB 170817A from Abbott et al. (2017b) we can constrain the mass of the graviton to \(m_g < 3.6 \times 10^{-21}\ \mathrm{eV}/c^2\). For an exceedingly optimal GW-GRB conditions (\(\sim \) 1 s known intrinsic time offset uncertainty, a few Gpc source distance, observations starting at 7 Hz) we could achieve \(m_g < 5.0 \times 10^{-23}\ \mathrm{eV}/c^2\).
The second method is through waveform-deviation tests (Will 1998). This is, in effect, the same test. For a massive graviton, the inspiral of a CBC would be altered due to relative propagation delays as a function of energy. That is, waves emitted earlier in the inspiral have a lower energy, and would thus arrive earlier than expected relative to the higher frequency waves emitted later in the inspiral. This method applies to all CBC, with the current best limits from BBHs observed by LIGO and Virgo (Abbott et al. 2019e).
These limits are already more stringent than the best case option for the multimessenger GW-GRB test presented above, which is why the method was not performed in Abbott et al. (2017b). This is due to the greater timing precision for observations of GW inspirals than we can achieve for the GW-GRB time offsets. For waveform-deviations, the sensitivities depend on the distance to the source, and since BBH mergers are more massive than NS mergers, they should result in more stringent tests with the same GW network, despite being observed over shorter frequencies. LISA constraints are also greater than what can be achieved with ground-based interferometers. In the more general GW dispersion tests, from Samajdar and Arun (2017), ground-based interferometers and space-based interferometers are more sensitive to different \(\alpha \) values. In neither case will NS mergers be the most sensitive test. We do not consider constraining the mass of the graviton to be a science driver for NS mergers.
8.4 Gravitational-wave polarization
Like EM radiation, GWs are polarized. In GR there are “plus” and “cross” tensor polarization modes. Such is the faith in GR that all waveforms used in GW searches and the description of the antenna patterns of GW interferometers are constructed from these modes. However, generic metric theories of gravity allow up to six polarization modes: the two tensor modes of GR, as well as two vector and two scalar modes (Eardley et al. 1973; Will 2018), with some theories requiring all six (e.g., Jacobson and Mattingly 2004). Any detection of non-tensor GW polarization would demonstrate a true failure of GR while also strictly limiting the allowable beyond-GR theories. We here follow the succinct description in Abbott et al. (2019d). For a more thorough summary of GW polarization from beyond-GR theories we refer to the discussion in Will (2014) and references therein.
The tensor modes (\(A_+\) and \(A_{\times} \)) are transverse to the direction of propagation. The scalar modes are split between a transverse mode referred to as the “breathing mode” (\(A_b\)) and a longitudinal mode referred to as the “longitudinal” mode (\(A_l\)). Both vector modes (\(A_{x}\) and \(A_{y}\)) are longitudinal. The GW strain measured by a given interferometer can be written as \(h(t) = F^A h_A\) with \(F^A\) the antenna response to the \(h_A\) component of the signal; with all six considered A = (\(+\), \(\times \), x, y, b, l). The response of an individual interferometer to a given polarization is determined by the detector orientation to the source, and we can constrain the contribution of polarization modes by enforcing consistency with observed signals in a network of interferometers (Chatziioannou et al. 2012). \(F_+\) and \(F_{\times} \) are the usual response functions; a derivation of the other four is available in Poisson and Will (2014).
The maximal test of GW polarization then has a total of eight unknowns: the six polarization modes and the extrinsic direction to the source. However, the response of quadrupolar antennas to the scalar breathing and longitudinal modes are degenerate and cannot be distinguished, preventing delineation by such GW interferometers (Will 2014; Abbott et al. 2019e). Therefore, the most general possible test of GW polarization by the ground-based GW network has 7 unknowns. External determination of the source position is particularly powerful for these investigations as it enables precise knowledge of the relative arrival times at the interferometers. NS mergers generally provide stronger tests of GW polarization because the EM counterparts allow for precise, external localizations, resolving two parameters.
Simulations of studying additional GW polarization modes with the ground-based GW polarization network confirm these tests are possible (Takeda et al. 2018). The authors note a more precise measurement of the chirp mass, dependent on the duration of the signal, enables more powerful GW polarization studies, further supporting the use of NS mergers over BBH mergers. We note that these tests are generally performed using waveforms constructed from GR (but see the restricted waveform-deviation tests described in Arun 2012), implicitly assuming additional modes do not alter the behavior of merging compact objects (Isi et al. 2017). This is a conservative assumption as alteration of the inspiral should produce more obvious deviations from GR.
For transient signals, any less than five contributing interferometers results in an underdetermined system for the full test, but interesting tests can be performed with fewer contributing interferometers. The LVC have performed basic tests of GW polarization modes for mergers detected in LIGO-Hanford, LIGO-Livingston, and Virgo, first performed with the BBH detection of GW170814 (Abbott et al. 2017e). These studies compare the agreement of strain data for pure tensor modes against pure vector or pure scalar modes; mixed-mode results have not yet been reported. The current value from BBH mergers (Abbott et al. 2019e) is several orders of magnitude less stringent than from GW170817 due to use of the EM-determined position (Abbott et al. 2019d).
The simulations and current results demonstrate why NS mergers with EM-determined positions are best suited for tests of beyond-GR GW polarizations. Table 3 shows the fraction of time a given network has a number of active interferometers. The maximum distance for a full network detection is determined by the least sensitive interferometer. Additional modes can also be studied with the ground-based GW network with continuous waves (Isi et al. 2017) or observations of the stochastic background (Callister et al. 2017). They may also be studied with PTAs (Yunes and Siemens 2013). In these cases the time to first detection is still somewhat uncertain.
As such we consider searches for additional GW polarization modes to be science drivers for NS mergers. These searches require multiple-interferometer detections, generally resulting in well-constrained GW-only localizations within the detection horizon of the least sensitive contributing interferometer. Given this, and the importance of these investigations, we can safely assume an EM counterpart will be found for such a detection. The number of (sufficiently sensitive) GW interferometers is the only unresolved technical requirement. With current plans we will have LIGO-Hanford, LIGO-Livingston, Virgo, and KAGRA in the next few years, with upgrades and the addition of LIGO-India expected by \(\sim \) 2026. We note LIGO-Hanford and LIGO-Livingston are coaligned (except for the curvature of Earth) to maximize detection prospects, which largely rules out their use as independent interferometers here. Such a network would enable searches for both vector or both scalar modes in addition to the GR tensor modes. We support the investment into Virgo, KAGRA, and LIGO-India.
Prospects for a fully-determined test are somewhat pessimistic, unless an additional interferometer is constructed. One option would be to extend the second generation ground-based interferometers into the third generation era, which is an attractive option for several reasons (calibration, maintaining good localization capability for nearby events, etc). Future planned (LISA) and proposed (e.g., mid-range interferometers, or the Einstein Telescope) triangular interferometer sets could contribute three independent measures (Gair et al. 2013; Sathyaprakash et al. 2012). These separate instruments could jointly observe sources that emit in the overlap frequencies between them, but such a possibility will not occur for a long time.
8.5 Extra large dimensions
In GR there are four dimensions of spacetime (\(\text{D}=4\)). Some alternative theories of gravity have a higher number of dimensions. We here discuss tests for additional large dimensions. Observational signatures include effects on the quasinormal modes of BBH mergers (Chakraborty et al. 2018), additional GW polarization modes (Andriot and Gómez 2017), and “leakage” of GWs amplitude into the additional dimensions (Deffayet and Menou 2007). The latter two are well-suited for study with NS mergers. Additional polarization modes is discussed in Sect. 8.4. Here we focus on GW leakage, following Deffayet and Menou (2007).
GW observations of CBCs directly measure the luminosity distance to the source, assuming GR, where \(h \propto d_L^{-1}\). With extra large dimensions conservation of flux dictates that
With studies on GWs this leakage is generally invoked with a screening mechanism that asymptotes to GR in the strong-field regime, maintaining GR-predicted waveforms. We adopt the form from Abbott et al. (2019d):
with \(R_c\) and n respectively the distance scale and transition steepness of the screening mechanism. When \(D > 4\) a given source will appear dimmer than a D = 4 equivalent as energy is lost to the higher dimensions, causing the inferred luminosity distance to be greater than the real value. With GW-only observations we would systematically measure a higher distance for all sources. With EM-determined distances we can compare the two measures. A detectable difference arises only when light and matter propagate in four dimensions of spacetime while gravity may experience more, which is the case in many extra-dimensional theories of gravity (Abbott et al. 2019d).
This test has been performed using \(d_L^{GW}\) for GW170817 and \(d_L^\mathrm{EM}\) as from the distance to the host galaxy (Pardo et al. 2018; Abbott et al. 2019d), where the distance between the source and the host galaxy is small compared to the distance to Earth. In both cases they separately constrain parameter space for D, \(R_c\) or n. The results are consistent with the 4 spacetime dimensions of GR and constrain the characteristic screening scale as a function of transition steepness, with smooth transitions constraining \(R_c\) through Hubble radius scales. With more distant NS mergers and a sample of NS mergers with both GW and EM determined distances these constraints will greatly improve. Pardo et al. (2018) also limit the graviton lifetime through an amplitude dependent decay-length and test for large dimensions without a screening mechanism.
In Abbott et al. (2019d) \(d_L^\mathrm{EM}\) for NGC 4993 is determined directly through surface brightness fluctuations from Cantiello et al. (2018). This has the advantage of not relying on an assuming \(H_0\) or cosmological model, but is limited to mergers in the nearby universe. In Pardo et al. (2018) the distance is determined through the redshift measurement and an assumed \(H_0\). Given the current disagreement in the value of \(H_0\) results assuming each are presented. For future observations it will be necessary to transition to the latter method, which should occur on similar timescales to the standard siren measure of \(H_0\) (which assumes \(D=4\)).
This test is uniquely performed by joint GW-EM detections. NS mergers are the canonical example, and we consider this a science driver. However, we note that LISA and partners may perform significantly more stringent measures (Deffayet and Menou 2007). Possible LISA sources can be detected to a redshift of several and the precision of their \(d_L^\mathrm{GW}\) measures (Cutler 1998) is greater than third generation interferometers will achieve for NS mergers. However, prospects for EM detection, identification, and association of EM counterparts to merging supermassive black hole binaries are promising, but speculative. The greatest prospects are for NS inspiral observations with mid-range space-based interferometers (Cutler and Holz 2009).
8.6 Gravitational parity
A parity transformation inverts spatial coordinates (\(x \rightarrow -x, y \rightarrow -y, z \rightarrow -z)\), creating an effective mirror image. This changes right-handed coordinate systems into left-handed ones (and vice versa). Parity is conserved when a system or process is identical in the original or inverted coordinate system, and violated when not. Such was the belief in the conservation of parity that it was referred to as a law of physics. This tenant remained unchallenged until Lee and Yang (1956) suggested on theoretical grounds that weak interactions may not conserve parity, which was very shortly experimentally confirmed (Wu et al. 1957; Garwin et al. 1957). In the Standard Model EM and strong interactions are parity conserving but the weak interaction has maximal parity violation as its gauge bosons couple only to left-handed particles (right-handed antiparticles). Then, it is worth considering if gravity conserves or violates parity.
In GR parity is conserved. Generic gravitational theories that are parity violating and still viable after GW170817 and GRB 170817A are now known to reduce to dynamical Chern–Simons gravity (Alexander and Yunes 2018; Nishizawa and Kobayashi 2018), an overview of which is available in Alexander and Yunes (2009). A theoretical motivation for such searches is the requirement of the Chern–Simons parity-violating term in some QFTs of gravity (e.g., Alvarez-Gaume and Witten 1984; Ashtekar et al. 1989; Taveras and Yunes 2008; Weinberg 2008) and as a potential explanation for baryogenesis (Alexander et al. 2006; Alexander and Gates 2006). More fundamentally, we should be certain if parity violation occurs in only one or in two fundamental forces. Testing gravitational parity with direct GW detections is reviewed with regards to ground-based interferometers and PTAs in Yunes and Siemens (2013) and LISA-like detectors in Gair et al. (2013). We here closely follow the description in Yunes and Siemens (2013).
Gravitational parity conservation requires left and right-handed circular polarizations to propagate equally. When gravitational parity is violated then this is not true and is referred to as amplitude birefringence.Footnote 12 We can write
where f is the GW frequency, t is time, \(h_{+,k}\) and \(h_{\times ,k}\) are the GW Fourier components with wavenumber k. \(u\) accounts for curvature effects and is equal to 1 in a flat background; \(v\) captures the degree of birefringence and is equal to 0 in GR. With the right and left-circular polarization components \(h_{R,L} = (h_+ \pm h_{\times} )/\sqrt{2}\),
Thus, depending on the sign of \(v\), there is an enhancement of right-handed (left-handed) circularly polarized waves with the suppression of left-handed (right-handed) circularly polarized waves during propagation. The strength of this effect should accumulate based on the number of wavelengths experienced by the GW over the full propagation distance, i.e., proportional to \(Df\) with \(D\) the distance to the source and \(f\) the GW frequency (Yunes et al. 2010).
The importance of NS mergers to these tests is evident from the previous paragraph, and was first described in Yunes et al. (2010) whose conclusions we summarize here. As we are dealing with careful measures of GW polarization, a precise determination of the position is extremely beneficial (see Sect. 8.4). NS mergers occur in the highest GW frequencies that we are capable of detecting and are the most distant EM-bright sources in that band. Lastly, an ideal observation for testing gravitational parity would be pure left or right-handed circularly polarized waves. Due to collimation and relativistic beaming (and presumed alignment of the jet to the total angular momentum axis) the detection of an associated SGRB requires us to be nearly face-on, isolating nearly pure left or right-handed GWs. Further, such detections have improved constraints on the luminosity distance due to its correlation with inclination.
Gravitational parity violation would manifest as a disagreement in the luminosity distance as measured by GWs, \(d_L^\mathrm{GW}\) (assuming GR), against \(d_L^\mathrm{EM}\) determined through EM follow-up (either a direct distance measure of the host galaxy or through a measured redshift and an assumed cosmology). If the waves were the enhanced case then we would measure \(d_L^\mathrm{GW} < d_L^\mathrm{EM}\) and in the suppressed case \(d_L^\mathrm{GW} > d_L^\mathrm{EM}\). At least two interferometers, that are not coaligned (i.e. excluding LIGO-Hanford and LIGO-Livingston) are required to determine if the detected GW is left or right handed, with additional interferometers providing tighter constraints.
Yunes et al. (2010) note NSBH mergers provide more stringent constraints owing to their greater detection volume.Footnote 13 They show population-level analysis improves constraints approximately as \(1/\sqrt{N}\), where a bimodality in \(d_L^{GW}/d_L^\mathrm{EM}\) would be evident. Lastly, they also consider less than ideal scenarios, such as a wide-angled SGRB, and show it only marginally weakens such searches. Full constraints require the separate detection of a left-handed and right-handed events.
To this last discussion we add one further suggestion to the ideal NS merger for tests of gravitational parity. From Fong et al. (2015) the range of half-jet opening angles for SGRBs goes from a few degrees to \(>25^\circ \). These values may not be perfectly valid because they were calculated assuming top-hat jets, but they demonstrate we may have GW-GRB detections at tens of degrees from the angular momentum axis, further shown with the off-axis detection of GRB 170817A. This event was sub-optimal due to this and the GW signal being significant only in coaligned interferometers. Robustly determining the inclination of the system to Earth will fully enable this test which requires detecting a narrowly collimated on-axis burst or, for off-axis bursts, determination of a narrow \(\theta _i\). Kilonova observations cannot provide a stringent enough constraint on inclination angle. The best determination will be done with observations of a jet break in the GRB afterglow which generally requires initial detections on the order of a few hours and sufficient follow-up to late-times. Therefore, the ideal event is a high SNR GW detection of a NS merger with at least two interferometers, with an associated prompt GRB, and confirmation of a small inclination angle. Note the last requirement requires a narrow angle as the measurement of the jet break constrains us only to be within that angle, not our angle within the jet.
There are other methods to study gravitational parity on cosmological scales. LISA will detect massive BBH binaries to high redshifts. If gravitational parity is violated then LISA will observe a change in the apparent orientation of the system as a function of time (Alexander et al. 2008). Despite the vastly greater detection distances, a face-on GW-GRB detection would provide more stringent constraints, due to the higher GW frequencies involved (Yunes et al. 2010), and this test will be available a decade sooner. This is true with the current generation of ground-based interferometers and would vastly improve with third generation interferometers. Gravitational parity violation may also cause observable effects in GW generation, which could be identified with the observation of a spin-precessing BBH or a spinning NSBH binary, with a further enhancement for eccentric systems (Alexander and Yunes 2018). This test would likely be more sensitive, but the detection rates for these systems is unknown. Alternatively tests of gravitational parity can be done with studies of the stochastic background (Crowder et al. 2013). We note there are non-GW tests for parity violation that could be far more stringent (Dyda et al. 2012).
However, the technical drivers necessary for this test are already, or soon-to-be, met. This test requires continued improvements to the ground-based GW network to increase both distance to which NS mergers can be detected in GWs, an increase in the high-frequency detection range, and an increase in the rate of GW-GRB detections. It requires all-sky coverage with GRB detectors and is greatly aided by the capability to detect GRB afterglow emission within about a day in GW-GRB localization regions. We note that a typical cosmological GRB that is face-on and within the detection horizon of the current ground-based interferometers would be sufficiently bright that the prompt GRB detectors and follow-up instruments may not need to be particularly sensitive. As we move to more sensitive GW interferometers that detect NS mergers to distances where even on-axis GRBs are difficult to detect, the GW-GRB detection rates will be sufficiently high that we should not require vast improvements to the non-thermal EM detection capabilities. However, instruments sensitive to GRB emission will improve the population-level constraints.
8.7 Electromagnetic dispersion
Quantum Gravity (QG) may result in observable energy-dependent propagation delay, which is also a signature of LIV. EM dispersion is then motivated by searches for evidence of QG. The next section contains the scientific importance of these studies in a larger context and is not discussed here. This section is distinct to match the separation of these types of tests in the literature.
Due to having short intrinsic timescales and detections at cosmological distances, SGRBs provide stringent tests of EM (in vacuo) dispersion. For pedagogical purposes we use the effective low-energy field theory formulation from Vasileiou et al. (2013), which assumes \(E \ll E_{QG}\) with \(E_{QG}\) the scale of QG effects. For a massless particle we can perform a series expansion
where E, p, and c have their usual meanings. \(\xi \) represents the sign of the violation: for the subluminal case it is equal to \(+1\) (with a negative correlation between photon speed and energy) and \(-1\) for the superluminal case (a positive correlation between photon speed and energy). Such a dispersion would lead to
Note that this equation is considering only the dominant term, which is not necessarily for \(n=1\) depending on the specific theory considered. Generally, specific terms and signs of violation are considered separately. For two particles of different energies, \(E_h > E_l\), from the same source and emitted at the same time, this will induce an arrival delay
where
is a comoving distance modified by the order of LIV (Jacob and Piran 2008). Therefore, the best constraints on \(\varDelta t_{LIV}\) come events with high energy photons, with low-energy photons as a baseline, that originate at cosmological distances, with small (or well known) intrinsic time offsets. For these tests, often only linear and quadratic LIV (\(n=1, 2\)) are (separately) considered; the small intrinsic time offset is most important for linear tests.
The use of GRBs to probe dispersive LIV limits was first performed in Amelino-Camelia et al. (1998) using bursts detected by CGRO. The detection of high energy photons from cosmological distances and intrinsic impulsive behavior allow for two-sided measures on LIV. The primary instrument on the Fermi Satellite is the LAT and the secondary is the GBM, which together can detect GRBs from \(\sim \) 10 keV to \(\sim \) 10s of GeV. A year into its mission, both instruments on-board the Fermi Satellite detected GRB 090510 (Ackermann et al. 2010). The burst is a best-case scenario for these tests: it was detected deep into the universe (at a redshift of 0.9), was detected to high energies with a low-energy base, and the impulsive nature constrained the intrinsic emission time offset between low and high energy photons to of order a second. This burst holds the current best limits for linear dispersion, pushing the scale of QG beyond the Planck scale, and competitive limits for the quadratic case (Abdo et al. 2009; Vasileiou et al. 2013). From the duration and hardness of GRB 090510 it is likely a SGRB, and likely originates from a NS merger.
Significant improvements to these measurements with existing gamma-ray telescopes is unlikely. GRB 090510 is about a once a decade event for Fermi. VHE detections enable improved constraints, but must overcome attenuation for cosmological VHE photons. Based on the first detection of a GRB at VHE with the long GRB 190114C (Mirzoyan et al. 2019) and the marginal signal following the short GRB 160821B (Palatiello et al. 2017) we could expect unambiguous detections of SGRBs with the upcoming CTA. However, these limits would be one-sided as they rely on follow-up detections of non-impulsive GRB afterglow emission. Existing wide-field VHE instruments have yet to detect any GRB (they should be capable, but the necessary events are rare). We likely require either wide-field VHE instruments with improved sensitivity or a partnership with GW early warning systems and IACTs.
8.8 Lorentz invariance
The Standard Model is a quantum description of three of the four (known) fundamental forces. GR is a classical description of gravity. If the four forces are to be unified, we almost certainly require a quantum theory of gravity. The scale of interest where QG effects may become important (\(E_{QG}\)) is expected to be of order the Planck Scale, \(E_{PL} \equiv \sqrt{(\hbar c^5)/G} \approx 1.2 \times 10^{19}\,\text{GeV}\). Lorentz Symmetry is the underlying assumption of Relativity that the laws of physics are the same for all observers with no preferred frame. If there is a fundamental length scale of the Universe, then there is an inertial reference frame where that length is an extrema. Therefore, these two axioms are mutually exclusive and searches for LIV are motivated by the quest for QG. We note that the unambiguous detection and confirmation of the breaking of Lorentz Symmetry would rewrite textbooks, but setting forever more stringent limits on LIV is unlikely to be particularly useful for theoretical development. Therefore, this section is written in terms of the possible sensitivities to LIV with a given test, rather than projected future constraints.
For reviews on theory implications of LIV we refer the reader to Smolin (2008), Mattingly (2005), Jacobson et al. (2006). In brief, LIV from QG models have been explored for loop quantum gravity (e.g., Gambini and Pullin 1999; Rovelli 2008), string theory (e.g., Kosteleckỳ and Samuel 1989; Ellis et al. 1999), and warped brane worlds (e.g., Burgess et al. 2002). LIV and Planck-scale effect investigations are also important for non-commutative geometry (e.g., Douglas and Nekrasov 2001), varying speed of light cosmologies (e.g., Moffat 1993; Magueijo 2003), cosmologically varying moduli (e.g., Damour and Polyakov 1994), spacetime-varying couplings (e.g., Kosteleckỳ et al. 2003; Bertolami et al. 2004), emergent gauge bosons (e.g., Kraus and Tomboulis 2002), a consistent theory of BHs (e.g., Rovelli 2008), the prevention of high-energy divergences in QFTs (e.g., Solodukhin 2011), spacetime foam (e.g., Amelino-Camelia et al. 1997), deformed relativity (e.g., Amelino-Camelia 2002), and condensed matter analogues of emergent gravity (e.g., Volovik 2001).
There is only one way that Lorentz Invariance can be preserved and numerous methods of violation. To enable the comparison of a wide range of theories against a wide range of observational tests of LIV, the Standard Model Extension (SME) framework was developed. It is a comprehensive effective field theory description for tests of LIV, which includes CPT violation. Its series expansion from Vasileiou et al. (2013), and using n from Sect. 8.7 rather than the typical mass dimension (\(d=n+4\)),
with \(\hat{n}\) the direction of the sources, \({}_{0} Y_{jm}(\hat{n})\) spin-weighted spherical harmonics, and \(c_{(I)m}^{(n+4)}\) the framework coefficients representing the LIV strength. This expansion encapsulates directional-dependent violation, dispersive and non-dispersive constraints, birefringent and non-birefringent constraints, and it allows for specie-specific tests by separately considering the photon, gravity, neutrino, and matter sectors. Kosteleckỳ and Russell (2011) contains a summary of the best constraints of each SME parameter, with an annually updated document available on the arXiv,Footnote 14 where several of the best existing limits arise from observations of NS mergers.
Observationally probing Planck-scale effects is difficult. \(E_{PL}\) is several orders of magnitude larger than the highest energy particles ever observed. Astrophysical observations provide some of the best coefficient constraints because very small effects can build up over cosmological baselines into observable effects. Again the short intrinsic time offsets for cosmological detections enable NS mergers to provide some of the best discovery space. Second, the multimessenger nature of these sources enable us to use constraints in one sector to probe LIV in other sectors.
As discussed in Sect. 8.7, in the EM sector NS mergers hold the record for linear dispersion and large discovery space for dispersion in general. These limits are non-birefringent, but still theoretically motivated (see discussion in Vasileiou et al. 2013). The EM birefringent limits are several orders of magnitude more constraining (Kosteleckỳ and Mewes 2008). In short, the effect of EM birefringence manifests in different propagation speeds for left or right-handed photons, splitting a beam into two components. The detection of linear polarization from a distant source then severely constrains birefringent LIV, as the rotation rate over cosmological baselines has to be incredibly tiny. The detection of polarization from GRBs provide the most stringent LIV limits, of which LGRBs are the better candidate due to their higher fluence.
These constraints allow us to use multimessenger detections to constrain non-birefringent violation in the other sectors by observing the relative arrival times of different messengers. This was done with GW170817 and GRB 170817A and improved some non-dispersive constraints in the gravity sector by ten orders of magnitude (Abbott et al. 2017b), for largely the same reasons as discussed in Sect. 8.2. NS mergers have the greatest discovery space for these kinds of LIV tests. As discussed in Sect. 8.3 other observations have larger discovery space for dispersive LIV in the gravity sector.
The best, unambiguous, non-dispersive limits on the neutrino sector come from SN 1987A (e.g., Longo 1987; Stodolsky 1988). Under the assumption that the \(\sim \) 200 TeV neutrino IceCube-170922A association to the Fermi-LAT blazar flare from TXS 0506+056 is true (Aartsen et al. 2018) and using the gamma-rays as the low-energy baseline, dispersive and non-dispersive (using the gamma-rays as the low energy signal and the high energy neutrino) are improved by orders of magnitude (Ellis et al. 2019) compared to the observations of SN 1987A (e.g., Ellis et al. 2008). Should high energy neutrinos be detected from SGRBs it could shatter these limits given the small timescales and cosmological baselines. The best dispersive limits come from observing the relative arrival times for neutrinos with measured energies in SN 1987A (Murayama and Yanagida 2001; Kostelecky and Mewes 2012). When MeV neutrino detectors are capable of detecting NS mergers they will likely detect at least an order of magnitude more CCSNe which can provide a similar test (Arnaud et al. 2002). In neither case do we consider NS mergers to be critical, given the uncertainties on detection prospects.
Altogether, NS mergers have large discovery space for searches of LIV. Within the SME framework, these sources are critical for dispersive (non-birefringent) measures in the photon sector and non-dispersive measures in the gravity sector. We consider these science drivers for NS mergers as detection of LIV would usher in a new era of physics.
8.9 The weak equivalence principle
The WEP states that gravitational and inertial masses are identical. It is the outcome of Einstein’s famous elevator thought experiment, though similar ideas had been around before the formulation of GR. Multimessenger detections provide a unique test of WEP by testing if different messengers experience gravity differently. It is a test of the foundation of gravitational theory itself. We first present here the field-standard test method for pedagogical purposes. We close this section with a discussion on the problems with the values from this approach and a new proposed test.
Particles which traverse gravitational potentials undergo a propagation delay due to the warping of spacetime. This was first described by Shapiro (1964) as a fourth test of GR by checking for predictions matching the observed time delay due to the gravitational well of the Sun by observing radar pulses reflecting off Venus and Mercury near conjunction. The Parametrized Post-Newtonian (PPN) parameter \(\gamma \) measures the amount of curvature of space due to unit rest mass (Will 2014). Its value in GR is 1, but this value is not unique to GR. Other theories of gravity have \(\gamma \ne 1\). Shapiro delay depends on \(\gamma \) as:
where U(r) is the gravitational potential along the path l, with integration limits from the distance of emission \(r_e\) to observation \(r_o\).
If two particles follow the same path through a gravitational potential but couple to different spacetime metrics (i.e. experience gravity differently) then they would experience different Shapiro de,lays, inducing a relative propagation arrival time. We define the relative Shapiro delay for particles 1 and 2, constraining the term \(\varDelta t_{\mathrm{WEP}}\) from Eq. (12) which is defined as
For two sided constraints we can rewrite Eq. (35)
Equation (36) (or its one-sided version) has been used to constrain deviations between messengers and within messengers. Such observations determine if the trajectory of particles are the same, a test of the WEP. The first multimessenger test of WEP was between photons and neutrinos with SN 1987A, which showed that neutrinos obey GR to the limits of the measurement (Krauss and Tremaine 1988; Longo 1988). These constraints can be improved using the likely association of IceCube-170922A to the flaring Fermi-LAT blazar (Aartsen et al. 2018; Wei et al. 2019). Tests have also been performed within photons, GWs, and neutrinos (e.g., Longo 1988; Gao et al. 2015; Wei et al. 2015, 2016; Kahya and Desai 2016). Several of these relative constraints exceed the best absolute bounds \(\gamma _{\mathrm{EM}}-1 = (2.1 \pm 2.3) \times 10^{-5}\) from tracking of the Cassini spacecraft during a close alignment with the Sun (Bertotti et al. 2003).
All of these analyses should be performed: any deviation between or within messengers would have profound implications for the Universe. “Dark Matter Emulators” were alternative theories of gravity that claimed some of our evidence for dark matter arose from light coupling to a different metric than gravity (Desai et al. 2008; Kahya 2011). While the evidence for dark matter vastly exceeded what such theories could explain, it would not necessarily be surprising if light and gravity coupled to different spacetime metrics, given the rules that govern force interactions with other particles. GW170817 provided the first opportunity to use gravity in a relative test of the WEP. GRB 170817A provides the best partner for this test, giving
(Abbott et al. 2017b). This measure ruled out most “Dark Matter Emulators” (Boran et al. 2018).
NS mergers again provide some of the best discovery space. The emission in the first few seconds includes emission over several decades of energy of photons and GW, and likely the same for neutrinos. GW-GRB joint detections are almost certain to set the best relative bounds for GWs and photons. Should SGRBs be detected in the prompt phase as neutrinos, then they are also likely to set the best relative constraints for photons and neutrinos. Given the broad energy range within EM radiation for prompt GRB emission and in GW radiation during the strongly chirping inspiral, NS mergers will also likely result in the most stringent limits within these messengers. For individual gravitational potentials, these constraints depend weakly on the distance to the events (e.g., improving constraints by a factor of 2 with GW170817 and GRB 170817A following the prescription in Abbott et al. 2017b would require a joint detection at 5 Gpc). Events with smaller intrinsic time offsets, or a greater understanding of that distribution, will provide more stringent tests.
Beyond the observed temporal offset, the dominant parameter for improving these constraints is the total gravitational potential experienced over the paths of the particles of interest. The limits in Eq. 37 account only for the Milky Way’s gravitational potential, assuming a conservative mass, a Keplerian potential, and integrated from 26 Mpc (the 95% lower bound of \(d_L\) as measured from GW170817) to within 100 kpc. Other papers attempted to account for more of the Milky Way’s gravitational potential (e.g., Shoemaker and Murase 2018) or contributions from intervening gravitational potentials (e.g., contributions from the Virgo supercluster; Wei et al. 2017). Forecasting future constraints with this method is difficult given the range of possible paths from source to Earth (e.g., contributions from the host galaxy, intervening galaxies or clusters). With our prior note of caution, we do not attempt to provide them here. Improvements to our understanding of the total mass of the Milky Way and the shape of its gravitational potential (e.g., as a result of the GAIA or LISA missions) will enable more precise statements on relative violations of the WEP, and can be applied ex post facto to prior joint detections. The most stringent constraints possible would be from a lensed GW-GRB, where the mass of the lensing system could exceed the Milky Way’s by orders of magnitude.
We now discuss the issues with this test, from Minazzoli et al. (2019). The formulation of Eq. (36) uses an implicit coordinate system that is not gauge-invariant, i.e., depending on the coordinate choice one can obtain positive or negative values (Gao and Wald 2000). In Minazzoli et al. (2019) they consider Fermi coordinates associated to an observer, such that the delay is expressed in terms of an observed proper time, which results in a sum of terms with opposing sign. Using reasonable constructions for contributions to the total gravitational well experienced by propagating particles by considering the sum of catalogs they show the induced total (absolute) Shapiro delay is not monotonic, and indeed crosses zero in some cases. Therefore, while we can use the small offsets for, e.g., GW-GRBs to state that we find no evidence for WEP violation, we cannot quantify robust limits on relative Shapiro delay. Minazzoli et al. (2019) suggest this as motivation for the development of tests for specific alternative theories of gravity. We note that if the WEP is violated we will find evidence for it, we will just be unable to quantify the degree of violation with this test.
Minazzoli (2019) propose a new multimessenger test of the WEP using strongly lensed events. From the time delay between two images i and j we can apply the usual PPN parametrization \(\varDelta _{ij} \rightarrow (1+\gamma )/2 \varDelta _{ij}/2\). By measuring the time delay between these images in two different messengers one can quantify the search for relative WEP violation by
The requirement for detecting and identify a strongly lensed GW-GRB is not an easy one, but the rate should be non-zero with Gen 3 GW interferometers and a suitable GRB monitor.
9 Recommendations for the future
The preceding sections have clearly demonstrated astrophysical observations of NS mergers enable phenomenal scientific return. Making and reliably interpreting these observations requires input from observers, theorists, and simulation, and advancement in other fields of physics. Below we highlight some recommendations on areas where these needs may not be met, or support existing efforts. In very broad terms these are guided by the following criteria:
-
A deep understanding of what occurs during NS mergers will enable greater scientific return from these sources. Observations of the inspiral, coalescence, and early times from GW and neutrino observations nicely complement the EM observations of the SGRB jet and quasi-isotropic outflows.
-
With GW170817 and its counterparts the loss of EM detection in any energy range would have resulted in significant loss of science. This will also be true for future events. Broadband EM coverage is necessary.
-
Observations that enable early localizations are crucial to enable sensitive characterization of these events.
We make a number of recommendations on observational resources required for a given messenger (separating the types of photons), the necessary communication improvements to enable time-domain multi-messenger astronomy, and comment on both the necessary work outside of astrophysical observations and the difficulties inherent to interdisciplinary work.
The previous science and above comments apply generally; however, some of the recommendations below are focused on U.S. interests, given the on-going Astro2020 Decadal process (which decides the large mission prioritization of the U.S.) and because I am most familiar with this system. We directly discuss the GW interferometers. For EM missions we directly discuss some proposed large-scale (\(\gtrsim \)$1B) missions proposed to the Astro2020 Decadal, as well as similar scale missions that are in advanced proposal rounds outside of the U.S. For smaller scale missions we make broad recommendations only.
9.1 Observational resources
The following sections discuss the existing, planned, proposed, and possible observational capabilities in GWs, the EM spectrum, and neutrinos. To prevent repetition we make the following blanket statements of support:
-
For missions that have dedicated instrument teams we support sufficient funding to adapt to the new era of GW multimessenger astronomy.
-
For instruments that determine observing time through guest investigator/observer programs we support the allocation of sufficient resources to the observations of NS mergers, as well as the necessary prioritization of these observations. When competing proposals for relevant science enter the same round, we suggest the selection of those with community service and prompt open data aspects.
-
When there are proposed missions that significantly advance the capabilities in a given energy range, we support those missions. We support technological development funding for the cases where sufficient advancements are not yet ready.
9.1.1 Gravitational waves
GW observations are necessary for the majority of the science discussed in this paper, either directly through their own observations or indirectly by identifying NS mergers for follow-up. It is widely understood that advancements in GW observations are necessary, so we do not summarize why here. The past, present, and funded GW network is shown in Fig. 2. Discussions on this and proposed interferometers is in Sect. 2.3.
We recommend sustained investment into the ground-based gravitational wave interferometers. Improved sensitivity in the \(\sim \) 10–1000 Hz range will greatly increase the rates of detections of NS mergers, enabling population studies. We generally require a network of several interferometers of comparable sensitivity to provide reasonably accurate localizations for most multimessenger studies. This has been directly demonstrated during O3 by the LV detection of GW190425, and a few other events. Under current plans this need will be met in the late Advanced era as Virgo and KAGRA sensitivities become more comparable to Hanford and Livingston. The funded improvements to A+ and similar upgrades for other interferometers are critical. Further, with a sufficiently large number of Advanced/+ interferometers, the downtime can be staggered to allow for continuous GW observations. We support consideration of this endeavor to ensure we capture rare, interesting events.
If fewer than three 3rd generation interferometers are funded then the localizations will not be sufficiently constrained for multimessenger studies of these sources. Additionally, the detected events will nearly all be too far to recover kilonova at these distances. One potential solution would be to maintain (sufficiently upgraded) second generation interferometers into the third generation era, allowing for well-constrained localizations for events nearby enough for successful EM follow-up. This is also advantageous for other reasons (e.g., early calibration of the new interferometers).
The currently funded upgrades do not significantly broaden the frequency range at which GW detections of NS mergers can occur. Sensitivity at high frequencies, that is a few to several kHz, is of paramount importance to studies of NS mergers. They allow direct observation of merger, and potentially ringdown. This gives some of the greatest tests on the NS EOS, will allow conclusive classification of more systems from the immediate GW detection, the direct determination of the immediate remnant object in BNS mergers, and all of the science derived from that knowledge. We support funding to advance the necessary technologies until they are implemented into the existing network. If possible, this upgrade could be included into the A+ network, which would be commensurate with several upcoming facilities (e.g., EM upgrades, the nuclear experiment FRIB, and the MeV neutrino experiment Hyper-Kamiokande). Alternatively, building an interferometer focused on this frequency range and utilizing it in partnership with lower frequency interferometers is likely to be a viable solution (e.g., Ackley et al. 2020).
For longer-term investment a space-based mid-range interferometer brings unique capabilities. It is the only method to achieve early warning of NS mergers with precise localizations far enough in advance to enable broadband EM observations of merger time. It is uniquely suited to enable precise standard siren cosmology, broadband studies of the prompt GRB emission, population-level studies of the early kilonova emission, and several tests of fundamental physics. These observations would be truly remarkable. We support heavy investment into the technologies necessary for such missions to allow one to be launched as soon as possible.
9.1.2 Gamma-rays
We support the extension of the Fermi mission as GBM is the most prolific detector of SGRBs. We also support the continuation of the Swift mission as, despite lower joint detection rates, the immediate arcminute localization of a GW-detected NS merger would allow immediate follow-up across the EM spectrum, and an enormously informative dataset. These missions should be extended at least until suitable replacements are launched.
An ideal instrument would provide precise localizations of large numbers of SGRBs. It is difficult to vastly increase the SGRB detection rates with partial coding masks, and the localization accuracy of GBM-like instruments is generally limited. Construction of a fourth IPN appears unlikely, as it is now difficult to place astrophysics instruments on planetary spacecraft, and the data downlink latency would remain slow. The best option to balance detection rates and localization precision is the construction of a large Compton telescope.
In Astro2020 the only relevant large-scale mission proposal is the Compton+pair conversion telescope AMEGO (McEnery et al. 2019). AMEGO would have a SGRB detection rate roughly an order of magnitude higher than Swift BAT, with \(\lesssim \)degree accuracy. For events with sufficiently high energy photons, to be detected through pair conversion, these localizations may be smaller. The LGRB detection rate is measured in hundreds per year. These would allow greater population studies of these sources and enable study of the prompt, afterglow, and other non-thermal emission in the tens of MeV, where it has not yet been well-studied. If suitable advancements in follow-up instruments can be made to identify SGRB afterglow in \(\lesssim \)deg localizations, which appears reasonable, such an instrument would allow the best determination of the source evolution of NS mergers and collapsars, with implications for heavy element enrichment,
With a commensurate ground-based network with A+ sensitivity, AMEGO would be capable of roughly 1 joint GW-GRB detection per month. The immediate localizations of the multimessenger detections would be of order \(\lesssim \)degree accuracy for events where we expect afterglow emission, and inform searches for afterglow. This would be roughly an order of magnitude improvement over typical GW localizations with several contributing interferometers, and a far greater improvement for most detections at these distances. The joint detections would typically occur within \(\sim \) 500 Mpc. This guides the necessary capabilities of potential follow-up instruments, e.g., \(\sim \) 23rd Mag for a KN170817-like event, which seems possible at that time. Together these would give great constraints on SGRBs and ultrarelativistic jets, provide a GW-GRB sample for cosmology, give the most precise measures of the GW-GRB time delay, be used for tests of fundamental physics, and enable early broadband EM observations key for understanding NS mergers themselves. This mission would also be beneficial for networks with fewer, but more sensitive GW interferometers.
AMEGO may detect early afterglow emission in SGRBs, though this has not been quantified. The relative balanced priority to the Compton and pair regimes has limited the narrow-line point source sensitivity. With the current design it would require a fortuitous nearby NS merger to detect the prompt nuclear gamma-rays from the kilonova. It may be capable of identifying a KNR in the Milky Way. We support technology advancement to improve the narrow-line point-source sensitivity. Given the localization method of Compton telescopes, this would have the added benefit of improved prompt SGRB localizations.
Should AMEGO be selected in Astro2020 it would not launch for about a decade from now. Until that time, or in the event we get no large-scale gamma-ray mission selected within the decade, we support the launch of sensitive gamma-ray scintillation missions, especially those that exceed the sensitivity of GBM from a few keV to several MeV. Even CubeSat missions can provide expanded sky coverage, additional localization constraints, and photon statistics, especially when treated as a network (Sect. 9.2.1).
9.1.3 X-rays
Given current sensitivities and the relative intrinsic emission, X-rays are the easiest method to detect SGRB afterglow emission. They are usually the highest energy detection of this synchrotron emission, enabling inferences like the jet-opening angle, jet structure, and circumburst densities. The temporal evolution in this range also contains several non-thermal signatures, including flares and plateaus, that may have implications for the NS EOS and jet physics. X-ray observatories can provide the earliest arcsecond localizations, necessary for most EM telescopes to observe these events, for robust host association, and some tests of fundamental physics. This is the best wavelength to precisely localize distant events.
Swift XRT utilizes (modified) galaxy targeting for follow-up of GW-detected NS mergers. It is critical in the current era. Chandra provides high spatial resolution in X-rays, enabling host galaxy association for bursts that it detects, and recovery of off-axis afterglows like GRB 170817A. We support the allocation of appropriate Chandra time for NS-merger follow-up. Future sensitive X-ray observatories with high spatial resolution are helpful for NS-merger science. XMM-Newton and ATHENA have spatial resolution that may be problematic to isolate SGRBs afterglow, as demonstrated with observations of GRB 170817A.
We would ideally launch a time-domain, wide-field X-ray telescope with sufficient sensitivity to recover a reasonable fraction of SGRB afterglows. Figure 6 shows the full Swift XRT observations of SGRB afterglows, with the nearest known SGRBs highlighted to demonstrate that they are not brighter than the full sample. Thus, a wide-field X-ray telescope must achieve XRT-like sensitivity to recover afterglows at reasonable efficiencies. Recently proposed missions that would utilize lobster eye optics for follow-up observations do not have sufficient sensitivity to recover most off-axis counterparts to most GW detections nor on-axis counterparts to SGRB detection. With a fiducial lobster sensitivity and an on-target time of 100 s (which is optimistic given the necessary tiling) only \(\sim \) 15% of XRT-detected afterglows would be recovered. Missions that have lobster eye optics instruments with a FOV \(\gtrsim \)10% of the sky, like THESEUS or Einstein Probe, may be more promising because they can observe the prompt emission, early afterglow, and potential magnetar plateau. These have somewhat similar detection prospects for low-energy partial coding masks with larger FOV, such as STROBE-X. While these latter missions provide useful observations for NS mergers, we support relevant technology advancements for significantly more sensitive, wide-field X-ray instruments built for the purposes of follow-up observations of NS mergers.
9.1.4 Ultraviolet
Bright UV emission was among the surprises of KN170817. Such observations are key to understanding these sources, by identifying what causes bright UV emission, determination of the remnant object, and are the earliest possible light from kilonovae, which allows arcsecond localizations, robust association with GW signals, and observations of the rise in optical and IR bands.
Swift UVOT is copointed with XRT, and follows-up GW-detected NS mergers with the (modified) galaxy-targeted technique. The only other active UV mission is Hubble, which is far more sensitive. We support the allocation of Hubble observing time for NS merger studies of SGRBs afterglow, kilonovae, and to uncover the origin of early UV emission. However, the current \(\sim \) 48 hour response time of Hubble is egregiously insufficient and needs to be significantly shortened.
Because UV emission is the earliest possible kilonova emission it would be ideal to have a wide-field UV telescope to follow-up GW detections. A baseline guidance for this mission would achieve \(\sim \) 21st Mag in \(\sim \) 10 min, with \(\sim 10\,\text{deg}^2\) FOV. This should be sufficient to recover KN170817-like events to \(\sim \) 150–200 Mpc with most GW localization regions, though greater sensitivity/FOV are obviously beneficial. There are several proposed missions that meet these requirements, suggesting the necessary technology already exists. Indeed ULTRASAT exceeds these requirements with a planned launch in 2023.
9.1.5 Optical
Optical is likely to be the key discovery wavelength for kilonovae and the most common detections giving arcsecond localizations. They are key to observing the early and middle evolution of kilonovae, and for the spectroscopic determination of redshift.
Of all wavelengths, optical is likely the most prepared for EM-counterpart searches of GW detections. There are numerous time-domain telescopes that use galaxy-targeting, several wide-field telescopes that can tile the GW localizations, and particularly sensitive telescopes to deeply study these events, including those capable of broadband (near-UV to NIR) spectroscopy.
With the upcoming LSST and thirty meter telescopes, these capabilities will continue to improve and meet requirements into the A+ era. These facilities offer unmatched capabilities that are beneficial for NS-merger studies. We support the construction of an X-shooter like spectrometer for the thirty meter telescopes.
9.1.6 Infrared
IR uniquely probes the effects of the lanthanides and actinides. They enable spectroscopic determination of redshift, and are key to doing so for distant events. They may be the discovery wavelengths for particularly (infra)red kilonova, which may be possible for some NSBH mergers.
NIR can now be reliably observed from the ground, even to deep limits. The existing 10m and upcoming thirty meter telescopes are capable of studying kilonovae weeks after merger. We again support a sensitive spectrometer for these future instruments. Wide-field NIR telescopes now exist, but are currently much less sensitive than optical telescopes, which may prevent the detection of some kilonova from NSBH mergers. We support technology development to improve the sensitivity of such instruments, with similar technical guidelines to the wide-field UV capabilities discussed above.
Hubble provides sensitive NIR coverage. Far IR can only be observed from space, or near-space. Spitzer will soon end observations. SOFIA observes this energy range. JWST will be available in the coming years and its key capabilities enable important study of late-time kilonova emission. It is likely to be joined by WFIRST a few years later which will enable identification of faint (infra)red kilonova due to nearby prompt collapse BNS mergers or more distant NSBH mergers for events that are well localized but beyond the capabilities of wider-field monitors. Three great observatory-class missions in a row prioritize the IR regime, proving reliable coverage for our narrow-field needs.
9.1.7 Radio
Radio observations probe the low end of the synchrotron radiation of SGRB afterglow and from the quasi-isotropic outflow interactions long after merger, and are likely to be the latest possible observations of these events. Radio interferometry is capable of directly observing bulk outflow of the jets, and can even do so for events that are not face-on. This is currently limited to particularly nearby events.
Sensitive wide-field radio transient surveys have been developed, and are providing a new aspect to time-domain astronomy. However, another important metric for radio observations to study NS mergers is likely narrow-field sensitivity. With improvements in gamma-ray and X-ray sensitivity we would require a commensurate improvement in radio observations to fully study GRB 170817A-like events to greater distances.
9.1.8 VHE
VHE facilities probe the highest energy emission from these sources which provide stringent tests of LIV, and probe the extreme non-thermal emission. Observations of SGRBs at these energies may be unlikely with current facilities, but possible with the upcoming CTA mission. We recommend investigations into staggered observations with the large telescopes to maximize coverage of GW early warning localizations before merger, to attempt prompt observations of a SGRB.
9.1.9 Neutrinos
Neutrino detections of NS mergers would be a new messenger from these sources and allow a wealth of new science. MeV detections are likely to be rare, even with the funded Hyper-Kamiokande. High-energy neutrino observations are also likely to be rare with IceCube, but potentially observable. We recommend relevant software and analysis investment from these facilities, and patience until the first neutrino detection of a NS merger.
9.2 Communication and combined data
Given the critical information revealed from early observations of NS mergers, the necessity of robust associations, the inherent multimessenger and multiwavelength nature, and the need of follow-up observations for most EM observations, rapid communication of relevant information is of the utmost importance.
9.2.1 Combined searches
Combining the GW interferometers into an effective coherent network for detection has enabled the detection of a far greater number of events, more precise localizations, and the announcement of events quickly after merger. Similar improvements are possible with other types of searches within similar instruments, and between instruments. These are particularly promising outcomes for detections of signals that are prompt (or early).
The first is the construction of a coherent GRB network. These missions are predominantly background-dominated, so joint sub-threshold searches can increase the effective total sensitivity to SGRBs. Further, the automation of the IPN technique would reduce the latency for the annuli to be made available, which may aide in searches for kilonovae. The second are combined GW-GRB searches, both for independent triggers and sub-threshold searches. The automatic association and combined localizations of GW-GRB detections can increase the number of GW detections and reduce the prompt localization region. The last are combined neutrino-GW searches. These joint detections will be rare for the foreseeable future, but when they do occur the science return will be enormous, and the neutrino observations will provide \(\sim \) deg scale localizations. So despite the likely low chance of success of, investment is warranted.
Pulling out sub-threshold signals requires studies of weaker signals than have been considered before, which is particularly difficult and requires a deep understanding of the instrument, its noise, and its data. These studies likely require heavy investment by the relevant instrument teams. First is the combination of independent detections to aid the follow-up effort, development of shared software, maximizing the likelihood of follow-up success, and rewarding the team investment by credit for discoveries.
9.2.2 Reporting systems
Reporting systems are the backbone of multimessenger astronomy. They enable near real-time reporting of transient identification, localization, and initial analysis. This rapid and automated communication is fundamental to the success of the field, which is scientifically obvious. Sociologically, fast reporting allows for the claim of discovery for events of interest while also enabling greater observations and study for key events of interest.
Fully realizing the potential of multimessenger science requires advancements to the existing reporting systems. We comment on some ideal capabilities that these systems should be capable of.
-
General automated notice types including those for independently discovered transients, potential counterpart and claimed counterpart reporting, classification of those counterparts, planned and actual observations for pointed telescopes, retractions.
-
It must be capable of distributing alert information for all relevant observatories. For example, radio transients cannot be distributed through some optical alert systems because they cannot provide the observation band and magnitude (which is nonsense for a radio observation). A system that works for all relevant observatories and their relevant information is necessary.
-
Distribute alerts in real time through various standards to enable ease of access, and maintain an active database that can be polled on demand. With the above capability, this will enable things like requesting all current candidate counterparts to GW observations at a given time.
-
Easy creation of new alert streams, including user-created streams. This would allow for a distributed system for the reporting of value-added information, allowing individuals to contribute their specific expertise. and the minimization of duplicated effort. Examples include combined GRB and joint GW-GRB skymaps, or the convolution of GW skymaps with galaxy catalogs.
-
It should not attempt to duplicate or supplant the roles of instrument teams. The reporting, individual or combined, should give credit to those who enable the work.
-
The ranking of candidates to allow for automatic prioritization.
-
No single point failures, including computers, individuals, and networks. A good option is the use of cloud providers, which provide redundancy and high livetime while also avoiding some potential headaches (e.g., network restrictions due to national security concerns for systems housed within a NASA network).
-
Be a general multimessenger reporting system, not focused on NS mergers.
-
Induce as little delay as possible to high priority alerts. The most extreme example would be the early warning systems from GW observations. Early reports will send alerts on the order of tens of seconds, where transmission delay of the report could prevent successful EM observation of the merger time.
-
Enable private alert streams. This was done by GCN for O1 and O2 alerts from the LVC to enable the maturation of GW astronomy and could be used for other facilities with private data. It would also allow joint sub-threshold searches to be performed through existing alert streams, without public announcement of all individual sub-threshold searches.
-
The transient name server is used to provide unique identifiers to astronomical transients, working between the identifiers specific to individual fields or instruments. These two systems must integrate.
-
Able to access relevant catalogs and use the information accordingly, e.g., report galaxy-weighted localizations.
-
Be able to promptly determine the recent observations from relevant instruments of a given position to report or help determine the last sensitive non-detection for transients of interest.
-
The core software has to be written predominantly by professional programmers.
There are several proposals for future reporting methods. LSST has opted to use Apache Kafka to allow for distributed analysis and reporting through data brokers, which is an architecture that handles several of these wanted capabilities. There is the SCIMMA proposal to the NSF for a multimessenger computing institute. There is the NASA funded GCN upgrade referred to as TACH. AMON is an on-going project that attempts to combine sub-threshold signals to elevate the significance of weak events. Treasure Map provides a method for follow-up teams to report planned observations and coordination. There are several other on-going, proposed, and funded projects with similar ideals.
We must prevent the bifurcation of the time-domain community. As an example, both NSF and NASA have facilities with unique capabilities for multimessenger studies, and each appears open to funding multi-instrument systems as necessary. There should be a single automated organization to distribute alerts of interest for time-domain, multimessenger astronomy. If there is not, then all follow-up groups will have to develop their own software to ingest multiple types of alerts from different systems and combine the information themselves. This is an inefficient allocation of taxpayer money and scientist time. Note that we are not suggesting a single entity be made responsible for multimessenger astronomy. Each sub-group of multimessenger astronomers (e.g., optical surveys, GRB monitors, GW observers) should develop the capabilities necessary to analyze their own data. However, information of interest to the full multimessenger community should be reporting into a unified alert system. This can even be disparate systems that are intentionally built to communicate with each other (which could be, e.g., TACH communicating with the transient name server and Treasure Map allowing for follow-up coordination).
For those who report, automatically or promptly, we list a set of recommendations for best-practices:
-
A unified skymap format for poor localizations. We suggest the HEALPix format to match LIGO/Virgo and Fermi-GBM. We would support the development of HEALPix maps for things neutrino alerts (both individual MeV, SNEWS, and high energy localizations), pair conversion telescopes, Compton telescopes, gamma-ray scintillators, and the IPN. The relevant teams should contribute to the shared software, e.g., broaden the use of the multi-resolution maps that will be critical in the next few years.
-
The development of automated association methods for independent triggers, including (but not limited to) GWs, prompt SGRBs, neutrino detections, and optically-identified transients. Further, the automatic combination of localization information.
-
Full use of the various notice types should be used. For example, the GCN candidate counterpart notice type is substantially underutilized, with the very notable exception of the Swift-XRT team. If this were widely used it would enable fully robotic prioritization.
-
The assignment of informative names. KN170817 is a much more useful name for multimessenger studies than AT2017gfo. This is made obvious when you consider having a dozen GW-kilonova detections and having to remember which kilonova name belongs to which GW. The GWTC-1 catalog (Abbott et al. 2019b) reports a set of marginal candidates, which are named with the YYMMDD format, with no prefix or suffix marking them as GW candidates. This is not helpful for studies that seek to use these signals for future work.
9.2.3 Real-time information
The LVC developed real-time alerts and localizations for the Advanced era. They have heavily improved the information that is distributed in real-time by releasing the initial distance determination (as a function of 2D position), the initial merger classification based on the template mass measurements, and a likelihood of the release of matter from the merger. They have also developed Superevents, to down-select multiple GW triggers on the same event due to the multiple search pipelines, which have enabled preliminary notices before any manual selection.
Several astronomers have requested that the LVC report additional information in real-time. One usual request is the initial mass measures, which can be determined relatively early during the full parameter estimation. This would enable follow-up observers to make their own inference on the likely system classification, and prioritization to follow-up particularly interesting events when GW-detections of NS mergers become more routine. Examples may be particularly low or high-mass BNS mergers, or NSBH mergers near the disruption threshold. In general we support the continued increase in initial reporting information from GW detections.
However, this should be balanced against ensuring fair credit for the LVC and its individual members. Two recent results include the heavy (likely) BNS merger GW190425 (Abbott et al. 2020a) and the potential NSBH merger where the secondary object falls into the putative primary mass gap range (Abbott et al. 2020c). This science is only possible because of years and decades of investment that made GW interferometers sensitive enough to bring us into the new era, and much of the science could be inferred from the initial mass measures. We return to this in Sect. 9.4.
We support the development of early warning systems for NS mergers in the near-future. As discussed, these may not provide particularly well constrained localizations before merger with ground-based interferometers. However, knowing the event time before merger can still be beneficial for several reasons, and there are EM facilities that could potentially make use of even rough localizations. These alerts are likely to be complicated, and they must be distributed, received, and reacted to in seconds to be useful. Building this entire system will take heavy investment, and work should begin sooner rather than later.
Improved initial reporting should not be limited to GW alerts. For example, the prompt GRB monitors should automatically classify events, mark likely SGRBs, and hopefully combine information in near real-time to support the follow-up effort. This can be broadened to considerations of prompt GRB consistency with cocoon origin, which can inform follow-up searches targeting both the quasithermal and non-thermal signals.
The follow-up community is, in general, reporting necessary information in real-time. This includes announcing candidates of interest and their location. This gives the team credit at discovery, while enabling follow-up searches to characterize and classify the transients, and other teams to inform on the last non-detection. This information is also generally reported as soon as possible. Improvements could obviously be made, but the balance of rewarding credit for early reporting of information necessary to maximize science should spread to other aspects of multimessenger astronomy.
9.2.4 Space-based communication
Space-based observatories provide key coverage of \(\sim \) MeV gamma-rays, X-rays, ultraviolet, and infrared wavelengths. They also provide some of the most sensitive and precise observations in optical. There are two communication limitations that matter for existing and proposed missions.
Data bandwidth is limited given the expensive downlink cost and (in most cases) technical limitations. Fermi GBM can achieve far more sensitive searches because of the downlink of individual time-tagged event data. This was only possible because this continuous data time is small compared to the data requirements of the primary instrument on Fermi. Enabling missions to downlink more data will allow for increased scientific return through software developments.
Second, prompt communication is key. The prompt downlink of triggers from GRB monitors enabled time-domain astronomy and the distribution of SGRB localizations within a minute of merger. This capability is not widely accessible, requiring access to the NASA TDRSS satellites or a large network of ground stations as done for INTEGRAL.
Prompt uplink is currently not possible. One of the main sources of delay to the initial Swift follow-up of GW detections is the time to send the commands up to the spacecraft. We strongly endorse advancements that minimize this requirement for Swift and other missions, including removal (or minimization) of human-in-the-loop approval. This would also allow for future missions to decouple telescopes to separate spacecraft, maximizing their individual scientific return.
Lastly, the limitation of prompt uplink and in some cases approval of targets of opportunity approval to normal working hours during a weekday is problematic. If a once in a lifetime event goes off at 6pm on a Friday in the US then some of the most sensitive facilities in existence may not even send the repoint command until Monday. This is unacceptable for well-funded missions. In contrast, Swift is on pace for \(\sim \) 1900 targets of opportunity in 2019 (A. Tohuvavohu, private communication).
9.3 Theory, simulation, and interdisciplinary studies
Theory and simulation development enabled the detection and study of GW170817. The advanced numerical relativity waveforms that were constructed to build the CBC template banks that enable the real-time searches are a relatively new result. Significant improvements to these templates to fill the existing parameter space and consider additional effects, and improvements to analytic models (calibrated against the numerical waveforms) are warranted.
This is also true of the kilonova simulations that combined several very complicated processes into consistent codes that predicted the broad behavior of KN170817. They also created the models that were used to infer the parameters of the ejecta, which so much science relies on. Again improvements are warranted, as discussed in Sect. 5. Similar improvements on the simulations of SGRB jets and their interaction with surrounding material are recommended. These recommendations also directly apply for general simulations of NS mergers. Lastly, these results rely on knowledge of laboratory astrophysics, particularly atomic and nuclear studies of heavy elements. Also, the inclusion of sophisticated nuclear physics simulations can improve multimessenger results.
We strongly support the necessary funding and allocation of computational and experimental resources to advance theory, improve simulations, and encourage interdisciplinary research. It is critical to nearly all of the potential science with NS mergers.
9.4 Cultural change
We close our recommendations with a somewhat contentious issue. The community did not handle the high pressure situation of GW170817 as well as it could have. In the future this will be somewhat alleviated because the open public alerts from the LVC and few individual discoveries will be as important. However, we should strive to be better and support individuals and teams that act in good faith.
Interdisciplinary work often does not succeed because it is particularly difficult and the funding mechanisms are often lacking. It appears that the interdisciplinary studies in multimessenger astronomy will succeed because of the great interest from scientists and the funding agencies, and the science that can only be uncovered through such means. Another potential mismatch is the support for individuals that fall between fields, such as those building the inter-mission software that enables multimessenger astronomy.
This means that communities that have historically valued different metrics of success must adapt. In very broad strokes, astronomy tends to reward individual or small-group efforts, as evidenced by the metrics for faculty positions or prize fellowships, the awards from the professional societies, and the intense competition in time-domain astronomy. In contrast, nuclear and particle physicists, and related communities like astroparticle (neutrino, cosmic ray, gamma-ray) groups and now the GW collaborations, tend to work in very large collaboration out of necessity. For multimessenger science to succeed the judgement on the capability of an individual would ideally consider the metrics of success from their field.
10 Conclusions
Multimessenger observations of NS mergers allow for complementary information on the physics occurring during these events. GWs and neutrino observations directly probe the central engine. Kilonovae arise from the unbound ejecta released during and after coalescence. The emission of SGRBs arise from ultralrelativistic jets powered by the accretion torus on the central engine. Together this information could allow NS mergers to become the best understood astronomical transient.
In return, we can use them as tools to understand the universe, from cosmology, the origin of heavy elements, extreme particle acceleration, supranuclear matter, and fundamental physics. The science possible with studies of these sources is enormous. We are entering a new era because of the on-set of GW astronomy, and are well prepared for the next few years. Beyond that, some necessary capabilities do not exist and are not yet funded. Ensuring these needs are met will maximize what we learn from these unique sources.
Notes
Some specify NSBH or BHNS depending on which object formed first. This is a useful convention for some studies but is not used here as the distinction is beyond the scope of such a general review.
Note that this is slightly below the historically quoted number, which has been refined due to a greater understanding of the noise from the optical coatings.
Note this applies only to the GW-GRB detection volume, and will not significantly affect the GW-only detection rate due to inclination effects. See Sect. 4.4.
The color label for this third component has been referred to as “green” or “purple”. By physical temperature considerations green is correct. By combination of red and blue, deeply rooted in elementary art classes, purple is the intuitive name. I do not use a name here to prevent confusion, as it does not affect the rest of the paper. Realistically there will be a range from (infra)red to blue, but if three component fits become standard I strongly suggest using a single consistent color name.
Also because that section is quite long, and this provides a natural split given the different necessary observations.
This is also referred to as mass quadrupole polarizability or tidal polarizability.
The original letter refers to them as “neutrons” as the particle now known by that designation was not yet known.
Inversely, it has been shown that if a massless spin-2 gauge boson exists it is a graviton.
The term is used in analogy with EM birefringence, but GWs are maintained as a single wave.
They consider a 30\(M_{\odot} \) BH which is not expected to result in a SGRB, but the general statement is correct.
Abbreviations
- BAO:
-
Baryon acoustic oscillation
- BAT:
-
Burst Alert Telescope
- BATSE:
-
Burst and Transient Source Experiment
- BBN:
-
Big Bang Nucleosynthesis
- BH:
-
Black Hole
- BBH:
-
Binary Black Hole
- BNS:
-
Binary Neutron Star
- CBC:
-
Compact Binary Coalescence
- CMB:
-
Cosmic Microwave Background
- CCSNe:
-
Core-Collapse Supernova explosion
- CGRO:
-
Compton Gamma-Ray Observatory
- CTA:
-
Cherenkov Telescope Array
- CO:
-
Compact Object
- CR:
-
Cosmic Ray
- EM:
-
Electromagnetic
- FAR:
-
False Alarm Rate
- FoV:
-
Field of View
- EOS:
-
Equation of State
- GBM:
-
Gamma-ray Burst Monitor
- GCN:
-
Gamma-ray Coordinates Network
- GR:
-
General Relativity
- GRB:
-
Gamma-ray burst
- GW:
-
Gravitational wave
- HAWC:
-
High-Altitude Water Cherenkov
- HMNS:
-
HyperMassive Neutron Star
- IACT:
-
Imaging Atmospheric Cherenkov Telescope
- INTEGRAL:
-
INTErnational Gamma-Ray Astrophysics Laboratory
- IPN:
-
Interplanetary Network
- IR:
-
Infrared
- ISCO:
-
Innermost Stable Circular Orbit
- ISM:
-
Interstellar medium
- JWST:
-
James Webb Space Telescope
- KAGRA:
-
Kamioka Gravitational Wave Detector
- KNR:
-
Kilonova remnant
- LAT:
-
Large Area Telescope
- LEO:
-
Low Earth Orbit
- LGRB:
-
Long Gamma-Ray Burst
- LIGO:
-
Laser Interferometer Gravitational-wave Observatory
- LIV:
-
Lorentz Invariance Violation
- LSST:
-
Large Synoptic Survey Telescope
- LVC:
-
The LIGO Scientific Collaboration and Virgo Collaboration
- LISA:
-
Laser Interferometer Space Antenna
- NIR:
-
Near infrared
- MAGIC:
-
Major Atmospheric Gamma Imaging Cherenkov Telescopes
- MCMC:
-
Markov Chain Monte Carlo
- MW:
-
Milky Way
- NS:
-
Neutron Star
- NSBH:
-
Neutron Star–Black Hole
- PPN:
-
Parametrized Post-Newtonian
- PTA:
-
Pulsar Timing Arrays
- QCD:
-
Quantum Chromodynamics
- QFT:
-
Quantum Field Theory
- QG:
-
Quantum Gravity
- RAVEN:
-
Rapid VOEvent Coincidence Monitor
- SAA:
-
South Atlantic Anomaly
- SFR:
-
Star Formation Rate
- SGRB:
-
Short Gamma-Ray Burst
- SMBH:
-
SuperMassive Black Hole
- SMNS:
-
Supramassive Neutron Star
- SNR:
-
Signal-to-Noise Ratio
- SME:
-
Standard Model Extension
- SNe:
-
Supernova explosion
- SNEWS:
-
Supernova Early Warning System
- SPI-ACS:
-
SPectrometer onboard INTEGRAL-Anti-Coincidence Shield
- SR:
-
Special Relativity
- SSC:
-
Synchrotron Self Compton
- TOV:
-
Tolman–Oppenheimer–Volkoff
- TTE:
-
Time-Tagged Event
- UHECR:
-
Ultra-High Energy Cosmic Ray
- UV:
-
Ultraviolet
- UVOIR:
-
Ultraviolet, Optical, and Infrared
- UVOT:
-
Ultraviolet/Optical Telescope
- VHE:
-
Very High Energy
- WEP:
-
Weak Equivalence Principle
- XRT:
-
X-ray telescope
- ZTF:
-
Zwicky Transient Facility
References
Aartsen MG, Ackermann M, Adams J, Aguilar JA, Ahlers M, Ahrens M, Altmann D, Anderson T, Arguelles C, Arlen TC et al (2014) Observation of high-energy astrophysical neutrinos in three years of IceCube data. Phys Rev Lett 113:101101. https://doi.org/10.1103/PhysRevLett.113.101101
Aartsen MG, Ackermann M, Adams J, Aguilar JA, Ahlers M, Ahrens M, Altmann D, Anderson T, Arguelles C, Arlen TC et al (2015) Search for prompt neutrino emission from gamma-ray bursts with IceCube. Astrophys J Lett 805:L5. https://doi.org/10.1088/2041-8205/805/1/L5
Aartsen M, Ackermann M, Adams J, Aguilar JA, Ahlers M et al (2018) Multimessenger observations of a flaring blazar coincident with high-energy neutrino IceCube-170922A. Science. https://doi.org/10.1126/science.aat1378
Aasi J et al (2015) Advanced LIGO. Class Quantum Grav 32:074001. https://doi.org/10.1088/0264-9381/32/7/074001
Abadie J et al (2010) Predictions for the rates of compact binary coalescences observable by ground-based gravitational-wave detectors. Class Quantum Grav 27:173001. https://doi.org/10.1088/0264-9381/27/17/173001
Abadie J et al (2012a) Implications for the origin of GRB 051103 from LIGO observations. Astrophys J 755:2. https://doi.org/10.1088/0004-637X/755/1/2
Abadie J et al (2012b) Sensitivity achieved by the LIGO and Virgo gravitational wave detectors during LIGO’s sixth and Virgo’s second and third science runs. arXiv e-prints arXiv:1203.2674
Abbasi R, Abdou Y, Abu-Zayyad T, Adams J, Aguilar JA, Ahlers M, Andeen K, Auffenberg J, Bai X, Baker M et al (2011) Limits on neutrino emission from gamma-ray bursts with the 40 string IceCube detector. Phys Rev Lett 106:141101. https://doi.org/10.1103/PhysRevLett.106.141101
Abbott B et al (2008) Implications for the origin of GRB 070201 from LIGO observations. Astrophys J 681:1419. https://doi.org/10.1086/587954
Abbott BP et al (2009) LIGO: the laser interferometer gravitational-wave observatory. Rep Progr Phys 72:076901. https://doi.org/10.1088/0034-4885/72/7/076901
Abbott BP et al (2016a) GW151226: observation of gravitational waves from a 22-solar-mass binary black hole coalescence. Phys Rev Lett 116:241103. https://doi.org/10.1103/PhysRevLett.116.241103
Abbott BP et al (2016b) Observation of gravitational waves from a binary black hole merger. Phys Rev Lett 116:061102. https://doi.org/10.1103/PhysRevLett.116.061102
Abbott BP et al (2016c) Upper limits on the rates of binary neutron star and neutron star-black hole mergers from advanced LIGO’s first observing run. Astrophys J Lett 832:L21. https://doi.org/10.3847/2041-8205/832/2/L21
Abbott BP et al (2017a) Exploring the sensitivity of next generation gravitational wave detectors. Class Quantum Grav 34:044001. https://doi.org/10.1088/1361-6382/aa51f4
Abbott BP et al (2017b) Gravitational waves and gamma-rays from a binary neutron star merger: GW170817 and GRB 170817A. Astrophys J Lett 848:L13. https://doi.org/10.3847/2041-8213/aa920c
Abbott BP et al (2017c) GW170817: observation of gravitational waves from a binary neutron star inspiral. Phys Rev Lett 119:161101. https://doi.org/10.1103/PhysRevLett.119.161101
Abbott BP et al (2017d) Multi-messenger observations of a binary neutron star merger. Astrophys J Lett 848:L12. https://doi.org/10.3847/2041-8213/aa91c9
Abbott BP et al (2017e) GW170814: a three-detector observation of gravitational waves from a binary black hole coalescence. Phys Rev Lett 119:141101. https://doi.org/10.1103/PhysRevLett.119.141101
Abbott BP et al (2017f) On the progenitor of binary neutron star merger GW170817. Astrophys J Lett 850:L40. https://doi.org/10.3847/2041-8213/aa93fc
Abbott BP et al (2017g) Search for gravitational waves associated with gamma-ray bursts during the first advanced LIGO observing run and implications for the origin of GRB 150906B. Astrophys J 841:89. https://doi.org/10.3847/1538-4357/aa6c47
Abbott BP et al (2017h) A gravitational-wave standard siren measurement of the Hubble constant. Nature 551:85–88. https://doi.org/10.1038/nature24471
Abbott BP et al (2018a) Prospects for observing and localizing gravitational-wave transients with Advanced LIGO, Advanced Virgo and KAGRA. Living Rev Relativ 21:3. https://doi.org/10.1007/s41114-018-0012-9
Abbott BP et al (2018b) GW170817: measurements of neutron star radii and equation of state. Phys Rev Lett 121:161101. https://doi.org/10.1103/PhysRevLett.121.161101
Abbott BP et al (2019a) Binary black hole population properties inferred from the first and second observing runs of Advanced LIGO and Advanced Virgo. Astrophys J Lett 882:L24. https://doi.org/10.3847/2041-8213/ab3800
Abbott BP et al (2019b) GWTC-1: a gravitational-wave transient catalog of compact binary mergers observed by LIGO and Virgo during the first and second observing runs. Phys Rev X 9:031040. https://doi.org/10.1103/PhysRevX.9.031040
Abbott BP et al (2019c) Properties of the binary neutron star merger GW170817. Phys Rev X 9:011001. https://doi.org/10.1103/PhysRevX.9.011001
Abbott BP et al (2019d) Tests of general relativity with GW170817. Phys Rev Lett 123:011102. https://doi.org/10.1103/PhysRevLett.123.011102
Abbott BP et al (2019e) Tests of general relativity with the binary black hole signals from the LIGO-Virgo catalog GWTC-1. Phys Rev D 100:104036. https://doi.org/10.1103/PhysRevD.100.104036
Abbott BP et al (2019f) Search for gravitational-wave signals associated with gamma-ray bursts during the second observing run of Advanced LIGO and Advanced Virgo. Astrophys J 886:75. https://doi.org/10.3847/1538-4357/ab4b48
Abbott BP et al (2020a) GW190425: observation of a compact binary coalescence with total mass \(\sim 3.4 M_{\odot }\). Astrophys J Lett 892:L3. https://doi.org/10.3847/2041-8213/ab75f5
Abbott BP et al (2020b) Model comparison from LIGO-Virgo data on GW170817’s binary components and consequences for the merger remnant. Class Quantum Grav 37:045006. https://doi.org/10.1088/1361-6382/ab5f7c
Abbott R et al (2020c) GW190814: gravitational waves from the coalescence of a 23 solar mass black hole with a 2.6 solar mass compact object. Astrophys J Lett 896:L44. https://doi.org/10.3847/2041-8213/ab960f
Abdo AA, Ackermann M, Ajello M, Asano K, Atwood WB, Axelsson M, Baldini L, Ballet J, Barbiellini G, Baring MG et al (2009) A limit on the variation of the speed of light arising from quantum gravity effects. Nature 462:331. https://doi.org/10.1038/nature08574
Abe K, others, Hyper-Kamiokande Proto-Collaboration (2018) Hyper-Kamiokande design report. arXiv e-prints arXiv:1805.04163
Acernese F, Agathos M, Agatsuma K et al (2015) Advanced Virgo: a second-generation interferometric gravitational wave detector. Class Quantum Grav 32:024001. https://doi.org/10.1088/0264-9381/32/2/024001
Ackermann M, Asano K, Atwood WB, Axelsson M, Baldini L, Ballet J, Barbiellini G, Baring MG, Bastieri D, Bechtol K et al (2010) Fermi observations of GRB 090510: a short-hard gamma-ray burst with an additional, hard power-law component from 10 keV to GeV energies. Astrophys J 716:1178. https://doi.org/10.1088/0004-637X/716/2/1178
Ackley K, Adya VB, Agrawal P, Altin P, Ashton G, Bailes M, Baltinas E, Barbuio A, Beniwal D, Blair C et al (2020) Neutron star extreme matter observatory: a kilohertz-band gravitational-wave detector in the global network. arXiv e-prints arXiv:2007.03128
Adler RJ, Casey B, Jacob OC (1995) Vacuum catastrophe: an elementary exposition of the cosmological constant problem. Am J Phys 63:620–626. https://doi.org/10.1119/1.17850
Ahlers M, Halser L (2019) Neutrino fluence from gamma-ray bursts: off-axis view of structured jets. Mon Not R Astron Soc 490:4935–4943. https://doi.org/10.1093/mnras/stz2980
Ahmad QR, Allen RC, Andersen TC, Anglin JD, Barton JC, Beier EW, Bercovitch M, Bigu J, Biller SD, Black RA et al (2002) Direct evidence for neutrino flavor transformation from neutral-current interactions in the Sudbury Neutrino Observatory. Phys Rev Lett 89:011301. https://doi.org/10.1103/PhysRevLett.89.011301
Ajello M, Arimoto M, Axelsson M, Baldini L, Barbiellini G, Bastieri D, Bellazzini R, Bhat PN, Bissaldi E, Blandford RD et al (2019) A decade of gamma-ray bursts observed by Fermi-LAT: the second GRB catalog. Astrophys J 878:52. https://doi.org/10.3847/1538-4357/ab1d4e
Alam S, Ata M, Bailey S, Beutler F, Bizyaev D, Blazek JA, Bolton AS, Brownstein JR, Burden A, Chuang CH et al (2017) The clustering of galaxies in the completed SDSS-III Baryon Oscillation Spectroscopic Survey: cosmological analysis of the DR12 galaxy sample. Mon Not R Astron Soc 470:2617–2652. https://doi.org/10.1093/mnras/stx721
Albert A, André M, Anghinolfi M, Ardid M, Aubert JJ, Aublin J, Avgitas T, Baret B, Barrios-Martí J, Basa S et al (2017) Search for high-energy neutrinos from binary neutron star merger GW170817 with ANTARES, IceCube, and the Pierre Auger Observatory. Astrophys J Lett 850:L35. https://doi.org/10.3847/2041-8213/aa9aed
Alexander SHS, Gates SJ Jr (2006) Can the string scale be related to the cosmic baryon asymmetry? JCAP 2006:018. https://doi.org/10.1088/1475-7516/2006/06/018
Alexander S, Yunes N (2009) Chern–Simons modified general relativity. Phys Rep 480:1–55. https://doi.org/10.1016/j.physrep.2009.07.002
Alexander SH, Yunes N (2018) Gravitational wave probes of parity violation in compact binary coalescences. Phys Rev D 97:064033. https://doi.org/10.1103/physrevd.97.064033
Alexander SHS, Peskin ME, Sheikh-Jabbari MM (2006) Leptogenesis from gravity waves in models of inflation. Phys Rev Lett 96:081301. https://doi.org/10.1103/PhysRevLett.96.081301
Alexander S, Finn LS, Yunes N (2008) Gravitational-wave probe of effective quantum gravity. Phys Rev D 78:066005. https://doi.org/10.1103/physrevd.78.066005
Alexander KD, Margutti R, Blanchard PK, Fong W, Berger E, Hajela A, Eftekhari T, Chornock R, Cowperthwaite PS, Giannios D et al (2018) A decline in the X-ray through radio emission from GW170817 continues to support an off-axis structured jet. Astrophys J Lett 863:L18. https://doi.org/10.3847/2041-8213/aad637
Aloy MA, Janka HT, Müller E (2005) Relativistic outflows from remnants of compact object mergers and their viability for short gamma-ray bursts. Astron Astrophys 436:273–311. https://doi.org/10.1051/0004-6361:20041865
Alpher RA, Herman R (1948) Evolution of the Universe. Nature 162:774. https://doi.org/10.1038/162774b0
Alpher R, Bethe H, Gamow G (1948) The origin of chemical elements. Phys Rev 73:803. https://doi.org/10.1103/physrev.73.803
Altarelli G (1989) Experimental tests of perturbative QCD. Annu Rev Nucl Part Sci 39:357–406. https://doi.org/10.1142/9789814354141_0005
Alvarez-Gaume L, Witten E (1984) Gravitational anomalies. Nucl Phys B 234:269–330. https://doi.org/10.1515/9781400854561.451
Amelino-Camelia G (2002) Relativity in spacetimes with short-distance structure governed by an observer-independent (Planckian) length scale. Int J Mod Phys D 11:35–59. https://doi.org/10.1142/s0218271802001330
Amelino-Camelia G, Ellis J, Mavromatos NE, Nanopoulos DV (1997) Distance measurement and wave dispersion in a Liouville-string approach to quantum gravity. Int J Mod Phys A 12:607–623. https://doi.org/10.1142/s0217751x97000566
Amelino-Camelia G, Ellis J, Mavromatos NE, Nanopoulos DV, Sarkar S (1998) Tests of quantum gravity from observations of \(\gamma \)-ray bursts. Nature 393:763. https://doi.org/10.1038/26793
Andriot D, Gómez GL (2017) Signatures of extra dimensions in gravitational waves. JCAP 2017:048. https://doi.org/10.1088/1475-7516/2017/06/048
Antoniadis J, Freire PC, Wex N, Tauris TM, Lynch RS, van Kerkwijk MH, Kramer M, Bassa C, Dhillon VS, Driebe T et al (2013) A massive pulsar in a compact relativistic binary. Science 340:1233232. https://doi.org/10.1126/science.1233232
Antonioli P, Fienberg RT, Fleurot F, Fukuda Y, Fulgione W, Habig A, Heise J, McDonald AB, Mills C, Namba T et al (2004) SNEWS: the supernova early warning system. New J Phys 6:114. https://doi.org/10.1088/1367-2630/6/1/114
Aprahamian A, Lapi S, Mantica P, Fatemi R, Velkovska J, Wilkerson J, Filippone B, Cirigliano V, Schukraft J, Ji X et al (2015) Reaching for the horizon: the 2015 long range plan for nuclear science. Technical report, U.S. Department of Energy. https://www.osti.gov/biblio/1296778-reaching-horizon-long-range-plan-nuclear-science
Aptekar RL, Frederiks DD, Golenetskii SV, Ilynskii VN, Mazets EP, Panov VN, Sokolova ZJ, Terekhov MM, Sheshin LO, Cline TL et al (1995) Konus-W gamma-ray burst experiment for the GGS Wind spacecraft. Space Sci Rev 71:265–272. https://doi.org/10.1007/bf00751332
Arcavi I (2018) The first hours of the GW170817 kilonova and the importance of early optical and ultraviolet observations for constraining emission models. Astrophys J Lett 855:L23. https://doi.org/10.3847/2041-8213/aab267
Arcavi I, Hosseinzadeh G, Howell DA, McCully C, Poznanski D, Kasen D, Barnes J, Zaltzman M, Vasylyev S, Maoz D et al (2017) Optical emission from a kilonova following a gravitational-wave-detected neutron-star merger. Nature 551:64. https://doi.org/10.1038/nature24291
Arnaud N, Barsuglia M, Bizouard MA, Cavalier F, Davier M, Hello P, Pradier T (2002) Gravity wave and neutrino bursts from stellar collapse: a sensitive test of neutrino masses. Phys Rev D 65:033010. https://doi.org/10.1103/physrevd.65.033010
Arun KG (2012) Generic bounds on dipolar gravitational radiation from inspiralling compact binaries. Class Quantum Grav 29:075011. https://doi.org/10.1088/0264-9381/29/7/075011
Ascenzi S, Coughlin MW, Dietrich T, Foley RJ, Ramirez-Ruiz E, Piranomonte S, Mockler B, Murguia-Berthier A, Fryer CL, Lloyd-Ronning NM et al (2019) A luminosity distribution for kilonovae based on short gamma-ray burst afterglows. Mon Not R Astron Soc 486:672–690. https://doi.org/10.1093/mnras/stz891
Ascenzi S, Oganesyan G, Salafia OS, Branchesi M, Ghirlanda G, Dall’Osso S (2020) High-latitude emission from the structured jet of \({\gamma }\)-ray bursts observed off-axis. Astron Astrophys 641:A61. https://doi.org/10.1051/0004-6361/202038265. arXiv:2004.12215
Ashtekar A, Balachandran AP, Jo S (1989) The CP problem in quantum gravity. Int J Mod Phys A 4:1493–1514. https://doi.org/10.1142/s0217751x89000649
Ashton G, Burns E, Dal Canton T, Dent T, Eggenstein HB, Nielsen AB, Prix R, Was M, Zhu SJ (2018) Coincident detection significance in multimessenger astronomy. Astrophys J 860:6. https://doi.org/10.3847/1538-4357/aabfd2
Aso Y, Michimura Y, Somiya K, Ando M, Miyakawa O, Sekiguchi T, Tatsumi D, Yamamoto H et al, KAGRA Collaboration (2013) Interferometer design of the KAGRA gravitational wave detector. Phys Rev D 88:043007. https://doi.org/10.1103/physrevd.88.043007
Atwood WB, Abdo AA, Ackermann M, Althouse W, Anderson B, Axelsson M, Baldini L, Ballet J, Band DL, Barbiellini G et al (2009) The Large Area Telescope on the Fermi gamma-ray space telescope mission. Astrophys J 697:1071
Audren B, Lesgourgues J, Bird S, Haehnelt MG, Viel M (2013) Neutrino masses and cosmological parameters from a Euclid-like survey: Markov Chain Monte Carlo forecasts including theoretical errors. JCAP 2013:026. https://doi.org/10.1088/1475-7516/2013/01/026
Bahcall JN (1964) Solar neutrinos. I. Theoretical. Phys Rev Lett 12:300. https://doi.org/10.1201/9780429502811-4
Baiotti L, Rezzolla L (2017) Binary neutron star mergers: a review of Einstein’s richest laboratory. Rep Prog Phys 80:096901. https://doi.org/10.1088/1361-6633/aa67bb
Baker T, Bellini E, Ferreira PG, Lagos M, Noller J, Sawicki I (2017) Strong constraints on cosmological gravity from GW170817 and GRB 170817A. Phys Rev Lett 119:251301. https://doi.org/10.1103/physrevlett.119.251301
Balantekin AB, Carlson J, Dean DJ, Fuller GM, Furnstahl RJ, Hjorth-Jensen M, Janssens RVF, Li BA, Nazarewicz W, Nunes FM et al (2014) Nuclear theory and science of the facility for rare isotope beams. Mod Phys Lett A 29:1430010. https://doi.org/10.1142/s0217732314300109
Balbus SA, Hawley JF (1991) A powerful local shear instability in weakly magnetized disks. I. Linear analysis. II. Nonlinear evolution. Astrophys J 376:214–233. https://doi.org/10.1086/170270
Barbieri C, Salafia OS, Colpi M, Ghirlanda G, Perego A, Colombo A (2019) Filling the mass gap: how kilonova observations can unveil the nature of the compact object merging with the neutron star. Astrophys J Lett 887:L35. https://doi.org/10.3847/2041-8213/ab5c1e
Barbieri C, Salafia OS, Perego A, Colpi M, Ghirlanda G (2020) Electromagnetic counterparts of black hole-neutron star mergers: dependence on the neutron star properties. Eur Phys J A 56:1–25. https://doi.org/10.1140/epja/s10050-019-00013-x
Baring MG, Harding AK (1997) The escape of high-energy photons from gamma-ray bursts. Astrophys J 491:663. https://doi.org/10.1086/304982
Barkov MV, Pozanenko AS (2011) Model of the extended emission of short gamma-ray bursts. Mon Not R Astron Soc 417:2161–2165. https://doi.org/10.1111/j.1365-2966.2011.19398.x
Barnes J, Kasen D (2013) Effect of a high opacity on the light curves of radioactively powered transients from compact object mergers. Astrophys J 775:18. https://doi.org/10.1088/0004-637x/775/1/18
Barnes J, Kasen D, Wu MR, Martínez-Pinedo G (2016) Radioactivity and thermalization in the ejecta of compact object mergers and their impact on Kilonova light curves. Astrophys J 829:110. https://doi.org/10.3847/0004-637X/829/2/110
Barsotti L, Fritschel P, Evans M, Gras S (2018) Updated Advanced LIGO sensitivity design curve. Technical report, LIGO. https://dcc.ligo.org/LIGO-T1800044/public
Barthelmy SD, Barbier LM, Cummings JR, Fenimore EE, Gehrels N, Hullinger D, Krimm HA, Markwardt CB, Palmer DM, Parsons A, Sato G, Suzuki M, Takahashi T, Tashiro M, Tueller J (2005) The Burst Alert Telescope (BAT) on the Swift Midex Mission. Space Sci Rev 120:143–164. https://doi.org/10.1007/s11214-005-5096-3
Bartos I, Marka S (2019) A nearby neutron-star merger explains the actinide abundances in the early Solar System. Nature 569:85. https://doi.org/10.1038/s41586-019-1113-7
Baumgarte TW, Shapiro SL, Shibata M (1999) On the maximum mass of differentially rotating neutron stars. Astrophys J Lett 528:L29. https://doi.org/10.1086/312425
Bauswein A, Stergioulas N (2015) Unified picture of the post-merger dynamics and gravitational wave emission in neutron star mergers. Phys Rev D 91:124056. https://doi.org/10.1103/physrevd.91.124056
Bauswein A, Baumgarte TW, Janka HT (2013a) Prompt merger collapse and the maximum mass of neutron stars. Phys Rev Lett 111:131101. https://doi.org/10.1103/physrevlett.111.131101
Bauswein A, Goriely S, Janka HT (2013b) Systematics of dynamical mass ejection, nucleosynthesis, and radioactively powered electromagnetic signals from neutron-star mergers. Astrophys J 773:78. https://doi.org/10.1088/0004-637x/773/1/78
Bauswein A, Just O, Janka HT, Stergioulas N (2017) Neutron-star radius constraints from GW170817 and future detections. Astrophys J Lett 850:L34. https://doi.org/10.3847/2041-8213/aa9994
Bauswein A, Bastian NUF, Blaschke DB, Chatziioannou K, Clark JA, Fischer T, Oertel M (2019) Identifying a first-order phase transition in neutron-star mergers through gravitational waves. Phys Rev Lett 122:061102. https://doi.org/10.1103/physrevlett.122.061102
Baym G, Hatsuda T, Kojo T, Powell PD, Song Y, Takatsuka T (2018) From hadrons to quarks in neutron stars: a review. Rep Prog Phys 81:056902. https://doi.org/10.1088/1361-6633/aaae14
Belczynski K, Kalogera V, Bulik T (2002) A comprehensive study of binary compact objects as gravitational wave sources: evolutionary channels, rates, and physical properties. Astrophys J 572:407. https://doi.org/10.1086/340304
Belczynski K, Perna R, Bulik T, Kalogera V, Ivanova N, Lamb DQ (2006) A study of compact object mergers as short gamma-ray burst progenitors. Astrophys J 648:1110. https://doi.org/10.1086/505169
Belczynski K, Kalogera V, Rasio FA, Taam RE, Zezas A, Bulik T, Maccarone TJ, Ivanova N (2008) Compact object modeling with the StarTrack population synthesis code. Astrophys J Suppl Ser 174:223. https://doi.org/10.1086/521026
Belczynski K, Wiktorowicz G, Fryer CL, Holz DE, Kalogera V (2012) Missing black holes unveil the supernova explosion mechanism. Astrophys J 757:91. https://doi.org/10.1088/0004-637x/757/1/91
Bellini E, Sawicki I (2014) Maximal freedom at minimum cost: linear large-scale structure in general modifications of gravity. JCAP 2014:050. https://doi.org/10.1088/1475-7516/2014/07/050
Bellm EC (2014) The Zwicky transient facility. In: Woźniak PR, Graham MJ, Mahabal AA, Seaman R (eds) Proceedings of the third hot-wiring transient universe workshop, SLAC
Beloborodov AM (2010) Collisional mechanism for gamma-ray burst emission. Mon Not R Astron Soc 407:1033–1047. https://doi.org/10.1111/j.1365-2966.2010.16770.x
Beloborodov AM, Mészáros P (2017) Photospheric emission of gamma-ray bursts. Space Sci Rev 207:87–110. https://doi.org/10.1007/978-94-024-1292-5_4
Beniamini P, Nakar E (2018) Observational constraints on the structure of gamma-ray burst jets. Mon Not R Astron Soc 482:5430–5440. https://doi.org/10.1093/mnras/sty3110
Beniamini P, Hotokezaka K, Piran T (2016) R-process production sites as inferred from Eu abundances in dwarf galaxies. Astrophys J 832:149. https://doi.org/10.3847/0004-637x/832/2/149
Beniamini P, Petropoulou M, Barniol Duran R, Giannios D (2019) A lesson from GW170817: most neutron star mergers result in tightly collimated successful GRB jets. Mon Not R Astron Soc 483:840–851. https://doi.org/10.1093/mnras/sty3093
Berger E (2014) Short-duration gamma-ray bursts. Annu Rev Astron Astrophys 52:43–105. https://doi.org/10.1146/annurev-astro-081913-035926
Berger E, Kulkarni SR, Pooley G, Frail DA, McIntyre V, Wark RM, Sari R, Soderberg AM, Fox DW, Yost S et al (2003) A common origin for cosmic explosions inferred from calorimetry of GRB030329. Nature 426:154–157. https://doi.org/10.1038/nature01998
Berger E, Fong W, Chornock R (2013) An r-process Kilonova associated with the short-hard GRB 130603B. Astrophys J Lett 774:L23. https://doi.org/10.1088/2041-8205/774/2/L23
Bernstein G (2006) Metric tests for curvature from weak lensing and baryon acoustic oscillations. Astrophys J 637:598. https://doi.org/10.1086/498079
Bertolami O, Lehnert R, Potting R, Ribeiro A (2004) Cosmological acceleration, varying couplings, and Lorentz breaking. Phys Rev D 69:083513. https://doi.org/10.1103/physrevd.69.083513
Bertotti B, Iess L, Tortora P (2003) A test of general relativity using radio links with the Cassini spacecraft. Nature 425:374. https://doi.org/10.1038/nature01997
Bhat PN, Fishman GJ, Meegan CA, Wilson RB, Brock MN, Paciesas WS (1992) Evidence for sub-millisecond structure in a \(\gamma \)-ray burst. Nature 359:217–218. https://doi.org/10.1038/359217a0
Bhat PN, Meegan CA, von Kienlin A, Paciesas WS, Briggs MS, Burgess JM, Burns E, Chaplin V, Cleveland WH, Collazzi AC, Connaughton V, Diekmann AM, Fitzpatrick G, Gibby MH, Giles MM, Goldstein AM, Greiner J, Jenke PA, Kippen RM, Kouveliotou C, Mailyan B, McBreen S, Pelassa V, Preece RD, Roberts OJ, Sparke LS, Stanbro M, Veres P, Wilson-Hodge CA, Xiong S, Younes G, Yu HF, Zhang B (2016) The third Fermi GBM gamma-ray burst catalog: the first six years. Astrophys J Suppl 223:28. https://doi.org/10.3847/0067-0049/223/2/28
Biesiada M, Piórkowska A (2009) Gravitational lensing time delays as a tool for testing Lorentz-invariance violation. Mon Not R Astron Soc 396:946–950. https://doi.org/10.1111/j.1365-2966.2009.14748.x
Biesiada M, Ding X, Piórkowska A, Zhu ZH (2014) Strong gravitational lensing of gravitational waves from double compact binaries-perspectives for the Einstein Telescope. JCAP 2014:080. https://doi.org/10.1088/1475-7516/2014/10/080
Bilenky SM, Giunti C, Grifols JA, Masso E (2003) Absolute values of neutrino masses: status and prospects. Phys Rep 379:69–148. https://doi.org/10.1016/s0370-1573(03)00102-9
Binns W, Israel MH, Rauch BF, Cummings AC, Davis AJ, Labrador AW, Leske RA, Mewaldt RA, Stone EC, Wiedenbeck ME, Brandt TJ, Christian ER, Link JT, Mitchell JW, de Nolfo GA, von Rosenvinge TT, Sakai K, Sasaki M, Waddington CJ, Janka HT, Melott AL, Mason GM, Seo ES, Adams JH, Thielemann FK, Heger A, Lugaro M, Westphal AJ (2019) Ultra-heavy cosmic-ray science: are r-process nuclei in the cosmic rays produced in supernovae or binary neutron star mergers? Bull Am Astron Soc 51:313
Biscoveanu S, Thrane E, Vitale S (2020) Constraining short gamma-ray burst jet properties with gravitational waves and gamma-rays. Astrophys J 893:38. https://doi.org/10.3847/1538-4357/ab7eaf
Blackburn L, Briggs MS, Camp J, Christensen N, Connaughton V, Jenke P, Remillard RA, Veitch J (2015) High-energy electromagnetic offline follow-up of LIGO-Virgo gravitational-wave binary coalescence candidate events. Astrophys J Suppl 217:8. https://doi.org/10.1088/0067-0049/217/1/8
Blandford R, Narayan R (1986) Fermat’s principle, caustics, and the classification of gravitational lens images. Astrophys J 310:568–582. https://doi.org/10.1086/164709
Blandford RD, Narayan R (1992) Cosmological applications of gravitational lensing. Annu Rev Astron Astrophys 30:311–358. https://doi.org/10.1146/annurev.aa.30.090192.001523
Blandford RD, Znajek RL (1977) Electromagnetic extraction of energy from Kerr black holes. Mon Not R Astron Soc 179:433–456. https://doi.org/10.1093/mnras/179.3.433
Blas D, Ivanov MM, Sawicki I, Sibiryakov S (2016) On constraining the speed of gravitational waves following GW150914. JETP Lett 103:624–626. https://doi.org/10.1134/s0021364016100040
Bloemen S, Groot P, Nelemans G, Klein-Wolt M (2015) The BlackGEM array: searching for gravitational wave source counterparts to study ultra-compact binaries. In: Rucinski SM, Torres G, Zejda M (eds) Living together: planets, host stars and binaries. ASP conference series, vol 496. Astronomical Society of the Pacific, San Francisco, p 254
Bloom JS, Frail DA, Sari R (2001) The prompt energy release of gamma-ray bursts using a cosmological k-correction. Astron J 121:2879. https://doi.org/10.1086/321093
Boran S, Desai S, Kahya EO, Woodard RP (2018) GW170817 falsifies dark matter emulators. Phys Rev D 97:041501. https://doi.org/10.1103/physrevd.97.041501
Bose S, Chakravarti K, Rezzolla L, Sathyaprakash BS, Takami K (2018) Neutron-star radius from a population of binary neutron star mergers. Phys Rev Lett 120:031102. https://doi.org/10.1103/PhysRevLett.120.031102
Bracco A (2017) The NuPECC long range plan 2017: perspectives in nuclear physics. Europhysics News 48:21–24. https://doi.org/10.1080/10619127.2017.1352311
Briggs MS, Paciesas WS, Pendleton GN, Meegan CA, Fishman GJ, Horack JM, Brock MN, Kouveliotou C, Hartmann DH, Hakkila J (1996) BATSE observations of the large-scale isotropy of gamma-ray bursts. Astrophys J 459:40. https://doi.org/10.1086/176867
Brito R, Cardoso V, Pani P (2013) Massive spin-2 fields on black hole spacetimes: instability of the Schwarzschild and Kerr solutions and bounds on the graviton mass. Phys Rev D 88:023514. https://doi.org/10.1103/physrevd.88.023514
Brown AGA, Vallenari A, Prusti T, De Bruijne JH, Babusiaux C, Bailer-Jones CAL, Biermann M, Evans DW, Eyer L, Jansen F et al (2018) Gaia data release 2-summary of the contents and survey properties. Astron Astrophys 616:A1. https://doi.org/10.1051/0004-6361/201833051
Bucciantini N, Quataert E, Arons J, Metzger BD, Thompson TA (2008) Relativistic jets and long-duration gamma-ray bursts from the birth of magnetars. Mon Not R Astron Soc Lett 383:L25–L29. https://doi.org/10.1111/j.1745-3933.2007.00403.x
Bucciantini N, Metzger BD, Thompson TA, Quataert E (2011) Short gamma-ray bursts with extended emission from magnetar birth: jet formation and collimation. Mon Not R Astron Soc 419:1537–1545. https://doi.org/10.1111/j.1365-2966.2011.19810.x
Bulla M (2019) POSSIS: predicting spectra, light curves, and polarization for multidimensional models of supernovae and kilonovae. Mon Not R Astron Soc 489:5037–5045. https://doi.org/10.1093/mnras/stz2495
Bullock JS, Boylan-Kolchin M (2017) Small-scale challenges to the \(\Lambda \)CDM paradigm. Annu Rev Astron Astrophys 55:343–387. https://doi.org/10.1146/annurev-astro-091916-055313
Burbidge EM, Burbidge GR, Fowler WA, Hoyle F (1957) Synthesis of the elements in stars. Rev Mod Phys 29:547. https://doi.org/10.1103/revmodphys.29.547
Burgess CP, Cline JM, Filotas E, Matias J, Moore GD (2002) Loop-generated bounds on changes to the graviton dispersion relation. J High Energy Phys 03:043. https://doi.org/10.1088/1126-6708/2002/03/043
Burgess JM, Kole M, Berlato F, Greiner J, Vianello G, Produit N, Li ZH, Sun JC (2019) Time-resolved GRB polarization with POLAR and GBM-simultaneous spectral and polarization analysis with synchrotron emission. Astron Astrophys 627:A105. https://doi.org/10.1051/0004-6361/201935056
Burles S, Nollett KM, Truran JW, Turner MS (1999) Sharpening the predictions of big-bang nucleosynthesis. Phys Rev Lett 82:4176. https://doi.org/10.1103/physrevlett.82.4176
Burns E (2017) Searching for prompt gamma ray signals around gravitational wave triggers. PhD thesis, The University of Alabama in Huntsville
Burns E, Connaughton V, Zhang BB, Lien A, Briggs MS, Goldstein A, Pelassa V, Troja E (2016) Do the Fermi Gamma-ray Burst Monitor and Swift Burst Alert Telescope see the same short gamma-ray bursts? Astrophys J 818:110. https://doi.org/10.3847/0004-637X/818/2/110
Burns E, Veres P, Connaughton V, Racusin J, Briggs MS, Christensen N, Goldstein A, Hamburg R, Kocevski D, McEnery J et al (2018) Fermi GBM observations of GRB 150101B: a second nearby event with a short hard spike and a soft tail. Astrophys J Lett 863:L34. https://doi.org/10.3847/2041-8213/aad813
Burrows DN, Falcone A, Chincarini G, Morris D, Romano P, Hill JE, Godet O, Moretti A, Krimm H, Osborne JP et al (2007) X-ray flares in early GRB afterglows. Philos Trans R Soc A Math Phys Eng Sci 365:1213–1226. https://doi.org/10.1098/rsta.2006.1970
Caldwell RR, Dave R, Steinhardt PJ (1998) Cosmological imprint of an energy component with general equation of state. Phys Rev Lett 80:1582. https://doi.org/10.1103/physrevlett.80.1582
Callister T, Biscoveanu AS, Christensen N, Isi M, Matas A, Minazzoli O, Regimbau T, Sakellariadou M, Tasson J, Thrane E (2017) Polarization-based tests of gravity with the stochastic gravitational-wave background. Phys Rev X 7:041058. https://doi.org/10.1103/physrevx.7.041058
Cameron AGW (1957) Nuclear reactions in stars and nucleogenesis. Publ Astron Soc Pac 69:201–222. https://doi.org/10.1086/127051
Cannon K, Cariou R, Chapman A, Crispin-Ortuzar M, Fotopoulos N, Frei M, Hanna C, Kara E, Keppel D, Liao L et al (2012) Toward early-warning detection of gravitational waves from compact binary coalescence. Astrophys J 748:136. https://doi.org/10.1088/0004-637x/748/2/136
Cano Z, Wang SQ, Dai ZG, Wu XF (2017) The observer’s guide to the gamma-ray burst supernova connection. Adv Astron. https://doi.org/10.1155/2017/8929054
Cantiello M, Jensen JB, Blakeslee JP, Berger E, Levan AJ, Tanvir NR, Raimondo G, Brocato E, Alexander KD, Blanchard PK et al (2018) A precise distance to the host galaxy of the binary neutron star merger GW170817 using surface brightness fluctuations. Astrophys J Lett 854:L31. https://doi.org/10.3847/2041-8213/aaad64
Canuel B, Bertoldi A, Amand L, Di Borgo EP, Chantrait T, Danquigny C, Álvarez MD, Fang B, Freise A, Geiger R et al (2018) Exploring gravity with the MIGA large scale atom interferometer. Sci Rep 8:14064. https://doi.org/10.1038/s41598-018-32165-z
Capano CD, Tews I, Brown SM, Margalit B, De S, Kumar S, Brown DA, Krishnan B, Reddy S (2020) Stringent constraints on neutron-star radii from multimessenger observations and nuclear theory. Nat Astron 4:625–632. https://doi.org/10.1038/s41550-020-1014-6. arXiv:1908.10352
Carbone C, Verde L, Wang Y, Cimatti A (2011) Neutrino constraints from future nearly all-sky spectroscopic galaxy surveys. JCAP 2011:030. https://doi.org/10.1088/1475-7516/2011/03/030
Caves CM (1980) Gravitational radiation and the ultimate speed in Rosen’s bimetric theory of gravity. Ann Phys 125:35–52. https://doi.org/10.1016/0003-4916(80)90117-7
Cenko SB, Frail DA, Harrison FA, Kulkarni SR, Nakar E, Chandra PC, Butler NR, Fox DB, Gal-Yam A, Kasliwal MM et al (2010) The collimation and energetics of the brightest Swift gamma-ray bursts. Astrophys J 711:641. https://doi.org/10.1088/0004-637x/711/2/641
Chakraborty S, Chakravarti K, Bose S, SenGupta S (2018) Signatures of extra dimensions in gravitational waves from black hole quasinormal modes. Phys Rev D 97:104053. https://doi.org/10.1103/physrevd.97.104053
Chattopadhyay T, Vadawale SV, Aarthy E, Mithun NPS, Chand V, Basak R, Rao AR, Mate S, Sharma V, Bhalerao V et al (2019) Prompt emission polarimetry of gamma-ray bursts with AstroSat CZT-imager. Astrophys J 884:123. https://doi.org/10.3847/1538-4357/ab40b7
Chatziioannou K, Yunes N, Cornish N (2012) Model-independent test of general relativity: an extended post-Einsteinian framework with complete polarization content. Phys Rev D 86:022004. https://doi.org/10.1103/physrevd.86.022004
Chen HY, Holz DE, Miller J, Evans M, Vitale S, Creighton J (2017) Distance measures in gravitational-wave astrophysics and cosmology. arXiv e-prints arXiv:1709.08079
Chen HY, Fishbach M, Holz DE (2018) A two per cent Hubble constant measurement from standard sirens within five years. Nature. https://doi.org/10.1038/s41586-018-0606-0
Chevallier M, Polarski D (2001) Accelerating universes with scaling dark matter. Int J Mod Phys D 10:213–223. https://doi.org/10.1142/s0218271801000822
Choudhury SR, Joshi GC, Mahajan S, McKellar BH (2004) Probing large distance higher dimensional gravity from lensing data. Astropart Phys 21:559–563. https://doi.org/10.1016/j.astropartphys.2004.04.001
Christensen L, Hjorth J, Gorosabel J (2004) Uv star-formation rates of GRB host galaxies. Astron Astrophys 425:913–926. https://doi.org/10.1051/0004-6361:20040361
Church RP, Levan AJ, Davies MB, Tanvir N (2011) Implications for the origin of short gamma-ray bursts from their observed positions around their host galaxies. Mon Not R Astron Soc 413:2004–2014. https://doi.org/10.1111/j.1365-2966.2011.18277.x
Clark J, Bauswein A, Cadonati L, Janka HT, Pankow C, Stergioulas N (2014) Prospects for high frequency burst searches following binary neutron star coalescence with advanced gravitational wave detectors. Phys Rev D 90:062004. https://doi.org/10.1103/physrevd.90.062004
Clark JA, Bauswein A, Stergioulas N, Shoemaker D (2016) Observing gravitational waves from the post-merger phase of binary neutron star coalescence. Class Quantum Grav 33:085003. https://doi.org/10.1088/0264-9381/33/8/085003
Collett TE (2015) The population of galaxy–galaxy strong lenses in forthcoming optical imaging surveys. Astrophys J 811:20. https://doi.org/10.1088/0004-637x/811/1/20
Collett TE, Bacon D (2017) Testing the speed of gravitational waves over cosmological distances with strong gravitational lensing. Phys Rev Lett 118:091101. https://doi.org/10.1103/physrevlett.118.091101
Connaughton V (2002) BATSE observations of gamma-ray burst tails. Astrophys J 567:1028. https://doi.org/10.1086/338695
Cook GB, Shapiro SL, Teukolsky SA (1994) Rapidly rotating neutron stars in general relativity: realistic equations of state. Astrophys J 424:823–845. https://doi.org/10.1086/173934
Cornish N, Blas D, Nardini G (2017) Bounding the speed of gravity with gravitational wave observations. Phys Rev Lett 119:161102. https://doi.org/10.1103/physrevlett.119.161102
Côté B, Fryer CL, Belczynski K, Korobkin O, Chruślińska M, Vassh N, Mumpower MR, Lippuner J, Sprouse TM, Surman R et al (2018) The origin of r-process elements in the Milky Way. Astrophys J 855:99. https://doi.org/10.3847/1538-4357/aaad67
Côté B, Lugaro M, Reifarth R, Pignatari M, Világos B, Yagüe A, Gibson BK (2019) Galactic chemical evolution of radioactive isotopes. Astrophys J 878:156. https://doi.org/10.3847/1538-4357/ab21d1
Coughlin MW, Dietrich T (2019) Can a black hole-neutron star merger explain GW170817, AT2017gfo, and GRB170817A? Phys Rev D 100:043011. https://doi.org/10.1103/physrevd.100.043011
Coughlin MW, Dietrich T, Doctor Z, Kasen D, Coughlin S, Jerkstrand A, Leloudas G, McBrien O, Metzger BD, O’Shaughnessy R et al (2018) Constraints on the neutron star equation of state from AT2017gfo using radiative transfer simulations. Mon Not R Astron Soc 480:3871–3878. https://doi.org/10.1093/mnras/sty2174
Coughlin MW, Ahumada T, Anand S, De K, Hankins MJ, Kasliwal MM, Singer LP, Bellm EC et al (2019a) GROWTH on S190425z: searching thousands of square degrees to identify an optical or infrared counterpart to a binary neutron star merger with the Zwicky Transient Facility and Palomar Gattini-IR. Astrophys J Lett 885:L19. https://doi.org/10.3847/2041-8213/ab4ad8. arXiv:1907.12645
Coughlin MW, Dietrich T, Margalit B, Metzger BD (2019b) Multimessenger Bayesian parameter inference of a binary neutron star merger. Mon Not R Astron Soc 489:L91–L96. https://doi.org/10.1093/mnrasl/slz133
Coughlin ER, Nixon CJ, Barnes J, Metzger BD, Margutti R (2020) Variability in short gamma-ray bursts: gravitationally unstable tidal tails. Astrophys J Lett 896:L38. https://doi.org/10.3847/2041-8213/ab9a4e. arXiv:2006.03174
Coulter DA, Foley RJ, Kilpatrick CD, Drout MR, Piro AL, Shappee BJ, Siebert MR, Simon JD, Ulloa N, Kasen D et al (2017) Swope Supernova Survey 2017a (SSS17a), the optical counterpart to a gravitational wave source. Science. https://doi.org/10.1126/science.aap9811
Cowan CL Jr, Reines F, Harrison FB, Kruse HW, McGuire AD (1956) Detection of the free neutrino: a confirmation. Science 124:103–104. https://doi.org/10.1126/science.124.3212.103
Cowan JJ, Sneden C, Lawler JE, Aprahamian A, Wiescher M, Langanke K, Martínez-Pinedo G, Thielemann FK (2019) Making the heaviest elements in the universe: a review of the rapid neutron capture process. arXiv e-prints arXiv:1901.01410
Cowperthwaite PS, Berger E (2015) A comprehensive study of detectability and contamination in deep rapid optical searches for gravitational wave counterparts. Astrophys J 814:25. https://doi.org/10.1088/0004-637x/814/1/25
Creminelli P, Vernizzi F (2017) Dark Energy after GW170817 and GRB170817A. Phys Rev Lett 119:251302. https://doi.org/10.1103/physrevlett.119.251302
Crowder SG, Namba R, Mandic V, Mukohyama S, Peloso M (2013) Measurement of parity violation in the early universe using gravitational-wave detectors. Phys Lett B 726:66–71. https://doi.org/10.1016/j.physletb.2013.08.077
Cuesta AJ, Niro V, Verde L (2016) Neutrino mass limits: robust information from the power spectrum of galaxy surveys. Phys Dark Universe 13:77–86. https://doi.org/10.1016/j.dark.2016.04.005
Curran PA, Van der Horst AJ, Wijers RA, Starling RL, Castro-Tirado AJ, Fynbo JPU, Gorosabel J, Järvinen AS, Malesani D, Rol E et al (2007) GRB 060206 and the quandary of achromatic breaks in afterglow light curves. Mon Not R Astron Soc Lett 381:L65–L69. https://doi.org/10.1111/j.1745-3933.2007.00368.x
Cutler C (1998) Angular resolution of the LISA gravitational wave detector. Phys Rev D 57:7089. https://doi.org/10.1103/physrevd.57.7089
Cutler C, Holz DE (2009) Ultrahigh precision cosmology from gravitational waves. Phys Rev D 80:104009. https://doi.org/10.1103/physrevd.80.104009
da Silva Schneider A, O’Connor E, Granqvist E, Betranhandy A, Couch SM (2020) Equation of state and progenitor dependence of stellar-mass black hole formation. Astrophys J 894:4. https://doi.org/10.3847/1538-4357/ab8308
Dai ZG, Lu T (1998) Gamma-ray burst afterglows and evolution of postburst fireballs with energy injection from strongly magnetic millisecond pulsars. Astron Astrophys 333:L87–L90
Dai ZG, Wang XY, Wu XF, Zhang B (2006) X-ray flares from postmerger millisecond pulsars. Science 311:1127–1129. https://doi.org/10.1126/science.1123606
Dalal N, Holz DE, Hughes SA, Jain B (2006) Short GRB and binary black hole standard sirens as a probe of dark energy. Phys Rev D 74:063006. https://doi.org/10.1103/physrevd.74.063006
Damour T, Polyakov AM (1994) The string dilation and a least coupling principle. Nucl Phys B 423:532–558. https://doi.org/10.1016/0550-3213(94)90143-0
Danby G, Gaillard JM, Goulianos K, Lederman LM, Mistry N, Schwartz M, Steinberger J (1962) Observation of high-energy neutrino reactions and the existence of two kinds of neutrinos. Phys Rev Lett 9:36. https://doi.org/10.1103/physrevlett.9.36
Davis R Jr, Harmer DS, Hoffman KC (1968) Search for neutrinos from the sun. Phys Rev Lett 20:1205. https://doi.org/10.1201/9780429502811-45
De S, Finstad D, Lattimer JM, Brown DA, Berger E, Biwer CM (2018) Tidal deformabilities and radii of neutron stars from the observation of GW170817. Phys Rev Lett 121:091102. https://doi.org/10.1103/physrevlett.121.091102
De Felice A, Tsujikawa S (2012) Conditions for the cosmological viability of the most general scalar-tensor theories and their applications to extended Galileon dark energy models. JCAP 2012:007. https://doi.org/10.1088/1475-7516/2012/02/007
de Naurois M (2019) GRB190829A: detection of VHE gamma-ray emission with H.E.S.S. Technical report, GSFC. https://gcn.gsfc.nasa.gov/gcn3/25566.gcn3
de Rham C (2014) Massive gravity. Living Rev Relativ 17:7. https://doi.org/10.12942/lrr-2014-7
Deffayet C, Menou K (2007) Probing gravity with spacetime sirens. Astrophys J Lett 668:L143. https://doi.org/10.1086/522931
Derishev E, Piran T (2019) The physical conditions of the afterglow implied by MAGIC’s sub-TeV observations of GRB 190114C. Astrophys J Lett 880:L27. https://doi.org/10.3847/2041-8213/ab2d8a
Desai S, Kahya EO, Woodard RP (2008) Reduced time delay for gravitational waves with dark matter emulators. Phys Rev D 77:124041. https://doi.org/10.1103/physrevd.77.124041
Dessart L, Ott CD, Burrows A, Rosswog S, Livne E (2008) Neutrino signatures and the neutrino-driven wind in binary neutron star mergers. Astrophys J 690:1681. https://doi.org/10.1088/0004-637x/690/2/1681
Dezalay JP, Barat C, Talon R, Sunyaev R, Terekhov O, Kuznetsov A (1991) Short cosmic events: a subset of classical GRBs? In: Paciesas W, Fishman GJ (eds) Gamma-ray bursts, American Institute of Physics, AIP conference proceedings, vol 265, pp 304–309. https://doi.org/10.1063/1.42799
Di Valentino E, Holz DE, Melchiorri A, Renzi F (2018) Cosmological impact of future constraints on \(H_0\) from gravitational-wave standard sirens. Phys Rev D 98:083523. https://doi.org/10.1103/physrevd.98.083523
Dichiara S, Guidorzi C, Frontera F, Amati L (2013) A search for pulsations in short gamma-ray bursts to constrain their progenitors. Astrophys J 777:132. https://doi.org/10.1088/0004-637x/777/2/132
Diehl T, Collaboration Dark Energy Survey et al (2012) The dark energy survey camera (DECam). Phys Procedia 37:1332–1340. https://doi.org/10.1016/j.phpro.2012.02.472
Dimopoulos S, Graham PW, Hogan JM, Kasevich MA, Rajendran S (2008) Atomic gravitational wave interferometric sensor. Phys Rev D 78:122002. https://doi.org/10.1103/physrevd.78.122002
Dominik M, Berti E, O’Shaughnessy R, Mandel I, Belczynski K, Fryer C, Holz DE, Bulik T, Pannarale F (2015) Double compact objects. III. Gravitational-wave detection rates. Astrophys J 806:263. https://doi.org/10.1088/0004-637x/806/2/263
Douglas MR, Nekrasov NA (2001) Noncommutative field theory. Rev Mod Phys 73:977. https://doi.org/10.1103/revmodphys.73.977
Drewes M (2013) The phenomenology of right handed neutrinos. Int J Mod Phys E 22:1330019. https://doi.org/10.1142/s0218301313300191
Duffell PC, Quataert E, Kasen D, Klion H (2018) Jet dynamics in compact object mergers: GW170817 likely had a successful jet. Astrophy J 866:3. https://doi.org/10.3847/1538-4357/aae084
Dyda S, Flanagan ÉÉ, Kamionkowski M (2012) Vacuum instability in Chern–Simons gravity. Phys Rev D 86:124031. https://doi.org/10.1103/physrevd.86.124031
Eardley DM, Lee DL, Lightman AP (1973) Gravitational-wave observations as a tool for testing relativistic gravity. Phys Rev D 8:3308. https://doi.org/10.1103/physrevd.8.3308
Einstein A (1905) Zur Elektrodynamik bewegter Körper. Ann Phys 322:891–921. https://doi.org/10.1002/andp.19053221004
Einstein A (1916) Näherungsweise Integration der Feldgleichungen der Gravitation. Sitzungsber Königl Preuß Akad Wiss. https://doi.org/10.1002/3527608958.ch7
Ellis J, Mavromatos NE, Nanopoulos DV (1999) Probing models of quantum space–time foam. arXiv e-prints arXiv:gr-qc/9909085
Ellis J, Harries N, Meregaglia A, Rubbia A, Sakharov AS (2008) Probes of Lorentz violation in neutrino propagation. Phys Rev D 78:033013. https://doi.org/10.1103/physrevd.78.033013
Ellis J, Mavromatos NE, Sakharov AS, Sarkisyan-Grinbaum EK (2019) Limits on neutrino Lorentz violation from multimessenger observations of TXS 0506+056. Phys Lett B 789:352–355. https://doi.org/10.1016/j.physletb.2018.11.062
Englert F, Brout R (1964) Broken symmetry and the mass of gauge vector mesons. Phys Rev Lett 13:321. https://doi.org/10.1103/physrevlett.13.321
Estevez D, Lieunard B, Marion F, Mours B, Rolland L, Verkindt D (2018) First tests of a Newtonian calibrator on an interferometric gravitational wave detector. Class Quantum Grav 35:235009. https://doi.org/10.1088/1361-6382/aae95f
Evans PA, Osborne JP, Kennea JA, Campana S, O’Brien PT, Tanvir NR, Racusin JL, Burrows DN, Cenko SB, Gehrels N (2015) Optimization of the Swift X-ray follow-up of Advanced LIGO and Virgo gravitational wave triggers in 2015–16. Mon Not R Astron Soc 455:1522–1537. https://doi.org/10.1093/mnras/stv2213
Evans PA, Kennea JA, Palmer DM, Bilicki M, Osborne JP, O’Brien PT, Tanvir NR, Lien AY, Barthelmy SD, Burrows DN et al (2016) Swift follow-up of gravitational wave triggers: results from the first aLIGO run and optimization for the future. Mon Not R Astron Soc 462:1591–1602. https://doi.org/10.1093/mnras/stw1746
Evans PA, Cenko SB, Kennea JA, Emery SW, Kuin NPM, Korobkin O, Wollaeger RT, Fryer CL, Madsen KK, Harrison FA et al (2017) Swift and NuSTAR observations of GW170817: detection of a blue kilonova. Science 358:1565–1570. https://doi.org/10.1126/science.aap9580
Ezquiaga JM, Zumalacárregui M (2017) Dark energy after GW170817: dead ends and the road ahead. Phys Rev Lett 119:251304. https://doi.org/10.1103/physrevlett.119.251304
Faber JA, Rasio FA (2012) Binary neutron star mergers. Living Rev Relativ 15:8. https://doi.org/10.12942/lrr-2012-8
Fan YZ, Zhang B, Proga D (2005) Linearly polarized X-ray flares following short gamma-ray bursts. Astrophys J Lett 635:L129. https://doi.org/10.1086/499489
Fan YZ, Wu XF, Wei DM (2013) Signature of gravitational wave radiation in afterglows of short gamma-ray bursts? Phys Rev D 88:067304. https://doi.org/10.1103/physrevd.88.067304
Fang K, Metzger BD (2017) High-energy neutrinos from millisecond magnetars formed from the merger of binary neutron stars. Astrophys J 849:153. https://doi.org/10.3847/1538-4357/aa8b6a
Feeney SM, Peiris HV, Williamson AR, Nissanke SM, Mortlock DJ, Alsing J, Scolnic D (2019) Prospects for resolving the Hubble constant tension with standard sirens. Phys Rev Lett 122:061105. https://doi.org/10.1103/physrevlett.122.061105
Fenimore EE, Epstein RI, Ho C (1993) The escape of 100 mev photons from cosmological gamma-ray bursts. Astron Astrophys Suppl 97:59–62
Ferdman RD, Freire PCC, Perera BBP, Pol N, Camilo F, Chatterjee S, Cordes JM, Crawford F, Hessels JWT, Kaspi VM et al (2020) Asymmetric mass ratios for bright double neutron-star mergers. Nature 583:211–214. https://doi.org/10.1038/s41586-020-2439-x
Fernández R, Metzger BD (2016) Electromagnetic signatures of neutron star mergers in the advanced LIGO era. Annu Rev Nucl Part Sci 66:23–45. https://doi.org/10.1146/annurev-nucl-102115-044819
Fernández R, Tchekhovskoy A, Quataert E, Foucart F, Kasen D (2018) Long-term GRMHD simulations of neutron star merger accretion discs: implications for electromagnetic counterparts. Mon Not R Astron Soc 482:3373–3393. https://doi.org/10.1093/mnras/sty2932
Fields BD, Molaro P, Sarkar S (2014) Big-bang nucleosynthesis. arXiv e-prints arXiv:1412.1408
Finn LS, Chernoff DF (1993) Observing binary inspiral in gravitational radiation: one interferometer. Phys Rev D 47:2198. https://doi.org/10.1103/physrevd.47.2198
Finn LS, Sutton PJ (2002) Bounding the mass of the graviton using binary pulsar observations. Phys Rev D 65:044022. https://doi.org/10.1103/physrevd.65.044022
Fong WF, Berger E (2013) The locations of short gamma-ray bursts as evidence for compact object binary progenitors. Astrophys J 776:18. https://doi.org/10.1088/0004-637x/776/1/18
Fong WF, Berger E, Chornock R, Margutti R, Levan AJ, Tanvir NR, Tunnicliffe RL, Czekala I, Fox DB, Perley DA, Cenko SB, Zauderer BA, Laskar T, Persson SE, Monson AJ, Kelson DD, Birk C, Murphy D, Servillat M, Anglada G (2013) Demographics of the galaxies hosting short-duration gamma-ray bursts. Astrophys J 769:56. https://doi.org/10.1088/0004-637X/769/1/56
Fong WF, Berger E, Margutti R, Zauderer BA (2015) A decade of short-duration gamma-ray burst broadband afterglows: energetics, circumburst densities, and jet opening angles. Astrophys J 815:102. https://doi.org/10.1088/0004-637x/815/2/102
Fong WF, Metzger BD, Berger E, Özel F (2016) Radio constraints on long-lived magnetar remnants in short gamma-ray bursts. Astrophys J 831:141. https://doi.org/10.3847/0004-637x/831/2/141
Fong WF, Berger E, Blanchard PK, Margutti R, Cowperthwaite PS, Chornock R, Alexander KD, Metzger BD, Villar VA, Nicholl M et al (2017) The electromagnetic counterpart of the binary neutron star merger LIGO/Virgo GW170817. VIII. A comparison to cosmological short-duration gamma-ray bursts. Astrophys J Lett 848:L23. https://doi.org/10.3847/2041-8213/aa9018
Fong W, Blanchard PK, Alexander KD, Strader J, Margutti R, Hajela A, Villar VA, Wu Y, Ye CS, Berger E, Chornock R, Coppejans D, Cowperthwaite PS, Eftekhari T, Giannios D, Guidorzi C, Kathirgamaraju A, Laskar T, Macfadyen A, Metzger BD, Nicholl M, Paterson K, Terreran G, Sand DJ, Sironi L, Williams PKG, Xie X, Zrake J (2019) The optical afterglow of GW170817: an off-axis structured jet and deep constraints on a globular cluster origin. Astrophys J Lett 883:L1. https://doi.org/10.3847/2041-8213/ab3d9e. arXiv:1908.08046
Foucart F (2012) Black-hole-neutron-star mergers: disk mass predictions. Phys Rev D 86:124007. https://doi.org/10.1103/physrevd.86.124007
Foucart F (2020) A brief overview of black hole-neutron star mergers. Front Astron Space Sci 7:46. https://doi.org/10.3389/fspas.2020.00046. arXiv:2006.10570
Foucart F, Deaton MB, Duez MD, O’Connor E, Ott CD, Haas R, Kidder LE, Pfeiffer HP, Scheel MA, Szilagyi B (2014) Neutron star-black hole mergers with a nuclear equation of state and neutrino cooling: dependence in the binary parameters. Phys Rev D 90:024026. https://doi.org/10.1103/physrevd.90.024026
Foucart F, Haas R, Duez MD, O’Connor E, Ott CD, Roberts L, Kidder LE, Lippuner J, Pfeiffer HP, Scheel MA (2016) Low mass binary neutron star mergers: gravitational waves and neutrino emission. Phys Rev D 93:044019. https://doi.org/10.1103/physrevd.93.044019
Foucart F, Hinderer T, Nissanke S (2018) Remnant baryon mass in neutron star-black hole mergers: predictions for binary neutron star mimickers and rapidly spinning black holes. Phys Rev D 98:081501. https://doi.org/10.1103/PhysRevD.98.081501
Fox DW, Yost S, Kulkarni SR, Torii K, Kato T, Yamaoka H, Sako M, Harrison FA, Sari R, Price PA et al (2003) Early optical emission from the \(\gamma \)-ray burst of 4 October 2002. Nature 422:284–286. https://doi.org/10.1038/nature01504
Fraija N, Dichiara S, do ES Pedreira ACC, Galvan-Gamez A, Becerra RL, Duran RB, Zhang BB (2019) Analysis and modeling of the multi-wavelength observations of the luminous GRB 190114C. Astrophys J Lett 879:L26. https://doi.org/10.3847/2041-8213/ab2ae4
Frail DA, Kulkarni SR, Nicastro L, Feroci M, Taylor GB (1997) The radio afterglow from the \(\gamma \)-ray burst of 8 May 1997. Nature 389:261–263. https://doi.org/10.1038/38451
Frail DA, Kulkarni SR, Sari R, Djorgovski SG, Bloom JS, Galama TJ, Reichart DE, Berger E, Harrison FA, Price PA et al (2001) Beaming in gamma-ray bursts: evidence for a standard energy reservoir. Astrophys J Lett 562:L55. https://doi.org/10.1086/338119
Frederiks DD, Palshin VD, Aptekar RL, Golenetskii SV, Cline TL, Mazets EP (2007) On the possibility of identifying the short hard burst GRB 051103 with a giant flare from a soft gamma repeater in the M81 group of galaxies. Astron Lett 33:19–24. https://doi.org/10.1134/S1063773707010021
Freedman WL, Madore BF (2010) The Hubble constant. Annu Rev Astron Astrophys 48:673–710. https://doi.org/10.1146/annurev-astro-082708-101829
Freiburghaus C, Rosswog S, Thielemann FK (1999) R-process in neutron star mergers. Astrophys J Lett 525:L121. https://doi.org/10.1086/312343
Friedmann A (1922) Über die Krümmung des Raumes. Z Physik 10:377–386. https://doi.org/10.1007/BF01332580
Fruchter AS, Thorsett SE, Metzger MR, Sahu KC, Petro L, Livio M, Ferguson H, Pian E, Hogg DW, Galama T et al (1999) Hubble Space Telescope and Palomar imaging of GRB 990123: implications for the nature of gamma-ray bursts and their hosts. Astrophys J Lett 519:L13. https://doi.org/10.1086/312094
Fruchter AS, Levan AJ, Strolger L, Vreeswijk PM, Thorsett SE, Bersier D, Burud I, Cerón JMC, Castro-Tirado AJ, Conselice C et al (2006) Long \(\gamma \)-ray bursts and core-collapse supernovae have different environments. Nature 441:463. https://doi.org/10.1038/nature04787
Fukuda Y, others, (Super-Kamiokande Collaboration) (1998) Evidence for oscillation of atmospheric neutrinos. Phys Rev Lett 81:1562. https://doi.org/10.1103/PhysRevLett.81.1562
Fukugita M, Yanagida T (1986) Barygenesis without grand unification. Phys Lett B 174:45–47. https://doi.org/10.1016/0370-2693(86)91126-3
Gair JR, Vallisneri M, Larson SL, Baker JG (2013) Testing general relativity with low-frequency, space-based gravitational-wave detectors. Living Rev Relativ 16:7. https://doi.org/10.12942/lrr-2013-7
Galama TJ, Vreeswijk PM, Van Paradijs J, Kouveliotou C, Augusteijn T, Böhnhardt H, Brewer JP, Doublier V, Gonzalez JF, Leibundgut B et al (1998) An unusual supernova in the error box of the \(\gamma \)-ray burst of 25 April 1998. Nature 395:670–672. https://doi.org/10.1038/27150
Gambini R, Pullin J (1999) Nonstandard optics from quantum space–time. Phys Rev D 59:124021. https://doi.org/10.1103/physrevd.59.124021
Gao S, Wald RM (2000) Theorems on gravitational time delay and related issues. Class Quantum Grav 17:4999. https://doi.org/10.1088/0264-9381/17/24/305
Gao WH, Fan YZ (2006) Short-living supermassive magnetar model for the early X-ray flares following short GRBs. Chin J Astron Astrophys 6:513. https://doi.org/10.1088/1009-9271/6/5/01
Gao H, Ding X, Wu XF, Zhang B, Dai ZG (2013) Bright broadband afterglows of gravitational wave bursts from mergers of binary neutron stars. Astrophys J 771:86. https://doi.org/10.1088/0004-637X/771/2/86
Gao H, Wu XF, Mészáros P (2015) Cosmic transients test Einstein’s equivalence principle out to GeV energies. Astrophys J 810:121. https://doi.org/10.1088/0004-637x/810/2/121
Gao H, Ai SK, Cao ZJ, Zhang B, Zhu ZY, Li A, Zhang NB, Bauswein A (2020) Relation between gravitational mass and baryonic mass for non-rotating and rapidly rotating neutron stars. Front Phys 15:24603. https://doi.org/10.1007/s11467-019-0945-9. arXiv:1905.03784
Garwin RL, Lederman LM, Weinrich M (1957) Observations of the failure of conservation of parity and charge conjugation in meson decays: the magnetic moment of the free muon. Phys Rev 105:1415. https://doi.org/10.1103/physrev.105.1415
Gehrels N, Sarazin CL, O’Brien PT, Zhang B, Barbier L, Barthelmy SD, Blustin A, Burrows DN, Cannizzo J, Cummings JR et al (2005) A short \(\gamma \)-ray burst apparently associated with an elliptical galaxy at redshift \(z= 0.225\). Nature 437:851–854. https://doi.org/10.1038/nature04142
Gehrels N, Spergel D, SDT W (2015) Wide-field infraRed survey telescope (WFIRST) mission and synergies with LISA and LIGO-Virgo. J Phys Conf Ser 610:012007. https://doi.org/10.1088/1742-6596/610/1/012007
Gehrels N, Cannizzo JK, Kanner J, Kasliwal MM, Nissanke S, Singer LP (2016) Galaxy strategy for LIGO-Virgo gravitational wave counterpart searches. Astrophys J 820:136. https://doi.org/10.3847/0004-637x/820/2/136
Gendreau KC, Arzoumanian Z, Okajima T (2012) The Neutron star Interior Composition ExploreR (NICER): an Explorer mission of opportunity for soft X-ray timing spectroscopy. In: Space telescopes and instrumentation 2012: ultraviolet to gamma ray, Proc. SPIE, vol 8443, p 844313. https://doi.org/10.1117/12.926396
Geng JJ, Zhang B, Kölligan A, Kuiper R, Huang YF (2019) Propagation of a short GRB jet in the ejecta: jet launching delay time, jet structure, and GW170817/GRB 170817A. Astrophys J Lett 877:L40. https://doi.org/10.3847/2041-8213/ab224b
Ghirlanda G, Salafia OS, Pescalli A, Ghisellini G, Salvaterra R, Chassande-Mottin E, Colpi M, Nappo F, D’Avanzo P, Melandri A et al (2016) Short gamma-ray bursts at the dawn of the gravitational wave era. Astron Astrophys 594:A84. https://doi.org/10.1051/0004-6361/201628993
Ghirlanda G, Nappo F, Ghisellini G, Melandri A, Marcarini G, Nava L, Salafia OS, Campana S, Salvaterra R (2018) Bulk Lorentz factors of gamma-ray bursts. Astron Astrophys 609:A112. https://doi.org/10.1051/0004-6361/201731598
Ghirlanda G, Salafia OS, Paragi Z, Giroletti M, Yang J, Marcote B, Blanchard J, Agudo I, An T, Bernardini MG et al (2019) Compact radio emission indicates a structured jet was produced by a binary neutron star merger. Science 363:968–971. https://doi.org/10.1126/science.aau8815
Giacomazzo B, Perna R (2013) Formation of stable magnetars from binary neutron star mergers. Astrophys J Lett 771:L26. https://doi.org/10.1088/2041-8205/771/2/l26
Giacomazzo B, Zrake J, Duffell PC, MacFadyen AI, Perna R (2015) Producing magnetar magnetic fields in the merger of binary neutron stars. Astrophys J 809:39. https://doi.org/10.1088/0004-637x/809/1/39
Gill R, Granot J, De Colle F, Urrutia G (2019) Numerical simulations of an initially top-hat jet and the afterglow of GW170817/GRB170817a. Astrophys J 883:15. https://doi.org/10.3847/1538-4357/ab3577
Gleyzes J, Langlois D, Piazza F, Vernizzi F (2015) Exploring gravitational theories beyond Horndeski. JCAP 2015:018. https://doi.org/10.1088/1475-7516/2015/02/018
Goldstein A, Burns E, Hamburg R, Connaughton V, Veres P, Briggs MS, Hui CM, The GBM-LIGO Collaboration (2016) Updates to the Fermi-GBM short GRB targeted offline search in preparation for LIGO’s Second Observing Run. ArXiv e-prints arXiv:1612.02395
Goldstein A, Veres P, Burns E, Briggs MS, Hamburg R, Kocevski D, Wilson-Hodge CA, Preece RD, Poolakkil S, Roberts OJ, Hui CM, Connaughton V, Racusin J, von Kienlin A, Dal Canton T, Christensen N, Littenberg T, Siellez K, Blackburn L, Broida J, Bissaldi E, Cleveland WH, Gibby MH, Giles MM, Kippen RM, McBreen S, McEnery J, Meegan CA, Paciesas WS, Stanbro M (2017a) An ordinary short gamma-ray burst with extraordinary implications: Fermi-GBM detection of GRB 170817A. Astrophys J Lett 848:L14. https://doi.org/10.3847/2041-8213/aa8f41
Goldstein A, Veres P, Burns E, Briggs MS, Hamburg R, Kocevski D, Wilson-Hodge CA, Preece RD, Poolakkil S, Roberts OJ et al (2017b) An ordinary short gamma-ray burst with extraordinary implications: Fermi-GBM detection of GRB 170817A. Astrophys J Lett 848:L14
Gompertz BP, O’Brien PT, Wynn GA (2013) Magnetar powered GRBs: explaining the extended emission and X-ray plateau of short GRB light curves. Mon Not R Astron Soc 438:240–250. https://doi.org/10.1093/mnras/stt2165
Gompertz BP, Levan AJ, Tanvir NR, Hjorth J, Covino S, Evans PA, Fruchter AS, González-Fernández C, Jin ZP, Lyman JD et al (2018) The diversity of kilonova emission in short gamma-ray bursts. Astrophys J 860:62. https://doi.org/10.3847/1538-4357/aac206
Goobar A, Amanullah R, Kulkarni SR, Nugent PE, Johansson J, Steidel C, Law D, Mörtsell E, Quimby R, Blagorodnova N et al (2017) iPTF16geu: a multiply imaged, gravitationally lensed type Ia supernova. Science 356:291–295. https://doi.org/10.1126/science.aal2729
Goodman J (1986) Are gamma-ray bursts optically thick? Astrophys J Lett 308:L47–L50. https://doi.org/10.1086/184741
Goodman J (1997) Radio scintillation of gamma-ray-burst afterglows. New Astron 2:449–460. https://doi.org/10.1016/S1384-1076(97)00031-6
Gorski KM, Hivon E, Banday AJ, Wandelt BD, Hansen FK, Reinecke M, Bartelmann M (2005) HEALPix: a framework for high-resolution discretization and fast analysis of data distributed on the sphere. Astrophys J 622:759. https://doi.org/10.1086/427976
Gottlieb O, Nakar E, Piran T, Hotokezaka K (2018) A cocoon shock breakout as the origin of the \(\gamma \)-ray emission in GW170817. Mon Not R Astron Soc 479:588–600. https://doi.org/10.1093/mnras/sty1462
Graham PW, Hogan JM, Kasevich MA, Rajendran S, Romani RW (2017) Mid-band gravitational wave detection with precision atomic sensors. arXiv e-prints arXiv:1711.02225
Granot J, Kumar P (2003) Constraining the structure of gamma-ray burst jets through the afterglow light curves. Astrophys J 591:1086. https://doi.org/10.1086/375489
Granot J, Guetta D, Gill R (2017) Lessons from the short GRB 170817A: the first gravitational-wave detection of a binary neutron star merger. Astrophys J Lett 850:L24. https://doi.org/10.3847/2041-8213/aa991d
Grove JE, Cheung CC, Kerr M, Mitchell LJ, Phlips BF, Woolf RS, Wulf E, Wilson-Hodge CA, Kocevski D, Briggs MS et al (2019) Glowbug, a gamma-ray telescope for bursts and other transients. https://pcos.gsfc.nasa.gov/physpag/meetings/head2019/. PCOS high energy astrophysics division (HEAD) 17th divisional meeting
Guidorzi C, Margutti R, Brout D, Scolnic D, Fong W, Alexander KD, Cowperthwaite PS, Annis J, Berger E, Blanchard PK, Chornock R, Coppejans DL, Eftekhari T, Frieman JA, Huterer D, Nicholl M, Soares-Santos M, Terreran G, Villar VA, Williams PKG (2017) Improved constraints on H\(_{0}\) from a combined analysis of gravitational-wave and electromagnetic emission from GW170817. Astrophys J Lett 851:L36. https://doi.org/10.3847/2041-8213/aaa009
Guiriec S, Briggs MS, Connaugthon V, Kara E, Daigne F, Kouveliotou C, Van der Horst AJ, Paciesas W, Meegan CA, Bhat PN et al (2010) Time-resolved spectroscopy of the three brightest and hardest short gamma-ray bursts observed with the Fermi gamma-ray burst monitor. Astrophys J 725:225. https://doi.org/10.1088/0004-637x/725/1/225
Guiriec S, Connaughton V, Briggs MS, Burgess M, Ryde F, Daigne F, Mészáros P, Goldstein A, McEnery J, Omodei N et al (2011) Detection of a thermal spectral component in the prompt emission of GRB 100724B. Astrophys J Lett 727:L33. https://doi.org/10.1088/2041-8205/727/2/l33
Guiriec S, Kouveliotou C, Hartmann DH, Granot J, Asano K, Mészáros P, Gill R, Gehrels N, McEnery J (2016) A unified model for GRB prompt emission from optical to \(\gamma \)-rays; exploring GRBs as standard candles. Astrophys J Lett 831:L8. https://doi.org/10.3847/2041-8205/831/1/L8
Gupta S, Desai S (2018) Limit on graviton mass using stacked galaxy cluster catalogs from SPT-SZ, Planck-SZ. and SDSS-redMaPPer. Ann Phys 399:85–92. https://doi.org/10.1016/j.aop.2018.09.017
Guralnik GS, Hagen CR, Kibble TW (1964) Global conservation laws and massless particles. Phys Rev Lett 13:585. https://doi.org/10.1103/physrevlett.13.585
Guth AH (1981) Inflationary universe: a possible solution to the horizon and flatness problems. Phys Rev D 23:347–356. https://doi.org/10.1103/PhysRevD.23.347
Gyulassy M, McLerran L (2005) New forms of QCD matter discovered at RHIC. Nucl Phys A 750:30–63. https://doi.org/10.1016/j.nuclphysa.2004.10.034
Haggard D, Nynka M, Ruan JJ, Kalogera V, Cenko SB, Evans P, Kennea JA (2017) A deep Chandra X-ray study of neutron star coalescence GW170817. Astrophys J Lett 848:L25
Hajela A, Margutti R, Alexander KD, Kathirgamaraju A, Baldeschi A, Guidorzi C, Giannios D, Fong W, Wu Y, MacFadyen A et al (2019a) Two years of nonthermal emission from the binary neutron star merger GW170817: rapid fading of the jet afterglow and first constraints on the kilonova fastest ejecta. Astrophys J Lett 886:L17. https://doi.org/10.3847/2041-8213/ab5226
Hajela A et al (2019b) Further Chandra observations of GW170817 581–583 days since merger. Technical report, GSFC. https://gcn.gsfc.nasa.gov/gcn/gcn3/24000.gcn3
Halzen F, Hooper D (2002) High-energy neutrino astronomy: the cosmic ray connection. Rep Progr Phys 65:1025. https://doi.org/10.1088/0034-4885/65/7/201
Hansen BMS, Lyutikov M (2001) Radio and X-ray signatures of merging neutron stars. Mon Not R Astron Soc 322:695. https://doi.org/10.1046/j.1365-8711.2001.04103.x
Harrison FA, Bloom JS, Frail DA, Sari R, Kulkarni SR, Djorgovski SG, Axelrod T, Mould J, Schmidt BP, Wieringa MH et al (1999) Optical and radio observations of the afterglow from GRB 990510: evidence for a jet. Astrophys J Lett 523:L121. https://doi.org/10.1086/312282
Hascoët R, Daigne F, Mochkovitch R, Vennin V (2012) Do Fermi Large Area Telescope observations imply very large Lorentz factors in gamma-ray burst outflows? Mon Not R Astron Soc 421:525–545. https://doi.org/10.1111/j.1365-2966.2011.20332.x
Heavens A, Jimenez R, Verde L (2014) Standard rulers, candles, and clocks from the low-redshift Universe. Phys Rev Lett 113:241302. https://doi.org/10.1103/physrevlett.113.241302
Hess VF (1912) Über Beobachtungen der durchdringenden Strahlung bei sieben Freiballonfahrten. Phys Z 13:1084–1091
Higgs PW (1964) Broken symmetries and the masses of gauge bosons. Phys Rev Lett 13:508. https://doi.org/10.1103/physrevlett.13.508
Hinderer T, Nissanke S, Foucart F, Hotokezaka K, Vincent T, Kasliwal M, Schmidt P, Williamson AR, Nichols DA, Duez MD et al (2019) Distinguishing the nature of comparable-mass neutron star binary systems with multimessenger observations: GW170817 case study. Phys Rev D 100:063021. https://doi.org/10.1103/physrevd.100.063021
Hirata K, Kajita T, Koshiba M, Nakahata M, Oyama Y, Sato N, Suzuki A, Takita M, Totsuka Y, Kifune T et al (1987) Observation of a neutrino burst from the supernova SN1987A. Phys Rev Lett 58:1490. https://doi.org/10.1016/0375-9474(88)90844-5
Hopkins AM, Beacom JF (2006) On the normalization of the cosmic star formation history. Astrophys J 651:142. https://doi.org/10.1086/506610
Horowitz CJ, Piekarewicz J (2001) Neutron star structure and the neutron radius of \(^{208}\)Pb. Phys Rev Lett 86:5647. https://doi.org/10.1103/physrevlett.86.5647
Horowitz CJ, Kumar KS, Michaels R (2014) Electroweak measurements of neutron densities in CREX and PREX at JLab, USA. Eur Phys J A 50:48. https://doi.org/10.1140/epja/i2014-14048-3
Hotokezaka K, Piran T (2015) Mass ejection from neutron star mergers: different components and expected radio signals. Mon Not R Astron Soc 450:1430–1440. https://doi.org/10.1093/mnras/stv620
Hotokezaka K, Kiuchi K, Kyutoku K, Okawa H, Yi Sekiguchi, Shibata M, Taniguchi K (2013) Mass ejection from the merger of binary neutron stars. Phys Rev D 87:024001. https://doi.org/10.1103/physrevd.87.024001
Hotokezaka K, Nissanke S, Hallinan G, Lazio TJW, Nakar E, Piran T (2016a) Radio counterparts of compact binary mergers detectable in gravitational waves: a simulation for an optimized survey. Astrophys J 831:190. https://doi.org/10.3847/0004-637X/831/2/190
Hotokezaka K, Wanajo S, Tanaka M, Bamba A, Terada Y, Piran T (2016b) Radioactive decay products in neutron star merger ejecta: heating efficiency and \(\gamma \)-ray emission. Mon Not R Astron Soc 459:35–43. https://doi.org/10.1093/mnras/stw404
Hotokezaka K, Beniamini P, Piran T (2018) Neutron star mergers as sites of r-process nucleosynthesis and short gamma-ray bursts. Int J Mod Phys D 27:1842005. https://doi.org/10.1142/S0218271818420051. arXiv:1801.01141
Hotokezaka K, Nakar E, Gottlieb O, Nissanke S, Masuda K, Hallinan G, Mooley KP, Deller AT (2019) A Hubble constant measurement from superluminal motion of the jet in GW170817. Nat Astron 3:940–944. https://doi.org/10.1038/s41550-019-0820-1
Howell EJ, Ackley K, Rowlinson A, Coward D (2019) Joint gravitational wave-gamma-ray burst detection rates in the aftermath of GW170817. Mon Not R Astron Soc 485:1435–1447. https://doi.org/10.1093/mnras/stz455
Hubble EP (1925) NGC 6822, a remote stellar system. Astrophys J. https://doi.org/10.1086/142943
Hubble E (1929a) A relation between distance and radial velocity among extra-galactic nebulae. Proc Natl Acad Sci USA 15:168–173. https://doi.org/10.1073/pnas.15.3.168
Hubble EP (1929b) A spiral nebula as a stellar system, Messier 31. Astrophys J. https://doi.org/10.1086/143167
Hulse RA, Taylor JH (1975) Discovery of a pulsar in a binary system. Astrophys J Lett 195:L51–L53. https://doi.org/10.1086/181708
Hurley K, Cline T, Mazets E, Barthelmy S, Butterworth P, Marshall F, Palmer D, Aptekar R, Golenetskii S, Il’Inskii V et al (1999) A giant periodic flare from the soft \(\gamma \)-ray repeater SGR1900+14. Nature 397:41–43. https://doi.org/10.1038/16199
Hurley K, Boggs SE, Smith DM, Duncan RC, Lin R, Zoglauer A, Krucker S, Hurford G, Hudson H, Wigger C et al (2005) An exceptionally bright flare from SGR 1806–20 and the origins of short-duration \(\gamma \)-ray bursts. Nature 434:1098–1103. https://doi.org/10.1038/nature03519
Hurley K, Golenetskii S, Aptekar R, Mazets E, Pal’Shin V, Frederiks D, Mitrofanov IG, Golovin D, Kozyrev A, Litvak M, Sanin AB, Boynton W, Fellows C, Harshman K, Starr R, von Kienlin A, Rau A, Yamaoka K, Ohno M, Fukazawa Y, Takahashi T, Tashiro M, Terada Y, Murakami T, Makishima K, Barthelmy S, Cummings J, Gehrels N, Krimm H, Cline T, Goldsten J, Del Monte E, Feroci M, Marisaldi M, Briggs M, Connaughton V, Meegan C, Smith DM, Wigger C, Hajdas W (2011) The third interplanetary network. In: McEnery JE, Racusin JL, Gehrels N (eds) Gamma ray bursts 2010. AIP conference series, vol 1358. American Institute of Physics, pp 385–388. https://doi.org/10.1063/1.3621810
Ioka K, Hotokezaka K, Piran T (2016) Are ultra-long gamma-ray bursts caused by blue supergiant collapsars, newborn magnetars, or white dwarf tidal disruption events? Astrophys J 833:110. https://doi.org/10.3847/1538-4357/833/1/110
Isi M, Pitkin M, Weinstein AJ (2017) Probing dynamical gravity with the polarization of continuous gravitational waves. Phys Rev D 96:042001. https://doi.org/10.1103/physrevd.96.042001
Ivezić Ž, Kahn SM, Tyson JA, Abel B, Acosta E, Allsman R, Alonso D, AlSayyad Y, Anderson SF, Andrew J et al (2019) LSST: from science drivers to reference design and anticipated data products. Astrophys J 873:111. https://doi.org/10.3847/1538-4357/ab042c
Iyer B, Souradeep T, Unnikrishnan CS, Dhurandhar S, Raja S, Sengupta A (2011) LIGO-India, proposal of the consortium for Indian initiative in gravitational-wave observations (IndIGO). Technical report, LIGO. https://dcc.ligo.org/LIGOM1100296/public
Jacob U, Piran T (2008) Lorentz-violation-induced arrival delays of cosmological particles. JCAP 2008:031. https://doi.org/10.1088/1475-7516/2008/01/031
Jacobson T, Mattingly D (2004) Einstein-aether waves. Phys Rev D 70:024003. https://doi.org/10.1103/physrevd.70.024003
Jacobson T, Liberati S, Mattingly D (2006) Lorentz violation at high energy: concepts, phenomena, and astrophysical constraints. Ann Phys 321:150–196. https://doi.org/10.1016/j.aop.2005.06.004
Ji AP, Frebel A, Chiti A, Simon JD (2016) R-process enrichment from a single event in an ancient dwarf galaxy. Nature 531:610. https://doi.org/10.1038/nature17425
Jiménez JB, Piazza F, Velten H (2016) Evading the Vainshtein mechanism with anomalous gravitational wave speed: constraints on modified gravity from binary pulsars. Phys Rev Lett 116:061101. https://doi.org/10.1103/physrevlett.116.061101
Jin ZP, Hotokezaka K, Li X, Tanaka M, D’Avanzo P, Fan YZ, Covino S, Wei DM, Piran T (2016) The Macronova in GRB 050709 and the GRB-macronova connection. Nat Commun 7:12898. https://doi.org/10.1038/ncomms12898
Johnson JA (2019) Populating the periodic table: nucleosynthesis of the elements. Science 363:474–478. https://doi.org/10.1126/science.aau9540
Johnson JA, Zasowski G, Weinberg D, Ting YS, Sobeck J, Smith V, Silva Aguirre V, Nataf D, Lucatello S, Kollmeier J, Hekker S, Cunha K, Chiappini C, Carlberg J, Bird J, Basu S, Anguiano B (2019) The origin of elements across cosmic time: Astro2020 science white paper. arXiv e-prints arXiv:1907.04388
Just O, Bauswein A, Pulpillo RA, Goriely S, Janka HT (2015) Comprehensive nucleosynthesis analysis for ejecta of compact binary mergers. Mon Not R Astron Soc 448:541–567. https://doi.org/10.1093/mnras/stv009
Just O, Obergaulinger M, Janka HT, Bauswein A, Schwarz N (2016) Neutron-star merger ejecta as obstacles to neutrino-powered jets of gamma-ray bursts. Astrophys J Lett 816:L30. https://doi.org/10.3847/2041-8205/816/2/l30
Kahya EO (2011) A useful guide for gravitational wave observers to test modified gravity models. Phys Lett B 701:291–295. https://doi.org/10.1016/j.physletb.2011.05.073
Kahya EO, Desai S (2016) Constraints on frequency-dependent violations of Shapiro delay from GW150914. Phys Lett B 756:265–267. https://doi.org/10.1016/j.physletb.2016.03.033
Kalogera V, Belczynski K, Kim C, O’Shaughnessy R, Willems B (2007) Formation of double compact objects. Phys Rep 442:75–108. https://doi.org/10.1016/j.physrep.2007.02.008
Kanner J, Camp J, Racusin J, Gehrels N, White D (2012) Seeking counterparts to Advanced LIGO/Virgo transients with Swift. Astrophys J 759:22. https://doi.org/10.1088/0004-637x/759/1/22
Karki S, Tuyenbayev D, Kandhasamy S, Abbott BP, Abbott TD, Anders EH, Berliner J, Betzwieser J, Cahillane C, Canete L et al (2016) The Advanced LIGO photon calibrators. Rev Sci Instrum 87:114503. https://doi.org/10.1063/1.4967303
Kasen D, Badnell NR, Barnes J (2013) Opacities and spectra of the r-process ejecta from neutron star mergers. Astrophys J 774:25. https://doi.org/10.1088/0004-637X/774/1/25
Kasen D, Metzger B, Barnes J, Quataert E, Ramirez-Ruiz E (2017) Origin of the heavy elements in binary neutron-star mergers from a gravitational-wave event. Nature 551:80. https://doi.org/10.1038/nature24453
Kasliwal MM, Nakar E, Singer LP, Kaplan DL, Cook DO, Van Sistine A, Lau RM, Fremling C, Gottlieb O, Jencson JE et al (2017) Illuminating gravitational waves: a concordant picture of photons from a neutron star merger. Science 358:1559–1565. https://doi.org/10.1126/science.aap9455
Kasliwal MM, Kasen D, Lau RM, Perley DA, Rosswog S, Ofek EO, Hotokezaka K, Chary RR, Sollerman J, Goobar A et al (2019) Spitzer mid-infrared detections of neutron star merger GW170817 suggests synthesis of the heaviest elements. Mon Not R Astron Soc Lett. https://doi.org/10.1093/mnrasl/slz007
Kathirgamaraju A, Tchekhovskoy A, Giannios D, Barniol Duran R (2019) EM counterparts of structured jets from 3D GRMHD simulations. Mon Not R Astron Soc Lett 484:L98–L103. https://doi.org/10.1093/mnrasl/slz012
Katz JI, Canel LM (1996) The long and the short of gamma-ray bursts. Astrophys J 471:915. https://doi.org/10.1086/178018
Kawaguchi K, Shibata M, Tanaka M (2020) Diversity of kilonova light curves. Astrophys J 889:171. https://doi.org/10.3847/1538-4357/ab61f6. arXiv:1908.05815
Kawamura S, Ando M, Seto N, Sato S, Nakamura T, Tsubono K, Kanda N, Tanaka T, Yokoyama J, Funaki I et al (2011) The Japanese space gravitational wave antenna: DECIGO. Class Quantum Grav 28:094011. https://doi.org/10.1088/0264-9381/28/9/094011
Keppel D, Ajith P (2010) Constraining the mass of the graviton using coalescing black-hole binaries. Phys Rev D 82:122001. https://doi.org/10.1103/physrevd.82.122001
Kimura SS, Murase K, Mészáros P, Kiuchi K (2017) High-energy neutrino emission from short gamma-ray bursts: prospects for coincident detection with gravitational waves. Astrophys J Lett 848:L4. https://doi.org/10.3847/2041-8213/aa8d14
Kimura SS, Murase K, Bartos I, Ioka K, Heng IS, Mészáros P (2018) Transejecta high-energy neutrino emission from binary neutron star mergers. Phys Rev D 98:043020. https://doi.org/10.1103/physrevd.98.043020
Kisaka S, Ioka K (2015) Long-lasting black hole jets in short gamma-ray bursts. Astrophys J Lett 804:L16. https://doi.org/10.1088/2041-8205/804/1/L16
Kiuchi K, Kyutoku K, Sekiguchi Y, Shibata M, Wada T (2014) High resolution numerical relativity simulations for the merger of binary magnetized neutron stars. Phys Rev D 90:041502. https://doi.org/10.1103/physrevd.90.041502
Kiuchi K, Sekiguchi Y, Kyutoku K, Shibata M, Taniguchi K, Wada T (2015) High resolution magnetohydrodynamic simulation of black hole-neutron star merger: mass ejection and short gamma ray bursts. Phys Rev D 92:064034. https://doi.org/10.1103/physrevd.92.064034
Kiuchi K, Kyutoku K, Shibata M, Taniguchi K (2019) Revisiting the lower bound on tidal deformability derived by AT 2017gfo. Astrophys J Lett 876:L31. https://doi.org/10.3847/2041-8213/ab1e45
Klebesadel RW, Strong IB, Olson RA (1973) Observations of gamma-ray bursts of cosmic origin. Astrophys J Lett 182:L85. https://doi.org/10.1086/181225
Knox L (2006) Precision measurement of the mean curvature. Phys Rev D 73:023503. https://doi.org/10.1103/physrevd.73.023503
Kobayashi S, Zhang B (2007) The onset of gamma-ray burst afterglow. Astrophys J 655:973. https://doi.org/10.1086/510203
Kocevski D, Butler N, Bloom JS (2007) Pulse width evolution of late-time X-ray flares in gamma-ray bursts. Astrophys J 667:1024. https://doi.org/10.1086/520041
Kocevski D, Burns E, Goldstein A, Dal Canton T, Briggs MS, Blackburn L, Veres P, Hui CM, Hamburg R, Roberts OJ, Wilson-Hodge CA, Connaughton V, Racusin J, Littenberg T, von Kienlin A, Bissaldi E (2018) Analysis of sub-threshold short gamma-ray bursts in Fermi GBM data. Astrophys J 862:152. https://doi.org/10.3847/1538-4357/aacb7b
Köppel S, Bovard L, Rezzolla L (2019) A general-relativistic determination of the threshold mass to prompt collapse in binary neutron star mergers. Astrophys J Lett 872:L16. https://doi.org/10.3847/2041-8213/ab0210
Korobkin O, Hungerford AM, Fryer CL, Mumpower MR, Misch GW, Sprouse TM, Lippuner J, Surman R, Couture AJ, Bloser PF, Shirazi F, Even WP, Vestrand WT, Miller RS (2020) Gamma rays from kilonova: a potential probe of r-process nucleosynthesis. Astrophys J 889:168. https://doi.org/10.3847/1538-4357/ab64d8. arXiv:1905.05089
Kostelecky A, Mewes M (2012) Neutrinos with Lorentz-violating operators of arbitrary dimension. Phys Rev D 85:096005. https://doi.org/10.1103/PhysRevD.85.096005
Kosteleckỳ VA, Mewes M (2008) Astrophysical tests of Lorentz and CPT violation with photons. Astrophys J Lett 689:L1. https://doi.org/10.1086/595815
Kosteleckỳ VA, Russell N (2011) Data tables for Lorentz and CPT violation. Rev Mod Phys 83:11. https://doi.org/10.1103/revmodphys.83.11
Kosteleckỳ VA, Samuel S (1989) Spontaneous breaking of Lorentz symmetry in string theory. Phys Rev D 39:683. https://doi.org/10.1103/physrevd.39.683
Kosteleckỳ VA, Lehnert R, Perry MJ (2003) Spacetime-varying couplings and Lorentz violation. Phys Rev D 68:123511. https://doi.org/10.1103/physrevd.68.123511
Kouveliotou C, Meegan CA, Fishman GJ, Bhat NP, Briggs MS, Koshut TM, Paciesas WS, Pendleton GN (1993) Identification of two classes of gamma-ray bursts. Astrophys J Lett 413:L101–L104. https://doi.org/10.1086/186969
Kraus P, Tomboulis ET (2002) Photons and gravitons as Goldstone bosons and the cosmological constant. Phys Rev D 66:045015. https://doi.org/10.1103/physrevd.66.045015
Krauss LM, Tremaine S (1988) Test of the weak equivalence principle for neutrinos and photons. Phys Rev Lett 60:176. https://doi.org/10.1103/physrevlett.60.176
Kruckow MU, Tauris TM, Langer N, Kramer M, Izzard RG (2018) Progenitors of gravitational wave mergers: binary evolution with the stellar grid-based code COMBINE. Mon Not R Astron Soc 481:1908–1949. https://doi.org/10.1093/mnras/sty2190
Kulkarni SR, Djorgovski SG, Odewahn SC, Bloom JS, Gal RR, Koresko CD, Harrison FA, Lubin LM, Armus L, Sari R et al (1999) The afterglow, redshift and extreme energetics of the \(\gamma \)-ray burst of 23 January 1999. Nature 398:389–394. https://doi.org/10.1038/18821
Kumar P, Granot J (2003) The evolution of a structured relativistic jet and gamma-ray burst afterglow light curves. Astrophys. J 591:1075. https://doi.org/10.1086/375186
Kumar P, Zhang B (2015) The physics of gamma-ray bursts and relativistic jets. Phys Rep 561:1–109. https://doi.org/10.1016/j.physrep.2014.09.008
Kuns KA, Yu H, Chen Y, Adhikari RX (2020) Astrophysics and cosmology with a decihertz gravitational-wave detector: TianGO. Phys Rev D 102:043001. https://doi.org/10.1103/PhysRevD.102.043001. arXiv:1908.06004
Kuzmin VA, Rubakov VA, Shaposhnikov ME (1985) On anomalous electroweak baryon-number non-conservation in the early universe. Phys Lett B 155:36–42. https://doi.org/10.1016/0370-2693(85)91028-7
Kyutoku K, Seto N (2017) Gravitational-wave cosmography with LISA and the Hubble tension. Phys Rev D 95:083525. https://doi.org/10.1103/physrevd.95.083525
Lamb GP, Tanvir NR, Levan AJ, de Ugarte Postigo A, Kawaguchi K, Corsi A, Evans PA, Gompertz B, Malesani DB, Page KL, Wiersema K, Rosswog S, Shibata M, Tanaka M, van der Horst AJ, Cano Z, Fynbo JPU, Fruchter AS, Greiner J, Heintz KE, Higgins A, Hjorth J, Izzo L, Jakobsson P, Kann DA, O’Brien PT, Perley DA, Pian E, Pugliese G, Starling RLC, Thöne CC, Watson D, Wijers RAMJ, Xu D (2019) Short GRB 160821B: a reverse shock, a refreshed shock, and a well-sampled kilonova. Astrophys J 883:48. https://doi.org/10.3847/1538-4357/ab38bb
Langer N, Norman CA (2006) On the collapsar model of long gamma-ray bursts: constraints from cosmic metallicity evolution. Astrophys J Lett 638:L63. https://doi.org/10.1086/500363
Lattimer JM (2012) The nuclear equation of state and neutron star masses. Annu Rev Nucl Part Sci 62:485–515. https://doi.org/10.1146/annurev-nucl-102711-095018
Lattimer JM, Prakash M (2000) Nuclear matter and its role in supernovae, neutron stars and compact object binary mergers. Phys Rep 333:121–146. https://doi.org/10.1016/s0370-1573(00)00019-3
Lattimer JM, Schramm DN (1974) Black-hole-neutron-star collisions. Astrophys J Lett 192:L145–L147. https://doi.org/10.1086/181612
Lazzati D, Ramirez-Ruiz E, Ghisellini G (2001) Possible detection of hard X-ray afterglows of short \(\gamma \)-ray bursts. Astron Astrophys 379:L39–L43. https://doi.org/10.1051/0004-6361:20011485
Lazzati D, Ghirlanda G, Ghisellini G (2005) Soft gamma-ray repeater giant flares in the BATSE short gamma-ray burst catalogue: constraints from spectroscopy. Mon Not R Astron Soc Lett 362:L8–L12. https://doi.org/10.1111/j.1745-3933.2005.00062.x
Lazzati D, Deich A, Morsony BJ, Workman JC (2017) Off-axis emission of short \(\gamma \)-ray bursts and the detectability of electromagnetic counterparts of gravitational-wave-detected binary mergers. Mon Not R Astron Soc 471:1652–1661. https://doi.org/10.1093/mnras/stx1683
Lazzati D, Perna R, Morsony BJ, Lopez-Camara D, Cantiello M, Ciolfi R, Giacomazzo B, Workman JC (2018) Late time afterglow observations reveal a collimated relativistic jet in the ejecta of the binary neutron star merger GW170817. Phys Rev Lett 120:241103. https://doi.org/10.1103/physrevlett.120.241103
Le Floc’h E, Duc PA, Mirabel IF, Sanders DB, Bosch G, Diaz RJ, Donzelli CJ, Rodrigues I, Greiner J, Mereghetti S et al (2003) Are the hosts of gamma-ray bursts sub-luminous and blue galaxies? Astron Astrophys 400:499–510. https://doi.org/10.1051/0004-6361:20030001
Leavitt HS (1908) 1777 variables in the magellanic clouds. Ann Harvard Coll Obs 60:87–108
Leavitt HS, Pickering EC (1912) Periods of 25 variable stars in the small magellanic cloud. Harvard Coll Obs Circ 173:1–3
Lee TD, Yang CN (1956) Question of parity conservation in weak interactions. Phys Rev 104:254. https://doi.org/10.1016/b978-0-08-006509-0.50010-7
Lee WH, Ramirez-Ruiz E (2007) The progenitors of short gamma-ray bursts. New J Phys 9:17. https://doi.org/10.1088/1367-2630/9/1/017
Lee HK, Wijers RAMJ, Brown GE (2000) The Blandford–Znajek process as a central engine for a gamma-ray burst. Phys Rep 325:83–114. https://doi.org/10.1016/s0370-1573(99)00084-8
Lei WH, Zhang B, Liang EW (2013) Hyperaccreting black hole as gamma-ray burst central engine. I. Baryon loading in gamma-ray burst jets. Astrophys J 765:125. https://doi.org/10.1088/0004-637x/765/2/125
Lei WH, Zhang B, Wu XF, Liang EW (2017) Hyperaccreting black hole as gamma-ray burst central engine. II. Temporal evolution of the central engine parameters during the prompt and afterglow phases. Astrophys J 849:47. https://doi.org/10.3847/1538-4357/aa9074
Leibler CN, Berger E (2010) The stellar ages and masses of short gamma-ray burst host galaxies: investigating the progenitor delay time distribution and the role of mass and star formation in the short gamma-ray burst rate. Astrophys J 725:1202–1214. https://doi.org/10.1088/0004-637X/725/1/1202
Lemaître G (1927) Un Univers homogène de masse constante et de rayon croissant rendant compte de la vitesse radiale des nébuleuses extra-galactiques. Ann Soc Sci Bruxelles 47:49–59
Lemaître G (1931) Expansion of the universe, A homogeneous universe of constant mass and increasing radius accounting for the radial velocity of extra-galactic nebulae. Mon Not R Astron Soc 91:483–490
Li LX (2000) Toy model for the Blandford–Znajek mechanism. Phys Rev D 61:084016. https://doi.org/10.1103/PhysRevD.61.084016
Li W, Chornock R, Leaman J, Filippenko AV, Poznanski D, Wang X, Ganeshalingam M, Mannucci F (2011) Nearby supernova rates from the Lick Observatory supernova search. III. The rate-size relation, and the rates as a function of galaxy Hubble type and colour. Mon Not R Astron Soc 412:1473–1507. https://doi.org/10.1111/j.1365-2966.2011.18162.x
Li X, Hu YM, Fan YZ, Wei DM (2016) GRB/GW Association: long-short GRB candidates, time lag, measuring gravitational wave velocity, and testing Einstein’s equivalence principle. Astrophys J 827:75. https://doi.org/10.3847/0004-637x/827/1/75
Li T, Xiong S, Zhang S, Lu F, Song L, Cao X, Chang Z, Chen G, Chen L, Chen T et al (2018) Insight-HXMT observations of the first binary neutron star merger GW170817. Sci China Phys Mech Astron 61:031011. https://doi.org/10.1007/s11433-017-9107-5
Li BA, Krastev PG, Wen DH, Zhang NB (2019) Towards understanding astrophysical effects of nuclear symmetry energy. Eur Phys J A 55:117. https://doi.org/10.1140/epja/i2019-12780-8
Lien A, Sakamoto T, Barthelmy SD, Baumgartner WH, Cannizzo JK, Chen K, Collins NR, Cummings JR, Gehrels N, Krimm HA, Markwardt CB, Palmer DM, Stamatikos M, Troja E, Ukwatta TN (2016) The third swift burst alert telescope gamma-ray burst catalog. Astrophys J 829:7. https://doi.org/10.3847/0004-637X/829/1/7
Linde AD (1982) A new inflationary universe scenario: a possible solution of the horizon, flatness, homogeneity, isotropy and primordial monopole problems. Phys Lett B 108:389–393. https://doi.org/10.1016/0370-2693(82)91219-9
Linder EV (2003) Exploring the expansion history of the universe. Phys Rev Lett 90:091301. https://doi.org/10.1103/PhysRevLett.90.091301
Linder EV (2005) Curved space or curved vacuum? Astropart Phys 24:391–399. https://doi.org/10.1016/j.astropartphys.2005.08.004
Linder EV (2011) Lensing time delays and cosmological complementarity. Phys Rev D 84:123529. https://doi.org/10.1103/physrevd.84.123529
Lippuner J, Fernández R, Roberts LF, Foucart F, Kasen D, Metzger BD, Ott CD (2017) Signatures of hypermassive neutron star lifetimes on r-process nucleosynthesis in the disc ejecta from neutron star mergers. Mon Not R Astron Soc 472:904–918. https://doi.org/10.1093/mnras/stx1987
Lipunov VM, Gorbovskoy E, Kornilov VG, Tyurina N, Balanutsa P, Kuznetsov A, Vlasenko D, Kuvshinov D, Gorbunov I, Buckley DAH et al (2017) MASTER optical detection of the first LIGO/Virgo neutron star binary merger GW170817. Astrophys J Lett 850:L1. https://doi.org/10.3847/2041-8213/aa92c0
Liska M, Hesp C, Tchekhovskoy A, Ingram A, van der Klis M, Markoff S (2017) Formation of precessing jets by tilted black hole discs in 3D general relativistic MHD simulations. Mon Not R Astron Soc Lett 474:L81–L85. https://doi.org/10.1093/mnrasl/slx174
Liska M, Tchekhovskoy A, Ingram A, Van Der Klis M (2019) Bardeen-Petterson alignment, jets, and magnetic truncation in GRMHD simulations of tilted thin accretion discs. Mon Not R Astron Soc 487:550–561. https://doi.org/10.1093/mnras/stz834
Lithwick Y, Sari R (2001) Lower limits on Lorentz factors in gamma-ray bursts. Astrophys J 555:540. https://doi.org/10.1086/321455
Littenberg TB, Farr B, Coughlin S, Kalogera V, Holz DE (2015) Neutron stars versus black holes: probing the mass gap with LIGO/Virgo. Astrophys J Lett 807:L24. https://doi.org/10.1088/2041-8205/807/2/l24
Longo MJ (1987) Tests of relativity from SN1987A. Phys Rev D 36:3276. https://doi.org/10.1103/physrevd.36.3276
Longo MJ (1988) New precision tests of the Einstein equivalence principle from SN1987A. Phys Rev Lett 60:173. https://doi.org/10.1103/physrevlett.60.173
Lorimer DR (2008) Binary and millisecond pulsars. Living Rev Relativ 11:8. https://doi.org/10.12942/lrr-2008-8
Lü HJ, Zhang B (2014) A test of the millisecond magnetar central engine model of gamma-ray bursts with swift data. Astrophys J 785:74. https://doi.org/10.1088/0004-637x/785/1/74
Lü HJ, Zhang B, Lei WH, Li Y, Lasky PD (2015) The millisecond magnetar central engine in short GRBs. Astrophys J 805:89. https://doi.org/10.1088/0004-637x/805/2/89
LVC (2017a) LIGO/Virgo G298048: Fermi GBM trigger 524666471/170817529: LIGO/Virgo Identification of a possible gravitational-wave counterpart. Technical report, GSFC. https://gcn.gsfc.nasa.gov/gcn3/21505.gcn3
LVC (2017b) LIGO/Virgo G298048: further analysis of a binary neutron star candidate with updated sky localization. Technical report, GSFC. https://gcn.gsfc.nasa.gov/gcn3/21513.gcn3
LVC (2017c) LIGO/Virgo Identification of a binary neutron star candidate coincident with Fermi GBM trigger 524666471/170817529. Technical report, GSFC. https://gcn.gsfc.nasa.gov/gcn3/21509.gcn3
LVC (2017d) LIGO/Virgo S190425z: updated localization from LIGO and Virgo data. Technical report, GSFC. https://gcn.gsfc.nasa.gov/gcn3/24228.gcn3
LVC (2017e) LIGO/Virgo S190718y: identification of a GW compact binary merger candidate. Technical report, GSFC. https://gcn.gsfc.nasa.gov/gcn3/25087.gcn3
LVC (2019) LIGO/Virgo S190425z: identification of a GW compact binary merger candidate. Technical report, GSFC. https://gcn.gsfc.nasa.gov/gcn/gcn3/24168.gcn3
LVC (2020) IPN triangulation of GRB 200415A (possible Magnetar Giant Flare in Sculptor Galaxy?). GRB Coordinates Network 27585. https://gcn.gsfc.nasa.gov/gcn/gcn3/27585.gcn3
Lynch R, Coughlin M, Vitale S, Stubbs CW, Katsavounidis E (2018) Observational implications of lowering the LIGO-Virgo alert threshold. Astrophys J Lett 861:L24. https://doi.org/10.3847/2041-8213/aacf9f
Lyutikov M, Pariev VI, Blandford RD (2003) Polarization of prompt gamma-ray burst emission: evidence for electromagnetically dominated outflow. Astrophys J 597:998. https://doi.org/10.1086/378497
Macias P, Ramirez-Ruiz E (2019) Constraining collapsar r-process models through stellar abundances. Astrophys J Lett 877:L24. https://doi.org/10.3847/2041-8213/ab2049
Madau P, Dickinson M (2014a) Cosmic star-formation history. Annu Rev Astron Astrophys 52:415–486. https://doi.org/10.1146/annurev-astro-081811-125615
Madau P, Dickinson M (2014b) Cosmic star-formation history. Annu Rev Astron Astrophys 52:415–486. https://doi.org/10.1146/annurev-astro-081811-125615
Magueijo J (2003) New varying speed of light theories. Rep Prog Phys 66:2025. https://doi.org/10.1088/0034-4885/66/11/r04
Maione F, De Pietri R, Feo A, Löffler F (2017) Spectral analysis of gravitational waves from binary neutron star merger remnants. Phys Rev D 96:063011. https://doi.org/10.1103/physrevd.96.063011
Majorana E (1937) Teoria simmetrica dell’elettrone e del positrone. Il Nuovo Cimento (1924-1942) 14:171. https://doi.org/10.1007/bf02961314
Maki Z, Nakagawa M, Sakata S (1962) Remarks on the unified model of elementary particles. Prog Theor Phys 28:870–880. https://doi.org/10.1143/ptp.28.870
Mandhai S, Tanvir N, Lamb G, Levan A, Tsang D (2018) The rate of short-duration gamma-ray bursts in the local universe. Galaxies 6:130. https://doi.org/10.22323/1.357.0047
Mao S, Paczynski B (1992) On the cosmological origin of gamma-ray bursts. Astrophys J 388:L45–L48. https://doi.org/10.1086/186326
Margalit B, Metzger BD (2019) The multi-messenger matrix: the future of neutron star merger constraints on the nuclear equation of state. Astrophys J Lett 880:L15. https://doi.org/10.3847/2041-8213/ab2ae2. arXiv:1904.11995
Margutti R, Berger E, Fong WF, Guidorzi C, Alexander KD, Metzger BD, Blanchard PK, Cowperthwaite PS, Chornock R, Eftekhari T et al (2017) The electromagnetic counterpart of the binary neutron star merger LIGO/Virgo GW170817. V. Rising X-ray emission from an off-axis jet. Astrophys J Lett 848:L20. https://doi.org/10.3847/2041-8213/aa9057
Margutti R, Alexander KD, Xie X, Sironi L, Metzger BD, Kathirgamaraju A, Fong WF, Blanchard PK, Berger E, MacFadyen A et al (2018) The binary neutron star event LIGO/Virgo GW170817 160 days after merger: synchrotron emission across the electromagnetic spectrum. Astrophys J Lett 856:L18. https://doi.org/10.3847/2041-8213/aab2ad
Martínez-Pinedo G, Fischer T, Lohs A, Huther L (2012) Charged-current weak interaction processes in hot and dense matter and its impact on the spectra of neutrinos emitted from protoneutron star cooling. Phys Rev Lett 109:251104. https://doi.org/10.1103/physrevlett.109.251104
Mather JC, Cheng ES, Cottingham DA, Eplee RE Jr, Fixsen DJ, Hewagama T, Isaacman RB, Jensen KA, Meyer SS, Noerdlinger PD et al (1994) Measurement of the cosmic microwave background spectrum by the COBE FIRAS instrument. Astrophys J 420:439–444. https://doi.org/10.1086/173574
Matsumoto T, Kimura SS, Murase K, Mészáros P (2020) Linking extended and plateau emissions of short gamma-ray bursts. Mon Not R Astron Soc 493:783–791. https://doi.org/10.1093/mnras/staa305
Mattingly D (2005) Modern tests of Lorentz invariance. Living Rev Relativ 8:5. https://doi.org/10.12942/lrr-2005-5
Mazets EP, Golenetskii SV, Il’inskii VN, Guryan YA et al (1979) Observations of a flaring X-ray pulsar in Dorado. Nature 282:587–589. https://doi.org/10.1038/282587a0
Mazets EP, Golenetskii SV, Il’inskii VN, Panov VN, Aptekar RL, Guryan YA, Proskura MP, Sokolov IA, Sokolova ZY, Kharitonova TV et al (1981) Catalog of cosmic gamma-ray bursts from the KONUS experiment data. Astrophys Space Sci 80:3–83. https://doi.org/10.1007/bf00649141
Mazets EP, Aptekar RL, Cline TL, Frederiks DD, Goldsten JO, Golenetskii SV, Hurley K, von Kienlin A, Pal’shin VD (2008) A giant flare from a soft gamma repeater in the Andromeda galaxy (M31). Astrophys J 680:545–549. https://doi.org/10.1086/587955
McClelland D, Evans M, Schnabel R, Lantz B, Martin I, Quetschke V (2014) Instrument science white paper. Technical report, LIGO. https://dcc.ligo.org/LIGO-T1400316/public
McEnery J, Barrio JA, Agudo I, Ajello M, Álvarez JM, Ansoldi S, Anton S, Auricchio N, Stephen JB, Baldini L et al (2019) All-sky medium energy gamma-ray observatory: exploring the extreme multimessenger universe. arXiv e-prints arXiv:1907.07558
Meegan CA, Fishman GJ, Wilson RB, Paciesas WS, Pendleton GN, Horack JM, Brock MN, Kouveliotou C (1992) Spatial distribution of \(\gamma \)-ray bursts observed by BATSE. Nature 355:143–145. https://doi.org/10.1038/355143a0
Meegan C, Lichti G, Bhat PN, Bissaldi E, Briggs MS, Connaughton V, Diehl R, Fishman G, Greiner J, Hoover AS, van der Horst AJ, von Kienlin A, Kippen RM, Kouveliotou C, McBreen S, Paciesas WS, Preece R, Steinle H, Wallace MS, Wilson RB, Wilson-Hodge C (2009) The Fermi Gamma-ray Burst Monitor. Astrophys J 702:791–804. https://doi.org/10.1088/0004-637X/702/1/791
Meng YZ, Geng JJ, Zhang BB, Wei JJ, Xiao D, Liu LD, Gao H, Wu XF, Liang EW, Huang YF et al (2018) The origin of the prompt emission for short GRB 170817A: photosphere emission or synchrotron emission? Astrophys J 860:72. https://doi.org/10.3847/1538-4357/aac2d9
Mertens S (2016) Direct neutrino mass experiments. J Phys Conf Ser 718:022013. https://doi.org/10.1088/1742-6596/718/2/022013
Messenger C, Read J (2012) Measuring a cosmological distance-redshift relationship using only gravitational wave observations of binary neutron star coalescences. Phys Rev Lett 108:091101. https://doi.org/10.1103/physrevlett.108.091101
Messick C, Blackburn K, Brady P, Brockill P, Cannon K, Cariou R, Caudill S, Chamberlin SJ, Creighton JD, Everett R et al (2017) Analysis framework for the prompt discovery of compact binary mergers in gravitational-wave data. Phys Rev D 95:042001. https://doi.org/10.1103/physrevd.95.042001
Mészáros P, Rees MJ (1997) Poynting jets from black holes and cosmological gamma-ray bursts. Astrophys J Lett 482:L29. https://doi.org/10.1086/310692
Mészáros P, Waxman E (2001) TeV neutrinos from successful and choked gamma-ray bursts. Phys Rev Lett 87:171102. https://doi.org/10.1103/physrevlett.87.171102
Mészáros P, Rees MJ, Wijers RAMJ (1998) Viewing angle and environment effects in gamma-ray bursts: sources of afterglow diversity. Astrophys J 499:301. https://doi.org/10.1086/305635
Metzger BD (2020) Kilonovae. Living Rev Relativ 23:1. https://doi.org/10.1007/s41114-019-0024-0
Metzger BD, Berger E (2012) What is the most promising electromagnetic counterpart of a neutron star binary merger? Astrophys J 746:48. https://doi.org/10.1088/0004-637x/746/1/48
Metzger BD, Fernández R (2014) Red or blue? A potential kilonova imprint of the delay until black hole formation following a neutron star merger. Mon Not R Astron Soc 441:3444–3453. https://doi.org/10.1093/mnras/stu802
Metzger BD, Piro AL (2014) Optical and X-ray emission from stable millisecond magnetars formed from the merger of binary neutron stars. Mon Not R Astron Soc 439:3916–3930. https://doi.org/10.1093/mnras/stu247
Metzger BD, Zivancev C (2016) Pair fireball precursors of neutron star mergers. Mon Not R Astron Soc 461:4435–4440. https://doi.org/10.1093/mnras/stw1800
Metzger BD, Piro AL, Quataert E (2008a) Time-dependent models of accretion discs formed from compact object mergers. Mon Not R Astron Soc 390:781–797. https://doi.org/10.1111/j.1365-2966.2008.13789.x
Metzger BD, Quataert E, Thompson TA (2008b) Short-duration gamma-ray bursts with extended emission from protomagnetar spin-down. Mon Not R Astron Soc 385:1455–1460. https://doi.org/10.1111/j.1365-2966.2008.12923.x
Metzger BD, Piro AL, Quataert E (2009) Neutron-rich freeze-out in viscously spreading accretion discs formed from compact object mergers. Mon Not R Astron Soc 396:304–314. https://doi.org/10.1111/j.1365-2966.2008.14380.x
Metzger BD, Martínez-Pinedo G, Darbha S, Quataert E, Arcones A, Kasen D, Thomas R, Nugent P, Panov IV, Zinner NT (2010) Electromagnetic counterparts of compact object mergers powered by the radioactive decay of r-process nuclei. Mon Not R Astron Soc 406:2650–2662. https://doi.org/10.1111/j.1365-2966.2010.16864.x
Metzger BD, Giannios D, Thompson TA, Bucciantini N, Quataert E (2011) The protomagnetar model for gamma-ray bursts. Mon Not R Astron Soc 413:2031–2056. https://doi.org/10.1111/j.1365-2966.2011.18280.x
Metzger BD, Bauswein A, Goriely S, Kasen D (2014) Neutron-powered precursors of kilonovae. Mon Not R Astron Soc 446:1115–1120. https://doi.org/10.1093/mnras/stu2225
Metzger BD, Thompson TA, Quataert E (2018) A magnetar origin for the kilonova ejecta in GW170817. Astrophys J 856:101. https://doi.org/10.3847/1538-4357/aab095
Mewes M (2019) Signals for Lorentz violation in gravitational waves. Phys Rev D 99:104062. https://doi.org/10.1103/physrevd.99.104062
Meyer BS, Howard WM, Mathews GJ, Hoffman R, Woosley SE (1992) The r-process in supernovae. In: Kubono S, Kajino T (eds) Unstable nuclei in astrophysics, vol 37. World Scientific, Singapore
Miller JM, Ryan BR, Dolence JC, Burrows A, Fontes CJ, Fryer CL, Korobkin O, Lippuner J, Mumpower MR, Wollaeger RT (2019a) Full transport model of GW170817-like disk produces a blue kilonova. Phys Rev D 100:023008. https://doi.org/10.1103/physrevd.100.023008
Miller MC, Lamb FK, Dittmann AJ, Bogdanov S, Arzoumanian Z, Gendreau KC, Guillot S, Harding AK, Ho WCG, Lattimer JM et al (2019b) PSR J0030+0451 mass and radius from NICER data and implications for the properties of neutron star matter. Astrophys J Lett 887:L24. https://doi.org/10.3847/2041-8213/ab50c5
Minaev PY, Pozanenko AS (2017) Precursors of short gamma-ray bursts in the SPI-ACS/INTEGRAL experiment. Astron Lett 43:1–20. https://doi.org/10.1134/s1063773717010017
Minazzoli O (2019) Strong lensing in multimessenger astronomy as a test of the equivalence principle. arXiv e-prints arXiv:1912.06891
Minazzoli O, Johnson-McDaniel NK, Sakellariadou M (2019) Shortcomings of Shapiro delay-based tests of the equivalence principle on cosmological scales. Phys Rev D 100:104047. https://doi.org/10.1103/PhysRevD.100.104047. arXiv:1907.12453
Mirshekari S, Yunes N, Will CM (2012) Constraining Lorentz-violating, modified dispersion relations with gravitational waves. Phys Rev D 85:024041. https://doi.org/10.1103/physrevd.85.024041
Mirzoyan R, Noda K, Moretti E, Berti A, Nigro C, Hoang J, Micanovic S, Takahashi M, Chai Y, Moralejo A et al (2019) MAGIC detects the GRB 190114C in the TeV energy domain. Technical report, GSFC. https://gcn.gsfc.nasa.gov/gcn/gcn3/23701.gcn3
Mochkovitch R, Hernanz M, Isern J, Martin X (1993) Gamma-ray bursts as collimated jets from neutron star/black hole mergers. Nature 361:236–238. https://doi.org/10.1038/361236a0
Moffat JW (1993) Superluminary universe: a possible solution to the initial value problem in cosmology. Int J Mod Phys D 2:351–365. https://doi.org/10.1142/s0218271893000246
Mogushi K, Cavaglià M, Siellez K (2019) Jet geometry and rate estimate of coincident gamma-ray burst and gravitational-wave observations. Astrophys J 880:55. https://doi.org/10.3847/1538-4357/ab1f76
Mohapatra RN, Smirnov AY (2006) Neutrino mass and new physics. Annu Rev Nucl Part Sci 56:569–628. https://doi.org/10.1146/annurev.nucl.56.080805.140534
Mooley KP, Deller AT, Gottlieb O, Nakar E, Hallinan G, Bourke S, Frail DA, Horesh A, Corsi A, Hotokezaka K (2018) Superluminal motion of a relativistic jet in the neutron-star merger GW170817. Nature 561:355–359. https://doi.org/10.1038/s41586-018-0486-3
Moore GD, Nelson AE (2001) Lower bound on the propagation speed of gravity from gravitational Cherenkov radiation. JHEP 2001:023. https://doi.org/10.1088/1126-6708/2001/09/023
Most ER, Weih LR, Rezzolla L, Schaffner-Bielich J (2018) New constraints on radii and tidal deformabilities of neutron stars from GW170817. Phys Rev Lett 120:261103. https://doi.org/10.1103/physrevlett.120.261103
Most ER, Papenfort LJ, Dexheimer V, Hanauske M, Schramm S, Stöcker H, Rezzolla L (2019) Signatures of quark-hadron phase transitions in general-relativistic neutron-star mergers. Phys Rev Lett 122:061101. https://doi.org/10.1103/physrevlett.122.061101
Mueller G, Baker J, Barke S, Bender PL, Berti E, Caldwell R, Conklin JW, Cornish N, Ferrara EC, Holley-Bockelmann K, Kamai B, Larson SL, Livas J, McWilliams ST, Mueller G, Natarajan P, Rioux N, Sankar SS, Schnittman J, Shoemaker D, Slutsky J, Stebbins R, Thorpe I, Ziemer J (2019) Space based gravitational wave astronomy beyond LISA. Bull Am Astron Soc 51:243
Murase K, Mészáros P, Zhang B (2009) Probing the birth of fast rotating magnetars through high-energy neutrinos. Phys Rev D 79:103001. https://doi.org/10.1103/physrevd.79.103001
Murase K, Toomey MW, Fang K, Oikonomou F, Kimura SS, Hotokezaka K, Kashiyama K, Ioka K, Mészáros P (2018) Double neutron star mergers and short gamma-ray bursts: long-lasting high-energy signatures and remnant dichotomy. Astrophys J 854:60. https://doi.org/10.3847/1538-4357/aaa48a
Murayama H, Yanagida T (2001) LSND, SN1987A, and CPT violation. Phys Lett B 520:263–268. https://doi.org/10.1016/s0370-2693(01)01136-4
Murguia-Berthier A, Montes G, Ramirez-Ruiz E, De Colle F, Lee WH (2014) Necessary conditions for short gamma-ray burst production in binary neutron star mergers. Astrophys J Lett 788:L8. https://doi.org/10.1088/2041-8205/788/1/l8
Nagakura H, Hotokezaka K, Sekiguchi Y, Shibata M, Ioka K (2014) Jet collimation in the ejecta of double neutron star mergers: a new canonical picture of short gamma-ray bursts. Astrophys J Lett 784:L28. https://doi.org/10.1088/2041-8205/784/2/l28
Nagano M, Watson AA (2000) Observations and implications of the ultrahigh-energy cosmic rays. Rev Mod Phys 72:689. https://doi.org/10.1103/revmodphys.72.689
Nakar E, Piran T (2011) Detectable radio flares following gravitational waves from mergers of binary neutron stars. Nature 478:82–84. https://doi.org/10.1038/nature10365
Nakar E et al (2012) Relativistic shock breakouts: a variety of gamma-ray flares: from low-luminosity gamma-ray bursts to type Ia supernovae. Astrophys J 747:88. https://doi.org/10.1088/0004-637x/747/2/88
Nishizawa A, Kobayashi T (2018) Parity-violating gravity and GW170817. Phys Rev D 98:124018. https://doi.org/10.1103/physrevd.98.124018
Nishizawa A, Nakamura T (2014) Measuring speed of gravitational waves by observations of photons and neutrinos from compact binary mergers and supernovae. Phys Rev D 90:044048. https://doi.org/10.1103/physrevd.90.044048
Nissanke S, Holz DE, Dalal N, Hughes SA, Sievers JL, Hirata CM (2013) Determining the Hubble constant from gravitational wave observations of merging compact binaries. arXiv e-prints arXiv:1307.2638
Norris JP, Bonnell JT (2006) Short gamma-ray bursts with extended emission. Astrophys J 643:266. https://doi.org/10.1086/502796
Nouri FH, Duez MD, Foucart F, Deaton MB, Haas R, Haddadi M, Kidder LE, Ott CD, Pfeiffer HP, Scheel MA et al (2018) Evolution of the magnetized, neutrino-cooled accretion disk in the aftermath of a black hole-neutron star binary merger. Phys Rev D 97:083014. https://doi.org/10.1103/physrevd.97.083014
Nynka M, Ruan JJ, Haggard D, Evans PA (2018) Fading of the X-ray afterglow of neutron star merger GW170817/GRB 170817A at 260 days. Astrophys J Lett 862:L19. https://doi.org/10.3847/2041-8213/aad32d
Oechslin R, Janka HT (2006) Torus formation in neutron star mergers and well-localized short gamma-ray bursts. Mon Not R Astron Soc 368:1489–1499. https://doi.org/10.1111/j.1365-2966.2006.10238.x
Oechslin R, Janka HT (2007) Gravitational waves from relativistic neutron-star mergers with microphysical equations of state. Phys Rev Lett 99:121102. https://doi.org/10.1103/physrevlett.99.121102
Ofek EO (2007) Soft gamma-ray repeaters in nearby galaxies: rate, luminosity function, and fraction among short gamma-ray bursts. Astrophys J 659:339. https://doi.org/10.1086/511147
Oganesyan G, Ascenzi S, Branchesi M, Salafia OS, Dall’Osso S, Ghirlanda G (2020) Structured jets and X-ray plateaus in gamma-ray burst phenomena. Astrophys J 893:88. https://doi.org/10.3847/1538-4357/ab8221
Oppenheimer JR, Volkoff GM (1939) On massive neutron cores. Phys Rev 55:374–381. https://doi.org/10.1103/PhysRev.55.374
Özel F, Freire P (2016) Masses, radii, and the equation of state of neutron stars. Annu Rev Astron Astrophys 54:401–440. https://doi.org/10.1146/annurev-astro-081915-023322
Paczynski B (1986) Gamma-ray bursters at cosmological distances. Astrophys J Lett 308:L43–L46. https://doi.org/10.1086/184740
Paczynski B, Rhoads JE (1993) Radio transients from gamma-ray bursters. Astrophys J Lett 418:L5. https://doi.org/10.1086/187102. arXiv:astro-ph/9307024
Palatiello M, Noda K, Inoue S, Colin P, Moretti E, Longo F (2017) MAGIC observation of a short nearby GRB 160821B. In: Proceedings of the 7th international Fermi symposium, held 15–20 October 2017, in Garmisch-Partenkirchen, Germany (IFS2017). https://doi.org/10.22323/1.312.0084
Palmer DM, Barthelmy S, Gehrels N, Kippen RM, Cayton T, Kouveliotou C, Eichler D, Wijers RAMJ, Woods PM, Granot J et al (2005) A giant \(\gamma \)-ray flare from the magnetar SGR 1806–20. Nature 434:1107–1109. https://doi.org/10.1038/nature03525
Panaitescu A (2005a) Jets, structured outflows and energy injection in gamma-ray burst afterglows: numerical modelling. Mon Not R Astron Soc 363:1409–1423. https://doi.org/10.1111/j.1365-2966.2005.09532.x
Panaitescu A (2005b) Models for achromatic light-curve breaks in gamma-ray burst afterglows: jets, structured outflows and energy injection. Mon Not R Astron Soc 362:921–930. https://doi.org/10.1111/j.1365-2966.2005.09352.x
Panaitescu A, Kumar P (2001) Jet energy and other parameters for the afterglows of GRB 980703, GRB 990123, GRB 990510, and GRB 991216 determined from modeling of multifrequency data. Astrophys J 554:667. https://doi.org/10.1086/321388
Pannarale F, Berti E, Kyutoku K, Lackey BD, Shibata M (2015) Gravitational-wave cutoff frequencies of tidally disruptive neutron star-black hole binary mergers. Phys Rev D 92:081504. https://doi.org/10.1103/physrevd.92.081504
Pardo K, Fishbach M, Holz DE, Spergel DN (2018) Limits on the number of spacetime dimensions from GW170817. JCAP 2018:048. https://doi.org/10.1088/1475-7516/2018/07/048
Pauli W (1930) Dear radioactive ladies and gentlemen. Phys Today 31:27
Penzias AA, Wilson RW (1965) A measurement of excess antenna temperature at 4080 Mc/s. Astrophys J 142:419–421. https://doi.org/10.1086/148307
Perley DA, Metzger BD, Granot J, Butler NR, Sakamoto T, Ramirez-Ruiz E, Levan AJ, Bloom JS, Miller AA, Bunker A et al (2009) GRB 080503: implications of a naked short gamma-ray burst dominated by extended emission. Astrophys J. https://doi.org/10.1088/0004-637x/696/2/1871
Perlmutter S, Aldering G, Goldhaber G, Knop RA, Nugent P, Castro PG, Deustua S, Fabbro S, Goobar A, Groom DE et al (1999) Measurements of \(\Omega \) and \(\Lambda \) from 42 high-redshift supernovae. Astrophys J 517:565. https://doi.org/10.1086/307221
Perna R, Keeton CR (2009) Gravitational lensing of anisotropic sources. Mon Not R Astron Soc 397:1084–1092. https://doi.org/10.1111/j.1365-2966.2009.15041.x
Perna R, Sari R, Frail D (2003) Jets in gamma-ray bursts: tests and predictions for the structured jet model. Astrophys J 594:379. https://doi.org/10.1086/376772
Peters PC, Mathews J (1963) Gravitational radiation from point masses in a Keplerian orbit. Phys Rev 131:435. https://doi.org/10.1103/PhysRev.131.435
Piran T (1999) Gamma-ray bursts and the fireball model. Phys Rep 314:575–667. https://doi.org/10.1016/s0370-1573(98)00127-6
Piran T, Nakar E, Rosswog S (2013) The electromagnetic signals of compact binary mergers. Mon Not R Astron Soc 430:2121–2136. https://doi.org/10.1093/mnras/stt037
Planck Collaboration (2020) Planck 2018 results. VI. Cosmological parameters. Astron Astrophys 641:A6. https://doi.org/10.1051/0004-6361/201833910
Poisson E, Will CM (2014) Gravity: newtonian, post-newtonian, relativistic. Cambridge University Press, Cambridge
Pontecorvo B (1957) Mesonium and antimesonium. Zhur Eksp Teor Fiz 33:549–551
Pontecorvo B (1958) Inverse \(\beta \) processes and nonconservation of lepton charge. Zhur Eksp Teor Fiz 34:247
Pontecorvo B (1967) Neutrino experiments and the question of leptonic-charge conservation. Zh Eksp Teor Fiz 53:1717–1725. https://doi.org/10.1016/b978-0-12-395657-6.50020-3
Pontecorvo B (1968) Neutrino experiments and the problem of conservation of leptonic charge. Sov Phys JETP 26:165
Popham R, Woosley SE, Fryer C (1999) Hyperaccreting black holes and gamma-ray bursts. Astrophys J 518:356. https://doi.org/10.1086/307259
Postnov KA, Yungelson LR (2014) The evolution of compact binary star systems. Living Rev Relativ 17:3. https://doi.org/10.12942/lrr-2014-3
Pruet J, Thompson TA, Hoffman RD (2004) Nucleosynthesis in outflows from the inner regions of collapsars. Astrophys J 606:1006. https://doi.org/10.1086/382036
Punturo M, Abernathy M, Acernese F, Allen B, Andersson N, Arun K, Barone F, Barr B, Barsuglia M, Beker M et al (2010) The Einstein Telescope: a third-generation gravitational wave observatory. Class Quantum Grav 27:194002
Qian YZ (2000) Supernovae versus neutron star mergers as the major r-process sources. Astrophys J Lett 534:L67. https://doi.org/10.1086/312659
Qian X, Vogel P (2015) Neutrino mass hierarchy. Progr Part Nucl Phys 83:1–30. https://doi.org/10.1016/j.ppnp.2015.05.002
Rachen JP, Mészáros P (1998) Photohadronic neutrinos from transients in astrophysical sources. Phys Rev D 58:123005. https://doi.org/10.1103/physrevd.58.123005
Racusin JL, Karpov SV, Sokolowski M, Granot J, Wu XF, Pal’shin V, Covino S, Van Der Horst AJ, Oates SR, Schady P et al (2008) Broadband observations of the naked-eye \(\gamma \)-ray burst GRB 080319B. Nature 455:183–188. https://doi.org/10.1038/nature07270
Racusin JL, Liang EW, Burrows DN, Falcone A, Sakamoto T, Zhang BB, Zhang B, Evans P, Osborne J (2009) Jet breaks and energetics of Swift gamma-ray burst X-ray afterglows. Astrophys J 698:43. https://doi.org/10.1088/0004-637x/698/1/43
Racusin J, Perkins JS, Briggs MS, de Nolfo G, Krizmanic J, Caputo R, McEnery JE, Shawhan P, Morris D, Connaughton V, Kocevski D, Wilson-Hodge C, Hui M, Mitchell L, McBreen S (2017) BurstCube: a CubeSat for gravitational wave counterparts. In: 35th international cosmic ray conference (ICRC2017), SISSA, Proceedings of Science, vol 301. https://doi.org/10.22323/1.301.0760, arXiv:1708.09292
Radice D, Perego A, Zappa F, Bernuzzi S (2018) GW170817: joint constraint on the neutron star equation of state from multimessenger observations. Astrophys J Lett 852:L29. https://doi.org/10.3847/2041-8213/aaa402
Raithel CA (2019) Constraints on the neutron star equation of state from GW170817. Eur Phys J A 55:80. https://doi.org/10.1140/epja/i2019-12759-5
Raithel CA, Özel F, Psaltis D (2018) Tidal deformability from GW170817 as a direct probe of the neutron star radius. Astrophys J Lett 857:L23. https://doi.org/10.3847/2041-8213/aabcbf
Ratra B, Peebles PJE (1988) Cosmological consequences of a rolling homogeneous scalar field. Phys Rev D 37:3406. https://doi.org/10.1103/physrevd.37.3406
Ravasio ME, Oganesyan G, Ghirlanda G, Nava L, Ghisellini G, Pescalli A, Celotti A (2018) Consistency with synchrotron emission in the bright GRB 160625B observed by Fermi. Astron Astrophys 613:A16. https://doi.org/10.1051/0004-6361/201732245
Ravi V, Lasky PD (2014) The birth of black holes: neutron star collapse times, gamma-ray bursts and fast radio bursts. Mon Not R Astron Soc 441:2433–2439. https://doi.org/10.1093/mnras/stu720
Read JS, Baiotti L, Creighton JD, Friedman JL, Giacomazzo B, Kyutoku K, Markakis C, Rezzolla L, Shibata M, Taniguchi K (2013) Matter effects on binary neutron star waveforms. Phys Rev D 88:044042. https://doi.org/10.1103/physrevd.88.044042
Rees MJ, Meszaros P (1994) Unsteady outflow models for cosmological gamma-ray bursts. Astrophys J Lett 430:L93. https://doi.org/10.1086/187446. arXiv:astro-ph/9404038
Refsdal S (1964) On the possibility of determining Hubble’s parameter and the masses of galaxies from the gravitational lens effect. Mon Not R Astron Soc 128:307–310. https://doi.org/10.1093/mnras/128.4.307
Reichart DE (1998) The redshift of GRB 970508. Astrophys J Lett 495:L99. https://doi.org/10.1086/311222
Reines F, Cowan CL Jr (1953) Detection of the free neutrino. Phys Rev 92:830. https://doi.org/10.1142/9789814343060_0006
Reitze D, Adhikari RX, Ballmer S, Barish B, Barsotti L, Billingsley G, Brown DA, Chen Y, Coyne D, Eisenstein R, Evans M, Fritschel P, Hall ED, Lazzarini A, Lovelace G, Read J, Sathyaprakash BS, Shoemaker D, Smith J, Torrie C, Vitale S, Weiss R, Wipf C, Zucker M (2019) Cosmic explorer: the U.S. contribution to gravitational-wave astronomy beyond LIGO. Bull Am Astron Soc 51:35
Rezzolla L, Takami K (2016) Gravitational-wave signal from binary neutron stars: a systematic analysis of the spectral properties. Phys Rev D 93:124051. https://doi.org/10.1103/PhysRevD.93.124051
Rezzolla L, Giacomazzo B, Baiotti L, Granot J, Kouveliotou C, Aloy MA (2011) The missing link: merging neutron stars naturally produce jet-like structures and can power short gamma-ray bursts. Astrophys J Lett 732:L6. https://doi.org/10.1088/2041-8205/732/1/L6
Rezzolla L, Most ER, Weih LR (2018) Using gravitational-wave observations and quasi-universal relations to constrain the maximum mass of neutron stars. Astrophys J Lett 852:L25. https://doi.org/10.3847/2041-8213/aaa401
Rhoads JE (1997) How to tell a jet from a balloon: a proposed test for beaming in gamma-ray bursts. Astrophys J Lett 487:L1. https://doi.org/10.1086/310876
Riess AG, Filippenko AV, Challis P, Clocchiatti A, Diercks A, Garnavich PM, Gilliland RL, Hogan CJ, Jha S, Kirshner RP et al (1998) Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron J 116:1009. https://doi.org/10.1086/300499
Riess AG, Macri LM, Hoffmann SL, Scolnic D, Casertano S, Filippenko AV, Tucker BE, Reid MJ, Jones DO, Silverman JM et al (2016) A 2.4% determination of the local value of the Hubble constant. Astrophys J 826:56. https://doi.org/10.3847/0004-637x/826/1/56
Riess AG, Casertano S, Yuan W, Macri L, Bucciarelli B, Lattanzi MG, MacKenty JW, Bowers JB, Zheng W, Filippenko AV et al (2018) Milky Way cepheid standards for measuring cosmic distances and application to Gaia DR2: implications for the Hubble constant. Astrophys J 861:126. https://doi.org/10.3847/1538-4357/aac82e
Riess AG, Casertano S, Yuan W, Macri LM, Scolnic D (2019) Large Magellanic Cloud cepheid standards provide a 1% foundation for the determination of the Hubble constant and stronger evidence for physics beyond \({\Lambda }\)CDM. Astrophys J 876:85. https://doi.org/10.3847/1538-4357/ab1422
Riley TE, Watts AL, Bogdanov S, Ray PS, Ludlam RM, Guillot S, Arzoumanian Z, Baker CL, Bilous AV, Chakrabarty D et al (2019) A NICER view of PSR J0030+0451: millisecond pulsar parameter estimation. Astrophys J Lett 887:L21. https://doi.org/10.3847/2041-8213/ab481c
Roberts LF, Reddy S, Shen G (2012) Medium modification of the charged-current neutrino opacity and its implications. Phys Rev C 86:065803. https://doi.org/10.1103/physrevc.86.065803
Rossi E, Lazzati D, Rees MJ (2002) Afterglow light curves, viewing angle and the jet structure of \(\gamma \)-ray bursts. Mon Not R Astron Soc 332:945–950. https://doi.org/10.1046/j.1365-8711.2002.05363.x
Rosswog S (2007) Fallback accretion in the aftermath of a compact binary merger. Mon Not R Astron Soc Lett 376:L48–L51. https://doi.org/10.1111/j.1745-3933.2007.00284.x
Rovelli C (2008) Loop quantum gravity. Living Rev Relativ 11:5. https://doi.org/10.22323/1.224.0005
Rowlinson A, O’Brien PT, Tanvir NR, Zhang B, Evans PA, Lyons N, Levan AJ, Willingale R, Page KL, Onal O et al (2010) The unusual X-ray emission of the short Swift GRB 090515: evidence for the formation of a magnetar? Mon Not R Astron Soc 409:531–540. https://doi.org/10.1063/1.3621770
Rowlinson A, O’Brien PT, Metzger BD, Tanvir NR, Levan AJ (2013) Signatures of magnetar central engines in short GRB light curves. Mon Not R Astron Soc 430:1061–1087. https://doi.org/10.1093/mnras/sts683
Rubin VC, Thonnard N, Ford WK Jr (1978) Extended rotation curves of high-luminosity spiral galaxies. IV. Systematic dynamical properties, SA through SC. Astrophys J 225:L107–L111. https://doi.org/10.1086/182804
Rubin VC, Ford WK Jr, Thonnard N (1980) Rotational properties of 21 Sc galaxies with a large range of luminosities and radii, from NGC 4605 (\(R = 4\) kpc) to UGC 2885 (\(R = 122\) kpc). Astrophys J 238:471–487
Ruffert M, Janka HT (1998) Colliding neutron stars. Gravitational waves, neutrino emission, and gamma-ray bursts. Astron Astrophys 338:535–555
Ruiz M, Shapiro SL (2017) General relativistic magnetohydrodynamics simulations of prompt-collapse neutron star mergers: the absence of jets. Phys Rev D 96:084063. https://doi.org/10.1103/physrevd.96.084063
Ryan G, van Eerten H, Piro L, Troja E (2020) Gamma-ray burst afterglows in the multimessenger era: numerical models and closure relations. Astrophys J 896:166. https://doi.org/10.3847/1538-4357/ab93cf. arXiv:1909.11691
Sadowski A, Belczynski K, Bulik T, Ivanova N, Rasio FA, O’Shaughnessy R (2008) The total merger rate of compact object binaries in the local universe. Astrophys J 676:1162. https://doi.org/10.1086/528932
Safarzadeh M, Berger E, Leja J, Speagle JS (2019) Measuring the delay time distribution of binary neutron stars. III. Using the individual star formation histories of gravitational-wave event host galaxies in the local universe. Astrophys J Lett 878:L14. https://doi.org/10.3847/2041-8213/ab24e3
Sagués Carracedo A, Bulla M, Feindt U, Goobar A (2020) Detectability of kilonovae in optical surveys: post-mortem examination of the LVC O3 run follow-up. arXiv e-prints arXiv:2004.06137
Sakstein J, Jain B (2017) Implications of the neutron star merger GW170817 for cosmological scalar-tensor theories. Phys Rev Lett 119:251303. https://doi.org/10.1103/physrevlett.119.251303
Salafia OS, Giacomazzo B (2020) Accretion-to-jet energy conversion efficiency in GW170817. arXiv e-prints arXiv:2006.07376
Salam A (1968) Weak and electromagnetic interactions. In: Elementary particle theory: proceedings of the eight Nobel symposium, Almqvist & Wiksell, Stockholm, p 367
Samajdar A, Arun KG (2017) Projected constraints on the dispersion of gravitational waves using advanced ground- and space-based interferometers. Phys Rev D 96:104027. https://doi.org/10.1103/physrevd.96.104027
Sari R, Piran T, Narayan R (1998) Spectra and light curves of gamma-ray burst afterglows. Astrophys J Lett 497:L17–L20. https://doi.org/10.1086/311269
Sari R, Piran T, Halpern JP (1999) Jets in gamma-ray bursts. Astrophys J Lett 519:L17–L20. https://doi.org/10.1086/312109
Sathyaprakash BS, Schutz BF, Van Den Broeck C (2010) Cosmography with the Einstein Telescope. Class Quantum Grav 27:215006. https://doi.org/10.1088/0264-9381/27/21/215006
Sathyaprakash B, Abernathy M, Acernese F, Ajith P, Allen B, Amaro-Seoane P, Andersson N, Aoudia S, Arun K, Astone P et al (2012) Scientific objectives of Einstein Telescope. Class Quantum Grav 29:124013. https://doi.org/10.1088/0264-9381/29/12/124013
Savchenko V, Ferrigno C, Kuulkers E, Bazzano A, Bozzo E, Brandt S, Chenevez J, Courvoisier TJL, Diehl R, Domingo A, Hanlon L, Jourdain E, von Kienlin A, Laurent P, Lebrun F, Lutovinov A, Martin-Carrillo A, Mereghetti S, Natalucci L, Rodi J, Roques JP, Sunyaev R, Ubertini P (2017) INTEGRAL detection of the first prompt gamma-ray signal coincident with the gravitational-wave event GW170817. Astrophys J Lett 848:L15. https://doi.org/10.3847/2041-8213/aa8f94
Schnittman JD, Dal Canton T, Camp J, Tsang D, Kelly BJ (2018) Electromagnetic chirps from neutron star-black hole mergers. Astrophys J 853:123. https://doi.org/10.3847/1538-4357/aaa08b
Schutz BF (1986) Determining the Hubble constant from gravitational wave observations. Nature 323:310. https://doi.org/10.1038/323310a0
Schutz BF (2002) Lighthouses of gravitational wave astronomy. In: Gilfanov M, Sunyeav R, Churazov E (eds) Lighthouses of the Universe: the most luminous celestial objects and their use for cosmology, ESO astrophysics symposia. Springer, Berlin, pp 207–224. https://doi.org/10.1007/10856495_29
Schutz BF (2011) Networks of gravitational wave detectors and three figures of merit. Class Quantum Grav 28:125023. https://doi.org/10.1088/0264-9381/28/12/125023
Sekiguchi Y, Kiuchi K, Kyutoku K, Shibata M (2011) Gravitational waves and neutrino emission from the merger of binary neutron stars. Phys Rev Lett 107:051102. https://doi.org/10.1103/physrevlett.107.051102
Senno N, Murase K, Mészáros P (2016) Choked jets and low-luminosity gamma-ray bursts as hidden neutrino sources. Phys Rev D 93:083003. https://doi.org/10.1103/physrevd.93.083003
Shapiro II (1964) Fourth test of general relativity. Phys Rev Lett 13:789. https://doi.org/10.1103/physrevlett.13.789
Shapley H (1918) Studies based on the colors and magnitudes in stellar clusters. VII. The distances, distribution in space, and dimensions of 69 globular clusters. Astrophys J. https://doi.org/10.1086/142423
Shibata M, Taniguchi K (2006) Merger of binary neutron stars to a black hole: disk mass, short gamma-ray bursts, and quasinormal mode ringing. Phys Rev D 73:064027. https://doi.org/10.1103/physrevd.73.064027
Shibata M, Uryū K (2000) Simulation of merging binary neutron stars in full general relativity: \(\Gamma = 2\) case. Phys Rev D 61:064001. https://doi.org/10.1103/physrevd.61.064001
Shibata M, Zhou E, Kiuchi K, Fujibayashi S (2019) Constraint on the maximum mass of neutron stars using GW170817 event. Phys Rev D 100:023015. https://doi.org/10.1103/PhysRevD.100.023015. arXiv:1905.03656
Shoemaker IM, Murase K (2018) Constraints from the time lag between gravitational waves and gamma rays: implications of GW170817 and GRB 170817A. Phys Rev D 97:083013. https://doi.org/10.1103/physrevd.97.083013
Shull JM, Smith BD, Danforth CW (2012) The baryon census in a multiphase intergalactic medium: 30% of the baryons may still be missing. Astrophys J 759:23. https://doi.org/10.1088/0004-637x/759/1/23
Siegel DM, Metzger BD (2017) Three-dimensional general-relativistic magnetohydrodynamic simulations of remnant accretion disks from neutron star mergers: outflows and r-process nucleosynthesis. Phys Rev Lett 119:231102. https://doi.org/10.1103/physrevlett.119.231102
Siegel DM, Barnes J, Metzger BD (2019) Collapsars as a major source of r-process elements. Nature 569:241. https://doi.org/10.1038/s41586-019-1136-0
Singer LP, Price LR (2016) Rapid Bayesian position reconstruction for gravitational-wave transients. Phys Rev D 93:024013. https://doi.org/10.1103/physrevd.93.024013
Singer LP, Price LR, Farr B, Urban AL, Pankow C, Vitale S, Veitch J, Farr WM, Hanna C, Cannon K et al (2014) The first two years of electromagnetic follow-up with Advanced LIGO and Virgo. Astrophys J 795:105. https://doi.org/10.1088/0004-637x/795/2/105
Smolin L (2008) Three roads to quantum gravity. Basic Books, New York
Smoot GF, Bennett CL, Kogut A, Wright EL, Aymon J, Boggess NW, Cheng ES, De Amici G, Gulkis S, Hauser MG et al (1992) Structure in the COBE differential microwave radiometer first-year maps. Astrophys J 396:L1–L5. https://doi.org/10.1086/186504
Soares-Santos M, Holz DE, Annis J, Chornock R, Herner K, Berger E, Brout D, Chen HY, Kessler R, Sako M et al (2017) The electromagnetic counterpart of the binary neutron star merger LIGO/Virgo GW170817. I. Discovery of the optical counterpart using the dark energy camera. Astrophys J Lett 848:L16. https://doi.org/10.3847/2041-8213/aa9059
Sokolsky P (2018) Introduction to ultrahigh energy cosmic ray physics. CRC Press, Boca Raton. https://doi.org/10.1201/9780429499654
Solodukhin SN (2011) Entanglement entropy of black holes. Living Rev Relativ 14:8. https://doi.org/10.12942/lrr-2011-8
Song HR, Ai SK, Wang MH, Xing N, Gao H, Zhang B (2019) Viewing angle constraints on S190425z and S190426c and the joint gravitational-wave/gamma-ray detection fractions for binary neutron star mergers. Astrophys J Lett 881:L40. https://doi.org/10.3847/2041-8213/ab3921
Starling RLC, Wijers RAMJ, Hughes MA, Tanvir NR, Vreeswijk PM, Rol E, Salamanca I (2005) Spectroscopy of the \(\gamma \)-ray burst GRB 021004: a structured jet ploughing through a massive stellar wind. Mon Not R Astron Soc 360:305–313. https://doi.org/10.1111/j.1365-2966.2005.09042.x
Starobinskiǐ AA (1979) Spectrum of relict gravitational radiation and the early state of the universe. Sov J Exp Theor Phys Lett 30:682. https://doi.org/10.1142/9789814317344_0078
Stodolsky L (1988) The speed of light and the speed of neutrinos. Phys Lett B 201:353–354. https://doi.org/10.1016/0370-2693(88)91154-9
Stone N, Loeb A, Berger E (2013) Pulsations in short gamma ray bursts from black hole-neutron star mergers. Phys Rev D 87:084053. https://doi.org/10.1103/physrevd.87.084053
Strong IB, Klebesadel RW, Olson RA (1974) A preliminary catalog of transient cosmic gamma-ray sources observed by the VELA satellites. Astrophys J 188:L1. https://doi.org/10.1086/181415
Sun H, Zhang B, Gao H (2017) X-ray counterpart of gravitational waves due to binary neutron star mergers: light curves, luminosity function, and event rate density. Astrophys J 835:7. https://doi.org/10.3847/1538-4357/835/1/7
Sun H, Li Y, Zhang BB, Zhang B, Bauer FE, Xue Y, Yuan W (2019) A unified binary neutron star merger magnetar model for the chandra X-ray transients CDF-S XT1 and XT2. Astrophys J 886:129. https://doi.org/10.3847/1538-4357/ab4bc7. arXiv:1908.01107
Svinkin DS, Hurley K, Aptekar RL, Golenetskii SV, Frederiks DD (2015) A search for giant flares from soft gamma-ray repeaters in nearby galaxies in the Konus-WIND short burst sample. Mon Not R Astron Soc 447:1028–1032. https://doi.org/10.1093/mnras/stu2436
Symbalisty E, Schramm DN (1982) Neutron star collisions and the r-process. Astrophys Lett 22:143–145
Tak D, Guiriec S, Uhm ZL, Yassine M, Omodei N, McEnery J (2019) Multiple components in the broadband \(\gamma \)-ray emission of the short GRB 160709A. Astrophys J 876:76. https://doi.org/10.3847/1538-4357/ab0e72
Takeda H, Nishizawa A, Michimura Y, Nagano K, Komori K, Ando M, Hayama K (2018) Polarization test of gravitational waves from compact binary coalescences. Phys Rev D 98:022008. https://doi.org/10.1103/physrevd.98.022008
Tamanini N, Caprini C, Barausse E, Sesana A, Klein A, Petiteau A (2016) Science with the space-based interferometer eLISA. III: probing the expansion of the universe using gravitational wave standard sirens. JCAP 2016:002. https://doi.org/10.1088/1475-7516/2016/04/002
Tanabashi M, Hagiwara K, Hikasa K, Nakamura K, Sumino Y, Takahashi F, Tanaka J, Agashe K, Aielli G, Amsler C et al (2018) Review of particle physics. Phys Rev D 98:030001
Tanaka M (2016) Kilonova/macronova emission from compact binary mergers. Adv Astron. https://doi.org/10.1155/2016/6341974
Tanaka M, Hotokezaka K (2013) Radiative transfer simulations of neutron star merger ejecta. Astrophys J 775:113. https://doi.org/10.1088/0004-637X/775/2/113
Tanvir NR, Levan AJ, Fruchter AS, Hjorth J, Hounsell RA, Wiersema K, Tunnicliffe RL (2013) A ‘kilonova’ associated with the short-duration \(\gamma \)-ray burst GRB 130603B. Nature 500:547. https://doi.org/10.1038/nature12505
Tanvir NR, Levan AJ, González-Fernández C, Korobkin O, Mandel I, Rosswog S, Hjorth J, D’Avanzo P, Fruchter AS, Fryer CL et al (2017) The emergence of a lanthanide-rich kilonova following the merger of two neutron stars. Astrophys J Lett 848:L27. https://doi.org/10.3847/2041-8213/aa90b6
Tauris TM, Kramer M, Freire PCC, Wex N, Janka HT, Langer N, Podsiadlowski P, Bozzo E, Chaty S, Kruckow MU et al (2017) Formation of double neutron star systems. Astrophys J 846:170. https://doi.org/10.3847/1538-4357/aa7e89
Taveras V, Yunes N (2008) Barbero-Immirzi parameter as a scalar field: K-inflation from loop quantum gravity? Phys Rev D 78:064070. https://doi.org/10.1103/physrevd.78.064070
Taylor JH, Weisberg JM (1982) A new test of general relativity: gravitational radiation and the binary pulsar PSR 1913+16. Astrophys J 253:908–920. https://doi.org/10.1086/159690
Taylor SR, Gair JR (2012) Cosmology with the lights off: standard sirens in the Einstein Telescope era. Phys Rev D 86:023502. https://doi.org/10.1103/physrevd.86.023502
Taylor GB, Frail DA, Berger E, Kulkarni SR (2004) The angular size and proper motion of the afterglow of grb 030329. Astrophys J Lett 609:L1. https://doi.org/10.1086/422554
Thompson C (1994) A model of gamma-ray bursts. Mon Not R Astron Soc 270:480–498. https://doi.org/10.1093/mnras/270.3.480
Timmes F, Fryer C, Timmes F, Hungerford AL, Couture A, Adams F, Aoki W, Arcones A, Arnett D, Auchettl K et al (2019) Catching element formation in the act; the case for a new MeV gamma-ray mission: radionuclide astronomy in the 2020s. BAAS 51:2. https://doi.org/10.2172/1498895
Tolman RC (1939) Static solutions of Einstein’s field equations for spheres of fluid. Phys Rev 55:364. https://doi.org/10.1103/physrev.55.364
Toma K, Sakamoto T, Zhang B, Hill JE, McConnell ML, Bloser PF, Yamazaki R, Ioka K, Nakamura T (2009) Statistical properties of gamma-ray burst polarization. Astrophys J 698:1042. https://doi.org/10.1088/0004-637x/698/2/1042
Troja E, Cusumano G, O’Brien PT, Zhang B, Sbarufatti B, Mangano V, Willingale R, Chincarini G, Osborne JP, Marshall FE, Burrows DN, Campana S, Gehrels N, Guidorzi C, Krimm HA, La Parola V, Liang EW, Mineo T, Moretti A, Page KL, Romano P, Tagliaferri G, Zhang BB, Page MJ, Schady P (2007) Swift observations of GRB 070110: an extraordinary X-ray afterglow powered by the central engine. Astrophys J 665:599–607. https://doi.org/10.1086/519450
Troja E, Rosswog S, Gehrels N (2010) Precursors of short gamma-ray bursts. Astrophys J 723:1711. https://doi.org/10.1088/0004-637x/723/2/1711
Troja E, Lipunov VM, Mundell CG, Butler NR, Watson AM, Kobayashi S, Cenko SB, Marshall FE, Ricci R, Fruchter A et al (2017a) Significant and variable linear polarization during the prompt optical flash of GRB 160625B. Nature 547:425. https://doi.org/10.1038/nature23289
Troja E, Piro L, van Eerten H, Wollaeger RT, Im M, Fox OD, Butler NR, Cenko SB, Sakamoto T, Fryer CL et al (2017b) The X-ray counterpart to the gravitational-wave event GW170817. Nature 551:71. https://doi.org/10.1038/nature24290
Troja E, Van Eerten H, Ryan G, Ricci R, Burgess JM, Wieringa MH, Piro L, Cenko SB, Sakamoto T (2019) A year in the life of GW 170817: the rise and fall of a structured jet from a binary neutron star merger. Mon Not R Astron Soc 489:1919–1926. https://doi.org/10.1093/mnras/stz2248
Tsang D, Read JS, Hinderer T, Piro AL, Bondarescu R (2012) Resonant shattering of neutron star crusts. Phys Rev Lett 108:011102. https://doi.org/10.1103/physrevlett.108.011102
Tso R, Isi M, Chen Y, Stein L (2017) Modeling the dispersion and polarization content of gravitational waves for tests of general relativity. In: Proceedings of the seventh meeting on CPT and Lorentz symmetry, World Scientific, pp 205–208. https://doi.org/10.1142/9789813148505_0052
Tunnicliffe RL, Levan AJ, Tanvir NR, Rowlinson A, Perley DA, Bloom JS, Cenko SB, O’Brien PT, Cobb BE, Wiersema K et al (2013) On the nature of the ‘hostless’ short GRBs. Mon Not R Astron Soc 437:1495–1510. https://doi.org/10.1093/mnras/stt1975
Usman SA, Nitz AH, Harry IW, Biwer CM, Brown DA, Cabero M, Capano CD, Dal Canton T, Dent T, Fairhurst S et al (2016) The PyCBC search for gravitational waves from compact binary coalescence. Class Quantum Grav 33:215004. https://doi.org/10.1088/0264-9381/33/21/215004
Usov VV (1992) Millisecond pulsars with extremely strong magnetic fields as a cosmological source of \(\gamma \)-ray bursts. Nature 357:472–474. https://doi.org/10.1038/357472a0
Valenti S, David J, Yang S, Cappellaro E, Tartaglia L, Corsi A, Jha SW, Reichart DE, Haislip J, Kouprianov V (2017) The discovery of the electromagnetic counterpart of GW170817: kilonova AT 2017gfo/DLT17ck. Astrophys J Lett 848:L24. https://doi.org/10.3847/2041-8213/aa8edf
van de Voort F, Pakmor R, Grand RJJ, Springel V, Gómez FA, Marinacci F (2020) Neutron star mergers and rare core-collapse supernovae as sources of r-process enrichment in simulated galaxies. Mon Not R Astron Soc 494:4867–4883. https://doi.org/10.1093/mnras/staa754. arXiv:1907.01557
Van Elewyck V, Ando S, Aso Y, Baret B, Barsuglia M, Bartos I, Chassande-Mottin E, Di Palma I, Dwyer J, Finley C et al (2009) Joint searches between gravitational-wave interferometers and high-energy neutrino telescopes: science reach and analysis strategies. Int J Mod Phys D 18:1655–1659. https://doi.org/10.1142/s0218271809015655
Van Paradijs J, Groot PJ, Galama T, Kouveliotou C, Strom RG, Telting J, Rutten RGM, Fishman GJ, Meegan CA, Pettini M et al (1997) Transient optical emission from the error box of the \(\gamma \)-ray burst of 28 February 1997. Nature 386:686. https://doi.org/10.1038/386686a0
Vasileiou V, Jacholkowska A, Piron F, Bolmont J, Couturier C, Granot J, Stecker FW, Cohen-Tanugi J, Longo F (2013) Constraints on Lorentz invariance violation from Fermi-Large Area Telescope observations of gamma-ray bursts. Phys Rev D 87:122001. https://doi.org/10.1103/physrevd.87.122001
Velasco R (2019) Discovery of late-time very high energy emission from a gamma-ray burst afterglow. In: 1st international Cherenkov telescope array symposium. https://indico.cta-observatory.org/event/1946/contributions/19893/
Veres P, Mészáros P, Goldstein A, Fraija N, Connaughton V, Burns E, Preece RD, Hamburg R, Wilson-Hodge CA, Briggs MS et al (2018) Gamma-ray burst models in light of the GRB 170817A-GW170817 connection. arXiv e-prints arXiv:1802.07328
Vietri M (1995) On the acceleration of ultra high energy cosmic rays in gamma ray bursts. arXiv e-prints arXiv:astro-ph/9506081
Villar VA, Guillochon J, Berger E, Metzger BD, Cowperthwaite PS, Nicholl M, Alexander KD, Blanchard PK, Chornock R, Eftekhari T, Fong W, Margutti R, Williams PKG (2017) The combined ultraviolet, optical, and near-infrared light curves of the kilonova associated with the binary neutron star merger GW170817: unified data set, analytic models, and physical implications. Astrophys J Lett 851:L21. https://doi.org/10.3847/2041-8213/aa9c84
Vitale S, Chen HY (2018) Measuring the Hubble constant with neutron star black hole mergers. Phys Rev Lett 121:021303. https://doi.org/10.1103/PhysRevLett.121.021303
Voges W, Aschenbach B, Boller T, Brauninger H, Briel U, Burkert W, Dennerl K, Englhauser J, Gruber R, Haberl F et al (2000) Rosat all-sky survey faint source catalogue. IAU Circ 7432:3
Volovik GE (2001) Superfluid analogies of cosmological phenomena. Phys Rep 351:195–348. https://doi.org/10.1016/s0370-1573(00)00139-3
von Kienlin A, Beckmann V, Rau A, Arend N, Bennett K, McBreen B, Connell P, Deluit S, Hanlon L, Hurley K, Kippen M, Lichti GG, Moran L, Preece R, Roques J-P, Schönfelder V, Skinner G, Strong A, Williams R (2003) INTEGRAL spectrometer SPI’s GRB detection capabilities. GRBs detected inside SPI’s FoV and with the anticoincidence system ACS. Astron Astrophys 411:L299–L305. https://doi.org/10.1051/0004-6361:20031231
von Kienlin A, Meegan CA, Paciesas WS, Bhat PN, Bissaldi E, Briggs MS, Burns E, Cleveland WH, Gibby MH, Giles MM et al (2020) The fourth Fermi-GBM gamma-ray burst catalog: a decade of data. Astrophys J 893:46. https://doi.org/10.3847/1538-4357/ab7a18
Wallner A, Faestermann T, Feige J, Feldstein C, Knie K, Korschinek G, Kutschera W, Ofan A, Paul M, Quinto F et al (2015) Abundance of live \(^{244}\)Pu in deep-sea reservoirs on Earth points to rarity of actinide nucleosynthesis. Nat Commun 6:5956. https://doi.org/10.1038/ncomms6956
Wanajo S (2013) The r-process in proto-neutron-star wind revisited. Astrophys J Lett 770:L22. https://doi.org/10.1088/2041-8205/770/2/L22
Wanajo S, Sekiguchi Y, Nishimura N, Kiuchi K, Kyutoku K, Shibata M (2014) Production of all the r-process nuclides in the dynamical ejecta of neutron star mergers. Astrophys J Lett 789:L39
Wanderman D, Piran T (2010) The luminosity function and the rate of Swift’s gamma-ray bursts. Mon Not R Astron Soc 406:1944–1958. https://doi.org/10.1111/j.1365-2966.2010.16787.x
Wanderman D, Piran T (2015) The rate, luminosity function and time delay of non-Collapsar short GRBs. Mon Not R Astron Soc 448:3026–3037. https://doi.org/10.1093/mnras/stv123
Wang JS, Peng FK, Wu K, Dai ZG (2018) Pre-merger electromagnetic counterparts of binary compact stars. Astrophys J 868:19. https://doi.org/10.3847/1538-4357/aae531
Wang XY, Liu RY, Zhang HM, Xi SQ, Zhang B (2019) Synchrotron self-compton emission from external shocks as the origin of the sub-TeV emission in GRB 180720B and GRB 190114C. Astrophys J 884:117. https://doi.org/10.3847/1538-4357/ab426c. arXiv:1905.11312
Waxman E (1995) Cosmological gamma-ray bursts and the highest energy cosmic rays. Phys Rev Lett 75:386. https://doi.org/10.1103/physrevlett.75.386
Waxman E, Bahcall J (1997) High energy neutrinos from cosmological gamma-ray burst fireballs. Phys Rev Lett 78:2292. https://doi.org/10.1103/physrevlett.78.2292
Wei JJ, Gao H, Wu XF, Mészáros P (2015) Testing Einstein’s equivalence principle with fast radio bursts. Phys Rev Lett 115:261101. https://doi.org/10.1103/physrevlett.115.261101
Wei JJ, Wang JS, Gao H, Wu XF (2016) Tests of the Einstein equivalence principle using TeV blazars. Astrophys J Lett 818:L2. https://doi.org/10.3847/2041-8205/818/1/l2
Wei JJ, Zhang BB, Wu XF, Gao H, Mészáros P, Zhang B, Dai ZG, Zhang SN, Zhu ZH (2017) Multimessenger tests of the weak equivalence principle from GW170817 and its electromagnetic counterparts. JCAP 2017:035. https://doi.org/10.1088/1475-7516/2017/11/035
Wei JJ, Zhang BB, Shao L, Gao H, Li Y, Yin QQ, Wu XF, Wang XY, Zhang B, Dai ZG (2019) Multimessenger tests of Einstein’s weak equivalence principle and Lorentz invariance with a high-energy neutrino from a flaring blazar. J High Energy Astrophys 22:1–4. https://doi.org/10.1016/j.jheap.2019.01.002
Weinberg S (1967) A model of leptons. Phys Rev Lett 19:1264. https://doi.org/10.1103/physrevlett.19.1264
Weinberg S (2008) Effective field theory for inflation. Phys Rev D 77:123541. https://doi.org/10.1103/physrevd.77.123541
Weinberg DH, Mortonson MJ, Eisenstein DJ, Hirata C, Riess AG, Rozo E (2013) Observational probes of cosmic acceleration. Phys Rep 530:87–255. https://doi.org/10.1016/j.physrep.2013.05.001
Will CM (1998) Bounding the mass of the graviton using gravitational-wave observations of inspiralling compact binaries. Phys Rev D 57:2061. https://doi.org/10.1103/physrevd.57.2061
Will CM (2014) The confrontation between general relativity and experiment. Living Rev Relativ 17:4. https://doi.org/10.12942/lrr-2014-4
Will CM (2018) Theory and experiment in gravitational physics. Cambridge University Press, Cambridge. https://doi.org/10.1017/9781316338612
Williams D, Clark JA, Williamson AR, Heng IS (2018) Constraints on short, hard gamma-ray burst beaming angles from gravitational wave observations. Astrophys J 858:79. https://doi.org/10.3847/1538-4357/aab847
Williamson AR, Biwer C, Fairhurst S, Harry IW, Macdonald E, Macleod D, Predoi V (2014) Improved methods for detecting gravitational waves associated with short gamma-ray bursts. Phys Rev D 90:122004. https://doi.org/10.1103/physrevd.90.122004
Willingale R, O’Brien PT, Osborne JP, Godet O, Page KL, Goad MR, Burrows DN, Zhang B, Rol E, Gehrels N et al (2007) Testing the standard fireball model of gamma-ray bursts using late X-ray afterglows measured by Swift. Astrophys J 662:1093. https://doi.org/10.1086/517989
Wollaeger RT, Korobkin O, Fontes CJ, Rosswog SK, Even WP, Fryer CL, Sollerman J, Hungerford AL, Van Rossum DR, Wollaber AB (2018) Impact of ejecta morphology and composition on the electromagnetic signatures of neutron star mergers. Mon Not R Astron Soc 478:3298–3334. https://doi.org/10.1093/mnras/sty1018
Wood J (2016) An all-sky search for bursts of very high energy gamma rays with HAWC. PhD thesis, University of Maryland, College Park. arXiv:1801.01550
Woosley SE (1993) Gamma-ray bursts from stellar mass accretion disks around black holes. Astrophys J 405:273–277. https://doi.org/10.1086/172359
Woosley SE, Bloom JS (2006) The supernova-gamma-ray burst connection. Annu Rev Astron Astrophys 44:507–556. https://doi.org/10.1063/1.2207927
Woosley SE, Hoffman RD (1992) The alpha-process and the r-process. Astrophys J 395:202–239. https://doi.org/10.1086/171644
Woosley SE, Wilson JR, Mathews GJ, Hoffman RD, Meyer BS (1994) The r-process and neutrino-heated supernova ejecta. Astrophys J 433:229–246. https://doi.org/10.1086/174638
Wu CS, Ambler E, Hayward RW, Hoppes DD, Hudson RP (1957) Experimental test of parity conservation in beta decay. Phys Rev 105:1413. https://doi.org/10.1016/b978-0-08-006509-0.50011-9
Wu MR, Banerjee P, Metzger BD, Martínez-Pinedo G, Aramaki T, Burns E, Hailey CJ, Barnes J, Karagiorgi G (2019) Finding the remnants of the Milky Way’s last neutron star mergers. Astrophys J 880:23. https://doi.org/10.3847/1538-4357/ab2593. arXiv:1905.03793
Xie X, Zrake J, MacFadyen A (2018) Numerical simulations of the jet dynamics and synchrotron radiation of binary neutron star merger event GW170817/GRB 170817A. Astrophys J 863:58. https://doi.org/10.3847/1538-4357/aacf9c
Xue YQ, Zheng XC, Li Y, Brandt WN, Zhang B, Luo B, Zhang BB, Bauer FE, Sun H, Lehmer BD, Wu XF, Yang G, Kong X, Li JY, Sun MY, Wang JX, Vito F (2019) A magnetar-powered X-ray transient as the aftermath of a binary neutron-star merger. Nature 568:198–201. https://doi.org/10.1038/s41586-019-1079-5
Yagi K, Yunes N (2013) I-Love-Q: unexpected universal relations for neutron stars and quark stars. Science 341:365–368. https://doi.org/10.1126/science.1236462
Yang B, Jin ZP, Li X, Covino S, Zheng XZ, Hotokezaka K, Fan YZ, Piran T, Wei DM (2015) A possible macronova in the late afterglow of the long-short burst GRB 060614. Nat Commun 6:7323. https://doi.org/10.1038/ncomms8323
Yang S et al (2017) LIGO/Virgo G298048: continued observation for DLT17ck. Technical report, GSFC. https://gcn.gsfc.nasa.gov/gcn3/21579.gcn3
Yonetoku D, Murakami T, Gunji S, Mihara T, Toma K, Morihara Y, Takahashi T, Wakashima Y, Yonemochi H, Sakashita T et al (2012) Magnetic structures in gamma-ray burst jets probed by gamma-ray polarization. Astrophys J Lett 758:L1. https://doi.org/10.1088/2041-8205/758/1/l1
Yost SA, Harrison FA, Sari R, Frail DA (2003) A study of the afterglows of four gamma-ray bursts: constraining the explosion and fireball model. Astrophys J 597:459. https://doi.org/10.1086/378288
Yu YW, Zhang B, Gao H (2013) Bright “Merger-nova” from the remnant of a neutron star binary merger: a signature of a newly born, massive, millisecond magnetar. Astrophys J Lett 776:L40. https://doi.org/10.1088/2041-8205/776/2/L40
Yunes N, Siemens X (2013) Gravitational-wave tests of general relativity with ground-based detectors and pulsar-timing arrays. Living Rev Relativ 16:9. https://doi.org/10.12942/lrr-2013-9
Yunes N, O’Shaughnessy R, Owen BJ, Alexander S (2010) Testing gravitational parity violation with coincident gravitational waves and short gamma-ray bursts. Phys Rev D 82:064017. https://doi.org/10.1103/physrevd.82.064017
Zalamea I, Beloborodov AM (2011) Neutrino heating near hyper-accreting black holes. Mon Not R Astron Soc 410:2302–2308. https://doi.org/10.1111/j.1365-2966.2010.17600.x
Zappa F, Bernuzzi S, Radice D, Perego A, Dietrich T (2018) Gravitational-wave luminosity of binary neutron stars mergers. Phys Rev Lett 120:111101. https://doi.org/10.1103/physrevlett.120.111101
Zhang B (2018) The physics of gamma-ray bursts. Cambridge University Press, Cambridge. https://doi.org/10.1017/9781139226530
Zhang B (2019) The delay time of gravitational wave: gamma-ray burst associations. Front Phys 14:64402. https://doi.org/10.1007/s11467-019-0913-4
Zhang B, Kumar P (2013) Model-dependent high-energy neutrino flux from gamma-ray bursts. Phys Rev Lett 110:121101. https://doi.org/10.1103/PhysRevLett.110.121101
Zhang B, Mészáros P (2001) Gamma-ray burst afterglow with continuous energy injection: signature of a highly magnetized millisecond pulsar. Astrophys J Lett 552:L35. https://doi.org/10.1086/320255
Zhang B, Mészáros P (2002) Gamma-ray burst beaming: a universal configuration with a standard energy reservoir? Astrophys J 571:876–879. https://doi.org/10.1086/339981
Zhang B, Yan H (2010) The internal-collision-induced magnetic reconnection and turbulence (ICMART) model of gamma-ray bursts. Astrophys J 726:90. https://doi.org/10.1088/0004-637x/726/2/90
Zhang B, Zhang BB, Liang EW, Gehrels N, Burrows DN, Mészáros P (2007) Making a short gamma-ray burst from a long one: implications for the nature of GRB 060614. Astrophys J Lett 655:L25. https://doi.org/10.1086/511781
Zhang BB, Zhang B, Sun H, Lei WH, Gao H, Li Y, Shao L, Zhao Y, Hu YD, Lü HJ et al (2018a) A peculiar low-luminosity short gamma-ray burst from a double neutron star merger progenitor. Nat Commun 9:447. https://doi.org/10.1038/s41467-018-02847-3
Zhang NB, Li BA, Xu J (2018b) Combined constraints on the equation of state of dense neutron-rich matter from terrestrial nuclear experiments and observations of neutron stars. Astrophys J 859:90. https://doi.org/10.3847/1538-4357/aac027
Zhang SN, Kole M, Bao TW, Batsch T, Bernasconi T, Cadoux F, Chai JY, Dai ZG, Dong YW, Gauvin N et al (2019) Detailed polarization measurements of the prompt emission of five gamma-ray bursts. Nat Astron 3:258. https://doi.org/10.1038/s41550-018-0664-0
Zhu S (2015) Precursors in gamma-ray bursts observed by Fermi. PhD thesis, University of Maryland, College Park. http://hdl.handle.net/1903/17258
Zhuge X, Centrella JM, McMillan SLW (1994) Gravitational radiation from coalescing binary neutron stars. Phys Rev D 50:6247. https://doi.org/10.1103/physrevd.50.6247
Zucker M, Vitale S, Sigg D (2016) Getting an A+: enhancing advanced LIGO. Technical report, LIGO. https://dcc.ligo.org/LIGO-G1601435/public
Zwicky F (1933) Die Rotverschiebung von extragalaktischen Nebeln. Helv Phys Acta 6:110–127
Zwicky F (1937) On the masses of nebulae and of clusters of nebulae. Astrophys J 86:217. https://doi.org/10.1086/143864
Acknowledgements
I would like to acknowledge the groups and individuals who I have worked with over many years, which greatly influenced the content of this paper. My close involvement in the Fermi-GBM+LIGO/Virgo working group has significantly advanced my understanding of this field. Individuals include, but are not limited to, Nelson Christensen, Regina Caputo, Valerie Connaughton, C. Michelle Hui, Dan Kocevski, Julie McEnery, Brian Metzger, Judith Racusin, Jay Tasson, Bing Zhang, who I have long worked with and/or provided direct feedback on this manuscript. I led an Astro2020 white paper from the Multimessenger Science Action Group on Multimessenger Science with Neutron Star Mergers. While this manuscript began before that work started, it greatly expanded the science discussed here, and I thank the individuals who contributed to that paper. I would also like to thank all of the scientists who provided feedback on the initial arXiv version. Lastly, I would like to thank both reviewers for providing helpful feedback on such a long manuscript.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Burns, E. Neutron star mergers and how to study them. Living Rev Relativ 23, 4 (2020). https://doi.org/10.1007/s41114-020-00028-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s41114-020-00028-7