1 Introduction

Fuzzy inference systems methods (FISs) are a framework for computation based on the fundamental concepts of fuzzy set theory proposed by Zadeh (1965), fuzzy rules, and fuzzy reasoning. Fuzzy sets were originally suggested by Zadeh (1965). Fuzzy sets have been used and are beneficial in several important papers in the literature such as Chen (1996), Chen and Chen (2002), Lin et al. (2006), Chen and Hsu (2008) and Chen and Lee (2010), Boltürk (2022), Nguyen-Huynh and Vo-Van (2023), Qian et al. (2023), Sobhi and Dick (2023), Nishad and Aggarwal (2023) and Minaev et al. (2023). FISs methods use fuzzy set theory to match the inputs to the outputs. FISs are composed of three elements: fuzzification, knowledge base (rule base or database), and defuzzification. In the fuzzification stage, a real-valued input is mapped to a fuzzy set through membership functions. At this stage, the input can also be a fuzzy set. The rule base phase is a database of language rules in if–then format. Using these If–Then rules, a judgment is performed by producing a fuzzy output according to the fuzzy input from the fuzzification phase. In the defuzzification phase, this fuzzy output is transformed to produce a crisp (real-valued) output. Among these factors, the fact that the knowledge base is based on expert knowledge and the number of inputs in the system increases makes the determination of rules very difficult and complex.

The fuzzy regression functions approach suggested by Türkşen (2008) utilizes fuzzy functions instead of complex relationships in the rule base. In the FRF method, the inputs and outputs of the system are first clustered with the fuzzy clustering method proposed by Bezdek et al. (1984), and membership values are obtained. These membership values are combined with the system inputs to form an independent variable matrix and an target vector corresponding to these inputs. Then, using ordinary least squares (OLS) based multiple regression analysis, the number of fuzzy functions is obtained as the number of fuzzy sets. There are several studies in the literature on FRF methods.

Beyhan and Alci (2010) developed the concept of fuzzy regression functions with exogenous input autoregressive modeling. Aladag et al. (2014) used fuzzy regression functions for forecasting of Australian beer consumption time series. Gasir and Crockett (2016) proposed a fuzzy regression tree to forecast complex datasets. Başkir (2016) used a fuzzy regression function with least square estimates for modeling Dupont analysis on the Turkish insurance sector. Aladag et al. (2016) proposed a fuzzy time series forecasting method based on a fuzzy regression function approach. Baser and Demirhan (2017) forecasted the horizontal global solar radiation by using a hybrid method based on fuzzy regression functions with a support vector machine. Tak (2018) proposed a meta-fuzzy regression functions approach that aggregates methods for the same purpose into functions. Tak et al. (2018) combined the autoregressive moving average model ARMA with the fuzzy regression functions approach. Bas et al. (2019) suggested a novel fuzzy regression function approach using ridge regression as a replacement for multiple linear regression.

Chakravarty et al. (2020) proposed a robust fuzzy regression functions approach against the outliers. Tak (2020) suggested a forecasting method based on fuzzy regression functions using a possibilistic fuzzy clustering method alternative to the fuzzy clustering method using maximum likelihood estimates for the parameters. Tak (2021a) proposed a forecast combination with meta-possibilistic fuzzy functions. Pehlivan and Turksen (2021) used a multiplicative fuzzy clustering algorithm instead of the fuzzy clustering method and proposed a multiplicative fuzzy regression function method. Tak (2021b) proposed meta-fuzzy functions based on feed-forward neural networks with a single hidden layer for forecasting. Bas (2022) proposed an approach to robust fuzzy regression functions that can be used even in the presence of outliers in the data set. Bas and Egrioglu (2022) replaced the fuzzy clustering algorithm with the Gustafson-Kessel clustering algorithm in their FRF approach. Chakravarty et al. (2022a) proposed a fuzzy regression functions approach by the use of a noise cluster within fuzzy clustering algorithms. Chakravarty et al. (2022b) proposed a modified fuzzy regression functions framework using a noise cluster for robust wind forecasting. Tak and İnan (2022) proposed a fuzzy regression method to employ an elastic net in fuzzy functions to overcome the multicollinearity problem. Cevik et al. (2023) proposed a forecast combination approach with meta-fuzzy functions for forecasting the number of immigrants within the maritime line security project in Turkey. In addition to these studies, there are numerous studies in the literature where both fuzzy methods and artificial neural network methods are used in the forecasting problem.

Chen and Phuong (2017) proposed a new fuzzy time series forecasting method based on optimal partitions of intervals in the universe of discourse and optimal weighting vectors of two-factor second-order fuzzy-trend logical relationship groups. Cheng et al. (2016) proposed a new fuzzy time series forecasting method for forecasting the Taiwan stock exchange capitalization-weighted stock index. Chen and Jian (2017) proposed a new fuzzy forecasting method based on two-factors second-order fuzzy-trend logical relationship groups, particle swarm optimization techniques, and similarity measures between the subscripts of fuzzy sets. Singh et al. (2018) proposed a firefly algorithm-based neural network for nonlinear discrete-time systems. Zeng et al. (2019) proposed a new clustering-based fuzzy time series forecasting method based on linear combinations of independent variables, the subtractive clustering algorithm, and the artificial bee colony algorithm. Chen et al. (2019) proposed a fuzzy time series forecasting model based on proportions of intervals and particle swarm optimization techniques. Gupta and Kumar (2019) proposed a novel high-order probabilistic fuzzy set-based forecasting method in the environment of both non-probabilistic and probabilistic uncertainties.

Chen et al. (2020) used fuzzy information granulation and deep neural networks combined to solve traffic-flow forecasting. Fan et al. (2021) suggested a deep-learning approach for financial market prediction. Pant and Kumar (2022a) proposed a fuzzy time series forecasting method based on hesitant fuzzy sets, particle swarm optimization, and support vector machines. Pant and Kumar (2022b) proposed a novel method for fuzzy time series forecasting based on particle swarm optimization and intuitionistic fuzzy set. Goyal and Bisht (2023) proposed an adaptive hybrid fuzzy time series forecasting technique based on particle swarm optimization. Samal and Dash (2023) developed a novel stock index trend predictor model by integrating multiple criteria decision-making with an optimized online sequential extreme learning machine. Song et al. (2024) proposed a hybrid time series forecasting model by developing linear and nonlinear series separately. Pant and Kumar (2024) proposed a hesitant fuzzy sets-based computational method for weighted fuzzy time series.

In this study, for the first time in the literature, the Gaussian Process Regression (GPR) method is used instead of OLS regression in the FRF method. The motivation for this paper is that the FRF method is based on OLS regression and OLS regression is not a suitable method for parameter estimation for nonlinear data. Based on this motivation, this study proposes a fuzzy inference system that can be used for nonlinear data. The contribution of this paper is to adapt the GPR method, which can provide uncertainty measures on forecasts and can work with both small data and nonlinear data, to the FRF method using the OLS method. Another contribution of the study is to propose a new FRF method based on the GPR method instead of the OLS regression-based FRF method, which is not suitable for parameter estimation using the ordinary least squares method for nonlinear data. The performance of the proposed fuzzy regression functions approach based on Gaussian process regression (FRF-GPR) is examined by analyzing randomly selected Bitcoin and crude oil time series.

The other sections of the paper are as follows. Section 2 briefly introduces the GPR method. Section 3 presents the step-by-step algorithm of the proposed FRF-GPR method. Section 4 reports the analysis results obtained by comparing the proposed method with alternative methods. Section 5 summarizes the discussion and conclusions of the study.

2 Gaussian process regression

GPR is a strong and versatile nonparametric regression technique. It is especially helpful where the association between input variables and output is not known explicitly or may be ambiguous. GPR is a Bayesian approximation that can model the uncertainty in forecasts.

Let a linear regression model be as given in Eq. (1).

$$y={x}^{T}\beta +\varepsilon$$
(1)

where \(\varepsilon \sim N\left(0,{\sigma }^{2}\right).\)

A GPR model describes the response by introducing latent variables, \(f({x}_{i})\), \(i=\mathrm{1,2},...,n\) and overt basis functions, \(h\), from a Gaussian process (GP). A GP is a collection of random variables with any finite number of common Gaussian distributions.

Let's consider the model given in Eq. (2).

$$h{\left(x\right)}^{T}\beta +f\left(x\right)$$
(2)

where \(f\left(x\right) \sim GP\left(0,k\left(x,{x}{\prime}\right)\right).\) So, \(f\left(x\right)\) has a zero mean with covariance function, \(k\left(x,{x}^{\mathrm{^{\prime}}}\right)\). The covariance function \(k\left(x,{x}^{\mathrm{^{\prime}}}\right)\) is typically characterized by a sequence of kernel parameters or hyperparameters. Different kernel functions can be used in GPR. In this study, the following squared exponential kernel function given by Eq. (3) is used.

$$k\left({x}_{i},{x}_{j}\backslash \theta \right)={\sigma }_{f}^{2}exp\left[-\frac{1}{2}\frac{{\left({x}_{i}-{x}_{j}\right)}^{T}\left({x}_{i}-{x}_{j}\right)}{{\sigma }_{l}^{2}}\right]$$
(3)

The response \(y\) can be modeled as in Eq. (4).

$$P\left(y\setminus f,X\right)\sim N\left(y\setminus HB+f,{\sigma }^{2}\mathrm{\rm I}\right)$$
(4)

where \(X=\left(\begin{array}{c}{x}_{1}^{T}\\ {x}_{2}^{T}\\ \vdots \\ {x}_{n}^{T}\end{array}\right) , y=\left(\begin{array}{c}{y}_{1}\\ {y}_{2}\\ \vdots \\ {y}_{n}\end{array}\right) , H=\left(\begin{array}{c}1, h\left({x}_{1}^{T}\right)\\ 1,h\left({x}_{2}^{T}\right)\\ \vdots \\ 1,h\left({x}_{n}^{T}\right)\end{array}\right)\) and \(f=\left(\begin{array}{c}f\left({x}_{1}\right)\\ f\left({x}_{2}\right)\\ \vdots \\ f\left({x}_{n}\right)\end{array}\right).h(x)\) is a sequence of elementary functions that transform the original feature vector x into a new feature vector\(h(x)\). To make the GPR model nonparametric, \(f\left({x}_{i}\right)\) is a latent variable for each observation\(x\). Parameter estimation in GPR is based on Eqs. (5) and (6).

$$logP\left(y\setminus X,\beta ,\theta ,\sigma \right)=-\frac{1}{2}{\left(y-H\beta \right)}^{T}{\left[k\left(x,{x}{\prime}\right)+{\sigma }^{2}{I}_{n}\right]}^{-1}\left(y-H\beta \right)-\frac{n}{2}log2\pi -\frac{1}{2}\left[k\left(x,{x}{\prime}\right)+{\sigma }^{2}{I}_{n}\right]$$
(5)
$$\left[\widehat{\beta },\widehat{\sigma ,}\widehat{\theta }\right]=\mathit{arg} \, \underset{\beta ,\theta ,\sigma }{{\text{max}}\mathit{log}}P\left(y\setminus X,\beta ,\theta ,\sigma \right)$$
(6)

The predictions or forecasts of the model can be obtained by using Eq. (7).

$$E\left({y}_{new} \backslash y,X,{x}_{new}, \beta ,\theta ,\sigma \right)=h{\left({x}_{new}\right)}^{T}\beta +\sum_{i=1}^{n}{\alpha }_{i}k\left({x}_{new},{x}_{i}/\theta \right)$$
(7)

The alphas in this equation are calculated by Eq. (8).

$$\alpha ={\left(K\left(X,X/\theta \right)+{\sigma }^{2}{I}_{n}\right)}^{-1}\left(y-H\beta \right)$$
(8)

3 The proposed method

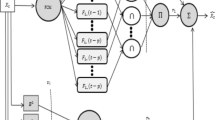
In this study, a fuzzy inference system method based on Gaussian process regression is proposed for the first time in the literature. In this new fuzzy inference system, the GPR method is used instead of OLS regression which was used for parameter estimation in the classical FRF method.

Thus, a fuzzy inference system that can be used for nonlinear data sets is proposed by using the GPR method, that does not require the linearity assumption that is valid in the OLS method. This new proposed fuzzy inference system method, FRF-GPR method, is presented step by step with the following algorithm.

Algorithm:

FRF-GPR.

Step 1. Setting the parameters of the FRF-GPR algorithm.

In this first step, the algorithm parameters are first determined.

\(c:\) The number of fuzzy clusters.

\(p:\) The number of lagged variables.

Step 2. The data set is separated into training and test set.

In this step, the test set length \((ntest)\) is first determined and the time series is divided into training \((ntrain)\) and test sets according to the determined test set length. Once this distinction is made, the proposed method starts to be applied to the training set.

Step 3. Creating the inputs and target of the FRF-GPR method.

The training set is first lagged by the number of lagged variables. Then, the target vector corresponding to this lagged time series are created. These lagged variables of the training set and the target vector corresponding to these lagged variables are put together in a matrix and clustered with FCM. Thus, membership values \(({\mu }_{ik},i=\mathrm{1,2},\cdots ,c;k=\mathrm{1,2},\cdots ,ntrain)\) are obtained. Where \(ntrain\) is the length of the training set.

For each fuzzy set, an input matrix is created with these membership values and some non-linear transformations of these membership values and the lagged variables of the training set. This input matrix and the target vector corresponding to this input matrix are given by Eqs. (9)–(13) respectively.

$${X}^{\left(i\right)}=\left[\begin{array}{ccc}I& \mu & LV\end{array}\right]$$
(9)
$$I=\left[\begin{array}{c}1\\ 1\\ \vdots \\ 1\end{array}\right]$$
(10)
$$\mu =\left[\begin{array}{cccc}{\mu }_{i1}& {{\mu }_{i1}}^{2}& {exp(\mu }_{i1})& ln\left(\frac{\left(1-{\mu }_{i1}\right)}{{\mu }_{i1}}\right)\\ {\mu }_{i2}& {{\mu }_{i2}}^{2}& {exp(\mu }_{i2})& ln\left(\frac{\left(1-{\mu }_{i2}\right)}{{\mu }_{i2}}\right)\\ \vdots & \vdots & \vdots & \vdots \\ {\mu }_{intrain}& {{\mu }_{intrain}}^{2}& {exp(\mu }_{intrain})& ln\left(\frac{\left(1-{\mu }_{intrain}\right)}{{\mu }_{intrain}}\right)\end{array}\right]$$
(11)
$$LV=\left[\begin{array}{cccc}{x}_{1}& {x}_{2}& \cdots & {x}_{p}\\ {x}_{2}& {x}_{3}& \cdots & {x}_{p+1}\\ \vdots & \vdots & \vdots & \vdots \\ {x}_{ntrain-p}& {x}_{ntrain-p+1}& \cdots & {x}_{ntrain-1}\end{array}\right]$$
(12)
$${Y}^{(i)}=\left[{x}_{p+1} {x}_{p+2} \vdots {x}_{n}\right]$$
(13)

The input matrix given by Eq. (9) is a combination of the unit matrix given by Eq. (10), the membership matrix consisting of membership values and various non-linear transformations of membership values given by Eq. (11), and the matrix of lagged variables of the time series given by Eq. (12).

Step 4. The fuzzy Gaussian regression functions for each fuzzy set are estimated by Gaussian process regression using Eqs. (9)–(13).

Step 5. The final outputs of the training set are derived by assigning weights to the membership values corresponding to the outputs obtained by Gaussian process regression as given in Eq. (9).

Step 6. The input matrix and the target vector for the test set are reconfigured by Eqs. (14)–(18) respectively. The final outputs of the test set are derived by assigning weights to the membership values corresponding to the outputs.

$${XT}^{\left(i\right)}=\left[\begin{array}{ccc}I2& \mu T& LVT\end{array}\right]$$
(14)
$$I2=\left[\begin{array}{c}1\\ 1\\ \vdots \\ 1\end{array}\right]$$
(15)
$$\mu T=\left[\begin{array}{cccc}{\mu }_{i,{\text{ntrain}}+1}& {{\mu }_{i,{\text{ntrain}}+1}}^{2}& {exp(\mu }_{i,{\text{ntrain}}+1})& ln\left(\frac{\left(1-{\mu }_{i,{\text{ntrain}}+1}\right)}{{\mu }_{i,{\text{ntrain}}+1}}\right)\\ {\mu }_{i,{\text{ntrain}}+2}& {{\mu }_{i,{\text{ntrain}}+2}}^{2}& {exp(\mu }_{i,{\text{ntrain}}+2})& ln\left(\frac{\left(1-{\mu }_{i,{\text{ntrain}}+2}\right)}{{\mu }_{i,{\text{ntrain}}+2}}\right)\\ \vdots & \vdots & \vdots & \vdots \\ {\mu }_{i,{\text{ntrain}}+{\text{ntest}}}& {{\mu }_{i,{\text{ntrain}}+{\text{ntest}}}}^{2}& {exp(\mu }_{i,{\text{ntrain}}+{\text{ntest}}})& ln\left(\frac{\left(1-{\mu }_{{\text{ntrain}}+{\text{ntest}}}\right)}{{\mu }_{{\text{ntrain}}+{\text{ntest}}}}\right)\end{array}\right]$$
(16)
$$LVT=\left[\begin{array}{cccc}{x}_{{\text{ntrain}}-\mathrm{ p}+1}& {x}_{{\text{ntrain}}-\mathrm{ p}+2}& \cdots & {x}_{{\text{ntrain}}}\\ {x}_{{\text{ntrain}}-\mathrm{ p}+2}& {x}_{{\text{ntrain}}-\mathrm{ p}+3}& \cdots & {x}_{{\text{ntrain}}+1}\\ \vdots & \vdots & \vdots & \vdots \\ {x}_{ntrain-p+ntest}& {x}_{ntrain-p+ntest+1}& \cdots & {x}_{ntrain+ntest-1}\end{array}\right]$$
(17)
$${YT}^{(i)}=\left[{x}_{ntrain+1} {x}_{ntrain+2} \vdots {x}_{ntrain+ntest}\right]$$
(18)

The input matrix given by Eq. (14) is a combination of the unit matrix given by Eq. (15), the membership matrix consisting of membership values and various non-linear transformations of membership values given by Eq. (16), and the matrix of lagged variables of the time series given by Eq. (17) for the test set.

4 Applications

The performance of the proposed FRF-GPR method is evaluated on Bitcoin and daily observed 1-year Crude Oil time series. In the analysis of these time series, different time series are created from each Bitcoin and Crude Oil time series. The information about these time series is given in Table 1.

Table 1 Information for the time series
Full size table

These time series are downloaded from the Yahoo Finance website (https://finance.yahoo.com/).

In the assessment of the analysis performance of the proposed FRF-GPR method, the FRF proposed by Türkşen (2008), the multilayer perceptron artificial neural network (MLP-ANN) proposed by Rumelhart et al. (1986), the multiplicative neuron model artificial neural network (SMNM-ANN) proposed by Yadav et al. (2007), Pi-sigma artificial neural network (PS-ANN) proposed by Shin and Ghosh (1991), long short term memory artificial neural network (LSTM-ANN) proposed by Hochreiter and Schmidhuber (1997) and fuzzy time series network (FTS-N) proposed by Bas et al. (2015) are utilized.

To determine the optimal number of inputs and the number of hidden layers \((m)\) for the MLP-ANN method, each parameter is increased one by one between one and five for different combinations. To determine the optimal number of inputs for the SMNM-ANN method, the number of inputs is increased by one between one and five. To determine the optimal number of inputs and the degree for the PS-ANN method, each parameter is increased one by one between one and five for different combinations. To determine the optimal number of inputs and the number of fuzzy clusters \((c)\) for the FRF-GPR, FRF, and FTS-N methods, the number of inputs is tried between one and ten, and the number of fuzzy clusters is tried between three and ten. To determine the optimal number of inputs, hidden layer unit \((h),\) and the number of hidden layers for the LSTM-ANN method \((m)\), each parameter is increased one by one between one and five for different combinations. The test set length is taken as 14 for each analyzed series.

The analysis results obtained from all methods are evaluated on the test set of each time series using the root mean square error criterion given by Eq. (19).

$$RMSE=\sqrt{\frac{1}{ntest}\sum_{t=1}^{ntest}{\left({x}_{t}-{\widehat{x}}_{t}\right)}^{2}}$$
(19)

Here \({ntest,x}_{t}\) and \({\widehat{x}}_{t}\) shows the number of test samples, the observed values, and the forecasts, respectively. Considering that each method will be affected by the initial solutions, thirty different solutions are realized using the optimal parameter values for each method. Each method is run 30 times with its optimal parameters and thus 30 different RMSE values are obtained for each method. Finally, the mean, median, standard deviation, interquartile range, and minimum and maximum statistics of these RMSE values are calculated.

The analysis results obtained for Series 1–5, which are different sub-time series derived from the Bitcoin time series, are given in Tables 2, 3, 4, 5, 6.

Table 2 Analysis results obtained for Series 1
Full size table
Table 3 Analysis results obtained for Series 2
Full size table
Table 4 Analysis results obtained for Series 3
Full size table
Table 5 Analysis results obtained for Series 4
Full size table
Table 6 Analysis results obtained for Series 5
Full size table

The analysis results obtained for Series 1 indicate that the proposed FRF-GPR method is the most effective analysis method in terms of mean, standard deviation, median, interquartile range and maximum statistics compared to other methods.

In the analysis results obtained for Series 2, it is seen that the proposed FRF-GPR method is the best method for the standard deviation statistic and the third-best method for the mean statistic.

Based on the analysis results obtained for Series 3, the proposed FRF-GPR method is again the best analysis method in terms of mean, standard deviation, median and maximum statistics.

The proposed FRF-GPR method is the most efficient analysis technique for the mean, standard deviation, median, interquartile range and maximum statistics as a result of the analysis results obtained for Series 4.

The analysis results obtained for Series 5 show that the proposed FRF-GPR method is better than the other analysis methods in terms of mean, standard deviation and maximum statistics. The results of the analysis obtained for different sub-series derived from the crude oil time series, Series 6–Series 10, are given in Tables 78, 9, 10, 11.

Table 7 Analysis results obtained for Series 6
Full size table
Table 8 Analysis results obtained for Series 7
Full size table
Table 9 Analysis results obtained for Series 8
Full size table
Table 10 Analysis results obtained for Series 9
Full size table
Table 11 Analysis results obtained for Series 10
Full size table

The results of the analysis of Series 6 reveal that the proposed FRF-GPR method stands out in the mean, median, standard deviation and maximum statistics.

In line with the analysis results of Series 7 given in Table 8, it can be said that the proposed FRF-GPR method is the second most successful method among all analysis methods in general when all statistics are considered.

In the analysis results of Series 8 given in Table 9, it is seen that the proposed FRF-GPR method ranks first again in the mean, median, and maximum statistics.

The analysis results for Series 9 in Table 10 show that the proposed FRF-GPR method is first in the maximum statistic and generally second in the other statistics. The results of the analysis given in Table 11 for Series 10 confirm that the proposed FRF-GPR method ranks first in all statistics.

The optimal parameters obtained from each method for the analyzed series are given in Tables 12 and 13. In addition, these optimal parameter values are obtained from the validation sets. Also, (–) indicates that the method does not have a corresponding value for a cell of the Tables 12 and 13.

Table 12 Optimum parameters obtained from each method for Series 1–5
Full size table
Table 13 Optimum parameters obtained from each method for Series 6–10
Full size table

5 Conclusions

In this study, for the first time in the literature, the GPR method is used for the parameter estimation phase of the FRF method instead of OLS regression. In this way, it is investigated whether GPR regression, which can also work with nonlinear data, is an advantage over the FRF method using OLS regression. The contribution of this paper to the literature is to propose a new approach of fuzzy regression functions using the GRP method instead of the OLS method, which is not suitable for parameter estimation of nonlinear data.

When the analysis results obtained from all methods are evaluated together, it can be said that the proposed FRF-GPR method obtains better forecasting results than the OLS-based FRF method. In addition, the proposed FRF-GPR method produced better forecasting results than many well-known shallow and deep artificial neural network methods in the literature. In future studies, the GPR method can also be used for parameter estimation of intuitionistic and picture fuzzy regression function methods.