1 Introduction

The aim of this article is to prove that the intuitionistic fuzzy numbers or values can be aggregated with the direct application of weighted geometric means. Our motivation is to show that this very simple method has never been established before; however, it gives a valid procedure for the aggregation of intuitionistic fuzzy numbers that generates a new multi-attribute group decision-making procedure in this popular framework.

Following the introduction of fuzzy sets (Zadeh 1965) and its multiple applications (Bellman and Zadeh 1970; Chen and Phuong 2017; Chen and Wang 2009), Atanassov (1986) first proposed to use a restricted class of “orthopairs” (i.e., pairs of numbers from the unit interval) as a way to assess belongingness to a set. The core principle that justifies this position is that non-membership is often evaluated separately from membership. Thus, the new model considered a pair of values in the unit interval, that assess the possible membership/non-membership of an element to the “orthopair fuzzy set”. Atanassov’s extension was called “intuitionistic fuzzy set” (IFS). Because belongingness is split between membership and non-membership (with some hesitancy allowed), this model assumes that for each orthopair, the sum of both values is less than or equal to 1.

Probably, the most successful generalization of intuitionistic fuzzy sets that still resorts to pairs of evaluations consists of q-rung orthopair fuzzy sets (Khan et al. 2021; Senapati et al. 2023; Yager 2017). Their semantics have been explored recently by Alcantud (2023). They are bound by a less restrictive condition: the sum of the \(\mathrm q-th\) power of the membership and non-membership values must not exceed 1. In this general framework, intuitionistic fuzzy sets become 1-rung orthopair fuzzy sets, and 2-rung orthopair fuzzy sets coincide with intuitionistic fuzzy sets of second type (Atanassov (1989), reprinted in Atanassov (2016), see also Atanassov et al. (2013)). This model gained traction under the name Pythagorean fuzzy sets (Yager 2014).

When the use of more than one evaluation was accepted and justified by applications, other types of extensions of fuzzy sets introduced an evaluation for the indeterminacy of the belongingness. This idea produced picture fuzzy sets (Cuong 2014), spherical fuzzy sets (Kutlu Gündoğdu and Kahraman 2019), and even more general models (Akram and Martino 2023; Akram et al. 2023), but we shall not refer to them in this paper.

Our research is motivated by the importance of aggregation in the framework of multi-attribute group decision-making (MAGDM). An intuitionistic fuzzy set associates an intuitionistic fuzzy number or value (IFN or IFV, respectively) with each element of a universal set of alternatives. Aggregation of IFSs is typically performed elementwise. This means that for each element, the IFN corresponding to its evaluation by an aggregate IFS is the result of the aggregation of all individual IFNs associated with the element. Therefore, aggregation of intuitionistic fuzzy sets reduces to aggregation of intuitionistic fuzzy numbers. And for this reason, aggregation operators on crisp numbers have been a source of inspiration for aggregators in the intuitionistic fuzzy field. The problems of intertemporal aggregation of intuitionistic fuzzy information (Alcantud et al. 2020), ranking IFNs (Ali et al. 2019; Feng et al. 2020; Liu et al. 2018), and information quantification (Ali et al. 2022), have also received considerable attention.

In relation with this idea, we note that already Xu and Yager (2006) discussed the aggregation of IFNs. They initiated a methodology that generates aggregation operators through operational laws that preserve the structure of IFNs. Another source of inspiration takes advantage of special aggregation operators on crisp numbers. Both approaches are not independent, and they are often combined in a single formula. Let us describe these two methodologies.

In relation with the first line of inspection, Xu and Yager (2006) introduced the intuitionistic fuzzy (respectively, ordered) weighted geometric operators and the intuitionistic fuzzy hybrid geometric operator. The intuitionistic fuzzy (respectively, ordered) weighted averaging operators and intuitionistic fuzzy hybrid aggregation operator appeared in Xu (2007). Afterwards Wei (2010) defined induced geometric aggregation operators and Garg (2017) used novel aggregation operators from improvements of the operational laws. Beliakov et al. (2011) suggested to resort to additive generators of the t-norm and t-conorm in the operational laws for IFNs. With the help of transformation techniques between intuitionistic fuzzy numbers and triangular fuzzy numbers, Chen and Chang (2016) produced renewed expressions for the operators in Xu and Yager (2006). These authors criticized and improved upon He et al. (2014).

Many examples exist that testify to the value of the second line of investigation. Intuitionistic fuzzy Bonferroni means and intuitionistic fuzzy power aggregation operators were the subjects of Xu and Yager (2011) and Xu (2011). In Wang and Liu (2011), the intuitionistic fuzzy Einstein (ordered) weighted geometric operators were introduced. The geometric Heronian mean inspired Yu (2013) to define the IFGHM (intuitionistic fuzzy weighted geometric) aggregation operator. Under the inspiration of the Heronian mean, Liu and Chen (2017) defined the IFAHA (intuitionistic fuzzy Archimedean Heronian aggregation, whose explicit formula is given in their Theorem 1) and IFWAHA (intuitionistic fuzzy weight Archimedean Heronian aggregation, whose explicit formula is given in their Theorem 5) aggregation operators. They were used to define an MAGDM methodology Liu and Chen (2017) (Sect. 4). Also, Kumar and Chen (2022) defined the AIFWHM (advanced intuitionistic fuzzy weighted Heronian mean) aggregation operators in their Eq. 8. They criticized the proposal in Liu and Chen (2017) with the argument that it does not always discriminate among alternatives Kumar and Chen (2022) (Sect. 4). In passing, we note that Beliakov et al. (2011); Chen and Chang (2016); He et al. (2014); Kumar and Chen (2022) use a variety of operational laws on IFNs.

In consideration of cases with correlated information, Xu (2010) used the Choquet integral to define intuitionistic fuzzy correlated averaging (respectively, geometric) aggregation operators from a fuzzy measure. Special cases included the intuitionistic fuzzy weighted averaging/geometric operators and the intuitionistic fuzzy weighted ordered weighted averaging/geometric operators. Relatedly, Xu and Xia (2011) developed induced generalized intuitionistic fuzzy Choquet ordered averaging.

Evidence of the impact of the research about aggregators of IFSs on decision-making can be found in articles such as Deng et al. (2022); Huang et al. (2023); Liu et al. (2020); Chen and Randyanto (2013); Wang et al. (2022), and their references. Other applications include the investigation of centroid transformation of IFVs (Feng et al. 2019). Also, the advancement of this field has a positive impact on other branches including the aggregation of complex intuitionistic fuzzy sets (Akram et al. 2021), a model that extends IFSs, or the measurement of similarities (Chen and Chen 2001).

Many aggregation operators for IFNs have resorted to the weighted geometric mean. However, it is surprising that neither of these methodologies operates on the orthopairs in the most direct and natural manner, to wit, by taking the weighted geometric means of both membership and non-membership degrees. To fill this unexpected gap in the literature, in this paper, we define the intuitionistic fuzzy direct weighted geometric operator on IFNs. Then we prove that our new formula produces a well-defined aggregation operator on IFNs, and we compare its performance with existing aggregators with the help of two proxies (the average of the Euclidean distances to the IFNs, and the sum of squared error or SSE inspired by the k-means clustering algorithm, v. Celebi et al. (2013)). Our mathematical proof allows us to show that the intuitionistic fuzzy direct weighted geometric operator is in fact a representable intuitionistic aggregation operator on IFNs. This class of aggregator has been studied by Kolesárová and Mesiar (2020). An application to group decision-making with an illustrative example supplements and motivates these achievements.

This paper is organized as follows. Sect. 2 recalls known concepts and facts about intuitionistic fuzzy sets and aggregation operators. Section 3 summarizes relevant antecedents on aggregation of intuitionistic fuzzy sets. General comments are made in Sect. 3.1. Operational laws for IFNs are described in Sects. 3.2, and 3.3 recalls how their implementation with weighted geometric averages leads to several aggregation operators on IFNs. Section  4 contains our contribution to the aggregation of IFNs and a comparison with existing aggregation operators. Multi-attribute group decision-making is the subject of Sect. 5. Section 6 concludes this article.

2 Preliminary concepts and results

This section revises some definitions and results. Section 2.1 recalls basic concepts, and Sect. 2.2 gives a brief overview of aggregation operators.

For convenience, we shall write the unit interval [0, 1] as \(\mathcal{I}\).

Henceforth, X denotes a set of alternatives.

2.1 Review of concepts

The next standard notions will be used in this paper.

Definition 1

(Yager 2017) A q-rung orthopair fuzzy set A over X is \(A = \{ \langle x, ( \mu _A(x),\nu _A(x) ) \rangle |\, x\in X \}.\) The mappings \(\mu _A,\nu _A: X \rightarrow \mathcal{I}\), respectively, encode the degrees of membership and non-membership of \(x\in X\) to A, with \(( \mu _A (x) )^q + ( \nu _A (x) )^q \le 1\) for all \(x\in X\).

Definition 1 produces an Atanassov’s intuitionistic fuzzy set (Atanassov 1986) when \(q=1\), and a Pythagorean fuzzy set when \(q=2\). Recently, Alcantud (2023) has generalized Definition 1 to complemental fuzzy sets, and he has provided a common semantic interpretation to all these models.

Focusing on Atanassov’s intuitionistic fuzzy sets, the interpretation of \(\langle x, ( \mu _A(x),\nu _A(x) ) \rangle\) is that for each \(x\in X\), the degree of membership of x in A (the IFS) lies in the closed interval \([\mu _A(x), 1-\nu _A(x)]\).

An orthopair is \((\mu , \nu )\), where \(0\le \mu , \nu \le 1\). And it is an intuitionistic fuzzy number (IFN) or intuitionistic fuzzy value (IFV), when \(0\le \mu + \nu \le 1\) (Xu and Yager 2006). The set of all IFNs will be denoted by \(\textbf{A}\).

Some IFNs can be compared with the help of the binary relation \(\succcurlyeq\) on IFNs defined as follows: for each pair \(( \mu _1, \nu _1 )\), \(( \mu _2, \nu _2)\) of IFNs, \(( \mu _1, \nu _1 ) \succcurlyeq ( \mu _2, \nu _2 )\) if and only if \(\mu _1 \geqslant \mu _2\) and \(\nu _2 \geqslant \nu _1\) (Atanassov 1986). The bottom and top elements of \(\succcurlyeq\) are \(\textbf{0}= (0, 1)\) and \(\textbf{1}= (1, 0)\), respectively.

This binary comparison is incomplete: for example, \(I_1=(0.3, 0.5)\) and \(I_2=(0.4, 0.6)\) cannot be compared by \(\succcurlyeq\). A more discriminating tool was built with the help of the score of an IFN \(I=(\mu , \nu )\), defined as \(S(I)=\mu - \nu\) in Chen and Tan (1994). IFNs with higher scores are preferred over IFNs with smaller scores. Because \(S(I_1)=S(I_2)=-0.2\), this rule declares that \(I_1\) and \(I_2\) are equally good. Clearly, ties will appear on a regular basis. To act as a tie-breaking rule for situations like this, the accuracy of I, defined as \(H(I)=\mu + \nu\) in Hong and Choi (2000), is commonly employed since Xu and Yager (2006) proposed its utilization. In a comparison of IFNs with the same score, the IFN with higher accuracy is preferred. In our example, \(H(I_1)=0.8 < H(I_2) = 1\), hence \(I_2\) is preferred over \(I_1\). The next definition summarizes this comparison law:

Definition 2

Xu and Yager (2006) [Definition 1] Suppose \(I_1 = ( \mu _1, \nu _1 )\) and \(I_2 = ( \mu _2, \nu _2 )\) are different IFNs. Then

  • If \(S(I_1)>S(I_2)\), then we declare \(I_1 > I_2\).

  • If \(S(I_2)>S(I_1)\), then we declare \(I_2 > I_1\).

  • If \(S(I_1)=S(I_2)\), then when \(H(I_1)>H(I_2)\) we declare \(I_1 > I_2\), and when \(H(I_2)>H(I_1)\) we declare \(I_2 > I_1\).

Recall that Xu (2007), Definition 3.1, explained that \(S(I_1)=S(I_2)\) and \(H(I_1) = H(I_2)\) only happen simultaneously when \(I_1=I_2\). Also, Xu (2007), Theorem 3.1, proved that the comparative rule in Definition 2 is finer than the binary relation \(\succcurlyeq\): \(I_1 \succcurlyeq I_2\) implies \(I_1 > I_2\) when \(I_1, I_2\) are different IFNs.

2.2 Aggregation operators

The concept of an aggregation operator is well known:

Definition 3

(Beliakov et al. 2007) A mapping \(\mathcal {A}: \mathcal{I}\times {\mathop {\ldots }\limits ^{n}} \times \mathcal{I}\rightarrow \mathcal{I}\) is called an aggregation operator when it satisfies:

  • Boundary condition: \(\mathcal {A}(0, {\mathop {\ldots }\limits ^{n}}, 0)=0\), \(\mathcal {A}(1, {\mathop {\ldots }\limits ^{n}}, 1)=1\).

  • Monotonicity: \(\mathcal {A}(a_1, {\ldots }, a_n) \geqslant \mathcal {A}(b_1, {\ldots }, b_n)\) if \(a_i, b_i\in \mathcal{I}\) (\(i=1, \ldots , n\)) and \((a_1, {\ldots }, a_n)\geqslant (b_1, {\ldots }, b_n)\).

We shall be especially concerned with two aggregation operators associated with \(\omega = (\omega _1, \ldots , \omega _n)\), a weighting vector. By this we mean \(\omega _1+ \ldots + \omega _n=1\) and \(\omega _j\in \mathcal{I}\) for each \(j=1, \ldots , n\) (v., Def. 2.5 of Beliakov et al. (2007)). When \((a_1, {\ldots }, a_n)\in \mathcal{I}\times {\mathop {\ldots }\limits ^{n}} \times \mathcal{I}\):

  1. 1.

    Its weighted arithmetic mean is (v., Def. 2.6 of Beliakov et al. (2007))

    $$\begin{aligned} M_{\omega } (a_1, \ldots , a_n) = \sum _{j=1}^n{\omega _j} a_j. \end{aligned}$$
    (1)
  2. 2.

    Its weighted geometric mean is (v., Def. 2.8 of Beliakov et al. (2007))

    $$\begin{aligned} G_{\omega } (a_1, \ldots , a_n) = \prod _{j=1}^n a_j^{\omega _j}. \end{aligned}$$
    (2)

Importantly, Beliakov et al. (2007), Eq. (2.4), states the geometric–arithmetic inequality \(G_{\omega } (a_1, \ldots , a_n)\leqslant M_{\omega } (a_1, \ldots , a_n)\).

3 Aggregation of IFSs: antecedents

This section contains some relevant antecedents that will serve us to formulate our main question. A brief introduction to the aggregation problem that we shall investigate is in Sect.  3.1. Then in Sect.  3.2, we recall some operations on IFNs. Section 3.3 defines known (families of) geometric aggregation operators.

3.1 Aggregation of intuitionistic fuzzy numbers

The aggregation of intuitionistic fuzzy sets is performed elementwise. Hence, it relies on aggregation of IFNs, which are the characteristics that define each element in X:

Definition 4

Beliakov et al. (2011) [Definition 5] An aggregation operator on n IFNs is a mapping \(f: \textbf{A}\times {\mathop {\ldots }\limits ^{n}} \times \textbf{A}\rightarrow \textbf{A}\) that is monotonic with respect to \(\succcurlyeq\) and satisfies \(f(\textbf{0}, {\mathop {\ldots }\limits ^{n}}, \textbf{0}) = \textbf{0}\), \(f(\textbf{1}, {\mathop {\ldots }\limits ^{n}}, \textbf{1}) = \textbf{1}\).

The following guiding principles have helped to aggregate IFNs (Liu and Chen 2017). The founding Xu and Yager (2006) suggested to use operations on IFNs to replace the standard arithmetic operations between numbers, and several articles followed this trend. Sections 3.2 and 3.3, respectively, deal with both technicalities. Section 3.3 focuses on references relating to the implementation with weighted geometric averages, our research arena. And as mentioned in the Introduction, a different principle builds on special aggregation operators on crisp numbers. We do not need to be explicit about these other cases in our article.

3.2 Algebraic operations on intuitionistic fuzzy numbers

Some aggregation operators were designed with the help of various operations on IFNs or IFVs. Originally, one had the next expressions:

Definition 5

(Atanassov 1994) Let \(I_1 =(\mu _1, \nu _1)\), \(I_2 =(\mu _2, \nu _2)\) be IFNs and \({\lambda }>0\). Then:

$$\begin{aligned}&I_{1} \oplus _{} I_{2} = (\mu _1+\mu _2-\mu _1\cdot \mu _2, \nu _1\cdot \nu _2),\\&I_{1} \otimes _{} I_{2} = (\mu _1 \cdot \mu _2, \nu _1 + \nu _2 -\nu _1\cdot \nu _2),\\&\lambda I_{1} = ( 1 - (1-\mu _1)^{\lambda }, \nu _1^{\lambda } ),\\&I_{1}^{\lambda } = ( \mu _1^{\lambda }, 1 - (1-\nu _1)^{\lambda } ). \end{aligned}$$

However, He et al. (2014) suggested the following alternative expressions for multiplication of IFNs and power operation on IFNs:

$$\begin{aligned} I_{1} \otimes _{} I_{2} =&( (1-\nu _1) (1-\nu _2) - ( 1 - (\mu _1 + \nu _1)) ( 1 - (\mu _2 + \nu _2)),\\&1 - (1-\nu _1) (1 - \nu _2) ),\\ I_{1}^{\lambda } =&( (1-\nu _1)^{\lambda } - (1-\mu _1-\nu _1)^{\lambda }, 1 - (1-\nu _1)^{\lambda } ). \end{aligned}$$

Some drawbacks found in the application of these operations motivated Chen and Chang (2016) to redefine them as follows:

$$\begin{aligned}&I_{1} \otimes _{} I_{2} = ( \mu _1+\mu _2-\mu _1\cdot \mu _2, \nu _1 ( 1 - \mu _2 -\nu _2) + \nu _2 ( 1-\mu _1 ) ),\\&I_{1}^{\lambda } = ( 1 - (1-\mu _1)^{\lambda }, (1-\mu _1)^{\lambda } - (1-\mu _1-\nu _1)^{\lambda } ). \end{aligned}$$

Now, let us see how these operations produce aggregation operators on IFNs.

3.3 Some geometric aggregation operators on intuitionistic fuzzy numbers

In this section, we let \(\omega = (\omega _1, \ldots , \omega _n)\) be a weight vector. To avoid a lengthy discussion, we keep our presentation focused on geometric-type aggregators, and skip the details concerning, e.g., arithmetic-type aggregation of intuitionistic fuzzy numbers.

Definition 6

(Xu and Cai 2013; Xu and Yager 2006) The intuitionistic fuzzy weighted geometric operator on n intuitionistic fuzzy numbers associated with \(\omega\) can be computed as follows: when \(\{ I_1 = (\mu _1, \nu _1), \ldots , I_n = (\mu _n, \nu _n) \}\) are IFNs,

$$\begin{aligned}{} & {} \textrm{IFWG}_{\omega } (I_1, \ldots , I_n) = \Bigr ( \prod _{j=1}^n \mu _j^{\omega _j}, \ 1- \prod _{j=1}^n (1-\nu _j)^{\omega _j} \Bigr ). \end{aligned}$$
(3)

This aggregation operator was defined in Xu and Yager (2006), Definition 2, and Xu and Cai (2013), Definition 1.3.2, with the help of the operations on IFNs that we have recalled in Definition 5. Specifically, it was defined as \(\textrm{IFWG}_{\omega } (I_1, \ldots , I_n) = \omega _1 I_1 \otimes _{} \ldots \otimes _{} \omega _n I_n\) where \(\otimes _{}\) refers to the first formula from Definition 5. It was characterized in Xu and Yager (2006), Theorem 2, and Xu and Cai (2013), Theorem 1.3.2, through the formula (3). In Xu et al. (2023), Definition 3.1, this operator is called IFWG operator with respect to \(\otimes _{}\).

The spirit of the OWA operator suggested the next variation Xu and Yager (2006)[Definition 3] which is also an aggregation operator on IFNs: in the conditions of Definition 6,

$$\begin{aligned} \begin{aligned}&\textrm{IFOWG}_{\omega } (I_1, \ldots , I_n) = \Bigr ( \prod _{j=1}^n \mu _{\sigma (j)}^{\omega _j}, \ 1- \prod _{j=1}^n (1-\nu _{\sigma (j)})^{\omega _j} \Bigr ) \end{aligned} \end{aligned}$$
(4)

with \((\sigma (1), \ldots , \sigma (n))\) being a permutation of \((1, 2, \ldots , n)\) such that \(I_{i-1}\geqslant I_{i}\) by the comparative rule in Definition 2, for each \(i=2, \ldots , n\). This operator was extended in Wei (2010), Definition 9, by the induced IFOWG (I-IFOWG) aggregation operator with the help of an order inducing variable.

The utilization of alternative expressions for the operations on IFNs (cf., Sect. 3.2) prompted the next proposal:

Definition 7

(Chen and Chang 2016, Definition 4.1) The intuitionistic fuzzy weighted geometric averaging (IFWGA) aggregation operator on n intuitionistic fuzzy numbers associated with \(\omega\) can be computed as follows: when \(\{ I_1 = (\mu _1, \nu _1), \ldots , I_n = (\mu _n, \nu _n) \}\) are IFNs,

$$\begin{aligned} {\text{IFWGA}}_{\omega } \,(I_{1} , \ldots ,I_{n} ) & = \Bigr (1 - \prod\limits_{{j = 1}}^{n} {(1 - \mu _{j} )^{{\omega j}} } , \\ & \prod\limits_{{j = 1}}^{n} {(1 - \mu _{j} )^{{\omega j}} } - \prod\limits_{{j = 1}}^{n} {(1 - \mu _{j} - v_{j} )^{{\omega j}} } \Bigr ) \\ \end{aligned}$$
(5)

The intuitionistic fuzzy ordered weighted geometric averaging (IFOWGA) aggregation operator (Chen and Chang 2016, Definition 4.2) is a variation of IFWGA that replicates the change introduced by IFOWG\(_{\omega }\) with respect to IFWG\(_{\omega }\).

The next operator was defined in Yu (2013), Definition 6, with the help of the operations in Definition 5. Then Yu (2013), Theorem 2, proves the lengthy formula provided in Definition 8:

Definition 8

(Yu 2013) The intuitionistic fuzzy geometric weighted Heronian mean aggregation operator on n intuitionistic fuzzy numbers associated with \(\omega\) and \(p\geqslant 0\), \(q\geqslant 0\) that do not vanish simultaneously, can be computed as follows: when \(\{ I_1 = (\mu _1, \nu _1), \ldots , I_n = (\mu _n, \nu _n) \}\) are IFNs,

$$\begin{gathered} IFGWHM_{\omega }^{{p,q}} (I_{1} , \ldots ,I_{n} ) \hfill \\ = \left( {1 - \left( {1 - \prod\limits_{{\mathop {j = 1}\limits_{{i = 1}} }}^{n} {\left( {1 - \left( {1 - \mu _{i}^{{\omega _{i} }} } \right)^{p} \left( {1 - \mu _{j}^{{\omega _{j} }} } \right)^{q} } \right)^{{\frac{2}{{n(n + 1)}}}} } } \right)^{{\frac{1}{{p + q}}}} ,} \right. \hfill \\ {\text{ }}\left. {\left( {1 - \prod\limits_{{\mathop {j = 1}\limits_{{i = 1}} }}^{n} {(1 - (} 1 - (1 - \nu _{i} )^{{\omega _{i} }} )^{p} (1 - (1 - \nu _{j} )^{{\omega _{j} }} )^{q} )^{{\frac{2}{{n(n + 1)}}}} } \right)^{{\frac{1}{{p + q}}}} } \right). \hfill \\ \end{gathered}$$

Remark 1

Xu (2007) defined the \(\textrm{IFWA}_{\omega }\) (for intuitionistic fuzzy weighted averaging) operator. In our analysis of geometric-inspired aggregators, it is timely to explain that in Xu et al. (2023), this operator is called IFWG operator with respect to \(\oplus _{}\). Its formula in the conditions of Definition 6 is

$$\begin{aligned} IFWA_{\omega } (I_{1} , \ldots ,I_{n} ) & = \left(1 - \prod\limits_{{j = 1}}^{n} {(1 - \mu _{j} )^{{\omega _{j} }} } ,\;\prod\limits_{{j = 1}}^{n} {\nu _{j}^{{\omega _{j} }} } \right) \\ {\text{ }} & = \omega _{1} I_{1} \oplus _{{}} \ldots \oplus _{{}} \omega _{n} I_{n} . \\ \end{aligned}$$
(6)

To conclude this section, we note that Xu et al. (2023) have performed an updated investigation of relationships among intuitionistic fuzzy weighted geometric operators.

Once the analysis of geometric-type aggregators on intuitionistic fuzzy numbers has been completed, we are ready to present our contribution.

4 The intuitionistic fuzzy direct weighted geometric aggregation operator

Section 3 has prepared the ground for the main concepts in this article. There we have witnessed the development of increasingly complicated expressions for geometric-mean-inspired aggregation operators for IFNs. Here, we produce aggregation operators that, despite their simplicity, are novel in this literature. We state them directly with the help of the weighted geometric mean, so henceforth in this section \(\omega = (\omega _1, \ldots , \omega _n)\) denotes a weight vector (cf., Sect. 3.3).

Definition 9

The intuitionistic fuzzy direct weighted geometric operator on n intuitionistic fuzzy numbers associated with \(\omega\) is defined as follows: for each collection of IFNs \(\{ I_1 = (\mu _1, \nu _1), \ldots , I_n = (\mu _n, \nu _n) \}\),

$$\begin{aligned}{} & {} \textrm{IFDG}_{\omega } (I_1, \ldots , I_n) = \Bigr ( \prod _{j=1}^n \mu _j^{\omega _j}, \ \prod _{j=1}^n \nu _j^{\omega _j} \Bigr ). \end{aligned}$$
(7)

When \(\omega = ( \frac{1}{n}, \ldots , \frac{1}{n} )\), we obtain the intuitionistic fuzzy direct geometric operator

$$\begin{aligned} \textrm{IFDG}(I_1, \ldots , I_n) = \Bigr ( \prod _{j=1}^n \mu _j^{\frac{1}{n}}, \ \prod _{j=1}^n \nu _j^{\frac{1}{n}} \Bigr ). \end{aligned}$$
(8)

\(\textrm{IFDG}_{\omega }\) inherits the idempotency and boundedness properties of the weighted geometric means. But it is not monotonic with respect to >, the comparative rule in Definition 2:

Example 1

Consider \(\omega =(0.3, 0.7)\), \(I_1 =(0.9, 0.1)\), \(I_2 =(0.5, 0.5)\), \(I_3 =(0.3, 0.2)\). Although \(I_3>I_2\), \(\textrm{IFDG}_{\omega }(I_1, I_3) > \textrm{IFDG}_{\omega }(I_1, I_2)\) is false because \(S(\textrm{IFDG}_{\omega }(I_1, I_3) ) = S (0.417, 0.162) = 0.255 < 0.287 = S( \textrm{IFDG}_{\omega }(I_1, I_2) ) = S (0.596, 0.309)\).

Our next section proves that (7) and (8) produce aggregation operators. Section 4.2 gives supplementary discussion.

4.1 Main result

We are ready to state and prove our main result in this paper:

Theorem 1

  \(\textrm{IFDG}_{\omega }\) is an aggregation operator on IFNs.

Proof

To prove that \(\textrm{IFDG}_{\omega }\) satisfies Definition 4, consider \(\{ I_1 = (\mu _1, \nu _1), \ldots , I_n = (\mu _n, \nu _n) \}\), a collection of IFNs. First we need to prove that \(\left( \prod _{j=1}^n \mu _j^{\omega _j}, \prod _{j=1}^n \nu _j^{\omega _j}\right)\) is an IFN, which boils down to \(\prod _{j=1}^n \mu _j^{\omega _j} + \prod _{j=1}^n \nu _j^{\omega _j}\leqslant 1\).

By definition of IFN, it must be the case that \(\nu _j \leqslant 1- \mu _j\) for each \(j=1, \ldots , n\). Therefore, the proof will be ended if we show \(\prod _{j=1}^n \mu _j^{\omega _j} + \prod _{j=1}^n (1-\mu _j)^{\omega _j}\leqslant 1\).

By the geometric–arithmetic inequality (cf., Sect. 2.2):

$$\begin{aligned}{} & {} \prod _{j=1}^n \mu _j^{\omega _j} + \prod _{j=1}^n (1-\mu _j)^{\omega _j}\leqslant \sum _{j=1}^n {\omega _j} \mu _j + \sum _{j=1}^n {\omega _j} (1-\mu _j) = 1. \end{aligned}$$

This completes the proof that \(\textrm{IFDG}_{\omega }: \textbf{A}\times {\mathop {\ldots }\limits ^{n}} \times \textbf{A}\rightarrow \textbf{A}\).

Idempotency guarantees \(f(\textbf{0}, {\mathop {\ldots }\limits ^{n}}, \textbf{0}) = \textbf{0}\), \(f(\textbf{1}, {\mathop {\ldots }\limits ^{n}}, \textbf{1}) = \textbf{1}\).

Monotonicity with respect to \(\succcurlyeq\) is routine: when \(I_i = (\mu _i, \nu _i) \succcurlyeq ( \bar{\mu }_i, \bar{\nu }_i) = \bar{I}_i\) for \(i=1, \ldots , n\), one immediately gets \(\textrm{IFDG}_{\omega } (I_1, \ldots , I_n) \succcurlyeq \textrm{IFDG}_{\omega } (\bar{I}_1, \ldots , \bar{I}_n)\). □

The application of Theorem 1 to \(\omega = ( \frac{1}{n}, \ldots , \frac{1}{n} )\) guarantees that \(\textrm{IFDG}\) is an aggregation operator.

4.2 Discussion

Compared to Theorem 1, Definition 6 bypasses the difficulty of the proof that \(\textrm{IFWG}_{\omega }\) is an aggregation operator by resorting to expressions defined from operational laws of IFNs. Then, the gist of the argument proving Xu and Yager (2006), Theorem 2, and Xu and Cai (2013), Theorem 1.3.2, becomes pretty simple and accessible. By contrast, the operator defined in Definition 9 also produces IFNs through a novel simpler formula; however, the demonstration that it is an aggregation operator is much harder without the utilization of the geometric–arithmetic inequality.

The next property establishes a remarkable comparison:

Proposition 1

In the conditions of Definitions 6 and 9: \(\textrm{IFDG}_{\omega }(I_1, \ldots , I_n) \succcurlyeq \textrm{IFWG}_{\omega }(I_1, \ldots , I_n)\). In particular, \(S(\textrm{IFDG}_{\omega }(I_1, \ldots , I_n) )\geqslant S(\textrm{IFWG}_{\omega }(I_1, \ldots , I_n))\).

Proof

The first claim reduces to \(\prod _{j=1}^n \nu _j^{\omega _j} \leqslant 1- \prod _{j=1}^n (1-\nu _j)^{\omega _j}\), or equivalently, \(\prod _{j=1}^n \nu _j^{\omega _j} + \prod _{j=1}^n (1-\nu _j)^{\omega _j} \leqslant 1\). The proof of Theorem 1 justifies this non-trivial inequality. The second claim is now immediate (cf., Sect. 2.1). □

Finally in this section, to ensure that Definition 9 produces a distinct aggregation operator for IFNs, the next example compares it with the most prominent intuitionistic fuzzy geometric operators found in the existing literature.

Example 2

For illustration, let us examine the results of the aggregation of the IFNs used in Example 1 of Xu and Yager (2006) by the focal intuitionistic fuzzy geometric operators whose expressions are given in section 3.3 (we avoid the \(\textrm{IFGWHM}_{\omega }^{p,q}\) class of operators, which depend upon extra parameters and would require a very lengthy analysis). Hence, we consider \(I_1 =(0.1, 0.7)\), \(I_2 =(0.4, 0.3)\), \(I_3 =(0.6, 0.1)\), and \(I_4 =(0.2, 0.5)\) and the vector of weights \(\omega =(0.2, 0.3, 0.1, 0.4)\).

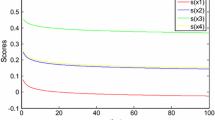
Figure 1 shows both \(I_1, I_2, I_3\), and \(I_4\), and their aggregation by \(\textrm{IFDG}_{\omega }\), \(\textrm{IFWG}_{\omega }\), \(\textrm{IFOWG}_{\omega }\), and \(\textrm{IFWGA}_{\omega }\).

Fig. 1
figure 1

A graphical comparison of the aggregate IFNs (circular dots) associated with the IFNs (squared dots) in Example 2: red dot—result obtained from the new \(\textrm{IFDG}_{\omega }\) in Equation 7—, black dot—result with \(\textrm{IFWG}_{\omega }\) in Equation (3)—blue dot—result with \(\textrm{IFOWG}{\omega }\) in Equation 4—and green dot—result with \(\textrm{IFWGA}{\omega }\) in Equation 5

Full size image

To compare the relative performance of these aggregation methodologies, we shall use two proxies. First, we employ the average of the Euclidean distances to the four IFNs. Second, we use the Sum of Squared Error (SSE) by inspiration of the k-means clustering algorithm (Celebi et al. 2013). Table 1 summarizes both the results of the aggregation by the four operators considered in this example, plus their respective average distances and SSEs. We observe that in this example \(\textrm{IFDG}_{\omega }\) outperforms \(\textrm{IFWG}_{\omega }\) and \(\textrm{IFOWG}_{\omega }\) in both dimensions, although it is much simpler.

Table 1 Results by four aggregation operators, average distances to the points, and SSEs, in Example 2
Full size table

Finally in this section, we explain that \(\textrm{IFDG}_{\omega }\) is an example of representable intuitionistic aggregation function Kolesárová and Mesiar (2020) [Section 3]. To introduce this concept, recall that the dual of the aggregation operator \(\mathcal {A}: \mathcal{I}\times {\mathop {\ldots }\limits ^{n}} \times \mathcal{I}\rightarrow \mathcal{I}\) is \(\mathcal {A}^d: \mathcal{I}\times {\mathop {\ldots }\limits ^{n}} \times \mathcal{I}\rightarrow \mathcal{I}\) defined as \(\mathcal {A}^d(a_1, {\ldots }, a_n) = 1 - \mathcal {A}(1-a_1, {\ldots }, 1-a_n)\) for each \(a_i\in \mathcal{I}\) (\(i=1, \ldots , n\)). Kolesárová and Mesiar argue that when \(\mathcal {B}\) is another aggregation operator such that \(\mathcal {A}^d \geqslant \mathcal {B}\), the next expression defines an aggregation operator on IFNs: for each collection of IFNs \(\{ I_1 = (\mu _1, \nu _1), \ldots , I_n = (\mu _n, \nu _n) \}\),

$$\begin{aligned}{} & {} (\mathcal {A},\mathcal {B})(I_1, \ldots , I_n) = \Bigr ( \mathcal {A}( \mu _1, \ldots \mu _n ), \ \mathcal {B}( \nu _1, \ldots \nu _n ) \Bigr ). \end{aligned}$$
(9)

If we apply this expression to the case \(\mathcal {A}= \mathcal {B}= G_{\omega }\) given by Eq. (2), then we obtain \(\textrm{IFDG}_{\omega } = (\mathcal {A},\mathcal {B})\). The crucial inequality \(G_{\omega }^d \geqslant G_{\omega }\) that is required by the definition of representable intuitionistic aggregation function is precisely what we demonstrate in the proof of Theorem 1.

In conclusion, although \(\textrm{IFDG}_{\omega }\) is a representable intuitionistic aggregation function, the fact that it is a new example of this class of aggregators necessitates a non-trivial mathematical proof that we produce in Theorem 1.

5 An application to multi-attribute group decision-making

This section produces an application of the intuitionistic fuzzy direct weighted geometric operator to group decision-making with the help of the comparison law in Definition 2. To this purpose, we adapt the methodology described in either Section 6 of Kumar and Chen (2022) or Section V of Liu and Chen (2017) by replacing their respective aggregation operators by an intuitionistic fuzzy direct weighted geometric operator in the corresponding steps of their algorithms.

We state this procedure below as Algorithm 1. The input is a list of IFSs. They are submitted by a group of agents. Two elective components are two vectors of weights \(\omega\) and w. They, respectively, capture the importance of the attributes that characterize the IFSs and the expertise of the agents. Then, the first step transforms attributes of cost type into benefit type (this standard procedure is called “normalization”). Step 2 uses \(\textrm{IFDG}_{w}\) to produce an aggregate IFS from the multi-agent information. At this point, for each alternative and characteristic we have one IFV. Step 3 uses \(\textrm{IFDG}_{\omega }\) to associate one IFV with each alternative. Finally, Step 4 computes the figures that are needed to apply the comparison law given in Definition 2 to the alternatives.

figure a

The next example gives both an illustrative application of Algorithm 1 and a comparative analysis with respect to two existing methodologies.

Example 3

For illustration, let us reconsider the example that was studied in both Example 6.1 of Kumar and Chen (2022) and Section V of Liu and Chen (2017) in the light of Algorithm 1.

The goal of this problem is to produce a ranking of five options \(O_1, \ldots , O_5\). To calculate it, three experts evaluate the alternatives in relation with four characteristics \(C_1, \ldots , C_4\). The values assigned to the opinions of the agents are measured by the vector of weights \(w = (0.35, 0.4, 0.25)\). And the relative values of the characteristics are measured by \(\omega = (0.1, 0.2, 0.3, 0.4)\).

The three experts submit their assessments by Tables 2-4, respectively.

Table 2 Ratings given by expert 1 in Example 3
Full size table
Table 3 Ratings given by expert 2 in Example 3
Full size table
Table 4 Ratings given by expert 3 in Example 3
Full size table

Let us apply Algorithm 1. Example 6.1 of Kumar and Chen (2022) and Section V of Liu and Chen (2017) explained that all characteristics are positive. Therefore, we do not need to do anything at Step 1.

At Step 2, the aggregate values across agents use the vector of weights \(w = (0.35, 0.4, 0.25)\) to produce the IFS defined by Table 5 with the help of \(\textrm{IFDG}_{w }\). For example, the cell corresponding to the evaluation of \(O_1\) under \(C_1\) is calculated as follows:

$$\begin{aligned}{} & {} \textrm{IFDG}_{w }\bigr ( (0.5, 0.4), (0.4, 0.5), (0.4, 0.2) \bigr ) \\{} & {} = (0.5^{0.35} 0.4^{0.4} 0.4^{0.25}, 0.5^{0.35} 0.4^{0.4} 0.4^{0.25}, \, 0.4^{0.35} 0.5^{0.4} 0.2^{0.25}) \\{} & {} = (0.432492, 0.367762). \end{aligned}$$
Table 5 Aggregate evaluation obtained after step 2 in Example 3
Full size table

Now, Step 3 aggregates the IFVs across characteristics using the vector of weights \(\omega = (0.1, 0.2, 0.3, 0.4)\) with the help of \(\textrm{IFDG}_{\omega }\). For example, the cell corresponding to the evaluation of \(O_1\) is calculated as follows:

$$\begin{aligned}{} {} \textrm{IFDG}_{\omega }&\bigr ( (0.432492, 0.367762), (0.537827, 0.230495),\\{} & {} (0.36282, 0.429), (0.462436, 0.299797) \bigr )\\ = &(0.432492^{0.1} 0.537827^{0.2} 0.36282^{0.3} 0.462436^{0.4}, \, \\& 0.367762^{0.1} 0.230495^{0.2} 0.429^{0.3} 0.299797^{0.4} ) \\ = & (0.440204, 0.323264). \end{aligned}$$

Then, Step 4 computes all the scores of the aggregate IFVs. Table 6 shows both aggregate values and their scores.

Table 6 Aggregate values and their scores in Example 3
Full size table

We conclude \(O_{2}> O_{4}> O_{5}> O_{1} > O_{3}\). This ranking coincides with the recommendations given by both Kumar and Chen (2022), Sect. 6, and Liu and Chen (2017), Section V, to this problem. This coincidence confirms that the methodology designed with our fundamental aggregation operator is consistent with existing approaches.

6 Concluding remarks

Many aggregation operators on IFNs have been defined since the pioneering articles by Xu and Yager (2006) and Xu (2007). Influential papers on the topic include Beliakov et al. (2011); Kolesárová and Mesiar (2020); Wei (2010); Xu and Yager (2011); Xu (2011); Wang and Liu (2011); Xu (2010); Xu et al. (2023), and Xu et al. (2023).

However, the intuitionistic fuzzy direct weighted geometric operator on IFNs defined in (7) remained unexplored. We have proven that it is an aggregation operator on IFNs and also that it as a new example of the class of representable intuitionistic fuzzy aggregators studied by Kolesárová and Mesiar (2020).

Finally, we have confirmed that the utilization of the intuitionistic fuzzy direct weighted geometric operator produces reliable results in multi-attribute group decision-making.