Trapezoidal interval type-2 fuzzy aggregation operators and their application to multiple attribute group decision making

Abstract

A type-2 fuzzy set, which is characterized by a fuzzy membership function, involves more uncertainties than the type-1 fuzzy set. As the most widely used type-2 fuzzy set, interval type-2 fuzzy set is a very useful tool to model the uncertainty in the process of decision making. As a special case of interval type-2 fuzzy set, trapezoidal interval type-2 fuzzy set can express linguistic assessments by transforming them into numerical variables objectively. The aim of this paper is to investigate the multiple attribute group decision-making problems in which the attribute values and the weights take the form of trapezoidal interval type-2 fuzzy sets. First, we introduce the concept of trapezoidal interval type-2 fuzzy sets and some arithmetic operations between them. Then, we develop several trapezoidal interval type-2 fuzzy aggregation operators for aggregating trapezoidal interval type-2 fuzzy sets and examine several useful properties of the developed operators. Furthermore, based on the proposed operators, we develop two approaches to multiple attribute group decision making with linguistic information. Finally, a practical example is given to illustrate the feasibility and effectiveness of the developed approach.

Appendices

Appendix 1: type-2 fuzzy sets

A type-2 fuzzy set $\tilde{A}$ in the universe of discourse X can be represented by a type-2 membership function $\mu_{{\tilde{A}}}$, shown as follows [20, 21, 56]:

$$\tilde{A} = \left\{ {\left( {\left( {x,u} \right),\mu_{{\tilde{A}}} \left( {x,u} \right)} \right)\left| {\forall x \in X,\quad \forall u \in J_{x} \subseteq \left[ {0,1} \right]} \right.} \right\},$$

where $0 \le \mu_{{\tilde{A}}} \left( {x,u} \right) \le 1$. The type-2 fuzzy set $\tilde{A}$ also can be represented as follows:

$$\tilde{A} = \int_{x \in X} {\int_{{u \in J_{x} }} {{{\mu_{{\tilde{A}}} \left( {x,u} \right)} \mathord{\left/ {\vphantom {{\mu_{{\tilde{A}}} \left( {x,u} \right)} {\left( {x,u} \right)}}} \right. \kern-0pt} {\left( {x,u} \right)}}} } = \int_{x \in X} {{{\left[ {\int_{{u \in J_{x} }} {{{\mu_{{\tilde{A}}} \left( {x,u} \right)} \mathord{\left/ {\vphantom {{\mu_{{\tilde{A}}} \left( {x,u} \right)} u}} \right. \kern-0pt} u}} } \right]} \mathord{\left/ {\vphantom {{\left[ {\int_{{u \in J_{x} }} {{{\mu_{{\tilde{A}}} \left( {x,u} \right)} \mathord{\left/ {\vphantom {{\mu_{{\tilde{A}}} \left( {x,u} \right)} u}} \right. \kern-0pt} u}} } \right]} x}} \right. \kern-0pt} x}} ,$$

where x is the primary variable, J _x  ⊆ [0, 1] is the primary membership of x, u is the secondary variable, and $\int_{{u \in J_{x} }} {{{\mu_{{\tilde{A}}} \left( {x,u} \right)} \mathord{\left/ {\vphantom {{\mu_{{\tilde{A}}} \left( {x,u} \right)} u}} \right. \kern-0pt} u}}$ is the secondary membership function (MF) at x. ∫ denotes union among all admissible x and u. For discrete universe of discourse, ∫ is replaced by Σ.

Let $\tilde{A}$ be a type-2 fuzzy set in the universe of discourse X represented by the type-2 membership function $\mu_{{\tilde{A}}} \left( {x,u} \right)$. If all $\mu_{{\tilde{A}}} \left( {x,u} \right) = 1$, then $\tilde{A}$ is called an interval type-2 fuzzy set. An interval type-2 fuzzy set $\tilde{A}$ can be regarded as a special case of a type-2 fuzzy set, shown as follows [21]:

$$\tilde{A} = \int_{x \in X} {\int_{{u \in J_{x} }} {{1 \mathord{\left/ {\vphantom {1 {\left( {x,u} \right)}}} \right. \kern-0pt} {\left( {x,u} \right)}}} } = \int_{x \in X} {{{\left[ {\int_{{u \in J_{x} }} {{1 \mathord{\left/ {\vphantom {1 u}} \right. \kern-0pt} u}} } \right]} \mathord{\left/ {\vphantom {{\left[ {\int_{{u \in J_{x} }} {{1 \mathord{\left/ {\vphantom {1 u}} \right. \kern-0pt} u}} } \right]} x}} \right. \kern-0pt} x}} ,$$

where x is the primary variable, J _x  ⊆ [0, 1] is the primary membership of x, u is the secondary variable, and $\int_{{u \in J_{x} }} {{1 \mathord{\left/ {\vphantom {1 u}} \right. \kern-0pt} u}}$ is the secondary membership function (MF) at x.

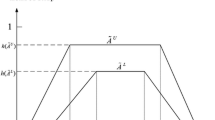
Uncertainty about an interval type-2 fuzzy set $\tilde{A}$ is conveyed by the union of all of the primary memberships, which is called the footprint of uncertainty (FOU) of $\tilde{A}$, i.e.,

$${\text{FOU}}\left( {\tilde{A}} \right) = \bigcup\nolimits_{x \in X} {J_{x} }$$

The upper membership function and lower membership function of $\tilde{A}$ are two type-1 membership functions that bound the FOU. The upper membership function is associated with the upper bound of ${\text{FOU}}\left( {\tilde{A}} \right)$ and is denoted by $\tilde{A}^{U}$, and the lower membership function is associated with the lower bound of ${\text{FOU}}\left( {\tilde{A}} \right)$ and is denoted by $\tilde{A}^{L}$.

Let $\tilde{A}$ be a trapezoidal type-1 fuzzy set, $\tilde{A} = \left( {a_{1} ,a_{2} ,a_{3} ,a_{4} ;H_{1} \left( {\tilde{A}} \right),H_{2} \left( {\tilde{A}} \right)} \right)$, as shown in Fig. 3, where $H_{1} \left( {\tilde{A}} \right)$ denotes the membership value of the element a ₂, $H_{2} \left( {\tilde{A}} \right)$ denotes the membership value of the element a ₃, $0 \le H_{1} \left( {\tilde{A}} \right) \le 1$ and $0 \le H_{2} \left( {\tilde{A}} \right) \le 1$. If a ₂ = a ₃, then the trapezoidal type-1 fuzzy set $\tilde{A}$ becomes a triangular type-1 fuzzy set.

Fig. 3

A trapezoidal type-1 fuzzy set

Appendix 2: some operational laws and comparison law

The operation between the trapezoidal interval type-2 fuzzy sets $\tilde{A}_{1} = \left( {\tilde{A}_{1}^{U} ,\tilde{A}_{1}^{L} } \right) = \left( {\left( {a_{11}^{U} ,a_{12}^{U} ,a_{13}^{U} ,a_{14}^{U} ;H_{1} \left( {\tilde{A}_{1}^{U} } \right),H_{2} \left( {\tilde{A}_{1}^{U} } \right)} \right),\quad \left( {a_{11}^{L} ,a_{12}^{L} ,a_{13}^{L} ,a_{14}^{L} ;H_{1} \left( {\tilde{A}_{1}^{L} } \right),H_{2} \left( {\tilde{A}_{1}^{L} } \right)} \right)} \right)$ and $\tilde{A}_{2} = \left( {\tilde{A}_{2}^{U} ,\tilde{A}_{2}^{L} } \right) = \left( {\left( {a_{21}^{U} ,a_{22}^{U} ,a_{23}^{U} ,a_{24}^{U} ;H_{1} \left( {\tilde{A}_{2}^{U} } \right),H_{2} \left( {\tilde{A}_{2}^{U} } \right)} \right),\quad \left( {a_{21}^{L} ,a_{22}^{L} ,a_{23}^{L} ,a_{24}^{L} ;H_{1} \left( {\tilde{A}_{2}^{L} } \right),H_{2} \left( {\tilde{A}_{2}^{L} } \right)} \right)} \right)$ is defined as follows [1, 18, 19]:

1.

$$\begin{aligned} \tilde{A}_{1} \oplus \tilde{A}_{2} & = \left( {\tilde{A}_{1}^{U} ,\tilde{A}_{1}^{L} } \right) \oplus \left( {\tilde{A}_{2}^{U} ,\tilde{A}_{2}^{L} } \right) \\ & = \left( \begin{array}{l} \left( {a_{11}^{U} + a_{21}^{U} ,a_{12}^{U} + a_{22}^{U} ,a_{13}^{U} + a_{23}^{U} ,a_{14}^{U} + a_{24}^{U} ;\, \hbox{min} \left\{ {H_{1} \left( {\tilde{A}_{1}^{U} } \right),H_{1} \left( {\tilde{A}_{2}^{U} } \right)} \right\},\,\hbox{min} \left\{ {H_{2} \left( {\tilde{A}_{1}^{U} } \right),H_{2} \left( {\tilde{A}_{2}^{U} } \right)} \right\}} \right), \hfill \\ \left( {a_{11}^{L} + a_{21}^{L} ,a_{12}^{L} + a_{22}^{L} ,a_{13}^{L} + a_{23}^{L} ,a_{14}^{L} + a_{24}^{L} ;\,\hbox{min} \left\{ {H_{1} \left( {\tilde{A}_{1}^{L} } \right),H_{1} \left( {\tilde{A}_{2}^{L} } \right)} \right\},\,\hbox{min} \left\{ {H_{2} \left( {\tilde{A}_{1}^{L} } \right),H_{2} \left( {\tilde{A}_{2}^{L} } \right)} \right\}} \right) \hfill \\ \end{array}\right) \\ \end{aligned}$$

2.

$$\begin{aligned} \tilde{A}_{1} \otimes \tilde{A}_{2} & = \left( {\tilde{A}_{1}^{U} ,\tilde{A}_{1}^{L} } \right) \otimes \left( {\tilde{A}_{2}^{U} ,\tilde{A}_{2}^{L} } \right) \\ {\kern 1pt} & = \left( \begin{array}{l} \left( {a_{11}^{U} \times a_{21}^{U} ,a_{12}^{U} \times a_{22}^{U} ,a_{13}^{U} \times a_{23}^{U} ,a_{14}^{U} \times a_{24}^{U} ;\, \hbox{min} \left\{ {H_{1} \left( {\tilde{A}_{1}^{U} } \right),H_{1} \left( {\tilde{A}_{2}^{U} } \right)} \right\},\, \hbox{min} \left\{ {H_{2} \left( {\tilde{A}_{1}^{U} } \right),H_{2} \left( {\tilde{A}_{2}^{U} } \right)} \right\}} \right), \hfill \\ \left( {a_{11}^{L} \times a_{21}^{L} ,a_{12}^{L} \times a_{22}^{L} ,a_{13}^{L} \times a_{23}^{L} ,a_{14}^{L} \times a_{24}^{L} ;\, \hbox{min} \left\{ {H_{1} \left( {\tilde{A}_{1}^{L} } \right),H_{1} \left( {\tilde{A}_{2}^{L} } \right)} \right\},\, \hbox{min} \left\{ {H_{2} \left( {\tilde{A}_{1}^{L} } \right),H_{2} \left( {\tilde{A}_{2}^{L} } \right)} \right\}} \right) \hfill \\ \end{array}\right) \\ \end{aligned}$$

3.

$$k\tilde{A}_{1} = \left( {k\tilde{A}_{1}^{U} ,k\tilde{A}_{1}^{L} } \right) = \left( \begin{aligned} \left( {k \times a_{11}^{U} ,k \times a_{12}^{U} ,k \times a_{13}^{U} ,k \times a_{14}^{U} ;\,H_{1} \left( {\tilde{A}_{1}^{U} } \right),H_{2} \left( {\tilde{A}_{2}^{U} } \right)} \right), \hfill \\ \left( {k \times a_{11}^{L} ,k \times a_{12}^{L} ,k \times a_{13}^{L} ,k \times a_{14}^{L} ;\,H_{1} \left( {\tilde{A}_{1}^{L} } \right),H_{2} \left( {\tilde{A}_{2}^{L} } \right)} \right) \hfill \\ \end{aligned} \right),\quad {\text{where}}\quad k > 0$$

4.

$$\tilde{A}_{1}^{k} = \left( {\left( {\tilde{A}_{1}^{U} } \right)^{k} ,\left( {\tilde{A}_{1}^{L} } \right)^{k} } \right) = \left( \begin{aligned} \left( {\left( {a_{11}^{U} } \right)^{k} ,\left( {a_{12}^{U} } \right)^{k} ,\left( {a_{13}^{U} } \right)^{k} ,\left( {a_{14}^{U} } \right)^{k} ;\,H_{1} \left( {\tilde{A}_{1}^{U} } \right),H_{2} \left( {\tilde{A}_{1}^{U} } \right)} \right), \hfill \\ \left( {\left( {a_{11}^{L} } \right)^{k} ,\left( {a_{12}^{L} } \right)^{k} ,\left( {a_{13}^{L} } \right)^{k} ,\left( {a_{14}^{L} } \right)^{k} ;\,H_{1} \left( {\tilde{A}_{1}^{L} } \right),H_{2} \left( {\tilde{A}_{1}^{L} } \right)} \right) \hfill \\ \end{aligned} \right),\quad {\text{where}}\quad k > 0$$

Let $\tilde{A} = \left( {\tilde{A}^{U} ,\tilde{A}^{L} } \right) = \left( {\left( {a_{1}^{U} ,a_{2}^{U} ,a_{3}^{U} ,a_{4}^{U} ;H_{1} \left( {\tilde{A}^{U} } \right),H_{2} \left( {\tilde{A}^{U} } \right)} \right),\left( {a_{1}^{L} ,a_{2}^{L} ,a_{3}^{L} ,a_{4}^{L} ;H_{1} \left( {\tilde{A}^{L} } \right),H_{2} \left( {\tilde{A}^{L} } \right)} \right)} \right)$ be a trapezoidal interval type-2 fuzzy set. Chen et al. [57] defined the ranking value $RV\left( {\tilde{A}} \right)$ of $\tilde{A}$ as follows:

$$\begin{aligned} {\text{RV}}\left( {\tilde{A}} \right) & = \left[ {\frac{{\left[ {\left( {a_{1}^{U} + K} \right) + \left( {a_{4}^{U} + K} \right)} \right]}}{2} + \frac{{\left( {H_{1} \left( {\tilde{A}^{U} } \right) + H_{2} \left( {\tilde{A}^{U} } \right) + H_{1} \left( {\tilde{A}^{L} } \right) + H_{2} \left( {\tilde{A}^{L} } \right)} \right)}}{4}} \right] \\ & \quad \times \frac{{\left[ {\left( {a_{1}^{U} + K} \right) + \left( {a_{2}^{U} + K} \right) + \left( {a_{3}^{U} + K} \right) + \left( {a_{4}^{U} + K} \right) + \left( {a_{1}^{L} + K} \right) + \left( {a_{2}^{L} + K} \right) + \left( {a_{3}^{L} + K} \right) + \left( {a_{4}^{L} + K} \right)} \right]}}{8} \\ \end{aligned}$$

where $K = \left\{ {\begin{array}{*{20}l} 0 \hfill & {{\text{if}}\quad a_{1}^{U} \ge 0,} \hfill \\ {\left| {a_{1}^{U} } \right|,} \hfill & {{\text{if}}\quad a_{1}^{U} < 0.} \hfill \\ \end{array} } \right.$

To rank any two trapezoidal interval type-2 fuzzy sets, Chen et al. [57] defined the following comparison laws: Let $\tilde{A}$ and $\tilde{B}$ be two trapezoidal interval type-2 fuzzy sets. If ${\text{RV}}\left( {\tilde{A}} \right) < {\text{RV}}\left( {\tilde{B}} \right)$, then we define $\tilde{A} < \tilde{B}$. If ${\text{RV}}\left( {\tilde{A}} \right) = {\text{RV}}\left( {\tilde{B}} \right)$, then we define $\tilde{A} = \tilde{B}$.