1 Introduction

One of the biggest obstacles to a wide industrial utilization of laser powder bed fusion (PBF-LB/M) is the extensive and costly quality assurance. There are commercial in situ monitoring systems on the market, but a reliable interpretation of the recorded data is challenging. In-process monitoring in metallic additive manufacturing (metal AM) is, therefore, still subject of Research and Development [1,2,3].

Due to the thermal nature of the process, the thermal radiation emitted is suitable as a process signature. It can be recorded contactless using thermography, pyrometry, or quotient pyrometry.

For thermography and pyrometry, the emissivity ε is generally estimated and considered to be constant. For the PBF-LB/M process, e.g., the consolidation plateau can serve as a good reference point [4, 5]. Often, the emissivity is just considered to be equals one.

Even by this assumption, Lought et al. were able to correlate thermal features extracted from monitored short-wave infrared radiation (SWIR, \({\lambda }_{SWIR}\)= 0.9 µm–1.7 µm) of a 304L stainless steel PBF-LB/M process to resulting yield strength and porosity of the produced parts [6]. Also, Oster et al. could predict porosity based on SWIR monitoring data with the help of Artificial Intelligence (AI) methods [7]. With the help of AI, also the near infrared (NIR, \({\lambda }_{NIR}\)=0.75–1.1 µm) signatures captured by an Optical Tomography System could be used to predict porosity in an IN718 PBF-LB/M process [8].

Quotient pyrometry, the monitoring of multiple wavelength ranges of the thermal signature simultaneously, is an also commonly used approach for in-process monitoring. The influence of the emissivity is neglected by assuming constant ratio of the emissivity for the monitored wavelengths (gray-body assumption) [9]. By monitoring two different wavelength ranges in the visible (VIS, \({\lambda }_{VIS}\)=0.40–0.75 µm) and NIR range, Vallabh et al. [10] and Becker et al. [11] could estimate approximate surface temperatures for the PBF-LB/M process. An approach by means of a spectrometer monitoring multiple wavelength ranges by Fernandez et al. [4] showed promising results.

Although promising results have already been obtained without deeper consideration of emissivity, it is difficult to transfer the measured results to other materials, machines or simply build processes. Here, the monitoring of real surface temperatures as absolute physical quantity would be a game changer for the transferability of monitoring systems.

Since both assumptions, constant emissivity for thermography and constant emissivity ratio for quotient pyrometry are not valid in general, one goal of this study is to check the validity and its limitations for the use case of PBF-LB/M.

The spectral directional emissivity \({{\varepsilon }^{\prime}}_{\lambda }\left(\varphi ,\lambda ,T\right)\) is a major source of error when determining temperatures with thermal camera systems. It depends on many influencing factors and is quite difficult to measure. Depending on the monitoring wavelength, the error resulting from an unknown \({{\varepsilon }^{\prime}}_{\lambda }\) can have drastic effects on the measured temperature [9], e.g., several 100 K for thermographic measurements of the PBF-LB/M process in the mid infrared wavelength range as used by Altenburg et al. [12] or Mohr et al. [13]. PBF-LB/M correlated emissivity investigations of metallic powders had already been done 1995 be Sih et al. [14]. A sophisticated measurement set-up for measuring the spectral directional emissivity \({{\varepsilon }^{\prime}}_{\lambda }\left(\varphi ,\lambda ,T\right)\) spatially resolved in the PBF/LBM process for one wavelength is realized by Deisenroth et al. [15].

As one step toward enabling monitoring systems to measure absolute temperatures, the spectral directional emissivity \({{\varepsilon }^{\prime}}_{\lambda }\left(\varphi ,\lambda ,T\right)\) occurring in the PBF-LB/M process is investigated by wavelength and viewing angle in this paper. To this end, measurements were carried out on PBF-LB/M samples and metallic powders of commonly used AM materials—stainless steels 316L and aluminum AlSi10Mg—using the emissivity measuring apparatus (EMMA) of the Center for Applied Energy Research (CAE), Würzburg, Germany.

2 Theory and measurement procedure

The spectral directional emissivity \({{\varepsilon }^{\prime}}_{\lambda }\left(\varphi ,\lambda ,T\right)\) of the surface of an opaque body is a measure of how much radiation it emits in comparison to an ideal heat radiator, a black body. It ranges between 0—absolute reflectance, and 1—absolute emittance. It depends on the chemical composition, the aggregate state (liquid or solid), surface condition (e.g., roughness), and temperature \({T}_{s}\) of the measured specimen as well as on the viewing angle (azimuth angle \(\varphi\)) and the measured wavelength \(\lambda\). Polarization can also be an influencing parameter for anisotropic surfaces, such as those created by the stripe pattern in the PBF-LB/M process. Furthermore, when measuring the emissivity of a specimen, the measured value is also strongly influenced by the measuring environment, e.g., the measurement atmosphere and the surrounding walls.

There are several techniques for measuring the emissivity of opaque targets (e.g., reference emitter, reference temperature, two temperature and reflectivity approach) [9, 16, 17]. To gain detailed information on the spectral and angular dependence of the emissivity, the direct radiometric method is chosen here [18]. A more detailed description of the measurement procedure and the underlying theory is introduced by Manara et al. in [17].

Note that when comparing literature values of emissivity, a distinction must be made between the often-stated total hemispherical emissivity \(\varepsilon \left(T\right)\) (e.g., measured by the calorimetric method) and the spectral directional emissivity \({{\varepsilon }^{\prime}}_{\lambda }\left(\varphi ,\lambda ,T\right)\) investigated here. The former is applicable to heat transfer problems, the latter is needed when looking at thermographic measurements as targeted here. In the following, the spectral directional emissivity \({{\varepsilon }^{\prime}}_{\lambda }\left(\varphi ,\lambda ,T\right)\) is referred to as emissivity.

Therefore, the measurable spectral directional radiative intensity \({I}_{mea}\) of a specimen consists of:

  • the intensity emitted by the specimen itself \({I}_{bb}\left(\lambda ,{T}_{S}\right)\cdot {{\varepsilon }^{\prime}}_{\lambda }\left(\varphi ,\lambda ,{T}_{S}\right)\) and

  • the intensity emitted by the hemispherical surrounding which is reflected by the specimen into the view of observation

\({I}_{Su}\left(\lambda ,{T}_{Su}\right)\cdot {\rho }_{\lambda }\left(\varphi ,\lambda ,{T}_{S}\right)\)resulting in:

$${I}_{\text{mea}}\left(\varphi ,\lambda ,{T}_{\text{S}},{T}_{\text{Su}}\right)={I}_{bb}\left(\lambda ,{T}_{S}\right)\cdot {{\varepsilon }^{\prime}}_{\lambda }\left(\varphi ,\lambda ,{T}_{S}\right)$$
$$+{I}_{Su}\left(\lambda ,{T}_{Su}\right)\bullet {\rho }_{\lambda }\left(\varphi ,\lambda ,{T}_{S}\right).$$
(1)

\({I}_{bb}\) gives the spectral directional radiative intensity of an ideal black body, \({\rho }_{\lambda }\left(\varphi ,\lambda ,{T}_{S}\right)\) is the spectral hemispherical-directional reflectivity of the specimen, and \({T}_{Su}\) is the temperature of the hemispherical surrounding. Due to Kirchhoff’s law, which describes the identity of spectral directional absorptivity \({\alpha }_{\lambda }\left(\varphi ,\lambda ,T\right)\) and emissivity \({{\varepsilon }^{\prime}}_{\lambda }\left(\varphi ,\lambda ,T\right)\) and the conservation of energy for nontransparent specimen (\({\alpha }_{\lambda }\left(\varphi ,\lambda ,T\right)+{\rho }_{\lambda }\left(\varphi ,\lambda ,T\right)=1\)), Eq. (1) can be solved for the emissivity:

$${\varepsilon ^{\prime}}_{\lambda }\left(\varphi ,\lambda ,{T}_{S}\right)=\frac{{I}_{\text{mea}}\left(\varphi ,\lambda ,{T}_{\text{S}},{T}_{\text{Su}}\right)-{I}_{Su}\left(\lambda ,{T}_{Su}\right)}{{I}_{bb}\left(\lambda ,{T}_{S}\right)-{I}_{Su}\left(\lambda ,{T}_{Su}\right)}.$$
(2)

Since the radiation coming from the surrounding influences the measurement, an environment as close as possible to an ideal black body with a constant and significantly lower, homogeneous temperature must be provided for the measurement.

For samples at ambient temperature \({T}_{amb}\), another method to measure the emissivity \({\varepsilon ^{\prime}}_{\lambda }\left(\varphi ,\lambda ,T\right)\) is used, since the emitted intensity is very low and no differentiation can be made between reflected and emitted radiation at ambient temperature\({T}_{amb}\). Therefore, an external light source with known intensity Iext and an integrating sphere with known spectral directional-hemispheric reflectivity \({\rho }_{Su,\lambda }\left(\varphi ,\lambda ,{T}_{amb}\right)\) is used.

Using the law of conservation of energy and Kirchhoff's law, the emissivity \({\varepsilon ^{\prime}}_{\lambda }\left(\varphi ,\lambda ,T\right)\) can be determined via its reflectivity:

$${\varepsilon ^{\prime}}_{\lambda }\left(\varphi ,\lambda ,{T}_{amb}\right)=1-\frac{{I}_{\text{mea}}\left(\varphi ,\lambda ,{T}_{amb}\right)}{{I}_{ext}\left(\lambda \right)\cdot {\rho }_{Su,\lambda }\left(\varphi ,\lambda ,{T}_{amb}\right)}.$$
(3)

Since the measurement results are strongly dependent on the knowledge of the surrounding, the reader should still consider that, despite very careful measurement methods and system design, a significant measurement uncertainty is unavoidable. Measurements from different publications often disagree by ≈ 10% [19].

3 Experimental details

In this work, the emissivity of PBF-LB/M specimens was determined using two different measurement apparatuses: one for ambient temperatures \({T}_{amb}\) and temperatures up to \({T}_{S}=\) 200 °C, and one for higher temperatures in the range between \({T}_{S}=\) 400 °C and 1290 °C. All measurements were performed at the Center for Applied Energy Research (CAE), Würzburg, Germany.

3.1 Emissivity measurement systems

3.1.1 Ambient temperature measurements

The schematic set-up for the measurement of the emissivity at ambient temperature is shown in Fig. 1. As measurement environment integrating spheres and standards from the same material as the sphere’s inner coating with known spectral directional-hemispheric reflectivity \({\rho }_{Su,\lambda }\left(\varphi ,\lambda ,{T}_{amb}\right)\) were used.

Fig. 1
figure 1

Schematic ambient temperature measurement set-up

Full size image

For measurements in the VIS, NIR and lower short-wave infrared (SWIR) (\({\lambda }_{SWIR-L}\) =1.1–2 µm) wavelength range, a VIS/NIR grating spectrometer (Lambda 950, Perkin Elmer, US) with integrated integrating sphere with PTFE coating and integrated deuterium and tungsten halogen light sources was used. As reference standard, a PTFE standard was used.

Measurements in the upper SWIR range (\({\lambda }_{SWIR-U}\) = 2–2.5 µm), mid wavelength infrared range (MWIR) (\({\lambda }_{MWIR}\) = 2.5–5.5 µm), long wavelength infrared range (LWIR) (\({\lambda }_{LWIR}\) = 8–14 µm), and up to \(\lambda\) = 20 µm were performed with a 4’’ golden integrating sphere (Labsphere, US) and a Fourier Transformation infrared spectrometer (IFS, Bruker, US). Appropriate diffusively reflecting gold standards and a silicon carbide thermal were used.

All measurements were performed with the specimen tilted by 8° to avoid direct reflections from its surface to the measurement opening.

3.1.2 High-temperature measurements

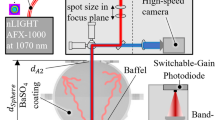
The apparatus used for measuring the spectral directional emissivity in the wavelength range between 1 and 20 µm at temperatures up to 2400 K (EMMA) is presented in detail by Arduini et al. in [17]. Therefore, just a brief overview will be given here.

The EMMA apparatus consists of a vacuum vessel with homogeneously tempered walls (\(\Delta T=\)± 0.5 K) and interior high emitting black coating (\({{\varepsilon }^{\prime}}_{\lambda }\left(\varphi ,\lambda ,T\right)=\) 0.975 ± 0.010), a connecting vacuum chamber and an FTIR-spectrometer (Vertex-70v, Bruker, US). The inner measuring and heating unit inside the vacuum vessel is shown in Fig. 2.

Fig. 2
figure 2

Heating and measuring unit inside the vacuum vessel

Full size image

Before each measurement, the apparatus is calibrated with a calibration procedure described in [20]. For the measurement of the emissivity, the specimen is placed in a movable graphite holder. With a linear actuator, the holder with specimen can be inserted into an inductive heating copper coil with fast heating rates of up to 200 K/min. It is then heated up homogeneously to the measuring temperature \({T}_{S}\). After reaching the targeted temperature, the holder is moved out of the coil and positions the specimen into the measuring beam. The measuring spot diameter here is \({d}_{m}\) = 6 mm. The emitted radiation \({I}_{\text{mea}}\) is guided by different mirrors to the spectrometer. Movable silver mirrors allow to manipulate the beam path and to measure the emissivity at different azimuth angles \(\varphi\) from normal to the specimen (\(\varphi\) = 0°) to \(\varphi\) = 70°. Note that \({d}_{m}\) is increased for \(\varphi >0\) in the tilted direction to up to 12 mm for \(\varphi\) = 70°.

The temperature of the vessel walls is determined by a contact thermometer. The temperature of the sample is elaborately determined and controlled as described in detail in [20]. To avoid influences from atmospheric gases, the whole beam path can be evacuated or be filled with specific process gases. For all measurements reported in this paper, an argon atmosphere was used.

3.2 Investigated specimens

In this investigation, two different PBF-LB/M materials were studied—stainless steel 316L and aluminum AlSi10Mg. Here, measurements were performed on as-delivered powder materials and as-printed specimens of the size of (24 × 24 × 3) mm3 or (24 × 50 × 3) mm3 for larger azimuth angles \(\varphi\). In Fig. 3, printed specimens are displayed exemplary.

Fig. 3
figure 3

Measured specimen (24 × 24 × 3) mm3 out of stainless steel 316L (left) and aluminum AlSi10Mg (right)

Full size image

The process parameters and equipment used for the printed specimens are summarized in Table 1. It should be noted that infill parameter sets were used since these are used for the majority of a printed component, i.e., the bulk part.

Table 1 Process information for the printed specimens
Full size table

Thicker powder samples were measured in graphite crucibles with a depth of approximately 4 mm. To analyze thinner powder layers, crucibles of the same material as the powder were printed and a protruding edge was ground to a defined height. The notch then was filled with powder and flattened using a blade. Figure 4 shows both types of powder samples in their crucibles after measurement. The particle size distribution of the 316L powder was 10–45 µm and that of the AlSi10Mg powder was 25–70 µm.

Fig. 4
figure 4

AlSi10Mg powder specimens in printed crucibles (left) and graphite crucibles (right)

Full size image

3.3 Investigated parameters

The viewing angle of off-axis monitoring systems on the build platform of PBF-LB/M systems is defined by optical window positions and changes between machines. The viewing angle also changes within the image, across the build platform. Therefore, in this study, besides wavelength \(\lambda\) and specimen temperature \({T}_{S}\), also the influence of the azimuth angle \(\varphi\) was investigated as well as the influence of the texture of PBF-LB/M surfaces with different scan angles \(\alpha\). Additionally, powder surfaces with different layer thickness \(t\) were investigated to study the influence of the diffusive radiation path within the powder on the emissivity.

For all high temperature measurements, the emissivity was measured in the wavelength range of \(\lambda\) = 1.5 µm–20 µm to estimate the influence of the measurement wavelength on the emissivity. To also estimate the emissivity in the VIS range, measurements were performed at ambient temperature \({T}_{amb}\) in the range \(\lambda\) = 0.4 µm–20 µm. This knowledge helps to choose suitable monitoring wavelength ranges for the PBF-LB/M process.

The PBF-LB/M process is characterized by large temperature gradients for melting and solidifying materials. A deeper understanding of the influence of the specimen temperature \({T}_{S}\) and aggregate changes on the emissivity is essential. Both powder and printed specimens, therefore, were measured at different specimen temperatures \({T}_{S}\).

It is well known that the surface condition influences the emissivity. Here, the influence of the wavy and rough surface of PBF-LB/M manufactured surfaces as well as the influence of the rough surface of a metal powder layer on the emissivity were investigated.

A general comparison of these two conditions was performed, and also the influence of the layer thickness \(t\) and the structured surface of PBF-LB/M specimens, as shown for one 316L specimen in Fig. 5, was investigated. The structured surface arises through the hatching of the scanning laser. Due to the often-used stripe pattern, as depicted in Fig. 3, the hatching shows one orientation per layer defined by the scan angle α. In this study, the influence of the orientation of the stripe pattern and the scan angle α were also investigated as influence factor on the emissivity.

Fig. 5
figure 5

Scanning electron microscope image of a 316L specimen with characteristic stripe pattern

Full size image

4 Results and discussion

In the following graphs (Figs. 6, 7, 8, 9, 10, 11, 12), it should be noted that the wavelength-axis \(\lambda\) is logarithmic. All measurements of powder specimens are shown with dashed or dotted lines, all solid lines represent PBF-LB/M specimen measurements. The relative uncertainty of each measurement curve is represented by a semi-transparent area.

Fig. 6
figure 6

Emissivity for different azimuth angles φ for (a) 316L PBF-LB/M specimens (TS=1290 °C, α = 45°) and (b) 316L powder specimens (TS=760–800 °C, t = 4 mm)

Full size image

4.1 Azimuth angle

The emissivity measured at various azimuth angles \(\varphi\) is shown in Fig. 6a) for 316L PBF-LB/M specimens (S) and in Fig. 6b) for 316L powder specimens (P). Similarly, the emissivity measured at various azimuth angles \(\varphi\) for AlSi10Mg PBF-LB/M specimens (S) is shown in Fig. 7a) and powder specimens (P) in Fig. 7b).

Fig. 7
figure 7

Emissivity for different azimuth angles for (a) AlSi10Mg PBF-LB/M specimens (TS=507 °C, α = 45°) and (b) AlSi10Mg powder specimens (TS=425–440 °C, t = 4°mm)

Full size image

The scan angle \(\alpha\) and the layer thickness were kept constant. To minimize the influence of the measurement process on the measurement results, the measurements were conducted in quick succession. Consequently, in some cases, there are slight deviations in the specimen temperatures \({T}_{S}\).

All figures show that changing the azimuth angle from 0° (normal to the specimen) to 25° show just low changes in emissivity for larger wavelengths. When changing the azimuth angle \(\varphi\) to 47° and 60°, a significant increase in emissivity can be seen for all tested PBF-LB/M specimens. This is in line with the findings of Sainz-Menchón et al. [21]. In contrast, for all powder specimens, a decrease of emissivity can be seen for large azimuth angles \(\varphi .\)

The powder surface can be thought of as a series of cavities. Due to its geometry, a cavity has a higher emissivity than a flat surface of the same material [14]. At large azimuth angle \(\varphi ,\) it can be assumed that the measured radiation comes from smaller penetration depths of the cavities between the powder particles. Therefore, the observed surface is closer to a flat surface and emissivity becomes smaller.

The deviating measurement results for wavelengths below 3 µm for the AlSi10Mg PBF-LB/M specimens need to be analyzed in more detail. One explanation could be oxidation of the specimen during measurement which is close to unavoidable for aluminum. The presence of oxidation of the sample can be shown by the clearly visible peaks at approx. λ = 11 µm. Their origin may be explained by the Berreman effect [22].

The peaks occurring at approx. λ = 8 µm for the 316L-PBF-LB/M specimens at higher azimuth angles \(\varphi\) results from the optical properties of a protective coating of the silver mirrors used in EMMA. Since the peak does not occur in all measurements, it can be assumed that there is a temperature, angle and polarization dependency for this effect.

The peak at about λ = 15 µm is probably caused by a chemical change over the measurement period. It is also being investigated whether the very precise agreement of the emissivity of the 316L specimens at wavelengths of less than λ = 2.5 µm is also caused by an influence from the measurement setup.

In general, the measurement results suggest that when monitoring the PBF-LB/M process at small viewing angles in relation to the building platform, the angle dependence of the emissivity has no significant effect. However, with systems mounted at a steeper viewing angle, a measurement error can be expected toward the edges of the building platform due to the lager occurring azimuth angle \(\varphi\).

4.2 Temperature

In Fig. 8, the emissivity versus wavelength is shown for 316L, both powder specimens (P) and PBF-LB/M specimens (S) with scan angle α = 45°, for different specimen temperatures \({T}_{S}\). The same is shown in Fig. 9 for AlSi10Mg.

Fig. 8
figure 8

Emissivity for different temperatures for 316L PBF-LB/M (α = 45°, φ = 25°) and powder specimens (φ = 25°, t = 1–4 mm)

Full size image
Fig. 9
figure 9

Emissivity for different temperatures for AlSi10Mg PBF-LB/M (α = 45°, φ = 25°) and powder specimens (φ = 25°, t = 160 µm, 4 mm)

Full size image

Except for the measurements performed at 20 °C and 200 °C, which were done with the ambient temperature set-up at an azimuth angle of \(\varphi\) = 8°, all measurements were performed with an azimuth angle of \(\varphi\) = 25°. Since the azimuth angle \(\varphi\) showes a minor influence on the measured emissivity for \(\varphi\) < 25° (see Sect. 4.1), the measurements are comparable.

The PBF-LB/M specimens show a clear increase in emissivity at higher \({T}_{S}\) for both 316L and AlSi10Mg, as expected by the Hagen–Rubens relation [19]. No dependency of the emissivity on \({T}_{S}\) can be seen for the 316L and AlSi10Mg powder specimens. This is expected because the relationship between temperature \({T}_{S}\) and emissivity is based here on the decreasing conductivity σ with increasing temperature \({T}_{S}\), but this occurs only to a limited extent with powders.

The higher emissivity of the powder specimens compared to the PBF-LB/M specimens is clearly recognizable. This is due to the already described higher emissivity of the powder cavities as stated and shown by Sih et al. [14] and Mohr et al. for 316L [13].

For the emissivity of 316L PBF-LB/M specimens in the MWIR wavelength range, Mohr et al. could show comparable, but slightly lower emissivity values of \({{\varepsilon }^{\prime}}_{\lambda }\)= 0.2 for \({T}_{S}\) = 175–300 °C and \({{\varepsilon }^{\prime}}_{\lambda }\)= 0.22–0.25 for \({T}_{S}\) = 350–580 °C. An emissivity of \({{\varepsilon }^{\prime}}_{\lambda }\)= 0.21–0.28 for \({T}_{S}\) = 200 °C was measured in this study.

For 316L powder specimens, Mohr et al. report lower emissivity values of \({{\varepsilon }^{\prime}}_{\lambda }\)= 0.39 for \({T}_{S}\) = 350–520 °C and \({{\varepsilon }^{\prime}}_{\lambda }\)= 0.4–0.47 for \({T}_{S}\) = 550–630 °C in the MWIR range for a powder layer with a thickness of t = 50 µm [13]. In this study, an emissivity of \({{\varepsilon }^{\prime}}_{\lambda }\)= 0.55–0.65 for \({T}_{S}\) = 400 °C was measured for a powder layer of t = 1 mm. The higher layer thickness in this study could contribute to the increased measured emissivity, as shown in Sect.  4.3.

The increased measured emissivity could also be explained by oxidation that possibly occurred during the measurement. Higher emissivity values for oxidized steel and steel alloys were shown by many publications [9, 23]. Nearly doubled emissivity of 0.42–0.57 in the MWIR range for oxidized PBF-LB/M were shown by Mohr et al. [13].

Chemical analyses of the specimen after the measurement are pending for this study.

Measurements were also carried out on liquid and resolidified samples as part of the study. However, due to difficulties like balling of the liquid surface and slag formation, no reliable results are available yet.

4.3 Layer thickness

The influence of the layer thickness \(t\) for powder layers on the emissivity is shown in Fig. 10 for 316L and in Fig. 11 for AlSi10Mg, for an azimuth angle of φ = 25°.

Fig. 10
figure 10

Emissivity for different layer thicknesses \(t\) for 316L powder specimens (φ = 25°) compared to one PBF-LB/M specimen (α = 45°, φ = 25°)

Full size image
Fig. 11
figure 11

Emissivity for different layer thicknesses \(\text{t}\) for AlSi10Mg powder specimens (φ = 25°) compared to one PBF-LB/M specimen (α = 45°, φ = 25°)

Full size image

It needs to be noted that most of the measurements were performed at different specimen temperatures TS. However, as seen in Sect. 4.2, for powder specimens the influence of the temperature TS is small for the used temperatures.

For both materials, thin layers of \(t\) = 80 µm or \(t\) = 160 µm show smaller emissivity over all wavelength ranges compared to thicker powder layers of \(t\) = 1 mm or \(t\) = 4 mm. Due to the high measurement uncertainty at small wavelengths, this tendency can only be definitively verified for wavelengths above 8 µm.

This could be due to the translucency of the underlying PBF-LB/M surface with comparable lower emissivity. Exemplary, curves for PBF-LB/M specimens are shown in both figures as solid black lines.

4.4 Scan angle

Figure 12 shows the emissivity of 316L PBF-LB/M specimens printed with different scan angles α of the topmost layer measured at an azimuth angle of φ = 25°. The same is shown in Fig. 13 for AlSi10Mg.

Fig. 12
figure 12

Emissivity for different scan angles for 316L PBF-LB/M specimens (TS=1290 °C, φ = 25°)

Full size image
Fig. 13
figure 13

Emissivity for different scan angles for AlSi10Mg PBF-LB/M specimens (TS=417–447 °C, φ = 25°)

Full size image

For 316L, no specific influence of the scan angle α on the emissivity can be recognized.

For AlSi10Mg, the same tendency can be seen in Fig. 13 for measurements taken at slightly different temperatures (± 12 K). Therefore, it can be assumed, that the scan angle α has a relatively low influence on the emissivity. However, more measurements are planned to evaluate the influence of the measurement itself on the measured results, since some deviations were found in other measurements.

The small influence of the scan angle α on the measured emissivity could also be attributed, for example, to the relatively large measurement spot of \({d}_{m}\) = 6 mm. At steep azimuth angles φ, the surface of the sample generally appears rough. The orientation of the waviness due to the scan angle α becomes dominant at flatter azimuth angles φ. Therefore, further investigations are needed for larger azimuth angles φ.

4.5 Measurement wavelength

All measurement graphs show the expected decrease of the emissivity toward longer wavelengths λ. This can be derived directly from the Hagen–Rubens relation [19]. This makes it clear that, for example, when using quotient pyrometry with use of gray-body assumption, no major errors occur for measurement wavelengths that are close together.

5 Conclusion and outlook

A deeper understanding of the emissivity in the PBF-LB/M process could significantly reduce the uncertainty in determining true surface temperatures with thermographic methods. By utilizing real temperature information, a deeper process understanding can be reached, e.g., due to improved process simulations. Also, the transferability between measurements on different machines or with different materials can be enhanced. Since the emissivity also varies within the melt pool [9], it is questionable whether this general information is sufficient to improve, e.g., AI predictions using thermographic data.

In this work, it could be shown that general trends for the behavior of the emissivity can be transferred to PBF-LB/M samples and powders.

It could be proven that the emissivity of PBF-LB/M or metal powder surfaces only weakly depends on the azimuth angle for \(\varphi\) < 25°. Thus, for the process monitoring of the PBF-LB/M process, measurement signals from systems mounted off-axis with a small azimuth angle \(\varphi\), e.g., normal to the build platform, are nearly not influenced by emissivity changes due to changing azimuth angle \(\varphi\). For larger azimuth angle \(\varphi\), increasing emissivity for PBF-LB/M specimens and in contrast declining emissivity for powder specimens could be shown. Therefore, care must be taken when measuring through the chamber door viewing port at large azimuth angles.

For all measurements, the expected rising of the emissivity with lower wavelengths could be proven. The weaker dependency on the specimen temperature \({T}_{S}\) of the emissivity in the upper wavelength range tends to favor those wavelengths for monitoring tasks, just considering the emissivity changes. However, as no particularly pronounced abrupt changes in emissivity over the wavelength were detected, no wavelength range can be ruled out as unfavorable for process monitoring in principle. A sound knowledge of emissivity, especially at short wavelengths, is still important, e.g., for quotient pyrometric approaches.

The measurements on PBF-LB/M specimens showed the expected but low tendency of rising emissivity with rising specimen temperature \({T}_{S}\) directly resulting from Planck’s law and the Hagen–Rubens relation [9, 19]. It was shown that this dependency is neglectable for powder specimens. Further investigations for liquid samples are still needed, since generally lower emissivity is expected [15].

In accordance with the literature, significantly higher emissivity were shown for powder surfaces compared to PBF-LB/M surfaces. In addition, also an influence of the powder layer thickness \(t\) was evident. Here too, more detailed measurements are planned, e.g., for thinner layer thicknesses \(t\) that are more common in the PBF-LB/M process.

It was shown that the scan angle \(\alpha\) does not have a significant influence on the emissivity for small azimuth angles \(\varphi\). Further measurements at larger \(\varphi\) are expected to show a higher influence.

Another open question is the repeatability of the measurement results for PBF-LB/M specimens in general. Therefore, further measurements of specimens printed on different machines and with different scanning parameters are planned.