1 Introduction

New challenges in manufacturing originating in emerging markets, such as the space industry or hydrogen-based energy storage and production, demand novel manufacturing strategies to fulfill all requirements. Consequently, PBF-LB/M and laser welding are becoming more attractive as fast and precise manufacturing tools for many applications. For example, in the space industry, the highly complex and individualized shapes of injection plates or the internal cooling structures of combustion chambers are exceptionally well suited for PBF-LB/M. On the other hand, producing individual cell plates of hydrogen fuel cells requires many welds to form cooling channels at a micrometer-width scale and meter-length scale. In this case, laser welding is very interesting because of its small spot size and high weld speeds. Novel materials like superalloys must be processed under specific conditions to further advance these high-end applications. Innovative advancements in laser processing, such as beam shaping or the increase of the spot size [1], could allow the manufacturing industry to keep up with these new demands [2]. However, the challenge in implementing innovative process strategies for manufacturing is the temporal and financial cost of developing new, reliable, and tailored processes. A lack of profound process understanding for these new laser-material combinations requires an empirical and iterative approach to identify suitable process parameters that allow the manufacturing of the part to be of sufficient quality.

This approach, particularly the ex situ specimen testing and analysis, makes the process development time- and labor-intensive. Therefore, there is a great potential for accelerating process development by replacing physical ex situ specimen testing with digital analysis of in situ monitoring data, significantly reducing the time and labor requirements of every iteration. For this, it is necessary to monitor a process characteristic that is directly tied to the process dynamic and behavior. Understanding this signal sufficiently is necessary to derive a beneficial process parameter adjustment from the monitoring data.

There are numerous approaches for in situ process monitoring in laser welding [3] or PBF/LB-M [4]. The approaches can be structured into optical, temperature, and acoustic monitoring. Optical monitoring with the means of an off- or coaxial camera can be used to detect various defects in PBF-LB/M [5]. A camera has also been used with auxiliary structured light in laser welding to determine keyhole depth [6]. However, image-based approaches generate a lot of data, which is difficult to process in a timely manner and often requires machine learning approaches. Another optical measuring technique is optical coherence tomography. It has been proven particularly suited to monitor the keyhole depth in laser welding [7] and PBF-LB/M [8]. Optical coherence tomography provides one-dimensional data, which significantly mitigates the challenges regarding data quantity. Still, the signal-to-noise ratio could be better, which requires elaborate data processing for analysis. Furthermore, the calibration effort connected to an optical coherence tomography system is high. In contrast to optical monitoring, temperature monitoring allows the detection of precursors for defect formation, such as steep temperature gradients, instead of detecting already-formed defects. This makes temperature monitoring attractive for real-time control purposes. The temperature can be monitored in different ways. For example, Vallabh et al. [9] predicted melt pool depth during PBF-LB/M using two-wavelength pyrometry, and Xiao et al. [10] identified the prevailing process regime during laser welding. One downside is the missing spatial resolution of point pyrometry. Infrared imaging can provide the required spatial resolution and has been beneficially used for in situ monitoring in laser welding [11] and PBF-LB/M [11, 12]. A significant hurdle in radiation-based temperature monitoring is the extensive calibration process to acquire results close to absolute temperature values. This is necessary due to the dynamic nature of the specific emissivity and its multiple dependencies. Acoustic monitoring has also been successfully used for in situ process monitoring. For example, PBF-LB/M acoustic emission monitoring allowed Drissi-Daoudi et al. [13] to detect any deviations from the conduction mode during the process and Kononenko et al. [14] to identify crack formation. For laser welding, the penetration classification from Luo et al. [15] is an example of acoustic monitoring. However, the significant additional noise during the acoustic measurement from sources such as the shielding gas flow requires extensive data preparation, and, due to the mere indirect connection of acoustic emission to the process, characterization requires complex data processing.

An emerging monitoring approach can fill the niche created by the individual disadvantages of the listed techniques. Reflection-based absorption monitoring allows us to derive the time-resolved absorption during the process by measuring the intensity of the reflected laser radiation with a photodiode. The photodiode provides a one-dimensional data stream with a high signal-to-noise ratio, which can be processed in a timely manner. The absorption rate governs the amount of energy introduced to the workpiece and thus determines the temperature field and process dynamics. Therefore, signal features can be interpreted as precursors for defect formation. There have been successful strides in using an absorption measurement for in situ process monitoring.

For example, Norris and Robino [16] identified the correlation between the different welding regimes and absorption values with an experimental setup based on two integrated spheres. Simonds et al. [17] proved the increase in coupling efficiency on the boundary from the conduction to the keyhole welding regime with a single integrated sphere. Allen et al. [18] further equipped the integrated sphere setup with optical coherence tomography to confirm the correlation between the highly dynamic vapor depression geometry in laser deep penetration welding and the laser energy absorption.

The laser absorption in powder material differs from that in solid material due to the powder bed’s different surface roughness and topology. In [19], Simonds et al. analyzed the optical coupling behavior of thin layers of stainless-steel powder 316L. The key finding was the higher absorption of powder compared to solid materials. The dynamic behavior of the absorptance reveals physical phenomena, including oxidation, melting, and keyhole formation. Even for powder material, this keyhole formation includes an increase in absorption, as Trapp et al. [20] demonstrated with direct calorimetric measurements. Simultaneous measurements of laser power absorption and high-speed X-ray imaging were made to correlate time-resolved keyhole geometry with laser energy absorption on laser welds of Ti6Al4V plates and powder [21, 22]. Wittemer and Wudy [23] developed a calibration-less measurement with an integrating sphere. They applied it in [24] to identify in situ the threshold between conduction and keyhole welding for high-intensity irradiation with high-throughput experiments.

These examples prove the possibility of identifying specific process characteristics, such as the prevailing process regime, based on the absorption signal. However, there has not been a continuous regime traversing link between the changes in absorptivity and changes in the process dynamic over an increase in radiation intensity. Therefore, this work investigates bead-on-plate welds with an integrating sphere in a wide range of radiation intensities. Additionally, coaxial high-speed footage and the resulting melt track width were examined to identify a regime traversing and intensity-dependent link between the process behavior and the changes in the degree of absorption.

2 Experimental setup and methods

The exploration for this investigation is conducted on a custom test rig. The test rig is equipped with a fiber laser and a three-dimensional scanner optic, which are discussed in more detail in Section 2.1. The test rig also includes the in situ absorbance measurement system with the integrating sphere at its core and a coaxial high-speed camera, which are discussed in Sections 2.4 and 2.5, respectively. A cross jet is mounted in the system to produce a strong airflow between the test specimen and the sphere to avoid contaminating the sphere’s inner surface with oxides. The complete experimental setup is schematically depicted in Fig. 1.

Fig. 1
figure 1

Schematic depiction of the experimental setup with the connection of all the components

Full size image

2.1 Optical setup

The optical system comprises a fiber laser with a wavelength of 1070 nm from the manufacturer nLIGHT with the trade name AFX-1000 and a 3D-scanner optic called AM-Module from the manufacturer RAYLASE. This unique combination allows a very variable choice of beam shapes in the laser spot. Firstly, the beam source provides seven different beam shapes, with an increasing portion of the laser power distributed in an outer ring around an inner Gaussian core. Secondly, the two independent z-axes of the optics facilitate a variable laser spot diameter at a constant focal length. This highly variable setup allowed us to conduct experiments with different combinations of spot sizes and beam shapes within the spot and investigate their influence. The available seven beam shapes vary in the power shares in the inner core and outer ring and range from a Gaussian beam shape for ID 95/5 over a distribution of 75% of the laser power in the Gaussian core and 25% of the power in the outer ring for ID 75/25, to 10% in the core and 90% in the ring for ID 10/90. The beam caustic of all seven beam shapes was measured using a CineSpot Tool Cinogy FBP-2KF by the company Cinogy. The imaged beam shapes are shown in the focus plane at a magnification factor of M = 1 in Fig. 2. These beam shapes were used at different magnification settings, which scale the shown distributions by a factor of \(M=1\), \(M=1.5\), and \(M=1.9\). Every configuration of beam shape and magnification factor results in a different spot diameter \({d}_{s}\), which was calculated based on the caustic measurements using the second-moment method for of \(M=1\), \(M=1.5\), and \(M=2\). The diameter for \(M=1.9\) was interpolated. The resulting equivalent diameters are listed in Table 1.

Fig. 2
figure 2

Tested beam shapes at a magnification factor of 1

Full size image
Table 1 Spot diameter depending on magnification factor and beam shape
Full size table

Additionally, the mean radiation intensity \({I}_{\text{mean}}(x)\) was calculated for every combination of beam shape, magnification factor, and laser power by dividing the laser power \({P}_{\text{Laser}}\) by the irradiated area A of the specific beam-shape-magnification combination:

$${I}_{\text{mean}}\left(\text{Index},M,{P}_{\text{Laser}}\right)=\frac{{P}_{\text{Laser}}}{A(\text{Index},M)}$$

The irradiated area A was calculated via the spot diameter \({d}_{s}\).

2.2 Process design and parameters

The inclusion of the integrating sphere in the setup restricts the angle of incidence of the laser between + 0.9° and − 0.9° to the surface normal for all experiments because of the size of the bottom aperture. This leads to a measuring area of about 1 cm2. Due to this restriction, the experiments were designed to fit this area. As shown in Fig. 3, every experiment consists of 16 melt tracks \(n=1-16\) at increasing laser powers, starting with 50 W at n = 1 to 800 W at n = 16. The power range is determined at the low end by the lowest emitable power and at the high end by the highest emitable power of the ID 95/5 configuration. Each melt track has a length of \(l=10 \text{mm}\) and is spaced 600 µm apart to avoid cross-influence. The scan vectors are orientated perpendicular to the cross-jet flow vector. All melt tracks are produced at a scan speed of \({v}_{\text{scan}} = 800 \text{mm}/\text{s}\). The scan speed was selected to be slow enough to provide enough measuring points per melt track to be statistically relevant and fast enough to be relevant in an industrial context. The experiments were conducted with various combinations of beam shapes and magnification factors. Every test series consists of one experiment per available beam shape for various magnification factors and applied sensory systems. Table 2 lists the executed test series and their parameters.

Fig. 3
figure 3

Schematically visualized process design for all experiments

Full size image
Table 2 List of tested combinations of beam shape and magnification factor
Full size table

2.3 Material

To investigate the absorption measurement on a well-understood and researched material, stainless steel AISI 316L was selected. The melt tracks were produced on hot-rolled plates with a thickness of 5 mm.

2.4 Absorption measurement

The absorbance measurement system utilizes two signal streams from two photodiodes: One is referred to as the integrating sphere signal (ISS), which indicates changes in the reflected laser radiation, and the other as the back reflection signal (BRS), which shows the changes in the laser output power. Both signals are sampled together at a frequency of \({f}_{M}=20\text{ kHz}\). The integrating sphere signal is acquired with a switchable gain diode sensor (Thorlabs PDA100A2), which is fiber coupled to the integrating sphere and thereby measures the intensity of the captured reflected radiation. The laser wavelength of 1070 nm is isolated with a bandwidth filter before the photodiode to avoid influences in the signal by other radiation sources, such as thermal radiation. As seen in Fig. 1, the integrating sphere consists of two halves made using laser-based powder bed fusion with PA12 material. It possesses an inner diameter of \({d}_{\text{Sphere}}=120 \text{mm}\). Two apertures are positioned in alignment with the laser’s propagation path, with diameters of \({d}_{\text{Aperture }1}=15 \text{mm}\) and \({d}_{\text{Aperture }2}=30 \text{mm}\), respectively. The bottom aperture is positioned at a distance of \({l}_{\text{Distance}}=20 \text{mm}\) above the target. The sphere’s inner surface is coated with multiple layers of barium sulfate (BaSO4) to create a near Lambertian surface for its diffuse and uniformly reflective properties. Therefore, the captured radiation is distributed homogenously by multiple reflections within the sphere to an average intensity. The back reflection signal is drawn from a sensor integrated into the beam source. This signal is directly proportional to the output power of the laser. In every experiment, the data is separately logged for every of the 16 melt tracks. This results in \({n}_{\text{points}}=250\) measuring points for every melt track and thus for every process parameter combination calculated by:

$${n}_{\text{points}}=\frac{10 \text{mm}\bullet 20000 1/\text{s}}{800\text{mm}/\text{s}},$$

because of the constant sampling frequency \({f}_{m}\), scan speed \({v}_{\text{scan}}\), and melt track length \(l\). This raw data is exemplary shown for one process parameter set in Fig. 4a. The raw data is processed in the following steps:

Fig. 4
figure 4

Data processing steps of the integrating sphere signal using the example of the experiment at ID 20/80 and magnification 1 with a focus on 400 W

Full size image

For every melt track, the integrating sphere data exhibits a significant peak at the beginning of the melt track, which corresponds to the initial formation of a melt pool. This phenomenon was also observed by Yang et al. [25]. This condition is temporary and does not represent the rest of the melt track. The same is true for the end of the melt track, where a drop in the signal corresponds to the emission cut-off. Thus, the first and last 5% of measuring points on every melt track are not considered for further analysis, resulting in 225 measuring points per melt track, as shown in Fig. 4b.

The diode signal can be visualized and statistically described for every melt track as a boxplot to compare the individual melt track data to other melt tracks. The specifications of this boxplot are depicted in Fig. 4c.

Due to the inherent geometric constraints imposed by the spherical setup, the monitoring of reflected radiation is subject to limitations, as it disregards the fraction of radiation that propagates beyond the boundaries of the sphere. Therefore, this unquantified fraction of reflected radiation, a direct calculation of absorption solely from the reflection, becomes infeasible despite excluding transmitted power from the power equation for AISI 316L at this specific thickness. Consequently, determining absorption information relies on qualitative reflection measurements, offering a qualitative assessment rather than a quantitative analysis.

To benefit from this qualitative data, the changes in absorption are consistently analyzed in relation to the increase in laser power. However, the integrating sphere signal is a consequence of the dual impact of laser power on the signal. Firstly, laser power can modify the process dynamics in a manner similar to other process parameters. Consequently, this alteration influences the laser reflection and subsequently affects the resulting measuring signal throughout the process. Secondly, even in scenarios where the absorption rate remains constant during the process, an increase in laser power still induces an overall elevation in the absolute reflection. Because of this twofold influence of the laser power on the integrating sphere signal, the impact of the changes in process dynamics on the signal must be isolated. Therefore, the diode signal must be referenced to the laser power. As shown in [24], the back-reflection can be used to determine the changes in the laser power and, in turn, to reference the integrating sphere signal to this power. This is achieved by setting the individual data streams of every melt in one experiment in relation to the first melt track of this experiment, meaning that for a multiplication of the laser power for melt track x by m in comparison to the laser power for the first melt track, melt track 1, the integrating sphere signal is divided by m to form the Referenced ISS.

$$\text{Referenced ISS }\left(\text{melt track }x\right)=\frac{\text{ISS }\left(\text{melt track }x\right)}{m},$$
$$m={p}_{\text{Laser}}(\text{melt track} 1)/{p}_{\text{Laser}}(\text{melt track} x)$$

The resulting referenced signals for all melt tracks of one experiment can be visualized together in on boxplot to analyze the qualitative signal changes for an increase in laser power.

2.5 High-speed imagery

To correlate the absorption signal to visible process characteristics, a high-speed camera was mounted coaxially to the laser beam at a framerate of 20 kHz. A CP90-3-M-540 by the company Optronis was used. For the introduced process design, this resulted in 250 images per melt track. An example of the resulting monochrome imagery can be seen in Fig. 5a. To analyze the development of the imagery in relation to an increase in laser power, the image data is processed to form the median illumination sum and median deviation per melt track. This is done in two steps. In the first step, the median illumination of every pixel along the timeline is calculated to form a median picture per melt track, as seen in Fig. 5b. Simultaneously, the standard deviation of every pixel along the timeline is calculated. In the second step, the illumination value of every pixel is summed up, resulting in a median illumination sum per melt track. Additionally, the pixel-wise standard deviation is added over all pixels and normalized to the value domain of the illumination sum. For every experiment, the resulting illumination sum can be plotted in arbitrary units over the laser power in W, as seen in Fig. 5c. Lastly, the relative change of the illumination sum´s standard deviation between one power level and the next was calculated and visualized, as seen in Fig. 5d.

Fig. 5
figure 5

Example of the monochrome high-speed imagery and the involved processing steps to form a median illumination sum and deviation per melt track at ID 20/80 and magnification 1

Full size image

2.6 Micrograph images

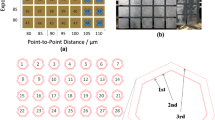
The micrographs were prepared to assess the melt track dimensions. This was accomplished by performing cross-sectional cuts on the produced test specimens. The cut-outs were then embedded in a transparent epoxy and subjected to a wet grinding process involving three stages using silicon carbide paper with varying grit sizes (180, 360, and 1200). Subsequently, the specimens underwent a two-stage polishing process utilizing polishing pastes with particle sizes of 3 µm and 1 µm, respectively. Lastly, the specimens were treated with Adler etchant for etching. Microscope images of the melt track cross-sections were captured. These images were analyzed to determine each melt track’s dimensions, width, and depth, as depicted in Fig. 6.

Fig. 6
figure 6

Exemplary micrograph images of a melt track and its width

Full size image

3 Results and discussion

3.1 Absorption signature

To gain a general understanding of the signal output of the absorption measurement, the signal sequence over the increase in laser power is investigated for all tested combinations of beam shape and magnification factor. This allows the signal characterization and comparison. For the signal description, the trend of the referenced diode signal in arbitrary units is shown as a boxplot diagram over the laser power from 50 to 800 W for ID 50/50 at \(M=1\) in Fig. 7. At low powers, the signal climes rapidly over an increase in laser power, as seen between 50 and 150 W. Due to the referencing procedure, the signal indicates the change in the portion of the input power, which is reflected in the process zone. This is referred to as the change in the degree of reflection or absorption. Therefore, the signal suggests that with increasing laser input power, the percentage of reflected power increases, and the absorbed portion presumably decreases. The rapid signal increase terminates at a maximum of 150 W. The maximum is followed by a rapid signal decrease for further power increase, as seen between 150 and 350 W. This suggests a significant reduction in the degree of reflection and, therefore, a substantial increase in the degree of absorption. After this, the signal decrease becomes less pronounced, and the curve flattens out at the end, as seen between 350 and 800 W. This hints toward a slight decline in the degree of reflection with increasing laser power after the significant signal drop.

Fig. 7
figure 7

Referenced diode signal over an increase in laser power for ID 50/50 at magnification 1

Full size image

Figure 8 shows in the center the referenced diode signal in arbitrary units over increasing laser power again for ID 50/50 at \(M=1\). For comparison, the signal of ID 95/5 at \(M=1\) is shown on the left and ID 10/90 at \(M=1\) on the right. This means the laser power is shifted from almost entirely in the inner core on the left to a pronounced ring shape on the right. The comparison shows a change in the signal curve with shifting power from the inner core to the outer ring. For one thing, the signal median at its maximum increases with the power portion in the ring. At ID 95/5, the signal reaches around 400 AU at its maximum, and at ID 10/90, it reaches around 575 AU. This suggests an overall increase in reflection and decreased absorption at the signal maximum with increased laser power in the outer ring. For another, the laser power at which the signal reaches its maximum shifts to higher powers for increased power in the ring. While the signal starts at or past its maximum at 50 W for ID 95/5, the maximum is reached at 250 W for ID 10/90.

Fig. 8
figure 8

Three examples of the referenced diode signal over an increase in laser power for three different beam shapes

Full size image

For further comparison, Fig. 9 shows the signal of ID 95/5 with an increasing magnification factor. On the left, the signal is shown at \(M=1\), in the middle at \(M=1.5\), and on the right at \(M=1.9\). The same trend can be seen for increasing magnification factor, as before with increasing power in the outer ring. The value of the signal maximum increases, and the maximum is reached at higher laser powers with an increasing magnification factor. Due to the significant enlargement of the irradiated area for an increase in the magnification factor or power portion in the ring, as seen in Table 1, the mean radiation intensity decreases in both cases. This means the signal maximum increases in value and shifts to higher laser powers for decreasing mean radiation intensities.

Fig. 9
figure 9

Three examples of the referenced diode signal over an increase in laser power for the tested magnifications

Full size image

Independent of the mean radiation intensity, the signal trend can be divided into two distinct sections schematically visualized in Fig. 10. Section 1 describes the steep incline to the maximum, and in Section 2, the sharp signal decreases past the maximum. This signal behavior over an increase in laser power seems characteristic of the laser’s interaction with 316L. Because of the close inverse connection of the signal to the changes in the degree of absorption, this behavior can be defined as the absorption signature of 316L for the tested conditions. The signal behavior is rooted in the process behavior because of the strong connection between the degree of absorption and the process characteristic. Thus, a profoundly understood link between the signal and process behavior can facilitate a signal-based process characterization. For this, the section-specific behavior of the absorption signature and, in particular, the thresholds between those sections were analyzed with additional sensory.

Fig. 10
figure 10

Schematic depiction of the absorption signature of 316L for the tested conditions with visualized division in two sections

Full size image

3.1.1 Section one of the absorption signature

To establish a link between the sharp signal increase in the first section of the absorption signature and the process result, the melt track dimensions in this section of the absorption signature and, in particular, at the end of the section are investigated. For this, the measured melt track widths and depths, as determined in Section 2.6, are visualized over the laser power, as shown exemplarily in Fig. 11 for the experiment at magnification 1.9 and ID 95/5. The development of the melt track depth exhibits a consistent linear increase over increasing laser power, and the development of the melt track width shows a linear increase with two sections of different gradients. From 50 to 250 W, the melt track width increases at a significantly higher rate than from 250 to 800 W. This change in gradient is differently pronounced and situated at different laser powers for varying combinations of beam shapes and magnification, but can be observed as a general commonality.

Fig. 11
figure 11

Changes of melt track dimensions over an increase in laser power for the experiment with ID 95/5 and magnification 1.9

Full size image

At the top of Fig. 13, this change in gradient of the melt track width increase can be seen for three additional examples: ID 95/5, ID 75/25, and ID 65/35 at magnification 1.9. At the bottom of Fig. 13, the corresponding diode signals of those experiments are shown. In a direct comparison of melt track width development and the diode signal over laser power increase, it becomes apparent that the diode signal maximum coincides with the change in gradient of the melt track width increase. This is marked in red in Fig. 13. This correlation suggests a link between the melt track width and the degree of absorption below a specific laser power threshold. This power threshold varies for different combinations of beam shapes and magnification. Above this power threshold, the increase of melt track width is lower than below this power threshold, which could be rooted in a change in the process dynamic. The increase of the diode signal, which indicates an increase in the reflected laser radiation during the increase of melt track width, could be explained by the significant change in surface roughness when transitioning from the rough surface of the test specimens to the mirror-like surface of the molten metal [26]. This transition is gradual as the melt pool size increases within the irradiated area of the laser spot. At low laser powers, the melt pool width is smaller than the spot diameter; thus, a smaller portion of the laser light interacts with the melt pool surface, and the rest hits the rough surface of the specimen. With increasing power, the melt pool size also increases, and a growing portion of the laser light hits the melt pool surface, thus leading to a gradual signal increase. At a certain laser power threshold, the melt pool size is equivalent to the irradiated area, and the growth of the melt pool beyond this point does not change the surface roughness of the interaction zone. Therefore, the melt pool growth past the laser power threshold does not affect the absorption behavior. This effect is visualized in Fig. 12.

Fig. 12
figure 12

Schematic visualization of the melt pool growth in relation to the laser spot size over an increase in laser power

Full size image

This link between the melt pool width and the absorption would only be valid while the melt pool grows within the periphery of the laser spot. Above this threshold, any further growth of the melt pool width does not influence the degree of reflection because the entire laser light already interacts with the melt pool surface. At the same time, the increase in melt pool size beyond the spot size is solemnly driven by thermal conduction instead of direct power absorption in the irradiated area. This can explain the change in the gradient of the melt pool size increase. This hypothesis is supported by the similarity of the melt track width at the threshold, as marked in Fig. 13, and the corresponding spot diameter in Table 1. While the growth of the melt pool beyond the limits of the laser spot can explain why the diode signal stops increasing at this point, it does not explain the sudden decrease beyond this threshold. This sudden decrease is discussed in Section 3.1.2.

Fig. 13
figure 13

Three examples of the referenced diode signal over an increase in laser power at the bottom and the corresponding change in melt track width at the top, as well as the red highlighted correlation between the diode signals maximum and the change in gradient in the melt track width increase

Full size image

3.1.2 Section two of the absorption signature

The second section of the absorption signature, the sharp decrease following the maximum, was investigated in detail utilizing high-speed imagery to identify the responsible change in the process characteristic, which is tied to the signal behavior. Figure 14 shows the illumination sum over the laser power of the experiment at magnification 1 and ID 20/80, which was derived as described in Section 2.5.

Fig. 14
figure 14

Exemplary illumination sum plot of ID 20/80 at magnification 1 with four exemplary snapshots from the high-speed imagery for 150 W and 300 W

Full size image

The plot shows a trend, which was apparent for all experiments with the high-speed camera. The illumination sum starts with small values at low laser powers and a slight deviation. Those low illumination sums and deviations remain relatively constant up to a specific laser power threshold, as is seen in Fig. 14, from 50 to 200 W. From this threshold, the illumination sum increases significantly with further power increases. At the same time, the deviation in the illumination of all pictures in one melt track rises significantly as well. The snapshots of the original high-speed imagery at four exemplary timestamps in Fig. 14 illustrate the reason behind the change in the illumination sum and deviation.

The snapshots from the plateauing region at 150 W display a relatively constant illumination, which is mainly limited to the saturated process zone. The snapshots from the rising area of the plot display the same saturated process zone but, additionally, a shifting white haze that surrounds the process zone. This haze and its rapidly shifting nature are the reasons for the rapid increase of the illumination sum and deviation starting at 250 W.

The comparison of this footage with [27] or [28] shows that the white haze shows the weld plume. The emergence of the weld plume especially impacts the standard deviation, though it is very dynamic in nature. This can be seen in Fig. 15, which shows the change in the standard deviation of the illumination sum from one power level to the next. As was also visible in Fig. 14, the relative change of the illumination sum’s standard deviation between 50 and 200 W is relatively small, with a slightly increasing trend. However, the change in the standard deviation between 200 and 250 W is high, with an increase of roughly 150%. This change marks the maximum before it decreases between 250 and 400 W, after which it remains relatively low, indicating an insignificant change in the standard deviation between 400 and 800 W. The maximum relative change of the standard deviation results from the onset of vapor formation, thereby allowing the detection of the threshold for vapor formation. Therefore, Fig. 16 shows four exemplary median illumination images of four melt tracks assigned to the corresponding diode signal boxplot to investigate the connection between the high-speed imagery and the referenced diode signal. While the median images of the melt tracks at 150 and 200 W are shown as examples of the median illumination before and at the maximum of the corresponding diode signal, the median images of the melt tracks at 250 and 300 W are shown as examples beyond the maximum. The comparison of the images at the top and bottom of the figure suggests that the drop of the diode signal past its maximum coincides with the onset of a visible vapor plume in the high-speed footage. This is further supported by the fact that the change in the standard deviation of the illumination sum reaches its maximum, going from 200 to 250 W, which indicates the threshold for vapor formation. The correlation between the sudden drop of the diode signal and the onset of vapor formation can be observed in all experiments and was validated by comparing the illumination sum and the relative change of the standard deviation with the corresponding diode signal. Figure 17 provides three examples of this comparison with the illumination sum plots at the top, the relative change of the standard deviation in the middle, and the referenced diode signal at the bottom. The red line marks the first laser power level after the maximum of the referenced diode signal. At the same time, this red line coincides with the maximum of the relative standard deviation change in the middle, indicating the highest standard deviation change in the corresponding illumination sum at the top from one power level to the next. This validates the correlation between the significant increase in absorption, indicated by the drop of the diode signal, and the onset of vapor formation, which is indicated by the sudden rise of the standard deviation. The change in process behavior can explain this correlation. At a specific power input, the material starts to vaporize. The condensation and oxidation of this vapor form the visible plume [29]. The vaporization leads to a depletion of the melt pool volume on the one hand and, on the other hand, to vapor pressure as a result of the expansion of the vapor due to the phase change. These two effects result in a vapor depression in the melt pool, which changes the topology of the melt pool surface [30, 31]. This topology change can influence the degree of absorption. For example, the changed topology results in a changed angle of incidence, which influences the degree of absorption [32]. However, this effect is too small to be solely responsible for the substantial change in the reflection signal. For deep vapor depressions with high aspect ratios, often called keyholes, the absorption increase can be significant compared to the flat molten pool surface due to multiple reflections in the vapor capillary [33]. Nevertheless, as the comparison with the high-speed footage showed, the drop in the reflection signal coincides with the onset of vapor depression formation. At this early stage, the aspect ratio is low [34]. Therefore, multiple reflections and the associated absorption increase are unlikely. However, the vapor reflection can also lead to a different scatter pattern in the reflection [35], which can change the diode signal because the portion of reflected radiation that escapes to the side without entering the sphere increases. Preliminary results suggest that this effect will impact the signal significantly. In the future, this effect will be investigated in detail using directional reflection measurement. On top of the named effects, partial absorption of the radiation in the plume [32] or by small particles in the plume [33] can increase the apparent degree of absorption and, therefore, the signal. These combined effects, emphasizing the shift in the predominant reflection direction, result in a sharp decrease in the diode signal in correlation with the onset of the vapor plume. The onset of a vapor depression has been used to define the beginning of the transition mode between conduction and keyhole mode [34, 36]. Together, this means the sharp decline past the maximum of the referenced diode signal indicates the start of the transition mode.

Fig. 15
figure 15

Change of the standard deviation of the illumination sum from one power level to the next for ID 20/80 at magnification 1

Full size image
Fig. 16
figure 16

Referenced diode signal over increasing laser power for ID 20/80 at magnification 1 and exemplary median illumination images of four melt tracks, two before and at the diode signal maximum and two after

Full size image
Fig. 17
figure 17

Three examples for the comparison of the illumination sum plot with the referenced diode signal from 50 to 800 W to validate the absorption signature threshold

Full size image

3.2 Influence of mean intensity on the absorption signature

The different presented examples of the referenced diode signal plots of the conducted experiments show that the identified and discussed absorption signature shifts to higher laser powers for increased magnifications or power share in the outer ring. Higher magnifications and increased power in the ring result in a decreased mean radiation intensity at constant laser power due to the increased irradiated area. This suggests that the absorption signature exhibits an intensity-dependent trend. To investigate this hypothesis, the referenced diode signal is plotted over the mean radiation intensity, calculated in Section 2.1 for every combination of magnification factor, beam shapes, and laser power. Figure 18 shows these plots for the same exemplary parameter sets, which were displayed in Figs. 8 and 9. The differences between the shown plots are mainly the diode value at the maximum, but the maximum occurs at a similar mean intensity. However, for the experiment at magnification 1 and ID 95/5, the signal starts at the maximum with the melt track at the lowest tested laser power. Generally, the maximum is reached at a characteristic mean intensity, which means that for combinations of beam shapes and magnification that result in an overall lower intensity, higher laser powers are required to reach the characteristic mean intensity. This results in more measurements before the maximum. Therefore, the maximum of the diode signal seems to depend on the irradiance’s mean intensity. Figure 19 illustrates the intensity dependency of the absorption signature by overlaying the referenced diode signals of 21 different combinations of beam shapes and magnification, plotted over their mean intensity. Especially the increase to the maximum follows a very similar trend in all plots. This maximum is reached between 0.48 and 1.1 106 W/cm2. Past the maximum, slightly higher discrepancies can be seen in the trend of the steep descent. Combined with the identified process behavior, which was linked to the absorption signature, the onset of vapor formation is closely tied to a characteristic mean intensity. This seems valid for ring-shaped beam profiles independent of the spot size for a specific combination of material and laser.

Fig. 18
figure 18

Referenced diode signal median in arbitrary units over increasing mean radiation intensity for selected combinations of beam shapes and magnification factor

Full size image
Fig. 19
figure 19

Overlay of the referenced diode signal median over their mean intensities of 21 different combinations of beam shapes and magnifications

Full size image

4 Conclusion and outlook

In this work, the changes in the reflected laser light over an increase in laser power were investigated to establish links to the changes in the process behavior over an increase in laser power. Additionally, the influence of the mean radiation intensity on the changes in reflection was evaluated. For this, bead-on-plate welds were produced on stainless steel AISI 316L, stepwise increasing laser power levels for various combinations of beam shapes and spot magnifications. During these experiments, the laser reflection was measured with an integrating sphere, and high-speed imagery was recorded using a coaxial camera. Ex situ to the process, the resulting melt track widths were measured in micrographical cross sections. The presented results lead to the following conclusions about links between absorption and process behavior based on the mean radiation intensity:

  • The diode signal exhibits a characteristic behavior over an increase in laser power independent of the beam shapes or magnification. This was defined as the absorption signature. The absorption signature can be divided into two distinct sections separated by the maximum of the diode signal. A steep increase at low laser powers toward the maximum is followed by a steep decrease, which merges into a plateauing section at high laser powers.

  • The steep increase in reflection was linked to the change in surface property during the growth of the melt pool within the boundaries of the laser spot.

  • The steep decrease in reflection was linked to the onset of vapor formation and the resulting vapor depression, which changes the melt pool topology and, in turn, the resulting reflection pattern. Therefore, the steep decrease can indicate the start of the transition mode between conduction and keyhole mode.

  • The comparison of the absorption signature over the mean intensity for various combinations of beam shapes and magnification shows a strong dependency of the reflection maximum on the mean radiation intensity.

The link between absorption signature and process behavior is the first step in an in situ absorption-based process characterization for laser-based material processing, which has the potential to accelerate process development significantly by reducing the dependency on resource-heavy ex situ characterization. Furthermore, the mean intensity dependency of the absorption signature suggests a transferability of individual process features, like the onset of vapor formation across different parameter combinations in the scope of the tested parameter space. This can facilitate a more targeted approach during process development, further accelerating parameter identification. In the future, the available measurement area should be increased by an improved sphere design to accelerate the exploration of this research, and the influence of additional parameters, such as the material or the scan speed on the absorption signature, should be investigated.