1 Introduction

DED-Arc is a rapidly developing manufacturing technique that allows the production of complex and large-scale structural components like bridges or steel nodes [1,2,3]. While DED-Arc offers many advantages, such as high build-up rates and reduced production time, design flexibility, and reduced material waste, it also presents a significant challenge: managing the temperature during the manufacturing process.

Controlling the temperature is essential to ensure that the geometrical and mechanical properties of the final product meet the desired specifications. The mechanical properties of steel are highly influenced by the process parameters employed during manufacturing, as they determine the resulting temperature-time (T-t) profile experienced by the material during the additive manufacturing process. As a result, they significantly impact the microstructure and subsequently influencing the mechanical behavior of the resulting part [4,5,6,7,8].

To qualify DED-Arc components for use in the building industry, individual case approvals may be obtained. However, reliable determination of the resulting mechanical properties is essential. Virtual component testing offers a solution by virtually simulating the behavior of a digital representation of the physical object, known as a “digital shadow”, using assigned parameters and properties [9, 10]. This enables the prediction of the component’s performance. To generate the digital shadow, the DED-Arc process needs to be monitored, and the recorded data must be integrated into a location-related model. This monitoring involves capturing data such as temperature profiles, geometric data, and relevant process parameters [11, 12]. By aligning this data with the model, a digital representation of the physical object is created for virtual testing of its mechanical behavior [13].

Thermography theoretically offers high potential for monitoring the DED-Arc process. By using an infrared camera to monitor the temperature of the workpiece in real time, thermography can provide precise temperature measurements and provides an imaging technique for T-t profiles at any desired region of the part to be produced. However, using thermography for monitoring the DED-Arc process presents some challenges [14]. One of the primary challenges is the dynamically changing emissivity of the material at different temperatures. Due to differences in surface characteristics and annealing colors at temperatures >550 °C for steel, the recorded temperatures must be corrected with the related emissivity coefficient.

2 State of the art

Thermography is a technique that uses, e.g., infrared radiation to measure the temperature of a surface. The principle of thermography is based on the fact that all objects emit infrared radiation proportional to their temperature. Infrared radiation is a type of electromagnetic radiation that lies beyond the visible spectrum of light, with longer wavelengths than visible light. The amount of infrared radiation emitted by an object is determined by its emissivity, which is a measure of its ability to emit radiation. Emissivity varies depending on the material and the surface conditions of the object. Objects with high emissivity, such as rough surfaces or dark-colored materials, emit more radiation than objects with low emissivity, such as shiny surfaces or light-colored materials. Mehmert [15] collected emissivity coefficients for different surface conditions of steel at different temperatures (Fig. 1).

Fig. 1
figure 1

Emissivity of steel with different surface conditions [15, 16]

Full size image

In addition to emissivity, transmissivity can also affect the accuracy of thermography measurements. Transmissivity refers to the ability of a material to transmit infrared radiation through it. For example, glass has low transmissivity and reflects most of the infrared radiation, making it challenging to measure the temperature of an object behind it. The transmission of air exhibits a significant dependence on the wavelength of the IR measurement system. In the long-wavelength atmospheric window, typically ranging from 8 to 14 μm, the transmission remains consistently high, allowing for efficient transmission over long distances. However, in the middle atmospheric window spanning from 3 to 5 μm, measurable attenuations occur due to the influence of the atmosphere, even at relatively short distances of a few tens of meters (compare Fig. 2). Accordingly, the influence of the transmissivity can be reduced by choosing a thermographic system that uses long wavelengths between 8 and 14 μm.

Fig. 2
figure 2

Spectral transmittance of air: path length L = 10 m, relative humidity u = 85 %, temperature T = 25 °C, air pressure p = 1013 mbar [17, 18]

Full size image

Regarding emissivity, a smooth surface will have a higher emissivity than a rough surface [19]. Sooty surfaces can also affect the emissivity of the material. During DED-Arc, smoke and fumes are generated due to the melting of the wire and deposition of the material. These smoke and fumes deposit on the surface of the material and affect its emissivity. Dark surfaces tend to have a higher emissivity than light surfaces, which can affect the accuracy of the temperature measurements obtained through thermography [20]. In some cases, the smoke and fumes can also block the infrared radiation, making it challenging to obtain accurate temperature readings.

The approach to monitor the AM process by thermography aiming at investigating the influence of thermal cycles on the material properties is followed by many research groups [21,22,23,24,25,26,27,28,29]. For laser powder bed fusion (LPBF), thermography is already deployed by industry and investigations on calibrating the emissivity and correlating material properties with thermal cycles are available [27, 29]. This is partly due to the earlier industrial application of the technology in general, but also to the more uniform surface of the components and more controlled energy source. For WAAM, there are investigations on the effect of thermal cycles on material and mechanical properties which are not considering the change of emissivity [22, 23]. Some people state that there is no change in emissivity [24, 26]. However, Baier et al. presented a methodology, to determine the emissivity coefficient in order to reliably track and control the interpass temperature for WAAM of titanium [21]. It must be noted that for the control of the interpass temperature only one value for the emissivity for a certain temperature is needed. So when thermography is used just to capture one specific interpass temperature that needs to be reached before the next layer is applied, it is enough to determine the emission coefficient for that specific temperature. If process monitoring is required, including the calculation of cooling rates and the analysis of thermal cycles, it is necessary to take into account changes in emissivity as well, especially for high temperatures.

The main findings of the analyzed investigations are as follows:

  • Process monitoring using thermography is of high interest.

  • Mechanical properties are influenced by the characteristic thermal cycle of WAAM.

  • To reliably determine temperatures during WAAM, it is necessary to correct the changes of the emission coefficient for different temperatures and surface conditions.

3 Experimental and analytical approach

The experiments were carried out in two stages. First, a workflow for generating a temperature-dependent function for the emission coefficient ε(T) is presented. In the second stage, this function is used to correct thermographic temperature measurements of the manufacturing of thin-walled samples and to analyze the effect of a wrongly set value for the emissivity.

The setup, material, and methodology are further described in the following sections.

3.1 Setup and material

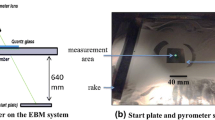
The manufacturing setup used for both stages of the investigation consisted of a Kuka 6-axis robot (KR 22) with a tilt-turn table. The Fronius TPS500i power source is connected to the robot, and the torch is mounted on the robotic handling system (compare Fig. 3).

Fig. 3
figure 3

General setup (left) and setup for the determination of ε(T) (right)

Full size image

The thermal camera used for the experiments is the VarioCAM HD head 900 from InfraTec. The thermal camera has a measuring range of −40 to 2000 °C, which depends on the calibration setting. For the experiments, a full-frame setting with a temperature range of 250 to 1200 °C is used. The measurement accuracy is ±1 °C, whereby the temperature is resolved with approx. 0.02 K. For temperature, recording is done with a spectral range of 7.5 to 14 μm and the detector type is an uncooled microbolometer focal plane array. The VarioCAM HD is set up on a tripod at a fixed distance (1 m) from the sample. For the measurement, the emission value is set to 1 and is then manually corrected to match the reference temperature. A detailed explanation on the correction of the emissivity is given in Section 3.2. The transmission is also set to 1 (compare Fig. 2) and the path temperature is assumed to be 20 °C.

Temperature measurement with thermocouples is carried out using a QuantumX MX1609KB from HBM. This has 16 galvanically isolated inputs and can measure temperatures from −100 to 1300 °C. The measuring rate can be set between 0.1 and 200 s−1. For these experiments, it was set to 10 s−1. The measurement deviations of the system result from a total error limit at 22 °C ambient temperature of ±0.7 K and a temperature drift of ±0.2 K/10 K [15]. The thermocouples used are the C20-KX thermocouples from TC Mess- und Regeltechnik GmbH. These thermocouples are of type K of the standard DIN EN 60584-1 [30] and can measure temperatures up to 800 °C. They were attached to the top layer by spot resistance welding before the actual WAAM process started.

The pyrometer used is the “CTratio 1MH” from Optris. The pyrometer can measure temperatures between 700 and 2000 °C in a spectral range of 0.8 to 1.1 μm and achieves a resolution of 0.1 K with a system accuracy of ±0.5% Tmeas+2 °C. The pyrometer can be used in single and dual channel operation. In dual-channel operation, the pyrometer automatically calculates the prevailing emissivity and applies it to the temperature measurement. The ratio pyrometer is placed next to the thermal camera, as this pyrometer is used as a reference temperature for the thermal camera for temperatures above 700 °C.

To ensure local comparability of measurements with the three different instruments, the measurement spot of the pyrometer was aligned with the measurement point of the attached thermocouples. The temperature-time profiles from the thermography measurements were generated at the pixels where the thermocouples were attached.

For the experiments, a high strength filler wire is utilized. The chemical composition is listed in Table 1. The shielding gas was M21 (18% CO2 and 82% argon) with a flow rate of 16 l/min and the energy input was around 2 kJ/cm (vwire = 3 m/min, vweld=45 cm/min).

Table 1 Chemical analysis of the used filler wire Böhler 3dprint AM80HD
Full size table

3.2 Methodology

3.2.1 Thermography and determination of ε(T)

The emission value of a material depends on several factors, such as the surface conditions and the color. The color is partly temperature-dependent, as the material begins to glow at high temperatures. Furthermore, welding produces condensed metal vapors, soot or carbon black, which give the layers further down a darker color. This is depicted in Fig. 4. For this reason, a temperature-dependent function must be created for the emissivity, which describes this change in the emissivity value by also considering the increasing impurity of the layers.

Fig. 4
figure 4

Increasing impurity of the surface by soot, carbon black, and slag of the WAAM process

Full size image

To determine the correct temperature and thus emission values, the ratio pyrometer and the thermocouples are used as a reference to determine the exact prevailing temperature. The ratio pyrometer is intended to measure the temperatures above 700°C. For the lower temperatures, the thermocouples are used. With the help of these measured temperatures, the temperature measured by the thermal camera is to be adjusted and the actual emission values for the thermal camera determined. For a simple adjustment, the emission value of the thermal camera is set to 1. Subsequently, the emission values of the thermal camera are corrected so that the temperature of the thermal camera corresponds to the reference temperature. The correction of the emission values is carried out using Eqs. (1), (2) and (3) for the correction of a temperature TA calculated by the measuring device with a wrongly set emission coefficient [14].

$${T}_M={T}_M^{\ast }+\delta T$$
(1)
$$\frac{{1}}{{{T}}_{{M}}^{\ast }}=\frac{{1}}{{{T}}_{{A}}}+\frac{{{\lambda}}_{{eff}}}{{{C}}_{{2}}}\;{\ln}\;{\varepsilon_k }$$
(2)
$${\delta} {T}=\frac{{{\varepsilon}}_{{k}}-{\varepsilon}}{{{\varepsilon}}_{{k}}}\ast \frac{{{\lambda}}_{{eff}}}{{{C}}_{\textbf{2}}}\ast {{{T}}_{{M}}^{\ast}}^{\textbf{2}}$$
(3)

TM is the corrected temperature, \({T}_M^{\ast }\)is a preliminary temperature, TA is the raw temperature measured by the IR camera, C2 is the Planck constant, εk is the set value for the emissivity during measuring, and ε is the actual emissivity. The value for the effective wavelength λeff is set to 10 μm taken from [14] for the wavelength range of the thermal camera, which is between 7.5 and 14 μm.

To record a representative T-t profile, thin-walled samples were manufactured. Subsequently, thermocouples were attached to the last deposited layer and the ratio pyrometer was also focused on the last deposited layer. After starting the measurement, three to four weld beads were added on top of the thin-walled sample. This allows the subdivision of the emission values to be calculated later into individual layers. The procedure was repeated for seven individual experiments to statistically validate the results.

Figure 5 describes graphically the determination of values for the emissivity at different temperatures. The black line is the reference temperature measured by the ratio pyrometer. At each intersection with one of the dashed lines, the emissivity (ε), the according real temperature (TM), and the temperature TA measured by the thermal camera with ε=1 (TA) are logged.

Fig. 5
figure 5

T-t curve measured by thermography with different, constant emissivity values and T-t curve of the ratio pyrometer, which accounts for change of emissivity

Full size image

After logging and plotting the data points in a ε(T) diagram, a Boltzmann fit, which uses non-linear curve fitting with Levenberg-Marquardt iteration, was applied to describe the emissivity as a function of temperature. This function was later used to correct the temperature in the second stage of this study.

3.3 Application of ε(T) for the thermal cycles during WAAM

In the second stage of the study, thin-walled samples (100 × 50 mm) with different interpass temperatures were manufactured and the process was recorded using the same setup and settings as described in Section 3.1. The welding source parameters were as follows: U=18 V, I=200 A, vwire=6 m/min, vweld=45 cm/min, IPTspecimen 1 = 400°C/IPTspecimen 2 = 200°C. After manufacturing, the T-t profile for certain locations on the specimens was exported and corrected.

4 Results

4.1 Thermography and determination of ε(T)

From the calibration of the thermal camera by ratio pyrometer and thermocouples, the following dependency between temperature, number of deposited layer, and emissivity can be derived (Figs. 6 and 7).

Fig. 6
figure 6

Emissivity of different layers/temperature peaks for a temperature TA recorded by IR thermography with ε = 1

Full size image
Fig. 7
figure 7

Emissivity of different layers/temperature peaks of the real temperature TM

Full size image

The data points can be subdivided into collectives that refer to the first, second, and third deposited layer, respectively, temperature peak. The emissivity for low temperatures increases with each further layer that is added to the structure, producing more condensed metal vapors, soot and carbon black. After a third layer is applied to the point of interest, there is no observable change in emissivity, which means that for further thermal cycles the function for layer 3 (green) can be used to correct the measured temperature. For high temperatures, the surface becomes more reflective and the emissivity decreases. To describe the data points, a Boltzmann function was fitted for each layer, Eq. (4).

$${Y}\left({x}\right)={{A}}_{\textbf{2}}+\frac{{{A}}_{{1}}-{{A}}_{{2}}}{{1}+{l{e}}^{\frac{{x}-{{x}}_{\textbf{0}}}{{dx}}}}$$
(4)

The parameters obtained by the fit are the following listed in Table 2.

Table 2 Parameters for the fitting of the data points
Full size table

From the values for A1 and A2, it can be seen that for layer 2 and layer 3 the asymptote is below 0. This is due to missing data points in the high temperature range, where the emissivity approaches its minimum. For correcting high temperatures occurring during WAAM, this leads to too high temperature values. For that reason, data points were manually added, assuming that the emissivity in the temperature range TA=1100…1250°C is more or less equal for all three layers. The corrected fit function and the parameters are presented in the Appendix.

Fig. 8 shows a time-temperature profile that is recorded by the ratio pyrometer (blue) and the according T-t profile obtained from thermography, which was corrected afterwards using Eq. (4) with the parameters in the Appendix.

Fig. 8
figure 8

Temperature of the thermal camera corrected with ε(T) and temperature of the ratio pyrometer as reference

Full size image

As can be seen, for temperatures between 700 and 1200 °C, which are the measuring limits of ratio pyrometer and thermal camera, the calculated function is suitable to correct the temperatures from thermography.

4.2 Application of ε(T) for the thermal cycles during WAAM

The time-temperature profiles of a wall with an interpass temperature of 400°C and a wall with 200°C were recorded using an infrared camera. The emissivity was set to 1 and corrected subsequently using the determined function. To illustrate the effect of a wrong emissivity, Figs. 9 and 10 depict the uncorrected T-t profile with an emissivity of 1, and for comparison, the gray line shows the corrected temperature. It can be seen that for higher temperatures the deviation due to incorrect emissivity is much higher than for lower temperatures.

Fig. 9
figure 9

T-t profile of the specimen with 400°C interpass temperature as recorded by IR thermal camera (e=1) and the corrected T-t profile using Eq. (4) and Appendix Fig. 13

Full size image
Fig. 10
figure 10

T-t profile of the specimen with 200°C interpass temperature as recorded by IR thermal camera (e=1) and the corrected T-t profile using Eq. (4) and Appendix Fig. 13

Full size image

After deposition, the curve reheats five times above A3 for IPT=400°C and four times for IPT=200°. Here, the material is austenitized for a short time, but at high temperatures. This may lead to fine grains due to the short period of time for grain growth. It can also be assumed that, during austenitization, the steel fully austenitizes, as the grains are very fine. The last peak in which the temperature rises above A3 is called critical cooling cycle [28]. For the second part of the profile, the material is still frequently reheated, but the temperature remains below A3. Although the temperature peaks for Tmax are decreasing steadily, the Tmin remains almost stable at 400°C, respectively, 200°C. In the case of IPT=400°C, the steel is exposed to high temperatures, especially temperatures between A3 and Ms, for a long time. For an IPT of 200°C, the material fully transformed after each cycle, while for IPT=400°C the Mf-temperature is only reached in the last cycle.

For a first description of the cooling behavior, t8/5 times provide an easy measure to estimate the compliance to requirements. The error occurring by choosing a wrong emissivity or by not correcting it is depicted in Figs. 11 and 12. Here, the t8/5 times were calculated for all peaks T> 800°C from the T-t profile in Fig. 10.

Fig. 11
figure 11

Comparison of t8/5 times of a T-t profile with different emission coefficients and corrected emissivity

Full size image
Fig. 12
figure 12

Deviation of t8/5 times for constant emissivity values from the corrected t8/5 times

Full size image

It can be seen that deviations in t8/5 times depend on the cooling rate. For longer cooling rates, the error is higher, for low cooling rates it becomes less distinct.

5 Discussion

In discussing the outcomes of this study, it is imperative to acknowledge that the derived curves illustrating changes in emissivity are subject to the characteristics of the measuring device, including wavelength and type. Different wavelengths and types of thermal cameras may exhibit variations in their sensitivity to emissivity changes. This nuance underscores the need for careful consideration of the specific measuring device employed, as its characteristics can influence the accuracy and reliability of the derived curves.

The study’s emphasis on the dependence of emissivity on temperature and surface purity aligns with existing literature, contributing valuable insights to the understanding of DED-Arc processes. The demonstrated ability of thermography to yield reliable temperature profiles, despite challenges associated with higher temperatures, underscores its potential for enhancing process monitoring. However, the study recognizes the difficulty in obtaining precise data points for extremely high temperatures, such as those found in the molten pool during the DED-Arc process. The limited exposure of the point of interest to such elevated temperatures, and when it does occur, often for a brief duration, introduces a high potential for error. One proposed approach for obtaining more data points in this challenging range involves increasing the energy input and potentially adjusting other process parameters, such as a higher interpass temperature. However, it is crucial to acknowledge that any added data points obtained in this manner are preliminary and represent rough assumptions. Nevertheless, for the analysis of the T-t profile in terms of resulting microstructure, the correct determination of temperatures around A3 is more crucial than for the temperatures of the molten pool [28].

Moreover, within the context of the three derived curves, it is crucial to highlight the significance of the emissivity function for temperature peak 3/layer 3 compared to those for peaks 1 and 2. This emphasis is rooted in the recognition that the evolution of microstructure during the DED-Arc process predominantly occurs in the so-called critical cooling cycle [28]. This cycle, marked by the peak temperature surpassing the A3 temperature for the last time, holds particular importance for understanding the transformation kinetics and resultant material properties.

6 Summary and conclusions

This study demonstrates the potential of thermography for monitoring and evaluating the DED-Arc process. By developing a calibration function for the emission coefficient and correcting and analyzing recorded temperature profiles, the importance of the correct determination of the emission coefficient for process monitoring was pointed out. While thermography offers a great potential, for a full field record of the temperature profiles of a product, it is important to also consider its limitations. Although thermal cameras can detect temperatures of up to 2000°C, it is very difficult for the molten pool. In this study, temperatures up to 1500°C could be reliably detected and emissivity values were calculated. By the application of the calibration function for the emissivity, the T-t profiles of two specimens, one with high and one with low IPT, were corrected and the effect of a wrong emission coefficient was shown by depicting them and calculating the t8/5 times for different emissivity values. The key findings of this study are as follows:

  • The emissivity during WAAM of high strength steel depends on the temperature as well as on the purity of the surface.

  • By considering the change of emissivity, reliable temperature profiles can be detected by thermography, although it is still a challenge for higher temperatures like in the molten pool.

  • The effect of wrong emissivity coefficient on the t5/8 times depends on the cooling speed and the set value for the emissivity.

Although the emissivity of the surface of a part to be produced by DED-Arc also depends on the deployed gas, wire material, and the arc power, the presented function gives an estimation about the change of emissivity and the error occurring by using a constant emission coefficient. For analyzing full field thermal cycles and correlating the temperature profile with high-resolution material and component tests, thermography contributes to the development of virtual component tests and thus the qualification and certification of large scale parts, e.g., for the construction industry.