A novel pressure transient analysis model for fracturing wells in fracture–cavity carbonate reservoirs

Abstract

Large-scale karst caves are the principal storage spaces for hydrocarbon resources in fracture–cavity carbonate reservoirs. Drilling directly into these caves is considered the ideal mode of development, but many wells do not effectively penetrate karst caves. Therefore, acid fracturing is employed to generate artificial fractures that can connect with these caves. However, there are no appropriate well test methods for fracturing wells in fracture–cavity reservoirs. This study establishes a novel pressure transient analysis model for such wells. A new mathematical model is proposed that couples linear flow in acid fracturing cracks with radial flow in the oil drainage area. The Laplace transform and Stehfest numerical inversion provided analytical solutions for the bottomhole pressure. Typical log–log well testing curves were plotted to analyze oil flow, which occurs in ten stages. During the flow stage in fracturing cracks, the pressure and pressure derivative curves are parallel lines with a slope of 0.5. In the stage of karst cave storage, the pressure derivative curve is a straight line with a slope of 1. A comparison with previous models confirmed the validity of the proposed model. The influence of key parameters on the behavior of typical curves is analyzed. A field case study of the proposed model was carried out. Parameters related to fracturing cracks and karst caves, such as the crack length and cave radius, were successfully estimated. The proposed model has great potential for determining formation parameters of fracture–cavity reservoirs.

Article highlights

• A new mathematical model for fracturing wells in fracture-cavity reservoirs is established by coupling the linear flow in fracturing cracks with the radial flow in oil drainage area.

• The cave flow stage characterized by a concave shape on pressure-derivative curve, which help the estimation of volume and location of large karst caves.

• A filed case shows the great potential of the proposed method to the fracture-cavity reservoirs with fractured wells.

1 Introduction

Carbonate reservoirs play an important role in the exploitation of global oil and gas resources (Flügel and Munnecke 2010). China has abundant hydrocarbon resources in carbonate rocks, which are primarily located in the Tahe oilfield, Puguang gas field, and Anyue gas field. Over the past few years, there has been significant growth in the production of crude oil and gas from these vast carbonate oil and gas fields. This has made carbonate reservoirs a crucial area for the exploration and development of domestic oil reservoirs and reserves growth (Li et al. 2018).

Fracture–cavity carbonate reservoirs have unique characteristics that distinguish them from traditional carbonate reservoirs (Golfier et al. 2015). Typical fracture–cavity reservoirs have a complex pore network that includes karst caves of various sizes, natural fractures, dissolved vuggy pores, and a tight matrix (Jiao 2019; Li et al. 2016). In general, the size of karst caves ranges from several meters to tens of meters, and these constitute the principal storage spaces for crude oil. Natural fractures and dissolved vuggy pores are widely distributed in reservoirs, while matrix pores are underdeveloped (Berre et al. 2019; Flemisch et al. 2018; Tian et al. 2019). Consequently, the complex pore structure characteristics of fracture–cavity carbonate reservoirs lead to difficulties in describing seepage characteristics (Fang et al. 2019; Sun et al. 2018). In the development of fracture–cavity reservoirs, it is common to estimate physical properties related to large-scale caves and fractures using pressure transient analysis (PTA) or rate transient analysis (RTA). Calculating these parameters accurately can provide valuable guidance for achieving more efficient and stable production from oil and gas wells (Wei et al. 2022).

Throughout the history of the development of well testing theory with regard to carbonate reservoirs, theoretical models can be mainly divided into two categories. One of these comprises theoretical models of multiple continuous-porosity systems, such as the classic fracture–matrix double-continuum and vug–fracture–matrix triple-continuum models (Abdassah and Ershaghi 1986; Warren and Root 1963). Multiple-continuum theoretical models are based on the assumptions that the dimensions of pores and fractures are small, usually below the millimeter scale, and that all types of pores are continuously and widely distributed in the reservoir (Berre et al. 2019). Over the past half-century, numerous well testing models based on dual and triple media have been established and have been widely used in carbonate reservoirs with microscale natural fractures and dissolved vuggy pores (Abdassah and Ershaghi 1986; Camacho-Velázquez et al. 2005; Gómez et al. 2014; Guo et al. 2012; Jia et al. 2013; Kazemi 1969; Warren and Root 1963). However, in the case of fracture–cavity reservoirs multiple-continuum models are no longer applicable because of the presence of large-scale karst caves and fractures, whereby the reservoir pore structure does not conform to the idealized continuum assumption. The location and volume of large-scale karst caves are the most significant parameters, but these cannot be determined by the conventional multiple-continuum reservoir models (Du et al. 2020).

Another type of well testing model is the discrete cavity–fracture model, which is no longer constrained by the assumption of continuous porosity and considers that fractures and cavities can exist discretely in the reservoir (Yao et al. 2010). The connectivity between karst caves and fractures is different in each fracture–cavity reservoir, which is one of the main reasons for the diversity of pressure and production performance (Berre et al. 2019; Zhu et al. 2015). Although research on the discrete cavity–fracture model is in the initial stage, some researchers have established corresponding well testing models based on different connectivities between large-scale karst caves and fractures (Du et al. 2022, 2020, 2019; He et al. 2018; Li et al. 2021, 2020; Nie et al. 2021; Wei et al. 2022; Xing et al. 2018; Xiong et al. 2017). Xiong et al. (2017) determined the transient-pressure response of a single fracture–cavity physical combination model by experimental testing. A mathematical model of a single fracture–cavity combination was established, and the analytical solution was obtained. Li et al. (2021) and Wei et al. (2022) proposed PTA models of wells drilled into beads-on-string caves, in which the flow in large-scale karst caves is assumed to correspond to free flow and the effect of gravity is considered. Li et al. (2020) and Li et al. (2022) studied RTA models of horizontal fracture–cavity systems connected in series or parallel and carried out analyses of sensitivity and field case applications.

If large-scale karst caves are considered as regions of discrete pore systems and natural fractures and dissolved vuggy pores are considered as double-continuum regions, coupling the oil flow in the two types of regions is another option for establishing a well testing model. Xing et al. (2018) developed an analytical well testing model for wells drilled into karst caves. In their model, the isopotential body assumption is adopted for the karst cave regions, while the outer zone of the reservoir is considered to be a fracture–vug dual-porosity system. Du et al. (2019) presented a new analytical well testing model that considers the coupling between oil flow and wave propagation. Their model adopts the wave equation to describe the fluid flow in a large-scale cave. By fitting measured pressure data to the type curve, reservoir parameters such as the cave volume can be calculated. Du et al. (2022) and Du et al. (2020) proposed a well testing model of multiple radial fracture–cavity regions, and the corresponding solutions of PTA and RTA were given.

It is worth mentioning that some researchers have investigated numerical well testing models of fracture–cavity reservoirs and have obtained some results (Chen et al. 2016; Gao et al. 2016; Wan et al. 2018, 2020; Wang et al. 2018; Yao et al. 2010). Because of the advantages of numerical solutions, numerical well testing models of fracture–cavity reservoirs can simulate the reservoir pressure and production characteristics of complex discretely distributed large-scale fractures and cavities, which cannot be solved easily in analytical models. Yao et al. (2010) developed a model of a discrete fracture–vug network based on the finite element method, in which the flow in porous rock and macrofracture systems obeys Darcy’s law. In contrast, the flow in macroscale vug systems obeys the Navier–Stokes equation. Chen et al. (2016) established a pressure analysis model by regarding caves as equipotential bodies and used the boundary element method to solve the mathematical model. Gao et al. (2016) maintained that the flow in karst caves corresponds to Barree–Conway high-speed non-Darcy flow and established a numerical well testing model for wells drilled into caves by the finite difference method. Wan et al. (2018) and Wan et al. (2020) developed a numerical pressure transient model for fracture–cavity reservoirs with unfilled cavities, in which the finite element method is applied in solving the mathematical model. The characteristic curves for two typical cases, namely, a well drilled into a karst cave and a well not drilled into a karst cave, are analyzed. Although numerical well testing models have various benefits, they also encounter certain problems, such as intricacies in geological modeling, meshing difficulties, and a lack of convergence in numerical solutions. These problems hinder the widespread use of such models.

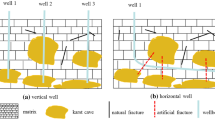
As was previously stated, in fracture–cavity carbonate reservoirs oil and gas are stored in large-scale karst caves. Consequently, drilling wells directly into these caves is the optimal method of development (Li et al. 2016). Despite the increasing rate at which wells are drilled into karst caves, many wells are still not effectively drilled into such caves, as depicted in Fig. 1a. In this situation, acid fracturing is commonly used to create artificial fractures that connect with karst caves (Wang et al. 2018). In addition, small natural fractures and dissolved vuggy pores are formed within the area of the reservoir unaffected by fracturing cracks and larger karst cavity regions (as shown in Fig. 1b).

Fig. 1

Schematic of the geological model with acid fracturing well: a Seismic features of a karst cave; b Schematic of the geological model

A novel analytical model for PTA is developed in this study for reservoirs with fracture–cavity systems in which fracturing wells have not penetrated karst caves. The model considers the cracks produced by acid fracturing that connect the wellbore to a karst cave. The area where oil drains radially is centered around a large karst cave, and the surrounding region outside the cave contains two types of pore spaces: natural fractures and dissolved vuggy pores. Firstly, we establish and solve a mathematical model by coupling the linear seepage equation for artificial cracks formed by acid fracturing with the radial seepage equation for the area of radial oil drainage. Then, the typical log–log well testing curve is plotted, and the effects of controlling parameters on the behavior of this curve are demonstrated in detail. Finally, a field case application of the proposed model is presented. This study introduces a new approach that combines linear flow in fractures produced by acid fracturing, free flow in karst caves, and radial flow in natural fractures and vuggy pores. This enables the simultaneous interpretation of multiple parameters, including fractures formed by acid fracturing, large-scale karst caves, natural fractures, and dissolved vuggy pores.

2 Physical model

2.1 Geological model

In the geological structural model, which is shown in Fig. 1, the wellbore is drilled near a karst cave, with which it is connected via acid fracturing cracks. Moreover, microscale natural fractures and dissolved vuggy pores are also developed in the region of macroscale cavities and fracturing cracks. The fluid flow in such fracture–cavity reservoirs represents a complex multiscale flow problem (Sun et al. 2018). To make this problem more manageable, some reasonable assumptions are essential. On the basis of these assumptions, the physical model is established.

2.2 Simplified physical model and assumptions

Figure 2 presents the physical model of a fracturing well in a fracture–cavity carbonate reservoir. Figure 2a illustrates the planar distribution characteristics of the pore system, including acid fracturing cracks, a large karst cave, natural fractures, and dissolved vuggy pores. Figure 2b shows the area of radial oil drainage formed with the cave as its center. In this model, the shape of the karst cave is assumed to be cylindrical, and the acid fracturing cracks are assumed to be horizontal plates. Figure 2c shows that the region outside the karst cave can be regarded as a dual-porosity reservoir comprising natural fractures and dissolved vuggy pores. Figure 2d shows the fluid flow of oil in the reservoir. Driven by a decrease in pressure, oil flows into natural fractures from dissolved vuggy pores, then flows from natural fractures to the karst cave, and finally flows into the wellbore from the karst cave through fracturing cracks. The basic assumptions of the physical model are as follows:

• (1) The vertical well produces oil at a constant rate. The fluid is single-phase slightly compressible crude oil, and the compressibility, viscosity, and formation volume factor of crude oil are assumed to be constants.

• (2) The effective thickness of the reservoir is constant, and a large-scale karst cave is developed near the wellbore, with which it is connected via the fracturing cracks. The fluid flow in the fracturing cracks corresponds to one-dimensional linear isothermal Darcy flow.

• (3) The karst cave is filled with crude oil, and the flow in the cave corresponds to isothermal free flow. The propagation of the pressure wave in the cave occurs very rapidly so that the pressure reaches equilibrium instantaneously at any position. Therefore, we ignore the flow process and dynamic changes inside the karst cave, the pressure at all points in the cave is equal (Du et al. 2019).

• (4) An area of radial drainage is formed with the cave as its center, and the flow in this area corresponds to isothermal Darcy flow. Natural fractures and dissolved vuggy pores are radially distributed in the region outside the karst cave, which is regarded as a double-continuum porous system (Xing et al. 2018). The matrix is so tight that its porosity and permeability are much smaller than those of dissolved vuggy pores and natural fractures, and therefore in this study matrix flow is ignored (Li et al. 2020).

• (5) At the initial time point, the reservoir pressure is equal at all positions and is equal to the original reservoir pressure.

• (6) The physical properties of the reservoir, such as permeability, porosity, and rock compressibility, are all constants.

• (7) The influences of the skin factor and wellbore storage constant are considered, while the effects of capillary force and gravity are ignored.

Fig. 2

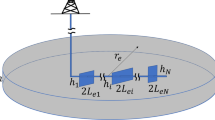
Schematic diagram of the physical model: a The wellbore is connected to the karst cave via the fracturing cracks; b The area of radial oil drainage is formed with the cave as its center (L_f = length of fracturing cracks; R_c = radius of karst cave); c The fracture–vug double-continuum outer formation; d Schematic diagram of the fluid flow process

3 Mathematical model

3.1 Establishment of the mathematical model

Schematic diagram of coupling the linear seepage equation in artificial acid fracturing cracks with the radial seepage equation in the radial oil drainage area is shown in Fig. 3. Firstly, a linear seepage equation for artificial acid fracturing cracks was established with the wellbore as the origin, where the inner boundary condition is the wellbore boundary condition and the outer boundary condition is the karst cave condition. Then, a radial seepage equation was established with the center of the karst cave as the origin, with the inner boundary condition being the karst cave condition. The karst cave connects the fractured area and the dual porosity area, whose flow rate and pressure serve as continuity conditions. By establishing a continuity equation between the flow rate and pressure of the karst cave, coupled with the seepage of the two zones, we ultimately established a comprehensive mathematical model.

Fig. 3

Schematic diagram of coupling mathematical model

On the basis of Darcy flow, the seepage velocity v in the fracturing cracks can be expressed as follows (Li et al. 2020):

$$ v = - \frac{{K_{f} }}{{\mu_{o} }}\frac{{\partial p_{f} }}{\partial x}\quad (r_{w} < x < L_{f} ) $$

(1)

There is no source term for the fracturing cracks, and the governing equation of the fracturing cracks can be written as:

$$ \frac{{\partial (\rho \varphi_{f} )}}{\partial t} + \nabla \cdot \left( {\rho v} \right) = 0 $$

(2)

Considering the compressibility of fluid and rock, the equation of state of fluid and rock in the fracturing cracks can be expressed as:

$$ \begin{aligned} \rho & = \rho_{0} \left[ {1 + C_{flu} \left( {p - p_{ref} } \right)} \right] \\ \varphi_{f} & = \varphi_{f0} \left[ {1 + C_{f} \left( {p - p_{ref} } \right)} \right] \\ \end{aligned} $$

(3)

where ρ₀ is the density of oil at the reference pressure p_ref and φ_f0 is the porosity of fracturing cracks at the reference pressure p_ref. By substituting Eq. (1) and Eq. (3) into Eq. (2), the one-dimensional differential governing equation for the fracturing cracks can be obtained:

$$ \frac{{K_{f} }}{{\varphi_{f} \mu_{o} C_{ft} }}\frac{{\partial^{2} p_{f} }}{{\partial x^{2} }} = \frac{{\partial p_{f} }}{\partial t}\quad (r_{w} < x < L_{f} ) $$

(4)

where C_ft is the total compressibility of the fracturing cracks and is defined as:

$$ C_{ft} = C_{flu} + C_{r,f} $$

(5)

The inner boundary condition of the wellbore is defined as:

$$ - \frac{{K_{f} W_{f} H_{f} }}{{\mu_{o} }} \cdot \frac{{\partial p_{f} }}{\partial x}\left| {_{{x = r_{w} }} } \right. = q_{o} B_{o} $$

(6)

The external boundary of the acid fracturing cracks is connected to the karst cave, and therefore the pressure here is equal to the pressure in the cave:

$$ \left. {p_{f} } \right|_{{x = L_{f} }} = p_{c} $$

(7)

On the basis of the assumption of fracture–vug double-continuum porous media (Jia et al. 2013), taking the center of the karst cave as the coordinate origin, the governing equation of natural fractures in the area outside the karst cave can be expressed as follows:

$$ \frac{{K_{fr} }}{{\mu_{o} }}\frac{{\partial^{2} p_{fr} }}{{\partial r^{2} }} + \frac{{K_{fr} }}{{\mu_{o} }}\frac{{\partial p_{fr} }}{\partial r} + \alpha \frac{{K_{vr} }}{{\mu_{o} }}(P_{vr} - P_{fr} ) = \varphi_{fr} C_{frt} \frac{{\partial p_{fr} }}{\partial t}\quad (r_{c} \le r \le r_{e} ) $$

(8)

where C_frt is the total compressibility of natural fractures and is defined as:

$$ C_{frt} = C_{flu} + C_{r,fr} $$

(9)

The differential governing equation of the dissolved vuggy pore system can be expressed as follows (Jia et al. 2013):

$$ - \alpha \frac{{K_{vr} }}{{\mu_{o} }}(P_{vr} - P_{fr} ) = \varphi_{vr} C_{vrt} \frac{{\partial p_{vr} }}{\partial t} $$

(10)

where C_vrt is the total compressibility of the natural dissolved vuggy pore system and is defined as:

$$ C_{vrt} = C_{flu} + C_{r,vr} $$

(11)

The external boundary condition of the area of radial drainage is as follows:

$$ p_{fr} (\infty ,t) = p_{i} \quad {\text{for}}\;{\text{the}}\;{\text{infinite}}\;{\text{reservoir}} $$

(12)

$$ \left. {\frac{{\partial p_{fr} }}{\partial r}} \right|_{{r = r_{e} }} = 0\quad {\text{for}}\;{\text{the}}\;{\text{closed}}\;{\text{boundary}} $$

(13)

$$ p_{fr} (r_{e} ,t) = p_{i} \quad {\text{for}}\;{\text{the}}\;{\text{constant - pressure}}\;{\text{boundary}} $$

(14)

The pressure at the internal boundary of natural fractures is equal to the pressure in the karst cave:

$$ \left. {p_{fr} } \right|_{{r = r_{c} }} = p_{c} $$

(15)

The rate of flow out of the karst cave through the fracturing cracks equals the elastic expansion plus the rate of flow from the natural fractures. Therefore, the flow continuous equation for flow out of the karst cave can be expressed as:

$$ - \frac{{K_{f} W_{f} H_{f} }}{{\mu_{o} }}\frac{{\partial p_{f} }}{\partial x}\left| {_{{x = L_{f} }} } \right. = - \pi r_{c}^{2} hC_{ct} \frac{{dp_{c} }}{dt} - \left. {2\pi r_{c} h\frac{{K_{fr} }}{{\mu_{o} }}\frac{{\partial p_{fr} }}{\partial r}} \right|_{{r = r_{c} }} $$

(16)

The initial condition is defined as:

$$ \left. {p_{fr} } \right|_{t = 0} = \left. {p_{vr} } \right|_{t = 0} = \left. {p_{v} } \right|_{t = 0} = \left. {p_{f} } \right|_{t = 0} = p_{i} $$

(17)

3.2 Dimensionless variables and solutions of the model

For the convenience of analysis, dimensionless variables were defined as presented in Table 1.

Table 1 Definitions of dimensionless variables

The following Laplace transform based on t_D is used to solve the partial differential equations:

$$ \overline{f}(r_{D} ,s) = \int\limits_{0}^{\infty } {f(r_{D} ,t_{D} )e^{{ - st_{D} }} dt_{D} } $$

(18)

By applying the dimensionless variables and Laplace transform, the mathematical model in Laplace space can be obtained.

The governing equations for natural fractures and dissolved vuggy pores in the area of radial oil drainage are expressed as:

$$ \frac{{d^{2} \overline{p}_{frD} }}{{dr_{D}^{2} }} + \frac{1}{{r_{D} }}\frac{{d\overline{p}_{frD} }}{{dr_{D} }} + \lambda (\overline{p}_{vrD} - \overline{p}_{frD} ) = \omega M_{D} s\overline{p}_{frD} $$

(19)

$$ (1 - \omega )s\overline{p}_{vrD} + \lambda (\overline{p}_{vrD} - \overline{p}_{frD} ) = 0 $$

(20)

The external boundary condition of the area of radial drainage is defined as:

$$ \overline{p}_{frD} (\infty ,s) = 0\quad {\text{for}}\;{\text{the}}\;{\text{infinite}}\;{\text{reservoir}} $$

(21)

$$ \left. {\frac{{d\overline{p}_{frD} }}{{dr_{D} }}} \right|_{{r_{D} = r_{eD} }} = 0\quad {\text{for}}\;{\text{the}}\;{\text{closed}}\;{\text{boundary}} $$

(22)

$$ \overline{p}_{frD} (r_{eD} ,s) = 0\quad {\text{for}}\;{\text{the}}\;{\text{constant - pressure}}\;{\text{boundary}} $$

(23)

The internal boundary condition of the area of radial oil drainage is defined as:

$$ \left. {\overline{p}_{frD} } \right|_{{r_{D} = r_{vD} }} = \overline{p}_{cD} $$

(24)

The governing equation of the fracturing cracks is as follows:

$$ \frac{{d^{2} \overline{p}_{fD} }}{{dx_{D}^{2} }} = s\overline{p}_{fD} $$

(25)

The inner boundary condition of the wellbore is defined as:

$$ A_{fD} \frac{{d\overline{p}_{fD} }}{{dx_{D} }}\left| {_{{x_{D} = 1}} } \right. = - \frac{1}{s} $$

(26)

The external boundary condition of the fracturing cracks is as follows:

$$ \left. {\overline{p}_{fD} } \right|_{{x_{D} = L_{fD} }} = \overline{p}_{cD} $$

(27)

The flow continuous equation for the karst cave is:

$$ - A_{fD} \frac{{d\overline{p}_{fD} }}{{dx_{D} }}\left| {_{{x_{D} = L_{fD} }} } \right. = - r_{cD}^{2} \eta_{1} s\overline{p}_{cD} - r_{cD} \eta_{2} \left. {\frac{{dp_{frD} }}{{dr_{D} }}} \right|_{{r_{D} = r_{cD} }} $$

(28)

Equations (19)–(27) represent the mathematical model in Laplace space. The process of solving the mathematical model in Laplace space is shown in Appendix 1.

When x_D = r_wD = 1, the bottomhole pressure in Laplace space can be written as:

$$ \overline{p}_{sD} = A_{1} e^{\sqrt s } + B_{1} e^{ - \sqrt s } $$

(29)

where A₁ and B₁ are the coefficients of the solution. The expressions for A₁ and B₁ under different external conditions are given in Appendix 1. Note that the expression for the bottomhole flow pressure $\overline{p}_{sD}$ does not consider the influence of the wellbore storage effect and skin effect. We can calculate the bottomhole pressure $\overline{p}_{wD}$ according to Duhamel’s principle to take the wellbore storage effect and skin effect into account (Ozkan and Raghavan 1991; Van Everdingen and Hurst 1949):

$$ \overline{p}_{wD} = \frac{{s\overline{p}_{sD} + S}}{{s + C_{D} s^{2} (s\overline{p}_{sD} + S)}} $$

(30)

The Stehfest method (Stehfest 1970) is used to convert the dimensionless bottomhole pressure or dimensionless production in Laplace space into the values in real space. The Stehfest numerical inversion method can be expressed as:

$$ p_{wD} \left( {t_{D} } \right) = \frac{\ln 2}{{t_{D} }}\sum\limits_{i}^{N} {L_{i} } \overline{p}_{wD} (s) $$

(31)

where

$$ L_{i} = ( - 1)^{{\frac{N}{2} + i}} \sum\limits_{{k = \left[ {\frac{i + 1}{2}} \right]}}^{{\min \left( {i,\frac{N}{2}} \right)}} {\frac{{k^{{\frac{N}{2} + 1}} (2k)!}}{{\left( {\frac{N}{2} - k} \right)!k!(k - i)!(i - k)!(2k - i)!}}} $$

(32)

4 Pressure transient analysis and validation

4.1 Typical curves

The typical curves for the dimensionless pressure and pressure derivative can be obtained from the above semianalytical solution for the bottomhole pressure. Figure 4 shows a typical log–log curve obtained by PTA for a fractured well in a fracture–cavity reservoir. This typical curve can be divided into ten flow stages, and the flow characteristics of each stage can be recognized.

• Flow stage I is the stage corresponding to the wellbore storage effect, in which the curves for the pressure and pressure derivative are coincident straight lines with a slope of 1.

• Flow stage II is the stage corresponding to the skin effect. The slope of the pressure curve decreases because of the influence of the skin coefficient, and the pressure derivative curve bends downward to form a smooth convex shape.

• Flow stage III is the stage of linear flow in the acid fracturing cracks, in which the curves for the pressure and the pressure derivative are parallel lines with a slope of 0.5.

• Flow stage IV is the first transitional flow stage. At this stage, the flow transitions from linear flow to cave storage, and the pressure derivative curve drops rapidly.

• Flow stage V is the period of storage in the large karst cave, which is similar to the stage of wellbore storage. The slope of the pressure derivative curve is equal to 1. Flow stages IV and V are caused by the large karst cave, and therefore we refer to these two flow stages as corresponding to the karst cave storage effect. Here, the pressure derivative curve bends downward to form a smooth concave shape. The characteristics of flow stages IV and V can be identified to judge whether there are caves in the reservoir.

• Flow stage VI is the second transitional flow stage. At this stage, the flow of crude oil transitions from cave storage to radial flow in natural fractures in the outer region. This stage is characterized by a drop in the pressure derivative curve, which gradually transitions to a horizontal line.

• Flow stage VII is the stage of radial flow in natural fractures in the outer region, and the pressure derivative curve is a horizontal line.

• Flow stage VIII is the stage of interporosity flow from the dissolved vuggy pores to the natural fractures in the outer region. At this stage, the pressure derivative curve drops to form a second concave shape.

• Flow stage IX is the stage of total radial flow in the oil drainage area of the system, and the pressure derivative curve is a horizontal line.

• Flow stage X is the stage of boundary-dominated flow. The characteristics of the curves at this stage are determined by the different external boundary conditions. For the infinite reservoir, the pressure derivative curve is a horizontal line. For the closed boundary, the curves for the pressure and pressure derivative rise rapidly and have a slope of 1. For the constant-pressure boundary, the pressure derivative curve drops rapidly.

Fig. 4

Typical curves for bottomhole pressure and pressure derivative

4.2 Validation of the model

As was stated in the introduction, Xing et al. (2018) established a well testing model for wells drilled into karst caves. In order to compare the results of this study with their results, the length of the fracturing cracks in the proposed model is set to zero. This means that there are no fracturing cracks in our model and the well is directly drilled into the karst cave. As shown in Fig. 5a, by setting the parameters of the fracturing cracks, the model in this study can be reduced to the model of a well drilled into a karst cave established by Xing et al. (2018). Figure 5 shows a comparison between the typical curves obtained using the proposed reduced model and the results of Xing et al. (2018). Although different dimensionless methods are used in this paper and the study by Xing et al. (2018), the results in this paper are highly consistent with those of the model established by Xing et al. (2018) when the same physical parameters are used. Furthermore, as also shown in Fig. 6, when the dimensionless length of the fracturing cracks is set to 30, in the typical curve an additional stage of linear flow in fracturing cracks is added in comparison with the model established by Xing et al. (2018). Under the influence of linear flow, the concave segment of the pressure derivative curve formed by the cave storage effect becomes shallower, but the subsequent flow stages are completely identical. This indirectly proves the correctness of the PTA model devised in this study.

Fig. 5

Simplified diagrams of the proposed model: a Model of well drilled into karst cave; b Single fracture–cavity model

Fig. 6

Comparison between our typical curves and those obtained by Xing et al. (2018)

Li et al. (2020) developed a well testing model for connections between multiple fractures and multiple karst caves. When the cave radius is set to a value equal to the radius of the outer boundary in the proposed model, this means that there is no reservoir outside the karst cave. In this case, the proposed model is identical to the single fracture–cavity model established by Li et al. (2020). As shown in Fig. 5b, by setting the radius of the outer boundary, the proposed model can be reduced to the single fracture–cavity model established by Li et al. (2020).

Figure 7 compares the typical curves obtained using the proposed model and the results obtained by Li et al. (2020). Our typical curve obtained using the reduced model is highly consistent with those obtained by Li et al. (2020) when the same physical parameters are employed. In addition, in a more general case, the boundary radius is not equal to the radius of the karst cave. In comparison with the typical curve obtained by Li et al. (2020), the model in this study has an additional stage of radial flow in the outer region and a stage of interporosity flow around the karst cave.

Fig. 7

Comparison between our typical curves and those obtained by Li et al. (2020)

5 Sensitivity analysis

Engineers primarily focus on identifying the parameters that define caves and artificial fracturing cracks in fracture–cavity carbonate reservoirs. In this section, the characteristic parameters of the proposed model are analyzed in detail, including the radius of the cave (r_cD), the length of fracturing cracks (x_fD), the cross-sectional area of fracturing cracks (A_fD), the storage ratio of natural fractures (ω_fr), and the crossflow coefficient (λ). These parameters have different influences on the shapes of the curves in different stages. The proposed model includes some basic parameters, such as C_D, S, and r_eD, whose effects on typical curves are widely understood. Hence, we will not discuss these parameters in detail.

5.1 Effect of cave radius

Figure 8 illustrates the influence of differences in the radius of the karst cave (r_cD) on the typical well testing curves obtained using the proposed model. The values of the karst cave radius and other relevant parameters are shown in Fig. 7. It can be observed that the karst cave radius mainly affects the stages of cave storage, i.e., stages IV and V. With an increase in the karst cave radius, the first concave segment of the pressure derivative curve in stages IV and V is deeper, and the transition from flow stage V to the stage of radial flow in natural fractures occurs later. This is mainly because the larger is the karst cave, the greater is the crossflow from the karst cave to the fracturing cracks, which results in a greater decrease in the pressure derivative curve.

Fig. 8

Typical curves obtained by pressure transient analysis (PTA) with different values of r_cD

5.2 Effect of length of fracturing cracks

Figure 9 illustrates the influence of differences in the length of fracturing cracks (L_fD) on the typical well testing curves obtained using the proposed model. The values of the fracturing crack length and other relevant parameters are shown in Fig. 8. It can be observed that the fracturing crack length mainly affects flow stage III. With an increase in the fracturing crack length, the longer is the area where the curves for the pressure and pressure derivative are parallel lines with a slope of 0.5, and the later is the time at which the first concave segment appears. This is mainly because the longer is the fracturing crack length, the longer is the duration of linear flow of crude oil in the fracturing cracks, and the later is the time at which the first transitional flow stage occurs.

Fig. 9

Typical curves obtained by PTA with different values of L_fD

5.3 Effect of cross-sectional area of fracturing cracks

Figure 10 illustrates the influence of differences in the cross-sectional area of fracturing cracks (A_fD) on the typical well testing curves obtained using the proposed model. The values of the cross-sectional area of fracturing cracks and other relevant parameters are shown in Fig. 9. It can be observed that the cross-sectional area of fracturing cracks mainly affects flow stages III and IV. Both the dimensionless pressure and the pressure derivative decrease with an increase in the cross-sectional area of fracturing cracks. The reason for this effect is that the greater is the cross-sectional area of the fracturing cracks, the faster is the flow through the fracturing cracks. Therefore, the dimensionless pressure and pressure derivative decrease. The value of A_fD also has a slight effect on the transitional flow stage IV.

Fig. 10

Typical curves obtained by PTA with different values of A_fD

5.4 Effect of storage ratios

Figure 11 illustrates the influence of differences in the storage ratio of natural fractures (ω_fr) on the typical well testing curves obtained using the proposed model. The values of the storage ratio of natural fractures and other relevant parameters are shown in Fig. 10. It can be observed that the storage ratio of natural fractures mainly affects flow stage VI and stage VIII. Undoubtedly, the storage ratio of natural fractures indicates the amount of oil accumulated in the natural fracture subsystem, and the range of the storage ratio must be 0–1. The smaller is the value of ω_fr, the wider and deeper is the concave segment of the pressure derivative curve in crossflow stage VIII, which indicates that more oil accumulates in the dissolved vuggy pore subsystem. In addition, the value of ω_fr has a slight effect on the second transitional flow stage VI.

Fig. 11

Typical curves obtained by PTA with different values of ω_fr and ω_vr

Note that the storage ratio of natural fractures (ω_fr) has a reciprocal relationship with the storage ratio of vuggy pores (ω_vr), which can be expressed as ω_fr + ω_vr = 1. Therefore, the effect of the storage ratio of vuggy pores on the behavior of typical well testing curves is opposite to that of the storage ratio of natural fractures, and hence we will not analyze it in detail. In particular, when ω_fr = 1, the model of dual-porosity media in the outer region is reduced to the model of a homogeneous reservoir.

5.5 Effect of crossflow coefficient

Figure 12 illustrates the influence of differences in the crossflow coefficient (λ) on the typical well testing curves obtained using the proposed model. The values of the natural crossflow coefficient and other relevant parameters are shown in Fig. 11. It can be seen from the characteristic curves that the crossflow coefficient mainly affects the stage of interporosity flow from the vuggy pore subsystem to the natural fracture subsystem. The larger is the crossflow coefficient, the earlier is the time at which interporosity flow of oil occurs. The crossflow coefficient only influences the initial time, but not the oil flow rate, of interporosity flow, which is different from the case of the storage ratios.

Fig. 12

Typical curves obtained by PTA with different values of λ

6 Field application

To demonstrate the application of the proposed model, an oil production well in the Tahe oilfield was selected for analysis. The drilling records, core analysis, and geological data for the sample well indicate that the reservoir is a typical fracture–cavity carbonate reservoir. Figure 13 shows the seismic response of the sample well. There is a large-scale karst cave near the well. The reservoir was reformed by acid fracturing with a total volume of fracturing fluid of 2589 m³. A pressure drop test was conducted for the sample well after fracturing fluid flowback was completed. Before the test, the bottomhole pressure was stabilized at 87.80 MPa, and the oil production rate was 49.8 m³/day. In this case, we assumed that the total compressibility was equal to that of acid fracturing cracks, the karst cave, natural fractures, and dissolved vuggy pores, i.e., C_t = C_frt = C_vrt = C_ct = C_ft. Table 2 lists the basic reservoir properties of the sample well.

Fig. 13

Seismic response of the sample well

Table 2 Reservoir properties of the sample well

Figures 14, 15 and 16 present the results of fitting a log–log typical curve, a semilog pressure drop curve, and a pressure history curve to the measured pressure data using the proposed model. Because the duration of the pressure drop test was insufficient, there is only one concave segment in the pressure derivative curve fitted to the field data, which is presented in Fig. 15. The log–log typical well testing curve was fitted closely in all flow stages, especially in the stage of linear flow in the acid fracturing cracks. In addition, both the pressure history curve and the semiparametric curve match the field data very well. The physical parameters of the reservoir can be calculated by using the proposed analytical model and are presented in Table 3. According to the seismic data, the estimated volume of the large karst cave is between 20,000 and 40,000 m³, which is consistent with the result of the interpretation 30,997.6 m³. The well test analysis shows that the acid fracturing cracks of the example well directly connect to the large-scale karst cave, allowing the crude oil in this cave to be effectively extracted. This is an important guarantee for the high oil production of this well, and also indicates that the acid fracturing effect is significant. It is important to point out that in this particular case study does not reflect the dual porosity flow characteristics in the surrounding area of the cave, that is, the second concave shape does not appear in the pressure derivative curve because of the short testing time. It can be observed from this case study that the proposed model can simulate the problem of complex transient flow for fracturing wells in fracture–cavity carbonate reservoirs. The matches between the field data and the typical curves are highly satisfactory, and hence we can calculate the most significant parameters, such as the cave volume.

Fig. 14

Semilog fitted curve for pressure drop in sample well

Fig. 15

Fitted curves for pressure and pressure derivative in sample well

Fig. 16

Fitted curve for pressure history of sample well

Table 3 Results of the interpretation

7 Conclusions

In this study a PTA model was established for fracturing wells in fracture–cavity carbonate reservoirs. On the basis of the results presented in this paper, the main conclusions are summarized as follows:

• (1) A novel well testing model for fracturing wells in fracture–cavity reservoirs was established. The well is connected to a large karst cave via fracturing cracks. An area of radial oil drainage is formed with the cave as its center, and the area outside the cave is a dual-porosity region comprising natural fractures and dissolved vuggy pores.

• (2) The typical well testing curves for the pressure and pressure derivative were plotted and analyzed in detail. Oil flow in the proposed model can be divided into ten stages, and two characteristic concave segments can be observed in the pressure derivative curve. In particular, the curves for the pressure and pressure derivative are characterized by parallel lines with a slope of 0.5 in the stage of flow in fracturing cracks. The stage of cave storage is similar to the stage of wellbore storage, in which the slope of the pressure derivative curve is equal to 1.

• (3) For an analysis of its validity, the proposed model was reduced to a single fracture–cavity model and a model of a well drilled into a karst cave. The results are consistent with those of the models established by Xing et al. (2018) and Li et al. (2020).

• (4) The influences of key parameters on the behavior of the typical curve were analyzed, especially those of parameters related to pressure fractures and karst caves. It can be concluded that the longer are the fracturing cracks, the longer is the duration of flow stage III. With an increase in the cave radius, the first concave segment of the pressure derivative curve becomes deeper.

• (5) As a field application, actual pressure drop data for a sample well in the Tahe oilfield were analyzed. The results of fitting the pressure and its derivative were satisfactory. According to the results of our interpretation, the fracture length is 52.4 m, and the cave volume is 30,997.6 m³, which are consistent with geological data. These results indicate that the proposed model is practical and suitable for PTA analysis.

In this model, we focus on the scenario of a single acid fracturing crack. The proposed model has the potential to be expanded to a more complex model of multiple fractures. In the future, we will further investigate the flow behavior with regard to complex flow in multistage fracturing cracks in fracture–cavity reservoirs.

Appendix 1: Solution of the mathematical model

In this section, a detailed derivation of the solution of the mathematical model in Laplace space is provided, and the expression for the solution is given. Equations (19)–(27) represent the mathematical model in Laplace space. We can substitute Eq. (20) into Eq. (19) to obtain:

$$ \frac{{\partial^{2} \overline{p}_{frD} }}{{\partial r_{D}^{2} }} + \frac{1}{{r_{D} }}\frac{{\partial \overline{p}_{frD} }}{{\partial r_{D} }} = M_{D} sf(s)\overline{p}_{frD} $$

(33)

where f(s) is the characteristic function:

$$ f(s) = \frac{\lambda + \omega (1 - \omega )s}{{\lambda + (1 - \omega )s}} $$

(34)

To simplify the equation, we introduce the following intermediate variables:

$$ \sigma_{0} = \sqrt {M_{D} sf(s)} $$

(35)

$$ \sigma_{1} = \sqrt s $$

(36)

$$ \zeta_{1} = r_{cD}^{2} h_{D} \eta_{1} $$

(37)

$$ \zeta_{2} = r_{cD}^{{}} h_{D} \eta_{2} $$

(38)

The general solution of Eq. (28) in Laplace space is:

$$ \overline{p}_{frD} = A_{0} I_{0} (r_{D} \sigma_{0} ) + B_{0} K_{0} (r_{D} \sigma_{0} ) $$

(39)

The derivation of Eq. (39) gives:

$$ \frac{{d\overline{p}_{frD} }}{{dr_{D} }} = A_{0} \sigma_{0} I_{1} (r_{D} \sigma_{0} ) - B_{0} \sigma_{0} K_{1} (r_{D} \sigma_{0} ) $$

(40)

The substitution of Eq. (39) into Eq. (26) gives:

$$ A_{0} I_{0} (r_{vD} \sigma_{0} ) + B_{0} K_{0} (r_{vD} \sigma_{0} ) = \overline{p}_{cD} $$

(41)

The substitution of Eqs. (39) and (40) into Eqs. (21)–(23) gives:

$$ A_{0} I_{0} (\infty ) + B_{0} K_{0} (\infty ) = 0\quad {\text{for}}\;{\text{the}}\;{\text{infinite}}\;{\text{reservoir}} $$

(42)

$$ A_{0} \sigma_{0} I_{1} (r_{eD} \sigma_{0} ) - B_{0} \sigma_{0} K_{1} (r_{eD} \sigma_{0} ) = 0\quad {\text{for}}\;{\text{the}}\;{\text{closed}}\;{\text{boundary}} $$

(43)

$$ A_{0} I_{0} (r_{{{\text{e}}D}} \sigma_{0} ) + B_{0} K_{0} (r_{eD} \sigma_{0} ) = 0\quad {\text{for}}\;{\text{the}}\;{\text{constant - pressure}}\;{\text{boundary}} $$

(44)

The general solution of Eq. (25) in Laplace space is:

$$ \overline{p}_{fD} = A_{1} e^{{\sigma_{1} x_{D} }} + B_{1} e^{{ - \sigma_{1} x_{D} }} $$

(45)

The derivation of Eq. (45) gives:

$$ \frac{{d\overline{p}_{fD} }}{{dx_{D} }} = \sigma_{1} A_{1} e^{{\sigma_{1} x_{D} }} - \sigma_{1} B_{1} e^{{ - \sigma_{1} x_{D} }} $$

(46)

The substitution of Eq. (46) into Eq. (26) gives:

$$ A_{fD} (\sigma_{1} A_{1} e^{{\sigma_{1} }} - \sigma_{1} B_{1} e^{{ - \sigma_{1} }} ) = - \frac{1}{s} $$

(47)

The substitution of Eq. (46) into Eq. (27) gives:

$$ A_{1} e^{{\sigma_{1} L_{fD} }} + B_{1} e^{{\sigma_{1} L_{fD} }} = \overline{p}_{cD} $$

(48)

Finally, the substitution of Eqs. (40) and (47) into Eq. (28) gives:

$$ - A_{fD} (\sigma_{1} A_{1} e^{{\sigma_{1} L_{fD} }} - \sigma_{1} B_{1} e^{{ - \sigma_{1} L_{fD} }} ) = \zeta_{1} s\overline{p}_{cD} - \zeta_{2} (A_{0} \sigma_{0} I_{1} (r_{cD} \sigma_{0} ) - B_{0} \sigma_{0} K_{1} (r_{cD} \sigma_{0} )) $$

(49)

Our mathematical model has five linear equations, namely, Eqs. (41), (47), (48), (49), and any of the external boundary equations, i.e., (42), (43), or (44). In addition, we need to solve five undetermined parameters, namely, A₀, B₀, A₁, B₁, and p_vD. Therefore, the solutions of the model in Laplace space can be obtained by using linear algebra. The solution for the bottomhole pressure is only related to the parameters A₁ and B₁, and therefore only the expressions for A₁ and B₁ are given in this paper. To simplify the formula, the following intermediate variable parameters are introduced:

$$ \begin{aligned} a_{1} & = \left( {s\zeta_{1} - A_{fD} \sigma_{1} } \right)K_{0} (r_{cD} \sigma_{0} ) + \zeta_{2} \sigma_{0} K_{1} (r_{cD} \sigma_{0} ) \\ a_{2} & = s\zeta_{1} K_{0} (r_{cD} \sigma_{0} ) + \zeta_{2} \sigma_{0} K_{1} (r_{cD} \sigma_{0} ) \\ a_{3} & = \left( {s\zeta_{1} + A_{fD} \sigma_{1} } \right)K_{0} (r_{cD} \sigma_{0} ) + \zeta_{2} \sigma_{0} K_{1} (r_{cD} \sigma_{0} ) \\ a_{4} & = \sinh (\sigma_{1} - L_{fD} \sigma_{1} ) \\ a_{5} & = \cosh (\sigma_{1} - L_{fD} \sigma_{1} ) \\ a_{6} & = A_{fD} \sigma_{1} K_{0} (r_{cD} \sigma_{0} ) \\ a_{7} & = {\text{e}}^{{ - L_{fD} \sigma_{1} }} \\ a_{8} & = A_{fD} s\sigma_{1} \\ a_{9} & = {\text{e}}^{{\sigma_{1} - 2L_{fD} \sigma_{1} }} \\ a_{10} & = A_{fD} \sigma_{1} \left[ {I_{1} (r_{eD} \sigma_{0} )K_{0} (r_{cD} \sigma_{0} ) + I_{0} (r_{cD} \sigma_{0} )K_{1} (r_{eD} \sigma_{0} )} \right] \\ a_{11} & = \left[ {\left( {s\zeta_{1} - A_{fD} \sigma_{1} } \right)I_{0} (r_{cD} \sigma_{0} ) - \zeta_{2} \sigma_{0} I_{1} (r_{{{\text{c}}D}} \sigma_{0} )} \right]K_{1} (r_{eD} \sigma_{0} ) \\ a_{12} & = \left[ {s\zeta_{1} I_{0} (r_{cD} \sigma_{0} ) - \zeta_{2} \sigma_{0} I_{1} (r_{cD} \sigma_{0} )} \right]K_{1} (r_{eD} \sigma_{0} ) \\ a_{13} & = \left[ {s\zeta_{1} K_{0} (r_{cD} \sigma_{0} ) + \zeta_{2} \sigma_{0} K_{1} (r_{cD} \sigma_{0} )} \right] \\ a_{14} & = \left[ {\left( {s\zeta_{1} + A_{fD} \sigma_{1} } \right)I_{0} (r_{cD} \sigma_{0} ) - \zeta_{2} \sigma_{0} I_{1} (r_{cD} \sigma_{0} )} \right]K_{1} (r_{eD} \sigma_{0} ) \\ a_{15} & = I_{1} (r_{eD} \sigma_{0} ) \\ a_{16} & = {\text{e}}^{{L_{fD} \sigma_{1} }} \\ a_{17} & = \left[ {\left( {s\zeta_{1} - A_{fD} \sigma_{1} } \right)I_{0} (r_{cD} \sigma_{0} ) - \zeta_{2} \sigma_{0} I_{1} (r_{cD} \sigma_{0} )} \right]K_{0} (r_{eD} \sigma_{0} ) \\ a_{18} & = \left[ { - s\zeta_{1} I_{0} (r_{cD} \sigma_{0} ) + \zeta_{2} \sigma_{0} I_{1} (r_{cD} \sigma_{0} )} \right]K_{0} (r_{eD} \sigma_{0} ) \\ a_{19} & = I_{0} (r_{eD} \sigma_{0} ) \\ a_{20} & = A_{fD} \sigma_{1} \left[ { - I_{0} (r_{eD} \sigma_{0} )K_{0} (r_{cD} \sigma_{0} ) + I_{0} (r_{cD} \sigma_{0} )K_{0} (r_{eD} \sigma_{0} )} \right] \\ a_{21} & = \left[ {\left( {s\zeta_{1} + A_{fD} \sigma_{1} } \right)K_{0} (r_{cD} \sigma_{0} ) + \zeta_{2} \sigma_{0} K_{1} (r_{cD} \sigma_{0} )} \right] \\ \end{aligned} $$

(50)

The expressions for A₁ and B₁ under different external boundary conditions can be written as follows:

For the infinite reservoir:

$$ \left\{ {\begin{array}{*{20}l} {A_{1} = \frac{{a_{1} a_{7} }}{{2a_{8} ( - a_{2} a_{5} + a_{6} a_{4} )}}} \hfill \\ {B_{1} = \frac{1}{{a_{8} {\text{e}}^{{ - \sigma_{1} }} + \frac{{a_{9} a_{1} a_{8} }}{{a_{3} }}}}} \hfill \\ \end{array} } \right. $$

(51)

For the closed boundary:

$$ \left\{ {\begin{array}{*{20}l} {A_{1} = \frac{{a_{7} (a_{15} a_{1} + a_{11} )}}{{2a_{8} [ - (a_{13} a_{15} + a_{12} )a_{5} + a_{10} a_{4} ]}}} \hfill \\ {B_{1} = \frac{{a_{16} (a_{15} a_{3} + a_{14} )}}{{2a_{8} [(a_{13} a_{15} + a_{12} )a_{5} - a_{10} a_{4} ]}}} \hfill \\ \end{array} } \right. $$

(52)

For the constant-pressure boundary:

$$ \left\{ {\begin{array}{*{20}l} {A_{1} = \frac{{a_{7} (a_{17} - a_{19} a_{1} )}}{{2a_{8} [(a_{18} + a_{19} a_{13} )a_{5} + a_{20} a_{4} ]}}} \hfill \\ {B_{1} = \frac{{a_{16} ( - a_{17} + a_{19} a_{21} )}}{{2a_{8} [(a_{18} + a_{19} a_{13} )a_{5} + a_{20} a_{4} ]}}} \hfill \\ \end{array} } \right. $$

(53)

When x_D = r_wD = 1, the bottomhole pressure can be written as:

$$ \overline{p}_{sD} = A_{1} e^{\sqrt s } + B_{1} e^{ - \sqrt s } $$

(54)