Dual-Porosity Dual-Permeability Rate Transient Analysis for Horizontal Wells with Nonuniform and Asymmetric Hydraulic Fractures

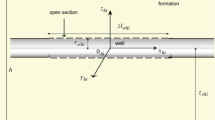
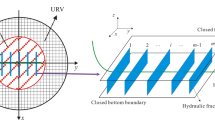
Abstract

Microseismic monitoring in the field has widely shown nonuniformity and asymmetry of hydraulic fractures resulted from multi-stage hydraulic fracturing operations. Considering these influential features of the hydraulic fractures, this paper presents semi-analytical solutions for the wellbore pressure (oil well) and pseudo-pressure (gas well) during production from multi-fractured horizontal wells (MFHW). The solutions further account for bounded and naturally fractured rock formations, recovering existing dual-porosity dual-permeability solutions for a vertical wellbore with one single hydraulic fracture and single-porosity solutions for MFHW. Instead of using the common and simple Warren and Root model, which neglects fluid flow in rock matrix, we adopt the Barenblatt model, which considers fluid flow in both rock matrix and natural fractures. We introduce a permeability ratio, ${k}_{D}$, and show that Warren and Root model becomes problematic when ${k}_{D}$ is larger than 0.05. Comparison analysis shows that the nonuniformity of the hydraulic fracture length distributed along the horizontal wellbore, the nonuniformity of the fracture height, and their asymmetry could have a bigger role than the spacing in the rate transient analysis. For the cases with symmetric and uniform hydraulic fractures, analytical expressions are derived for the classical + 1/2, 0, and + 1 slopes with six characteristic times related to the flow regimes. The application of the semi-analytical solutions to rate transient analysis is demonstrated through five field case studies, consisting of two horizontal and three vertical wells.

Appendices

Appendix 1: Definitions of the Dimensionless Variables

The dimensionless variables are defined by

$$\begin{array}{c}{p}_{D}^{I}=\frac{2\pi {k}^{II}h{p}^{I}}{\mu q}.\end{array}$$

(26)

$$\begin{array}{c}{p}_{D}^{II}=\frac{2\pi {k}^{II}h{p}^{II}}{\mu q}.\end{array}$$

(27)

$$\begin{array}{c}{r}_{D}=\frac{r}{{r}_{e}}.\end{array}$$

(28)

$$\begin{array}{c}{t}_{D}=\frac{{k}^{II}t}{\mu \left({\omega }^{I}+{\omega }^{II}\right){r}_{e}^{2}}.\end{array}$$

(29)

$$\begin{array}{c}\omega =\frac{{\omega }^{I}}{{\omega }^{I}+{\omega }^{II}}.\end{array}$$

(30)

$$\begin{array}{c}{k}_{D}=\frac{{k}^{I}}{{k}^{II}}.\end{array}$$

(31)

$$\begin{array}{c}{\lambda }_{D}=\frac{\mu {r}_{e}^{2}\lambda }{{k}^{II}},\end{array}$$

(32)

where $q$ is the production rate whose dimensionless form is defined by

$$\begin{array}{c}{q}_{D}=\frac{q}{{q}_{sc}},\end{array}$$

(33)

where ${q}_{sc}$ is the production rate at the standard conditions.

Appendix 2: Dual-Porosity Dual-Permeability Semi-analytical Solutions for Rate Transient Analysis for Nonuniform and Asymmetric Hydraulic Fractures

2.1 Dual-Porosity Dual-Permeability Analytical Solution for MFHW

In this section, the point source and line source solutions are derived. As we know, the use of point source and line source is not new and dates back to (Ozkan and Raghavan 1991). However, the dual-porosity dual-permeability semi-analytical solutions for the MFHW together with the analytical expressions for the slopes and time markers presented in this paper are brand new.

Equation 1 provides the governing equations of pore pressure for oil wells. For gas wells, Al-Hussainy et al. (Al-Hussainy et al. 1966) introduced the concept of pseudo-pressure, $m(p)$, defined by:

$$\begin{array}{c}m\left(p\right)=2{\int }_{{p}_{0}}^{p}\frac{p}{\mu Z}dp,\end{array}$$

(34)

where Z is the gas compressibility factor. They showed that the governing equations of the pseudo-pressure for gas wells have the same form with the ones for oil wells. As a result, the solutions of pore pressure for oil well and pseudo-pressure for gas well take the same form. Without confusion, Eqs. (3) and (4) are re-written as follows,

$$\begin{array}{c}\omega \frac{\partial {f}_{D}^{I}}{\partial {t}_{D}}={k}_{D}\left(\frac{\partial {f}_{D}^{I}}{\partial {r}_{D}^{2}}+\frac{1}{{r}_{D}}\frac{\partial {f}_{D}^{I}}{\partial {r}_{D}}\right)+{\lambda }_{D}\left({f}_{D}^{II}-{f}_{D}^{I}\right),\end{array}$$

(35)

$$\begin{array}{c}\left(1-\omega \right)\frac{\partial {f}_{D}^{II}}{\partial {t}_{D}}=\frac{\partial {f}_{D}^{II}}{\partial {r}_{D}^{2}}+\frac{1}{{r}_{D}}\frac{\partial {f}_{D}^{II}}{\partial {r}_{D}}-{\lambda }_{D}\left({f}_{D}^{II}-{f}_{D}^{I}\right),\end{array}$$

(36)

where the two variables ${f}_{D}^{I}$ and ${f}_{D}^{II}$ stand for ${p}_{D}^{I}$ and ${p}_{D}^{II}$, or ${m}_{D}\left({p}^{I}\right)$ and ${m}_{D}\left({p}^{II}\right)$, respectively. The dimensionless pseudo-pressure, ${m}_{D}(p)$, is defined by,

$$\begin{array}{c}{m}_{D}\left(p\right)=\frac{\pi {k}^{II}\mathrm{hZm}(p)}{\mathrm{Bpq}},\end{array}$$

(37)

where $B \left(=\frac{T{p}_{\mathrm{sc}}Z}{{T}_{\mathrm{sc}}p}\right)$ is the gas volume factor, ${p}_{\mathrm{sc}}$ and ${T}_{\mathrm{sc}}$ are the pressure and temperature at standard conditions.

Applying Laplace transform to Eqs. (35) and (36), considering Eq. (5), and rearranging the equation, we have:

$$\begin{array}{c}{D}_{D}^{-1}\left(s{A}_{D}-{\Gamma }_{D}\right)\left[\begin{array}{c}{\tilde{f }}_{D}^{I}\\ {\tilde{f }}_{D}^{II}\end{array}\right]={\nabla }_{D}^{2}\left[\begin{array}{c}{\tilde{f }}_{D}^{I}\\ {\tilde{f }}_{D}^{II}\end{array}\right],\end{array}$$

(38)

where $\sim$ stands for the Laplace transform, ${\nabla }_{D}^{2}=\frac{{d}^{2}}{d{r}_{D}^{2}}+\frac{1}{{r}_{D}}\frac{d}{d{r}_{D}}$, and

$$\begin{array}{c}{A}_{D}=\left[\begin{array}{cc}\omega & 0\\ 0& 1-\omega \end{array}\right];\;{D}_{D}=\left[\begin{array}{cc}{k}_{D}& 0\\ 0& 1\end{array}\right];\\ {\Gamma }_{D}={\lambda }_{D}\left[\begin{array}{cc}-1& 1\\ 1& -1\end{array}\right].\end{array}$$

(39)

Solutions of Eq. (38) can be derived using the decoupled method given by Farlow (Farlow 1993). To begin with, we introduce a new matrix, $P$, which is to be determined, and two variables, ${\tilde{g }}_{D}^{I}$ and ${\tilde{g }}_{D}^{II}$, such that,

$$\begin{array}{c}\left[\begin{array}{c}{\tilde{f }}_{D}^{I}\\ {\tilde{f }}_{D}^{II}\end{array}\right]=P\left[\begin{array}{c}{\tilde{g }}_{D}^{I}\\ {\tilde{g }}_{D}^{II}\end{array}\right].\end{array}$$

(40)

Substitution of Eq. (40) into Eq. (38) gives,

$$\begin{array}{c}{D}_{D}^{-1}\left(s{A}_{D}-{\Gamma }_{D}\right)P\left[\begin{array}{c}{\tilde{g }}_{D}^{I}\\ {\tilde{g }}_{D}^{II}\end{array}\right]=P{\nabla }_{D}^{2}\left[\begin{array}{c}{\tilde{g }}_{D}^{I}\\ {\tilde{g }}_{D}^{II}\end{array}\right].\end{array}$$

(41)

i.e.,

$$\begin{array}{c}{P}^{-1}{D}_{D}^{-1}\left(s{A}_{D}-{\Gamma }_{D}\right)P\left[\begin{array}{c}{\tilde{g }}_{D}^{I}\\ {\tilde{g }}_{D}^{II}\end{array}\right]={\nabla }_{D}^{2}\left[\begin{array}{c}{\tilde{g }}_{D}^{I}\\ {\tilde{g }}_{D}^{II}\end{array}\right].\end{array}$$

(42)

We choose the matrix $P$ such that the following equation is satisfied:

$$\begin{array}{c}{P}^{-1}{D}^{-1}\left(sA-{\Gamma }_{D}\right)P=\left[\begin{array}{cc}{\lambda }^{I}& 0\\ 0& {\lambda }^{II}\end{array}\right].\end{array}$$

(43)

The matrix $P$ is denoted by

$$\begin{array}{c}P=\left[\begin{array}{cc}{m}_{11}& {m}_{12}\\ {m}_{21}& {m}_{22}\end{array}\right].\end{array}$$

(44)

Substitution of Eq. (43) into Eq. (42) gives the following two decoupled differential equations:

$$\begin{array}{c}{\lambda }^{I}{\tilde{g }}_{D}^{I}={\nabla }_{D}^{2}{\tilde{g }}_{D}^{I}.\end{array}$$

(45)

$$\begin{array}{c}{\lambda }^{II}{\tilde{g }}_{D}^{II}={\nabla }_{D}^{2}{\tilde{g }}_{D}^{II}.\end{array}$$

(46)

For a circularly bounded formation, the general solutions to Eq. (45) are expressed in a linear combination of ${K}_{0}\left(\sqrt{{\lambda }^{I}}{r}_{D}\right)$ and ${I}_{0}\left(\sqrt{{\lambda }^{I}}{r}_{D}\right)$, where ${I}_{0}(x)$ and ${K}_{0}\left(x\right)$ and are the modified Bessel functions of the first and second kind. The general solutions to Eq. (46) are expressed in a linear combination of ${K}_{0}\left(\sqrt{{\lambda }^{II}}{r}_{D}\right)$ and ${I}_{0}\left(\sqrt{{\lambda }^{II}}{r}_{D}\right)$. Further considering Eq. (40), the general solutions to Eq. (38) for a continuous point source with unit intensity take the form

$$\begin{array}{c}{\left[\begin{array}{c}{\tilde{f }}_{D}^{I}\\ {\tilde{f }}_{D}^{II}\end{array}\right]}_{\mathrm{cp}}=P\left[\begin{array}{c}{C}_{11}{K}_{0}\left(\sqrt{{\lambda }^{I}}{r}_{D}\right)+{C}_{12}{I}_{0}\left(\sqrt{{\lambda }^{I}}{r}_{D}\right)\\ {C}_{21}{K}_{0}\left(\sqrt{{\lambda }^{II}}{r}_{D}\right)+{C}_{22}{I}_{0}\left(\sqrt{{\lambda }^{II}}{r}_{D}\right)\end{array}\right],\end{array}$$

(47)

where ${C}_{ij}$ are the coefficients to be determined by boundary conditions.

For the continuous point source solution, we consider that the unit production rate at the point source, ${r}_{D}=0$, is the sum of the production rates from the two porous media, i.e., the following mass conservation equation is satisfied

$$\begin{array}{c}\underset{{r}_{D}\to 0}{\mathrm{lim}}\left({\phi }^{I}{k}_{D}\frac{\partial {\tilde{f }}_{D,\mathrm{cp}}^{I}}{\partial {r}_{D}}+{\phi }^{II}\frac{\partial {\tilde{f }}_{D,\mathrm{cp}}^{II}}{\partial {r}_{D}}\right){r}_{D}=-\frac{1}{s}.\end{array}$$

(48)

Using Eq. (47), the variation of pore pressure at the fracture mouth of the ith hydraulic fracture caused by a continuous line source with a uniform unit intensity along the jth hydraulic fracture can be obtained by integrating the point source solutions along the length, as illustrated in Fig. 32, and expressed as follows,

Fig. 32

source at the jth hydraulic fracture

Illustration of the variation of pore pressure at the fracture mouth of the ith hydraulic fracture caused by a continuous line

$$\begin{array}{c}{\left[\begin{array}{c}{\tilde{f }}_{D}^{I}\\ {\tilde{f }}_{D}^{II}\end{array}\right]}_{\mathrm{cl},ij}=P{\int }_{-{L}_{{eD}_{j1}}}^{{L}_{{eD}_{j2}}}\left[\begin{array}{c}{\tilde{f }}_{{D}_{\mathrm{cp},ij}}^{I}\\ {\tilde{f }}_{{D}_{\mathrm{cp},ij}}^{II}\end{array}\right]d{x}_{D},\end{array}$$

(49)

where

$$\begin{array}{c}{\tilde{f }}_{{D}_{\mathrm{cp},ij}}^{I}={C}_{11}{K}_{0}\left(\sqrt{{\lambda }^{I}}\sqrt{{x}_{D}^{2}+{\Delta }_{{D}_{ij}}^{2}}\right)\\ +{C}_{12}{I}_{0}\left(\sqrt{{\lambda }^{I}}\sqrt{{x}_{D}^{2}+{\Delta }_{{D}_{ij}}^{2}}\right).\end{array}$$

(50)

$$\begin{array}{c}{\tilde{f }}_{{D}_{\mathrm{cp},ij}}^{II}={C}_{21}{K}_{0}\left(\sqrt{{\lambda }^{II}}\sqrt{{x}_{D}^{2}+{\Delta }_{{D}_{ij}}^{2}}\right)\\ +{C}_{22}{I}_{0}\left(\sqrt{{\lambda }^{II}}\sqrt{{x}_{D}^{2}+{\Delta }_{{D}_{ij}}^{2}}\right).\end{array}$$

(51)

The average intensity for the line source from the ${j}^{th}$ hydraulic fracture is calculated to be $\frac{{q}_{{D}_{j}}}{2{h}_{{D}_{j}}{L}_{{\mathrm{eD}}_{j}}}$, where ${h}_{{D}_{j}}\left(=\frac{{h}_{j}}{{r}_{e}}\right)$ is the dimensionless height of the jth hydraulic fracture. Considering that Eq. (49) is for a uniform unit intensity, the variation of pore pressure at the fracture mouth of the ith hydraulic fracture caused by a continuous line source from the jth hydraulic fracture with a uniform intensity of $\frac{{q}_{{D}_{j}}}{2{h}_{{D}_{j}}{L}_{{\mathrm{eD}}_{j}}}$ can be obtained as follows,

$$\begin{array}{c}{\left[\begin{array}{c}{\tilde{f }}_{D}^{I}\\ {\tilde{f }}_{D}^{II}\end{array}\right]}_{ij}=\frac{{q}_{{D}_{j}}}{2{h}_{{D}_{j}}{L}_{{\mathrm{eD}}_{j} }}{\left[\begin{array}{c}{\tilde{f }}_{D}^{I}\\ {\tilde{f }}_{D}^{II}\end{array}\right]}_{cl,ij}.\end{array}$$

(52)

Accounting for the $N$ stages of hydraulic fractures, the variation of pore pressure at the mouth of the jth fracture is expressed as follows,

$$\begin{array}{c}{\left[\begin{array}{c}{\tilde{f }}_{D}^{I}\\ {\tilde{f }}_{D}^{II}\end{array}\right]}_{i}={\sum }_{j=1}^{N}{\left[\begin{array}{c}{\tilde{f }}_{D}^{I}\\ {\tilde{f }}_{D}^{II}\end{array}\right]}_{ij}.\end{array}$$

(53)

At the fracture mouth of each hydraulic fracture, the pore pressure in the primary porosity is equal to that in the secondary porosity. Either of the two can be set as the wellbore pressure at the fracture mouth. Therefore, we can set,

$$\begin{array}{c}{\tilde{f }}_{{\mathrm{wD}}_{i}}={\tilde{f }}_{{D}_{i}}^{II},\end{array}$$

(54)

where ${\tilde{f }}_{w{D}_{i}}$ is the wellbore pressure or pseudo-pressure at the mouth of the ith hydraulic fracture.

In the following paragraphs, the $N+4$ unknown parameters, including four coefficients ${C}_{ij}$ and $N$ unknowns ${q}_{{D}_{i}}$, are to be determined based on the boundary conditions.

Applying the Laplace transform to the boundary conditions, Eqs. (6), (7), (8), and (9), we can see that the boundary conditions in the Laplace domain take the same forms as those in the time domain. These equations together with Eq. (48) generate $N+4$ independent equations which are presented as below.

$$\begin{array}{c}{m}_{11}\sqrt{{\lambda }^{I}}\left[{K}_{1}\left(\sqrt{{\lambda }^{I}}\right){C}_{11}-{I}_{1}\left(\sqrt{{\lambda }^{I}}\right){C}_{12}\right]\\ +{m}_{12}\sqrt{{\lambda }^{II}}\left[{K}_{1}\left(\sqrt{{\lambda }^{II}}\right){C}_{21}-{I}_{1}\left(\sqrt{{\lambda }^{II}}\right){C}_{22}\right]=0.\end{array}$$

(55)

$$\begin{array}{c}{m}_{21}\sqrt{{\lambda }^{I}}\left[{K}_{1}\left(\sqrt{{\lambda }^{I}}\right){C}_{11}-{I}_{1}\left(\sqrt{{\lambda }^{I}}\right){C}_{12}\right]\\ +{m}_{22}\sqrt{{\lambda }^{II}}\left[{K}_{1}\left(\sqrt{{\lambda }^{II}}\right){C}_{21}-{I}_{1}\left(\sqrt{{\lambda }^{II}}\right){C}_{22}\right]=0.\end{array}$$

(56)

$$\begin{array}{c}\left({m}_{11}-{m}_{21}\right){K}_{0}\left(\sqrt{{\lambda }^{I}}{w}_{D}\right){C}_{11}\\ +\left({m}_{11}-{m}_{21}\right){I}_{0}\left(\sqrt{{\lambda }^{I}}{w}_{D}\right){C}_{12}\\ +\left({m}_{12}-{m}_{22}\right){K}_{0}\left(\sqrt{{\lambda }^{II}}{w}_{D}\right){C}_{21}\\ +\left({m}_{12}-{m}_{22}\right){I}_{0}\left(\sqrt{{\lambda }^{II}}{w}_{D}\right){C}_{22}=0.\#\end{array}$$

(57)

For $i=\mathrm{1,2},\cdots ,N-1$

$$\begin{array}{c}{\sum }_{j=1}^{N}\frac{{q}_{{D}_{j}}}{2{h}_{{D}_{j}}{L}_{{\mathrm{eD}}_{j}}}{\int }_{-{L}_{{\mathrm{eD}}_{j1}}}^{{L}_{{\mathrm{eD}}_{j2}}}\left({m}_{21}^{ij}+{m}_{22}^{ij}\right)dx=0.\end{array}$$

(58)

$$\begin{array}{c}{\sum }_{i=1}^{N}{q}_{{D}_{i}}={q}_{D}.\end{array}$$

(59)

$$\begin{array}{c}\left({\phi }^{I}{k}_{D}{m}_{11}+{\phi }^{II}{m}_{21}\right){C}_{11}\\ +\left({\phi }^{I}{k}_{D}{m}_{12}+{\phi }^{II}{m}_{22}\right){C}_{21}=\frac{1}{s}.\end{array}$$

(60)

where

$$\begin{array}{c}{m}_{21}^{ij}={m}_{21}\left[\begin{array}{c}{K}_{0}\left(\sqrt{{\lambda }^{I}}\sqrt{{x}_{D}^{2}+{\Delta }_{{D}_{ij}}^{2}}\right)\\ -{K}_{0}\left(\sqrt{{\lambda }^{I}}\sqrt{{x}_{D}^{2}+{\Delta }_{{D}_{i+1,j}}^{2}}\right)\end{array}\right]{C}_{11}\\ +{m}_{21}\left[\begin{array}{c}{I}_{0}\left(\sqrt{{\lambda }^{I}}\sqrt{{x}_{D}^{2}+{\Delta }_{{D}_{ij}}^{2}}\right)\\ -{I}_{0}\left(\sqrt{{\lambda }^{I}}\sqrt{{x}_{D}^{2}+{\Delta }_{{D}_{i+1,j}}^{2}}\right)\end{array}\right]{C}_{12}.\end{array}$$

(61)

$$\begin{array}{c}{m}_{22}^{ij}={m}_{22}\left[\begin{array}{c}{K}_{0}\left(\sqrt{{\lambda }^{II}}\sqrt{{x}_{D}^{2}+{\Delta }_{{D}_{ij}}^{2}}\right)\\ -{K}_{0}\left(\sqrt{{\lambda }^{II}}\sqrt{{x}_{D}^{2}+{\Delta }_{{D}_{i+1,j}}^{2}}\right)\end{array}\right]{C}_{21}\\ +{m}_{22}\left[\begin{array}{c}{I}_{0}\left(\sqrt{{\lambda }^{II}}\sqrt{{x}_{D}^{2}+{\Delta }_{{D}_{ij}}^{2}}\right)\\ -{I}_{0}\left(\sqrt{{\lambda }^{II}}\sqrt{{x}_{D}^{2}+{\Delta }_{{D}_{i+1,j}}^{2}}\right)\end{array}\right]{C}_{22}.\end{array}$$

(62)

Using the linear algebra algorithm, the above $N+4$ independent equations can be solved to obtain four coefficients, ${C}_{ij}$, and $N$ unknowns, ${q}_{{D}_{i}}$. The solutions are presented in the Laplace domain. We can apply the Stehfest algorithm to obtain the solutions in the time domain.

It is worthwhile to further discuss how the solution couples the local coordinate system with the polar coordinates of the cylindrical reservoir. The radial distance, ${r}_{D}$, in the continuous point source solution presented in Eq. (47) is associated with the local polar coordinates of each individual point source. The horizontal well is assumed to lay at the center of the formation. When applying the no-flow external cylindrical boundary condition to the point source solution, strictly speaking, the radial distance, ${r}_{\mathrm{pD}}$, should be applied to the point source, as illustrated in Fig. 32. Note that this ${r}_{\mathrm{pD}}$ varies along the cylindrical boundary. Considering that the length of hydraulic fractures and that the horizontal well is relatively smaller than the reservoir radius while also avoiding the complexity of mathematical derivation, we reasonably use 1 as the dimensionless radius when applying the no-flow cylindrical boundary conditions, as shown in Eq. (55) and (56).

2.2 Single-Porosity Single-Permeability Semi-analytical Solution for MFHW

The single-porosity single-permeability semi-analytical solution for a MFHW can be obtained from the dual-porosity dual-permeability semi-analytical solution by setting $\omega =0.5$ and ${k}_{D}=1$.

2.3 Dual-Porosity Dual-Permeability Semi-analytical Solution for a Hydraulically Fractured Vertical Well

For a vertical wellbore with one single hydraulic fracture with production rate of${q}_{D}$, the solution of wellbore pressure or pseudo-pressure can be obtained by multiplying Eq. (49) by an intensity factor, $\frac{{q}_{D}}{2{h}_{D}{L}_{\mathrm{eD}}}$, i.e.,

$$\begin{array}{c}{\left[\begin{array}{c}{\tilde{f }}_{D}^{I}\\ {\tilde{f }}_{D}^{II}\end{array}\right]}_{w}=\frac{{q}_{D}}{2{h}_{D}{L}_{\mathrm{eD}}}P{\int }_{-{L}_{\mathrm{eD}1}}^{{L}_{\mathrm{eD}2}}\left[\begin{array}{c}{\tilde{f }}_{D,\mathrm{cp}}^{I}\\ {\tilde{f }}_{D,\mathrm{cp}}^{II}\end{array}\right]d{x}_{D},\end{array}$$

(63)

where

$$\begin{array}{c}{\tilde{f }}_{D,\mathrm{cp}}^{I}={C}_{11}{K}_{0}\left(\sqrt{{\lambda }^{I}}{x}_{D}\right)+{C}_{12}{I}_{0}\left(\sqrt{{\lambda }^{I}}{x}_{D}\right).\end{array}$$

(64)

$$\begin{array}{c}{\tilde{f }}_{D,\mathrm{cp}}^{II}={C}_{21}{K}_{0}\left(\sqrt{{\lambda }^{II}}{x}_{D}\right)+{C}_{22}{I}_{0}\left(\sqrt{{\lambda }^{II}}{x}_{D}\right).\end{array}$$

(65)

The 4 coefficients ${C}_{ij}$ can be determined from Eqs. (55), (56), (57), and (60).

The semi-analytical solutions are expressed in Laplace domain. We use the following Stehfest method to numerically evaluate the solutions in time domain:

$$\begin{array}{c}g\left(t\right)=\frac{\mathrm{ln}2}{t}{\sum }_{k=1}^{M}{h}_{k}\tilde{g }\left(\frac{k\mathrm{ln}2}{t}\right),\end{array}$$

(66)

where $\tilde{g }$ is the Laplace transform of $g$, $M$ is an even positive integer less than or equal to 20, and

$$ \begin{array}{*{20}c} {h_{k} = } \\ {\sum _{{i = \left\lfloor {(k + 1)/2} \right\rfloor }}^{{{\text{min}}(k,\frac{M}{2})}} \frac{{\left( { - 1} \right)^{{k + \frac{M}{2}}} i^{{\frac{M}{2}}} \left( {2i} \right)!}}{{\left( {\frac{M}{2} - i} \right)!i!\left( {i - 1} \right)!\left( {k - i} \right)!(2i - k)}}.} \\ \end{array} $$

(67)

Figure 33 shows that the numerical evaluations of the semi-analytical solution in time domain are identical for three values of M, i.e., 8, 12, and 16. We set M as 8 in this paper.

Fig. 33

Evaluations of the semi-analytical solution in time domain for three values of M