1 Introduction

Mineral resources play an indispensable role in social progress and industrial production, and are an important foundation for economic development (Ali et al. 2017; Yu et al. 2020). With the rapid development of industrialization, the demand for mineral resources has gradually increased (Daw 2017; Guo et al. 2022; Wood 2017). The non-renewability of resources and gradual exhaustion of shallow resources have caused the mining of mineral resources to shift toward deep mining (Li et al. 2017; Liang et al. 2017; Westergård 2018). In China, most mines have shifted to the stage of deep resource mining, and approximately 60 mines have reached the maximum mining depth of more than one kilometer (Mei et al. 2020). In the deep mining stage, roadway engineering is not only responsible for the tasks of mining and transportation, but also contributes to geological exploration and ore prospecting tasks. Compared with a shallow rock mass, the mechanical properties of deep rock may change from rigid to flexible under the environment of high in-situ stress and high temperature. In addition, deep rock masses can exhibit obvious rheological phenomena (Kang et al. 2015; Wang et al. 2017; Zhang et al. 2020), which are particularly significant in soft rock and broken zones (Sun et al. 2020b; Yao et al. 2019). The rheological properties of the surrounding rock cause the deformation of the roadway to increase gradually over time. The surrounding rock can be destroyed by the release of stored plastic strain energy, resulting in failure of the roadway support, which will make it difficult to maintain the normal production function of the roadway (Tan et al. 2017). Moreover, a large number of repaired roadway support projects will inevitably influence the mining production and increase the economic expenditure (Kang et al. 2015; Wang et al. 2000; Yang et al. 2017), which will have unfavorable impacts on the economy of the mine.

The roadway support also affects the deformation and stability of the roadway. Effective roadway support and combined support methods play very important roles in the control of roadway deformation. However, the roadway may undergo large deformation owing to the rheological phenomena of the surrounding rock under high in-situ stress (Gao et al. 2018; Meng et al. 2017; Shen 2014; Zhang et al. 2020); thus, greater resistance should be provided to ensure the normal function of the roadway (Lu and Jiang 1998). Previous studies have shown that it is very uneconomical to simply increase the support resistance to control the deformation of the roadway, and roadway support should fully utilize the self-supporting role of the surrounding rock (Huang and Zheng 2016; Nagy 2018). In roadway support engineering, the strength of the surrounding rock plays a major role in the choice of support pattern. A single support form or a combined pattern of bolt + steel mesh and sprayed concrete are commonly adopted in strata with higher surrounding rock strengths, whereas support forms such as steel arches, poured concrete, or grouting may be adopted in fracture zones and weak surrounding rock (Li et al. 2020; Srivastava and Singh 2015; Yang et al. 2017).

Roadway support is generally carried out immediately after excavation of the working face. For roadways with obvious rheological phenomena, it is usually difficult to meet the requirements of stability through primary support measures, and thus secondary support is required after the primary support and violent release of the plastic strain energy of the surrounding rock (Malan 2002; Yu et al. 2019, 2018). If the secondary support is installed too early, the plastic strain energy of the surrounding rock cannot be fully released, and the surrounding stress can be shifted to the support body, resulting in damage to the support. However, the self-support capacity of the surrounding rock may decrease if the secondary support is installed too late, possibly because the surrounding rock has been destroyed and crushed under the effect of high in-situ stress. Therefore, greater support resistance must be provided to maintain the stability of the roadway (Cong et al. 2020; Luo et al. 2017; Sun et al. 2021).

Generally, the failure of roadway support can be attributed to unreasonable support strengths and support times. The primary support should be flexible to release the pressure of the surrounding rock effectively, whereas the secondary support should be rigid to control the surface deformation of the surrounding rock of the roadway. Previous studies have shown that the determination of the secondary support time is mainly based on deformation monitoring of the surrounding rock (Luo et al. 2017; Öge 2020). When the surrounding rock deformation is in a stable state or the deformation rate is lower than a certain value, secondary support will be carried out. However, deformation monitoring of the surrounding rock indicates that it usually takes several months for the surrounding rock deformation to stabilize, which is very unfavorable and may pose significant risks for safe production. Considering the obvious rheological phenomena of roadway surrounding rock under the action of high in-situ stress in the deep mining stage, its rheological rate is also different as the mining depth increases. Therefore, by carrying out the creep tests of surrounding rock under different in-situ stress conditions, the corresponding stable creep rate can be obtained, then according to the radial displacement change of the surrounding rock of the roadway, the reasonable time of secondary support can be determined. This will greatly shorten the determination of secondary support time compared to the field deformation monitoring. In addition, optimizing the combined support parameters will further reduce the support costs and avoid the large-scale maintenance of the support projects. This will be beneficial to ensure the normal operation of daily mine production and to minimize support costs.

This study focuses on a deep mining superseding roadway with a maximum mining depth of approximately 1500 m from the surface at the Huize lead–zinc mine in Yunnan province, China. First, the effects of the existing support for the deep mine roadway are investigated, and then a rheological test of the surrounding rock is conducted to determine the secondary support time. Finally, numerical simulations and orthogonal tests are applied to optimize the support parameters. The research results can provide a technical reference for deep roadway support.

2 Project site investigation and preliminary design of secondary support

2.1 Project status

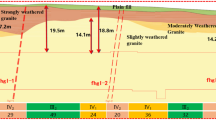
The mine is located in Huize County, Yunnan Province, China. The construction roadway is located at a depth of approximately 1500 m in the mine and is considered a deep resource replacement project; the detailed strata histogram is shown in Fig. 1. The main exposed surrounding rock of the roadway is Baizuo Fm, which has a lithology of grayish white, beige, and flesh-red coarse crystalline dolomite. This is partially mingled with light gray limestone and dolomitic limestone, while a few parts consisting of Datang Fm, which has a lithology of gray or dark gray cryptocrystalline limestone, flint bands, and clumps, are seen locally. The field measurements show that the maximum and minimum horizontal principal stresses and vertical principal stress of the roadway are 41.5 MPa, 15.2 MPa, and 20.8 MPa, respectively. The angle between the roadway trend and direction of the maximum horizontal principal stress is 85°.

Fig. 1
figure 1

Strata histogram and geological description of the roadway surrounding rock

Full size image

The existing support methods are mainly bolt + steel mesh and sprayed concrete applied as a single support form or combined pattern, while support forms of steel arches or poured concrete may be adopted in fracture zones or areas of weak surrounding rock. Figure 2a shows the non-standardized construction of bolts, e.g., bolts that are not installed perpendicular to the surface of the roadway (an overly large angle between the bolts and the normal direction of the roadway surface, which results in exposed lengths of the bolts). This will reduce the effective anchoring length of the bolt, resulting in a reduction in the suspension effect of the bolt on the rock, which adversely affects the formation of an effective combined arch. The existing support scheme does not consider the floor support, which will cause pressure to be released along the floor and bottom angles of both sides after roadway excavation, resulting in floor heave and deformation of the bottom angle on both sides. This is particularly obvious in areas of water accumulation, as shown in Fig. 2b. Figure 2c shows that the presence of water corrodes the bolts exposed to air, which reduces the adhesion and friction between the bolts and the surrounding rock, resulting in roadway shrinkage (two-sided shrinkage). The surrounding rock exhibiting sidewall spalling is due to the redistribution of the in-situ stress, as shown in Fig. 2d. Owing to the weakening effect of water on the strength of the surrounding rock and the influence of swelling deformation, large-scale spalling occurs in local areas of the weak surrounding rock, resulting in collapses soon after excavation of the roadway (Fig. 2e). In areas of structurally fractured and weak surrounding rock, the low self-supporting ability results in the surrounding rock undergoing a larger deformation under the action of high in-situ stress, causing fracture of the back slab of the roof and sidewall steel arch, as shown in Fig. 2f.

Fig. 2
figure 2

Present situation and failure modes of the roadway support

Full size image

2.2 Preliminary design of secondary support

The main function of the support is to improve the stress state of the plastic fracture zone of the surrounding rock, control the roadway deformation and plastic fracture zone size, and ensure the functioning of the roadway over a reasonable service period (Yu et al. 2020). Previous studies have shown that a self-stable equilibrium arch can be formed owing to the effect of squeezing stress in the fracture zone of the surrounding rock, and roadway support should fully consider the self-stabilization balance time of the surrounding rock collapse (Cong et al. 2020; Yu et al. 2015; Zhou et al. 2014).

Based on the physical and mechanical properties of the exposed surrounding rock, the investigation of the roadway support situation, and the experience of support technology and support materials supply in early engineering practice, the combined support method of bolt + steel mesh + sprayed concrete continues to be recommended for use as secondary support for roadways. The secondary support design mainly includes the determination of support timing and the optimization of support parameters, i.e., the selection of the appropriate sprayed concrete thickness, bolt lengths, bolt row spacing, and bolt diameters.

3 Analysis of the secondary support time

Owing to the obvious rheology of the surrounding rock of the roadway under the effect of high in-situ stress, it is difficult to realize complete release of the plastic strain energy in the plastic zone with a premature secondary support time. However, with an excessively long secondary support time, the self-support capacity of the surrounding rock will be reduced, and greater surrounding rock stress will be exerted on the supporting body. Therefore, it is necessary to consider the coupling between the secondary support time and the self-support strength of the surrounding rock comprehensively to select a reasonable secondary support time (Shi et al. 2020; Wang et al. 2021). It is generally believed that secondary support should be applied when the deformation of the roadway is in a stable stage. Considering the obvious rheological effects exhibited by the surrounding rock of the deep roadway under the action of high in-situ stress, in this section, the strain rate of the exposed surrounding rock of the roadway in the stable creep stage was investigated using creep tests. Then, combined with the changes in the radial displacement of the roadway, the appropriate secondary support time was determined.

3.1 Creep test materials, equipment, and process

Rock materials for testing were obtained from the exposed surrounding rock of the Baizuo Fm after excavation of the roadway and were processed into standard rock specimens with dimensions of Φ50 mm × 100 mm in the laboratory. The processing accuracy complied with the “Engineering Rock Mass Test Method Standard” (National Standard of the People's Republic of China GB/T 50266-2013). Abnormal specimens were removed using wave velocity tests. An MTS 815 rock mechanics testing machine was used for the creep experiments, as shown in Fig. 3, and the creep test loads were 30, 40, 50, 55, and 60 MPa. A loading rate of 0.5 MPa/s was applied to reach the preset value, after which the load was maintained. According to relevant specifications and the deformation monitoring results of roadway convergence reported in previous investigations (Cong et al. 2020; Sun et al. 2020a), the loading time was designed as 5 h or when the specimen reached the stable stage of the creep test, after which the next level of loading was applied.

Fig. 3
figure 3

MTS 815 rock mechanics testing machine

Full size image

3.2 Results of the creep tests

The creep test curves with different loads are shown in Fig. 4. Under a load of 60 MPa, the specimen failed after 1 h, and the curve exhibits three obvious stages: the initial creep stage, stable creep stage, and accelerating creep stage. Under the other loads, after an obvious instantaneous elastic deformation, the creep test curves gradually enter the stable creep stage; as the load increases, the instantaneous elastic deformation increases, and the initial creep stage becomes more obvious.

Fig. 4
figure 4

Creep test curves

Full size image

According to previous studies, the Burgers model can describe rock creep in the initial and stable stages (Huang et al. 2020; Yang et al. 2015; Zhang et al. 2020; Zhao et al. 2018). The Burgers model is shown in Fig. 5.

Fig. 5
figure 5

Burgers creep model

Full size image

The constitutive equation of the Burgers model is:

$$\ddot{\sigma } + \left( {\frac{{E_{2} }}{{\eta_{1} }} + \frac{{E_{2} }}{{\eta_{2} }} + \frac{{E_{1} }}{{\eta_{1} }}} \right)\dot{\sigma } + \frac{{E_{1} E_{2} }}{{\eta_{1} \eta_{2} }}\sigma = E_{2} \ddot{\varepsilon } + \frac{{E_{1} E_{2} }}{{\eta_{1} }}\dot{\varepsilon }.$$
(1)

The creep equation is:

$$\varepsilon = \frac{{\sigma_{0} }}{{E_{2} }} + \frac{{\sigma_{0} }}{{\eta_{2} }}t + \frac{{\sigma_{0} }}{{E_{1} }}\left( {1 - e^{{ - \frac{{E_{1} }}{{\eta_{1} }}t}} } \right).$$
(2)

where η1 and η2 are viscosity parameters, E1 and E2 are the elastic moduli, σ represents the stress, ε is the strain, t is the time, and σ0 is the instantaneous stress.

Equation (2) was used to fit the data in Fig. 4, and the parameters of the Burgers creep model for the Baizuo Fm surrounding rock at different stress levels are listed in Table 1. The fitting accuracy for all stress levels was greater than 0.98, which demonstrates a reasonable choice of the creep model.

Table 1 Creep model parameters
Full size table

3.3 Determination of the secondary support time

A section of the deep roadway was designed for a three-center arch with a height of 2.85 m and a width of 2.80 m. Using the equivalent circle process, the equivalent radius is 1.80 m, as shown in Fig. 6.

Fig. 6
figure 6

Equivalent circle treatment of the roadway section

Full size image

A differential operator is used to transform Eq. (1), yielding the following:

$$\left[ {1 + \left( {\frac{{\eta_{2} }}{{E_{2} }} + \frac{{\eta_{1} }}{{E_{1} }} + \frac{{\eta_{2} }}{{E_{1} }}} \right)D + \left( {\frac{{\eta_{1} \eta_{2} }}{{E_{1} E_{2} }}} \right)D^{2} } \right]\sigma = \left[ {\eta_{2} D + \left( {\frac{{\eta_{1} \eta_{2} }}{{E_{1} }}} \right)D^{2} } \right]\varepsilon ,$$
(3)

where D is the ordinary differential operator with respect to time, t. The meanings of the other symbols are the same as those described above.

Considering the creep damage effect, the creep damage variable, ωp, was introduced to modify the constitutive relationship, and Eq. (3) can be rewritten as follows:

$$\left[ {1 + \left( {\frac{{\eta_{2} }}{{E_{2} }} + \frac{{\eta_{1} }}{{E_{1} }} + \frac{{\eta_{2} }}{{E_{1} }}} \right)D + \left( {\frac{{\eta_{1} \eta_{2} }}{{E_{1} E_{2} }}} \right)D^{2} } \right]\frac{\sigma }{{1 - \omega_{p} }} = \left[ {\eta_{2} D + \left( {\frac{{\eta_{1} \eta_{2} }}{{E_{1} }}} \right)D^{2} } \right]\varepsilon .$$
(4)

Rewriting both sides of Eq. (3) in the form of f(D)σ = g(D)ε, we can obtain the following:

$$\begin{aligned} f(D) & = {{\left[ {1 + \left( {\frac{{\eta_{2} }}{{E_{2} }} + \frac{{\eta_{1} }}{{E_{1} }} + \frac{{\eta_{2} }}{{E_{1} }}} \right)D + \left( {\frac{{\eta_{1} \eta_{2} }}{{E_{1} E_{2} }}} \right)D^{2} } \right]} \mathord{\left/ {\vphantom {{\left[ {1 + \left( {\frac{{\eta_{2} }}{{E_{2} }} + \frac{{\eta_{1} }}{{E_{1} }} + \frac{{\eta_{2} }}{{E_{1} }}} \right)D + \left( {\frac{{\eta_{1} \eta_{2} }}{{E_{1} E_{2} }}} \right)D^{2} } \right]} {(1 - \omega_{p} )}}} \right. \kern-0pt} {(1 - \omega_{p} )}} \\ g(D) & = \eta_{2} D + \left( {\frac{{\eta_{1} \eta_{2} }}{{E_{1} }}} \right)D^{2} . \\ \end{aligned}$$
(5)

The meaning of each symbol in Eq. (5) is the same as described above. Therefore,

$$E = \sigma {/}\varepsilon = g\left( {\text{D}} \right)/f(D).$$
(6)

Many scholars have studied the elastic–plastic deformation of circular tunnels based on the Hoek–Brown criterion and the following equation for the radial displacement of an excavation roadway has been obtained (Carranza-Torres 2004; Sharan 2005, 2008; Zhang et al. 2012):

$$\Delta u = \frac{1 + \mu }{{E\left( {1 - \omega_{p} } \right)}}r_{0} P_{0} ,$$
(7)

where Δu is the surface displacement of the roadway, μ is the Poisson's ratio, P0 is the in-situ stress, r0 is the equivalent circle radius of the roadway, and E represents the elastic modulus of the surrounding rock.

Substituting g(D)/f(D) in place of E and performing the Laplace transform and inverse transform on Eq. (7), we obtain the following:

$$\Delta u(t) = \frac{{r_{0} P_{0} }}{{2E_{2} \left( {1 - \omega_{p} } \right)}}\left\{ {1 + \frac{{E_{2} }}{{\eta_{2} }}t + \frac{{E_{2} }}{{E_{1} }}\left[ {1 - \exp \left( { - \frac{{E_{1} }}{{\eta_{1} }}t} \right)} \right]} \right\}.$$
(8)

Differentiating Eq. (8) with respect to time, t, the expression for the deformation rate, Δ(t), can be obtained as follows:

$$\Delta \dot{u}(t) = \frac{{r_{0} P_{0} }}{{2E_{2} \left( {1 - \omega_{p} } \right)}}\left\{ {\frac{{E_{2} }}{{\eta_{2} }} + \frac{{E_{2} }}{{\eta_{1} }}\left[ {\exp \left( { - \frac{{E_{1} }}{{\eta_{1} }}t} \right)} \right]} \right\},$$
(9)

where \(\Delta \dot{u}(t)\) is the deformation rate of the radial displacement, and the meanings of the other symbols are the same as described above.

Based on research results for the time effect of the damage variable of the Burgers creep model in the literature (Cai and Cao 2016), the creep damage variable can be determined as

$$\omega_{p} = \frac{{E_{2} }}{{E_{2} + E_{1} }}.$$
(10)

Substituting Eq. (10) into Eq. (9), we can obtain the relationship between the time, t, and the creep deformation rate, creep model parameters, in-situ stress, and equivalent circle radius, as follows:

$$t = - \frac{{\eta_{1} }}{{E_{1} }}\ln \left\{ {\left[ {2\Delta \dot{u}(t)\frac{{E_{1} E_{2} }}{{r_{0} P_{0} \left( {E_{2} + E_{1} } \right)}} - \frac{{E_{2} }}{{\eta_{2} }}} \right]\frac{{\eta_{1} }}{{E_{2} }}} \right\}.$$
(11)

The deformation rate of the radial displacement is replaced with the creep deformation rate in the stable creep stage, and the creep model parameters under different stresses are substituted into Eq. (11) to obtain the reasonable secondary support time for the Baizuo Fm surrounding rock under different stress levels, as summarized in Table 2.

Table 2 Secondary support times for the Baizuo Fm surrounding rock
Full size table

The measured maximum horizontal in-situ stress of the roadway is 41.5 MPa. According to Table 2, the stable deformation rate of the Baizuo Fm surrounding rock under this in-situ stress can be approximately regarded as 0.0024 mm/h. Thus, the secondary support time is approximately 170 h after excavation of the roadway.

4 Optimization of the secondary support parameters

4.1 Optimization analysis process

An orthogonal test was adopted to optimize the secondary support parameters. After excavation of the roadway, the stress of the surrounding rock is redistributed (Ma and Wu 2021; Zhao and Zhang 2017). When the stress of the surrounding rock exceeds its own bearing strength, the roadway surrounding rock deforms and expands to the free surface, which manifests as displacement and deformation of the roof, floor, and both sides of the roadway, and a plastic zone is formed inside the surrounding rock (Xie et al. 2019; Zang et al. 2020). Therefore, roof subsidence, floor heave displacement, side displacement, and formation of aplastic zone were selected as the test indicators for the orthogonal tests. According to the previous engineering practice of bolt + steel mesh + spayed concrete roadway support, the thickness of the sprayed concrete layer, bolt length, bolt row spacing, and bolt diameter were selected as the test factors, and five levels were defined for each factor. The factors and levels are listed in Table 3.

Table 3 Factors and levels for the orthogonal test
Full size table

The L25(54) orthogonal table was adopted to determine each factor and level in the table, as summarized in Table 4. The numbers 25, 5 and 4 in L25(54) indicate that there are 25 experiments to be conducted, with 5 different factors being studied, and each factor has 4 levels.

Table 4 Orthogonal design scheme
Full size table

FLAC3D was used to establish the calculation model for numerical simulation of the deformation of the roadway surrounding rock and expansion of the plastic zone. The calculation range of the numerical model was 20 m (X) × 10 m (Y) × 20 m (Z). Stress constraints were imposed on the upper boundary of the model, and displacement constraints were imposed on the other boundaries. The model had a total of 29,600 units and 32,769 nodes. The Mohr–Coulomb strength model was adopted for the surrounding rock, according to the experiment of previous mechanical properties of Baizuo FM, parameters for the numerical simulation are listed in Table 5. The bolt and sprayed concrete layer were simulated using cable and shell models, respectively. Taking support scheme S1 as an example, the calculation model and calculation results are shown in Fig. 7.

Table 5 Basic parameters of the surrounding rock
Full size table
Fig. 7
figure 7

Numerical simulation of the surrounding rock deformation with support scheme S1, a calculation model; b calculation results

Full size image

4.2 Results and analysis

The indexes obtained in the numerical simulations with different factors and levels are listed in Table 6.

Table 6 Results of the numerical simulations
Full size table

Table 6 lists the results of the 25 calculations in the orthogonal tests. There are no direct comparisons of two parameters or levels in these experiments. Therefore, the optimal combination of support parameters cannot be directly derived from these calculation results. However, a pragmatic conclusion can be obtained by comparing the calculation results for the same parameter or same level as a whole. Here, ki is defined as the average value of the calculation results of an index, which corresponds to the i-th level of a factor in the orthogonal test. For instance, A3 is a sprayed concrete layer thickness of 100 mm, which appears five times in the orthogonal tests, as indicated in Table 6. Then, k3 is the average value of one of the four indexes in these five tests. The range, R, is the difference between the maximum and minimum values of ki under a certain experimental design factor, which reflects the degree of significance of the influence of different factors on the index in the orthogonal experiment. The range analysis results are summarized in Table 7.

Table 7 Range analysis
Full size table

The relationship between the index mean value, ki, of each factor and the level is shown in Fig. 8. With an increase in the thickness of the sprayed concrete layer of factor A, the roof subsidence, floor heave displacement, and side displacement decrease gradually, and these indexes reach minimum values of 5.43, 14.81, and 18.43 mm, respectively, when the thickness of the sprayed concrete layer is 140 mm. After excavation of the roadway, the original rock stress is redistributed. The surrounding rock can be effectively sealed with the sprayed concrete in time, which will form a whole with the surrounding rock to prevent weathering. Simultaneously, a flexible arch beam ring is formed on the surface of the roadway and can provide radial support, thereby effectively restraining the deformation of the surrounding rock of the roadway. The plastic zone decreases with an increase in the thickness of the sprayed concrete layer. On the other hand, the sprayed concrete will severely fall off if the thickness of a single sprayed concrete layer is too large. Engineering practice has shown that the thickness of a single sprayed concrete layer should not exceed 150 mm. Research also shows that the mechanical properties of the sprayed concrete layer gradually changed from flexible to rigid with an increase in the thickness of the sprayed layer (Yu et al. 2020); this will limit the deformation of the surrounding rock, resulting in an increased load imposed on the sprayed concrete, which is then more likely cause deformation and failure of the surrounding rock. Therefore, a thickness of 140 mm is selected as the secondary support parameter value for the sprayed concrete.

Fig. 8
figure 8

Graph of index mean values and levels for different factors: a roof subsidence, T1; b floor heave displacement, T2; c side displacement, T3; d plastic zone, T4

Full size image

When the bolt row spacing of factor C is less than 0.7 m, the roof subsidence, floor heave displacement, and side displacement remain basically unchanged; with increasing bolt row spacing exceeding 0.7 m, these three indexes gradually increase. On both sides of the roadway, the effect of the arch beam formed by the sprayed concrete is weakened. Under the action of gravity and the stress of the surrounding rock, the sprayed concrete layer and separated rock masses have a tendency to move to the free surface of the roadway, resulting in an increase in the displacement and deformation of the two sides of the roadway. Through a reasonable arrangement of the bolt row spacing, the surrounding rock and sprayed concrete layer can be formed as an integral structure with the deep rock layer through the effect of compression and reinforcement of the bolts, which can prevent deformation of the roadway surrounding rock. In addition, with a bolt row spacing of 0.7 m, the surrounding rock has a minimum plastic zone of 31.67 m3. Therefore, 0.7 m is selected as the secondary support parameter value for the bolt row spacing. The bolt length of factor B and the bolt diameter of factor D have little effect on the deformation and failure of the roadway surrounding rock. The index values for the roof subsidence, floor heave displacement, and side displacement remain basically unchanged with varying bolt lengths and diameters. When the bolt length and bolt diameter are 1.9 m and 42 mm, respectively, the roadway surrounding rock has the minimum plastic zone. Therefore, 1.9 m and 42 mm are chosen as the secondary support parameter values for the bolt length and bolt diameter, respectively.

5 Conclusion

In view of the obvious rheological phenomena in the surrounding rock of a deep roadway under high in-situ stress in the Huize lead–zinc mine, Yunnan, a survey was undertaken to investigate the roadway support situation and failure modes. The results showed that it was difficult for the initial support to maintain the stability of the roadway, and it was necessary to implement secondary support in a reasonable time to ensure the main function of the roadway. Through creep tests of the main exposed surrounding rock, the creep rate of the stable creep stage was obtained, and the Burgers creep model was employed, which could effectively describe the initial and the stable creep stages. Then, according to the equation for the radial displacement change derived based on the Hoek–Brown criterion, the reasonable time for secondary support was determined to be approximately 170 h after excavation of the Baizuo Fm surrounding rock under an in-situ stress of 41.5 MPa. The need for continuous geological exploration and ore prospecting of deep resources in the mine will inevitably lead to an increase in the amount of roadway construction and support required, thus increasing the mining cost. To reduce the support costs while meeting requirements for stability and functionality of the roadway, numerical simulations and orthogonal test methods were employed to optimize and analyze the secondary support parameters. The optimized parameters obtained were a sprayed concrete thickness of 140 mm, bolt row spacing of 0.7 m, bolt length of 1.9 m, and bolt diameter of 42 mm. The research methods and conclusions in this study can provide a scientific basis and technical support for deep roadway support. In addition, it is recommended that additional roadway field monitoring tests be conducted in future work. These tests can be used to modify the creep model and further verify the rationality of the secondary support time.