1 Introduction

Enhanced geothermal systems (EGS) are human engineered geothermal reservoirs enabled for cost-effective heat mining from initially low-permeability high temperature rocks via hydraulic stimulation. This technology involves the injection of cold water at well-controlled rates into the target geothermal reservoir over a long uncased interval to enhance permeability through reactivating pre-existing fractures or creating new fractures (Evans et al. 2005; Gelet et al. 2012; McClure and Horne 2014; Xie and Min 2016; Fan and Parashar 2019; Li et al. 2022). As fluids travel through the fractured rock, they are heated to economic temperatures, allowing heat harvesting. Continuous injection of large-volume fluids into the reservoir causes volumetric expansion of the reservoir due to the poroelastic effect. On the other hand, injection of cold fluids into the hot reservoir leads to shrinkage of the reservoir due to the thermoelastic effect. The net effect depends on the injection operations (rate, duration, volume) and the physical properties of the rock matrix (Fan et al. 2020). A better understanding of the interaction and feedback between multi-physical processes during hydraulic stimulation of an EGS reservoir requires the employment of fully coupled thermoporoelasticity.

The classical thermoporoelasticity is a natural extension of the isothermal theory of Biot poroelasticity to include the thermal effects, where an instantaneous local thermal equilibrium (LTE) between the solid and fluid phases is generally assumed and the temperatures of the two phases are assumed to be identical. The prerequisite for this implicit assumption is large heat transfer coefficients between the solid and fluid phases (Cheng 2016). Despite the widespread applications of LTE thermoporoelasticity in many engineering practices (Ding et al. 2020; Gao et al. 2021), a local thermal equilibrium may not be established due to the huge difference in thermal properties (thermal expansion coefficients and specific heat) of the solids and fluids, especially at short time scales. In particular, when cold fluid is injected at a high rate into the wellbore, it may take a long time for the solid and fluid temperatures to equilibrate in the vicinity of the wellbore. Under such conditions, the influence of local thermal non-equilibrium (LTNE), hence the two distinct temperatures for the solid and fluid phases, has to be taken into account. Contrary to the LTE theory, LTNE is achieved by coupling the heat transfer in the solid and fluid phases through an additional source term quantifying heat exchange between the two phases (Nied and Bejan 2006).

Recently, LTNE based thermoporoelasticity has been employed to address a wide variety of engineering problems in petroleum engineering, subsurface hydrogeology, and biological systems (Kim and Jang 2002; Rees et al. 2008; Gelet et al. 2013; Jin and He 2013; Roshan et al. 2014; Straughan 2013; Eltayeb 2015; Dehghan et al. 2016; Heinze and Blocher 2019; Wang et al. 2019; Zhai and Atefi-Monfared 2020). For example, He and Jin (2010) developed a LNTE thermoporoelastic theory incorporating the LTNE effect through introducing a weighted average temperature for the solid and fluid. He and Jin (2010) applied the model to solve the problem of a wellbore subjected to uniform fluid pressure and temperature variations and found, particularly for a short time, that LTNE influences the stress and pore pressure fields considerably. He et al. (2012) further examined the impact of convective cooling/heating on pore pressure and stresses around a borehole using LNTE thermoporoelasticity. Gao et al. (2017) derived the analytical solution of an inclined borehole subjected to far-field non-hydrostatic in situ stress in a transversely isotropic formation in the framework of LTNE thermoporoelasticity. Gandomkar and Gray (2019) analyzed the LTNE effect on the stability of a wellbore considering both conductive and convective heat transfers within the porous matrix. Li et al. (2018) extended the analysis of Gao et al. (2017) to include the effect of dual porosity to allow mass and heat transfer between pores and fractures while accounting for the LTNE effect. Gelet et al. (2013) employed a mixture theory to examine the LTNE effect on heat mining in an EGS system.

In addition, a wide variety of analytical solutions have been derived in the context of fully coupled poroelasticity/thermopoelasticity to address injection-induced stress perturbations and temperature changes (Abouslaiman and Cui 1998; Abousleiman and Chen 2010; Bai and Li 2009; Fan et al. 2016, 2019, 2023; Kanfar et al. 2016; Fan and Parashar 2020; Gao et al. 2021; Fan and Jin 2023). Among such solutions, two popular boundaries are frequently used for the temperature conditions at the borehole surface: 1. a constant temperature (Wang and Papamichos 1994; Wang and Dusseault 2003) and 2. a constant heat flux (Mctigue 1990; Alazmi and Vafai 2002). Most of the time, a constant pore pressure is assumed for the pore pressure boundary conditions at the borehole (Abousleiman and Ekbote 2005; Jin and He 2013). For hydraulic stimulation conducted in an EGS, the uncased section of the borehole is subjected to a non-isothermal fluid flux. Adopting a fluid flux boundary condition for pore pressure (Rajapakse 1993; Mehrabian and Abousleiman 2013; Celli et al. 2013; Chen and Abousleiman 2016; Chen 2019; Huang and Chen 2021) and a convective cooling boundary condition for temperature (He et al. 2012; Barletta et al. 2015; Lagziri and Bezzazi 2019) would be more appropriate to mimic the thermoporoelastic response of the reservoir. To the best of the authors’ knowledge, the analytical solutions accounting for the LTNE effect and convective cooling during hydraulic stimulation of an EGS in the framework of fully coupled thermoporoelasticity have not been reported.

The main objective of the present study is to analyze the effects of LNTE between fluid and solid phases on the transient distribution of stresses, pore pressure, and temperatures around a wellbore subjected to a non-isothermal fluid flux and convective cooling. The load decomposition technique and integral transform method are applied to solve the governing equations. The analytical solutions presented in this work may aid in the design of hydraulic stimulation in EGS and may also serve as a benchmark solution for validation in thermoporoelasticity.

2 Governing equations for fully coupled thermopoelasticity under LTNE conditions

For low-permeability porous rocks, heat transfer through convection can be neglected (McTigue 1986; Kurashige 1989). Considering the heat transfer across fluid and rock frame with disparate thermal properties and accounting for the dynamic interplay between solid and fluid temperature gradients, for the solid phase, the governing equation is given by (Nied and Bejan 2006)

$$\left( {1 - \phi_{0} } \right)\rho_{s} c_{s} \frac{{\partial \theta_{s} }}{\partial t} = \left( {1 - \phi_{0} } \right)k_{Ts} \nabla^{2} \theta_{s} + h_{{\text{int}}} \left( {\theta_{f} - \theta_{s} } \right)$$
(1)

where θs and θf are the changes in temperature for solid and fluid, respectively, and t is time. The material constants involved are: the reference porosity ϕ0, the solid–fluid interface heat transfer coefficient hint, ρs, cs and kTs are the mass density, specific heat, and thermal conductivity of solid, respectively, ρf, cf and kTf are the mass density, specific heat, and thermal conductivity of fluid, respectively. Similarly, for the fluid phase, the governing equation is written as

$$\phi_{0} \rho_{f} c_{f} \frac{{\partial \theta_{f} }}{\partial t} = \phi_{0} k_{Tf} \nabla^{2} \theta_{f} - h_{{\text{int}}} \left( {\theta_{f} - \theta_{s} } \right)$$
(2)

In the above, the last term \(h_{{\text{int}}} \left( {\theta_{f} - \theta_{s} } \right)\) characterizes the heat transfer between fluid and solid under the LTNE condition.

The weighted average temperature for the fluid-saturated porous rock θave is defined by (He and Jin 2010)

$$\theta_{ave} = \left( {1 - \phi_{0} } \right)\theta_{s} + \phi_{0} \theta_{f}$$
(3)

The constitutive equations for thermo-poroelastic fluid-saturated rocks accounting for LTNE effect are given by (Mctigue 1986; He and Jin 2010)

$$\sigma_{ij} = 2G\varepsilon_{ij} + \frac{2G\nu }{{1 - 2\nu }}\varepsilon_{kk} \delta_{ij} - \alpha p\delta_{ij} - K\alpha_{{\text{s}}} \theta_{{{\text{ave}}}} \delta_{ij}$$
(4)
$$\zeta = \alpha \left( {\frac{{\varepsilon_{kk} }}{3} + \frac{p}{{K_{u} B}}} \right) - \phi_{0} \left( {\alpha_{f} - 3\alpha_{s} } \right)\theta_{{{\text{ave}}}}$$
(5)

where the total stresses σij and the increment of fluid content ζ are expressed in terms of the strains εij, the excess pore pressure p, and the weighted average temperature θave. The following material constants are introduced: the shear modulus G, the drained Poisson’s ratio ν, the Biot coefficient α, the drained bulk modulus of fluid-saturated rock K, the linear thermal expansion coefficient of solid matrix αs, the undrained bulk modulus of fluid-saturated rock Ku, the Skempton’s coefficient B, and the volumetric thermal expansion coefficient of the pore fluid αf.

Substituting the constitutive Eqs. (4) and (5) into the equilibrium equations \(\sigma_{ji,j} = 0\) and utilizing the strain–displacement relationship \(\varepsilon_{ij} = \frac{1}{2}\left( {u_{i,j} + u_{j,i} } \right)\) yield the governing equation for displacement as follows (Kurashige 1989)

$$G\nabla ^{2} u_{i} + \frac{G}{{1 - 2\nu }}\varepsilon _{{kk,i}} - \alpha p_{{,i}} - 3K\alpha _{s} \theta _{{ave,i}} = 0$$
(6)

Similarly, substituting the constitutive equation into the mass conservation equation \(\frac{\partial \zeta }{{\partial t}} + q_{i,i} = 0\) and using the Darcy’s law \(q_{i} = - \frac{k}{{\mu_{f} }}p_{,i}\), we obtain the governing differential equation for pore pressure

$$\frac{\alpha (1 - \alpha B)}{{BK}}\frac{\partial p}{{\partial t}} - \frac{k}{{\mu_{f} }}\nabla^{2} p = - \alpha \frac{{\partial \varepsilon_{kk} }}{\partial t} + \left[ {\phi \left( {\alpha_{f} - 3\alpha_{s} } \right) + 3\alpha \alpha_{s} } \right]\frac{{\partial \theta_{ave} }}{\partial t}$$
(7)

In the above, qi is the fluid flux, k is the intrinsic permeability and µf is the pore fluid viscosity. For an axisymmetric deformation in an infinite domain, pore pressure and displacement become uncoupled, and Eq. (7) can be simplified as (Kurashige 1989; He and Jin 2010)

$$\frac{\partial p}{{\partial t}} - c\nabla^{2} p = c^{\prime} \frac{{\partial \theta_{ave} }}{\partial t}$$
(8)

where \(c = \frac{k}{{\mu_{f} }}\frac{{2GB^{2} \left( {1 + \nu_{u} } \right)^{2} \left( {1 - \nu } \right)}}{{9\left( {1 - \nu_{u} } \right)\left( {\nu_{u} - \nu } \right)}}\) is the hydraulic diffusivity and \(c^{\prime } = \frac{c}{{{k \mathord{\left/ {\vphantom {k {\mu_{f} }}} \right. \kern-0pt} {\mu_{f} }}}}\left[ {\phi \left( {\alpha_{f} - 3\alpha_{s} } \right) + \frac{{6\alpha_{s} \left( {\nu_{u} - \nu } \right)}}{{B\left( {1 - \nu } \right)\left( {1 + \nu_{u} } \right)}}} \right]\) is the pore pressure–temperature coupling coefficient.

In the next section, we demonstrate how to solve the full set of Eqs. (1), (2), (6), and (8) for the temperatures, pore pressure, and stresses for an injection well subjected to a non-isothermal fluid flux and convective cooling in an EGS reservoir.

3 Problem formation and analytical solutions

3.1 Problem formulation

Consider a well of radius a embedded in a thermoporoelastic rock matrix. The uncased segment of the well is exposed to a non-isothermal fluid flux qw and convective cooling. The initial temperature of the formation is T0. The temperature of the injected fluid is Tw. The boundary conditions at the borehole wall (\(r = a\)) are given by

$$\, \left\{ {\begin{array}{*{20}l} {\left. {\sigma_{r} } \right|_{{_{r = a} }} = - p_{w} {\text{(t)}}H{\text{(t), }}\left. {\sigma_{r\theta } } \right|_{{_{r = a} }} = 0{, }} \\ {\left. {q_{r} } \right|_{r = a} = q_{w} H{\text{(t), }}} \\ {\left. { - k_{Ts} {{\partial T_{s} } \mathord{\left/ {\vphantom {{\partial T_{s} } {\partial r}}} \right. \kern-0pt} {\partial r}}} \right|_{r = a} = \left. {h_{TS} \left[ {T_{W} H{\text{(t)}} - T_{s} } \right]} \right|_{r = a} {, }\left. {T_{f} } \right|_{r = a} = T_{W} H{\text{(t)}}} \\ \end{array} } \right.$$
(9)

In the above, σr and σrθ are the radial stress and shear stress, respectively, H(t) is the Heaviside function, pw is the time-dependent fluid pressure that must be maintained at the borehole wall in order to drive a constant fluid flux into the formation, and \(q_{w} = \left. { - \frac{k}{{\mu_{f} }}\frac{{dp_{w} {(}r{,}t{)}}}{dr}} \right|_{r = a}\) is the constant fluid flux at the borehole wall.

The initial conditions for the temperatures are as follows,

$$\left. {T_{s} \left( {r,t} \right)} \right|_{t = 0} = T_{0} {, }\left. {T_{f} \left( {r,t} \right)} \right|_{t = 0} = T_{0}$$
(10)

At the far field

$$\left. {T_{s} \left( {r,t} \right)} \right|_{r \to \infty } = T_{0} {, }\left. {T_{f} \left( {r,t} \right)} \right|_{r \to \infty } = T_{0} \,$$
(11)

The initial and boundary conditions for the temperatures can also be described in terms of the changes in temperature for solids and fluids θs and θf

$$\left. {\theta_{s} \left( {r,t} \right)} \right|_{t = 0} = 0, \, \left. {\theta_{f} \left( {r,t} \right)} \right|_{t = 0} = 0$$
(12)
$$\left. { - k_{Ts} \frac{{\partial \theta_{s} \left( {r,t} \right)}}{\partial r}} \right|_{r = a} = \left. {h_{Ts} \left[ {\left( {T_{w} - T_{0} } \right)H{\text{(t)}} - \theta_{s} } \right]} \right|_{r = a} {, }\left. {\theta_{f} \left( {r,t} \right)} \right|_{r = a} = \left( {T_{w} - T_{0} } \right)H{\text{(t)}}$$
(13)
$$\left. {\theta_{s} \left( {r,t} \right)} \right|_{r \to \infty } = 0, \, \left. {\theta_{f} \left( {r,t} \right)} \right|_{r \to \infty } = 0$$
(14)

To make our problem analytically tractable, following Detournay and Cheng (1988), we decompose the loading into two modes, and the corresponding boundary conditions are given below.

Mode 1

$$\, \left\{ {\begin{array}{*{20}l} {\left. {\sigma_{r}^{(1)} } \right|_{{_{r = a} }} = - p_{w} {\text{(t)}}H{\text{(t), }}\left. {\sigma_{r\theta }^{(1)} } \right|_{{_{r = a} }} = 0{, }} \\ {\left. {q_{r}^{(1)} } \right|_{r = a} = 0{, }} \\ {\left. {\theta_{s}^{(1)} \left( {r,t} \right)} \right|_{r = a} = 0, \, \left. {\theta_{f}^{(1)} \left( {r,t} \right)} \right|_{r = a} = 0} \\ \end{array} } \right.$$
(15)

Mode 2

$$\, \left\{ {\begin{array}{*{20}l} {\left. {\sigma_{r}^{(2)} } \right|_{{_{r = a} }} = 0{, }\left. {\sigma_{r\theta }^{(2)} } \right|_{{_{r = a} }} = 0{, }} \\ {\left. {q_{r}^{(2)} } \right|_{r = a} = q_{w} H{\text{(t), }}} \\ {\left. { - k_{Ts} {{\partial \theta_{s}^{(2)} } \mathord{\left/ {\vphantom {{\partial \theta_{s}^{(2)} } {\partial r}}} \right. \kern-0pt} {\partial r}}} \right|_{r = a} = \left. {h_{Ts} \left[ {\left( {T_{w} - T_{0} } \right)H{\text{(t)}} - \theta_{s} } \right]} \right|_{r = a} {, }\left. {\theta_{f}^{(2)} } \right|_{r = a} = \left( {T_{w} - T_{0} } \right)H{\text{(t)}}} \\ \end{array} } \right.$$
(16)

In the above, the superscripts (1) and (2) denote the two loading modes, respectively. The decomposition of the boundary conditions into different modes enables the resolution of the intricate problem through the application of superposition. The final solution to the problem is obtained by superposition of the solutions induced by mode 1 loading and mode 2 loading.

3.2 Analytical solutions

3.2.1 Mode 1 loading solution

For this loading mode, Eqs. (1) and (2) under the boundary conditions (15) have trivial solutions. It follows from Eq. (8) that the induced pore pressure p = 0. The induced stress components are given by

$$\frac{{k\sigma_{r}^{(1)} }}{{q_{w} \mu a}} = - \frac{{kp_{w} }}{{q_{w} \mu a}}\frac{{a^{2} }}{{r^{2} }}$$
(17)
$$\frac{{k\sigma_{\theta }^{(1)} }}{{q_{w} \mu a}} = \frac{{kp_{w} }}{{q_{w} \mu a}}\frac{{a^{2} }}{{r^{2} }}$$
(18)

We note that pw is the time-dependent fluid pressure acting on the wellbore wall to drive a constant fluid flux into the formation, which will be calculated from the mode 2 loading solution, as shown below.

3.2.2 Mode 2 loading solution

Application of the Laplace transform to Eqs. (1–2) with respect to the time t results in

$$s\tilde{\theta }_{s} = \kappa_{s} \nabla^{2} \tilde{\theta }_{s} + h(\tilde{\theta }_{f} - \tilde{\theta }_{s} )$$
(19)
$$sb_{1} \tilde{\theta }_{f} = b_{2} \kappa_{s} \nabla^{2} \tilde{\theta }_{f} - h(\tilde{\theta }_{f} - \tilde{\theta }_{s} )$$
(20)

where s is the Laplace transform parameter. Following He et al. (2012), we introduced the following symbols

$$\kappa_{s} = \frac{{k_{Ts} }}{{\rho_{s} c_{s} }},h = \frac{{h_{{\text{int}}} }}{{\left( {1 - \phi_{0} } \right)\rho_{s} c_{s} }},b_{1} = \frac{{\phi_{0} \rho_{f} c_{f} }}{{\left( {1 - \phi_{0} } \right)\rho_{s} c_{s} }},b_{2} = \frac{{\phi_{0} k_{Tf} }}{{\left( {1 - \phi_{0} } \right)k_{Ts} }},b_{4s} = \frac{{k_{Ts} }}{{ah_{Ts} }}$$

In the above, \(\kappa_{s}\) is the thermal diffusivity of the solid, h characterizes the heat transfer between the solid and fluid, b1 is the effective heat capacity ratio between the fluid and the solid, b2 is the effective thermal conductivity ratio between the fluid and the solid, b4s is the inverse of the Biot number of the solid.

Elimination of \(\tilde{\theta }_{f}\) from (19) and (20) yields

$$b_{2} \kappa_{s}^{2} \nabla^{2} \nabla^{2} \tilde{\theta }_{s} - \kappa_{s} \left[ {s\left( {b_{1} + b_{2} } \right) + h\left( {1{ + }b_{2} } \right)} \right]\nabla^{2} \tilde{\theta }_{s} + \left[ {b_{1} s^{2} + sh\left( {1{ + }b_{1} } \right)} \right]\tilde{\theta }_{s} = 0$$
(21)

The boundary conditions in the Laplace domain are

$$\left. { - k_{Ts} \frac{{\partial \tilde{\theta }_{s} \left( {r,t} \right)}}{\partial r}} \right|_{r = a} = \left. {h_{Ts} \left( {\frac{{T_{w} - T_{0} }}{s} - \tilde{\theta }_{s} } \right)} \right|_{r = a} \,, \left. {\tilde{\theta }_{s} \left( {r,t} \right)} \right|_{r \to \infty } = 0$$
(22)

Solving Eq. (21) under the boundary condition (22), we obtain the solution for the changes in solid temperature (He et al. 2012)

$$\begin{aligned} \tilde{\theta }_{s} \left( {r,s} \right) & = \frac{{T_{w} - T_{0} }}{{sc_{3} }}\left[ {s - \kappa_{s} \lambda_{2} - ab_{4s} h\sqrt {\lambda_{2} } \frac{{K_{1} \left( {a\sqrt {\lambda_{2} } } \right)}}{{K_{0} \left( {a\sqrt {\lambda_{2} } } \right)}}} \right]\frac{{K_{0} \left( {r\sqrt {\lambda_{1} } } \right)}}{{K_{0} \left( {a\sqrt {\lambda_{1} } } \right)}} \\ & \quad - \frac{{T_{w} - T_{0} }}{{sc_{3} }}\left[ {s - \kappa_{s} \lambda_{1} - ab_{4s} h\sqrt {\lambda_{1} } \frac{{K_{1} \left( {a\sqrt {\lambda_{1} } } \right)}}{{K_{0} \left( {a\sqrt {\lambda_{1} } } \right)}}} \right]\frac{{K_{0} \left( {r\sqrt {\lambda_{2} } } \right)}}{{K_{0} \left( {a\sqrt {\lambda_{2} } } \right)}} \\ \end{aligned}$$
(23)

Substituting the above into Eq. (19) and solving the resulting equation gives (He et al. 2012)

$$\begin{aligned} \tilde{\theta }_{f} \left( {r,s} \right) & = \frac{{T_{w} - T_{0} }}{{sc_{3} }}\left[ {s - \kappa_{s} \lambda_{2} - ab_{4s} h\sqrt {\lambda_{2} } \frac{{K_{1} \left( {a\sqrt {\lambda_{2} } } \right)}}{{K_{0} \left( {a\sqrt {\lambda_{2} } } \right)}}} \right]\frac{{K_{0} \left( {r\sqrt {\lambda_{1} } } \right)}}{{K_{0} \left( {a\sqrt {\lambda_{1} } } \right)}}\left( {1 + \frac{{s - \kappa_{s} \lambda_{1} }}{h}} \right) \\ & \quad - \frac{{T_{w} - T_{0} }}{{sc_{3} }}\left[ {s - \kappa_{s} \lambda_{1} - ab_{4s} h\sqrt {\lambda_{1} } \frac{{K_{1} \left( {a\sqrt {\lambda_{1} } } \right)}}{{K_{0} \left( {a\sqrt {\lambda_{1} } } \right)}}} \right]\frac{{K_{0} \left( {r\sqrt {\lambda_{2} } } \right)}}{{K_{0} \left( {a\sqrt {\lambda_{2} } } \right)}}\left( {1 + \frac{{s - \kappa_{s} \lambda_{2} }}{h}} \right) \\ \end{aligned}$$
(24)

where

\(\lambda_{1} { = }\frac{1}{{\kappa_{s} }}\left( {A_{1} s + A_{2} + \sqrt {A_{3} s^{2} + A_{4} s + A_{2}^{2} } } \right)\), \(\lambda_{2} { = }\frac{1}{{\kappa_{s} }}\left( {A_{1} s + A_{2} - \sqrt {A_{3} s^{2} + A_{4} s + A_{2}^{2} } } \right)\),\(A_{1} { = }\frac{1}{2}\left( {1{ + }\frac{{b_{1} }}{{b_{2} }}} \right)\), \(A_{2} { = }\frac{h}{2}\left( {1{ + }\frac{1}{{b_{2} }}} \right)\), \(A_{3} { = }\frac{1}{4}\left( {\frac{{b_{1} }}{{b_{2} }} - 1} \right)^{2}\), \(A_{4} { = }\frac{h}{2}\left( {\frac{1}{{b_{2} }} - 1} \right)\left( {\frac{{b_{1} }}{{b_{2} }} - 1} \right)\), and

$$c_{3} = \kappa_{s} \left( {\lambda_{1} - \lambda_{2} } \right) + ab_{4s} h\sqrt {\lambda_{1} } \left( {1 + \frac{{s - \kappa_{s} \lambda_{2} }}{h}} \right)\frac{{K_{1} \left( {a\sqrt {\lambda_{1} } } \right)}}{{K_{0} \left( {a\sqrt {\lambda_{1} } } \right)}} - ab_{4s} h\sqrt {\lambda_{2} } \left( {1 + \frac{{s - \kappa_{s} \lambda_{1} }}{h}} \right)\frac{{K_{1} \left( {a\sqrt {\lambda_{2} } } \right)}}{{K_{0} \left( {a\sqrt {\lambda_{2} } } \right)}}$$

Substituting (23) and (24) into (3), we get the weighted average temperature for the fluid-saturated porous rock \(\tilde{\theta }_{ave}^{(2)}\) in the Laplace domain.

$$\begin{aligned} \tilde{\theta }_{ave}^{(2)} & = \frac{{T_{w} - T_{0} }}{{sc_{3} }}\left[ {s - \kappa_{s} \lambda_{2} - ab_{4s} h\sqrt {\lambda_{2} } \frac{{K_{1} \left( {a\sqrt {\lambda_{2} } } \right)}}{{K_{0} \left( {a\sqrt {\lambda_{2} } } \right)}}} \right]\frac{{K_{0} \left( {r\sqrt {\lambda_{1} } } \right)}}{{K_{0} \left( {a\sqrt {\lambda_{1} } } \right)}}\left[ {1 + \frac{{\phi_{0} \left( {s - \kappa_{s} \lambda_{1} } \right)}}{h}} \right] \\ & \quad - \frac{{T_{w} - T_{0} }}{{sc_{3} }}\left[ {s - \kappa_{s} \lambda_{1} - ab_{4s} h\sqrt {\lambda_{1} } \frac{{K_{1} \left( {a\sqrt {\lambda_{1} } } \right)}}{{K_{0} \left( {a\sqrt {\lambda_{1} } } \right)}}} \right]\frac{{K_{0} \left( {r\sqrt {\lambda_{2} } } \right)}}{{K_{0} \left( {a\sqrt {\lambda_{2} } } \right)}}\left[ {1 + \frac{{\phi_{0} \left( {s - \kappa_{s} \lambda_{2} } \right)}}{h}} \right] \\ \end{aligned}$$
(25)

Application of Laplace transforms in (8) results in

$$\frac{{d^{2} \tilde{p}^{(2)} }}{{dr^{2} }} + \frac{1}{r}\frac{{d\tilde{p}^{(2)} }}{dr} - \frac{s}{c}\tilde{p}^{(2)} = - \frac{{c^{\prime}}}{c}s\tilde{\theta }_{ave}^{(2)}$$
(26)

which is subjected to the following boundary conditions

$$\left. {\frac{{d\tilde{p}^{(2)} }}{dr}} \right|_{r = a} = - \frac{{\mu q_{w} }}{ks}, \, \left. {\tilde{p}^{(2)} } \right|_{r \to \infty } = 0$$

The resulting solution is given by

$$\begin{aligned} \frac{{\tilde{p}^{(2)} ks}}{{q_{w} \mu a}} & = \frac{{K_{0} \left( \xi \right)}}{{\beta K_{1} \left( \beta \right)}}\left[ {1{ + }\frac{ks}{{q_{w} \mu }}\frac{{c^{\prime } m_{1} \sqrt {\lambda_{1} } }}{{c\lambda_{1} - s}}\frac{{K_{1} \left( {a\sqrt {\lambda_{1} } } \right)}}{{K_{0} \left( {a\sqrt {\lambda_{1} } } \right)}}{ + }\frac{ks}{{q_{w} \mu }}\frac{{c^{\prime } m_{2} \sqrt {\lambda_{2} } }}{{c\lambda_{2} - s}}\frac{{K_{1} \left( {a\sqrt {\lambda_{2} } } \right)}}{{K_{0} \left( {a\sqrt {\lambda_{2} } } \right)}}} \right] \\ & \quad - \frac{ks}{{q_{w} \mu a}}\left[ {\frac{{c^{\prime } m_{1} }}{{c\lambda_{1} - s}}\frac{{K_{0} \left( {r\sqrt {\lambda_{1} } } \right)}}{{K_{0} \left( {a\sqrt {\lambda_{1} } } \right)}} + \frac{{c^{\prime } m_{2} }}{{c\lambda_{2} - s}}\frac{{K_{0} \left( {r\sqrt {\lambda_{2} } } \right)}}{{K_{0} \left( {a\sqrt {\lambda_{2} } } \right)}}} \right] \\ \end{aligned}$$
(27)

where \(m_{1} \left( s \right) = \frac{{T_{w} - T_{0} }}{{c_{3} }}\left[ {s - \kappa_{s} \lambda_{2} - ab_{4s} h\sqrt {\lambda_{2} } \frac{{K_{1} \left( {a\sqrt {\lambda_{2} } } \right)}}{{K_{0} \left( {a\sqrt {\lambda_{2} } } \right)}}} \right]\left[ {1 + \frac{{\phi_{0} \left( {s - \kappa_{s} \lambda_{1} } \right)}}{h}} \right]\),

\(m_{2} \left( s \right) = - \frac{{T_{w} - T_{0} }}{{c_{3} }}\left[ {s - \kappa_{s} \lambda_{1} - ab_{4s} h\sqrt {\lambda_{1} } \frac{{K_{1} \left( {a\sqrt {\lambda_{1} } } \right)}}{{K_{0} \left( {a\sqrt {\lambda_{1} } } \right)}}} \right]\left[ {1 + \frac{{\phi_{0} \left( {s - \kappa_{s} \lambda_{2} } \right)}}{h}} \right]\),

\(\xi = r\sqrt {{\raise0.7ex\hbox{$s$} \!\mathord{\left/ {\vphantom {s c}}\right.\kern-0pt} \!\lower0.7ex\hbox{$c$}}}\), and \(\beta = a\sqrt {{\raise0.7ex\hbox{$s$} \!\mathord{\left/ {\vphantom {s c}}\right.\kern-0pt} \!\lower0.7ex\hbox{$c$}}}\).

Once the pore pressure and temperatures are obtained, the stress components are determined as follows (McTigue 1986)

$$\sigma_{r} = - \frac{2\eta }{{r^{2} }}\int\limits_{a}^{r} {p(\psi ,t)} \psi d\psi - \frac{{E\alpha_{s} }}{1 - \nu }\frac{1}{{r^{2} }}\int\limits_{a}^{r} {T(\psi ,t)} \psi d\psi + c_{1} (t) + c_{2} (t)\frac{1}{r}$$
(28)
$$\sigma_{\theta } = 2\eta \left[ {\frac{1}{{r^{2} }}\int\limits_{a}^{r} {p(\psi ,t)} \psi d\psi - p} \right] + \frac{{E\alpha_{s} }}{1 - \nu }\left[ {\frac{1}{{r^{2} }}\int\limits_{a}^{r} {T(\psi ,t)} \psi d\psi - T} \right] + \frac{{2Gc_{1} (t)}}{1 - 2\nu } + \frac{{2Gc_{2} (t)}}{{r^{2} }}$$
(29)

c1 = c2 = 0 is required to guarantee that radial and hoop stresses are bound as r → ꝏ. Transforming (28) and (29) into the Laplace domain and substituting (25) and (27) into the transformed equations results in

$$\begin{aligned} \frac{{\tilde{\sigma }_{r}^{(2)} ks}}{{q_{w} \mu a}} & = - 2\eta \frac{{F_{1} }}{{\beta K_{1} \left( \beta \right)}}\left[ {1{ + }\frac{ks}{{q_{w} \mu }}\frac{{c^{\prime } m_{1} \sqrt {\lambda_{1} } }}{{c\lambda_{1} - s}}\frac{{K_{1} \left( {a\sqrt {\lambda_{1} } } \right)}}{{K_{0} \left( {a\sqrt {\lambda_{1} } } \right)}}{ + }\frac{ks}{{q_{w} \mu }}\frac{{c^{\prime } m_{2} \sqrt {\lambda_{2} } }}{{c\lambda_{2} - s}}\frac{{K_{1} \left( {a\sqrt {\lambda_{2} } } \right)}}{{K_{0} \left( {a\sqrt {\lambda_{2} } } \right)}}} \right] \\ & \quad { + }2\eta \frac{ks}{{q_{w} \mu a}}\left[ {\frac{{c^{\prime } m_{1} }}{{c\lambda_{1} - s}}\frac{{F_{2} }}{{K_{0} \left( {a\sqrt {\lambda_{1} } } \right)}} + \frac{{c^{\prime } m_{2} }}{{c\lambda_{2} - s}}\frac{{F_{3} }}{{K_{0} \left( {a\sqrt {\lambda_{2} } } \right)}}} \right] \\ & \quad - \frac{{Ek\alpha_{s} }}{{q_{w} \mu a\left( {1 - \nu } \right)}}\left[ {c_{1} s\left( {1 + \phi_{0} \frac{{s - \kappa_{s} \lambda_{1} }}{h}} \right)F_{2} + c_{2} s\left( {1 + \phi_{0} \frac{{s - \kappa_{s} \lambda_{2} }}{h}} \right)F_{3} } \right] \\ \end{aligned}$$
(30)
$$\begin{aligned} \frac{{\tilde{\sigma }_{\theta }^{{(2)}} ks}}{{q_{w} \mu a}} & = \frac{{Ek\alpha _{s} }}{{q_{w} \mu a\left( {1 - \nu } \right)}}\left\{ {c_{1} s\left( {1 + \phi _{0} \frac{{s - \kappa _{s} \lambda _{1} }}{h}} \right)\left[ {F_{2} - K_{0} \left( {r\sqrt {\lambda _{1} } } \right)} \right]} \right. \\ & \quad \left. { + c_{2} s\left( {1 + \phi _{0} \frac{{s - \kappa _{s} \lambda _{2} }}{h}} \right)\left[ {F_{3} - K_{0} \left( {r\sqrt {\lambda _{2} } } \right)} \right]} \right\} \\ & \quad + \frac{{2\eta }}{{\beta K_{1} \left( \beta \right)}}\left[ {F_{1} - K_{0} \left( \xi \right)} \right]\left\{ {1 + \frac{{ks}}{{q_{w} \mu }}\left[ {\frac{{c^{\prime } m_{1} \sqrt {\lambda _{1} } }}{{c\lambda _{1} - s}}\frac{{K_{1} \left( {a\sqrt {\lambda _{1} } } \right)}}{{K_{0} \left( {a\sqrt {\lambda _{1} } } \right)}} + \frac{{c^{\prime } m_{2} \sqrt {\lambda _{2} } }}{{c\lambda _{2} - s}}\frac{{K_{1} \left( {a\sqrt {\lambda _{2} } } \right)}}{{K_{0} \left( {a\sqrt {\lambda _{2} } } \right)}}} \right]} \right\} \\ & \quad - 2\eta \frac{{ks}}{{q_{w} \mu a}}\left[ {\frac{{c^{\prime } m_{1} }}{{c\lambda _{1} - s}}\frac{{F_{2} - K_{0} \left( {r\sqrt {\lambda _{1} } } \right)}}{{K_{0} \left( {a\sqrt {\lambda _{1} } } \right)}} + \frac{{c^{\prime } m_{2} }}{{c\lambda _{2} - s}}\frac{{F_{3} - K_{0} \left( {r\sqrt {\lambda _{2} } } \right)}}{{K_{0} \left( {a\sqrt {\lambda _{2} } } \right)}}} \right] \\ \end{aligned}$$
(31)

where \(F_{1} = \frac{{\beta K_{1} \left( \beta \right) - \xi K_{1} \left( \xi \right)}}{{\xi^{2} }}\), \(F_{2} = \frac{{a\sqrt {\lambda_{1} } K_{1} \left( {a\sqrt {\lambda_{1} } } \right) - r\sqrt {\lambda_{1} } K_{1} \left( {r\sqrt {\lambda_{1} } } \right)}}{{r^{2} \lambda_{1} }}\), and

\(F_{3} = \frac{{a\sqrt {\lambda_{2} } K_{1} \left( {a\sqrt {\lambda_{2} } } \right) - r\sqrt {\lambda_{2} } K_{1} \left( {r\sqrt {\lambda_{2} } } \right)}}{{r^{2} \lambda_{2} }}\).

As far as the authors are aware, Eqs. (27), (30) and (31) are the analytical solutions during hydraulic stimulation of an Enhanced Geothermal System (EGS) addressing both the LTNE effect and convective cooling within the framework of fully coupled thermoporoelasticity, which have not been presented before.

Setting r = a, it follows from (27) that the transformed pore pressure at the borehole is given by

$$\begin{aligned} \left. {\frac{{\tilde{p}_{w}^{(2)} ks}}{{q_{w} \mu a}}} \right|_{r = a} & = \frac{{K_{0} \left( \beta \right)}}{{\beta K_{1} \left( \beta \right)}}\left[ {1{ + }\frac{ks}{{q_{w} \mu }}\frac{{c^{\prime } m_{1} \sqrt {\lambda_{1} } }}{{c\lambda_{1} - s}}\frac{{K_{1} \left( {a\sqrt {\lambda_{1} } } \right)}}{{K_{0} \left( {a\sqrt {\lambda_{1} } } \right)}}{ + }\frac{ks}{{q_{w} \mu }}\frac{{c^{\prime } m_{2} \sqrt {\lambda_{2} } }}{{c\lambda_{2} - s}}\frac{{K_{1} \left( {a\sqrt {\lambda_{2} } } \right)}}{{K_{0} \left( {a\sqrt {\lambda_{2} } } \right)}}} \right] \\ & \quad - \frac{ks}{{aq_{w} \mu }}\left( {\frac{{c^{\prime } m_{1} }}{{c\lambda_{1} - s}} + \frac{{c^{\prime } m_{2} }}{{c\lambda_{2} - s}}} \right) \\ \end{aligned}$$
(32)

The stresses for mode 1 loading in the Laplace domain are obtained by applying the Laplace transform to Eqs. (17) and (18) and replacing the resulting \(\tilde{p}_{w}\) by \(\tilde{p}_{w}^{(2)}\) in (32).

The final solutions to the original problem are obtained by superposition of the solutions of modes 1 and 2.

$$\theta = \theta^{(2)}$$
(33)
$$p = p_{0} + p^{(2)}$$
(34)
$$\sigma_{r} = \sigma_{r}^{(1)} + \sigma_{r}^{(2)}$$
(35)
$$\sigma_{\theta } = \sigma_{\theta }^{(1)} + \sigma_{\theta }^{(2)}$$
(36)

3.3 Model validation

3.3.1 Comparison with existing analytical solutions

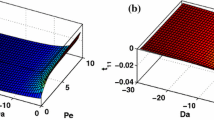
To verify the derived solutions, we compared them with those available in published papers (Fig. 1).

Fig. 1
figure 1

A wellbore is subjected to a non-isothermal fluid flux and convective cooling under LTNE conditions

Full size image

When the interface heat transfer coefficient hint approaches infinity, local thermal equilibrium between the solid and fluid phases is achieved. The transformed temperature is given by

$$\tilde{\theta } = \frac{{T_{w} - T_{0} }}{s}\frac{{K_{0} \left( {\xi_{h} } \right)}}{{K_{0} \left( {\beta_{h} } \right) + K_{1} \left( {\beta_{h} } \right){{\beta_{h} } \mathord{\left/ {\vphantom {{\beta_{h} } {B_{i} }}} \right. \kern-0pt} {B_{i} }}}}$$
(37)

where \(\xi_{h} = r\sqrt {{\raise0.7ex\hbox{$s$} \!\mathord{\left/ {\vphantom {s {c_{h} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${c_{h} }$}}}\), \(\beta_{h} = a\sqrt {{\raise0.7ex\hbox{$s$} \!\mathord{\left/ {\vphantom {s {c_{h} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${c_{h} }$}}}\), ch = kT/(ρC) is the thermal diffusivity for the bulk material and \(B_{i} = a{{h_{TS} } \mathord{\left/ {\vphantom {{h_{TS} } {k_{T} }}} \right. \kern-0pt} {k_{T} }}\) is the Biot number. \(\rho C = \left( {1 - \phi_{0} } \right)\rho_{s} C_{s} + \phi_{0} \rho_{f} C_{f}\) and \(k_{T} = \left( {1 - \phi_{0} } \right)k_{{T{\text{s}}}} + \phi_{0} k_{Tf}\). Equation (37) is consistent with Eq. (27) of He et al. (2012).

Under the local thermal equilibrium conditions, the induced pore pressure is given by

$$\frac{{\tilde{p}ks}}{{q_{w} \mu a}} = \frac{{K_{0} \left( \xi \right)}}{{\beta K_{1} \left( \beta \right)}} + \frac{{c^{\prime} k\left( {T_{w} - T_{0} } \right)}}{{q_{w} \mu a\left( {1 - {c \mathord{\left/ {\vphantom {c {c_{h} }}} \right. \kern-0pt} {c_{h} }}} \right)}}\frac{{K_{0} \left( {\xi_{h} } \right) - {{\sqrt {{c \mathord{\left/ {\vphantom {c {c_{h} }}} \right. \kern-0pt} {c_{h} }}} K_{1} \left( {\beta_{h} } \right)K_{0} \left( \xi \right)} \mathord{\left/ {\vphantom {{\sqrt {{c \mathord{\left/ {\vphantom {c {c_{h} }}} \right. \kern-0pt} {c_{h} }}} K_{1} \left( {\beta_{h} } \right)K_{0} \left( \xi \right)} {K_{1} \left( \beta \right)}}} \right. \kern-0pt} {K_{1} \left( \beta \right)}}}}{{\left[ {K_{0} \left( {\beta_{h} } \right) + K_{1} \left( {\beta_{h} } \right){{\beta_{h} } \mathord{\left/ {\vphantom {{\beta_{h} } {B_{i} }}} \right. \kern-0pt} {B_{i} }}} \right]}}$$
(38)

Equation (38) agrees with the Eq. (34) of Fan et al. (2020).

3.3.2 Comparison with numerical solutions

In this study, we conducted an extensive comparative analysis between our derived analytical solutions and finite element simulations performed using Comsol Multiphysics. Figure 2 represents the selection of a domain size of 40 a, specifically chosen to mitigate potential boundary condition effects in the far field, where a = 0.1 m denotes the wellbore radius. To optimize computational efficiency, one quarter of the model was judiciously adopted, leveraging its inherent symmetry. The finite element model, shown in Fig. 2, comprises 4800 four-node quadrilateral elements, designed with a refined mesh focused around the borehole vicinity. Each nodal point within this model was characterized by five specified degrees of freedom: encompassing solid temperature, fluid temperature, displacement (in two dimensions), and pore pressure. By utilizing the material parameters outlined in Table 1 (McTigue (1986), Wang (2000), and Cheng (2016)) and integrating the boundary conditions as detailed in Eqs. (9) and (11), we successfully obtained the temporal-spatial distribution of pore pressure. Subsequently, the simulation results underwent comparison with the analytical solution (27), as demonstrated in Fig. 3. The consistent alignment observed between our analytical approach and the simulation outcomes serves as compelling validation, reinforcing the reliability and credibility of our methodology.

Fig. 2
figure 2

a One-quarter finite element model for an EGS well under a non-isothermal fluid flux and convective cooling b Refined mesh is used in the vicinity of the borehole

Full size image
Table 1 Material parameters used in the numerical analysis
Full size table
Fig. 3
figure 3

Comparison between analytical solutions and numerical results from Comsol Multiphysics simulation

Full size image

4 Numerical results and discussion

In the Laplace domain, the induced stresses, pore pressure, and temperature changes are given by Eqs. 33–36. We performed an inverse Laplace transform utilizing the Stehfest algorithm to obtain the time domain solutions, which is given by

$$f(t) = \frac{\ln 2}{t}\sum\limits_{i = 1}^{N} {V_{i} } \tilde{f}(\frac{\ln 2}{t}i)$$
(39)

where

$$V_{i} = ( - 1)^{i + N/2} \sum\limits_{{k = \left[ {\frac{i + 1}{2}} \right]}}^{{\min \left( {i,N/2} \right)}} {\frac{{k^{N/2} \left( {2k} \right)!}}{{\left( {N/2 - k} \right)!k!(k - 1)!(i - k)!(2k - i)!}}}$$
(40)

The numerical results are presented in this section. We focus on the impact of LTNE on the transient evolution of stresses and pore pressure induced by hydraulic stimulation of a geothermal reservoir. From McTigue (1986), Wang (2000), and Cheng (2016), Table 1 shows the physical properties of the granite used in the numerical calculations as a representative rock type for geothermal reservoirs.

4.1 Effect of LTNE on temperature fields

The typical range for the convective heat transfer coefficient, hTS, is 5–1000 W/ (m2 K) (He and Jin 2010; Zhao 2014; Bai et al. 2017; Heinze et al. 2017). To evaluate the effect of LTNE on temperature fields, we choose hTS = 500 W/(m2 K), resulting in a Biot number Bi = 20 for a wellbore with a radius of 0.1 m. Figure 4 shows the radial distribution of the normalized temperature drops (normalized by \({{q_{w} \mu_{f} a} \mathord{\left/ {\vphantom {{q_{w} \mu_{f} a} k}} \right. \kern-0pt} k}\)) in the LTNE theory and in the classical LTE theory at a nondimensional time of t* = 1 (t* = ct/a2). As anticipated, with increasing distance from the wellbore, the temperature decreases rapidly. There is a noticeable difference in the temperature between LTNE and the classical LTE theory, especially in the vicinity of the borehole wall. The classical LTE theory underestimates the temperature drop, hence the induced thermal contraction.

Fig. 4
figure 4

Normalized temperature drop versus radial distance from the wellbore at a nondimentional time t* = ct/a2 = 1

Full size image

4.2 Pore pressure fields

According to Eq. (34), hydraulic stimulation induced changes in pore pressure are caused by two factors: the first is the temperature difference between injected fluid and native fluid; and the second is the fluid flux at the wellbore wall. To gain some insight into the transient evolution of pore pressure, a decomposition technique is utilized to quantify the separate contributions of convective cooling and fluid injection to the variation in pore pressure, as shown in Figs. 5 and 6. Figure 5 shows the evolution of hydraulically induced pore pressure by the injection of an isothermal fluid at a constant flux qw, where LTNE has no effect on the pore pressure evolution. Pore pressure decreases dramatically with increasing distance from the wellbore over time. At a given location, pore pressure increases steadily with increasing time. In contrast to the constant pore pressure boundary adopted by He et al. (2012), we observed that the pore pressure at the borehole wall keeps increasing with time to drive fluid into the formation at a constant flux.

Fig. 5
figure 5

Normalized pore pressure versus radial distance induced by the injection of an isothermal fluid at a constant flux

Full size image
Fig. 6
figure 6

Convective cooling induced pore pressure versus radial distance at different normalized times

Full size image

Figure 6 shows thermally induced pore pressure along the radial direction at different nondimentional times, where LTNE plays an active role in the pore pressure evolution. From Fig. 6, it is clear that thermally induced pore pressure decreases with increasing distance from the borehole. The LTNE theory predicts a slightly higher pore pressure than the LTE theory, despite the fact that both theories predict a similar distribution pattern for thermally induced pore pressure along the radial direction. We note that the injection induced pore pressure is partially offset by the thermally induced pore pressure.

4.3 Stress field

Figures 7 and 8 show the evolution of hydraulically induced radial stress and hoop stress (normalized by \({{q_{w} \mu_{f} a} \mathord{\left/ {\vphantom {{q_{w} \mu_{f} a} k}} \right. \kern-0pt} k}\)) along the radial direction, respectively. It is observed that at a specific location, the magnitude of injection induced hoop stress increases with increasing time. At a certain time, injection induced hoop stress decays with increasing distance from the borehole.

Fig. 7
figure 7

Hydraulically induced radial stress versus radial distance caused by the injection of an isothermal fluid at a constant flux at different normalized times

Full size image
Fig. 8
figure 8

Hydraulically induced hoop stress versus radial distance caused by injection of an isothermal fluid at a constant flux at different normalized times

Full size image

Figures 9 and 10 show the thermally induced radial stress and hoop stress as a function of radial distance at different times, respectively. In Fig. 9, we observe a non-monotonic evolution behavior of thermally induced radial stress in the classical LTE theory. A gradual increase in radial stress occurs as the distance from the borehole increases, culminating in a peak. With increasing time, the magnitude of the peak radial stress also increases. While in the LTNE theory, thermally induced radial stress decreases progressively with increasing distance from the borehole. The sharp difference in the distribution pattern of thermally induced radial stress between the classical LTE and LNTE theories highlights the significance of incorporating LTNE in the geomechanical analysis of hydraulic stimulation of EGS. From Fig. 10, it is clear that LTNE has a profound effect on the evolution of thermally induced hoop stress along the radial direction. In the LTNE theory, the hoop stress changes from compressive to tensile with increasing distance from the borehole. On the contrary, the classical LTE theory predicts that hoop stress is tensile in the vicinity of the borehole and becomes compressive at further distances. The tensile domain expands with increasing time.

Fig. 9
figure 9

Convective cooling induced radial stress versus radial distance from the borehole at different normalized times

Full size image
Fig. 10
figure 10

Convective cooling induced hoop stress versus radial distance from the borehole at different normalized times

Full size image

5 Conclusions

In this paper, we present an analytical solution for a well subjected to a non-isothermal fluid flux and convective cooling within a thermoporoelastic medium under LTNE conditions, with applications to hydraulic stimulation in EGS. Load decomposition and superposition techniques are employed to derive the hydraulic stimulation induced temperatures, pore pressure, and stresses. The separate contributions of fluid injection and convective cooling to the induced pore pressure and stresses are qualitatively determined. We reach the following conclusions:

  1. (1)

    At early times, convective cooling reduces pore pressure, counteracting the pressure increase caused by fluid injection.

  2. (2)

    The LTNE theory predicts marginally higher thermally induced pore pressure compared to the LTE theory.

  3. (3)

    LTNE has a significant influence on the distribution pattern of thermally induced radial and hoop stresses, distinct from the patterns predicted by classical LTE theory.