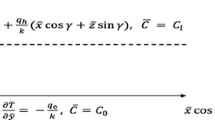Abstract
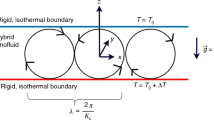
The contribution of Robin boundaries on the onset of convection in a horizontal saturated porous layer covered by a free surface on the top is investigated here. The saturated solid matrix is assumed in a regime where the temperature profile of the solid phase differs from a fluid one. Two energy equations are adopted as a consequence of the local thermal non-equilibrium model (LTNE), and four Biot numbers are arising out of the third kind of boundaries imposed on both surfaces. The dimensionless parameters H and \(\gamma \) which rule the transition from local thermal equilibrium (LTE) to non-equilibrium one or vice versa are taken into account. The cases of equal and different Biot numbers have been considered beside the asymptotic limits of LTE and LTNE one. A linear stability analysis of the basic motionless state has been performed. The perturbation terms of the main steady flows are evaluated in the form of plane waves. The eigenvalue problem is solved either analytically or numerically depending on the temperature gradient of the fluid phase. The analytical solution is handled through a dispersion relation, while the numerical one is computed by the Runge–Kutta solver combined with the shooting method. The variation in Darcy–Rayleigh number and wave number is obtained with respect to Biot numbers for all resulting cases.








Similar content being viewed by others
References
Banu, N., Rees, D.A.S.: Onset of Darcy–Bénard convection using a thermal nonequilibrium model. Int. J. Heat Mass Transf. 45, 2221–2228 (2002)
Barletta, A.: Thermal instabilities in a fluid saturated porous medium. In: Öchsner, A., Murch, G.E. (eds.) Heat Transfer in Multi-phase Materials, pp. 381–414. Springer, New York (2011)
Barletta, A., Celli, M., Lagziri, H.: Instability of a horizontal porous layer with local thermal non-equilibrium: effects of free surface and convective boundary conditions. Int. J. Heat Mass Transf. 89, 75–89 (2015)
Celli, M., Kuznetsov, A.: A new hydrodynamic boundary condition simulating the effect of rough boundaries on the onset of Rayleigh–Bénard convection. Int. J. Heat Mass Transf. 116, 581–586 (2018)
Celli, M., Lagziri, H., Bezzazi, M.: Local thermal non-equilibrium effects in the Horton–Rogers–Lapwood problem with a free surface. Int. J. Therm. Sci. 116, 254–264 (2017)
Horton, C.W., Rogers, F.T.: Convection currents in a porous medium. J. Appl. Phys. 16, 367–370 (1945)
Kaviany, M.: Thermal nonequilibrium between fluid and solid phases. In: Principles of Heat Transfer in Porous Media, 2nd edn, pp. 391–424. Springer
Kuznetsov, A.V.: Thermal nonequilibrium forced convection in porous media. In: Ingham, D.B., Pop, I. (eds.) Transport Phenomena in Porous Media, pp. 103–129. Pergamon, Oxford (1998)
Lapwood, E.R.: Convection of a fluid in a porous medium. Proc. Camb. Philos. Soc. 44, 508–521 (1948)
Nield, D.A.: A note on local thermal non-equilibrium in porous media near boundaries and interfaces. Transp. Porous Med. 95(3), 581–584 (2012)
Rees, D.A.S.: Stability of Darcy–Bénard convection. In: Vafai, K. (ed.) Handbook of Porous Media, pp. 521–558. Begell House, Redding, CT (2000)
Rees, D.A.S., Pop, I.: Local thermal non-equilibrium in porous medium convection. In: Ingham, D.B., Pop, I. (eds.) Transport Phenomena in Porous Media III, pp. 147–173. Pergamon, Oxford (2005)
Siddheshwa, P.G.: Convective instability of ferromagnetic fluids bounded by fluid-permeable, magnetic boundaries. J. Magn. Magn. Mater. 149, 148–150 (1995)
Tyvand, P.A.: Onset of Rayleigh–Bénard convection in porous bodies. In: Ingham, D.B., Pop, I. (eds.) Transport Phenomena in Porous Media II, pp. 82–112. Pergamon, Oxford (2002)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A : The Principle of Exchange of Instabilities for Limiting Case \(H\rightarrow 0\)
Appendix A : The Principle of Exchange of Instabilities for Limiting Case \(H\rightarrow 0\)
The eigenvalue problem obtained for the case characterized by no transfer of the heat is carried out between the two phases is
Multiplying Eqs. (48a), (48b) by the complex conjugate quantities \(\bar{\psi }\) and \(\bar{\theta }\), respectively, gives rise to two complex resulting equations. These equations are integrated by part with the use of boundary conditions, namely
After multiplying Eq. (49a) by the parameter \(\dfrac{-\gamma {{\tilde{B}}}_{f12}}{R(1+\gamma )}\), we can now add it to Eq. (49b) to obtain
The two parts of real and imaginary in Eq. (50) have to be independently equal to zero to satisfy the condition of
Equation (51) defines two different assumptions. The first one is \(\theta =0 \) which means no secondary flow exists in the basic state. This condition cannot be acceptable because it would imply a contradiction with what we are looking for. Thus, this result supports the validity of the second assumption which is \(\omega _R=0\). Consequently, we can assure that the eigenvalue problem of this limiting cases holds the principle of exchange of instabilities.
Rights and permissions
About this article
Cite this article
Lagziri, H., Bezzazi, M. Robin Boundary Effects in the Darcy–Rayleigh Problem with Local Thermal Non-equilibrium Model. Transp Porous Med 129, 701–720 (2019). https://doi.org/10.1007/s11242-019-01301-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11242-019-01301-2