Control of Three-Phase Voltage Source Converters with the Derivative-Free Nonlinear Kalman Filter

Abstract

The paper is concerned with proving differential flatness of the three-phase voltage source converter (VSC) model and its resulting description in the Brunovsky (canonical) form. For the linearized canonical model of the converter a feedback controller is designed. At a second stage, a novel Kalman Filtering method (Derivative-free nonlinear Kalman Filtering) is introduced. The proposed Kalman Filter is redesigned as disturbance observer for estimating additive input disturbances to the VSC model. These estimated disturbance terms are finally used by a feedback controller that enables the DC output voltage track desirable setpoints. The efficiency of the proposed state estimation-based control scheme is tested through simulation experiments.

Introduction

The paper proposes a nonlinear control scheme for three-phase voltage source converters (VSCs) where estimation of disturbances and variations of the load current is performed with the use of a new nonlinear filtering approach, the so-called Derivative-free nonlinear Kalman Filter. VSCs, are three-phase filtered rectifiers, that are widely used in the electric power grid (mainly for power flow control). VSCs are the main building blocks of power flow controllers in transmission lines. For example, VSCs are contained in unified power flow controllers, or distribution-static synchronous compensators. VSCs enable control of the amplitude and phase angle of the AC terminal voltages. Moreover, their bidirectional power flow capabilities allow VSCs to perform real and/or reactive power flow control in AC transmission lines [1].

The dynamic model of VSCs is a nonlinear one and several nonlinear control methods have been proposed for it. Linearization round certain operating points with the computation of Jacobian matrices and control with the use of linear feedback control methods have to cope with the approximate linearization errors [2, 3]. Operation range is restricted and a relatively big capacitor is needed for keeping a constant DC-voltage in presence of a varying load. Initial nonlinear control approaches consider the representation of the VSC dynamics in the dq reference frame and use PI compensators. Passivity-based control methods have been proposed in [4]. Neural/fuzzy control methods for VSCs have been analyzed in [5–8]. Back-stepping control approaches have been proposed in [9]. State estimation-based control for VSCs has been studied in [10–12]. The power matching modulation approach has been proposed in [13, 14], while the virtual flux control method has been analyzed in [15, 16].

Other control approaches consider input–output linearization, as well as input-state linearization [17]. The latter methods transform the nonlinear system into a decoupled linear one. It is also known that one can attempt transformation of the nonlinear VSC model into the linear canonical (Brunovsky) form through the application of Lie-algebra. With the application of Lie-algebra methods it is possible to arrive at a description of the system in the linear canonical form if the relative degree of the system is equal to the order of the system. However, this linearization procedure requires the computation of Lie derivatives (partial derivatives on the vector fields describing the system dynamics) and this can be a cumbersome computation procedure.

Moreover, differential flatness theory has been proposed for VSC control [18–20]. Differential flatness theory is currently a main direction in nonlinear dynamical systems and enables linearization for a wider class of systems than the one succeeded with Lie-algebra methods [21–23]. To find out if a dynamical system is differentially flat, the following should be examined: (i) the existence of the so-called flat output, i.e., a new variable which is expressed as a function of the system’s state variables. The flat output and its derivatives should not be coupled in the form of an ordinary differential equation (ODE), (ii) the components of the system (i.e., state variables and control input) should be expressed as functions of the flat output and its derivatives [24–27]. In certain cases the differential flatness theory enables transformation to a linearized form (canonical Brunovsky form) for which the design of the controller becomes easier. In other cases by showing that a system is differentially flat, one can easily design a reference trajectory as a function of the so-called flat output and can find a control law that assures tracking of this desirable trajectory [25, 26].

This paper is concerned with proving differential flatness of the three-phase VSC model and its resulting description in the Brunovsky (canonical) form [28]. It is shown that for the linearized converter’s model it is possible to design a feedback controller. At a second stage, a novel Kalman Filtering method, the Derivative-free nonlinear Kalman Filter, is proposed for estimating the non-measurable elements of the state vector of the linearized system. With the redesign of the proposed Kalman Filter as a disturbance observer, it becomes possible to estimate disturbance terms which are due to variations of the load current and to use these terms in the feedback controller. By avoiding linearization approximations, the proposed filtering method, improves the accuracy of estimation, and results in smooth control signal variations and in minimization of the tracking error of the associated control loop [29–32].

The structure of the paper is as follows: in “Linearization of the Converter’s Model Using Lie Algebra” section the dynamic model of the VSC is analyzed. Moreover, it is shown how linearization of the model of the VSC can be performed by applying Lie-algebra theory. In “Differential Flatness of the Voltage Source Converter” section it is proven that the model of the VSC is a differentially flat one and that it can be transformed to the linear canonical form. In “Kalman Filter-Based Disturbance Observer for the VSC Model” section it is shown that the Derivative-free nonlinear Kalman Filter can be redesigned in the form of a disturbance observer so as to enable estimation of disturbance terms which are due to load current variations. In “Simulation Tests” section simulation tests are provided to evaluate the performance of the proposed nonlinear control scheme. Finally, in “Conclusions” section concluding remarks are stated.

Linearization of the Converter’s Model Using Lie Algebra

Dynamic Model of the Voltage Source Converter

The VSC model in the rotating dq reference frame is given by [11, 20]:

$$\begin{aligned}&L{\dot{i}_d}={-}R{i_d}+L{\omega }{i_q}+v_d-{V_{dc} \over 2}{u_1},\nonumber \\&L{\dot{i}_q}={-}L{\omega }{i_d}-R{i_q}+v_q-{V_{dc} \over 2}{u_2}, \\&{C_{DC}}{\dot{V}_{DC}}={-}{1 \over R_c}V_{DC}+{3 \over 4}{i_d}{u_1}+{3 \over 4}{i_q}{u_2},\nonumber \end{aligned}$$

(1)

where ${i_d},\,{i_q}$ are the line currents $(i_a,\,i_b,\,i_c)$ after transformation in the dq reference frame, and equivalently ${v_d},\,{v_q}$ are the phase voltages ${v_a},\,{v_b},\,{v_c}$ after transformation in the dq reference frame. Variable $V_{dc}$ denotes the DC voltage output of the converter, $u_1=\eta _d$ and $u_2=\eta _q$ stand for control inputs. The line losses and the transformer conduction losses are modelled by R and the inverter switching losses are modeled by $R_c.$ Moreover, $v_q$ is taken to be 0.

In Fig. 1 the electric circuit of the VSC is depicted. Denoting $x=[i_d,\,i_q,\,V_{dc}]^T$ as the state vector, $y=[e_c,\,i_q]^T$ as the output and $u=[\eta _d,\,\eta _q]^T$ as the input vector, the MIMO nonlinear one of the VSC is written in the state-space form

$$\begin{aligned}&\dot{x}=f(x)+G(x)u,\nonumber \\&y=h(x), \end{aligned}$$

(2)

where

$$\begin{aligned}&f=\begin{pmatrix} -{R \over L}{x_1}+{\omega }{x_2}+{v_d \over L} \\ -{\omega }{x_1}-{R \over L}x_2 \\ -{x_3 \over {{C_DC}{R_c}}} \end{pmatrix},\quad \nonumber \\&G=\left[ g_1 \ g_2\right] = \begin{pmatrix} -{x_3 \over {2L}} &{}\quad 0 \\ 0 &{}\quad -{x_3 \over {2L}} \\ {{3{x_1}} \over {4C_{dc}}} &{}\quad {{3{x_1}} \over {4C_{dc}}} \end{pmatrix}, \end{aligned}$$

(3)

$$\begin{aligned}&h=\begin{pmatrix} h_1 \\ h_2 \end{pmatrix}= \begin{pmatrix} e_c \\ i_q \end{pmatrix}= \begin{pmatrix} {3 \over 4}L(x_1^2+x_2^2)+{C_{dc} \over 2}{x_3^2} \\ x_2 \end{pmatrix}. \end{aligned}$$

(4)

Fig. 1

Electrical circuit of the voltage source converter

Linearization of the Converter’s Model Using Lie-Algebra

Linearization of the converter’s model will be performed using Lie-algebra and with the computation of the associated Lie derivatives [33, 34]. The following state variables are defined: $z_1=h_1(x),\,z_2={L_f}h_1(x),$ and $z_3=h_2(x).$ After intermediate computations (see “Appendix: Linearization of the Converter’s Model Using Lie-Algebra” section) one arrives at the following equations

$$\begin{aligned} \dot{z}_1= & {} z_2,\nonumber \\ \dot{z}_2= & {} v_1,\nonumber \\ \dot{z}_3= & {} v_2, \end{aligned}$$

(5)

or in state-space description

$$\begin{aligned}&\begin{pmatrix} \dot{z}_1 \\ \dot{z}_2 \\ \dot{z}_3 \end{pmatrix}= \begin{pmatrix} 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \end{pmatrix} \begin{pmatrix} z_1 \\ z_2 \\ z_3 \end{pmatrix}+ \begin{pmatrix} 0 &{}\quad 0 \\ 1 &{}\quad 0 \\ 0 &{}\quad 1 \end{pmatrix} \begin{pmatrix} v_1 \\ v_2 \end{pmatrix},\nonumber \\&\begin{pmatrix} y_1 \\ y_2 \end{pmatrix}= \begin{pmatrix} 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 \end{pmatrix} \begin{pmatrix} z_1 \\ z_2 \\ z_3 \end{pmatrix}, \end{aligned}$$

(6)

where the new control inputs are defined as

$$\begin{aligned} v_1= & {} {L_f^2}{h_1}(x)+{L_{g_1}}{L_f}{h_1}(x){u_1}+{L_{g_2}}{L_f}{h_2}(x){u_2},\nonumber \\ v_2= & {} f_{21}+g_{22}{u_2}. \end{aligned}$$

(7)

Therefore, the initial nonlinear system of the VSC is transformed into the linear canonical form. The linearized system is controllable and observable.

Differential Flatness of the Voltage Source Converter

Definition of Differentially Flat Systems

Differential flatness is a structural property of a class of nonlinear systems, denoting that all system variables (such as state vector elements and control inputs) can be written in terms of a set of specific variables (the so-called flat outputs) and their derivatives. The following nonlinear system is considered:

$$\begin{aligned} \dot{x}(t)=f(x(t),\,u(t)). \end{aligned}$$

(8)

The time is $t{\in }R,$ the state vector is $x(t){\in }R^n$ with initial conditions $x(0)=x_0,$ and the input is $u(t){\in }R^m.$ Next, the properties of differentially flat systems are given [21–27, 35].

The finite dimensional system of Eq. (8) can be written in the general form of an ODE, i.e., $S_i\,(w,\,\dot{w},\,\ddot{w},\ldots ,\,w^{(i)}),\, i=1,\,2,\ldots ,q.$ The term w is a generic notation for the system variables [these variables are for instance the elements of the system’s state vector x(t) and the elements of the control input u(t)] while $w^{(i)},\,i=1,\,2,\ldots ,q$ are the associated derivatives. Such a system is differentially flat if there are m functions $y=(y_1,\ldots ,y_m)$ of the system variables and of their time-derivatives, i.e., $y_i=\phi (w,\,\dot{w},\,\ddot{w},\ldots ,w^{(\alpha _i)}), \,i=1,\ldots ,m$ satisfying the following two conditions [23–28, 35]:

• (1) There does not exist any differential relation of the form $R(y,\,\dot{y},\ldots ,y^{(\beta )})=0$ which implies that the derivatives of the flat output are not coupled in the sense of an ODE, or equivalently it can be said that the flat output is differentially independent.

• (2) All system variables (i.e., the elements of the system’s state vector w and the control input) can be expressed using only the flat output y and its time derivatives $w_i={\psi _i}\,(y,\,\dot{y},\ldots ,y^{(\gamma _i)}), \, i=1,\ldots ,s.$ An equivalent definition of differentially flat systems is as follows:

Definition: The system $\dot{x}=f(x,\,u),\,x{\in }{R^n},\,u{\in }{R^m}$ is differentially flat if there exist relations

$$\begin{aligned}&h{\text {:}}\,{R^n}{\times }{{\left( R^m\right) }^{r+1}}{\rightarrow }{R^m},\nonumber \\&\phi {\text {:}}\,{\left( R^m\right) ^r}{\rightarrow }{R^n} \, \text {and}\nonumber \\&\psi {\text {:}}\, \left( R^m\right) ^{r+1}{\rightarrow }{R^m}, \end{aligned}$$

(9)

such that

$$\begin{aligned} y= & {} h\left( x,\,u,\,\dot{u},\ldots ,u^{(r)}\right) , \nonumber \\ x= & {} \phi \left( y,\,\dot{y},\ldots ,y^{(r-1)}\right) , \, \text {and} \nonumber \\ u= & {} \psi \left( y,\,\dot{y},\ldots ,y^{(r-1)},\,y^{(r)}\right) . \end{aligned}$$

(10)

This means that all system dynamics can be expressed as a function of the flat output and its derivatives, therefore the state vector and the control input can be written as

$$\begin{aligned} x(t)= & {} \phi \left( y(t),\,\dot{y}(t),\ldots ,y^{(r-1)}(t)\right) , \,\text {and}\nonumber \\ u(t)= & {} \psi \left( y(t),\,\dot{y}(t),\ldots ,y^{(r)}(t)\right) . \end{aligned}$$

(11)

It is noted that for linear systems the property of differential flatness is equivalent to that of controllability.

Differential Flatness of the Voltage Source Converter’s Model

It will be shown that the dynamic model of the VSC is a differentially flat one, i.e., it holds that all state variables and its control inputs can be written as functions of the flat outputs and their derivatives. Moreover, it will be shown that by expressing the elements of the state vector as functions of the flat outputs and their derivatives one obtains a transformation of the VSC model into the linear canonical (Brunovsky) form.

The following flat outputs are defined

$$\begin{aligned}&y_{f_1}={h_1}={{3L} \over 4}\left( x_1^2+x_2^2\right) +{C_{{dc}_2} \over 2}x_3^2, \end{aligned}$$

(12)

$$\begin{aligned}&y_{f_2}={h_2}=i_q. \end{aligned}$$

(13)

It holds that

$$\begin{aligned} \dot{y}_{f_1}={-}{3 \over 2}R\left( x_1^2+x_2^2\right) +{3 \over 2}{v_d}{x_1}-{1 \over R_c}{x_3^2}, \end{aligned}$$

(14)

while deriving once more with respect to time one gets

$$\begin{aligned} \ddot{y}_{f_1}= & {} {{3R^2} \over 2}\left( x_1^2+x_2^2\right) -{{3R} \over L}{v_d}{x_1}+{{2{x_3^2}} \over {{C_{dc}}{R_c^2}}}\nonumber \\&+\left( -{{3R} \over {2L}}{x_1}{x_3}-{3 \over {4L}}{v_d}{x_3}-{{3{x_1}{x_3}} \over {2{R_c}C_{dc}}}\right) {u_1}\nonumber \\&+\left( {{3R{x_2}{x_3}} \over {2L}}-{{3{x_2}{x_3}} \over {2{R_c}{C_{dc}}}}\right) {u_2}. \end{aligned}$$

(15)

Moreover,

$$\begin{aligned} \dot{y}_{f_2}=\left( {-}\omega {x_1}-{R \over L}x_2\right) -{x_3 \over {2L}}{u_2}. \end{aligned}$$

(16)

It can be confirmed that all state variables and the control inputs of the VSC model can be written as functions of the flat outputs $y_{f_1},\,y_{f_2}$ and of their derivatives. It holds that $y_{f_2}=x_2=i_q.$ Moreover, using the definition of the flat outputs it holds

$$\begin{aligned}&\dot{y}_{f_1}={-}{3 \over 2}R\left( x_1^2+x_2^2\right) +{3 \over 2}{v_d}{x_1}-{1 \over R_c}{x_3^2}, \end{aligned}$$

(17)

$$\begin{aligned}&y_{f_2}=x_2. \end{aligned}$$

(18)

Solving Eq. (17) with respect to $x_3^2$ one obtains

$$\begin{aligned} x_3^2={R_c}\left[ -{3 \over 2}R{x_1^2}-{3 \over 2}R{y_{f_2}^2}+{3 \over 2}{v_d}{x_1}-\dot{y}_{f_1}\right] . \end{aligned}$$

(19)

By substituting Eq. (19) into Eq.  (12) one gets

$$\begin{aligned} y_{f_1}= & {} {3 \over 4}L{x_1^2}+{3 \over 4}L{y_{f_2}^2}\\&+\,{C_{dc} \over 2}{R_c}\left[ -{3 \over 2}R{x_1^2}-{3 \over 2}R{y_2^2}+{3 \over 2}{v_d}{x_1}-\dot{y}_{f_1}\right] \\&\Rightarrow \left( {{3L-3{C_{dc}{R_c}R}} \over 4}\right) {x_1^2}+{{3{C_{dc}}{R_c}{v_d}} \over 4}{x_1}\\&+\left( {3 \over 4}L{y_{f_2}^2}-{{3{C_{dc}}{R_c}R} \over 4}{y_{f_2}^2} -{{{C_{dc}}{R_c}} \over 2}\dot{y}_{f_1}-y_{f_1}\right) =0. \end{aligned}$$

By computing the roots of the binomial given in the above equation it becomes possible to express state variable $y_1$ as a function of the flat outputs and their derivatives. Thus, by keeping the maximum of the binomial’s root’s one obtains

$$\begin{aligned} x_1=f_a\left( y_{f_1},\,\dot{y}_{f_1},\,y_{f_2}\right) . \end{aligned}$$

(20)

Using the relation for $x_1$ described in Eq. (20) into Eq. (19) one has

$$\begin{aligned} x_3^2= & {} R_c\left[ -{3 \over 2}R{f_a}\left( y_{f_1},\,\dot{y}_{f_1},\,y_{f_2}\right) -{3 \over 2}R{y_{f_2}^2}\right. \\&\left. +\,{3 \over 2}{v_d}f_a\left( y_{f_1},\,\dot{y}_{f_1},\,y_{f_2}\right) -\dot{y}_1\right] {\Rightarrow } x_3\\= & {} {R_c}\left[ -{3 \over 2}R{f_a}\left( y_{f_1},\,\dot{y}_{f_1},\,y_{f_2}\right) -{3 \over 2}R{y_{f_2}^2}\right. \\&\left. +\,{3 \over 2}{v_d}f_a\left( y_{f_1},\,\dot{y}_{f_1},\,y_{f_2}\right) -\dot{y}_1\right] ^{1 \over 2}{\Rightarrow } {x_3}\\= & {} f_b\left( y_{f_1},\,\dot{y}_{f_1},\,y_{f_2}\right) . \end{aligned}$$

From the first line of the state-space description of the system given in Eq. (2) and Eqs. (3)–(4) it holds that

$$\begin{aligned}&\dot{x}_1=\left( -{R \over L}{x_1}+{\omega }{x_2}+{v_d \over L}\right) -{x_3 \over {2L}}u_1{\Rightarrow }\nonumber \\&u_1={{\left( -{R \over L}{x_1}+{\omega }{x_2}+{v_d \over L}\right) -\dot{x}_1} \over {{x_3} \over {2L}}}{\Rightarrow }\nonumber \\&u_1={f_c}\left( y_{f_1},\,\dot{y}_{f_1},\,y_{f_2}\right) . \end{aligned}$$

(21)

Similarly, from the second line of the state-space description of the system given in Eq. (2) and Eqs. (3)–(4) it holds that

$$\begin{aligned}&\dot{x}_2=\left( -{\omega }{x_1}-{R \over L}{x_2}\right) -{x_3 \over {2L}}u_2{\Rightarrow }\nonumber \\&u_2={{{-}{\omega }{x_1}-{R \over L}x_2-\dot{x}_2} \over {x_3 \over {2L}}}{\Rightarrow }\nonumber \\&u_2={f_d}\left( y_{f_1},\,\dot{y}_{f_1},\,y_{f_2}\right) . \end{aligned}$$

(22)

Consequently, all state variables and the control inputs in the model of the VSC can be written as functions of the flat outputs and their derivatives. Thus, the VSC model is a differentially flat one.

Linearization of the Converter’s Model Using Differential Flatness Theory

Using the definitions of the flat outputs $y_{f_1}$ and $y_{f_2}$ for the VSC model, and considering the new state variables $z_1=y_{f_1},\,z_2=\dot{y}_{f_1}$ and $z_3=y_{f_2}$ one obtains

$$\begin{aligned} \dot{z}_1= & {} z_2,\nonumber \\ \dot{z}_2= & {} {{3R^2} \over 2}\left( x_1^2+x_2^2\right) -{{3R} \over L}{v_d}{x_1}+{{2{x_3^2}} \over {{C_{dc}}{R_c^2}}}\nonumber \\&+\left( {{3R} \over {2L}}{x_1}{x_3}-{3 \over {4L}}{v_d}{x_3}-{{3{x_1}{x_3}} \over {2{R_c}C_{dc}}}\right) u_1\nonumber \\&+\left( {{{3R}{x_2}{x_3}} \over {2L}}-{{3{x_2}{x_3}} \over {2{R_c}C_{dc}}}\right) {u_2},\nonumber \\ \dot{z}_3= & {} \left( -{\omega }{x_1}-{R \over L}{x_2}\right) -{{x_3} \over {2L}}{u_2}, \end{aligned}$$

(23)

or equivalently

$$\begin{aligned} \dot{z}_1=z_2, \nonumber \\ \dot{z}_2=v_1, \nonumber \\ \dot{z}_3=v_2, \end{aligned}$$

(24)

which can be also written in state-space form

$$\begin{aligned}&\begin{pmatrix} \dot{z}_1 \\ \dot{z}_2 \\ \dot{z}_3 \end{pmatrix}= \begin{pmatrix} 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \end{pmatrix} \begin{pmatrix} z_1 \\ z_2 \\ z_3 \end{pmatrix}+ \begin{pmatrix} 0 &{}\quad 0 \\ 1 &{}\quad 0 \\ 0 &{}\quad 1 \end{pmatrix} \begin{pmatrix} v_1 \\ v_2 \end{pmatrix},\nonumber \\&\begin{pmatrix} \dot{y}_1 \\ \dot{y}_2 \end{pmatrix}= \begin{pmatrix} 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 \end{pmatrix} \begin{pmatrix} z_1 \\ z_2 \\ z_3 \end{pmatrix}. \end{aligned}$$

(25)

As already noted, the linearized system is controllable and observable. The new control inputs $v_i, \, i=1,\,2$ are the same as the ones defined in the Lie algebra-based approach [see Eq. (50) in “Appendix: Linearization of the Converter’s Model Using Lie-Algebra” section]. The linearized model of the VSC can be described by the following two equations

$$\begin{aligned} \ddot{z}_1= & {} v_1,\nonumber \\ \dot{z}_3= & {} v_2. \end{aligned}$$

(26)

The control inputs which enable convergence to the desirable setpoints are

$$\begin{aligned} v_1= & {} \ddot{z}_1^d-{k_1^1}\left( \dot{z}_1^1-\dot{z}_1^d\right) -{k_2^1}\left( z_1-z_1^d\right) ,\nonumber \\ v_2= & {} \dot{z}_3^d-{k_1^2}\left( z_3-z_3^d\right) . \end{aligned}$$

(27)

The control law of Eq. (27) succeeds the following tracking error dynamics

$$\begin{aligned}&\ddot{e}_1+{k_1^1}\dot{e}_1+{k_2^1}e_1=0,\nonumber \\&\dot{e}_3+{k_1^2}{e_3}=0, \end{aligned}$$

(28)

which results into $lim_{t{\rightarrow }\infty }e_1(t)=0$ and $lim_{t{\rightarrow }\infty }e_3(t)=0.$ It can be noticed that the linearized model of the converter obtained after the application of differential flatness theory is the same with the one obtained with the use of the Lie derivative approach. It holds that

$$\begin{aligned} v_1= & {} {L_f^2}{h_1}(x)+{L_{g_1}}{L_f}{h_1}(x){u_1} +{L_{g_2}}{L_f}{h_1}(x){u_2},\nonumber \\ v_2= & {} {L_f}{h_2}(x)+{L_{g_1}}{h_2}(x){u_1}+{L_{g_2}}{h_2}(x){u_2}, \end{aligned}$$

(29)

or, in matrix form

$$\begin{aligned} \begin{pmatrix} v_1 \\ v_2 \end{pmatrix}= & {} \begin{pmatrix} {L_f^2}{h_1}(x) \\ {L_f}{h_2}(x) \end{pmatrix}\nonumber \\&+ \begin{pmatrix} {L_{g_1}}{L_f}{h_1}(x) &{}\quad {L_{g_2}}{L_f}{h_1}(x) \\ {L_{g_1}}h_2(x) &{}\quad {L_{g_2}}h_2(x) \end{pmatrix} \begin{pmatrix} u_1 \\ u_2 \end{pmatrix}. \end{aligned}$$

(30)

It holds that

$$\begin{aligned}&\begin{pmatrix} v_1 \\ v_2 \end{pmatrix}\nonumber \\&\quad = \begin{pmatrix} {{3R^2} \over 2}(x_1^2+x_2^2)-{{3R} \over L}{v_d}{x_1}+{{2{x_3^2}} \over {{C_{dc}}{R_c^2}}} \\ -{\omega }{x_1}-{R \over L}{x_2} \end{pmatrix}\nonumber \\&\quad +\begin{pmatrix} {{3R} \over {2L}}{x_1}{x_3}-{3 \over {4L}}{v_d}{x_3}-{{3{x_1}{x_3}} \over {2{R_c}C_{dc}}} &{}\quad {{{3R}{x_2}{x_3}} \over {2L}}-{{3{x_2}{x_3}} \over {2{R_c}{C_{dc}}}} \\ 0 &{}\quad -{x_3 \over {2L}} \end{pmatrix} \begin{pmatrix} u_1 \\ u_2 \end{pmatrix}. \end{aligned}$$

(31)

According to the above, the VSC dynamic model can be also written in a more compact form as

$$\begin{aligned} \tilde{v}= & {} \tilde{f}+M\tilde{u}{\Rightarrow }\nonumber \\ \tilde{u}= & {} M^{-1}(\tilde{v}-\tilde{f}). \end{aligned}$$

(32)

Outlining the previous linearization approach one starts from Eqs. (12) and (13) which provide the flat outputs of the system. By successive derivations of these flat outputs with respect to time one arrives at an input–output linearized equivalent description which can be also written in the linear canonical (Brunovsky) form. Thus linearization of the system’s dynamics is achieved and from that point on the solution of the feedback control and of the state estimation problems becomes possible. The flat outputs for a dynamical system are chosen to be functions of its state vector elements. In a large part of the relevant bibliography there is no systematic approach for selecting flat outputs, as there is no systematic way to choose a Lyapunov function for a control loop. However, as noted in [35], recently there have been developed methods which enable to compute analytically the flat outputs of dynamical systems is based on expressing the system in the so-called implicit form and in computing the associated differential matrix [24].

To solve state estimation problems in the VSC model the Derivative free nonlinear Kalman Filter will be introduced next. The Derivative-free nonlinear Kalman Filter stands for a new contribution to the field of nonlinear estimation and under certain conditions it is proven to maintain the optimality features of the standard Kalman Filter. By proving that the monitored system is differentially flat, its transformation to the linear canonical (Brunovsky) form becomes possible. This enables to solve both the control and the state estimation problem. The novelty of the article is primarily in the used nonlinear estimation method, which is the Derivative-free nonlinear Kalman Filter. The filter consists of (i) a nonlinear transformation (diffeomorphism) which enables to write the state-space model of the system into the linear canonical form, (ii) application of the Kalman Filter recursion to the equivalent linearized model, and (iii) an inverse transformation, based again on differential flatness theory, which enables to obtain state estimates for the initial nonlinear model. This filtering method is a new and genuine result in nonlinear estimation theory which under specific conditions retains the optimality features of the standard Kalman Filter. Moreover, the use of the aforementioned filter as a disturbances estimator is also a novel element in this research work. The filter estimates simultaneously the non-measurable state vector elements of the converters and disturbances or modelling error terms that affect its functioning. Comparing to other nonlinear estimators the new filter provides state estimates of improved accuracy (minimum variance). Moreover, in [35] it has been demonstrated that this filter is computationally faster than other nonlinear filters (extended and unscented Kalman Filter or particle filter).

Kalman Filter-Based Disturbance Observer for the VSC Model

The simultaneous estimation of the non-measurable elements of the VSC state vector (e.g., $\dot{y}_{f_1}$) as well as the estimation of additive disturbance terms (e.g., associated with variations of the load current $i_L$) is possible with the use of a disturbance estimator [36–40].

Next, it will be considered that additive input disturbances (e.g., due to load variations) affect the VSC model. Thus, it is assumed that the third row of the state-space equations of the VSC of Eq. (2) includes a disturbance term

$$\begin{aligned} \dot{x}_3=-{{x_3} \over {C_{dc}{R_c}}}+{{3{x_1}} \over {4{C_DC}}}u_1+{{3{x_2}} \over {4{C_DC}}}u_2+\tilde{d}. \end{aligned}$$

(33)

By describing the system’s dynamics using the differential flatness theory approach and using the definition of the input $v_1$ given in Eq. (31), the disturbances’ effects appear as follows

$$\begin{aligned} \ddot{y}_{f_1}=v_1+\left( -{2 \over R_c}{x_3}\tilde{d}\right) , \end{aligned}$$

(34)

which means that the additive disturbance term is now described by

$$\begin{aligned} \tilde{T}_d=-{2 \over R_c}{x_3}\tilde{d}. \end{aligned}$$

(35)

The disturbance $\tilde{T}_d$ may also comprise additional uncertainty terms associated with the numerical values of the parameters of the VSC model. It is assumed that the aggregate dynamics of term $\tilde{T}_d$ is described by its third order derivative

$$\begin{aligned} \tilde{T}_d^{(3)}={f_L}\left( y_{f_1},\,\dot{y}_{f_1},\,y_{f_2}\right) . \end{aligned}$$

(36)

Thus, it holds that $z_1=y_{f_1},\,z_2=\dot{y}_{f_1},\, z_3=y_{f_2},\,z_4=\tilde{T}_d,\,z_5=\dot{\tilde{T}}_d$ and $z_6=\ddot{\tilde{T}}_d.$ The dynamics of the extended state-space model is written as

$$\begin{aligned}&\dot{z}_1=z_2\quad \dot{z}_2=v_1+\tilde{T}_d\quad \dot{z}_3=v_2, \nonumber \\&\dot{z}_4=z_5\quad \dot{z}_5=z_6\quad \dot{z}_6=f_L\left( y_{f_1},\,\dot{y}_{f_1},\,y_{f_2}\right) , \end{aligned}$$

(37)

or in matrix form one has

$$\begin{aligned}&\dot{\tilde{z}}=\tilde{A}\tilde{z}+\tilde{B}\tilde{v},\nonumber \\&\tilde{y}=\tilde{C}{\tilde{z}}, \end{aligned}$$

(38)

$$\begin{aligned} \begin{pmatrix} \dot{z}_1 \\ \dot{z}_2 \\ \dot{z}_3 \\ \dot{z}_4 \\ \dot{z}_5 \\ \dot{z}_6 \end{pmatrix}= & {} \begin{pmatrix} 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \end{pmatrix} \begin{pmatrix} z_1 \\ z_2 \\ z_3 \\ z_4 \\ z_5 \\ z_6 \end{pmatrix}\nonumber \\&\quad +\begin{pmatrix} 0 &{}\quad 0 &{}\quad 0 \\ 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 \end{pmatrix} \begin{pmatrix} v_1 \\ v_2 \\ f_L(y_{f_1},\,\dot{y}_{f_1},\,y_{f_2}) \end{pmatrix},\nonumber \\ \begin{pmatrix} y_1 \\ y_2 \end{pmatrix}= & {} \begin{pmatrix} 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 \end{pmatrix} \begin{pmatrix} z_1 \\ z_2 \\ z_3 \\ z_4 \\ z_5 \\ z_6 \end{pmatrix}. \end{aligned}$$

(39)

The associated state estimator is

$$\begin{aligned} \hat{\dot{\tilde{z}}}={\tilde{A}_o}{\hat{\tilde{z}}}+{\tilde{B}_o}{\tilde{v}}_1+{K_o}(\tilde{y}-\tilde{C}\hat{\tilde{z}}), \end{aligned}$$

(40)

where

$$\begin{aligned} \tilde{A}_o= & {} \begin{pmatrix} 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \end{pmatrix},\quad \tilde{B}_o= \begin{pmatrix} 0 &{}\quad 0 &{}\quad 0 \\ 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \end{pmatrix},\nonumber \\ \tilde{C}_o= & {} \begin{pmatrix} 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 \end{pmatrix}, \end{aligned}$$

(41)

while the estimator’s gain ${K_o}{\in }R^{6{\times }2}$ is obtained from the standard Kalman Filter recursion [41–44].

Defining as $\tilde{A}_d,\,\tilde{B}_d,$ and $\tilde{C}_d,$ the discrete-time equivalents of matrices $\tilde{A}_o,\,\tilde{B}_o$ and $\tilde{C}_o,$ respectively, the Derivative-free nonlinear Kalman Filter can be designed for the aforementioned representation of the system dynamics [23, 31]. The associated Kalman Filter-based disturbance estimator is given by

Measurement update

$$\begin{aligned}&K(k)={P^{-}(k)}{\tilde{C}_d^T}\left[ \tilde{C}_d{\cdot }P^{-}(k){\tilde{C}_d^T}+R\right] ^{-1},\nonumber \\&{\hat{\tilde{z}}(k)}={\hat{z}^{-}(k)}+K(k)\left[ \tilde{C}_d{\tilde{z}}(k)-\tilde{C}_d{\hat{\tilde{z}}^{-}(k)}\right] ,\\&P(k)=P^{-}(k)-K(k){\tilde{C}_d}P^{-}(k),\nonumber \end{aligned}$$

(42)

Time update

$$\begin{aligned}&P^{-}(k+1)={\tilde{A}_d(k)}P(k){\tilde{A}_d^T}(k)+Q(k),\nonumber \\&{\hat{\tilde{z}}^{-}(k+1)}=\tilde{A}_d(k)\hat{\tilde{z}}(k)+\tilde{B}_d(k)\tilde{v}(k). \end{aligned}$$

(43)

It is of worth to give a brief comparison between global linearization and control for the VSC model using differential flatness theory and Lie algebra. One should point out that whereas necessary and sufficient conditions for the use of Lie algebra-based control exist only if the system is input-to-state linearizable, for the use of flatness-based control necessary and sufficient conditions are the system to be differentially flat which also means input–output linearizable. Obviously, input–output linearizable systems are a wider class than input-to-state linearizable systems and consequently flatness-based control can be applied to a wider class of nonlinear dynamical systems.

Simulation Tests

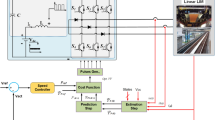
To evaluate the performance of the proposed nonlinear control scheme, that uses Kalman Filtering to estimate the nonmeasurable disturbances of the VSC model, simulation experiments have been carried out. Different DC voltage setpoints $V_{DC}$ have been assumed. Moreover, different external disturbance terms $\tilde{d}$ (e.g., due to load perturbations) have been considered to affect the VSC dynamic model. The control loop used in the VSC control is shown in Fig. 2. It can be noticed that the aggregate control signal comprises the flatness-based control input and the term for the annihilation of the disturbances which is based on the estimation provided by the Kalman Filter.

Fig. 2

Control loop for the VSC comprising a flatness-based nonlinear controller and a Kalman Filter-based disturbances estimator. The aggregate control input comprises

Fig. 3

a Control of the state variables (blue line) of the VSC in case of reference setpoint 1 (red line), and b estimation of disturbance input (first diagram green line) and variation of the control inputs (second and third blue lines)

Fig. 4

a Control of the state variables (blue line) of the VSC in case of reference setpoint 2 (red line), and b estimation of disturbance input (first diagram green line) and variation of the control inputs (second and third blue lines)

Fig. 5

a Control of the state variables (blue line) of the VSC in case of reference setpoint 3 (red line), and b estimation of disturbance input (first diagram green line) and variation of the control inputs (second and third diagrams blue line)

Fig. 6

a Control of the state variables of the VSC (blue line) in case of reference setpoint 4 (red line), and b estimation of disturbance input (first diagram green line) and variation of the control inputs (second and third diagrams blue line)

Several cases of VSC operation under different perturbation terms have been presented. The disturbance dynamics was completely unknown to the controller and its identification was performed in real time by the disturbance estimator. It is shown that the Derivative-free nonlinear Kalman Filter redesigned as a disturbance observer is capable of estimating with accuracy the unknown disturbance input $\tilde{d}$. The associated results are presented in Figs. 3, 4, 5 and 6. In these diagrams the setpoints are drawn with the red line, the real values of the state vector elements of the converter are depicted with the blue line, while the state estimates which are provided by the Derivative-free nonlinear Kalman Filter are printed with a green line. Several reference setpoints have been defined for the VSC state variables, i.e., currents $i_d,\,i_q$ and the output voltage $V_{dc}$ and as it can be observed from the associated diagrams, the proposed control scheme resulted in fast and accurate convergence to these setpoints. The disturbance observer that was based on the Derivative-free nonlinear Kalman Filter was capable of estimating the unknown and time-varying input disturbances affecting the VSC model.

Fig. 7

Convergence of the output voltage $V_{dc}$ (blue line) to the reference setpoint (red line) a without using the disturbance observer and b when using the disturbance observer

The simulation experiments have confirmed that the proposed state estimation-based control scheme not only enables implementation of VSC control through the measurement of a small number of variables (e.g., the ones appearing in the flat outputs $y_{f_1}$ and $y_{f_2}$) but also improves the robustness of the VSC control loop in case of disturbances.

The improvement in the performance of the control loop that is due to the use of a disturbance observer based on the Derivative-free nonlinear Kalman Filter is explained as follows: (i) compensation of the disturbance terms which are generated by parametric uncertainty or unknown external inputs and (ii) more accurate estimation of the disturbance terms because the filtering procedure is based on an exact linearization of the system’s dynamics and does not introduce numerical errors (as for example in the case of the extended Kalman Filter). This is shown in Fig. 7.

The disturbances depicted in Figs. 3, 4, 5 and 6 of the article represent the cumulative effects of modelling uncertainty and of external perturbations. Modelling uncertainties can be due to parametric variations in the electric circuit of the VSC, while the external perturbations can be induced by voltage variations in the grid (e.g., voltage sags, harmonics distortions, etc.). It is shown that by using the Derivative-free nonlinear Kalman Filter as a disturbance estimator it is possible to estimate simultaneously the non-measurable state vector elements of the converter and the aggregate perturbation inputs. By knowing such disturbance inputs it is possible to compensate for them by introducing an additional term to the feedback control input.

As an outline of the previous analytical and experimental results it can be stated that by proving that the VSC model is differentially flat, its transformation to the linear canonical (Brunovsky) form becomes possible. This enables to solve both the control and the state estimation problem. The novelty of the article is primarily in the used nonlinear estimation method, which is the Derivative-free nonlinear Kalman Filter. This filtering method is a new and genuine result in nonlinear estimation theory which under specific conditions retains the optimality features of the standard Kalman Filter. Moreover, the use of the aforementioned filter as a disturbances estimator is also a novel element in this research work. The filter estimates simultaneously the non-measurable state vector elements of the converter and disturbances or modelling error terms that affect its functioning. Additionally, one can compare control based on global linearization methods and the differential flatness theory approach, against control based on approximate linearization. It has been confirmed that flatness-based control is of improved robustness. Finally, comparing to adaptive control methods the proposed flatness-based control approach is computationally simpler.

Conclusions

The paper has proposed a nonlinear control scheme for three-phase VSCs. Estimation of disturbances terms due to variations of the load current has been performed with the use of a new nonlinear filtering approach, the so-called Derivative-free nonlinear Kalman Filter. First, it was proven that the dynamic model of the three-phase VSC is a differentially flat one, and this enabled its description in the Brunovsky (linear canonical) form. It has been shown that for the linearized converter’s model it is possible to design a state feedback controller. At a second stage, a novel Kalman Filtering method, the Derivative-free nonlinear Kalman Filter, has been proposed for estimating the non-measurable elements of the dynamic model of the VSC.

It has been shown that by avoiding linearization approximations, the proposed filtering method, improves the accuracy of estimation, and results in smooth control signal variations and in minimization of the tracking error of the VSC control loop. Moreover, with the redesign of the proposed Kalman Filter as a disturbance observer, it became possible to obtain estimates of disturbance terms associated with variations of the load current. The VSC’s control input was generated by including in the state-feedback control law an input that is based on the estimate of the disturbance terms. Simulation tests have been provided to evaluate the performance of the nonlinear control scheme. A comparison between the approach that was based on differential flatness theory and Lie algebra-based linearization of the converter’s model has been performed.

Appendix: Linearization of the Converter’s Model Using Lie-Algebra

Linearization of the converter’s model can be also performed using Lie-algebra and with the computation of the associated Lie derivatives [33, 34]. The following state variables are defined: $z_1=h_1(x),\,z_2={L_f}h_1(x),$ and $z_3=h_2(x).$ Thus one gets

$$\begin{aligned} {L_f}{h_1}(x)= & {} {{{\partial }{h_1}} \over {{\partial }{x_1}}}{f_1}+{{{\partial }{h_1}} \over {{\partial }{x_2}}}{f_2}+{{{\partial }{h_1}} \over {{\partial }{x_3}}}{f_3}{\Rightarrow } {L_f}{h_1}(x)\\= & {} {3 \over 2}L{x_1}\left( -{R \over L}{x_1}+{\omega }{x_2}+{v_d \over L}\right) \nonumber \\&+\,{3 \over 2}L{x_2}\left( -\omega {x_1}-{R \over L}x_2\right) \\&+\,C_{dc}{x_3}\left( -{x_3 \over {{C_{dc}}{R_c}}}\right) {\Rightarrow }{z_2^1}={L_f}{h_1}(x)\\= & {} -{3 \over 2}R\left( x_1^2+x_2^2\right) +{3 \over 2}{v_d}{x_1}-{1 \over R_c}x_3^2. \end{aligned}$$

Similarly, one has

$$\begin{aligned} {\dot{z}_2}={L_f^2}{h_1}(x)+{L_{g_1}}{L_f}{{h_1}(x)}{u_1}+{L_{g_2}}{L_f}{{h_2}(x)}{u_2}, \end{aligned}$$

(44)

where

$$\begin{aligned} {L_f^2}{h_1}(x)= & {} {{{\partial }{z_2^1}} \over {{\partial }{x_1}}}{f_1}+{{{\partial }{z_2^1}} \over {{\partial }{x_2}}}{f_2}+{{{\partial }{z_2^1}} \over {{\partial }{x_3}}}{f_3}{\Rightarrow }{L_f^2}{h_1}(x)\\= & {} \left( -3R{x_1}+{3 \over 2}v_d\right) \left( -{R \over L}{x_1}+{\omega }{x_2} +{v_d \over L}\right) \\&+\left( -3R{x_2}\right) \left( -{\omega }{x_1}-{R \over L}{x_2}\right) \\&+\left( -{2 \over R_c}{x_3}\right) \left( -{x_3 \over {{C_{dc}}{R_c}}}\right) {\Rightarrow }{L_f^2}{h_1}(x)\\= & {} {{3R^2} \over L}\left( x_1^2+x_2^2\right) -{{3R} \over L}{v_d}{x_1}+{{2{x_3^2}} \over {{C_{dc}}{R_c^2}}}, \end{aligned}$$

while it also holds

$$\begin{aligned} {L_{g_1}}{L_f}{h_1}(x)= & {} {{{\partial }{z_2^1}} \over {{\partial }{x_1}}}{g_{11}}+{{{\partial }{z_2^1}} \over {{\partial }{x_2}}}{g_{21}}+{{{\partial }{z_2^1}} \over {{\partial }{x_3}}}{g_{31}}{\Rightarrow }{L_{g_1}}{L_f}{h_1}(x)\\= & {} \left( -3R{x_1}+{3 \over 2}v_d\right) \left( -{x_3 \over {2L}}\right) +\left( -3R{x_2}\right) 0\\&+\left( -{2 \over R_c}x_3\right) \left( {{3{x_1}} \over {4{C_{dc}}}}\right) {\Rightarrow } {L_{g_1}}{L_f}{h_1}(x)\\= & {} {{3R} \over {2L}}{x_1}{x_3}-{3 \over {4L}}{v_d}{x_3}-{{3{x_1}{x_3}} \over {2{R_c}{C_{dc}}}}, \end{aligned}$$

and also

$$\begin{aligned} {L_{g_2}}{L_f}{h_1}(x)= & {} {{{\partial }{z_2^1}} \over {{\partial }{x_1}}}{g_{12}}+{{{\partial }{z_2^1}} \over {{\partial }{x_2}}}{g_{22}}+{{{\partial }{z_2^1}} \over {{\partial }{x_3}}}{g_{32}}{\Rightarrow }\\ {L_{g_2}}{L_f}{h_1}(x)= & {} \left( -3R{x_1}+{3 \over 2}v_d\right) 0 +\left( -3R{x_2}\right) \left( -{x_3 \over {2L}}\right) \\&+\left( -{2 \over R_c}x_3\right) \left( {{3{x_2}} \over {4C_{dc}}}\right) {\Rightarrow }{L_{g_2}}{L_f}{h_1}(x)\\= & {} {{3R{x_2}{x_3}}\over {2L}}-{{3{x_2}{x_3}} \over {2{R_c}{C_{dc}}}}. \end{aligned}$$

Therefore, one has

$$\begin{aligned}&\dot{z}_1=z_2,\nonumber \\&\dot{z}_2={L_f^2}{h_1}(x)+{L_{g_1}}{L_f}{h_1}(x){u_1} +{L_{g_2}}{L_f}{h_1}(x){u_2}. \end{aligned}$$

(45)

It can be confirmed that it holds $\dot{z}_1=z_2.$ Indeed one has $z_1=h_1(x)$ therefore

$$\begin{aligned} {\dot{z}_1}= & {} {{{\partial }{z_1^1}} \over {{\partial }{x_1}}}{\dot{x}_1}+{{{\partial }{z_1^1}} \over {{\partial }{x_2}}}{\dot{x}_2}+{{{\partial }{z_1^1}} \over {{\partial }{x_3}}}{\dot{x}_3}{\Rightarrow }{\dot{z}_1}\\= & {} {3 \over 2}L{x_1}\left( -{R \over L}{x_1}+{\omega }{x_2} +{v_d \over L}\right) +{3 \over 2}L{x_2}\left( -{\omega }{x_1}-{R \over L}{x_2}\right) \\&+\,{C_{dc}}{x_3}\left( -{{x_3} \over {{C_{dc}}{R_c}}}\right) {\Rightarrow }{\dot{z}_1}=-{3 \over 2}R{x_1^2}\\&+\,{3 \over 2}L{\omega }{x_1}{x_2}+{3 \over 2}{v_d}{x_1}-{3 \over 2}R{x_2^2}-{3 \over 2}L{\omega }{x_1}{x_2}-{1 \over {R_C}}{x_3^2}. \end{aligned}$$

Thus, one finally obtains

$$\begin{aligned} \dot{z}_1=-{3 \over 2}R\left( x_1^2+x_2^2\right) +{3 \over 2}{v_d}{x_1}-{1 \over R_c}x_3^2. \end{aligned}$$

(46)

Equation (44) can be also confirmed. Indeed, using that $z_2={L_f}{h_1}(x)=-{3 \over 2}R(x_1^2+x_2^2)+{3 \over 2}{v_d}{x_1}-{1 \over R_c}x_3^2$ one obtains

$$\begin{aligned} {\dot{z}_2}= & {} {{{\partial }{z_2^1}} \over {{\partial }{x_1}}}{\dot{x}_1}+{{{\partial }{z_2^1}} \over {{\partial }{x_2}}}{\dot{x}_2}+{{{\partial }{z_2^1}} \over {{\partial }{x_3}}}{\dot{x}_3}{\Rightarrow }{\dot{z}_2}\nonumber \\= & {} \left( -3R{x_1}+{3 \over 2}v_d\right) \left( -{R \over L}{x_1}+{\omega }{x_2}+{v_d \over L}-{x_3 \over {2L}}u_1\right) \nonumber \\&+\left( -3R{x_2}\right) \left( -{\omega }{x_1}-{R \over L}{x_2}-{x_3 \over {2L}}u_2\right) \nonumber \\&+ \left( -{2 \over R_c}{x_3}\right) \left( -{x_3 \over {{C_{dc}}{R_c}}}+{{3{x_1}} \over {4C_{dc}}}u_1+{{3{x_2}} \over {4C_{dc}}}u_2\right) {\Rightarrow }\nonumber \\ {\dot{z}_2}= & {} {{3R^2} \over L}\left( x_1^2+x_2^2\right) -{{3R} \over L}{v_d}{x_1}+{{2{x_3^2}} \over {{C_{dc}}{R_c^2}}}\nonumber \\&+\left( {{3R} \over {2L}}{x_1}{x_3}-{3 \over {4L}}{v_d}{x_3}-{{3{x_1}{x_3}} \over {2{R_c}{C_{dc}}}}\right) u_1\nonumber \\&+\left( {{3R{x_2}{x_3}} \over {2L}}-{{3{x_2}{x_3}} \over {2{R_c}{C_{dc}}}}\right) u_2, \end{aligned}$$

(47)

which through the previous relations about ${L_f^2}h_1(x),\, {L_{g_1}}{L_f}{h_1}(x)$ and ${L_{g_2}}{L_f}{h_1}(x)$ confirms finally Eq. (44).

The third state variable is also examined, that is $z_3={h_2}(x)=i_q.$ It holds that

$$\begin{aligned} {L_f}{h_2}(x)= & {} {{{\partial }{h_2}} \over {{\partial }{x_1}}}{f_1}+{{{\partial }{h_2}} \over {{\partial }{x_2}}}{f_2}+ {{{\partial }{h_2}} \over {{\partial }{x_3}}}{f_3}{\Rightarrow }\nonumber \\ {L_f}{h_2}(x)= & {} 0{f_1}+1{f_2}+0{f_3}{\Rightarrow }\nonumber \\ {L_f}{h_2}(x)= & {} {-}{\omega }{x_1}-{R \over L}{x_2}. \end{aligned}$$

(48)

Equivalently, one gets

$$\begin{aligned} {L_{g_1}}{h_2}(x)= & {} {{{\partial }{h_2}} \over {{\partial }{x_1}}}{g_{11}}+ {{{\partial }{h_2}} \over {{\partial }{x_2}}}{g_{21}}+ {{{\partial }{h_2}} \over {{\partial }{x_3}}}{g_{31}}{\Rightarrow }\nonumber \\ {L_{g_1}}{h_2}(x)= & {} 0g_{11}+1g_{21}+0g_{31}{\Rightarrow }\nonumber \\ {L_{g_1}}{h_2}(x)= & {} 0, \end{aligned}$$

(49)

and similarly one has

$$\begin{aligned} {L_{g_2}}{h_2}(x)= & {} {{{\partial }{h_2}} \over {{\partial }{x_1}}}{g_{12}}+ {{{\partial }{h_2}} \over {{\partial }{x_2}}}{g_{22}}+ {{{\partial }{h_2}} \over {{\partial }{x_3}}}{g_{32}}{\Rightarrow }\nonumber \\ {L_{g_2}}{h_2}(x)= & {} 0g_{12}+1g_{22}+0g_{32}{\Rightarrow }\nonumber \\ {L_{g_2}}{h_2}(x)= & {} {-}{{x_3} \over {2L}}. \end{aligned}$$

(50)

Therefore, it holds

$$\begin{aligned} \dot{z}_3= & {} {L_f}{h_2}(x)+{L_{g_1}}{h_2}(x){u_1}+{L_{g_2}}{h_2}(x){u_2}{\Rightarrow }\nonumber \\ \dot{z}_3= & {} \left( {-}{\omega }{x_1}-{R \over L}{x_2}\right) +0{u_1}-{{x_3} \over {2L}}{u_2},\nonumber \\ \dot{z}_3= & {} \left( {-}{\omega }{x_1}-{R \over L}{x_2}\right) -{{x_3} \over {2L}}u_2. \end{aligned}$$

(51)

Equation (51) corresponds to the second line of the state-space equations of $V_{dc}$ and therefore confirms the relation

$$\begin{aligned} \dot{z}_3={{L_f}{h_2}(x)}+{L_{g_1}}{h_2}(x){u_1}+{L_{g_1}}{h_2}(x){u_2}. \end{aligned}$$

(52)

Therefore one arrives at the following equations

$$\begin{aligned} \dot{z}_1= & {} z_2,\nonumber \\ \dot{z}_2= & {} {L_f^2}{h_1}(x)+{L_{g_1}}{L_f}{h_1}(x){u_1}+{L_{g_2}}{L_f}{h_2}(x){u_2},\nonumber \\ \dot{z}_3= & {} f_{21}+g_{22}u_2, \end{aligned}$$

(53)

where the new control inputs are defined as

$$\begin{aligned} v_1= & {} {L_f^2}{h_1}(x)+{L_{g_1}}{L_f}{h_1}(x){u_1} +{L_{g_2}}{L_f}{h_2}(x){u_2},\nonumber \\ v_2= & {} f_{21}+g_{22}{u_2}. \end{aligned}$$

(54)

Consequently, one gets

$$\begin{aligned} \dot{z}_1= & {} z_2,\nonumber \\ \dot{z}_2= & {} v_1,\nonumber \\ \dot{z}_3= & {} v_2, \end{aligned}$$

(55)

or in state-space description

$$\begin{aligned} \begin{pmatrix} \dot{z}_1 \\ \dot{z}_2 \\ \dot{z}_3 \end{pmatrix}= & {} \begin{pmatrix} 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \end{pmatrix} \begin{pmatrix} z_1 \\ z_2 \\ z_3 \end{pmatrix}+ \begin{pmatrix} 0 &{}\quad 0 \\ 1 &{}\quad 0 \\ 0 &{}\quad 1 \end{pmatrix} \begin{pmatrix} v_1 \\ v_2 \end{pmatrix},\nonumber \\ \begin{pmatrix} y_1 \\ y_2 \end{pmatrix}= & {} \begin{pmatrix} 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 \end{pmatrix} \begin{pmatrix} z_1 \\ z_2 \\ z_3 \end{pmatrix}. \end{aligned}$$

(56)

Therefore, the initial nonlinear system of the VSC is transformed into the linear canonical form.