Identifying discrete behavioural types: a re-analysis of public goods game contributions by hierarchical clustering

Abstract

We propose a framework for identifying discrete behavioural types in experimental data. We re-analyse data from six previous studies of public goods voluntary contribution games. Using hierarchical clustering analysis, we construct a typology of behaviour based on a similarity measure between strategies. We identify four types with distinct stereotypical behaviours, which together account for about 90% of participants. Compared to the previous approaches, our method produces a classification in which different types are more clearly distinguished in terms of strategic behaviour and the resulting economic implications.

1 Introduction

The heterogeneity in decision-making behaviour observed in both field settings and their laboratory counterparts is by turns a great joy and a great frustration to practitioners of behavioural economics. The richness in the variety of individual behaviour is evidence that people are indeed different, and approach the same economic decision-making task in a variety of ways. However, parsimonious, practical, and tractable economic models try to capture the commonalities in behaviour. Extracting those commonalities from the embarrassment of riches offered by the data is an important challenge in the development of behavioural economics and game theory.

One approach is to group behaviour into a small number of distinct types, which we refer to as a typology. In this paper, we will focus on the case of public goods voluntary contribution games (VCGs), for which Fischbacher et al. (2001) (FGF) have proposed one such typology, which groups participants into four types. We choose this as an interesting setting, because the P-experiment protocol introduced by FGF, based on the linear VCG (Ledyard 1997), has been employed as a standard methodology by many studies conducted in various languages and locations (Kocher et al. 2008). The analysis we conduct in this paper benefits from being able to re-use data from a number of studies using a sufficiently similar protocol.

Although a number of papers have used variants of the FGF typology, the literature in experimental economics has not employed a framework for defining or evaluating candidate typologies. To address this, we introduce techniques from machine learning, in which exactly these types of classification problems have been studied in depth. Ideally, a typology represents the data well when the behaviours of two participants classified as the same type are similar, while the behaviours of two participants classified as different types are dissimilar. Machine learning provides methods for evaluating the trade-offs between within-type similarity and across-type dissimilarity and for constructing classifications which are optimal according to some criterion with respect to these trade-offs. Machine learning is commonly associated with data sets with large numbers of observations, a problem experimental economists rarely face. However, it also studies the organisation of multi-dimensional data. In the data we analyse, a participant’s type is determined based on a 21-dimensional conditional contribution strategy elicited by the P-experiment protocol.

We use data from six previous studies using the P-experiment protocol to construct alternative typologies using hierarchical cluster analysis (Kaufman and Rousseeuw 1990). Our typologies differ from FGF in the organisation of conditionally cooperative participants. FGF propose to categorise these participants primarily into conditional cooperators and non-monotonic “hump-shaped” contributors. In contrast, cluster analysis identifies a group of strong conditional cooperators, centred on participants who match group contributions on a one-for-one basis, and a group of weak conditional cooperators, centred on those who match group contributions at approximately a one-for-two rate.

Machine learning offers tools for visualising the properties of classifications of high-dimensional data, such as our behavioural typologies. We use silhouette analysis (Rousseeuw 1987) to assess the cohesion of types using both approaches, and illustrate that, in the FGF typology, participants grouped in the same type exhibit behaviours with heterogeneous consequences in the VCG.

To be useful in understanding economic and strategic behaviour, the classifications in a typology should correlate with choices made by the same participants which are not used in the classification process. In the P-experiment, participants make two types of choices: conditional contributions, which are used in the classification, and unconditional contributions, which are not. Across our data set, FGF’s conditional cooperators and hump-shaped contributors do not differ in their unconditional contributions. In contrast, participants classified as strong conditional cooperators make generally higher unconditional contributions than those classified as weak conditional cooperators. This supports the strong/weak conditional cooperator distinction as being a more insightful description of the data and that the underpinnings of the behaviour of weak conditional cooperators may be distinct from those of strong conditional cooperators.

2 The game

The experiments used in our analysis involve one-shot interaction among participants in a VCG. Participants are anonymously placed into groups with M members. Each participant receives G tokens. She can allocate any number of tokens between 0 and G to a group account; tokens not allocated to the group account are kept in her private account. We refer to the tokens allocated to the group account as her contribution. The participant receives a point for each token kept in her private account. Each token contributed to the group account yields $P>1$ points, which are then split equally among the group members. The parameters P and M are chosen, so that the marginal per-capita return (MPCR), P/M, is less than one. With these parameters, a participant who cares only about maximising her own earnings has a strictly dominant strategy, which is to contribute no tokens. In contrast, the strategy profile that maximises total earnings of the group is for each member to contribute all G tokens.

In the P-experiment protocol, contributions are made in two stages. In Stage 1, $M-1$ members make their contributions. The remaining member learns the average contribution of other members, and then decides on her contribution. A participant does not know whether she will make her contribution in Stage 1 or Stage 2, nor, if she is to be the Stage 2 contributor, what the average contribution of the other members in Stage 1 will turn out to be. Decisions are, therefore, elicited using the strategy method (Selten 1967). Each participant i states what her contribution will be if she is chosen to contribute in Stage 1; we write the unconditional contribution of participant i as $u^i$. She also states her contribution in Stage 2, for each possible realisation of the average contribution of the other members of her group.¹ We call these Stage 2 contributions the contribution strategy. We write the contribution strategy of i as a vector $c^i$. The component $c^i_g$ is the contribution of participant i in Stage 2 if the other members contribute g tokens on average in Stage 1. The contribution strategy is the basis for identifying behavioural types.

3 Typologies

Let ${\mathcal {N}}$ denote the set of participants, and ${\mathcal {C}}=\{(i,c^i)\}_{i\in {\mathcal {N}}}$ be the set of all participants paired with their contribution strategies. We define a typology T as a partition of ${\mathcal {C}}$ into equivalence classes. Each equivalence class is interpreted as a distinct behavioural type. We write T(i) as the type of participant i in typology T.

The existing state-of-the-art in the literature is the typology based on Fischbacher et al. (2001), which we will call $T^F$. $T^F$ partitions participants into one of four types.

• Free riders (FR) always maximise individual earnings by keeping all tokens in the private account, irrespective of the outcome of the first stage.

• Conditional cooperators (CC) increase their contributions to the group account based on higher contributions by others in the first stage. A participant i is deemed a conditional cooperator by testing whether the Spearman’s $\rho$ correlation coefficient between the vector $[0,1,\ldots ,G]$ of possible average contributions g and the participant’s strategy $\left[ c^i_0,c^i_1,\ldots ,c^i_G\right]$ is significantly positive at significance level $\le 0.001$. We separately tabulate exact conditional contributors (XC), who match exactly one-for-one, labeling other CC as inexact conditional contributors (IC).

• Hump-shaped (HS) contributors are identified based on visual classification of contribution strategies, in which $c^i_0$ and $c^i_G$ are small, but $c^i_g$ is larger for some intermediate values $0<g<G$; these strategies often have a triangular shape when plotted.

• Others (OT) is the residual type, comprised of participants, whose contribution strategies do not satisfy the criteria defining the other types.

The $T^F$ procedure is implemented by defining a stereotypical behaviour, combined with a formal or informal criterion for deciding when a given contribution strategy is “similar enough” to the stereotype. This similarity is a matter of judgment; alternative proposals for inclusion criteria have been made in subsequent papers (e.g., Rustagi et al. 2010; Fischbacher et al. 2012). By adjusting the classification criteria, one can make the residual “other” group smaller, but with the possibility that a participant’s contribution strategy might satisfy the criteria for more than one other type. The most recent refinement of the criteria by Thöni and Volk (2018) encounters this problem, requiring a further criterion for assigning contribution strategies that satisfy their versions of both the CC and HS criteria.

The stereotypical behaviours in $T^F$ are chosen based on an ad-hoc combination of theoretical models and inspection of the data. We are interested first in assessing the performance of this classification in identifying coherent types.

Question 1

How does the four-type typology $T^F$ compare with other candidate groupings of the data into four types?

One approach to systematically constructing alternate candidate typologies with a specified number of types is hierarchical cluster analysis with Ward’s minimum variance method (Ward 1963). Cluster analysis takes as a starting point a metric of (dis-)similarity between two objects. We define the dissimilarity between the contribution strategies $c^i$ of participant i and $c^j$ of participant j as the Manhattan distance $d(c^{i} ,c^{j} ) = \sum\nolimits_{{g = 0}}^{G} {\left| {c_{g}^{i} - c_{g}^{j} } \right|}$. This is the expected difference between the Stage 2 contributions of participants i and j if the average contribution g of other group members is chosen uniformly at random. Two contribution strategies separated by a smaller distance are more similar.

For any fixed $C=1,2,\ldots ,|{\mathcal {C}}|$, Ward’s method generates a candidate typology $T^H(C)$ which partitions ${\mathcal {C}}$ into exactly C groups. The partition $T^H(C)$ is one that minimises the within-group sum of squared errors among all possible partitions with exactly C groups. We propose the typology $T^H(4)$ as an alternative to $T^F$ maintaining the same number of types.²

By maintaining the same number of types, two candidate typologies will differ only in which four types they identify. Therefore, one can, for example, read off any differences in the stereotypical behaviours of the types between typologies. However, there is no a priori reason to have exactly four types, and it may be that more (or fewer) types provide a more satisfactory description.

Question 2

Given the distribution of contribution strategies in the data, what is an appropriate number of types to include in a typology?

Ward’s method proposes a partition for each C, which has the property that the partition $T^H(C)$ can be computed efficiently given $T^H(C+1)$ by combining together the two “most similar” elements of $T^H(C+1)$. The trade-off in having more (resp., fewer) types is that the variability within a type will be less (resp., more). For example, there is a trivial, but unsatisfying, clustering which assigns each contribution strategy to its own distinct type. The resulting types are by definition perfectly coherent, having zero variability, but fail to capture that there may be many strategies which differ, for example, by only one token in one contingency.

There are several approaches in the literature to analysing this trade-off. Recall that solutions $T^H(C)$ and $T^H(C+1)$ differ in that one cluster in T(C) is divided into two in $T^H(C+1)$. There are exactly two members $t_1,t_2 \in T^H(C+1)$, such that $t_1\not =t_2$ and $t_1\cup t_2\in T^H(C)$. Let W(t) denote the sum of squared errors in cluster t. Duda and Hart (1973) define the index

$$\begin{aligned} \mathrm {Je(2)/Je(1)}= \frac{W(t_1)+W(t_2)}{W(t_1\cup t_2)}. \end{aligned}$$

(1)

Because Ward’s method minimises the within-cluster sum of squared errors, $\mathrm {Je(2)/Je(1)}\le 1$. This is considered in conjunction with the value of a pseudo-$T^2$ statistic:

$$\begin{aligned} {\text {PT}}^2=\left\{ \frac{1}{\mathrm {Je(2)/Je(1)}} - 1\right\} \times \left\{ |t_1|+|t_2|-2\right\} = \left\{ \frac{W(t_1\cup t_2)}{W(t_1)+W(t_2)} - 1\right\} \times \left\{ |t_1|+|t_2|-2\right\} , \end{aligned}$$

(2)

where |t| is the number of members of cluster t. Duda and Hart recommend preferring clusterings with relatively high $\mathrm {Je(2)/Je(1)}$ and relatively low ${\text {PT}}^2$ values.

The criteria of Duda and Hart refer specifically to the output of hierarchical clustering. Another measurement of type coherence, which can be applied to any typology T, is silhouette analysis (Rousseeuw 1987). For any participant i, the average distance from i’s contribution strategy to the contribution strategies of other participants of a given type $t\in T$ is

$$\begin{aligned} a(i,t) = \frac{\sum _{j\not = i:T(j)=t} d(c^i,c^j)}{\sum _{j\not = i:T(j)=t} 1}. \end{aligned}$$

(3)

For i, the distance to the “closest” type which is different from the type to which i is assigned is

$$\begin{aligned} b(i) = \min _{t\not =T(i)} a(i,t). \end{aligned}$$

(4)

The participant’s silhouette index is then defined as

$$\begin{aligned} s(i) = \frac{b(i)-a(i,T(i))}{\max \{b(i),a(i,T(i))\}}. \end{aligned}$$

(5)

The silhouette index ranges from − 1 to + 1. Values greater than zero indicate that the members of i’s type are closer, on average, than the members of the next closest type.

In the trivial typology that assigns each distinct strategy to its own cluster, the silhouette index is + 1 for all strategies. Taken to the other extreme, fixing a small number C of groups and assigning strategies at random to the groups leads to silhouette indices distributed with a median near zero and small absolute values. Although hierarchical clustering does not construct its solution for C groups at random, but by combining two similar groups from its solution for $C+1$ groups, any grouping of heterogeneous strategies under one type necessarily decreases the silhouette index. Kaufman and Rousseeuw (1990) suggest selecting an appropriate number of clusters C by analysing the levels and distributions of silhouette indices as an indicator of the trade-off between within-cluster similarity and across-cluster dissimilarity.

4 Results

We re-analyse the data from six VCG experiments using the P-experiment protocol, published between 2001 and 2016. We surveyed the literature for studies which met these criteria:

• P-experiment protocol published in a peer-reviewed journal as of September 2016.

• Participants played the VCG in groups of 4.

• Participants were endowed with 20 tokens.

• MPCR equal to 0.4 points per token.

We identified a total of nine studies satisfying these criteria; the authors of six of these kindly provided us with their data sets.³ These six experiments were conducted in four different countries and four different languages, with a total of $N=551$ participants: Fischbacher et al. (2001) (Switzerland, $N=44$); Herrmann and Thöni (2009) (Russia, $N=160$); Fischbacher and Gächter (2010) (Switzerland, $N=140$); Fischbacher et al. (2012) (United Kingdom, $N=136$); Cartwright and Lovett (2014) (United Kingdom, $N=31$); and Préget et al. (2016) (France, $N=40$).

There are 397 distinct contribution strategies chosen by the 551 participants. Of these, 86 are perfect free riders, with $c_g=0$ for all g; a further 44 are perfect one-to-one matchers, with $c_g=g$ for all g. There are 5 who unconditionally contribute all their tokens, $c_g=20$ for all g. Overall, only 16 contribution strategies are chosen by more than one participant, leaving 381 participants, whose contribution strategy is unique within the data set. The objective of a typology is to offer an organisation of this heterogeneous data.

4.1 Definition of the typology

Result 1

$T^H(4)$ creates a more cohesive grouping than the four-type typology $T^F$.

We begin by visualising, using heatmaps, the patterns of behaviour associated with the different types in $T^H(4)$ compared to those in $T^H$. The heatmap for type t is produced from the contribution strategies of all participants assigned to t by constructing the set $\{(k,c^i_k)\}_{T(i)=t,k=0,\ldots ,20}$. The frequencies of the ordered pairs in this set are used to generate the heatmaps, as shown in Fig. 1; darker shades correspond to higher frequencies. For each type, we plot the medoid of the type using unfilled diamonds. The medoid is defined as the contribution strategy which has the smallest average distance from other strategies in the type, and is one method of expressing a “typical” member of the type. These medoids motivate our naming of the four types:⁴

• Own maximisers (OWN, 25.8% of participants), with a modal allocation of zero in all contingencies;

• Strong conditional cooperators (SCC, 38.8%), who match average contributions exactly or approximately one-for-one;

• Weak conditional cooperators (WCC, 18.9%), who have generally increasing contribution strategies, but at a rate of less than one-for-one;

• Various (VAR, 16.5%), which as the residual type includes various behaviours, such as those who contribute most or all tokens irrespective of what others do, with an average contribution of about one-half the endowment in all contingencies.

Each participant has a type generated by $T^H(4)$ and one generated by $T^F$.⁵ Table 1 compares the typologies by giving the shares of participants classified in each possible pair of types $(t^h,t^f)\in T^H(4) \times T^F$. The key difference between the two typologies is in their categorisation of the modes of conditional cooperation. $T^H(4)$ produces types which capture strong versus weak versions of conditional cooperation, with the strong version anchored by the 44 participants who match exactly one-for-one (XC), while the weak version clusters around a medoid in which contributions are matched roughly one-for-two. Conversely, the conditional cooperators in $T^F$ appear in all four types in $T^H(4)$. Hump-shaped contributors split primarily between own maximisers and weak conditional cooperators.

Table 1 Comparison of the $T^F$ and $T^H(4)$ typologies

Fig. 1

Heatmaps of contribution strategies of the participants classified in each type

These observations suggest that conditional cooperators and hump-shaped contributors under $T^F$ are not cohesive types, insofar as they group within the same type behaviours with dissimilar contribution consequences. Figure 2 plots the silhouette indices of the members of each type. The plot is generated by sorting members of each type in decreasing order by their silhouette index s(i), and plotting those sorted s(i) values against the participant’s sorted rank. In $T^F$, a majority of participants identified as hump-shaped contributors (25 of 39) have strategies which are on average closer to one of the other three types’ strategies, than to other hump-shaped contributors. Among those identified as others, 65 of 97 have strategies closer on average to one of the other three types than to the rest of those considered others. Many conditional cooperators likewise have negative indices.

We compare this with the silhouette plot for the types generated by typology $T^H$.⁶ All own maximisers have positive indices, as do most strong conditional cooperators (197 of 214). The distinction between strong conditional cooperators and weak conditional cooperators eliminates the large negative indices observed among $T^F$’s conditional cooperators. The heterogeneity of the remaining participants classified as various is evident in the range of indices among the participants; although a majority (54 of 91) have negative indices, the magnitudes are much smaller than those measured for the others type in $T^F$. Overall, 66.6% of the participants have a higher index in $T^H(4)$ than $T^F$. The average index increases from 0.17 in $T^F$ to 0.40 in $T^H(4)$, and the median from 0.23 to 0.43. The medians are significantly different ($p<0.001$ using sign-rank test).

Fig. 2

Silhouette plots of type clusters. Each participant is assigned an index in $[-1,1]$, comparing the average distance between the participant’s strategy and the strategies of participants of the same type, against the average distance to participants’ strategies who are classified in the next closest type. a Typology $T^F$. b Typology $T^H(4)$

Result 2

The typology $T^H(5)$ identifies a unconditional high contributors as a distinct type.

We address Question 2 with a two-stage procedure. In the first stage, we select a range of possible candidate typologies, using the Duda–Hart selection criterion. The Duda–Hart $\mathrm {Je(2)/Je(1)}$ and ${\text {PT}}^2$ exclude typologies with fewer four clusters; solutions with four or more clusters all exhibit high $\mathrm {Je(2)/Je(1)}$ and low ${\text {PT}}^2$ values. Among these candidate solutions, we calculate in the second stage the mean silhouette index for each. The choice of five clusters provides the highest index (0.42), compared to 0.40 for $T^H(4)$ and 0.37 for $T^H(6)$.⁷ We, therefore, select the five-type typology $T^H(5)$ as the most appropriate. This typology differs from $T^H(4)$ by identifying as a distinct type unconditional high contributors, comprising 4.7% of subjects who contribute most or all tokens irrespective of what others do.⁸ Figure 3 provides the heatmaps after the disaggregation of unconditional high contributors from the remaining contributors classed as Various. Among the 26 participants classified as unconditional high contributors, 25 have a positive silhouette index, with an average of 0.47 across the cluster.

Fig. 3

Heatmaps of clusters combined in $T^H(5)$ to yield $T^H(4)$. Unconditional high contributors are considered a distinct type in $T^H(5)$

4.2 Out-of-sample prediction of unconditional contributions

Fig. 4

Boxplots of Stage 1 contributions by type, for each typology. Boxes indicate the interquartile range of the distribution; unfilled diamonds indicate medians. a Typology $T^F$. b Typology $T^H(5)$

Experiments using the P-experiment protocol all generate Stage 1 unconditional contributions $u^i$ for each participant i. These are not used in constructing $T^F$ or $T^H(5)$. There is no previous evidence that the $T^F$ typology is useful in explaining variations in Stage 1 contributions.

Result 3

In contrast to $T^F$, different types in $T^H(5)$ generate distinct patterns of Stage 1 contributions.

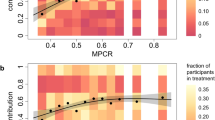
Figure 4 shows the distributions of Stage 1 contributions, grouped by type assignment based on Stage 2 contribution strategies. In the $T^F$ typology, free riders allocate on average 2.15 tokens (with a mode at zero), while the other three types have dispersed distributions of Stage 1 contributions with means and medians near half of the endowment of 20 tokens. The Stage 1 contribution of free riders is different from other types (all Bonferroni multiple comparisons tests $p<0.001$), while there is no significant difference in Stage 1 allocations among the remaining types.

Using $T^H(5)$, the ranking and magnitude of average allocations are consistent with the classification based on Stage 2 strategies. Own maximisers contribute the least (3.20 tokens), followed by weak conditional cooperators (8.23), strong conditional cooperators (10.04), various (11.42) and unconditional high (13.96). Stage 1 contributions are significantly different across the five types. The mean allocation of own maximisers is significantly lower than all other clusters (one-way analysis of variance with multiple comparisons and Bonferroni correction, all $p\le 0.001$). There is a significant difference in contributions between weak conditional cooperators and strong conditional cooperators ($p=0.088$, Bonferroni corrected), but no significant differences between the strong conditional cooperators and various, nor between the various and unconditional high (all other comparisons $p<0.011$, Bonferroni corrected).⁹

This analysis of Stage 1 contributions is convenient, because all P-experiment protocols generate this data, and so are included in all the studies we survey. This can be interpreted as an internal validity check on the protocol. If the types constructed from Stage 2 strategies are meaningful, at minimum, they should correlate with Stage 1 decisions made in the same play of the game. A theory of types would be even more robustly founded if types predicted playing other iterations of the game, or in other games. In a companion paper, Fallucchi et al. (2018), we use the five-type classification and confirm that strong and weak conditional cooperators react differently to changes in the financial incentives across non-linear versions of the VCG. This provides additional support for the strong–weak conditional cooperation distinction.

4.3 A deterministic version of the clustering-based typology

The qualitative structure of the clusters reported in $T^H(4)$ and $T^H(5)$ is robust to using subsamples of the data set: the four-cluster and five-cluster solutions centre consistently on the medoids plotted in Fig. 1. However, with 397 distinct contribution strategies in the data set, most participants do not exactly match one of the stereotypical strategies. Classification, therefore, inherently requires some measure of what it means for a contribution strategy to be “similar enough” to a stereotype. The classifications we report as $T^F$ are based on the original (Fischbacher et al. 2001) criteria. As noted, subsequent authors have proposed modifications to the inclusion criteria. The effect of these variations on what it means to be “similar enough” is to change which contribution strategies are included at the periphery of the types, while not significantly affecting the type’s medoid.

Clustering differs in its approach to defining inclusion criteria. The criteria developed by clustering are determined by the data; that is, what constitutes “similar enough” is defined relative to the distribution of the data. This endogenous determination is implemented in Ward’s method by minimising the sum of squared errors within types. Nevertheless, for some applications, it is useful to have a deterministic rule for determining a priori the type membership for any given contribution strategy.

The key insight from the clustering approach is the identification of a set of candidates for the type-defining stereotypical behaviours, which are distinct from the set used in $T^F$. In the spirit of the approach used by $T^F$, clustering suggests, for a typology with five types, this stepwise classification scheme:

Step 1:

SCC: all $c^i$ “similar enough” to the stereotype strategy of matching exactly one-for-one.

Step 2:

OWN: all $c^i$ “similar enough” to the stereotype strategy of always contributing zero.

Step 3:

UCH: all $c^i$ “similar enough” to the stereotype strategy of always contributing all tokens.

Step 4:

WCC: all $c^i$ not yet classified who contribute less than the exact one-for-one matching amount in a “substantial majority” of contingencies g.

Step 5:

All remaining strategies are in VAR.

To construct a four-type version, omit Step 3.

As with $T^F$-like schemes, this method requires the user to fill in what it means for a contribution strategy to be “similar enough” to one of the stereotypes. In the Online Appendix, we use the results of the clusters generated on our data set to suggest parameters for distance bounds to determine inclusion in these types.

Our data set is drawn from experiments conducted in traditional laboratory settings. Even within these settings, heterogeneity in contribution strategies is substantial. In studies conducted in the field (e.g., Rustagi et al. 2010) or in natural experiments targeting broader, more representative samples of participants (e.g., Slonim et al. 2013), heterogeneity in responses often increases. Cluster analysis offers a framework for measuring and evaluating whether a given typology continues to be a satisfactory organisation of the data when an experiment is taken to these new environments. In these situations, the endogenous determination of “similar enough” as a function of the data may be seen as a strength, as it provides a way of distinguishing whether coherent-looking types remain even in the face of potentially greater heterogeneity.

5 Discussion

We introduce hierarchical cluster analysis as a useful tool for evaluating whether a model with a discrete number of behavioural types is an appropriate description of experimental data. In VCGs using the P-experiment protocol, we confirm that own maximisers and strong conditional cooperators (matching the contributions of others one-to-one) emerge as the cores of clearly distinguished behavioural groups. Importantly, strong and weak conditional cooperation are identified as distinct modes of behaviour. This provides an independent justification for a similar distinction among types of conditional cooperator which has been proposed in several previous studies, including Chaudhuri and Paichayontvijit (2006), Rustagi et al. (2010), Gächter et al. (2012), and Cheung (2014).

The toolkit of cluster analysis provides methods to evaluate and select from competing potential solutions. Therefore, one can evaluate, for example, the candidate $T^H(4)$ against $T^H(5)$, or even whether any discrete clustering at all is a satisfactory description of the data. Silhouette plots like those in Fig. 2 help to provide a measure of the coherence of types according to some metric. In the case of these plots, we are comparing types generated by clustering on the same distance metric, versus those generated by FGF, which uses a different notion of similarity. Therefore, they illustrate the differences in character of the type classifications produced by the two approaches. This does not reduce to a “horse race” between the approaches; different descriptions of data may prove to be useful for different purposes. Indeed, a theme in the application of machine-learning techniques is the interaction between provable guarantees (e.g., that the solutions $T^H(C)$ minimise the sum of within-cluster sum of squared errors) and heuristic judgments (e.g., using silhouette indices and the criteria of Duda and Hart to recommend a preferred number of clusters).

Machine learning emphasises the importance of cross validation in evaluating clustering. In this paper, we do this by an out-of-sample comparison of the levels of unconditional contributions by the same participants in the same experiment, and find that the cluster-based typology distinguishes these better than the FGF approach. Out-of-sample validation can also be done by applying clustering techniques to two or more sets of decisions made by the same participants. Poncela-Casasnovas et al. (2016) cluster subjects into four different types based on their behaviour in a set of dyadic games. Results show that subjects are consistent across games and that differences exist between young and adults, and between male and female participants. Similarly, in our companion paper (Fallucchi et al. 2018), we apply clustering techniques to contribution strategies of the same participants in linear and non-linear VCGs, as a measure of the consistency of behaviour and portability of types.

Interesting experimental designs often generate unanticipated results, which call for the development of improved or new models. Unsupervised classification methods such as clustering are one option for a structured approach to informing that process. Parametric mixture models (Bardsley and Moffatt 2007) likewise organise experimental data through the lens of multiple discrete types. However, to implement a mixture model, one must first specify the types. The medoids arising from cluster analysis can provide a first glimpse for the types to consider in a mixture model analysis.¹⁰