Abstract
We study \({\mathbb {Q}}\)-factorial terminal Fano 3-folds whose equations are modelled on those of the Segre embedding of  . These lie in codimension 4 in their total anticanonical embedding and have Picard rank 2. They fit into the current state of classification in three different ways. Some families arise as unprojections of degenerations of complete intersections, where the generic unprojection is a known prime Fano 3-fold in codimension 3; these are new, and an analysis of their Gorenstein projections reveals yet other new families. Others represent the “second Tom” unprojection families already known in codimension 4, and we show that every such family contains one of our models. Yet others have no easy Gorenstein projection analysis at all, so prove the existence of Fano components on their Hilbert scheme.
. These lie in codimension 4 in their total anticanonical embedding and have Picard rank 2. They fit into the current state of classification in three different ways. Some families arise as unprojections of degenerations of complete intersections, where the generic unprojection is a known prime Fano 3-fold in codimension 3; these are new, and an analysis of their Gorenstein projections reveals yet other new families. Others represent the “second Tom” unprojection families already known in codimension 4, and we show that every such family contains one of our models. Yet others have no easy Gorenstein projection analysis at all, so prove the existence of Fano components on their Hilbert scheme.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Fano 3-folds, Gorenstein rings and 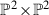
A Fano 3-fold is a complex projective variety X of dimension 3 with \({\mathbb {Q}}\)-factorial terminal singularities and \(-K_X\) ample. We construct several new Fano 3-folds, and others which explain known phenomena. The anticanonical ring

of a Fano 3-fold X is Gorenstein, and provides an embedding \(X\subset \mathrm{w}\mathbb P\) in weighted projective space (wps) that we exploit here, focusing on the case \(X\subset \mathrm{w}\mathbb P^7\) of codimension 4.
According to folklore, when seeking Gorenstein rings in codimension 4 one should look to  and
and  . Each embeds by the Segre embedding as a projectively normal variety in codimension 4 with Gorenstein coordinate ring (by [16, Section 5] since their hyperplane sections are subcanonical). We consider
. Each embeds by the Segre embedding as a projectively normal variety in codimension 4 with Gorenstein coordinate ring (by [16, Section 5] since their hyperplane sections are subcanonical). We consider  , expressed as
, expressed as

or, in words, as the locus where a generic  matrix of forms drops rank. As part of a more general theory of weighted homogeneous varieties, the case of
matrix of forms drops rank. As part of a more general theory of weighted homogeneous varieties, the case of  was worked out by Szendrői [32], which was the inspiration for our study here.
was worked out by Szendrői [32], which was the inspiration for our study here.
The number of deformation families of Fano 3-folds is finite [20, 21], and the Graded Ring Database (Grdb) [4, 6] has a list of rational functions  that includes all Hilbert series
that includes all Hilbert series  of Fano 3-folds with
of Fano 3-folds with  . (In fact, we do not know of any Fano 3-fold whose Hilbert series is not on that list, even without this additional condition.) An attempt at an explicit classification, outlined in [2], aims to describe all deformation families of Fano 3-folds for each such Hilbert series. All families whose general member lies in codimension \(\leqslant 2\) are known [12], and almost certainly those in codimension 3 are too [2, 6]. An analysis of (Gorenstein) projections [8, 24, 34] provides much of the classification in codimension 4, but it is not complete, and codimension 4 remains at the cutting edge.
. (In fact, we do not know of any Fano 3-fold whose Hilbert series is not on that list, even without this additional condition.) An attempt at an explicit classification, outlined in [2], aims to describe all deformation families of Fano 3-folds for each such Hilbert series. All families whose general member lies in codimension \(\leqslant 2\) are known [12], and almost certainly those in codimension 3 are too [2, 6]. An analysis of (Gorenstein) projections [8, 24, 34] provides much of the classification in codimension 4, but it is not complete, and codimension 4 remains at the cutting edge.
We use the methods of [8] freely, although we work through an example in detail in Sect. 3 and explain any novelties as they arise.
1.2 The aims of this paper
We describe families of Fano 3-folds \(X\subset \mathrm{w}\mathbb P^7\) whose equations are a specialisation of the format (1); that is, they are regular pullbacks, as in Sect. 2. It is usually hard to describe the equations of varieties in codimension 4—see papers from Kustin and Miller [22] to Reid [31]—but if we decree the format in advance, then the equations come almost for free, and the question becomes how to put a grading on them to give Fano 3-folds. Our results come in three broad flavours, which we explain in Sects. 4–6 and summarise here.
Section 4: Unprojecting Pfaffian degenerations. We find new varieties in  format that have the same Hilbert series as known Fano 3-folds but lie in different deformation families. From another point of view, we understand this as the unprojection analysis of degenerations of complete intersections, and this treatment provides yet more families not exhibited by [8]. (The key point is that the unprojection divisor \(D\subset Y\) does not persist throughout the degeneration \(Y\leadsto Y_0\), and so the resulting unprojection is not a degeneration in a known family.)
format that have the same Hilbert series as known Fano 3-folds but lie in different deformation families. From another point of view, we understand this as the unprojection analysis of degenerations of complete intersections, and this treatment provides yet more families not exhibited by [8]. (The key point is that the unprojection divisor \(D\subset Y\) does not persist throughout the degeneration \(Y\leadsto Y_0\), and so the resulting unprojection is not a degeneration in a known family.)
For example, No. 1.4 in Takagi’s analysis [33] exhibits a single family of Fano 3-folds with Hilbert series

this is number 26989 in the Grdb. Our  analysis finds another family with
analysis finds another family with  , and a subsequent degeneration–unprojection analysis of the situation finds a third family.
, and a subsequent degeneration–unprojection analysis of the situation finds a third family.
Theorem 1.1
There are three deformation families of Fano 3-folds X with Hilbert series  . Their respective general members
. Their respective general members  all lie in codimension 4 with degree \(-K_X^3 = 17/2\) and a single orbifold singularity \(\frac{1}{2}(1,1,1)\), and with invariants:
all lie in codimension 4 with degree \(-K_X^3 = 17/2\) and a single orbifold singularity \(\frac{1}{2}(1,1,1)\), and with invariants:
We prove this particular result in Sect. 3; the last two columns of the table refer to the unprojection calculation (N is the number of nodes, as described in Sect. 3), which is explained in the indicated sections. The Euler characteristic e(X) is calculated during the unprojection following [8, Section 7] and the other invariants follow. We do not know whether there are any other deformation families realising the same Hilbert series  .
.
We calculate the Hodge number \(h^{2,1}(X)\) in Family 3 using Ilten’s computer package [19] for the computer algebra system Macaulay2 [17] following [15]: denoting the affine cone over X by \(A_X\), [15, Theorem 2.5] gives
and this is exactly what [19] calculates (compare [5, Section 4.1.3]).
In this case, all three families lie in codimension 4. It is more common that the known family lies in codimension 3 and we find new families in codimension 4. Thus the corresponding Hilbert scheme contains different components whose general members are Fano 3-folds in different codimensions, a phenomenon we had not seen before.
Further analysis of degenerations finds yet more new Fano 3-folds even where there is no  model; the following result is proved in Sect. 4.2.
model; the following result is proved in Sect. 4.2.
Theorem 1.2
There are two deformation families of Fano 3-folds X with Hilbert series \(P_X = P_{548}\). Their respective general members X have degree \(-K_X^3 = 1/15\), and are distinguished by their embedding in wps and Euler characteristics as follows:
\(X\subset \mathrm{w}\mathbb P\) | e(X) | \(\#\,\mathrm{nodes}\) | |
|---|---|---|---|
Family 1 |
| \(-\,42\) | 8 |
Family 2 |
| \(-\,40\) | 9 |
In this case there is no  model: such a model would come from a specialised Tom unprojection, but the Tom and Jerry analysis outlined in Sect. 4.2 rules this out.
model: such a model would come from a specialised Tom unprojection, but the Tom and Jerry analysis outlined in Sect. 4.2 rules this out.
Section 5: Second Tom. The Big Table [9] lists all (general) Fano 3-folds in codimension 4 that have a Type I projection. Such projections can be of Tom type or Jerry type (see [8, 2.3]). The result of that paper is that every Fano 3-fold admitting a Type I projection has at least one Tom family and one Jerry family. However in some cases there is a second Tom or second Jerry (or both). Two of these cases were already known to Szendrői [32], even before the Tom and Jerry analysis was developed.
Euler characteristic is of course constant in families, but whenever there is a second Tom, the Euler characteristics of members of the two Tom families differ by 2. Theorem 5.1 below says that in this case the Tom family with smaller Euler characteristic always contains special members in  format.
format.
Section 6: No Type I projection. Finally, we find some Fano 3-folds that are harder to describe, including some that currently have no construction by Gorenstein unprojection. Such Fano 3-folds were expected to exist, but this is the first construction of them in the literature we are aware of. It may be the case that there are other families of such Fano 3-folds having Picard rank 1, but our methods here cannot answer that question.
 format (number of nodes is given as a superscript to \(\mathrm{Tom}\)/\(\mathrm{Jer}\))
format (number of nodes is given as a superscript to \(\mathrm{Tom}\)/\(\mathrm{Jer}\))1.3 Summary of results
Our approach starts with a systematic enumeration of all possible  formats that could realise the Hilbert series of a Fano 3-fold after appropriate specialisation. In Sect. 7, following [7, 27], we find 53 varieties in
formats that could realise the Hilbert series of a Fano 3-fold after appropriate specialisation. In Sect. 7, following [7, 27], we find 53 varieties in  format that have the Hilbert series of a Fano 3-fold. We summarise the fate of each of these 53 cases in Table 1; the final column summarises our results, as we describe below, and the rest of the paper explains the calculations that provide the proof.
format that have the Hilbert series of a Fano 3-fold. We summarise the fate of each of these 53 cases in Table 1; the final column summarises our results, as we describe below, and the rest of the paper explains the calculations that provide the proof.
The columns of Table 1 are as follows. Column k is an adjunction index, described in Sect. 7.1, and columns a and b refer to the vectors in Sect. 2 that determine the weights on the weighted  . Column Grdb lists the number of the Hilbert series in [6], column c indicates the codimension of the usual model suggested there, and \(\mathrm{w}\mathbb P\) its ambient space. Column T/J shows the number of distinct Tom and Jerry components according to [8]. For example, TTJ indicates there are two Tom unprojections and one Jerry unprojection in the Big Table [9]. We write ‘no I’ when the Hilbert series does not admit a numerical Type I projection, and so the Tom and Jerry analysis does not apply, and ‘n/a’ if the usual model is in codimension 3 rather than 4.
. Column Grdb lists the number of the Hilbert series in [6], column c indicates the codimension of the usual model suggested there, and \(\mathrm{w}\mathbb P\) its ambient space. Column T/J shows the number of distinct Tom and Jerry components according to [8]. For example, TTJ indicates there are two Tom unprojections and one Jerry unprojection in the Big Table [9]. We write ‘no I’ when the Hilbert series does not admit a numerical Type I projection, and so the Tom and Jerry analysis does not apply, and ‘n/a’ if the usual model is in codimension 3 rather than 4.
The final column describes the results of this paper; it is an abbreviation of more detailed results. For example, Theorem 1.1 expands out the first line of the table, \(k=4\), and other lines of the table that are not indicated as failing have analogous theorems that the final column summarises. If the  model fails to realise a Fano 3-fold at all, it is usually because the general member does not have terminal singularities; we say, for example, ‘bad 1/4 point’ if the format forces a non-quasismooth, non-terminal index 4 point onto the variety.
model fails to realise a Fano 3-fold at all, it is usually because the general member does not have terminal singularities; we say, for example, ‘bad 1/4 point’ if the format forces a non-quasismooth, non-terminal index 4 point onto the variety.
When the Grdb model is in codimension 3, we list which Tom and Jerry unprojections of a degeneration work to give alternative varieties in codimension 4, indicating the number of nodes as a superscript and the codimension 4 ambient space. (We do not say which Tom or Jerry since that depends on a choice of rows and columns.) In each case the Tom unprojection gives the  model determined by the parameters a and b. The usual codimension 3 model arises by Type I unprojection with number of nodes being one more that that of the
model determined by the parameters a and b. The usual codimension 3 model arises by Type I unprojection with number of nodes being one more that that of the  Tom model.
Tom model.
When the Grdb model is in codimension 4 with two Tom unprojections, the  always works to give the second of the Tom families. The further Tom and Jerry analysis of the unprojection is carried out in [8] and we do not repeat the result here. When the Grdb model is in codimension 4 with only a single Tom unprojection, the model usually fails. The exception is family 12,960, which does work as a
always works to give the second of the Tom families. The further Tom and Jerry analysis of the unprojection is carried out in [8] and we do not repeat the result here. When the Grdb model is in codimension 4 with only a single Tom unprojection, the model usually fails. The exception is family 12,960, which does work as a  model. There is also a case of a Hilbert series, number 11,157, where the Grdb offers a prediction of a variety in codimension 5, but this fails as a
model. There is also a case of a Hilbert series, number 11,157, where the Grdb offers a prediction of a variety in codimension 5, but this fails as a  model.
model.
In Sect. 7.1, we outline a computer search that provides the a, b parameters of Table 1 which are the starting point of the analysis here. In Sect. 7.2, we summarise the results of [32] that provide the most general form of the Hilbert series of a variety in  format; that paper also discovered cases 11,106 and 11,021 of Table 1 that inspired our approach here. First we introduce the key varieties of the
format; that paper also discovered cases 11,106 and 11,021 of Table 1 that inspired our approach here. First we introduce the key varieties of the  format in Sect. 2.
format in Sect. 2.
2 The key varieties and weighted 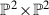 formats
formats
The affine cone  on
on  is defined by the equations (1) on \({\mathbb {C}}^9\). It admits a 6-dimensional family of \({\mathbb {C}}^*\) actions, or equivalently six degrees of freedom in assigning positive integer gradings to its (affine) coordinate ring. We express this as follows.
is defined by the equations (1) on \({\mathbb {C}}^9\). It admits a 6-dimensional family of \({\mathbb {C}}^*\) actions, or equivalently six degrees of freedom in assigning positive integer gradings to its (affine) coordinate ring. We express this as follows.
Let  and \(b=(b_1,b_2,b_3)\) be two vectors of integers that satisfy \(a_1\leqslant a_2\leqslant a_3\), and similarly for the \(b_i\), and that \(a_1+b_1\geqslant 1\). We define a weighted
and \(b=(b_1,b_2,b_3)\) be two vectors of integers that satisfy \(a_1\leqslant a_2\leqslant a_3\), and similarly for the \(b_i\), and that \(a_1+b_1\geqslant 1\). We define a weighted  as
as

where the variables have weights

Thus  , where the \({\mathbb {C}}^*\) action is determined by the grading. We treat
, where the \({\mathbb {C}}^*\) action is determined by the grading. We treat  as a key variety for each different pair a, b. (Note that the entries of a and b may also all lie in \(\frac{1}{2}+\mathbb Z\), without any change to our treatment here).
as a key variety for each different pair a, b. (Note that the entries of a and b may also all lie in \(\frac{1}{2}+\mathbb Z\), without any change to our treatment here).
Proposition 2.1
 is a 4-dimensional, \({\mathbb {Q}}\)-factorial projective toric variety of Picard rank \(\rho _V = 2\).
is a 4-dimensional, \({\mathbb {Q}}\)-factorial projective toric variety of Picard rank \(\rho _V = 2\).
Proof
First we describe a toric variety  by its Cox ring. The input data is the weight matrix (3), which is weakly increasing along rows and down columns. The key is to understand the freedom one has to choose alternative vectors \(a^{(i)}\!,b^{(i)}\), for \(i = 1,2\), to give the same matrix. For example, if we choose \(a^{(1)}_1\!=0\), then \(b^{(1)}\) is determined by the top row, and then \(a^{(1)}_2\) and \(a^{(1)}_3\) are determined by the first column. Alternatively, choosing \(b^{(2)}_1\!=0\) determines different vectors \(a^{(2)}\) and \(b^{(2)}\). Concatenating the a and b vectors to give
by its Cox ring. The input data is the weight matrix (3), which is weakly increasing along rows and down columns. The key is to understand the freedom one has to choose alternative vectors \(a^{(i)}\!,b^{(i)}\), for \(i = 1,2\), to give the same matrix. For example, if we choose \(a^{(1)}_1\!=0\), then \(b^{(1)}\) is determined by the top row, and then \(a^{(1)}_2\) and \(a^{(1)}_3\) are determined by the first column. Alternatively, choosing \(b^{(2)}_1\!=0\) determines different vectors \(a^{(2)}\) and \(b^{(2)}\). Concatenating the a and b vectors to give  determines a 2-dimensional \({\mathbb {Q}}\)-subspace \(U=U_{a,b}\subset {\mathbb {Q}}^6\) together with a chosen integral basis .
determines a 2-dimensional \({\mathbb {Q}}\)-subspace \(U=U_{a,b}\subset {\mathbb {Q}}^6\) together with a chosen integral basis .
We define  as a quotient of \({\mathbb {C}}^6\) by
as a quotient of \({\mathbb {C}}^6\) by  as follows. In terms of Cox coordinates, it is determined by the polynomial ring R in variables \(u_1,u_2,u_3\), \(v_1,v_2,v_3\), bi-graded by the columns of the matrix (giving the two \({\mathbb {C}}^*\) actions)
as follows. In terms of Cox coordinates, it is determined by the polynomial ring R in variables \(u_1,u_2,u_3\), \(v_1,v_2,v_3\), bi-graded by the columns of the matrix (giving the two \({\mathbb {C}}^*\) actions)
The irrelevant ideal is , and

If  is well formed, then it is a toric variety determined by a fan (.07emthe image of all non-irrelevant cones of the fan of \({\mathbb {C}}^6\) under projection to a complement of U). The bilinear map
is well formed, then it is a toric variety determined by a fan (.07emthe image of all non-irrelevant cones of the fan of \({\mathbb {C}}^6\) under projection to a complement of U). The bilinear map

is an isomorphism onto its image  , and the conclusions of the proposition all follow at once. (\({\mathbb {Q}}\)-factoriality holds since the Cox coordinates correspond to the 1-skeleton of the fan, and so any maximal cone with at least five rays must contain all \(u_i\) or all
, and the conclusions of the proposition all follow at once. (\({\mathbb {Q}}\)-factoriality holds since the Cox coordinates correspond to the 1-skeleton of the fan, and so any maximal cone with at least five rays must contain all \(u_i\) or all  , contradicting the choice of irrelevant ideal.)
, contradicting the choice of irrelevant ideal.)
If  is not well formed, then, just as for wps, there is a different weight matrix that is well formed and determines a toric variety \(W'\) isomorphic to
is not well formed, then, just as for wps, there is a different weight matrix that is well formed and determines a toric variety \(W'\) isomorphic to  . (See Iano-Fletcher [18, 6.9–20] for wps and Ahmadinezhad [1, 2.3] for the general case.) The proposition follows using \(W'\). \(\square \)
. (See Iano-Fletcher [18, 6.9–20] for wps and Ahmadinezhad [1, 2.3] for the general case.) The proposition follows using \(W'\). \(\square \)
The well forming process used in the proof is easy to use. For example, if an integer \(n>1\) divides every entry of some row of the weight matrix (4), then we may divide that row through by n; the subspace \(U\subset {\mathbb {Q}}^6\) is unchanged by this. Or if an integer \(n>1\) divides all columns except one, then the corresponding Cox coordinate u appears only as \(u^n\) in the coordinate rings of standard affine patches and we may truncate R by replacing the generator u by \(u^n\); this does not change the coordinate rings of the affine patches, and so the scheme it defines is isomorphic to the original (c.f. [1, Lemma 2.9] for the more general statement). This multiplies the u column of (4) by n, changing the subspace \(U\subset {\mathbb {Q}}^6\), and then we may divide the whole matrix by n as before. See [1, 2.3] for the complete process.
Having said that, in practice we will work with non-well-formed quotients if they arise, since they still admit regular pullbacks that are well formed, and the grading on the target wps is something we fix in advance. More importantly for us here is that well forming step \(u\leadsto u^n\) destroys the  structure, so we avoid it.
structure, so we avoid it.
Example 2.2
Consider  for \(a=(1,1,1)\), \(b=(1,1,2)\). Selecting \(a^{(i)}\) and \(b^{(i)}\) as above gives bi-grading matrix
for \(a=(1,1,1)\), \(b=(1,1,2)\). Selecting \(a^{(i)}\) and \(b^{(i)}\) as above gives bi-grading matrix

on variables \(u_1,u_2,u_3\), \(v_1,v_2,v_3\). (We use the vertical line in the bi-grading matrix to indicate the irrelevant ideal  .) The map \(\mathrm{\Phi }\) of (5) is then
.) The map \(\mathrm{\Phi }\) of (5) is then

since the monomials having gradings \(\left( {\begin{matrix}2\\ 2\end{matrix}}\right) \) and \(\left( {\begin{matrix}3\\ 3\end{matrix}}\right) \), as necessary. The image  is defined by (2), and we often write the target weights of \(\mathrm{\Phi }\) in matching array:
is defined by (2), and we often write the target weights of \(\mathrm{\Phi }\) in matching array:
In this case  is not well formed: the locus
is not well formed: the locus  has dimension 3 (by Hilbert–Burch), so has codimension 1 in
has dimension 3 (by Hilbert–Burch), so has codimension 1 in  but nontrivial stabiliser \(\mathbb Z/2\) in the wps. Well forming the gradings using \(v_3^2\), as above, gives a new bi-grading
but nontrivial stabiliser \(\mathbb Z/2\) in the wps. Well forming the gradings using \(v_3^2\), as above, gives a new bi-grading

That process is well established, but has a problem: for this presentation \(W'\) of W, the Segre map is not bi-linear: \(u_1v_1\) has bidegree \(\left( {\begin{matrix} 1\\ 1 \end{matrix}}\right) \), but \(u_1v_3\) has an independent bidegree \(\left( {\begin{matrix} 3\\ 2 \end{matrix}}\right) \). We could use \(u_1^2v_3\) instead, which has proportional bidegree \(\left( {\begin{matrix} 3\\ 3 \end{matrix}}\right) \). Taking  , where R is the graded ring of forms of degrees \(\left( {\begin{matrix} m\\ m \end{matrix}}\right) \) for \(m\geqslant 0\), gives
, where R is the graded ring of forms of degrees \(\left( {\begin{matrix} m\\ m \end{matrix}}\right) \) for \(m\geqslant 0\), gives  , which is now well formed, but we have lost the codimension 4 property of V we want to exploit. In a case like this, we work directly with the non-well-formed
, which is now well formed, but we have lost the codimension 4 property of V we want to exploit. In a case like this, we work directly with the non-well-formed  and its non-well-formed image
and its non-well-formed image  .
.
We use the varieties  as key varieties to produce new varieties from by regular pullback; see [30, Section 1.5] or [7, Section 2]. In practical terms, that means writing equations in the form of (1) inside a wps \(\mathrm{w}\mathbb P^7\) where the \(x_i\) are homogeneous forms of positive degrees, and the resulting loci \(X\subset \mathrm{w}\mathbb P^7\) are the Fano 3-folds we seek.
as key varieties to produce new varieties from by regular pullback; see [30, Section 1.5] or [7, Section 2]. In practical terms, that means writing equations in the form of (1) inside a wps \(\mathrm{w}\mathbb P^7\) where the \(x_i\) are homogeneous forms of positive degrees, and the resulting loci \(X\subset \mathrm{w}\mathbb P^7\) are the Fano 3-folds we seek.
Alternatively, we may treat X as a complete intersection in a projective cone over  , as in Sect. 3.2 below, where the additional cone vertex variables may have any positive degrees; this point of view is taken by Corti-Reid and Szendrői in [14, 26, 29, 32]. It follows from this description that the Picard rank of X is 2.
, as in Sect. 3.2 below, where the additional cone vertex variables may have any positive degrees; this point of view is taken by Corti-Reid and Szendrői in [14, 26, 29, 32]. It follows from this description that the Picard rank of X is 2.
3 Unprojection and the proof of Theorem 1.1
The Hilbert series number 26989 in the Graded Ring Database (Grdb) [6] is

In Sect. 3.1 we describe the known family of Fano 3-folds  that realise this Hilbert series, \(P_{X^{(1)}}\! = P\). These 3-folds are not smooth: the general member of the family has a single \(\frac{1}{2}(1,1,1)\) quotient singularity. We exhibit a different family in Sect. 3.2 with the same Hilbert series in
that realise this Hilbert series, \(P_{X^{(1)}}\! = P\). These 3-folds are not smooth: the general member of the family has a single \(\frac{1}{2}(1,1,1)\) quotient singularity. We exhibit a different family in Sect. 3.2 with the same Hilbert series in  format, and the subsequent “Tom and Jerry” analysis yields a third distinct family in Sect. 3.3.
format, and the subsequent “Tom and Jerry” analysis yields a third distinct family in Sect. 3.3.
Recall (from [8, Section 4], for example) that if \(X\dasharrow Y\supset D\) is a Gorenstein unprojection and Y is quasismooth away from N nodes, all of which lie on D, then
3.1 The classical 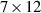 family
family
A general member of the first family can be constructed as the unprojection of a coordinate \(D = \mathbb P^2\) inside a c.i.  (see, for example, Papadakis [23]). In general, Y has six nodes that lie on D: in coordinates x, y, z, u, v, w, t of
(see, for example, Papadakis [23]). In general, Y has six nodes that lie on D: in coordinates x, y, z, u, v, w, t of  , setting
, setting  , the general Y has equations defined by
, the general Y has equations defined by
for general linear forms \(A_{i,j}\); singularities occur when the  matrix drops rank, which is calculated by evaluating the numerator of the Hilbert series of that locus at 1:
matrix drops rank, which is calculated by evaluating the numerator of the Hilbert series of that locus at 1:

The coordinate ring of X has a  free resolution. If \(Y_{\mathrm {gen}}\) is a nonsingular small deformation of Y, then
free resolution. If \(Y_{\mathrm {gen}}\) is a nonsingular small deformation of Y, then  (by the usual Chern class calculation, since \(Y_{\mathrm {gen}}\) is a smooth 2, 2, 2 complete intersection) so, by (6),
(by the usual Chern class calculation, since \(Y_{\mathrm {gen}}\) is a smooth 2, 2, 2 complete intersection) so, by (6),

This family is described by Takagi [33]; it is no. 1.4 in the tables there of Fano 3-folds of Picard rank 1.
3.2 A 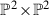 family with Tom projection
family with Tom projection
Consider the  key variety
key variety  , where \(a = \bigl (\frac{1}{2},\frac{1}{2},\frac{1}{2}\bigr )\) and \(b=\bigl (\frac{1}{2},\frac{1}{2},\frac{3}{2}\bigr )\). We define a quasismooth variety
, where \(a = \bigl (\frac{1}{2},\frac{1}{2},\frac{1}{2}\bigr )\) and \(b=\bigl (\frac{1}{2},\frac{1}{2},\frac{3}{2}\bigr )\). We define a quasismooth variety  in codimension 4 as a regular pullback.
in codimension 4 as a regular pullback.
In explicit terms, in coordinates x, y, z, t, u, v, w, s on  , a
, a  matrix M of forms of degrees
matrix M of forms of degrees
gives a quasismooth  ; for example,
; for example,
works. Alternatively, note that \(X^{(2)}\) may be viewed as a complete intersection

where  is the projective cone over \(V_{a,b}\) on a vertex of degree 1 (by introducing a new variable of degree 1), and \(Q_i\) are general quadrics (which are quasilinear, and so may be used to eliminate two variables of degree 2). The general such \(X^{(2)}\) is quasismooth (since in particular the intersection misses the vertex). Described in these terms, \(C_1V_{a,b}\) has Picard rank 2, and so \(\rho _{X^{(2)}}\! = 2\).
is the projective cone over \(V_{a,b}\) on a vertex of degree 1 (by introducing a new variable of degree 1), and \(Q_i\) are general quadrics (which are quasilinear, and so may be used to eliminate two variables of degree 2). The general such \(X^{(2)}\) is quasismooth (since in particular the intersection misses the vertex). Described in these terms, \(C_1V_{a,b}\) has Picard rank 2, and so \(\rho _{X^{(2)}}\! = 2\).
Any such \(X^{(2)}\) has a single quotient singularity \(\frac{1}{2}(1,1,1)\), at the coordinate point \(P_s\in X^{(2)}\) as the explicit equations make clear, since y, z, u, v are implicit functions in a neighbourhood of \(P_s\in X^{(2)}\). The Gorenstein projection from this point \(P_s\) has image  , where
, where
is an antisymmetric  matrix, and \(\mathrm{Pf}\,N\) denotes the sequence of five maximal Pfaffians of N. (The nonzero entries of N are those of \(M^T\) with the entry s deleted.)
matrix, and \(\mathrm{Pf}\,N\) denotes the sequence of five maximal Pfaffians of N. (The nonzero entries of N are those of \(M^T\) with the entry s deleted.)
This Y contains the projection divisor  and has five nodes on D (either by direct calculation, or by the formula of [8, Section 7]). The divisor \(D\subset Y\) is in Tom\(_3\) configuration: entries \(n_{i,j}\) of the skew
and has five nodes on D (either by direct calculation, or by the formula of [8, Section 7]). The divisor \(D\subset Y\) is in Tom\(_3\) configuration: entries \(n_{i,j}\) of the skew  matrix N defining Y lie in the ideal \(I_D = (y,z,u,v)\) if both \(i\not =3\) and \(j\not =3\); that is, all entries off row 3 and column 3 of N are in \(I_D\). Thus, in particular, we can reconstruct \(X^{(2)}\) from \(D\subset Y\) as the Tom\(_3\) unprojection. It follows from Papadakis–Reid [25, Section 2.4] that \(\omega _{X^{(2)}} = \mathscr {O}_{X^{(2)}}(-1)\) and so \(X^{(2)}\) is a Fano 3-fold.
matrix N defining Y lie in the ideal \(I_D = (y,z,u,v)\) if both \(i\not =3\) and \(j\not =3\); that is, all entries off row 3 and column 3 of N are in \(I_D\). Thus, in particular, we can reconstruct \(X^{(2)}\) from \(D\subset Y\) as the Tom\(_3\) unprojection. It follows from Papadakis–Reid [25, Section 2.4] that \(\omega _{X^{(2)}} = \mathscr {O}_{X^{(2)}}(-1)\) and so \(X^{(2)}\) is a Fano 3-fold.
It remains to show that  , so that this Fano 3-fold must lie in a different deformation family from the classical one constructed in Sect. 3.1.
, so that this Fano 3-fold must lie in a different deformation family from the classical one constructed in Sect. 3.1.
The degree of the (1, 2) entry \(f_{1,2}\) of N is in fact zero while the degree of \(f_{4,5}\) is 2, although each entry is of course the zero polynomial in this case; we denote this by indicating the degrees of the entries with brackets around those that are zero in this case:
We may deform Y by varying these two entries to  and
and  , where \(\varepsilon \not =0\) and f is a general quadric on
, where \(\varepsilon \not =0\) and f is a general quadric on  (and, of course, the skew symmetric entries in \(f_{2,1}\) and \(f_{5,4}\)). Denoting the deformed matrix by \(N_\varepsilon \), and
(and, of course, the skew symmetric entries in \(f_{2,1}\) and \(f_{5,4}\)). Denoting the deformed matrix by \(N_\varepsilon \), and  , we see a small deformation of Y to a smooth Fano 3-fold
, we see a small deformation of Y to a smooth Fano 3-fold  that is a 2, 2, 2 complete intersection. (The nonzero constant entries of \(N_\varepsilon \) provide two syzygies that eliminate two of the five Pfaffians.) As in Sect. 3.1, the smoothing \(Y_\varepsilon \) has Euler characteristic
that is a 2, 2, 2 complete intersection. (The nonzero constant entries of \(N_\varepsilon \) provide two syzygies that eliminate two of the five Pfaffians.) As in Sect. 3.1, the smoothing \(Y_\varepsilon \) has Euler characteristic  , so by (6) we have that
, so by (6) we have that  .
.
Note that the Pfaffian smoothing \(Y_\varepsilon \) of Y destroys the unprojection divisor \(D\subset Y\): for D to lie inside \(Y_\varepsilon \) the entries \(f_{3,4}\) and \(f_{3,5}\) of \(N_\varepsilon \) would have to lie in \(I_D\) (so \(N_\varepsilon \) would be in Jer\(_{4,5}\) format with the extra constraint \(f_{4,5}=0\)), but then Y would be singular along D since three of the five Pfaffians would lie in \(I_D^2\).
3.3 A third family by Jerry unprojection
A Tom and Jerry analysis following [8] shows that varieties  defined by Pfaffians as in Sect. 3.2 by the maximal Pfaffians of a syzygy matrix N with weights
defined by Pfaffians as in Sect. 3.2 by the maximal Pfaffians of a syzygy matrix N with weights
can also be constructed in Jer\(_{1,3}\) format: that is, with all entries \(f_{i,j}\) of N lying in \(I_D\) whenever i or j lie in \(\{1,3\}\). The general such \(D\subset Y\) has seven nodes on D. Unprojecting \(D\subset Y\) gives a general member \(X^{(3)}\) of a third family with  .
.
This completes the proof of Theorem 1.1.
4 Unprojecting Pfaffian degenerations
4.1
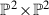 models with a codimension 3 Pfaffian component
models with a codimension 3 Pfaffian component
Each of the Fano Hilbert series 1396, 5302, 5858, 5962, 11436, 20543 is realised by a codimension 3 Pfaffian model, which is the simple default model presented in the Grdb. (So too are 4999, 5844 and 10,984, but we do not find new models for these.) We show that they can also be realised by a  model in a different deformation family (and sometimes a third model too). The key point is that a projection of the usual model admits alternative degenerations in higher codimension that also contain a divisor that can be unprojected.
model in a different deformation family (and sometimes a third model too). The key point is that a projection of the usual model admits alternative degenerations in higher codimension that also contain a divisor that can be unprojected.
For example, consider series number 20543

There is a well-known family that realises this as  in codimension 3, where M has degrees
in codimension 3, where M has degrees
A typical member of this family has a two \(\frac{1}{2}(1,1,1)\) quotient singularities, and making the Gorenstein projection from either of them presents X as a Type I unprojection of

In general, Y has eight nodes lying on D, and it smooths to a nonsingular Fano 3-fold \(Y_{\mathrm {gen}}\) with Euler characteristic  . Thus a general X has Euler characteristic
. Thus a general X has Euler characteristic  .
.
A quasismooth  family. We can write another (quasismooth) model
family. We can write another (quasismooth) model  in codimension 4 in
in codimension 4 in  format with weights
format with weights
Projecting from \(\frac{1}{2}(1,1,1)\) has image  where M has degrees
where M has degrees
and Y has seven nodes lying on D; in coordinates x, y, z, t, u, w, v, we may take \(D=\mathbb P^2\) to be  . By varying the (1, 2) entry from zero to a unit, Y has a deformation to a quasismooth 3, 3 complete intersection \(Y_{\mathrm {gen}}\) as before, and so,
. By varying the (1, 2) entry from zero to a unit, Y has a deformation to a quasismooth 3, 3 complete intersection \(Y_{\mathrm {gen}}\) as before, and so,  . Thus these
. Thus these  models are members of a different deformation family from the original one.
models are members of a different deformation family from the original one.
More is true in this case: the general member of this new deformation family is in  format. Starting with matrix (7) and \(D=\mathbb P^2\) as above, the (1, 2) entry of the general Tom\(_3\) matrix is necessarily the zero polynomial. In general, the four entries (1, 4), (1, 5), (2, 4) and (2, 5) of the matrix are in the ideal
format. Starting with matrix (7) and \(D=\mathbb P^2\) as above, the (1, 2) entry of the general Tom\(_3\) matrix is necessarily the zero polynomial. In general, the four entries (1, 4), (1, 5), (2, 4) and (2, 5) of the matrix are in the ideal  , and for the general member these four variables are dependent on those entries. Thus the (4, 5) entry can be arranged to be zero by row-and-column operations.
, and for the general member these four variables are dependent on those entries. Thus the (4, 5) entry can be arranged to be zero by row-and-column operations.
Another family in codimension 4. There is a third deformation family in this case. The codimension 3 format (7) also admits a Jerry\(_{15}\) unprojection with nine nodes on D, giving  in codimension 4 with
in codimension 4 with  .
.
4.2 Pfaffian degenerations of codimension 2 Fano 3-folds
The key to the cases in Sect. 4.1 that the  model exposes is the degeneration of a codimension 2 Fano 3-fold. More generally, Table 3 of [3] lists 13 cases of Fano 3-fold degenerations where the generic fibre is a codimension 2 complete intersection and the special fibre is a codimension 3 Pfaffian. In each case, the anti-symmetric
model exposes is the degeneration of a codimension 2 Fano 3-fold. More generally, Table 3 of [3] lists 13 cases of Fano 3-fold degenerations where the generic fibre is a codimension 2 complete intersection and the special fibre is a codimension 3 Pfaffian. In each case, the anti-symmetric  syzygy matrix of the special fibre has an entry of degree 0, which is the zero polynomial in the degeneration, but when nonzero serves to eliminate a single variable. (In fact [3] describes the graded rings of K3 surfaces, but these extend to Fano 3-folds by the usual extension–deformation method introducing a new variable of degree 1.)
syzygy matrix of the special fibre has an entry of degree 0, which is the zero polynomial in the degeneration, but when nonzero serves to eliminate a single variable. (In fact [3] describes the graded rings of K3 surfaces, but these extend to Fano 3-folds by the usual extension–deformation method introducing a new variable of degree 1.)
For example,  degenerates to codimension 3
degenerates to codimension 3
Both of these realise Fano Hilbert series number 547, and the Euler characteristic of a general member is  .
.
The codimension 2 family has a subfamily whose members contain a Type I unprojection divisor,

on which Y has eight nodes; the unprojection of \(D\subset Y\) gives the codimension 3 Pfaffian family

Imposing the same unprojection divisor \(D\subset Y^{0}\) can be done in two distinct ways, coming from different Tom and Jerry arrangments. In one way, there are degenerations \(Y^{t}_{12,13} \leadsto Y^{0}\) which contain the same D in every fibre \(Y_t\). These unproject to a degeneration of the family (8) by the following lemma: indeed unprojection commutes with regular sequences by [10, Lemma 5.6], and so unprojection commutes with flat deformation, if one fixes the unprojection divisor; so the lemma is a particular case of [10, Lemma 5.6].
Lemma 4.1
Let  be any wps and fix
be any wps and fix  , for some \(d\leqslant s-2\). Suppose \(Y_t\subset \mathscr {Y}\rightarrow \mathscr {T}\) is a flat 1-dimensional family of projectively Gorenstein subschemes of \(\mathbb P\) over smooth base \(0\in \mathscr {T}\), each one containing D and with \(\dim Y_t = \dim D + 1=d+1\), and with \(\omega _Y=\mathscr {O}_Y(k_Y)\). Let
, for some \(d\leqslant s-2\). Suppose \(Y_t\subset \mathscr {Y}\rightarrow \mathscr {T}\) is a flat 1-dimensional family of projectively Gorenstein subschemes of \(\mathbb P\) over smooth base \(0\in \mathscr {T}\), each one containing D and with \(\dim Y_t = \dim D + 1=d+1\), and with \(\omega _Y=\mathscr {O}_Y(k_Y)\). Let  be the unprojection of
be the unprojection of  , where \(b = k_Y-k_D = a_0+\cdots +a_d-1\). Then \(\mathscr {X}\) is flat over \(\mathscr {T}\), and for each closed point \(t\in \mathscr {T}\) the fibre \(X_t\in \mathscr {X}\) is the unprojection of \(D\subset Y_t\).
, where \(b = k_Y-k_D = a_0+\cdots +a_d-1\). Then \(\mathscr {X}\) is flat over \(\mathscr {T}\), and for each closed point \(t\in \mathscr {T}\) the fibre \(X_t\in \mathscr {X}\) is the unprojection of \(D\subset Y_t\).
But the \(\mathrm{Jer}_{24}\) unprojection is different: small deformations of \(Y^{0}\) do not contain D. Indeed, in this \(D\subset Y^0\) model, \(Y^{0}\) has nine nodes on D, which is a numerical obstruction to any such deformation. This \(D\subset Y^{0}\) unprojects to a codimension 4 Fano 3-fold

with the same Hilbert Series No. 548 as (8) but lying in a different component: it has Euler characteristic  . This proves Theorem 1.2.
. This proves Theorem 1.2.
5
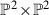 and the second Tom
and the second Tom
The Big Table [9], which contains the results of [8], lists deformation families of Fano 3-folds in codimension 4 that have a Type I projection to a Pfaffian 3-fold in codimension 3. The components are listed according to the Tom or Jerry type of the projection: the type of projection is invariant for sufficiently general members of each component. The result of this section gives an interpretation of the Big Table of [8], but does not describe any new families of Fano 3-folds.
Theorem 5.1
For every Hilbert series listed in the Big Table [9] that is realised by two distinct Tom projections, there is a Fano 3-fold in  format that lies on the family containing 3-folds with the smaller (more negative) Euler characteristic.
format that lies on the family containing 3-folds with the smaller (more negative) Euler characteristic.
The theorem is proved simply by constructing each case. There are 29 Hilbert series that have two Tom families. Using ‘TTJ’ to indicate a series realised by two Tom components and one Jerry component and ‘TTJJ’ to indicate two of each, they are (Table 2).
 format that admit a second Tom unprojection
format that admit a second Tom unprojectionFor example, for Hilbert Series No. 4839,

[9] describes four deformation families of Fano 3-folds

A general such X has Type I projections from both \(\frac{1}{5}(1,1,4)\) and \(\frac{1}{9}(1,1,8)\). (It is enough to consider just one of these centres of projection, but [8] calculates both, drawing the same conclusion twice.)
We construct a  model for \(P_{4839}\). Consider \(\mathbb P=\mathbb P^7(1,1,4,5,6,7,8,9)\) with coordinates x, y, z, t, u, v, w, s. The
model for \(P_{4839}\). Consider \(\mathbb P=\mathbb P^7(1,1,4,5,6,7,8,9)\) with coordinates x, y, z, t, u, v, w, s. The  minors of the matrix
minors of the matrix
define quasismooth \(X\subset \mathbb P\) with quotient singularities \(\frac{1}{2}(1,1,1)\), \(\frac{1}{5}(1,1,4)\) and \(\frac{1}{9}(1,1,8)\).
Eliminating either the variable t of degree 5 or s of degree 9 computes the two possible Type I projections, with image a nodal codimension 3 Fano 3-fold Y containing  or \({D=\mathbb P(1,1,8)}\) with 20 or 13 nodes lying on D respectively. (Both t and s appear only once in the matrix, so eliminating them simply involves omitting that entry and mounting the rest of the matrix in a skew matrix, as usual.)
or \({D=\mathbb P(1,1,8)}\) with 20 or 13 nodes lying on D respectively. (Both t and s appear only once in the matrix, so eliminating them simply involves omitting that entry and mounting the rest of the matrix in a skew matrix, as usual.)
6 Cases with no numerical Type I projection
The five Hilbert series 360, 577, 648, 878 and 1766 do not admit a Type I projection, and so the analysis of [8] does not apply. Nevertheless each is realised by a variety in  format exist, although only two of these are Fano 3-folds.
format exist, although only two of these are Fano 3-folds.
In the two cases 360 and 648 the general  model is not quasismooth and has a non-terminal singularity, so there is no
model is not quasismooth and has a non-terminal singularity, so there is no  Fano model. (Each of these admit Type II\(_1\) projections, so are instead subject to the analysis of [24]; this is carried out by Taylor [34].) In the case 577, the
Fano model. (Each of these admit Type II\(_1\) projections, so are instead subject to the analysis of [24]; this is carried out by Taylor [34].) In the case 577, the  model is quasismooth, but it has a \(\frac{1}{4}(1,1,1)\) quotient singularity and so is not a terminal Fano 3-fold and again there is no
model is quasismooth, but it has a \(\frac{1}{4}(1,1,1)\) quotient singularity and so is not a terminal Fano 3-fold and again there is no  Fano model.
Fano model.
However, there is a quasismooth Fano 3-fold  in
in  format with weights
format with weights
realising Hilbert series 878. It has  ,
,  quotient singularities. There is also a quasismooth Fano 3-fold
quotient singularities. There is also a quasismooth Fano 3-fold  in
in  format with weights
format with weights
realising Hilbert series 1799. It has  ,
,  quotient singularities. Each of these two admit only Type II\(_2\) projections, and an analysis by Gorenstein projection has not yet been attempted. Presumably such an analysis can in principle work, once we have much better understanding of Type II unprojection, but until then our models are the only Fano 3-folds known to realise these two Hilbert series.
quotient singularities. Each of these two admit only Type II\(_2\) projections, and an analysis by Gorenstein projection has not yet been attempted. Presumably such an analysis can in principle work, once we have much better understanding of Type II unprojection, but until then our models are the only Fano 3-folds known to realise these two Hilbert series.
7 Enumerating 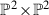 formats
formats
7.1 Enumerating  formats and cases that fail
formats and cases that fail
The Hilbert series  of such Gorenstein rings R(X) satisfy the orbifold integral plurigenus formula [11, Theorem 1.3]
of such Gorenstein rings R(X) satisfy the orbifold integral plurigenus formula [11, Theorem 1.3]

where \(P_{\mathrm {ini}}\) is a function only of the genus g of X, where \(g+2=h^0(-K_X)\), and \(P_{\mathrm {orb}}\) is a function of a quotient singularity \(Q = \frac{1}{r}(1,a,-a)\), the collection of which form the basket \(\mathscr {B}\) of X (see [13, Section 9]). When \(X\subset \mathrm{w}\mathbb P\) is quasismooth, and so is an orbifold, the basket \(\mathscr {B}\) is exactly the collection of quotient singularities of X. Thus the numerical data \(g, \mathscr {B}\) gives the basis for a systematic search of Hilbert series with given properties, which we develop further here.
We may enumerate all  formats
formats  and then list all genus–basket pairs \(g,\mathscr {B}\) whose corresponding series (9) has matching numerator. This algorithm is explained in [7, Section 4]. It works systematically through increasing \(k\in \mathbb N\), where \(k=3\bigl (\sum a_i + \sum b_i\bigr )\), the sum of the weights of the ambient space of the image of \(\mathrm{\Phi }\) in (5).
and then list all genus–basket pairs \(g,\mathscr {B}\) whose corresponding series (9) has matching numerator. This algorithm is explained in [7, Section 4]. It works systematically through increasing \(k\in \mathbb N\), where \(k=3\bigl (\sum a_i + \sum b_i\bigr )\), the sum of the weights of the ambient space of the image of \(\mathrm{\Phi }\) in (5).
The enumeration does not have a termination condition, even though there can only be finitely many solutions for Fano 3-folds, so this does not directly give a classification. Nevertheless, we search for  formats for each \(k=1,\dots ,31\) to start the investigation. This reveals 53 cases whose numerical data (basket and genus) match those of a Fano 3-fold. The number # of cases found per value of k is:
formats for each \(k=1,\dots ,31\) to start the investigation. This reveals 53 cases whose numerical data (basket and genus) match those of a Fano 3-fold. The number # of cases found per value of k is:

This hints that we may have found all Fano Hilbert series that match some  format, since the algorithm stops producing results after \(k=23\). Of course that is not a proof that there are no other cases, and we do not claim that; the results here only use the outcome of this search as their starting point, so how that outcome arises is not relevant.
format, since the algorithm stops producing results after \(k=23\). Of course that is not a proof that there are no other cases, and we do not claim that; the results here only use the outcome of this search as their starting point, so how that outcome arises is not relevant.
7.2 Weighted 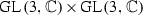 varieties according to Szendrői
varieties according to Szendrői
The elementary considerations we deploy for the key varieties  are part of a more general approach to weighted homogeneous spaces by Grojnowski and Corti–Reid [14], with other cases developed by Qureshi and Szendrői [28, 29]. The particular case of
are part of a more general approach to weighted homogeneous spaces by Grojnowski and Corti–Reid [14], with other cases developed by Qureshi and Szendrői [28, 29]. The particular case of  was worked out detail by Szendrői [32], which we sketch here.
was worked out detail by Szendrői [32], which we sketch here.
In the treatment of [32],  , for the maximal torus \(T\subset G\). The construction of a weighted
, for the maximal torus \(T\subset G\). The construction of a weighted  , denoted \(\mathrm{w}\Sigma (\mu ,u)\), is determined by the choice of a coweight vector \(\mu \in \mathrm{Hom}(M,\mathbb Z)\), in coordinates say
, denoted \(\mathrm{w}\Sigma (\mu ,u)\), is determined by the choice of a coweight vector \(\mu \in \mathrm{Hom}(M,\mathbb Z)\), in coordinates say  , and an integer \(u\in \mathbb Z\). These data are subject to the positivity conditions that all
, and an integer \(u\in \mathbb Z\). These data are subject to the positivity conditions that all  . The construction of \(\mathrm{w}\Sigma (\mu ,u)\) is described in [28, Section 2.2]. It embeds in wps
. The construction of \(\mathrm{w}\Sigma (\mu ,u)\) is described in [28, Section 2.2]. It embeds in wps

with image defined by  minors
minors

with respect to the weights
The following theorem then follows from the general Hilbert series formula of [28, Theorem 3.1].
Theorem 7.1
(Szendrői [32]) The Hilbert series of \(\mathrm{w}\Sigma (\mu ,u)\) in the embedding (10) is

where the Hilbert numerator  is
is

with \(s=a_1+a_2+a_3+b_1+b_2+b_3\).
This numerator exposes the  resolution. The
resolution. The  minors in (11) are visible in the first parentheses; for example \(t^{-a_1-b_1}t^{2u+s} = t^{(a_2+b_2+u) + (a_3+b_3+u)}\) carries the degree of \(x_5x_9=x_6x_8\). First syzygies appear in the second parentheses; for example, the syzygy
minors in (11) are visible in the first parentheses; for example \(t^{-a_1-b_1}t^{2u+s} = t^{(a_2+b_2+u) + (a_3+b_3+u)}\) carries the degree of \(x_5x_9=x_6x_8\). First syzygies appear in the second parentheses; for example, the syzygy
has degree  . The additional parameter \(u\in \mathbb Z\) in this treatment is absorbed into the \(a_i\) in our naive treatment of Sect. 2, so the key varieties we enumerate are the same.
. The additional parameter \(u\in \mathbb Z\) in this treatment is absorbed into the \(a_i\) in our naive treatment of Sect. 2, so the key varieties we enumerate are the same.
References
Ahmadinezhad, H.: On pliability of del Pezzo fibrations and Cox rings. J. Reine Angew. Math. 723, 101–125 (2017)
Altınok, S., Brown, G., Reid, M.: Fano 3-folds, \(K3\) surfaces and graded rings. In: Berrick, A.J., Leung, M.C., Xu, X. (eds.) Topology and Geometry: Commemorating SISTAG. Contemporary Mathematics, vol. 314, pp. 25–53. American Mathematical Society, Providence (2002)
Brown, G.: Graded rings and special \(K3\) surfaces. In: Bosma, W., Cannon, J. (eds.) Discovering Mathematics with Magma. Algorithms and Computation in Mathematics, vol. 19, pp. 137–159. Springer, Berlin (2006)
Brown, G.: A database of polarized \(K3\) surfaces. Experiment. Math. 16(1), 7–20 (2007)
Brown, G., Fatighenti, E.: Hodge numbers and deformations of Fano 3-folds (2017). arXiv:1707.00653
Brown, G., Kasprzyk, A.M.: The graded ring database. http://www.grdb.co.uk/
Brown, G., Kasprzyk, A.M., Zhu, L.: Gorenstein formats, canonical and Calabi–Yau threefolds (2014). arXiv:1409.4644
Brown, G., Kerber, M., Reid, M.: Fano 3-folds in codimension 4, Tom and Jerry. Part I. Compositio Math. 148(4), 1171–1194 (2012)
Brown, G., Kerber, M., Reid, M.: Tom and Jerry: big table (2012). http://grdb.co.uk/Downloads
Brown, G., Reid, M.: Diptych varieties. I. Proc. London Math. Soc. 107(6), 1353–1394 (2013)
Buckley, A., Reid, M., Zhou, S.: Ice cream and orbifold Riemann–Roch. Izv. Math. 77(3), 461–486 (2013)
Chen, J.-J., Chen, J.A., Chen, M.: On quasismooth weighted complete intersections. J. Algebraic Geom. 20(2), 239–262 (2011)
Corti, A., Pukhlikov, A., Reid, M.: Fano \(3\)-fold hypersurfaces. In: Corti, A., Reid, M. (eds.) Explicit Birational Geometry of 3-Folds. London Mathematical Society Lecture Note Series, vol. 281, pp. 175–258. Cambridge University Press, Cambridge (2000)
Corti, A., Reid, M.: Weighted Grassmannians. In: Beltrametti, M.C., et al. (eds.) Algebraic Geometry, pp. 141–163. de Gruyter, Berlin (2002)
Di Natale, C., Fatighenti, E., Fiorenza, D.: Hodge theory and deformations of affine cones of subcanonical projective varieties. J. London Math. Soc. (2017). https://doi.org/10.1112/jlms.12073, arXiv:1512.00835
Goto, S., Watanabe, K.: On graded rings. I. J. Math. Soc. Japan 30(2), 179–213 (1978)
Grayson, D.R., Stillman, M.E.: Macaulay2, a software system for research in algebraic geometry. http://www.math.uiuc.edu/Macaulay2/
Iano-Fletcher, A.R.: Working with weighted complete intersections. In: Corti, A., Reid, M. (eds.) Explicit Birational Geometry of 3-Folds. London Mathematical Society Lecture Note Series, vol. 281, pp. 101–173. Cambridge University Press, Cambridge (2000)
Ilten, N.O.: Versal deformations and local Hilbert schemes. J. Softw. Algebra Geom. 4, 12–16 (2012)
Kawamata, Y.: Boundedness of \(Q\)-Fano threefolds. In: Bokut, L.A., Ershov, Yu.L., Kostrikin, A.I. (eds.) Proceedings of the International Conference on Algebra, Part 3. Contemporary Mathematics, vol. 131, pp. 439–445. American Mathematical Society, Providence (1992)
Kollár, J., Miyaoka, Y., Mori, S., Takagi, H.: Boundedness of canonical \(\mathbf{Q}\)-Fano 3-folds Proc. Japan Acad. Ser. A Math. Sci. 76(5), 73–77 (2000)
Kustin, A.R., Miller, M.: Constructing big Gorenstein ideals from small one. J. Algebra 85(2), 303–322 (1983)
Papadakis, S.A.: Kustin–Miller unprojection with complexes. J. Algebraic Geom. 13(2), 249–268 (2004)
Papadakis, S.A.: The equations of type \({\rm II}_2\) unprojection. J. Pure Appl. Algebra 212(10), 2194–2208 (2008)
Papadakis, S.A., Reid, M.: Kustin–Miller unprojection without complexes. J. Algebraic Geom. 13(3), 563–577 (2004)
Qureshi, M.I.: Constructing projective varieties in weighted flag varieties II. Math. Proc. Cambridge Philos. Soc. 158(2), 193–209 (2015)
Qureshi, M.I.: Computing isolated orbifolds in weighted flag varieties. J. Symbolic Comput. 79(Part 2), 457–474 (2017)
Qureshi, M.I., Szendrői, B.: Constructing projective varieties in weighted flag varieties. Bull. London Math. Soc. 43(4), 786–798 (2011)
Qureshi, M.I., Szendrői, B.: Calabi–Yau threefolds in weighted flag varieties. Adv. High Energy Phys. 2012, # 547317 (2012)
Reid, M.: Fun in codimension 4 (2011). https://homepages.warwick.ac.uk/~masda/3folds/Fun.pdf
Reid, M.: Gorenstein in codimension 4: the general structure theory. In: Kawamata, Y. (ed.) Algebraic Geometry in East Asia—Taipei 2011. Advanced Studies in Pure Mathematics, vol. 65, pp. 201–227. Mathematical Society Japan, Tokyo (2015)
Szendrői, B.: On weighted homogeneous varieties (2005) (Unpublished manuscript)
Takagi, H.: On classification of \({\mathbb{Q}}\)-Fano 3-folds of Gorenstein index 2. I, II. Nagoya Math. J. 167(117–155), 157–216 (2002)
Taylor, R.: Fano 3-Folds and Type II Unprojection. PhD thesis, University of Warwick (In preparation)
Author information
Authors and Affiliations
Corresponding author
Additional information
AMK was supported by EPRSC Fellowship EP/N022513/1. MIQ was supported by a Lahore University of Management Sciences (LUMS) faculty startup research grant (STG-MTH-1305) and an LMS research in pairs grant for a visit to the UK.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Brown, G., Kasprzyk, A.M. & Qureshi, M.I. Fano 3-folds in  format, Tom and Jerry.
European Journal of Mathematics 4, 51–72 (2018). https://doi.org/10.1007/s40879-017-0200-2
format, Tom and Jerry.
European Journal of Mathematics 4, 51–72 (2018). https://doi.org/10.1007/s40879-017-0200-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-017-0200-2





 formats
formats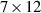 family
family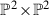 family with Tom projection
family with Tom projection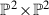 models with a codimension 3 Pfaffian component
models with a codimension 3 Pfaffian component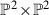 and the second Tom
and the second Tom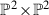 formats
formats formats and cases that fail
formats and cases that fail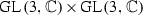 varieties according to Szendrői
varieties according to Szendrői varieties that provided our initial motivation and the tools of Sect.
varieties that provided our initial motivation and the tools of Sect.