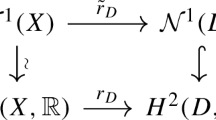Fano 4-folds with $b_{2}>12$ are products of surfaces

Abstract

Let $X$ be a smooth, complex Fano 4-fold, and $\rho _{X}$ its Picard number. We show that if $\rho _{X}>12$, then $X$ is a product of del Pezzo surfaces. The proof relies on a careful study of divisorial elementary contractions $f\colon X\to Y$ such that $\dim f(\operatorname{Exc}(f))=2$, together with the author’s previous work on Fano 4-folds. In particular, given $f\colon X\to Y$ as above, under suitable assumptions we show that $S:=f(\operatorname{Exc}(f))$ is a smooth del Pezzo surface with $-K_{S}=(-K_{Y})_{|S}$.

1 Introduction

Smooth, complex Fano varieties have been classically intensively studied, and have attracted a lot of attention also in the last decades, due to their role in the framework of the Minimal Model Program. The Fano condition is a natural positivity condition of the tangent bundle, and it ensures a rich geometry, from both the points of view of birational geometry and of families of rational curves.

It has been known since the 90’s that Fano varieties form a bounded family in each dimension. Del Pezzo surfaces are known classically, and the classification of Fano 3-folds have been in achieved in the 80’s, there are 105 families.

Starting from dimension 4, there are probably too many families to get a complete classification; still we aim to better understand and describe the behavior and properties of these varieties. In this paper we focus on Fano 4-folds $X$ with “large” Picard number $\rho _{X}$; let us recall that since $X$ is Fano, $\rho _{X}$ is equal to the second Betti number $b_{2}(X)$. We show the following result.

Theorem 1.1

Let $X$ be a smooth Fano 4-fold with $\rho _{X}> 12$. Then $X\cong S_{1}\times S_{2}$, where $S_{i}$ are del Pezzo surfaces.

To the author’s knowledge, all known examples of Fano 4-folds which are not products of surfaces have $\rho \leq 9$, so that we do not know whether the condition $\rho > 12$ in Theorem 1.1 is sharp. We refer the reader to [7, §6] for an overview of known Fano 4-folds with $\rho \geq 6$; there are few examples and it is an interesting problem to construct new ones.

As $\rho _{S_{1}\times S_{2}}=\rho _{S_{1}}+\rho _{S_{2}}$, and del Pezzo surfaces have $\rho \leq 9$, Theorem 1.1 implies the following.

Corollary 1.2

Let $X$ be a smooth Fano 4-fold. Then $\rho _{X}\leq 18$.

Let us note that Theorem 1.1 and Corollary 1.2 generalize to dimension 4 the analogous result for Fano 3-folds, established by Mori and Mukai in the 80’s:

Theorem 1.3

[15], Theorem 1.2

Let $X$ be a smooth Fano 3-fold with $\rho _{X}> 5$. Then $X\cong S\times \mathbb{P}^{1}$ where $S$ is a del Pezzo surface. In particular $\rho _{X}\leq 10$.

The proof of Theorem 1.1 relies on a careful study of elementary contractions of $X$ of type $(3,2)$, together with the author’s previous work on Fano 4-folds. To explain this, let us introduce some notation.

Let $X$ be a Fano 4-fold. A contraction is a surjective morphism $f\colon X\to Y$, with connected fibers, where $Y$ is normal and projective; $f$ is elementary if $\rho _{X}-\rho _{Y}=1$. As usual, an elementary contraction can be of fiber type, divisorial, or small.

We say that an elementary contraction $f\colon X\to Y$ is of type $(3,2)$ if it is divisorial with $\dim S=2$, where $E:=\operatorname{Exc}(f)$ and $S:=f(E)\subset Y$. Such $f$ can have at most finitely many 2-dimensional fibers; outside the images of these fibers, $Y$ and $S$ are smooth, and $f$ is just the blow-up of the surface $S$. If $y_{0}\in S$ is the image of a two-dimensional fiber, then either $Y$ or $S$ are singular at $y_{0}$; these singularities have been described by Andreatta and Wiśniewski, see Theorem 2.1. In any case, $Y$ has at most isolated locally factorial and terminal singularities, while $S$ can be not normal.

We denote by $\mathcal{N}_{1}(X)$ the real vector space of one-cycles with real coefficients, modulo numerical equivalence; we have $\dim \mathcal{N}_{1}(X)=\rho _{X}$. For any closed subset $Z\subset X$, we set

$$ \mathcal{N}_{1}(Z,X):=\iota _{*}(\mathcal{N}_{1}(Z))\subset \mathcal{N}_{1}(X) $$

where $\iota \colon Z\hookrightarrow X$ is the inclusion, so that $\mathcal{N}_{1}(Z,X)$ is the subspace of $\mathcal{N}_{1}(X)$ spanned by classes of curves in $Z$, and $\dim \mathcal{N}_{1}(Z,X)\leq \rho _{Z}$.

We study an elementary contraction $f\colon X\to Y$ of type $(3,2)$ under the hypothesis that:

$$ \dim \mathcal{N}_{1}(E,X)\geq 4. $$

In particular this implies that $Y$ is Fano too (Lemma 2.3).

We would like to compare $(-K_{Y})_{|S}$ to $-K_{S}$, but since $S$ may be singular, we consider the minimal resolution of singularities $\mu \colon S'\to S$ and set $L:=\mu ^{*}((-K_{Y})_{|S})$, a nef and big divisor class on $S'$. We show that $K_{S'}+L$ is semiample (Proposition 3.1). Then our strategy is to look for curves in $S'$ on which $K_{S'}+L$ is trivial, using other elementary contractions of $X$ of type $(3,2)$ whose exceptional divisor intersects $E$ in a suitable way.

Hence let us assume that $X$ has another elementary contraction $g_{1}$ of type $(3,2)$ whose exceptional divisor $E_{1}$ intersects $E$, and such that $E\cdot \Gamma _{1}=0$ for a curve $\Gamma _{1}$ contracted by $g_{1}$. Set $D:=f(E_{1})\subset Y$. We show that an irreducible component $C_{1}$ of $D\cap S$ is a $(-1)$-curve contained in the smooth locus $S_{\mathit{reg}}$, and such that $-K_{Y}\cdot C_{1}=1$ (Proposition 3.4, see Figure 1). If $C_{1}'\subset S'$ is the transform of $C_{1}$, we have $(K_{S'}+L)\cdot C_{1}'=0$.

Fig. 1

The varieties in Proposition 3.4.

Finally let us assume that $X$ has three elementary contractions $g_{1}$, $g_{2}$, $g_{3}$, all of type $(3,2)$, satisfying the same assumptions as $g_{1}$ above. We also assume that $E_{1}\cdot \Gamma _{2}>0$ and $E_{1}\cdot \Gamma _{3}>0$, where $E_{1}=\operatorname{Exc}(g_{1})$ and $\Gamma _{2}$, $\Gamma _{3}$ are curves contracted by $g_{2}$, $g_{3}$ respectively. Then we show that $S$ is a smooth del Pezzo surface with $-K_{S}=(-K_{Y})_{|S}$ (Propositions 3.7 and 3.9); let us give an overview of the proof.

The previous construction yields three distinct $(-1)$-curves $C_{1}',C_{2}',C_{3}'\subset S'$ such that $(K_{S'}+L)\cdot C_{i}'=0$ and $C_{1}'$ intersects both $C_{2}'$ and $C_{3}'$. This shows that the contraction of $S'$ given by $K_{S'}+L$ cannot be birational, namely $K_{S'}+L$ is not big. We also rule out the possibility of a contraction onto a curve, and conclude that $K_{S'}+L\equiv 0$. Finally we show that $\omega _{S}\cong \mathcal{O}_{Y}(K_{Y})_{|S}$, where $\omega _{S}$ is the dualizing sheaf of $S$, and conclude that $S$ is smooth and del Pezzo.

We believe that these results can be useful in the study of Fano 4-folds besides their use in the present work. It would be interesting to generalize this technique to higher dimensions.

Let us now explain how we use these results to prove Theorem 1.1. We define the Lefschetz defect of $X$ as:

$$ \delta _{X}:=\max \bigl\{ \operatorname{codim}\mathcal{N}_{1}(D,X)\,| \,D\subset X\text{ a prime divisor}\bigr\} . $$

This invariant, introduced in [3], measures the difference between the Picard number of $X$ and that of its prime divisors; we refer the reader to [7] for a survey on $\delta _{X}$.

Fano 4-folds with $\delta _{X}\geq 3$ are classified, as follows.

Theorem 1.4

[3], Theorem 3.3

Let $X$ be a smooth Fano 4-fold. If $\delta _{X}\geq 4$, then $X\cong S_{1}\times S_{2}$ where $S_{i}$ are del Pezzo surfaces, and $\delta _{X}=\max _{i}\rho _{S_{i}}-1$.

Theorem 1.5

[8], Proposition 1.5

Smooth Fano 4-folds with $\delta _{X}=3$ are classified. They have $5\leq \rho _{X}\leq 8$, and if $\rho _{X}\in \{7,8\}$ then $X$ is a product of surfaces.

Therefore in our study of Fano 4-folds we can assume that $\delta _{X}\leq 2$, that is, $\operatorname{codim}\mathcal{N}_{1}(D,X)\leq 2$ for every prime divisor $D\subset X$. To prove that $\rho _{X}\leq 12$, we look for a prime divisor $D\subset X$ with $\dim \mathcal{N}_{1}(D,X)\leq 10$.

To produce such a divisor, we look at contractions of $X$. If $X$ has an elementary contraction of fiber type, or a divisorial elementary contraction $f\colon X\to Y$ with $\dim f(\operatorname{Exc}(f))\leq 1$, it is not difficult to find a prime divisor $D\subset X$ such that $\dim \mathcal{N}_{1}(D,X)\leq 3$, hence $\rho _{X}\leq 5$ (Lemmas 2.6 and 2.7).

The case where $X$ has a small elementary contraction is much harder and is treated in [6], where the following result is proven.

Theorem 1.6

[6], Theorem 1.1

Let $X$ be a smooth Fano 4-fold. If $X$ has a small elementary contraction, then $\rho _{X}\leq 12$.

We are left with the case where every elementary contraction $f\colon X\to Y$ is of type $(3,2)$. In this case we show (Theorem 4.1) that, if $\rho _{X}\geq 8$, we can apply our previous study of elementary contractions of type $(3,2)$, so that if $E:=\operatorname{Exc}(f)$ and $S:=f(E)\subset Y$, then $S$ is a smooth del Pezzo surface. This implies that $\dim \mathcal{N}_{1}(S,Y)\leq \rho _{S}\leq 9$, $\dim \mathcal{N}_{1}(E,X)=\dim \mathcal{N}_{1}(S,Y)+1\leq 10$, and finally that $\rho _{X}\leq 12$, proving Theorem 1.1.

The structure of the paper is as follows. In §2 we gather some preliminary results. Then in §3 we develop our study of elementary contractions of type $(3,2)$, while in §4 we prove Theorem 1.1.

1.1 Notation

We work over the field of complex numbers.

We will frequently use the definitions and apply the techniques of birational geometry and the Minimal Model Program, without explicit references. We refer the reader to [9, 13, 14] for background and details.

Let $X$ be a projective variety.

We denote by $\mathcal{N}_{1}(X)$ (respectively, $\mathcal{N}^{1}(X)$) the real vector space of one-cycles (respectively, Cartier divisors) with real coefficients, modulo numerical equivalence; $\dim \mathcal{N}_{1}(X)=\dim \mathcal{N}^{1}(X)=\rho _{X}$ is the Picard number of $X$.

For any closed subset $Z\subset X$, we denote by $\mathcal{N}_{1}(Z,X)$ the subspace of $\mathcal{N}_{1}(X)$ spanned by classes of curves in $Z$.

Let $C$ be a one-cycle of $X$, and $D$ a Cartier divisor. We denote by $[C]$ (respectively, $[D]$) the numerical equivalence class in $\mathcal{N}_{1}(X)$ (respectively, $\mathcal{N}^{1}(X)$). We also denote by $D^{\perp}\subset \mathcal{N}_{1}(X)$ the orthogonal hyperplane to the class $[D]$.

The symbol ≡ stands for numerical equivalence (for both one-cycles and divisors), and ∼ stands for linear equivalence of divisors.

$\operatorname{NE}(X)\subset \mathcal{N}_{1}(X)$ is the convex cone generated by classes of effective curves, and $\overline{\operatorname{NE}}(X)$ is its closure. An extremal ray $R$ is a one-dimensional face of $\overline{\operatorname{NE}}(X)$. If $D$ is a Cartier divisor in $X$, we write $D\cdot R>0$, $D\cdot R=0$, and so on, if $D\cdot \gamma >0$, $D\cdot \gamma =0$, and so on, for a non-zero class $\gamma \in R$. We say that $R$ is $K$-negative if $K_{X}\cdot R<0$.

A contraction is a surjective morphism, with connected fibers, between normal projective varieties.

Suppose that $X$ has terminal and locally factorial singularities, and is Fano. Then $\operatorname{NE}(X)$ is a convex polyhedral cone. Given a contraction $f\colon X\to Y$, we denote by $\text{NE}(f)$ the convex subcone of $\text{NE}(X)$ generated by classes of curves contracted by $f$; we recall that there is a bijection between contractions of $X$ and faces of $\operatorname{NE}(X)$, given by $f\mapsto \operatorname{NE}(f)$. Moreover $\dim \operatorname{NE}(f)=\rho _{X}-\rho _{Y}$, in particular $f$ is elementary (that is, $\rho _{X}-\rho _{Y}=1$) if and only if $\operatorname{NE}(f)$ is an extremal ray.

When $\dim X=4$, we say that an extremal ray $R$ is of type $(3,2)$ if the associated elementary contraction $f$ is of type $(3,2)$, namely if $f$ is divisorial with $\dim f(\operatorname{Exc}(f))=2$. We also set $E_{R}:=\operatorname{Exc}(f)$ and denote by $C_{R}\subset E_{R}$ a general fiber of $f_{|E_{R}}$; note that $E_{R}\cdot C_{R}=-1$ and $-K_{X}\cdot C_{R}=1$.

We will also consider the cones $\operatorname{Eff}(X)\subset \mathcal{N}^{1}(X)$ of classes of effective divisors, and $\operatorname{mov}(X)\subset \mathcal{N}_{1}(X)$ of classes of curves moving in a family covering $X$. Since $X$ is Fano, both cones are polyhedral; we have the duality relation $\operatorname{Eff}(X)=\operatorname{mov}(X)^{\vee}$.

If $\mathcal{N}$ is a real vector space and $S\subset \mathcal{N}$ is a subset, we denote by $\mathbb{R}S$ the linear span of $S$.

2 Preliminaries

In this section we gather some preliminary results that will be used in the sequel.

Andreatta and Wiśniewski have classified the possible 2-dimensional fibers of an elementary contraction of type $(3,2)$ of a smooth Fano 4-fold. In doing this, they also describe precisely the singularities both of the target, and of the image of the exceptional divisor, as follows.

Theorem 2.1

[1], Theorem on p. 256

Let $X$ be a smooth Fano 4-fold and $f\colon X\to Y$ an elementary contraction of type $(3,2)$. Set $S:=f(\operatorname{Exc}(f))$.

Then $f$ can have at most finitely many 2-dimensional fibers. Outside the images of these fibers, $Y$ and $S$ are smooth, and $f$ is the blow-up of $S$.

Let $y_{0}\in S\subset Y$ be the image of a 2-dimensional fiber; then one of the following holds:

$(i)$:

$S$ is smooth at $y_{0}$, while $Y$ has an ordinary double point at $y_{0}$, locally factorial and terminal;

$(ii)$:

$Y$ is smooth at $y_{0}$, while $S$ is singular at $y_{0}$. More precisely either $S$ is not normal at $y_{0}$, or it has a singularity of type $\frac{1}{3}(1,1)$ at $y_{0}$ (as the cone over a twisted cubic).

In particular the singularities of $Y$ are at most isolated, locally factorial, and terminal.

We will need the following elementary estimates on $\dim \mathcal{N}_{1}(Z,X)$ in terms of a contraction $f\colon X\to Y$ and of $f(Z)\subset Y$.

Remark 2.2

Let $f\colon X\to Y$ be a contraction between normal projective varieties, and $Z\subset X$ an irreducible closed subset. Consider the pushforward of one-cycles $f_{*}\colon \mathcal{N}_{1}(X)\to \mathcal{N}_{1}(Y)$. We have the following:

$(a)$:

$f_{*}(\mathcal{N}_{1}(Z,X))=\mathcal{N}_{1}(f(Z),Y)$;

$(b)$:

$\dim \mathcal{N}_{1}(Z,X)\leq \rho _{X}-\rho _{Y}+\dim \mathcal{N}_{1}(f(Z),Y)$;

$(c)$:

if $\dim f(Z)\leq 1$, then $\dim \mathcal{N}_{1}(Z,X)\leq \rho _{X}-\rho _{Y}+1$.

Indeed $(a)$ follows from the definitions and the surjectivity of $f$, and $(b)$ follows from $(a)$ because $f_{*}$ is a surjective linear map. For $(c)$, we have $\mathcal{N}_{1}(f(Z),Y)=\{0\}$ if $f(Z)=\{pt\}$, and $\mathcal{N}_{1}(f(Z),Y)=\mathbb{R}[f(Z)]$ if $f(Z)$ is a curve; in any case $\dim \mathcal{N}_{1}(f(Z),Y)\leq 1$, and we apply $(b)$.

Now we give some simple preliminary results on extremal rays of type $(3,2)$.

Lemma 2.3

Let $X$ be a smooth Fano 4-fold and $f\colon X\to Y$ an elementary contraction of type $(3,2)$; set $E:=\operatorname{Exc}(f)$. If $\dim \mathcal{N}_{1}(E,X)\geq 4$, then $E\cdot R\geq 0$ for every extremal ray $R$ of $X$ different from $\operatorname{NE}(f)$, and $Y$ is Fano.

Proof

It follows from [5, Lemma 2.16 and Remark 2.17] that $\operatorname{NE}(f)$ is the unique extremal ray of $X$ having negative intersection with $E$, $-K_{X}+E=f^{*}(-K_{Y})$ is nef, and $(-K_{X}+E)^{\perp}\cap \operatorname{NE}(X)=\operatorname{NE}(f)$, so that $-K_{Y}$ is ample. □

Lemma 2.4

Let $X$ be a smooth Fano 4-fold and $R_{1}$, $R_{2}$ extremal rays of $X$ of type $(3,2)$ such that $\dim \mathcal{N}_{1}(E_{R_{1}},X)\geq 4$ and $E_{R_{1}}\cdot R_{2}=0$.

Then $E_{R_{2}}\cdot R_{1}=0$ and $R_{1}+R_{2}$ is a face of $\operatorname{NE}(X)$ whose associated contraction is birational, with exceptional locus $E_{R_{1}}\cup E_{R_{2}}$.

Proof

Let $H$ be a nef divisor on $X$ such that $H^{\perp}\cap \operatorname{NE}(X)=R_{2}$, and set $H':=H+(H\cdot C_{R_{1}})E_{R_{1}}$. Then $H'\cdot C_{R_{1}}= H'\cdot C_{R_{2}}=0$, and if $R_{3}$ is an extremal ray of $\operatorname{NE}(X)$ different from $R_{1}$ and $R_{2}$, we have $E_{R_{1}}\cdot R_{3}\geq 0$ by Lemma 2.3, hence $H'\cdot R_{3}>0$. Therefore $H'$ is nef and $(H')^{\perp}\cap \operatorname{NE}(X)=R_{1}+R_{2}$ is a face of $\operatorname{NE}(X)$.

If $\Gamma \subset X$ is an irreducible curve with $[\Gamma ]\in R_{1}+R_{2}$, then $H'\cdot \Gamma =0$, so that either $E_{R_{1}}\cdot \Gamma <0$ and $\Gamma \subset E_{R_{1}}$, or $H\cdot \Gamma =0$, $[\Gamma ]\in R_{2}$ and $\Gamma \subset E_{R_{2}}$. This shows that the contraction of $R_{1}+R_{2}$ is birational with exceptional locus $E_{R_{1}}\cup E_{R_{2}}$.

We show that $E_{R_{2}}\cdot R_{1}=0$. By contradiction, suppose that $E_{R_{2}}\cdot R_{1}\neq 0$. If $E_{R_{2}}\cdot R_{1}<0$, then $E_{R_{1}}=E_{R_{2}}$, thus $\dim \mathcal{N}_{1}(E_{R_{2}},X)\geq 4$, contradicting Lemma 2.3.

Suppose that $E_{R_{2}}\cdot R_{1}>0$, and let $f_{i}$ be the contraction of $R_{i}$, $i=1,2$. Since $E_{R_{2}}\cdot R_{1}>0$, $E_{R_{2}}$ meets every non-trivial fiber of $f_{1}$, and $f_{1}(E_{R_{1}}\cap E_{R_{2}})=f_{1}(E_{R_{1}})$; let $Z$ be an irreducible component of $E_{R_{1}}\cap E_{R_{2}}$ such that $f_{1}(Z)=f_{1}(E_{R_{1}})$.

On the other hand $E_{R_{1}}\cdot R_{2}=0$, thus $E_{R_{1}}\cap E_{R_{2}}$ is a union of fibers of $f_{2}$, and $\dim f_{2}(Z)\leq 1$. This yields $\dim \mathcal{N}_{1}(Z,X)\leq 2$ by Remark 2.2$(c)$.

We also have $f_{1}(Z)=f_{1}(E_{R_{1}})$, thus $(f_{1})_{*}(\mathcal{N}_{1}(E_{R_{1}},X))=(f_{1})_{*}(\mathcal{N}_{1}(Z,X))$ by Remark 2.2$(a)$, and $\dim (f_{1})_{*}(\mathcal{N}_{1}(E_{R_{1}},X))\leq \dim \mathcal{N}_{1}(Z,X) \leq 2$. We deduce that $\dim \mathcal{N}_{1}(E_{R_{1}},X)\leq 3$ by Remark 2.2$(b)$, against our assumptions. □

Lemma 2.5

Let $X$ be a smooth Fano 4-fold and $R_{1}$, $R_{2}$ distinct extremal rays of $X$ of type $(3,2)$ with $\dim \mathcal{N}_{1}(E_{R_{i}},X)\geq 4$ for $i=1,2$. If there exists a birational contraction $g\colon X\to Z$ with $R_{1},R_{2}\subset \operatorname{NE}(g)$, then $E_{R_{1}}\cdot R_{2}=E_{R_{2}}\cdot R_{1}=0$.

Proof

We note first of all that $E_{R_{i}}\cdot R_{j}\geq 0$ for $i\neq j$ by Lemma 2.3. Suppose that $E_{R_{1}}\cdot R_{2}>0$. Then $E_{R_{1}}\cdot (C_{R_{1}}+C_{R_{2}})=E_{R_{1}}\cdot C_{R_{2}}-1\geq 0$. Moreover $E_{R_{2}}\cdot R_{1}>0$ by Lemma 2.4, so that $E_{R_{2}}\cdot (C_{R_{1}}+C_{R_{2}})\geq 0$. On the other hand for every prime divisor $D$ different from $E_{R_{1}}$, $E_{R_{2}}$ we have $D\cdot (C_{R_{1}}+C_{R_{2}})\geq 0$, therefore $[C_{R_{1}}+C_{R_{2}}]\in \operatorname{Eff}(X)^{\vee}= \operatorname{mov}(X)$. Since $[C_{R_{1}}+C_{R_{2}}]\in \operatorname{NE}(g)$, $g$ should be of fiber type, a contradiction. □

Lemma 2.6

Let $X$ be a smooth Fano 4-fold with $\delta _{X}\leq 2$, and $g\colon X\to Z$ a contraction of fiber type. Then $\rho _{Z}\leq 4$.

Proof

This follows from [3]; for the reader’s convenience we report the proof.

If $\dim Z\leq 1$, then $\rho _{Z}\leq 1$. If $Z$ is a surface, take any prime divisor $D\subset X$ such that $g(D)\subsetneq Z$, namely $\dim g(D)\leq 1$. We have $\dim \mathcal{N}_{1}(D,X)\leq \rho _{X}-\rho _{Z}+1$ by Remark 2.2$(c)$, thus $\operatorname{codim}\mathcal{N}_{1}(D,X)\geq \rho _{Z}-1$. Therefore $\delta _{X}\leq 2$ yields $\rho _{Z}\leq 3$.

Suppose now that $\dim Z=3$. By [2, Lemma 2.6] we know that $Z$ has some elementary contraction $h\colon Z\to W$. If $\dim W\leq 2$, by applying the first part of the proof to $h\circ g\colon X\to W$, we get $\rho _{W}\leq 3$ and hence $\rho _{Z}\leq 4$.

If $h$ is birational and divisorial, then $\dim h(\operatorname{Exc}(h))\leq 1$, and Remark 2.2$(c)$ yields $\dim \mathcal{N}_{1}(\operatorname{Exc}(h),Z)\leq 2$. Moreover we can take a prime divisor $D\subset X$ such that $g(D)\subseteq \operatorname{Exc}(h)$, thus $\dim \mathcal{N}_{1}(g(D),Z)\leq 2$. Reasoning as above we conclude that $\operatorname{codim}\mathcal{N}_{1}(D,X)\geq \rho _{Z}-2$ and $\rho _{Z}\leq 4$.

Finally we assume that $h$ is birational and small. Then $\operatorname{Exc}(h)$ is a curve in $Z$, and $\mathcal{N}_{1}(\operatorname{Exc}(h),Z)=\mathbb{R}\operatorname{NE}(h)$ is one-dimensional. We show that there exists a prime divisor $D\subset X$ such that $g(D)\subseteq \operatorname{Exc}(h)$. We consider the lifting of $h$ in $X$ (see [2, §2.5]), which is an elementary contraction $h'\colon X\to W'$ fitting into a commutative diagram:

and such that $g_{*}(\operatorname{NE}(h'))=\operatorname{NE}(h)$. If $F\subset X$ is a non-trivial fiber of $h'$, then $g$ must be finite on $F$ and $g(F)\subseteq \operatorname{Exc}(h)$. This implies that $h'$ is a $K$-negative birational elementary contraction with fibers of dimension $\leq 1$, therefore it must be of type $(3,2)$ (see [16, Theorem 1.2]); let $D$ be its exceptional divisor. Then $g(D)\subseteq \operatorname{Exc}(h)$.

Hence $\dim \mathcal{N}_{1}(g(D),Z)=1$, and reasoning as above we get $\operatorname{codim}\mathcal{N}_{1}(D,X)\geq \rho _{Z}-1$ and $\rho _{Z}\leq 3$. □

Lemma 2.7

[5], Remark 2.17(1)

Let $X$ be a smooth Fano 4-fold. If $X$ has a divisorial elementary contraction not of type $(3,2)$, then $\rho _{X}\leq 5$.

3 Showing that $S$ is a del Pezzo surface

In this section we study elementary contractions of type $(3,2)$ of a Fano 4-fold. We focus on the surface $S$ which is the image of the exceptional divisor; as explained in the Introduction, our goal is to show that under suitable assumptions, $S$ is a smooth del Pezzo surface.

Recall that $S$ has isolated singularities by Theorem 2.1.

Proposition 3.1

Let $X$ be a smooth Fano 4-fold and $f\colon X\to Y$ an elementary contraction of type $(3,2)$. Set $E:=\operatorname{Exc}(f)$ and $S:=f(E)$, and assume that $\dim \mathcal{N}_{1}(E,X)\geq 4$.

Let $\mu \colon S'\to S$ be the minimal resolution of singularities, and set $L:= \mu ^{*}((-K_{Y})_{|S})$. Then $K_{S'}+L$ is semiample.

If moreover $K_{S'}+L\equiv 0$, then $S$ is a smooth del Pezzo surface, and $-K_{S}=(-K_{Y})_{|S}$.

Proof

Note that $-K_{Y}$ is Cartier by Theorem 2.1, and ample by Lemma 2.3, so that $L$ is nef and big on $S'$, and for every irreducible curve $\Gamma \subset S'$, we have $L\cdot \Gamma =0$ if and only if $\Gamma$ is $\mu$-exceptional.

Consider the pushforward of one-cycles $f_{*}\colon \mathcal{N}_{1}(X)\to \mathcal{N}_{1}(Y)$. Then $f_{*}(\mathcal{N}_{1}(E, X))=\mathcal{N}_{1}(S,Y)$, therefore $\rho _{S'}\geq \rho _{S}\geq \dim \mathcal{N}_{1}(S,Y)\geq 3$.

Recall that by the Cone Theorem we have:

$$ \overline{\operatorname{NE}}(S')=\overline{\operatorname{NE}}(S')_{K_{S'} \geq 0}+\sum _{i} R_{i} $$

where $R_{i}$ are the $K_{S'}$-negative extremal rays of $\overline{\operatorname{NE}}(S')$ (and they are at most countably many). We show that $K_{S'}+L$ is nef; for this it is enough to show that it is non-negative on each summand.

Since $L$ is nef, if $\gamma \in \overline{\operatorname{NE}}(S')_{K_{S'}\geq 0}$, we have $(K_{S'}+L)\cdot \gamma =K_{S'}\cdot \gamma +L\cdot \gamma \geq 0$.

Suppose now that $\overline{\operatorname{NE}}(S')$ has a $K_{S'}$-negative extremal ray $R$. The contraction associated to $R$ can be onto a point (if $S'\cong \mathbb{P}^{2}$), onto a curve (so that $\rho _{S'}=2$), or the blow-up of a smooth point (see for instance [14, Theorem 1-4-8]). Since $\rho _{S'}>2$, $R$ is generated by the class of a $(-1)$-curve $\Gamma$, that cannot be $\mu$-exceptional, because $\mu$ is minimal. Then $L\cdot \Gamma >0$ and $(K_{S'}+L)\cdot \Gamma =L\cdot \Gamma -1\geq 0$.

We conclude that $K_{S'}+L$ is nef on $S'$, and also semiample by the Base-Point-Free Theorem.

We assume now that $K_{S'}+L\equiv 0$. In particular $-K_{S'}$ is nef and big, namely $S'$ is a weak del Pezzo surface.

Set for simplicity $\mathcal{F}:=\mathcal{O}_{Y}(K_{Y})_{|S}$, invertible sheaf on $S$, and let $\omega _{S}$ be the dualizing sheaf of $S$. We have $K_{S'}\equiv \mu ^{*}(\mathcal{F})$, and since $S'$ is rational, we also have $\mathcal{O}_{S'}(K_{S'})\cong \mu ^{*}(\mathcal{F})$. By restricting to the open subset $\mu ^{-1}(S_{\mathit{reg}})$, we conclude that $(\omega _{S})_{|S_{\mathit{reg}}}\cong \mathcal{F}_{|S_{ \mathit{reg}}}$. Now we use the following.

Lemma 3.2

Let $S$ be a reduced and irreducible projective surface with isolated singularities, and $\omega _{S}$ its dualizing sheaf. If there exists an invertible sheaf ℱ on $S$ such that $(\omega _{S})_{|S_{\textit{reg}}}\cong \mathcal{F}_{|S_{\textit{reg}}}$, then $S$ is normal and $\omega _{S}\cong \mathcal{F}$.

This should be well-known to experts, we include a proof for lack of references. We postpone the proof of Lemma 3.2 and carry on with the proof of Proposition 3.1.

By Lemma 3.2 we have that $S$ is normal and $\omega _{S}\cong \mathcal{F}$, in particular $\omega _{S}$ is locally free. If $y_{0}$ is a singular point of $S$, then by Theorem 2.1$y_{0}$ is a singularity of type $\frac{1}{3}(1,1)$, but this contradicts the fact that $\omega _{S}$ is locally free. We conclude that $S$ is smooth, and finally that $-K_{S}=(-K_{Y})_{|S}$ is ample, so that $S$ is a del Pezzo surface.  □

Remark 3.3

In the setting of Proposition 3.1, when $K_{S'}+L\equiv 0$ we cannot conclude that $Y$ is smooth. A priori $Y$ could have isolated singularities at some $y_{0}\in S$; by [1] in this case $f^{-1}(y_{0})\cong \mathbb{P}^{2}$.

Proof of Lemma 3.2

Recall that $S$ has isolated singularities. The surface $S$ is reduced, thus it satisfies condition ($S_{1}$), namely

$$ \operatorname{depth}\mathcal{O}_{S,y}\geq 1\quad \text{for every }y \in S. $$

Then by [12, Lemma 1.3] the dualizing sheaf $\omega _{S}$ satisfies condition ($S_{2}$):

$$ \operatorname{depth}\omega _{S,y}\geq 2\quad \text{for every }y\in S, $$

where $\operatorname{depth}\omega _{S,y}$ is the depth of the stalk $\omega _{S,y}$ as an $\mathcal{O}_{S,y}$-module.

Then, for every open subset $U\subset S$ such that $S\smallsetminus U$ is finite, we have $\omega _{S}=j_{*}((\omega _{S})_{|U})$, where $j\colon U\hookrightarrow S$ is the inclusion. This is analogous to the properties of reflexive sheaves on normal varieties, see [11, Propositions 1.3 and 1.6] and [12, Remark 1.8]; for the reader’s convenience, we recall the proof using local cohomology [10].

Set $\{y_{1},\ldots ,y_{m}\}:=S\smallsetminus U$. We have $\operatorname{depth}_{\{y_{1},\ldots ,y_{m}\}}\omega _{S}:=\min _{i} \operatorname{depth}\omega _{S,y_{i}}\geq 2$ [10, p. 43]. By [10, Theorem 3.8] this is equivalent to $\underline{H}^{i}_{\{y_{1},\ldots ,y_{m}\}}(\omega _{S})=0$ for $i=0,1$, where $\underline{H}^{i}_{\{y_{1},\ldots ,y_{m}\}}(\omega _{S})$ is the $i$th local cohomology sheaf of $S$ with coefficients in $\omega _{S}$ and supports in $\{y_{1},\ldots ,y_{m}\}$ [10, §1], in particular $\underline{H}^{0}_{\{y_{1},\ldots ,y_{m}\}}(\omega _{S})$ is the subsheaf of $\omega _{S}$ of sections with support contained in $\{y_{1},\ldots ,y_{m}\}$. There is an exact sequence of sheaves:

$$ 0\longrightarrow \underline{H}^{0}_{\{y_{1},\ldots ,y_{m}\}}(\omega _{S}) \longrightarrow \omega _{S} \longrightarrow j_{*}\bigl((\omega _{S})_{|U} \bigr)\longrightarrow \underline{H}^{1}_{\{y_{1},\ldots ,y_{m}\}}( \omega _{S})\longrightarrow 0 $$

[10, Corollary 1.9], hence $\underline{H}^{i}_{\{y_{1},\ldots ,y_{m}\}}(\omega _{S})=0$ for $i=0,1$ is in turn equivalent to $\omega _{S}=j_{*}((\omega _{S})_{|U})$.

For $U=S_{\mathit{reg}}$ we have $\omega _{S}=j_{*}((\omega _{S})_{|S_{\mathit{reg}}})$. Since ℱ is locally free, we get

$$ \omega _{S}=j_{*}\bigl((\omega _{S})_{|S_{\mathit{reg}}}\bigr)\cong j_{*}( \mathcal{F}_{|S_{\mathit{reg}}} )=\mathcal{F}, $$

in particular $\omega _{S}$ is an invertible sheaf and for every $y\in Y$ we have $\omega _{S,y}\cong \mathcal{O}_{S,y}$ as an $\mathcal{O}_{S,y}$-module, thus $\operatorname{depth}\mathcal{O}_{S,y}=2$. Therefore $S$ has property $(S_{2})$, and it is normal by Serre’s criterion. □

Proposition 3.4

Let $X$ be a smooth Fano 4-fold and $f\colon X\to Y$ an elementary contraction of type $(3,2)$. Set $E:=\operatorname{Exc}(f)$ and $S:=f(E)$, and assume that $\dim \mathcal{N}_{1}(E,X)\geq 4$. Let $\mu \colon S'\to S$ be the minimal resolution of singularities, and set $L:=\mu ^{*}((-K_{Y})_{|S})$.

Suppose that $X$ has an extremal ray $R_{1}$ of type $(3,2)$ such that:

$$ E\cdot R_{1}=0\quad \textit{and}\quad E\cap E_{R_{1}}\neq \emptyset . $$

Set $D:=f(E_{R_{1}})\subset Y$.

Then $D_{|S}=C_{1}+\cdots +C_{r}$ where $C_{i}$ are pairwise disjoint $(-1)$-curves contained in $S_{\textit{reg}}$, $E_{R_{1}}=f^{*}(D)$, and $f_{*}(C_{R_{1}})\equiv _{Y} C_{i}$. Moreover if $C_{i}'\subset S'$ is the transform of $C_{i}$, we have $(K_{S'}+L)\cdot C_{i}'=0$ for every $i=1,\ldots ,r$.

Proof

By Lemma 2.4 we have $E_{R_{1}}\cdot \operatorname{NE}(f)=0$ and $\operatorname{NE}(f)+R_{1}$ is a face of $\operatorname{NE}(X)$, whose associated contraction $h\colon X\to Z$ is birational with $\operatorname{Exc}(h)=E\cup E_{R_{1}}$. We have a diagram (see Figure 1):

(3.5)

where $g$ is an elementary, $K$-negative, divisorial contraction, with $\operatorname{Exc}(g)=D$ (recall that $Y$ is locally factorial by Theorem 2.1, and Fano by Lemma 2.3).

Since $E_{R_{1}}\cdot \operatorname{NE}(f)=E\cdot R_{1}=0$, $E\cap E_{R_{1}}$ is both a union of fibers of $f$ and of fibers of the contraction of $R_{1}$. This implies that $\dim f(E\cap E_{R_{1}})\leq 1$, that $\mathcal{N}_{1}(E\cap E_{R_{1}})=\ker f_{*} \oplus \mathbb{R}R_{1}= \ker h_{*}$, and that $\dim h(E\cap E_{R_{1}})=0$.

We also note that both $E$ and $E_{R_{1}}$ have non-positive intersection with every irreducible curve contracted by $h$, thus they are both unions of fibers of $h$, and

$$ E\cap E_{R_{1}}=h^{-1}\bigl(h(E)\bigr)\cap h^{-1}\bigl(h(E_{R_{1}}) \bigr)=h^{-1}\bigl(h(E)\cap h(E_{R_{1}})\bigr). $$

Both $h(E)$ and $h(E_{R_{1}})$ are surfaces in $Z$, and the general fiber of $h$ over these surfaces is one-dimensional. Moreover $h(E)\cap h(E_{R_{1}})=h(E\cap E_{R_{1}})$ is finite, and the connected components of $E\cap E_{R_{1}}$ are 2-dimensional fibers of $h$ over these points.

Using the classification of the possible 2-dimensional fibers of $h$ in [1], as in [6, Lemma 4.15] we see that every connected component $T_{i}$ of $E\cap E_{R_{1}}$ (which is non-empty by assumption) is isomorphic to $\mathbb{P}^{1}\times \mathbb{P}^{1}$ with normal bundle $\mathcal{O}(-1,0)\oplus \mathcal{O}(0,-1)$, for $i=1,\ldots ,r$. Set $C_{i}:=f(T_{i})$, so that $D\cap S=f(E\cap E_{R_{1}})=f(\cup _{i} T_{i})=\cup _{i}C_{i}$. Then $C_{i}\cong \mathbb{P}^{1}$, $C_{i}\cap C_{j}=\emptyset$ if $i\neq j$, and $f$ has fibers of dimension one over $C_{i}$, therefore $C_{i}\subset S_{\mathit{reg}}$ and $C_{i}\subset Y_{\mathit{reg}}$ by Theorem 2.1.

Moreover $g(D)=h(E_{R_{1}})$ is a surface, namely $g$ is of type $(3,2)$, and $C_{i}$ is a one-dimensional fiber of $g$ contained in $Y_{\mathit{reg}}$, hence $K_{Y}\cdot C_{i}=D\cdot C_{i}=-1$. We also have $E_{R_{1}}=f^{*}(D)$ and $f_{*}(C_{R_{1}})\equiv _{Y} C_{i}$.

Since $C_{i}\subset S_{\mathit{reg}}$, it is a Cartier divisor in $S$, and we can write $D_{|S}=m_{1}C_{1}+\cdots +m_{r}C_{r}$ with $m_{i}\in \mathbb{Z}_{>0}$ for every $i=1,\ldots ,r$. In $S$ we have $C_{i}\cdot C_{j}=0$ for $i\neq j$, hence for $i\in \{1,\ldots ,r\}$ we get

$$ -1=D\cdot C_{i}=(m_{1}C_{1}+\cdots +m_{r}C_{r})\cdot C_{i}=m_{i} C_{i}^{2} $$

and we conclude that $m_{i}=1$ and $C_{i}^{2}=-1$, so that $C_{i}$ is a $(-1)$-curve in $S$.

Finally $-K_{S}\cdot C_{i}=-K_{Y}\cdot C_{i}=1$, hence if $C_{i}'\subset S'$ is the transform of $C_{i}$, we have $(K_{S'}+L)\cdot C_{i}'=0$. □

Corollary 3.6

Let $X$ be a smooth Fano 4-fold and $f\colon X\to Y$ an elementary contraction of type $(3,2)$. Set $E:=\operatorname{Exc}(f)$, and assume that $\dim \mathcal{N}_{1}(E,X)\geq 4$. Suppose that $X$ has an extremal ray $R_{1}$ of type $(3,2)$ such that $E\cdot R_{1}=0$.

Then $R_{1}':=f_{*}(R_{1})$ is an extremal ray of $Y$ of type $(3,2)$, and $E_{R_{1}}=f^{*}(E_{R_{1}'})$.

Proof

If $E\cap E_{R_{1}}\neq \emptyset$, we are in the setting of Proposition 3.4; consider the elementary contraction $g\colon Y\to Z$ as in (3.5). Then $\operatorname{NE}(g)=f_{*}(R_{1})=R_{1}'$ is an extremal ray of $Y$ of type $(3,2)$, and $f^{*}(E_{R_{1}'})=E_{R_{1}}$.

If $E\cap E_{R_{1}}=\emptyset$, then we still have a diagram as (3.5), where $g$ is locally isomorphic to the contraction of $R_{1}$ in $X$, and the statement is clear. □

Proposition 3.7

Let $X$ be a smooth Fano 4-fold and $f\colon X\to Y$ an elementary contraction of type $(3,2)$. Set $E:=\operatorname{Exc}(f)$ and $S:=f(E)$, and assume that $\dim \mathcal{N}_{1}(E,X)\geq 4$. Let $\mu \colon S'\to S$ be the minimal resolution of singularities, and set $L:=\mu ^{*}((-K_{Y})_{|S})$.

Suppose that $X$ has two extremal rays $R_{1}$, $R_{2}$ of type $(3,2)$ such that:

$$ E_{R_{1}}\cdot R_{2}>0 \textit{ and } E\cdot R_{i}=0,\ E\cap E_{R_{i}} \neq \emptyset \ \textit{for } i=1,2. $$

Then one of the following holds:

$(i)$:

$K_{S'}+L\equiv 0$;

$(ii)$:

there is a contraction $g\colon S'\to B$ with $\dim B=1$ such that $\operatorname{NE}(g)=(K_{S'}+L)^{\perp}\cap \overline{\operatorname{NE}}(S')$, and $E_{R_{1}}\cdot C_{R_{2}}=E_{R_{2}}\cdot C_{R_{1}}=1$.

Proof

We apply Proposition 3.4 to $f$, $R_{1}$ and to $f$, $R_{2}$. Write $f(E_{R_{1}})_{|S}=C_{1}+\cdots +C_{r}$, and let $\Gamma _{2}$ be an irreducible component of $f(E_{R_{2}})_{|S}$, so that $C_{1},\ldots ,C_{r},\Gamma _{2}$ are $(-1)$-curves contained in $S_{\mathit{reg}}$, and $\Gamma _{2}\equiv f_{*}(C_{R_{2}})$. Then

$$ 0< E_{R_{1}}\cdot C_{R_{2}}=f^{*}(f(E_{R_{1}}))\cdot C_{R_{2}}=f(E_{R_{1}}) \cdot \Gamma _{2}=(C_{1}+\cdots +C_{r})\cdot \Gamma _{2},$$

(3.8)

hence $C_{i}\cdot \Gamma _{2}>0$ for some $i$, say $i=1$. Since $C_{1}$ cannot be a component of $f(E_{R_{2}})_{|S}$, we also get $E_{R_{2}}\cdot C_{R_{1}}=f(E_{R_{2}})_{|S}\cdot C_{1}\geq \Gamma _{2} \cdot C_{1}>0$.

Let $\Gamma _{2}'$ and $C_{1}'$ in $S'$ be the transforms of $\Gamma _{2}$ and $C_{1}$ respectively; then $\Gamma _{2}'$ and $C_{1}'$ are disjoint from the $\mu$-exceptional locus, are $(-1)$-curves in $S'$, $C_{1}'\cdot \Gamma _{2}'>0$, and still by Proposition 3.4 we have $(K_{S'}+L)\cdot C_{1}'=(K_{S'}+L)\cdot \Gamma _{2}'=0$.

Recall that $K_{S'}+L$ is semiample by Proposition 3.1. In particular, the face $(K_{S'}+L)^{\perp}\cap \overline{\operatorname{NE}}(S')$ contains the classes of two distinct $(-1)$-curves which meet. This means that the associated contraction cannot be birational, and we have two possibilities: either $K_{S'}+L\equiv 0$, or $K_{S'}+L$ yields a contraction $g\colon S'\to B$ onto a smooth curve. We show that this second case yields $(ii)$.

Let $F\subset S'$ be a general fiber $F$ of $g$, so that $-K_{S'}\cdot F=L\cdot F$. Since $F$ is not $\mu$-exceptional, we have $L\cdot F>0$ and hence $-K_{S'}\cdot F>0$. Thus there is a non-empty open subset $B_{0}\subseteq B$ such that $(-K_{S'})_{|g^{-1}(B_{0})}$ is $g$-ample, therefore $g_{|g^{-1}(B_{0})}\colon g^{-1}(B_{0})\to B_{0}$ is a conic bundle, $F\cong \mathbb{P}^{1}$, and $-K_{S'}\cdot F=2$.

The curves $C'_{1}$ and $\Gamma _{2}'$ are components of the same fiber $F_{0}$ of $g$, and $-K_{S'}\cdot F_{0}=2=-K_{S'}\cdot (C_{1}'+\Gamma _{2}')$. For any irreducible curve $C_{0}$ contained in $F_{0}$ we have $-K_{S'}\cdot C_{0}=L\cdot C_{0}\geq 0$, so that if $C_{0}$ is different from $C_{1}'$ and $\Gamma _{2}'$, we must have $-K_{S'}\cdot C_{0}=L\cdot C_{0}= 0$ and $C_{0}$ is $\mu$-exceptional. But $C_{1}'$ and $\Gamma _{2}'$ are disjoint from the $\mu$-exceptional locus, thus $C_{0}\cap (C_{1}'\cup \Gamma _{2}')=\emptyset$. Since $F_{0}$ is connected, we conclude that $F_{0}= C_{1}'+\Gamma _{2}'$ and $F_{0}\subset g^{-1}(B_{0})$, hence $F_{0}$ is isomorphic to a reducible conic.

This also shows that $C'_{i}$ for $i>1$ are contained in different fibers of $g$, so that

$$ C_{1}\cdot \Gamma _{2}=\Gamma _{2}\cdot C_{1}=1\quad \text{and}\quad C_{i} \cdot \Gamma _{2}=0\quad \text{for every }i=2,\ldots ,r, $$

and finally using (3.8)

$$ E_{R_{1}}\cdot C_{R_{2}}=(C_{1}+\cdots +C_{r})\cdot \Gamma _{2}=1. $$

Similarly we conclude that $E_{R_{2}}\cdot C_{R_{1}}=1$. □

Proposition 3.9

Let $X$ be a smooth Fano 4-fold and $f\colon X\to Y$ an elementary contraction of type $(3,2)$. Set $E:=\operatorname{Exc}(f)$ and $S:=f(E)$, and assume that $\dim \mathcal{N}_{1}(E,X)\geq 4$.

Suppose that $X$ has three distinct extremal rays $R_{1}$, $R_{2}$, $R_{3}$ of type $(3,2)$ such that:

$$ E\cdot R_{i}=0,\ E\cap E_{R_{i}}\neq \emptyset \ \textit{for } i=1,2,3, \textit{ and } E_{R_{1}}\cdot R_{j}>0\ \textit{for } j=2,3. $$

Then $S$ is a smooth del Pezzo surface and $-K_{S}=(-K_{Y})_{|S}$.

Proof

We apply Proposition 3.7 to $f$, $R_{1}$, $R_{2}$ and to $f$, $R_{1}$, $R_{3}$; we show that we are in case $(i)$, which yields the statement by Proposition 3.1.

By contradiction, suppose that we are in case $(ii)$; we keep the same notation as in the proof of Proposition 3.7. Then $K_{S'}+L$ yields a contraction $g\colon S'\to B$ onto a curve, $E_{R_{2}}\cdot R_{1}>0$, and $E_{R_{3}}\cdot R_{1}>0$.

Let $C_{1}\subset S$ be an irreducible component of $f(E_{R_{1}})_{|S}$, and $C_{1}'\subset S'$ its transform. For $j\in \{2,3\}$ write $f(E_{R_{j}})_{|S}=\Gamma _{j1}+\cdots +\Gamma _{jr_{j}}$, and let $\Gamma _{ji}'\subset S'$ be the transform of $\Gamma _{ji}$.

Using (3.8) as in the proof of Proposition 3.7, we see that $(\Gamma _{j1}+\cdots +\Gamma _{jr_{j}})\cdot C_{1}>0$, hence $\Gamma _{ja_{j}}\cdot C_{1}>0$ for some $a_{j}\in \{1,\ldots ,r_{j}\}$, and $\Gamma _{ja_{j}}'\cdot C_{1}'>0$ in $S'$. Then the proof of Proposition 3.7 shows that $C_{1}'+\Gamma _{2a_{2}}'$ and $C_{1}'+\Gamma _{3a_{3}}'$ are both fibers of $g$, so they should coincide, but $\Gamma _{2a_{2}}'\neq \Gamma _{3a_{3}}'$ because $R_{2}\neq R_{3}$, and we get a contradiction. □

Corollary 3.10

Let $X$ be a smooth Fano 4-fold with $\delta _{X}\leq 2$. Suppose that $X$ has four distinct extremal rays $R_{0}$, $R_{1}$, $R_{2}$, $R_{3}$ of type $(3,2)$ such that:

$$ E_{R_{0}}\cdot R_{i}=0\ \textit{for } i=1,2,3, \textit{ and } E_{R_{1}} \cdot R_{j}>0\ \textit{for } j=2,3. $$

Then one of the following holds:

$(i)$:

$\dim \mathcal{N}_{1}(E_{R_{i}},X)\leq 3$ for some $i\in \{0,1,2,3\}$, in particular $\rho _{X}\leq 5$;

$(ii)$:

$\dim \mathcal{N}_{1}(E_{R_{0}},X)\leq 10$, in particular $\rho _{X}\leq 12$. Moreover if $f\colon X\to Y$ is the contraction of $R_{0}$ and $S:=f(E_{R_{0}})$, then $S$ is a smooth del Pezzo surface and $-K_{S}=(-K_{Y})_{|S}$.

Proof

We assume that $\dim \mathcal{N}_{1}(E_{R_{i}},X)\geq 4$ for every $i=0,1,2,3$, and prove $(ii)$.

We show that $E_{R_{0}}\cap E_{R_{i}}\neq \emptyset$ for every $i=1,2,3$. If $E_{R_{0}}\cap E_{R_{i}}=\emptyset$ for some $i\in \{1,2,3\}$, then for every curve $C\subset E_{R_{0}}$ we have $E_{R_{i}}\cdot C=0$, so that $[C]\in (E_{R_{i}})^{\perp}$, and $\mathcal{N}_{1}(E_{R_{0}},X)\subset (E_{R_{i}})^{\perp}$.

Since the classes $[E_{R_{1}}],[E_{R_{2}}],[E_{R_{3}}]\in \mathcal{N}^{1}(X)$ generate distinct one dimensional faces of $\operatorname{Eff}(X)$ (see [4, Remark 2.19]), they are linearly independent, hence in $\mathcal{N}_{1}(X)$ we have

$$ \operatorname{codim}\bigl((E_{R_{1}})^{\perp}\cap (E_{R_{2}})^{\perp} \cap (E_{R_{3}})^{\perp}\bigr)=3. $$

On the other hand $\operatorname{codim}\mathcal{N}_{1}(E_{R_{0}},X)\leq \delta _{X} \leq 2$, thus $\mathcal{N}_{1}(E_{R_{0}},X)$ cannot be contained in the above intersection. Then $\mathcal{N}_{1}(E_{R_{0}},X)\not \subset (E_{R_{h}})^{\perp}$ for some $h\in \{1,2,3\}$, hence $E_{R_{0}}\cap E_{R_{h}}\neq \emptyset$. In particular, since $E_{R_{0}}\cdot R_{h}=0$, there exists an irreducible curve $C\subset E_{R_{0}}$ with $[C]\in R_{h}$.

For $j=2,3$ we have $E_{R_{1}}\cdot R_{j}>0$, and by Lemma 2.4 also $E_{R_{j}}\cdot R_{1}>0$. This implies that $E_{R_{0}}\cap E_{R_{i}}\neq \emptyset$ for every $i=1,2,3$. For instance say $h=3$: then $E_{R_{1}}\cdot R_{3}>0$ yields $E_{R_{1}}\cap C\neq \emptyset$, hence $E_{R_{0}}\cap E_{R_{1}}\neq \emptyset$. Then there exists an irreducible curve $C'\subset E_{R_{0}}$ with $[C']\in R_{1}$, and $E_{R_{2}}\cdot R_{1}>0$ yields $E_{R_{0}}\cap E_{R_{2}}\neq \emptyset$.

Finally we apply Proposition 3.9 to get that $S$ is a smooth del Pezzo surface and $-K_{S}=(-K_{Y})_{|S}$. Therefore $\dim \mathcal{N}_{1}(S,Y)\leq \rho _{S}\leq 9$ and $\dim \mathcal{N}_{1}(E_{R_{0}},X)=\dim \mathcal{N}_{1}(S,X)+1\leq 10$, so we get $(ii)$. □

4 Proof of Theorem 1.1

In this section we show how to apply the results of §3 to bound $\rho _{X}$; the following is our main result.

Theorem 4.1

Let $X$ be a smooth Fano 4-fold with $\delta _{X}\leq 2$ and $\rho _{X}\geq 8$, and with no small elementary contraction.

Then $\rho _{X}\leq \delta _{X}+10\leq 12$. Moreover every elementary contraction $f\colon X\to Y$ is of type $(3,2)$, and $S:=f(\operatorname{Exc}(f))\subset Y$ is a smooth del Pezzo surface with $-K_{S}=(-K_{Y})_{|S}$.

In the proof we will use the following terminology: if $R_{1}$, $R_{2}$ are distinct one-dimensional faces of a convex polyhedral cone $\mathcal{C}$, we say that $R_{1}$ and $R_{2}$ are adjacent if $R_{1}+R_{2}$ is a face of $\mathcal{C}$. A facet of $\mathcal{C}$ is a face of codimension one. We will also need the following elementary fact.

Lemma 4.2

Let $\mathcal{C}$ be a convex polyhedral cone not containing non-zero linear subspaces, and $R_{0}$ a one-dimensional face of $\mathcal{C}$. Let $R_{1},\ldots ,R_{m}$ be the one-dimensional faces of $\mathcal{C}$ that are adjacent to $R_{0}$.

Then the linear span of $R_{0},R_{1},\ldots ,R_{m}$ is $\mathbb{R}\mathcal{C}$.

Proof

We can assume that $\mathcal{C}\subset \mathbb{R}^{n}$ with $n=\dim \mathcal{C}$. Since $\mathcal{C}$ does not contain non-zero linear subspaces, there exists an affine hyperplane $H\subset \mathbb{R}^{n}$ such that $P:=H\cap \mathcal{C}$ is an $(n-1)$-dimensional convex polytope, and $\mathcal{C}$ is the cone over $P$. Then $v_{i}:=R_{i}\cap H$ is a vertex of $P$ for $i=0,1,\ldots ,m$, and $v_{1},\ldots ,v_{m}$ are the vertices of $P$ that are adjacent to $v_{0}$. The claim is that the affine span of $v_{0},v_{1},\ldots ,v_{m}$ is $H$.

Up to translation we can assume that $v_{0}=0$ in $H=\mathbb{R}^{n-1}$. Let $\mathcal{D}\subset H$ be the convex cone generated by $v_{1},\ldots ,v_{m}$, with vertex $v_{0}$. Since $P$ is convex, we have $P\subset \mathcal{D}$, and $\dim \mathcal{D}=\dim P=n-1$. Thus the affine span of $v_{0},v_{1},\ldots ,v_{m}$ has dimension $n-1$, and coincides with $H$. □

Proof of Theorem 4.1

Let $f\colon X\to Y$ be an elementary contraction; note that $\rho _{Y}=\rho _{X}-1\geq 7$. Then $f$ is not of fiber type by Lemma 2.6, and not small by assumption, so that $f$ is divisorial. Moreover $f$ is of type $(3,2)$ by Lemma 2.7.

Set $E:=\operatorname{Exc}(f)$ and $S:=f(E)\subset Y$; we have $\dim \mathcal{N}_{1}(E,X)\geq \rho _{X}-\delta _{X}\geq 6$, and if $R'\neq \operatorname{NE}(f)$ is another extremal ray of $X$, we have $E\cdot R'\geq 0$ by Lemma 2.3. Moreover, if $R'$ is adjacent to $\operatorname{NE}(f)$, then $E\cdot R'=0$. Indeed the contraction $g\colon X\to Z$ of the face $R'+\operatorname{NE}(f)$ cannot be of fiber type by Lemma 2.6, thus it is birational and we apply Lemma 2.5.

We are going to show that there exists three extremal rays $R_{1}'$, $R_{2}'$, $R'_{3}$ adjacent to $\operatorname{NE}(f)$ such that $E_{R_{1}'}\cdot R_{j}'>0$ for $j=2,3$, and then apply Corollary 3.10.

Let us consider the cone $\operatorname{NE}(Y)$. It is a convex polyhedral cone whose extremal rays $R$ are in bijection with the extremal rays $R'$ of $X$ adjacent to $\operatorname{NE}(f)$, via $R=f_{*}(R')$, see [2, §2.5].

By Corollary 3.6, $R$ is still of type $(3,2)$, and $f^{*}(E_{R})=E_{R'}$. Thus for every pair $R_{1}$, $R_{2}$ of distinct extremal rays of $Y$, with $R_{i}=f_{*}(R_{i}')$ for $i=1,2$, we have $E_{R_{1}}\cdot R_{2}=E_{R'_{1}}\cdot R'_{2}\geq 0$.

If $R_{1}$ and $R_{2}$ are adjacent, we show that $E_{R_{1}}\cdot R_{2}=E_{R_{2}}\cdot R_{1}=0$. Indeed consider the contraction $Y\to Z$ of the face $R_{1}+R_{2}$ and the composition $g\colon X\to Z$, which contracts $R_{1}'$ and $R_{2}'$. Again $g$ cannot be of fiber type by Lemma 2.6, thus it is birational and we apply Lemma 2.5 to get $E_{R_{1}'}\cdot R_{2}'=E_{R_{2}'}\cdot R_{1}'=0$, thus $E_{R_{1}}\cdot R_{2}=E_{R_{2}}\cdot R_{1}=0$.

Fix an extremal ray $R_{1}$ of $Y$. We show that there exist two distinct extremal rays $R_{2}$, $R_{3}$ of $Y$ with $E_{R_{1}}\cdot R_{j}>0$ for $j=2,3$.

Indeed since $E_{R_{1}}$ is an effective divisor, there exists some curve $C\subset Y$ with $E_{R_{1}}\cdot C>0$, hence there exists some extremal ray $R_{2}$ with $E_{R_{1}}\cdot R_{2}>0$.

By contradiction, let us assume that $E_{R_{1}}\cdot R=0$ for every extremal ray $R$ of $Y$ different from $R_{1}$, $R_{2}$. This means that the cone $\operatorname{NE}(Y)$ has the extremal ray $R_{1}$ in the halfspace $\mathcal{N}_{1}(Y)_{E_{R_{1}}<0}$, the extremal ray $R_{2}$ in the halfspace $\mathcal{N}_{1}(Y)_{E_{R_{1}}>0}$, and all other extremal rays in the hyperplane $(E_{R_{1}})^{\perp}$.

Fix $R\neq R_{1},R_{2}$, and let $\tau$ be a facet of $\operatorname{NE}(Y)$ containing $R$ and not $R_{1}$. Note that $\mathbb{R}\tau \neq (E_{R_{1}})^{\perp}$, as $E_{R_{1}}$ and $-E_{R_{1}}$ are not nef. By Lemma 4.2 the rays adjacent to $R$ in $\tau$ cannot be all contained in $(E_{R_{1}})^{\perp}$. We conclude that $R_{2}$ is adjacent to $R$, therefore $E_{R_{2}}\cdot R=0$, namely $R\subset (E_{R_{2}})^{\perp}$.

Summing up, we have shown that every extremal ray $R\neq R_{1},R_{2}$ of $Y$ is contained in both $(E_{R_{1}})^{\perp}$ and $(E_{R_{2}})^{\perp}$. On the other hand these rays include all the rays adjacent to $R_{1}$, so by Lemma 4.2 their linear span must be at least a hyperplane. Therefore $(E_{R_{1}})^{\perp}=(E_{R_{2}})^{\perp}$ and the classes $[E_{R_{1}}],[E_{R_{2}}]\in \mathcal{N}^{1}(Y)$ are proportional, which is impossible, because they generate distinct one dimensional faces of the cone $\operatorname{Eff}(Y)$ (see [4, Remark 2.19]).

We conclude that there exist two distinct extremal rays $R_{2}$, $R_{3}$ of $Y$ with $E_{R_{1}}\cdot R_{j}>0$ for $j=2,3$.

For $i=1,2,3$ we have $R_{i}=f_{*}(R'_{i})$ where $R'_{i}$ is an extremal ray of $X$ adjacent to $\operatorname{NE}(f)$, so that $E\cdot R_{i}'=0$. Moreover for $j=2,3$ we have $E_{R'_{1}}\cdot R'_{j}=E_{R_{1}}\cdot R_{j}>0$.

We apply Corollary 3.10 to $\operatorname{NE}(f)$, $R_{1}'$, $R_{2}'$, $R_{3}'$. We have already excluded $(i)$, and $(ii)$ yields the statement. □

We can finally prove the following more detailed version of Theorem 1.1.

Theorem 4.3

Let $X$ be a smooth Fano 4-fold which is not a product of surfaces.

Then $\rho _{X}\leq 12$, and if $\rho _{X}=12$, then there exist $X\stackrel{\varphi }{\dasharrow} X'\stackrel{g}{\to} Z$ where $\varphi$ is a finite sequence of flips, $X'$ is smooth, $g$ is a contraction, and $\dim Z=3$.

Proof

Since $X$ is not a product of surfaces, we have $\delta _{X}\leq 3$ by Theorem 1.4. Moreover $\delta _{X}=3$ yields $\rho _{X}\leq 6$ by Theorem 1.5, while $\delta _{X}\leq 2$ yields $\rho _{X}\leq 12$ by Theorems 1.6 and 4.1.

If $\rho _{X}=12$, the statement follows from [6, Theorems 2.7 and 9.1]. □