Skip to main content
SpringerLink
Log in

The Lefschetz defect of Fano varieties

  • Published:
Rendiconti del Circolo Matematico di Palermo Series 2 Aims and scope Submit manuscript

Abstract

Smooth, complex Fano varieties are a very natural class of projective varieties, and have been intensively studied both classically and in recent times, due to their significance in the framework of the Minimal Model Program. The Lefschetz defect is an invariant of smooth Fano varieties that has been recently introduced in [7]; it is related to the Picard number \(\rho _X\) of X, and to the Picard number of prime divisors in X. This paper is a survey on this new invariant and its properties: we explain the definition of the Lefschetz defect \(\delta _X\) and its origin, the known results, and several examples, especially in dimensions 3 and 4; we do not give new theoretical results. In particular, we explain how the results on the Lefschetz defect allow to recover the classification of Fano 3-folds with \(\rho _X\ge 5\), due to Mori and Mukai. We also review the known examples of Fano 4-folds with \(\rho _X\ge 6\), that are remarkably few: apart products and toric examples, there are only 6 known families, with \(\rho _X\in \{6,7,8,9\}\).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Notes

  1. A smooth projective variety X is of Fano type if there exists an effective \(\mathbb {Q}\)-divisor \(\Delta \) such that the pair \((X,\Delta )\) is log Fano, namely \((X,\Delta )\) has klt singularities and \(-(K_X+\Delta )\) is ample, see [27].

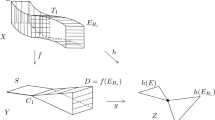
  2. For instance, if \(L_1\) is globally generated, then the vector bundle \(L_1\oplus \mathcal {O}_T\oplus \mathcal {O}_T\) is globally generated, thus H is too, and by Bertini \(S_1\) is smooth.

References

  1. Ando, T.: On extremal rays of the higher dimensional varieties. Invent. Math. 81, 347–357 (1985)

    Article  MathSciNet  MATH  Google Scholar 

  2. Batyrev, V.V.: On the classification of toric Fano 4-folds. J. Math. Sci. (N. Y.) 94, 1021–1050 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  3. Birkar, C., Cascini, P., Hacon, C.D., McKernan, J.: Existence of minimal models for varieties of log general type. J. Am. Math. Soc. 23, 405–468 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  4. Bonavero, L., Campana, F., Wiśniewski, J.A.: Variétés complexes dont l’éclatée en un point est de Fano. C. R. Math. Acad. Sci. Paris 334, 463–468 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  5. Casagrande, C.: Toric Fano varieties and birational morphisms. Int. Math. Res. Not. 27, 1473–1505 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  6. Casagrande, C.: On Fano manifolds with a birational contraction sending a divisor to a curve. Mich. Math. J. 58, 783–805 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  7. Casagrande, C.: On the Picard number of divisors in Fano manifolds. Ann. Sci. Éc. Norm. Supér. 45, 363–403 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  8. Casagrande, C.: On the birational geometry of Fano 4-folds. Math. Ann. 355, 585–628 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  9. Casagrande, C.: Numerical invariants of Fano 4-folds. Math. Nachr. 286, 1107–1113 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  10. Casagrande, C.: On some Fano manifolds admitting a rational fibration. J. Lond. Math. Soc. 90, 1–28 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  11. Casagrande, C.: Rank \(2\) quasiparabolic vector bundles on \({\mathbb{P} }^1\) and the variety of linear subspaces contained in two odd-dimensional quadrics. Math. Z. 280, 981–988 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  12. Casagrande, C.: Fano 4-folds with a small contraction. Adv. Math. 405, 1–55 (2022), paper no. 108492

  13. Casagrande, C., Codogni, G., Fanelli, A.: The blow-up of \({\mathbb{P} }^4\) at \(8\) points and its Fano model, via vector bundles on a del Pezzo surface. Rev. Mát. Comput. 32, 475–529 (2019)

    MATH  Google Scholar 

  14. Casagrande, C., Druel, S.: Locally unsplit families of large anticanonical degree on Fano manifolds. Int. Math. Res. Not. 2015, 10756–10800 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  15. Casagrande, C., Romano, E.A.: Classification of Fano 4-folds with Lefschetz defect 3 and Picard number 5. J. Pure Appl. Algebra 226 (2022), no. 3, 13 pp., paper no. 106864

  16. Casagrande, C., Romano, E.A., Secci, S.A.: Fano manifolds with Lefschetz defect 3. J. Math. Pures Appl. 163 (2022), 625–653, corrigendum: published online 13 October (2022)

  17. Della Noce, G.: On the Picard number of singular Fano varieties. Int. Math. Res. Not. 2014, 955–990 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  18. Hu, Y., Keel, S.: Mori dream spaces and GIT. Mich. Math. J. 48, 331–348 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  19. Iskovskikh, V.A., Prokhorov, Yu.G.: Algebraic geometry V - Fano varieties, Encyclopaedia Math. Sci. vol. 47. Springer (1999)

  20. Kollár, J., Mori, S.: Birational Geometry of Algebraic Varieties, Cambridge Tracts in Mathematics, vol. 134. Cambridge University Press, Cambridge (1998)

    Book  Google Scholar 

  21. Kreuzer, M., Skarke, H.: Classification of reflexive polyhedra in three dimensions. Adv. Theor. Math. Phys. 1(2), 853–871 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  22. Küchle, O.: On Fano \(4\)-folds of index \(1\) and homogeneous vectos bundles over Grassmannians. Math. Z. 218, 563–575 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  23. Manivel, L.: A four-dimensional cousin of the Segre cubic. arXiv:2211.16154 (2022)

  24. Mori, S., Mukai, S., Classification of Fano \(3\)-folds with \(b_2\ge 2\), I, Algebraic and Topological Theories—to the memory of Dr. Takehiko Miyata (Kinosaki: Kinokuniya. Tokyo 1986, 496–545 (1984)

  25. Mori, S., Mukai, S.: Erratum: “classification of Fano \(3\)-folds with \(b_2\ge 2\)’’. Manuscr. Math. 110, 407 (2003)

    Article  Google Scholar 

  26. Mukai, S.: Counterexample to Hilbert’s fourteenth problem for the \(3\)-dimensional additive group, RIMS Preprint n. 1343, Kyoto (2001)

  27. Prokhorov, Yu.G., Shokurov, V.V.: Towards the second main theorem on complements. J. Algebr. Geom. 18, 151–199 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  28. Sato, H.: Toward the classification of higher-dimensional toric Fano varieties. Tôhoku Math. J. 52, 383–413 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  29. Scaramuzza, A.: Algorithms for projectivity and extremal classes of a smooth toric variety. Exp. Math. 18, 71–84 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  30. Secci, S.A.: Fano 4-folds having a prime divisor of Picard number 1. arXiv:2103.16140. To appear in Advances in Geometry (2022)

  31. Tsukioka, T.: Classification of Fano manifolds containing a negative divisor isomorphic to projective space. Geom. Dedic. 123, 179–186 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  32. Wiśniewski, J.A.: On contractions of extremal rays of Fano manifolds. J. Reine Angew. Math. 417, 141–157 (1991)

    MathSciNet  MATH  Google Scholar 

  33. Xie, Z.: Anticanonical geometry of the blow-up of \({\mathbb{P}}^4\) in 8 points and its Fano model. Math. Z., published online 19 September (2022)

Download references

Author information

Authors and Affiliations

  1. Dipartimento di Matematica, Università di Torino, via Carlo Alberto 10, 10123, Torino, Italy

    C. Casagrande

Authors
  1. C. Casagrande
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to C. Casagrande.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Casagrande, C. The Lefschetz defect of Fano varieties. Rend. Circ. Mat. Palermo, II. Ser 72, 3061–3075 (2023). https://doi.org/10.1007/s12215-022-00846-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12215-022-00846-4

Keywords

Search

Navigation