Abstract
The importance of a mobility system based on railway technology as the backbone of public transport is now widely acknowledged. Indeed, rail systems are green, high performing, smart and able to ensure a high degree of safety. Therefore, modal split should be steered towards rail transport by increasing the attractiveness of this transport mode. In this context, a key element is represented by the timetabling design phase, which must aim to guarantee an appropriate degree of robustness of rail operations in order to ensure a high degree of system reliability and increase service quality. A crucial factor in the task of timetabling entails evaluating dwell times at stations. The innovative feature of this paper is the analytical definition of dwell times as flow dependent. Our proposal is based on estimating dwell times according to the crowding level at platforms and related interaction between passengers and the rail service in terms of user behaviour when a train arrives. An application in the case of a real metro system is provided in order to show the feasibility of the proposed approach.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The key role of the timetabling design phase in rail transport management lies in the fact that the results of this planning task have a direct impact on service quality, hence on passenger satisfaction [1]. The timetabling process is made ever more difficult by the constant increase in travel demand, and the consequent need to provide sufficient transport capacity, avoid train and platform congestion and guarantee a good level of service reliability is increasingly felt. It is therefore necessary to develop suitable methodologies to enable service providers to provide a timetable which is as robust and stable as possible, so as to increase the attractiveness of rail systems.
Timetable planning consists in establishing for each train line a feasible schedule of arrival and departure times at the stations served consecutively, consistent with the safety and signalling system, transfer connections and regulations. For this purpose, several factors have to be taken into account, such as train running times, blocking times and minimum headway between two successive convoys, dwell times at stations and possible buffer times. In particular, the paper focuses on the dwell time estimation problem. However, although mass transit agencies may adopt a statistical approach for determining dwell times as a function of confidence degrees (expressed, for instance, in terms of percentiles), the planning phase is implemented when the service is not yet in operation (for instance, in the case of a new line, new services or new timetables), and therefore, there are no available data for implementing such procedures. Hence, in these cases, it is necessary to adopt a modelling approach for simulating future and hypothetical conditions. Our proposal aims to provide an analytical tool for supporting planning phases. Moreover, since mass transit agencies may adopt some control strategies to increase the compliant between the real and the scheduled timetables, the use of a decision support system which allows to estimate actual dwell times may direct the use of proper intervention actions such as the adoption of additional rolling stock, the increase or reduction in stop duration of a convoy or the limitation of passengers flows on platform. In the literature, contributions on dwell times follow mainly two kinds of approaches, namely regression and micro-simulation methodologies. Methods based on the former approach aim to provide, on the basis of the data observed, a regression model which expresses dwell times as a sum of constant and variable predictors. In particular, fixed values are related to the unlocking, opening and closing times of doors together with any planned buffer times; indeed, they are invariant once rolling stock features and train dispatching times are set up. By contrast, variable parameters are a function of the users alighting and boarding times which, in turn, depend on passenger flows. Statistical techniques were the first kind of approach proposed in the literature [2, 3] and were borrowed from the bus service sector [4,5,6]. More recent contributions in this field are provided by [7,8,9,10]. However, broadly speaking, these methods are not generic enough to be applied in contexts other than those in which they were developed, and moreover, they provide no details about passenger behavioural rules when a train arrives.
On the other hand, methods based on a micro-simulation approach analyse pedestrian behaviour on platforms explicitly, especially in crowded conditions [11, 12], and relate it to delays and to other aspects of rail service performance.
In this context, [13] extended the simulation methodology proposed by [14], introducing the evaluation of the mutual interaction between dwell times and train delays. By contrast, [15] simulated the cooperation and negotiation process between boarding and alighting passengers by means of a cellular automata-based model and [16] proposed a multi-agent simulation method which is able to take into account passenger congestion both on the platform and inside trains. Moreover, in order to overcome the shortages of discrete approaches, [17] proposed an extension of a traditional floor field cellular automata pedestrian model, which is specifically developed for simulating high-density contexts. Furthermore, [18] addressed the problem of defining passenger service time and other related factors (i.e. user density on trains and platforms, pedestrian level of service and passenger dissatisfaction) by combining micro-simulation tasks with laboratory experiments.
Albeit based on statistical techniques, regression methods are mostly deterministic, in the sense that their results can be viewed as the expected values of dwell times which are required for completing the boarding and alighting process. By contrast, micro-simulation approaches are better able to take into account the stochasticity of the analysed phenomenon which lies in several factors: the temporal and spatial distribution of passengers, passenger and train driver behaviours, and train delays. Stochastic variations in dwell time are taken into account in [19], while [20] addressed the problem by determining dwell times by separating them into both deterministic and stochastic sub-processes.
Other methodologies proposed in the literature for estimating dwell times are based on the use of artificial neural networks: [21] modelled human behaviour and interaction between different groups of passengers by applying artificial intelligence-based techniques and especially by means of a fuzzy logic approach, while [22] addressed the problem by using the so-called Extreme Learning Machine (ELM), a very fast training speed algorithm described by [23].
From the above, we may identify some of the elements which influence dwell times such as rolling stock and passenger flows with their features. Rolling stock plays a role in the problem of dwell time estimation due to many factors: the control system, number and width of doors [24], kind of service performed [25], horizontal and vertical gaps between the train and platform [26, 27] and interior layout of the convoy seen as number and position of seats [28] or as passenger distance to exit doors and potential free space that the passenger is inclined to occupy [29]. As shown by [30], also fare collection methods may influence dwell times at stations.
Moreover, the importance of considering the number and characteristics of passengers (gender, age, mobility, luggage) for determining alighting and boarding times is self-evident [31]. This element is the hardest to evaluate, since it depends on uncertain conditions such as the interaction between different groups of passengers on the same platform and between passengers on the platform and those on the train [32].
An important factor to be taken into account is also the forecast of queue length of passengers who fail to take the train due to a lack of residual capacity on the convoy: these users will influence the next alighting and boarding process. In this regard, [33] proposed a methodology for supporting pedestrian flow management which is able to provide a theoretically quantitative prediction for the queue length of stranded passengers by means of probabilistic theory and discrete time Markov chain theory.
In addition, also station layout and rail operations affect dwell times. The former includes the position of access/egress facilities on the platform [34] and train stop type (e.g. short stop or large stations [35]). The latter (i.e. rail operation) presents a relationship of reciprocal influence with dwell times at stations, which are key factors in order to optimise the reliability of rail systems [36,37,38,39]. Dwell times play an important role especially in propagating delays [40,41,42,43]. Indeed, when a first delay occurs, if the timetable is neither stable nor flexible enough, the perturbation propagates and generates secondary delays, reducing service quality and hence passenger satisfaction. In this context, a careful estimate of dwell times, as a function of passenger flows, is the most critical task in order to design a robust timetable and make it able to absorb delays by avoiding disturbance propagation.
Clearly, this requirement becomes increasingly felt with the worsening of crowded conditions. Indeed, as shown by [44], the dynamic interaction between passengers and the rail service produces the so-called snowball effect: the number of passengers on the platform influences the dwell times of trains at stations which, in turn, cause increasing delays; this implies an increase in headways which could generate more passenger flows on the platform (generally proportional to the headway increase), producing a further extension of dwell times. However, the snowball effect does not evolve indefinitely, but converges towards an equilibrium state according to proper theoretical conditions, as shown in Sect. 2.
Given the close relationship between dwell times, the timetable and reliability of rail service [45, 46], together with the need to evaluate boarding and alighting times as a function of passenger flows, the majority of contributions in the literature have concentrated on dwell time estimation in the planning phase: [47] focused on the definition of run times and station dwell times in order to minimise transfer waiting times, while [48] analysed the possibility of adjusting dwell times so as to increase station capacity. Nevertheless, some have also proposed models for managing disruptions [49] and real-time rescheduling tasks [50], or even making more effective energy-saving measures [51].
In this context, this paper proposes a methodology whose aim is to support the timetabling planning process by providing an accurate estimation of train dwell times at stations, so as to increase timetabling robustness and hence rail service reliability. Dwell times are computed as a function of travel demand flows evaluated by simulating explicitly user behaviour on the platform when a train arrives. Moreover, the proposed methodology also takes account of station layout, assuming, as proposed by [34], that passengers during the boarding process choose the door on the basis of their exit position (for example, stairs or elevator) in the alighting stop so as to minimise the walking distance at their own destination station. Obviously, the choice of the preferred door cannot be always satisfied, especially in high crowding conditions. Indeed, in these cases, passengers tend to modify the selected door (choosing adjacent doors and/or adjacent coaches) as a function of the crowding degree in order to board as soon as possible. Hence, in these contexts, the assumption on the starting position of passengers on the platform (according to the approach proposed by [34] or other equivalent approaches) represents only the initialisation of the loading algorithm.
The paper is structured as follows. Section 2 describes the simulation framework for modelling the interaction between rail system components, focusing on the estimation of dwell times as flow-dependent variables and their influence on the achievable service performance. Section 3 shows the feasibility of the suggested approach by recourse to an application in the case of a real metro line. Finally, conclusions and future research are summarised in Sect. 4.
2 Simulation of Interaction Between Rail System Components
Rail service is characterised by a high degree of complexity because of the large amount of interactions existing between its components: infrastructure, signalling system, rolling stock and timetable. In addition, the reciprocal influence between rail service and travel demand has to be taken into account: passengers on the platform influence dwell times at stations and this represents one of the main disturbances of high-frequency service lines. As a result, a realistic analysis of rail operations should consider the effects of delays resulting from travel demand both in the phase of network design and in real-time management.
The proposed modelling framework is based on the adoption of three different models (Fig. 1):
-
a Supply Model;
-
a Travel Demand Model;
-
a Service Simulation Model.
The first two models provide, respectively, supply characteristics and travel demand related to the analysed context. By means of their interaction, it is possible to evaluate passenger flows on the network and performance of elements of the transportation systems analysed.
In particular, the Supply Model (SuM) provides the features of all public transport systems within the study area, including the rail system. In this way, split demand among transport modes can be taken into account. Indeed, rail and metro lines, particularly within cities, are part of the public transportation system and cannot be considered individually. Hence, knowing the characteristics of the other transport modes can also provide better estimation of the arrival rate at each station.
The Travel Demand Model is the most innovative part of the procedure. It is split into two further sub-models: a Pre-Platform Model (PPM) and an On-Platform Model (OPM).
The former estimates the number of passengers arriving at stations as a result of the interaction with the Supply Model (SuM) by reproducing the decision-making process made by passengers who choose, among all possible alternatives (i.e. different transport modes), the one which maximises their utility. The results of this model allow arrival rates of passengers at platforms to be determined.
The latter explicitly simulates passenger behaviour on the platform by considering the maximum capacity of each train and estimating the dwell time required to complete the boarding/alighting process. This model is based on a First-In First-Out (FIFO) approach where it must be considered that passengers on the same platform may have different destinations and hence different alighting stations. In this way, travel demand is simulated dynamically according to rail service performance which, in turn, is influenced by passenger flows.
This reciprocal interaction between travel demand and rail service generates, as we will see, a fixed-point problem and takes place in a simulation environment provided by the Service Simulation Model (SeSM). Indeed, given their complexity, railway systems cannot be described in terms of a closed-form analytical solution, but it is necessary to rely on specific simulation techniques. The SeSM is a microscopic synchronous simulation model and is able to provide rail network performance as a function of infrastructure, rolling stock, signalling system, planned timetable and travel demand.
In our case, the simulation of the rail system can be performed by using commercial software (such as OpenTrack ® software [52]), appropriately integrated with ad hoc external tools in order to include travel demand as input data and, therefore, to take into account variations in dwell times at stations just due to variations in travel demand. Moreover, both deterministic and stochastic simulations can be performed.
More detail on the formulation of these models can be found in [53, 54]. However, it is worth pointing out that by means of this new conception of the Travel Demand Model and especially through the On-Platform sub-model, we may capture the interaction between passenger flows and the rail service taking place at stations. This phenomenon is the key factor to be simulated in order to perform a reliable estimation of dwell times. This will, in turn, generate a robust timetable which is able to absorb delays, avoiding their propagation.
Therefore, evaluation of dwell time is a fundamental scheduling task of the wider process of timetabling which directly influences service reliability and passenger satisfaction. Herein lies the motivation behind our proposal.
In particular, the proposed methodology estimates dwell times at station by considering, as input, passenger flows, station configurations and a function expressing the dependence of dwell times on the number of passengers at the most loaded door.
Qualitatively, this function presents constant values of dwell time for low passenger flows, and then, the dwell time increases as the number of passengers rises. However, since the factors which influence this relationship vary for different railway networks, the function has to be suitably calibrated on the specific system analysed.
Moreover, although interchange with bus services may seem to transfer irregularity to a metro system, the low values of transferred passengers (the capacity of a bus generally has a lower order of magnitude than a metro context) do not yield significant effects. Likewise, if in the interchange node numerous bus lines converge, the overlap of irregularities tends to compensate, and therefore, also in this case transfer irregularities can be neglected. Finally, in the case of interchange with rail systems (regional trains, metros or funiculars), where the flows involved may be substantial, the regular structure of arrivals tends to stabilise travel demand variations. However, in order to prevent any kind of irregularity, we propose to perform analyses by considering different levels of travel demand in order to take even more severe conditions into account.
In planning dwell times, the greatest challenge is to be able to model the interaction between passengers and trains during the boarding/alighting process by capturing the above-mentioned snowball effect and the complex phenomenon of negotiation and cooperation between passengers. In particular, the proposed approach considers three levels of interaction.
First of all, on the basis of the station configuration, passengers move towards the door they prefer. In particular, the assumption is that passengers prefer to board the train with their final destination in mind so as to maximise their own utility, according to the theory of the rational decision maker (see, for instance, [55]). Indeed, especially commuters, who have experience of the system, choose the door of the train which is as close as possible to the stairs or the elevators so as to minimise their walking distance at the alighting station. When in front of a door there is a larger group of passengers than a set value (which, obviously, varies from case to case), they start moving to the adjacent doors in the same coach. In the case of crowded situations, the customer’s target is to get on the train as rapidly as possible, trying to remain close to the first favourite door. Once the capacity constraints of the coach are reached, passengers move towards the other doors which attract flow according to their available capacity. This means that the emptier the coach, the more passengers will board it.
The assumption to be made, for the procedure in question, is that the door chosen to board the train will be the same as that to alight from it. This is supported by the lack of freedom of movement for passengers within the coach, especially in crowded conditions.
However, it is worth noting that, although in the literature there are few studies on the microscopic behaviour of passengers on the platform, we adopted the proposal of [34] for determining the initial position of passengers when a train arrives. Another equivalent approach would be based on distributing passengers uniformly on the platform. Obviously, in the cases of low crowding conditions, each passenger is able to board quickly through the preferred door without affecting the dwell time duration, and therefore, the two approaches would provide similar results. Likewise, in the case of high crowding conditions, the congestion of doors and coaches affects user choices aimed at reducing boarding times. Hence, also in these conditions, the initial position of passengers on platform being calculated with both approaches would provide similar results in terms of dwell time duration, since the loading algorithm converges to a solution depending on the train congestion level.
Therefore, by modelling the boarding/alighting process as a threefold interaction phenomenon, we may compute the number of passengers at the most loaded door and, by means of the calibrated function (expressing the relation between the number of passengers and dwell times for the specific context analysed), provide dwell times for each simulated train and at each station. In addition, by estimating the door chosen to board the train, the proposed model provides information about the crowding level within each coach (Fig. 2). This result is extremely useful for calculating the on-board disutility perceived by passengers and could enable a fleet composition to be planned which is closer to customers’ needs. Furthermore, Intelligent Transportation Systems (ITS) could also be designed to inform customers about the crowding levels of the approaching train and to suggest positioning along the platform or which coach of the train should be preferred, so as to optimise the boarding/alighting process and reduce dwell times.
It is worth noting that, should the maximum capacity of the train be reached, the proposed methodology is able to estimate the passenger surplus (i.e. the number of passengers who are forced to remain on the platform due to capacity constraints of the whole convoy being reached) who has to board following trains.
This task makes the simulation more realistic, especially in the case of breakdowns, because it allows for propagation of the disturbance. Hence, besides the planning phase addressed herein, the proposed model can be easily adjusted to deal with rescheduling measures in an off-line dimension (see, for instance, [56]).
From a mathematical standpoint, the snowball effect, and therefore the reciprocal dependence between headways and dwell times, results in a fixed-point problem formulation. For this purpose, let
be a function to be calibrated which expresses the dependence of dwell times on the number of boarding/alighting passengers, where dwt and td represent, respectively, dwell time and travel demand vectors. Obviously, function \(\vartheta \left( \cdot \right)\) has to consider that there is a threshold value of boarding/alighting passengers below which the dwell time is constant.
Likewise, let
be the relation providing headways (i.e. vector hd) as a function of dwell times (i.e. vector dwt) by means of the simulation performed by the SeSM.
Since the frequency of a metro rail service strongly affects the congestion level on the platform, assuming within a short time interval the arrival rate of passengers at station s as constant, the travel demand (i.e. the number of passengers waiting on the platform) at each station s may be calculated as:
where td s,d,r is the number of passengers arriving at the platform of station s for travelling towards destination d during the time interval between run r − 1 and run r; upf s,d,r is the arrival rate of passengers at platform of station s for travelling towards destination d during time interval between run r − 1 and run r; hd r,s is the headway between run r − 1 and run r at station s. Obviously, td s,d,r and hd r,s express, respectively, the component of vector td and vector hd. Hence, Eq. (3) may be expressed in vector notation as:
Obviously, the PPM provides arrival rates (upf s,d,r) associated with each origin–destination station and each time interval between two successive runs.
Therefore, combining the above-mentioned functions, the following is obtained:
or equivalently:
The explicit formulation of relations in Eq. (5), or equivalently in Eq. (6), can be expressed in closed form in the case of function \(\vartheta \left( \cdot \right)\) (whose details are provided in Sect. 3) and function \(\gamma \left( \cdot \right)\) (whose formulation is provided in Eq. 3). Differently, function \(\psi \left( \cdot \right)\) may not be expressed in closed form since it represents a system of differential equations whose solution requires the implementation of proper simulation software. In particular, in Sect. 3, we propose the use of the commercial software OpenTrack ® [52] for solving this task numerically.
A first remark concerns the relationship between the travel demand (in terms of arrival rate) in a station and the related dwell time. Indeed, although Eq. (1) shows the direct dependence of dwell times on travel demand (i.e. the higher the travel demand, the higher the dwell time), Eq. (3) (or, equivalently, Eq. 4) shows the direct dependence of travel demand on headway which, by means of Eq. (2), in turn depends on dwell times in previous stations. Hence, the dwell time in a station is a function of the arrival rate in that station, the arrival rates in the previous stations and the framework of the travel demand (in terms of alighting flows). For this reason, in general, it is not possible to state that higher flows (in terms of arrival rates) necessarily imply higher dwell times.
However, the problem formulated by Eq. (6) highlights the need to find a dwell time vector which produces a headway vector which generates travel demand on platform which provides the initial dwell time vector. According to the theory of the fixed-point problem, this particular case is called ‘compound fixed-point problem’. The mathematical conditions which ensure the existence of the solution of (6) are expressed by Brouwer’s theorem [57]. In our case, since all conditions are satisfied, we may state that the snowball effect always evolves towards an equilibrium condition. Likewise, Banach’s theorem [58] (or equivalently its version in the case of weaker conditions proposed by Cantarella [59]) allows us to state the uniqueness of the fixed-point solution. However, in our case, the uniqueness conditions are not satisfied and this has an impact on the selected resolution procedure. More specifically, two different methods were considered, namely an ‘iterative algorithm’ and an ‘MSA (Method of Successive Average) framework algorithm’ [59, 60]; for both of them it is worth analysing convergence properties.
With respect to the iterative algorithm, the convergence cannot be stated analytically, and hence, it cannot be excluded that the algorithm diverges. On the other hand, the issue of the convergence of the MSA algorithm requires a more detailed assessment. Indeed if, in general, the convergence of this algorithm for the resolution of the compound fixed-point problem is guaranteed by Blum’s theorem [61]; in our case, the convergence of the algorithm cannot be demonstrated since, as explained above, the uniqueness of the solution cannot be assured mathematically. However, this does not mean that the solution is not unique, but that there are no mathematical bases to be sure of this assumption according to traditional proof proposed in the literature.
Hence, it is necessary to look for numerical evidence that the solution of this fixed-point problem could be unique. In particular, it is provided by [62] which applied both algorithms in the case of a real metro line and verified as well their convergence to the same configuration of dwell time.
Moreover, in contrast to the iterative algorithm, the MSA generates decimal values at each iteration. Obviously, such values need to be rounded up/down to the nearest integer before being set up within the simulation model. However, this process can cause theoretical problems for the achievement of the solution by causing a slowdown in reaching convergence.
Therefore, the iterative algorithm appears easier and faster than the MSA procedure, which was why it was selected as the resolution approach to be adopted. However, obviously, in order to prevent the algorithm from performing an infinite number of iterations, a termination test has to be established, based on the maximum number of solutions analysed.
3 Application of the Methodology in the Case of a Real Metro Line
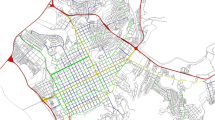
In order to show its feasibility, the proposed approach was applied to Line 1 of the Naples metro system in its 17-station configuration. The line is about 18 km long and has a somewhat directional travel demand since it connects the suburbs (Piscinola) with the city centre (Garibaldi). Hence, morning flows are directed towards the city centre and afternoon/evening flows towards the suburbs. Figure 3 shows the framework of Line 1, highlighting interchange points with other transportation systems.
The choice of a metro network was no accident: due to the close distance between two successive stations, dwell times are frequently comparable to travel times. Thus, the need to provide a reliable estimation of dwell times becomes even more important.
Currently, for most of the days, there is a headway of 8 min between two successive convoys on the line. Together with the demand flows involved, this makes the snowball effects not very apparent. However, since our aim is to verify the capacity of the methodology to capture this phenomenon, in the application we stressed the system by simulating a denser timetable, up to a headway of 3 min.
However, the application of the proposed methodology has required two kinds of surveys: a survey of passenger flows for estimating travel demand and a survey of boarding/alighting flows and train stop durations for determining the passenger flow dwell time function.
The first approach has been performed periodically in all stations and in all time periods since 2012 by surveying both the count of passengers waiting on platforms and turnstile data. The second campaign was performed in a shorter period (May–June 2013) by collecting 172 data surveyed in 14 stations during the morning and afternoon peak hours.
Travel demand was estimated according to [63], and the simulation model was calibrated in terms of infrastructure, signalling system, rolling stock and timetable as shown by [64]. Moreover, in order to investigate the sensitivity of the methodology to different crowding conditions, the proposed approach was applied in relation to three different levels of travel demand obtained by means of the first type of surveys, whose results, expressed in terms of a distribution function, are shown in Fig. 4.
The capacity constraints set for simulating the threefold interaction between passengers and convoys in this specific network are as follows:
-
20 passengers per door (according to the experimental evidence during surveys);
-
216 passengers per carriage (according to the capacity of the rolling stock adopted on the line);
-
wherever the capacity of the carriage was reached, the surplus is distributed in proportion to the residual capacity of the remaining wagons.
The function expressing the relation between passenger flows and dwell times in this specific network was calibrated by adopting the second kind of surveys (calibration details may be found in [56]), whose results are shown in Fig. 5. In particular, the analytical formulation is:
where \(td_{\text{s}}^{\hbox{max} }\) represents the sum of passengers boarding and alighting at the most loaded door (obviously expressed in terms of passenger number instead of passenger flow); \({{Cap}}_{\text{rc}}\) is the capacity of the rail coach which represents the maximum number of boarding passengers or, equivalently, the maximum number of alighting passengers. Hence, the worst case consists in a completely full coach, which first unloads all passengers and then loads them again (in this case, the number of transiting passengers is equal to \(2 \cdot {{Cap}}_{\text{rc}}\)). This implies that, since \(td_{\text{s}}^{\hbox{max} }\) has a maximum value, the dwell time is upper bounded.
However, the R 2 test in the case of function (7) has provided a result equal to 0.81.
The basic idea of the following application is to stress the system in order to point out the presence of the snowball effect and the fact that dwell times need to be planned according to travel demand flows, rather than as fixed values. For this purpose, we analysed different timetables with a decreasing value of headways between two successive convoys and a fixed planned dwell time for each station and for each run, without any differences between peak hours and off-peak hours.
Hence, for each timetable, by means of the above-mentioned modelling framework and the implementation of the iterative algorithm, we simulated the threefold interaction between passengers and trains and solved the fixed-point problem (6), estimating dwell time as well for each station and for each run as a flow-dependent value.
Our simulation focused on the morning peak hour (6.00–9.00). As we will see, the resulting dwell times, which are estimated by simulating rail service performance dynamically according to passenger flows, represent much more reliable values to be set into the timetable, in order to improve its robustness and resilience to delays.
The steps of the procedure are as follows. First of all, a starting random value of the dwell time vector \({\boldsymbol{dwt}}^{0}\) is set up, and then, the SeSM evaluates the new headways according to the dwell time vector \({\boldsymbol{dwt}}^{ \, i}\) provided at iteration i. The next step consists in simulating the threefold interaction between passengers and the train so as to estimate a new dwell time vector, that is \({\boldsymbol{dwt}}^{{\left( {i + 1} \right)}}\), based on the headways obtained by SeSM.
At this point, the termination test has to be verified, that is:
where M is a set number which expresses the maximum number of iterations (for instance, M = 1000). Therefore, if the test is satisfied the algorithm stops; otherwise, it is necessary to calculate the new headways. However, to be more accurate, it is worth noting that the proposed procedure has the following limitation: since the dwell time is a random variable, the value obtained should be considered as the expected value of the dwell time required for the boarding/alighting process, and thus, information about its statistical distribution is not available.
The iterative algorithm, whose flow chart is shown in Fig. 6, was implemented for each planned headway analysed (i.e. from 8 to 3 min) and for each level of travel demand (i.e. 50th, 85th and 95th percentile), amounting to a total of 18 processed scenarios (i.e. algorithm implementations).
The number of runs for each planned headway is shown in Table 1 (detailed for the outward and return trip), together with the number of iterations which need to be implemented to solve the fixed-point problem in the case of each planned headway and each travel demand level. Interestingly, the maximum number of iterations, which is set as a termination test requirement, is never reached, and therefore, the algorithm reaches the convergence in each scenario analysed. As can be seen, the number of iterations varies from a minimum of 6 to a maximum of 18, presenting a significant increase with the reduction in the planned headway due to growing system instability. Obviously, the lower is the planned headway to be analysed, the higher the number of runs and hence the computational time. However, since our proposal addresses a planning task, time is not the main variable to be considered.
In terms of analysis of results, it is worth noting the asymmetry between outward and return trips due to the asymmetry in the network. In particular, the depot (i.e. the place where each rail convoy starts the service every day and is housed every night) is located at one end of the line (i.e. at the beginning of the outward trip). Hence, achievement of the frequency regime conditions requires a transitory phase which implies a different number of runs.
The outcome of the addressed fixed-point problem is represented by an estimation of dwell times for each station and for each run. By way of illustration, Tables 2, 3 and 4 show the converging dwell times for a planned headway of 8 min, detailed for the three levels of travel demand analysed. Obviously, this type of result was also produced for the other planned headways tested: the structure and the rationale are the same, but the numerical values provided are different and the number of runs rises as the headway decreases.
Moreover, since we also considered rolling stock constraints and hence the real use of trains, it is important to provide also dwell times in the case of the first station in order to show that the timetable was planned to ensure the preservation of headways (i.e. the train is able to perform the outward trip, the return trip and the outward trip again without being delayed).
The dwell times can be observed to vary both along the columns (i.e. the stations) and rows (i.e. the runs with a certain planned departure time associated). This implies that dwell times experience both spatial and temporal variabilities. Moreover, the same run at the same station could have a different dwell time on different days, according to the travel demand level at that time and hence the flows of boarding/alighting passengers involved.
As shown in the tables, dwell times in some cases can reach also values above 90 sec. The reason lies in the fact that these values represent the converging dwell times, i.e. the dwell times reached at the end of the evolution of the snowball effect, which, as mentioned before, magnifies the involved quantities.
Moreover, these values are amplified by the congestion which affects the alighting/boarding time and makes this process very chaotic. Indeed, as shown by [24, 65], this is a nonlinear phenomenon: a certain number of users, which constitutes a mixed flow (i.e. some users must board and others must alight), needs a greater time, with respect to the case that they represent an unidirectional flow, for going through the same door.
In addition, also the congestion inside the coach (i.e. standing passengers on-board close to doors) and on the platform extends dwell times. In particular, in the analysed context, the former is accentuated by the fact that doors do not open on the same side in all stations, hence could happen that passengers who boarded on the right side must to move inside the coach in order to alight on the left side or vice versa, while the latter is due to the fact that passengers are not aware of the exact position of each door while the train is approaching, and therefore, they walk on the platform in a chaotic way.
Furthermore, it is worth nothing that, even if generally dwell times increase as the travel demand increases, as stated in Sect. 2, the dwell time in a station depends on arrival rates in that station, the arrival rates in the previous stations and the framework of the travel demand (in terms of alighting flows).
Hence, it is not possible to identify a simple evolution in dwell time values because these values represent the converging values at the equilibrium state. Therefore, since the equilibrium points of investigated flows are different (because boundary conditions are different), the comparison between results related to different percentiles is nonsense. This makes each solved fixed-point problem as stand-alone and prevents a comparison between results related to different conditions. Therefore, results show the uniqueness of each condition and confirm the necessity to make use of suitable simulation techniques which are able to reproduce the complexity of phenomenon and catch its unpredictable evolution.
The possible variation in dwell times between two successive runs may generate variations in headway in each station. However, the timetable was planned so as to ensure that headway was constant on average. In order to highlight this phenomenon, Figs. 7, 8 and 9 show for each planned headway and for each travel demand level, the maximum and the minimum actual headways obtained by implementing the converging dwell times in the simulation model and then selecting the maximum and minimum values among all the resulting headways (i.e. for each run and for each station). Moreover, it is shown that average values of actual headways coincide perfectly with planned ones.
This outcome points out the fact that an erroneous estimation of dwell times makes the system unstable and hence unreliable in the minds of passengers, since the planned timetable is not being respected. The phenomenon which takes place is so-called platooning: trains no longer travel evenly spaced but in bunches. Indeed, the headway between two successive convoys fluctuates so strongly between low and high values that some trains are very close, while others are very far apart. This entails an increase in both the mean and variance of passenger waiting times and the presence of overcrowded trains followed by empty ones, with a further decrease in the provided level of service.
This proves the importance of computing dwell times as flow-dependent factors so as to optimise the timetabling design phase and increase system reliability.
Finally, although it is not possible to state that there is a simple dependence between arrival rate in a station and related dwell time at the equilibrium conditions, it is possible to highlight that in some interchange points (i.e. Piscinola, Vanvitelli and Garibaldi which are, respectively, the 1st, the 9th and the 17th station in the outward trip) we obtained great values of dwell times. However, the generally low values in the other transfer stations (i.e. Chiaiano, Medaglie d’Oro and Museo which are, respectively, the 2nd, the 8th and the 13th station in the outward trip) may be related to low interchange flows due to the low quality of bus (Chiaiano and Medaglie d’Oro) and metro (Museo) services. Obviously, similar remarks can be carried out also in the case of the return trip.
4 Conclusions and Research Prospects
The paper addressed the importance of estimating dwell times at rail stations as flow-dependent factors, rather than as fixed values, providing a methodology which is able to capture the threefold interaction between passengers and trains and the associated snowball effect. The effectiveness of the proposed approach was confirmed by a test application on a real metro line.
Providing an accurate estimate of dwell times is a fundamental task to perform in order to design a robust timetable which presents a high degree of flexibility and resilience to propagation of disturbances. It is thus possible to ensure a high-quality service and increase the attractiveness of the system.
Given the significance of dwell times within the timetable planning phase, the suggested approach has considerable potential which is worth investigating in greater depth in forthcoming works. First of all, it would be possible to include the rail crowding theory in the proposed modelling architecture by providing further important information which would enrich the analysis, enabling an estimate of en route passenger discomfort, perhaps even differentiating between passengers standing or sitting. This could contribute to improve the traditional approach proposed in the literature, according to which waiting time is worth three times on-board time.
Moreover, the rail crowding model would also enable overcrowding conditions to be simulated, in which passengers could decide not to take the first arriving train, but wait for the following one (hoping it will be less crowded), although this would entail an increase in their waiting time. In this way, the simulation could become even more realistic. Another important research prospect consists in operationalising the proposed simulation tools for supporting the planning of energy-efficient driving measures so as to increase their effectiveness, or for assisting the design of dedicated ITS systems which could inform passengers about crowding conditions on the train. Furthermore, it would be interesting to strengthen the random component of the procedure by enabling it to estimate the probability distribution of dwell times and not only their average value. Finally, as future developments, we propose to investigate other resolution methods for the fixed-point problem and test the procedure on different network contexts.
References
Niu H, Zhou X, Gao R (2015) Train scheduling for minimizing passenger waiting time with time-dependent demand and skip-stop patterns: nonlinear integer programming models with linear constraints. Transp Res Part B 76:117–135
Wirasinghe SC, Szplett D (1984) An investigation of passenger interchange and train scheduling time at LRT stations: (ii) estimation of standing time. J Adv Transp 18(1):13–24
Lam WHK, Cheung C-Y, Lam CF (1999) A study of crowding effects at the Hong Kong light rail transit stations. Transp Res Part A 33(5):401–415
Levinson HS (1983) Transit travel time performance. Transp Res Rec 915:1–6
Guenthner RP, Hamat K (1988) Transit dwell time under complex fare structure. J Transp Eng 114(3):367–379
Levine J, Torng G (1994) Dwell-time effects of low-floor bus design. J Transp Eng 120(6):914–929
Harris NG, Anderson RJ (2007) An international comparison of urban rail boarding and alighting rates. Proc Inst Mech Eng Part F J Rail Rapid Transit 221(4):521–526
Vuchic VR (2005) Urban transit operations, planning and economics. Wiley, Hoboken
Kecman P, Goverde RMP (2015) Predictive modelling of running and dwell times in railway traffic. Public Transp 7(3):295–319
Hansen IA, Goverde RMP, van der Meer DJ (2010) Online train delay recognition and running time prediction. In: Proceedings of 13th international IEEE annual conference on intelligent transportation systems (IEEE-ITSC 2010), Funchal, Portugal, September 2010, pp 1783–1788
Lam WHK, Cheung CY, Poon YF (1998) A study of train dwelling time at the Hong Kong mass transit railway system. J Adv Transp 32(3):285–295
Tirachini A, Hensher DA, Rose JM (2013) Crowding in public transport systems: effects on users, operation and implications for the estimation of demand. Transp Res Part A 53:36–52
Jiang Z, Xie C, Ji T, Zou X (2015) Dwell time modelling and optimized simulations for crowded rail transit lines based on train capacity. Promet 27(2):125–135
Jiang Z, Li F, Xu R, Gao P (2012) A simulation model for estimating train and passenger delays in large-scale rail transit networks. J Cent South Univ 19:3603–3613
Zhang Q, Han B, Li D (2008) Modeling and simulation of passenger alighting and boarding movement in Beijing metro stations. Transp Res Part C 16(5):635–649
Yamamura A, Koresawa M, Aadchi S, Inagi T, Tomii N (2013) Dwell time analysis in railway lines using multi agent simulation. In: Proceedings of 13th world conference on transportation research (WCTR 2013), Rio de Janeiro, Brazil, July 2013
Bandini S, Mondini M, Vizzari G (2014) Modelling negative interaction among pedestrians in high density situations. Transp Res Part C 40:251–270
Seriani S, Fernandez R (2015) Pedestrian traffic management of boarding and alighting in metro stations. Transp Res Part C 53:76–92
Larsen R, Pranzo M, D’Ariano A, Corman F, Pacciarelli D (2014) Susceptibility of optimal train schedules to stochastic disturbances of process times. Flex Serv Manuf J 26(4):466–489
Longo G, Medeossi G (2013) An approach for calibrating and validating the simulation of complex rail networks. In: Proceedings of transportation research board 92nd annual meeting, Washington DC, USA, January 2013, pp 1–19
Berbey A, Galan R, Sanz Bobi JD, Caballero R (2012) A fuzzy logic approach to modelling the passengers’ flow and dwelling time. WIT Trans Built Environ 128:359–369
Chu W-J, Zhang X-C, Chen J-H, Xu B (2015) An ELM-based approach for estimating train dwell time in urban rail traffic. Math Probl Eng 2015:1–9
Huang G-B, Zhu Q-Y, Siew C-K (2006) Extreme learning machine: theory and applications. Neurocomputing 70:489–501
Weston JG (1989) Train service model—technical guide. London Underground operational research note 89/18
Jong J, Chang E (2011) Investigation and estimation of train dwell time for timetable planning. In: Proceedings of 9th world congress on railway research, Lille, France, May 2011
Buchmuller S, Weidmann U, Nash A (2008) Development of a dwell time calculation model for timetable planning. WIT Trans Built Environ 103:525–534
Wiggenraad PBL (2001) Alighting and boarding times of passengers at dutch railway stations analysis of data collected at 7 stations in October 2000. Dissertation, TRAIL Research School, Delft University of Technology, Delft, The Netherlands
Harris NG (2006) Train boarding and alighting rates at high passenger loads. J Adv Transp 40(3):249–263
Baee S, Eshghi F, Hashemi SM, Moienfar R (2012) Passenger boarding/alighting management in urban rail transportation. In: Proceedings of the joint rail conference (JRC’12), Philadelphia, USA, April 2012, pp 823–829
Fletcher G, El-Geneidy A (2013) The effects of fare payment types and crowding on dwell time: a fine-grained analysis. Transp Res Rec 2351:124–132
Daamen W, Lee Y, Wiggenraad P (2008) Boarding and alighting experiments: overview of setup and performance and some preliminary results. Transp Res Rec 2042(1):71–81
Puong A (2000) Dwell time model and analysis for the MBTA red line. Research Memo, Massachusetts Institute of Technology, Cambridge (MA), USA
Xu X, Liu J, Li H, Zhou Y (2013) Probabilistic model for remain passenger queues at subway station platform. J Cent South Univ 20:837–844
Kunimatsu T, Hirai C, Tomii N (2012) Train timetable evaluation from the viewpoint of passengers by microsimulation of train operation and passenger flow. Electr Eng Jpn 181(4):51–62
Li D, Goverde RMP, Daamen W, He H (2014) Train dwell time distributions at short stop stations. In: Proceedings of 17th international IEEE conference on intelligent transportation systems (IEEE-ITCS 2014), Qingdao, China, October 2014, pp 2410–2415
Hadas Y, Ceder A (2010) Optimal coordination of public-transit vehicles using operational tactics examined by simulation. Transp Res Part C 18:879–895
Carey M, Carville S (2000) Testing schedule performance and reliability for train stations. J Oper Res Soc 51:666–682
Heimburger DE, Herzenberg AY, Wilson NHM (1999) Using simple simulation models in operational analysis of rail transit lines: case study of Boston’s red line. Transp Res Rec 1667:21–30
Dewilde T, Sels P, Cattrysse D, Vansteenwegen P (2014) Improving the robustness in railway station areas. Eur J Oper Res 235:276–286
Cui Y, Martin U, Zhao W (2016) Calibration of disturbance parameters in railway operational simulation based on reinforcement learning. J Rail Transp Plan Manag 6:1–12
Ceder A, Hassold S (2015) Applied analysis for improving rail-network operations. J Rail Transp Plan Manag 5:50–63
Burdett RL, Kozan E (2014) Performance profiling for predictive train schedules. J Rail Transp Plan Manag 4:98–114
Büker T, Seybold B (2012) Stochastic modelling of delay propagation in large networks. J Rail Transp Plan Manag 2:34–50
Kanai S, Shiina K, Harada S, Tomii N (2011) An optimal delay management algorithm from passengers’ viewpoints considering the whole railway network. J Rail Transp Plan Manag 1:25–37
Pouryousef H, Lautala P (2015) Hybrid simulation approach for improving railway capacity and train schedules. J Rail Transp Plan Manag 5:211–224
Sato K, Tamura K, Tomii N (2013) A MIP-based timetable rescheduling formulation and algorithm minimizing further inconvenience to passengers. J Rail Transp Plan Manag 3:38–53
Wong RCW, Yuen TWY, Fubg KW, Leung JMY (2008) Optimizing timetable synchronization for rail mass transit. Transp Sci 42(1):57–69
Landex A, Jensen LW (2013) Measures for track complexity and robustness of operation at stations. J Rail Transp Plan Manag 3:22–35
Kepaptsoglou K, Karlaftis MG (2010) A model for analyzing metro station platform conditions following a service disruption. In: Proceedings of 13th international IEEE annual conference on intelligent transportation systems (IEEE-ITSC 2010), Funchal, Portugal, September 2010, pp 1789–1794
Li D, Daamen W, Goverde RMP (2016) Estimation of train dwell time at short stops based on track occupation event data: a study at a Dutch railway station. J Adv Transp 50:877–896
Xiaoming X, Keping L, Xiang L (2016) A multi-objective subway timetable optimization approach with minimum passenger time and energy consumption. J Adv Transp 50:69–95
Nash A, Huerlimann D (2004) Railroad simulation using OpenTrack. Comput Railw 9:45–54
D’Acierno L, Gallo M, Montella B, Placido A (2013) The definition of a model framework for managing rail systems in the case of breakdowns. In: Proceedings of 16th international IEEE annual conference on intelligent transportation systems (IEEE-ITSC 2013), The Hague, The Netherlands, October 2013, pp 1059–1064
D’Acierno L, Placido A, Botte M, Montella B (2016) A methodological approach for managing rail disruptions with different perspectives. Int J Math Models Methods Appl Sci 10:80–86
Domencich TA, McFadden D (1975) Urban travel demand: a behavioural analysis. American Elsevier, New York
Placido A, D’Acierno L, Botte M, Montella B (2015) Effects of stochasticity on recovery solutions in the case of high-density rail/metro networks. In: Proceedings of 6th international conference on railway operations modelling and analysis, Tokyo, Japan, March 2015
Brouwer LEJ (1912) Uber Abbildung der Mannigfaltigkeiten. Math Ann 71:97–115
Banach S (1922) Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales. Fund Math 3:133–181
Cantarella GE (1997) A general fixed-point approach to multimodal multi-user equilibrium assignment with elastic demand. Transp Sci 31:107–128
Sheffi Y, Powell WB (1981) A comparison of stochastic and deterministic traffic assignment over congested networks. Transp Res Part B 15:53–64
Blum JR (1954) Multidimensional stochastic approximation methods. Ann Math Stat 25:737–744
Placido A (2015) The definition of a model framework for the planning and the management phases of the rail system in any kind of service condition. Ph.D. dissertation, Federico II University of Naples, Naples, Italy
Ercolani M, Placido A, D’Acierno L, Montella B (2014) The use of micro-simulation models for the planning and management of metro systems. WIT Trans Built Environ 135:509–521
D’Acierno L, Gallo M, Montella B, Placido A (2012) Analysis of the interaction between travel demand and rail capacity constraints. WIT Trans Built Environ 128:197–207
Douglas N (2012) Modelling train and passenger capacity. Report to transport for NSW by DOUGLAS economics, Sydney, Australia
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Editor: Xuesong Zhou
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
D’Acierno, L., Botte, M., Placido, A. et al. Methodology for Determining Dwell Times Consistent with Passenger Flows in the Case of Metro Services. Urban Rail Transit 3, 73–89 (2017). https://doi.org/10.1007/s40864-017-0062-4
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40864-017-0062-4