Introduction

In 1859, James Prescot Joule published a paper entitled, On some thermo-dynamic properties of solids [1]. The abstract of this paper starts with the sentence: After finding the numerical relation between heat and work in 1843, it immediately occurred to me to investigate various phenomena in which heat is involved by mechanical means… These phenomena in which heat is involved by mechanical means provide the basis of caloric effects. Actually, a caloric effect can be defined in terms of the reversible thermal response of a given material to the work exchanged when it is subjected to an external field [2]. In his paper, Joule assumed that work was of mechanical nature but, in fact, it can be performed by application or removal of any kind of external field, either mechanical, electric or magnetic, and the corresponding caloric effect is denoted as mechanocaloric, electrocaloric or magnetocaloric, respectively. Joule reported measurements of the temperature change in solids such as natural rubber caused by the removal of a uniaxial force [3]. This corresponds to a kind of mechanocaloric effect that, at present, is denoted as the elastocaloric effect. Unfortunately, the measured temperature changes were very small, due to an inefficient measurement technique. Perhaps this negative result has been responsible for the fact that solid-state cooling using this mechanical method has remained unexplored for very long.

It has been often considered that giant elastocaloric effect was reported for the first time by Rodríguez and Brown [4]. In that paper, the authors aimed at determining the martensitic transition entropy change of a Cu–Al–Ni shape-memory alloy and for that purpose they used a method that is often used to characterize caloric effects. However, the authors did not mention either that the measured thermal effect was related to other caloric effects nor its interest for refrigeration applications. In fact, the resurgence of the elastocaloric effect must be attributed to Nikitin et al. who back in 1992 reported a large effect near room temperature in FeRh [5]. The possibility giant elastocaloric effects in shape-memory alloys and its potential use for solid-state refrigeration was established in [6]. That paper established the thermodynamic analogies of the mechanocaloric effect and other caloric effects such as the magnetocaloric and electrocaloric effects, which prompted research on the study of the elastocaloric effect and the development of new elastocaloric materials with improved properties for refrigeration applications. Later on, Cui et al. showed the high efficiency of elastocaloric cooling in NiTi shape-memory wires from direct measurement of cooling effects induced by adiabatic release of an applied load [7].

The possibility of inducing other mechanocaloric effects was confirmed soon after the elastocaloric effect was established. Particularly, the possibility of a giant barocaloric effect, which is a mechanocaloric effect induced by hydrostatic pressure, was confirmed to occur in the Ni–Mn–In metamagnetic shape-memory alloy, thanks to the anomalously large volume change accompanying the symmetry change of the unit cell at the martensitic transition [8]. The paper already corroborated that the volume change in this class of shape-memory materials is a consequence of the huge change of magnetization taking place at the martensitic transition. Moreover, it opened up the possibility of multicaloric effects since it clearly established the existence of materials where caloric effects may be induced by application of multiple fields.

At present, elastocaloric effect is a well-known subject with a great potential for refrigeration applications [9, 10]. As a matter of fact, the U.S. Department of Energy has acknowledged that thermoelastic cooling technology based on the elastocaloric effect in shape-memory materials has the highest potential for avoiding the environment impact of the conventional and widely used vapour-compression technology in near room-temperature refrigeration applications [11].

The present paper aims at briefly reviewing elastocaloric effects in shape-memory materials. It is organized as follows. First, the thermodynamics of the elastocaloric effect is summarized in "Thermodynamics of the Elastocaloric Effect" section. Recent advances in elastocaloric effect in shape-memory alloys are discussed in "Elastocaloric Materials" section, and the combination of the uniaxial stress with non-mechanical fields as a strategy to optimize caloric effects is considered in "Multicaloric Effects" section. Finally, we summarize and conclude.

Thermodynamics of the Elastocaloric Effect

In general, a mechanocaloric effect is quantified from the entropy change isothermally and reversibly induced in a material by application or removal of stress, or by the corresponding temperature change that occurs when the stress is applied or removed adiabatically. In contrast with the electrocaloric and magnetocaloric effects in which electric and magnetic fields have a vectorial nature, stress is a rank-2 tensor. The most immediate consequence of this fact is that even in elastically isotropic materials, a complete characterization of the mechanocaloric effect requires studying the thermal response of the material to two independent stress modes such as hydrostatic pressure and shear [9]. For practical reasons, instead of shear, the response to a uniaxial stress, which is a combination of hydrostatic pressure and shear, is often considered. In this case, the components of a uniaxial stress applied in a given direction \(\mu\) are of the form, \({\sigma }_{ij}=\sigma {\delta }_{i\mu }{\delta }_{j\mu }\). Here, \({\delta }_{ij}\) is a Krönecker delta and subscripts indicate space direction. Note that \(\sigma >0\) represents an applied tension and \(\sigma <0\) a compression. On the other hand, for an hydrostatic pressure, \({\sigma }_{ij}=-p{\delta }_{ij}\), where the minus sign is included to take into account that hydrostatic pressure corresponds to an isotropic compression effect. It is interesting to note that in both cases the relevant fields, \(\sigma\) and \(p\) can be treated as scalars.

For the elastocaloric effect, the isothermal response to an applied stress \(\sigma\) is given as, \({\xi }_{T}= {\left(\partial S/\partial \sigma \right)}_{T}={\left(\partial \varepsilon /\partial T\right)}_{\sigma }\) and the adiabatic one as, \({\xi }_{S}= {\left(\partial T/\partial \sigma \right)}_{S}={-\left(\partial \varepsilon /\partial S\right)}_{\sigma } = -\left(T/C\right){\xi }_{T}\), where \(\varepsilon\) is the strain induced in the direction of the applied stress, \(S\) entropy, \(T\) temperature and \(C\) heat capacity. In both cases, adequate Maxwell relations have been taken into account. Therefore, the corresponding isothermal change of entropy, \(\Delta S\), and adiabatic change of temperature, \(\Delta T\), induced by application of a uniaxial stress \(\sigma\), are obtained by integration of the corresponding response functions as

$$\Delta S\left(0\to \sigma \right)=\int_0^{\sigma}{\xi }_{T} {\text{d}}\sigma ,$$
(1)

and

$$\Delta T\left(0\to \sigma \right)=T\left[{\text{exp}}\left(-\int_0^{\sigma}\frac{{\xi }_{T}}{C} {\text{d}}\sigma \right)-1\right].$$
(2)

Note that in the second equation \(T\) is in fact the initial temperature at \(\sigma =0.\) Usually, the change of temperature is small, \(\Delta T/T\ll 1\), and assuming that \(C\) is stress independent, \(\Delta T\) can be simply given as

$$\Delta T\left(0\to \sigma \right)\cong -\frac{T\Delta S\left(0\to \sigma \right)}{C}.$$
(3)

Both \(\Delta S\) and \(\Delta T\) may be very large when \({\xi }_{T}\) is large. This is expected to occur in the neighbourhood of a structural phase transition involving a change of symmetry and volume of the unit cell. It is worth to note that when the transition involves only a volume change, the material will show both barocaloric and elastocaloric effects but, instead, when it is only associated with a change of symmetry given by a pure shear, it will only display elastocaloric effect since barocaloric effect requires volume change. The latter case is precisely the case corresponding to martensitic transitions in non-magnetic alloys, which occur through a dominant shear mechanism with a negligibly small volume change.

For \({\xi }_{T}<0\) the entropy will increase while temperature will decrease under an applied stress, which corresponds to the conventional elastocaloric effect. Note that when the stress is removed the entropy will increase and the temperature will decrease (cooling effect) by exactly the same amounts if the process is strictly reversible. The inverse case occurs for \({\xi }_{T}>0\). In that case entropy will increase and temperature decrease under an applied stress and entropy will decrease and temperature increase when the stress is removed. It is interesting to indicate that the pure elastic contribution to the elastocaloric effect is usually inverse due to the fact that when a material is under a uniaxial stress, volume increases when it is heated, and consequently, as illustrated in Fig. 1, \({\left(\partial \varepsilon /\partial T\right)}_{\sigma }>0\) which gives rise to an inverse elastocaloric effect. Nevertheless, few materials exist that show negative thermal expansion. This is the case, for instance, of the ZrW2O8 compound [12]. In this material, atoms are arranged in a network of octahedra and tetrahedra. The negative thermal expansion is a consequence of the low energy of the optical modes associated with a mixing of librational modes of the tetrahedra and translational modes of oxygen atoms. While no experiments have been reported yet, it is expected that the elastocaloric effect in this material will be conventional.

Fig. 1
figure 1

Schematic illustration of the inverse elastocaloric effect associated with volume dilatation elastic materials and conventional effect associated with a martensitic transition

Full size image

The situation is different in the neighbourhood of a martensitic or ferroelastic transition. Consider the simple example illustrated in Fig. 1 where a model material that undergoes a martensitic transition from a square to a rectangular phase with no volume change is considered. In this case, for symmetry reasons, the two variants—long and short—shown in the figure can grow at the transition. In the absence of an applied stress, they form a twined structure with 50% of each variant (with a negligible total volume change). Application of stress (tensile, for instance) breaks the symmetry and the long variant is favoured. Consequently, deformation increases as temperature decreases and the resulting elastocaloric effect is conventional. Note that it is also conventional in the case of an applied compression stress, which has a negative sign, and favours the short variant. In general, when more variants grow at the transition, as occurs in real cases, under an applied stress there is always one (or few) variant which is favoured and the above argument applies too.

The isothermal entropy change that quantifies the elastocaloric effect is usually determined from measurements of the temperature and stress dependence of the strain. Then, from Eq. 1\(\Delta S\) is numerically obtained as

$$\Delta S\left(T+\delta T/2,\sigma \right)\approx \frac{1}{\Delta T}\left[\int_0^{\sigma} \varepsilon \left(T+\delta T,\sigma \right){\text{d}}\sigma -\int_0^{\sigma} \varepsilon \left(T,\sigma \right){\text{d}}\sigma \right],$$
(4)

where \(\sigma\) is estimated as the ratio of the applied force, \(F\), over the cross-section area,\({A}_{0}\), of the unstressed studied specimen, and \(\varepsilon \cong \left(L-{L}_{0}\right)/{L}_{0},\) where \(L\) is the actual length of the sample at a given stress \(\sigma\) and \({L}_{0}\) a reference length at zero stress. Note that the preceding Eq. (4) renders the entropy change per unit volume. Using the mass density, it can be transformed to entropy per unit mass.

This method was used to study the elastocaloric effect of a Cu–Zn–Al shape-memory crystal in [6]. In general, mechanical experiments are performed with commercial hard screw machines that are well adapted to have a good control of the strain (or displacement) which is the thermodynamically conjugated variable of the stress. However, in that paper, stress controlled experiments were performed using a special extra soft machine that permitted a very good control of the applied stress. Results obtained with that machine were compared with those obtained with standard hard machine. In this strain controlled case, the entropy change isothermally induced by a strain \(\varepsilon\) is obtained from integration of the Maxwell relation \({\left(\partial S/\partial \varepsilon \right)}_{T}={-\left(\partial \sigma /\partial T\right)}_{\varepsilon }\) and it is given as

$$\Delta S\left(0\to \varepsilon \right)=-\int_0^{\varepsilon} {\left(\frac{\partial \sigma }{\partial T}\right)}_{\varepsilon } {\text{d}}\varepsilon .$$
(5)

Results obtained using both machines are shown in Fig. 2. The comparison confirmed that in spite of the huge displacement associated with the martensitic transition (transformation strain \(\sim\) 10%), both kind of measurements provide very similar results. Actually, the most remarkable difference arises from the transition hysteresis, which is much larger in stress controlled than in strain controlled measurements [13]. These results corroborated that standard mechanical stress–strain measurements are adequate to conveniently characterize the elastocaloric properties of shape-memory materials.

Fig. 2
figure 2

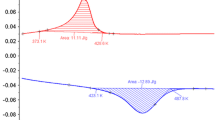
Example of a strain–stress loading curves at temperatures (from left to right) T = 294.6, 295.3, 296.1, 297.9, 298.8, 299.9, 302.0, 303.1, 305.4, 306.0, 307.5, 309.4 and 310.5 K in a Cu68.13Zn15.74Al16.13 single crystal. This alloy transforms martensitically from a cubic (L21) parent phase to a monoclinic (18R) phase. The transition temperature at zero stress is \({T}_{{\text{M}}}\) = 234 K. The red discontinuous curve is the unloading curve at 294.5 K and illustrates the stress hysteresis. b Stress–strain curves at temperatures (from bottom to top) T = 295.0, 297.8, 303.1 and 307.8 K. The red discontinuous curve is the unloading curve at 295.0 K that illustrates the strain hysteresis. Note that strain hysteresis is much smaller than stress hysteresis. c Isothermal stress-induced entropy change curves corresponding to increasing applied stress values (from left to right) \(\sigma =\) 105, 110, 115, 120, 125, 130, 135, 140, 143 MPa. d Isothermal strain-induced entropy change corresponding to increasing strain values (from bottom to top) \(\varepsilon =\) 0.01, 0.02, 0.03, 0.04, 0.05, 0.06, 0.07, 0.08. Note that in this alloy 1 mol = 57.937 g and its molar volume is 7.52 cm3/mole. Therefore, 1 J/K mole = 17.26 J/K kg = 0.133 J/K cm3

Full size image

For a strictly equilibrium first-order transition, the variable \(X\) (the strain \(\varepsilon\) in the case of a martensitic transition) thermodynamically conjugated to the field \(y\) (the stress \(\sigma\) in the case of a martensitic transition), and \(S\) show a discontinuity at the transition and the validity in using the Maxwell equation \({\left(\partial S/\partial y\right)}_{T}={\left(\partial X/\partial T\right)}_{\sigma }\) has been questioned. In fact, integration of this Maxwell relation in the vicinity of the transition discontinuity renders the Clausius–Clapeyron equation. This result can be proved as follows [6]. For a martensitic transition, suppose that the strain is a function of temperature and stress of the general form,

$$\varepsilon \left(T,\sigma \right)={\varepsilon }_{0}\left(T,\sigma \right)+{\varepsilon }_{{\text{t}}}\mathcal{F}\left\{\left[{T}_{{\text{t}}}\left(\sigma \right)-{T}_{{\text{t}}}\left(0\right)\right]/\delta T\right\},$$
(6)

where \(\mathcal{F}\) is a shape-function that varies from 0 to 1 within the temperature range \(\delta T\), \({\varepsilon }_{{\text{t}}}\) the transition strain, \({T}_{{\text{t}}}\left(\sigma \right)\) the transition temperature corresponding to a stress \(\sigma\) and \({\varepsilon }_{0}\left(T,\sigma \right)\) a function giving the temperature and stress dependence of the strain outside the transition. For a strict first-order transition, \(\mathcal{F}\) should approach a Heaviside function and then the stress-induced contribution to the change of entropy only associated with the phase transition is given as

$$\Delta S\left(0\to \sigma \right)=\int_0^{\sigma}{\left(\frac{\partial \varepsilon }{\partial T}\right)}_{\sigma }{\text{d}}\sigma =\left\{\begin{array}{c}-\frac{{\varepsilon }_{{\text{t}}}}{\alpha } \; {\text {for}} \; T \;\; {\text {in the range}} \;\;\;\; \left[{T}_{{\text{t}}}\left(0\right),{T}_{{\text{t}}}\left(\sigma \right)\right],\\ 0 \; {\text{for}} \; T \; {\text{outside the range}} \; \left[{T}_{{\text{t}}}\left(0\right),{T}_{{\text{t}}}\left(\sigma \right)\right],\end{array}\right.$$
(7)

where \(\alpha ={\text{d}}{T}_{{\text{t}}}/{\text{d}}\sigma\) and it has been taken into account that the derivative of the Heaviside function is the Dirac \(\delta\)-function. Therefore, this shows that \(\Delta S\left(0\to \sigma \right)\) is the transition entropy \(\Delta {S}_{{\text{t}}}\) given by the Clausius–Clapeyron equation,

$$\frac{{\text{d}}{T}_{{\text{t}}}}{{\text{d}}\sigma }= - \frac{\Delta {S}_{{\text{t}}}}{{\varepsilon }_{{\text{t}}}}.$$
(8)

This is a general result that can be applied to any first-order phase transition, either ferroelastic/martensitic, ferromagnetic or ferroelectric.

Actually, the Clausius–Clapeyron equation has often been used to determine the elastocaloric change of entropy associated with martensitic transitions. It is worth remarking again that this method only provides the entropy change contribution associated with a well-defined first-order transition, while contributions to the elastocaloric effect arising from any temperature dependence of \(\varepsilon\) outside the transition are not taken into account. Since these effects are often very small in the case of martensitic transitions, the estimation of the entropy change based on the Clausius–Clapeyron equation provides quite good results [14].

The elastocaloric effect can also be quantified from calorimetric measurements performed under selected values of the applied stress (or strain). From these measurements and the knowledge of the temperature dependence of the heat capacity outside the transition, the entropy as a function of stress and temperature, \(S\left(T,\sigma \right)\), can be determined. Then, the entropy change induced by isothermal application of a stress \(\sigma\) can be obtained as

$$\Delta S\left(0\to \sigma \right)= S\left(T,\sigma \right)-S\left(T,0\right).$$
(9)

This kind of estimation of the entropy change requires special calorimeters that can run under well-controlled stress or strain (see for instance [14]). However, it is worth to mention that it is difficult to design calorimeters that enable applying high enough uniaxial loads that yield a complete characterization of the elastocaloric properties of the studied materials under applied loads. In contrast, this kind of measurements are very well adapted to the study of barocaloric effects [15].

A commonly used technique to study elastocaloric effects is to measure the temperature change induced by adiabatic application or removal of either stress or strain by means of a thermocouple attached to the studied sample or, alternatively, using non-contact infrared thermometry. Infrared thermometry has the advantage of allowing the determination of the spatial distribution of temperature in the studied sample [16]. This is important when the elastocaloric effect in the vicinity of a martensitic transition is studied since depending on specific issues of the material very different distributions can occur. Furthermore, by appropriate numerical data treatment, it is possible to track the dynamics of heat sources and heat sinks during the martensitic transition [17].

The temperature change can also be obtained from the calorimetrically computed \(S\left(T,\sigma \right)\) curves as

$$\Delta T\left(0\to \sigma \right)= T\left(S,\sigma \right)-T\left(S,0\right).$$
(10)

It is worth indicating that the intrinsic hysteresis associated with first-order phase transitions is an important issue to take into account for a proper and complete characterization of the elastocaloric properties of a given material. Actually, hysteresis has a highly detrimental effect as it restricts the range of reversibility associated with the application and removal of a given field. As a consequence, in elastocaloric materials showing large hysteresis, larger stresses are required in order to reach reproducible isothermal entropy changes and adiabatic temperature changes comparable to those displayed by materials with lower hysteresis.

Finally, it is useful to indicate that a complete characterization of the caloric properties of a given material requires a good knowledge of the reversible contributions of both \(\Delta S\) and \(\Delta T\). In the case of the elastocaloric effect while \(\Delta T\) can be determined quite easily, the determination of \(\Delta S\) is more challenging. For this reason, \(\Delta T\) is usually employed to define a figure of merit suitable for technological applications that conveniently quantifies the refrigeration capacity of the considered material.

Elastocaloric Materials

Among the different families of elastocaloric materials, the one constituted by shape-memory alloys is undoubtedly the most studied one and probably that displaying better performances. Conventional shape-memory alloys are non-magnetic alloys in which the distortion at the transition is predominantly determined by a pure shear. Therefore, the transition is very sensitive to an applied uniaxial stress while almost insensitive to hydrostatic pressure. In fact, in its parent phase, these materials have the ability of recovering, upon loading and unloading, a huge deformation (in some cases larger than 10%) associated with the stress- or strain-induced transformation with a quite low hysteresis. This unique property is called superelasticity, which together with the significant latent heat involved in the transition are responsible for the excellent elastocaloric properties of this class of materials.

As already indicated, first studies of the elastocaloric effect in shape-memory alloys were performed in Cu-based alloys [6]. In these materials, the transition can be described by a pure shear of the {110} planes along the \(\langle 1\overline{1 }0\rangle\) directions. An isothermal entropy change of about 20 J/kg K was induced in a Cu–Zn–Al single crystal with a relatively low uniaxial stress of 100 MPa applied along the [100] crystallographic direction (see Fig. 2). Maximum adiabatic temperature changes of more than 10 K were expected. However, measured values were slightly lower due to lack of adiabaticity in the measurements [16]. An interesting aspect is the fact that both the isothermal entropy and adiabatic temperature changes are large and highly reproducible upon field cycling over a very broad temperature span of about 130 K [18].

Soon after, it was shown that Ti–Ni shape-memory alloys show larger adiabatic temperature changes than Cu-based alloys [7]. Near the 50–50 composition, this alloy undergoes a transition from a cubic B2 phase to monoclinic B19′ martensitic phase, with a much larger latent heat than in Cu-based alloys. Actually, in this material, the entropy difference between the two phases includes, in addition to a vibrational contribution as in Cu-based alloys, a significant electronic contribution, which is responsible for the large latent heat and excellent elastocaloric properties. Adiabatic temperature changes of about 15 K were measured for an applied stress of 500 MPa, which correspond to an isothermal entropy change of about 70 J/kg K. The inconvenience of this class of alloys is the fact that the transition occurs with a hysteresis significantly larger than in Cu-based alloys. Furthermore, these materials show some degradation of elastocaloric properties along cycling across the transition. It is interesting to note that under compression mode the transition occurs with slightly lower hysteresis than in tension mode and has better fatigue properties due to a lower crack mobility [19, 20].

Interestingly, in Ni–Ti, the martensitic transition can occur via an intermediate transition towards a rhombohedral phase (R-phase), depending on heat treatment and doping. In some circumstances, this intermediate transition can be studied separately from the transition to the B19′ phase, thanks to the fact that the former occurs with a much lower hysteresis than the latter [21]. While the distortion and latent heat associated with the transition to the R-phase are quite small, its low hysteresis gives rise to a high degree of reversibility for low applied stresses which results in excellent elastocaloric properties [22].

The advances in the study of the elastocaloric effect and materials in recent years have been noteworthy. Nowadays, Ni–Ti is still one of the most interesting materials for refrigeration applications but new ones have been developed showing outstanding properties. Interesting results have been reported in some magnetic shape-memory alloys [23, 24]. However, this class of materials are very brittle, which limits the possibility of applying large stresses to reach high enough values of the isothermal entropy and adiabatic temperature changes. In any case, the family of all-3-d Heusler alloys that undergo a martensitic transition is worth mentioning [25]. It has been shown that in its paramagnetic region reversible adiabatic temperature changes of more than 30 K can be reached by application and removal of 700 MPa with almost no degradation along cycling [26]. The colossal elastocaloric effect occurs thanks to the large volume change taking place at the martensitic transition, which contributes significantly to the large latent heat and also provides to these materials with excellent barocaloric properties [27].

An interesting strategy to improve elastocaloric properties of given materials consists of judiciously engineer their microstructure. This also opens a possible route to adapt well-known materials to a particular elastocaloric behaviour required for specific applications. With this idea in mind, additive manufacturing of Ni–Ti has been used to design nanocomposite compounds comprising nickel-rich intermetallic compound interspersed among a binary alloy matrix that allows quasi-linear stress–strain behaviour with extremely small hysteresis [28]. Similar behaviour was also reported in nano-grain Ni–Ti obtained by severe cold-working. These cold-rolled alloys also show quasi-linear superelasticity, which enables large recoverable strains of about 4% and very low hysteresis effects induced by high tensile stresses up to 1 GPa [29, 30]. On the other hand, it has been shown that very large reversible strains can also be induced by low compressive stresses in tweed textured Fe–Pd alloys [31]. The striking mechanical behaviour displayed by all these materials, which occurs with high reproducibility along cycling, gives rise to a significant elastocaloric effect quantified by a large adiabatic temperature decrease under stress removal, taking place very homogeneously over the whole studied specimen. Actually, it is expected that shape-memory materials with appropriate microstructure might be the most successful alternative route to design elastocaloric materials with optimal properties for refrigeration applications.

The strategy based on engineering the microstructure has also been proposed to design materials that show inverse elastocaloric effect associated with a martensitic transition. This is accomplished by growing nanoprecipitates within the parent matrix with a selected orientation that creates an internal stress that opposes the external applied stress. Therefore, in a certain range of applied stresses, variants compatible with the internal stress grow at the expenses of the variants compatible with the external stress. As a consequence, while the external stress does not overcome the internal one, the material shows an inverse elastocaloric effect [32, 33]. It is worth to note that an inverse elastocaloric effect can also occur due to the interplay of structural and secondary degrees of freedom. This has been shown to occur in the Co–Cr–Al–Si alloy where the inverse effect is a consequence of a reentrant behaviour of its martensitic transformation induced by magnetism [34]. It is worth to note that materials showing inverse effect could be useful for designing refrigeration cycles with improved efficiency, thanks to work recovering based on the inverse effect.

Multicaloric Effects

Multiferroic materials with significant interplay between different ferroic properties are expected to show cross-response to the different fields thermodynamically conjugated to these properties. Therefore, in these materials, entropy and temperature changes can be driven by simultaneous or sequential application/removal of multiple fields, which give rise to a multicaloric effect [35]. At present, the thermodynamics behind multicaloric effects is well established [36]. The main result is that the multicaloric effect induced by two different fields is not the simple sum of the corresponding monocaloric effects but instead it includes a contribution from the cross-coupling response of the material.

Magnetic shape-memory alloys belong to this class of materials where a multicaloric effect can be induced by uniaxial stress, \(\sigma\), and magnetic field, \(B\). It can be shown that in this case the entropy change isothermally induced by application of these fields is given by

$$\Delta S\left[T,\left(\mathrm{0,0}\right)\to \left(B,\sigma \right)\right]= \Delta S\left(0\to \sigma \right)+\Delta S\left(0\to B\right)+\int_0^{\sigma}\int_0^B \frac{\partial {\chi }_{\sigma -B}}{\partial T}{\text{d}}\sigma {\text{d}}B,$$
(11)

where the two first terms in the right-hand side quantify the elastocaloric and magnetocaloric effects and the last term is the cross-coupling contribution. It is interesting to note, that this last contribution is related to the temperature derivative of the cross-susceptibility which is expressed as

$$\frac{\partial {\chi }_{\sigma -B}}{\partial T}= \frac{{\partial }^{2}S}{\partial B\partial \sigma }.$$
(12)

Therefore, this result indicates that the cross-coupling term arises from the curvature of the entropy surface in the \(T-\sigma -B\) coordinate space, which always occurs in the presence of a phase transition.

The study of actual multicaloric effects in specific materials has started quite recently but very interesting results have already been achieved. A thorough study of multicaloric effects induced by stress and magnetic field in the Ni–Mn–In metamagnetic shape-memory alloy has been reported in [37]. Results were obtained using a unique calorimeter working under magnetic field and uniaxial load. From these results isothermal and isofield (stress and magnetic field) entropy surfaces can be obtained from which multicaloric entropy changes can be determined. In this material, while the magnetocaloric effect is inverse the elastocaloric effect is conventional and, to take advantage of the response to the two fields it is convenient to proceed by applying one field and removing the second one. It is worth remarking that multicaloric materials showing one conventional and one inverse caloric effect opens the possibility of taking advantage of the hysteresis for refrigeration purposes. This has been shown in [38] where a refrigeration cycle has been proposed that takes advantage of the magnetic hysteresis to lock-in the ferromagnetic phase as the magnetizing field is removed and the cycle is then closed by application of stress. This strategy drastically reduces the volume of the magnetic field source and so reduces the amount of expensive permanent magnets required in magnetic refrigerating devices.

At present it is acknowledged that the use of more than one driving field can induce larger thermal changes, with smaller field magnitudes, over broader ranges of operating temperature, and can also eliminate hysteresis in one control field by transferring it to another field [39]. Overall, it is expected that multicaloric materials could contribute to opening new routes for future developments of high efficiency cooling devices [40].

Conclusions

The excellent elastocaloric properties of shape-memory alloys have great potential for room-temperature refrigeration, heat pumping and harvesting applications. The study of the elastocaloric effect started much recently than the study of electrocaloric and especially magnetocaloric effects. Nevertheless, advances in the study of the elastocaloric effect and materials have been noteworthy in recent years and, at present, elastocaloric materials have been designed that show caloric performances perfectly comparable to those of the best magnetocaloric materials and certainly much better than electrocaloric ones [41]. This is illustrated in Fig. 3 where \(\Delta S\) values as a function of the corresponding \(\Delta T\) for prototypical elastocaloric, magnetocaloric and electrocaloric materials are depicted. The distribution of data for elastocaloric materials might suggest that there is still room for improvement. Note that the low values of electrocaloric materials correspond to bulk samples. In fact, much larger values have been reported in thin films where, for a given voltage, the resulting electric field is much larger. Recently, it has been shown that the limitations associated with the need of thin samples can be overcome to some extent by using multilayers capacitors [42].

Fig. 3
figure 3

Measured maximum values of the reversible isothermal entropy changes as a function of the corresponding adiabatic temperature change for prototypical caloric materials. Squares: elastocaloric materials (NiMnTiB: values measured in a (Ni50Mn31.5Ti18.5)99.8B0.2 sample at 308 K under application of 700 MPa [26]. NiTi: averaged values measured in near stoichiometric alloys at 295 K under application of ca. 700 MPa [7, 47, 48]. Cu-based: averaged values measured in Cu68.1Zn15.8Al16.1 and Cu69.6Al27.7Ni2.7 alloys at ca. 300 K under application of ca. 150 MPa [4, 6]. Fe–Pd: values measured in a Fe68.8Pd31.2 alloy at 250 K under application of 100 MPa [49]). Circles: magnetocaloric (LaFeSiH: values measured in a LaFe11.57Si1.43H1.3 compound at 291 K under application of 5 T [50]. Gd5Si2Ge2: values measured in the stoichiometric alloy at 280 K under application of 5 T [51]. Gd: measured in a sample of 99.9 wt% purity at 294 K (near the critical point) under application of 5 T [52]. NiMnInCo: measured in a Ni45.2Mn36.7In13Co5.1 sample at 317 K under application of 2 T [53]). Triangles: electrocaloric materials (BaTiO3 measured in a bulk sample at 397 K under application of 4 kV/cm [54]. PNZS: measured in a bulk sample of Pb0.99Nb0.02(Zr0.05Sn0.20Ti0.05)0.98O3 at 434 K under application of 30 kV/cm [55]). For the sake of comparison, it is worth to indicate that values of \(\Delta S\) of about 500 J/K kg have been reported in some barocaloric plastic crystals [15]. The corresponding \(\Delta T\) is more moderated of about 10 K

Full size image

Actually, a number of prototypes and demonstrators have already been proposed based on Ni–Ti alloys. In relation to magnetocaloric materials, the great advantage of elastocaloric materials is the fact that they are usually constituted of elements which are non-critical, relatively cheap, quite abundant and non-toxic. In addition, they have very good thermal conductivity, which is a crucial property for an efficient heat exchange in actual devices. Moreover, devices based on the elastocaloric effect are quite easily scalable. To this respect, it is interesting to remark that superelastic effect has been demonstrated to occur with associated large latent heat in nanopillars [43], which opens up the possibility of designing miniature refrigeration devices based on this technology.

Another interesting aspect is the fact that in elastocaloric materials the caloric effect can be induced by non-homogeneous stress modes that give, for instance, rise to bending or twisting. In the first case the corresponding caloric effect is denoted as flexocaloric effect, while in the second it is denoted twistcaloric effect. In both cases, large strain gradients occur in region of maximum curvature [44]. This permits to concentrate a larger caloric response in these regions with low applied forces [45]. Compared to the homogeneous elastocaloric effect, non-homogeneous effects are more efficient since a larger caloric response can be obtained with less exchanged work. This is a consequence of the fact that, in the superelastic region above the martensitic transition temperature, a larger threshold must be overcome to nucleate the martensitic phase by application of a uniaxial stress than by bending [46].

The main drawback of elastocaloric shape-memory alloys is the fact that elastocaloric properties degrade along cycling across the martensitic transition. This is basically due to a deficient elastic accommodation of the martensitic phase within the parent matrix. At present, however, materials with suitable microstructures have been designed which support a large number of cycles. For instance, the growth of adequate precipitates permits improving elastic accommodation of martensitic domains in the parent phase and strongly improves fatigue properties, and a stable martensitic transition has been recorded for more than ten million cycles [47].

To conclude, we can state that elastocaloric materials have open up encouraging prospects for developing an environmentally friendly solid-state cooling technology that may efficiently replace conventional technology currently used in refrigeration and heat pumping devices.