Introduction

It is widely acknowledged that besides shape-memory and superelastic properties, shape-memory materials display many other functional capabilities, which make them desirable for a broad spectrum of technological applications. Among these capabilities, during the last few years a lot of attention has been paid to their excellent caloric response which suggests that these materials have a great potential for solid-state refrigeration and energy harvesting applications [1, 2]. The large thermal response is a consequence of the release or absorption of the latent heat intrinsically associated with the first-order martensitic transition, which is at the origin of the memory properties exhibited by shape-memory materials [3].

The caloric response of solids is defined as the reversible thermal changes that can be induced by application or removal of an external field, either magnetic, electric or mechanical. In shape-memory materials, mechanocaloric effects are induced by changing the stress or strain applied to the materials. So far, most of the work has been performed by application and removal of uniaxial stress or hydrostatic pressure and the corresponding caloric effects are usually denoted as elastocaloric and barocaloric effects, respectively. These effects may be very large when they occur in the vicinity of a phase transition associated with an order parameter thermodynamically conjugated to stress or hydrostatic pressure [4]. In these two cases the applied stress is uniform but caloric effects associated with non-uniform stresses inducing, for instance, bending or twisting can also be considered. These caloric effects are usually denoted as flexocaloric and twistocaloric, respectively [5, 6].

It is usually claimed that inducing mechanocaloric effects by the application of non-uniform stresses is more efficient than by the application of uniform stresses since a lower driving force is required to induce a large caloric response [7, 8]. Nevertheless, the quantitative comparison of uniform and non-uniform effects is not straightforward due to, precisely, the non-uniform character of both stress and strain in the non-uniform case. The aim of the present paper is to quantitatively compare the flexocaloric and the elastocaloric effects associated with a martensitic transition in a shape-memory material. For illustrative purposes here we propose a two-dimensional (2D) model for a shape-memory material that undergoes a square-to-rectangle transition which can be induced by a uniaxial stress and by bending. We show that a reliable comparison of the corresponding elastocaloric and flexocaloric effects requires that the mechanical work exchanged in both cases is the same. The comparison confirms that the flexocaloric effect is more efficient at low work since less driving force is required to nucleate the martensitic phase by bending.

Thermodynamics

From a general point of view, a caloric effect is a phenomenon in which a reversible thermal change is induced in a given material by mechanical or electromagnetic means. According to the first law of thermodynamics if the effect is strictly adiabatic then the work, W, exchanged in the process must result in a change of internal energy, \(\Delta U = W\). Therefore, the amount of work exchanged represents the driving force of the caloric effect. In the adiabatic case the caloric effect is measured by the change of temperature of the body. When instead, the work is performed in isothermal conditions, heat must be exchanged with a reservoir in order to keep the temperature constant and, thus, the thermal effect is measured by the change of entropy of the body. If the work is performed by controlling a given external field \({\varvec{p}}\), then the appropriate response functions corresponding to the adiabatic and isothermal situations are \(\xi _S =(\partial T/\partial {\varvec{p}})_S\) and \(\xi _T = (\partial S/\partial {\varvec{p}})_T\), respectively. These two functions are, in general, position dependent if the field is not uniform. Using Maxwell’s relations it is obtained that these response functions can be determined as

$$\begin{aligned} \xi _T= & {} \displaystyle \left( \frac{\partial {\varvec{B}}}{\partial T} \right) _{{\varvec{p}}}, \end{aligned}$$
(1)
$$\begin{aligned} \xi _S= & {} \displaystyle -\left( \frac{\partial {\varvec{B}}}{\partial S} \right) _{{\varvec{p}}} = - \frac{T}{C} \left( \frac{\partial {\varvec{B}}}{\partial T} \right) _{{\varvec{p}}} = - \frac{T}{C} \xi _T, \end{aligned}$$
(2)

where \({\varvec{B}}\) is the work conjugate of the field \({\varvec{p}}\) and C is a heat capacity.

In the case of an elastic body subjected to a stress \(\sigma ({\varvec{r}})\) that induces a non-uniform deformation \(\varepsilon ({\varvec{r}})\), mechanical work is given by \(\int _{\Omega } d{\varvec{r}} \int d\varepsilon \sigma\) [9], where the first integral is performed over the body’s volume \(\Omega\). The elastocaloric effect is induced by a uniform uniaxial stress, \(\sigma\), and, thus, the work is simply given by \(\Omega \int d\varepsilon \sigma\). In this case the changes of entropy and temperature corresponding to a finite change of stress can be determined from the equations,

$$\begin{aligned} \Delta S = S(T, \sigma ) - S(T, 0)= & {} \int _0^{\sigma } \xi _T d \sigma, \end{aligned}$$
(3)
$$\begin{aligned} \ln \left( 1 + \frac{\Delta T}{T_i} \right)= & {} - \int _0^{\sigma } \frac{\xi _T}{C} d \sigma , \end{aligned}$$
(4)

where \(\Delta T = T(S, \sigma ) - T(S, 0)\) and \(T_i = T(S, 0)\) is the initial temperature of the body. When \(\Delta T \ll T_i\) and C can be assumed independent of \(\sigma\), \(\Delta T \simeq - (T_i \Delta S)/C\), which is often a good approximation to estimate the adiabatic change of temperature close to room temperature. These changes are expected to be very large when they occur close to a phase transition where \(\xi _T\) is expected to be large. In this sense, particularly interesting are first-order ferroelastic or martensitic transitions. In this case the large thermal response is a consequence of the latent heat that is released or absorbed when the transition is induced by the application or removal of stress.

When the stress is not homogeneous the above expressions for \(\Delta S\) and \(\Delta T\) are no longer adequate and, in general, these quantities must be determined by direct computation of the entropy induced by the actual distribution of applied stresses. In this general situation the most convenient way to compare the caloric responses induced by given distributions of stresses is in terms of the corresponding ratios \(\Delta S /W\), where W is the work exchanged with the material to isothermally induce a given change of entropy.

Model

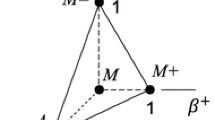
In this section we present a mesoscopic model for a ferroelastic material as the constituent of a 2D macroscopic beam of size \(L_x \times L_y\) with free boundary conditions (Fig. 1a). The beam is considered to be the projection onto a 2D space of a three-dimensional sheet of width \(L_x\), thickness \(L_y\), and with no boundaries in z-direction. Thus, all results will be given per unit length in z-direction, assuming that all physical variables describing the beam are constant along this direction.

Fig. 1
figure 1

a Beam of size \(L_x \times L_y\) in the absence of external forces or stresses, b with applied bending forces \(f_y\) and c with an applied homogeneous deviatoric stress

Full size image

The model is based on that presented in Ref. [6] but it will be extended to study homogeneous deformations by minimization of the thermodynamic potential. Its main features are summarized as follows.

The Helmholtz free energy of the beam is written as the sum of the cohesive energy and the free energy of a set of 3N classical harmonic oscillators which are the building blocks of the beam,

$$\begin{aligned} {{\mathcal {F}}} = E_{coh} + {{\mathcal {F}}}_{vib} \end{aligned}$$
(5)

with

$$\begin{aligned} {{\mathcal {F}}}_{vib}= k_BT \sum _{i=1}^{3N} \ln \left( \frac{\hbar \omega _i}{k_BT} \right) \end{aligned}.$$
(6)

The vibrational free energy is divided into two terms,

$$\begin{aligned} {{\mathcal {F}}}_{vib} = {{\mathcal {F}}}_{\omega } + {{\mathcal {F}}}_{T}, \end{aligned}$$
(7)

the first term, \({{\mathcal {F}}}_\omega\), containing the dependence of vibrational free energy on the frequencies of the oscillators, and the second term, \({{\mathcal {F}}}_{T}\), that only depends on temperature,

$$\begin{aligned} \begin{array}{l} \displaystyle {{\mathcal {F}}}_{\omega } = k_BT \sum _{i=1}^{3N} \ln \left( \frac{\hbar \omega _i}{U} \right) , \\ \displaystyle {{\mathcal {F}}}_T = -3Nk_BT \ln \left( \frac{k_BT}{U} \right) , \end{array} \end{aligned}$$
(8)

where U is the reduced unit of energy. Both the cohesive energy and the frequencies of the oscillators depend on the deformation of the beam. Thus, we define an elastic free energy as

$$\begin{aligned} {{\mathcal {F}}}_{el}=E_{coh}+{{\mathcal {F}}}_{\omega } \end{aligned}$$
(9)

which is written as a functional of the 2D mesoscopic strain fields, \(e_m\), and the 2D strain gradients, \(\partial e_{m}/\partial X_i\), of the beam,

$$\begin{aligned} {{\mathcal {F}}}_{el}= \int f_{el}(e_{m}, \partial e_{m}/\partial X_i) d{\varvec{X}}, \end{aligned}$$
(10)

where \(X_i\) is the i-th component of the position vector of a volume element of the beam in the undistorted configuration. The elastic free energy density \(f_{el}\) is modeled using a Ginzburg–Landau expansion,

$$\begin{aligned} \begin{array}{lll} f_{el} &{} = &{} \displaystyle \frac{1}{2} A (T-T_c)e_2^2 + \frac{1}{4} \beta e_2^4 + \frac{1}{6} \gamma e_2^6 + \frac{1}{2} A_1 e_1^2 \\ &\quad{} + &{} \displaystyle \frac{1}{2} A_3 e_3^2 + \displaystyle \frac{1}{2} \kappa _1 |\nabla e_1 |^2 + \frac{1}{2} \kappa _2 |\nabla e_2 |^2 \\ &\quad{} + &{} \displaystyle \frac{1}{2} \kappa _{3} |\nabla e_3 |^2, \end{array} \end{aligned}$$
(11)

where T is the temperature, \(T_c\) is the stability limit of the square phase, and \(e_1=(\varepsilon _{xx} +\varepsilon _{yy})/\sqrt{2}\), \(e_2=(\varepsilon _{xx} -\varepsilon _{yy})/\sqrt{2}\), and \(e_3=\varepsilon _{xy}\) are the symmetry-adapted strains, which are written in terms of the components of the Lagrangian strain tensor, \(\varepsilon _{ij}\). The dependence of the elastic free energy on the frequencies of the oscillators is thus included through the parameters of the Ginzburg–Landau model.

The dynamical equation of the displacement, \({\varvec{u}}\), of a volume element of the beam can be written as follows:

$$\begin{aligned} \rho _0 {\ddot{u}}_i = \rho _0 g_i + \sum _j \frac{\partial \tau _{ij}}{\partial X_j}, \end{aligned}$$
(12)

where the dots stand for time derivative, \(\rho _0\) is the density of the undistorted beam, \(g_i\) is the i-th component of an external force (per unit mass), and \(\tau _{ij}\) are the components of the first Piola–Kirchhoff stress tensor [10]. The first Piola–Kirchhoff stress tensor is the work conjugate of the deformation gradient, \(F_{ij}\), which is defined as follows:

$$\begin{aligned} F_{ij}= \frac{\partial u_i}{\partial X_j}+\delta _{ij}, \end{aligned}$$
(13)

where \(\delta _{ij}\) is the Kronecker delta. Thus, using the chain rule the first Piola–Kirchhoff stress tensor can be obtained from the Helmholtz free energy as follows:

$$\begin{aligned} \tau _{ij} = \frac{\delta {{\mathcal {F}}}}{\delta F_{ij}} = \sum _{m=1}^3 \frac{\delta {{\mathcal {F}}}_{el}}{\delta e_{m}} \frac{\partial e_{m}}{\partial F_{ij}}. \end{aligned}$$
(14)

A damping force derived from a Rayleigh potential is also included to dissipate the excess free energy during relaxation.

The model parameters and the size of the beam are the same as in Ref. [6]. With these parameters the square-to-rectangle phase transition in the absence of applied forces or stresses occurs at \(T_0=T_c+3\beta ^2/16A\gamma =1.029T_c\).

The thermal response of the beam to bending is studied by numerical integration of Eq. (12) using a distribution of bending forces applied to the long edge of the beam, as shown schematically in Fig. 1b. Analytically the forces are given by the expression,

$$\begin{aligned} \begin{array}{l} f_y({X,Y=0})= \left\{ \begin{array}{l} 2f_0X/L_x, \quad X \le L_x/2\\ 2f_0- 2f_0X/L_x, \quad X> L_x/2, \end{array} \right. \\ f_y({X,Y=L_y})= \left\{ \begin{array}{l} - f_0+ 2f_0X/L_x, \quad X \le L_x/2\\ f_0 - 2f_0X/L_x, \quad X > L_x/2, \end{array} \right. \end{array} \end{aligned}$$
(15)

where \(X=X_x\), \(Y=X_y\), and \(f_0\) is a parameter.

A uniaxial stress is a combination of a deviatoric stress, \(\sigma _2 =(\sigma _{xx}-\sigma _{yy})/\sqrt{2}\), and hydrostatic pressure. In the vicinity of a square-to-rectangle transformation the elastic constant associated with the deviatoric deformation, \(C^\prime\), is much softer than the bulk modulus. Thus, under an applied uniaxial stress the deformation of the material is essentially deviatoric. Therefore, as a simplification, to study the caloric response of the beam to a uniaxial stress we consider an applied deviatoric stress only. In this approximation the thermodynamic potential is the Gibbs free energy,

$$\begin{aligned} {{\mathcal {G}}}= {{\mathcal {F}}} - \int \sigma _2 e_2 d\textbf{X}, \end{aligned}$$
(16)

where the stress \(\sigma\) needs to be interpreted as the second Piola–Kirchhoff stress tensor, as this is the work conjugate of the Lagrangian strain tensor \(\varepsilon\). The caloric response of the beam to a homogeneous deviatoric deformation (Fig. 1c) can be efficiently obtained by minimization of this Gibbs free energy. Thus, in this case, no numerical integration of the dynamical equations of the beam is performed.

Flexocaloric Effect

In this section we present the results of the elastic and caloric response of the beam to bending.

First, we show the deviatoric strain pattern of the bent beam at two different temperatures using a gray scale (Fig. 2). At \(T=1.05T_c\), above the transition temperature in the absence of stress, the low symmetry rectangular phase is induced by bending (Fig. 2a). We note that the two different variants of the rectangular phase nucleate at opposite sides of the beam, as on one side the lattice is stretched, whereas on the other side it is compressed. The two transformed regions are separated by a broad region where the stress is small and the square lattice remains untransformed. This results in a strain microstructure where only a fraction of the original square phase is transformed to the low symmetry rectangular phase.

Fig. 2
figure 2

a Deviatoric strain pattern of a bent beam at \(T=1.05T_c\), above the transition temperature in the absence of stress, \(T_0=1.029T_c\). Light (dark) regions represent positive (negative) strain. The strain generated microstructure is enlarged, showing the nucleation of the two different variants of the rectangular phase at opposite sides of the beam, while the central part remains untransformed. b Characteristic zig-zag strain microstructure of the rectangular phase obtained at \(T=0.8T_c\), well below the transition temperature. c Microstructural changes associated with bending observed experimentally in Cu–Al–Ni (Ref. [11])

Full size image

At \(T=0.8T_c\), well below the transition temperature, the thermodynamically stable structure is the rectangular phase. In this case, a zig-zag domain boundary separating the two variants of the rectangular phase allows the transformation of the whole square lattice while accommodating the stress induced by bending (Fig. 2b). This kind of zig-zag microstructure compares very well with the pattern induced by bending in Cu–Al–Ni reported by Otsuka and collaborators (Fig. 2c) [11]. This excellent agreement with experiments gives support to the model proposed above to study caloric effects.

To study the caloric response of the beam to bending we first compute the total entropy which is obtained as, follows:

$$\begin{aligned} \begin{array}{lll} S &{} = &{} \displaystyle - \frac{\partial {{\mathcal {F}}}}{\partial T} = - \frac{A}{2} \int e_2^2 d\textbf{X} \\ &\quad{} + &{} \displaystyle 3Nk_B \left[ 1+ \ln \left( \frac{k_BT}{U} \right) \right] . \end{array} \end{aligned}$$
(17)

The entropy of the beam vs temperature for different values of the parameter \(f_0\) controlling the strength of the applied forces is shown in Fig. 3. The entropy is plotted with respect to the entropy in the absence of applied forces at \(T=1.5T_c\). In the absence of applied forces the result shown corresponds to equilibrium, with a discontinuity at the transition temperature. For small applied forces (\(f_0 \le 1\times 10^{-5}\) reduced units) a tiny thermal hysteresis has been observed. In this case, the results shown correspond to the entropy obtained when cooling the beam.

Fig. 3
figure 3

Entropy of the bent beam vs temperature for several values of the parameter \(f_0\), which controls the strength of the applied forces. The entropy is plotted relative to its value at \(T=1.5T_c\) in the absence of applied forces

Full size image

Ignoring the tiny thermal hysteresis of the bent beam, these entropy curves are used to determine the isothermal entropy change (Fig. 4) and the adiabatic temperature change (Fig. 5) of the beam when applying the distribution of external forces. It is obtained that both the isothermal entropy change and the adiabatic temperature change have a single discontinuity associated with the discontinuity of the entropy curve in the absence of applied forces. As a general trend, the caloric response is larger slightly above the transition temperature. In this temperature region, the response relative to the applied forces is larger for small forces. For large applied forces, however, the decay of the caloric response as the temperature increases is much slower.

Fig. 4
figure 4

Isothermal entropy change of the beam when applying the external forces vs temperature. The results are plotted for several values of the strength of the applied forces

Full size image
Fig. 5
figure 5

Adiabatic temperature change of the beam when applying the external forces vs the initial temperature. The results are given for several values of the strength of the applied forces

Full size image

Elastocaloric Effect

In this section we present the results of the caloric response of the beam to a homogeneous deviatoric stress.

Minimization of the Gibbs free energy of the beam [Eq. (16)] yields the homogeneous deviatoric strain induced by application of a homogeneous deviatoric stress. The total entropy of the beam is then obtained as follows:

$$\begin{aligned} \begin{array}{lll} S= & {} \displaystyle - \frac{\partial {{\mathcal {G}}}}{\partial T} = - \frac{A}{2} e_2^2 \Omega + 3Nk_B \left[ 1+ \ln \left( \frac{k_BT}{U} \right) \right] \end{array} \end{aligned}.$$
(18)

The entropy of the beam vs temperature for different values of the applied stress is shown in Fig. 6. A discontinuity in the entropy curves is observed for stresses smaller than \(\sigma _2^\textrm{cri}=4.89 \times 10^{-4}\) (in reduced units) where a critical point exists [6]. From these curves we obtain the isothermal entropy change and the adiabatic temperature change when a homogeneous deviatoric stress is applied to the beam. The results are shown in Figs. 7 and 8.

Fig. 6
figure 6

Entropy of the beam vs temperature for several values of the applied deviatoric stress, \(\sigma _2\). The entropy is plotted relative to its value at \(T=1.5T_c\) in the absence of applied stress

Full size image
Fig. 7
figure 7

Isothermal entropy change of the beam when applying a deviatoric stress vs temperature. The results are plotted for several values of the applied stress

Full size image
Fig. 8
figure 8

Adiabatic temperature change of the beam when applying a deviatoric stress vs the initial temperature. The results are given for several values of the applied stress

Full size image

For stresses smaller than the critical stress the isothermal entropy change has two discontinuities associated with the discontinuities of the entropy curves with and without the applied stress. Regarding the adiabatic temperature change, only a single discontinuity is obtained, but the caloric response relative to the applied stress is especially large slightly above the transition temperature in the absence of stress. For stresses larger than the critical stress only the discontinuity associated with the discontinuity of the entropy curve in the absence of stress is observed in both the isothermal entropy change and the adiabatic temperature change. As obtained when studying the flexocaloric effect, the elastocaloric response of the beam is larger slightly above the transition temperature. In this temperature region, the response relative to the applied stress is larger for small stresses. For large applied stresses, however, the decay of the caloric response as the temperature increases is slower.

Also, comparison of the caloric response of the beam to bending with the caloric response to a homogeneous deformation shows that in the latter case the caloric response decays faster as the temperature increases.

Comparison Between the Flexocaloric and the Elastocaloric Effects

In order to be able to compare the caloric response of the beam to a homogeneous deformation with the caloric response of the beam to bending from a quantitative point of view, the stress values corresponding to the curves shown in Sect. 5 have been chosen so that the work done in the homogeneous deformation equals the work done by bending the beam in the curves shown in Sect. 4. As the displacement/strain depends on temperature, the work done for a given applied stress or distribution of forces depends on temperature as well. Thus, the equivalence of the works done by a homogeneous deformation and by bending is only established at \(T=1.05T_c\).

The work done by external forces to bend the beam is computed as follows:

$$\begin{aligned} W_\textrm{bend}= \rho _0 \int d\Omega \int f_y d\textbf{u}, \end{aligned}$$
(19)

whereas for homogeneous deformations the work done by a homogeneous deviatoric stress is evaluated as follows:

$$\begin{aligned} W_\textrm{hom}= \Omega \int \sigma _2 de_2 \end{aligned}.$$
(20)

In the first case [Eq. (19)] the computation of the integral requires the applied force (per unit mass) vs displacement curve for each volume element where an external force is applied. In the second case [Eq. (20)], the stress vs strain curve is needed.

The correspondence between bending forces and homogeneous stresses is as follows. The work done when bending the beam with a distribution of forces with \(f_0=1 \times 10^{-6}\) at \(T=1.05T_c\) is the same as by application of a homogeneous stress \(\sigma _2=1.4 \times 10^{-4}\). Due to the discontinuity of the phase transition, the work done by bending the beam with \(f_0=2\times 10^{-6}\) and \(f_0=5\times 10^{-6}\) cannot be obtained in a homogeneous deformation where the stress is the control parameter. The values of the homogeneous stresses giving rise to the same work as bending with \(f_0=1 \times 10^{-5}\), \(f_0=2 \times 10^{-5}\), and \(f_0=5 \times 10^{-5}\) are \(\sigma _2=6 \times 10^{-4}\), \(\sigma _2=2 \times 10^{-3}\), and \(\sigma _2=6 \times 10^{-3}\), respectively.

Comparison of the isothermal entropy change when bending at \(T=1.05T_c\) (Fig. 4) to the isothermal entropy change associated with a homogeneous deformation at the same temperature (Fig. 7) reveals that at equal work the caloric response to a homogeneous deformation is larger. This comparison is done in a broader force/stress range in Fig. 9 where the isothermal entropy change is directly plotted vs the work done for both bending (symbols) and application of a homogeneous deviatoric stress (solid line).

For large values of the work done, the isothermal entropy change due to a homogeneous stress is systematically larger than the caloric response to bending. This result is associated with the smaller transformed fraction of the beam when bending.

We also note a discontinuity (indicated with a dashed line) in the caloric response to a homogeneous deformation. This is due to the first-order character of the phase transition. When bending, the nucleation of the rectangular phase occurs with much less work, and the associated discontinuity cannot be seen in the figure. Thus, when the stress is the control parameter, the caloric response to a homogeneous deformation can only be large if the work done is sufficiently large to induce the phase transition. Intermediate caloric responses are not allowed. On the contrary, bending allows to obtain moderate caloric responses with moderate work. Moreover, for small work, the caloric response of the beam to bending is larger than the caloric response to a homogeneous deviatoric stress.

In summary, bending may have the advantage over homogeneous deformations of giving a larger caloric response relative to the work done in the limit of small work. Moreover, it also allows to operate at intermediate work.

Fig. 9
figure 9

Isothermal entropy change vs work done when bending (circles) and when applying a homogeneous deviatoric stress (solid line). The dashed line indicates a discontinuity of the solid line. The same curves are shown in the inset at a larger scale

Full size image

Conclusion

We have proposed a Ginzburg–Landau model suitable to study mechanocaloric effects in the vicinity of a martensitic transition with associated shape-memory and superelastic effects. The model has been used to compare the elastocaloric effect induced by a uniform uniaxial stress to the flexocaloric effect induced by bending. We have shown that a reliable comparison of both caloric effects must be done for equal amounts of exchanged work. Results corroborate that the flexocaloric effect is more efficient for refrigeration applications since a larger caloric response can be obtained in the range of low exchanged work. This is a consequence of the fact that, in the superelastic region above the martensitic transition temperature, a larger threshold must be overcome to induce the transformation by application of a uniaxial stress than by bending. In real materials the difference of both caloric effects might be even larger due to the inverse response associated with the volumetric effect [12] that dominates the caloric response in the elastic deformation region of the parent phase.

From the model it is deduced that another advantage of the flexocaloric effect compared to the elastocaloric effect is the low hysteresis, which originates only from nucleation effects. In any case, it has been recently shown that in real systems the evolution of the transformation fronts through avalanches results in much larger hysteresis, comparable with the hysteresis observed in the elastocaloric case [13].