Introduction

Shape Memory Alloys (SMAs) are a special class of materials that are able to recover an original shape even after experiencing very large deformations [1]. Among the SMA materials, the most commercialized ones are the nickel–titanium (NiTi) alloys, thanks to their excellent mechanical and functional features, as well as good corrosion resistance and biocompatibility [2]. Shape recovery properties of SMAs are directly linked to the so-called thermoelastic martensitic transformation (TMT). This latter consists in a reversible solid-state transition between two different phases: the body-centered cubic austenite (A) and the monoclinic martensite (M). Phase transformation can occur either by temperature variation (TIM, thermally induced martensite) or by mechanical stress (SIM, stress-induced martensite). In the first case, phase transition is triggered by characteristic temperatures (TTs, Transformation Temperatures), obtaining the shape memory effect (SME). In the latter one, instead, transformation occurs when characteristic stresses (TSs, Transformation Stresses) are applied, representing the pseudoelastic effect (PE).

Due to these unique features, NiTi alloys are currently used in several engineering applications, ranging from robotics [3], automotive [4], aerospace [5], and civil engineering [6, 7], where both SME and PE are used for the realization of active and/or tunable components and devices.

NiTi alloys have been widely used in many biomedical fields, like dental, orthopedic, vascular, neurosurgical, and surgical, and especially to produce mini-invasive instruments and implants [8, 9]. One of the most significant applications is represented by cardiovascular stents for vessel revascularization.

Self-expanding mechanism and pseudoelastic characteristics allow to obtain a more uniform expansion of the device. In fact, it has been demonstrated how NiTi stents are less traumatic than balloon-expandable stents, reducing vascular injury and thrombogenicity [8]. Moreover, NiTi stents are characterized by enhanced radial strength and flexibility and by the capacity to recover from crushing [10, 11].

As a direct consequence of this increasing interest, many efforts were devoted in the last years to study the thermo-mechanical characteristics of NiTi alloys [1]. However, many aspects are still unknown, especially when dealing with fatigue and fracture mechanics because phase transformations significantly affect the damage initiation and propagation mechanisms. It is well known, in fact, that in the near crack tip region local transformation occurs as a consequence of the high localized stresses and this leads to a stress redistribution that cannot be directly analyzed by common elastic or elasto-plastic theories. To this aim, Finite Element (FE) codes, proper constitutive models for SMAs [12, 13], and analytical approaches [14,15,16] were developed to investigate the fracture properties of SMAs. In addition, special and ad hoc investigation techniques were also developed and exploited to study the crack formation and propagation mechanisms under static [17,18,19,20,21] and cyclic loadings [22,23,24,25] by both local and global analyses [26, 27]. An example is represented by synchrotron X-ray micro-diffraction (XRD) [18, 19], infrared thermography (IR) [20, 25], and Digital Image Correlation (DIC) [21, 22, 28,29,30,31,32] that allow to demonstrate that phase transition phenomena significantly affect the fatigue properties of the material as well as the functional response, [26, 27].

However, the relation between micro- and macro-scale damage mechanisms as well as the functional evolution, occurring during fatigue loading still represents an open issue. In this context, the investigation of mechanical properties of SMAs at micro- and nanoscale is fundamental, especially when dealing with biomedical applications, where devices are typically characterized by small sizes. Microindentation and nanoindentation are some of the most important and efficient non-destructive techniques to measure the mechanical properties (i.e., elastic moduli, hardness) of materials at small scale. In the last years, many efforts were spent in modeling micro- and nanoindentation for the numerical characterization of SMAs [33,34,35,36,37] and several experiments were also carried out to study the local transformation mechanisms by nanoindentation [38,39,40,41,42,43,44,45].

In particular, forward and reverse phase transformations in small volumes were analyzed by Frick et al. [38]. Pseudoelastic recovery and the effects of temperature on indentation response were investigated by Wood et al. [39]. Stress-induced transformation mechanisms generated by indenting single grains of NiTi alloy were investigated by Laplanche et al. [40]. The effects of crystallographic anisotropies and grain orientation on the indentation response were analyzed by Pfetzing et al. [41] and by Gall et al. [42]. Interesting investigations were carried out by Maletta et al. [35], by Yan et al. [43], and by Amini et al. [44] where it was demonstrated the spherical tip is less sensitive to the local anisotropies of SMAs, due to the lower stress/strain gradients and larger indentation/process zone compared to sharp tips as the Berkovich. Nanoindentation technique was also proposed as an efficient methodology to identify phase transformation mechanisms in SMAs [46, 47], using spherical indenters and relatively large indentation loads (400 mN).

Recently, micro- and nanoindentation have been also used to analyze the effect of localized cyclic contact stress on functionally graded TiN/TiNi films [48]. The adopted investigation methodology consists in advanced testing indentations that allow in applying cyclic penetrations to a sample.

The aim of this work is to use such approach to investigate, from a nanoscale point of view, the cyclic functional evolution of a NiTi superelastic alloy when “multicycle” indentations are applied. The investigation of the local functional evolution of SMAs is of great interest, especially when dealing with biomedical applications [9, 49], such as cardiovascular stents. Such devices, in fact, are subjected to cyclic loadings, generated by the cardiac rhythm and the musculoskeletal movement that can strongly affect their functional response [50, 51]. Cyclic nanoindentation can provide very useful information in this field. In addition, single loading–unloading indentations were also carried out both experimentally with the aim to investigate the evolution of the main functional parameters and numerically by finite element simulations in order to estimate the size of the transformation zone under the tip as a function of the indentation load. The experiments were performed using both Berkovich and spherical tip to highlight the differences in the deformation field.

Materials and Methods

Material

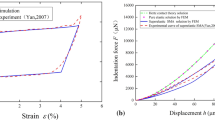
In the present work a commercial NiTi pseudoelastic alloy was analyzed (50.8% Ni, 49.2% Ti). The mechanical properties were obtained from a quasi-static loading–unloading tensile test at room temperature (\(T=25^\circ \mathrm{C}\) and \(\dot{\varepsilon }=2.5\cdot {10}^{-4} {\mathrm{s}}^{-1}\)). The experiment was carried out in displacement control until the complete stress-induced transformation was recorded. Figure 1a reports the obtained stress–strain response with a highlight of the main mechanical properties, i.e., the elastic modulus of the austenite \({E}_{A}\) and martensite \({E}_{M}\), transformation stresses \({\sigma }_{s}^{AM}\), \({\sigma }_{f}^{AM}\), \({\sigma }_{s}^{MA}\), and \({\sigma }_{f}^{MA}\), and transformation strain \({\varepsilon }_{L}\). Obtained values are listed in Table 1. This latter also reports transformation temperatures \({M}_{s}\), \({M}_{f}\), \({A}_{s}\), and \({A}_{f}\) that were measured by Differential Scanning Calorimetry (DSC) experiments, as represented in Fig. 1b.

Fig. 1
figure 1

a Stress–strain response of the analyzed NiTi alloy and main measured mechanical and functional properties. Test conducted in quasi-static isothermal conditions (\(T=25^\circ \mathrm{C}\) and \(\dot{\varepsilon }=2.5\cdot {10}^{-4} {\mathrm{s}}^{-1}\)). b Differential scanning calorimetry (DSC) thermograms of the analyzed NiTi alloy together with the measured values of the transformation temperatures (TTs)

Full size image

For a better understanding of the nanoindentation results, the microstructure was revealed by chemical etching with a mixture of acids (45-ml H2O, 45-ml HNO3, and 10-ml HF). Sample was cut, mounted using cold mounting epoxy resin, to avoid temperature effects on the material, and polished starting with wet SiC grinding papers and then by diamond solution and silica both with polishing cloths. Finally, microstructural characterization was carried out by light micrographic investigations (DM4000 M, Leica, Germany).

Figure 2 reports the etched micrographs of the NiTi sample. As shown, the material is mainly based on a near-equiatomic NiTi phase matrix (nominally austenite) surrounded by minor phases mainly made of Ni3Ti, Ti2Ni, and Ti3Ni4 precipitates [52, 53].

Fig. 2
figure 2

Etched microstructure at different magnifications of NiTi sample: a 50 × and b 100 ×

Full size image

This heterogeneity has to be attributed to the heat treatments typically carried out on such material to reduce structural defects, residual stresses, and anisotropy resulting from the manufacturing process that totally deteriorates the shape memory response. Applying heat treatments such as annealing, solution treatment (at high temperatures), and aging (depending on the operating temperature range) may results in microstructural phase changes. Like many other alloys, precipitations generate within the structure when the saturated state has reached during heating treatment. It occurs when the content of Ni exceeds the solubility limit of NiTi after the quenching process. It is well known, in fact, that higher cooling rates result in the formation of a large amount of Ni3Ti phase. Therefore, the saturation limit is reached by solutionizing the NiTi alloy at high temperatures and subsequent quenching. Aging at lower temperatures promotes the precipitation of Ni-rich phases in the matrix [54]. In fact, as reported in [55] where the same material made by the same supplier was tested, it is shown that such heat treatment, typically made at 400–500 °C, generates intermetallic phases within the NiTi matrix, as the lenticular-shaped Ti3Ni4 particles, that affect the Ni concentration of the matrix with a consequent increase of the \({M}_{s}\) temperature. In addition, Ti3Ni4 particles affect the features of the martensitic transformation in supporting the formation of the R phase [56], as observed in the DSC thermograph reported in Fig. 1b.

Ti2Ni is a secondary phase in NiTi alloys that is undesirable but not completely disposable. One of the main challenges in the production of nitinol has always been the minimization of these low-melting point oxides in the microstructure. In fact, several studies have already focused on reducing the content of the Ti2Ni [57] by solution heat treatment. However, even though a reduction was observed, the complete elimination of these oxides is not achievable.

Nanoindentation Experiments

Nanoindentation tests were carried out on a sample, cut from a NiTi lamina 0.5 mm thick, by a nanoindentation platform (NHT, CSM Instruments, Switzerland) with a load capacity of 500 mN, at room temperature. Experiments were carried out using both Berkovich and spherical (radius 20 μm) tips.

Figure 3 shows a schematic depiction of the nanoindentation response of a NiTi alloy, i.e., the force vs penetration depth curve, together with the main parameters used to capture the material evolution in terms of maximum penetration depth (\({h}_{max}\)), recovered and residual depths after unloading (\({h}_{rec}\) and \({h}_{res}\)), and maximum force (\({P}_{max}\)). Figure also shows two additional functional parameters that can be obtained from nanoindentation data, i.e., recovered work (\({W}_{rec}\)), that represents the energy spent in elastic deformation, and dissipated work (\({W}_{dis}\)) that represents the energy spent in inelastic deformation. Please consider that by simply summing these latter parameters, one can obtain the total energy \({W}_{total}\) available during the indentation.

Fig. 3
figure 3

Schematic depiction of the force–penetration response obtained by nanoindentation experiment. Figure also reports the functional parameters of interest

Full size image

Finally, also the elastic modulus \(E\) of the investigated material can be also estimated from the load-penetration response. In particular, according with the Oliver and Pharr’s method [58], if the contact stiffness (\(S\)), i.e., the slope of the initial unloading path, see Fig. 3, is known the so-called reduced Young’s modulus, \({E}_{r}\), can be obtained through Eq. 1:

$${E}_{r}=\frac{S}{2 \beta }\cdot \sqrt{\frac{\pi }{A({h}_{c})}},$$
(1)

where \(A({h}_{c})\) is the projected area at the contact depth \({h}_{c}\) and \(\beta\) is a geometric correction factor equal to 1.00 for the spherical tip and 1.034 for the Berkovich one. It is important to remark that \(S\) has to be estimated by fitting the unloading path of the nanoindentation curve from 98 to 40% of the maximum load, \({P}_{max}\) [52]. Based on this assumption, the elastic modulus of the material \(E\) can be calculated from \({E}_{r}\) as follows:

$$\frac{1}{{E}_{r}}=\frac{\left(1-{\nu }^{2}\right)}{E}+\frac{\left(1-{\nu }_{i}^{2}\right)}{{E}_{i}},$$
(2)

where \(E\), \(\nu\), \({E}_{i}\), and \({v}_{i}\) are the elastic modulus and the Poisson’s coefficient of the material and indenter tip, respectively. Please consider that in this case, \({v}_{i}=0.07, {E}_{i}=1141 \mathrm{GPa}\).

It is important to underline that NiTi alloys are characterized by two different phases, austenite and martensite, which can coexist under the application of mechanical stresses. From a phenomenological point of view, when an austenitic NiTi sample is indented, contact stress drives austenite to transform into stress-induced martensite, as schematically shown in Fig. 4.

Fig. 4
figure 4

Schematic depiction of an austenitic SMA indentation with the highlight of the characteristic zones of the deformed region beneath the indenter, i.e., plastically deformed martensite, elastically deformed martensite, transformation zone, elastically deformed austenite, and stress-free zone

Full size image

As a consequence, the reduced Young’s modulus, reported in Eq. 2, strongly depends on the evolution of the stress-induced martensite beneath the indenter and, therefore, on SMA’s material properties \({E}_{A}\), \({E}_{M}\), \({\sigma }_{s}^{AM}\), \({\sigma }_{f}^{AM}\), \({\sigma }_{s}^{MA}\), \({\sigma }_{f}^{MA}\), \({\nu }_{a}\), \({\nu }_{m}\), \({\varepsilon }_{L}\), as well as the maximum indentation depth \({h}_{max}\) and tip geometry [59]. An understanding of the complex mechanisms involved within the indentation process zone is not an easy task, and numerical analyses are required. Details about numerical investigations are reported in Section “Finite Element Analyses.”

In this work, two different experiments were carried out. The first one consists in loading–unloading depth-controlled indentations for the investigation of the recovered depth ratio, i.e., \({h}_{rec}/{h}_{max}\), the recovered energy ratio, i.e., \({W}_{rec}/{W}_{tot}\), and the evolution of the reduced Young’s modulus, \({E}_{r}\), as a function of the maximum penetration depth, \({h}_{max}\). The \({h}_{max}\) values were properly selected, for both the Berkovich and spherical tips, to avoid in exceeding the maximum load capability of the platform (500 mN) and to avoid big noise on the measured data. For statistical purposes, matrices of 30 indentations were performed with both the Berkovich and the spherical tip. In both cases, 100 μm of distance between the imprints, along the horizontal and vertical directions, was set to avoid the interaction and interference effects among the measurements.

Furthermore, with the aim to analyze the effect of localized cyclic load on the functional parameters, previously identified (\({h}_{rec}/{h}_{max}\), \({W}_{rec}/{W}_{tot}\), and \({E}_{r}\)), “multicycle” nanoindentations, consisting in indenting the same point for multiple times, were carried out. Figure 5 schematically shows the load profile used for the multicycle test that is composed by the following steps:

  1. 1.

    loading: linear increasing of the load up to a maximum value (\({P}_{max}\));

  2. 2.

    holding at \({P}_{max}\): the maximum load is held for a specified time interval, \(\Delta {t}_{max}\) (pause at maximum load);

  3. 3.

    unloading: load is linearly decreased up to a minimum value (\({P}_{min}\));

  4. 4.

    holding at \({P}_{min}\): the minimum load is held for a specified time interval,\(\Delta {t}_{min}\) (pause at minimum load).

Fig. 5
figure 5

Load profile used for the multicycle test. Sample is indented until load reaches a prefixed limit (maximum load). The maximum load is held for a specified time interval (pause at maximum load). Later, load decreases up to a minimum value (minimum load), which is held for a specified time interval (pause at minimum load)

Full size image

When the Berkovich tip was used, the following parameters were set: \({P}_{max}=100 \mathrm{mN}\), \({P}_{min}=2 \mathrm{mN}\), loading and unloading rates 100 mN/min, \(\Delta {t}_{max}=15 \mathrm{s}\), and \(\Delta {t}_{min}=2 \mathrm{s}\). When the spherical tip was used, the following parameters were set: \({P}_{max}=150 \mathrm{mN}\), \({P}_{min}=2 \mathrm{mN}\), loading and unloading rates 100 mN/min, \(\Delta {t}_{max}=20 \mathrm{s}\), \(\Delta {t}_{min}=2 \mathrm{s}\). In this investigation 150 cyclic indentations were carried out.

Furthermore, in order to investigate possible creep mechanisms of the material under nanoindentation, the following tests were carried out:

  • Specimen indented with Berkovich tip up to a maximum load of 100 mN reached in 30 s and held for 15 min; results are presented in Fig. 6a.

  • Specimen indented with the spherical tip up to a maximum load of 150 mN reached in 30 s and held for 30 min; results are presented in Fig. 6b.

Fig. 6
figure 6

a Creep test performed on the NiTi sample with Berkovich tip; b creep test performed on the NiTi sample with spherical tip

Full size image

Figure 6a and b clearly shows that the material does not exhibit any creep effect.

Finite Element Analyses

To deeply investigate the evolution of austenite and martensite during indentation tests, a finite element model (FEM) of the nanoindentation process was built using the commercial code ABAQUS CAE (Dassault Systems, 2020). Thanks to symmetry, a quarter of the geometry was modeled. Temperature effects are not involved in the analysis. The model is composed of two parts:

  1. 1.

    Indenter: 3D discrete rigid part. The Berkovich tip is modeled as an equivalent cone with an apex angle of 70.3°(Fig. 7a); the spherical tip is modeled as a cone with an apex angle of 45° and a tip radius of 20 μm (Fig. 7b). The indenter is discretized in almost 30,000 R3D4 elements; mesh is refined close to the contact zone.

  2. 2.

    Specimen: 3D deformable part. The specimen is modeled as a cube of 2 mm × 2 mm × 2 mm; the sizes of the specimen are two orders of magnitude greater than the indentation-involved zone sizes to avoid edge effects on the simulation results. The specimen is discretized in almost 400,000 C3D4 elements; mesh is refined close to the contact zone.

Fig. 7
figure 7

Finite element model of nanoindentation testing with a Berkovich tip and b Spherical tip. Figure highlights the contact zone of indenter and specimen

Full size image

The Auricchio–Taylor’s model [60, 61] was used to simulate the pseudoelastic behavior of the material and the parameters listed in Table 1 were set. Please consider that these latter are referred to the tensile response. For the compressive behavior of the material, the Auricchio–Taylor’s model only requires the definition of the compression start transformation stress. As no experimental data were available, it was calculated by a tuning process that aimed in minimizing the error between the numerical and experimental force–penetration responses. The obtained value is 560 MPa. Finally, the martensitic hardening was reconstructed according to Fig. 1a. For more details about the pseudoelastic model, see ABAQUS/CAE 2020 User’s Manual, Online Documentation Help, Dassault systems [62].

The contact between parts was defined as a frictionless master (indenter) and slave (specimen) interaction as the effect of friction on numerical results can be considered as negligible [59].

The main outcome of the numerical simulation is the evolution of the martensitic region during the penetration of the indenter into the specimen. Figure 8 reports the schematic evolution of the martensite volume fraction, MVF, under Berkovich and spherical tips. MVF ranges from 0 (totally austenitic zone) to 1 (totally martensitic zone); intermediate values indicate that both austenite and martensite exist, that is, the transformation zone. The radius of the martensitic zone, \({r}_{M}\), is the length along the indenter symmetry axes of the totally martensitic zone (MVF = 1); the radius of the transformation zone, \({r}_{AM}\), is the length along the indenter symmetry axes of the totally martensitic zone (MVF = 1) and the transformation zone (0 < MVF < 1). As a consequence of the high strain gradients, induced by the sharp Berkovich tip, stress-induced martensite is generated at the contact surface, even for very small penetration depths. By contrast, for the spherical tip, the shape of the MVF map changes for small and high penetration depths. In fact, according to the Hertzian contact theory, the maximum stress level is not at the contact surface between the indenter and the sample but a bit below it. Consequently, for small penetration depths, the contact region between the bodies is in austenitic phase (MVF = 0); at high penetration depths the martensite evolves until the contact surface. Figure 8 depicts these differences.

Fig. 8
figure 8

Scheme of the martensitic volume fraction under Berkovich and spherical tips during nanoindentation

Full size image

Results and Discussion

Single Indentation Tests

Figure 9 shows nanoindentation curves obtained using the Berkovich (Fig. 9a) and the spherical (Fig. 9b) tips when a maximum penetration depth, ranging from \({h}_{max}=500\) to \({h}_{max}=3000\) nm, is applied. Due to the limited load capability of the nanoindentation apparatus (500 mN), the maximum penetration \({h}_{max}\) of 3000 nm cannot be reached using the spherical tip. Figure 9 also shows the residual imprint of the tips into the sample.

Fig. 9
figure 9

Nanoindentation curves obtained in depth control mode for different maximum depths with the highlight of the residual imprint: a load–depth profile obtained using Berkovich indenter tip and b load–depth profile obtained using spherical tip

Full size image

The obtained mechanical responses, reported in Fig. 9, are quite dissimilar because of the different deformation field induced by the tips. In fact, due to the sharp geometry of the Berkovich indenter, highly localized deformations, characterized by high magnitude and plastic phenomena, are generated. On the contrary, the strain field induced by the blunt spherical tip involves a wider region and is characterized by lower gradients [63].

This aspect is confirmed by the analysis of the recovered penetration depth \({h}_{rec}\), reported in Fig. 10a. In particular, in the whole \({h}_{max}\) investigated range, \({h}_{rec}\) is higher for the spherical tip than for the Berkovich one. In fact, as a consequence of the high strain gradient induced by the Berkovich tip, the recovery capability is reduced by inelastic phenomena.

Fig. 10
figure 10

Evolution of the main investigated parameters as a function of the maximum penetration depth (\({h}_{max}\)) for both Berkovich and spherical tip: a recovered indentation depth (\({h}_{rec}\)); b recovered depth ratio (\({h}_{rec}/{h}_{max}\)); c recovered energy ratio (\({W}_{rec}/{W}_{tot}\)); and d reduced Young’s modulus (\({E}_{r}\)) obtained from Oliver and Pharr’s method

Full size image

Figure 10b reports the recovered depth ratio, \({h}_{rec}/{h}_{max}\), as a function of maximum penetration depth, \({h}_{max}\), for both Berkovich and spherical tips, showing an almost constant trend in the case of Berkovich indentations. The reason can be found in the geometrical similarity of the different indentations, meaning that the extension of the strain map increases directly with \({h}_{max}\), whereas the magnitude of the strain does not change. The direct consequence is that the recovery capability is independent of \({h}_{max}\). On the other hand, the recovered penetration ratio, \({h}_{rec}/{h}_{max}\), decreases by increasing the maximum penetration depth, \({h}_{max}\). Such trend can be attributed to the non-geometrical similarity of the spherical indentations. Furthermore, according to the Hertzian theory and as depicted in Fig. 8, in the region immediately under the indenter, stress-induced martensite appears when \({h}_{max}\) reaches a certain value resulting in a decrease of the recovery capability.

Figure 10c reports the evolution of the recovered energy ratio, \({W}_{rec}/{W}_{tot}\), as a function of the maximum penetration depth for both spherical and Berkovich tips, showing the same trend observed for the recovered depth ratio, \({h}_{rec}/{h}_{max}\).

Figure 10d reports the reduced Young’s modulus, \({E}_{r}\), obtained using the Oliver and Pharr’s method, showing a decreasing trend with the maximum penetration depth for both tips. This result can be also explained by analyzing the microstructure of the material highlighted in Fig. 2. In particular, when the maximum penetration depth is increased, the dimension of the contact area increases as well, as shown in Fig. 11, and the slips between grain boundaries and precipitates become more significant resulting in the decreasing \({E}_{r}\) trend. It is important to remark that stiffness of materials tends to decrease in the case of high concentration of grain boundaries, due to the presence of intergranular cracks through the grain structure [64, 65]. Moreover, since the deformed zone and therefore the number of grains involved during the indentation directly depends on the maximum penetration depth, different results can be expected varying \({h}_{max}\), i.e., the so-called size effect.

Fig. 11
figure 11

Highlight of the residual imprints of nanoindentations and schematic depiction of the contact area in the examined \({h}_{max}\) range on the etched NiTi surface: a Berkovich tip and b spherical tip

Full size image

Since the process region under the spherical tip is wider than the one under the Berkovich tip, the influence of grain boundaries/precipitates on the material response is more significant for the spherical tip. As a result, increasing \({h}_{max}\), the volume of the process zone increases with the cube of \({h}_{max}\) and, consequently, the slope of \({E}_{r}\) trend is expected to be greater for the spherical tip. Actually, this assumption is observed in Fig. 10d for \(500\le {h}_{max}\le 1500\) nm. Instead, for \(1500\le {h}_{max}\le 2500\) nm, the slope of \({E}_{r}\) trend is lower for the spherical tip than for the Berkovich one. This behavior can be addressed in the evolution of the martensitic zone under the indenter tip, investigated through FEM analysis as reported in Fig. 12. In this latter, the total radius, \({r}_{tot}\), that is the length of the process zone along the indenter symmetry axes, determined via FEA, is \({r}_{tot}=13{ h}_{max}\) for Berkovich indenter tip, whereas is \({r}_{tot}=18{ h}_{max}\) for spherical indenter tip.

Fig. 12
figure 12

FEA evolution of the martensitic zone radius, rM, the transformation zone radius, rAM, and the maps of martensitic volume fraction, MVF, as a function of the penetration depth for a Berkovich tip and b spherical tip

Full size image

Thanks to the geometrical similarity of the Berkovich indentations, both the ratios \({r}_{M}/{r}_{tot}\) and \({r}_{AM}/{r}_{tot}\) remain constant when increasing the maximum penetration depth \({h}_{max}\) (see Fig. 12a). Consequently, the decreasing trend of the reduced Young’s modulus cannot be attributed to the increase of martensitic zone beneath the Berkovich tip, confirming what was previously assessed. By contrast, for the spherical tip, these ratios vary with \({h}_{max}\) (see Fig. 12b). In the range \(500\le {h}_{max}\le 1500\) nm, \({r}_{M}/{r}_{tot}\) remains almost constant, while \({r}_{AM}/{r}_{tot}\) decreases linearly. This implies a small increase in the austenitic region within the process zone that causes a stiffer response of the material mitigating the observed size effect. Instead, in the range \(1500\le {h}_{max}\le 2500\) nm, both \({r}_{M}/{r}_{tot}\) and \({r}_{AM}/{r}_{tot}\) decrease linearly and, in particular, \({r}_{AM}/{r}_{tot}\) decreases slower than for the smaller values of \({h}_{max}\). This implies a reduced volume of martensite, respect to the whole process zone, generating a stiffer behavior of the specimen resulting in a stronger mitigation of the size effect. This latter phenomenon directly affects the reduced Young’s modulus that decreases with increasing \({h}_{max}\) but slower respect to the range \(500\le {h}_{max}\le 1500\) nm, as clearly shown in Fig. 10d.

Furthermore, the reduced Young’s modulus measured with Berkovich indenter tip is higher than the one obtained using the spherical tip (see Fig. 10d). This result can be considered a combination of the size effect and the MVF evolution. In fact, the comparison between Fig. 12a and b shows that both the ratios \({r}_{M}/{r}_{tot}\) and \({r}_{AM}/{r}_{tot}\) are greater for the spherical tip than for the Berkovich one in the whole investigated \({h}_{max}\) range. Consequently, the amount of austenite in the involved zone for Berkovich tip is greater than for spherical tip resulting in a stiffer response of the sample.

Multicycle Indentation Tests

Figure 13 reports the force–penetration curves obtained from a multicycle nanoindentation test using both a Berkovich tip, Fig. 13a, and a spherical tip, Fig. 13b. Results show a marked evolution of the local mechanical response of the NiTi sample that tends to stabilize after around 100 cycles. This behavior was also observed from a macroscopic point of view in “standard” fatigue experiments [26], where ratcheting effects were observed until 100/150 fatigue cycles. The modification of the force–penetration response of the material, observed after multicycle indentations, can be attributed to several microstructural mechanisms that occur beneath the indenter tip, such as the generation of stabilized martensite, detwinning mechanisms, and slips. These latter can be related to the presence of precipitates, i.e., Ni3Ti, Ti2Ni and Ni4Ti3, which alter the resistance of the material to both martensitic transformation and dislocation motion [66, 67].

Fig. 13
figure 13

Load–penetration response obtained from a multicycle nanoindentation test using a a Berkovich tip and b a spherical tip

Full size image

In several works the presence of coherent precipitates in NiTi alloys is found to increase the resistance to functional fatigue as a consequence of the reduction of the dislocation activity [68]. This phenomenon was also analyzed by Gall et al. in [69]. In particular, NiTi alloys with 10-nm Ni4Ti3 precipitates are characterized by the presence of stabilized martensite, as a consequence of mechanical cycling, as well the absence of dislocation activity. In fact, although precipitates with small size prevent the dislocation motion, the martensite interfaces tend to remain pinned at the small precipitates and cause permanent strain accumulation. On the contrary, in samples with large Ni4Ti3 precipitates (500 nm) mechanical cycling caused a more significant dislocation activity as well as stabilized martensite, because materials with larger precipitate sizes do not exhibit permanent pinning of martensite as a dominant mode, but plastic flow represents the main strain accumulation mechanism [69].

These mechanisms cause a gradual evolution of functional parameters, as can be seen in the trend of the maximum penetration depth, \({h}_{max}\), recovered depth ratio, \({h}_{rec}/{h}_{max}\), recovered energy ratio, \({W}_{res}/{W}_{tot}\), and reduced Young’s modulus, \({E}_{r}\), that are reported in Fig. 14 as a function of indentation cycles and for both tips (Table 1).

Fig. 14
figure 14

Cyclic evolution of the investigated functional parameters as a function of the indentation cycles for both Berkovich and spherical tip: a maximum penetration depth (\({h}_{max}\)); b recovered depth ratio (\({h}_{rec}/{h}_{max}\)); c recovered energy ratio (\({W}_{rec}/{W}_{tot}\)); and d reduced Young’s modulus (\({E}_{r}\))

Full size image
Table 1 Material properties
Full size table

From a local point of view, recovered depth ratio, \({h}_{rec}/{h}_{max}\), and recovered energy depth, \({W}_{rec}/{W}_{tot}\), are important functional fatigue parameters because they represent a quantitative measure of the localized cyclic evolution of the pseudoelastic properties of the alloy during loading history. Moreover, a rapid increase of \({h}_{max}\) during the first few indentations can be observed in Fig. 14a for both the indenters, mainly due to the accumulation of stabilized martensite and slip phenomena.

Additionally, Fig. 14b shows that the recovered depth ratio, \({{h}_{rec}/h}_{max}\), tends to stabilize increasing the number of cyclic indentations, close to 100, meaning that the material reaches a pseudoelastic steady state condition. Repeated loadings tend to inhibit the recovery capability of the material resulting in a decreasing trend of \({{h}_{rec}/h}_{max}\). In addition, Fig. 14b shows that more cycles are required to reach a stable response for the spherical tip compared to the Berkovich one. This behavior can be attributed to the bigger process zone involved during the spherical indentation test.

Figure 14c shows the evolution of the recovered energy ratio, i.e., \({W}_{rec}/{W}_{tot}\). An increasing trend with the indentation cycles can be observed for both tips, reaching a stabilized condition after almost 100 cycles, as observed for the other functional parameters.

It is interesting to note that in the first few cycles (see insert A of Fig. 14c) for the Berkovich tip, the evolution of \({W}_{rec}/{W}_{tot}\) is quicker than the spherical tip. In particular, in the first cycle carried out with the Berkovich tip a higher amount of energy is dissipated. This phenomenon is mainly due to the sharpness of the Berkovich tip that implies a higher strain gradient, whereas the energy dissipated during the additional cycles can be attributed to the generation of stabilized martensite and slips that occur beneath the indenter tip during the cyclic test. On the contrary, in the case of spherical indenter, the work spent by inelastic mechanisms during the first cycle is lower than the Berkovich even if \({P}_{max}\) is higher.

Figure 14d reports the evolution of the reduced Young’s modulus obtained for both tips, calculated for each loading–unloading cycle according with the Oliver and Pharr’s theory. Results show that, as well as for the penetration depth data, also the reduced Young’s modulus decreases during the indentation cycles until the stabilization. This latter can be attributed to the accumulation of stabilized martensite and slips. In fact, the increase in the amount of martensite results in a decrease in the material stiffness until stabilization. Figure 14d also shows that the reduced Young’s modulus obtained from the Berkovich indentation is greater than the one obtained for the spherical tip as discussed in Section “Single Indentation Tests.” The percentual difference between \({E}_{r}\) at first cycle and the stabilized value is about 32% for the Berkovich tip and 30% for the spherical one.

Conclusion

The functional evolution mechanisms of NiTi shape memory alloy were analyzed at the nanoscale using nanoindentation. Two types of experiments have been carried out, using both Berkovich and spherical tips: (i) single indentations in depth control mode at different maximum penetration depths and (ii) multicycle indentations for 150 cycles. In particular, functional evolution was analyzed in terms of the recovery capability (recovered depth ratio and recovered energy ratio) and reduced Young’s modulus for both tips. The effect of the microstructural morphology on the evolution of functional parameters was studied, and it was demonstrated that the nanoindentation response is strongly affected by the concentration of grain boundaries and precipitates. Furthermore, the evolution of the martensitic and transformation zone beneath the indenter was also analyzed by numerical simulations. The main findings are summarized as follows:

  • for the single indentations, the material exhibited higher recovery capability when it is indented with the spherical tip than with the Berkovich one. The recovery capability decreases with the increase in the maximum penetration depth, \({h}_{max}\), when the spherical tip is used and remains almost constant for the Berkovich one.

  • for the single indentations, the reduced Young’s modulus, \({E}_{r}\), decreases with the increase in \({h}_{max}\) due to the size effect and the evolution of the stress-induced martensitic region in the process zone, for both tips. In detail, due to the increase in the dimension of the contact area with \({h}_{max}\), the slips between the grain boundaries/precipitates tend to be more significant (size effect), as shown also by micrographic analysis. Moreover, numerical simulations allow to investigate the evolution of the martensitic radius in the process zone for both tips. FEA and micrographs confirm the experimental results. Furthermore, the Berkovich indentations produce a stiffer response of the material than the spherical ones for the same reasons previously addressed.

  • for multicycle indentations, the maximum penetration depth, \({h}_{max}\), increases, and the recovery depth ratio, \({{h}_{rec}/h}_{max}\), decreases with the loading–unloading cycles due to the accumulation of stabilized martensite and slips for both tips. This result is also confirmed from an energetic point of view with the stabilization of the recovered energy ratio, \({W}_{rec}/{W}_{tot}\), after almost 100 cycles. Furthermore, in the first few cycles, the Berkovich-induced strain map produces a greater energy dissipation and a faster evolution of \({W}_{rec}/{W}_{tot}\) respect to the spherical tip.

  • for multicycle indentations, the reduced Young’s modulus, \({E}_{r}\), decreases when the material is subjected to loading–unloading cycles and stabilizes after almost 100 cycles, because of the accumulation of stabilized martensite and slips.

Finally, this work is a first approach to the SMAs nanoscale functional fatigue, which can represent a powerful tool for future fatigue analysis of small size devices, such as biomedical ones. Future development will involve the detailed analysis of the main parameters set in the multicycle tests (i.e., maximum load and loading/unloading rate) and the comparison between the functional responses of different SMA alloys.