Introduction

Nickel–titanium (NiTi)-based shape memory alloys (SMAs) are increasingly used in a large number of medical and industrial applications in last years [1, 2]. This is due to the ever-increasing effort by both scientific and technical communities, whose aim is to better understand their unique functional and mechanical response as well as to develop effective and reliable design methods.

In fact, starting from early successful applications and consolidated market position in the medical field, NiTi alloys have been becoming exceptional candidates in several industrial applications due to the unique combination of functional and structural properties as well as to the good corrosion resistance and chemical stability. Both the pseudoelastic properties and thermal recovery, namely pseudoelasticity (PE) and shape memory effect (SME) [3], are increasingly exploited to develop smart components with active and/or tunable functional responses combined with high load bearing properties. Thanks to their exceptionally high stress and strain recovery capabilities, NiTi alloys are able to exploit very high specific work but they are also subjected to cyclic loading often under severe stress conditions. In such applications, NiTi components are serious candidates for crack generation and propagation phenomena that actually limit the NiTi spread in several emerging applications of automotive, aeronautic, aerospace, oil and gas and robotic sectors [2].

Unfortunately, standard procedures/methods based on solid mechanics theories cannot be directly applied to predict fracture and fatigue properties of SMAs, due to their complex thermomechanical constitutive response associated with phase changes at the crystal scale. In fact, the functional properties of SMAs are due to a reversible diffusionless phase transition, the so-called thermoelastic martensitic transformation (TMT), between two distinct crystal structures, the parent austenite (B2) and the product martensite (B19’) phases. Austenite is a relatively ordered body-centered cubic structure that is stable at high temperatures and low stresses, whereas martensite is a less ordered monoclinic phase stable at low temperatures and high stresses. As a consequence, TMT can be activated either by temperature (TIM, thermal-induced martensite) or mechanical stresses (SIM, stress-induced martensite). Both TIM and SIM play a significant role on crack formation and propagation mechanisms under both static and/or fatigue loadings. Unfortunately, these effects cannot be captured by standard solid mechanics theories and ad-hoc methods must be developed.

Within this context, several studies were carried out in recent years with the aim of analyzing the effects of SIM and TIM on fatigue and fracture properties of SMAs, as discussed in recent review papers [4,5,6,7]. Both low- and high-cycle fatigue properties of NiTi SMAs were analyzed within the framework of modified approaches for common engineering metals [8,9,10,11,12,13,14,15]. Fracture-mechanics-based approaches were also used to analyze fatigue crack growth in SMAs [16,17,18,19]. Some of these works were motivated by special/critical needs for use in biomedical applications, such as the endovascular stents [20,21,22].

These literature works highlighted a marked effect of near-crack-tip transformations on crack formation and propagation mechanisms and special investigation techniques were applied to capture such phase changes. Texture evolutions were analyzed by synchrotron X-ray micro-diffraction (XRD) [23,24,25,26,27]. It was shown that highly localized stresses, arising at the crack-tip region, cause stress-induced martensitic transformations and detwinning of martensite variants at the very crack tip. Dislocation plasticity and retained martensite were also captured after fracture. Localized near-crack-tip martensitic transformations were also observed by infrared thermography (IR) [28, 29] and instrumented nanoindentation [30,31,32]. Furthermore, digital image correlation (DIC) was used to analyze the strain field in the proximity of the crack tip [16, 29, 30, 33,34,35,36,37] and special correlations methods were developed to estimate the effective stress intensity factor (SIF) [30, 34,35,36,37] by a fitting to the William’s solution [38].

To better understand the role of crack-tip transformations on both static and fatigue cracks, ad-hoc FE (Finite Element) models for SMAs were developed [39,40,41,42,43,44,45,46,47,48] and the effects of complex thermo-mechanical coupling were analyzed [47, 48]. In addition, special analytical models were developed [49,50,51,52,53] that are based on modified linear elastic or elastic plastic theories, with the aim of developing effective design methods as well as to define special fracture and fatigue control parameters for SMAs. However, many aspects related to the role of stress-induced martensite and martensite reorientation on fracture and fatigue properties of austenitic and martensitic NiTi are still unknown and deserve deeper systematic studies. In fact, the two alloy types exhibit different fracture and fatigue properties even though crack generates and propagates in detwinned martensite crystal structure in both alloys [23,24,25,26,27].

This work aims to analyze fatigue crack growth in two near-equiatomic NiTi alloys having austenitic and martensitic structure at room temperature, resulting from different transformation temperatures (TTs). Systematic studies involving standard fatigue crack propagation experiments coupled with high-resolution DIC and an ad-hoc analytical model were carried out with the aim of better understanding the underlying physics of crack propagation in the two crystal structures. In particular, mode I crack growth experiments were carried out by using eccentrically loaded single-edge (ESE) crack specimens. Crack propagation and near-crack-tip displacements were captured by in-situ high-resolution DIC, and a special nonlinear fitting procedure, based on the William’s expansion series, was used to estimate the effective stress intensity factor (SIF) range. The SIF range was also computed by linear elastic fracture mechanics (LEFM) as well as by a special analytical method for SMAs [50, 51]. It was shown that this latter method can be successfully used to analyze both fracture properties and fatigue crack propagation of austenitic NiTi SMAs [34, 35]. However, the method is applied for the first time in this study to analyze the effects of nonlinear crack-tip transformation phenomena in martensitic NiTi alloys.

Results revealed a significant difference in the crack growth rate for the two alloys. These differences are attributed to dissimilar dissipative phenomena as well as to different crack-tip stress and strain fields, as also directly observed by DIC strain maps. Finally, it was shown that both DIC and the analytical method are able to predict the different crack propagation curves for both alloys, whereas LEFM is not able to capture such differences.

Materials and Methods

Materials

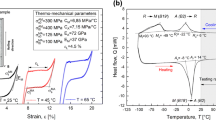
Two near-equiatomic NiTi alloys, namely Type M and Type S, were used in this investigation. The two alloys have different transformation temperatures (TTs), as shown in the DSC thermograms of Fig. 1, resulting from a slightly dissimilar chemical composition and distinct thermo-mechanical processing conditions. Type M has a monoclinic martensitic structure at room temperature (T0 < Mf), whereas Type S has body-centered cubic austenite structure (T0 > Af), as shown in the DSC thermograms of Fig. 1.

Fig. 1
figure 1

Differential scanning calorimetry (DSC) thermograms of the two alloys together with the measured values of the transformation temperatures (TTs)

Full size image

Figure 2 illustrates the isothermal quasi-static strain-controlled stress–strain curves of the two alloys, at room temperature (T0 = 25 °C). The measured values of the main mechanical parameters are also shown in the figure, namely transformation stresses, transformation strain and Young’s moduli.

Fig. 2
figure 2

Isothermal stress–strain response of the two alloys at room temperatures (T0 = 25 °C) together with the measured values of the main mechanical parameters

Full size image

Crack Growth Experiments

Eccentrically loaded single edge crack (ESE) specimens (see Fig. 3) were used for fatigue crack growth experiments. The samples were manufactured from as-received NiTi plates with thickness t = 0.5 mm, by electrodischarge machining (EDM), with the rolling direction parallel to the loading axis. The samples were fatigue precracked starting from the EDM notch (r = 100 μm), up to a length to width ratio (a/W) around 0.20 according to recommendations of the ASTM E647 standard [54].

Fig. 3
figure 3

Eccentrically loaded single edge crack (ESE) specimen and experimental setup

Full size image

Isothermal fatigue crack propagation tests were subsequently carried out at room temperature, at a frequency f = 5 Hz, a load ratio R = Pmin/Pmax = 0.05 and a maximum load Pmax = 100 N. Almost straight crack paths normal to the load direction, initiating from the EDM notch, were always obtained as shown in Fig. 3.

Crack growth was monitored in-situ by a CCD Camera (Sony ICX 625—Prosilica GT 2450) with a resolution of 2448 × 2050 pixels. A suitable objective was adopted to focus the crack-tip region (Rodagon f. 80 mm—Rodenstock), resulting in a resolution of 450 pixels/mm. Digital correlation was carried out by a commercial software (VIC-2D®, Correlated Solutions).

ASTM E647 Method

ASTM E647 standard was used to calculate the mode I stress intensity range (\({\Delta K}_{I}\)) as follows:

$$\Delta K_{I} = \frac{\Delta P}{{B\sqrt W }}F$$
(1)

where \(\Delta P\) (95 N) is the load range, \(W\) and \(B\) are the specimen width and thickness, respectively, whereas \(F\) is a function of the crack-to-width ratio (\(a/W\)):

$$F = \left( \frac{a}{W} \right)^{1/2} \left( {1.4 + \frac{a}{W}} \right)\left( {1 - \frac{a}{W}} \right)^{ - 3/2} G$$
(2)

with \(G\) given by:

$$G = 3.97 - 10.88\left( \frac{a}{W} \right) + 26.25\left( \frac{a}{W} \right)^{2} - 38.9\left( \frac{a}{W} \right)^{3} + 30.15\left( \frac{a}{W} \right)^{4} - 9.27\left( \frac{a}{W} \right)^{5}$$
(3)

However, small-scale transformation conditions must be verified to apply ASTM E647 standard that can be enforced by the following equation:

$$\left( {W - a} \right) \ge \frac{4}{\pi }\left( {\frac{{K_{Imax} }}{{\sigma_{tr}^{s} }}} \right)^{2}$$
(4)

where \(\left(W-a\right)\) is the uncracked ligament and the term at the right end side is a measure of the extent of the crack-tip transformation zone. The equation is obtained from ASTM E647 by substituting the yield strength (\({S}_{Y}\)) with the start transformation stress (\({\sigma }_{tr}^{s}\)). This latter parameter can be regarded either as the stress for A-M transformation in austenitic alloy (\({\sigma }_{AM}^{s}\)) or as the reorientation/detwinning stress in martensitic alloy (\({\sigma }_{det}^{s}\)). Equation (4) is illustrated in the graphs in Fig. 4 for the ESE specimen subjected to a load range \(\Delta P\)=95 N for both austenitic and martensitic structures. The intersection points between the curves represent the limits for predominantly elastic region, that is the maximum values of the SIF defining the small-scale transformation condition. It is found that the ASTM linear elastic model can be accepted for \({K}_{I}\) values lower than about 11 MPa m1/2 and 22 MPa m1/2 for martensitic (Type M) and austenitic (Type S) structure, respectively.

Fig. 4
figure 4

Graphical representation of the small-scale transformation condition for the ESE sample subjected to a load rang ∆P = 95 N for both austenitic and martensitic structures

Full size image

Analytical Method

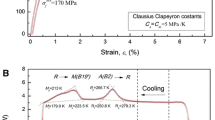
The analytical model by Maletta et al. [51] was used to estimate the stress intensity range \({\Delta K}_{I}\) during fatigue crack growth experiments. The model can be adapted to both austenitic and martensitic crystallographic structure, as they exhibit a similar monotonic stress–strain response as shown in Fig. 5 and Table 1.

Fig. 5
figure 5

Schematic depiction of the monotonic stress–strain curve of a NiTi SMAs and contours of crack-tip stress-induced transformation phenomena: transformation \(\left({r}_{tr}^{s}\right)\), fully transformed \(\left({r}_{tr}^{f}\right)\) and plastic \({(r}_{pl})\)

Full size image
Table 1 Mechanical parameters of the stress–strain curve for the two crystal structures of NiTi
Full size table

A summary description of the model is reported in the following for the sake of completeness and readability. The method is based on a modified Irwin’s correction of the LEFM and considers an increased effective crack length (\({a}_{e}\)) and stress intensity factor (\({K}_{Ie}\)):

$$a_{e} = a + \Delta r$$
(5)
$$K_{eI} = f\left( {a_{e} } \right)$$
(6)

where the function \(f({a}_{e})\) depends on the specific geometry and loading condition and for the ESE specimen is obtained by Eqs. (1–3). The quantity \(\Delta r\) is a function of the extent of the transformation region:

$$\Delta r = r_{tr}^{s} - \frac{1}{2\pi }\left( {\frac{{K_{I} }}{{\sigma_{tr}^{s} }}} \right)^{2}$$
(7)

where \({r}_{tr}^{s}\) represents the maximum extent of the transformation region (see Fig. 5) and can be obtained from the following equation:

$$r_{tr}^{s} = \frac{{2\left( {1 - b} \right)K_{Ie}^{2} }}{{\pi \sigma_{tr}^{s} \left( {\sigma_{tr}^{s} + \sigma_{tr}^{f} } \right)}} + \frac{{2\left( {E_{1} \varepsilon_{L} + \alpha^{ - 1} \sigma_{tr}^{f} - \sigma_{tr}^{s} } \right)r_{tr} + 4\left( {1 - \nu - b\nu } \right)K_{Ie} \sqrt {2r_{tr}^{f} /\pi } }}{{\left( {1 - b} \right)\alpha^{ - 1} + \left( {b + 1} \right)\left( {1 - 2\nu } \right)\left( {\sigma_{tr}^{s} + \sigma_{tr}^{f} } \right)}} + r_{tr}^{f}$$
(8)

\(r_{tr}^{f}\) represents the extent of the fully transformed region (see Fig. 5) and it given by:

$$r_{tr}^{f} = \frac{2}{\pi }\left( {\frac{{\left( {1 - \nu - b\nu } \right)\left( {1 - b} \right)K_{Ie} }}{{\left( {1 - b} \right)E_{1} \varepsilon_{L} + \left( {b + 1} \right)\left( {1 - 2\nu } \right)\sigma_{tr}^{f} + \left( {1 - b} \right)\sigma_{tr}^{s} }}} \right)^{2}$$
(9)

where \(\alpha ={E}_{2}/{E}_{1}\) is the Young’s modulus ratio, ν is the Poisson’s ratio, b = 0 for plane stress and b = 2ν for plane strain. The crack-tip stress distribution along the crack direction (θ = 0) in both untransformed elastic and fully transformed regions (\({\sigma }_{e}(r)\) and \({\sigma }_{t}(r)\)) can be obtained from equilibrium and compatibility conditions:

$$\sigma_{e i} \left( r \right) = g_{i} \frac{{K_{Ie} }}{{\sqrt {2\pi \left( {r - {\Delta }r} \right)} }}$$
(10)
$$\sigma_{t i} \left( r \right) = g_{i} \frac{{2\left( {1 - \nu - b\nu } \right)K_{Ie} /\sqrt {2\pi r} - E_{1} \varepsilon_{L} + \alpha^{ - 1} \sigma_{tr}^{f} - \sigma_{tr}^{s} }}{{\left( {1 - b} \right)\alpha^{ - 1} + \left( {b + 1} \right)\left( {1 - 2\nu } \right)}}$$
(11)

where \({g}_{i}=1\) for i = 1,2 and \({g}_{i}=b\) for i = 3. The effective mode I austenitic SIF in the elastic domain, namely \({K}_{Ie}\), can be directly obtained from stress distribution (Eq. 10) by considering the distance from the effective crack tip (\(\tilde{r }=r-\Delta r\)), according to the Irwin’s assumption:

$$K_{Ie} = \mathop {{\text{lim}}}\limits_{{\tilde{r} \to 0}} \sqrt {2\pi \tilde{r}} \sigma_{e 2} \left( {\tilde{r}} \right)$$
(12)

It is worth noting that the knowledge of the extent of transformation region, in terms of both \({r}_{tr}^{s}\) and \({r}_{tr}^{f}\), is required to calculate \({K}_{Ie}\) by an iterative approach, similarly to the Irwin’s correction for elastic–plastic materials.

DIC Regression Method

The effective stress intensity factor was estimated from a nonlinear regression analysis of the DIC measured displacement field by the William’s expansion series (see Fig. 6). In the following, a summary description of the method is provided for the sake of completeness but full details about the nonlinear regression are given in [34].

Fig. 6
figure 6

Schematic depiction of the workflow to estimate the effective crack length (\({a}_{e}\)) and stress intensity factor (\({K}_{Ie}\)) by the DIC nonlinear correlation method

Full size image

The analytical solution of the near crack-tip displacement field, for an isotropic material under mode I loading, is given by:

$$\left\{ {\varvec{u}} \right\} = \left[ {{\varvec{\uppsi}}} \right]\left\{ {\varvec{U}} \right\}$$
(13)

where \(\left\{{\varvec{u}}\right\}={\{{u}_{x} {u}_{y}\}}^{T}\) is a vector of displacement components along x and y axes; \(\left[{\varvec{\uppsi}}\right]\) is a matrix containing the William’s expansion equations referred to the physical crack-tip position (\({x}_{0}\), \({y}_{0}\)); \(\left\{{\varvec{U}}\right\}={\left\{\begin{array}{ccccc}{K}_{I}& T& A& {B}_{x}& {B}_{y}\end{array}\right\}}^{T}\) is the vector of the unknown parameters, where \({K}_{I}\) is the mode I stress intensity factor, T is the T-stress parameter, A is the rigid body rotation term, \({B}_{x}\) and \({B}_{y}\) are the rigid body motions along x and y axis.

An overdetermined system of linear equations is obtained if Eq. 13 is applied to a set of m DIC measurements points that can be solved by the least square method:

$$\left\{ {\varvec{U}} \right\} = \left( {\left[ {{{\varvec{\uppsi}}}^{\user2{*}} } \right]^{T} \left[ {{{\varvec{\uppsi}}}^{\user2{*}} } \right]^{ - 1} } \right)\left[ {{{\varvec{\uppsi}}}^{\user2{*}} } \right]^{T} \left\{ {\varvec{d}} \right\}$$
(14)

where \(\left\{ {\varvec{d}} \right\}\) is the experimentally measured displacement vector obtained from DIC in the m points and superscript (*) indicates that quantity is applied to the measurement points.

However, the William’s solution is based on LEFM assumptions and therefore this method can be used only in the case of limited crack-tip nonlinearities, that is under the assumption of small-scale transformation [53]. If crack-tip nonlinearities are predominant, an effective crack length \(a_{e}\) must be considered for the best-fit solution. Therefore, the effective crack-tip position \(\left( {x_{e} ,y_{e} } \right)\) has to be included in the vector of unknown parameters \(\left\{ {\varvec{U}} \right\} = \left\{ {\begin{array}{*{20}c} {K_{I} } & T & A & {B_{x} } & {B_{y} } & {x_{e} } & {y_{e} } \\ \end{array} } \right\}^{T}\).

This leads to a new set of nonlinearly coupled equations and, as reported in [34], the estimation of the new unknowns requires a nonlinear fitting process by an iterative procedure based on Newton–Raphson method. To this aim, Eq. (13) can be written as a series of iterative equations based on Taylor’s series expansions as follows:

$$\left\{ {\varvec{d}} \right\} - \left\{ {{\varvec{u}}^{\user2{*}} } \right\}_{i} = \mathop \sum \limits_{n = 1}^{7} \left[ {\frac{{\partial \left\{ {\varvec{u}} \right\}}}{{\partial U_{n} }}\Delta U_{n} } \right]_{i} = \left[ {{{\varvec{\upxi}}}^{\user2{*}} } \right]_{i} \left\{ {\Delta {\varvec{U}}} \right\}_{i}$$
(15)

where the subscript i indicates the i-th iteration step, \({\left[{{\varvec{\upxi}}}^{\boldsymbol{*}}\right]}_{i}\) is the displacement gradient with respect to the unknown terms \(\left\{{\varvec{U}}\right\}\) and \({\left\{\Delta {\varvec{U}}\right\}}_{i}={\left\{\begin{array}{ccccccc}{\Delta K}_{I}& \Delta T& \Delta A& \Delta {B}_{x}& \Delta {B}_{y}& \Delta {x}_{e}& \Delta {y}_{e}\end{array}\right\}}_{i}^{T}\) is the correction to the estimation of the vector \(\left\{{\varvec{U}}\right\}\) at the i-th step. Least squares regression gives the best fit of \({\left\{\Delta {\varvec{U}}\right\}}_{i}\):

$$\left\{ {\Delta {\varvec{U}}} \right\}_{i} = \left( {\left[ {{{\varvec{\upxi}}}^{\user2{*}} } \right]_{i}^{T} \left[ {{{\varvec{\upxi}}}^{\user2{*}} } \right]_{i} } \right)^{ - 1} \left[ {{{\varvec{\upxi}}}^{\user2{*}} } \right]_{i}^{T} \left\{ {\Delta {\varvec{u}}^{\user2{*}} } \right\}_{i}$$
(16)

The solution of the system gives the correction vector of unknowns for prior estimates of the coefficients. The procedure described above is repeated until the corrections \({\left\{\Delta {\varvec{U}}\right\}}_{i}\) become acceptably small. Figure 6 reports the complete workflow for the unknown parameters estimation.

Results and Discussions

Figure 7 reports the evolution of the stress intensity range (\({\Delta K}_{I}\)) as a function of the normalized crack length (\(a/W\)) for the two alloys, as obtained from the DIC regression method, analytical model and ASTM. Good agreement was observed between DIC and analytical results for both alloy types. ASTM method, instead, underestimates the \({\Delta K}_{I},\) and it does not consider any difference between the two materials as it is based on linear elastic assumptions that neglect crack-tip nonlinearities. Negligible differences were observed between the two materials for small crack lengths (\(a/W<0.3\)), where the three methods provide similar results due to small crack-tip nonlinearities and, consequently, linear elastic assumption can be applied. Large differences, instead, were observed at higher crack lengths between Type M and Type S alloys due to distinct crack-tip stress-induced transformations as shown in Fig. 8. This latter reports a comparison of the near-crack-tip von Mises strain contours for two crack length (a/W = 0.35 and 0.46) and for the two materials. It is clearly shown that martensitic alloy exhibits a much larger transformation region (red area in the figures) than the austenitic one and differences further increase with increasing the crack length.

Fig. 7
figure 7

Mode I stress intensity range (\({\Delta K}_{I}\)) as a function of the normalized crack length (\(a/W\)) for martensitic (Type M) and austenitic (Type S) alloys as obtained by the regression method, analytical model and ASTM

Full size image
Fig. 8
figure 8

Near-crack-tip von Mises strain maps obtained from DIC measurements at two crack lengths and for the two alloys: a Type S,\(a/W\)=0.35; b Type S, \(a/W\)=0.46; a Type M, \(a/W\)=0.35; b Type M, \(a/W\)=0.46

Full size image

The larger transformation zone observed in martensitic NiTi is attributed to the lower critical stress for martensite reorientation with respect to austenite. The transformation zone causes an increase of the effective crack length and stress intensity range (\({a}_{e}\) and \({\Delta K}_{Ie}\)), and this effect becomes more evident when increasing the crack length, as shown in Fig. 7.

Figure 9 reports the evolution of the normalized crack length (a/W, Fig. 9a) and the fatigue crack growth rate (da/dN, Fig. 9b) as a function of the number of cycles (N) during fatigue experiments for both alloys, starting from the same initial crack length (a/W ~ 0.2).

Fig. 9
figure 9

Evolution of fatigue crack versus the number of cycles for martensitic (Type M) and austenitic (Type S) alloys: a Normalized crack length (\(a/W\)) and b crack growth rate (\(da/dN\))

Full size image

Figure 9a shows that martensitic alloy exhibits a much longer fatigue life than the austenitic one. This is also confirmed by the graphs in Fig. 9b; that is, Type S alloy always shows higher values of the crack growth rate than Type M.

This is an unexpected result, because Type M alloys experiences larger values of the effective stress intensity range as shown in Fig. 7. This can be attributed to the large cyclic dissipative phenomena occurring in the martensitic structure, due to pseudoplasticity associated with martensite detwinning. In particular, most of the strain energy developed in the loading step (\(\dot{P}>0\)), due to near-crack-tip martensite reorientation, is mainly dissipated and only a small fraction is elastically recovered upon unloading (\(\dot{P}<0\)), as schematically shown in Fig. 10. Conversely, the austenite phase upon unloading (\(\dot{P}<0\)) releases a larger fraction of strain energy accumulated in the loading step (\(\dot{P}>0\)) due to pseudoelastic recovery (see Fig. 10). Furthermore, compressive residual stresses are expected in the near-crack-tip region upon unloading in martensitic NiTi, due to the elastic recovery of the sample against a pseudoplastically deformed crack-tip region. These crack-tip irreversibility and dissipative phenomena are considered as key factors for the reduced fatigue crack growth in Type M alloy.

Fig. 10
figure 10

Schematic of the cyclic crack-tip transformation phenomena in austenitic and martensitic crystal structures

Full size image

Figure 11 shows the crack propagation curves (\(da/dN\) vs \({\Delta K}_{I}\)) as obtained from the three methods for Type S (Fig. 11a) and Type M (Fig. 11b) alloys. Figure 11a shows a satisfactory agreement between the three solutions in Type S alloy for \({\Delta K}_{I}\) values lower than around 20 MPa m1/2, that is under the assumption of small-scale transformation, as schematically shown in Fig. 4. Good agreement between regression data and analytical results is still observed beyond this limit, where ASTM results provide much higher crack propagation rates, resulting in an evident increase in the slope of the propagation curve. This is actually attributed to the underestimation of \({\Delta K}_{I}\) by the ASTM method when increasing the SIF, as also shown in Fig. 7, due to the increased crack-tip transformation zone.

Fig. 11
figure 11

Crack propagation curves \(da/dN\) vs \({\Delta K}_{I}\) obtained by DIC regression method, analytical model and ASTM method: a austenitic alloy (Type S) and b martensitic alloy (Type M)

Full size image

These effects are even more evident in the martensitic (Type M) alloy as shown in Fig. 11b. In fact, ASTM method provides increasingly higher estimates of the propagation rate when increasing the stress intensity range, starting from around 9 MPm1/2 that is close to the small-scale transformation condition of Fig. 4. In particular, an almost sharp variation in the slope of the ASTM propagation curve is observed at this critical value of ∆KI, suggesting a significant change in the fatigue crack propagation mechanisms. It is attributed to a significant increase of the crack-tip transformation zone that causes an increase of the effective SIF that is not taken into account by the ASTM method. In fact, this slope change is not observed in neither regressed nor analytical results that are always in good agreements.

Effective crack propagation data were fitted to the Paris law (\(da/dN=C\bullet\Delta {K}_{I}^{m}\)), as reported in Fig. 12. The reduced crack propagation rates (\(da/dN\)) in Type M alloy are confirmed by the coefficient C that is more than one order of magnitude lower than in Type S alloy (5.3 10–9 vs 1.4 10–7). On the contrary, the exponent m is slightly higher in Type M alloy (3.25 vs 2.53), due to the more rapid increase of the crack-tip transformation zone with increasing \({\Delta K}_{I}\) as also illustrated in Fig. 8.

Fig. 12
figure 12

Comparison between the effective crack propagation curves obtained from DIC of martensitic (Type M) and austenitic (Type S) alloys and fittings to the Paris law equation

Full size image

Figure 12 also reports near-threshold SIF values, namely \(\Delta {K}_{th}^{*}\), that were estimated from the lowest measured values of \(da/dN\) as obtained from DIC. However, it is worth noting that this value does not represent a standard material parameter, as most of the conditions given by the standard ASTM E647 are not satisfied, where K-decreasing methods are recommended to capture lower values of the crack growth rate. In any case, the two materials show similar values of \(\Delta {K}_{th}^{*}\) that are around 4.6 MPa m1/2. This is the expected result because nonlinear effects in the near threshold region become negligible due to the reduced crack-tip transformation zone and, consequently, to predominantly elastic conditions. However, crack growth rate is still much lower in Type M alloy due to the cyclic dissipative phenomena described above.

Conclusions

Fatigue crack growth of SMAs under both austenitic and martensitic conditions was analyzed by testing two near-equiatomic NiTi alloys with different crystal structure at room temperature. The digital image correlation (DIC) method was used to capture local transformation phenomena as well as to estimate the effective stress intensity factor (SIF) by a special nonlinear fitting procedure involving the William’s expansion series. The SIF range was also computed by a special analytical model that takes into account the crack-tip transformation mechanisms in SMAs.

The main outcomes can be summarized as follows:

  • the two crystal structures exhibit a largely different behavior: that is, martensitic alloy exhibits a much lower crack propagation rate than the austenitic one;

  • the different fatigue response is attributed to dissimilar dissipative phenomena in the two alloys as well as to different crack-tip stress and strain fields, as also directly observed by DIC strain maps;

  • the prediction of the special analytical method is in good agreement with effective results obtained by DIC. On the contrary, very large mismatch was observed with the LEFM predictions that is not able to consider crack-tip nonlinearities in SMAs;

  • the analytical model can be actually used to analyze fatigue crack propagation in both martensitic and austenitic NiTi, even though they exhibit a very different behavior due to distinct crack-tip transformation mechanisms;

  • future studies will be aimed at analyzing fatigue crack propagation in martensitic SMAs under complex thermo-mechanical loading conditions, that is to consider the role of both stress-induced and thermally induced transformation mechanisms.