Introduction

Since abnormal deposition of macromolecules in the arterial wall is believed by many to play a significant role in diseases such as coronary artery disease (CAD)—the foremost cause of morbidity in the industralised world, a number of mathematical models has been developed which elucidate our ability in understanding the treatments available. The gold standard medical treatment consists of deploying a drug-eluting stent in the occluded vessel in order to restore luminal blood flow and to resist the tendency of the body to re-occlude the artery by means of local and controlled release of drug from DES. The first DES to gain commercial approval from the Food and Drug Administration (FDA) in the United States was the Cypher stent, which was developed by Cardis Corporation (Miami, FL, USA). The first generation DES exhibited considerable effect on reducing restenosis rates, compared to bare metal stent (BMS) (cf. [1]). A successful DES deployment is defined by its ability to transport the right proportion of an appropriate drug within the correct time frame that will prevent post-operative in-stent restenosis (ISR). The degree of initial stenosis, the presence of thrombus on the stent and even the advent of re-endothelialisation will all contribute to the DES’s ability to transport drug throughout the porous arterial wall.

Keeping this in mind, several studies were carried out in the recent past covering different aspects of the problem by disregarding luminal flow (cf. [2–16]). Due to porosity of the arterial wall, flow within it must consider the influence of the tissue permeability. A number of studies has been carried out by taking into account the interstitial flow within the porous arterial wall (cf. [17–24]).

In view of these, an attempt is made in the present investigation to explore the influence of diffusivity (Peclet number) on the transport of drug within a porous arterial wall eluted from a coronary stent in which the interstitial fluid (plasma) is treated to be Newtonian. The governing equations of motion of unsteady flow phenomena together with the drug transport equation are successfully solved numerically by MAC method primarily introduced by [25] to achieve the desired degree of accuracy. The primary objective of the present investigation is to explore the effect of diffusivity of drug on the drug deposition within the arterial wall quantitatively by using a relatively simple finite-difference scheme. The novelty of the present study lies with the inclusion of DES and unsteadiness of the mass transport within a porous arterial wall which closely resemble the pathological situation.

Governing Equations and Boundary Conditions

The governing equations representing the interstitial flow within a porous arterial wall are Brinkman equations and continuity equation whose dimensionless forms in two-dimensional Cartesian co-ordinate system may be written as

$$\begin{aligned} {\partial u_x \over \partial t} + {\partial u_x^2 \over \partial x} + {\partial (u_xu_y) \over \partial y}= & {} -{\partial p \over \partial x} + {1\over Re} \bigg [{\partial ^2u_x \over \partial x^2} + {\partial ^2u_x \over \partial y^2}\bigg ] - \frac{1}{Re k_p}{u_x}, \end{aligned}$$
(1)
$$\begin{aligned} {\partial u_y \over \partial t} + {\partial (u_xu_y) \over \partial x} + {\partial u_y^2 \over \partial y}= & {} -{\partial p \over \partial y} + {1\over Re} \bigg [{\partial ^2u_y \over \partial x^2} + {\partial ^2u_y \over \partial y^2} \bigg ] - \frac{1}{Re k_p}{u_y}, \end{aligned}$$
(2)
$$\begin{aligned} \mathrm{and} \;\;\;{\partial u_x \over \partial x} + {\partial u_y \over \partial y}= & {} 0, \end{aligned}$$
(3)

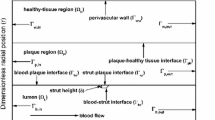
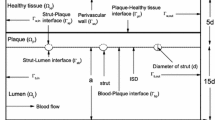
where \(x\) and \(y\) are the dimensionless co-ordinates scaled with respect to \(r_0\), the width of the domain [cf. Fig. 1]. The dimensionless axial and transmural components of velocity \(u_x\) and \(u_y\) are scaled with respect to the transmural filtration velocity \(U_\mathrm{filt}\). The Reynolds number (\(Re\)) and the dimensionless pressure (\(p\)) may be defined as

Fig. 1
figure 1

Schematic of computational model used for the study

Full size image
$$\begin{aligned} Re={{r_o U_\mathrm{filt}\rho } \over \mu },\quad p={p^{\prime } \over {\rho U_\mathrm{filt}^2}}, \end{aligned}$$

in which \(\rho \) is the density of the interstitial fluid, \(\mu \), the viscosity and \(p^{\prime }\), the pressure. Here, \(k_p=\frac{k}{r_0^2}\); \(k\) being the Darcy permeability.

The convection–diffusion equation representing the transport of drug within the arterial wall can be written in dimensionless form as

$$\begin{aligned} {\partial c_t \over \partial t} + u_x{\partial c_t \over \partial x} + u_y{\partial c_t \over \partial y} = {1\over Pe} \bigg [{\partial ^2c_t \over \partial x^2}+ {\partial ^2c_t \over \partial y^2} \bigg ], \end{aligned}$$
(4)

in which the Peclet number \(Pe= \frac{r_0 U_\mathrm{filt}}{D_t}\); \(D_t\), the coefficient of diffusion. Here time and drug concentration are scaled as follows:

$$\begin{aligned} t\rightarrow {t U_\mathrm{filt} \over r_o},\quad {c_t\rightarrow {c_t\over {c_s}}}, \end{aligned}$$

where \(c_s\) is the reference concentration at the strut.

The computational domain consists of a long section of length \(L\) idealised as a rectangle and the arterial wall thickness is taken to be 10 times the strut width. As the drug at the lumen-tissue interface (\(\Gamma _{bt}\)) becomes exposed to flowing blood, it is assumed that blood is extremely efficient at washing out mural-adhered drug, modelled as a zero concentration condition by (cf. [26])

$$\begin{aligned} u_y= & {} 1, u_x=0\hbox { and }\; c_t=0 \quad \mathrm{{for}}\quad x \in \Gamma _{bt}, \quad y=0;\\ u_y= & {} 0 = u_x, c_t=1 \quad \mathrm{{for}}\quad x \in \Gamma _{bs}, \quad y=0. \end{aligned}$$

At the perivascular wall (\(\Gamma _{tp}\)), zero variations in normal direction for the drug concentration and velocities are assumed [cf. [27]] which may be mathematically written as

$$\begin{aligned} {\partial u_x \over \partial y}=0={\partial u_y \over \partial y},\;\; {\partial c_t \over \partial y}=0\hbox { at }y=1. \end{aligned}$$

Moreover, along the proximal (\(\Gamma _{ti}\)) and distal \((\Gamma _{to})\) boundaries \(\Gamma _{to} \) [cf. [21]], the conditions are as follows:

$$\begin{aligned} u_x=0, {\partial u_y \over \partial x}=0, {\partial c_t \over \partial x} =0 \;\; \mathrm{on}\;\;\Gamma _{ti}\hbox { and }{\partial u_x \over \partial x}=0={\partial u_y \over \partial x},\;\; {\partial c_t \over \partial x}=0 \;\; \mathrm{on}\;\;\Gamma _{to}. \end{aligned}$$

Method of Solutions

The above governing equations along with the boundary conditions are solved numerically by finite-difference method. Control volume-based finite-difference discretisation of those equations is carried out in staggered grids, usually known as Marker and Cell (MAC) proposed initially by [25]. In this type of grid alignment, the interstitial velocities, the pressure and the drug concentration are calculated at different locations of the control volume, as indicated in Fig. 2. The discretisation of the time derivative terms are based on the first order accurate two-level forward time differencing formula while those for the convective terms in the momentum equations are accorded with a hybrid formula consisting of central differencing and second order unwinding. The diffusive terms, however, are discretised by second order accurate three-point central difference formula.

Fig. 2
figure 2

A typical MAC cell

Full size image

The equation for pressure is derived from the discretised momentum and continuity equations which is solved iteratively by Successive-over-Relaxation (S.O.R.) method with the chosen value of over-relaxation parameter as 1.2, in order to get the intermediate pressure-field using the interstitial velocity field. Subsequently, the maximum cell divergence of the velocity field is calculated and checked for its tolerance. If the tolerance limit is not satisfied, then the pressure at each cell of the domain is corrected and the interstitial velocities at each cell are adjusted accordingly by repeating the process. Thus, in the finite-difference formula, we assume \(x_i=i\delta x, y_j=j\delta y, t_n=n \delta t\) in which \(n\) refers to the time direction, \(\delta t\), the time increment. Here, \(\delta x\) and \(\delta y\) denote the space step sizes along the axial and transmural directions respectively. The computational code based on the following algorithm has been successfully programmed using FORTRAN language.

The MAC method consists of the following two stages:

Stage 1:

  1. (i)

    \({u_x}^{n}_{i+\frac{1}{2},j}, {u_y}^{n}_{i,j+\frac{1}{2}}\) and \(c^{n}_{t_{i,j}}\) are initialised at each cell \((i,j)\). This is done either from result of the previous cycle or from the prescribed initial conditions.

  2. (ii)

    Time step \(\delta t\) calculated from stability criteria.

  3. (iii)

    The equation for pressure is solved to get the intermediate pressure-field \(p^{*}_{i,j}\) using interstitial velocities \({u_x}^{n}_{i+\frac{1}{2},j}, {u_y}^{n}_{i,j+\frac{1}{2}}\) of the \( {n}^\mathrm{{th}}\) time step.

  4. (iv)

    The momentum equations representing interstitial flow are solved to get intermediate velocities \({u_x}^{*}_{i+\frac{1}{2},j}, {u_y}^{*}_{i,j+\frac{1}{2}}\) in an explicit manner using the previously known velocities and pressure.

Stage 2:

  1. (v)

    The maximum cell divergence of the velocity-field is calculated and checked for its tolerance. If the tolerance limit is satisfied, then the drug transport equation is solved to get drug concentration \(c^{n+1}_{t_{i,j}}\) within the arterial tissue in an explicit manner and steady-state convergence is checked for whether to stop calculation. If the maximum divergence of the velocity-field is found to be greater than the tolerance limit at any cell in absolute sense, go to step (vi).

  2. (vi)

    The pressure at each cell of the domain is corrected and subsequently the velocities at each cell are adjusted to get \({u_x}^{n+1}_{i+\frac{1}{2},j}\) and \({u_y}^{n+1}_{i,j+\frac{1}{2}}\). Then step (v) is again performed. This completes the necessary calculations for advancing flow-field through one cycle in time. The process is to be repeated until steady-state convergence is achieved.

Numerical Stability: Time-stepping Procedure

Amsden and Harlow [28] suggested that the number of calculation cycles and hence the running time could be reduced by the use of an adaptive time stepping routine which, at a given cycle, would automatically choose the time step most appropriate to the velocity-field at that cycle. Welch et al. [29] discussed the stability and accuracy requirements for the MAC method. They suggested stability restriction involving the Reynolds number:

$$\begin{aligned} \delta t_1 \le Min \Bigg [{Re \over 2}{{\delta x^2 \delta y^2} \over {\delta x^2 + \delta y^2}} \Bigg ]_{i,j}. \end{aligned}$$

This stability condition is related to viscous effect [cf. [30]] which can be applied directly to select an appropriate time step.

A more appropriate treatment used by [31], among others, is to require that no particles should cross more than one cell boundary in a given time interval, that is,

$$\begin{aligned} \delta t_2 \le Min \Bigg [{{\delta x \over |u_x| } , {\delta y \over |u_y|}} \Bigg ]_{i,j}. \end{aligned}$$

The time step to be used at a given point in the calculation will be

$$\begin{aligned} \delta t = a\; Min \Big [{\delta t_1, \delta t_2}\Big ], \end{aligned}$$

where \(0 < a \le 1\); the reason for this extra added factor \(a\) led to a considerable computational savings.

Results and Discussion

For the purpose of numerical computation of the desired quantities of major physiological significance, the computational domain has been confined with a finite nondimensional length of 1.7 in which the onset and offset lengths have been selected to be 8 times the width of the strut. For this computational domain, solutions are computed through the generation of staggered grids with a size of \(86 \times 51\).

Figure 3a, b display respectively the axial and the transmural velocity contours of the interstitial fluid streaming through the porous arterial wall for \(Re\) = 0.00005 and \(Pe=15.\) The velocity contour, as appeared in Fig. 3a, has some interesting features to note that when the interstitial fluid crosses the middle of the strut, the corresponding axial velocity becomes negative and the asymmetry of the contour about the middle of the strut is observed. One may also observe that within the domain under study, there should be a separatrix (a boundary separating two distinct signs of axial velocity) along which the axial velocity vanishes. Furthermore, one may observe that the transmural velocity contour (cf. Fig. 3b), reflecting the asymmetry about the middle of the strut, is maximum along the lumen-tissue interface (non-strut region) and diminishes gradually as one moves away from it. However, a reverse trend is observed in the region where the strut is well apposed with the arterial tissue. This observation may be justified in the sense that in the lumen-tissue interface, filtration of blood plasma from the lumen takes place whereas the transmural velocity vanishes owing to the so-slip conditons in the strut-tissue interface.

Fig. 3
figure 3

a Axial velocity contour for Re = 0.00005 and Pe = 15. b Transmural velocity contour for Re = 0.00005 and Pe = 15

Full size image

Figure 4a exhibits the profile for drug concentration through the depth of the arterial wall at \(Re=0.00005\) and \(Pe=15.\) It is to be noted from the results of this figure that the drug concentration vanishes at the non-strut region owing to the clearing out of mural-adhered drug by the blood stream and then increases up to some upper bound as one moves away from the interface, and then finally decays steadily. However, the concentration is all time higher (\(x=0.85\)) throughout the depth of the arterial wall just beneath the strut. This observation is in good agreement with those of [32]. Figure 4b shows the results of concentration profiles for different \(Pe.\) Simulations for six values of \(Pe\) in a compatible range are carried out to show the trend of the solution. One may observe that the drug concentration reduces with increasing \(Pe\) as the convection velocity sweeps the drug away from the wall, where it is dispersed. At the intermediate instances, the profiles may appear bulged and therefore a more uniform concentration is guaranteed [cf. Fig. 4c].

Fig. 4
figure 4

a Transmural concentration profile for different axial positions at Re = 0.00005 and Pe = 15. b Transmural concentration profile at the middle of the strut for different Pe at Re = 0.00005. c Transmural concentration profile for different times at Re = 0.00005 and Pe = 15 (non-dimensional time one = 4.79  h)

Full size image

The unsteady nature of the concentration profile of drug for three distinct times (\(t=0.1,0.5,1\)) is portrayed in Fig. 5a. The concentration of drug increases with increasing time and the rate of increase is maximum for smaller times, and thereafter attains a steady state (cf. Figs. 4c, 6). Moreover, it is clear that peaks of the concentration are attained immediately beneath the contact surface of the strut which has further been established in Fig. 5b, c. Axial dependence of drug concentration within the arterial tissue for different \(Pe\) is plotted in Fig. 5b. The results of this figure reveal that the drug concentration reduces with increasing \(Pe\), as anticipated. All the above observations are in conformity to those of [33]. Figure 6 exhibits the evolution of drug concentration at the upstream of the stent corresponding to \(Re = 0.00005\) for different \(Pe\). Comparing the results of this figure, one may conclude that the mass balance reached the quasi-steady state faster for large \(Pe\).

Fig. 5
figure 5

a Axial variation of the drug concentration for different times (Re = 0.00005, Pe = 15). b Variation of the drug concentration at y = 0.11 for Re = 0.00005. c Contour plot of drug distribution within the porous arterial wall for Re = 0.00005 and Pe = 15

Full size image
Fig. 6
figure 6

Temporal distribution of dimensionless drug concentration in the tissue for different Pe at Re = 0.00005

Full size image

Conclusion

In this study, a two-dimensional model of interstitial flow and drug transport within a porous arterial tissue is proposed. The interstitial fluid is taken to be Newtonian and the transport of drug is considered to be governed by unsteady convection–diffusion equation. The analysis shows that the concentration of drug within the arterial tissue is maximum just beneath the stent strut which decreases with increasing Pe. One may also observe the asymmetry of the distribution of drug about the middle of the strut.

With the rapid ascent of stent-based drug elution in the treatment of vascular disease, many important issues concerning drug distribution and drug targeting need to be addressed. The application of drug transport through porous media in biological tissues is an ever-expanding field of research. Although advancing rapidly, there are many challenges in modelling of the transport of drug eluted from DES. The multi-layer model of the arterial wall describes the arterial anatomy most accurately. Some aspects of transport through porous arterial wall have not been properly addressed and more fundamental research is warranted. For instance, more accurate measurement of diffusivity for different layers and for different compositions of plaque, porosity, permeability and tortuosity may be taken into account in future investigations of the problem.