1 Introduction

Asperity degradation and grinding during rock joint shearing process play an essential role in the mechanical and hydraulic behaviour of the rock joints. Numerous laboratory experiments were conducted by various researchers (Pereira and de Freitas 1993; Seidel and Haberfield 1995, 2002; Lee et al. 2001; Hossaini et al. 2014) to describe the asperity sliding and damage caused by overriding of asperities and overstressing upon shearing. However, a number of outstanding issues of importance relating to rock joint fracturing still remain (Barton 2013), such as asperity degradation and breakage—induced gouge production and grinding (Jing and Stephansson 2007). The asperity degradation and associated gouge production and grinding may affect the shape of a joint surface and the subsequent response of the rock joints. Thus, improved understanding of the asperity degradation and gouge grinding is essential to characterize the mechanical and hydraulic behaviour of the rock joints, which have important applications in a variety of fields including rock slope engineering, mining, tunnelling, petroleum engineering and earth sciences.

Asperity degradation has been studied by directly assessing the surface morphology of a rough rock joint before and after shearing. Assuming the asperities on the rock joint surface had identical shape and same inclination angle, Patton (1966) developed the first theoretical model to predict the shear strength of rough rock joints. Although it took into account the effect of roughness of rock joint on its shear strength by a two-dimensional simplification, Patton’s model ignored the scale effect, interlocking effect between the asperities, and roughness evolution during the shearing and damage process of the rock joint. Ladanyi and Archambault (1969) proposed a non-linear theoretical model to predict the shear strength of rough rock joints, which provides better non-linear normal stress - shear stress curves than Patton’s model. However, the application of the non-linear model required more parameters and some special tests, and some parameters couldn’t well describe the irreversible effect of the roughness on the rock joint shear strength. Barton and Choubey (1977) proposed the well-known shear strength criterion for rough rock joints with the roughness explicitly denoted using the joint roughness coefficient (JRC). Plesha (1987) took into account roughness degradation and developed a two-dimensional theoretical model for rough rock joints on the basis of the theory of plasticity and the assumption of uniform tooth-shaped asperities. Amadei and Saeb (1990) developed a two-dimensional nonlinear elastic constitutive model for rough rock joints, which considered the different normal deformability of rock joints with mated and unmated initial positions and the effect of the deformability on the failure behaviour. Souley et al. (1995) extended the Amadei-Saeb model to include the shear behaviour of rough rock joints under cyclic loading. Haberfield and Johnston (1994) developed a mechanically-based model for rough rock joints capable of capturing the basic mechanisms of movement and making reasonably accurate predictions of shear displacement behaviour. Maksimovic (1996) proposed a non-linear joint failure model of hyperbolic type with three parameters: the basic angle of friction, the roughness angle and the median angle pressure. More recently, many joint constitutive models have been developed for the physical–mechanical behaviour of rock joints (Indraratna and Haque 2000; Olsson and Barton 2001; Seidel and Haberfield 2002; Serrano et al. 2014; Indraratna et al. 2015; Hencher and Richards 2015; Shrivastava and Rao 2015). However, these constitutive models have difficulty in implementing the real geometry of rock joints and the input parameters of these models are predefined by the user, which hampers the predictive capability of these models (Bahaaddini et al. 2015). Moreover, they are unable to trace the process of asperity shearing and degradation, and gouge formation and grinding, and the crack propagation inside the intact materials of the joint surfaces.

With the development of computational geomechanics, numerical method based on continuous and discontinuous mechanics has been become a promising approach to study the shear behaviour of rock joints. Son et al. (2004) conducted elasto-plastic simulation of a direct shear test on rough rock joints using a finite element method (FEM) with a joint finite element of 6-node and zero thickness. Their results reproduced salient phenomena commonly observed in actual shear test of rock joints, including the shear strength hardening, softening and dilation. Roosta et al. (2006) developed a visco-plastic multilaminate model to model the shear stress-shear displacement and normal displacement—shear displace of artificial joint specimen at constant normal load conditions. Liu et al. (2009) implemented the rock failure process analysis (RFPA) model (Tang 1997) into the finite element software package ABAQUS using its user subroutine UMAT interface to simulate the shearing process of a three-dimensional (3D) rough rock joints on the basis of the interface modelling technique and found that a curved failure surface developed from the loading asperity and approximately intersected the trailing face of the asperity. Lin et al. (2012) used a continuum approach to simulate direct shear tests on flat and wave-like rock joints. A new methodology is proposed by Nguyen et al. (2014) to combine shear box testing and corresponding continuous mechanics—based numerical simulations with the natural joint roughness at the micro-scale taken into account. However, most numerical simulations of the shearing process of rough rock joints are conducted using discontinuous methods, especially the commercial discrete element method (DEM)—Particle Flow Code (PFC) developed by Itasca Consulting Group Inc. Cundall (1999) implemented a bounded particle model into PFC2D to model the nonlinear relation between peak shear strength and normal stress, and the dependence of the peak dilation angle on the normal stress in shearing rock joints and rough faults. Indraratna and Haque (2000) used PFC2D to simulate the shear behaviour of artificial regular rock joints. Guo and Morgan (2008) simulated the breakdown of fault blocks using PFC2D to study the frictional strength, mechanical behaviour and stress and strain rate of evolving fault gouge and their dependence on normal stress and uniaxial compressive strength. Park and Song (2009, 2013) carried out an extensive series of simulations for direct shear tests of rock joints using PFC3D to demonstrate the feasibility of reproducing a rock joint using the bonded particle model and examine the effect of the geometrical features and the micro-properties of a joint on its shear behaviour. Shrivastava et al. (2011) used PFC2D to simulate direct shear tests on rock joints with asperity inclinations of 15° and 30° at different normal stresses. Zhao (2013) implemented PFC2D to simulate single and multi-gouge particles in a rough fracture segment undergoing shear. Huang et al. (2014) simulated the dynamic direct-shear tests on the rough rock joints with 3D both sinusoidal and random surface morphologies using the discrete element method. Bahaaddini et al. (2015) studied the shear behaviour of rock joints in a direct shear test using the particle flow code PFC2D taken into account the micro-scale properties of the smooth joint model.

As can be seen from the review on numerical modelling of rock joint shear process above, the continuous method usually model the joint shear process using either joint elements or contact surfaces with complicated constitutive models, which are developed on the basis of theoretical analysis or experimental observation of the relationship between shear stress and shear displacement when the rock joint is subjected to shear load. Thus, the continuous method has not modelled explicitly the asperity degradation and gouge grinding during the rock joint shear process. Through the bounded particle model, the discontinuous method has successfully modelled the fracture of asperity and the formation of circular or sphere gouge. However, the discontinuous method has the limitation of modelling the asperity degradation before its fracture, the transition from continuum to discontinuum through asperity degradation and fracture, the formation of irregular-shaped gouge, and the further fragmentation of the irregular-shaped gouge through the gouge grinding. This study implements a hybrid continuous-discontinuous method, i.e., a recently developed hybrid finite-discrete element method (Liu et al. 2015a), to model the asperity degradation and gouge grinding during the shearing process of rough rock joints. Compared with FEM, the hybrid method is more robust and efficient after the asperity degradation, especially tracing the gouge formation, movement and grinding. Compared with DEM, the hybrid method is more versatile in modelling asperity degradation before fracture, crack initiation and propagation during fracture, and irregular-shaped gouge grinding. This study extends an initial study on direct shearing of rock joints conducted by the authors and presented in a conference (Liu et al. 2015b). In the following sections, the hybrid finite-discrete element method is firstly introduced. Then the rock failure processes in the basic rock mechanics tests, i.e., the uniaxial compressive strength test and the Brazilian tensile strength test, are modelled using the hybrid method and the modelled results are compared with those well documented in literatures to calibrate the hybrid method. After that, the asperity degradation and gouge grinding in the direct shear tests of a rough rock joint are studied using the hybrid finite-discrete method. Finally, the hybrid method is used to investigate the effect of various shearing rates and roughness on the asperity degradation and gouge grinding during the shearing processes of rock joints.

2 Hybrid finite-discrete element method for modelling direct shearing of rock joints

A hybrid finite-discrete element method has been developed by the authors (Liu et al. 2015a) using C++ and OpenGL on the basis of our 2D (Liu et al. 2004) and 3D (Liu 2010) enriched finite element codes for modelling progressive failure processes of geomaterials and the 2D and 3D open-source finite-discrete element libraries originally developed by Munjiza (2004) and Xiang et al. (2009), respectively. The hybrid finite-discrete element method considers a problem to be modelled consists of a single discrete body or a number of interactive discrete bodies such as that shown in Fig. 1a. The interaction of the discrete bodies is governed by the so-called contact law: a stiffness (i.e., spring) in the normal direction and a stiffness and friction angle (i.e., spring-slip) in the tangential directions, as shown in Fig. 1a. The interaction forces developed at contact points are determined using linear functions of the deformations of the spring and/or spring-slip surfaces and resolved into normal and tangential components. Each individual discrete body is of a general shape and size and is modelled by a single discrete element. Each discrete element is then discretised into finite elements to analyse its deformability, as shown in Fig. 1b. An explicit and large strain Lagrangian formulation for the 10-node tetrahedral elements in 3D or constant strain elements in 2D is used to represent the element deformations. The displacement field of the 10-node tetrahedral elements varies nonlinearly and the faces of the elements become curved while the displacement field the constant strain elements varies linearly and the edges of the elements remain planar. The 10-node tetrahedral elements are used in 3D, which results in curved boundary surfaces, complicates the contact-detection algorithms and in turn increases computation times. Based on Gauss’ theorem to convert volume integrals into surface integrals in 3D or area integrals into line integrals in 2D, the increments of element strain can be obtained for each time step. The stress increments can then be obtained by invoking the constitutive equations of the modelled materials.

Fig. 1
figure 1

Calculation cycles in the hybrid finite-discrete element method. a Interactive discrete bodies through contacts in hybrid finite-discrete element model, b Finite element discretisation of discrete bodies and their deformabilities, c Fracture and fragmentation of discrete bodies, d Motion of discrete element after fracturing

Full size image

In the hybrid finite-discrete element method, the discrete elements may fracture and fragment depending on the calculated stress and strain of the discretised finite elements in the discrete elements. The fracture and fragmentation of the discrete elements result in the transition from continuum to discontinuum, which is the key component of the hybrid finite-discrete element method and makes the hybrid method different from the FEM originally developed for continua, such as ABAQUS, ANSYS, PHASE and PLAXIS, and the DEM originally developed for discontinua, such as PFC, UDEC and 3DEC. As shown in Fig. 1c), the finite elements are bonded together before fracturing and the cracks are assumed to coincide with the element surfaces during fracturing. Separation of these surfaces induces a bonding stress, which is taken to be a function of the size of separation. At any point on the surfaces of a crack, the separation δ can be divided into two components in Eq. (1)

$$\delta = \delta_{n} \varvec{n} + \delta_{s} \varvec{t}$$
(1)

where, n and t are the unit vectors in the normal and tangential directions, respectively, of the surface at such a point, δ n and δ s are the magnitudes of the components of δ. Accordingly, the traction vector p during fracture and fragmentation can be divided into two components in Eq. (2)

$$p = \sigma_{n} \varvec{n} + \tau \varvec{t}$$
(2)

where, \(\sigma_{n}\) and \(\tau\) are the normal and tangential stresses. In the limit no separation of adjacent edges takes place, i.e., \(\delta_{n} = \delta_{tp} = 0\) (tensile) or \(\delta_{s} = \delta_{sp} = 0\) (shear) as shown in Fig. 1c), the bonding stress is equal to the peak stress \(\sigma_{n} = f_{tp}\) (tensile) or \(\tau = f_{sp}\) (shear). With increasing separation \(0 < \delta_{n} \le \delta_{tp}\) (tensile) or \(0 < \delta_{s} \le \delta_{sp}\). (shear), the bonding stress decreases and the decreased bonding stress is a function of peak strength and separation (Munjiza 2004), which can be described using Eqs. (3) and (4)

$$\sigma_{n} = \left[ {2\frac{{\delta_{n} }}{{\delta_{tp} }} - \left( {\frac{{\delta_{n} }}{{\delta_{tp} }}} \right)^{2} } \right]f_{tp}$$
(3)
$$\tau = 2\frac{{\delta_{s} }}{{\delta_{sp} }}f_{sp}$$
(4)

With continuously increasing separation \(\delta_{tp} < \delta_{n} < \delta_{tu}\) (tensile) or \(\delta_{sp} < \delta_{s} < \delta_{su}\) (shear), the bonding stress decreases and the decreased bonding stress is a function of damage index D a peak strength \(f_{p}\). described using Eqs. (5) and (6)

$$\sigma = g\left( D \right)f_{tp}$$
(5)
$$\tau = h\left( D \right)f_{sp} ,$$
(6)

where, \(\sigma\) and \(\tau\) are the bonding stress, \(D\) is the damage index, \(f_{tp}\) and \(f_{sp}\) is the peak tensile and shear strength, respectively, and \(g\left( D \right)\) and \(h\left( D \right)\) are the damage function. At separation, \(\delta_{n} \ge \delta_{tu}\) (tensile) or \(\delta_{s} \ge \delta_{su}\) (shear), the bonding stress becomes zero and the crack is assumed to propagate. However, in the case of shear, a friction stress will develop if the fracture surface is rough, as shown in Fig. 1c.

After fracture and fragmentation, an explicit central difference scheme is applied in the hybrid finite-discrete element method to integrate the equations of motion of either the initially discrete elements or the discrete elements formed by the fracture and fragmentation algorithm. The unknown variables, i.e., contact forces on the discrete ements’ boundary or stresses in the internal elements are determined locally at each time step from the known variables on the boundaries and in the elements and their immediateeighbours, as shown in Fig. 1d.

In sum, the hybrid finite-discrete element method involves in the following algorithms: (1) the numerical model is assumed to consist of an assemblage of discrete deformable bodies and the interaction between discrete deformable bodies is solved using the contact law. (2) The rigid body movement of the discrete deformable bodies is solved to produce the inertial and interaction forces for each of the discrete bodies and gross rigid body translational and rotational displacement of the discrete body as a whole. (3) The inertial and interaction forces are applied on each of the discrete deformable bodies to determine its deformation, displacement and strain and stress fields according to the finite element method. (4) If the calculated deformation and stress fields satisfy the failure criteria, fracture and fragmentation occur and the discrete deformable body is fragmented into two or more discrete deformable bodies through fracture and fragmentation algorithms. (5) The calculated deformation fields are supposed over the gross rigid body motion displacements to calculate new positions of each of discrete deformable body. Thus, the hybrid finite-discrete element method uses the continuous method, i.e., FEM, to model continuum-based phenomena and the discontinuous method, i.e., DEM, to model discontinuum-based phenomena. Compared with FEM, the hybrid finite-discrete element method is more robust in modelling rock failure, especially fracture, fragmentation, and fragment movements resulting in tertiary fractures. Compared with DEM, the hybrid finite-discrete element method is more versatile in dealing with irregular-shaped, deformable and breakable particles. Please refer to our recent paper (Liu et al. 2015a) for the detail coding and implementation of the hybrid finite-discrete element method in computers.

Moreover, in order to consider the effect of loading rate on the deformation and fracture behaviour of rock during dynamic shearing of rough rock joints, Eq. (7) initially proposed by Zhao (2000) is implemented into the hybrid finite-discrete element method

$$\sigma_{cd} = A{ \log }\left( {\frac{{\dot{\sigma }_{cd} }}{{\dot{\sigma }_{c} }}} \right) + \sigma_{c}$$
(7)

where, \(\sigma_{cd}\) is the dynamic uniaxial compressive strength (MPa), \(\dot{\sigma }_{cd}\) is the dynamic loading rate (MPa/s), \(\dot{\sigma }_{c}\) is the quasi-static loading rate (approximately \(5 \times 10^{ - 2}\) MPa/s), \(\sigma_{c}\) is the uniaxial compressive strength at the quasi-static loading rate (MPa) and \(A\) is a material parameter, which is 11.9 for the Bukit Timah granite (Zhao 2000).

3 Calibration of the hybrid finite-discrete element method by modelling UCS and BTS

In this section, the failure processes in the uniaxial compressive strength (UCS) test and Brazilian tensile strength (BTS) test, which are usually conducted in rock mechanics laboratory, are modelled using the hybrid finite-discrete element method. The modelled results are compared with those documented in literatures to calibrate the hybrid finite-discrete element method. Figure 2 depicts the numerical models constructed for the UCS and BTS tests following the standards of International Society of Rockechanics (ISRM 1978, 1979). The material properties of the rock specimens are Young’s modulus \(E = 60\,{\text{GPa}}\), Poisson’s ratio \(v = 0.25\), density \(\rho = 2600\,{\text{kg}}/{\text{m}}^{3}\), tensile sength \(\sigma_{t} = 20\,{\text{MPa}}\), compressive strength \(\sigma_{c} = 200\,{\text{MPa}}\), internal friction angle \(\emptyset = 30^{^\circ }\), surface friction coefficient \(\mu = 0.2\), and fracture energy \(G_{f} = 50\,{\text{N}}/{\text{m}}\). The material properties of the loading plates follow those of standard steel. The penalty terms of the rock specimen and loading plates are assumed to be equal to elastic modulus of the rock specimen and half of that of the steel, respectively. During the UCS test, a constant displacement increment of 1 m/s is applied on the top loading plate in the vertical direction while the bottom loading plate is fixed in both vertical and horizontal directions. During the BTS test, the constant displacement increment of 1 m/s is applied on both the top and bottom loading plates in the vertical direction but both the top and bottom loading plates are fixed in the horizontal direction.

Fig. 2
figure 2

Numerical models for calibrating the hybrid finite-discrete element method. a UCS test, b BTS test

Full size image

Figure 3 depicts the modelled rock failure process in terms of the distributions of the maximum shear stress and the initiated cracks during the UCS test. It can be seen from Fig. 3a that the load is applied on the top loading plate and transferred to the rock specimen through the contact between the top loading plate and the rock specimen. T load then propagates through the rock specimen to form a uniform stress field between the top and bottom plates. As the load increases, two shear cracks are formed, as shown in Fig. 3b, which divide the rock specimen into three pieces. Further loading causes the three pieces sliding along the formed two shear cracks. Microstructure or statistical methods, such as those proposed by Liu et al. (2012), may be introduced based on the actual texture of rock to obtain reasonable failure pattern as observed in experiments.

Fig. 3
figure 3

Hybrid finite-discrete element modelling of uniaxial compressive strength test, a Max shear stress distribution, b Failure process

Full size image

Figure 4 visually illustrates the modelled rock disc splitting failure process in terms of the distributions of the minor principal stress (the compressive stress) and the initiated cracks during the BTS test while the corresponding force and displacement curve is shown in Fig. 5. As the top and bottom loading plates contact the rock specimen, high stress concentrations are induced at the loading areas (Fig. 4a-A). As the loading plates further move toward each other, the induced stress propagates through the rock disc (Fig. 4a-B) to form a rather uniform stress distribution near the central line of the disc (Fig. 4a-C). According to literatures (Liu et al. 2007), a constant tensile stress in the horizontal direction is generated along the loading line, which forces the specimen to fail in tension along the loading line. As modelled in Fig. 4b-C, a tensile crack is initiated at the centre of the specimen and then propagates along the loading line (Fig. 4b-D). It should be noted that, in Fig. 4b, tensile crack is marked using the red colour while the compressive crack and the boundaries are denoted using the blue colour. After that, the formed tensile crack unstably propagates radially towards the two loading areas at the two ends of the specimen, where compressive cracks are initiated due to the high compressive stress concentration and the release of the confinement through the central tensile crack, as shown in Fig. 4b-E. At the same time, the specimen gradually loses its load bearing capacity (Fig. 4F). Finally, as the loading plates further move towards each other, the central tensile crack splits the specimen into two halves (Fig. 4G) while at the same time, more cracks are initiated around the two loading areas and the central tensile crack.

Fig. 4
figure 4

Hybrid finite-discrete element modelling of Brazilian tensile strength test. a Major principal stress distribution, b Failure process

Full size image
Fig. 5
figure 5

Force–displacement curve obtained during hybrid modelling of the BTS test

Full size image

The force–displacement curve of the BTS test recorded in Fig. 5 presents the typical behaviour of brittle rock under compression: a compressive deformation region (AB), a linear-elastic deformation region (BC), a non-linear deformation region (CD), a strain-softening deformation region (DEF) and a residual deformation region (FG), in which the alphabets correspond to those in Fig. 4. The maximum load \(P_{ \hbox{max} }\) at Point D can be used to calculate the tensile strength \(\sigma_{t}\) of the Brazilian disc at failure according to Eq. (8):

$$\sigma_{t} = \frac{{2{{P}}_{ \hbox{max} } }}{\pi Dt} = \frac{2 \times 2869814}{3.14 \times 0.054 \times 1} = 33.85 \times 10^{6} {\text{N}}/{\text{m}}^{2} = 34 \, {\text{MPa}}$$
(8)

where, \(\sigma_{t}\) is the tensile strength, \(P_{ \hbox{max} }\) is the maximum load at the peak of the force–displacement curve, \(D\) is the diameter of the specimen and \(t\) is the thickness of the specimen. It can be seen that the obtained dynamic strength of the specimen (34 MPa) is higher than the input static strength of the specimen (20 MPa), which is probably caused by the effects of the loading rate. As mentioned previously, the loading rate used in the BTS modelling is 1 m/s, which is much higher than that used in laboratory static experiments (around 0.01 mm/s). According to literatures (Zhang et al. 1999; Zhao 2000), the loading rate has important influences on rock properties. To take the influence into account, Eq. (7) is implemented into the hybrid finite-discrete element method. According to the modelled dynamic strength of the specimen and the input static strength, the material parameter A in Eq. (7) should be chosen as 20 for this specimen. In this case, theynamic strength of the specimen can be calculated according to Eq. (9)

$$\sigma_{cd} = A\log \left( {\frac{{\dot{\sigma }_{cd} }}{{\dot{\sigma }_{c} }}} \right) + \sigma_{c} = 20 \times \log \left( {\frac{{1\,{\text{m/s}}}}{{0.01\,{\text{mm/s}}}}} \right) + 20 = 34\,{\text{MPa}}$$
(9)

However, further studies are needed for the hybrid finite-discrete element method to model the effect of the loading rate on the dynamic strength of rock through implementing Eq. (7).

4 Hybrid finite-discrete element modelling of rock joint failure in direct shear test

After the calibration in Sect. 3, the hybrid finite-discrete element method is implemented in this section to model the asperity shearing and degradation, and the resultant gouge sliding and arching during the direct shear test of a rough rock joint. The majority of direct shearing tests of rock joints have been conducted under normal stress constraint in literatures (Roosta et al. 2006; Park and Song 2013; Indraratna et al. 2015). However, several researchers (Seidel and Haberfield 2002; Thirukumaran and Indraratna 2016), argued that progresses in the direct shear tests under constant displacement would provide a better understanding of the mechanical behaviour of rock fractures under confined situations such as underground rock engineering since shear strengthening is the major feature of rocks fractures under this loading condition, contrary to the shear weakening under constant normal stress corresponding to near free surface conditions. Correspondingly, the direct shearing test under constant displacement is studied here. As shown in Fig. 6a-A, the numerical model consists of two discrete rock blocks, which perfectly match each other along a saw-tooth shape joint. The upper and bottom discrete rock blocks are forced to move in the opposite directions, i.e., the right and left directions, respectively, with an initial velocity of 1 m/s, to shear the upper and bottom discrete rock blocks along the saw-tooth shape joint. The top and bottom boundaries of the upper and bottom discrete rock blocks, respectively, are fixed in the vertical direction to provide constraints for the constant displacement conditions. Each of the discrete rock blocks is discretised into triangular finite elements using the Delaunay triangulation algorithm shown in Fig. 6b-A. As argued by Kazerani (2013), this kind of polygonal configuration generated through the Delaunay triangulation algorithm or the Voronoi diagram generator may be the most representative of the mineral structure observed in rocks although the vast majority of micromechanical models have been carried out by rounded (disc-shaped) particles (e.g. Potyondy and Cundall 2004). The material properties of both rock blocks are the same as those of the UCS and BTS specimens described in Sect. 2.

Fig. 6
figure 6

Hybrid modelling of rock joint fracture process during shearing. a Fracture process, b Max shear stress distribution

Full size image

Figure 6 records the modelled rock joint fracturing process during direct shearing in terms of the distribution of the initiated cracks and the maximum shear stress while the corresponding vertical force versus horizontal shear displacement curve is plotted in Fig. 7, in which the alphabetical labels correspond to those in Fig. 6. It should be noted that, in Fig. 6a, the shear cracks are marked using the red colour while the blue colour is used to denote the boundaries and the tensile cracks. As can be seen from Fig. 6, before shearing, the two halves of the rock joint are assumed to be in intimate contact with both faces of each asperity in full contact. As soon as the horizontal shear displacement is applied on the top and bottom rock blocks, the interface slip is initiated (Fig. 6a-B) and the contact area between the two halves of the joint is restricted to one asperity face (Fig. 6b-B). The contact area progressively reduces as shear displacement progresses, which is the asperity sliding phase (Fig. 7A-B). There is little damage and fracture induced during the asperity sliding phase, as show in Fig. 6A-B. As the shear displacement increases, local normal stresses increase both as a consequence of the reduced contact area and as a result of the increasing normal stresses due to the contact normal stiffness condition. A critical normal stress (Fig. 7B) is reached at which the asperity can no longer sustain the loading and individual asperity failure results. Since the rocks on both sides of the interface have the same physical–mechanical properties, failures occur at localized regions of high stress at both leading and trailing points of contact of each asperity, as shown in Fig. 6C and D. It can be seen from Fig. 6C and D, the majorities of the failures are initiated in shear mode (the red colour in Fig. 6a-C) but further propagate in the tensile mode (the blue colour in Fig. 6a-C) due to the low tensile strength of the rock compared with its shear strength. As the shear displacement increases, failures gradually progressed from these localized regions until complete failure of most asperities and therefore of the whole interface) occurred, which is the asperity shearing phase. This resulted in a significant reduction in the measured force–displacement curve, as shown in Fig. 7B-D. Further shear displacement causes shear sliding (Fig. 6D-E) again, which results in the recorded load increases again due to the residual asperities and failure-resultant gouges, as shown in Fig. 7D-E. After that, the shearing phase occurs again due to the failure of the residual asperities and the resultant gouges (Fig. 6E, F), and the recorded load decreases (Fig. 7E, F) correspondingly. The sliding and shearing phases may repeat in several cycles (Figs. 6, 7F–H) with the residual asperities and failure-resultant gouges being subjected to further shear until a smooth shear surface is formed and the residual shear strength of the rock joint is achieved.

Fig. 7
figure 7

Normal force–shearing displacement curve obtained during hybrid modelling of rock joint fracture process in shearing

Full size image

Figure 8 compares the obtained shear failure pattern from the numerical simulation with that predicted by Seidel and Haberfield (2002). Seidel and Haberfield (2002) conducted a number of direct shear tests on rough rock joints with regular triangular asperities and concluded that, during the asperity shearing phase, the shear failure developed along a curved failure surface emanating from the apex of the loading concrete asperity and intersected the trailing face of the rock asperity, as shown in Fig. 8a. It can be seen from Fig. 8b, the modelled shear failure develops following the trend proposed by Seidel and Haberfield (2002) but the details of the shear failure development are much more complicated than that predicted in the theoretical model. This may be caused by the shearing of both sides of the joint interface since the top rock block and the bottom rock block have the same physical–mechanical properties in this study while only the rock on one side of the joint interface is supposed to fail in the theoretical model proposed by Seidel and Haberfield (2002). Moreover, Seidel and Haberfield (2002) also observed that further shear displacement did not occur on the curved failure surface, but rather on a chord linking the intersection points of the initial failure surface with the leading and trailing asperity faces. The numerical model again presented much more complicated shear failure envelope, as depicted in Fig. 8b. The force-shear displacement curve depicted in Fig. 7 and introduced above agrees with the evolvement of the rock joint strength described in literatures (Huang et al. 2002; and Morgan 2004). First of all, the rock joint strengthens rapidly from zero to a peak. After the peak, it weakens exponentially from the peak to a steady state value over a critical slip distance. Finally, the rock joint strength stays approximately constant, with some fluctuations caused by local stick–slip events.

Fig. 8
figure 8

Comparison between the fracture patterns obtained by theoretical model and numerical simulation. a Schematic representation according to theoretical model (Seidel and Haberfield 2002), b Two steps from numerical simulation

Full size image

Therefore, as can be seen from Figs. 7 and 8, the hybrid finite-discrete element modelling explain the shear resistance evolution mechanism of the joint during the direct shear test. At the early stage of the direct shear test, the shear resistance of the joint is completely provided by the increasing static friction. As the shear displacement increases, the static frictions in some joint asperities consistently lose and transform into the sliding friction, but the static friction in the surrounding asperities gradually increases. During the asperity sliding process, the intact asperities on the two surfaces of the joint ride up each other to provide increasing joint shear resistance through a combination of the static and sliding frictions. The joint shear resistance reaches its peak when the intact asperities start to damage and break forming gauges between the two joint surfaces. During the asperity shearing process, the joint resistance gradually decreases and the majority of the asperities becomes damaged and broken although there may be still unbroken joint asperities. During the strain-softening stage after the peak, the broken joint asperities provide the joint shear resistance through sliding friction while the unbroken joint asperities and the resultant gauges formed between the two joint surfaces may ride up to provide the joint shear resistance by a combination of the static, sliding and rotating frictions. The break of the joint asperities leads to the stress concentrations in surrounding unbroken joint asperities and gauges, which may cause the joint shear resistance does not decrease monotonically but increase a little bit in some stage. This process may repeat in several cycles depending on the matching of the formed new joint surfaces and the grinding and rotation of the resultant gauges. Finally all of the asperities are broken and it becomes easy for the resultant gauges to grind or rotate between the formed new joint surface, in which the shear resistance is completely provided by the sliding and rotating frictions. Correspondingly, the shear resistance decreases to the residual shear stress. In sum, the hybrid finite-discrete element modelling reproduces all the shear failure mechanisms during the rock joint shearing process described in literature (Guo and Morgan 2008): asperity damage, contact sliding and grain rotation except the volume change, which is, however, indirectly reproduced through the increased asperity degradation since the constant displacement conditions in the vertical boundaries of the model suppressed the dilation and compaction but promotes the asperity degradation.

5 Discussions

5.1 Dynamic shear behaviour of rock joints under different shearing rates

The dynamic shear behaviour of rock joints is significant to a number of mining and civil engineering applications (Huang et al. 2014). Moreover, the studies on the dynamic shear behaviour of rock joints can shed light on the origin and evolvement of fault slip, which consequently leads to earthquakes and landslides (Marone 1998). Correspondingly, the same numerical model with the same rock joint is sheared under different shearing rates to investigate the dynamic shear behaviour of rock joints. Figures 9a–c depict the normal force–shear displacement curves and final failure patterns obtained from the direct shear tests of the same rock joint under the shearing rates of 1, 10 and 100 m/s, respectively. The comparison among the obtained three fracture patterns indicates higher shearing rate causes more severe joint asperity degradation and gouge grinding and then smoother residual joint surface. The comparison among the obtained three normal force–shear displacement curves shows that the higher the shearing rate, the bigger the peak shear load is, the more severe non-linear the pre-peak curve is, the smoother the post-peak curve is and the lower the residual load is. All these observed phenomena can be explained through the asperity degradation and gouge grinding occurred in the direct shear tests. According to Eq. (7), high loading rates increase the rock strength, i.e., the joint asperities have higher dynamic strength in the direct shear test under higher shearing rates, which suppresses the joint asperity degradation but promotes the shearing sliding along the joint asperities. The shearing sliding should cause the volume dilation. However, since the direct shear test is conducted under the constant displacement loading condition instead of the constant normal stress loading condition, the fixed top and bottom boundaries of the model do not allow the volume dilation to occur. Correspondingly, the normal forces at these boundaries increase to provide strong confinements, which explains why the higher the shearing rate, the bigger the normal force is. Moreover, the strong confinements suppress the shearing sliding along the joint asperities. At the same time, the higher shearing rate induces higher stress concentrations in the joint asperities, which promotes the asperity degradations and the gouge formation. That is why the force–shear displacement curve becomes more non-linear before the peak and why more joint asperities are sheared and more gouges are formed and grinded between the two joint surfaces in the direct shear test of the rock joint under higher shearing rate. During the post-failure stage, almost all joint asperities are damaged and broken and almost all formed gouges are grinded between the two joint surfaces, which results in the smooth new joint surfaces and the smooth post-failure force-shear displacement curve. However, in the direct shear test under the low shearing rate, the low normal force provides low confinements, which promotes the shearing sliding and suppresses the asperity degradation. That is why less joint asperities are sheared, smaller peak load is presented, less gouges are formed, and rough new joint surfaces are resulted. During the post-failure stage, the newly formed rough joint surfaces, the shearing sliding and the resultant gouge rotation together cause some joint asperities are not completely sheared at once and the gouges are not completed grinded at once but they are gradually sheared or grinded, which is why there are more fluctuations during the post-peak stage of the force-shear displacement curve. In sum, the higher shearing rate promotes the joint asperity degradation and the resultant gouge grinding.

Fig. 9
figure 9

Effects of loading rate on the normal force–shearing displacement curves and fracture patterns during rock joint fracture process in shearing. a Shearing rate: 1 m/s, b Shearing rate: 10 m/s, c Shearing rate: 100 m/s

Full size image

5.2 Direct shearing of rock joints with various roughness

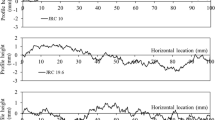
In this section, the direct shear tests of rock joints with various roughness are modelled using the hybrid finite-discrete element method to investigate the effect of joint roughness on the shear failure process. Figure 10 depicts the geometric and numerical models of rock joints with various roughness profiles. The roughness profile is defined according to the height and inclination of the joint asperities. For example, 17.5° × 9.5 mm means the joint asperity is inclined to the horizontal direction with an angle of 17.5° and has a height of 9.5 mm above the horizontal joint surface. Figure 11 compares the modelled fracture patterns of the rock joints with various roughness profiles in terms of the distributions of the maximum shear stress and the initiated cracks. It should be noted that only the fracture patters for three roughness profiles depicted in Fig. 10 are illustrated in Fig. 11 in order to save spaces. As can be seen from Fig. 11 and the failure process of rock joints under shearing introduced in detail in Sect. 4, for rough rock joints with deep asperities, the joint asperity degradation and the gouge formation and grinding are the main mechanism of the joint shear resistance evolution. However, for the relatively smooth rock joints with shallow asperities, the joint asperity sliding is the main mechanism of the joint shear resistance evolution.

Fig. 10
figure 10

Numerical model for direct shearing of rock joints with various roughness. a Geometrical model, b Numerical model and c Various roughness profiles

Full size image
Fig. 11
figure 11

Effects of roughness on the fracture patterns of rock joints during shearing (Top Max shear stress distribution. Bottom Failure pattern). a 27.5° × 23 mm, (b) 17.5° × 9.5 mm and (c) 5° × 3.75 mm

Full size image

6 Conclusions

In this study, a hybrid finite-discrete element method is implemented to model the shear failure process of rough rock joints in direct shear tests under the constant displacement loading conditions. The calculation cycles of the hybrid finite-discrete element method are firstly introduced. The hybrid finite-discrete element method is then calibrated by simulating the rock failure processes in the UCS and BTS tests and comparing them against these in literatures. After that, the direct shear test of a rough rock joint is modelled using the hybrid finite-discrete element method to investigate the joint shear resistance evolution by focusing on the joint asperity degradation and gouge grinding. Finally, the effects of the shearing rate and the joint roughness on the asperity sliding and degradation, and the gouge formation and grinding are discussed. Throughout this study, the following conclusions can be drawn:

  1. (1)

    The hybrid finite-discrete element method reproduces the joint shear resistance evolution process during the direct shear test of rough rock joints, such as from asperity sliding to degradation and from gouge formation to grinding. Compared with FEM, the hybrid method is more efficient in modelling the asperity sliding and the gouge formation and grinding due to the asperity degradation, which FEM has difficulty to deal with. Compared with DEM, the hybrid method is more robust in modelling the transition from continuum to discontinuum due to the asperity degradation and the formation and grinding of irregular-shaped gouges. Thus, the hybrid finite-discrete element method is a valuable numerical tool better than FEM and DEM for the studies on the asperity degradation and gouge grinding during the shear resistance evolution process of rock joints under shearing and even the fracture and fragmentation of rocks under static and impact loads.

  2. (2)

    Higher shearing rate in the direct shear tests of rough rock joints under the constant normal displacement loading conditions promotes the asperity degradation but constraints the volume dilation, which result in higher peak shear resistance, more gouge formation and grinding, and smoother new joint surfaces.

  3. (3)

    Roughness affects the joint shear resistance evolution through influencing the joint fracture micro-mechanism. The asperity degradation and gouge grinding are the main micro-mechanism occurred in shearing rough rock joints with deep asperities while the asperity sliding is the main micro-mechanism happened in shearing smooth rock joints with shallow asperities.