Abstract
In mathematics education, the research on proof by contradiction (PBC) often claims that this activity is more difficult for students than direct proof, or simply difficult in general. Many hypotheses have been offered to support or explain this belief, yet they span a disorientingly wide swath of journal articles, conference papers, dissertations, book chapters, etc. In addition, few attempts have been made to organize these hypotheses or carefully test them. In this paper, we conduct a thorough literature review on PBC, organize existing hypotheses about challenges with PBC into a Hypothesis Framework for (Students’ Difficulty with) Proof By Contradiction (HFPBC), discuss the state of research related to each hypothesis, and offer thoughts on the future study of these hypotheses.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The practice of mathematical proof is arguably the defining characteristic of mathematics as a discipline, playing a role similar to that of experimentation in the sciences. Proof provides the epistemological basis of confidence in mathematical knowledge as well as the functions of explanation, systematization, discovery, and communication of that knowledge (de Villiers 1990). Understanding and constructing proofs are important prerequisites for students’ full participation in the field and a key element of their enculturation into it, and many universities have instituted “Introduction to Proof” courses to facilitate this. The teaching and learning of proof have accordingly been of central interest to researchers in mathematics education for many years (Hanna & de Villiers 2012).
Proof by contradiction (PBC) is an essential form of indirect proof (IP) across all mathematical content areas. Students routinely use this approach to prove the nonexistence of objects in geometry, the infinitude of primes in number theory, and the irrationality of \(\sqrt {2}\) in analysis. Indirect argumentation is also common in everyday life. People often frame their reasoning indirectly: “If A were true, then how do you explain B?” and “If suspect A were the murderer, then we would know B and C. But ...”. Despite the presence of indirect thinking in both everyday and academic settings, some mathematics educators and researchers have noted that students face difficulty when using such arguments. As such, a literature base was born to study the use of indirect reasoning, such as PBC, in mathematics.
Two main themes arise as one begins reading the research on PBC. The first is how new this body of research is. Speaking to its infancy as a field, Baccaglini-Frank et al. (2013) wrote that “although much research has been conducted on the themes of proof and argumentation in mathematics education, rarely do the studies focus on particular proof structures, such as proof by contradiction” (p. 63). Bedros (2003) shared this sentiment ten years earlier:
Only a few comprehensive studies or systematic accounts in the mathematics education literature deal solely and deeply with undergraduate students’ difficulties in understanding the indirect aspects of proving. Thus, very little is known about students’ perceptions and understandings of indirect processes. (p. 25)
The second theme centers on the contrast between PBC (or IP more generally, for some authors) and direct proof (DP). For example, Antonini and Mariotti (2008) wrote that “at any school level, students’ difficulties with indirect proof seem to be greater than those related to direct proof” (p. 401). These authors earlier noted that the “current literature agrees on the fact that students show much more difficulties with indirect than direct proofs” (Antonini & Mariotti 2006, p. 65) and referenced the “unanimously recognized difficulties with indirect proofs” (Antonini & Mariotti 2008, p. 403). Similarly, Jourdan and Yevdokimov (2016) stated that “there is a consensus that learners do find indirect types of proof quite difficult and do struggle with the conceptual and technical aspects of indirect proofs” (p. 63). They go on to cite Epp (1998) who wrote that “students find proof by contradiction considerably harder to master than direct proof” (p. 711). Writing even earlier, Robert and Schwarzenberger (1991) spoke of “proofs by contradiction presenting particular difficulties” (p. 130), and even further back, Lazar (1947) inclusively wrote that “philosophers, logicians, mathematicians, commentators, textbook writers, teachers, and, of course, pupils, have expressed dissatisfaction with this method of proof [IP]” (p. 225).
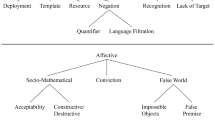
It is interesting to note that these two themes are somewhat at odds: It is difficult to clearly establish the relative challenge/dissatisfaction offered by PBC/IP and DP in a literature base that is in its infancy. Indeed, many of the above quotes comparing IP and DP were made without citational support, so the strength of these claims is not immediately clear. To add to the muddiness of the PBC landscape, thinkers have offered a vast array of reasons why PBC may be more difficult than DP. As an example, Pasztor and Alacaci (2005) noted that “Our study focuses on students’ error patterns when negating quantified sentences [emphasis added], which are the single most important cause for their difficulties with indirect proofs and proofs by contradiction” (p. 1714). This reason is but one of 16 separate reasons (see Fig. 1) given by authors for the supposed disparity between students’ fluency with DP and PBC (or for challenges with PBC alone). Also at issue is precisely what is more difficult when comparing these types of proof. This “what” might refer to knowing when to use PBC, how to produce proofs with PBC, or even the conviction behind and comprehension of PBCs.
To make matters more complicated, when researchers actually do empirical studies comparing DP and IP, or exploring the “difficulties” of IP, the results can be contradictory. For example, Brown (2018) found that when given two proofs of the same theorem (one a DP, one an IP), students preferred a direct approach for some theorems and an indirect approach for other theorems. In summarizing her findings, Brown wrote: “it seems that length, complexity, and familiarity are criteria students bring to bear on proofs before considerations of proof type when selecting the most convincing proof” (p. 17). As another example, when exploring preservice mathematics teachers’ fluency with PBC, a study on teachers in Ankara, Turkey suggested that they generally were quite strong with the topic (Demiray & Bostan 2017), while a study of American teachers found they “had a superficial understanding of the ‘proof by contradiction’ mode of argumentation” (Bleiler et al., 2014, p. 105).
Finally, the literature on IP/PBC has not been as careful as possible in distinguishing theories based on anecdotal evidence from those that have been carefully explored through qualitative and quantitative research. As an example, in an important paper by Uri Leron (1985), the author advanced what we call the “Constructive/Destructive Hypothesis” and “False World Hypotheses” (see below). The author was quite forthright about the nature of his theory, writing “I begin with observation, continue with generalization and end with speculation”(p. 321), later noting that “I cannot claim any factual basis for it” (p. 324) where “it” is the false world metaphor he created as part of the article. While Leron’s speculation was based on anecdotal teaching experience and a single class of student teachers around a single theorem (the PBC of the infinitude of primes), this paper is cited over 90 times (according to Google Scholar) in the last 30 years, with varying degrees of faithfulness to the speculative nature of the original work.
Given the nascent and confusing research on PBC, we thought it would be productive to organize those ideas that have been clearly or repeatedly advanced by scholars into a Hypothesis Framework for (Students’ Difficulties with) PBC (HFPBC, see Fig. 1). In addition to giving new researchers a sense of the state/structure of the field, we hope that the HFPBC and its careful description will inform current researchers as to what is known regarding each hypothesis. Also, this framework can help scholars move beyond poorly-specified claims (e.g., saying IP/PBC is more “difficult” than DP) and overly-simplified claims (e.g., citing a particular hypothesis in the framework as the main cause of student confusion). Furthermore, we believe this framework will be useful to educators as they explore the potential sources of trouble students might face when engaging with PBC. Indeed, one goal of our organizational efforts is to facilitate the call-to-arms of Hanna and de Villiers (2012) who, when looking at works from their volume, pleaded “for additional empirical research, longitudinal studies, and investigations on the long-term effects of the different approaches to proof” (p. 6).
Literature Review
In order to gain a complete picture of the existing work on PBC, we conducted a systematic review of the field. In the initial identification stage, we searched for works primarily focused on PBC or IP. In particular, we followed this plan:
-
Databases (subcollections) to search: ERIC, EBSCO (Education Source, Academic Search Complete, MathSciNet, and OpenDissertations collections), ProQuest (Dissertations & Theses, PsycARTICLES, PsycINFO collections), Google Scholar
-
Allowable dates: Any time up to and including October 2019
-
Language of search: English
-
Articles to search from: Those with electronic access in the above repositories (or where electronic access could be found more globally on the internet)
-
Search terms: “proof by contradiction” or “indirect proof” in the title or abstract (when available); the bodies of texts were not included because initial searches included too many false positives
-
Inclusion criteria: Work focuses primarily on the act of PBC (either from a historical, empirical, philosophical, or pedagogical perspective within mathematics) and discusses understanding of PBC; work may be from any type of source (refereed journals, published/unpublished dissertations, books, etc.) and focus on any constituency (teachers, students of any level, etc.), or center on theory development/epistemology
-
Exclusion criteria: Work is solely a collection of activities or resources for teachers related to PBC; work presents a mathematical proof that happens to use PBC; work is not centrally focused on PBC/IP in general; work does not discuss/explore understanding of PBC/IP; work is duplicated in another search; electronic access is not possible; work references a poster presentation; work is exclusively related to mathematical logic
While it was possible to search for both “proof by contradiction” and “indirect proof” using a single search string, we chose to conduct separate searches in the event this extra granularity might benefit other researchers in the future. Table 1 presents a list of the numbers of works returned from each search (“Raw Number of Articles”), how many of these met the inclusion criteria and did not appear in an earlier search (“Number New Included”), and how many were seen previously or met the exclusion criteria (“Number Excluded”).
In addition to searching large databases, we also searched the websites of prominent journals in mathematics education using the above guidelines. This step was important because databases often maintain only a subset of available content from a given journal (e.g. years 1980-2015). To select these journals, we referred to Williams and Leatham (2017), which explored journal quality in mathematics education using a variety of metrics. The searched journals included Educational Studies in Mathematics (ESM), Journal for Research in Mathematics Education (JRME), Journal of Mathematical Behavior (JMB), Journal of Mathematics Teacher Education (JMTE), International Journal on Mathematics Education (ZDM), Mathematical Teaching & Learning (MTL), and For the Learning of Mathematics (FLM). While these journals were well-represented in the database searches, three additional articles were identified for inclusion (see Table 1).
As an initial sense of the infancy of the field, one sees that of the 615 works meeting search terms (this total includes duplicates), only 35 works in these databases/journals met the inclusion criteria for our review. Furthermore, this total includes works from a vast array of sources: research journals, conferences, dissertations, book chapters, etc. Table 2 (see Appendix) lists these articles and the particular search that led to their inclusion. This lack of research focused primarily on PBC is not unexpected. When Brown (2012) looked through the 94 papers presented at the ICMI Study 19 Conference (focused on “Proof and Proving in School Mathematics”), she found that “only 9 mention indirect proofs and only 1 of those 9 explicitly investigated indirect proofs” (p. 8). Thus, among works specifically related to proof, only a fraction mention IP, and a fraction of that fraction focus on IP. In a similar exploration of the 2008 through 2010 conference proceedings from SIGMAA on RUME (Special Interest Group of the Mathematical Association of America on Research in Undergraduate Mathematics Education), 0 of the 241 papers focused on student understanding of IP/PBC (Brown 2012).
Given the lack of papers focused on IP/PBC, we expanded our search to look for other important works that contained significant mention of IP/PBC (and, to catch those works focused on IP/PBC that fell through the cracks). By reading the 35 initial articles and checking their bibliographies, we identified additional important articles to include. By looking through the bibliographies of those new articles (and so on, i.e., an iterative bibliographic exploration), we ultimately identified 25 additional articles that had important sections, results, or were from fields outside of mathematics but still relevant. These articles are listed in Table 3 (see Appendix). We hope this list of 60 total articles (Tables 2 and 3) will be useful to those interested in studying PBC or IP.
The Hypothesis Framework for (Students’ Difficulties with) Proof By Contradiction (HFPBC)
With our literature base set, we turned to the second task of this paper. Our goal was to identify and structure the existing theories for why students might struggle when engaged with PBC. Interestingly, while the inclusion/exclusion criteria of the review did not demand a focus on students’ understanding of PBC (just understanding of PBC), virtually all the works did focus on students, including those papers with a strong historical or theoretical bent. In Fig. 1, we propose a framework that organizes the current major hypotheses surrounding students’ difficulties with PBC. At a high level, the hypotheses fall into one of three categories: “Operational Hypotheses” (those centered on the act of producing a PBC), “Affective Hypotheses” (the emotional and attitudinal views held by students and communities related to PBC), and “Foundational Hypotheses” (the theoretical and logical issues that underpin PBC). The framework was constructed by carefully reviewing the above articles and noting every hypothesis offered by scholars (whether original or citing the work of others). This initial pass produced an extensive list that was then refined by collapsing hypotheses mentioned repeatedly, removing hypotheses that were infrequently discussed or developed, and uniting micro-hypotheses into larger categories with sufficient substance. Thus, the 16 leaf nodes of the HFPBC are the hypotheses in the literature that had sufficient development, substance, mention, empirical evidence, and/or promise to be included. The internal nodes of the HFPBC represent our efforts to organize these into a coherent structure.
In the end, the structuring and naming that appear in Fig. 1 are the product of an extensive series of drafts born from a grounded approach to theory development (Corbin & Strauss, 1990), (Strauss & Corbin, 1994). Furthermore, this macro-structuring of hypotheses should not be seen as mutually exclusive: leaf nodes in the framework could easily be placed in different positions of the hierarchy; we have simply placed them where we think they have the most natural fit. As an example, when constructing a PBC, students must work toward a contradiction, but it is not clear in advance what this contradiction will be (e.g., steps that result in a statement like 0 = 1, or perhaps a contradiction to a well-known theorem). We call this the “Lack of Target Hypothesis” and place it under the “Contradiction Hypotheses” label, but we suspect this unease regarding the proof’s destination will also engender an emotional response worthy of mention somewhere under the “Affective Hypotheses” root node.
In the sections that follow, we dive into each of the internal and leaf nodes of the HFPBC. After doing so, we offer a discussion around the value this organizational structure could bring to the field. Before moving forward, we want to clarify our use of the word “hypothesis”. In this paper, we use this term to mean a narrative advanced by the PBC literature that aims to explain phenomena related to PBC. While this term comes with different definitions and expectations in various domains, we sought a single label to refer to each of the components of Fig. 1 but faced the challenge of referencing settings with widely disparate degrees of empirical and theoretical backing. In the end, we chose a conservative term that would remind readers of the developing nature of these ideas. Indeed, we believe that even those hypotheses with the most development are still developmental; the studies that underpin them are often restricted to certain people (e.g., university students) or certain types of PBC problems (e.g., showing the irrationality of a given number), and hence, the generalizability of their findings remains an open question. To help the reader get a sense for the development of each hypothesis, we have chosen to label the leaf-nodes (i.e., the non-organizational hypotheses) with one of four terms: Unstudied (hypotheses with no known empirical work on students), Emerging (hypotheses for which we know of 1 or 2 empirical studies about students’ difficulties which agree), Supported (3+ convergent empirical studies), and Inconsistent (2+ divergent studies). We use the term “Supported” rather than “Proven” or “Verified” because future studies could conflict with existing work, and the possible causes of student difficulty with PBC may shift over time. We begin and end the discussion of each non-organizational hypothesis (see headers and concluding sentences) with the label to orient the reader.
Finally, it is important to note that the HFPBC was born from a perspective focused on inclusivity. As mentioned above, one goal was not to include only those hypotheses that had become butterflies, but rather, to add some caterpillars to the framework with the hope that future researchers would take up the mantle of development. Indeed, any hypothesis that was clearly stated, mentioned by multiple authors, or for which theoretical/empirical work had been done was ultimately included in the framework in some way. This spirit of inclusion also extended to the perspectives of the authors we examined. Readers familiar with the PBC literature will recognize that the papers in our review take different views on what PBC is and what type of student activity to focus on (e.g., producing PBC proofs, analyzing others’ proofs, identifying proof types, etc.). We have chosen not to limit our discussion to a particular PBC definition or type of student activity because we believe that the HFPBC is strengthened (as an organizing force for the field) when it works to be as inclusive as possible. As such, individual researchers may wish to consider only those hypotheses with a certain level of empirical support, those that make sense within their personal definitions of PBC, or those that can be operationalized based on the targeted student activity. In total, we feel the HFPBC is coherent (in general) based on its encyclopedic foundation, and coherent to particular users after subsetting based on personal lenses.
Operational Hypotheses
Hypotheses under this label focus primarily on the act of constructing a PBC, from the initial steps of deciding PBC is appropriate, to forming the negation of the conclusion, to working toward the contradiction, and finally, to recognizing and asserting that a contradiction has been reached.
Training Hypotheses
This collection of hypotheses centers on the idea that the educational system fails to give students the support and opportunities they need to meet with success when doing PBC. Antonini and Mariotti (2007) described the state of affairs bluntly: “Indirect proofs do not find an adequate attention in school practice, at any school level” (p. 541). Thompson (1996) added: “Given the minor emphasis on this proof technique in the secondary curriculum, it is no wonder that students find the technique difficult to understand and use” (p. 474). This lack of emphasis might be surprising to some given PBC’s early development [dating to (at least) 375 B.C. by Eudoxus] and prevalance in the work of famous mathematicians − for example, 16 of 31 proofs in Euclid’s Elements, Book III were indirect (Lazar 1947).
Historically, it appears some difficulty around operationalizing IP stemmed from poor instructional materials and pedagogy. Lazar (1947) noted three trends: “very few books take the trouble to give a definition of the crucial terms ‘direct proof’ and ‘indirect proof”’ (p. 226), “until the early years of this century very few geometry books took the trouble to give the logical basis underlying the method of indirect proof” (p. 236) and that “of late, the tendency has arisen to use the indirect proof only in cases where direct proof is impossible or very difficult” (p. 233). If textbooks fail to articulate an idea and teachers use it only as a last resort, it is no wonder students might struggle to operationalize it. Leadbeater (1937) shared these sentiments even earlier: “To what then are we to attribute the disrepute into which the indirect method has fallen? In the writer’s opinion it is due solely to bewildering and illogical presentations often given by writers of textbooks” (p. 25). Byham (1969), a student of Lazar, carefully catalogued these “bewildering and illogical presentations” in his dissertation, perhaps the most thorough review of the development of IP in geometry texts. By analyzing 37 different books, he found authors used seven different names for indirect proof, which were often poorly presented and inconsistent across books.
In addition to the issue of textbook training, one must consider the training of PBC that happens in classrooms. Some researchers have begun to explore different pedagogical approaches to PBC. For example, Amit and Portnov-Neeman (2017) studied students’ performance on PBC when trained using the “explicit teaching approach” (experimental group, EG) as compared to standard methods (control group, CG). Over a six month training cycle, they found that talented sixth graders improved their PBC performance using either approach, but that gains in the EG far outpaced those in the CG. To date, few studies have explored how different approaches to training PBC affect student understanding and success.
Deployment Hypothesis [Emerging]
The Deployment Hypothesis suggests that students struggle to recognize the signs that PBC could be a helpful technique for proving a proposition (in general, and for a specific problem). In order to better understand these tip-offs in general, Lin et al. (2003) analyzed interviews with six mathematicians and found two deployment-related themes: 1) PBC is helpful when the given statement is awkward to build from (e.g., “Prove there are no integers that …”), and 2) PBC is useful when the negation has a nice representation (e.g., assuming \(\sqrt 2\) is rational). They note that these themes may not be clear to students. Barnard and Tall (1997) raised another issue related to deployment: to deploy a technique requires that one know of its existence in advance or to be able to create it for the first time. In a group of students (aged 15 to first-year-college) who had not seen the standard PBC of the irrationality of \(\sqrt 2\), they found that none was able to spontaneously use this line of reasoning, noting that the students “are unfamiliar with the possibility of proving something true by initially supposing it to be false – a conflict likely to provoke cognitive tension and insecurity”(p. 43). This hypothesis is labeled Emerging because we know students struggle to deploy PBC before its formal introduction and that mathematicians have some criteria for deploying PBC, but we don’t yet understand the growth between these extremes.
Template Hypothesis
Both DP and IP feature patterns of argumentation that arise frequently. For example, when students first learn to prove the existence of limits from the epsilon-delta definition, they are trained to consider an arbitrary positive epsilon, and then use this (in conjunction with algebra related to the function) to define a delta that will cause the remainder of the definition to hold. Similarly, in set theory, students know they can show the equality of two sets by showing that each is a subset of the other. The Template Hypothesis suggests that these common ways of reasoning in PBC are either less numerous, less accessible to students, or less trained by teachers than those seen in DP. While various authors (Antonini & Mariotti 2008; Brown 2018; Hanna & de Villiers 2012; Tall 1979; Thompson 1996) have mentioned this idea, it does not appear that any scholars have empirically explored it (Unstudied).
Resource Hypothesis
When students engage in the act of proving, they bring resources (previous knowledge, intuition, examples, etc.) to bear on the challenges they face. The Resource Hypothesis explores whether the way these resources (both productive and non-productive) are used is altered when engaging with PBC. Brown (2018) articulated the core of this hypothesis when writing:
What is at issue is not one’s knowledge sources but rather the activities required. In other words, it may be that IPs demand particular activities, that is, ways of reasoning with one’s knowledge sources, and that students experience difficulties meeting these demands. (p. 3)
While socio-cultural and situated views of cognition argue from a high level that one’s setting definitely matters (Brown, Collins, & Duguid 1989; Forman 2003; Vygotsky 1987), mathematics education researchers who study proof, in particular, have explored this idea in less detail. Dawkins and Karunakaran (2016) stressed this point for the setting of content area (analysis vs. algebra vs. number theory etc.) writing: “We are concerned that framing mathematical proving as a single, content-general practice may inappropriately downplay the role particular mathematics content plays therein” (p. 65). In relation to IP, the authors write: “we observe students who on one task treat contrapositive statements as equivalent while in others fail to see the equivalence and show no conscious knowledge of the general logical relationship” (p. 72). Other authors have also highlighted the critical role particular content knowledge plays in the creation and understanding of proof for undergraduate math majors and preservice mathematics teachers (Bleiler et al., 2014; Ko & Knuth 2013). While this hypothesis has promise given the central role of resources in learning, proving, and IP mentioned above, their influence in PBC specifically remains Unstudied.
Negation Hypotheses
This macro-category focuses on issues related to formulating ¬q (not q) when using PBC on a conditional of the form p⇒q. These hypotheses appear to be the most developed and researched in the field, in part because fields outside of mathematics use negation as well (e.g., computer science and philosophy) and because negation is a smaller, self-contained, procedural, and easily-observable part of PBC. Indeed, Inglis and Simpson (2008) wrote that “it is of course well known that students have difficulty negating complex quantified statements in mathematical contexts (e.g. Barnard, 1995; Dubinsky et al., 1988)” (p. 199).
Quantifier Hypothesis [Supported]
To negate a quantified statement (e.g., a statement involving a “for all” or “there exists”), students must first understand what quantifiers are present. If statements are written in informal ways, the transition to a logic-based equivalent can be difficult (Selden & Selden 1995). Even after arriving at a formal logical statement, students struggle to understand the importance of order and scope when multiple quantifiers are present (Dubinsky & Yiparaki 2000). To add to these issues, Shipman (2016) noted that quantifiers can be hidden by our pedagogical approaches and ways of writing statements. For example, educators often use truth tables to show that the negation of P⇒Q is P ∧¬Q (here, ∧ means “and”). However, mathematical statements often take the form P(x)⇒Q(x), or more carefully: ∀x ∈ S, P(x)⇒Q(x), with the negation: ∃x ∈ S, P(x) ∧¬Q(x). These subtleties are often overlooked when beginning a PBC. For example, a student might begin a proof of “If \(q \in \mathbb {Q} \wedge r \in \overline {\mathbb {Q}}\), then \(q+r \in \overline {\mathbb {Q}}\)” by simply writing: “Suppose not. Let q + r be rational.” (\(\overline {\mathbb {Q}}\) is the irrational numbers). This step ignores the hidden “for all” quantifiers on q and r, and hence, their conversion to “there exists” quantifiers in the negation (Shipman 2016). Lin et al. (2003) explored students’ abilities to negate statements like “all people are my friends” and “no angle of triangle ABC is acute”, and found that overall, negation of statements without any (hidden) quantifiers was easiest for students, followed by “some” statements (harder), “all” statements (harder), and “only one” statements (hardest).
In one of the earlier studies of negations and quantifiers, Barnard (1995) gave 78 first year undergraduates and 78 second/third year undergraduates a collection of seven statements to negate. These ranged from easy (“x satisfies P, for all x in X) to hard (“Given x in X, there exists y in Y such that S(x, z) is true for all z in Z”) (p. 3). These statements were each presented in three contexts: everyday with answers chosen via multiple choice (All people living in Cheltenham watch ‘Neighbours’), mathematical with answers chosen via multiple choice (For all integers a, a2 ≥ 0), and everyday with students providing negations (All people living in Neasden have black hair) (prompts from pp. 5-7). In general, the performance was better when comparing older students to younger students, easier prompts to harder prompts, and multiple choice answers to student-generated answers. In general, student success rates were low, roughly between 30% and 70% on most problems. This hypothesis is Supported by the research.
Language Filtration Hypothesis
While mathematicians may negate statements in formal logical settings, students often face statements presented in real-world contexts that use spoken and written language to set up problems. This hypothesis suggests that students might struggle with negation, and hence PBC, because of the movement between natural language and mathematics, the way thinking filters through/is influenced by language, and by the idiosyncrasies common in language. As an example, Lin et al. (2003) noted in an exploration of Chinese students’ negations that subtle word ordering and semantic issues can influence how students negate statements. In Mandarin, the statement “I have only one brother” is actually ordered “only-have-one”. Many students negate this as “not-only-have-one” which converts to “more than one” in Mandarin (rather than the correct negation of “0 or more than 1”).
English has its share of issues as well: speakers are often not clear whether they mean an exact amount or an inequality: “Yeah, I’ve got a brother!” (1 or at least 1?) or “What is the probability of drawing 2 green balls?” (exactly 2 or more than 1?). This makes negation difficult when problems rely on textual prompts, rather than purely mathematical prompts. As Shipman (2016) noted: “Students may be working with colloquial meanings of English or may be learning English as a foreign language” (p. 48). Pasztor and Alacaci (2005) extended these ideas by citing the literature on polarization, divisive politics, and either-or thinking. They offer simple examples like “Some horses are slow” (negated as “Some horses are not slow” or “Some horses are fast”) to show how negation in everyday language might differ from that in mathematics. Similar themes have also been explored by Barnard (1995), Antonini (2001), and Epp (2003). This hypothesis is Supported by a variety of researchers across many settings.
Cognitive Demand Hypothesis [Unstudied]
The Cognitive Demand Hypothesis is derived from research on cognitive load theory (CLT) from information processing (Centre for Education Statistics and Evaluation 2017; Sweller 1988, 1994). The idea behind this hypothesis is that PBC places large mental demands on students and that this can overwhelm the cognitive bandwidth students have available for thinking. At a basic level, PBC demands more information be considered than DP: Rafetseder, Schwitalla, and Perner (2013) wrote that “people keep two models (“p and q” as well as “not p and not q”) in mind to understand counterfactual statements, whereas they keep only one model (“p and q”) in mind to understand indicative statements” (p. 399). Antonini and Mariotti (2008) noted that additional psychological forces may be at play when doing PBC: “It may be too demanding to assume that what is to be proved is false, and it is extremely hard for one’s mind to follow the deductive steps when false hypotheses and contradictions are involved” (p. 402). This theme appears to have been first articulated in Leron’s (1985) important paper (see also the “False World Hypotheses”):
The moment the negative assumption is declared, along with the intention of falsifying it by means of a future contradiction, a cognitive strain is set up in the mind of the learner, perhaps because of the difficulty of living in a false world, still operating as if it were real. This cognitive strain grows (linearly?) with the time spent living in this world, i.e. with the distance between the negative assumption and the terminal contradiction. Perhaps the feeling of frustration and incomprehensibility is proportional to the length of the ‘negative stretch’ of the proof. (p. 324)
Although much work has been done in building a general theory of cognitive load (e.g., the different types of load, gathering evidence for CLT, how to adapt teaching based on CLT), it appears that almost no empirical work has gone into measuring/studying the relationship between PBC and CLT, hence the Unstudied label.
Contradiction Hypotheses
These hypotheses center on a unique feature of a PBC: the contradiction itself. Given that it is not present in other types of proof, one might suspect that the act of seeking out and identifying the presence of a contradiction could provide additional challenges for students.
Recognition Hypothesis [Unstudied]
The Recognition Hypothesis suggests that students may struggle to identify that a contradiction has been reached when in fact it has, or they may believe a contradiction has been reached when it has not. One reason for the former issue is that a mathematical statement may contradict a wide variety of things: itself, a common fact the student does not know/has forgotten, a statement from elsewhere in the proof, the supposition of the problem, an axiom, etc. This recognition failure might lead to backtracking or not finishing the proof, or the student might continue on to reach a later contradiction, resulting in a less efficient argument. Chamberlain (2017) wrote that “students have even more diffculty identifying a contradiction when it does not directly relate to the primary statement they are trying to prove” (p. 32). In contrast, a student might believe a contradiction has been reached when it has not because mathematical expressions can be subtler than they appear. For example, if a student arrives at “\((\sqrt 3 + \sqrt 6)^{2} + (\sqrt 2 - \sqrt 9)^{2}\) is rational”, they might (falsely) claim a contradiction based on the appearance of the mathematical expression (which reduces to 20). We can find no empirical work exploring this Unstudied hypothesis.
Lack of Target Hypothesis [Unstudied]
With DP, the proposition provides two important guideposts in the proving process. If we must show p⇒q, then we can begin at p with the clear objective of q, or start at q workng backwards toward p. With IP, students must explore the dark abyss of mathematics until a contradiction is uncovered, having neither a clear goal to head toward nor a landing spot from which to work backward. In this sense, no destination, or target, is evident, and the range of possibilities for the contradiction is immense. Antonini (2010) gave a sense of the landscape: “Sometimes, R [the contradiction] could stand for a figure with strange lines or angles that bad (sic) represents a geometrical concept (as it happens in proof by contradiction), an uncommon proposition, a situation not expected because of the didactical contract, etc.” (p. 155). Indeed, Jourdan and Yevdokimov (2016) provided simple examples revealing that a contradiction may arise to a given, an internal result to the proof, or to an external result (see examples 2-6, pp. 60-63). Chamberlain (2017) noted how some problems have many natural targets. In proving ab = 0⇒a = 0 or b = 0, a student using PBC might end at a = 0 and a≠ 0, b = 0 and b≠ 0, or 1 = 0 and 1 ≠ 0. While some authors have discussed the variety of possible targets and hinted at the difficulty a lack of target may create, there appears to be no research for this Unstudied hypothesis.
Affective Hypotheses
The Affective Hypotheses focus on issues related to the emotional and social space in which mathematics is done. Some issues are related to the psychology of students, while others are shaped by teachers, communities of practice, and historical trends.
Socio-Mathematical Hypotheses
Various authors have argued that mathematics, like many disciplines, cannot be understood apart from the social milieu in which it is developed and enacted. While the image of a student sitting alone at home writing a PBC may suggest an act with no social connections, Vygotsky (1987) would disagree: “Writing is also speech without an interlocutor, addressed to an absent or imaginary person or to no one in particular … it is a conversation with a blank sheet of paper” (p. 181). In this sense, writing (or proving) is communication with an imagined audience (and a real audience during grading or publishing), and as such, comes imbued with the expectations of classrooms and societies.
Acceptability Hypothesis [Unstudied]
The Acceptability Hypothesis summarizes the idea that PBC is less accepted or less palatable than other forms of proof (usually, DP). Historical trends are believed to be one force behind this hypothesis. Antonini (2019) noted “in many cases throughout history some mathematicians have discussed its [PBC] acceptability and have proposed to exclude proof by contradiction from proving methods” (p. 794). Gasser (1992) outlined some of these historical moments dating back to at least 1662, many of which argued that while PBC might show that something is true, PBC often falls short of explaining why that thing is true. Furthermore, Gasser explained, from a logical perspective, why people may have felt this way. Compared to an IP, a DP creates a series of true statements, like lights on a strand:
The reasoner who knows that the premises are true will know not only that the conclusion is too, but also that each consequence in the series is also true. Each proposition of the chain of reasoning that goes from the premises to the conclusion constitutes an intermediate conclusion known to be true by the reasoner; each proposition represents new knowledge. Each is a ground for recognizing the truth of further consequences. (p. 44)
Mancosu (1991) catalogued additional historical examples noting the “lower epistemological status” (p. 26) of IP and the failure to engender the feeling of causality that DP often does. More recently, Brown (2017) cited modern resistance to indirect methods, including opposition to Hilbert’s non-constructive proof of the Hilbert Basis Theorem and a recent critique of Cantor’s non-constructive proof establishing the existence of transcendental numbers. As one might expect, these historical themes gained traction in pedagogical spaces (see comments under “Training Hypotheses”). In a 1932 defense of PBC, Seidlin (1932) collected 80 examples (printing only 10) of anti-PBC rhetoric found in DP teaching materials of high school teachers. These included “It [PBC] is the laughing stock of students” and “... it doesn’t really prove” (p. 5). Seidlin concluded his article by writing: “Shall we condemn a method because it has been needlessly disfigured by textbook writers!” (p. 17).
This derision might seem antiquated to current scholars. As Gasser (1992) wrote: “It is also noteworthy that nowadays no one but the intuitionnists [sic] reject indirect proof and even they do not reject it entirely” (p. 45). This turnaround is due, in part, to the 1957 publication of Polya’s “How to Solve It”, wherein the author “claimed that using indirect proof is the height of intellectual achievement, and that it promotes students’ thinking to higher levels” (Hine 2019, p. 29). To date, the influence of these philosophical, historical, and pedagogical trends on students’ understanding of PBC appears largely Unstudied.
Constructive/Destructive Hypothesis
This hypothesis appears to have its origins in Leron’s (1985) paper outlining anecdotal evidence from his own teaching. In brief, his idea is that in mathematics, students prefer to operate in a way that constructs knowledge, always moving from a universe of known results to a larger universe. When writing a PBC, he noted that:
We are about to enter a false, impossible world, and all our subsequent efforts are directed towards ‘destroying’ this world, proving it is indeed false and impossible. We are thus involved in an act of mathematical destruction, not construction. (p. 323)
In essence, he argued that humans would much prefer to erect buildings, rather than show certain designs are not possible by attempting to construct them, all the while waiting for collapse. Antonini and Mariotti (2008) furthered this idea, writing that “students can feel confused and dissatisfied because of the unexpected destruction of the mathematical objects on which the proof was based” (p. 402). Brown (2018) folded these ideas into her “constructive hypothesis” (the source of our name) and notes that this preference for constructive approaches might lessen conviction and understanding in students when working via PBC. Specifically, PBC steers “learners to reason against, rather than with, that which they perceive to be ‘real’” (Brown 2018, p. 4). Other papers have briefly touched on this idea, noting the tension that can arise for students when no mathematical object is constructed by the proof’s end (Bedros 2003, Brown 2013, Harel and Sowder 1998). While this idea is over 30 years old, it appears little empirical work has been done to explore the prevalence and importance of this Unstudied hypothesis.
Conviction Hypothesis
Conviction refers to the degree of certainty a reader has regarding the truth of a mathematical argument or statement. While conviction can be derived from the deductive logic present in proof, students and mathematicians also derive conviction from other sources, including empirical evidence, worked examples, authority, etc. (Weber, Inglis, & Mejia-Ramos 2014). The Conviction Hypothesis suggests that students have greater difficulty deriving conviction from PBCs than via other types of proof.
For some readers, the Conviction Hypothesis may feel like a consequence of students’ difficulties with PBC, rather than a cause. Indeed, when students struggle with an idea, they have trouble deriving conviction from it. We include the Conviction Hypothesis because, while the above logic is certainly in play, so too is the fact that lower conviction can erode the use of an idea (just as distrust in an institution is both the cause and effect of that institution’s decline). Thus, we see PBC and the conviction derived from its use as components in a cyclic system.
Many researchers have explored this issue, offering anecdotal, philosophical, and empirical evidence. Bedros (2003) summarized the early work on conviction:
Past research (Lewis, 1986; Goetting, 1995; Saeed, 1996) that has dealt with students’ preferences and understanding of proofs in general, has indicated that most students find indirect arguments non-convincing. Also, if given the choice, they prefer DPs to indirect ones even when the IPs presented to them are easier to construct and understand. (p. 5)
Despite this statement, the situation is more complex. Brown (2018) noted that for IP “there is a scarcity of empirical evidence to support current claims regarding students’ lacking a sense of conviction” (p. 2). Indeed, evidence to the contrary exists. Tall (1979) gave first-year university students the standard PBC of the irrationality of \(\sqrt 2\) and a more direct argument that focused on prime factorization. He found no statistically significant difference in the proportions that chose each when students selected based on which proof was more understandable/less confusing. In a second study with a less familiar prompt (\(\sqrt {5/8}\)), he found students did prefer a more direct approach when asked to choose based on degree of understanding/confusion. Brown (2018) explored conviction via a series of comparative tasks and ultimately concluded “rather than demonstrating links between students’ sense of conviction and the directness of a proof, what is shown is that familiarity influenced students’ sense of conviction” (p. 12). Furthermore, by analyzing student feedback, Brown was able to show that additional elements are responsible for instilling conviction, like simplicity, conciseness, and the degree to which an argument aligns with a student’s thinking patterns. Thus, we have Inconsistent findings for this hypothesis: While some authors have seen evidence that PBC fails to instill conviction (Bedros 2003; Harel & Sowder 1998; Leron 1985), others have found evidence explicitly contradicting this and pointing to the influence of confounding variables (Brown 2011, 2012, 2018; Tall 1979).
False World Hypotheses
If a statement of the form p⇒q is actually true, then a proof by contradiction, which begins with the assumption of p ∧¬q, will force the student to inhabit a logical world that, in fact, cannot exist. The hypotheses that fall under this label center around the issues that come with this territory.
Impossible Objects Hypothesis [Supported]
Often, the assumption of p ∧¬q in a PBC leads to the postulation of a mathematical object which cannot exist or cannot be drawn. In some cases, this impossibility can be hidden behind notation (e.g., a number which must be both even and odd can be written simply as n). In other cases, the PBC places assumptions on a geometric object which preclude drawing it (e.g., a planar triangle with angle sum more than 180 degrees, lines that must be parallel and intersect, etc.). As such, there was historical pushback on IP as a general method: “Some of the arguments given against usual indirect proof are that it often leads to a distorted and inexact figure ... and that it [IP] requires that [the figure] to be constructed which is actually impossible” (Lazar 1947, p. 234). Documented concerns about impossible figures go back even further: Leadbeater (1937) recounted a paper from about 1907 that objected to PBC because “it required that to be constructed which was experimentally impossible” (p. 28). The Impossible Objects Hypothesis states that the impossible objects sometimes created when using a PBC act as an affective (and operational) hurdle to students.
The evidence for this hypothesis mostly comes in the form of observing how students behave when faced with impossible objects. In some settings, students skirt the affective hurdle by falling back on the imprecise nature of hand-sketching (Baccaglini-Frank et al., 2013; Mariotti and Antonini 2009). This might occur if a “triangle” in a PBC is supposed to have two right angles and the student draws a figure with two nearly right angles. In other research, students will seek out new objects to bridge the impossible and possible worlds. In some cases, this is done through a process known as “abduction” (Antonini 2019; Antonini and Mariotti 2009; Mariotti and Antonini 2009), and in other cases, through a “pseudo-object” (Baccaglini-Frank et al., 2013, 2018; Leung and Lopez-Real (2002). Finally, Koichu (2012) found that “definitions and axioms of geometry can be intellectually necessitated for students by means of the exploration of impossible objects” (p. 2). By using the Penrose tribar and an impossible plane in a tetrahedon (optical illusions that can be drawn but not created), Koichu leveraged the affective discomfort of impossible objects to motivate the selection of particular axioms in Euclidean geometry.
Beyond the representational difficulties inherent to and affordances of impossible objects, students must also have the courage to work with these objects and expect that known theorems may be applied to them (Antonini & Mariotti 2006, 2008). Overall, the Impossible Objects Hypothesis appears Supported, although most of the papers mentioned above are case studies involving small sample sizes.
False Premise Hypothesis [Supported]
This hypothesis suggests that people have difficulty using a statement they suspect is false (p ∧¬q) as the starting point for a series of logical implications. Hine (2019) summarized this idea nicely: “reasoning based on false assumptions induces cognitive strain, because the student does not know what is or what is not true” (p. 31). Researchers have explored this hypothesis for at least the last fifty years. For example, Thompson (1996) cited a 1979 dissertation by Edgar Williams who found that 60% of his sample of Albertan high school students would not make deductions from false hypotheses. Bedros (2003) cited dissertations from the 1980s and 1990s with similar findings in calculus and number theory. Durand-Guerrier (2003) asked students which integers between 1 and 20 would make this implication true: “If n is even, then n + 1 is prime”. She found that students, using the logic of everyday life, first reduced their thinking to those numbers that make the antecedent true (evens), and then checked if they made the consequent true, missing the fact that odd numbers create a false antecedent, and hence, a true conditional. The aversion of working from a false premise has also been observed outside of mathematical settings (Luria 1976; Norenzayan, Choi, & Peng 2007).
Within the mathematical space, Brown (2018) offered a possible explanation for this trepidation. She noted that most students are raised with a standard Euclidean view of logic (axioms are truth, logic creates more truth), while PBC forces a “hypothetico-deductive” view of logic (axioms may or may not be true, logic creates new statements which are valid deductions even if their premises are false). Given this contrast, each act of PBC is then a revolt against the tradition laid down in high school mathematics. While other authors in mathematics education have explored these ideas for students new to PBC (Antonini & Mariotti 2006, 2008; Durand-Guerrier, Boero, Douek, Epp, & Tanguay 2012; Harel & Sowder 1998; Jourdan & Yevdokimov 2016), Davis (2009) explored the hypothesis in experienced mathematicians/scientists. For this group, reasoning from falseness appeared to be a natural act, and Davis catalogued examples of this behavior. These included the advancement of the topology of manifolds, the use of Newtonian physics in classical continuum mechanics, the process of finding roots by substituting best guesses, and even simple situations where one might check for the equality of \(\frac {8}{11}\) and \(\frac 57\) by setting them equal and cross-multiplying. In all these cases, the thinker knows they are likely arguing from falseness, and yet progress can be made by reasoning this way. Taken together, existing research suggests the hypothesis is Supported for students newer to PBC, and that the hypothesis holds less influece for experts.
Foundational Hypotheses
Foundational Hypotheses are related to the logical bedrock on which PBC is built. While “Operational Hypotheses” and “Affective Hypotheses” center on the act of doing PBC and the concomitant emotions at play, Foundational Hypotheses deal with higher-level questions like: Why is PBC valid, what are its logical foundations, and how does it relate to other indirect forms of argumentation? Gasser (1992) pointed out some of the issues at play:
Principles of logic such as those of excluded middle and noncontradiction are also at work [in PBC], but as Aristotle pointed out, these almost always remain unsaid in the course of a proof... It would seem that such principles of logic are (or – what is just as important – are perceived as being) more present in indirect proof than in other sorts of reasoning. For in indirect proof these principles are present not vaguely and abstractly, as being ‘at the basis of all deductive activity’, but they play an active argumentative role in the deduction that is being carried out. (p. 48)
In essence, the hypotheses that follow are based on a simple notion: the logic of how PBC works is simply more complex, more foregrounded, and less normative than that of DP.
Metatheoretical Hypothesis
We take the name “metatheoretical hypothesis” from Brown (2018) whose description and development are based on the work of several other scholars (primarily, Antonini & Mariotti 2008). The idea here is that every statement to prove is actually part of a triplet (S, P, T) consisting of a statement, proof, and theory (e.g., Euclidean axiomatics) in which the proof derives the statement. A PBC is special in that the student does not directly prove S (say, p⇒q) via P, but instead, demonstrates a secondary statement, S∗ (say, p ∧¬q⇒r ∧¬r) via a direct proof P∗ and the same theory T. In addition, the student needs a way (i.e., the logical argument behind why PBC works) of showing that the triplet (S∗,P∗,T) can give rise to (S, P, T), which Antonini and Mariotti (2008) called the “meta-theorem” (MS, MP, MT). With this nomenclature, the Metatheoretical Hypothesis is the claim that students struggle to know the triplet (MS, MP, MT), or fail to see that the triplet (S, P, T) is proved via an alternate triplet (S∗,P∗,T) and a metatheory that relates the two triplets. Brown (2018) summarized her hypothesis by writing that “students’ difficulties gaining conviction from and reasoning with IPs are tied to students’ difficulties reasoning with or accepting the metatheorems required” (p. 5). Epp (2009) spoke to this complexity as well noting that “Even rather simple proofs and disproofs are built atop a normally unexpressed substructure of great logical and linguistic complexity” (p. 313). Note that this hypothesis is not suggesting DP is devoid of a meta-theory (indeed, students of logic will be familiar with terms like “modus ponens”). Rather, the hypothesis suggests that the meta-theory in PBC is more problematic, possibly because the meta-theory of DP is so standard/taken-for-granted that students may forget it is even there.
To date, some research has explored this hypothesis to varying degrees of specificity. For example, when Thompson (1992) asked students to explain how IP functions, almost two-thirds of participants received poor scores when students’ rationales were holistically scored. Bleiler et al. (2014) found similar issues with teachers, noting that they were “focusing on (local) specifics of an argument but overlooking the (global) logical structure of an argument” (p. 107). In an important conference paper, Brown (2016) showed that metatheoretical issues change over time. Students were given two statements: “For all positive integers n, if n mod 3 ≡ 2 then n is not a perfect square” (Theorem 5 in the paper; S in the above notation) and “There exists no positive integer n such that n mod 3 ≡ 2 and n is a perfect square” (Statement A in the paper; S∗, essentially). Students were then asked if one could prove Theorem 5 by proving Statement A. Among 35 undergraduates who had taken Introduction to Proof, Real Analysis, and Abstract Algebra classes, 83% correctly answered yes, suggesting knowledge that S∗⇒S. Among a group of 21 novice provers, 42.8% answered incorrectly and 23.8% showed hesitancy by answering “Yes-no-yes”. In the same study, 100% of 6 mathematicians answered correctly. Finally, when asked which statement they would pursue first when attempting to prove Theorem 5, novices preferred Theorem 5 (76.2% Theorem 5, 9.5% Statement A, 14.3% No Response), while this preference dissolved among experienced proof writers (57.1% Theorem 5, 42.9% Statement A) and mathematicians (33.3% Theorem 5, 33.3% Statement A, 33.3% Either).
In the related setting of proof by contraposition (here S∗ is ¬q⇒¬p), Antonini and Mariotti (2008) described a college student Fabio who was confident in the proof that n odd ⇒n2 odd [(S∗,P∗,T)], but was unsure if this result proved the original claim that n2 even ⇒n even [(S, P, T)], perhaps due to weaknesses in the metatheory that connected the two triplets. Similarly, Stylianides et al. (2004) found specific examples of students who believed in the veracity of the secondary statement, S∗ (¬q⇒¬p), but who failed to see how this could be related to the primary statement, S (p⇒q). Inglis and Simpson (2008) looked more generally at the connections students held among the four statements p⇒q, ¬p⇒¬q, q⇒p, and ¬q⇒¬p. In this more general setting, the authors found that students struggle with questions related to conditionals, suggesting weaknesses in basic logic, and hence, suggesting that advanced logic (such as appears in PBC) might suffer. Overall, this hypothesis is Supported by research from many authors.
Argumentation Rift Hypothesis [Supported]
Some scholars find the logical challenges asserted by the “Metatheoretical Hypothesis” somewhat counterintuitive. As Reid and Dobbin (1998) wrote: “Formal proofs by contradiction are difficult for many students, however, the ease with which quite young students use contradiction in arguments suggests that it is not the reasoning itself which causes the problem” (p. 46). Indeed, research has shown that children naturally engage in counterfactual/indirect reasoning in everyday life and unprompted mathematical settings (Antonini 2003; Freudenthal 1973; Maher et al., 2007; Rafetseder et al., 2013; Reid and Dobbin 1998). The Argumentation Rift Hypothesis claims that some divide exists between the indirect thinking people do in everyday life and more formal PBC settings, and as such, skills in the former do not immediately carry over to the latter.
Some work has been done to understand and verify the existence of this divide. For example, Reid and Dobbin (1998) conjectured that it is due, in part, to an absence of “emotioning” in formal mathematical PBC settings compared to its presence in everyday argumentation. As an example, Reid and Dobbin found that children playing the game Set needed to be sure they had found the complete solution (emotioning present). In some mathematical settings that use PBC, it is possible that this drive is not present. For example, the authors point to the proof that \(\sqrt 2\) is irrational, noting that the statement is already part of most students’ concept images by the time they encounter the formal proof (see also Lin et al., 2003; Tall 1979). To increase emotioning, thereby facilitating the work of PBC, Hadas et al. (2000) argued for the use of dynamic geometry systems, while Harel and Sowder (1998) stressed the importance of authentic inquiry.
Another possible cause for the rift is the differing logic present in PBC and everyday settings (Lazar 1947; Lin et al., 2003). Brown (2016) noted: “There is a profusion of research from cognitive psychology demonstrating that humans’ ways of reasoning do not fully align with the forms of reasoning used in standard logic” (p. 581). As a simple example of these differences, Stylianides et al. (2004) offered students the prompts: “If a car doesn’t have fuel, it will not move” and “The car has fuel”. They then asked about the conclusion “The car will definitely move”. Several students argued correctly (the car may not move), not by thinking about logical statements, but based on personal experiences with driving (e.g., the engine might be broken). The authors wrote that “adult reasoners’ application of knowledge about judgments of necessity is affected by personal knowledge or beliefs about the argument content” (p. 155).
An additional reason for the rift between indirect argumentation and proof is that argumentation often takes place in the verbal, not symbolic, context. Stylianides et al. (2004) studied the importance of the reasoning domain when exploring logical ability. They found that education majors were able to reason about contraposition far more effectively in verbal domains (67% correct) compared to symbolic domains (20%, n = 70). Some will find this result unsurprising, for even within the quantitative space, not all forms of indirect reasoning are logically equivalent. For example, Otani (2019) used Toulmin’s (2005) argumentation model to contrast PBC with null hypothesis significance testing (NHST). By comparing the data, warrant, backing, qualifier, rebuttal, and claim in each setting, the author highlighted key differences between the two forms of argument. For example, when arriving at a contradiction (data) in a PBC, classical logic (backing) guarantees (qualifier) that p⇒q (claim). In NHST, finding a p-value < α based on observations (data) allows one to tentatively (qualifier) reject H0 (claim) based on probability theory (backing). While both techniques have an indirect flavor, PBC advances with logical certainty, while NHST advances with probabilistic hopefulness. Otani offered a caution within the quantitative space that likely applies as one thinks more generally about the argumentation rift: “Many students tend to fall into the illusion that the analogical approach with mathematical proof by contradiction is applicable to hypothesis testing in spite of the fact that the analogy does not actually work” (p. 2). Overall, this hypothesis is Supported in the literature.
Conflation Hypothesis [Supported]
The Conflation Hypothesis states that people experience difficulty with PBC because it shares structural and logical elements with other forms of IP (e.g., proof by contraposition, proof by counterexample). Specifically, some PBCs argue from p ∧¬q to ¬p, hence arriving at the contradiction p ∧¬p. If the assumption of p is not actually used to derive ¬p, these arguments can be presented more simply as ¬q⇒¬p, a proof by contraposition. Given that many students learn these techniques within a short span (say, in an Introduction to Proof course), it is understandable why they might intertwine in students’ minds. To date, some work has been done on this topic, often in the form of research asking participants to identify the type of proof being used in some prompt. For example, Bleiler et al. (2014) found that teachers had trouble articulating differences between proof by contraposition and PBC when offering feedback to students, but not when differentiating these settings for themselves. In a different study of eight prospective primary school mathematics teachers, five misidentified a PBC as a proof by contraposition (Doruk and Kaplan 2018). In a larger study of 172 preservice teachers (Doruk 2019), only 36% could correctly identify a PBC as such, while 37% incorrectly chose proof by contraposition as the proof type. Confusion was present even among those who answered correctly, for in interviews, subjects tended to focus on superficial features, such as particular phrases (“whether or not”, “the contrary”), when identifying proof types, rather than deep logical structures. The tendency to confuse PBC and contraposition has also been seen in students (Goetting 1995; Stylianides et al., 2004). To add to the confusion, Thompson (1996) found evidence of students interchanging PBC and proof by counterexample. Given the above work on both teachers and students, the Conflation Hypothesis is Supported.
Discussion and Future Directions
In the previous two sections, we discussed our systematic review of the research on PBC and then leveraged this literature base to build the HFPBC. In this section, we offer some high-level thoughts for the field moving forward.
First, while organizational tools like Fig. 1 can be helpful in structuring knowledge and orienting researchers, they also can mislead people. For example, while the leaf nodes are printed using the same size and darkness of font, this does not imply they are equally developed or impactful for students. We hope our labelling system (Unstudied, Emerging, Inconsistent, and Supported) will remind the field of the lay of the land. In addition, the physical space between these hypotheses does not imply they are independent. To the contrary, we believe they have strong interaction effects. For example, Brown (2016) noted that students’ difficulties with understanding how PBC works (“Foundational Hypotheses”) were partly the result of textbooks not adequately training students on formal logic (“Training Hypotheses”). Antonini (2019) argued that “even if a person formally knows that a statement has been proved, this knowledge is not always associated with the feeling that the statement is necessarily true” (p. 794). That is, logical clarity (“Foundational Hypotheses”) is not a sufficient condition for instilling conviction (“Conviction Hypothesis”). Together, these authors trace a path from training through logic to conviction, each layer influencing its successor.
Figure 1 also hides the important influence of context. That is, there is not simply one version of the HFPBC, but rather many, depending on the who, what, when, where, why, and how that a particular researcher is studying. The critical role of context was seen in many of the above hypotheses. For example, Stylianides et al. (2004) found differences between education majors and mathematics majors when exploring proof by contraposition. Certain groups, like mathematicians and Olympiad-level problem solvers have shown great skill in using PBC (Tall et al., 2012). Said simply: what holds for one population (the “who”) may not hold for another. Furthermore, the “Language Filtration Hypothesis” showed that the “where” matters: Mandarin and English structure everyday language differently, presenting unique challenges for negation. Similarly, studies on preservice teachers in Turkey (Demiray & Bostan 2017) and the United States (Bleiler et al., 2014) revealed differences in their understanding of PBC. The importance of “when” was seen in Brown (2016) which revealed differences in views related to PBC among novice, mature, and expert proof writers. Amit and Portnov-Neeman (2017) showed that the “how” of PBC matters: students trained in PBC using one approach performed differently than students trained using a second approach. This study underscored the fact that PBC cannot be viewed as pedagogically agnostic. To speak about the challenges posed by PBC, one must necessarily consider how it was taught, to whom, at what stage of maturity, where in the world, and with what goals.
Looking to the future, we would like to again caution researchers about using language that suggests that DP is easier, more preferred, more convincing, or more anything than IP (or PBC, specifically). While the focus of our review was on identifying possible difficulties surrounding PBC, the explicit comparison of DP and IP was a much-discussed theme in (and natural subset of) the reviewed papers. Surprisingly, we found little empirical evidence supporting any such claims, despite a long list of anecdotal, historical, and philosophical reasons why they might be the case. In addition, we feel these claims ignore the nuances that underpin a real conversation comparing the two proof types (e.g., for whom? in what settings? at what experience levels? on what particular problems? with what training?). Some of the best work comparing DP and IP comes from Brown (2011, 2018), who found that comparisons across proof types are muddied by a multitude of confounding variables including proof simplicity, conciseness, familiarity, and alignment with students’ existing thinking.
One option moving forward is to stop the binary focus on DP versus IP and to simply explore the challenges present within PBC. The tripartite structure of Fig. 1 suggests that the situation is incredibly complex, and the research literature backs this up. Antonini (2019) provided an important example of this using the case of Fabio, a senior undergraduate (and probably the most-cited student in the entire PBC literature). Despite understanding the structure of PBC (“Foundational Hypotheses”) and producing PBCs (“Operational Hypotheses”), he appeared to have strong affective reservations with the technique, noting “the absurdity is ... at least embarrassing. You reach a contradiction ... so what? You haven’t proved anything! ... [Y]ou haven’t shown it to me” (p. 797). This vignette suggests that even when behavior and logic are in place, affect may be out of step. As such, attending to only certain hypotheses or sub-trees of the HFPBC may leave researchers with an incomplete view of PBC in a given population.
Finally, researchers will need to reconcile the HFPBC with their own views on PBC. Because Fig. 1 was created from a position of inclusivity, some of the hypotheses may be incompatible with certain theoretical viewpoints or methodological approaches to studying PBC. Indeed, we saw a huge range of approaches to the latter: high-level statistics for performance on a single (or many) PBC problems, surveys asking students to identify which proof type is used in a given proof, side-by-side comparisons of DP and PBC, clinical interviews related to PBC, naturalistic mathematical settings with and without technology in which students use PBC, non-mathematical settings that use indirect argumentation, teaching experiments, and historical/textbook analyses. As an example of the above-mentioned reconciliation, readers might explore our companion paper (Rabin and Quarfoot, in press) which focused on PBC problems within an “Introduction to Proof” course. We found the most success by looking at a small subset of the hypotheses using an approach combining students’ homework solutions, exam solutions, and interviews. Students’ written work was useful for thinking about “Operational Hypotheses”, while interviews gave the chance to explore all three sub-trees of Fig. 1. Whatever methodology researchers choose, they should take care to ensure their tools can actually help study the hypotheses they are interested in developing.
Ultimately, it is the job of researchers within a given field to bring organization to their growing universe. We believe our literature review and its distillation into the HFPBC are an important step forward for those interested in PBC, and proof more generally. Indeed, we sense that the research on direct proof might also benefit from such an effort. Furthermore, we hope this paper can act as a PBC field-wide reset, inspiring researchers to revisit supposed truths (e.g., comparing DP to IP, citing specific hypotheses as paramount, etc.) and offering new directions for additional work.
References
Amit, M., & Portnov-Neeman, Y. (2017). Explicit teaching of strategies - The case of proof by contradiction. In Mathematics education for the future project 14th international conference: Challenges in mathematics education for the next decade. Hungary.
Antonini, S. (2001). Negation in mathematics: Obstacles emerging from an exploratory study. In M. van den Heuvel-Panhuizen (Ed.) Proceedings of the 25th conference of the international group for the psychology of mathematics education, (Vol. 2 pp. 49–56). The Netherlands: Utrecht.
Antonini, S. (2003). Non-examples and proof by contradiction. In N.A. Pateman, B.J. Dougherty, & J. Zillox (Eds.) Proceedings of the 2003 joint meeting of PME and PMENA. Honolulu, (Vol. 2 pp. 49–55).
Antonini, S. (2010). A model to analyse argumentations supporting impossibilities in mathematics. In Proceedings of the 34th conference of the international group for the psychology of mathematics education. Belo Horizonte, (Vol. 2 pp. 153–160).
Antonini, S. (2019). Intuitive acceptance of proof by contradiction. ZDM Mathematics Education, 51(5), 793–806. https://doi.org/10.1007/s11858-019-01066-4.
Antonini, S., & Mariotti, M. A. (2006). Reasoning in an absurd world: Difficulties with proof by contradiction. In Proceedings of the 30th PME conference. Prague, Czech Republic, (Vol. 2 pp. 65–72).
Antonini, S., & Mariotti, M.A. (2007). Indirect proof: An interpreting model. In D. Pitta-Pantazi G. Philippou (Eds.) Proceedings of the Ffth Congress of the European Society for Research in Mathematics Education CERME5. Larnaca, Cyprus: University of Cyprus and ERME (pp. 541–550).
Antonini, S., & Mariotti, M. A. (2008). Indirect proof: What is specific to this way of proving? ZDM Mathematics Education, 40(3), 401–412. https://doi.org/10.1007/s11858-008-0091-2.
Antonini, S., & Mariotti, M. A. (2009). Abduction and the explanation of anomalies: The case of proof by contradiction. In V. Durand-Guerrier, S. Soury-Lavergne, & F. Arzarello (Eds.) Proceedings of the Sixth Congress of the European Mathematical Society for Research in Mathematics Education, (pp. xx–xx). Lyon, France: Institut National de Recherche Pédagogique and ERME.
Baccaglini-Frank, A., Antonini, S., Leung, A., & Mariotti, M. A. (2013). Reasoning by contradiction in dynamic geometry. PNA, 7(2), 63–73.
Baccaglini-Frank, A., Antonini, S., Leung, A., & Mariotti, M. A. (2018). From pseudo-objects in dynamic explorations to proof by contradiction. Digital Experiences in Mathematics Education, 4(2-3), 87–109.
Barnard, A. D. (1995). The impact of meaning on students’ ability to negate statements. In L. Meira D. Carraher (Eds.) Proceedings of the nineteenth international conference for the psychology of mathematics education. Recife, Brazil, (Vol. 2 pp. 3–10).
Barnard, T., & Tall, D. (1997). Cognitive units, connections and mathematical proof. In E. Pehkonen (Ed.) Proceedings of PME 21. Lahti, Helsinki, (Vol. 2 pp. 41–48).
Bedros, V. (2003). An exploratory study of undergraduate students’ perceptions and understandings of indirect proofs. (Doctoral dissertation). Available from ProQuest database. (3094873).
Bleiler, S. K., Thompson, D. R., & Krajčevski, M. (2014). Providing written feedback on students’ mathematical arguments: Proof validations of prospective secondary mathematics teachers. Journal of Mathematics Teacher Education, 17(2), 105–127. https://doi.org/10.1007/s10857-013-9248-1.
Brown, J. S., Collins, A., & Duguid, P. (1989). Situated cognition and the culture of learning. Educational Researcher, 18, 32–41.
Brown, S. (2011). An investigation of students’ proof preferences: The case of indirect proofs. In S. Brown, S. Larsen, K. Marrongelle, & M. Oehrtmann (Eds.) Proceedings of the 14th annual conference on research in undergraduate mathematics education, (Vol. 4 pp. 31–36).
Brown, S. (2012). Making jumps: An exploration of students’ difficulties interpreting indirect proofs. In S. Brown, S. Larsen, K. Marrongelle, & M. Oehrtmann (Eds.) Proceedings of the 15th annual conference on research in undergraduate mathematics education, (Vol. 2 pp. 7–16).
Brown, S. (2013). Partial unpacking and indirect proofs: A study of students’ productive use of the symbolic proof scheme. In S. Brown, G. Karakok, K.H. Roh, & M. Oehrtman (Eds.) Proceedings of the 16th annual conference on research in undergraduate mathematics education. Denver, CO, (Vol. 2 pp. 47–54).
Brown, S. (2016). When nothing leads to everything: Novices and experts working at the level of a logical theory. In T. Fukawa-Connelly, N. Infante, M. Wawro, & S. Brown (Eds.) Proceedings of the 19th annual conference on research in undergraduate mathematics education (pp. 579–587).
Brown, S. (2017). Who’s there? A study of students’ reasoning about a proof of existence. International Journal of Research in Undergraduate Mathematics Education, 3(3), 466–495. https://doi.org/10.1007/s40753-017-0053-6.
Brown, S. (2018). Are indirect proofs less convincing? A study of students’ comparative assessments. The Journal of Mathematical Behavior, 49, 1–23. http://www.sciencedirect.com/science/article/pii/S0732312316302000.
Byham, F. C. (1969). Indirect proof in geometry from Euclid to the present. Unpublished doctoral dissertation, The Ohio State University.
Centre for Education Statistics and Evaluation. (2017). Cognitive load theory: Research that teachers really need to understand (Tech Rep.). Sydney NSW, Australia.
Chamberlain Jr., D.J. (2017). Investigating the development of proof comprehension: The case of proof by contradiction. Unpublished doctoral dissertation. https://scholarworks.gsu.edu/cgi/viewcontent.cgi?article=1051&context=math_diss.
Corbin, J. M., & Strauss, A. (1990). Grounded theory research: Procedures, canons, and evaluative criteria. Qualitative Sociology, 13(1), 3–21. https://doi.org/10.1007/BF00988593.
Davis, C. (2009). The role of the untrue in mathematics. The Mathematical Intelligencer, 31(3), 4–8.
Dawkins, P.C., & Karunakaran, S.S. (2016). Why research on proof-oriented mathematical behavior should attend to the role of particular mathematical content. The Journal of Mathematical Behavior, 44, 65–75. http://www.sciencedirect.com/science/article/pii/S0732312316301304.
Demiray, E., & Bostan, M. I. (2017). Pre-service middle school mathematics teachers’ evaluations of discussions: The case of proof by contradiction. Mathematics Education Research Journal, 29(1), 1–23.
de Villiers, M. (1990). The role and function of proof in mathematics. Pythagoras, 24, 17–24.
Doruk, M. (2019). Preservice mathematics teachers’ determination skills of the proof techniques: The case of integers. International Journal of Education in Mathematics Science and Technology (IJEMST), 7(4), 335–348.
Doruk, M., & Kaplan, A. (2018). Prospective mathematics teachers’ strategies for evaluating the accuracy of proofs in the field of analysis. Çukurova Üniversitesi Eğitim Fakültesi Dergisi, 47(2), 623–666.
Dubinsky, E., & Yiparaki, O. (2000). On student understanding of AE and EA quantification. In E. Dubinsky, A. Schoenfeld, & J. Kaput (Eds.) Research in collegiate mathematics education, IV (pp. 239–289). Providence: American Mathematical Society.
Durand-Guerrier, V. (2003). Which notion of implication is the right one? From logical considerations to a didactic perspective. Educational Studies in Mathematics, 53(1), 5–34. https://doi.org/10.1023/A:1024661004375.
Durand-Guerrier, V., Boero, P., Douek, N., Epp, S.S., & Tanguay, D. (2012). Examining the role of logic in teaching proof. In G. Hanna M. de Villiers (Eds.) Proof and proving in mathematics education: The 19th ICMI study. https://doi.org/10.1007/978-94-007-2129-6_16 (pp. 369–389). Dordrecht: Springer.
Epp, S.S. (1998). A unified framework for proof and disproof. The Mathematics Teacher, 91(8), 708–713. http://www.jstor.org/stable/27970751.
Epp, S. S. (2003). The role of logic in teaching proof. The American Mathematical Monthly, 110(10), 886–899. https://doi.org/10.1080/00029890.2003.11920029.
Epp, S. S. (2009). The use of logic in teaching proof. In B. Hopkins S. Epp (Eds.) Discrete mathematics resource guide (pp. 313–324). MAA Publications.
Forman, E. A. (2003). A sociocultural approach to mathematics reform: Speaking, inscribing, and doing mathematics within communities of practice. In J. Kilpatrick, W. G. Martin, & D. Schifter (Eds.) A research companion to principles and standards for school mathematics (pp. 333–352). Reston: National Council of Teachers of Mathematics.
Freudenthal, H. (1973). Mathematics as an educational task. Dordrecht: Kluwer Academic Publishers.
Gasser, J. (1992). Argumentative aspects of indirect proof. Argumentation, 6(1), 41–49.
Goetting, M. (1995). The college student’s understanding of mathematical proof. Unpublished doctoral dissertation. University of Maryland, College Park.
Hadas, N., Hershkowitz, R., & Schwarz, B.B. (2000). The role of contradiction and uncertainty in promoting the need to prove in dynamic geometry environments. Educational Studies in Mathematics, 44(1), 127–150. https://doi.org/10.1023/A:1012781005718.
Hanna, G., & de Villiers, M. (2012). Proof and proving in mathematics education: The 19th ICMI study, Vol. 15. Berlin: Springer Science & Business Media.
Harel, G., & Sowder, L. (1998). Students’ proof schemes: Results from exploratory studies. In A. H. Schoenfeld, J. Kaput, & E. Dubinsky (Eds.) Research in collegiate mathematics. III. Providence, RI: American Mathematical Society and Washington, DC: Mathematical Association of America, (Vol. 7 pp. 234–283).
Hine, G. (2019). Proof by contradiction: Teaching and learning considerations in the secondary mathematics classroom. Australian Mathematics Education Journal, 1(3), 28–33.
Inglis, M., & Simpson, A. (2008). Conditional inference and advanced mathematical study. Educational Studies in Mathematics, 67(3), 187–204. https://doi.org/10.1007/s10649-007-9098-9.
Jourdan, N., & Yevdokimov, O. (2016). On the analysis of indirect proofs: Contradiction and contraposition. Australian Senior Mathematics Journal, 30(1), 55–64.
Ko, Y.-Y., & Knuth, E.J. (2013). Validating proofs and counterexamples across content domains: Practices of importance for mathematics majors. The Journal of Mathematical Behavior, 32(1), 20–35. http://www.sciencedirect.com/science/article/pii/S0732312312000363.
Koichu, B. (2012). Enhancing an intellectual need for defining and proving: A case of impossible objects. For the Learning of Mathematics, 32(1), 2–7.
Lazar, N. (1947). The logic of the indirect proof in geometry: Analysis, criticism and recommendations. The Mathematics Teacher, 40(5), 225–240.
Leadbeater, J. G. (1937). Indirect proof in geometry. A defence. The Mathematical Gazette, 21(242), 25–32.
Leron, U. (1985). A direct approach to indirect proofs. Educational Studies in Mathematics, 16(3), 321–325. https://doi.org/10.1007/BF00776741.
Leung, A., & Lopez-Real, F. (2002). Theorem justification and acquisition in dynamic geometry: A case of proof by contradiction. International Journal of Computers for Mathematical Learning, 7(2), 145–165.
Lin, F. L., Lee, Y. S., & Wu Yu, J. Y. (2003). Students’ understanding of proof by contradiction. In N.A. Pateman, B.J. Dougherty, & J. Zilliox (Eds.) Proceedings of the 2003 Joint Meeting of PME and PMENA, (Vol. 4 pp. 443–449). Honolulu.
Luria, A. R. (1976). Cognitive development: Its cultural and social foundations (M. Lopez-Morillas, L. Solotaroff Trans.) London: Harvard University Press.
Maher, C.A., Mueller, M., & Weber, K. (2007). Tracing middle school students’ construction of arguments. In S. Brown, G. Karakok, K.H. Roh, & M. Oehrtman (Eds.) Proceedings of the 29th annual meeting of the North American chapter of the international group for the psychology of mathematics education (pp. 581–587).
Mancosu, P. (1991). On the status of proofs by contradiction in the seventeenth century. Synthese, 88(1), 15–41.
Mariotti, M. A., & Antonini, S. (2009). Breakdown and reconstruction of figural concepts in proofs by contradiction in geometry. In F. L. Lin, F. J. Hsieh, G. Hanna, & M. de Villiers (Eds.) Proof and proving in mathematics education, ICMI study 19 conference proceedings. Taiwan, Taipei, (Vol. 2 pp. 82–87).
Norenzayan, A., Choi, I., & Peng, K. (2007). Perception and cognition. In S. Kitayama D. Cohen (Eds.) Handbook of cultural psychology (pp. 569–594). New York: Guilford Press.
Otani, H. (2019). Comparing structures of statistical hypothesis testing with proof by contradiction: In terms of argument. Hiroshima Journal of Mathematics Education, 12, 1–12.
Pasztor, A., & Alacaci, C. (2005). On people’s incorrect either-or patterns in negating quantified statements: A study. In S. Brown, G. Karakok, K.H. Roh, & M. Oehrtman (Eds.) Proceedings of the 27th annual conference of the cognitive science society, (Vol. 27 pp. 1714–1719). Hillsdale: Erlbaum.
Rafetseder, E., Schwitalla, M., & Perner, J. (2013). Counterfactual reasoning: From childhood to adulthood. Journal of Experimental Child Psychology, 114(3), 389–404. http://www.sciencedirect.com/science/article/pii/S0022096512002007.
Reid, D., & Dobbin, J. (1998). Why is proof by contradiction difficult? In A. Olivier K. Newstead (Eds.) Proceedings of the 22th conference of the international group for the psychology of mathematics education, (Vol. 4 pp. 41–48). South Africa: Stellenbosch.
Robert, A., & Schwarzenberger, R. (1991). Research in teaching and learning mathematics at an advanced level. In D. Tall (Ed.) Advanced mathematical thinking (pp. 127–139). Dordrecht: Kluwer.
Seidlin, J. (1932). In defense of the “indirect” proof. Mathematics News Letter, 4–17.
Selden, J., & Selden, A. (1995). Unpacking the logic of mathematical statements. Educational Studies in Mathematics, 29(2), 123–151. https://doi.org/10.1007/BF01274210.
Shipman, B. A. (2016). Subtleties of hidden quantifiers in implication. Teaching Mathematics and Its Applications: International Journal of the IMA, 35(1), 41–49.
Strauss, A., & Corbin, J. M. (1994). Grounded theory methodology: An overview. In N. K. Denzin Y. S. Lincoln (Eds.) Handbook of qualitative research (pp. 273–285). Thousand Oaks: Sage Publications.
Stylianides, A. J., Stylianides, G. J., & Philippou, G. N. (2004). Undergraduate students’ understanding of the contraposition equivalence rule in symbolic and verbal contexts. Educational Studies in Mathematics, 55, 133–162.
Sweller, J. (1988). Cognitive load during problem solving: Effects on learning. Cognitive Science, 12(2), 257–285.
Sweller, J. (1994). Cognitive load theory, learning difficulty, and instructional design. Learning and Instruction, 4(4), 295–312.
Tall, D. (1979). Cognitive aspects of proof, with special reference to the irrationality of \(\sqrt 2\). In S. Brown, G. Karakok, K.H. Roh, & M. Oehrtman (Eds.) Proceedings of the third international conference for the psychology of mathematics education (pp. 203–205). UK: Warwick.
Tall, D., Yevdokimov, O., Koichu, B., Whiteley, W., Kondratieva, M., & Cheng, Y. -H. (2012). Cognitive development of proof. In G. Hanna M. de Villiers (Eds.) Proof and proving in mathematics education (pp. 13–49). Dordrecht: Springer.
Thompson, D. R. (1992). An evaluation of a new course in precalculus and discrete mathematics. Unpublished doctoral dissertation. University of Chicago, Department of Education.
Thompson, D. R. (1996). Learning and teaching indirect proof. The Mathematics Teacher, 89(6), 474–482.
Toulmin, S. E. (2005). The uses of argument (Updated ed.) Cambridge: Cambridge University Press.
Vygotsky, L. S. (1987). Thought and language. Cambridge: MIT Press.
Weber, K., Inglis, M., & Mejia-Ramos, J. P. (2014). How mathematicians obtain conviction: Implications for mathematics instruction and research on epistemic cognition. Educational Psychologist, 49(1), 36–58. https://doi.org/10.1080/00461520.2013.865527.
Williams, S. R., & Leatham, K. R. (2017). Journal quality in mathematics education. Journal for Research in Mathematics Education, 48(4), 369–396.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interests
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix: Literature Review Articles
Appendix: Literature Review Articles
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Quarfoot, D., Rabin, J.M. A Hypothesis Framework for Students’ Difficulties with Proof By Contradiction. Int. J. Res. Undergrad. Math. Ed. 8, 490–520 (2022). https://doi.org/10.1007/s40753-021-00150-z
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40753-021-00150-z