Abstract
Engineering students particularly struggle with mathematics in the first year of their university studies. A result of these difficulties are high drop-out rates among the engineering students. There are various measures to support the students in their studies such as preparatory courses or bridging courses. The contribution of this research is to investigate the impact of certain factors on engineering students’ success in their first year of studies in a supportive environment which includes a preparatory course, tutorials, a bridging course and a drop-in centre. First, we ask how the students’ use of support measures impact the students’ success. Second, we clarify which affective, motivational and cognitive factors affect the students’ success in mathematics. Our further aim is to investigate the relationships between the factors that impact students’ success. We consider potential factors during the first year of studies. Our results suggest that particularly students’ mathematical abilities before the first semester and a support in tutorials during the first semester account for students’ success in the final exams in the first year of engineering studies.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Mathematics can act as either a “gateway to engineering” or a “gatekeeper, denying entry to otherwise talented would-be engineers” (Winkelman 2009, p. 315). On the one side, mathematics is an important part of the syllabus for engineers that “should enable students to understand, set up and use the mathematical concepts, models and procedures that are used in the application subjects like engineering mechanics, machine dynamics or control theory” (Alpers 2010, p. 2). On the other side, mathematics has been identified as an obstacle for engineering students, particularly those in their first year of study (e.g. Croft and Grove 2006; Harris et al. 2015). Although engineering students seem to perceive mathematics as “an important tool used by competent engineers”, for them, university mathematics often turns out to be a “(usually unwelcome) surprise” (Harris et al. 2015, p. 322).
One result of these problems with mathematics courses was reports of high drop-out rates from various countries (e.g. Godfrey et al. 2010; Heublein 2014; Søgaard Larsen 2013; Troelsen and Laursen 2014). Gómez-Chacón et al. (2015), p. 2117) stated that engineering students “encounter epistemological/cognitive, sociological/cultural and didactical obstacles”. Heublein et al. (2010) identified excessive demands and lack of motivation as the main reasons for an individual to drop out. As a reason for the lack of motivation, some researchers refer to a gap between abstract university mathematics and mathematics that is actually needed to practice the profession (Filho et al. 2016; Wood et al. 2012).
The excessive demands of mathematics – sometimes also reported as a general transition problem (Gueudet 2008; de Guzmán et al. 1998) – cause cognitive problems. As a consequence, various ways of providing educational support were integrated in the first year of engineering students’ studies (e.g. SEFI 2016). Examples are mathematics courses before the regular studies (preparatory courses; cf. Andra 2017), bridging courses during the first semesters or drop-in centres for help from tutors (e.g. Matthews et al. 2013). Suggestions have also been made for improving students’ motivation. For example, Holm et al. (2008) reported that students suggest a “more inductive way of introducing first year students to theoretical mathematical concepts” (Troelsen and Laursen 2014, p. 492) as a strategy to ensure successful study in the first year of university. Härterich et al. (2012) described a project in which the content of the first-year mathematics lectures was connected with practical applications.
Our contribution in this paper is based on a learning environment of a German university that includes established ways for support students in their first year of engineering studies. Thus, regarding a supply-use model (Fend 2002), we refer to engineering students of a German university who have access to several measures of support concerning mathematics, namely preparatory courses, bridging courses during the first semester, weekly exercises and a drop-in centre. However, although engineering students are assisted by several support measures in most German universities, the effectiveness of the support measures is unclear. For example, the drop-out rates of engineering studies remain high. High drop-out rates of about 50% are particularly found for specialised engineering study programmes such as electrical engineering or computer sciences (Heublein and Schmelzer 2018).
For this reason, the aim of this study is to build on existing support measures and to investigate factors concerning students’ motivational, affective and cognitive characteristics as well as factors involved in engineering students’ use of support measures in their first year of studies. Our main questions are:
-
1.
which affective or motivational factors impact students’ success in mathematics in a support environment?
-
2.
which (cognitive) factors concerning previous mathematical knowledge impact students’ success in mathematics in a support environment?
-
3.
which factors concerning the use of support measures impact students’ success in mathematics?
-
4.
which of these factors are main factors affecting students’ success in mathematics if different factors are combined?
To investigate these questions, in this paper, we first describe the aspects of the supply-use model in greater detail. Thus we describe the theoretical constructs presented in the supply-use model and outline the characteristics of the measures to support engineering students. We further discuss the relevant aspects of students’ motivational, affective and cognitive preconditions of learning. Further, we outline our method to analyse about 270 engineering students (in electrical engineering and computer sciences) concerning motivational, affective, and cognitive factors and the students’ use of support measures. Using a statistical approach, we analyse the data in an exploratory way and analyse the impact of individual factors, as well as combinations of different factors, on students’ success in mathematics. On this basis, we discuss the findings concerning our four main research questions, which suggest that students’ mathematical abilities prior to the first semester and support in the form of tutorials during the first semester particularly account for students’ success in the final exams in the first year of engineering studies.
Theoretical Constructs
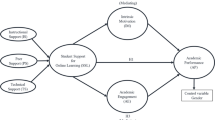
We structure factors that potentially have an impact on students’ success in a supply-use model (Fig. 1). This model was proposed by Fend (2002). The main idea was a theoretical separation of the impact of the supply of learning opportunities, on the one hand, and the use of learning opportunities, on the other hand, on students’ learning results. This model has been used in several studies, in which the factors defined as a supply or a use varied. Similar ideas of how to model factors of students’ learning results or students’ success are discussed for example in Neuville et al. (2007) or in meta-studies of impacts on students’ achievement by Richardson et al. (2012) or Schneider and Preckel (2017). For example, Schneider and Preckel (2017) use the terms “instruction” for factors that impact students’ success concerning a supply. Moreover, they use the term “students” for a student’s use and a student’s preconditions for learning. We outline in the following the specific form of a supply for engineering students, and we outline the decision for investigating specific factors concerning the use of learning opportunities by the engineering students and specific factors concerning the engineering students’ preconditions for learning. Finally, we explain our definition of student success.
Supply-use model of Fend (2002)
With respect to the given environment at the university, the engineering students of our study can access a variety of support measures. This supportive environment is the basis for our study and is briefly outlined in Fig. 2. A more detailed description with regard to the quantity and quality of the supply, including several support measures, is given in Section 2.1.
It seems obvious to assume that the extent of the use of learning opportunities impacts the students’ success. Thus, use is a main aspect in the supply-use model of Fend (2002). Empirical research supports this assumption. For example, as a result of a meta-study, Credé et al. (2010) found that a use of learning opportunities in the form of class attendance is the best predictor of students’ success. Schneider and Preckel (2017), citing the study of Credé et al. (2010), state that class attendance is one of the three most important factors for students’ success. In fig. 3, we outline the aspects of students’ use of learning opportunities, which we further describe in a little more detail in Section 2.2.
There is an enormous number of different factors to consider when measuring motivational, affective and cognitive preconditions for students’ learning (Schneider and Preckel 2017; Richardson et al. 2012). Some of these factors were found to strongly impact the student success, while others showed only a minor impact. For this reason, one rationale for choosing a specific precondition as a possible factor in engineering students’ success is that findings exist which suggest a major impact of these factors on students’ success. One problem with using this method to determine factors for investigation is that the cited meta-studies refer to various university studies that potentially have very different bases for students’ success (e.g. Vedel 2016). For this reason, a second strategy for determining factors to investigate regarding engineering students’ success was pursued, which was to ensure that success in mathematics was an aspect of the findings in the studies on student success. A further aim of selecting possible factors was to find a common theoretical basis for the factors. Finally, several researchers stated that many factors that impact students’ success are known, but that there is little knowledge about how different factors interact to affect students’ success (e.g. Robbins et al. 2004; Isleib et al. 2019). For this reason, one goal of our research is to investigate the impact of not only individual factors on students’ success, but also that of combined factors. We outline motivational and cognitive preconditions for students’ learning as possible factors for students’ success in fig. 4. In Section 2.3, we describe the constructs behind the factors and discuss some empirical findings concerning the significance of the factors.
Finally, although it is possible to define students’ success differently (e.g. Fleischer et al. 2019), we follow Schneider and Preckel (2017) and specifically define students’ success as “grades or performance on an educational achievement test” (Steinmayr et al. 2014). In our case, the test is a written final exam in linear algebra after the first semester and in analysis after the second semester.
Supply Including Support Measures
The university where our study took place provides a syllabus that is common for engineering studies in Germany. The support measures available there for engineering students are also provided by several German universities. To briefly illustrate the syllabus in mathematics and the scope of support measures, we refer to the specific topic of differential calculus. The ability to manipulate sequences and identify the convergence of sequences is a basic goal of the analysis course that is compulsory for the engineering students in the second semester. This basic goal is also tested in a written exam at the end of the second semester. In a written exam, a task for testing this basic goal was to compute the limit of the sequence \( {\left({a}_n\right)}_{n=0}^{\infty } \) with \( {a}_n=\frac{\cos (n)+4}{5n+1} \) (1).
A preparatory course for the future engineering students is provided before the first semester. The preparatory course lasts six weeks and includes daily lectures along with small group exercises. In this course, the students review the essential material of mathematics learnt in school such as rational and real numbers, elementary algebra or functions. Further, students examine subjects such as complex numbers, elements of logic, elements of differential calculus and integral calculus. In the preparatory course, several prerequisites for identifying the limit of the sequence (1) are addressed. For example, trigonometric functions such as the cosine function that are taught in upper secondary schools are reviewed. Also, the solving of inequalities such as \( \frac{3}{5n+1}\le \frac{\cos (n)+4}{5n+1}\le \frac{5}{5n+1} \) is introduced. Finally, the manipulation of polynomials is practised and computing the limits of polynomial sequences is introduced.
In the first week of the first semester, the students are required to pass a preliminary test of skills that includes topics that were addressed in the preparatory course. For example, one task in a preliminary test was to compute \( \underset{n\to \infty }{\lim}\frac{6{n}^2-1}{n-5{n}^2} \). If a student does not pass this test, he or she is required to attend a bridging course during the first semester and to repeat the preliminary test at the end of the first semester. For the students who pass the test, attending the bridging course is voluntary. Taught in the bridging course are the topics from secondary school mathematics that are covered in the preparatory course, on the one hand, and first semester topics, on the other hand.
In accordance with the mathematics curriculum proposed by the European Society for Engineering Education (SEFI 2013), the mathematics syllabus of the engineering students in our study consists of two parts: linear algebra (first semester) and analysis (second semester). In every one of the 15 weeks during a semester, the students received two lectures lasting 90 min each. The syllabus of the analysis lectures contains, for example, the topics real and complex numbers, infimum and supremum, sequences and convergence, series, continuity, limits of functions, one-dimensional differential and integral calculus, the fundamental theorem of calculus, Taylor series, power series, and an outlook to n-dimensional differential and integral calculus. In the analysis lecture, a proof is provided for every theorem and content is provided with mathematical rigor, for example, including ε − δ-definitions for continuity. However, compared to a typical analysis course for mathematics students, the analysis lecture for engineers is less abstract and contains a reduced number of theorems and an extended number of examples. In the lecture, the theoretical background needed for computing the limit of the sequence in (1) is given, i.e. the sandwich rule. That is, suppose that \( \underset{n\to \infty }{\lim }{a}_n=a \) and \( \underset{n\to \infty }{\lim }{c}_n=a \) and that ∀nϵN : an ≤ bn ≤ cn. Then, \( \underset{n\to \infty }{\lim }{b}_n=a \).
In every week of the semester, tutorials were offered for the engineering students. Tutorials were divided in a tutorial for the whole group and small group tutorials, where student tutors would provide exercises as well as personal support for individual engineering students. In every week of the semester, the students received a homework assignment comprised of several tasks. For example, to have them practise finding the limit of a sequence, one task was to examine the convergence of \( {\left({a}_n\right)}_{n=1}^{\infty } \) with \( {a}_n=\frac{\sin (n)}{n} \). The students were required to hand the completed homework assignments over to the tutors. Thus, the effectiveness of the tutorials was measured by the achievement of homework tasks, which was a prerequisite for permission to take the final exam at the end of the semester. Student tutors were made available in a drop-in centre, and they would offer help for individual mathematical problems.
The content regarding sequences should illustrate two characteristics of the supply and the support measures. First, a specific concept from the mathematical syllabus for engineering students, such as the convergence of sequences, is introduced in the lecture with mathematical rigor. The introduction of the concept is done mainly in an applied way, meaning that basic mathematical techniques that are a prerequisite for applying a concept are presented again or are newly provided in a preparatory course and applying of the technique is practised in the tutorials and homework. Thus, according to Alpers (2010), the mathematics lectures for engineering students aim to help them understand mathematical concepts particularly for the purpose of applying them. Second, the written final exams mainly ask that mathematical concepts be applied in procedural tasks (cf. Rittle-Johnson and Schneider 2014). Only a minor portion of the tasks correspond to conceptual tasks (ibid.) such as giving a definition or developing a proof. For this reason, success on the written exam represents the main goal of the mathematics syllabus.
Use of Support Measures
We define the use of a support measure by the participation in a support measure. In the case of the preparatory course and the bridging course, we defined for participation a dichotomous variable (participation/no participation). Furthermore, we define the use of support measures by the number of weeks in which a student participates. This is the case for the weekly tutorials. As outlined above, students’ class attendance was found to have a strong effect on students’ success (Credé et al. 2010).
In addition, we define the use of support measures by achievement. The achievement of the preparatory course is measured by the preliminary test. The achievement in tutorials is measured by the achievement in the tasks of the homework assignment. Following Kuncel and Hezlett (2007), achievement on an academic test is a strong predictor of students’ success. Also, the meta-study of Schneider and Preckel (2017) suggest that prior achievement is an important factor in students’ success.
Affective/Motivational and Cognitive Preconditions for Learning
Self-efficacy and also the further affective constructs in this section could be understood as motivational constructs that are part of a mathematics-related affect (Hannula 2012). According to Bandura (e.g. Bandura 2012), a student’s self-efficacy is his or her belief in his or her “ability to plan and to execute the skills necessary to produce a certain behaviour” (Schneider and Preckel 2017, p. 591). In this study, the certain behaviour is to succeed in a written final exam. Similar to the construct of self-concept outlined below, self-efficacy refers to “individuals’ expectancies for success and perceptions of ability on different tasks [that] play a prominent role in their motivation to perform these tasks” (Wigfield and Eccles 1992, p. 109). The basis for the construct of self-efficacy and all other constructs outlined below is a social-cognitive theory including the assumption that “human functioning is a product of the interplay of intrapersonal influences, the behavior individuals engage in, and the environmental forces that impinge upon them” (Bandura 2012, p. 11). The research of Schneider and Preckel (2017) implies that self-efficacy is the most important affective factor for students’ success. Related research results are given by Zimmerman (2000) or Neuville et al. (2007).
Similar to self-efficacy, the construct of self-concept is a self-belief that is found to impact students’ achievement (Shavelson et al. 1982). Also, Hattie (2009) reported a considerable effect of students’ self-concept on students’ success. In contrast to self-efficacy, the construct of self-concept comprises the whole information of a person about himself or herself. Thus, a student’s expectancy of success in a specific domain such as mathematics is part of this student’s self-concept. A mathematical self-concept could be defined as an individual’s beliefs about his or her mathematical ability and mathematical preferences that impact the student’s success (Byrne 1990).
In addition to constructs representing an individual’s expectancy of success, motivation theory explores constructs that refer to an individual’s value of this success (Wigfield and Eccles 1992; Bandura 2012). Richardson et al. (2012) report motivational factors that are related to assignment of value as possible impacts on students’ success, although the impact is somewhat low. Schneider and Preckel (2017) also refer to various value-related motivational factors that impact students’ success. However, a large percentage of these motivational factors seem to have a low impact on students’ success. By contrast, Neuville et al. (2007) emphasise value according to the expectancy-value theory of Wigfield and Eccles (1992) as a predictive for students’ success. Also, German studies report the impact of these motivational factors on students’ success (Heublein et al. 2010; Fleischer et al. 2019). In the expectancy-value theory of Wigfield and Eccles (1992), achievement-related values are a main part of an individual’s motivation for doing a task. An intrinsic value, an attainment value, a utility value and costs are part of achievement-related values. An intrinsic value includes a student’s interest. Interest could be understood as a student’s development of an appreciation for a specific subject such as mathematics (Wild and Möller 2009). This definition involves the necessity to regard interest in a given context. Attainment value is defined “as the personal importance of doing well on the task”, “utility value is determined by how well a task relates to current and future goals” and costs are “conceptualized in terms of the negative aspects of engaging in the task, such as performance anxiety [or] the amount of effort needed to succeed” (Eccles and Wigfield 2002, pp. 119–120).
Affective constructs beyond motivational constructs seem to have merely a minor impact on students’ success (e.g. Richardson et al. 2012). All the motivation constructs that we selected could be integrated in the well-developed motivation theory of Wigfield and Eccles (1992), that is, expectancy-value theory.
The relationships mentioned so far are partly based on studies in which the focus is not on mathematics. However, the reported results concerning relationships between motivational variables and students’ success serve as an orientation for our study. Finally, research has yielded ambiguous results concerning the development of motivational variables in the first year of study, showing some motivational variables as increasing and some decreasing (Brahm and Jenert 2014; Kyndt et al. 2015).
Concerning cognitive preconditions for students’ learning, we consider the students’ grades in final school exams. Although we restrict the cognitive preconditions for learning to this single variable, the meta-study of Schneider and Preckel (2017) suggests that the grade in the final exam is a strong predictor of students’ success. Various other studies agree with this finding (e.g. Robbins et al. 2004; Blömeke 2009; Fleischer et al. 2019).
Method
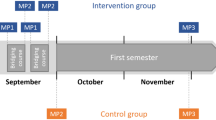
This research is part of the research in the Competence Centre for Higher Education in Mathematics (Kompetenzzentrum Hochschuldidaktik Mathematik, khdm; www.khdm.de). The sample in this study consists of engineering students from a German university. Students in Germany do not need specific grades at the end of secondary school to enter an engineering study programme. For this reason, engineering students are heterogeneous with respect to their final school grades. The university where the study took place is a regional university that is not among the universities whose degree programme for engineering students has a high rank. Data were collected within the first year of engineering studies, as visualised in Fig. 5. None of the authors is directly related to the teaching staff of engineering studies.
In the first semester, we collected the data of 274 engineering students, and in the second semester, we collected the data of 216 students. Since the measurements took place at different points within the first year of studies, the number of students is different in every measurement and, thus, the number of students differs for every analysis provided in the result section. For this reason, we give the specific number of students for each analysis in the result section.
All data collection was voluntary. The students used codes that ensure anonymity. The data collection was in accordance with the ethical standards of the university in which the students were enrolled.
We firstly collected data on the students’ use of support measures regarding:
-
participation in the preparatory course and in the bridging course (dichotomous variables),
-
the number of weeks, in which the students participated in the tutorials (metric variable),
-
the achievement in the preliminary test, and
-
the achievement after tutorials (homework).
The achievement in the preliminary test is a metric variable, since for each task, a dichotomous score (solved, not solved) is used. Cronbach’s alpha for all items in the test is above 0.9. For this reason, we computed the sum of the scores to measure the achievement in the preliminary test.
For different tasks in the homework, different numbers of points are given. Some of the students seem to stop turning in homework after gaining 50% of the points, since 50% of the points in homework allows students to take the final exam. Finally, research has shown that students tend to copy homework instead of solving the tasks for themselves (Göller 2020). For this reason, the results concerning achievement in homework have to be carefully interpreted. Nevertheless, we used this factor as a heuristic.
Secondly, we collected data concerning motivational factors that we outlined in the former section through questionnaires. The questionnaires are based on existing instruments with Likert scales. For every Likert scale, we defined possibilities to rate a statement from 1 (no agreement) to 5 (full agreement). Due to the exploratory design of our study, we assume Likert distances between each choice (cf. Sullivan and Artino 2013). We used the following scales (we provide the items in an open repository: https://osf.io/5m36f/):
-
Self-efficacy: Kunter et al. (2002), 4 items;
-
Self-concept: Adaption of Schöne et al. (2002) in Biehler et al. (2018), 4 items;
-
Interest: Schiefele et al. (1993), 9 items (adapted);
-
Values: Eccles and Wigfield (2002), 8 items (the sub-construct interest is measured with a separate scale; the original items of the other sub-constructs were reduced to items that produced the highest Cronbach’s alpha in a pilot study).
Furthermore, we collected data on cognitive preconditions for learning, which was given by grades on final school exams. Regarding these grades, we made a distinction between a general grade that is an average of grades concerning all subjects in school and the final grade concerning mathematics. The grades were provided by the students.
Finally, we collected data concerning the final exams at the end of the first semester (linear algebra exam) and at the end of the second semester (analysis exam). We also collected data on several demographic variables such as age, sex, schooling, etc. However, we do not refer to these variables in this paper.
One main aim of our study is to investigate the impact of different factors on students’ success in an exploratory way. Therefore, we first make a correlation analysis to measure a possible impact of single factors on students’ success. In this analysis, it is a theoretical assumption that a specific factor predicts students’ success. We report every correlation coefficient which significantly differs from 0. Although hypothesis testing has been criticised in recent decades (e.g. Nickerson 2000), we use these p values in an exploratory way, as a “familiar and useful” way to summarise statistical findings (Spiegelhalter 2017, p. 41). In accordance with the ASA statement on p values, we also report values above 0.05 and report the p values together with effect sizes (c.f. Wasserstein and Lazar 2016). Following Cohen (2013), we understand correlations above 0.5 as high effect and that between 0.3 and 0.5 as medium effect. A further aim of our study is to determine which of the factors mainly have impact on the students’ success and which factors include redundant information. For this, we conduct a multiple regression analysis. Finally, we selectively analyse differences between motivational variables between the first and the second semester using a t-test. For this test, we report Cohen’s d as an effect size. Following Cohen (2013), we understand a d value of 0.2 as small effect, 0.5 as medium effect and 0.8 as strong effect.
Results
The scales that we used to measure the motivational constructs of self-efficacy, self-concept, interest and values showed an appropriate reliability concerning Cronbach’s alpha of at least 0.75. To analyse the relationships among the different constructs in the supply-use model, we restrict the focus to the first semester. Afterwards, we examine the development of both the constructs and the relationships among constructs in the first year of engineering studies.
Relationships among Theoretical Constructs
First, we analysed relationships among the variables and, particularly, between the variables and students’ achievement in the final exam by correlation. In accordance with the supply-use model (Fend 2002), we differentiate in the correlation analysis motivational, affective or cognitive dispositions regarding use of support measures.
A correlation analysis concerning the use of support measures and students’ achievement in the final exam is shown in Table 1. The results of this analysis give evidence that support measures matter. The use of the preparatory course and also the use of the tutorials measured by participation and achievement correlate considerably with the students’ achievement. Only the use of a bridging course seems to have merely a weak influence on the students’ achievement in the final exam. We excluded students’ attendance in the drop-in centre, since only very few students used this support measure.
A correlation analysis concerning students’ cognitive preconditions for learning and students’ achievement in the final exam is shown in Table 2. The correlations among cognitive preconditions and engineering students’ achievement in the final exam in the first semester are significant, although they might be weaker than expected. It is remarkable that the general achievement in the final school exam shows a higher correlation to engineering students’ achievement than the achievement in the school mathematics exam.
A correlation analysis concerning motivational factors and students’ achievement in the final exam is shown in Table 3. The motivational constructs are significantly correlated. The correlations between these factors and students’ achievement in the final exam in the first semester are weaker, but are still statistically significant. Only the correlation between the students’ self-efficacy and the students’ achievement is not significant. The latter result is in contrast to the finding in other studies (e.g. Richardson et al. 2012). We interpret this result as a specific feature of the first two mathematics courses at university, which tend to put excessive demands on students. For this reason, a construct that is more independent of an actual task, like the mathematical self-concept, seems to be more appropriate to measure the expectance of engineering students. For this reason, we focus on the students’ mathematical self-concept.
The correlation analysis provides a lot of statistically significant correlations between the different variables. For this reason, a further task in our research was to identify structures of variables that are predictive for students’ achievement in finals exams. We investigate this question by a multiple regression analysis.
We firstly used regression analysis to investigate the influence of the variables that we assigned to the use of support measures. The sample size in this analysis is n = 81 (engineering students). Since participation in the bridging course showed a weak correlation to the students’ achievement, we excluded this variable from the regression analysis. We also excluded the dichotomous variable regarding the participation in the preparatory course.
The results of the regression analysis (Table 4) gives again evidence that some of the support measures have a strong impact on the students’ achievement. Furthermore, 45.4% of the variance of the students’ achievement can be explained by the use of support measures (corrected R2). Interestingly, a differentiated analysis shows that beyond the achievement in the preliminary test, participation in tutorials seems to have a stronger impact on students’ achievement in final exams than in the students’ achievement in the tutorials. We interpret this finding as a result of students’ tendency to copy homework, which is the basis for achievement in tutorials, instead of paying attention during tutorials (Göller 2020).
Second, we investigated the influence of the motivational factors, that is, self-concept, interest and values. The sample size in this analysis is n = 112. We excluded self-efficacy from this analysis due to the weak correlation of this construct to the students’ achievement in the final exam. The three variables explain only 14.3% of the variance of students’ achievement (R2 = 0.143). According to the correlation analysis, the influence of the motivational disposition is different. As shown in Table 5, only self-concept would show a significant change concerning R2 if this construct is excluded from the regression analysis.
Concerning the influence of the cognitive preconditions for learning, we only refer to the achievement in the final school exam (general). The sample size in this analysis is n = 110. This variable explains only 8.9% of the variance of students’ achievement and has a standardised beta of 0.312, which is statistically significant.
In a further regression analysis, we integrated all variables. Due to the sample size of n = 69 for this analysis (cf. Bortz & Döring for an appropriate sample size in a regression analysis), the following result must be understood as heuristic for building a model for predictive constructs for students’ achievement. As a result of this analysis, the constructs that we used to predict engineering students’ achievement in final exams seem to be considerably redundant. Only the variables achievement in the preliminary test and participation in tutorials result in significant changes in the explained variance when excluded from the regression analysis (Table 6).
Development of Theoretical Constructs in the First Year of Study
A further question in our research refers to the development of engineering students in the first year of studies. Addressing this question, we first compared the scores for the motivational variables, that is, self-efficacy, self-concept, interest and values (see Table 7). For every construct, a decrease during the first year of study is apparent. A remarkable result is the different strengths of the correlations when dividing the four constructs in two groups. Whereas the constructs of values and self-efficacy show a strong correlation between the first two semesters, the constructs of interest and self-concept show a weaker correlation. Except for values (medium effect), the decrease of motivational factors shows a small effect concerning Cohen’s d.
Second, we investigated correlations between further variables that were measured in both semesters, that is, participation in tutorials, achievement in tutorials and achievement in final exams (see Table 8). Each of the correlations is statistically significant. Although a significant correlation was expected between the two final exams, after the first and after the second semester, the strength of this correlation is remarkable.
Finally, we analyse changes in the model of predictors of students’ achievement in the final exam that we developed for the first semester. First, the strong influence of the tutorials is not apparent in the second semester. The standardised beta coefficients show no significant change compared to the first semester. Based on a sample size of 68 students, neither the participation nor the achievement in the tutorials have a significant influence on the achievement in the final exam.
The motivational variables show an increased influence on the students’ achievement. Thus, the constructs of self-concept, of values and of interest explain 24.7% of the variance of students’ achievement in the second semester final exam (analysis). Accordingly, the standardised beta coefficients are slightly higher than in the first semester (Table 9). However, this is also affected by the small sample size (n = 60). Only the values construct shows a significant result when excluded from the regression analysis.
Again, we integrated all factors in a multiple regression analysis. Again, most factors that we used to predict engineering students’ achievement in final exams seem to provide redundant information. Only the variables achievement in the preliminary test and students’ achievement in the first-semester exam concerning linear algebra result in significant changes in the explained variance when excluded from the regression analysis (Table 10). Both variables concerning a sample size of n = 43 students explain 58.1% of the variance in the calculus exam.
Discussion
Since first-year engineering students struggle particularly with mathematics, several support measures including innovative teaching approaches are proposed to facilitate engineering students’ mathematical learning. Although the support measures were mostly developed and used at German universities to reduce the number of students dropping out, the drop-out rates at German universities are still high, because drop out is strongly impacted by excessive demands in mathematics and motivational problems. Based on this finding, two strategies of a further development of the mathematical part of engineering studies are conceivable: First, it is possible to develop further support measures to potentially improve students’ success and to reduce drop-out rates. Second, it is possible to investigate students’ use of support measures, including students’ motivational and cognitive preconditions for learning (cf. Fend 2002), to gain an empirical basis for a further development of engineering studies. The main aim of this paper is to contribute to the second strategy by investigating factors that potentially influence students’ success in mathematics. Thus, applying a supply-use model (Fend 2002), we took the existing supportive environment for granted and regarded individual preconditions for learning and the individual use of support measures as variables that potentially influence first-year students’ success in mathematics.
Regarding our first three research questions, our results show that most of the factors concerning students’ preconditions for learning and students’ use of support measures have a significant impact on students’ success with not less than a medium effect. Since we selected the potential factors on the basis of existing research including meta-studies that indicate these factors as considerably impacting students’ success, our results could be interpreted as expectable. In this sense, our study replicated existing findings concerning engineering studies. However, our fourth research question refers to the impact of combinations of potentially predictive factors for students’ success. In the following, we outline the results concerning single factors and combined factors for the students’ use of support measures and preconditions for learning.
First, students’ use of support measures and tutorials as well as the achievement in a preliminary test or in tutorials are significantly correlated to students’ success. For this reason, support measures seem to matter. Only the bridging course seems to have no impact on students’ success. However, results from multiple regression analysis indicate that only the achievement in a preliminary test and a participation in tutorials are predictive for students’ success, whereas the other factors provide redundant information. This model including achievement in the preliminary test and participation in tutorials explains about 45% of the variance of students’ success. For this reason, the analysis of combinations of factors concerning the use of support measures enhance the results compared to a simple correlation analysis. For students’ success in the second semester, the predictive model including achievement in the preliminary test and achievement in the final exam after the first semester explains about 60% of the variance of students’ success.
Our results regarding the students’ use of support measures may have two implications. The first implication concerns guidance of students when beginning engineering studies. The contribution of this study is not solely that a good result in a preliminary test is worthwhile, but that the result of this preliminary test is predictive for success in mathematics at least in the first year of studies and, thus potentially for success in engineering studies as a whole. A further contribution to a guidance for the students is given by a closer look at the preliminary test. First, differences in the achievement in the preliminary test for engineering students were mostly based on different achievements in tasks concerning elementary functions and elementary algebra. Thus, shortcomings in both subjects seem to be predictive for the students’ success in mathematics and engineering studies in the long term. Thus, referencing Winkelman (2009), the elementary functions and elementary algebra may serve as gateways or gatekeepers to engineering studies. A detailed analysis of this thesis could be a topic for future research.
A second implication of the results concerning students’ use of support measures is to consider a more obligatory use of tutorials in the first semester, since particularly the participation in tutorials seems to impact the students’ success in their first semester. Our interpretation of this result is that constantly working with exercises in mathematical concepts provided in the lectures affects students’ success. By contrast, the achievement in the tutorials, which is measured by the amount of successfully finished homework, provides no further predictive information. Furthermore, a participation in tutorials in the second semester provides no predictive information for the students’ success in their second semester. Our interpretation of this result is as follows. The tutorials in the first semester successfully develop first-year students’ learning strategies (Magen-Nager 2016). However, after the first semester and after developing learning strategies for university studies, tutorials only have a partial further influence on students’ achievement. For investigating this interpretation, the aim of an ongoing study is to collect data of first-year students’ learning strategies.
Finally, since a participation in the bridging course is not correlated with the students’ success, an implication of our research is to reconsider the existence and/or the conception of this support measure.
An unexpected result in this study was that every one of the other factors that correlates with students’ success could be reduced from a predictive model without a loss of information. For example, the achievement in final school exams is not predictive for students’ success in our model, as shown in Table 6 and Table 10. Our results are in contrast to the findings of Blömeke (2009) or Harackiewicz et al. (2002). Also, motivational factors, although significantly correlated with students’ success, seem to have no predictive value for students’ success. Thus, every motivational factor could be excluded from a model predicting students’ success without a significant loss of information. Although this result agrees with the findings of Kuncel and Hezlett (2007), the result is remarkable, since an enormous number of studies refer to the importance of motivational factors for students’ success (e.g. Richardson et al. 2012). However, we do not propose neglecting motivational factors altogether. For example, in our sample, we found a decrease of every motivational variable that was also reported in Brahm and Jenert (2014) or, concerning statistics laden studies, in Eichler and Zapata-Cordona (2016). For this reason, it may be a question for future research whether for example a broader view on applying mathematics in an engineering context, as proposed by Wood et al. (2012) or Filho et al. (2016), would change the development of motivational factors and change the influence of motivational factors on students’ success. A further question is how a decrease of motivation is related to a drop out and, thus, the impact of motivation on students’ success and students’ dropping out is different.
Although our model explains about 45% of the variance of students’ achievement in the first semester and about 60% of the variance of students’ achievement in the second semester, there is still the crucial question of whether further constructs and related factors could explain parts of the remaining variance. As suggested earlier, investigation of learning strategies might serve as a purposeful approach for this investigation. Furthermore, increase of the sample size is desirable. Although we started with 274 students in the first semester, the number of students who participated in our study from the preliminary test to the final exam in the second semester decreased to 43 students. In a future study, we will collect data from a second cohort of engineering students, with the aim of aggregating the samples. However, apart from one analysis, we met the requirements of statistical analyses suggested in Bortz and Döring (2006). Finally, we defined students’ success by the achievement in the final exam. However, it would be a reasonable approach to measure success by a broader construct including further sub-constructs, for example success in other subjects for first-year engineering students or success in developing a professional identity.
Conclusion
First-year engineering students’ success in mathematics could mainly be predicted by mathematical abilities that engineering students demonstrate in a preliminary test before the first semester. The results in this test predict both the achievement in the final exam after the first semester and that in the final exam after the second semester. A further influencing factor on students’ success seems to be the use of support measures during the first semester. However, only a portion of the support measures is used by the students and, thus, could potentially be supportive for engineering students’ success. For this reason, a support measure such as a bridging course may be questioned, whereas measures like a preliminary test may serve as a major instrument for guidance of students. Our results could serve to inform how students could be prepared mathematically for the difficult transition from secondary school to a university study programme. Furthermore, our results imply that an analysis of a combination of factors representing students’ use of a mathematical supply and students’ cognitive and motivational preconditions for learning is important to identify redundant information within the factors. For example, affective and motivational variables as well as the achievement in school exams are found to show considerable correlations to the students’ success in mathematics, but provide only redundant information in comparison to achievement in a preliminary test or the use of tutorials. For this reason, the importance of these factors on students’ achievement could be reconsidered.
Data Availability
Material and data will be provided in an open repository (https://osf.io/5m36f/).
References
Alpers, B. (2010). Studies on the mathematical expertise of mechanical engineers. Journal of Mathematical Modelling and Application, 1(3), 2–17.
Andra, C. (2017). An analysis of freshmen engineering students’ notes during a preparatory mathematics course. In T. Dooley & G. Gueudet (Eds.), Proceedings of the Tenth Congress of the European Society for Research in Mathematics Education (CERME10, February 1–5, 2017) (pp. 1977–1985). Dublin: DCU Institute of Education & ERME.
Bandura, A. (2012). Self-efficacy: The exercise of control. New York: Freeman.
Biehler, R., Hänze, M., Hochmuth, R., Becher, S., Fischer, E., Püschl, J., & Schreiber, S. (2018). Lehrinnovation in der Studieneingangsphase „Mathematik im Lehramtsstudium“ – Hochschuldidaktische Grundlagen, Implementierung und Evaluation (khdm-report 18-07) [teaching innovations at the beginning of mathematics studies in a teacher education program. Conception, implementation, evaluation]. Retrieved from https://kobra.uni-kassel.de/handle/123456789/11018 (28.06.2020).
Blömeke, S. (2009). Ausbildungs- und Berufserfolg im Lehramtsstudium im Vergleich zum Diplom-Studium – Zur prognostischen Validität kognitiver und psycho-motivationaler Auswahlkriterien [success in a teacher training program compared to specialized programs. Predictive value of cognitive and motivational factors]. Zeitschrift für Erziehungswissenschaft, 12(1), 82–110. https://doi.org/10.1007/s11618-008-0044-0.
Bortz, J., & Döring, N. (2006). Forschungsmethoden und Evaluation [methods in research and evaluation]. Heidelberg: Springer-Medizin-Verl.
Brahm, T., & Jenert, T. (2014). The crucial first year: The development of students’ motivation at a business school - a mixed methods study. Leuven.
Byrne, B. M. (1990). Self-concept and academic achievement: Investigating their importance as discriminators of academic track membership in high school. Canadian Journal of Education / Revue Canadienne De L’éducation, 15(2), 173. https://doi.org/10.2307/1495374.
Cohen, J. (2013). Statistical power analysis for the behavioral sciences. Hoboken: Taylor and Francis.
Credé, M., Roch, S. G., & Kieszczynka, U. M. (2010). Class attendance in college. Review of Educational Research, 80(2), 272–295. https://doi.org/10.3102/0034654310362998.
Croft, T., & Grove, M. (2006). Mathematics support: Support for the specialist mathematician and the more able student. MSOR Connections, 6(2), 1–5.
Eccles, J. S., & Wigfield, A. (2002). Motivational beliefs, values, and goals. Annual Review of Psychology, 53, 109–132. https://doi.org/10.1146/annurev.psych.53.100901.135153.
Eichler, A., & Zapata-Cordona, L. (2016). Empirical research in statistics education: Springer Verlag.
Fend, H. (2002). Mikro- und Makrofaktoren eines Angebot-Nutzungsmodells von Schulleistungen [micro-factors and macro-factors in a use-supply model for students‘ achievement]. Zeitschrift für Pädagogische Psychologie, 16(3/4), 141–149. https://doi.org/10.1024//1010-0652.16.34.141.
Filho, P. L., Mercat, C., El-Demerdash, M., & Trgalová, J. (2016). Students’ perceptions of mathematics in engineering courses from partners of MetaMath and MathGeAr projects. In T. Niemi & H.-M. Järvinen (Eds.), Proceedings of the 44th SEFI annual conference 2016 (12th–15th September 2016), Tampere, Finland. European Society for Engineering Education SEFI: Tampere.
Fleischer, J., Leutner, D., Brand, M., Fischer, H., Lang, M., Schmiemann, P., & Sumfleth, E. (2019). Vorhersage des Studienabbruchs in naturwissenschaftlich-technischen Studiengängen [Predicting drop-outs in science studies]. Zeitschrift für Erziehungswissenschaft, 22(5), 1077–1097. https://doi.org/10.1007/s11618-019-00909-w.
Godfrey, E., Aubrey, T., & King, R. (2010). Who leaves and who stays? Retention and attrition in engineering education. Engineering Education, 5(2), 26–40. https://doi.org/10.11120/ened.2010.05020026.
Göller, R. (2020). Selbstreguliertes Lernen im Mathematikstudium [self-regulated learning in mathematics studies]. Wiesbaden: Springer Fachmedien Wiesbaden. https://doi.org/10.1007/978-3-658-28681-1.
Gómez-Chacón, I. M., Griese, B., Rösken-Winter, B., & Gónzalez-Guillén, C. (2015). Engineering students in Spain and Germany – Varying and uniform learning strategies. In K. Krainer & N. Vondrova (Eds.), CERME9: Proceedings of the ninth congress of the European Society for Research in mathematics education (pp. 2117–2126). Prague: Charles University.
Gueudet, G. (2008). Investigating the secondary–tertiary transition. Educational Studies in Mathematics, 67(3), 237–254. https://doi.org/10.1007/s10649-007-9100-6.
de Guzmán, M., Hodgson, B. R., Robert, A., & Villani, V. (1998). Difficulties in the passage from secondary to tertiary education. In G. Fischer (Ed.), Documenta mathematica, proceedings of the international congress of mathematicians: Extra volume ICM, Berlin, 18–27 august 1998 (pp. 747–762). Rosenheim: Geronimo.
Hannula, M. S. (2012). Exploring new dimensions of mathematics-related affect: Embodied and social theories. Research in Mathematics Education, 14(2), 137–161. https://doi.org/10.1080/14794802.2012.694281.
Harackiewicz, J. M., Barron, K. E., Tauer, J. M., & Elliot, A. J. (2002). Predicting success in college: A longitudinal study of achievement goals and ability measures as predictors of interest and performance from freshman year through graduation. Journal of Educational Psychology, 94(3), 562–575. https://doi.org/10.1037/0022-0663.94.3.562.
Harris, D., Black, L., Hernandez-Martinez, P., Pepin, B., Williams, J., & Team, W. T. T. (2015). Mathematics and its value for engineering students: What are the implications for teaching? International Journal of Mathematical Education in Science and Technology, 46(3), 321–336. https://doi.org/10.1080/0020739X.2014.979893.
Härterich, J., Kiss, C., Rooch, A., Mönnigmann, M., Schulze Darup, M., & Span, R. (2012). MathePraxis – Connecting first-year mathematics with engineering applications. European Journal of Engineering Education, 37(3), 255–266. https://doi.org/10.1080/03043797.2012.681295.
Hattie, J. (2009). Visible learning: A synthesis of over 800 meta-analyses relating to achievement. London: Routledge.
Heublein, U. (2014). Student drop-out from German higher education institutions. European Journal of Education, 49(4), 497–513. https://doi.org/10.1111/ejed.12097.
Heublein, U., Hutzsch, C., & Schreiber, J. (2010). Ursachen des Studienabbruchs in Bachelor- und in herkömmlichen Studiengängen. Forum Hochschule [reasons for drop-outs in bachelor programs and traditional programs]. Hannover: Deutsches Zentrum für Hochschul- und Wissenschaftsforschung.
Heublein, U., & Schmelzer, R. (2018). Die Entwicklung der Studienabbruchquoten an den deutschen Hochschulen [The development of drop-out rates at German universities]. Hannover: DZHW.
Holm, C., Laursen, K. B., & Winsløw, C. (2008). Hvorfor gik de ud? En analyse af frafald på årgang 2006 af matematikstudiet [why did they leave? An analysis of drop-outs in year 2006 of the mathematics study]. Copenhagen: University of Copenhagen.
Isleib, S., Woisch, A., & Heublein, U. (2019). Ursachen des Studienabbruchs: Theoretische basis und empirische Faktoren [reasons for a drop-out. Theoretical basis and empirical factors]. Zeitschrift für Erziehungswissenschaft, 22(5), 1047–1076. https://doi.org/10.1007/s11618-019-00908-x.
Kuncel, N. R., & Hezlett, S. A. (2007). Assessment. Standardized tests predict graduate students’ success. Science (New York, N.Y.), 315(5815), 1080–1081, https://doi.org/10.1126/science.1136618.
Kunter, M., Schümer, G., Artelt, C., Baumert, J., Klieme, E., Neubrand, M., Prenzel, K., Schiefele, U., Schneider, W., Stanat, P., Tillmann, K.-J., & Weiß, M. (2002). PISA 2000: Dokumentation der Erhebungsinstrumente. Materialien aus der Bildungsforschung: Nr. 72 [PISA 2000: Documentation of instruments. Materials from educationsl research no 72]. Berlin: Max-Planck-Institut für Bildungsforschung.
Kyndt, E., Coertjens, L., van Daal, T., Donche, V., Gijbels, D., & van Petegem, P. (2015). The development of students’ motivation in the transition from secondary to higher education: A longitudinal study. Learning and Individual Differences, 39, 114–123. https://doi.org/10.1016/j.lindif.2015.03.001.
Magen-Nager, N. (2016). The effects of learning strategies on mathematical literacy: A comparison between lower and higher achieving countries. International Journal of Science and Mathematics Education, 2(2), 306–321.
Matthews, J., Croft, T., Lawson, D., & Waller, D. (2013). Evaluation of mathematics support centres: A literature review. Teaching Mathematics and Its Applications, 32(4), 173–190. https://doi.org/10.1093/teamat/hrt013.
Neuville, S., Frenay, M., Schmitz, J., Boudrenghien, G., Noël, B., & Wertz, V. (2007). Tinto's theoretical perspective and expectancy-value paradigm: A confrontation to explain freshmen's academic achievement. Psychologica Belgica, 47(1), 31. https://doi.org/10.5334/pb-47-1-31.
Nickerson, R. S. (2000). Null hypothesis significance testing: A review of an old and continuing controversy. Psychological Methods, 5(2), 241–301. https://doi.org/10.1037/1082-989x.5.2.241.
Richardson, M., Abraham, C., & Bond, R. (2012). Psychological correlates of university students' academic performance: A systematic review and meta-analysis. Psychological Bulletin, 138(2), 353–387. https://doi.org/10.1037/a0026838.
Rittle-Johnson, B., & Schneider, M. (2014). Developing conceptual and procedural knowledge of mathematics. In R. Cohen Kadosh, A. Dowker, B. Rittle-Johnson, & M. Schneider (Eds.), The Oxford handbook of numerical cognition. Oxford University Press.
Robbins, S. B., Lauver, K., Le, H., Davis, D., Langley, R., & Carlstrom, A. (2004). Do psychosocial and study skill factors predict college outcomes? A meta-analysis. Psychological Bulletin, 130(2), 261–288. https://doi.org/10.1037/0033-2909.130.2.261.
Schneider, M., & Preckel, F. (2017). Variables associated with achievement in higher education: A systematic review of meta-analyses. Psychological Bulletin, 143(6), 565–600. https://doi.org/10.1037/bul0000098.
Schiefele, U., Krapp, A., Wild, K.-P., & Winteler, A. (1993). Der Fragebogen zum Studieninteresse (FSI) [questionnaire for interest concering studies (FSI)]. Diagnostica, 39(4), 335–351.
Schöne, C., Dickhäuser, O., Spinath, B., & Stiensmeier-Pelster, J. (2002). Skalen zur Erfassung des schulischen Selbstkonzepts (SESSKO) [Scales for measuring self-concept in school (SESSKO)]. Göttingen: Hogrefe.
SEFI (2013). A framework for mathematics curricula in engineering education. Brussels. Brussels: European Society for Engineering Education (SEFI).
SEFI (Ed.). (2016). Proceedings of the 18th SEFI mathematics working group seminar. Gothenburg: University of Gothenburg.
Shavelson, R. J., Hubner, J. J., & Stanton, G. C. (1982). Self-concept: Validation of construct interpretations. Journal of Educational Psychology, 74(1), 3–17. https://doi.org/10.3102/00346543046003407.
Søgaard Larsen, M. (2013). Dropout phenomena at universities: What is dropout? Why does dropout occur? What can be done by the universities to prevent or reduce it?: A systematic review. Clearinghouse - research series: 2013:15: Danish clearinghouse for educational research.
Spiegelhalter, D. (2017). Too familiar to ditch. Significance, 14(2), 41.
Steinmayr, R., Meißner, A., Weidinger, A. F., & Wirthwein, L. (2014). Oxford bibliographies online datasets. https://doi.org/10.1093/obo/9780199756810-0108.
Sullivan, G. M., & Artino, A. R. (2013). Analyzing and interpreting data from likert-type scales. Journal of Graduate Medical Education, 5(4), 541–542. https://doi.org/10.4300/JGME-5-4-18.
Troelsen, R., & Laursen, P. F. (2014). Is drop-out from university dependent on national culture and policy? The case of Denmark. European Journal of Education, 49(4), 484–496. https://doi.org/10.1111/ejed.12094.
Vedel, A. (2016). Big five personality group differences across academic majors: A systematic review. Personality and Individual Differences, 92, 1–10. https://doi.org/10.1016/j.paid.2015.12.011.
Wasserstein, R. L., & Lazar, N. A. (2016). The ASA statement on p -values: Context, process, and purpose. The American Statistician, 70(2), 129–133. https://doi.org/10.1080/00031305.2016.1154108.
Wigfield, A., & Eccles, J. S. (1992). The development of achievement task values: A theoretical analysis. Developmental Review, 12(3), 265–310. https://doi.org/10.1016/0273-2297(92)90011-P.
Wild, E., & Möller, J. (2009). Pädagogische Psychologie [Pedagogical psychology]. Berlin: Springer-Verlag Berlin Heidelberg.
Winkelman, P. (2009). Perceptions of mathematics in engineering. European Journal of Engineering Education, 34(4), 305–316. https://doi.org/10.1080/03043790902987378.
Wood, L. N., Mather, G., Petocz, P., Reid, A., Engelbrecht, J., Harding, A., et al. (2012). University students’ views of the role oh mathematics in their future. International Journal of Science and Mathematics Education, 10(1), 99–119. https://doi.org/10.1007/s10763-011-9279-y.
Zimmerman, B. J. (2000). Self-efficacy: An essential motive to learn. Contemporary Educational Psychology, 25(1), 82–91. https://doi.org/10.1006/ceps.1999.1016.
Funding
Open Access funding enabled and organized by Projekt DEAL. This study was funded by the Hessen State Ministry for Higher Education, Research and the Arts.
Author information
Authors and Affiliations
Contributions
Both authors contribute to the paper.
Corresponding author
Ethics declarations
Conflicts of Interest
None.
Code Availability (Software Application or Custom Code)
None.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Eichler, A., Gradwohl, J. Investigating Motivational and Cognitive Factors which Impact the Success of Engineering Students. Int. J. Res. Undergrad. Math. Ed. 7, 417–437 (2021). https://doi.org/10.1007/s40753-020-00127-4
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40753-020-00127-4