Introduction

In numerous instances of engineering practice and scientific research, multi-objective optimization problems (MOPs) [1] are prevalent. Their objectives often conflict with each other, and optimization of these objectives must be done simultaneously. As a consequence, what is usually obtained in MOPs is a group of solutions that are relatively superior among the objectives, known as Pareto optimal solutions [2]. Obtaining a group of solutions that converge to the true Pareto front (PF) [3] as much as feasible and are uniformly distributed on it is the most critical purpose of solving MOPs.

Due to the universality and group-based search characteristics of multi-objective evolutionary algorithms (MOEAs), which can generate multiple solutions in parallel. As a result, MOEAs have been greatly developed, and a significant number of MOEAs have been successfully applied to solve MOPs, for instance, firefly algorithm (FA) [4], genetic algorithm (GA) [5], ant colony optimization (ACO) [6], differential evolution (DE) [7], and particle swarm optimization (PSO) [8]. Among them, PSO was inspired by the foraging behavior of birds. It has the advantages of fast convergence, a simple mechanism, and so on. After some studies, it was found that PSO has good potential to be extended to solve MOPs.

Since the presentation of multi-objective particle swarm optimization (MOPSO) [9] in 2002, many researchers have improved it. MOPSOs can be approximately subdivided into three categories according to different strategies. The first category is MOPSOs based on Pareto dominance relationship. The representative MOPSOs include the speed-constrained MOPSO (SMPSO) [10], the MOPSO based on global margin ranking (MOPSO/GMR) [11], and the vortex MOPSO (MOVPSO) [12]. The second category is indicator-based MOPSOs. The representative MOPSOs include the MOPSO based on virtual Pareto front (MOPSO/vPF) [13], the MOPSO based on R2 indicator (ANMPSO) [14], and the MOPSO based on hypervolume (MOPSOhv) [15]. The third category is decomposition-based MOPSOs. The representative MOPSOs include the MOPSO based on decomposition (dMOPSO) [16], the decomposition-based MOPSO (MPSO/D) [17], the MOPSO based on multiple search strategies (MMOPSO) [18], and the external archive-guided MOPSO (AgMOPSO) [19].

Although the above algorithms improved MOPSO from different perspectives to solve MOPs, there are still two problems that need to be further solved in an expansion of PSO to settle MOPs. How to select appropriate personal best (pbest) and global best (gbest) is the first issue that needs to be solved. Because different pbest and gbest will pilot particles to approximate the true PF in different directions, which influences the search ability of algorithm in the evolutionary process. Selecting appropriate pbest and gbest can efficiently find optimal solutions with good properties. How to effectively maintain the external archive is the second issue that needs to be solved. Since the role of archive is to reserve non-dominated solutions, it provides good candidate solutions for the selection of gbest. Therefore, it is inevitably crucial to maintain the external archive effectively in order to reduce the computational complexity of the algorithm as well as to ensure that the non-dominated solutions in the external archive remain well-distributed.

For the past few years, numerous researchers have intensively investigated the above two problems and put forward many improved MOPSOs. For example, the new selection strategies of pbest and gbest were proposed in the literature [13, 20,21,22]. Li et al. [13] proposed a newly defined virtual generational distance indicator to select appropriate gbest, and designed an adaptive selection strategy of pbest based on different evolutionary states to promote the search efficiency of the algorithm and adaptively strengthen the exploitation and exploration abilities of particles. Wu et al. [20] designed a new selection strategy of gbest according to different evolutionary states monitored by ESE, which adaptively selected global best solutions to enhance the equilibrium between exploration and exploitation. Han et al. [21] chose an appropriate gbest adaptively by introducing the solution distribution entropy, thus improving the search performance in terms of convergence speed and convergence accuracy. Sharma et al. [22] chose the solution with the minimum penalty boundary intersection as gbest of the particle, which improves the performance of algorithm in terms of diversity and convergence. In addition, many researchers [23,24,25] effectively maintained external archive. Han et al. [23] used the gradient method to maintain the external archive and used the gradient information to solve the MOPs, which can obtain good Pareto sets, achieve smaller test errors at a faster rate, and improve the speed of convergence and local exploitation during the evolutionary process. Cui et al. [24] designed the diversity archive and the convergence archive by introducing the two-archive strategy into MOPSO and updated them in different ways to achieve a balance between convergence and diversity. Li et al. [25] updated the external archive by using a method based on dominant difference to improve the discriminability of particles that are difficult to obtain in high-dimensional space, and the experimental results also show that the method has better performance in terms of convergence and diversity and low complexity. From the above-mentioned literature, it is evident that the performance of algorithms depends greatly on the choice of the two best solutions and archive maintenance.

On the basis of the above review and analysis, a multi-objective particle swarm optimization with a competitive hybrid learning strategy (CHLMOPSO) is put forward for the sake of advancing algorithm robustness and achieving harmonious equilibrium between the convergence and diversity in dealing with MOPs. The distinctive contributions of CHLMOPSO that have been put forward are as follows:

(1) CHLMOPSO proposes a new update strategy of pbest. For further enhancement of the optimization ability of the particles, the derivative treatment of the stagnant particles without better pbest is carried out, which is more helpful to find better pbest.

(2) An adaptive strategy is devised to adjust the flight parameters in accordance with the evolutionary state of the particles, which is adjusted by using their ability to find their personal best solutions. This strategy can equilibrate the exploitation and exploration abilities of algorithm.

(3) A competitive hybrid learning strategy is proposed. This strategy mainly combines the advantages of MOPSO and competitive swarm optimizer (CSO) [26], determines the winners and losers through multiple methods of competition, and then updates them by using the updating strategies of MOPSO and CSO, respectively.

(4) An optimal angle distance strategy is proposed to maintain the archive effectively. The optimal angle distance considers the convergence distance of solutions and their minimum angle with other solutions at the same time, so as to increase the convergence speed of algorithm.

The arrangement of the remainder of this paper is as follows. Sections "Preliminaries and Background" and "The Proposed CHLMOPSO" describe the related work and the details of CHLMOPSO, respectively. Sections "Experimental Settings" and "Comparison of Experimental Results" present the experimental portion, in which CHLMOPSO is compared with the comparison algorithms on three suits of benchmark problems to assess the effectiveness of algorithms. In the end, the conclusions of CHLMOPSO are provided in section "Conclusion".

Preliminaries and background

MOPs

In a general case, a MOP [27, 28] can be expressed as:

$$ \begin{gathered} \min \;F\left( x \right) = \left( {f_{1} \left( x \right),f_{2} \left( x \right), \cdots ,f_{M} \left( x \right)} \right)^{T} \hfill \\ \;s.t.\;\;x = \left( {x_{1} ,x_{2} , \cdots ,x_{D} } \right) \in X \hfill \\ \end{gathered} $$
(1)

where \(F\left( x \right)\) represents the objective vector of M-dimension, \(f_{i} \left( x \right)\) represents the objective function of the i-th dimension, M is the number of objectives, and x is a D-dimensional decision vector in the decision space \(X \subset R^{D}\).

The Pareto dominance relationship could be utilized to evaluate the quality of solutions in MOPs for the reason that the objectives of MOPs are in conflict with each other. That is, a solution \(x_{\alpha }\) dominates the other solution \(x_{\beta }\), denoted as \(x_{\alpha } \prec x_{\beta }\), if and only if \(\forall u \in \left\{ {1,2, \cdots ,m} \right\}:f_{u} \left( {x_{\alpha } } \right) \le f_{u} \left( {x_{\beta } } \right) \wedge \exists v \in \left\{ {1,2, \cdots ,m} \right\}:f_{v} \left( {x_{\alpha } } \right) < f_{v} \left( {x_{\beta } } \right)\). A solution in MOPs is generally referred to as a Pareto optimal solution if it is not dominated by any other solution. The set of all Pareto optimal solutions in the decision space is known as Pareto optimal set (PS), and its image in the objective space is termed as Pareto front (PF).

MOPSO

Each particle i in MOPSO [9] encompasses a velocity vector \(v_{i} = \left( {v_{i,1} ,v_{i,2} , \cdots ,v_{i,D} } \right)\) and a position vector \(x_{i} = \left( {x_{i,1} ,x_{i,2} , \cdots ,x_{i,D} } \right)\), where \(i = 1,2, \cdots ,N\), N denotes population size, and D is the dimension of decision space. Subsequently, throughout the t + 1-th iteration, the velocity of the i-th particle is updated as follows:

$$ v_{i,d}^{t + 1} = \omega v_{i,d}^{t} + c_{1} r_{1} \left( {pb_{i,d}^{t} - x_{i,d}^{t} } \right) + c_{2} r_{2} \left( {gb_{i,d}^{t} - x_{i,d}^{t} } \right) $$
(2)

where t is the number of iterations, \(d = 1,2, \cdots ,D\), \(pb_{i}^{t} = \left( {pb_{i,1}^{t} ,pb_{i,2}^{t} , \cdots ,pb_{i,D}^{t} } \right)\) and \(gb_{i}^{t} = \left( {gb_{i,1}^{t} ,gb_{i,2}^{t} , \cdots ,gb_{i,D}^{t} } \right)\) represent pbest and gbest of the i-th particle, respectively, \(\omega\) stands for inertia weight, \(c_{1}\) and \(c_{2}\) denote learning factors, and \(r_{1}\) and \(r_{2}\) represent two random numbers uniformly generated in [0,1]. Then, its position is updated as follows:

$$ x_{i,d}^{t + 1} = x_{i,d}^{t} + v_{i,d}^{t + 1} $$
(3)

The proposed CHLMOPSO

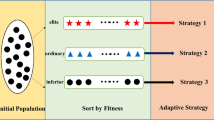
The present paper puts forward a competitive hybrid learning MOPSO to increase the holistic performance of algorithm. The algorithm is primarily made up of four components, and its main framework is shown in Fig. 1. First and foremost, the derivative treatment strategy is carried out on the stagnant particles without better pbest, which is more helpful to find better pbest. In the next place, for the sake of balancing the abilities of exploration and exploitation of algorithm, the flight parameters are adjusted adaptively in accordance with the evolutionary state of particles. Additionally, the winners and losers are determined through multiple competitions, and the hybrid learning strategies of MOPSO and CSO are used to guide them to fly. Finally, the optimal angle distance strategy is set forward to maintain the archive efficiently. The following sections go into great depth on the essential components of CHLMOPSO.

Fig. 1
figure 1

The framework of CHLMOPSO

Full size image

The derivative treatment strategy of stagnant particles

Most present MOPSOs choose their pbest by the Pareto dominance relationship between the existing pbest and the newly discovered solution, while ignoring the evolutionary state of population. Additionally, when the existing pbest and the newly discovered solution do not dominate each other, randomly selecting one of them may cause the particles to fall into the oscillation search process, thus affecting the search efficiency of population.

Here, a derivative treatment strategy is put forward for the sake of ameliorating the issues mentioned above. The algorithm initially determines if there is a dominance relationship between the newly discovered candidate pbest (marked as pbestnew) and the existing pbest (denoted as pbestold) when the particle discovers a new candidate pbest. If pbestnew dominates pbestold, it means that the pbest of the current generation of the particle is better than the pbest of the previous generation, thus indicating that the particle is learning and evolving without stagnation, then pbestnew is determined to be the pbest of the current generation of the particle. Otherwise, if pbestold dominates pbestnew or the two do not dominate each other, which means that the pbest of the particle has not been updated to get new information, that is, there is a stagnation phenomenon, which we call the stagnant particle, and pbestold of the particle will be derived. This strategy helps the stagnant particles to find new possible candidate pbest. The particular description of the derivative process of pbest of the stagnant particles is presented hereunder.

Procedure 1: Adaptively determine the derivative number of new candidate pbest for the stagnant particles during each iteration, where the number of derivatives is constrained by the upper and lower limits of derivatives. Additionally, the number of candidate pbest here is adaptively reduced with the number of iterations. This is to derive a more appropriate number of candidate pbest and improve the optimization ability of particles. Inspired by [29], at the t-th iteration, the derivative number of pbestold of each stagnant particle is determined by Eq. (4):

$$ p\left( t \right) = \left\{ {\begin{array}{*{20}c} {\left( {up - lp} \right) \times \left( {1 - 2 \times \left( {{t \mathord{\left/ {\vphantom {t T}} \right. \kern-0pt} T}} \right)^{2} + {{lp} \mathord{\left/ {\vphantom {{lp} {\left( {up - lp} \right)}}} \right. \kern-0pt} {\left( {up - lp} \right)}}} \right),\;\;\;\;\;0 \le t \le \left( {{T \mathord{\left/ {\vphantom {T 2}} \right. \kern-0pt} 2}} \right)\;\;\;\;\;\;\;\;\;} \\ {\left( {up - lp} \right) \times \left( {2 \times \left( {{{\left( {T - t} \right)} \mathord{\left/ {\vphantom {{\left( {T - t} \right)} T}} \right. \kern-0pt} T}} \right)^{2} + {{lp} \mathord{\left/ {\vphantom {{lp} {\left( {up - lp} \right)}}} \right. \kern-0pt} {\left( {up - lp} \right)}}} \right),\;\left( {{T \mathord{\left/ {\vphantom {T 2}} \right. \kern-0pt} 2}} \right) \le t \le T\;\;\;\;\;\;\;\;} \\ \end{array} } \right. $$
(4)

where \(p\left( t \right)\) is the quantity of candidate pbest that each stagnant particle created for the t-th iteration, T stands for the number of maximum iteration, \(1 \le lp \le up \le 5\), up is the maximum amount of derivatives, and lp is the minimum amount of derivatives.

Procedure 2: After determining the number of candidate pbest to be derived, new candidate personal best solutions \(canpbest = \left\{ {canpbest_{1} ,canpbest_{2} , \cdots ,canpbest_{p(t)} } \right\}\) are generated by deriving the pbestold of the stagnant particles. These are the concrete steps:

$$ canpbest_{i,j} \left( t \right) = pbest_{{old_{\;i,j} }} \left( t \right) - \Delta x\left( t \right)\left( {ub_{j} - lb_{j} } \right) $$
(5)
$$ \Delta x\left( t \right) = \left\{ {\begin{array}{ll} {\left( {x_{u} - x_{l} } \right) \times \left( {2r^{2} + {{x_{l} } \mathord{\left/ {\vphantom {{x_{l} } {\left( {x_{u} - x_{l} } \right)}}} \right. \kern-0pt} {\left( {x_{u} - x_{l} } \right)}}} \right),\;\;\;\;\;\;\;\;\;\;\;\;0 \le r \le 0.5} \\ {\left( {x_{u} - x_{l} } \right) \times \left( {1 - 2\left( {r - 1} \right)^{2} + {{x_{l} } \mathord{\left/ {\vphantom {{x_{l} } {\left( {x_{u} - x_{l} } \right)}}} \right. \kern-0pt} {\left( {x_{u} - x_{l} } \right)}}} \right),\;0.5 < r \le 1} \\ \end{array} } \right. $$
(6)
$$ x_{u} = r_{u} \times ub_{j} \;,x_{l} = r_{l} \times lb_{j} , $$
(7)

where \(canpbest_{i,j} \left( t \right)\) is the j-th dimension of the i-th derivative candidate pbest, \(ub_{j}\) and \(lb_{j}\) represent the upper limit and lower limit, respectively. \(\Delta x\left( t \right)\) represents the additional distance derived, \(x_{u}\) represents the maximum additional distance derived, which is determined by the product of the user-defined upper limit ratio \(r_{u}\) and \(ub_{j}\), \(x_{l}\) represents the minimum additional distance derived, which is determined by the product of the user-defined lower limit ratio \(r_{l}\) and \(lb_{j}\), and r is the absolute value of a Gaussian random number with a mean of 0 and a variance of 1/9. Similar to the literature [29], the parameters \(r_{u}\) and \(r_{l}\) in this paper are selected in the ranges (0.02, 0.7) and [0, 0.02], respectively.

Procedure 3: Firstly, the derivative particles are compared with the pbestold by Pareto dominance. If there is a dominance relationship, the algorithm will determine who becomes pbest of the stagnant particle. If there is no dominance relationship, the algorithm randomly selects one of them as the pbest of the stagnant particles. Algorithm 1 gives the pseudo-code of the derivative treatment strategy of stagnant particles.

figure a

Adaptive strategy for parameters adjustment

The three flight parameters \(\omega\), \(c_{1}\), and \(c_{2}\) are critical in MOPSO. The majority of experiments [21, 23, 24] have demonstrated that the larger \(\omega\) and \(c_{1}\), and the smaller \(c_{2}\) can stimulate better global exploration, while the smaller \(\omega\) and \(c_{1}\), and the larger \(c_{2}\) are conducive to better local exploitation. As a consequence, for the purpose of equilibrating the exploration and exploitation abilities, an adaptive flight parameter adjustment strategy is designed through the evolutionary state of each particle.

Procedure 1: Through the above analysis, the evolutionary state of each particle is first evaluated with respect to the dominance relationship between the current pbest and the previous pbest, thereby designing an adaptive flight parameter strategy.

$$ Ap_{i} \left( t \right) = \frac{{dis_{\max }^{pbest} \left( t \right) + dis_{\min }^{pbest} \left( t \right)}}{{dis_{\max }^{pbest} \left( t \right) + dis_{i} \left( t \right)}} $$
(8)

where \(Ap_{i} \left( t \right)\) is the adaptive parameter of the i-th particle, \(dis_{\max }^{pbest} \left( t \right)\) and \(dis_{\min }^{pbest} \left( t \right)\) stand for the maximum and minimum distance between all particles and pbest, respectively, and \(dis_{i} \left( t \right)\) signifies the distance between the i-th particle and its corresponding pbest.

Procedure 2: Based on the above considerations, according to the adaptive parameters of each particle, the adaptive flight parameters proposed in this paper are expressed as:

$$ \omega_{i} \left( t \right) = \left\{ {\begin{array}{*{20}c} {\omega_{o} \times \left( {1 - Ap_{i} \left( t \right)} \right),\;\;if\;pbest_{i} \left( {t - 1} \right) \prec pbest_{i} \left( t \right)\;\;\;} \\ {\omega_{o} \times \left( {1 + Ap_{i} \left( t \right)} \right),\;\;if\;pbest_{i} \left( {t - 1} \right) \succ pbest_{i} \left( t \right)\;\;\;} \\ {\omega_{o} ,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;if\;pbest_{i} \left( {t - 1} \right) \prec \succ pbest_{i} \left( t \right)\;} \\ \end{array} } \right. $$
(9)
$$ c_{1,i} \left( t \right) = \left\{ {\begin{array}{*{20}c} {c_{{1_{o} }} \times \left( {1 - Ap_{i} \left( t \right)} \right),\;\;if\;pbest_{i} \left( {t - 1} \right) \prec pbest_{i} \left( t \right)\;\;\;} \\ {c_{{1_{o} }} \times \left( {1 + Ap_{i} \left( t \right)} \right),\;\;if\;pbest_{i} \left( {t - 1} \right) \succ pbest_{i} \left( t \right)\;\;\;} \\ {c_{{1_{o} }} ,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;if\;pbest_{i} \left( {t - 1} \right) \prec \succ pbest_{i} \left( t \right)\;} \\ \end{array} } \right. $$
(10)
$$ c_{2,i} \left( t \right) = \left\{ {\begin{array}{*{20}c} {c_{{2_{o} }} \times \left( {1 - Ap_{i} \left( t \right)} \right),\;\;if\;pbest_{i} \left( {t - 1} \right) \succ pbest_{i} \left( t \right)\;\;\;} \\ {c_{{2_{o} }} \times \left( {1 + Ap_{i} \left( t \right)} \right),\;\;if\;pbest_{i} \left( {t - 1} \right) \prec pbest_{i} \left( t \right)\;\;\;} \\ {c_{{2_{o} }} ,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;if\;pbest_{i} \left( {t - 1} \right) \prec \succ pbest_{i} \left( t \right)\;} \\ \end{array} } \right. $$
(11)

where \(\omega_{o} = 0.4,\;c_{{1_{o} }} = 2,\;c_{{2_{o} }} = 2\). During the search process, the proposed adaptive flight parameter adjustment strategy can find the appropriate flight parameters for each particle. This is beneficial to accelerate convergence speed of the algorithm approaching the true PF and balance global exploration and local exploitation abilities of the algorithm.

The competitive hybrid learning strategy

In most meta-heuristic algorithms, it is fundamental to effectively promote convergence and diversity. In the standard MOPSO [9], every particle in the population learns in the same way, so the learning mode of particles is too single, which affects the exploration ability and the diversity. Therefore, inspired by the way of improving population diversity in CSO [26], this part puts forward a competitive hybrid learning strategy to update the particles. Algorithm 2 displays the corresponding pseudo-code.

figure b

Procedure 1: The pairwise competition mechanism in typical CSO only compares the fitness values of two particles, so the method of comparison is relatively simple. Therefore, in this section, a multi-competition method is proposed to determine the winners and losers. Firstly, the basic principle of Pareto dominance is introduced into the competition mechanism to judge whether there is dominance relationship between two randomly selected particles. The non-dominated particle wins and the dominated particle loses if there is a dominance relationship. Otherwise, an evolutionary ability comparison is used to distinguish the winner and loser. The particle with strong evolutionary ability is the winner, and the particle with weak evolutionary ability is the loser. The evolutionary ability here stands for the ability of particles to discover their own personal best. The evolutionary ability of the i-th particle is described as:

$$ E_{i} \left( t \right) = \sqrt {\sum\limits_{m = 1}^{M} {\left( {f_{i,m}^{pbest} \left( t \right) - f_{i,m}^{pbest} \left( {t - 1} \right)} \right)^{2} } } $$
(12)

where \(f_{i,m}^{pbest} \left( t \right)\) and \(f_{i,m}^{pbest} \left( {t - 1} \right)\) denote the m-th fitness value of the personal best solutions of the i-th particle, and M is the number of objectives.

Procedure 2: After the above competition, the hybrid learning strategy is proposed to update the winners and losers. The winners and losers are updated in different ways, and the MOPSO method and CSO method update the winners and losers, respectively, thus increasing convergence and diversity. By combining the updating strategies in MOPSO and CSO, the algorithm has attained favorable equilibrium in convergence and diversity. Therefore, the winners are updated by (2) and (3). Accordingly, the losers are updated to:

$$ v_{l}^{t + 1} = r_{3} v_{l}^{t} + r_{4} \left( {NS_{l}^{t} - x_{l}^{t} } \right) $$
(13)
$$ x_{l}^{t + 1} = x_{l}^{t} + v_{l}^{t + 1} $$
(14)

where \(r_{3}\) and \(r_{4}\) represent two random numbers uniformly generated in [0,1], and \(NS_{l}^{t}\) is a sample of learning randomly selected by the losers from the archive.

The archive maintenance of optimal angle distance

In most existing MOPSOs, as the number of iterations of the algorithm increases, so does the number of non-dominated solutions. Due to the limited size of the archive, an adequate strategy is needed for the effective maintenance of archive. Therefore, in CHLMOPSO, a strategy combining the adaptive grid and the optimal angle distance (OAD) is proposed to maintain the external archive. As shown in Algorithm 3, when the number of non-dominated solutions in the archive is larger than predefined archive size, the solutions with high density in the adaptive grid are deleted by using the OAD strategy, so that the number of stored solutions does not exceed the predefined archive size, so as to improve convergence speed of the algorithm in the evolution process.

Procedure 1: The optimal angle distance considers both the convergence distance (ConD) of solutions and their minimum angle to other solutions with high density. First of all, the convergence distance of the non-dominated solutions is calculated, and the fitness values of solutions need to be transformed before calculation. Denote the fitness values of all solutions in the grid G which have the largest density as \(F_{G} = \left\{ {F\left( {NS_{1} } \right),F\left( {NS_{2} } \right), \cdots ,F\left( {NS_{\left| G \right|} } \right)} \right\}\), where \(\left| G \right|\) is the number of solutions in G. Transform \(F_{G}\) to \(F_{G}{\prime} = \left\{ {F{\prime} \left( {NS_{1} } \right),F{\prime} \left( {NS_{2} } \right), \cdots ,F{\prime} \left( {NS_{\left| G \right|} } \right)} \right\}\) by the following method:

$$ F{\prime} \left( {NS_{i} } \right) = F\left( {NS_{i} } \right) - z_{G}^{\min } $$
(15)

where \(NS_{i}\) is the i-th non-dominated solution in the grid G, \(i = 1,2, \cdots ,\left| G \right|\), \(F\left( {NS_{i} } \right)\) and \(F{\prime} \left( {NS_{i} } \right)\) are the fitness values before and after the transformation of the i-th non-dominated solution in the grid G, respectively, and \(z_{G}^{\min } = \left( {z_{G,1}^{\min } ,z_{G,2}^{\min } , \cdots ,z_{G,m}^{\min } } \right)\) represents the smallest fitness value in each dimension of \(F_{G}\). Then, the convergence distance of the solutions is calculated by Eq. (16).

$$ ConD\left( {NS_{i} } \right) = \left\| {F{\prime} \left( {NS_{i} } \right)} \right\|_{2} $$
(16)

Procedure 2: Next, the optimal angle distance strategy for external archive maintenance is described. As shown in Eq. (17), the OAD consists of the ratio of the convergence distance of the non-dominated solution to the minimum angle, hence, the solutions can be evaluated more comprehensively. The smaller OAD value, the better quality of the solutions. The OAD is defined as:

$$ OAD\left( {NS_{i} } \right) = \frac{{ConD\left( {NS_{i} } \right)}}{{\mathop {\min }\limits_{{NS_{j} \in G,j \ne i}} \left\langle {F\left( {NS_{i} } \right),F\left( {NS_{j} } \right)} \right\rangle }} $$
(17)

where \(F\left( {NS_{i} } \right)\) and \(F\left( {NS_{j} } \right)\) stand for the fitness values of the solutions \(NS_{i}\) and \(NS_{j}\), respectively, and \(\left\langle {F\left( {NS_{i} } \right),F\left( {NS_{j} } \right)} \right\rangle\) is the angle between the vectors \(F\left( {NS_{i} } \right)\) and \(F\left( {NS_{j} } \right)\).

figure c

General framework of CHLMOPSO

The main components of CHLMOPSO are introduced in detail above, namely the derivative treatment of pbest of the stagnant particles, the adaptive adjustment of flight parameters, the competitive hybrid learning strategy, and the maintenance of external archive through the optimal angle distance. The pseudo-code of CHLMOPSO is shown in Algorithm 4.

At first, the initial population P and archive A are generated in the initialization stage of lines 1–2. After that, CHLMOPSO begins the cycle of the population search process in lines 3–8. In line 4, firstly, the pbest of stagnant particles is derived by Algorithm 1. Then, in line 5, as described in section "Adaptive strategy for parameters adjustment", the flight parameters are adjusted adaptively with respect to the evolutionary state of particles to balance the exploration and exploitation abilities. Then, in line 6, the competitive hybrid learning strategy in Algorithm 2 is used to update the particles. Finally, in line 7, the optimal angle distance of Algorithm 3 is used to effectively maintain the archive. The above-mentioned evolutionary process is duplicated until the maximum number of iterations is achieved and the final archive A is output.

figure d

Experimental settings

Experimental comparison algorithms

For the sake of estimating the performance of CHLMOPSO more objectively, ten algorithms are selected for comparison, including five advanced MOPSOs (CMOPSO [30], NMPSO [31], MPSOD [17], MOPSOCD [32], and MOPSO [9]) and five competitive MOEAs (DGEA [33], NSGAIISDR [34], SPEAR [35], MOEADD [36], and NSGAIII [37]). All relevant parameters set by the comparison algorithms remain consistent with the original references to guarantee the impartiality of algorithm performance comparison. Each algorithm runs independently for 30 times on each test problem, and the average and standard deviation of the IGD and HV values are recorded. The experimental results of all algorithms are implemented on an Intel(R) Core(TM) i7-6700 CPU @ 3.40 GHz 3.40 GHz Windows 7 system by MATLAB R2021b. The PlatEMO [38] provides source codes of comparison algorithms.

Test problems

Moreover, we selected 22 test problems from three different benchmark test suits, ZDT [39], UF [40], and DTLZ [41], to test the performance of these algorithms. They have different characteristics and complex Pareto front features, such as concavity and convexity, multi-mode, disconnected, and irregular PF shapes, etc., which can well verify the reliability of the algorithm. There are relevant parameter settings in Table 1, where FEs represents the maximum number of evaluations.

Table 1 Parameter settings of test problems
Full size table

Comprehensive performance evaluation indicators

The performance of algorithms is assessed by adopting the extensively acknowledged inverted generational distance (IGD) [42] and hypervolume (HV) [43]. The quality of the Pareto optimal solution set that the algorithm ultimately generates is superior with the smaller IGD value (or the larger HV value) of an algorithm.

Comparison of experimental results

In this paper, a competitive hybrid learning MOPSO is put forward. We compared CHLMOPSO with other MOPSOs and MOEAs to further assess its effectiveness and analyzed the overall performance of CHLMOPSO from the following aspects.

Comparison of IGD data

The average and standard deviation of the IGD values for CHLMOPSO and other MOPSOs and MOEAs on 22 test problems are displayed in Tables 2 and 3, respectively, and are denoted by ‘A’ and ‘S’. The best IGD values are displayed in bold. Furthermore, for the purpose of ensuring statistically reliable conclusions, and the data of all algorithms are tested for normality, it is found that some data do not conform to the normal distribution, so we introduced a non-parametric statistical hypothesis test to process the experimental results. At the significance level of \(\alpha = 0.05\), the Wilcoxon rank sum test [44] is utilized to evaluate if there are meaningful differences between the algorithms. The corresponding symbols ‘+’, ‘−’, and ‘≈’ represent that the results of other algorithms are apparently superior to CHLMOPSO, apparently inferior to CHLMOPSO, and statistically similar to CHLMOPSO, respectively.

Table 2 IGD values of CMOPSO, NMPSO, MPSOD, MOPSOCD, MOPSO, and CHLMOPSO on 22 test problems
Full size table
Table 3 IGD values of DGEA, NSGAIISDR, SPEAR, MOEADD, NSGAIII, and CHLMOPSO on 22 test problems
Full size table

The comprehensive performance of CHLMOPSO is superior to MOPSOs and MOEAs. In accordance with the results of the Wilcoxon rank sum test from Table 2, among all the 22 test problems considered, the comparison algorithms CMOPSO, NMPSO, MPSOD, MOPSOCD, and MOPSO perform significantly worse than CHLMOPSO on 9, 10, 17, 17, and 18 test problems, respectively, and obtain similar results with CHLMOPSO on 3, 4, 1, 4, and 1 test problems, respectively. Additionally, as can be observed from Table 3, CHLMOPSO is noticeably superior to the comparison algorithms DGEA, NSGAIISDR, SPEAR, MOEADD, and NSGAIII on 19, 17, 14, 14, and 13 of the 22 test problems, respectively, and similar results are obtained on 0, 2, 2, 2, and 3 test problems, respectively. Moreover, the standard deviations demonstrate that when compared with the other comparison algorithms, CHLMOPSO has a certain advantage in terms of stability.

The outcomes listed above demonstrate that CHLMOPSO performs well on most of the test problems. This manifests that the competitive hybrid learning strategy improves the exploration ability and effectively balances the exploitation and exploration abilities.

Comparison of HV data

The outcomes of the best HV values in Table 4 are similar to those of IGD values in Table 2. Compared with the five MOPSOs, CHLMOPSO obtains 11 best HV values on 22 test problems. Moreover, CHLMOPSO performs better than CMOPSO, NMPSO, MPSOD, MOPSOCD, and MOPSO on 9, 10, 17, 16, and 16 test problems, respectively. Similarly, Table 5 displays that CHLMOPSO acquires 13 best HV values on 22 test problems compared with five MOEAs. In addition, CHLMOPSO performs better than the comparison algorithms DGEA, NSGAIISDR, SPEAR, MOEADD, and NSGAIII on 18, 14, 14, 14, and 13 of 22 test problems, respectively. In addition, from the comparison of standard deviations of algorithms in the two tables, it can also be found that CHLMOPSO has favorable stability.

Table 4 HV values of CMOPSO, NMPSO, MPSOD, MOPSOCD, MOPSO, and CHLMOPSO on 22 test problems
Full size table
Table 5 HV values of DGEA, NSGAIISDR, SPEAR, MOEADD, NSGAIII, and CHLMOPSO on 22 test problems
Full size table

All the above statistical results prove that CHLMOPSO is still very competitive compared with the selected algorithms. CHLMOPSO has better convergence and diversity in contrast to the selected comparison algorithms on ZDT and UF test problems on 22 test problems, which may be due to the competitive hybrid learning strategy of our proposed algorithm can obtain a better performance guarantee.

Friedman rank test

In the above two sections, CHLMOPSO is compared with MOPSOs and MOEAs in IGD indicator and HV indicator. Next, we also conduct the Friedman rank test [45] on the results in Tables 2, 3, 4, 5 to further compare the overall performance of CHLMOPSO and the selected comparison algorithms, and the smaller value of the test result, the better. Tables 6 and 7 show the Friedman rank test and ranking of IGD and HV values of all algorithms on ZDT, UF, and DTLZ, respectively. The minimum values of the Friedman test and the minimum rankings in the tables are displayed in bold.

Table 6 Friedman rank test of IGD values of CHLMOPSO and all comparison algorithms
Full size table
Table 7 Friedman rank test of HV values of CHLMOPSO and all comparison algorithms
Full size table

Table 6 clearly demonstrates that CHLMOPSO carries out significantly better than other algorithms on ZDT and UF with respect to the ranking of IGD values, and its ranking of the Friedman rank test is the first. Although the ranking on DTLZ is not ideal, from the overall result, CHLMOPSO still ranks first in Friedman rank test. Similarly, according to the ranking of HV values in Table 7, CHLMOPSO ranks first in Friedman rank test for both ZDT and UF test problems. Although it ranks second in the overall ranking, it is also second only to NMPSO. The aforementioned results illustrate that CHLMOPSO is considerably better overall than the other ten algorithms on the chosen test problems.

Comparison of box plots

To intuitively compare the stability on three suits of benchmark test problems ZDT, UF, and DTLZ, Fig. 2 exhibits statistical box plots of IGD values distribution acquired by CHLMOPSO and other ten algorithms running independently for 30 times on some test problems. Among them, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, and 11 on the horizontal axis of the box plots are CMOPSO, NMPSO, MPSOD, MOPSOCD, MOPSO, DGEA, NSGAIISDR, SPEAR, MOEADD, NSGAIII, and CHLMOPSO in turn. It can be observed from the box plots that the gap between CHLMOPSO and CMOPSO is not obvious on ZDT1, ZDT2, and ZDT3. However, CHLMOPSO is slightly superior to CMOPSO on ZDT1 and ZDT3 from the IGD values in Table 2. On the most of other problems, the gaps between CHLMOPSO and other algorithms are clear at a glance. The IGD values of CHLMOPSO on the most test problems are smaller, the abnormal values of experimental data are less, and the gaps between the upper and lower quartiles of CHLMOPSO are smaller, that is, the boxes are flatter. These findings demonstrate that CHLMOPSO outperforms the ten algorithms in terms of both solution outcomes and algorithm stability.

Fig. 2
figure 2

Box statistics of the IGD values of eleven algorithms on different test problems

Full size image

Comparison of Pareto front

For the sake of displaying the optimization results of all algorithms intuitively, the distribution of Pareto optimal solution sets of CHLMOPSO and other ten comparison algorithms on ZDT3, UF9, and DTLZ6 is shown in Figs. 3, 4, 5, respectively. The distribution of Pareto optimal solution sets can clearly demonstrate the convergence and diversity of algorithms. It is obvious from Figs. 3, 4, 5 that the majority of the selected comparison algorithms obviously lack convergence and diversity on ZDT3, UF9, and DTLZ6, while the performance of CHLMOPSO is relatively satisfactory.

Fig. 3
figure 3

Approximation PF of eleven algorithms on ZDT3 test problem

Full size image
Fig. 4
figure 4

Approximation PF of eleven algorithms on UF9 test problem

Full size image
Fig. 5
figure 5

Approximation PF of eleven algorithms on DTLZ6 test problem

Full size image

In relation to the two-objective test problem ZDT3, the approximate PF distribution obtained by all algorithms is showcased in Fig. 3, only CMOPSO and CHLMOPSO can approximate the true PF, and the distribution is relatively uniform. Only a few solutions of NMPSO converge, while other algorithms do not achieve satisfactory convergence. Compared with the two-objective problems, the three-objective problems have higher requirements for the selected algorithms. In Fig. 4, comparing the distribution of Pareto optimal solution set of each algorithm on UF9, CHLMOPSO is well distributed near the true PF, while other algorithms show obvious insufficient convergence and diversity. In Fig. 5, although CMOPSO, NMPSO, MOPSOCD, and CHLMOPSO all have good convergence on DTLZ6, NMPSO and MOPSOCD still have the problem of insufficient diversity, and their Pareto optimal solution sets are not evenly distributed. However, the convergence and distribution of other algorithms are not ideal, so only CMOPSO and CHLMOPSO have better distribution and convergence.

The above experiments demonstrate that CHLMOPSO has more stable and significant performance than the selected comparison algorithms. This shows that the proposed competitive hybrid learning strategy can achieve significant convergence while ensuring the uniform distribution of solutions.

Comparison of IGD indicator convergence

Along with the quality of solutions, a vital measurement of performance is the speed at which algorithms convergence. Figure 6 depicts the convergence trajectories of the IGD values generated through all algorithms following 10,000 evaluations on ZDT3, UF9, and DTLZ6. In contrast to the ten comparison algorithms, CHLMOPSO has a swift convergence speed. Additionally, it can be seen from the termination state of each algorithm in the convergence process that CHLMOPSO has the smallest IGD value, which more clearly emphasizes that CHLMOPSO has remarkable convergence performance. As can be recognized, the competitive hybrid learning strategy proposed by CHLMOPSO can enhance the convergence and search efficiency of the algorithm.

Fig. 6
figure 6

IGD convergence trajectories of CHLMOPSO and ten comparison algorithms on ZDT3, UF9, and DTLZ6 test problems

Full size image

Ablation study

In CHLMOPSO, four key strategies are proposed to improve the overall performance of the algorithm. With the aim of investigating their respective contributions, we set up the experiments to compare the performance of CHLMOPSO with its four variants: (1) the CHLMOPSO without the derivative treatment strategy of pbest (CHLMOPSO-I); (2) the CHLMOPSO without adaptive flight parameters (CHLMOPSO-II); (3) the CHLMOPSO without competitive hybrid learning strategy (CHLMOPSO-III); (4) the CHLMOPSO without optimal angle distance to maintain external archive (CHLMOPSO-IV). The effectiveness of these four strategies will be discussed in depth in this subsection.

In order to ensure the fairness in the comparison of algorithm performance, the parameter settings of these four variants are consistent with CHLMOPSO. The four variants are tested on the ZDT, UF, and DTLZ test suites and run independently for 30 times on each test problem to obtain statistical average and standard deviation (in parenthesis) results with respect to the IGD and HV indicators. The comparison results are presented in Tables 8, 9, 10, 11, the best results of each test problem are shown in bold, and the Wilcoxon rank sum test is performed to detect whether there are significant performance differences between CHLMOPSO and the four variants.

Table 8 The comparison results of IGD and HV for CHLMOPSO and variant CHLMOPSO-I on 22 test problems
Full size table
Table 9 The comparison results of IGD and HV for CHLMOPSO and variant CHLMOPSO-II on 22 test problems
Full size table
Table 10 The comparison results of IGD and HV for CHLMOPSO and variant CHLMOPSO-III on 22 test problems
Full size table
Table 11 The comparison results of IGD and HV for CHLMOPSO and variant CHLMOPSO-IV on 22 test problems
Full size table

The experimental results indicate that CHLMOPSO performs significantly better than its four variants on most of the test problems, which confirms that the combination of the four proposed strategies improves the comprehensive performance of CHLMOPSO and has an important role in this algorithm. Additionally, as can be seen from Tables 8, 9, 10, 11, the variants CHLMOPSO-III and CHLMOPSO-IV perform worse than CHLMOPSO relative to those of CHLMOPSO-I and CHLMOPSO-II, which demonstrates that the proposed competitive hybrid learning strategy and the optimal angle distance strategy to maintain the external archive have made relatively great contributions to CHLMOPSO. In the variant CHLMOPSO-III, the performance of the competitive hybrid learning strategy is more significant on UF test suite. And in the variant CHLMOPSO-IV, the performance improvement of the optimal angle distance strategy to maintain the external archive is predominantly manifested on the ZDT test suite. However, in terms of the overall results, after removing the competitive hybrid learning strategy, the performance of variant CHLMOPSO-III is obviously worse, thus verifying that the competitive hybrid learning strategy has the greatest contribution to CHLMOPSO. This is because some studies have shown that the update of particles through the competitive mechanism in CSO can significantly increase the diversity of population, thus avoiding premature convergence. And our proposed competitive hybrid learning strategy combines the updating strategy of CSO with that of MOPSO to achieve a good equilibrium between convergence and diversity.

Conclusion

For improvements in the comprehensive performance of algorithm, a competitive hybrid learning MOPSO is put forward. CHLMOPSO proposes an updating strategy of pbest to derive pbest of the stagnant particles without evolution for the purpose of enhancing the ability of particles to explore. Subsequently, the flight parameters are transformed adaptively in accordance with the evolutionary state of particles. In the proposed competitive hybrid learning strategy, the algorithm selects different updating strategies. Additionally, the optimal angle distance strategy is applied to effectively maintain the archive, thereby speeding up algorithm convergence.

On three suits of benchmark problems, the simulation experiments compared CHLMOPSO with the selected MOPSOs and MOEAs. The IGD and HV indicators are utilized to assess its performance as a whole, and two non-parametric statistical tests, the Wilcoxon rank sum test and the Friedman rank test, are used to process experimental results. The findings from the experiments also verify the effectiveness of CHLMOPSO, which can better equilibrate the convergence and diversity.

However, according to the experimental results, it can be observed that the performance of the proposed CHLMOPSO needs to be further improved on some MOPs (such as DTLZ) with complex PF features that are multi-modal and concave. In addition, it can also be concluded from the ablation experiments that the adaptive parameters strategy in CHLMOPSO does not make a significant contribution to the algorithm, which may be due to the fact that the proposed adaptive flight parameters strategy only takes into account the evolutionary ability of the particles but not that of the population. Therefore, in our future work, it will be meaningful to design an adaptive parameters strategy that takes into account both the evolutionary ability of the population and the particles to obtain more accurate and better diversity of solutions for the particles. This can better balance the global exploration and local exploitation abilities of the algorithm to solve concave and multi-modal MOPs. Furthermore, the effective application of CHLMOPSO to solve practical problems such as vehicle routing, network communication, and production scheduling is also one of the future research.