Introduction

The notion of fuzzy set (FS) was defined by Zadeh [1] in 1965 to model some problems involving uncertainty. The FS has found application in many different fields such as computer science, medical science, clustering, robotic, optimization, and data mining. For example, Gadekallu and Gao [2] proposed a model using an approach based on rough sets for reducing the attributes and fuzzy logic system for classification for prediction of the Heart and Diabetes diseases; Sankaran et al. [3] proposed a method to provide a multi-path and multi-constraint Qualify of Service based on Reliable Fuzzy and Heuristic Concurrent Ant Colony Optimization. These studies are two example made in 2021 related to application of fuzzy logic and sets.

Zadeh [1] characterize an FS by the membership function of which codomain is interval [0, 1]. In an FS, if the membership degree (MD) of an element is \(\mu \), then its non-membership degree (NMD) is \(1-\mu \). Namely, in an FS, hesitation degree of an element is accepted as “0”. However, this perspective has some constraints. To overcome with this constraints, Atanassov [4] introduced the concept of intuitionistic FS (IFS) as a generalization of FSs. An IFS is defined by assigning two values from the range [0,1], named MD \( \mu \) and NMD \( \nu \), under the condition \( \mu + \nu \le 1 \) for all elements of the working universe. However, this set is not useful when \( \mu + \nu > 1 \). Therefore, Yager [5, 6] defined the Pythagorean FS (PyFS) as an extension of IFS under condition \(\mu ^2 + \nu ^2\le 1\). Another extension of IFS is Picture FS (PFS) defined by Cuong [7, 8]. PFS is a useful tool for representing human opinion, because a PFS can model judgments about an object or idea using degrees of yes, abstention, no, and rejection. A PFS is identified three degrees of an element, called MD \((\mu )\), abstinence degree (AD) or neutral degree \((\gamma )\), and NMD \((\nu )\) with the condition \(0\le \mu + \gamma + \nu \le 1\). Although PFS has wide applications in some field such as decision-making (DM) [9,10,11,12,13,14,15], similarity measure [16,17,18,19,20], correlation coefficient [21, 22], and clustering [23, 24], it is not sufficient in modelling some problems when \(\mu +\gamma +\nu >1\). For this reason, Gungogdu and Kahraman [25, 26] inaugurated the design of spherical FS (SFS) which is an extension of PFS satisfying the condition \(0\le \mu ^2 +\gamma ^2+\nu ^2 \le 1\). They also studied on SFS operations and applications of this set in DM problems. Kahraman et al. [25] proposed a DM method by integrating the SFS and TOPSIS method, and gave an application of the proposed method in the selection of hospital location. Mahmood et al. [27] defined the T-spherical FS (T-SFS) as an extension of the SFS with condition \(0 \le \mu ^q + \gamma ^q + \nu ^q\le 1\) and gave some applications in medical diagnosis and decision-making problems of T-SFS and SFS. Ullah et al. [28] introduced the similarity measures for T-SFSs and presented an application in pattern recognition. Garg et al. [29] presented improved interactive aggregation operators for T-SFSs and studied on operational laws of these operators. Ullah et al. [30] described some ordered weighted geometric (OWG) and hybrid geometric (HG) operators, and gave a numerical example involving multi-attribute decision-making (MADM) problem. Ullah et al. [31] introduced the concept of interval-valued T-SFS (IVT-SFS) and basic operations of them. They also defined two aggregation operators including weighted averaging and weighted geometric operators for IVT-SFS, and presented an MCDM method. Liu et al. [32] pointed out some limitations in operational laws of SFS and T-SFS, and suggested some novel operational laws for SFS and T-SFS. They also introduced Power Muirhead Mean Operator for T-SFS by combining power average operator with Muirhead Mean operator and presented an MAGDM method based on proposed operators. Recently, T-SFS has gained attention of researchers working on MCDM methods, MCGDM methods, and aggregation operators. For example, divergence measure of T-SFSs [33], immediate probabilistic Interactive averaging aggregation operators of T-SFSs [34], T-SF soft sets and their aggregation operators [35], generalized T-SF weighted aggregation operators on neutrosophic sets [36], T-SF Einstein Hybrid Aggregation operators [37], correlation coefficients for T-SFSs [38], T-SF Hamacher aggregation operators [39], complex T-SF aggregation operators [40], and T-spherical Type-2 fuzzy sets [41] are some of them.

The hesitant FS (HFS) is another extension of the FS for modelling the problems in which decision-makers have different opinions about an alternative or element in considered universe. The HFS was defined by Torra and Narukawa in [42, 43]. To explain the basic idea behind of the concept of the hesitant fuzzy set, we give an example: two decision-makers discuss the membership grade of an element to a set, and while one of them assigns membership grade 0.7 for the element, the other may assign 0.3. In such cases, making a common decision is difficult. In a such case, the HFS is a useful tool. Because of advantages of HFS, many researchers have been developed multiple decision-making methods and they have presented their applications under HF environment [44,45,46,47,48,49]. Xia et al. [50] described some HF aggregation operators and developed a group decision-making method. Chen et al. [51] interpreted the idea of interval-valued hesitant fuzzy sets (IvHFSs) which is a generalization of HFS. Peng et al. [52] investigated the continuous HF aggregation operators with the aid of continuous OWA operator, and they defined the C-HFOWA operator and C-HFOWG operator with their essential properties. They also extended these operators interval-valued HFS. Mu et al. [53] introduced a novel aggregation principle for HF elements (HFE). Amin et al [54] defined some aggregation operators for triangular cubic linguistic hesitant fuzzy sets. Fahmi et al. [55] defined some new operation laws for trapezoidal cubic hesitant fuzzy (TrCHF) numbers and introduced some new aggregation operators. Jiang et al. [56] defined the concept of interval-valued dual HFS, and described aggregation operators under interval-valued dual HF environment based on Hamacher t-norm and t-conorm. Liu et al. [57] introduced the Dombi aggregation operators of interval-valued hesitant fuzzy set based on Dombi t-norm and t-conorm. Some studies related to aggregation operator of HFS, extension of HFS, and decision-making can be found [58,59,60,61,62,63,64,65,66,67,68,69,70,71,72].

It has been mentioned above that HFSs are an important set structure in modelling problems involving multiple decision-makers, in terms of revealing the ideas of decision-makers. In an HFS, the HFEs are subsets of the interval [0,1]. In other words, the elements of an HFE express their degree of membership. It is insufficient to express non-membership and neutral status. As mentioned above, TSFS is defined as a generalization of FS, IFS, PyFS, PFS, qROFS, and SFS, and finds application in decision-making problems. Some generalizations of HFSs are available in the literature. To use the advantages of HFSs and T-SFSs together, in this article, we define a novel concept called the hesitant T-spherical fuzzy set (HT-SFS) by combining concepts of HFs and T-SFS. In HT-SFS, more than one T-spherical fuzzy value can be assigned to elements of the set containing the elements to be evaluated. T-SFS theory deals only one T-spherical fuzzy value for an element. Therefore, it does not suffice to model problems including disagreements of the opinion of decision-makers about an element or object. On the other hand, an HT-SFS can handle such situation. We also introduce some aggregation operators based on Dombi operators, including hesitant T-spherical Dombi fuzzy weighted arithmetic averaging (HTSDFWAA) operator, hesitant T-spherical Dombi fuzzy weighted geometric averaging (HTSDFWGA) operator, hesitant T-spherical Dombi fuzzy ordered weighted arithmetic averaging (HTSDFOWAA) operator, and hesitant T-spherical Dombi fuzzy ordered weighted geometric averaging (HTSDFOWGA) operator, and obtain some properties of them. Furthermore, we give a multi-criteria group decision-making (MCGDM) method and algorithm of the proposed method under the HT-SF environment. To show the process of of proposed method, we present an example related to the selection of most suitable person for the assistant professorship position in a university. Besides this, we have presented a comparison of the proposed methods with each other and a comparison table of the proposed clusters with other extensions of the FS.

Preliminaries

This section provides some basic definitions and operations that will be needed in the next sections. First, for the reader’s convenience, a table of notations by chapter is given in Table 1.

Table 1 Frequently used notations in “Preliminaries”, “Hesitant T-spherical fuzzy sets”, and “Hesitant T-spherical Dombi fuzzy aggregation operators”
Full size table

Definition 1

[25] An SFS \({\mathbb {S}}\) on a universe \({\mathfrak {X}}\) is represented as follows:

$$\begin{aligned} {\mathbb {S}}=\{(x,s(x),i(x),d(x)):x\in {\mathfrak {X}}\}, \end{aligned}$$

where \(s(x),i(x),d(x)\in [0,1],\) \(0\le s^2(x)+i^2(x)+d(x)^2\le 1\) for all \(x\in {\mathfrak {X}}.\) We consider the triplet (s, i, d) as SF number (SFN). Here, s,  i, and d are the membership degree (MD), abstinence degree (AD), and non-membership degree (NMD) of \(x\in {\mathbb {S}}\), respectively. Further \(\pi _{{\mathbb {S}}}(x)=\sqrt{1-(s^2(x)+i^2(x)+d^2(x))}\) is the hesitancy degree of x in \({\mathbb {S}}.\)

Definition 2

[27] A T-SF Set (T-SFS) on \({\mathfrak {X}}\) is defined as

$$\begin{aligned} T=\{(x,s(x),i(x),d(x)): x \in {\mathfrak {X}}\}, \end{aligned}$$

where \( s,i,d:{\mathfrak {X}} \longrightarrow [0,1]\) are membership, abstinence, and non-membership functions with a condition that

$$\begin{aligned} 0 \le s^{n}(x)+i^{n}(x)+d^{n}(x)\le 1. \end{aligned}$$

The refusal degree of T-SFS is defined as

$$\begin{aligned} r(x)=\root n \of {1-(s^{n}(x)+i^{n}(x)+d^{n}(x))}, \end{aligned}$$

and the triplet (s, i, d) is called the T-SF number (T-SFN).

Definition 3

[42, 43] Let \({\mathfrak {X}}\) be a fixed set, a hesitant fuzzy set (HFS) on \({\mathfrak {X}}\) is in terms of a function that applied to \({\mathfrak {X}}\) returns of [0, 1].The mathematical symbol of HFS

$$\begin{aligned} A=\{<x,h_{A}(x)> : x\in {\mathfrak {X}}\}, \end{aligned}$$

where \( h_{A}(x)\) is a set of some values in [0, 1], denoting the possible membership degrees of the element \(x\in {\mathfrak {X}}\) to the set A. \(h=h_{A}(x)\) is called an HF element (HFE).

From now on, set of all T-spherical fuzzy numbers is denoted by \(\Upsilon .\)

Hesitant T-spherical fuzzy sets

In this part, we define the concept of hesitant T-Spherical fuzzy sets and their set-theoretical operations.

Definition 4

Let \(\mathfrak {{\mathfrak {X}}}\) be a nonempty set. A hesitant T-SFS (HT-SFS) over \({\mathfrak {X}}\) denoted by \({\mathbb {T}}_{H}\) is defined as follows:

$$\begin{aligned} {\mathbb {T}}_H=\big \{(x, {\mathfrak {h}}(x)): {\mathfrak {h}}(x)\subseteq \Upsilon , x\in {\mathfrak {X}} \big \}. \end{aligned}$$

Here, \({\mathfrak {h}}(x)=\mathfrak {{\mathfrak {h}}}\) is collection of T-SFNs and \({\mathfrak {h}}\) is called HT-SF element (HT-SFE). The number of elements of an HT-SFE is called length of HT-SFE \({\mathfrak {h}}\) and denoted by \(\ell _{{\mathfrak {h}}}\).

In other words, an HT-SFS is collection of HT-SFEs.

Example 1

Let us consider a set \({\mathfrak {X}}=\{x_1,x_2,x_3,x_4\}\). Then, for \(t=3\), we can write an HT-SFS \({\mathbb {T}}\) as follows:

$$\begin{aligned}&{\mathbb {T}} = \Big \{\big (x_1,\{(0.6,0.8,0.4),(0.4,0.5,0.9),(0.6,0.2,0.7)\}\big ),\\&\quad \big (x_2,\{(0.3,0.9,0.5),(0.2,0.4,0.7)\}\big ),\\&\quad \big (x_3,\{(0.9,0.3,0.2),(0.6,0.6,0.6),(0.4,0.3,0.8),\\&\quad (0.5,0.7,0.6)\}\big ),\big (x_4,\{(0.7,0.2,0.2)\}\big )\Big \}. \end{aligned}$$

Definition 5

Let \({\mathfrak {h}}\) be an HT-SFE. Then, score value of HT-SFE \({\mathfrak {h}}\) denoted by SV\(({\mathfrak {h}})\) is defined as

$$\begin{aligned} SV({\mathfrak {h}})=\frac{1}{\ell _{{\mathfrak {h}}}}\sum _{k=1}^{\ell _{{\mathfrak {h}}}}(s_k^n-d_k^n) \end{aligned}$$
(1)

for some positive integer n. Here, SV\(({\mathfrak {h}})\in [-1,1].\)

Definition 6

Let \({\mathfrak {h}}\) be an HT-SFE. Then, accuracy value of HT-SFE \({\mathfrak {h}}\) denoted by AV\(({\mathfrak {h}})\) is defined as

$$\begin{aligned} AV({\mathfrak {h}})=\frac{1}{\ell _{{\mathfrak {h}}}}\sum _{k=1}^{\ell _{{\mathfrak {h}}}}(s_k^n+i_k^n+d_k^n) \end{aligned}$$

for the positive integer n. Here, AV\(({\mathfrak {h}})\in [0,1].\)

Definition 7

Let \({\mathfrak {h}}_1\) and \({\mathfrak {h}}_2\) be two HT-SFEs, SV\(({\mathfrak {h}}_1)\) and SV\(({\mathfrak {h}}_2)\) are the score values of \({\mathfrak {h}}_1\) and \({\mathfrak {h}}_2\), respectively, and AV\(({\mathfrak {h}}_1)\) and AV\(({\mathfrak {h}}_2)\) are the accuracy values of \({\mathfrak {h}}_1\) and \({\mathfrak {h}}_2\), respectively. Then

  1. 1.

    If SV\(({\mathfrak {h}}_1)<\mathrm{{SV}}({\mathfrak {h}}_2)\) then \({\mathfrak {h}}_1< {\mathfrak {h}}_2\)

  2. 2.

    If SV\(({\mathfrak {h}}_1)>\mathrm{{SV}}({\mathfrak {h}}_2)\) then \({\mathfrak {h}}_1> {\mathfrak {h}}_2\)

  3. 3.

    If SV\(({\mathfrak {h}}_1)=\mathrm{{SV}}({\mathfrak {h}}_2)\), there are three cases

    1. (a)

      If AV\(({\mathfrak {h}}_1)<\mathrm{{AV}}({\mathfrak {h}}_2)\), then \({\mathfrak {h}}_1< {\mathfrak {h}}_2\)

    2. (b)

      If AV\(({\mathfrak {h}}_1)>\mathrm{{AV}}({\mathfrak {h}}_2)\), then \({\mathfrak {h}}_1> {\mathfrak {h}}_2\)

    3. (c)

      If AV\(({\mathfrak {h}}_1)=\mathrm{{AV}}({\mathfrak {h}}_2)\) , then \({\mathfrak {h}}_1={\mathfrak {h}}_2\).

Example 2

Let us consider HT-SFEs \({\mathfrak {h}}_{1}=\{(0.6,0.8,0.4),(0.4,0.5,0.9),(0.6,0.2,0.7)\} \) and \({\mathfrak {h}}_{2}=\{(0.3,0.9,0.5),(0.2,0.4,0.7)\}\) of HT-SFS \({\mathbb {T}}\) given in Example 1, \( n=3 \); then

$$\begin{aligned} SV({\mathfrak {h}}_1)= & {} \frac{1}{\ell _{{\mathfrak {h}}_{1}}}\Big [(0.6^{3}-0.4^{3})+(0.4^{3}-0.9^{3})\\&+(0.6^{3}-0.7^{3})\Big ]\\= & {} -0.2133,\\ SV({\mathfrak {h}}_2)= & {} \frac{1}{\ell _{{\mathfrak {h}}_{2}}}[(0.3^{3}-0.5^{3})+(0.2^{3}-0.7^{3})]\\= & {} -0.2165. \end{aligned}$$

Definition 8

Let \({\mathbb {T}}_1=\{(x, {\mathfrak {h}}_1(x)): x\in {\mathfrak {X}}\}\) and \({\mathbb {T}}_2=\{(x, {\mathfrak {h}}_2(x)): x\in {\mathfrak {X}}\}\) be two HT-SFSs over a common universe \({\mathfrak {X}}\). If, for all \(x\in {\mathfrak {X}}\) SV\(({\mathfrak {h}}_1(x))\le SV({\mathfrak {h}}_2(x))\), then it is said that \({\mathbb {T}}_1\) is an HT-SF subset of \({\mathbb {T}}_2\), and denoted by \({\mathbb {T}}_1\triangleleft {\mathbb {T}}_2\).

Example 3

Let \({\mathbb {T}}_1\) and \({\mathbb {T}}_2\) be two HT-SFSs over \({\mathfrak {X}}=\{x_{1},x_{2},x_{3}\}\) for \(n=3\) given as follows:

$$\begin{aligned} {\mathbb {T}}_1= & {} \Big \{(x_{1},\{(0.5,0.4,0.3),(0.6,0.5,0.4),(0.7,0.2,0.6)\}),\\&(x_{2},\{(0.6,0.2,0.4),(0.7,0.1,0.6),(0.5,0.5,0.2)\}),\\&(x_{3},\{(0.9,0.6,0.1),(0.4,0.4,0.4),(0.6,0.2,0.5)\})\Big \}\\ {\mathbb {T}}_2= & {} \Big \{(x_{1},\{(0.7,0.6,0.5),(0.7,0.5,0.5),(0.8,0.3,0.6)\}),\\&(x_{2},\{(0.8,0.3,0.3),(0.6,0.2,0.2),(0.5,0.7,0.1)\}),\\&(x_{3},\{(0.7,0.3,0.3),(0.9,0.2,0.2),(0.5,0.1,0.3)\})\Big \}. \end{aligned}$$

Then, using Eq. (1), for \(x_i\in {\mathfrak {X}} (i=1,2,3)\), SVs of HT-SFEs are obtained as follows:

 

\(x_1\)

\(x_2\)

\(x_3\)

SV\(({\mathfrak {h}}_1)\)

0.126

0.132

0.273

SV\(({\mathfrak {h}}_2)\)

0.244

0.270

0.378

From the table, it is clear that \({\mathbb {T}}_1\triangleleft {\mathbb {T}}_2.\)

Set-theoretical operations of HT-SFSs

In this section union, intersection and complement of an HT-SFS are defined with their examples.

Definition 9

Let \({\mathfrak {h}}=\{(s_{t},i_{t},d_{t}): 1\le t \le \ell _{{\mathfrak {h}}}\}\) be a T-SFE over \({\mathfrak {X}}\). Then, lower and upper bounds of \({\mathfrak {h}}\) are defined as follows:

$$\begin{aligned} {\mathfrak {h}}^{-}= & {} \underset{t}{\min }(s_t^n-d_t^n)\\ {\mathfrak {h}}^{+}= & {} \underset{t}{\max }(s_t^n-d_t^n), \end{aligned}$$

respectively.

The following example can be given to explain lower and upper bound of \({\mathfrak {h}}\).

Let \({\mathfrak {h}}=\{(0.5,0.4,0.3),(0.6,0.5,0.4),(0.7,0.2,0.5)\}\) be an HT-FS element, \( n=3, l_{{\mathfrak {h}}}=3 \)

$$\begin{aligned} {\mathfrak {h}}^{-}= & {} \min \{(0.5^3-0.3^3),(0.6^3-0.4^3),(0.7^3-0.5^3)\}\\= & {} \min \{0.116,0.152,0.218\}\\= & {} 0.116,\\ {\mathfrak {h}}^{+}= & {} \max \{0.116,0.152,0.218\}\\= & {} 0.218. \end{aligned}$$

Definition 10

Let \({\mathbb {T}}_1\) and \({\mathbb {T}}_2\) be two HT-SFSs over \({\mathfrak {X}}\) and let \(\mathfrak {h_1}\) and \(\mathfrak {h_2}\) be HT-SFEs of \({\mathbb {T}}_1\) and \({\mathbb {T}}_2\) for all \(x\in {\mathfrak {X}}.\) Then, based on HT-SFEs, set-theoretical operations between \({\mathbb {T}}_1\) and \({\mathbb {T}}_2\) are defined as follows:

  1. 1.

    Union:

    $$\begin{aligned}&{\mathbb {T}}_1\Cup {\mathbb {T}}_2= \bigcup _{x\in {\mathfrak {X}}}\left\{ \left( x, \bigcup _{{\begin{array}{l}(s_{1},i_{1},d_{1})\in {\mathfrak {h}}_1\\ (s_{2},i_{2},d_{2})\in {\mathfrak {h}}_2\end{array}}}\{(s_k,i_k,d_k):\right. \right. \\&\left. \left. \quad s_k^n-d_k^n=\max \{s_1^n-d_1^n,s_2^n-d_2^n\}, k=1,2\}\right) .\right\} \end{aligned}$$
  2. 2.

    Intersection:

  3. 3.

    Complement:

    $$\begin{aligned} {\mathbb {T}}_1^c=\bigcup _{x\in {\mathfrak {X}}}\left\{ \left( x, \bigcup _{{\begin{array}{l}(s_{1},i_{1},d_{1})\in {\mathfrak {h}}_1\end{array}}}\{(d_{1},i_{1},s_{1})\}\right) \right\} . \end{aligned}$$

Example 4

Let \({\mathbb {T}}_1\) and \({\mathbb {T}}_2\) be two HT-SFSs over \({\mathfrak {X}}=\{x_{1},x_{2},x_{3}\}\) for \(n=4\) given as follows:

$$\begin{aligned} {\mathbb {T}}_1= & {} \Big \{(x_{1},\{(0.5,0.7,0.9),(0.3,0.2,0.7),(0.6,0.5,0.4)\}),\\&(x_{2},\{(0.4,0.6,0.3),\\&(0.2,0.5,0.9)\}),(x_{3},\{(0.8,0.4,0.3)\})\Big \}\\ {\mathbb {T}}_2= & {} \Big \{(x_{1},\{(0.4,0.8,0.5),(0.5,0.7,0.6)\}),\\&(x_{2},\{(0.2,0.7,0.6),(0.4,0.3,0.8)\}),\\&(x_{3},\{(0.5,0.4,0.8),(0.6,0.7,0.2),(0.9,0.2,0.4)\})\Big \}.\\ \end{aligned}$$

Then, using Definition 10, union, intersection. and complement of HT-SFEs are \({\mathbb {T}}_1\) and \({\mathbb {T}}_2\) are obtained as follows:

$$\begin{aligned}&{\mathbb {T}}_1\Cup {\mathbb {T}}_2\\&\quad =\Big \{(x_{1},\{(0.4,0.8,0.5),(0.5,0.7,0.6),(0.6,0.5,0.4)\}),\\&\qquad (x_{2},\{(0.4,0.6,0.3),(0.2,0.7,0.6),(0.4,0.3,0.8)\}),\\&\qquad (x_{3},\{(0.8,0.4,0.3),(0.9,0.2,0.4)\})\Big \},\\&{\mathbb {T}}_1\Cap {\mathbb {T}}_2\\&\quad =\Big \{(x_{1},\{(0.5,0.7,0.9),(0.3,0.2,0.7),(0.4,0.8,0.5),\\&\qquad (0.5,0.7,0.6)\}),\\&\qquad (x_{2},\{(0.2,0.7,0.6),(0.4,0.3,0.8),(0.2,0.5,0.9)\}),\\&\qquad (x_{3},\{(0.5,0.4,0.8),(0.6,0.7,0.2),(0.8,0.4,0.3)\})\Big \},\\ \end{aligned}$$

and

$$\begin{aligned} {\mathbb {T}}^c_1= & {} \Big \{(x_{1},\{(0.9,0.7,0.5),(0.7,0.2,0.3),(0.4,0.5,0.6)\}),\\&(x_{2},\{(0.3,0.6,0.4),\\&(0.9,0.5,0.2)\}),(x_{3},\{(0.3,0.4,0.8)\})\Big \},\\ \end{aligned}$$

respectively.

Hesitant T-spherical Dombi fuzzy aggregation operators

Aggregation operators are an important tool for obtaining a single value from many values. In this section, first, we define Dombi operators for two HT-SFEs based on Dombi t-norm and t-conorm. An HT-SFE is a collection of T-SFEs which have three components called MD, AD, and NMD. In summation (\(\oplus \)) operation between HT-SFEs, we use Dombi t-conorm for MDs, Dombi t-norm for AD, and Dombi t-norm for NMD. In product (\(\otimes \)) operation between HT-SFEs, we use Dombi t-conorm for MDs, Dombi t-norm for AD, and Dombi t-norm for NMD. Then, we define hesitant T-spherical Dombi fuzzy weighted arithmetic averaging operators and hesitant T-spherical Dombi fuzzy weighted geometric averaging operators as a generalization of the Dombi operators for two HT-SFEs. In these operations, only HT-SFEs are weighted and ignored the importance of the ordered position of HT-SFEs. This is a drawback, and to avoid this drawback, we introduce hesitant T-spherical Dombi fuzzy ordered weighted arithmetic (geometric) averaging operators. In these operators, we consider both the weights of the elements and the importance degrees of the hesitant fuzzy elements according to the score functions. Namely, First, we sort the HT-SFEs according to their score values using the score function we defined, then upon this ordering, we discard the weight vectors given at the beginning without changing the order. The basic idea related to the ordered weighted averaging (OWA) is presented in [73].

Dombi t-norm and t-conorm

Dombi product and Dombi sum which are specific types of triangular norms and conorms given in [74] as follows:

Definition 11

[74] Let f and g be two real numbers in the interval [0, 1]. Then, Dombi t-norm is given by

$$\begin{aligned} f\otimes g= \dfrac{1}{1+\bigg (\bigg ( \dfrac{1-f}{f}\bigg )^{\gamma }+\bigg ( \dfrac{1-g}{g}\bigg )^{\gamma }\bigg ) ^{\dfrac{1}{\gamma }}}, ~~\gamma > 0. \end{aligned}$$

Dombi t-conorm is given by

$$\begin{aligned} f\oplus g=1-\dfrac{1}{1+\bigg (\bigg (\dfrac{1-f}{f}\bigg )^{ -\gamma }+\bigg (\dfrac{1-g}{g}\bigg )^{ -\gamma }\bigg )^{\dfrac{1}{\gamma }}}, ~~\gamma >0, \end{aligned}$$

respectively.

Dombi operations of HT-SFEs

In this subsection, we define some Dombi operations between HT-SFEs.

Definition 12

Let \({\mathfrak {h}}_1=\{(s_{1t},i_{1t},d_{1t}): 1\le t \le \ell _{{\mathfrak {h}}_1}\}\) and \({\mathfrak {h}}_2=\{(s_{2r},i_{2r},d_{2r}): 1\le r \le \ell _{{\mathfrak {h}}_2}\}\) be two HT-SFEs and \(\gamma > 0\), and the Dombi operations for HT-SF elements are defined as follows:

  1. 1.
    $$\begin{aligned}&{\mathfrak {h}}_1\oplus {\mathfrak {h}}_2={\mathop {\bigcup }\nolimits _{{\begin{array}{l}(s_{1t},i_{1t},d_{1t})\in {\mathfrak {h}}_1\\ (s_{2r},i_{2r},d_{2r})\in {\mathfrak {h}}_2\end{array}}}}\\&\quad \left\{ \left( \root n \of {1-\frac{1}{1+\Big \{\Big (\frac{s_{1t}^n}{1-s_{1t}^n}\Big )^{\gamma }+ \Big (\frac{s_{2r}^n}{1-s_{2r}^n}\Big )^{\gamma }\Big \}^{\frac{1}{\gamma }}}},\right. \right. \\&\qquad \root n \of {\frac{1}{1+\Big \{\Big (\frac{1-i_{1t}^n}{i_{1t}^n}\Big )^{\gamma }+ \Big (\frac{1-i_{2r}^n}{i_{2r}^n}\Big )^{\gamma }\Big \}^{\frac{1}{\gamma }}}},\\&\left. \left. \qquad \root n \of {\frac{1}{1+\Big \{\Big (\frac{1-d_{1t}^n}{d_{1t}^n}\Big )^{\gamma }+ \Big (\frac{1-d_{2r}^n}{d_{2r}^n}\Big )^{\gamma }\Big \}^{\frac{1}{\gamma }}}} \right) \right\} \end{aligned}$$
  2. 2.
    $$\begin{aligned}&{\mathfrak {h}}_1\otimes {\mathfrak {h}}_2={\mathop {\bigcup }\nolimits _{{\begin{array}{l}(s_{1t},i_{1t},d_{1t})\in {\mathfrak {h}}_1\\ (s_{2r},i_{2r},d_{2r})\in {\mathfrak {h}}_2\end{array}}}}\\&\quad \left\{ \left( \root n \of {\frac{1}{1+\Big \{\Big (\frac{1-s_{1t}^n}{s_{1t}^n}\Big )^{\gamma }+ \Big (\frac{1-s_{2r}^n}{s_{2r}^n}\Big )^{\gamma }\Big \}^{\frac{1}{\gamma }}}},\right. \right. \\&\quad \root n \of {\frac{1}{1+\Big \{\Big (\frac{1-i_{1t}^n}{i_{1t}^n}\Big )^{\gamma }+ \Big (\frac{1-i_{2r}^n}{i_{2r}^n}\Big )^{\gamma }\Big \}^{\frac{1}{\gamma }}}},\\&\left. \left. \quad \root n \of {1-\frac{1}{1+\Big \{\Big (\frac{d_{1t}^n}{1-d_{1t}^n}\Big )^{\gamma }+ \Big (\frac{d_{2r}^n}{1-d_{2r}^n}\Big )^{\gamma }\Big \}^{\frac{1}{\gamma }}}} \right) \right\} \end{aligned}$$
  3. 3.
    $$\begin{aligned}&\lambda {\mathfrak {h}}_1={\mathop {\bigcup }\nolimits _{(s_{1t},i_{1t},d_{1t})\in {\mathfrak {h}}_1}} \left\{ \left( \root n \of {1-\frac{1}{1+\Big \{\lambda \Big (\frac{s_{1t}^n}{1-s_{1t}^n}\Big )^{\gamma }\Big \}^{\frac{1}{\gamma }}}},\right. \right. \\&\quad \root n \of {\frac{1}{1+\Big \{\lambda \Big (\frac{1-i_{1t}^n}{i_{1t}^n}\Big )^{\gamma }\Big \}^{\frac{1}{\gamma }}}},\\&\quad \left. \left. \root n \of {\frac{1}{1+\Big \{\lambda \Big (\frac{1-d_{1t}^n}{d_{1t}^n}\Big )^{\gamma }\Big \}^{\frac{1}{\gamma }}}} \right) \right\} \end{aligned}$$
  4. 4.
    $$\begin{aligned}&{\mathfrak {h}}_1^{\lambda }={\mathop {\bigcup }\nolimits _{(s_{1t},i_{1t},d_{1t})\in {\mathfrak {h}}_1}} \left\{ \left( \root n \of {\frac{1}{1+\Big \{\lambda \Big (\frac{1-s_{1t}^n}{s_{1t}^n}\Big )^{\gamma }\Big \}^{\frac{1}{\gamma }}}},\right. \right. \\&\quad \root n \of {\frac{1}{1+\Big \{\lambda \Big (\frac{1-i_{1t}^n}{i_{1t}^n}\Big )^{\gamma }\Big \}^{\frac{1}{\gamma }}}},\\&\quad \left. \left. \root n \of {1-\frac{1}{1+\Big \{\lambda \Big (\frac{d_{1t}^n}{1-d_{1t}^n}\Big )^{\gamma }\Big \}^{\frac{1}{\gamma }}}} \right) . \right\} \end{aligned}$$

Example 5

Let us consider \({\mathfrak {h}}(x_1)={\mathfrak {h}}_1=\{(0.6,0.8,0.4),(0.4,0.5,0.9),(0.6,0.2,0.7)\} \) and \({\mathfrak {h}}(x_2)={\mathfrak {h}}_2=\{(0.3,0.9,0.5),(0.2,0.4,0.7)\}\) in Example 1. For \(n=3\), \(\gamma =1\), and \(\lambda =2\)

$$\begin{aligned}&{\mathfrak {h}}_1\oplus {\mathfrak {h}}_2\\&\quad =\{(0.6151,0.7549,0.3536),\\&\qquad (0.6045,0.3922,0.3849),(0.4443,0.4925,0.4925),\\&\qquad (0.4141,0.3536,0.6726),(0.6151,0.1998,0.4655),\\&\qquad (0.6045,0.1928,0.5915)\}\\&{\mathfrak {h}}_1\otimes {\mathfrak {h}}_2\\&\quad =\{(0.2908,0.7549,0.5587),\\&\qquad (0.1981,0.3922,0.7187),(0.2685,0.4925,0.9041),\\&\qquad (0.1928,0.3536,0.9136),(0.2908,0.1998,0.7364),\\&\qquad (0.1981,0.1928,0.7994)\}\\&2{\mathfrak {h}}_1=\{(0.7082,0.7007,0.3209),\\&\qquad (0.4937,0.4055,0.8309),(0.7082,0.1590,0.5915)\}\\&{\mathfrak {h}}_1^2=\{(0.4947,0.7007,0.4937),\\&\qquad (0.3209,0.4055,0.9448),(0.4947,0.1590,0.7994)\}. \end{aligned}$$

Hesitant T-spherical Dombi fuzzy weighted arithmetic averaging operator

Definition 13

Let \({\mathcal {H}}^m=\{{\mathfrak {h}}_k=\{(s_{kj},i_{kj},d_{kj}): 1\le j \le \ell _{{\mathfrak {h}}_k}, k=1,2,\ldots ,m\}\) be an m dimensional collection of HT-SFEs. A hesitant T-spherical Dombi fuzzy weighted averaging (HTSDFWAA) operator is defined by a function HTSDFWAA: \({\mathcal {H}}^m \rightarrow {\mathcal {H}}\) as follows:

$$\begin{aligned}&\mathrm{{HTSDFWAA}}({\mathfrak {h}}_1,{\mathfrak {h}}_2,{\mathfrak {h}}_3,\ldots ,{\mathfrak {h}}_m)\\&\quad =\bigoplus _{z=1}^m(w_z {\mathfrak {h}}_z)\\&\quad =(w_1 {\mathfrak {h}}_1)\oplus (w_2 {\mathfrak {h}}_2)\oplus \cdots \oplus (w_m {\mathfrak {h}}_m), \end{aligned}$$

where \(w_z\) is weight of \({\mathfrak {h}}_z (z=1,2,\ldots ,m)\), \(0 \le w_z\le 1\) and \(\sum _{z=1}^{m}w_z=1.\)

We get the following theorem that follows the Dombi operations on HT-SFEs.

Theorem 1

Let \({\mathfrak {h}}_k\in {\mathcal {H}}^m\). Then

$$\begin{aligned}&HTSDFWAA({\mathfrak {h}}_1,{\mathfrak {h}}_2,\ldots ,{\mathfrak {h}}_m)\\&\quad =\bigoplus _{z=1}^m(w_z{\mathfrak {h}}_z)\\&\quad =\bigcup _{{\begin{array}{c} (s_1,i_1,d_1)\in {\mathfrak {h}}_1 \\ (s_2,i_2,d_2)\in {\mathfrak {h}}_2 \\ \cdots \\ (s_m,i_m,d_m)\in {\mathfrak {h}}_m \\ \end{array}}}\left( \begin{array}{c} \root n \of {1-\frac{1}{1+\left( \sum _{z=1}^{m}w_z\left( \frac{s_z^n}{1-s_z^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}}, \\ \root n \of {\frac{1}{1+\left( \sum _{z=1}^{m}w_z\left( \frac{1-i_z^n}{i_z^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}}, \\ \root n \of {\frac{1}{1+\left( \sum _{z=1}^{m}w_z\left( \frac{1-d_z^n}{d_z^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}} \\ \end{array} \right) , \end{aligned}$$

where \( \omega =(w_{1},w_{2},\ldots ,w_{m})\) be the m weight vector of \( {\mathfrak {h}}_k (k=1,2,\ldots ,m)\), such that \(\omega _{k}>0\) and \(\sum _{k=1}^{m}w_{k}=1 .\)

Proof

The theorem can be proved by the method of mathematical induction as follows:

  1. (i)

    When \(m=2\), based on Dombi operations on HT-SFEs, we obtain the following results:

    $$\begin{aligned}&w_{1}{\mathfrak {h}}_1=\bigcup _{{ (s_1,i_1,d_1)\in {\mathfrak {h}}_1 }}\left( \begin{array}{c} \root n \of {1-\frac{1}{1+\left( w_1\left( \frac{s_1^n}{1-s_1^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}}, \\ \root n \of {\frac{1}{1+\left( w_1\left( \frac{1-i_1^n}{i_1^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}}, \\ \root n \of {\frac{1}{1+\left( w_1\left( \frac{1-d_1^n}{d_1^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}} \\ \end{array} \right) \\&w_{2}{\mathfrak {h}}_2=\bigcup _{{ (s_2,i_2,d_2)\in {\mathfrak {h}}_2}}\left( \begin{array}{c} \root n \of {1-\frac{1}{1+\left( w_2\left( \frac{s_2^n}{1-s_2^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}}, \\ \root n \of {\frac{1}{1+\left( w_2\left( \frac{1-i_2^n}{i_2^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}}, \\ \root n \of {\frac{1}{1+\left( w_2\left( \frac{1-d_2^n}{d_2^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}} \\ \end{array} \right) \\&w_{1}{\mathfrak {h}}_1 \oplus w_{2}{\mathfrak {h}}_2\\&\quad =\bigcup _{{\begin{array}{c} (s_1,i_1,d_1)\in {\mathfrak {h}}_1 \\ (s_2,i_2,d_2)\in {\mathfrak {h}}_2 \\ \end{array}}}\left( \begin{array}{c} \root n \of {1-\frac{1}{1+\left( w_1\left( \frac{s_1^n}{1-s_1^n}\right) ^{\gamma }+w_2\left( \frac{s_2^n}{1-s_2^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}}, \\ \root n \of {\frac{1}{1+\left( w_1\left( \frac{1-i_1^n}{i_1^n}\right) ^{\gamma }+w_2\left( \frac{1-i_2^n}{i_2^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}}, \\ \root n \of {\frac{1}{1+\left( w_1\left( \frac{1-d_1^n}{d_1^n}\right) ^{\gamma }+w_2\left( \frac{1-d_2^n}{d_2^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}}, \\ \end{array} \right) \\&w_{1}{\mathfrak {h}}_1 \oplus w_{2}{\mathfrak {h}}_2\\&\quad =\bigcup _{{\begin{array}{c} (s_1,i_1,d_1)\in {\mathfrak {h}}_1 \\ (s_2,i_2,d_2)\in {\mathfrak {h}}_2 \\ \end{array}}}\left( \begin{array}{c} \root n \of {1-\frac{1}{1+\left( \sum _{z=1}^{2}w_z\left( \frac{s_z^n}{1-s_z^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}}, \\ \root n \of {\frac{1}{1+\left( \sum _{z=1}^{2} w_z\left( \frac{1-i_z^n}{i_z^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}}, \\ \root n \of {\frac{1}{1+\left( \sum _{z=1}^{2}w_z\left( \frac{1-d_z^n}{d_z^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}} \\ \end{array} \right) . \end{aligned}$$

    Then, the theorem holds for \( m=2 \)

  2. (ii)

    Suppose the theorem holds when \(z=k\)

    that is

    $$\begin{aligned}&\oplus _{z=1}^{k}(w_{z}{\mathfrak {h}}_z)\\&\quad =\bigcup _{{\begin{array}{c} (s_1,i_1,d_1)\in {\mathfrak {h}}_1 \\ (s_2,i_2,d_2)\in {\mathfrak {h}}_2\\ \cdots \\ (s_k,i_k,d_k)\in {\mathfrak {h}}_k \end{array}}}\left( \begin{array}{c} \root n \of {1-\frac{1}{1+\left( \sum _{z=1}^{k}w_z\left( \frac{s_z^n}{1-s_z^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}}, \\ \root n \of {\frac{1}{1+\left( \sum _{z=1}^{k} w_z\left( \frac{1-i_z^n}{i_z^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}}, \\ \root n \of {\frac{1}{1+\left( \sum _{z=1}^{k}w_z\left( \frac{1-d_z^n}{d_z^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}} \\ \end{array} \right) . \end{aligned}$$

    When \( z=k+1 \)

    $$\begin{aligned}&\oplus _{z=1}^{k}(w_{z}{\mathfrak {h}}_z)\oplus w_{k+1}{\mathfrak {h}}_{k+1}\\&\quad =\bigcup _{{\begin{array}{c} (s_1,i_1,d_1)\in {\mathfrak {h}}_1 \\ (s_2,i_2,d_2)\in {\mathfrak {h}}_2\\ \cdots \\ (s_k,i_k,d_k)\in {\mathfrak {h}}_k \\ \end{array}}}\left( \begin{array}{c} \root n \of {1-\frac{1}{1+\left( \sum _{z=1}^{k}w_z\left( \frac{s_z^n}{1-s_z^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}}, \\ \root n \of {\frac{1}{1+\left( \sum _{z=1}^{k} w_z\left( \frac{1-i_z^n}{i_z^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}}, \\ \root n \of {\frac{1}{1+\left( \sum _{z=1}^{k}w_z\left( \frac{1-d_z^n}{d_z^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}} \\ \end{array} \right) \\&\quad \oplus w_{k+1}{\mathfrak {h}}_{k+1}\\&\oplus _{z=1}^{k}(w_{z}{\mathfrak {h}}_z)\oplus w_{k+1}{\mathfrak {h}}_{k+1}\\&\quad =\bigcup _{{\begin{array}{c} (s_1,i_1,d_1)\in {\mathfrak {h}}_1 \\ (s_2,i_2,d_2)\in {\mathfrak {h}}_2\\ \cdots \\ (s_k,i_k,d_k)\in {\mathfrak {h}}_k \\ \end{array}}}\left( \begin{array}{c} \root n \of {1-\frac{1}{1+\left( \sum _{z=1}^{k}w_z\left( \frac{s_z^n}{1-s_z^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}}, \\ \root n \of {\frac{1}{1+\left( \sum _{z=1}^{k} w_z\left( \frac{1-i_z^n}{i_z^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}}, \\ \root n \of {\frac{1}{1+\left( \sum _{z=1}^{k}w_z\left( \frac{1-d_z^n}{d_z^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}} \\ \end{array} \right) \oplus \\&\bigcup _{\begin{array}{c} (s_{k+1},i_{k+1},d_{k+1})\in {\mathfrak {h}}_{k+1} \\ \end{array}}\left( \begin{array}{c} \root n \of {1-\frac{1}{1+\left( w_{k+1}\left( \frac{s_{k+1}^n}{1-s_{k+1}^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}}, \\ \root n \of {\frac{1}{1+\left( w_{k+1}\left( \frac{1-i_{k+1}^n}{i_{k+1}^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}}, \\ \root n \of {\frac{1}{1+\left( w_{k+1}\left( \frac{1-d_{k+1}^n}{d_{k+1}^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}} \\ \end{array} \right) \\&\oplus _{z=1}^{k+1}(w_{z}{\mathfrak {h}}_z)\\&\quad =\bigcup _{{\begin{array}{c} (s_1,i_1,d_1)\in {\mathfrak {h}}_1 \\ (s_2,i_2,d_2)\in {\mathfrak {h}}_2\\ \cdots \\ (s_{k+1},i_{k+1},d_{k+1})\in {\mathfrak {h}}_{k+1} \\ \end{array}}}\left( \begin{array}{c} \root n \of {1-\frac{1}{1+\left( \sum _{z=1}^{k+1}w_z\left( \frac{s_z^n}{1-s_z^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}}, \\ \root n \of {\frac{1}{1+\left( \sum _{z=1}^{k+1} w_z\left( \frac{1-i_z^n}{i_z^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}}, \\ \root n \of {\frac{1}{1+\left( \sum _{z=1}^{k+1}w_z\left( \frac{1-d_z^n}{d_z^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}} \\ \end{array} \right) . \end{aligned}$$

    Then, the theorem holds for \(z=k+1\). Hence, the theorem is proved for all \( z\in \mathbb {N}.\)

\(\square \)

Example 6

Let us consider \({\mathfrak {h}}_1=\{(0.6,0.8,0.4),(0.4,0.5,0.9),(0.6,0.2,0.7)\} \), \({\mathfrak {h}}_2=\{(0.3,0.9,0.5), (0.2,0.4,0.7)\}\), and \({\mathfrak {h}}_3=\{(0.5,0.4,0.3)\}\) for \(n=3\). When \(\gamma =1\), with weighted vector \(\omega =(0.5,0.3,0.2)\), we get

$$\begin{aligned}&\mathrm{{HTSDFWAA}}({\mathfrak {h}}_1,{\mathfrak {h}}_2,{\mathfrak {h}}_3)= \oplus _{z=1}^{3}(w_{z}{\mathfrak {h}}_z)\\&=\bigcup _{{\begin{array}{c} (s_1,i_1,d_1)\in {\mathfrak {h}}_1 \\ (s_2,i_2,d_2)\in {\mathfrak {h}}_2\\ (s_3,i_3,d_3)\in {\mathfrak {h}}_3 \\ \end{array}}}\left( \begin{array}{c} \root n \of {1-\frac{1}{1+\left( \sum _{z=1}^3w_z\left( \frac{s_z^n}{1-s_z^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}}, \\ \root n \of {\frac{1}{1+\left( \sum _{z=1}^3 w_z\left( \frac{1-i_z^n}{i_z^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}}, \\ \root n \of {\frac{1}{1+\left( \sum _{z=1}^3 w_z\left( \frac{1-d_z^n}{d_z^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}} \\ \end{array} \right) \\&\mathrm{{HTSDFWAA}}({\mathfrak {h}}_1,{\mathfrak {h}}_2,{\mathfrak {h}}_3)\\&\quad =\{(0.5298,0.6051,0.3843),(0.5246,0.4846,0.3961),\\&\qquad (0.4049,0.5100,0.4568),(0.3941,0.4391,0.4813),\\&\qquad (0.5298,0.2474,0.4461),(0.5246,0.2423,0.4683)\}. \end{aligned}$$

Theorem 2

(Idempotency) Let \({\mathfrak {h}}_k \, (k=1,2,\ldots ,m)\) be a number of HT-SFNs. Then, \({\mathfrak {h}}_k=(s_{k},i_{k},d_{k}) (k=1,2,\ldots ,m)\) be a number of HT-SFEs are all equal, i.e., \({\mathfrak {h}}_k= {\mathfrak {h}} \) for all k , then HTSDFWAA \(({\mathfrak {h}}_1,{\mathfrak {h}}_2,\ldots ,{\mathfrak {h}}_m)={\mathfrak {h}}\).

Hesitant T-spherical Dombi fuzzy weighted geometric averaging (HTSDFWGA) operator

Definition 14

Let \({\mathcal {H}}^m=\{{\mathfrak {h}}_k=\{(s_{kj},i_{kj},d_{kj}): 1\le j \le \ell _{{\mathfrak {h}}_k}, k=1,2,\ldots ,m\}\) be an m-dimensional collection of HT-SFEs. An HTSDFWGA operator is defined by a function HTSDFWGA: \({\mathcal {H}}^m \rightarrow {\mathcal {H}}\) as follows:

$$\begin{aligned}&\mathrm{{HTSDFWGA}}({\mathfrak {h}}_1,{\mathfrak {h}}_2,{\mathfrak {h}}_3,\ldots ,{\mathfrak {h}}_m)\\&\quad =\bigotimes _{z=1}^m( {\mathfrak {h}}_z^{w_z})\\&\quad =({\mathfrak {h}}^{w_1}_1)\otimes ({\mathfrak {h}}^{w_2}_2)\otimes \cdots \otimes ({\mathfrak {h}}^{w_m}_m), \end{aligned}$$

where \(w_z\) is weight of \({\mathfrak {h}}_z (z=1,2,\ldots ,m)\), \(0 \le w_z\le 1\) and \(\sum _{z=1}^{m}w_z=1.\)

Theorem 3

Let \({\mathfrak {h}}_k\in {\mathcal {H}}^m\). Then

$$\begin{aligned}&\mathrm{{HTSDFWGA}}({\mathfrak {h}}_1,{\mathfrak {h}}_2,\ldots ,{\mathfrak {h}}_m)=\bigotimes _{z=1}^m({\mathfrak {h}}_z^{w_{z}})\nonumber \\&\quad =\bigcup _{{\begin{array}{c} (s_1,i_1,d_1)\in {\mathfrak {h}}_1 \\ (s_2,i_2,d_2)\in {\mathfrak {h}}_2 \\ \cdots \\ (s_m,i_m,d_m)\in {\mathfrak {h}}_m \\ \end{array}}}\left( \begin{array}{c} \root n \of {\frac{1}{1+\left( \sum _{z=1}^{m}w_z\left( \frac{1-s_z^n}{s_z^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}}, \\ \root n \of {\frac{1}{1+\left( \sum _{z=1}^{m}w_z\left( \frac{1-i_z^n}{i_z^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}}, \\ \root n \of {1-\frac{1}{1+\left( \sum _{z=1}^{m}w_z\left( \frac{d_z^n}{1-d_z^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}} \end{array} \right) , \end{aligned}$$
(2)

where \( \omega =(w{1},w_{2},\ldots ,w_{m})\) be the m weighted vector of \( {\mathfrak {h}}_k (k=1,2,\ldots ,m)\), such that \(w_{k}>0\) and \(\sum _{k=1}^{m}w_{k}=1.\)

Proof

The theorem can be proved by the mathematical induction as follows:

  1. (i)

    When \(m=2\), we have

    $$\begin{aligned}&{\mathfrak {h}}^{w_{1}}_1=\\&\quad \bigcup _{{\begin{array}{c} (s_1,i_1,d_1)\in {\mathfrak {h}}_1 \\ \end{array}}}\left( \begin{array}{c} \root n \of {\frac{1}{1+\left( w_1\left( \frac{s_1^n}{1-s_1^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}}, \root n \of {\frac{1}{1+\left( w_1\left( \frac{1-i_1^n}{i_1^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}}, \\ \root n \of {1-\frac{1}{1+\left( w_1\left( \frac{1-d_1^n}{d_1^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}} \end{array} \right) \\&{\mathfrak {h}}^{w_{2}}_2=\\&\quad \bigcup _{{\begin{array}{c} (s_2,i_2,d_2)\in {\mathfrak {h}}_2 \\ \end{array}}}\left( \begin{array}{c} \root n \of {\frac{1}{1+\left( w_2\left( \frac{s_2^n}{1-s_2^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}}, \root n \of {\frac{1}{1+\left( w_2\left( \frac{1-i_2^n}{i_2^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}}, \\ \root n \of {1-\frac{1}{1+\left( w_2\left( \frac{1-d_2^n}{d_2^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}} \\ \end{array} \right) \end{aligned}$$

    and

    $$\begin{aligned}&{\mathfrak {h}}^{w_{1}}_1 \otimes {\mathfrak {h}}^{w_{2}}_2\\&=\bigcup _{{\begin{array}{c} (s_1,i_1,d_1)\in {\mathfrak {h}}_1 \\ (s_2,i_2,d_2)\in {\mathfrak {h}}_2 \\ \end{array}}}\left( \begin{array}{c} \root n \of {\frac{1}{1+(w_1\left( \frac{s_1^n}{1-s_1^n}\right) ^{\gamma }+w_2\left( \frac{s_2^n}{1-s_2^n}\right) ^{\gamma })^{\frac{1}{\gamma }}}}, \\ \root n \of {\frac{1}{1+(w_1\left( \frac{1-i_1^n}{i_1^n}\right) ^{\gamma }+w_2\left( \frac{1-i_2^n}{i_2^n}\right) ^{\gamma })^{\frac{1}{\gamma }}}}, \\ \root n \of {1-\frac{1}{1+(w_1\left( \frac{1-d_1^n}{d_1^n}\right) ^{\gamma }+w_2\left( \frac{1-d_2^n}{d_2^n}\right) ^{\gamma })^{\frac{1}{\gamma }}}}, \\ \end{array} \right) \\&{\mathfrak {h}}^{w_{1}}_1 \otimes {\mathfrak {h}}^{w_{2}}_2\\&=\bigcup _{{\begin{array}{c} (s_1,i_1,d_1)\in {\mathfrak {h}}_1 \\ (s_2,i_2,d_2)\in {\mathfrak {h}}_2 \\ \end{array}}}\left( \begin{array}{c} \root n \of {\frac{1}{1+\left( \sum _{z=1}^{2}w_z\left( \frac{s_z^n}{1-s_z^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}}, \\ \root n \of {\frac{1}{1+\left( \sum _{z=1}^{2} w_z\left( \frac{1-i_z^n}{i_z^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}}, \\ \root n \of {1-\frac{1}{1+\left( \sum _{z=1}^{2}w_z\left( \frac{1-d_z^n}{d_z^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}} \\ \end{array} \right) . \end{aligned}$$

    Then, the theorem holds for \( m=2. \)

  2. (ii)

    Suppose that the theorem holds for \(z=k\), that is

    $$\begin{aligned}&\otimes _{z=1}^{k}({\mathfrak {h}}^{w_{z}}_z)\\&=\bigcup _{{\begin{array}{c} (s_1,i_1,d_1)\in {\mathfrak {h}}_1 \\ (s_2,i_2,d_2)\in {\mathfrak {h}}_2\\ \cdots \\ (s_k,i_k,d_k)\in {\mathfrak {h}}_k \\ \end{array}}}\left( \begin{array}{c} \root n \of {\frac{1}{1+\left( \sum _{z=1}^{k}w_z\left( \frac{s_z^n}{1-s_z^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}}, \\ \root n \of {\frac{1}{1+\left( \sum _{z=1}^{k} w_z\left( \frac{1-i_z^n}{i_z^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}}, \\ \root n \of {1-\frac{1}{1+\left( \sum _{z=1}^{k}w_z\left( \frac{1-d_z^n}{d_z^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}} \\ \end{array} \right) . \end{aligned}$$

    We prove that equation is true for \( z=k+1 \)

    $$\begin{aligned}&\otimes _{z=1}^{k}({\mathfrak {h}}^{w_{z}}_z)\otimes {\mathfrak {h}}^{w_{k+1}}_{k+1}\\&\quad =\bigcup _{{\begin{array}{c} (s_1,i_1,d_1)\in {\mathfrak {h}}_1 \\ (s_2,i_2,d_2)\in {\mathfrak {h}}_2\\ \cdots \\ (s_k,i_k,d_k)\in {\mathfrak {h}}_k \\ \end{array}}}\left( \begin{array}{c} \root n \of {\frac{1}{1+\left( \sum _{z=1}^{k}w_z\left( \frac{s_z^n}{1-s_z^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}}, \\ \root n \of {\frac{1}{1+\left( \sum _{z=1}^{k} w_z\left( \frac{1-i_z^n}{i_z^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}}, \\ \root n \of {1-\frac{1}{1+\left( \sum _{z=1}^{k}w_z\left( \frac{1-d_z^n}{d_z^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}} \\ \end{array} \right) \\&\otimes {\mathfrak {h}}^{\omega _{k+1}}_{k+1}\otimes _{z=1}^{k}({\mathfrak {h}}^{w_{z}}_z)\otimes {\mathfrak {h}}^{w_{k+1}}_{k+1}\\&\quad =\bigcup _{{\begin{array}{c} (s_1,i_1,d_1)\in {\mathfrak {h}}_1 \\ (s_2,i_2,d_2)\in {\mathfrak {h}}_2\\ \cdots \\ (s_k,i_k,d_k)\in {\mathfrak {h}}_k \\ \end{array}}}\left( \begin{array}{c} \root n \of {\frac{1}{1+\left( \sum _{z=1}^{k}w_z\left( \frac{s_z^n}{1-s_z^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}}, \\ \root n \of {\frac{1}{1+\left( \sum _{z=1}^{k} w_z\left( \frac{1-i_z^n}{i_z^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}}, \\ \root n \of {1-\frac{1}{1+\left( \sum _{z=1}^{k}w_z\left( \frac{1-d_z^n}{d_z^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}} \\ \end{array} \right) \otimes \\&\bigcup _{\begin{array}{c} (s_{k+1},i_{k+1},d_{k+1})\in {\mathfrak {h}}_{k+1} \\ \end{array}}\left( \begin{array}{c} \root n \of {\frac{1}{1+(w_{k+1}\left( \frac{s_{k+1}^n}{1-s_{k+1}^n}\right) ^{\gamma })^{\frac{1}{\gamma }}}}, \\ \root n \of {\frac{1}{1+(w_{k+1}\left( \frac{1-i_{k+1}^n}{i_{k+1}^n}\right) ^{\gamma })^{\frac{1}{\gamma }}}}, \\ \root n \of {1-\frac{1}{1+(w_{k+1}\left( \frac{1-d_{k+1}^n}{d_{k+1}^n}\right) ^{\gamma })^{\frac{1}{\gamma }}}} \\ \end{array} \right) \\&\otimes _{z=1}^{k+1}({\mathfrak {h}}^{w_{z}}_z)\\&\quad =\bigcup _{{\begin{array}{c} (s_1,i_1,d_1)\in {\mathfrak {h}}_1 \\ (s_2,i_2,d_2)\in {\mathfrak {h}}_2\\ \cdots \\ (s_{k+1},i_{k+1},d_{k+1})\in {\mathfrak {h}}_{k+1} \\ \end{array}}}\left( \begin{array}{c} \root n \of {\frac{1}{1+\left( \sum _{z=1}^{k+1}w_z\left( \frac{s_z^n}{1-s_z^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}}, \\ \root n \of {\frac{1}{1+\left( \sum _{z=1}^{k+1} w_z\left( \frac{1-i_z^n}{i_z^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}}, \\ \root n \of {1-\frac{1}{1+\left( \sum _{z=1}^{k+1}w_z\left( \frac{1-d_z^n}{d_z^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}} \\ \end{array} \right) . \end{aligned}$$

    Then, the theorem holds for \(z=k+1\). Hence, the proof is completed.\(\square \)

Example 7

Let us consider HT-SFEs given in Example 6. Then, we get

$$\begin{aligned}&\mathrm{{HTSDFWGA}}({\mathfrak {h}}_1,{\mathfrak {h}}_2,{\mathfrak {h}}_3)=\otimes _{z=1}^{3}({\mathfrak {h}}^{w_{z}}_z) \\&\quad =\bigcup _{{\begin{array}{c} (s_1,i_1,d_1)\in {\mathfrak {h}}_1 \\ (s_2,i_2,d_2)\in {\mathfrak {h}}_2\\ (s_3,i_3,d_3)\in {\mathfrak {h}}_3 \\ \end{array}}}\left( \begin{array}{c} \root n \of {\frac{1}{1+\left( \sum _{z=1}^3w_z\left( \frac{s_z^n}{1-s_z^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}}, \\ \root n \of {\frac{1}{1+\left( \sum _{z=1}^3 w_z\left( \frac{1-i_z^n}{i_z^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}}, \\ \root n \of {1-\frac{1}{1+\left( \sum _{z=1}^3 w_z\left( \frac{1-d_z^n}{d_z^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}} \\ \end{array} \right) \\&\mathrm{{HTSDFWGA}}({\mathfrak {h}}_1,{\mathfrak {h}}_2,{\mathfrak {h}}_3)\\&\quad =\{(0.4053,0.6051,0.4241),(0.2890,0.4846,0.5475),\\&\qquad (0.3652,0.5100,0.8350),(0.2773,0.4391,0.8440),\\&\qquad (0.4052,0.2474,0.6183),(0.2890,0.2423,0.6675)\}. \end{aligned}$$

Theorem 4

(Idempotency) Let \({\mathfrak {h}}_k\in {\mathcal {H}}^m\) \((k=1,2,\ldots ,m)\). If \({\mathfrak {h}}_k={\mathfrak {h}}\) for \(k=1,2,\ldots ,m\), then HTSDFWGA\(({\mathfrak {h}}_1,{\mathfrak {h}}_2,\ldots ,{\mathfrak {h}}_m)={\mathfrak {h}}.\)

Proof

Straightforward. Therefore, the proof is omitted. \(\square \)

Hesitant T-spherical Dombi fuzzy ordered weighted arithmetic averaging (HTSDFOWAA) operator

Definition 15

Let \({\mathcal {H}}^m=\{{\mathfrak {h}}_k=\{(s_{kj},i_{kj},d_{kj}): 1\le j \le \ell _{{\mathfrak {h}}_k}, k=1,2,\ldots ,m\}\) be an m dimensional collection of HT-SFEs. An HTSDFOWAA operator is defined by a function HTSDFOWAA: \({\mathcal {H}}^m \rightarrow {\mathcal {H}}\) as follows:

$$\begin{aligned}&\mathrm{{HTSDFOWAA}}({\mathfrak {h}}_1,{\mathfrak {h}}_2,{\mathfrak {h}}_3,\ldots ,{\mathfrak {h}}_m)\\&\quad =\bigoplus _{z=1}^m(w_z {\mathfrak {h}}_{\sigma (z)})\\&\quad =(w_1 {\mathfrak {h}}_{\sigma (1)})\oplus (w_2 {\mathfrak {h}}_{\sigma (2)})\oplus \cdots \oplus (w_m {\mathfrak {h}}_{\sigma (m)}), \end{aligned}$$

where \( {\mathfrak {h}}_{\sigma (z)}\) is the zth largest of \({\mathfrak {h}}_z\) and \(w_z\) is weighted vector of \({\mathfrak {h}}_z (z=1,2,\ldots ,m)\), \(0 \le w_z\le 1\) and \(\sum _{z=1}^{m}w_z=1.\)

Theorem 5

Let \({\mathfrak {h}}_k\in {\mathcal {H}}^m\) \((k=1,2,\ldots ,m)\). Then

$$\begin{aligned}&\mathrm{{HTSDFOWAA}}({\mathfrak {h}}_1,{\mathfrak {h}}_2,\ldots ,{\mathfrak {h}}_m)=\bigoplus _{z=1}^m(w_z{\mathfrak {h}}_{\sigma (z)})\nonumber \\&\quad =\bigcup _{{\begin{array}{c} (s_1,i_1,d_1)\in {\mathfrak {h}}_1 \\ (s_2,i_2,d_2)\in {\mathfrak {h}}_2 \\ \cdots \\ (s_m,i_m,d_m)\in {\mathfrak {h}}_m \\ \end{array}}}\left( \begin{array}{c} \root n \of {1-\frac{1}{1+\left( \sum _{z=1}^{m}w_z\left( \frac{s_{\sigma (z)}^n}{1-s_{\sigma (z)}^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}}, \\ \root n \of {\frac{1}{1+\left( \sum _{z=1}^{m}w_z\left( \frac{1-i_{\sigma (z)}^n}{i_{\sigma (z)}^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}}, \\ \root n \of {\frac{1}{1+\left( \sum _{z=1}^{m}w_z\left( \frac{1-d_{\sigma (z)}^n}{d_{\sigma (z)}^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}} \\ \end{array} \right) , \end{aligned}$$

where\( {\mathfrak {h}}_{\sigma (z)}\) is the zth largest of \({\mathfrak {h}}_z\) and \( \omega =(w_{1},w_{2},\ldots ,w_{m})\) be the m weighted vector of \( {\mathfrak {h}}_k (k=1,2,\ldots ,m)\), such that \( 0<w_{k}<1 \) and \(\sum _{k=1}^{m}w_{k}=1 \)

Proof

The proof is made by similar way to proof of Theorem 1. \(\square \)

Hesitant T-spherical Dombi fuzzy ordered weighted geometric averaging (HTSDFOWGA) operator

Definition 16

Let \({\mathcal {H}}^m=\{{\mathfrak {h}}_k=\{(s_{kj},i_{kj},d_{kj}): 1\le j \le \ell _{{\mathfrak {h}}_k}\}, k=1,2,\ldots ,m\}\) be an m dimensional collection of HT-SFEs. An HTSDFOWGA operator is defined by a function HTSDFOWGA: \({\mathcal {H}}^m \rightarrow {\mathcal {H}}\) as follows:

$$\begin{aligned}&\mathrm{{HTSDFOWGA}}({\mathfrak {h}}_1,{\mathfrak {h}}_2,{\mathfrak {h}}_3,\ldots ,{\mathfrak {h}}_m)\\&\quad =\bigotimes _{z=1}^m( {\mathfrak {h}}_{\sigma (z)}^{w_{z}})\\&\quad =({\mathfrak {h}}^{w_1}_1)\otimes ({\mathfrak {h}}^{w_2}_2)\otimes \cdots \otimes ({\mathfrak {h}}^{w_m}_{\sigma (m)}), \end{aligned}$$

where \(w_z\) is weighted vector of \({\mathfrak {h}}_z (z=1,2,\ldots ,m)\), \(0 \le w_z\le 1\) and \(\sum _{z=1}^{m}w_z=1.\)

Theorem 6

Let \({\mathfrak {h}}_k\in {\mathcal {H}}^m\). Then

$$\begin{aligned}&\mathrm{{HTSDFOWGA}}({\mathfrak {h}}_{\sigma (1)},{\mathfrak {h}}_{\sigma (2)},\ldots ,{\mathfrak {h}}_m)=\bigotimes _{z=1}^m( {\mathfrak {h}}_{\sigma (z)}^{w_{z}})\\&\quad =\bigcup _{{\begin{array}{c} (s_{\sigma (1)},i_{\sigma (1)},d_{\sigma (1)})\in {\mathfrak {h}}_{\sigma (1)} \\ (s_{\sigma (2)},i_{\sigma (2)},d_{\sigma (2)})\in {\mathfrak {h}}_{\sigma (2)} \\ \cdots \\ (s_{\sigma (m)},i_{\sigma (m)},d_{\sigma (m)})\in {\mathfrak {h}}_{\sigma (m)} \\ \end{array}}}\left( \begin{array}{c} \root n \of {\frac{1}{1+\left( \sum _{z=1}^{m}w_z\left( \frac{1-s_{\sigma (z)}^n}{s_{\sigma (z)}^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}}, \\ \root n \of {\frac{1}{1+\left( \sum _{z=1}^{m}w_z\left( \frac{1-i_{\sigma (z)}^n}{i_{\sigma (z)}^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}}, \\ \root n \of {1-\frac{1}{1+\left( \sum _{z=1}^{m}w_z\left( \frac{d_{\sigma (z)}^n}{1-d_{\sigma (z)}^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}} \\ \end{array} \right) , \end{aligned}$$

where \( {\mathfrak {h}}_{\sigma (z)}\) is the zth largest of \({\mathfrak {h}}_z \) and \( \omega =(w_{1},w_{2},\ldots ,w_{m})\) be the m weighted vector of \( {\mathfrak {h}}_k (k=1,2,\ldots ,m)\), such that \(0<w_{k}<1 \) and \(\sum _{k=1}^{m}w_{k}=1. \)

Example 8

Let us consider \({\mathfrak {h}}_1=\{(0.6,0.8,0.4),(0.4,0.5,0.9),(0.6,0.2,0.7)\} \), \({\mathfrak {h}}_2=\{(0.3,0.9,0.5),(0.2,0.4,0.7)\}\) and \({\mathfrak {h}}_3=\{(0.5,0.4,0.3)\}\) for \(n=3\). When \(\gamma =1\), with weight vector \(\omega =(0.5,0.3,0.2)\), we get

$$\begin{aligned}&\mathrm{{HTSDFOWGA}}({\mathfrak {h}}_{\sigma (1)},{\mathfrak {h}}_{\sigma (2)},{\mathfrak {h}}_3)=\bigotimes _{z=1}^3( {\mathfrak {h}}_{\sigma (z)}^{w_{z}})\\&\quad =\bigcup _{{\begin{array}{c} (s_{\sigma (1)},i_{\sigma (1)},d_{\sigma (1)})\in {\mathfrak {h}}_{\sigma (1)} \\ (s_{\sigma (2)},i_{\sigma (2)},d_{\sigma (2)})\in {\mathfrak {h}}_{\sigma (2)} \\ (s_{\sigma (3)},i_{\sigma (3)},d_{\sigma (3)})\in {\mathfrak {3}}_{\sigma (3)} \\ \end{array}}}\left( \begin{array}{c} \root n \of {\frac{1}{1+\left( \sum _{z=1}^{3}w_z\left( \frac{1-s_{\sigma (z)}^n}{s_{\sigma (z)}^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}}, \\ \root n \of {\frac{1}{1+\left( \sum _{z=1}^{3}w_z\left( \frac{1-i_{\sigma (z)}^n}{i_{\sigma (z)}^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}}, \\ \root n \of {1-\frac{1}{1+\left( \sum _{z=1}^{3}w_z\left( \frac{d_{\sigma (z)}^n}{1-d_{\sigma (z)}^n}\right) ^{\gamma }\right) ^{\frac{1}{\gamma }}}} \\ \end{array} \right) . \end{aligned}$$

Using Eq. (1), SVs of HT-SFEs are obtained as follows:

$$\begin{aligned} \mathrm{{SV}}({\mathfrak {h}}_{1})= & {} -0.2133,\\ \mathrm{{SV}}({\mathfrak {h}}_{2})= & {} -0.2165,\\ \mathrm{{SV}}({\mathfrak {h}}_{3})= & {} 0.089. \end{aligned}$$

Here, \( \mathrm{{SV}}({\mathfrak {h}}_{3})> \mathrm{{SV}}({\mathfrak {h}}_{1})> \mathrm{{SV}}({\mathfrak {h}}_{2}) \) and

$$\begin{aligned} {\mathfrak {h}}_{\sigma (1)}= & {} {\mathfrak {h}}_{3}=\{(0.5,0.4,0.3)\} \\ {\mathfrak {h}}_{\sigma (2)}= & {} {\mathfrak {h}}_1=\{(0.6,0.8,0.4),(0.4,0.5,0.9),(0.6,0.2,0.7)\}\\ {\mathfrak {h}}_{\sigma (3)}= & {} {\mathfrak {h}}_{2}=\{(0.3,0.9,0.5),(0.2,0.4,0.7)\}. \\ \end{aligned}$$

Then

$$\begin{aligned}&\mathrm{{HTSDFOWGA}}({\mathfrak {h}}_1,{\mathfrak {h}}_2,{\mathfrak {h}}_3)=\{(0.4275,0.4867,0.3898),\\&\quad (0.3961,0.4569,0.7716),(0.4275,0.2799,0.5496),\\&\quad (0.3205,0.3105,0.4958),(0.3096,0.3051,0.7833),\\&\quad (0.3205,0.2423,0.5997)\}. \end{aligned}$$

Theorem 7

(Idempotency property) Let \({\mathfrak {h}}_k\in {\mathcal {H}}^m\) \((k=1,2,\ldots ,m)\). If \({\mathfrak {h}}_k={\mathfrak {h}}\) for \(k=1,2,\ldots ,m\), then HTSDFOWGA\(({\mathfrak {h}}_1,{\mathfrak {h}}_2,\ldots ,{\mathfrak {h}}_m)={\mathfrak {h}}.\)

Proof

Straightforward. \(\square \)

Multiple criteria group decision-making (MCGDM) method under HT-SF information

In this section, we develop a multiple criteria group decision-making method. First, we give frequently used notation in Table 2 for convenience.

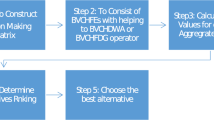
Table 2 Frequently used notations in “Multiple criteria group decision-making (MCGDM) method under HT-SF information” and other
Full size table

Let \(\kappa =\{\kappa _1,\kappa _2,\ldots ,\kappa _l\}\) be set of alternatives, \(\epsilon =\{\epsilon _1,\epsilon _2,\ldots ,\epsilon _s\}\) be a set of criteria and \(\partial =\{\partial _1,\partial _2,\ldots ,\partial _t\}\) be a set of decision-makers. Let us consider \(w=(w_1,w_2,\ldots ,w_s)\), such that \(w_j\in (0,1]\) and \(\sum _{j=1}^{s}w_j=1\) as the weight vector of the criteria which is determined by decision-makers. The steps of the MCGDM method are given as follows:

Step 1: The evaluation of the alternative \(\kappa _i\) according to criteria \(\epsilon _j\) performed by decision-makers \(\partial _y\) \((y=1,2,\ldots ,t)\) can be written as \(\zeta _{yj} (i=1,2,\ldots ,l; j=1,2,\ldots ,s; y=1,2,\ldots ,t)\). Hence, HT-SF-decision matrix \(DM_{\kappa _i}=[\zeta _{yj}]_{t\times s}\) can be constructed as follows:

$$\begin{aligned} D_{\kappa _i}=[\zeta _{yj}]_{t\times s}=\left( \begin{array}{cccc} \zeta _{11} &{}\qquad \zeta _{12} &{}\qquad \cdots &{}\qquad \zeta _{1s} \\ \zeta _{21} &{}\qquad \zeta _{22} &{}\qquad \cdots &{}\qquad \zeta _{2s} \\ \vdots &{}\qquad \vdots &{}\qquad \cdots &{}\qquad \vdots \\ \zeta _{t1} &{}\qquad \zeta _{t2} &{}\qquad \cdots &{}\qquad \zeta _{ts} \\ \end{array} \right) . \end{aligned}$$

Step 2: For all \(i=1,2,\ldots ,l\), HT-SFS denoted by HTSF\(_i\) is obtained as follows:

$$\begin{aligned} HTSF_i=\Big \{(\epsilon _j,{\mathfrak {h}}_{\epsilon _j}): j=1,2,\ldots ,s \Big \}. \end{aligned}$$

Here \({\mathfrak {h}}_{\epsilon _j}=\cup _{y=1}^t\{\zeta _{yj}\}.\)

Step 3: For \(\kappa _i, i=1,2,3,\ldots ,l \) HT-SF element related to \(\kappa _i\) denoted by \({\mathfrak {A}}_i\), is defined as follows:

$$\begin{aligned} {\mathfrak {A}}_i=\bigoplus _{j=1}^s w_j{\mathfrak {h}}_{\epsilon _j}. \end{aligned}$$

Step 4: Find score values of \({\mathfrak {A}}_i\) \((i=1,2,3,\ldots ,l).\)

Step 5: Order score values of \({\mathfrak {A}}_i\) \((i=1,2,3,\ldots ,l)\).

Step 6: Choose the alternative which has maximum score value.

Flowchart of the algorithm is given in Fig. 1.

Fig. 1
figure 1

Flowchart of the proposed method

Full size image

Illustrative example

We consider that a university wants for filling the position of one assistant professorship in a department. After the announcement for this vacant position, seven candidates \(\kappa _1,\kappa _2,\ldots ,\kappa _{7}\) apply for the position. University rector assigns three experts \(\partial _1, \partial _2\), and \(\partial _3\) to evaluate alternatives according to criterion \(\epsilon _1=\) experience, \(\epsilon _2=\) scientific works, and \(\epsilon _3=\) quality of the researches. After interview, experts determine the weight vector of the criteria as \((0.35,0.25,0.40)^T\).

Step 1: Experts evaluate the alternatives by HT-SFNs corresponding to linguistic variables given in Table 3 for each criteria and \(n=4\).

Table 3 Linguistic variable table for evaluation of the candidates
Full size table
  

\(\epsilon _1\)

\(\epsilon _2\)

\(\epsilon _3\)

\(D_{\kappa _1}\)

\(\partial _1\)

(0.633, 0.436, 0.367)

(0.233, 0.634, 0.767)

*

\(\partial _2\)

(0.100, 0.700, 0.900)

(0.900, 0.300, 0.100)

(0.500, 0.500, 0.500)

\(\partial _3\)

*

(0.764, 0.370, 0.234)

*

\(D_{\kappa _2}\)

\(\partial _1\)

*

(0.233, 0.634, 0.767)

*

\(\partial _2\)

(0.233, 0.634, 0.767)

(0.367, 0.567, 0.634)

(0.500, 0.500, 0.500)

\(\partial _3\)

(0.764, 0.370, 0.234)

(0.100, 0.700, 0.900)

(0.633, 0.436, 0.367)

\(D_{\kappa _3}\)

\(\partial _1\)

(0.367, 0.567, 0.634)

(0.633, 0.436, 0.367)

(0.100, 0.700, 0.900)

\(\partial _2\)

(0.900, 0.300, 0.100)

(0.764, 0.370, 0.234)

*

\(\partial _3\)

(0.633, 0.436, 0.367)

(0.100, 0.700, 0.900)

(0.500, 0.500, 0.500)

\(D_{\kappa _4}\)

\(\partial _1\)

(0.900, 0.300, 0.100)

(0.500, 0.500, 0.500)

(0.100, 0.700, 0.900)

\(\partial _2\)

(0.900, 0.300, 0.100)

*

(0.500, 0.500, 0.500)

\(\partial _3\)

*

(0.100, 0.700, 0.900)

(0.500, 0.500, 0.500)

\(D_{\kappa _5}\)

\(\partial _1\)

(0.367, 0.567, 0.634)

(0.500, 0.500, 0.500)

(0.100, 0.700, 0.900)

\(\partial _2\)

(0.100, 0.700, 0.900)

(0.367, 0.567, 0.634)

(0.633, 0.436, 0.367)

\(\partial _3\)

(0.900, 0.300, 0.100)

(0.100, 0.700, 0.900)

(0.500, 0.500, 0.500)

\(D_{\kappa _6}\)

\(\partial _1\)

(0.500, 0.500, 0.500)

(0.633, 0.436, 0.367)

(0.764, 0.370, 0.234)

\(\partial _2\)

*

(0.367, 0.567, 0.634)

(0.633, 0.436, 0.367)

\(\partial _3\)

*

(0.233, 0.634, 0.767)

(0.500, 0.500, 0.500)

\(D_{\kappa _7}\)

\(\partial _1\)

(0.500, 0.500, 0.500)

(0.633, 0.436, 0.367)

(0.500, 0.500, 0.500)

\(\partial _2\)

(0.367, 0.567, 0.634)

(0.100, 0.700, 0.900)

(0.233, 0.634, 0.767)

\(\partial _3\)

(0.233, 0.634, 0.767)

(0.100, 0.700, 0.900)

*

Step 2: Using HT-SF decision matrices given in Step 1, HTSF\(_i \, (i=1,2,\ldots ,7)\) are obtained as follows:

$$\begin{aligned}&HTSF_1=\Big \{\Big (\epsilon _1, \{(0.633,0.436,0.367),\\&\quad \Big (\epsilon _2,\{(0.233,0.634,0.767),\\&\qquad (0.900,0.300,0.100),(0.764,0.370,0.234)\}\Big ),\\&\quad \Big (\epsilon _3,\{(0.500,0.500,0.500)\}\Big )\Big \},\\&HTSF_2=\Big \{\Big (\epsilon _1, \{(0.764,0.370,0.234),\\&\quad (0.233,0.634,0.767\}\Big ),\Big (\epsilon _2,\{(0.100,0.700,0.900),\\&\qquad (0.233,0.634,0.767),(0.367,0.567,0.634)\}\Big ),\\&\quad \Big (\epsilon _3,\{(0.500,0.500,0.500),(0.633,0.436,0.367)\}\Big )\Big \},\\&HTSF_3=\Big \{\Big (\epsilon _1, \{(0.367,0.567,0.634),\\&\qquad (0.900,0.300,0.100),(0.633,0.436,0.367)\}\Big ),\\&\quad \Big (\epsilon _2,\{(0.633,0.436,0.367),\\&\qquad (0.764,0.370,0.234),(0.100,0.700,0.900)\}\Big ),\\&\quad \Big (\epsilon _3,\{(0.100,0.700,0.900),(0.500,0.500,0.500)\}\Big )\Big \},\\&HTSF4=\Big \{\Big (\epsilon _1, \{(0.900,0.300,0.100),\\&\quad (0.900,0.300,0.100)\}\Big ),\Big (\epsilon _2,\{(0.100,0.700,0.900),\\&\quad (0.500,0.500,0.500)\}\Big ),\Big (\epsilon _3,\{(0.100,0.700,0.900),\\&\qquad (0.500,0.500,0.500),(0.500,0.500,0.500)\}\Big )\Big \},\\&HTSF_5=\Big \{\Big (\epsilon _1, \{(0.367,0.567,0.634),\\&\qquad (0.100,0.700,0.900),(0.900,0.300,0.100)\}\Big ),\\&\quad \Big (\epsilon _2,\{(0.500,0.500,0.500),\\&\qquad (0.367,0.567,0.634),(0.100,0.700,0.900)\}\Big ),\\&\quad \Big (\epsilon _3,\{(0.100,0.700,0.900),\\&\qquad (0.633,0.436,0.367),(0.500,0.500,0.500)\}\Big )\Big \},\\&HTSF_6=\Big \{\Big (\epsilon _1, \{(0.500,0.500,0.500)\}\Big ),\\&\quad \Big (\epsilon _2,\{(0.633,0.436,0.367),\\&\qquad (0.367,0.567,0.634), (0.233,0.634,0.767)\}\Big ),\\&\quad \Big (\epsilon _3,\{(0.764,0.370,0.234),\\&\qquad (0.633,0.436,0.367),(0.500,0.500,0.500)\}\Big )\Big \},\\&HTSF_7=\Big \{\Big (\epsilon _1, \{(0.500,0.500,0.500),\\&\qquad (0.367,0.567,0.634),(0.233,0.634,0.767)\}\Big ),\\&\quad \Big (\epsilon _2,\{(0.633,0.436,0.367),\\&\qquad (0.100,0.700,0.900),(0.100,0.700,0.900)\}\Big ),\\&\quad \Big (\epsilon _3,\{(0.500,0.500,0.500),(0.233,0.634,0.767)\}\Big )\Big \}. \end{aligned}$$
Table 4 HTSDFWAA and HTSDFWGA values of HTSF\(_i \, (i=1,2,\ldots ,7)\)
Full size table
Table 5 Score values of \({\mathfrak {A}}_i\) according to HTSDFWAA and HTSDFWGA values
Full size table
Table 6 Score values of \({\mathfrak {A}}_i\) obtained using HTSDFWAA and HTSDFWGA operators
Full size table
Table 7 Ranking order for different \(\gamma \) values in the HTSDFWAA operator
Full size table
Table 8 Ranking order for different \(\gamma \) values in the HTSDFWGA operator
Full size table

Step 3: For \(n=4\) and \(\gamma =1\), HTSDFWAA and HTSDFWGA values of HTSF\(_i, \, (i=1,2,\ldots ,7)\) are obtained as in Table 4

Step 4: Score values of \({\mathfrak {A}}_i, (i=1,2,\ldots ,7) \) under score function are obtained as in Table 5.

Step 5: Using Eq. (1), ordering of the candidates is obtained as in Table 6.

Step 6: From the above illustration, although overall ranking values of the alternatives are different through the use of two operators, optimum alternatives are \(\kappa _4\) and \(\kappa _6\) for the two operators, respectively.

Fig. 2
figure 2

Ranking order for different \(\gamma \) values in the HTSDFWAA operator

Full size image
Fig. 3
figure 3

Ranking order for different \(\gamma \) values in the HTSDFWGA operator

Full size image
Table 9 Comparison table of the HT-SFS with some extensions of fuzzy
Full size table

Analysis of the effect of parameter \(\gamma \) on the results

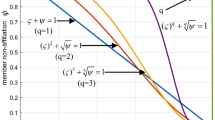
To show the effect of the \(\gamma \) variable in the formula of HTSDFWAA and HTSDFWGA on MCGDM results, we assign different values to \(\gamma \) from 1 to 10 and order candidates according to score values based on HTSDFWAA and HTSDFWGA. Ranking orders of the candidates according to score values and their ranking orders based on HTSDFWAA and HTSDFWGA operators are shown in Table 7. It is clear when \(\gamma \) value is changed in the formula HTFD WAS, the optimum candidate is always the same person, and orderings of candidates (SV\(({\mathfrak {A}}_4)>\mathrm{{SV}}({\mathfrak {A}}_1)>\mathrm{{SV}}({\mathfrak {A}}_3)>\mathrm{{SV}}({\mathfrak {A}}_5)>\mathrm{{SV}}({\mathfrak {A}}_2)>\mathrm{{SV}}({\mathfrak {A}}_6)>\mathrm{{SV}}({\mathfrak {A}}_7)\)) are same except in condition \(\gamma =1\). By Table 8, it is clear that when the value of \(\gamma \) is changed for HTSDFWGA operator, and the ranking orders of candidates (SV\(({\mathfrak {A}}_6)>\mathrm{{SV}}({\mathfrak {A}}_1)>\mathrm{{SV}}({\mathfrak {A}}_2)>\mathrm{{SV}}({\mathfrak {A}}_3)>\mathrm{{SV}}({\mathfrak {A}}_5)>\mathrm{{SV}}({\mathfrak {A}}_7)>\mathrm{{SV}}({\mathfrak {A}}_4)\)) are same except from in case \(\gamma =1\). In addition, best suitable candidate is identical for \(1\le \gamma \le 10\).

Graphical representation of Table 7 is given in Fig. 2.

Graphical representation of Table 7 is given in Fig. 3.

Using HTSDFWAA operator and score function, we obtain alternative \({\mathfrak {A}}_4\) which has maximum score value as an optimum element. Also, using HTSDFWGA operator and score function of HT-SFEs, we obtain alternative \({\mathfrak {A}}_6\) which has maximum score value. We see that different alternatives which are maximum score values are obtained each of proposed aggregation operators. In Table 5, for \(\gamma =2,3,4,\ldots ,10\) alternative \({\mathfrak {A}}_4\) which has minimum score value. In HTSDFWGA operator, since third competent of a TSFE is obtained using Dombi t-conorm and it has a negative effect over score value, alternative \({\mathfrak {A}}_4\) which has minimum score can be considered optimum element. Furthermore, we can give this relation by \(1-S{\mathfrak {A}}_i\) for score value obtained using result of HTSDFWGA operator.

Comparative analysis and discussion

In this section, we compare HT-SFS with other extensions of the fuzzy sets. Let \({\mathbb {T}}_H=\Big \{(x,\{(s_k,i_k,d_k): 1\le k \le l_x \}): x\in {\mathfrak {X}} \Big \}\). Then, comparison table can be given as in Table 9.

Here, we see that HT-SFS is an extension of sets specified in the Table 9. Therefore, the set structure defined in this paper has advantages of the other extensions of fuzzy sets specified in Table 9 in the modelling. It also models some problems which cannot be modelled existing set theories. In the following example, relation between these sets is explained.

Conclusion

In this paper, the concept of hesitant T-spherical sets and its set theoretical operations such as union, intersection, and complement have been defined. To be more understandable, some examples are given related to defined operations. Based on Dombi t-norm and Domb t-conorm operations, arithmetic operations between two HT-SFEs and

some aggregation operators such as HTSDFWAA, HTSDFWGA, HTSDFOWAA, and HTSDFOWGA operators have been introduced. Furthermore, an MCGDM method has been developed and presented an application to MCGDM problem involving selecting a person for a vacant position in any department of the university. Obtained results have been compared for different parameters. Also, the proposed set structure has been compared by other extensions of the fuzzy sets and mentioned its advantages. In future, our targets are to study on other aggregation operators, similarity measures, distance measures, and decision-making method based on TOPSIS, VIKOR, AHP, etc.